Abstract
The max-cut problem is a well-known topic in combinatorial optimization, with a wide range of practical applications. Given its NP-hard nature, heuristic approaches—such as genetic algorithms, tabu search, and harmony search—have been extensively employed. Recent research has demonstrated that harmony search can outperform genetic algorithms by effectively avoiding redundant searches, a strategy similar to tabu search. In this study, we propose a modified genetic algorithm that integrates tabu search to enhance solution quality. By preventing repeated exploration of previously visited solutions, the proposed method significantly improves the efficiency of traditional genetic algorithms and achieves performance levels comparable to harmony search. The experimental results confirm that the proposed algorithm outperforms standard genetic algorithms on the max-cut problem. This work demonstrates the effectiveness of combining tabu search with genetic algorithms and offers valuable insights into the enhancement of heuristic optimization techniques. The novelty of our approach lies in integrating solution-level tabu constraints directly into the genetic algorithm’s population dynamics, enabling redundancy prevention without additional memory overhead, a strategy not previously explored in the proposed hybrids.
Keywords:
genetic algorithm; tabu search; max-cut problem; hybrid metaheuristics; redundant search prevention; combinatorial optimization MSC:
68T20; 68W50; 90C27
1. Introduction
The max-cut problem is a fundamental problem in combinatorial optimization. Formally, given an undirected graph , where V is the set of vertices and E is the set of edges, the objective is to partition the vertex set V into two disjoint subsets S and such that the number (or total weight) of edges crossing between the two subsets is maximized. This leads to the definition of the cut value:
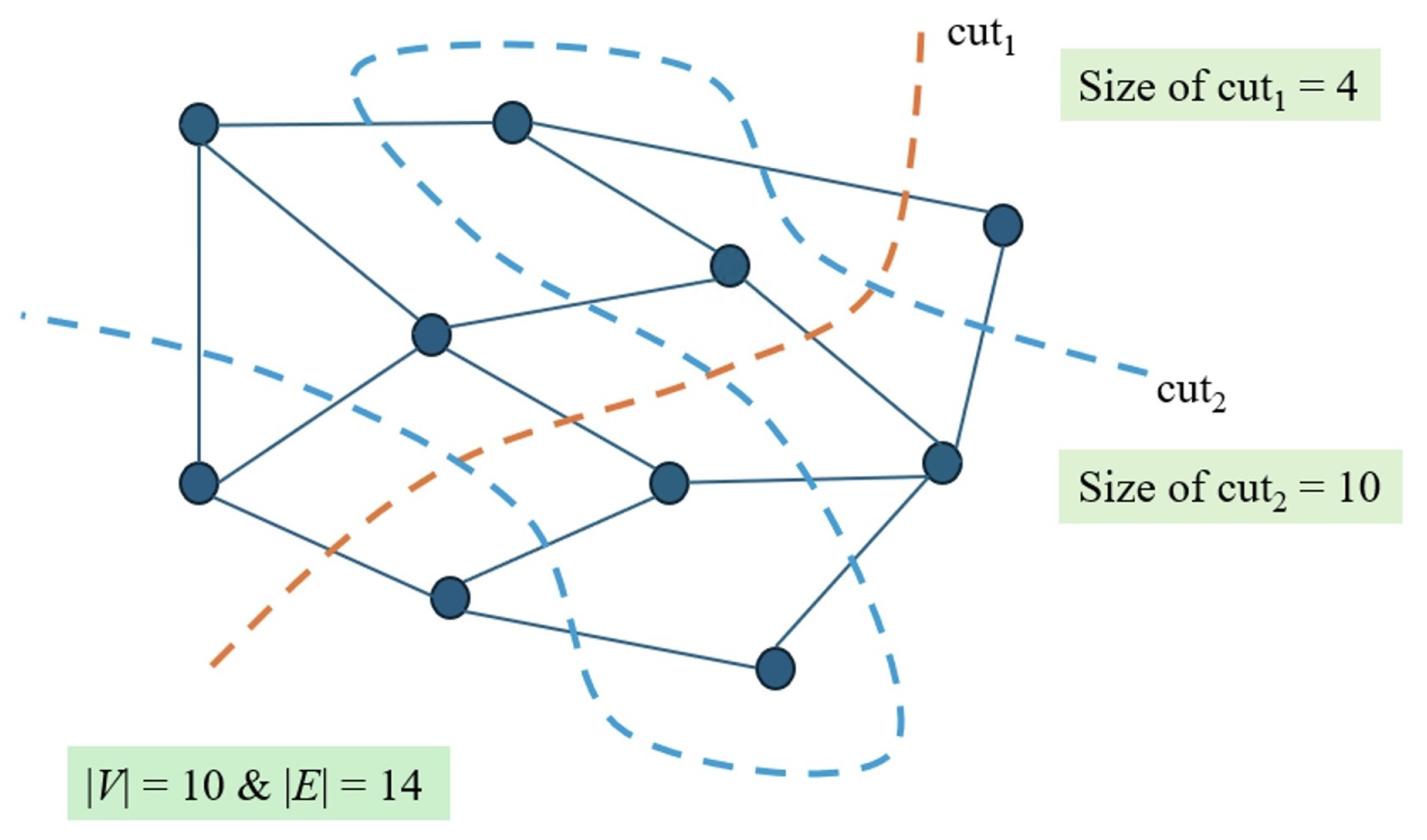
where denotes the weight of the edge . In the case of unweighted graphs, for all edges. The goal is to find a subset that maximizes . Figure 1 illustrates an example of a graph with 10 vertices and 14 edges, and how different partitions lead to different cut sizes. As the figure shows, selecting an optimal partition significantly impacts the overall cut value. The max-cut problem is classified as NP-hard [1,2], which implies that no known polynomial-time algorithm can solve all instances optimally. Due to this computational difficulty, a wide variety of heuristic and metaheuristic approaches have been proposed to find high-quality approximate solutions efficiently. The problem has practical significance in many areas [3], such as VLSI design, statistical physics (e.g., the Ising model [4]), network design, and clustering tasks in machine learning.
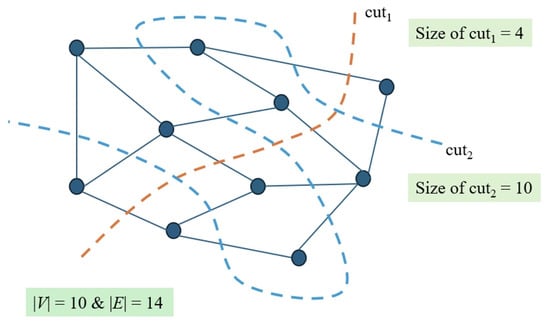
Figure 1.
An illustrative example of the max-cut problem on a graph with 10 vertices and 14 edges. The figure demonstrates how different vertex partitions (cuts) result in different cut sizes. The objective of the max-cut problem is to find the partition that maximizes the number of edges crossing between the two subsets.
Notable techniques include simulated annealing [5,6,7], genetic algorithms (GAs) [8,9,10], harmony search (HS) [11], and tabu search (TS) [6,12,13]. In addition to these methods, other metaheuristic frameworks such as scatter search [14], estimation of distribution algorithms (EDAs) [15], particle swarm optimization combined with EDAs [16], and ant colony optimization [17] have been extensively studied for solving the max-cut problem. These approaches have demonstrated effectiveness, particularly for large-scale instances where exact methods become computationally impractical. Beyond metaheuristics, neural network-based approaches have also been explored as alternative strategies for tackling the max-cut problem [18]. Notably, the discrete Hopfield neural network [19] leverages neural dynamics to iteratively refine solution quality. These machine learning-inspired techniques introduce a different paradigm compared to traditional metaheuristics, focusing on adaptive optimization processes.
While metaheuristics and neural network-based methods provide effective heuristics for large-scale instances, exact and combinatorial optimization approaches remain crucial for obtaining optimal solutions or strong theoretical bounds. Research in this area has examined branch-and-bound techniques [20] and exact algorithms, particularly in sparse graphs [21]. Moreover, semidefinite programming relaxations [20,22,23] have been widely applied to derive strong upper bounds. Notably, rank-two relaxation heuristics [24] and polyhedral cut-and-price methods [23] have been proposed to improve computational efficiency.
Among the various metaheuristic approaches, recent studies have particularly highlighted the effectiveness of the harmony search (HS) algorithm in solving the max-cut problem. A study by Kim et al. [11] demonstrated that the HS algorithm outperforms GAs in solving the max-cut problem. One of the key features of HS is its mechanism for generating initial solutions in a way that avoids redundancy, preventing the algorithm from repeatedly exploring the same solutions. This characteristic is similar to the strategy employed by TS, which avoids revisiting previously explored solutions by maintaining a memory structure known as the tabu list. In our interpretation, this feature enables HS to utilize the search space more effectively and potentially improve the quality of solutions. In contrast, while GA maintains diversity among candidate solutions, it may still suffer from repeatedly exploring similar regions in the solution space, which can lead to inefficiencies. To address this, we propose a new approach to enhance GA performance by incorporating key aspects of HS’s search strategy.
In this study, we introduce a novel hybrid algorithm that combines GA and TS to improve GA’s performance and introduce a search behavior similar to that of HS. By integrating TS’s exploration constraint mechanisms into GA, we aim to mitigate the issue of redundant solution exploration and improve the overall efficiency of the search process. In addition, we compare the performance of the proposed algorithm with that of conventional GA and HS to demonstrate its effectiveness. Through this comparison, we try to establish that the combination of GA and TS not only outperforms GA alone, but also shares similarities with HS in terms of search behavior.
This study makes three key contributions. First, we propose a novel GATS algorithm that incorporates the constraints of TS to improve the search efficiency of GA and prevent repetitive exploration of solutions. Second, we empirically validate that GATS outperforms conventional GA in solving the max-cut problem while maintaining competitive performance with HS. Third, based on previous research showing HS’s superiority over GA, we analyze how GATS exhibits similar search behavior to HS and discuss the implications of this within the broader context of recent trends in metaheuristic algorithms.
The structure of the paper is as follows. Section 2 reviews recent research, discussing existing algorithms for the max-cut problem and recent research trends. In Section 3, we introduce the genetic algorithms used in this study. Section 4 details the proposed GATS algorithm, including its design and integration strategy. Section 5 presents experimental results, comparing the performance of GATS with that of conventional GA and HS. Finally, Section 6 provides a summary of the main findings and outlines potential directions for future work.
2. Recent Work
Over the past decade, extensive research has been conducted on the max-cut problem, leading to the development of various algorithmic approaches, ranging from classical optimization techniques to advanced machine learning-based methods.
One prominent line of research focuses on classical optimization approaches. The Goemans–Williamson algorithm [25], based on semidefinite programming (SDP), remains one of the most influential methods for the max-cut problem. Building on this, Rodriguez-Fernandez et al. [26] explored whether replacing the random vector selection in this algorithm with clustering techniques such as k-means and k-medoids could yield better graph partitions. Mohades and Kahaei [27] took a different approach by reformulating the max-cut problem as an unconstrained optimization problem on a Riemannian manifold and applying a Riemannian gradient-based optimization algorithm. Meanwhile, Chen et al. [28] analyzed the limitations of local algorithms in large random hypergraphs, demonstrating that such methods struggle to find near-optimal max-cuts due to the overlap gap property. More recently, Kadhim and Al-jilawi [29] compared numerical SDP solvers—including bundle, interior point, and augmented Lagrangian methods—and reported that the bundle method achieved the fastest convergence on large benchmark instances.
Another significant research direction has focused on heuristic and metaheuristic methods for efficiently solving the max-cut problem. Wu et al. [30] introduced a hybrid evolutionary algorithm incorporating tabu search with a distance-and-quality-based solution combination operator and neighborhood-based search strategies. Lin and Zhu [31] proposed a memetic algorithm that integrates local search, a novel crossover operator, and a population update mechanism designed to balance solution quality and diversity. Similarly, Zeng et al. [32] improved upon this approach by employing edge-state learning instead of vertex-position-based methods to enhance solution quality.
Various population-based heuristics have also been explored. Kim et al. [11] compared the harmony search algorithm with genetic algorithms, concluding that the former achieved superior results with fewer parameters and greater efficiency. In a related study, Kim et al. [33] proposed an incremental genetic algorithm that gradually expanded subproblems by adding edges or vertices in a structured manner. Soares and Araújo [34] further extended the genetic algorithm approach by integrating tabu search and optimality cuts, demonstrating their effectiveness in enhancing solution quality. Wang et al. [35] took a different perspective by classifying and refining greedy heuristics. Their relation tree-based framework categorized algorithms into vertex-oriented Prim-class approaches (e.g., Sahni–Gonzalez [36] variants) and edge-oriented Kruskal-class methods (e.g., edge contraction and its refinements). Chen et al. [37] introduced a hybrid binary artificial bee colony algorithm that combined surjection mapping with local search to improve solution efficiency. Šević et al. [38] introduced a learning-based fixed-set search (FSS) metaheuristic, which extracts common substructures from high-quality solutions and reuses them to guide new solution construction, outperforming traditional GRASP-based methods.
Recently, machine learning-based approaches have gained traction in solving the max-cut problem. Gu and Yang [18] pioneered the use of a pointer network-based model trained with supervised learning to tackle the problem. They later extended this work [39] by incorporating reinforcement learning strategies, making the approach more effective for large-scale instances. Yao et al. [40] investigated the performance of graph neural networks (GNNs) on the max-cut problem, showing that GNNs performed comparably to semidefinite relaxation but were outperformed by extremal optimization. Jin and Liu [41] proposed a physics-inspired method that formulated the max-cut problem as an Ising system, using the Hamiltonian of this system as a loss function to train a recurrent neural network for approximating the ground-state transition distribution. Garmendia et al. [42] further examined neural methods in combinatorial optimization, highlighting both the generalization potential of neural models trained on diverse graphs and the computational limitations that still prevent them from matching the reliability of traditional solvers.
Additionally, Gao [43] proposed a randomized fuzzy logic-based algorithm for computing local max-cuts in RP time, demonstrating significantly faster performance compared to IBM CPLEX solvers, especially on signed graphs with non-PSD Laplacians. Islam et al. [44] also developed a Harris Hawk Optimization (HHO) variant for max-cut, with additional operators like crossover, mutation, and repair to enhance both exploration and exploitation capabilities.
Finally, several recent studies have focused on experimental comparisons of different max-cut algorithms. Mirka and Williamson [45] conducted a comparative study of max-cut approximation algorithms, finding that spectral methods were significantly faster while often achieving results comparable to those of semidefinite programming. In addition, Kang et al. [46] demonstrated a neuromorphic hardware-based spiking Boltzmann machine that solves max-cut problems using probabilistic sampling and parallelism in phase-change memory circuits.
More recently, quantum computing-based approaches have been proposed as a promising direction for solving the max-cut problem. The quantum approximate optimization algorithm (QAOA) [47] utilizes quantum circuits to approximate near-optimal cuts and has shown potential in benchmark settings. Hybrid methods combining QAOA with classical pre- and post-processing have also demonstrated scalability on large graphs [48]. Furthermore, quantum GAs that integrate Grover search with divide-and-conquer evolutionary strategies have been introduced and shown to outperform classical heuristics in specific instances [49]. These advances illustrate the growing relevance of quantum-enhanced optimization techniques in combinatorial problems like max-cut. These developments suggest that quantum-enhanced algorithms may become increasingly viable for tackling NP-hard problems like max-cut, especially as quantum hardware and software continue to evolve.
These diverse research efforts illustrate the continuous advancements in max-cut problem solving, with developments spanning classical optimization techniques, heuristic and metaheuristic approaches, emerging machine learning-driven methodologies, and now, quantum computing paradigms. These collective advances underline a continued effort to improve both the efficiency and exploratory capability of max-cut solvers. However, population-based heuristics such as GAs still suffer from redundant exploration. This motivates our proposed method, GATS (genetic algorithm with tabu search), which introduces solution-level tabu constraints to prevent revisiting previously explored solutions, inspired by mechanisms used in both TS and HS. As demonstrated in subsequent sections, GATS offers improved performance while maintaining computational efficiency.
3. Genetic Algorithms
Genetic algorithms (GAs) [50], as a representative technique of evolutionary computation [51], are widely used in combinatorial optimization problems such as graph partitioning [52,53,54]. They have also been extensively applied to the max-cut problem [8,9,10,11]. In this section, we introduce the GA used by Seo et al. [10] and propose an improved GA.
3.1. Generational Model
We now summarize the approach to the max-cut problem proposed by Seo et al. [10], where they consider two chromosome-encoding strategies for representing solutions to the max-cut problem:
- Vertex-based encoding: Each chromosome is a binary string of length , where each gene corresponds to a vertex in the graph . A gene value of 0 indicates that the corresponding vertex belongs to subset S, and 1 indicates it belongs to . This encoding allows for simple and intuitive computation of the cut size by counting the number of edges crossing between the two subsets.
- Edge-set encoding based on a spanning tree: As proposed by Seo et al. [10], this encoding represents each solution as a binary string of length , corresponding to a subset of edges from a predefined spanning tree of the graph. Each gene indicates whether the corresponding edge in the tree is included in the cut set. This representation enables structured exploration of the cut space by leveraging the properties of spanning trees.
These encoding methods serve as the basis for the genetic algorithms described in the following sections.
Seo et al. utilized a generational GA with the framework illustrated in Algorithm 1 and parameter settings detailed in Table 1. The algorithm employs tournament selection to choose candidate chromosomes, followed by one-point crossover and random bit-wise mutation. For implementation, Seo et al. [10] used Open Beagle [55] in combination with the Boost Graph Library (http://boost.org). Each execution of the genetic algorithm generates approximately 10,000 candidate solutions.
| Algorithm 1 Pseudo-code of the generational genetic algorithm proposed by Seo et al. [10] |
|

Table 1.
Configuration of the generational genetic algorithm as described by Seo et al. [10].
3.2. Steady-State Model
We developed a new GA aimed at improving upon the approach described in Section 3.1, utilizing a steady-state GA framework, as illustrated in Algorithm 2. Each chromosome represents a partition of a given graph and consists of genes, where each gene corresponds to a vertex in G. A gene is assigned a value of 0 if the corresponding vertex belongs to S, and 1 otherwise. This encoding method follows the vertex-based encoding strategy used in [10]. Each solution (chromosome) in our algorithm is represented by a binary vector:
where indicates that vertex belongs to subset S, and indicates membership in . The fitness of a solution is evaluated by the total number of edges crossing the partition, formally defined as
where is the indicator function, returning 1 if the edge connects two nodes in different subsets, and 0 otherwise. This formulation directly corresponds to the cut size of the solution.
The crossover operator used is uniform crossover, which creates offspring by randomly selecting each gene from one of the two parent chromosomes with equal probability. Mutation is applied bit-wise with a fixed probability , flipping each gene independently. The algorithm starts by initializing a population of randomly generated chromosomes. The fitness of each chromosome is determined by its cut size, and parent selection is performed randomly. A crossover operation generates two offspring by recombining genetic material from two parent chromosomes. We employ uniform crossover [56] and apply random bit-wise mutation. Once the offspring are generated, the GA replaces the least fit individual in the population with the fitter offspring. The algorithm runs for a fixed number of generations, denoted as T. Through experimentation, we found that setting results in execution times comparable to those of the method proposed by Seo et al. [10]. Over the course of each GA execution, approximately 10,000 candidate solutions are generated, following a Genitor-style replacement strategy [57].
| Algorithm 2 Pseudo-code of our steady-state genetic algorithm |
|
4. Proposed Algorithm
4.1. Overview of the Proposed Algorithm
Tabu search (TS), introduced by Glover [58], is a metaheuristic originally developed for operations research. It explores the solution space by iteratively modifying a single current solution. In each iteration, neighboring solutions are generated and evaluated. The best candidate not marked as tabu—or one that meets an aspiration criterion—is selected as the next current solution. The tabu list prevents cycling by restricting recently visited solutions. This process continues until a stopping condition is met, typically when no improvement is observed over several iterations.
The proposed method, genetic algorithm with tabu search (GATS), aims to enhance the performance of standard genetic algorithms (GAs) by integrating tabu search (TS) to prevent redundant exploration. Unlike conventional GAs, which often revisit previously explored solutions, GATS incorporates a tabu mechanism to enhance search efficiency and preserve solution diversity.
The memory mechanism in tabu search can assist a GA in escaping local minima and progressing toward a near-optimal solution. For combining GA with TS, we regard the population of GA as a tabu list. In this case, a solution obtained by crossover and mutation of GA is accepted only if it is not in the population. If the same solution already exists in the population, the solution is discarded and another solution is generated by applying crossover and mutation again. In this manner, we can design GA for exploring the solution space beyond local optimality and the GA combined with TS is expected to show improved performance.
4.2. Implementation of the Proposed Algorithm
The GATS framework follows the standard GA structure but incorporates tabu constraints at key stages. To formally describe the tabu mechanism, let the tabu list be denoted by
which stores recently accepted solutions. A newly generated candidate solution is accepted into the population only if
After acceptance, the tabu list is updated to include , and the worst element is removed if exceeds the predefined size . This maintains a fixed-size short-term memory that promotes exploration by avoiding repeated evaluations of the same solutions.
The algorithm starts with an initial population of solutions, each representing a potential max-cut partition. Parent selection follows a steady-state GA approach, using uniform crossover and random bit-wise mutation. However, instead of allowing duplicate solutions, a tabu list is maintained to track previously explored solutions. If a newly generated solution exists in the tabu list, it is discarded, and the search continues. This ensures that the search space is explored more effectively, reducing premature convergence. To detect duplicate solutions, the current implementation uses full-solution comparison. Although effective, this can be computationally demanding for large graphs. In future work, we plan to adopt a hash-based representation to improve scalability and performance.
Algorithm 3 shows the pseudo-code of the proposed algorithm combining GA with TS. The framework of the algorithm is almost the same as that of the steady-state GA introduced in Section 3.2. The algorithm employs vertex-based binary encoding [10], as outlined in Section 3.2. It starts by generating a population of 50 random chromosomes. These chromosomes are evaluated by calculating their cut sizes, and a given number of them are used to form a tabu list. For each generation, two chromosomes are selected randomly, and two new offspring are created using uniform crossover and random bit-wise mutation. If the fitter offspring is not in the tabu list, the GA replaces the least fit member of the entire population with the fitter offspring. However, if the fitter offspring is in the tabu list, it is simply discarded and the next generation begins. Note that the generation count increases regardless of whether a newly generated offspring is accepted or rejected. This design ensures consistent iteration control but may result in generations where no population update occurs.
| Algorithm 3 Pseudo-code of our genetic algorithm combined with tabu search |
|
4.3. Comparison with Traditional GA-TS Hybrids
A key distinction between the proposed GATS approach and existing hybridizations of GA with TS lies in how the tabu list is managed. While some recent studies have proposed hybrid GA-TS algorithms for the max-cut problem, they typically apply tabu mechanisms at the component or move level, such as tracking vertex-level changes. In contrast, our approach employs solution-level memory constraints, which, to the best of our knowledge, have not been extensively explored in the recent literature. Traditional GA-TS hybrids typically apply tabu constraints at the vertex level, tracking individual vertex movements to prevent cycling back to recently explored local optima [13,30,34]. While this method effectively improves local search performance, it does not prevent GA from generating redundant solutions at the global solution level, leading to inefficiencies in broader exploration.
In contrast, our proposed GATS (genetic algorithm with tabu search) integrates tabu search at the solution level, treating the GA population itself (or a part of it) as an implicit tabu list. This ensures that redundant solutions are eliminated at the crossover and mutation stages, thereby maintaining search diversity and improving overall efficiency. By restricting the reproduction of previously visited solutions, GATS achieves better exploration-exploitation balance compared to conventional GA-TS hybrids.
Although GATS is rooted in the GA framework, its solution-level memory mechanism strategically aligns it with the exploration behavior of harmony search (HS), rather than conventional GA-TS hybrids. Harmony search [59] maintains a memory structure that prevents redundant solution generation, ensuring continuous exploration of new regions. Similarly, GATS enforces solution-level constraints within GA’s evolutionary process, promoting a more structured and effective search. This distinction is crucial, as it allows GATS to avoid unnecessary recomputation while maintaining population diversity, ultimately leading to superior performance in combinatorial optimization problems.
In sum, unlike traditional GA-TS hybrid methods that apply tabu constraints at a local level—such as tracking recent moves of individual vertices—the proposed GATS algorithm operates at the global solution level by treating the entire population (or a part of it) as an implicit tabu list. This global-level constraint reduces redundancy and sustains diversity, avoiding the need for additional memory structures required in conventional TS. As a result, GATS ensures a broader exploration of the solution space while avoiding the complexity of managing explicit memory structures as typically required in conventional TS mechanisms.
This population-as-memory mechanism distinguishes GATS as a novel hybridization framework, streamlining memory usage and enhancing search breadth. The effectiveness of this approach is further validated in Section 5 through experimental comparisons with HS.
This mechanism enables the algorithm to maintain diversity within the population by preventing the reintroduction of recently explored solutions, which could otherwise lead to premature convergence.
To better position the proposed GATS method within the context of existing approaches, we compare it with representative studies that have addressed solution duplication in GAs. Several prior studies have proposed methods to mitigate redundancy and improve diversity. For example, Mumford [60] introduced a replacement strategy in a steady-state multi-objective evolutionary algorithm that explicitly rejects phenotypically duplicate offspring from entering the population. Raidl and Hu [61] proposed a complete archive for binary-encoded GAs, utilizing a trie-based structure that stores all evaluated solutions and transforms revisited candidates into similar but unvisited ones using a controlled perturbation process. Additionally, Wang et al. [62] proposed a nonrevisiting genetic algorithm based on a binary space partitioning (BSP) tree that not only records visited regions but also guides the search through multiple regions to avoid local optima.
Compared to these approaches, the GATS algorithm employs a fixed-length, solution-level tabu list that maintains a short-term memory of recently accepted solutions. This list is maintained separately from the population and is used to restrict the reinsertion of previously accepted individuals. Unlike trie-based or BSP-based global memory structures that require additional transformation logic or landscape modeling, our approach imposes a lightweight, recency-based avoidance strategy that integrates seamlessly with steady-state GA dynamics. Thus, while GATS shares the overarching goal of avoiding duplicate solutions and maintaining diversity, its implementation reflects a distinct balance between simplicity and effectiveness. In this sense, it represents a pragmatic hybridization of GA and TS principles, incorporating short-term memory without incurring significant computational overhead.
5. Experiments
All experiments were implemented in C and conducted on an Ubuntu 16.04.7 Linux system using a 2.8 GHz Intel i5 CPU. To ensure reproducibility, fixed random seeds were used in every run.
5.1. Test Graphs
We conducted experiments using 31 benchmark graphs commonly referenced in the literature [10,11,52,63]. These graphs represent different structural types and can be described as follows:
- G: A randomly generated graph consisting of n vertices, where each edge is included with probability p. For example, G1000.01 denotes a random graph with 1000 vertices and an edge probability of 0.01.
- U: A geometric random graph with n vertices, where the expected degree of each vertex is d. As an example, U500.10 represents a geometric random graph with 500 vertices and an expected degree of 10.
- breg: A 3-regular random graph with n vertices, constructed so that the optimal bisection size is close to b with high probability, which increases as n becomes larger.
- cat.n: A caterpillar graph with n vertices, where each node on the main spine is connected to six additional nodes. The variant rcat.n represents a modified caterpillar graph with n vertices, where each node along the spine has approximately legs.
- grid: A grid graph with n vertices, where the minimum cut size is b. The variant w-grid denotes a modified version with additional edges connecting opposite boundaries, forming a wrapped grid.
5.2. Determination of Tabu List Size
Selecting an appropriate size for the tabu list plays a critical role in guiding short-term search behavior [64], particularly when integrated with GAs. An overly small tabu list may allow repeated visits to previously explored solutions, while an excessively large list may overly restrict exploration and hinder convergence.
To determine the optimal size, we evaluated various tabu list sizes ranging from small to large values. The performance was assessed using the average of the percentage difference ratio, defined as , where is the best solution found across all experiments for a given graph, and is the average solution obtained from 30 runs of the algorithm. Lower values indicate better performance.
As shown in Table 2, the smallest average difference ratio was achieved when the tabu list size was set to 5. This indicates that a size of 5 provides the most effective balance between promoting exploration and avoiding redundant searches. In contrast, performance gradually deteriorates as the tabu list size increases beyond this point. This can be attributed to excessive restriction in solution acceptance, which may reduce diversity in the search space.

Table 2.
Impact of tabu list size on solution quality (average of percentage difference ratio).
Based on these findings, we adopted a tabu list size of 5 as the default configuration in our proposed GATS algorithm.
5.3. Comparison of Genetic Algorithms
In this subsection, we compare the performance of different GA variants applied to the max-cut problem, including the generational genetic algorithm (GGA) proposed by Seo et al. [10], our steady-state genetic algorithm (SGA), and our hybrid approach incorporating tabu search (GATS). To evaluate their effectiveness, we conducted experiments using benchmark graph instances, running each algorithm 30 times per instance and computing the average and standard deviation of the cut sizes. Table 3 compares their performance, where a multi-start algorithm (MSA) generates 10,000 random cuts and returns the best. The results indicate that SGA consistently outperforms GGA in our experiments, suggesting that the steady-state approach may be more effective than the generational model in maintaining solution quality under the given settings. Furthermore, GATS achieves superior results compared to SGA, highlighting the benefits of integrating tabu search to prevent redundant exploration and enhance search efficiency.

Table 3.
Cut sizes and runtime comparison among four algorithms.
To confirm the statistical significance of these findings, we performed one-tailed t-tests comparing the results of GGA, SGA, and GATS. The p-values indicate that the improvements from GGA to SGA and from SGA to GATS are statistically significant, reinforcing the conclusion that our modifications lead to meaningful performance gains. Additionally, we analyzed computational efficiency and found that GATS maintains a runtime comparable to SGA while significantly improving solution quality. This suggests that incorporating tabu search does not introduce excessive computational overhead, making GATS a viable alternative to conventional GAs.
Overall, the comparison reveals a clear performance hierarchy among the tested methods, where GGA is outperformed by SGA, which in turn is outperformed by GATS. The steady-state approach in SGA contributes to better convergence, while the integration of TS in GATS further refines the search process by mitigating local optima entrapment. These results confirm that our proposed hybrid method effectively balances exploration and exploitation, leading to a more robust optimization strategy for the max-cut problem. Overall, the performance ranking of the methods can be summarized as follows: MSA ≪ GGA ≪ SGA ≪ GATS, where “A ≪ B” means that B significantly outperforms A.
5.4. Analysis of Crossover Operator Impact
To better understand the source of performance improvement in the proposed steady-state genetic algorithm (SGA), we conducted a decomposition analysis, comparing the contribution of the evolutionary scheme and the crossover operator separately. While GGA employs a generational model with one-point crossover, the proposed SGA uses a steady-state model with uniform crossover.
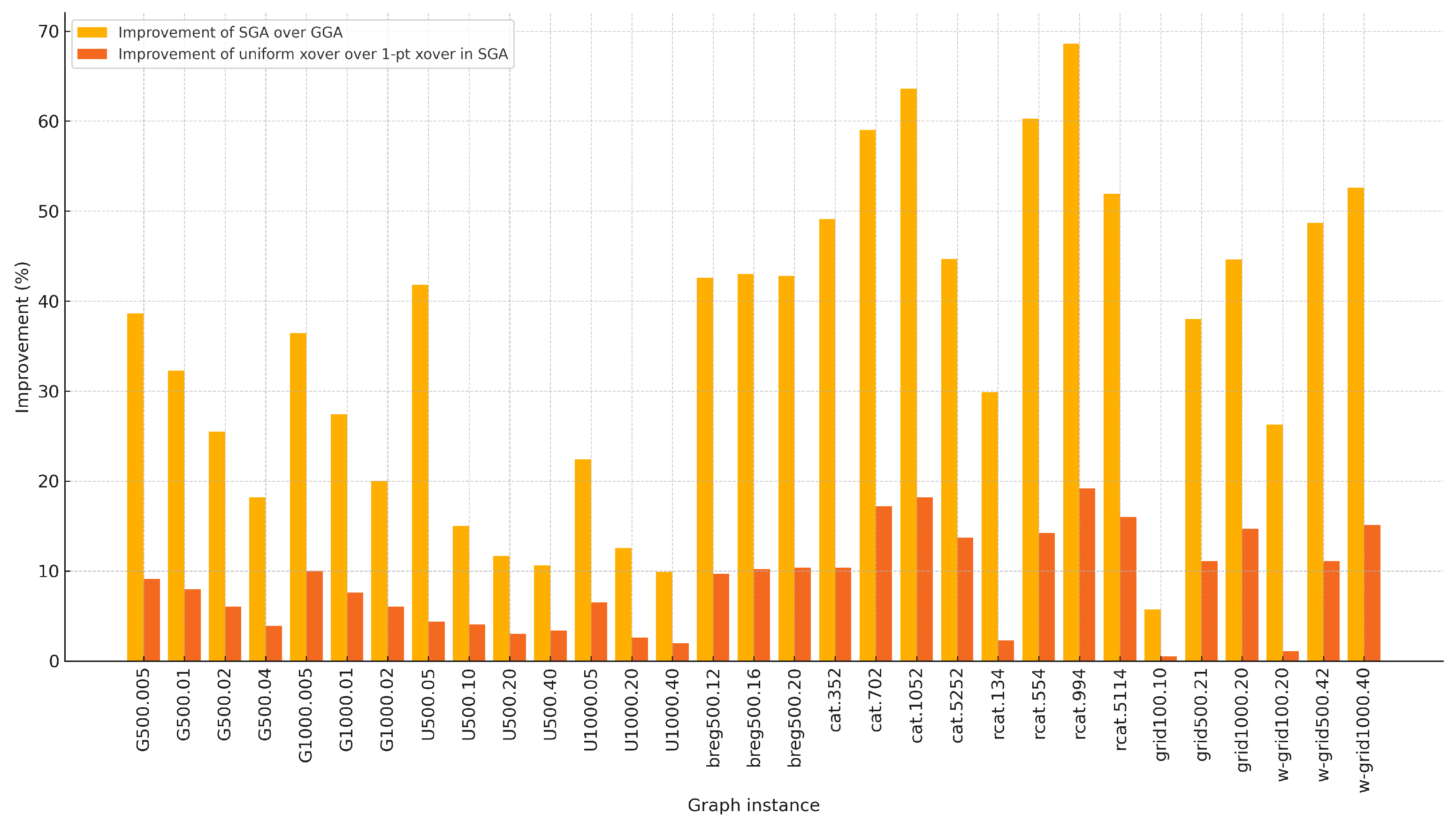
To isolate the effect of the crossover operator, we implemented a variant of SGA that adopts one-point crossover instead of uniform crossover. Figure 2 presents the comparative improvement rates across 31 benchmark instances: the yellow bars represent the improvement of SGA (with uniform crossover) over GGA, while the orange bars indicate the improvement achieved solely by switching from one-point to uniform crossover within the SGA framework.
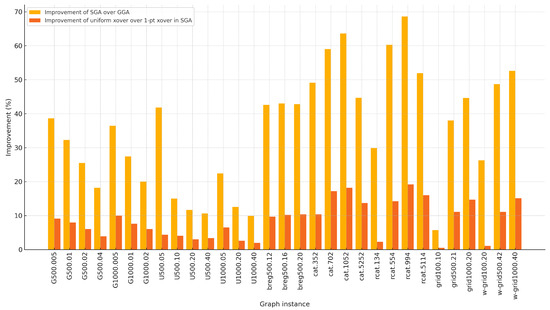
Figure 2.
Comparative improvement analysis showing the contribution of steady-state evolution and uniform crossover. Yellow bars indicate the improvement of SGA over GGA, while orange bars indicate the performance gain due to the use of uniform crossover over one-point crossover in SGA.
As shown in the figure, uniform crossover contributes significantly to the overall performance gain in many instances. In particular, instances such as prcart.994, pcart.1052, and rcat.554 show that more than one-fourth of the total improvement comes from the crossover operator alone. These results suggest that both the steady-state scheme and the choice of crossover operator play important and complementary roles in enhancing the effectiveness of the algorithm.
5.5. Convergence Analysis
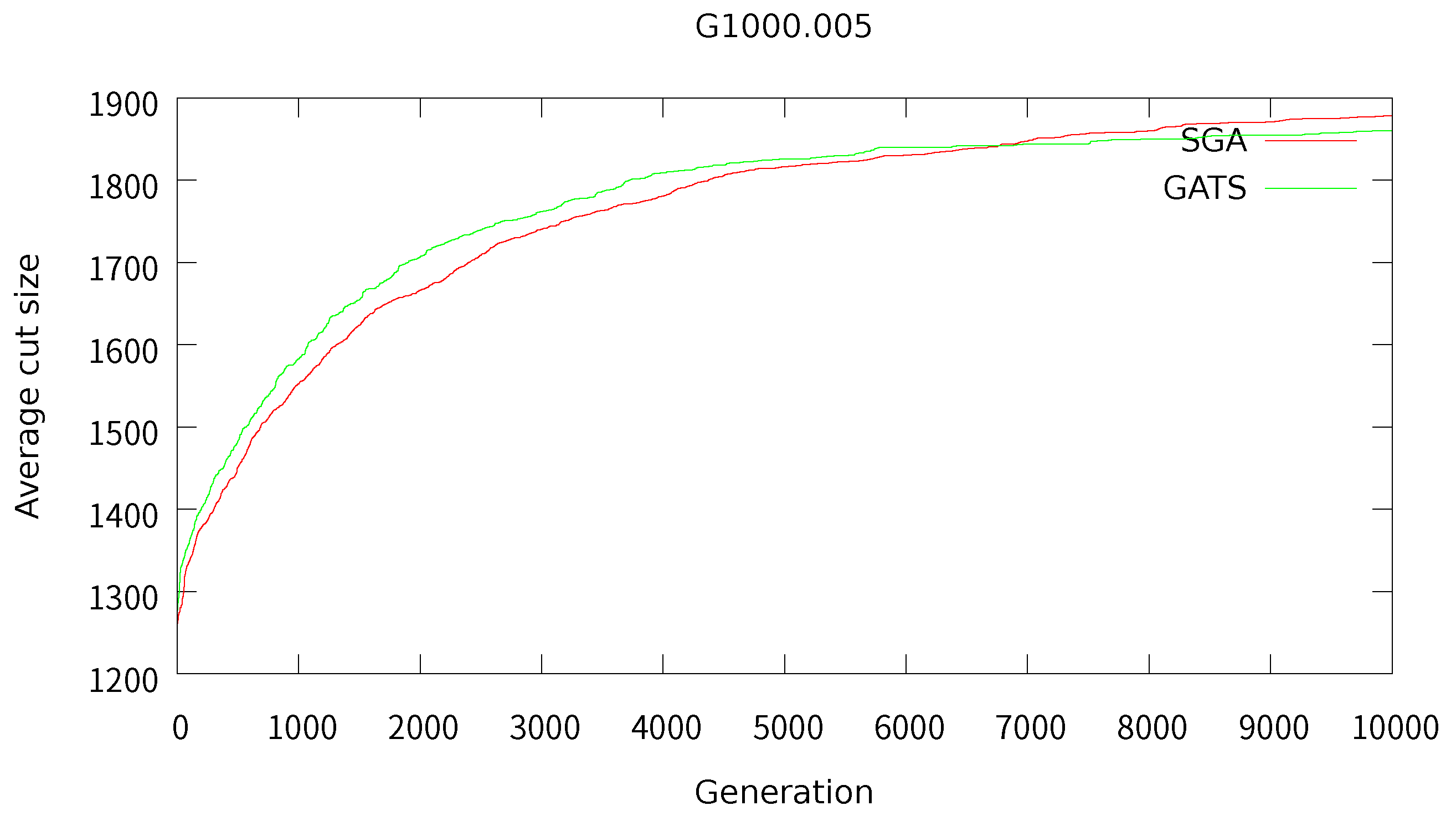
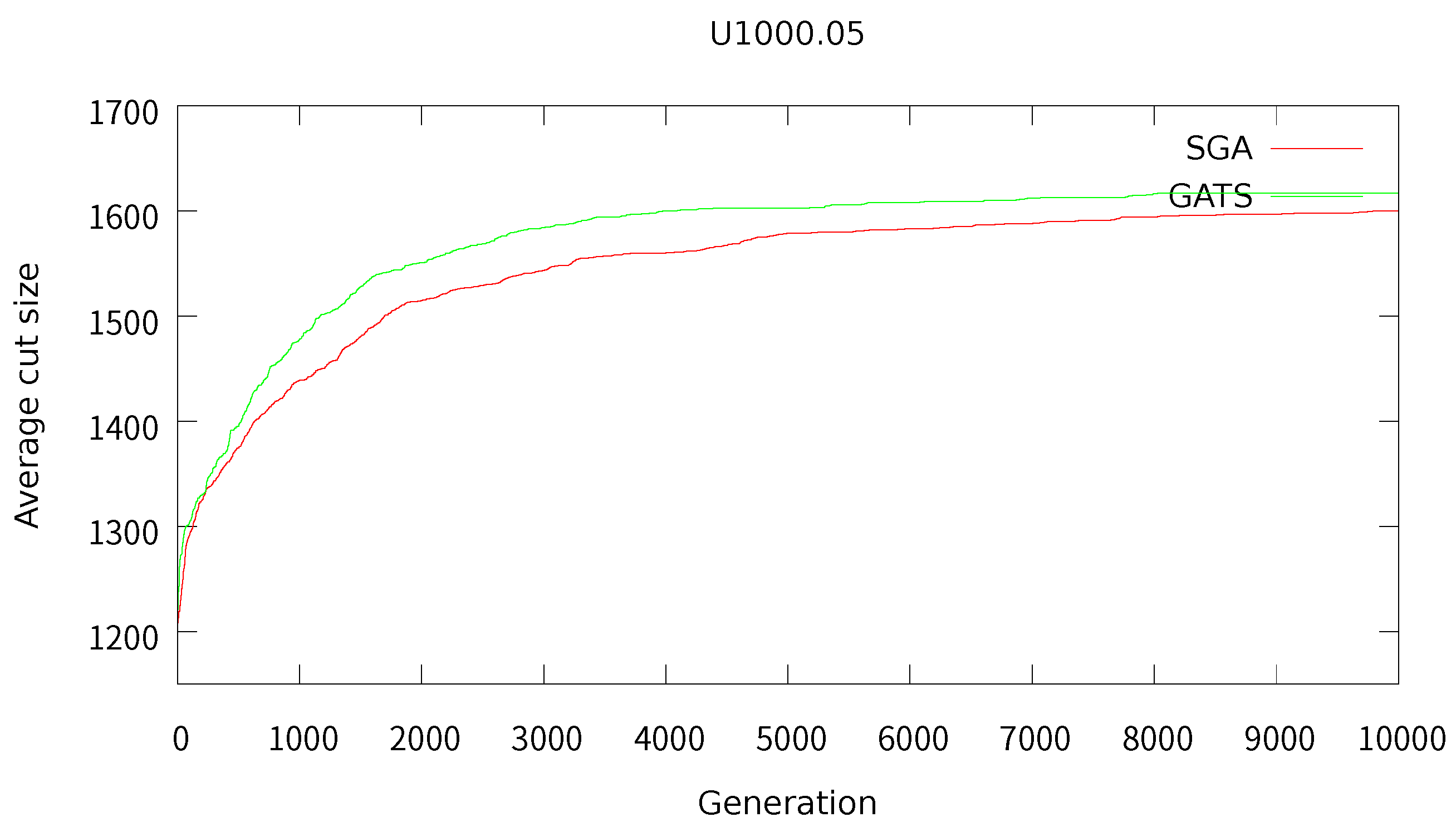
To further investigate the convergence behavior of the proposed GATS algorithm, we compared its performance against SGA over generations. Specifically, we measured the average cut size of the entire population at each generation for two representative graph instances: G1000.005 and U1000.05.
Figure 3 and Figure 4 present the convergence curves for these instances. As shown in the plots, GATS not only achieves higher average cut sizes throughout the evolution process but also exhibits more stable convergence than SGA. These results support the claim that the integration of a solution-level tabu list in GATS not only improves population diversity but also contributes to more efficient and effective convergence.
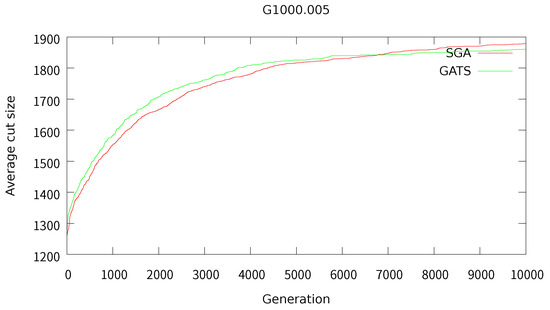
Figure 3.
Convergence behavior on instance G1000.005: average cut size over generations.
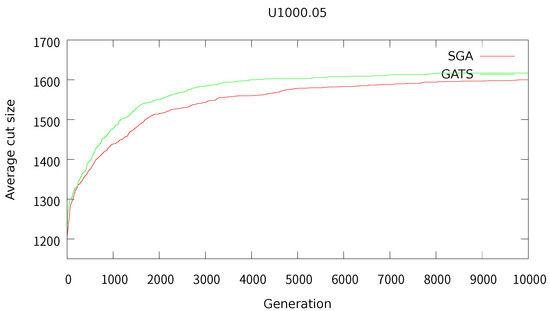
Figure 4.
Convergence behavior on instance U1000.05: average cut size over generations.
5.6. Comparison with Harmony Search
In this subsection, we analyze the results presented in Table 4, which compare the performance of GATS and HS. The results indicate that the two algorithms exhibit generally similar performance, with only minor differences in most cases. The average cut sizes obtained by GATS and HS are comparable across various test graphs, and the standard deviations remain consistently close, suggesting that GATS effectively incorporates the advantages of TS while maintaining search behavior similar to HS.

Table 4.
Performance comparison of the proposed method and harmony search.
However, certain test instances reveal notable performance differences between the two algorithms. In particular, HS significantly outperforms GATS in specific graphs such as cat.5252 and rcat.5114. For these cases, HS achieves substantially larger cut sizes, indicating that its search strategy is more effective for these graph structures. On the other hand, GATS performs slightly better than HS in a few instances, such as G1000.01 and breg500.12, though the differences in these cases are relatively small. The statistical significance analysis further supports these observations. While the majority of test cases yield p-values greater than 0.1, suggesting that the differences between the two algorithms are not statistically significant, certain cases, including cat.5252 and rcat.5114, exhibit extremely low p-values, confirming that HS significantly outperforms GATS for these specific graphs. Conversely, in cases where GATS shows marginally better results, such as G1000.01, the difference is relatively minor but still noticeable.
Another important aspect to consider is the execution time of the two algorithms. The results indicate that GATS and HS require nearly identical computation times, implying that the introduction of TS in GATS does not impose additional computational overhead. This suggests that while TS effectively prevents redundant solution exploration, it achieves this without compromising efficiency.
In sum, the comparison between GATS and HS demonstrates that the two algorithms achieve similar performance, with HS exhibiting an advantage in certain graph instances and GATS performing slightly better in others. The negligible computational cost of integrating TS in GATS further reinforces its practical utility. These findings indicate that GATS serves as an effective alternative to HS while maintaining the strengths of GA-based search strategies. Future research could further explore the underlying reasons why HS outperforms GATS in certain cases and investigate potential hybrid approaches that incorporate additional features of HS into GATS to enhance its overall performance.
The results from Section 5 collectively demonstrate that GATS not only enhances GA performance but also provides a competitive alternative to HS across a range of graph types.
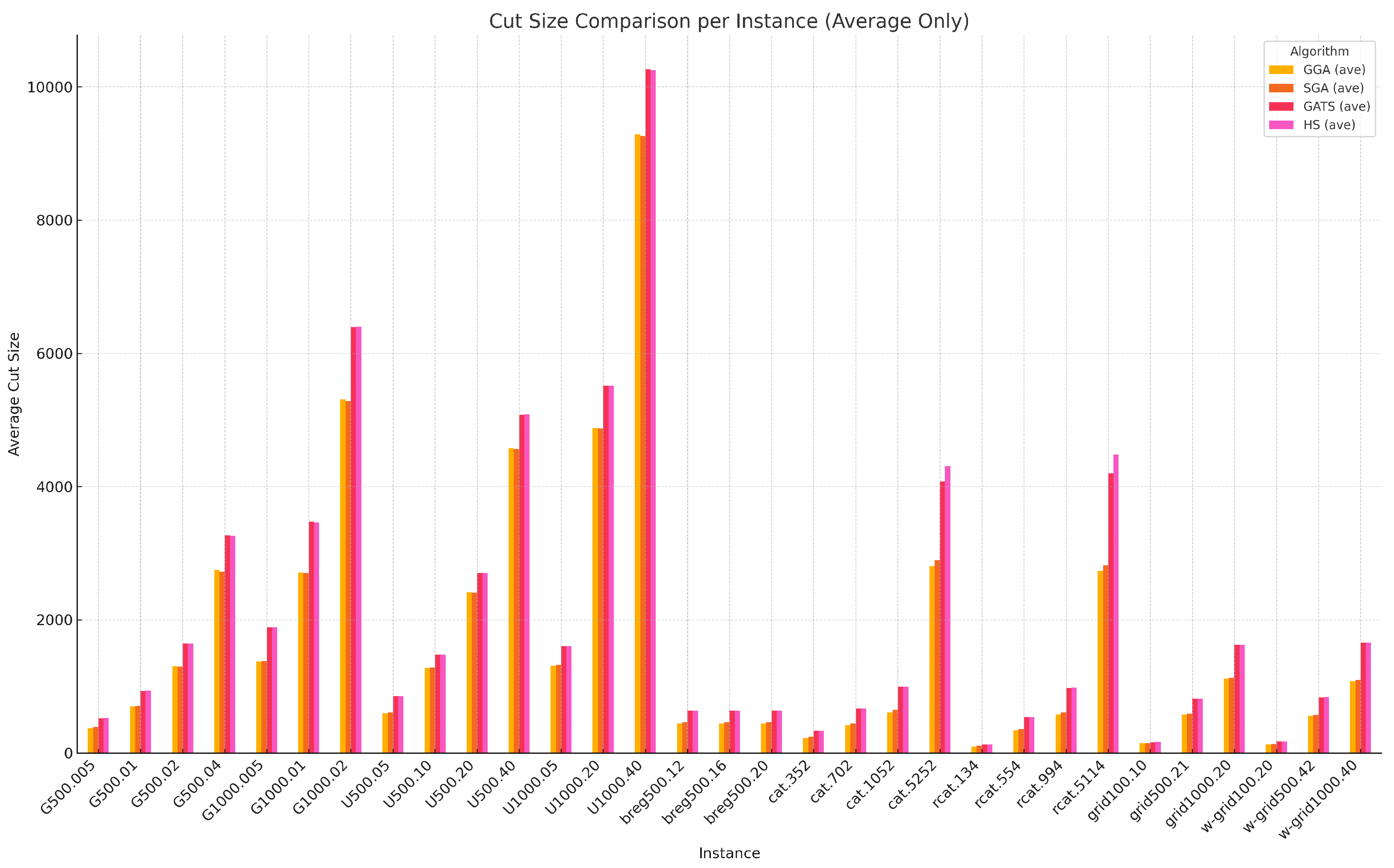
To further illustrate the performance differences among the algorithms, we present a bar chart in Figure 5. This visualization complements the numerical results shown in Table 3 and Table 4, allowing for a more intuitive comparison. As seen in the figure, the GATS and HS algorithms consistently outperform GGA and SGA across most benchmark instances, with HS showing a noticeable advantage in some specific cases (e.g., cat.5252, rcat.5114).
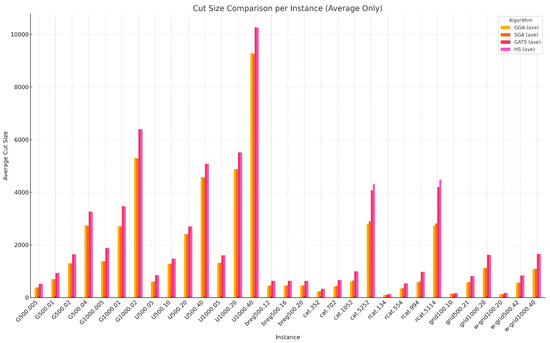
Figure 5.
Bar chart comparing the average cut sizes achieved by four algorithms (GGA, SGA, GATS, and HS) across all benchmark graph instances. This visualization complements the tabulated results and illustrates the relative performance more clearly.
In particular, HS appears to perform better than GATS in instances such as cat.5252 and rcat.5114. One possible reason is that HS generates new solutions by combining components from multiple existing solutions (i.e., a multi-parent mechanism), which may allow for more flexible exploration compared to the two-parent crossover in GA. This approach could be more effective for certain graph structures, such as tree-like graphs, where diverse component mixing helps escape local optima. These observations suggest that the recombination strategy in GATS may be less suited to specific topologies.
6. Conclusions and Future Work
This study proposed a hybrid genetic algorithm that incorporates tabu search (GATS) to improve the performance of GAs in solving the max-cut problem. By integrating TS, the proposed method effectively mitigates redundant exploration, leading to a more efficient search process. The experimental results confirm that GATS outperforms the standard GAs while exhibiting search behavior similar to harmony search (HS). This suggests that mitigating repetitive searches via tabu mechanisms contributes to more effective combinatorial optimization.
The findings of this study highlight the potential of combining GAs with TS to improve search efficiency. The results indicate that this approach can serve as an alternative to HS, which has been shown to be effective in previous studies. Furthermore, the similarities in search strategies between GATS and HS suggest that such hybridization may bridge the performance gap between various heuristic methods and provide a unified framework for efficient combinatorial optimization.
Unlike previous GA-TS hybrids, the proposed GATS method applies tabu constraints at the solution level, effectively balancing exploration and exploitation by discarding previously visited solutions at the generation stage. This novel mechanism contributes to improved performance without increasing computational complexity.
Future Research Directions
While the proposed method demonstrates promising performance improvements, several aspects can be explored in future research:
- Theoretical analysis of GATS efficiency: While the empirical results validate the effectiveness of GATS, a more rigorous theoretical analysis is required to explain why the method performs better than standard GAs. Future work could analyze the impact of tabu constraints on exploration efficiency and convergence properties using mathematical models.
- Diversity maintenance and search space coverage: The tabu list in GATS prevents redundant solutions, but its effect on search space coverage and genetic diversity has not been explicitly measured. Future studies could investigate the diversity preservation mechanisms of GATS using entropy-based or distribution-based metrics. Additionally, visualizing search trajectory patterns could provide further insights into how GATS explores the solution space differently compared to traditional GAs.
- Performance on different graph structures: While the proposed algorithm has been tested on a variety of benchmark graphs, further experiments on larger or structurally different graph types, such as real-world network graphs, could enhance our understanding of its generalizability. In particular, cases where HS significantly outperforms GATS, such as cat.5252 and rcat.5114, require a deeper analysis to identify potential limitations of the current approach.
- Comparisons with other metaheuristic techniques: Future work could explore hybridizing GATS with other metaheuristic algorithms [65] beyond HS. Techniques such as simulated annealing or reinforcement learning-based search strategies could be incorporated to enhance adaptability and convergence efficiency. Evaluating how these hybrid approaches perform against state-of-the-art heuristics would provide valuable insights.
- Computational complexity and optimization: Although GATS does not introduce significant computational overhead, further optimization of the algorithm could improve its scalability for large-scale instances. Investigating more efficient tabu list management strategies or parallelized implementations could enhance runtime efficiency while maintaining solution quality. Additionally, future studies could explore combining GATS with reinforcement learning-guided selection mechanisms to dynamically adapt tabu constraints during the search.
By addressing these research directions, future work can further refine the effectiveness of hybrid GAs in solving combinatorial optimization problems and extend their applicability to broader domains.
Author Contributions
Conceptualization, Y.-H.K. and Y.Y.; methodology, Y.-H.K.; software, Y.-H.K.; validation, Y.Y.; formal analysis, Y.Y.; investigation, Z.W.G. and Y.Y.; resources, Y.-H.K.; data curation, Y.-H.K.; writing—original draft preparation, Y.-H.K.; writing—review and editing, Z.W.G. and Y.Y.; visualization, Y.Y.; supervision, Z.W.G. and Y.Y.; project administration, Z.W.G. and Y.Y.; funding acquisition, Y.-H.K. and Z.W.G. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Korea Institute of Energy Technology Evaluation and Planning (KETEP) and the Ministry of Trade, Industry & Energy, Republic of Korea (RS-2024-00442817) and also supported by the Korea Institute of Marine Science & Technology Promotion (KIMST) funded by the Ministry of Oceans and Fisheries, Korea (RS-2022-KS221629).
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Acknowledgments
The present research has been conducted by the Research Grant of Kwangwoon University in 2024.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| GA | Genetic algorithm |
| HS | Harmony search |
| TS | Tabu search |
| EDA | Estimation of distribution algorithms |
| GNN | Graph neural network |
| MSA | Multi-start algorithm |
| GGA | Generational GA |
| SGA | Steady-state GA |
| GATS | GA combined with TS |
References
- Karp, R.M. Reducibility among combinatorial problems. In Complexity of Computer Computations; Plenum Press: New York, NY, USA, 1972; pp. 85–103. [Google Scholar]
- Garey, M.R.; Johnson, D.S.; Stockmeyer, L.J. Some simplified NP-complete graph problems. Theor. Comput. Sci. 1976, 1, 237–267. [Google Scholar] [CrossRef]
- Barahona, F.; Grotschel, M.; Junger, M.; Reinelt, G. An application of combinatorial optimization to statistical physics and circuit layout design. Oper. Res. 1988, 36, 493–513. [Google Scholar] [CrossRef]
- Anderson, C.A.; Jones, K.F.; Ryan, J. A Two-Dimensional Genetic Algorithm for The Ising Problem. Complex Syst. 1991, 5, 327–333. [Google Scholar]
- Homer, S.; Peinado, M. Design and performance of parallel and distributed approximation algorithms for maxcut. J. Parallel Distrib. Comput. 1997, 46, 48–61. [Google Scholar] [CrossRef]
- Arráiz, E.; Olivo, O. Competitive simulated annealing and tabu search algorithms for the max-cut problem. In Proceedings of the 11th Annual Conference on Genetic and Evolutionary Computation, Montréal, QC, Canada, 8–12 July 2009; pp. 1797–1798. [Google Scholar] [CrossRef]
- Myklebust, T. Solving maximum cut problems by simulated annealing. arXiv 2015, arXiv:1503.05774. [Google Scholar]
- Kim, S.H.; Kim, Y.H.; Moon, B.R. A hybrid genetic algorithm for the MAX CUT problem. In Proceedings of the Genetic and Evolutionary Computation Conference, San Francisco, CA, USA, 7–11 July 2001; pp. 416–423. [Google Scholar]
- Wu, Q.; Hao, J.K. A memetic approach for the Max-Cut problem. In Proceedings of the PPSN 2012—Parallel Problem Solving from Nature-PPSN XII: 12th International Conference, Taormina, Italy, 1–5 September 2012; Coello, C.A.C., Cutello, V., Deb, K., Forrest, S., Nicosia, G., Pavone, M., Eds.; LNCS. Springer: Heidelberg/Berlin, Germany, 2012; Volume 7492, pp. 297–306. [Google Scholar] [CrossRef]
- Seo, K.; Hyun, S.; Kim, Y.H. An edge-set representation based on a spanning tree for searching cut space. IEEE Trans. Evol. Comput. 2015, 19, 465–473. [Google Scholar] [CrossRef]
- Kim, Y.; Yoon, Y.; Geem, Z. A comparison study of harmony search and genetic algorithm for the max-cut problem. Swarm Evol. Comput. 2019, 44, 130–135. [Google Scholar] [CrossRef]
- Palubeckis, G. Application of multistart tabu search to the MaxCut problem. Inform. Technol. Control 2004, 2, 29–35. [Google Scholar]
- Kochenberger, G.; Hao, J.; Lü, Z.; Wang, H.; Glover, F. Solving large scale Max Cut problems via tabu search. J. Heuristics 2013, 19, 565–571. [Google Scholar] [CrossRef]
- Martí, R.; Duarte, A.; Laguna, M. Advanced scatter search for the Max-Cut problem. INFORMS J. Comput. 2009, 21, 26–38. [Google Scholar] [CrossRef]
- de Sousa, S.; Haxhimusa, Y.; Kropatsch, W. Estimation of distribution algorithm for the max-cut problem. In Proceedings of the Graph-Based Representations in Pattern Recognition: 9th IAPR-TC-15 International Workshop, GbRPR 2013, Vienna, Austria, 15–17 May 2013; Proceedings 9. Springer: Berlin/Heidelberg, Germany, 2013; pp. 244–253. [Google Scholar] [CrossRef]
- Lin, G.; Guan, J. An Integrated Method Based on PSO and EDA for the Max-Cut Problem. Comput. Intell. Neurosci. 2016, 2016, 3420671. [Google Scholar] [CrossRef] [PubMed]
- Gao, L.; Zeng, Y.; Dong, A. An ant colony algorithm for solving Max-cut problem. Prog. Nat. Sci. 2008, 18, 1173–1178. [Google Scholar] [CrossRef]
- Gu, S.; Yang, Y. A pointer network based deep learning algorithm for the max-cut problem. In Proceedings of the Neural Information Processing: 25th International Conference, ICONIP 2018, Siem Reap, Cambodia, 13–16 December 2018; Proceedings, Part I 25. Springer International Publishing: Berlin/Heidelberg, Germany, 2018; pp. 238–248. [Google Scholar] [CrossRef]
- Wang, J. An improved discrete Hopfield neural network for Max-Cut problems. Neurocomputing 2006, 69, 1665–1669. [Google Scholar] [CrossRef]
- Rendl, F.; Rinaldi, G.; Wiegele, A. A branch and bound algorithm for Max-Cut based on combining semidefinite and polyhedral relaxations. In Proceedings of the IPCO—Integer Programming and Combinatorial Optimization: 12th International IPCO Conference, Ithaca, NY, USA, 25–27 June 2007; Fischetti, M., Williamson, D.P., Eds.; LNCS. Springer: Berlin/Heidelberg, Germany, 2007; Volume 4513, pp. 295–309. [Google Scholar] [CrossRef]
- Crocea, F.; Kaminskib, M.; Paschosc, V. An exact algorithm for MAX-CUT in sparse graphs. Oper. Res. Lett. 2007, 35, 403–408. [Google Scholar] [CrossRef]
- Krislock, N.; Malick, J.; Rouoin, F. Improved semidefinite bounding procedure for solving Max-Cut problems to optimality. Math. Program. 2014, 143, 61–86. [Google Scholar] [CrossRef]
- Krishnan, K.; Mitchell, J. A semidefinite programming based polyhedral cut and price approach for the maxcut problem. Comput. Optim. Appl. 2006, 33, 51–71. [Google Scholar] [CrossRef]
- Burer, S.; Monteiro, R.; Zhang, Y. Rank-two relaxation heuristics for max-cut and other binary quadratic programs. SIAM J. Optim. 2002, 12, 503–521. [Google Scholar] [CrossRef]
- Goemans, M.X.; Williamson, D.P. Improved approximation algorithms for maximum cut and satisfiability problems using semidefinite programming. J. ACM 1995, 42, 1115–1145. [Google Scholar] [CrossRef]
- Rodriguez-Fernandez, A.; Gonzalez-Torres, B.; Menchaca-Mendez, R.; Stadler, P. Clustering improves the Goemans–Williamson approximation for the max-cut problem. Computation 2020, 8, 75. [Google Scholar] [CrossRef]
- Mohades, M.; Kahaei, M. An Efficient Riemannian Gradient Based Algorithm for Max-Cut Problems. IEEE Trans. Circuits Syst. II: Express Briefs 2021, 69, 1882–1886. [Google Scholar] [CrossRef]
- Chen, W.K.; Gamarnik, D.; Panchenko, D.; Rahman, M. Suboptimality of local algorithms for a class of max-cut problems. Ann. Probab. 2019, 47, 1587–1618. [Google Scholar] [CrossRef]
- Kadhim, F.J.; Al-jilawi, A.S. A Hybrid Approximate Algorithms of Numerical Optimization for Solving the Max-Cut Problem. arXiv 2024. [Google Scholar] [CrossRef]
- Wu, Q.; Wang, Y.; Lü, Z. A tabu search based hybrid evolutionary algorithm for the max-cut problem. Appl. Soft Comput. 2015, 34, 827–837. [Google Scholar] [CrossRef]
- Lin, G.; Zhu, W.X. A memetic algorithm for the max-cut problem. Int. J. Comput. Sci. Manag. 2015, 10, 67–544. [Google Scholar] [CrossRef]
- Zeng, Z.; Yu, X.; Wu, Q.; Wang, Y.; Zhou, Z. A memetic algorithm based on edge-state learning for max-cut. Expert Syst. Appl. 2022, 209, 118077. [Google Scholar] [CrossRef]
- Kim, J.; Yoon, Y.; Moon, B. Solving maximum cut problem with an incremental genetic algorithm. In Proceedings of the 2016 on Genetic and Evolutionary Computation Conference Companion, Denver, CO, USA, 20–24 July 2016; ACM: New York, NY, USA, 2016; pp. 49–50. [Google Scholar] [CrossRef]
- Soares, P.; Araújo, C. Genetic Algorithms with Optimality Cuts to the Max-Cut Problem. In Proceedings of the Brazilian Conference on Intelligent Systems, Belo Horizonte, Brazil, 25–29 September 2023; Springer: Cham, Switzerland, 2023; pp. 17–32. [Google Scholar] [CrossRef]
- Wang, J.; Wu, C.; Zuo, F. More on greedy construction heuristics for the MAX-CUT problem. arXiv 2023, arXiv:2312.10895. [Google Scholar]
- Sahni, S.; Gonzalez, T. P-complete approximation problems. J. ACM 1976, 23, 555–565. [Google Scholar] [CrossRef]
- Chen, X.; Lin, G.; Xu, M. Applying a binary artificial bee colony algorithm to the max-cut problem. In Proceedings of the 2019 12th International Congress on Image and Signal Processing, BioMedical Engineering and Informatics (CISP-BMEI), Suzhou, China, 19–21 October 2019; IEEE: New York, NY, USA, 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Šević, I.; Jovanovic, R.; Urošević, D.; Davidović, T. Fixed Set Search Applied to the Max-Cut Problem. In Proceedings of the 8th IEEE Energy Conference (ENERGYCON), Doha, Qatar, 4–7 March 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Gu, S.; Yang, Y. A deep learning algorithm for the max-cut problem based on pointer network structure with supervised learning and reinforcement learning strategies. Mathematics 2020, 8, 298. [Google Scholar] [CrossRef]
- Yao, W.; Bandeira, A.; Villar, S. Experimental performance of graph neural networks on random instances of max-cut. In Proceedings of the Wavelets and Sparsity XVIII, San Diego, CA, USA, 13–15 August 2019; SPIE: Bellingham, WA, USA, 2019; Volume 11138, pp. 242–251. [Google Scholar] [CrossRef]
- Jin, A.; Liu, X. A Fast Machine Learning Algorithm for the MaxCut Problem. In Proceedings of the 2023 IEEE MIT Undergraduate Research Technology Conference (URTC), Cambridge, MA, USA, 6–8 October 2023; IEEE: New York, NY, USA, 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Garmendia, A.I.; Ceberio, J.; Mendiburu, A. Exploring the Capabilities and Limitations of Neural Methods in the Maximum Cut. In Proceedings of the Advances in Artificial Intelligence, CAEPIA 2024, A Coruña, Spain, 19–21 June 2024; Alonso-Betanzos, A., Guijarro-Berdiñas, B., Bolón-Canedo, V., Hernández-Pereira, E., Fontenla-Romero, O., Camacho, D., Rabuñal, J.R., Ojeda-Aciego, M., Medina, J., Riquelme, J.C., et al., Eds.; Lecture Notes in Computer Science. Springer: Cham, Switzerland, 2024; Volume 14640. [Google Scholar] [CrossRef]
- Gao, L. Finding local Max-Cut in graphs in randomized polynomial time. Soft Comput. 2024, 28, 3029–3048. [Google Scholar] [CrossRef]
- Islam, M.R.; Islam, M.S.; Boni, P.K.; Sarker, A.S.; Anam, M.A. Solving the maximum cut problem using Harris Hawk Optimization algorithm. PLoS ONE 2025, 19, e0315842. [Google Scholar] [CrossRef]
- Mirka, R.; Williamson, D. An experimental evaluation of semidefinite programming and spectral algorithms for max cut. ACM J. Exp. Algorithmics 2023, 28, 1–18. [Google Scholar] [CrossRef]
- Kang, Y.G.; Ishii, M.; Park, J.; Shin, U.; Jang, S.; Yoon, S.; Kim, M.; Okazaki, A.; Ito, M.; Nomura, A.; et al. Solving Max-Cut Problem Using Spiking Boltzmann Machine Based on Neuromorphic Hardware with Phase Change Memory. Adv. Sci. 2024, 11, 2406433. [Google Scholar] [CrossRef]
- Farhi, E.; Goldstone, J.; Gutmann, S. A Quantum Approximate Optimization Algorithm. arXiv 2014, arXiv:1411.4028. [Google Scholar]
- Angone, A.; Liu, X.; Shaydulin, R.; Safro, I. Hybrid Quantum-Classical Multilevel Approach for Maximum Cuts on Graphs. arXiv 2023, arXiv:2309.08815. [Google Scholar]
- Viana, P.A.; de Paula Neto, F.M. A Quantum Genetic Algorithm Framework for the MaxCut Problem. arXiv 2024, arXiv:2501.01058. [Google Scholar]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization and Machine Learning; Addison-Wesley: Boston, MA, USA, 1989. [Google Scholar]
- Kim, Y.H.; Caraffini, F. Preface to “Swarm and Evolutionary Computation—Bridging Theory and Practice”. Mathematics 2023, 11, 1209. [Google Scholar] [CrossRef]
- Kim, Y.H.; Moon, B.R. Lock-gain based graph partitioning. J. Heuristics 2004, 10, 37–57. [Google Scholar] [CrossRef]
- Moraglio, A.; Kim, Y.H.; Yoon, Y.; Moon, B.R. Geometric Crossovers for Multiway Graph Partitioning. Evol. Comput. 2007, 15, 445–474. [Google Scholar] [CrossRef]
- Kim, J.; Hwang, I.; Kim, Y.H.; Moon, B.R. Genetic approaches for graph partitioning: A survey. In Proceedings of the 13th Annual Conference on Genetic and Evolutionary Computation, Dublin, Ireland, 12–16 July 2011; Association for Computing Machinery: New York, NY, USA, 2011; pp. 473–480. [Google Scholar] [CrossRef]
- Gagné, C.; Parizeau, M. Genericity in evolutionary computation software tools: Principles and case study. Int. J. Artif. Intell. Tools 2006, 15, 173–194. [Google Scholar] [CrossRef]
- Syswerda, G. Uniform Crossover in Genetic Algorithms. In Proceedings of the Third International Conference on Genetic Algorithms, Fairfax, WV, USA, 1 June 1989; pp. 2–9. [Google Scholar]
- Whitley, D.; Kauth, J. GENITOR: A different genetic algorithm. In Proceedings of the Rocky Mountain Conference on Artificial Intelligence, Saint Paul, MN, USA, 21–26 August 1988; pp. 118–130. [Google Scholar]
- Glover, F. Future paths for integer programming and links to artificial intelligence. Comput. Oper. Res. 1986, 13, 533–549. [Google Scholar] [CrossRef]
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V. Harmony search as a metaheuristic algorithm. J. Heuristic 2001, 6, 259–281. [Google Scholar] [CrossRef]
- Mumford, C.L. Simple Population Replacement Strategies for a Steady-State Multi-objective Evolutionary Algorithm. In Proceedings of the Genetic and Evolutionary Computation—GECCO 2004, Seattle, WA, USA, 26–30 June 2004; Deb, K., Ed.; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2004; Volume 3102, pp. 1360–1371. [Google Scholar] [CrossRef]
- Raidl, G.R.; Hu, B. Enhancing Genetic Algorithms by a Trie-Based Complete Solution Archive. In Proceedings of the Evolutionary Computation in Combinatorial Optimization (EvoCOP 2010), Istanbul, Turkey, 7–9 April 2010; Cowling, P., Merz, P., Eds.; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2010; Volume 6022, pp. 239–251. [Google Scholar] [CrossRef]
- Wang, Q.; Sang, C.; Ma, H.; Wang, C. A nonrevisiting genetic algorithm based on multi-region guided search strategy. Complex Intell. Syst. 2025, 11, 22. [Google Scholar] [CrossRef]
- Bui, T.N.; Moon, B.R. Genetic algorithm and graph partitioning. IEEE Trans. Comput. 1996, 45, 841–855. [Google Scholar] [CrossRef]
- Salhi, S. Defining tabu list size and aspiration criterion within tabu search methods. Comput. Oper. Res. 2002, 29, 67–86. [Google Scholar] [CrossRef]
- Talbi, E.G. A taxonomy of hybrid metaheuristics. J. Heuristics 2002, 8, 541–564. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).