Probability Density Function Distance-Based Augmented CycleGAN for Image Domain Translation with Asymmetric Sample Size

Abstract

Many image-to-image translation tasks face an inherent problem of asymmetry in the domains, meaning that one of the domains is scarce—i.e., it contains significantly less available training data in comparison to the other domain. There are only a few methods proposed in the literature that tackle the problem of training a CycleGAN in such an environment. In this paper, we propose a novel method that utilizes pdf (probability density function) distance-based augmentation of the discriminator network corresponding to the scarce domain. Namely, the method involves adding examples translated from the non-scarce domain into the pool of the discriminator corresponding to the scarce domain, but only those examples for which the assumed Gaussian pdf in VGG19 net feature space is sufficiently close to the GMM pdf that represents the relevant initial pool in the same feature space. In experiments on several datasets, the proposed method showed significantly improved characteristics in comparison with a standard unsupervised CycleGAN, as well as with Bootstraped SSL CycleGAN, where translated examples are added to the pool of the discriminator corresponding to the scarce domain, without any discrimination. Moreover, in the considered scarce scenarios, it also shows competitive results in comparison to fully supervised image-to-image translation based on the pix2pix method.

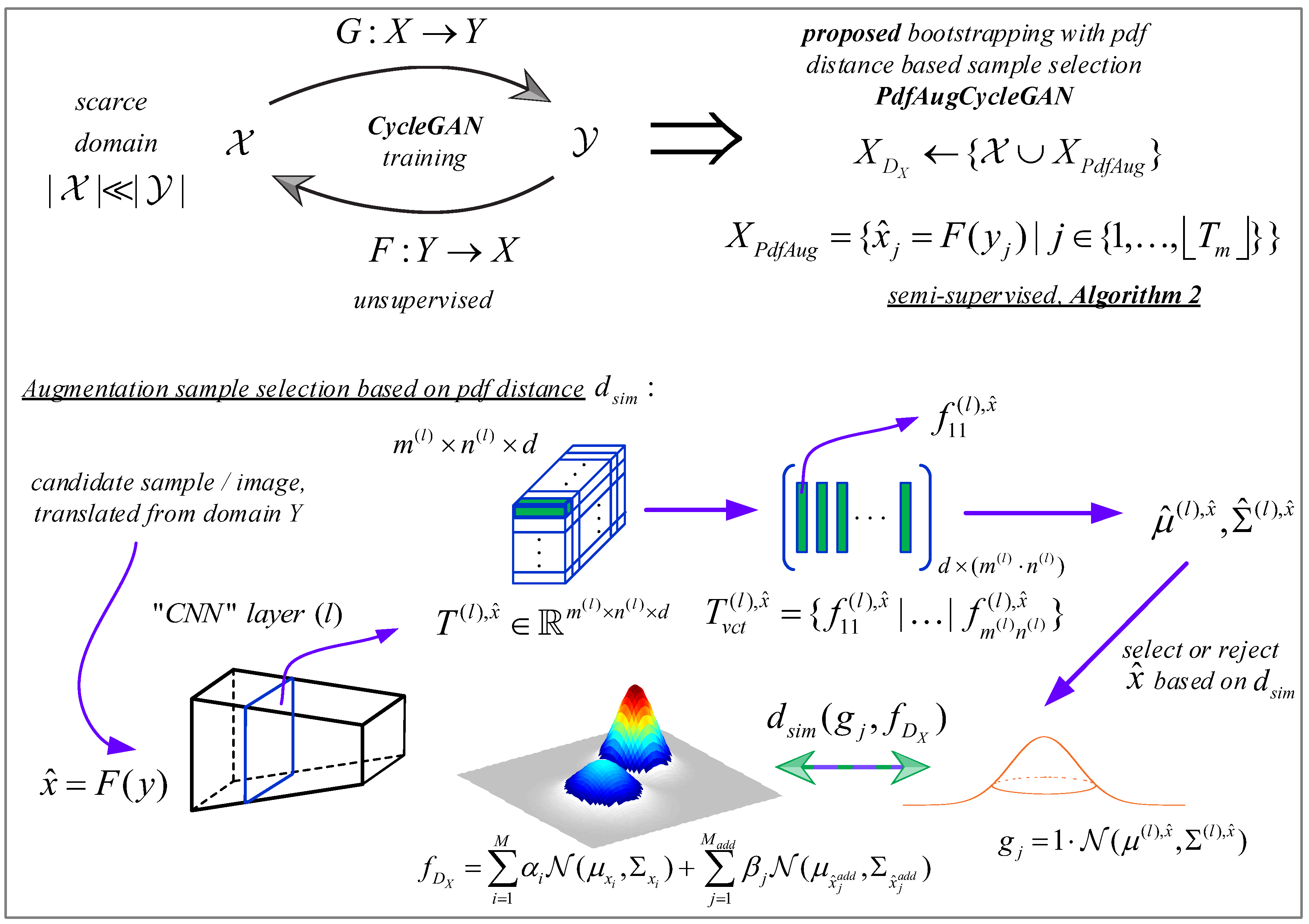
1. Introduction

Image-to-image (I2I) translation tasks are a key component of many image processing, computer graphics, and computer vision problems, as well as other similar problems. Some I2I methods that have been proposed are given in, for example, [1,2,3,4] for semantic image synthesis, [5,6,7,8] for image-to-image translation, and [9,10] for image super-resolution. They consist of constructing the mapping that translates images from one (source) domain to another (target) domain (or many of these), thus preserving the content of the image while the style of the image belonging to the first domain is changed to that of the second domain. The best performances of the I2I translations are obtained in the fully supervised training scenario, where in the training phase, all images in the source and the target (scarce) domain are assumed to be available in pairs (paired images). Those methods were developed first (see [11] for the pix2pix learning strategy) and are mostly based on conditional Generative Adversarial Networks (cGANs). However, the method was further developed by [12,13,14], whose solutions still failed to capture the complex structural relationships of scenes in cases when two domains had drastically different views while trying to achieve mapping through a single translation network. Moreover, despite improvements, the main drawback of supervised methods is related to the insufficient amount of paired image data that are available in most real-world I2I translation problems and the high cost of creating such datasets.

In order to cope with the previously mentioned problem, an unsupervised CycleGAN I2I method was proposed in [15]. It uses two GANs oriented in opposite directions, i.e., from one domain into another, and vice versa. The problem of highly under-constrained mappings, which are introduced in this approach, was dealt with by introducing a cycle consistency loss, which forces the mentioned mappings to be as close to bijective as possible. The method was proved to be very effective for preserving the semantic information of the data with respect to I2I translations, as well as other domain transfer tasks, such as the following: image-to-image translation [15], emotion style transfer [16], and speech enhancement [17]. Nevertheless, all of those mentioned, as well as many other domain transfer tasks, have inherent domain asymmetry, meaning that one of the domains has significantly less available training data (noted as scarce domain). There have been few studies reported in the literature devoted to resolving this problem. In [18], an augmented cyclic adversarial learning model that enforces the cycle consistency constraint via an external task-specific model is proposed. Additionally, in [19], the authors add semi-supervised task-specific attention modules to generate images that are used for improving performance in a medical image classification task. Recently, in [20], a bootstrapped SSL CycleGAN architecture was proposed, where the aforementioned problem was overcome using the following two strategies. Firstly, by using a relatively small percentage of available labeled training data from the reduced (scarce) domain and a Semi-Supervised Learning (SSL) approach, the method prevents overfitting of the discriminator belonging to the reduced domain, which would otherwise occur during initial training iterations due to the small amount of available training data in the scarce domain. Secondly, after initial learning guided by the described SSL strategy, additional augmentation of the reduced data domain is performed by inserting artificially generated training examples into the training poll of the data discriminator belonging to the scarce domain. Bootstrapped samples are generated by the neural network that performs the transfer from the fully observable domain to the scarce domain with its currently trained parameters. Moreover, in [21], the method for image translation is adapted for an application in which the fully observable image domain contains additional semantic information (in the form of associated text inputs). This presence of cross-modal information makes possible a different learning strategy design, in comparison to our method, which was designed and extensively tested for exclusively visual inputs. In [22], the fully observable domain has clearly distinguishable object classes, which correspond to similar categories, enabling fine-grained partitioning of the image domain into disjoint subsets (modes) for each of the known classes.

The problem of “imbalanced” or asymmetric sample size is also present in the tasks of training a multi-class classifier with an unequal number of training instances per category, e.g., in [23,24,25], where the CycleGAN model is used to compensate for an unequal number of training instances per category in different classification tasks that are of interest. However, these types of problems differ from the one investigated in this study.

In this work, we propose an extension of the methodology given in [20]. Namely, instead of just adding all of examples that are translated from the fully observable to the scarce domain (translated images of the training samples from the fully observable domain that do not have a pair in the scarce domain) and adding them to the training poll of the data discriminator belonging to the scarce domain, as implemented in [20], we implement this process selectively, in a more subtle manner. We actually add only those translated examples whose probability density function (pdf) in some predefined feature space is sufficiently close, in terms of distances or similarity measures between pdfs of feature vectors, to the pdf that represents the original pool of discriminator data in the scarce domain, obtained in the same feature space. To achieve an adequate feature space, we utilize a pre-trained VGG19 convolutional neural network (CNN) and extract feature maps from certain network layers [26].

The primary concept of the method proposed in this paper is to expand the pool of discriminator training samples in the scarce domain by adding translated images of unpaired samples from the fully observable domain. However, only images translated from the fully observable domain that have a pdf for their feature vectors (CNN-based image representations) that closely resembles (in terms of pdf similarity measure) the pdf of training samples that have already been assigned to the discriminator in the scarce domain (within the same CNN based feature space) will be included.

For the pdf representing the translated example that has the potential to be added to the pool of the discriminator of the scarce domain, we assume a multivariate Gaussian distribution and estimate its mean and covariance using the maximum likelihood (ML) method. On the other hand, for the pdf that represents the actual data from the discriminator pool (original images from the scarce domain), we assume a Gaussian mixture model (GMM) of their CNN-based representations with some small number of components, which is estimated over the same feature space obtained by the convolutional layers of the VGG19 CNN. Although several GMM similarity measures can be used to compare GMM pdfs, in this paper, we use one of the computationally most efficient [27,28,29]. The choice of feature space is also important. For this purpose, we chose the reshaped tensors representing convolutional feature maps from the layers of the pretrained VGG19 CNN proposed in [26] (e.g., see also [30,31]) as image features. The efficiency of this approach has already been demonstrated in various image recognition tasks, as well as image style transfer tasks (see [32,33,34]). Similar to what was done in [20], we use semi-supervised learning (SSL) on a predefined amount of available paired data to ensure that the generator performing translation to the scarce domain becomes sufficiently well trained. The initial SSL strategy that is based on a small set of paired observations allows the discriminator as well as the generator that are residing in the scarce domain to avoid overfitting and learn necessary parameters to some extent. After a sufficient number of iterations, the corresponding generator of the fully observable domain of the CycleGAN is periodically called to translate additional examples to the scarce domain (first phase of the propose bootstrapping process), from which some of them are chosen to be added in the training pool of the discriminator of the scarce domain (second phase), based on the previously mentioned pdf distance criteria.

This paper is organized as follows: In Section 2, we give a brief description of the baseline CycleGAN, first proposed in [15], as well as the bootstrapped SSL (BTS-SSL) CycleGAN proposed in [20]. In Section 3, the novel pdf distance-based augmented CycleGAN for asymmetric image domains (PdfAugCycleGAN further in the text) is proposed and described. In Section 4, the experimental results and comparisons of the proposed PdfAugCycleGAN to the baseline CycleGAN and BTS-SSLCycleGAN, as well as the fully supervised pix2pix method [11], are presented on several real datasets with varying amounts of data in the scarce domain. Finally, in Section 5, we provide the corresponding conclusions. The list of mathematical symbols is provided in Appendix A.

2. Baseline CycleGAN Methods

In [35], a non-parametric method called a Generative Adversarial Network (GAN) that learns the true data distribution based on competitive learning of two networks (generator and discriminator) was presented and has since quickly become ground-breaking in many applications of machine learning involving generative models. The key ingredient that underlies the game theoretic nature of the method is the Nash equilibrium, expressed by the minimax loss of the training procedure given by the following cross-entropy type loss:

$$\underset{G}{min}\underset{D}{max}{\mathbb{E}}_{y\sim p_Y\left(y\right)}ln\left(D\left(y\right)\right)+{\mathbb{E}}_{z\sim p_Z\left(z\right)}ln(1-D\left(G\left(z\right)\right))$$

(1)

Namely, adversarial training consists of the discriminator network D trying to discriminate between the synthetic samples artificially generated by the generator network G and the ground truth observations y available in the training data. Generator G is trying to deceive the discriminator by providing synthetic examples that are as similar as possible to the ground truth.

To perform I2I translation (and other domain transfer tasks), a supervised (using paired examples) version of the GAN architecture, named conditional GAN (cGAN), was proposed in [36] and applied to I2I in [11], named the pix2pix method. Namely, in contrast, conditional GANs learn a mapping from an observed image x and a random noise vector z to y, i.e., $G:(x,z)\to y$. Adversarial training is similar to the case of GAN, except that both the discriminator D and the generator G have input $(x,z)$, contrary to the case of an ordinary GAN network:

$$\underset{G}{min}\underset{D}{max}{\mathbb{E}}_{x\sim p_X\left(x\right),y\sim p_Y\left(y\right)}ln\left(D(x,y)\right)+{\mathbb{E}}_{x\sim p_X\left(x\right),z\sim p_Z\left(z\right)}ln(1-D(x,G(x,z))),$$

(2)

where $p_X$ and $p_Y$ are data distributions that correspond to domains X and Y, respectively, while $p_Z$ is a distribution of the latent variable z (commonly a normal distribution).

Although the pix2pix method showed superior performance in the presence of a large number of paired examples, in real applications, it is very hard to obtain such a large amount of labeled data, as this requires significant annotation effort, which is hard to obtain. The CycleGAN network emerged in [15] in order to perform I2I, as well as style transfer from one domain into another, without using any supervisor, i.e., paired data examples. This is done by invoking the cycle consistency loss in the overall loss function by designing two domain translators or mappers $G:X\to Y$ and $F:Y\to X$ in mutually opposite directions, where X and Y denote two image domains, i.e., style transfer domains. Cycle consistency loss encourages mappings F and G to be as close to a bijection (F and G are inverse to each other) to a sufficient extent, i.e., by making $G\left(F\right(y\left)\right)\approx y$, as well as $F\left(G\right(x\left)\right)\approx x$. It defines the diameter of the regions in X that are mapped by G to the same point $y\in Y$, and in principle, the same for F. If we denote the discriminator networks corresponding to domains X and Y by $D_X$ and $D_Y$, respectively, we utilize the following adversarial costs:

$$\begin{array}{ccc}& & {\mathcal{L}}_{adv}(G,D_Y)={\mathbb{E}}_{y\sim p_Y\left(y\right)}[ln\left(D_Y\left(y\right)\right)]+{\mathbb{E}}_{x\sim p_X\left(x\right)}(1-D_Y\left(G\left(x\right)\right))\hfill \\ & & {\mathcal{L}}_{adv}(F,D_X)={\mathbb{E}}_{x\sim p_X\left(x\right)}[ln\left(D_X\left(x\right)\right)]+{\mathbb{E}}_{y\sim p_Y\left(y\right)}(1-D_X\left(F\left(y\right)\right)),\hfill \end{array}$$

(3)

as well as the cycle consistency cost:

$${\mathcal{L}}_{cycle}(G,F)={\mathbb{E}}_{x\sim p_X\left(x\right)}{\parallel F\left(G\left(x\right)\right)-x\parallel }_{l_1}+{\mathbb{E}}_{y\sim p_Y\left(y\right)}{\parallel G\left(F\left(y\right)\right)-y\parallel }_{l_1},$$

(4)

so that the full optimization cost optimized by the learning strategy of CycleGAN as follows:

$$\mathcal{L}(G,F,D_X,D_Y)={\mathcal{L}}_{adv}(G,D_Y)+{\mathcal{L}}_{adv}(F,D_X)+{\lambda }_{cycle}{\mathcal{L}}_{cycle}(G,F),$$

(5)

where ${\lambda }_{cycle}>0$ controls the forcing of the cycle consistency.

The basic CycleGAN training procedure is given by the following pseudo-code in Algorithm 1:

Algorithm 1 CycleGAN training procedure

procedure CycleGAN     N—number of iterations; m—minibatch size; $\eta >0$, learning rate; $X\in \mathcal{X}$, $Y\in \mathcal{Y}$, unpaired or unlabeled training sets, such that $\left|X\right|\ll \left|Y\right|;$     Randomly initialize the parameters of the discriminators $D_X$, $D_Y$, and generators $G_{X\to Y}$, $G_{Y\to X}$: ${\theta }_{D_X}$, ${\theta }_{D_Y}$, ${\theta }_{G_{X\to Y}}$, ${\theta }_{G_{Y\to X}}$     for $k=1$ to N do         Sample minibatch of unpaired training data $\{x_1,\dots ,x_m\}\subset X$, $\{y_1,\dots ,y_m\}\subset Y$         ${\widehat{\mathcal{L}}}_{adv}(G_{X\to Y},D_Y)={\displaystyle \frac{1}{m}}{\sum }_{i=1}^{m}ln{D}_Y\left(y_i\right)+{\displaystyle \frac{1}{m}}{\sum }_{i=1}^{m}ln\left(1-D_Y\left(G_{X\to Y}\left(x_i\right)\right)\right)$         ${\widehat{\mathcal{L}}}_{adv}(G_{Y\to X},D_X)={\displaystyle \frac{1}{m}}{\sum }_{i=1}^{m}ln{D}_X\left(x_i\right)+{\displaystyle \frac{1}{m}}{\sum }_{i=1}^{m}ln\left(1-D_X\left(G_{Y\to X}\left(y_i\right)\right)\right)$         ${\theta }_{D_X}^{(k+1)}⟵{\theta }_{D_X}^{\left(k\right)}-\eta {\nabla }_{{\theta }_{D_X}}{\widehat{\mathcal{L}}}_{adv}(G_{Y\to X},D_X)$         ${\theta }_{D_Y}^{(k+1)}⟵{\theta }_{D_Y}^{\left(k\right)}-\eta {\nabla }_{{\theta }_{D_Y}}{\widehat{\mathcal{L}}}_{adv}(G_{X\to Y},D_Y)$         ${\theta }_{G_{Y\to X}}^{(k+1)}⟵{\theta }_{G_{Y\to X}}^{\left(k\right)}-\eta {\nabla }_{{\theta }_{G_{Y\to X}}}\left[{\widehat{\mathcal{L}}}_{adv}(G_{Y\to X},D_X)+{\lambda }_{cyc}{\mathcal{L}}_{cyc}(G_{X\to Y},G_{Y\to X})\right]$         ${\theta }_{G_{X\to Y}}^{(k+1)}⟵{\theta }_{G_{X\to Y}}^{\left(k\right)}-\eta {\nabla }_{{\theta }_{G_{X\to Y}}}\left[{\widehat{\mathcal{L}}}_{adv}(G_{X\to Y},D_Y)+{\lambda }_{cyc}{\mathcal{L}}_{cyc}(G_{X\to Y},G_{Y\to X})\right]$     end for end procedure

In the semi-supervised learning (SSL) case, i.e., in the case where there is a limited amount of paired (labeled) data, the additional SSL cost is added to (5), defined as follows:

$${\mathcal{L}}_{SSL}(G,F)={\displaystyle \frac{1}{\left|\mathcal{P}\right|}}\sum _{p\in \mathcal{P}}[\parallel G\left(x_p\right)-y_p{\parallel }_{l_1}+\parallel F\left(y_p\right)-x_p{\parallel }_{l_1}],$$

(6)

with $\mathcal{P}$ denoting set of indices of paired data samples. Thus, the overall cost of SSL CycleGAN is given as follows:

$$\begin{array}{ccc}\hfill \mathcal{L}(G,F,D_X,D_Y)& =& {\mathcal{L}}_{adv}(F,D_X)+{\mathcal{L}}_{adv}(G,D_Y)\hfill \\ & +& {\lambda }_{cycle}{\mathcal{L}}_{cycle}(G,F)+{\lambda }_{SSL}{\mathcal{L}}_{SSL}(G,F),\hfill \end{array}$$

(7)

with ${\lambda }_{SSL}>0$ controlling the influence of SSL cost on the overall cost.

Bootstrapped SSL CycleGAN for Asymmetric Domain Transfer

In order to deal with the mutually asymmetric domains, i.e., a problem where one of the domains involved in the translation task is scarce, meaning that it lacks a sufficient amount of data, Bootstrapped SSL CycleGAN (BTS-SSLCycleGAN) is proposed in [20]. It utilizes two concepts in addition to the standard CycleGAN. The first is SSL training, which uses cost (7) and assumes that some number of paired training samples is preventing overfitting of the discriminator network during the initial iterations of the learning process. The second concept is a bootstrapping strategy that aims to overcome the difference in the amount of training data between the scarce and non-scarce domains by artificially expanding the amount of the unlabeled training pool of the discriminator $D_X$ on the scarce domain X. This is achieved as follows.

In the initial phase of the training procedure, the parameters of the CycleGAN model are first optimized for some time using the previously mentioned SSL strategy. After the initial training of the generator $G_{Y\to X}$ (i.e., F), and when it is considered “reliable enough”, it is used as a bootstrapping sampler for data augmentation of the discriminator $D_X$. This is done by periodically translating a predefined percentage (sampled by uniform distribution) of available examples from the domain Y to the scarce domain X and adding those to the pool of the discriminator $D_X$, thus bootstrapping the statistics ${\widehat{p}}_X\left(x\right)$ of the scarce domain X, which approximates the ground truth $p_X\left(x\right)$.

3. Pdf Distance-Based Augmented CycleGAN

In this section, we propose and describe a novel method we call pdf distance-based augmented CycleGAN (PdfDistCycleGAN). In this approach, we expand on the previous idea of BTS-SSLCycleGAN by adding to the data pool of the discriminator $D_X$ of the scarce domain X only those translated samples from the domain Y which agree in some way, which we will specify soon in the text, and to some extent, to the currently estimated pdf ${\widehat{p}}_X\left(x\right)$ of the scarce domain X. We do this implicitly by measuring the similarity between the Gaussian pdf that corresponds to the particular bootstrapping sample translated from Y to X to the GMM that corresponds to the pool of the discriminator $D_X$ in some specified feature space. We specify the previous information as follows.

3.1. Proposed PdfAugCycleGAN Data Augmentation Process

We utilize the feature maps of the pretrained VGG19 convolutional network VGG19 Net, which is 19 layers deep and trained on the ImageNet database [30,31], to obtain the feature space in which pdf similarity is measured, i.e., the actual domain of $p_X$. For the translated example $\widehat{x}=F\left(y\right)$, for some particular $y\in Y$, we bring $\widehat{x}$ to the input of the instance of a pre-trained VGG19 CNN, and we use the obtained feature map tensor $T^{\left(l\right),\widehat{x}}\in {\mathbb{R}}^{m^{\left(l\right)}\times n^{\left(l\right)}\times d}$ from some specified l-th feature map level (or more of those). Thus, by vectorizing $T^{\left(l\right),\widehat{x}}$, we obtain the set of d dimensional feature vectors $T_{vct}^{\left(l\right),\widehat{x}}=\{f_{11}^{\left(l\right),\widehat{x}}|\dots |f_{m^{\left(l\right)}{n}^{\left(l\right)}}^{\left(l\right),\widehat{x}}\}$ from which, by assuming that these are generated by single multivariate Gaussian pdf $\mathcal{N}({\mu }^{\left(l\right),\widehat{x}},{\Sigma }^{\left(l\right),\widehat{x}})$, by using the ML technique [37,38], we obtain the estimates $({\widehat{\mu }}^{\left(l\right),\widehat{x}},{\widehat{\Sigma }}^{\left(l\right),\widehat{x}})$ of these as follows:

$$\begin{array}{ccc}& & {\widehat{\mu }}^{\left(l\right),\widehat{x}}={\displaystyle \frac{1}{m^{\left(l\right)}{n}^{\left(l\right)}}}\sum _{i=1}^{m^{\left(l\right)}}\sum _{j=1}^{n^{\left(l\right)}}{f}_{ij}^{\left(l\right),\widehat{x}}\hfill \\ & & {\widehat{\Sigma }}^{\left(l\right),\widehat{x}}={\displaystyle \frac{1}{m^{\left(l\right)}{n}^{\left(l\right)}-1}}\sum _{i=1}^{m^{\left(l\right)}}\sum _{j=1}^{n^{\left(l\right)}}\left(f_{ij}^{\left(l\right),\widehat{x}}-{\mu }^{\left(l\right),\widehat{x}}\right){\left(f_{ij}^{\left(l\right),\widehat{x}}-{\mu }^{\left(l\right),\widehat{x}}\right)}^T\hfill \end{array}$$

(8)

On the other hand, for the pool of existing training samples of the discriminator $D_X$ corresponding to the scarce domain X, we assign the Gaussian mixture pdf:

$$\begin{array}{ccc}& & f_{D_X}=\sum _{i=1}^M{\alpha }_i\mathcal{N}({\mu }_{x_i},{\Sigma }_{x_i})+\sum _{j=1}^{M_{add}}{\beta }_j\mathcal{N}({\mu }_{{\widehat{x}}_j^{add}},{\Sigma }_{{\widehat{x}}_j^{add}}),\hfill \\ & & {\alpha }_i,{\beta }_j\ge 0,\sum _{i=1}^M{\alpha }_i+\sum _{j=1}^{M_{add}}{\beta }_j=1,\mathrm{for} \mathrm{all}i,j\hfill \end{array}$$

(9)

where M is the number of original image examples $x_i$ of the pool corresponding to $D_X$, while $M_{add}$ is the number of translated examples ${\widehat{x}}_j^{add}=G\left(y_j\right)$, which have already been added to the pool corresponding to $D_X$. Estimates ${\mu }_{{\widehat{x}}_j^{add}}$ and ${\Sigma }_{{\widehat{x}}_j^{add}}$, corresponding to previously translated and added bootstrapping image samples ${\widehat{x}}_j$, are obtained using VGG19 features, as described by (8). The same also holds for original image samples $x_i$ in (9).

In this way, all parameters of single multivariate Gaussian distributions that make GMM are estimated exclusively from feature vectors of individual image samples. Thus, on the domain level, Gaussians corresponding to individual image samples are combined into a Gaussian mixture.

The actual mechanics of obtaining the component weights in GMM are given as follows. We assign ${\tilde{\alpha }}_i=\alpha ,i=1\dots ,M$, ${\tilde{\beta }}_j=\beta ,j=1,\dots ,M_{add}$, $\alpha >\beta >0$, with:

$$\begin{array}{ccc}& & {\alpha }_i={\displaystyle \frac{\widetilde{{\alpha }_i}}{{\sum }_{i=1}^M\widetilde{{\alpha }_i}+{\sum }_{j=1}^{M_{add}}\widetilde{{\beta }_j}}},i=1\dots ,M,\hfill \end{array}$$

(10)

$$\begin{array}{ccc}& & {\beta }_j={\displaystyle \frac{\widetilde{{\beta }_j}}{{\sum }_{i=1}^M\widetilde{{\alpha }_i}+{\sum }_{j=1}^{M_{add}}\widetilde{{\beta }_j}}},j=1,\dots ,M_{add},\hfill \end{array}$$

(11)

so that the constraints from the Equation (9) in the original manuscript still hold. Thus, we assign higher weights to the original examples belonging to the scarce domain, as we consider those to be more significant than the ones that are translated. We use $\beta ={\displaystyle \frac{1}{2}}\alpha$.

Another, more sophisticated approach is to weight individual contributions of the translated examples according to the distance of their corresponding Gaussians to the currently estimated GMM $f_{D_X}$ of the training samples that are already in the training pool of the discriminator in the scarce domain, which is given by Equation (9) in the original manuscript. Of course, in this case, we assign equal weights for all examples that are already in the training pool of the discriminator in the scarce domain X. One possible solution is given by the following weighting scheme:

$$\begin{array}{ccc}& & {\alpha }_i={\displaystyle \frac{1}{2M}},\hfill \end{array}$$

(12)

$$\begin{array}{ccc}& & {\beta }_j={\displaystyle \frac{1}{2}}{\displaystyle \frac{d_{sim}(g_j,f_{D_X})}{{\sum }_{\tilde{j}=1}^{M_{add}}{d}_{sim}(g_{\tilde{j}},f_{D_X})}},\hfill \end{array}$$

(13)

where $d_{sim}(·,·)$ denotes utilized GMM similarity measure (see Section 3.3), and $g_j$ is the Gaussian pdf obtained in VGG19 feature space, corresponding to the particular translated example ${\widehat{x}}_j\in X$, where it holds that ${\widehat{x}}_j=F\left(y_j\right)$, $y_j\in Y$. Thus, Equation (9) from the original manuscript still holds, but with more appropriate weight assignment. Nevertheless, in the experiments that we have conducted, we obtained unnoticeable differences in accuracy on the tested datasets. Therefore, we have presented only results with the weighting methodology presented in (10) and (11).

To decide whether or not the translated example ${\widehat{x}}_j$ is to be added to the pool of discriminator $D_X$, Figure 1, some particular GMM similarity measure $d_{sim}(g_j,f_{D_X})$ between the Gaussian $\mathcal{N}({\mu }_{{\widehat{x}}_j},{\Sigma }_{{\widehat{x}}_j})$, corresponding to the translated example ${\widehat{x}}_j$ (mixture is then defined as $g_j=1·\mathcal{N}({\mu }_{{\widehat{x}}_j},{\Sigma }_{{\widehat{x}}_j})$), and the mixture $f_{D_X}$, representing the pool of the discriminator $D_X$, is evaluated, where both mixtures are over the same specified CNN feature space (e.g., layer l values after forward pass in VGG19).

The adopted bootstrapping strategy (BTS) is that some predefined percentage P of the lowest score $d_{sim}(g_j,f_{D_X})$ translated examples, obtained via translation from unpaired examples $y_j$ belonging to the non-scarce domain Y, are added to the pool of discriminator $D_X$ periodically. We note that the parameters of the CNN implementing translation mapping F are the currently trained parameters, i.e., the parameters trained up to the moment when the translation of the novel examples into the scarce domain occurs.

Thus, the pool of discriminator $D_X$ is periodically boosted based on newly added images generated via image translation from the unpaired examples in the fully observable domain. The translation mapping is performed based on the currently determined parameters of the translation network, but only those translated examples that do not “spoil” the original distribution $p_X$ are added to the pool corresponding to $D_X$, thus preventing the presence of outliers in the augmentation process. Next, the generator $F:Y\to X$, as well as the discriminator $D_X$ are trained on the augmented pool of the discriminator $D_X$ by using the adversarial cost ${\mathcal{L}}_{adv}(F,D_X)$ from (3), as well as the cycle consistency cost (4) and SSL cost (7). This update is also made periodically, after the previously described process of data augmentation of the scarce domain X is finished.

3.2. PdfAugCycleGAN Training Procedure

Algorithm 2 begins by performing the SSL strategy, during the first $K_0$ out of N iterations to avoid overfitting of the discriminator of the scarce domain $D_X$. The previously described augmentation strategy is then invoked, and it is performed periodically. Here we formalize the training procedure of the previously proposed PdfAugCycleGAN based on the following pseudo-code in Algorithm 2.

We note that the proposed mechanism for the selection of new augmented training samples first preselects only the percent P of translated examples that have pdfs in VGG19 feature space and are the closest ones to the GMM corresponding to the samples already in the training pool of the discriminator in the scarce domain. Thus, the reported performance improvement of PdfAugCycleGAN in comparison to the baseline BTS-SSLCycleGAN comes from the fact that translated examples that can be considered as outliers for the discriminator training are excluded from the training pool in the case of PdfAugCycleGAN. In contrast, in baseline BTS-SSLCycleGAN, all samples translated from the fully observable domain are always included in the scarce domain discriminator training.

Algorithm 2 PdfAugCycleGAN training

procedure PdfAugCycleGAN     N—number of iterations; $K_0$—number of initial SSL iterations, $K_0\ll N$; K—period of the proposed bootstrapping strategy (BTS) repetition; $M_{SSL}=\left|{\mathcal{P}}_{data}\right|$, number of paired samples in ${\mathcal{P}}_{data}=\left\{(x_i^p,y_i^p)\right|i=1,\dots ,M_{SSL}\}=X_p\times Y_p$; $m_{SSL}$—SSL minibatch size, $m_{SSL}<M_{SSL}$; m—minibatch size after initial SSL phase; $P\in (0,1)$, percentage of unpaired samples translated from Y to X during the BTS minibatch that will be used to augment the original training pool corresponding to $D_X$; P controls the number of selected translated examples with the lowest score $d_{sim}(g_j,f_{D_X})$ of all the translated examples ${\widehat{x}}_j=G\left(y_j\right)$, which will be added to the training pool of $D_X$; $d_{sim}$ is a measure of similarity between GMMs; $\eta >0$, learning rate; $X_u\subset X$, $Y_u\subset Y$, unpaired training subsets, while $X_p\subset X,Y_p\subset Y$ are paired training subsets, such that $|Y_p|\ll |Y_u|$, $|X_p|\ll |X_u|$, and $\left|X\right|\ll \left|Y\right|$;     Randomly initialize the parameters of $D_X$, $D_Y$, and  $G_{X\to Y}$, $G_{Y\to X}$: ${\theta }_{D_X}$, ${\theta }_{D_Y}$, ${\theta }_{G_{X\to Y}}$, ${\theta }_{G_{Y\to X}}$     for $k=1$ to N do         Sample minibatch of unpaired training data $\{x_1,\dots ,x_m\}\subset X_u$, $\{y_1,\dots ,y_m\}\subset Y_u$         Sample minibatch of paired training data $\{(x_1^p,y_1^p),\dots ,(x_{m_{SSL}}^p,y_{m_{SSL}}^p)\}\subset X_p\times Y_p$         ${\mathcal{L}}_1={\widehat{\mathcal{L}}}_{adv}(G_{Y\to X},D_X)+{\lambda }_{cyc}{\mathcal{L}}_{cyc}(G_{X\to Y},G_{Y\to X})+{\lambda }_{SSL}{\widehat{\mathcal{L}}}_{SSL}(G_{X\to Y},G_{Y\to X})$         ${\mathcal{L}}_2={\widehat{\mathcal{L}}}_{adv}(G_{X\to Y},D_Y)+{\lambda }_{cyc}{\mathcal{L}}_{cyc}(G_{X\to Y},G_{Y\to X})+{\lambda }_{SSL}{\widehat{\mathcal{L}}}_{SSL}(G_{X\to Y},G_{Y\to X})$         ${\theta }_{D_X}^{(k+1)}⟵{\theta }_{D_X}^{\left(k\right)}-\eta {\nabla }_{{\theta }_{D_X}}{\widehat{\mathcal{L}}}_{adv}(G_{Y\to X},D_X)$         ${\theta }_{D_Y}^{(k+1)}⟵{\theta }_{D_Y}^{\left(k\right)}-\eta {\nabla }_{{\theta }_{D_Y}}{\widehat{\mathcal{L}}}_{adv}(G_{X\to Y},D_Y)$         ${\theta }_{G_{Y\to X}}^{(k+1)}⟵{\theta }_{G_{Y\to X}}^{\left(k\right)}-\eta {\nabla }_{{\theta }_{G_{Y\to X}}}{\mathcal{L}}_1$         ${\theta }_{G_{X\to Y}}^{(k+1)}⟵{\theta }_{G_{X\to Y}}^{\left(k\right)}-\eta {\nabla }_{{\theta }_{G_{X\to Y}}}{\mathcal{L}}_2$         if $\left((k>K_0)\wedge (((k-K_0)modK)==0)\right)$ then            Perform the augmentation of the training pool of discriminator $D_X$:            Sort all translated examples ${\widehat{x}}_j=G_{Y\to X}\left(y_j\right)$, $j\in \{1,\dots ,m\}$, by the increasing            values of $d_{sim}(g_j,f_{D_X})$, so that $\{{\widehat{x}}_j=G_{Y\to X}\left(y_j\right)\}$ is sorted in that manner, then            select the first $\lfloor Tm\rfloor$ that correspond to the percent P of the translated samples            from $Y_u$, i.e., $T_m=P\left|Y_u\right|$, and extend the training pool of $D_X$:            $X_{D_X}\leftarrow \{X\cup X_{PdfAug}\}$, $X_{PdfAug}=\{{\widehat{x}}_j=F\left(y_j\right)|j\in \{1,\dots ,\lfloor Tm\rfloor \}\}$         end if     end for end procedure

3.3. Measure of Similarity Between GMM Mixtures Used in Data Augmentation Process

The KL divergence, defined as $KL\left(p\right|\left|q\right)={\int }_{{\mathbb{R}}^d}p\left(x\right)ln{\displaystyle \frac{p\left(x\right)}{q\left(x\right)}}dx$, is the most natural measure between two probability distributions p and q. For the proposed pdf distance mentioned in the previous section, $d_{sim}$, we use the GMM similarity measure based on KL divergence between GMMs. Since it does not exist in closed form, an approximation based on the closed form expression for KL divergence between corresponding multivariate Gaussian components can be given by Equation (15).

Let us denote two GMMs as $f={\sum }_{i=1}^n{\alpha }_i{f}_i$ and $g={\sum }_{j=1}^m{\beta }_j{g}_j$, with $f_i=\mathcal{N}({\mu }_{f_i},{\Sigma }_{f_i})$ and $g_j=\mathcal{N}({\mu }_{g_j},{\Sigma }_{g_j})$ representing Gaussian components of the corresponding mixtures, with weights ${\alpha }_i\ge 0$, ${\beta }_j\ge 0$${\sum }_{i=1}^n{\alpha }_i=1$, ${\sum }_{j=1}^m{\beta }_j=1$. Terms ${\mu }_{f_i},{\mu }_{g_j}$ are means, while ${\Sigma }_{f_i},{\Sigma }_{g_j}$ are covariance matrices of $f_i$ and $g_j$. Then, the KL divergence between two Gaussian components $KL\left(f_i\right|\left|g_j\right)$ exists in the closed form given as follows:

$$\begin{array}{ccc}& & KL(f_i\left|\right|g_j)=ln{\displaystyle \frac{|{\Sigma }_{f_i}|}{|{\Sigma }_{g_j}|}}+Tr\left[{\Sigma }_{g_j}^{-1}{\Sigma }_{f_i}\right]+{({\mu }_{f_i}-{\mu }_{g_j})}^T{\Sigma }_{g_j}^{-1}({\mu }_{f_i}-{\mu }_{g_j})-d.\hfill \end{array}$$

(14)

Thus, the roughest approximation for KL divergence between GMMs, based on the convexity of the KL divergence, is given as follows:

$$KL\left(f\right|\left|g\right)\le K{L}_{WA}\left(f\right|\left|g\right)=\sum _{i,j}{\alpha }_i{\beta }_{j}KL(f_i\left|\right|g_j),$$

(15)

where $KL\left(f_i\right|\left|g_j\right)$, $i=1,\dots ,n$, $j=1,\dots ,m$ are given by (14).

For this paper, we use the approximation of the KL divergence between GMMs f and g based on averaging. Namely, GMMs f and g are replaced with multivariate Gaussians $\widehat{f}=\mathcal{N}({\mu }_{\widehat{f}},{\Sigma }_{\widehat{f}})$ nad $\widehat{g}=\mathcal{N}({\mu }_{\widehat{g}},{\Sigma }_{\widehat{g}})$ with

$$\begin{array}{ccc}& & {\mu }_{\widehat{f}}=\sum _i{\alpha }_i{\mu }_{f_i}\hfill \\ & & {\Sigma }_{\widehat{f}}=\sum _i{\alpha }_i\left({\Sigma }_{f_i}+({\mu }_{f_i}-{\mu }_{\widehat{f}}){({\mu }_{f_i}-{\mu }_{\widehat{f}})}^T\right).\hfill \end{array}$$

(16)

and similarly for g and $\widehat{g}$. Those estimates for $\widehat{f}$ and $\widehat{g}$ obtain minimum $KL\left(\tilde{f}\right|\left|\tilde{g}\right)$, with $\tilde{f},\tilde{g}$ in the class of multivariate Gaussians with a predefined dimension. Thus, the KL divergence between f and g is approximated by $KL\left(f\right|\left|g\right)\approx KL(\widehat{f},\widehat{g})$, where $KL(\widehat{f},\widehat{g})$ is evaluated using (14).

4. Experimental Results

In this section, we present the experiments obtained on several real-world datasets, in the problem of image translation: (1) Semantic label ↔ photo task on CityScapes dataset [11,39]. This dataset consists of 2975 training images of the size $128\times 128$, as well as an evaluation set for testing; (2) Architectural labels ↔ photo task [11,40] on the CMP Facade dataset, containing 400 training images; (3) Map ↔ aerial photo task on Google Maps dataset [11], containing 1096 training images of the size $256\times 256$.

The experimental setup for all datasets was designed to simulate an imbalanced, i.e., scarce domain scenario, where the left or the target domain X in the image translation task is considered scarce (with significantly less training data in comparison to the source domain Y). This is achieved using a setup in which only a certain percentage of the original left domain is used for I2I model training.

Each of the described experiments compares the proposed PdfAugCycleGAN image translation method against the following baseline methods: (1) original unsupervised CycleGAN proposed in [15], (2) fully supervised pix2pix method proposed in [11], (3) semi-supervised BTS-SSLCycleGAN method proposed in [20].

In order to compare the performance over the aforementioned tasks and datasets, we used Peak Signal-to-Noise Ratio (PSNR), as well as the more advanced Structural Similarity Index Measure (SSIM), which is a more advanced perception-based model that considers image degradation as perceived change in image structural information. The PSNR is evaluated as $PSNR=20log\left(MA{X}_I/\sqrt{MSE}\right)$, where $MA{X}_I$ is the maximum possible pixel value of the ground truth images, while $MSE$ is the squared Euclidean norm between the generated and ground truth images. The SSIM measure between generated images and ground truth images is calculated on various windows x, y of an image, as follows:

$$SSIM(x,y)={\displaystyle \frac{(2{\mu }_x{\mu }_y+c_1)(2{\sigma }_{xy}+c_2)}{({\mu }_x^2+{\mu }_y^2+c_1)({\sigma }_x^2+{\sigma }_y^2+c_2)}}$$

(17)

where ${\mu }_x$ and ${\mu }_y$ are the average values of x and y, while ${\sigma }_x^2$ and ${\sigma }_y^2$ are variances and $c_1$ and $c_2$ are constants, set as reported in [41].

4.1. Experimental Setup

Through all experiments (all datasets, all baselines, as well as the proposed method), we varied the percentage of the data that was considered as available in the scarce domain in the following steps: $25\%$, $50\%$, and $100\%$.

For the baseline BTS-SSLCycleGAN and the proposed PdfAugCycleGAN, in all experiments, after the initial $K_0$ iterations, during the next $k+K$ training iterations, where $K=50$, the examples from the fully observable (original) domain were transformed by $G_{Y\to X}$ and added to the training pool of the discriminator $D_X$ to perform the proposed data augmentation strategy (BTS). This periodical bootstrapping of the scarce domain during model training was done such that $20\%$ of randomly chosen examples (by uniform distribution) was generated for BTS-SSLCycleGAN in each BTS iteration.

For the proposed PdfAugCycleGAN, in each BTS iteration (on every K iteration of model training after $K_0$) the fixed percent of $50\%$ ($p=0.5$) of examples translated by $G_{Y\to X}$ with the lowest $d_{sim}(g_j,f_{D_X})$ score was selected for augmentation of the $D_X$ training pool, where $g_j$, $f_{D_X}$, and $d_{sim}$ are defined in Section 3.3 (these were the percents for which we obtained the best results). The described bootstrapping procedure was repeated (with the same rate as in the baseline BTS-SSLCycleGAN method), and new translated samples were periodically added into the training pool of the scarce domain X during the proposed CycleGAN model training strategy with sample selection based on pdf distance.

Since all the considered datasets originally contained paired images, we also used a fixed $20\%$ of paired training examples from the scarce domain for the initial semi-supervised learning stage of both BTS-SSLCycleGAN and PdfAugCycleGAN. The rest of the available data in the scarce domain were prepared in such a way that their corresponding pairs from the original dataset were discarded from the target domain in each of the experiments. In the asymmetric I2I translation task that was of the most interest for the proposed data augmentation method (scenario in which the total sample size of the scarce domain corresponds to only $25\%$ of original paired data), the result of the described setup was that only a relatively small amount of paired data was available for the SSL stage ($5\%$ of the original dataset), while the remaining $20\%$ of the available (unpaired) data in the scarce domain were reserved for the investigation of the proposed unsupervised model training strategy. Through sample selection involving pdf distance computation, Algorithm 2, the scarce domain was then periodically extended during the PdfAugCycleGAN model training procedure.

Considering the actual CycleGAN generator network architecture, we used the one originally proposed in [15] and also utilized in [17], as well as in [20]. It contains two stride-2 convolutions, several residual blocks, and two fractionally strided convolutions (stride ${\displaystyle \frac{1}{2}}$). It also utilizes six blocks for $128\times 128$ and nine blocks for $256\times 256$ and higher-resolution type images and also instance normalization, as in [15,42,43]. Considering the discriminator network, we used $70\times 70$ PatchGAN.

Considering the VGG19 network used in the evaluation of image feature maps and the construction of corresponding pdfs $g_j$, $f_{D_X}$, on which the computation of the selection score $d_{sim}(g_j,f_{D_X})$ is based, we use the standard pretrained VGG19, as described in Section 3.1 (see also [26]).

Considering the training procedure, instead of the loss function in Equation (3), we used a more stable $L_2$ adversarial loss (as reported in [44]). We also use the history of 50 generated images in order to calculate the average score. For all experiments, we used ${\lambda }_{cyc}={\lambda }_{SSL}=10$, $m=m_{SSL}=50$ with a learning rate $\eta =0.0002$, which was kept constant during the first 100 epochs, linearly decaying to zero during the next 100 epochs. Network parameters were initialized by using random samples drawn from the normal distribution $\mathcal{N}(0,0.02)$.

4.2. Result Analysis and Discussion

In

Table 1. Experimental comparison between proposed PdfAugCycleGAN and the baseline CycleGAN, BTS-SSLCycleGAN, and fully supervised pix2pix, under different scenarios: varying sample size ${\mathcal{S}}_X$ of scarce domain $\mathcal{X}$, as well as when applied to different tasks/datasets—CityScapes, Facade dataset, Google Maps. Bold values indicate better performance among the last two methods.

	${\mathcal{S}}_{\mathit{X}}$	pix2pix		CycleGAN		BTS-SSLCycleGAN		PdfAugCycleGAN
	[%]	PSNR	SSIM	PSNR	SSIM	PSNR	SSIM	PSNR	SSIM
CityScapes	25	19.89	0.60	17.20	0.56	18.77	0.61	19.10	0.64
	50	20.45	0.64	17.00	0.55	19.04	0.64	19.22	0.67
	100	19.51	0.59	17.12	0.54	20.47	0.65	21.23	0.68
Facade dataset	25	13.78	0.35	10.93	0.25	11.83	0.32	12.14	0.34
	50	14.24	0.40	11.00	0.25	13.75	0.40	13.92	0.42
	100	14.25	0.42	10.98	0.27	13.21	0.41	13.57	0.43
Google Maps	25	30.35	0.67	30.47	0.71	31.20	0.77	30.90	0.76
	50	30.55	0.68	29.78	0.72	30.88	0.79	30.21	0.76
	100	30.01	0.69	30.24	0.73	31.23	0.81	30.89	0.79

, the experimental results of the proposed PdfAugCycleGAN in comparison to the baseline pix2pix, CycleGAN, and BTS-SSLCycleGAN are presented in terms of PSNR and SSIM measures on several databases.

It can be seen that, in the majority of experiments involving unpaired (unsupervised) or semi-supervised I2I translation tasks, the proposed PdfAugCycleGAN obtained improvements in comparison to the baseline BTS-SSLCycleGAN, as well as the classical CycleGAN method, in both PSNR as well as SSIM measures. More specifically, in experiments obtained on CityScapes and Facade datasets, the proposed PdfAugCycleGAN obtained better results in comparison to all baseline methods, while in experiments on the Google Maps dataset, the BTS-SSLCycleGAN performed slightly better, i.e., for that particular dataset, the proposed selective bootstrapping methodology failed to improve the I2I translation results. However, the proposed PdfAugCycleGAN did achieve better PSNR performance on the particular dataset in the I2I translation scenario with the smallest sample size of the scarce domain X.

In general, the reported PSNR advantage of PdfAugCycleGAN over BTS-SSLCycleGAN is always present under the challenging scenario of a small sample size of X (when only $25\%$ of dataset samples was considered as available for the experiment), and even higher in the case of other I2I tasks and datasets.

Besides the unfavorable I2I translation scenario with asymmetric sample size, where PdfAugCycleGAN outperformed the competing BTS-SSL on both CityScapes and Facade datasets (thanks to the proposed selective approach to data augmentation), in the case of the same sample size (${\mathcal{S}}_X=100\%$ in Table 1), PdfAugCycleGAN also achieved better performance in comparison to the fully supervised pix2pix method, which further justifies the proposed selective BTS strategy.

Overall, the results in Table 1 confirm that the proposed more subtle handling of the translated examples, concerning whether those should be added into the pool of the discriminator $D_X$ of the scarce domain, can improve the performance of the augmented CycleGAN system.

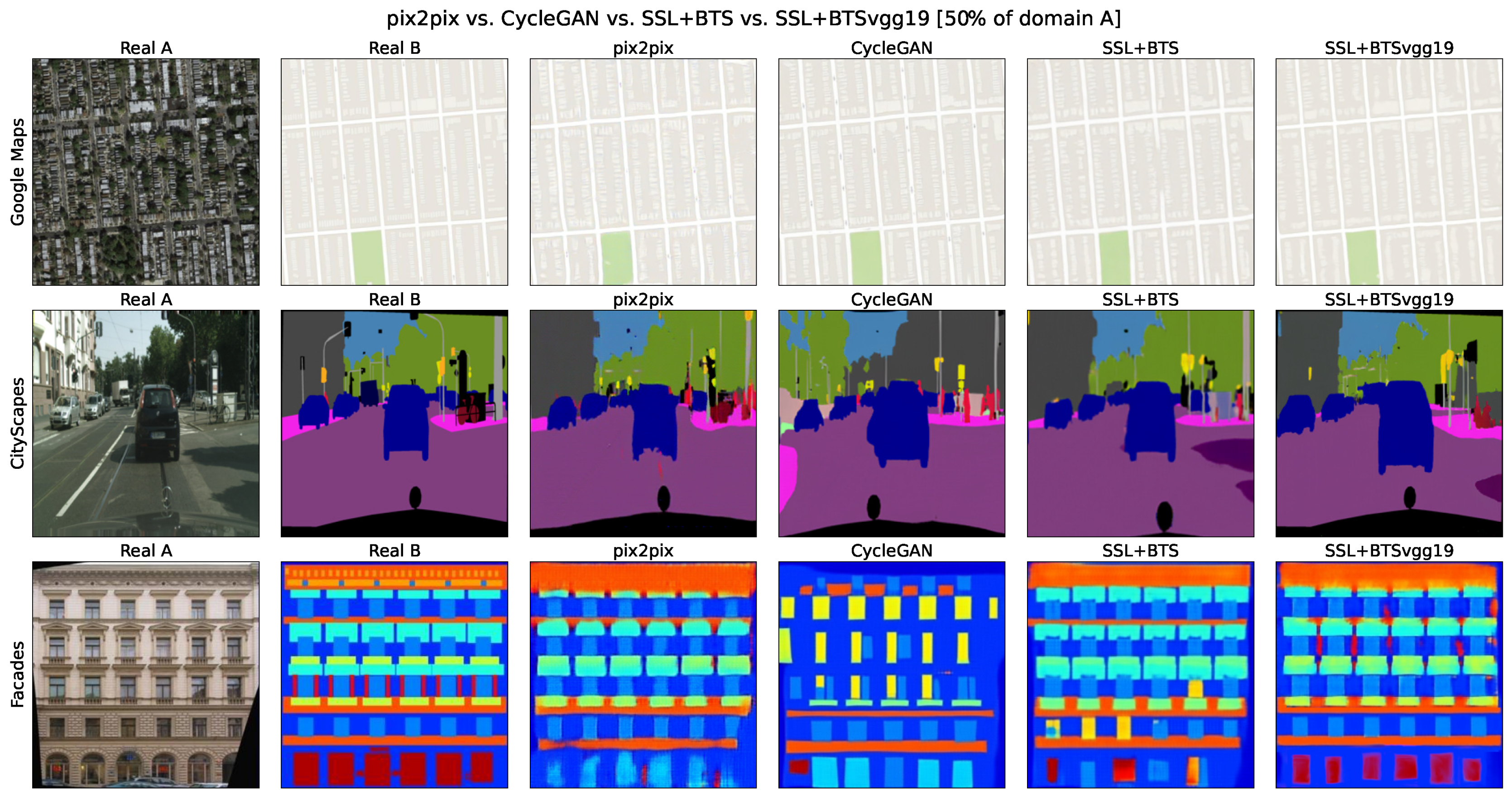
In Figure 2, visual examples are given for the proposed PdfAugCycleGAN vs. baseline CycleGAN, semi-supervised BTS-SSLCycleGAN, and fully supervised pix2pix algorithm comparisons for $50\%$ of the scarce domain data used. Real A (fully observable domain) and Real B (scarce, target domain) correspond to image pair examples. Examples are shown for Google Maps, CityScapes, and Facade datasets. It can be seen that in these examples, the proposed PdfAugCycleGAN obtains visually more accurate results than the baseline methods.

Based on additional analysis of reported values of PSNR [dB] and SSIM in Table 1, which are shown in Figure 3 we can also observe the following.

The relative gain $\gamma$ of the proposed PdfAugCycleGAN is consistently positive in comparison to competing baseline methods (CycleGAN and BTS-SSLCycleGAN) when measured over CityScapes and Facade datasets under all training data conditions (25%, 50%, and 100% of available training data). It is computed as the normalized difference of the performance metric values:

$$\begin{array}{c}\hfill \gamma =\frac{\zeta \left(\mathit{PdfAugCycleGAN}\right)-\zeta \left(\mathit{baseline}\right)}{\zeta \left(\mathit{baseline}\right)}·100\%,\end{array}$$

(18)

where $\zeta (·)$ denotes either PSNR or SSIM metric, i.e., performance values corresponding to the proposed PdfAugCycleGAN and selected baseline method of interest.

From the presented results, it is also possible to see that this gain is not significantly lower in the case of the 25% scenario in comparison to the 50% and 100% experiments in the case of comparisons with the CycleGAN and BTS-SSLCycleGAN methods. However, in the case of certain experiments where the evaluation of the proposed method is performed over the Google Maps dataset, the obtained relative gain against BTS-SSLCycleGAN was negative, as shown in Figure 3. The values indicate that the proposed method, for CityScapes and Facade datasets, provides consistent improvement with respect to BTS-SSLCycleGAN, including a relative increase of PSNR in the range of 1.2–3.7%, and a relative increase of SSIM in the range of 4.6–6.2%. Losses are observed for the Google Maps dataset, less than 2.2% for PSNR and less than 3.8% for SSIM. Slightly lower performance metrics on the Google Maps dataset can be explained by the fact that the proposed augmented model training is utilizing sample selection that is dependent on VGG19 feature space. This means that pdf estimation is relying on a feature extraction CNN that is pre-trained on natural image scenes, which are completely different from the satellite image scenes present in the Google Maps dataset. Thus, the proposed pdf distance computation is to some extent dependent on the type of images (scenes) on which the pre-trained feature extraction network is trained. Therefore, the proposed adaptive augmentation of the scarce domain in PdfAugCycleGAN is affected by the characteristics of the selected pre-trained feature space (character of the side information). This leads to better results over CityScapes and Facade datasets in comparison to Google Maps, which has a different type of scenes (significantly different from the ones on which VGG19 was trained).

At the end, we note that other limitations could also come from the choice and type of the training datasets and methods, e.g., the authors in [21,22] use dataset types which are problem-specific and significantly different from the ones used in the presented experiments (presence of cross-modal semantic information or clearly distinguishable classes), as already discussed in Section 1.

5. Conclusions

In this paper, we have proposed a novel approach for the CycleGAN training strategy in the case of unfavorable domain translation scenarios in which the original data domain has a substantially smaller number of samples in comparison to the target data domain. The method is based on periodical boosting of scarce domain statistics through data augmentation based on selective sampling of novel data samples generated via domain translation from the fully observable domain. The described data augmentation and learning are performed in a fully unsupervised manner, after a short initial semi-supervised stage that prevents the overfitting of the discriminator network in the scarce data domain. This process is periodically repeated throughout the model training process and significantly improves the overall model performance in comparison to the unsupervised learning baseline. In comparison to the similar previously proposed semi-supervised learning strategy, which also relies on data augmentation through transfer of samples from the fully observable domain, the proposed method achieves selective bootstrapping and thus better performance in cases when the sample size in the scarce domain is several times smaller than the number of samples in the fully observable domain.

In addition to the training strategy, this paper also proposes a novel sample selection criterion based on pdf distance between distributions of feature vectors corresponding to learned image representations obtained by a pretrained CNN. Thus, the proposed similarity measure between the specific sample and the pool of existing samples in the system could also apply to other types of problems involving adaptive sample selection or distance computation in the learned feature space characteristic for some specific signal modality.

The presented results also confirm that selective or more subtle strategies for data augmentation could be a key for more efficient model learning in the case of imbalanced domain translation tasks.