On the Total Version of Triple Roman Domination in Graphs

Abstract

In this paper, we describe the study of total triple Roman domination. Total triple Roman domination is an assignment of labels from $\{0,1,2,3,4\}$ to the vertices of a graph such that every vertex is protected by at least three units either on itself or its neighbors while ensuring that none of its neighbors remains unprotected. Formally, a total triple Roman dominating function is a function $f:V\left(G\right)\to \{0,1,2,3,4\}$ such that $f\left(N\right[v\left]\right)\ge |AN(v)|+3$, where $AN\left(v\right)$ denotes the set of active neighbors of vertex v, i.e., those assigned a positive label. We investigate the algorithmic complexity of the associated decision problem, establish sharp bounds regarding graph structural parameters, and obtain the exact values for several graph families.

1. Introduction

This study introduces a variation of the Roman domination problem in graphs. In previous works, we explored the $\left[k\right]$-Roman domination model, which involves defending against single attacks that require at least k units, focusing on the $k=3$ case. In this work, we extend the model by ensuring that stronger vertices, i.e., those with some legion deployed on them, are not isolated.

The Roman domination model originates from Emperor Constantine I’s defensive strategies [1,2,3,4]. His defensive strategy aimed to position the smallest possible number of legions across the empire while ensuring that each city housed between 0 and 2 legions. Cities without legions had to be adjacent to at least one city with two legions that could provide protection without remaining unprotected itself. This was first modeled by Cockayne et al. [5] in 2004. Since then, many variants have been studied to enhance its efficiency [6,7,8,9,10].

This model assigns labels $\{0,1,2\}$ to cities based on the number of legions. A city labeled with 0 must be adjacent to a city labeled with 2 to ensure defense without leaving other cities unprotected. This defines a Roman dominating function (RDF), and its minimum weight is called the Roman domination number, ${\gamma }_R\left(G\right)$.

A total dominating set S in a graph G guarantees that any vertex has a neighbor in S. Liu et al. [11] introduced the total Roman domination number for graphs without isolated vertices, denoted ${\gamma }_{tR}\left(G\right)$, which minimizes the weight of an RDF, making sure that the set of vertices with a positive label form a total dominating set.

The double Roman domination, introduced by Beeler et al. [12], uses labels $\{0,1,2,3\}$, ensuring that two legions can defend each city. Shao et al. [13] and Hao et al. [14] extended this to total double Roman domination, combining both conditions.

Ahangar et al. [15] introduced the $\left[k\right]$-Roman domination model, focusing on the $k=3$ case, called triple Roman domination. This assigns labels $\{0,1,\dots ,k+1\}$ to vertices such that each vertex with $f\left(u\right)<k$ satisfies $f\left(N\right[u\left]\right)\ge k+|AN(u)|$, where $AN\left(u\right)$ stands for the active neighbors (neighbors with a positive label) of u. The minimum weight of such a function is the $\left[k\right]$-Roman domination number, ${\gamma }_{\left[kR\right]}\left(G\right)$. Hajjari et al. [16] provided bounds, including ${\gamma }_{\left[3R\right]}\left(G\right)\le {\displaystyle \frac{3n}{2}}$ for graphs with $\delta \left(G\right)\ge 2$.

The concept of total domination can be incorporated into the triple Roman domination model to prevent there being isolated vertices among labeled ones, strengthening the network at the potential cost of higher expense.

A total triple Roman dominating function (t3RDF) satisfies both triple Roman domination and secures no isolated vertices in the induced subgraph by vertices with positive labels. The total triple Roman domination number, ${\gamma }_{\left[t3R\right]}\left(G\right),$ is the minimum weight of a t3RDF.

This paper introduces the total triple Roman domination model. We examine the algorithmic complexity of the decision problem, provide bounds, describe extremal graphs, and find exact values for several graph families.

The rest of this paper is organized as follows: Section 2 establishes the necessary notation and preliminaries. In Section 3, we prove the NP-completeness of the associated decision problem, even for bipartite graphs. Section 4 presents sharp bounds for the total triple Roman domination number in terms of structural parameters like maximum degree and girth. Section 5 derives exact values for specific graph families, including paths and cycles. Finally, Section 6 discusses the implications of our results and suggests future research directions.

2. Notation

Throughout this paper, we consider simple, finite, and undirected graphs. Let $G=(V,E)$ be a graph with vertex set $V\left(G\right)$ and edge set $E\left(G\right)$. The order of a graph G is the number of vertices, denoted by $|V(G)|$, and the size of the graph is the number of edges. The degree of a vertex v, denoted $d_G\left(v\right)$ or simply $d\left(v\right)$ when no confusion is possible, is the number of edges incident to v. The maximum degree and minimum degree of G are denoted by $\Delta \left(G\right)$ and $\delta \left(G\right)$, respectively. The neighborhood of a vertex v in a graph G is the set of all vertices adjacent to v, denoted by $N\left(v\right)$. A vertex v is called an isolated vertex if it has no adjacent vertices, i.e., if its neighborhood is empty, $N\left(v\right)=\varnothing$. The closed neighborhood of a vertex v is denoted by $N\left[v\right]$, and it is defined as $N\left(v\right)\cup \left\{v\right\}$. The induced subgraph $G\left[S\right]$ of a graph G is formed by a subset $S\subseteq V\left(G\right)$ of vertices, along with all edges in G that have both endpoints in S. A graph is regular if all of its vertices have the same degree, that is, it is k-regular if each vertex has degree k. A universal vertex in a graph is a vertex that is adjacent to all other vertices in the graph, meaning its degree is $|V(G)|-1$, where $|V(G)|$ is the number of vertices in the graph.

A path $P_n$ on length $n-1$ is a graph with n vertices arranged in a linear sequence, where each vertex (except the endpoints) has a degree of 2. A cycle $C_n$ of length n is a graph with n vertices forming a closed path, where each vertex has a degree of 2. The girth of a graph is defined as the length of the shortest cycle in the graph. If no cycles exist, the girth is said to be infinite. The distance between two vertices u and v, denoted by $d(u,v)$, is the length of a shortest path with end-vertices u and v. A set of vertices that is a k-independent set is where every pair of vertices of the set are at a distance, as least k. The star graph$S_{1,q}$ consists of a central vertex adjacent to q leaves. A tree is a connected graph containing no cycles. A graph is said to be connected if there is a path between every pair of vertices. From now on, we refer to a non-trivial connected graph as an ntc-graph. The complete graph $K_n$ has an edge between every pair of vertices and the complete bipartite graph $K_{p,q}$ consists of two disjoint sets of vertices of orders p and q, where each vertex in one set is adjacent to all vertices in the other set.

A leaf is a vertex of degree one. A weak support vertex is a vertex adjacent to a leaf, while a strong support vertex is a vertex adjacent to at least two leaves.

The corona product of two graphs G and H, denoted by $G\circ H$, is obtained by taking one copy of G, called the center graph, and a number of copies of H equal to the order of G. Then, each copy of H is assigned a vertex in G, and that one vertex is attached to each vertex in its corresponding H copy by an edge (see Figure 1).

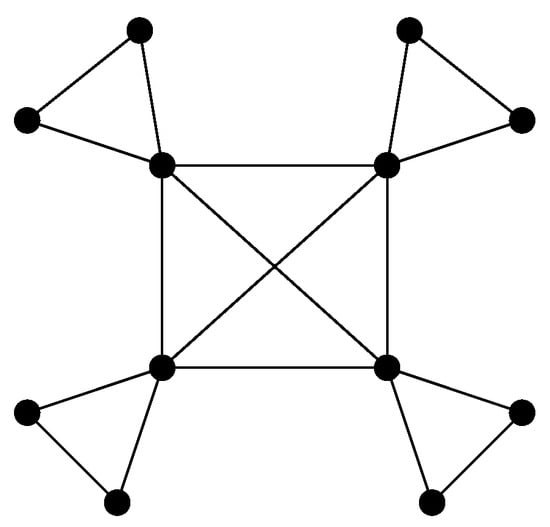
Figure 1. The corona product $K_4\circ K_2.$

Regarding domination in graphs, a dominating set (for short, d-set) of G is a set $D\subseteq V\left(G\right)$ such that every vertex in $V\left(G\right)\setminus D$ has a neighbor in D. The domination number $\gamma \left(G\right)$ is the minimum cardinality of a dominating set. A γ-set is a dominating set with cardinality equal to $\gamma =\gamma \left(G\right).$ A Roman dominating function on G (for short, RDF) is a function $f:V\left(G\right)\to \{0,1,2\}$ such that every vertex with $f\left(v\right)=0$ has a neighbor u with $f\left(u\right)=2$. The Roman domination number (RDN) ${\gamma }_R\left(G\right)$ is the minimum weight ${\sum }_{v\in V\left(G\right)}f\left(v\right)$ over all such functions. A $\left[k\right]$-Roman dominating function (kRDF) is a function $f:V\left(G\right)\to \{0,1,\dots ,k+1\}$ satisfying the stronger condition that every vertex v with $f\left(v\right)<k$ has at least one neighbor u with $f\left(N\right[u\left]\right)\ge k+|AN(u)|$. A total triple Roman dominating function (t3RDF) is a 3RDF such that the set of vertices with a positive label induces an isolated-free subgraph. Analogously, the total triple Roman domination number (t3RDN) of a graph G is denoted by ${\gamma }_{\left[t3R\right]}\left(G\right)$.

In Figure 2, we can find two total triple Roman dominating functions in a graph G. We may readily check that the one depicted on the right has the minimum weight.

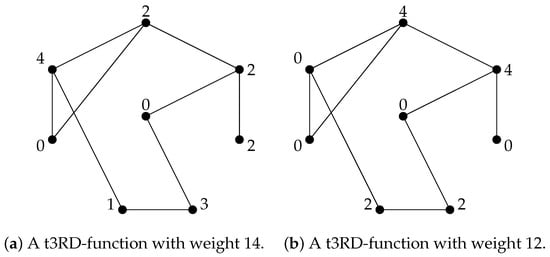
Figure 2. Two different total triple Roman dominating functions.

All notation follows the standard conventions in graph theory.

3. Complexity

The goal of this section is to prove that the total triple Roman domination decision problem (t3RDP) is NP-complete even for bipartite graphs.

We prove this by showing the equivalence of any instance of the t3RDP with an instance of one of the Exact 3-Cover (X3C) problem. Formally, we consider the following decision problems:

• $\mathit{t}\mathbf{3}\mathit{RDP}$ PROBLEM
• Instance: Graph $G=(V,E)$ and a positive integer K.
• Question: Does G have a t3RD function f with $f\left(V\right)\le K$?
• X3C PROBLEM
• Instance: A finite set $X,$ $|X|=3q,$ and a collection C of 3-element subsets of X.
• Question: Does there exist a subset $C^{\prime }\subseteq C$ such that every element of X appears in exactly one element of $C^{\prime }$?

Proposition 1.

t3RDP is $NP$-complete for bipartite graphs.

Proof. 

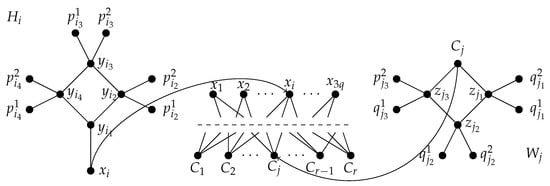
We can readily prove that t3RDP is in the NP-class because any potential solution can be verified in polynomial time. We now show that converting any instance of X3C to an instance of t3RDP results in equivalent solutions for both problems. Consider $X=\{x_1,x_2,\dots ,x_{3q}\}$ and $C=\{C_1,C_2,\dots ,C_r\}$, an instance $(X,C)$ of X3C. For each $x_i\in X$, we include a gadget $H_i$ by adding two pendant vertices $\{p_{ik}^1,p_{ik}^2\}$ to each vertex $y_{ik}$ for $k=2,3,4$ of the cycle $\{y_{i1},y_{i2},y_{i3},y_{i4}\}$. Additionally, for each $C_j\in C$, we construct the gadget $W_j$ by adding two pendant vertices $\{q_{jl}^1,q_{jl}^2\}$ to each vertex $z_{jl}$ of the path $\{z_{j1},z_{j2},z_{j3}\}$.

We construct the graph $\Gamma =\Gamma (X,C)$ as follows: We start with a bipartite graph where the vertex set consists of $X\cup C$. Each $x_i\in X$ is adjacent to a vertex $C_j\in C$ if and only if $x_i$ is one of the three elements belonging to the 3-element subset $C_j$ (i.e., $C_j=\{x_{j_1},x_{j_2},x_{j_3}\}$ and $x_i\in \{x_{j_1},x_{j_2},x_{j_3}\}$). We then incorporate the gadgets $H_i$ by adding an edge between $x_i$ and $y_{i1}$ for $i=1,\cdots ,3q$. Similarly, we attach the gadgets $W_j$ to $\Gamma$ by adding edges joining the vertices $\{C_j,z_{j1}\}$ and $\{C_j,z_{j3}\}$, respectively, for $j=1,\cdots ,r$ (see Figure 3).

Figure 3. Gadgets attached to $x_i$ and $C_j$ when constructing the bipartite graph $\Gamma$.

Clearly, the constructed graph is bipartite with vertex classes

$$\{x_i,y_{i_2},y_{i_4},p_{i_3}^1,p_{i_3}^2:1\le i\le 3q\}\cup \{z_{j_1},z_{j_3},q_{j_2}^1,q_{j_2}^2:1\le j\le r\}$$

and

$$\{y_{i_1},y_{i_3},p_{i_2}^1,p_{i_2}^2,p_{i_4}^1,p_{i_4}^2:1\le i\le 3q\}\cup \{C_j,z_{j_2},q_{j_1}^1,q_{j_1}^2,q_{j_3}^1,q_{j_3}^2:1\le j\le r\}.$$

Now, assume that there exists $C^{\prime }\subseteq C$, which is an exact cover for the set $X.$ Let f be a function over the vertices of $\Gamma$, defined as follows: $f\left(v\right)=4$ if

$$v\in \{C_j:C_j\in C^{\prime }\}\cup \{y_{i_k}:1\le i\le 3q,2\le k\le 4\}\cup \{z_{j_l}:1\le j\le r,1\le l\le 3\}$$

and $f\left(v\right)=0$ otherwise. Since $C^{\prime }$ is a solution of the X3C for the instance $(X,C),$ we may deduce that $|C^{\prime }|=q$. On the other hand, $f\left(N\right[v\left]\right)\ge |AN(v)|+3$ for all $v\in V(\Gamma )$ and the induced subgraph by the set of vertices with a positive label has no isolated vertices. Hence, f is a t3RD function with $w\left(f\right)=f\left(V\right(\Gamma \left)\right)=40q+12r.$

To complete the proof, suppose that f is a t3RDF with $f\left(V\right(\Gamma \left)\right)\le 40q+12r.$ Since $f\left(y_{i_k}\right)$ are support vertices and f is a t3RDF, we may assume that $f\left(v\right)=4$ for all $v\in \{y_{i_k}:1\le i\le 3q,2\le k\le 4\}.$ Analogously, without loss of generality, we may assume that $f\left(v\right)=4$ for $v\in \{z_{j_l}:1\le j\le r,1\le l\le 3\}.$

If $f\left(y_{i_1}\right)\ne 0$ for some $1\le i\le 3q$, then we may define a new function $f^{*}$ as follows: $f^{*}\left(y_{i_1}\right)=0$, $f^{*}\left(C_{j_i}\right)=min\{f\left(C_{j_i}\right)+f\left(y_{i_1}\right),4\}$, where $C_{j_i}$ is a clause containing $x_i$. As the vertex $y_{i_1}$ is total triple dominated by any of the vertices $y_{i_k},$ with $k=2,3,4,$ we have that $f^{*}$ is a t3RDF with weight at most $f\left(V\right)$. So, we may assume that $f\left(y_{i_1}\right)=0$ for all $i=1,\dots ,3q.$

Analogously, if $f\left(x_i\right)\ne 0$ for some $1\le i\le 3q$, the function $f^{*}\left(x_i\right)=0$, $f^{*}\left(C_{j_i}\right)=min\{f\left(C_{j_i}\right)+f\left(x_i\right),4\}$, where $C_{j_i}$ is a clause containing $x_i$. Since the vertices $C_j$ are adjacent to both $z_{j_k},$ with $k\in \{1,3\}$, then we have that $f^{*}$ is a t3RDF with weight at most $f\left(V\right)$. Then, we may assume that $f\left(x_i\right)=0$ for all $i=1,\dots ,3q.$

In such a case, we have that $f\left(V(\Gamma )\right)=12r+36q+{\sum }_{1\le j\le r}f\left(C_j\right)\le 40q+12r,$ which implies that ${\sum }_{1\le j\le r}f\left(C_j\right)\le 4q.$

Let $C^{\prime }$ be $\{C_j:f\left(C_j\right)=4\}$ and suppose that $|C^{\prime }|=s<q.$ Then, the number of vertex $x_i\in X$ with a neighbor in $C^{\prime }$ is at most $3s.$ As a result, $|x_i:N\left(x_i\right)\cap C^{\prime }=\varnothing |\ge 3q-3s$ and $f\left(N\left[x_i\right]\right)\ge |AN\left(x_i\right)|+3\ge 5$ for each vertex $x_i\in X$ without neighbours in $C^{\prime }.$ Also, given that the cardinality of $C_j$ is three, it must be that

$$\begin{array}{ccc}\hfill {\displaystyle \sum _{1\le j\le r}f\left(C_j\right)}& =& {\displaystyle \sum _{C_j\in C^{\prime }}f\left(C_j\right)+\sum _{C_j\in C\setminus C^{\prime }}f\left(C_j\right)}\hfill \\ \hfill {\displaystyle }& =& {\displaystyle 4s+\frac{1}{3}\sum _{x_i\notin N\left(C^{\prime }\right)}f\left(N\left[x_i\right]\right)}\hfill \\ & \ge & {\displaystyle 4s+\frac{5}{3}(3q-3s)=5q-s>4q,}\hfill \end{array}$$

which is a contradiction.

Therefore, $|C^{\prime }|=q$ with $f\left(v\right)=4$ if $v\in C^{\prime }$ and $f\left(v\right)=0$ if $v\in C\setminus C^{\prime }.$ As $f\left(x_i\right)=0$ and $f\left(y_i\right)=0$ for all $i,$ then there exist $C_{j_i}^{\prime }\in C^{\prime }$ with $x_i\in C_{j_i}^{\prime }$. Taking into account that $|X|=3q$ and the cardinality of $C_j$ is three, then the elements of $C^{\prime }$ are disjoint from each other.

Hence, $C^{\prime }$ solves the instance $(X,C)$ of the X3C problem.  □

Although the proof of the result is lengthy, the key insight lies in constructing a bipartite graph associated with the decision problem. This graph is built from the elements $x_i\in X$ and the clauses $C_j$ (3-element subsets $\{x_{j_1},x_{j_2},x_{j_3}\}$), which establishes the equivalence between the existence of a solution to the X3C problem and the existence of a total triple Roman domination function with the given weight.

4. Bounds

Once it is shown that calculating the exact value of the total triple Roman domination number (t3RDN) is NP-hard, it is a natural step forward to bound this parameter in terms of well-known structural features of a graph.

Clearly, the t3RDN of a disconnected graph is the sum of the t3RDN of its components. As we have mentioned above, the total version of this domination problem only makes sense for isolated vertex-free graphs. Therefore, since we need any undefended vertex to be able to receive at least 3 units from its active neighbors, it is straightforward to derive a first upper bound by assigning a label of 2 to each vertex in the graph.

Proposition 2.

Let G be a connected graph of order n. Then, ${\gamma }_{\left[t3R\right]}\left(G\right)\le 2n$. Equality holds if and only if G is the corona product $H\circ K_1$ of a connected graph H with a $K_1$.

Proof. 

To prove the inequality, we consider f to be the function defined as $f\left(v\right)=2$ for all $v\in V\left(G\right).$ Clearly, f is a t3RDF and, therefore, ${\gamma }_{\left[t3R\right]}\left(G\right)\le 2n.$

Next, we characterize the graphs that attain equality.

First, if $G=H\circ K_1$ and f is a ${\gamma }_{\left[t3R\right]}\left(G\right)$-function, then $n=|V(G)|$ is an even integer and $f\left(u\right)+f\left(v\right)\ge 4$ for each leaf $u,$ where v is the corresponding support vertex. Hence, ${\gamma }_{\left[t3R\right]}\left(G\right)=w\left(f\right)\ge 4{\displaystyle \frac{n}{2}}=2n$ and the equality holds.

On the other hand, suppose that ${\gamma }_{\left[t3R\right]}\left(G\right)=2n=2|V\left(G\right)|$. If $n=2$, then $G=K_2=K_1\circ K_1$ and the result holds. So, we may assume that $n\ge 3.$ If $\Delta \left(G\right)=n-1$, then ${\gamma }_{\left[t3R\right]}\left(G\right)\le 5,$ which is impossible because ${\gamma }_{\left[t3R\right]}\left(G\right)=2n.$ So, assume that $\Delta \left(G\right)\le n-2.$

Let v be a vertex with maximum degree in G and denote by $N\left(v\right)=\{z_1,\dots ,z_{\Delta }\}$ its neighborhood. First, suppose that $\delta \left(G\right)\ge 2$. If there exists a vertex w such that $N\left(w\right)\subseteq N\left(v\right)$, then consider such a vertex having the minimum degree and denote by $N\left(w\right)=\{z_{j_1},\dots ,z_{j_{d\left(w\right)}}\}$ its neighbors. Now, we may define a function f as follows: $f\left(v\right)=3$; $f\left(z_{j_2}\right)=\dots =f\left(z_{j_{d\left(w\right)}}\right)=0$; and $f\left(x\right)=2$ otherwise. By our choice of w, every vertex labeled with a 2 is adjacent to a vertex with a positive label. The vertices with a label of 0 are adjacent to both v and w; therefore, f is a t3RDF in G and ${\gamma }_{\left[t3R\right]}\left(G\right)\le w\left(f\right)=3+2(n-1-(d\left(w\right)-1))\le 3+2(n-1-(2-1))=2n-1,$ a contradiction. If $N\left(w\right)\neg \subseteq N\left(v\right)$ for all $w\in V\setminus N\left[v\right]$, then we may define a function f as follows: $f\left(v\right)=3$; $f\left(z_1\right)=1,f\left(z_2\right)=\dots =f\left(z_{\Delta }\right)=0$; and $f\left(x\right)=2$ otherwise. We can readily check that f is a t3RDF in G and, hence, ${\gamma }_{\left[t3R\right]}\left(G\right)\le w\left(f\right)\le 3+1+2(n-\Delta \left(G\right)-1)\le 2n-2,$ again a contradiction.

So, we can deduce that it must be $\delta \left(G\right)=1$. If there exists a strong support vertex v such that $\{z_1,\dots ,z_p:p\ge 2\}$ are its leaves, then we can define a function f as follows: $f\left(v\right)=4;f\left(z_1\right)=1,f\left(z_2\right)=\dots =f\left(z_p\right)=0$; and $f\left(x\right)=2$ otherwise. It is straightforward to check that f is a t3RDF, and then ${\gamma }_{\left[t3R\right]}\left(G\right)\le w\left(f\right)=5+2(n-p-1)\le 2n-1.$ Hence, there are only weak support vertices in G. If there exists a vertex $v\in V\left(G\right)$ that is neither a leaf nor a support vertex, then we may define a function f as follows: $f\left(v\right)=1$ and $f\left(x\right)=2$ otherwise. Since $d\left(v\right)\ge 2$, then f is a t3RDF and ${\gamma }_{\left[t3R\right]}\left(G\right)\le 2n-1,$ which is not possible.

Then, every vertex in G is either a leaf or a weak support vertex, which finishes the proof.  □

Our next results give us an upper bound for the t3RDN in terms of the maximum degree of the graph.

Proposition 3.

Let G be an ntc-graph of order n and maximum degree $\Delta \left(G\right)\ge 2$. Then, ${\gamma }_{\left[t3R\right]}\left(G\right)\le 3n-2\Delta \left(G\right)$.

Proof. 

Consider a vertex $v\in V\left(G\right)$ with maximum degree $\Delta \left(G\right)$ and let $N\left(v\right)=\{z_j:j=1,\dots ,\Delta \left(G\right)\}$ be the neighborhood of v. Let us define the function $f:V\to \{0,1,2,3,4\}$ as follows: $f\left(v\right)=3,$ $f\left(z_j\right)=1$ for $j=1,\dots ,\Delta \left(G\right)$ and $f\left(u\right)=3$ for the remaining vertices. Then, f is t3RDF and ${\gamma }_{\left[t3R\right]}\left(G\right)\le w\left(f\right)=3(n-\Delta \left(G\right))+\Delta \left(G\right)=3n-2\Delta \left(G\right).$  □

Some graphs, including the path $P_3$ and the cycle $C_3$, attain this bound. Furthermore, we can readily verify that the upper bound given in Proposition 3 improves upon the one presented in Proposition 2 whenever $\Delta \left(G\right)>⌈{\displaystyle \frac{n}{2}}⌉$.

Proposition 4.

Let G be an ntc-graph of order n, $\delta \left(G\right)\ge 2$, girth $g\ge 5$, and maximun degree $\Delta \left(G\right)\le n-2.$ Then,

$${\gamma }_{\left[t3R\right]}\left(G\right)\le 2(n-\Delta \left(G\right)+1).$$

Proof. 

Consider a vertex $v\in V\left(G\right)$ with maximum degree $\Delta \left(G\right)$ and let $N\left(v\right)=\{z_j:j=1,\dots ,\Delta \left(G\right)\}$ be the neighborhood of v. Let us define the function $f:V\to \{0,1,2,3,4\}$ as follows: $f\left(v\right)=3,f\left(z_1\right)=1,f\left(z_j\right)=0$ for $j\ne q$ and $f\left(u\right)=2$ for the remaining vertices. Let z be any vertex belonging to $V\setminus N\left[v\right]$. Since $\delta \left(G\right)\ge 2$ and $g\ge 5$, then $N\left(z\right)\cap (V\setminus N[v\left]\right)\ne \varnothing$. Therefore, there exists $w\in N\left(z\right)$ such that $f\left(w\right)=2$ and $f\left(N\right[z\left]\right)\ge 3+|AN(z)|.$ Since $G[V\setminus V_0]$ has no isolated vertices, then f is a t3RDF and

$${\gamma }_{\left[t3R\right]}\left(G\right)\le w\left(f\right)=3+1+2(n-\Delta \left(G\right)-1)=2(n-\Delta \left(G\right)+1).$$

□

As shown in Table 1, these bounds are not comparable. There are graphs for which each bound is better (boxed) than the others.

Table 1. $K_4^{-}$ stands for a complete graph $K_4$ without an edge. Bound boxed is better than the others obtained bounds for the corresponding graph.

Bounds	${\mathit{C}}_5$	${\mathit{P}}_4\circ {\mathit{K}}_1$	${\mathit{K}}_4^{-}$
Proposition 2	10	$\boxed{16}$	8
Proposition 3	11	17	$\boxed{5}$
Proposition 4	$\boxed{8}$	-	-

The upper bound can be significantly improved in the case of dealing with a regular graph, as demonstrated by the result we prove next.

Proposition 5.

Let G be an r-regular connected graph of order n and girth $g\ge 7$. Then, ${\gamma }_{\left[t3R\right]}\left(G\right)\le 2n-2r^2+3r-1.$

Proof. 

Let v be any vertex of the graph G and let us denote $N_0=\left\{v\right\}$, $N_1=N\left(v\right)$, and $N_2=N\left(N_1\right)-N_0$. Clearly, $|N_0|=1,|N_1|=r$ and $|N_2|=r(r-1)$ because the girth is at least $7.$ Consider the function $f:V\to \{0,1,2,3,4\}$, defined as follows: $f\left(v\right)=1;f\left(z\right)=3$ for all $z\in N_1;f\left(z\right)=0$ for all $z\in N_2;$ and $f\left(z\right)=2$ otherwise. Since $r\ge 2$ and the girth is greater than or equal to 7, we may readily verify that f is a t3RDF. Hence,

$${\gamma }_{\left[t3R\right]}\left(G\right)\le w\left(f\right)=1+3r+2(n-1-r-r(r-1))=2n-2r^2+3r-1.$$

□

Although the upper bound matches the exact value, for example, of ${\gamma }_{\left[t3R\right]}\left(C_7\right)$, it is worth pointing out that the girth condition is essential. It is not difficult to check that ${\gamma }_{\left[t3R\right]}\left(C_5\right)=8$, whereas the upper bound given by Proposition 5 would imply that ${\gamma }_{\left[t3R\right]}\left(C_5\right)\le 7.$

In what follows, it is important to keep in mind certain conditions that, without loss of generality, we may assume that a ${\gamma }_{\left[t3R\right]}\left(G\right)$-function satisfies.

Remark 1.

Let f be a ${\gamma }_{\left[t3R\right]}\left(G\right)$-function of an ntc-graph G. Let v be a support vertex whose leaves are the vertices $u_i$, with $i\in \{1,\dots ,r\}$. Then,

• If v is a weak support vertex, then $f\left(u_1\right)\ne 4,f\left(v\right)\ne 0$, and $f\left(u\right)+f\left(v\right)=4.$
• If v is a strong support vertex such that $f\left(w_j\right)=0$ for all $w_j\in N\left(v\right)\setminus \{u_i:i=1,\dots ,r\}$, then we may suppose that $f\left(u_1\right)=1$, $f\left(v\right)=4$, and $f\left(u_i\right)=0$ for all $i\ne 1.$
• If v is a strong support vertex such that there is a vertex $w_{j_0}\in N\left(v\right)\setminus \{u_i:i=1,\dots ,r\}$ with $f\left(w_{j_0}\right)\ne 0$, then we may assume that $f\left(v\right)=4$ and $f\left(u_i\right)=0$ for all the leaves $u_i$.

To close this section, we prove several results in which we bound the total triple Roman domination number of a graph in terms of other domination parameters such as the (total) domination number or the total double Roman domination number.

Proposition 6.

Let G be an ntc-graph; then, ${\gamma }_{\left[t3R\right]}\left(G\right)\le 5\gamma \left(G\right)$.

Proof. 

Let D be a $\gamma$-set and $D_1\subseteq D$ the isolated vertices in the induced subgraph $G\left[D\right]$. For each $v\in D_1$, we consider a vertex $\tilde{v}\in N\left(v\right)$, and let us denote $D_2=\{\tilde{v}:v\in D_1\}\subseteq V\setminus D$. Consider the function $f:V\to \{0,1,2,3,4\}$, defined as follows: $f\left(z\right)=4$ for all $z\in D;$ $f\left(z\right)=1$ for all $z\in D_2;$ and $f\left(z\right)=0$ for the remaining vertices. Then,

$${\gamma }_{\left[t3R\right]}\left(G\right)\le 4|D|+|D_2|\le 4\gamma +|D_1|\le 4\gamma +\gamma =5\gamma .$$

(1)

□

This bound is met by infinitely many graphs, such as those that contain a universal vertex.

Corollary 1.

Let G be an ntc-graph. If ${\gamma }_{\left[t3R\right]}\left(G\right)=5\gamma$, then every γ-set is a 3-independent set.

Proof. 

If ${\gamma }_{\left[t3R\right]}\left(G\right)=5\gamma$, then the inequalities in (1) become equalities. Therefore, $|D_1|=\gamma$ and all the dominating vertices are isolated in $G\left[D\right]$. Since $|D_2|=\gamma$, there is no common neighbor $\tilde{v}\in N\left(v\right)\cap N\left(v^{\prime }\right)$ for any pair $v,v^{\prime }\in D_1$ of distinct vertices. Consequently, every $\gamma$-set is a 3-independent set.  □

We can readily check that the reciprocal is not always true by considering, for example, the cycle graph $C_9,$ for which ${\gamma }_{\left[t3R\right]}\left(C_9\right)\le 14<5\gamma \left(C_9\right)=15$ (see Figure 4).

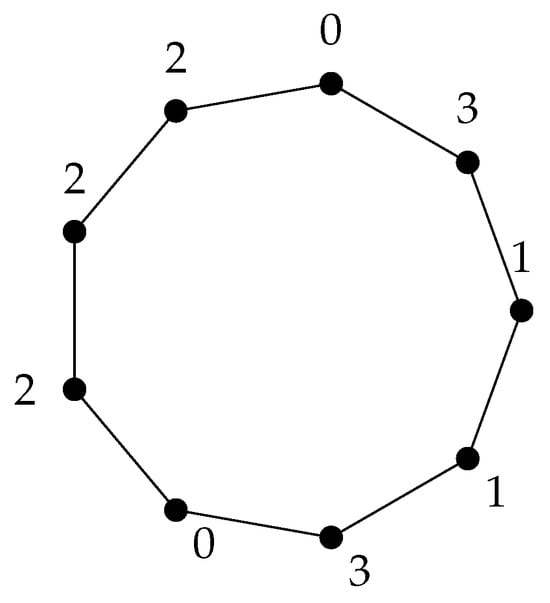
Figure 4. A total triple Roman dominating function on $C_9$.

Proposition 7.

Let G be an ntc-graph with at least 3 vertices. Then, ${\gamma }_t\left(G\right)+3\le {\gamma }_{\left[t3R\right]}\left(G\right)\le 4{\gamma }_t\left(G\right)$.

Proof. 

Let S be a ${\gamma }_t$-set of G and let $v\in S$. We can readily prove the upper bound by considering a function g such that $g\left(z\right)=4$ for all $z\in S$. This function g is a t3RDF and, hence, ${\gamma }_{\left[t3R\right]}\left(G\right)\le 4{\gamma }_t\left(G\right).$

Next, we prove the lower bound. Assume that $f=(V_0,V_1,V_2,V_3,V_4)$ is a ${\gamma }_{\left[t3R\right]}\left(G\right)$-function. Since $V\setminus V_0$ is a total dominating set, we have that

$$\begin{array}{ccc}\hfill {\gamma }_t\left(G\right)& \le & |V_1|+|V_2|+|V_3|+|V_4|\hfill \\ & =& |V_1|+2|V_2|+3|V_3|+4|V_4|-|V_2|-2|V_3|-3|V_4|\hfill \\ & =& {\gamma }_{\left[t3R\right]}\left(G\right)-|V_2|-2|V_3|-3|V_4|.\hfill \end{array}$$

If $V_4\ne \varnothing$, then ${\gamma }_t\left(G\right)\le {\gamma }_{\left[t3R\right]}\left(G\right)-3$ and we are finished. So, assume that $V_4=\varnothing .$ If $V_0\ne \varnothing$, then either $|V_2|\ge 3$, $\{|V_2|\ge 1,|V_3|\ge 1\}$, or $|V_3|\ge 2$ and, therefore, ${\gamma }_t\left(G\right)\le {\gamma }_{\left[t3R\right]}\left(G\right)-3.$ So, the only case that remains to consider is $V_0=V_4=\varnothing .$ But, in this situation, ${\gamma }_t\left(G\right)\le n-1<n+2\le {\gamma }_{\left[t3R\right]}\left(G\right),$ which concludes the proof.  □

Proposition 8.

Let G be an ntc-graph. Then,

$${\gamma }_{tdR}\left(G\right)<{\gamma }_{\left[t3R\right]}\left(G\right)\le min\left\{5\gamma ,⌊{\displaystyle \frac{3}{2}}{\gamma }_{tdR}\left(G\right)⌋\right\}.$$

Proof. 

First, to prove the lower bound, consider $f=(V_0,V_1,V_2,V_3,V_4)$ a ${\gamma }_{\left[t3R\right]}\left(G\right)$-function. If $V_4\ne \varnothing$, then $g=(V_0,V_1,V_2,V_3\cup V_4)$ is a tdRDF with weight $w\left(g\right)\le w\left(f\right)-1$ and, hence, ${\gamma }_{tdR}\left(G\right)<{\gamma }_{\left[t3R\right]}\left(G\right).$

Assume now that $V_4=\varnothing$, which implies that $V_2\cup V_3\ne \varnothing$. Let $v\in V_2\cup V_3$ be a vertex and consider the function $g=(V_0^g,V_1^g,V_2^g,V_3^g)$, defined as follows: $g\left(v\right)=f\left(v\right)-1$ and $g\left(z\right)=f\left(z\right)$ otherwise. First, observe that the set $V\setminus V_0$ still total-dominates the graph G. On the other hand, the set of active neighbors of all vertices of V does not change regardless of which function, f or g, we consider. Therefore, if $g\left(u\right)<2$ and $u\notin N\left(v\right)$, then $g\left(N\right[u\left]\right)=f\left(N\right[u\left]\right)\ge |AN(u)|+3\ge |AN(u)|+2.$ If $g\left(u\right)<2$ and $u\in N\left(v\right)$, then $g\left(N\right[u\left]\right)=f\left(N\right[u\left]\right)-1\ge |AN(u)|+2.$ Hence, g is a tdRD function with a weight of $w\left(g\right)=w\left(f\right)-1$ and ${\gamma }_{tdR}\left(G\right)<{\gamma }_{\left[t3R\right]}\left(G\right).$

To prove the upper bound, we consider $g=(V_0,V_1,V_2,V_3)$ a ${\gamma }_{tdR}\left(G\right)$-function. Let us define the following function: $f\left(v\right)=4$ if $v\in V_3;$ $f\left(v\right)=3$ if $v\in V_2;$ and $g\left(z\right)=f\left(z\right)$ otherwise. Then, f is a t3RDF of G and we may readily deduce that

$$\begin{array}{ccc}\hfill {\gamma }_{\left[t3R\right]}\left(G\right)& \le & f\left(V\right)=|V_1|+3|V_2|+4|V_3|\le ⌊{\displaystyle |V_1|+\frac{3}{2}(2|V_2|+3|V_3|)}⌋\hfill \\ & \le & ⌊{\displaystyle \frac{3}{2}(|V_1|+2|V_2|+3|V_3|)}⌋=⌊{\displaystyle \frac{3}{2}{\gamma }_{tdR}\left(G\right)}⌋.\hfill \end{array}$$

This fact, and the bound given by Proposition 6, lead us to the desired result.  □

We conclude by providing two lower bounds in terms of the order, maximum degree, and domination number of the graph, some of which follow from well-known bounds for the triple Roman domination number.

Proposition 9.

Let G be an ntc-graph with $n\ge 3$. Then, ${\gamma }_{\left[t3R\right]}\left(G\right)\ge {\gamma }_t\left(G\right)+\gamma \left(G\right).$

Proof. 

Let f be a ${\gamma }_{\left[t3R\right]}\left(G\right)$-function of G. Then,

$$\begin{array}{ccc}\hfill {\gamma }_{\left[t3R\right]}\left(G\right)& =& 3|V_3|+2|V_2|+|V_1|\hfill \\ & =& (|V_3|+|V_2|+|V_1|)+(|V_3|+|V_2|)+|V_3|\hfill \\ & \ge & {\gamma }_t\left(G\right)+\gamma \left(G\right),\hfill \end{array}$$

because $V_1\cup V_2\cup V_3$ (resp. $V_2\cup V_3$) is a total dominating (resp. dominating) set of $G.$  □

Proposition 10.

Let G be an ntc-graph of order n. Then,

$${\gamma }_{\left[t3R\right]}\left(G\right)\ge ⌈{\displaystyle \frac{2n+(\Delta (G)-1)\gamma }{\Delta \left(G\right)}}⌉.$$

Proof. 

This bound is an immediate consequence of ${\gamma }_{\left[t3R\right]}\left(G\right)\ge {\gamma }_{\left[3R\right]}\left(G\right)$ and the following lower bound, proved in [15]:

$${\gamma }_{\left[3R\right]}\left(G\right)\ge ⌈{\displaystyle \frac{2n+(\Delta (G)-1)\gamma }{\Delta \left(G\right)}}⌉.$$

□

By applying the upper bound proved in [17], we may derive the following remark.

Remark 2.

For any ntc-graph G of order $n\ge 2$ and maximum degree $\Delta \left(G\right)\ge 3$, we have that

$${\gamma }_{\left[t3R\right]}\left(G\right)\ge ⌈{\displaystyle \frac{4n}{\Delta \left(G\right)+1}}⌉.$$

5. Exact Values of the Total Triple Roman Domination Number

Our aim in this section is to characterize those graphs that have the first few smallest values of the parameter ${\gamma }_{t3R}\left(G\right)$. Also, we prove several results regarding the exact values of the t3RD-number for certain graph families. In what follows, we make use of the following notation. Given a positive integer $n\ge 3$, let $M_4=8$ and

$$M_n=\left\{\begin{array}{ccc}{\displaystyle ⌈\frac{3n}{2}⌉}& & \mathrm{if}n\equiv 0,1,3,5,7(\mathrm{mod}8),\mathrm{with}n\ne 7.\hfill \\ {\displaystyle ⌈\frac{3n}{2}⌉+1}& & \mathrm{if}n=7\mathrm{or}n\equiv 2,4,6(\mathrm{mod}8),\mathrm{with}n\ne 4.\hfill \end{array}\right.$$

Proposition 11.

Let G be an ntc-graph with order $n\ge 3$. Then, ${\gamma }_{\left[t3R\right]}\left(G\right)=5$ if and only if $\Delta \left(G\right)=n-1.$

Proof. 

Let u be a vertex with maximum degree and $v\in N\left(u\right)$. Consider a function defined as follows: $f\left(u\right)=4;f\left(v\right)=1;$ and $f\left(z\right)=0$ for all $z\ne v,u.$ We can readily check that f is a t3RDF of G. Hence, ${\gamma }_{\left[t3R\right]}\left(G\right)\le 5.$ On the other side, assume that G is an ntc-graph with at least 3 vertices and let $f=(V_0,V_1,V_2,V_3,V_4)$ be a ${\gamma }_{\left[t3R\right]}\left(G\right)$-function. If $V_0=\varnothing$, then for any vertex $u\in V$, we have that $f\left(N\right[u\left]\right)\ge 3+|AN(u)|=5$ and, therefore, ${\gamma }_{\left[t3R\right]}\left(G\right)=w\left(f\right)\ge 5.$ If $u\in V_0$, then either $V_4\ne \varnothing$, which implies that $|V\setminus V_0|\ge 2$, or $|V_3|\ge 1$ and $|V_2\cup V_3|\ge 2$ or $|V_2|\ge 3.$ In any case, we deduce that ${\gamma }_{\left[t3R\right]}\left(G\right)=w\left(f\right)\ge 5.$

Assume now that ${\gamma }_{\left[t3R\right]}\left(G\right)=5$ and $n\ge 3$. Let $f=(V_0,V_1,V_2,V_3,V_4)$ be a ${\gamma }_{\left[t3R\right]}\left(G\right)$-function. If $V_0\ne \varnothing$, then either $|V_2|=|V_3|=1$ or $|V_1|=|V_4|=1$. In any case, since f is a t3RDF, the vertex labeled 3 or 4 is universal. Hence, $\Delta \left(G\right)=n-1$.

Otherwise, suppose that $V_0=\varnothing$, which implies that $V_4=\varnothing$ because f has the minimum weight. Since $n\ge 3$, we have that either $|V_2|=2,|V_1|=1$ and $|V_3|=0$ or $|V_3|=1,|V_1|=2$ and $|V_2|=0$. In these cases, $G\in \{P_3,C_3\}$ and we are finished.  □

Proposition 12.

There is no ntc-graph G such that ${\gamma }_{\left[t3R\right]}\left(G\right)=6.$

Proof. 

Let G be an ntc-graph with ${\gamma }_{\left[t3R\right]}\left(G\right)=6$ and let $f=(V_0,V_1,V_2,V_3,V_4)$ be a ${\gamma }_{\left[t3R\right]}\left(G\right)$-function of G. If either $|V_4|=1,|V_1|=2$, $|V_4|=1,|V_2|=1$, $|V_3|=2$, or $|V_3|=1,|V_2|=1,|V_1|=1$, then the vertex with the greatest label is a universal vertex because f is a t3RD function, which is a contradiction with Proposition 11.

If $|V_3|=1$ and $|V_1|=3$, then $V_0=\varnothing$, and, once again, we deduce that the vertex in $V_3$ is universal. Hence, $\Delta \left(G\right)=n-1$. If $|V_2|=3$, then at least one of the vertices in $V_2$ must be adjacent to the other two vertices in $V_2$. Furthermore, since every vertex in $V_0$ must be adjacent to each vertex in $V_2$, we conclude that $\Delta \left(G\right)=n-1$, once again leading us to a contradiction.

Lastly, suppose that $|V_2|=2$ and $|V_1|=2$, which implies that $V_0=\varnothing$. The vertices in $V_2$ must all be adjacent, and each vertex in $V_1$ must be adjacent to both vertices in $V_2$. Therefore, both vertices in $V_2$ are universal, which completes the proof.  □

Next, we provide some technical results that allow us to establish the main results of this section concerning the exact value of the t3RD number for paths and cycles.

Lemma 1.

Let G be an ntc-graph of order n and $\Delta \left(G\right)\le 2.$ Let f be a ${\gamma }_{\left[t3R\right]}\left(G\right)$-function such that the number of vertices assigned 0 under f is minimized and let $\{v_{i_0-2},v_{i_0-1},v_{i_0},v_{i_0+1},v_{i_0+2}\}$ be an ordered set of vertices that induces a path in G. Then, the following conditions hold:

L1 

$f\left(v\right)\ne 4$ for all $v\in V\left(G\right)$.

L2 

If $f\left(v_{i_0-1}\right)=3$ and $f\left(v_{i_0}\right)=0$, then there exists a ${\gamma }_{\left[t3R\right]}\left(G\right)$-function g such that $g\left(v_{i_0-1}\right)=3,g\left(v_{i_0}\right)=0$ and $g\left(v_{i_0+1}\right)=2$.

L3 

If $f\left(v_{i_0-1}\right)=0$ and $f\left(v_{i_0}\right)=2$, then there exists a ${\gamma }_{\left[t3R\right]}\left(G\right)$-function g such that $g\left(v_{i_0-1}\right)=0,g\left(v_{i_0}\right)=2$ and $g\left(v_{i_0+1}\right)=2$.

L4 

If $f\left(v_{i_0-1}\right)=0$ and $f\left(v_{i_0}\right)=3$, then there exists a ${\gamma }_{\left[t3R\right]}\left(G\right)$-function g such that $g\left(v_{i_0-1}\right)=0,g\left(v_{i_0}\right)=3$ and $g\left(v_{i_0+1}\right)=1$.

Proof. 

Since G is an ntc-graph with $\Delta \left(G\right)\le 2$, it follows that G is either a path or a cycle. Let $\{v_1,v_2,\dots ,v_n\}$ be the vertices of G.

L1. Suppose a vertex exists, say $v_i$, such that $f\left(v_i\right)=4$. If $f\left(v_{i-1}\right)\ge 1$ and $f\left(v_{i+1}\right)\ge 1$, then we can define g as follows: $g\left(v_i\right)=3$ and $g\left(v_j\right)=f\left(v_j\right)$ for $j\ne i$. So, g is a t3RDF of G with weight $w\left(f\right)-1$, which is a contradiction. Without loss of generality, assume that $f\left(v_{i-1}\right)\ge 1$ and $f\left(v_{i+1}\right)=0$. Then, the function g defined by $g\left(v_i\right)=3,g\left(v_{i+1}\right)=1$, and $g\left(v_j\right)=f\left(v_j\right)$ for $j\notin \{i,i+1\}$ is a t3RDF of G with weight $w\left(f\right)$. Thus, g is also a ${\gamma }_{\left[t3R\right]}\left(G\right)$-function, with $|V_0^g|<|V_0^f|,$ against our assumptions. Therefore, the result holds.

L2. Since f is a t3RD function, $f\left(v_{i_0-1}\right)=3$ and $f\left(v_{i_0}\right)=0$, so it must be that $f\left(v_{i_0+1}\right)\ge 2$. On the other hand, as $f\left(v_{i_0}\right)=0$ and $f\left(v_{i_0+1}\right)=3$, we have that $i_0+1<n.$ So, we can define a function g as follows: $g\left(v_{i_0+1}\right)=2,g\left(v_{i_0+2}\right)=min\{f\left(v_{i_0+2}\right)+1,3\}$, and $g\left(v_j\right)=f\left(v_j\right)$ otherwise. Hence, g would be a t3RDF of G with weight $w\left(g\right)\le w\left(f\right)$ and $g\left(v_{i_0+1}\right)=2.$ The proof of items L3 and L4 are quite similar, so we omit them.  □

Lemma 2.

Let G be an ntc-graph with $\Delta \left(G\right)\le 2.$ If $\{v_{i_0-2},v_{i_0-1},v_{i_0},v_{i_0+1},v_{i_0+2}\}$ is an ordered set of vertices that induces a path in G, then there exists a ${\gamma }_{\left[t3R\right]}\left(G\right)$-function g such that $0\in \{g\left(v_j\right):i_0-2\le j\le i_0+2\}.$

Proof. 

Let f be a ${\gamma }_{\left[t3R\right]}\left(G\right)$-function such that the number of vertices labeled with a 0 under f is minimized and let $\{v_1,v_2,\dots ,v_n\}$ be the set of vertices of G. Suppose, on the contrary, that $f\left(v_i\right)\ne 0$ for all $i_0-2\le i\le i_0+2$. We have to consider several cases.

Case 1. If $f\left(v_{i_0}\right)=1$ and $f\left(v_j\right)\ge 1$ for all $i_0-2\le j\le i_0+2$ and $j\ne i_0$, then we can define a function g in the following way: $g\left(v_{i_0}\right)=0$, $g\left(v_{i_0+1}\right)=min\{f\left(v_{i_0+1}\right)+1,3\}$ and $g\left(v_j\right)=f\left(v_j\right)$ otherwise. Therefore, g is a t3RDF of G with weight $w\left(g\right)\le w\left(f\right)$ and $g\left(v_{i_0}\right)=0$.

Case 2. If $f\left(v_{i_0}\right)=2$ and $f\left(v_j\right)\ge 1$ for all $i_0-2\le j\le i_0+2$, then we can define g as $g\left(v_{i_0}\right)=0$, $g\left(v_{i_0-1}\right)=min\{f\left(v_{i_0-1}\right)+1,3\}$, $g\left(v_{i_0+1}\right)=min\{f\left(v_{i_0+1}\right)+1,3\}$, and $g\left(v_j\right)=f\left(v_j\right)$ otherwise. Therefore, g is a t3RDF of G with weight $w\left(g\right)\le w\left(f\right)$ and $g\left(v_{i_0}\right)=0$.

Case 3. If $f\left(v_{i_0}\right)=3$ and, without loss of generality $g\left(v_{i_0-1}\right)=1$ and $g\left(v_{i_0+1}\right)\ge 2$, then we consider $g\left(v_{i_0-1}\right)=0$, $g\left(v_{i_0-2}\right)=min\{f\left(v_{i_0-2}\right)+1,3\}$, and $g\left(v_j\right)=f\left(v_j\right)$ otherwise. Therefore, g is a t3RD function with weight $w\left(g\right)\le w\left(f\right)$ and $g\left(v_{i_0-1}\right)=0$.

Case 4. If $f\left(v_{i_0}\right)=3$, $f\left(v_{i_0-1}\right)=1$, $f\left(v_{i_0+1}\right)=1$, $f\left(v_{i_0-2}\right)=1$, and $f\left(v_{i_0+2}\right)=1$, then $f\left(v_{i_0-3}\right)=3$. We can define a new function g such that $g\left(v_{i_0-1}\right)=0$, $g\left(v_{i_0-2}\right)=2$, and $g\left(v_j\right)=f\left(v_j\right)$ otherwise. Hence, g is a t3RDF of G with weight $w\left(g\right)=w\left(f\right)$ and $g\left(v_{i_0-1}\right)=0$.  □

Proposition 13.

Let G be an ntc-graph with the maximum degree $\Delta \left(G\right)\le 2$, order $n\ge 5$, and let $f=(V_0,V_1,V_2,V_3,V_4)$ be a ${\gamma }_{\left[t3R\right]}\left(G\right)$-function such that $|V_0|$ is minimized. Then, ${\gamma }_{\left[t3R\right]}\left(G\right)\ge \lceil {\displaystyle \frac{6n}{5}}\rceil +2$.

Proof. 

First of all, note that since ${\gamma }_{\left[t3R\right]}\left(P_n\right)\ge {\gamma }_{\left[t3R\right]}\left(C_n\right)$, we only have to prove the result for cycles. For $C_5,C_6$, we may readily check that ${\gamma }_{\left[t3R\right]}\left(C_5\right)=8,{\gamma }_{\left[t3R\right]}\left(C_6\right)=10$, which satisfies the inequality.

Let us suppose that $n\ge 7$, f is a ${\gamma }_{\left[t3R\right]}\left(C_n\right)$-function, and $\{v_{i_0-2},$ $v_{i_0-1},$ $v_{i_0},$ $v_{i_0+1},$ $v_{i_0+2}\}$ are consecutive vertices of $C_n$. Without loss of generality, by applying Lemmas 1 and 2, we only have to consider the following situation: $f\left(v_{i_0-2}\right)=1,f\left(v_{i_0-1}\right)=3,$ $f\left(v_{i_0}\right)=0,f\left(v_{i_0+1}\right)=2,f\left(v_{i_0+2}\right)=2.$

If $f\left(v_{i_0+3}\right)\le 1$, then $f\left(v_{i_0+4}\right)\ge 2$. Therefore, the function g defined as $g\left(v_{i_0-1}\right)=2,$ $g\left(v_{i_0+2}\right)=1$, and $g\left(z\right)=f\left(z\right)$ otherwise is a total double Roman dominating function in the cycle $C_n$ with weight $w\left(g\right)=w\left(f\right)-2.$ By applying Proposition 8, since ${\gamma }_{[tdR]}\left(C_n\right)=\lceil {\displaystyle \frac{6n}{5}}\rceil$, we can conclude that

$${\gamma }_{\left[t3R\right]}\left(C_n\right)=w\left(f\right)=w\left(g\right)+2\ge {\gamma }_{\left[tdR\right]}\left(C_n\right)+2=⌈{\displaystyle \frac{6n}{5}}⌉+2.$$

□

Proposition 14.

Let G be an ntc-graph with $\Delta \left(G\right)\le 2$, $n\ge 5$, and let $f=(V_0,V_1,V_2,V_3,\varnothing )$ be a t3RDF on G, such that the number of vertices assigned 0 under f is the minimum. Then, ${\gamma }_{\left[t3R\right]}\left(G\right)\le \lceil {\displaystyle \frac{8n}{5}}\rceil$.

Proof. 

Since ${\gamma }_{\left[t3R\right]}\left(C_n\right)\le {\gamma }_{\left[t3R\right]}\left(P_n\right)$, we can restrict ourselves to proving the result for paths. To do this, we proceed by induction on the order $n\ge 5$ of the path. The labeling shown in Table 2 permit us to state that the bound is correct for all $5\le n\le 12.$

Table 2. t3RD functions for $5\le n\le 12$.

n	${\mathit{v}}_1$	${\mathit{v}}_2$	${\mathit{v}}_3$	${\mathit{v}}_4$	${\mathit{v}}_5$	${\mathit{v}}_6$	${\mathit{v}}_7$	${\mathit{v}}_8$	${\mathit{v}}_9$	${\mathit{v}}_{10}$	${\mathit{v}}_{11}$	${\mathit{v}}_{12}$	$\mathit{w}\left(\mathit{f}\right)$	$\lceil \frac{8\mathit{n}}{5}\rceil$
5	1	3	0	2	2								8	8
6	1	3	1	1	3	1							10	10
7	1	3	0	2	2	3	1						12	12
8	1	3	0	2	2	0	3	1					12	13
9	1	3	0	2	2	2	0	3	1				14	15
10	1	3	0	2	2	2	2	0	3	1			16	16
11	1	3	0	2	2	1	2	2	0	3	1		17	18
12	1	3	0	2	2	1	2	2	2	0	3	1	19	20

So, let us assume that $n\ge 13$ and ${\gamma }_{\left[t3R\right]}\left(P_{n_0}\right)\le \lceil {\displaystyle \frac{8n_0}{5}}\rceil$ for all $5\le n_0<n.$ Denote $P_n=P_8\cup P_{n-8}$, where $P_8=v_1{v}_2\dots v_8$ and $P_{n-8}=v_9\dots v_n,$ and consider $f:V\left(P_{n-8}\right)\to \{0,1,2,3,4\}$ a ${\gamma }_{\left[t3R\right]}\left(P_{n-8}\right)$-function. Then, the function g defined as $g\left(v_1\right)=g\left(v_8\right)=1,g\left(v_2\right)=g\left(v_7\right)=3,g\left(v_3\right)=g\left(v_6\right)=0,g\left(v_4\right)=g\left(v_5\right)=2$, and $g\left(v_i\right)=f\left(v_i\right)$ for all $9\le i\le n$ is a t3RDF in $P_n$ with weight

$$\begin{array}{ccc}\hfill w\left(g\right)& =& {\displaystyle \sum _{i=1}^{n}g\left(v_i\right)=\sum _{i=1}^{8}g\left(v_i\right)+\sum _{i=9}^{n}g\left(v_i\right)}\hfill \\ & =& {\displaystyle 12+{\gamma }_{\left[t3R\right]}\left(P_{n-8}\right)\le 12+⌈\frac{8(n-8)}{5}⌉}\hfill \\ & =& {\displaystyle ⌈\frac{8n-64+60}{5}⌉\le ⌈\frac{8n}{5}⌉.}\hfill \end{array}$$

This finishes the proof.  □

Let us point out that by Propositions 13 and 14, we know that $⌈{\displaystyle \frac{6n}{5}}⌉+2\le {\gamma }_{\left[t3R\right]}\left(G\right)\le ⌈{\displaystyle \frac{8n}{5}}⌉$ for any path or cycle G of order $n\ge 5$.

Lemma 3.

Let T be a tree and v be a leaf vertex of T. Let M be the tree obtained from T and the star $K_{1,s}$, with $s\ge 1,$ by adding an edge between v and a leaf of the star $K_{1,s}$. Then,

• If $s=1$, then ${\gamma }_{\left[t3R\right]}\left(T\right)+1\le {\gamma }_{\left[t3R\right]}\left(M\right)\le {\gamma }_{\left[t3R\right]}\left(T\right)+4.$
• If $s=2$ and there exists a ${\gamma }_{\left[t3R\right]}\left(T\right)$-function f such that $f\left(v\right)\ge 2$, then ${\gamma }_{\left[t3R\right]}\left(M\right)={\gamma }_{\left[t3R\right]}\left(T\right)+4.$
• If $s=2$ and $f\left(v\right)\le 1$ for all ${\gamma }_{\left[t3R\right]}\left(T\right)$-function f, then ${\gamma }_{\left[t3R\right]}\left(M\right)={\gamma }_{\left[t3R\right]}\left(T\right)+5$.
• Otherwise, we have that ${\gamma }_{\left[t3R\right]}\left(T\right)+4\le {\gamma }_{\left[t3R\right]}\left(M\right)\le {\gamma }_{\left[t3R\right]}\left(T\right)+5.$

Proof. 

To begin with, let us assume that $s=1$. Let $f_1$ be a ${\gamma }_{\left[t3R\right]}$-function on T and let $u_1$ and $u_2$ be the vertices of $K_{1,1}$ such that $u_1$ is adjacent to v in M. Let g be a function defined as $g\left(u_j\right)=2$ and $g\left(z\right)=f_1\left(z\right)$ for all $z\in V\left(T\right).$ So, g is a t3RDF on M and

$${\gamma }_{\left[t3R\right]}\left(M\right)\le w\left(f_1\right)+4={\gamma }_{\left[t3R\right]}\left(T\right)+4.$$

On the other hand, let f be a ${\gamma }_{\left[t3R\right]}\left(M\right)$-function and let $u\in N\left(v\right)-u_1$ be the neighbor of v in T. By applying Remark 1, we have that $f\left(u_1\right)+f\left(u_2\right)=4$ and, therefore, ${\gamma }_{\left[t3R\right]}\left(M\right)=f\left(V\left(T\right)\right)+4.$

If $f\left(v\right)\ge 2$, then the function g, defined as $g\left(z\right)=f\left(z\right)$ for every $z\in V\left(T\right)-\{u,v\}$ and $g\left(z\right)=min\{4,f(z)+1\}$ otherwise, is a t3RDF in T with weight, at most, ${\gamma }_{\left[t3R\right]}\left(M\right)-2$, and we are finished.

Now, if $f\left(v\right)=1$, then the function g, defined as $g\left(z\right)=f\left(z\right)$ for every $z\in V\left(T\right)-\left\{u\right\}$ and $g\left(u\right)=min\{4,f(u)+3\},$ is a t3RDF in T with weight, at most, ${\gamma }_{\left[t3R\right]}\left(M\right)-1$, as desired.

On the contrary, if $f\left(v\right)=0,$ then we have that $f\left(u_1\right)\le 3$ and, hence, $f\left(u\right)\ge 2,$ because v must be total triple Roman dominated by $f.$ Hence, the function g, defined as $g\left(z\right)=f\left(z\right)$ for every $z\in V\left(T\right)-\left\{v\right\}$ and $g\left(v\right)=2,$ is a t3RDF in T with weight, at most, ${\gamma }_{\left[t3R\right]}\left(M\right)-2$.

Let us now assume that $s=2$ and that there is a ${\gamma }_{\left[t3R\right]}\left(T\right)$-function f such that $f\left(v\right)\ge 2.$ Since f is a ${\gamma }_{\left[t3R\right]}\left(T\right)$-function such that $f\left(v\right)\ge 2$, then we can define a function g in the following way: $g\left(z\right)=f\left(z\right)$ for all $z\in V\left(T\right)$, $g\left(u_1\right)=0,$ $g\left(u_2\right)=3,$ and $g\left(u_3\right)=1$, which is a t3RDF on M, and, hence,

$${\gamma }_{\left[t3R\right]}\left(M\right)\le w\left(g\right)=w\left(f\right)+4={\gamma }_{\left[t3R\right]}\left(T\right)+4.$$

Moreover, if g is a ${\gamma }_{\left[t3R\right]}\left(M\right)$-function, then by Remark 1, we have that ${\gamma }_{\left[t3R\right]}\left(M\right)=g\left(V\left(T\right)\right)+g\left(u_1\right)+4$. Let us define the function $g^{*}$ on T as follows: $g^{*}\left(u\right)=min\{4,g\left(u\right)+g\left(u_1\right)\}$ and $g^{*}\left(z\right)=g\left(z\right)$ otherwise. The function $g^{*}$ is a t3RDF on T and, therefore, ${\gamma }_{\left[t3R\right]}\left(T\right)\le w\left(g^{*}\right)\le g\left(V\left(T\right)\right)+g\left(u_1\right)={\gamma }_{\left[t3R\right]}\left(M\right)-4$, which leads us to ${\gamma }_{\left[t3R\right]}\left(M\right)\ge {\gamma }_{\left[t3R\right]}\left(T\right)+4,$ as desired.

Next, let us suppose that $s=2$ and $f\left(v\right)\le 1$ for all ${\gamma }_{\left[t3R\right]}\left(T\right)$-function $f.$ If f is any ${\gamma }_{\left[t3R\right]}\left(T\right)$-function, then the function $g\left(z\right)=f\left(z\right)$ for all $z\in T$ and $g\left(u_1\right)=g\left(u_3\right)=1,$ $g\left(u_2\right)=3$ is a t3RDF on M, leading us to ${\gamma }_{\left[t3R\right]}\left(M\right)\le {\gamma }_{\left[t3R\right]}\left(T\right)+5.$

Now, to prove the other inequality, let us consider g a ${\gamma }_{\left[t3R\right]}\left(M\right)$-function. Then, by Remark 1, we have that ${\gamma }_{\left[t3R\right]}\left(M\right)=g\left(V\left(T\right)\right)+g\left(u_1\right)+g\left(u_2\right)+g\left(u_3\right)=g\left(V\left(T\right)\right)+g\left(u_1\right)+4$. If $g\left(u_1\right)=0$, then the restriction of the function g to the subset $V\left(T\right)\subseteq V$, denoted by $g_{|V(T)}$, is a ${\gamma }_{\left[t3R\right]}\left(T\right)$-function and, by our assumptions, $g\left(v\right)$ must be less than or equal to 1, which implies that $g\left(u_2\right)=4$ and $g\left(u_3\right)\ge 1,$ a contradiction because $g\left(u_2\right)+g\left(u_3\right)=4.$ So, it must be $g\left(u_1\right)\ge 1.$

Reasoning by contradiction, let us suppose that ${\gamma }_{\left[t3R\right]}\left(M\right)\le {\gamma }_{\left[t3R\right]}\left(T\right)+4$ and, hence, $g\left(V\left(T\right)\right)+g\left(u_1\right)\le {\gamma }_{\left[t3R\right]}\left(T\right).$ As $g\left(u_1\right)\ge 1$, we may deduce that $g_{|V(T)}$ is not a t3RDF. This may be due to either $g\left(u\right)=0$ or $g\left(u\right)+g\left(v\right)\le 3.$ We can define a function $g^{*}$ on T as follows: $g^{*}\left(v\right)=min\{4,g\left(v\right)+g\left(u_1\right)-(1-min\{g\left(u\right),1\})\},$ $g^{*}\left(u\right)=max\{g\left(u\right),1\}$ and $g^{*}\left(z\right)=g\left(z\right)$ otherwise. Then, $g^{*}\left(u\right)\ge 1$ and $g^{*}\left(u\right)+g^{*}\left(v\right)\ge max\{g\left(u\right),1\}+g\left(v\right)+g\left(u_1\right)-(1-min\{g\left(u\right),1\})=g\left(v\right)+g\left(u_1\right)+g\left(u\right)\ge 4$ because g is a t3RDF and $u_1$ is an active neighbor of v. Hence, $g^{*}$ is a t3RD function on T. Moreover, if $g\left(u\right)=0$, then $g\left(v\right)+g\left(u_1\right)\ge 4$, and if $g\left(u\right)\ge 1$, then $g\left(u_1\right)\ge 2$ because $g\left(u\right)+g\left(v\right)\le 3$, whereas $g\left(u\right)+g\left(v\right)+g\left(u_1\right)\ge 5$. In any case, $g^{*}\left(v\right)\ge 2,$ against our assumption.

The proof of the case $s>2$ is analogous to the earlier case.  □

In a sufficiently long path, considering eight consecutive intermediate vertices, the optimal labeling from the perspective of total triple Roman domination is $1,3,0,2,2,0,3,1.$ These labels sum up to 12 units for those eight vertices. On average, this results in a cost of $12n/8=3n/2$ units. Obviously, the formula needs to be refined, as only integer values can be considered, and it must also be adapted to specific cases.

The latter leads us to consider the value $M_n$ and prove the following theorem.

Theorem 1.

Let $n\ge 3$ be a positive integer. Then, ${\gamma }_{\left[t3R\right]}\left(P_n\right)=M_n$.

Proof. 

We can readily check that ${\gamma }_{\left[t3R\right]}\left(P_n\right)=M_n$ whenever $2\le n\le 4$. By applying Propositions 13 and 14, we know that ${\gamma }_{\left[t3R\right]}\left(P_5\right)=8$ and ${\gamma }_{\left[t3R\right]}\left(P_6\right)=10$.

Let $f=(V_0,V_1,V_2,V_3,\varnothing )$ be a ${\gamma }_{\left[t3R\right]}\left(P_n\right)$-function on $P_n$ such that the number of vertices assigned 0 under f is the minimum. For simplicity, we occasionally represent a domination function $f,$ defined on a path $P_n$ with n vertices denoted by $V\left(P_n\right)=\{v_1,v_2,\dots ,v_n\}$, as an ordered n-tuple $f=(a_1,a_2,\dots ,a_n)$, where $a_j=f\left(v_j\right)$ for each $j\in \{1,2,\dots ,n\}$.

Let us note that ${\gamma }_{\left[t3R\right]}\left(P_4\right)={\gamma }_{\left[t3R\right]}\left(P_5\right)=8,$ ${\gamma }_{\left[t3R\right]}\left(P_6\right)=10$ and the following labeling, $(2,2,2,2),$ $(1,3,0,2,2),$ $(1,3,0,2,2,2)$, corresponds to ${\gamma }_{\left[t3R\right]}\left(P_n\right)$-functions for $n=4,5,6$, respectively. Therefore, by applying Lemma 3, we derive that ${\gamma }_{\left[t3R\right]}\left(P_7\right)={\gamma }_{\left[t3R\right]}\left(P_8\right)=12,$ ${\gamma }_{\left[t3R\right]}\left(P_9\right)=14.$

Analogously, since ${\gamma }_{\left[t3R\right]}\left(P_7\right)=12$ and the labeling $(1,3,0,2,2,2,2)$ is a ${\gamma }_{\left[t3R\right]}\left(P_7\right)$-function, it follows from Lemma 3 that ${\gamma }_{\left[t3R\right]}\left(P_{10}\right)=16$. It is straightforward to see that $(1,3,0,2,2,0,3,1)$ and $(1,3,0,2,2,2,0,3,1)$ are the only minimum possible labelings of $P_8$ and $P_9$, respectively. Thus, by applying Lemma 3 again, we deduce that ${\gamma }_{\left[t3R\right]}\left(P_{11}\right)=17$ and ${\gamma }_{\left[t3R\right]}\left(P_{12}\right)=19$.

Let $n\ge 13,k$ and q be positive integers such that $n=8k+q$ with $0\le q\le 7$. Let us denote $V\left(P_n\right)=\left\{v_{ij},w_l:1\le i\le k,1\le j\le 8,1\le l\le q\right\}$ whenever $q>0$ and $V\left(P_n\right)=\left\{v_{ij}:1\le i\le k,1\le j\le 8\right\}$ otherwise.

We define the following function: $f_q\left(v_{i1}\right)=f_q\left(v_{i8}\right)=1,$ $f_q\left(v_{i2}\right)=f_q\left(v_{i7}\right)=3,$ $f_q\left(v_{i3}\right)=f_q\left(v_{i6}\right)=0,$ $f_q\left(v_{i4}\right)=f_q\left(v_{i5}\right)=2$ whenever $1\le i\le k-1$. If $q\ne 1$, then $f_q\left(v_{k1}\right)=f_q\left(v_{k8}\right)=1,$ $f_q\left(v_{k2}\right)=f_q\left(v_{k7}\right)=3,$ $f_q\left(v_{k3}\right)=f_q\left(v_{k6}\right)=0,$ and $f_q\left(v_{k4}\right)=f_q\left(v_{k5}\right)=2$. Finally, if $q=1$, then $f_1\left(v_{k1}\right)=1,$ $f_q\left(v_{k2}\right)=f_q\left(v_{k8}\right)=3,$ $f_q\left(v_{k3}\right)=f_q\left(v_{k7}\right)=0,$ and $f_q\left(v_{k4}\right)=f_q\left(v_{k5}\right)=f_q\left(v_{k6}\right)=2$. For the remainder vertices, we establish the values of $f_q\left(w_l\right)$ in Table 3.

Table 3. Values of $f_q\left(w_l\right),1\le q\le 7,1\le l\le q$.

	${\mathit{f}}_{\mathit{q}}\left({\mathit{w}}_1\right)$	${\mathit{f}}_{\mathit{q}}\left({\mathit{w}}_2\right)$	${\mathit{f}}_{\mathit{q}}\left({\mathit{w}}_3\right)$	${\mathit{f}}_{\mathit{q}}\left({\mathit{w}}_4\right)$	${\mathit{f}}_{\mathit{q}}\left({\mathit{w}}_5\right)$	${\mathit{f}}_{\mathit{q}}\left({\mathit{w}}_6\right)$	${\mathit{f}}_{\mathit{q}}\left({\mathit{w}}_7\right)$
$q=1$	1
$q=2$	1	3
$q=3$	1	3	1
$q=4$	3	0	3	1
$q=5$	1	3	0	3	1
$q=6$	1	3	0	2	3	1
$q=7$	3	0	2	2	0	3	1

Observe the following:

• If $q=0$, then $w\left(f_q\right)=12k=⌈{\displaystyle \frac{3n}{2}}⌉=M_n.$
• If $q=1$, then $w\left(f_q\right)=12(k-1)+13+1=12k+2=⌈{\displaystyle \frac{3(8k+1)}{2}}⌉=M_n.$
• If $q=2$, then $w\left(f_q\right)=12k+4=⌈{\displaystyle \frac{3(8k+2)}{2}}⌉+1=M_n.$
• If $q=3$, then $w\left(f_q\right)=12k+5=⌈{\displaystyle \frac{3(8k+3)}{2}}⌉=M_n.$
• If $q=4$, then $w\left(f_q\right)=12k+7=⌈{\displaystyle \frac{3(8k+4)}{2}}⌉+1=M_n.$
• If $q=5$, then $w\left(f_q\right)=12k+8=⌈{\displaystyle \frac{3(8k+5)}{2}}⌉=M_n.$
• If $q=6$, then $w\left(f_q\right)=12k+10=⌈{\displaystyle \frac{3(8k+6)}{2}}⌉+1=M_n.$
• If $q=7$, then $w\left(f_q\right)=12k+11=⌈{\displaystyle \frac{3(8k+7)}{2}}⌉=M_n.$

Therefore, we have that ${\gamma }_{\left[t3R\right]}\left(P_n\right)=M_n$ for all $n\le 12$ and that ${\gamma }_{\left[t3R\right]}\left(P_n\right)\le M_n$ for all $n\ge 13.$

To prove that ${\gamma }_{\left[t3R\right]}\left(P_n\right)\ge M_n$ for all $n\ge 13$, we reason by induction. Let $n\ge 13$ be an integer and assume that ${\gamma }_{\left[t3R\right]}\left(P_m\right)\ge M_m$ for all $2\le m<n.$ Let us denote $V\left(P_n\right)=\{u_j:1\le j\le n\}$ such that the edges of the path are $\left\{u_j{u}_{j+1}\right\}$ whenever $j\le n-1.$ So, we know that ${\gamma }_{\left[t3R\right]}\left(P_{n-8}\right)\ge M_{n-8}$ and, by applying Lemma 3, we may derive that ${\gamma }_{\left[t3R\right]}\left(P_{n-5}\right)\ge M_{n-8}+4$. Analogously, it is deduced that ${\gamma }_{\left[t3R\right]}\left(P_{n-2}\right)\ge M_{n-8}+8=M_n-4$.

Let g be a ${\gamma }_{\left[t3R\right]}\left(P_n\right)$-function such that the number of vertices with a label 0 is the minimum. By Remark 1, we have that $g\left(u_n\right)+g\left(u_{n-1}\right)=4$ and, without loss of generality, we may suppose that $g\left(u_n\right)=1,g\left(u_{n-1}\right)=3.$ If $g\left(V\left(P_{n-2}\right)\right)\ge M_n-4$, then we are finished because ${\gamma }_{\left[t3R\right]}\left(P_n\right)=w\left(g\right)=g\left(V\left(P_{n-2}\right)\right)+1+3\ge M_n.$

Hence, assume that $g\left(V\left(P_{n-2}\right)\right)<M_n-4,$ which implies that $g_{|P_{n-2}}$ is not a t3RDF in $P_{n-2}$ because $M_n-4\le M_{n-2}.$ This may be due to several reasons, and we must study different situations.

• Case 1: $\mathit{g}\left({\mathit{u}}_{\mathit{n}-\mathbf{2}}\right)=\mathbf{0}$. In this case, by Lemma 1, we have that $g\left(u_{n-3}\right)=2$ and $g\left(u_{n-4}\right)=2.$ If $g\left(u_{n-5}\right)=1$, then we have to study two different possibilities: either $\mathit{g}\left({\mathit{u}}_{\mathit{n}-\mathbf{6}}\right)=\mathbf{2}$ and $\mathit{g}\left({\mathit{u}}_{\mathit{n}-\mathbf{7}}\right)\ge \mathbf{2}$ or $\mathit{g}\left({\mathit{u}}_{\mathit{n}-\mathbf{6}}\right)=\mathbf{3}$ and $\mathit{g}\left({\mathit{u}}_{\mathit{n}-\mathbf{7}}\right)\ge \mathbf{0}$. In both cases, we may define the following function: $g^{\prime }\left(u_{n-5}\right)=0,$ $g^{\prime }\left(u_{n-6}\right)=3,$ $g^{\prime }\left(u_{n-7}\right)=1,$ $g^{\prime }\left(u_{n-8}\right)=min\{3,g\left(u_{n-8}\right)+g\left(u_{n-5}\right)+g\left(u_{n-6}\right)+g\left(u_{n-7}\right)-4\}$, and $g^{\prime }\left(z\right)=g\left(z\right)$ otherwise. The function $g^{\prime }$ is a t3RDF with the same weight as g. We can proceed similarly if $g\left(u_{n-5}\right)=2$ or $g\left(u_{n-5}\right)=3.$ Therefore, we may assume that $g\left(u_n\right)=1,$ $g\left(u_{n-1}\right)=3,$ $g\left(u_{n-2}\right)=0,$ $g\left(u_{n-3}\right)=2,$ $g\left(u_{n-4}\right)=2,$ $g\left(u_{n-5}\right)=0,$ $g\left(u_{n-6}\right)=3,$ and $g\left(u_{n-7}\right)=1.$ Since $V_4=\varnothing ,$ then $g\left(u_{n-8}\right)\ge 1.$

Case 1.1: $\mathbf{1}\le \mathit{g}\left({\mathit{u}}_{\mathit{n}-\mathbf{8}}\right)\le \mathbf{2}$. Then, $g\left(u_{n-9}\right)\ge 2$ and $g\left(u_{n-8}\right)+g\left(u_{n-9}\right)\ge 4$. Thus, $g_{|P_{n-8}}$ is a t3RDF in $P_{n-8}$ and, consequently, $g\left(V\left(P_{n-8}\right)\right)\ge {\gamma }_{\left[t3R\right]}\left(P_{n-8}\right)\ge M_{n-8}$, implying that ${\gamma }_{\left[t3R\right]}\left(P_n\right)=w\left(g\right)\ge M_{n-8}+12=M_n.$

Case 1.2: $\mathit{g}\left({\mathit{u}}_{\mathit{n}-\mathbf{8}}\right)=\mathbf{3}$. Then, we may define the following function: $g^{\prime }\left(u_{n-8}\right)=1,$ $g^{\prime }\left(u_{n-9}\right)=min\{3,g\left(u_{n-9}\right)+2\}$, and $g^{\prime }\left(z\right)=g\left(z\right)$ otherwise. The function $g^{\prime }$ is a t3RDF under the conditions of Case 1.1.

• Case 2: $\mathit{g}\left({\mathit{u}}_{\mathit{n}-\mathbf{2}}\right)\ne \mathbf{0},$ $\mathit{g}\left({\mathit{u}}_{\mathit{n}-\mathbf{3}}\right)=\mathbf{0}.$ In this case, we may define the function $g^{\prime }\left(u_{n-2}\right)=0,$ $g^{\prime }\left(u_{n-3}\right)=g\left(u_{n-2}\right)$, and $g^{\prime }\left(z\right)=g\left(z\right)$ otherwise, which is a t3RDF under the conditions of Case 1.
• Case 3: $\mathit{g}\left({\mathit{u}}_{\mathit{n}-\mathbf{2}}\right)=\mathbf{1},\mathit{g}\left({\mathit{u}}_{\mathit{n}-\mathbf{3}}\right)\ne \mathbf{0}.$ Clearly, $g\left(u_{n-3}\right)\le 2,$ because $g_{|P_{n-2}}$ is not a t3RDF in $P_{n-2}.$ $g\left(u_{n-3}\right)+g\left(u_{n-4}\right)\ge 4$, and we have that $g_{|P_{n-3}}$ is a t3RDF in $P_{n-3}$, and so ${\gamma }_{\left[t3R\right]}\left(P_n\right)=w\left(g\right)=g\left(V\left(P_{n-3}\right)\right)+g\left(u_{n-2}\right)+g\left(u_{n-1}\right)+g\left(u_n\right)\ge M_{n-3}+5\ge M_n$.
• Case 4: $\mathit{g}\left({\mathit{u}}_{\mathit{n}-\mathbf{2}}\right)\ge \mathbf{2},\mathit{g}\left({\mathit{u}}_{\mathit{n}-\mathbf{3}}\right)\ne \mathbf{0}.$ We can define the function $g^{\prime }\left(u_{n-2}\right)=1,$ $g^{\prime }\left(u_{n-3}\right)=min\{3,g\left(u_{n-3}\right)+g\left(u_{n-2}\right)-1\}$ and $g^{\prime }\left(z\right)=g\left(z\right)$ otherwise, which is a t3RDF under the conditions of Case 3.

Summarizing, we have shown that ${\gamma }_{\left[t3R\right]}\left(P_n\right)\ge M_n,$ which concludes the proof.  □

Theorem 2.

Let be $n\ge 3$ a positive integer. Then,

$${\gamma }_{\left[t3R\right]}\left(C_n\right)=\left\{\begin{array}{ccc}\lceil {\displaystyle \frac{3n}{2}}\rceil & & if n\equiv 0,1,3,5,7\left(\mathrm{mod}8\right).\hfill \\ \lceil {\displaystyle \frac{3n}{2}}\rceil +1& & if n\equiv 2,4,6\left(\mathrm{mod}8\right).\hfill \end{array}\right.$$

Proof. 

Let us denote

$${\overline{M}}_n=\left\{\begin{array}{ccc}\lceil {\displaystyle \frac{3n}{2}}\rceil & & if n\equiv 0,1,3,5,7\left(\mathrm{mod}8\right).\hfill \\ \lceil {\displaystyle \frac{3n}{2}}\rceil +1& & if n\equiv 2,4,6\left(\mathrm{mod}8\right).\hfill \end{array}\right.$$

Note that ${\overline{M}}_n=M_n$ whenever $n\ne 4,7$ and ${\overline{M}}_n=M_n-1$ for $n\in \{4,7\}.$

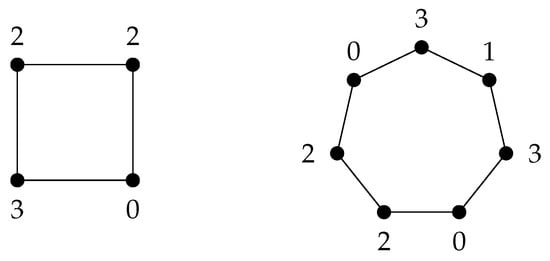
First, as shown in Figure 5, we have that ${\gamma }_{\left[t3R\right]}\left(C_n\right)\le {\overline{M}}_n$ for $n\in \{4,7\}$. On the other side, since ${\gamma }_{\left[t3R\right]}\left(C_n\right)\le {\gamma }_{\left[t3R\right]}\left(P_n\right)$, then we also have that ${\gamma }_{\left[t3R\right]}\left(C_n\right)\le {\gamma }_{\left[t3R\right]}\left(P_n\right)=M_n={\overline{M}}_n$ for all $n\ne 4,7.$

Figure 5. Total triple Roman dominating functions for $C_4$ and $C_7$.

To prove the other inequality, we proceed by induction on the order of the cycle. By Proposition 13, we have that

$${\gamma }_{\left[t3R\right]}\left(C_n\right)\ge ⌈{\displaystyle \frac{6n}{5}}⌉+2={\overline{M}}_n\mathrm{for}n\le 8.$$

Let $n\ge 9$ be an integer, and assume that ${\gamma }_{\left[t3R\right]}\left(C_{n^{\prime }}\right)\ge {\overline{M}}_{n^{\prime }}$ for all $3\le n^{\prime }<n.$ Denote by $V\left(C_n\right)=\{u_1,\dots ,u_n\}$ the set of consecutive vertices of the cycle. Let f be a ${\gamma }_{\left[t3R\right]}\left(C_n\right)$-function such that the number of vertices labeled with 0 is the minimum, which, by applying Lemma 1, implies that $V_4=\varnothing$. Since $n\ge 9$, we may consider five consecutive vertices, say $\{u_{i-2},u_{i-1},u_i,u_{i+1},u_{i+2}\}$. By Proposition 2, we can assume that $g\left(u_i\right)=0$ and, again by Lemma 1, we may suppose, without loss of generality, that $f\left(u_{i-2}\right)=f\left(u_{i-1}\right)=2,f\left(u_{i+1}\right)=3,f\left(u_{i+2}\right)=1$ and $f\left(u_{i+3}\right)\ne 0.$ We have to discuss some different possibilities.

• Case 1: $\mathit{f}\left({\mathit{u}}_{\mathit{i}-\mathbf{3}}\right)=\mathbf{0}.$ In this case, it must be that $f\left(u_{i-4}\right)=3,$ $f\left(u_{i-5}\right)=1$ and $f\left(u_{i-6}\right)\ne 0.$

Case 1.1: $\mathit{f}\left({\mathit{u}}_{\mathit{i}-\mathbf{6}}\right)+\mathit{f}\left({\mathit{u}}_{\mathit{i}+\mathbf{3}}\right)\ge \mathbf{4}.$ We can readily check that ${\gamma }_{\left[t3R\right]}\left(C_n\right)\ge {\overline{M}}_n$ for $n=9,10$. Let $n\ge 11$ and consider the cycle $C^{\prime }$ or order $n-8$ obtained by joining $u_{i-6}$ and $u_{i+3}.$ Thus, $f_{|C^{\prime }}$ is a t3RDF and ${\gamma }_{\left[t3R\right]}\left(C_n\right)=f\left(V\left(C_n\right)\right)=f\left(V\left(C^{\prime }\right)\right)+f\left(u_{i-5}\right)+f\left(u_{i-4}\right)+f\left(u_{i-3}\right)+f\left(u_{i-2}\right)+f\left(u_{i-1}\right)+f\left(u_i\right)+f\left(u_{i+1}\right)+f\left(u_{i+2}\right)\ge \overline{M}(n-8)+12\ge {\overline{M}}_n.$

Case 1.2: $\mathit{f}\left({\mathit{u}}_{\mathit{i}-\mathbf{6}}\right)=\mathit{f}\left({\mathit{u}}_{\mathit{i}+\mathbf{3}}\right)=\mathbf{1}.$ Then, it must be that $f\left(u_{i-7}\right)=f\left(u_{i+4}\right)=3,$ and the cycle $C^{\prime }$ or order $n-8$ obtained by joining $u_{i-6}$ and $u_{i+3}$ satisfies that $f_{|C^{\prime }}$ is a t3RDF with ${\gamma }_{\left[t3R\right]}\left(C_n\right)=f\left(V\left(C_n\right)\right)=f\left(V\left(C^{\prime }\right)\right)+f\left(u_{i-5}\right)+f\left(u_{i-4}\right)+f\left(u_{i-3}\right)+f\left(u_{i-2}\right)+f\left(u_{i-1}\right)+f\left(u_i\right)+f\left(u_{i+1}\right)+f\left(u_{i+2}\right)\ge \overline{M}(n-8)+12\ge {\overline{M}}_n.$

Case 1.3: $\mathit{f}\left({\mathit{u}}_{\mathit{i}-\mathbf{6}}\right)=\mathbf{2},\mathit{f}\left({\mathit{u}}_{\mathit{i}+\mathbf{3}}\right)=\mathbf{1},$ which implies that $f\left(u_{i+4}\right)=3$ and $f\left(u_{i-7}\right)\ge 2.$ If $i+4=i-7$, then $n=11$ and ${\gamma }_{\left[t3R\right]}\left(C_{11}\right)=w\left(f\right)=18\ge 17={\overline{M}}_{11}.$ Thus, assume that $n\ge 12.$ If $u_{i+4}$ is adjacent to $u_{i-7}$, then $n=12$ and ${\gamma }_{\left[t3R\right]}\left(C_{12}\right)=w\left(f\right)\ge 20\ge 19={\overline{M}}_{12}.$ Thus, assume that $n\ge 13$ and consider the cycle $C^{\prime }$ or order $n-8$ obtained by joining $u_{i-6}$ and $u_{i+3}$. Again, $f_{|C^{\prime }}$ is a t3RDF with ${\gamma }_{\left[t3R\right]}\left(C_n\right)=f\left(V\left(C_n\right)\right)=f\left(V\left(C^{\prime }\right)\right)+f\left(u_{i-5}\right)+f\left(u_{i-4}\right)+f\left(u_{i-3}\right)+f\left(u_{i-2}\right)+f\left(u_{i-1}\right)+f\left(u_i\right)+f\left(u_{i+1}\right)+f\left(u_{i+2}\right)\ge \overline{M}(n-8)+12\ge {\overline{M}}_n.$

• Case 2: $\mathit{f}\left({\mathit{u}}_{\mathit{i}-\mathbf{3}}\right)=\mathbf{1}.$ Then, it must be that $f\left(u_{i-4}\right)\ge 2.$ Let $C^{\prime }$ be the cycle or order $n-1$ obtained by joining $u_{i-4}$ and $u_{i-2}.$ We have that ${\gamma }_{\left[t3R\right]}\left(C_n\right)=f\left(V\left(C_n\right)\right)=f\left(V\left(C^{\prime }\right)\right)+f\left(u_{i-3}\right)\ge \overline{M}(n-1)+2\ge {\overline{M}}_n.$
• Case 3: $\mathit{f}\left({\mathit{u}}_{\mathit{i}-\mathbf{3}}\right)\ge \mathbf{2}.$ If so, we may consider the cycle $C^{\prime }$ or order $n-1$ obtained by joining $u_{i-3}$ and $u_{i-1}.$ We can readily check that $f_{|C^{\prime }}$ is a t3RDF and ${\gamma }_{\left[t3R\right]}\left(C_n\right)=f\left(V\left(C_n\right)\right)=f\left(V\left(C^{\prime }\right)\right)+f\left(u_{i-2}\right)\ge \overline{M}(n-1)+2\ge {\overline{M}}_n.$

This concludes the proof.  □

In this section, we characterized those graphs with the minimum possible value of ${\gamma }_{\left[t3R\right]}\left(G\right)=5$ and proved that there are no graphs with ${\gamma }_{\left[t3R\right]}\left(G\right)=6.$ We also determined the exact values of the total triple Roman domination number ${\gamma }_{\left[t3R\right]}$ for paths and cycles. For paths $P_n$ of order $n\ge 3$, we established that ${\gamma }_{\left[t3R\right]}\left(P_n\right)=M_n$, where $M_n$ is defined based on modular arithmetic conditions (Theorem 1). For cycles $C_n$, we showed that ${\gamma }_{\left[t3R\right]}\left(C_n\right)=\lceil {\displaystyle \frac{3n}{2}}\rceil$ when $n\equiv 0,1,3,5,7(mod8)$ and ${\gamma }_{\left[t3R\right]}\left(C_n\right)=\lceil {\displaystyle \frac{3n}{2}}\rceil +1$ when $n\equiv 2,4,6(mod8)$ (Theorem 2). These results highlight the structural differences between paths and cycles and provide a foundation for further exploration of this parameter in other graph families.

6. Discussion

In this paper, we introduced a novel concept called total triple Roman domination in graphs, which represents a variant of the classical Roman domination problem by requiring additional conditions on dominating sets to provide greater robustness and reliability for a graph. The new concept was formally defined, and it was shown that the associated decision problem is NP-complete even when restricted to bipartite graphs. Moreover, several sharp upper and lower bounds for the parameter were obtained, as well as the exact value for some particular graphs. The total triple Roman domination model has potential uses in real-world scenarios requiring layered defense mechanisms, such as the below.

• Cybersecurity networks, where nodes with higher labels represent multi-layered firewalls.
• Urban planning, ensuring backup resources (e.g., hospitals, police stations) are optimally placed.
• Robust sensor coverage in IoT systems, minimizing blind spots.

As a future line of research, we intend to prove that the problem remains NP-complete in general but can be reduced to a linear problem in specific families of graphs, such as trees. Additionally, the exact value of the parameter should be investigated for other graphs or graph families with specific structural properties.