Neuronal Mesh Reconstruction from Image Stacks Using Implicit Neural Representations
Abstract
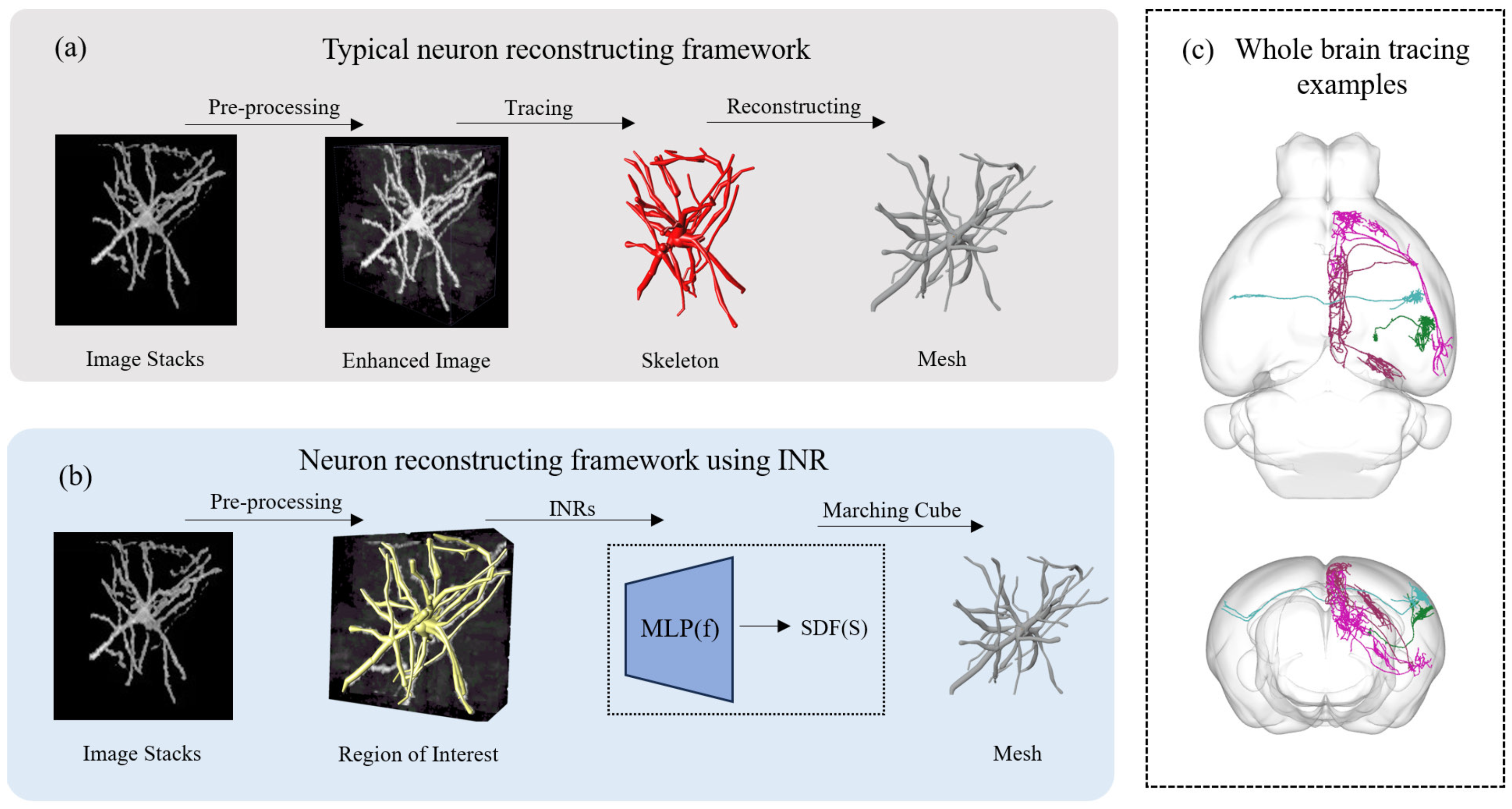
1. Introduction
- We present a new deep learning framework capable of extracting neuronal membrane surfaces from image stacks in an end-to-end manner.
- We propose a framework for neuronal reconstruction that integrates a GCN with attention mechanisms to accurately extract neural structural features.
- The proposed method demonstrates superior performance in both the detailed reconstruction of local dendritic regions and the global reconstruction of complete neuronal dendritic structures.
2. Related Work
2.1. Neuron Tracing from Light Microscopy Images
2.2. Neuron Reconstruction from Morphology Skeletons
2.3. Implicit Neural Representation
3. Methods
3.1. Using SDF to Represent Neurons
3.2. Implicit Representation Modeling
3.3. Neural Network Architecture
4. Experiment Results
4.1. Data
4.2. Reconstruction Analysis
4.2.1. Quantitative Analysis
4.2.2. Visualization Analysis
4.3. Space of INR
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| MLP | Multi-layer perceptron |
| INR | Implicit Neural Representations |
| SDF | Signed distance function |
| GCN | Graph convolutional networks |
| GAT | Graph attention network |
| BCE | Binary Cross-Entropy |
| 3D | Three-dimensional |
| 2D | Two-dimensional |
| AFM | Automation-Following-Manual |
References
- Senft, S.L. A Brief History of Neuronal Reconstruction. Neuroinformatics 2011, 9, 119–128. [Google Scholar] [CrossRef]
- Markram, H.; Muller, E.; Ramaswamy, S.; Reimann, M.; Abdellah, M.; Sanchez, C.; Ailamaki, A.; Alonso-Nanclares, L.; Antille, N.; Arsever, S.; et al. Reconstruction and Simulation of Neocortical Microcircuitry. Cell 2015, 163, 456–492. [Google Scholar] [CrossRef]
- Kim, J.; Zhao, T.; Petralia, R.S.; Yu, Y.; Peng, H.; Myers, E.; Magee, J.C. mGRASP Enables Mapping Mammalian Synaptic Connectivity with Light Microscopy. Nat. Methods 2012, 9, 96–102. [Google Scholar] [CrossRef]
- Parekh, R.; Ascoli, G. Neuronal Morphology Goes Digital: A Research Hub for Cellular and System Neuroscience. Neuron 2013, 77, 1017–1038. [Google Scholar] [CrossRef]
- Iascone, D.M.; Li, Y.; Sümbül, U.; Doron, M.; Chen, H.; Andreu, V.; Goudy, F.; Blockus, H.; Abbott, L.F.; Segev, I.; et al. Whole-Neuron Synaptic Mapping Reveals Spatially Precise Excitatory/Inhibitory Balance Limiting Dendritic and Somatic Spiking. Neuron 2020, 106, 566–578.e8. [Google Scholar] [CrossRef]
- Mörschel, K.; Breit, M.; Queisser, G. Generating Neuron Geometries for Detailed Three-Dimensional Simulations Using AnaMorph. Neuroinformatics 2017, 15, 247–269. [Google Scholar] [CrossRef]
- Hepburn, I.; Chen, W.; Wils, S.; De Schutter, E. STEPS: Efficient Simulation of Stochastic Reaction–diffusion Models in Realistic Morphologies. BMC Syst. Biol. 2012, 6, 36. [Google Scholar] [CrossRef]
- Yuan, X.; Trachtenberg, J.T.; Potter, S.M.; Roysam, B. MDL Constrained 3-D Grayscale Skeletonization Algorithm for Automated Extraction of Dendrites and Spines from Fluorescence Confocal Images. Neuroinformatics 2009, 7, 213–232. [Google Scholar] [CrossRef]
- Al-Kofahi, K.; Lasek, S.; Szarowski, D.; Pace, C.; Nagy, G.; Turner, J.; Roysam, B. Rapid Automated Three-dimensional Tracing of Neurons from Confocal Image Stacks. IEEE Trans. Inf. Technol. Biomed. 2002, 6, 171–187. [Google Scholar] [CrossRef]
- Rodriguez, A.; Ehlenberger, D.B.; Dickstein, D.L.; Hof, P.R.; Wearne, S.L. Automated Three-Dimensional Detection and Shape Classification of Dendritic Spines from Fluorescence Microscopy Images. PLoS ONE 2008, 3, e1997. [Google Scholar] [CrossRef]
- Rodriguez, A.; Ehlenberger, D.B.; Hof, P.R.; Wearne, S.L. Three-dimensional Neuron Tracing by Voxel Scooping. J. Neurosci. Methods 2009, 184, 169–175. [Google Scholar] [CrossRef]
- Choromanska, A.; Chang, S.F.; Yuste, R. Automatic Reconstruction of Neural Morphologies with Multi-Scale Tracking. Front. Neural Circuits 2012, 6, 25. [Google Scholar] [CrossRef]
- Wang, Y.; Narayanaswamy, A.; Tsai, C.L.; Roysam, B. A Broadly Applicable 3-D Neuron Tracing Method Based on Open-Curve Snake. Neuroinformatics 2011, 9, 193–217. [Google Scholar] [CrossRef]
- Cohen, L.D.; Kimmel, R. Global Minimum for Active Contour Models: A Minimal Path Approach. Int. J. Comput. Vis. 1997, 24, 57–78. [Google Scholar] [CrossRef]
- Peng, H.; Long, F.; Myers, G. Automatic 3D Neuron Tracing Using All-path Pruning. Bioinformatics 2011, 27, i239–i247. [Google Scholar] [CrossRef]
- Xiao, H.; Peng, H. APP2: Automatic tracing of 3D neuron morphology based on hierarchical pruning of a gray-weighted image distance-tree. Bioinformatics 2013, 29, 1448–1454. [Google Scholar] [CrossRef]
- Basu, S.; Condron, B.; Aksel, A.; Acton, S. Segmentation and Tracing of Single Neurons from 3D Confocal Microscope Images. IEEE Trans. Inf. Technol. Biomed. Publ. IEEE Eng. Med. Biol. Soc. 2012, 17, 319–335. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, D.; Song, Y.; Peng, H.; Cai, W. Automated 3-D Neuron Tracing With Precise Branch Erasing and Confidence Controlled Back Tracking. IEEE Trans. Med. Imaging 2018, 37, 2441–2452. [Google Scholar] [CrossRef]
- Yang, J.; Hao, M.; Liu, X.; Wan, Z.; Zhong, N.; Peng, H. FMST: An Automatic Neuron Tracing Method Based on Fast Marching and Minimum Spanning Tree. Neuroinformatics 2019, 17, 185–196. [Google Scholar] [CrossRef] [PubMed]
- Dorkenwald, S.; Schneider-Mizell, C.M.; Brittain, D.; Halageri, A.; Jordan, C.; Kemnitz, N.; Castro, M.A.; Silversmith, W.; Maitin-Shephard, J.; Troidl, J.; et al. CAVE: Connectome Annotation Versioning Engine. bioRxiv 2023. [Google Scholar] [CrossRef]
- Wang, S.; Li, X.; Mitra, P.; Wang, Y. Topological Skeletonization and Tree-Summarization of Neurons Using Discrete Morse Theory. bioRxiv 2018. [Google Scholar] [CrossRef]
- Gala, R.; Chapeton, J.; Jitesh, J.; Bhavsar, C.; Stepanyants, A. Active Learning of Neuron Morphology for Accurate Automated Tracing of Neurites. Front. Neuroanat. 2014, 8, 37. [Google Scholar] [CrossRef]
- Wang, C.W.; Lee, Y.C.; Pradana, H.; Zhou, Z.; Peng, H. Ensemble Neuron Tracer for 3D Neuron Reconstruction. Neuroinformatics 2017, 15, 185–198. [Google Scholar] [CrossRef]
- Li, Q.; Shen, L. Neuron Segmentation Using 3D Wavelet Integrated Encoder–decoder Network. Bioinformatics 2022, 38, 809–817. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, D.; Song, Y.; Liu, S.; Huang, H.; Chen, M.; Peng, H.; Cai, W. Multiscale Kernels for Enhanced U-Shaped Network to Improve 3D Neuron Tracing. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Long Beach, CA, USA, 16–17 June 2019; pp. 1105–1113. [Google Scholar]
- Yang, B.; Liu, M.; Wang, Y.; Zhang, K.; Meijering, E. Structure-Guided Segmentation for 3D Neuron Reconstruction. IEEE Trans. Med. Imaging 2022, 41, 903–914. [Google Scholar] [CrossRef]
- Megjhani, M.; Rey-Villamizar, N.; Merouane, A.; Lu, Y.; Mukherjee, A.; Trett, K.; Chong, P.; Harris, C.; Shain, W.; Roysam, B. Population-scale three-dimensional reconstruction and quantitative profiling of microglia arbors. Bioinformatics 2015, 31, 2190–2198. [Google Scholar] [CrossRef]
- Becker, C.; Rigamonti, R.; Lepetit, V.; Fua, P. Supervised Feature Learning for Curvilinear Structure Segmentation. In Advanced Information Systems Engineering; Hutchison, D., Kanade, T., Kittler, J., Kleinberg, J.M., Mattern, F., Mitchell, J.C., Naor, M., Nierstrasz, O., Pandu Rangan, C., Steffen, B., et al., Eds.; Springer: Berlin/Heidelberg, Gernamy, 2013; pp. 526–533. [Google Scholar]
- Liu, Y.; Wang, G.; Ascoli, G.A.; Zhou, J.; Liu, L. Neuron Tracing from Light Microscopy Images: Automation, Deep Learning and Bench Testing. Bioinformatics 2022, 38, 5329–5339. [Google Scholar] [CrossRef]
- Manubens-Gil, L.; Zhou, Z.; Chen, H.; Ramanathan, A.; Liu, X.; Liu, Y.; Bria, A.; Gillette, T.; Ruan, Z.; Yang, J.; et al. BigNeuron: A Resource to Benchmark and Predict Performance of Algorithms for Automated Tracing of Neurons in Light Microscopy Datasets. Nat. Methods 2023, 20, 824–835. [Google Scholar] [CrossRef]
- Glaser, J.R.; Glaser, E.M. Neuron Imaging with Neurolucida—A PC-based System for Image Combining Microscopy. Comput. Med. Imaging Graph. 1990, 14, 307–317. [Google Scholar] [CrossRef]
- Gleeson, P.; Steuber, V.; Silver, R.A. neuroConstruct: A Tool for Modeling Networks of Neurons in 3D Space. Neuron 2007, 54, 219–235. [Google Scholar] [CrossRef] [PubMed]
- Eberhard, J.; Wanner, A.; Wittum, G. NeuGen: A Tool for The Generation of Realistic Morphology of Cortical Neurons and Neural Networks in 3D. Neurocomputing 2006, 70, 327–342. [Google Scholar] [CrossRef]
- Wilson, M.A.; Bhalla, U.S.; Uhley, J.D.; Bower, J.M. GENESIS: A System for Simulating Neural Networks. In Proceedings of the 2nd International Conference on Neural Information Processing Systems, Cambridge, MA, USA, 1 January 1988; NIPS’88; pp. 485–492. [Google Scholar]
- Brito, J.P.; Mata, S.; Bayona, S.; Pastor, L.; DeFelipe, J.; Benavides-Piccione, R. Neuronize: A Tool for Building Realistic Neuronal Cell Morphologies. Front. Neuroanat. 2013, 7, 15. [Google Scholar] [CrossRef]
- Garcia-Cantero, J.J.; Brito, J.P.; Mata, S.; Bayona, S.; Pastor, L. NeuroTessMesh: A Tool for the Generation and Visualization of Neuron Meshes and Adaptive On-the-Fly Refinement. Front. Neuroinform. 2017, 11, 38. [Google Scholar] [CrossRef]
- Abdellah, M.; Hernando, J.; Eilemann, S.; Lapere, S.; Antille, N.; Markram, H.; Schürmann, F. NeuroMorphoVis: A Collaborative Framework for Analysis and Visualization of Neuronal Morphology Skeletons Reconstructed from Microscopy Stacks. Bioinformatics 2018, 34, i574–i582. [Google Scholar] [CrossRef]
- Abdellah, M.; Guerrero, N.R.; Lapere, S.; Coggan, J.S.; Keller, D.; Coste, B.; Dagar, S.; Courcol, J.D.; Markram, H.; Schürmann, F. Interactive Visualization and Analysis of Morphological Skeletons of Brain Vasculature Networks with VessMorphoVis. Bioinformatics 2020, 36, i534–i541. [Google Scholar] [CrossRef]
- Abdellah, M.; Foni, A.; Zisis, E.; Guerrero, N.R.; Lapere, S.; Coggan, J.S.; Keller, D.; Markram, H.; Schürmann, F. Metaball Skinning of Synthetic Astroglial Morphologies into Realistic Mesh Models for in silico Simulations and Visual Analytics. Bioinformatics 2021, 37, i426–i433. [Google Scholar] [CrossRef]
- Zhu, X.; Liu, X.; Liu, S.; Shen, Y.; You, L.; Wang, Y. Robust Quasi-uniform Surface Meshing of Neuronal Morphology Using Line Skeleton-based Progressive Convolution Approximation. Front. Neuroinform. 2022, 16, 953930. [Google Scholar] [CrossRef]
- Mildenhall, B.; Srinivasan, P.P.; Tancik, M.; Barron, J.T.; Ramamoorthi, R.; Ng, R. NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis. Commun. ACM 2022, 65, 99–106. [Google Scholar] [CrossRef]
- Mescheder, L.; Oechsle, M.; Niemeyer, M.; Nowozin, S.; Geiger, A. Occupancy Networks: Learning 3D Reconstruction in Function Space. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 4455–4465. [Google Scholar]
- Park, J.J.; Florence, P.; Straub, J.; Newcombe, R.; Lovegrove, S. DeepSDF: Learning Continuous Signed Distance Functions for Shape Representation. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 165–174. [Google Scholar]
- Zang, G.; Idoughi, R.; Li, R.; Wonka, P.; Heidrich, W. IntraTomo: Self-supervised Learning-based Tomography via Sinogram Synthesis and Prediction. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 11–17 October 2021; pp. 1940–1950. [Google Scholar]
- Wu, Q.; Li, Y.; Sun, Y.; Zhou, Y.; Wei, H.; Yu, J.; Zhang, Y. An Arbitrary Scale Super-Resolution Approach for 3D MR Images via Implicit Neural Representation. IEEE J. Biomed. Health Inform. 2023, 27, 1004–1015. [Google Scholar] [CrossRef] [PubMed]
- Shen, L.; Pauly, J.; Xing, L. NeRP: Implicit Neural Representation Learning With Prior Embedding for Sparsely Sampled Image Reconstruction. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 770–782. [Google Scholar] [CrossRef] [PubMed]
- Wu, Q.; Li, Y.; Xu, L.; Feng, R.; Wei, H.; Yang, Q.; Yu, B.; Liu, X.; Yu, J.; Zhang, Y. IREM: High-Resolution Magnetic Resonance Image Reconstruction via Implicit Neural Representation. In Medical Image Computing and Computer Assisted Intervention—MICCAI 2021; De Bruijne, M., Cattin, P.C., Cotin, S., Padoy, N., Speidel, S., Zheng, Y., Essert, C., Eds.; Springer International Publishing: Cham, Switzerland, 2021; Volume 12906, pp. 65–74. [Google Scholar]
- Sun, Y.; Liu, J.; Xie, M.; Wohlberg, B.; Kamilov, U. CoIL: Coordinate-Based Internal Learning for Tomographic Imaging. IEEE Trans. Comput. Imaging 2021, 7, 1400–1412. [Google Scholar] [CrossRef]
- Wolterink, J.M.; Zwienenberg, J.C.; Brune, C. Implicit Neural Representations for Deformable Image Registration. In Proceedings of Machine Learning Research PMLR, Proceedings of the 5th International Conference on Medical Imaging with Deep Learning, Zurich, Switzerland, 6–8 July 2022; Konukoglu, E., Menze, B., Venkataraman, A., Baumgartner, C., Dou, Q., Albarqouni, S., Eds.; ML Research Press: Cambridge, MA, USA, 2022; Volume 172, pp. 1349–1359. [Google Scholar]
- Sun, S.; Han, K.; You, C.; Tang, H.; Kong, D.; Naushad, J.; Yan, X.; Ma, H.; Khosravi, P.; Duncan, J.S.; et al. Medical Image Registration via Neural Fields. Med. Image Anal. 2024, 97, 103249. [Google Scholar] [CrossRef] [PubMed]
- Yang, R.; Xiao, T.; Cheng, Y.; Cao, Q.; Qu, J.; Suo, J.; Dai, Q. SCI: A Spectrum Concentrated Implicit Neural Compression for Biomedical Data. Proc. AAAI Conf. Artif. Intell. 2023, 37, 4774–4782. [Google Scholar] [CrossRef]
- Yang, R. TINC: Tree-Structured Implicit Neural Compression. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 18–22 June 2023; pp. 18517–18526. [Google Scholar]
- Zhang, H.; Wang, R.; Zhang, J.; Li, C.; Yang, G.; Spincemaille, P.; Nguyen, T.B.; Wang, Y. NeRD: Neural Representation of Distribution for Medical Image Segmentation. arXiv 2021, arXiv:2103.04020. [Google Scholar]
- Wiesner, D.; Suk, J.; Dummer, S.; Svoboda, D.; Wolterink, J.M. Implicit Neural Representations for Generative Modeling of Living Cell Shapes. In Medical Image Computing and Computer Assisted Intervention—MICCAI 2022; Wang, L., Dou, Q., Fletcher, P.T., Speidel, S., Li, S., Eds.; Springer Nature: Cham, Switzerland, 2022; Volume 13434, pp. 58–67. [Google Scholar]
- Alblas, D.; Hofman, M.; Brune, C.; Yeung, K.K.; Wolterink, J.M. Implicit Neural Representations for Modeling of Abdominal Aortic Aneurysm Progression. In Functional Imaging and Modeling of the Heart; Bernard, O., Clarysse, P., Duchateau, N., Ohayon, J., Viallon, M., Eds.; Springer Nature: Cham, Switzerland, 2023; pp. 356–365. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Liò, P.; Bengio, Y. Graph Attention Networks. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Lorensen, W.E.; Cline, H.E. Marching Cubes: A High Resolution 3D Surface Construction Algorithm. ACM SIGGRAPH Comput. Graph. 1987, 21, 163–169. [Google Scholar] [CrossRef]
- Zhou, Y.; Tuzel, O. VoxelNet: End-to-End Learning for Point Cloud Based 3D Object Detection. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 4490–4499. [Google Scholar]
- Li, Q.; Jia, X.; Zhou, J.; Shen, L.; Duan, J. Rediscovering BCE Loss for Uniform Classification. arXiv 2024, arXiv:2403.07289. [Google Scholar]
- Lin, T.Y.; Goyal, P.; Girshick, R.; He, K.; Dollar, P. Focal Loss for Dense Object Detection. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2999–3007. [Google Scholar]
- Li, X.; Sun, X.; Meng, Y.; Liang, J.; Wu, F.; Li, J. Dice Loss for Data-imbalanced NLP Tasks. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, Online, 5–10 July 2020; pp. 465–476. [Google Scholar]
- Peng, H.; Xie, P.; Liu, L.; Kuang, X.; Wang, Y.; Qu, L.; Gong, H.; Jiang, S.; Li, A.; Ruan, Z.; et al. Morphological Diversity of Single Neurons in Molecularly Defined Cell Types. Nature 2021, 598, 174–181. [Google Scholar] [CrossRef]
- Peng, H.; Hawrylycz, M.; Roskams, J.; Hill, S.; Spruston, N.; Meijering, E.; Ascoli, G. BigNeuron: Large-Scale 3D Neuron Reconstruction from Optical Microscopy Images. Neuron 2015, 87, 252–256. [Google Scholar] [CrossRef]
- Mancini, M.; Jones, D.K.; Palombo, M. Lossy Compression of Multidimensional Medical Images Using Sinusoidal Activation Networks: An Evaluation Study. In Computational Diffusion MRI; Cetin-Karayumak, S., Christiaens, D., Figini, M., Guevara, P., Pieciak, T., Powell, E., Rheault, F., Eds.; Springer Nature: Cham, Switzerland, 2022; Volume 13722, pp. 26–37. [Google Scholar]
- Sitzmann, V.; Martel, J.N.P.; Bergman, A.W.; Lindell, D.B.; Wetzstein, G. Implicit neural representations with periodic activation functions. In Proceedings of the NIPS’20: Proceedings of the 34th International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 6–12 December 2020; Curran Associates Inc.: Red Hook, NY, USA, 2020. [Google Scholar]
- Gao, T.; Sun, S.; Liu, H.; Gao, H. Exploring the Impact of Activation Functions in Training Neural ODEs. In Proceedings of the Thirteenth International Conference on Learning Representations, Singapore, 24–28 April 2025. [Google Scholar]
- Kingma, D.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the International Conference on Learning Representations, Banff, AB, Canada, 14–16 April 2014. [Google Scholar]







| Dataset | Original | Ours | DeepSDF | Wiesner |
|---|---|---|---|---|
| Peng | 25,247.3 ± 16,013.2 | 27,081.7 ± 10,657.1 | 1504.0 ± 1151.8 | 2928.3 ± 1280.1 |
| gold166 | 4,869,980.7 ± 3,471,001.5 | 4,957,674.0 ± 99,378.0 | 523,663.0 ± 5,430,585.7 | 165,344.0 ± 17,911.9 |
| Dataset | Original | Ours | DeepSDF | Wiesner |
|---|---|---|---|---|
| Peng | 25,122.3 ± 8887.2 | 28,860.0 ± 5462.3 | 1483.6 ± 824.2 | 3942.0 ± 943.1 |
| gold166 | 887,116.5 ± 591,552.0 | 761,935.0 ± 46,552.1 | 326,129.7 ± 246,538.4 | 25,914.5 ± 26,041.1 |
| Dataset | Ours | Deepsdf | Wiesner |
|---|---|---|---|
| Peng | 92.7% | 5.9% | 11.6% |
| gold166 | 98.2% | 10.8% | 3% |
| Dataset | Ours | Deepsdf | Wiesner |
|---|---|---|---|
| Peng | 85.1% | 5.9% | 15.7% |
| gold166 | 85.9% | 36.8% | 2.9% |
| Method | CD ↓ | IoU ↑ | Localized IoU ↑ |
|---|---|---|---|
| Ours | 14.9 | 0.85 | 0.77 |
| DeepSDF | 94.1 | 0.05 | 0.045 |
| Wiesner | 84.3 | 0.10 | 0.09 |
| Method | CD ↓ | IoU ↑ | Localized IoU ↑ |
|---|---|---|---|
| Ours | 14.1 | 0.90 | 0.81 |
| DeepSDF | 63.2 | 0.08 | 0.07 |
| Wiesner | 97.1 | 0.02 | 0.018 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, X.; Zhao, Y.; You, L. Neuronal Mesh Reconstruction from Image Stacks Using Implicit Neural Representations. Mathematics 2025, 13, 1276. https://doi.org/10.3390/math13081276
Zhu X, Zhao Y, You L. Neuronal Mesh Reconstruction from Image Stacks Using Implicit Neural Representations. Mathematics. 2025; 13(8):1276. https://doi.org/10.3390/math13081276
Chicago/Turabian StyleZhu, Xiaoqiang, Yanhua Zhao, and Lihua You. 2025. "Neuronal Mesh Reconstruction from Image Stacks Using Implicit Neural Representations" Mathematics 13, no. 8: 1276. https://doi.org/10.3390/math13081276
APA StyleZhu, X., Zhao, Y., & You, L. (2025). Neuronal Mesh Reconstruction from Image Stacks Using Implicit Neural Representations. Mathematics, 13(8), 1276. https://doi.org/10.3390/math13081276








