The Elitist Non-Dominated Sorting Crisscross Algorithm (Elitist NSCA): Crisscross-Based Multi-Objective Neural Architecture Search

Abstract

In recent years, neural architecture search (NAS) has been proposed for automatically designing neural network architectures, which searches for network architectures that outperform novel human-designed convolutional neural network (CNN) architectures. Related research has always been a hot topic. This paper proposes a multi-objective evolutionary algorithm called the elitist non-dominated sorting crisscross algorithm (elitist NSCA) and applies it to neural architecture search, which considers two optimization objectives: the accuracy and network parameters. In the algorithm, an innovative search space borrowed from the latest residual block and dense connection is proposed to ensure the quality of the compact architectures. A variable-length crisscross optimization strategy, which creatively iterates the evolution through inter-individual horizontal crossovers and intra-individual vertical crossovers, is employed to simultaneously optimize the microstructure parameters and macroscopic architecture of the CNN. In addition, a corresponding mutation operator is added pertinently based on the performance of the proxy model, and the elitist strategy is improved through pruning to reduce the impact of abnormal fitnesses. The experimental results on multiple datasets show that the proposed algorithm has a higher accuracy and robustness than those of certain state-of-the-art algorithms.

1. Introduction

With the rapid development of deep learning, the architectural design of deep neural networks has become an active research area in the past few years. In addition to the classical convolutional neural network architectures, such as DenseNet (Dense Convolutional Network), ResNet (Residual Neural Network), VGGNet (Visual Geometry Group Network), and GoogleNet (Google Inception Net), many new network architectures have been designed. The design of these architectures usually requires manual labor by experienced researchers with rich professional knowledge, and the design process is time-consuming, so it is difficult to specifically design a high-performance neural network architecture that can fulfill the requirements of a specific task.

Neural architecture search (NAS) has emerged to address these problems, which refers to the automatic search for task-specific neural networks [1,2,3]. NAS greatly reduces the requirements and time required for the architecture’s design, making the design of neural network architectures automatic and efficient. At present, the types of NAS can be divided into three main categories: (1) reinforcement-learning-based (RL-based), (2) differentiable-based (D-based), and (3) evolutionary-algorithm-based (EA-based). RL guides the search for the optimal architecture through a reward mechanism, which has strong adaptability. However, RL-based strategies usually have high resource requirements and take long search times [4]. D-based strategies utilize gradient descent for the architecture search, which has the advantages of a low computational cost and a fast search speed. However, the D-based strategies suffer from vanishing gradients and exploding gradients. Moreover, the D-based strategies have a limited search space, which means that they cannot cover complex search spaces [5]. Evolutionary algorithms simulate the natural evolutionary procedure to search for network architectures, and they are suitable for non-continuous and non-differentiable search spaces, which can be applied to a wide range of search tasks. To go further, evolutionary algorithms only evaluate a limited number of models and require lower computational costs compared to reinforcement learning [6]. In addition, many new technologies are also used in NAS, such as attention mechanisms [7], knowledge distillation [1], and pruning [8]. NAS has also been successfully applied in many fields, including object detection [9], image denoising [10], and image segmentation [7].

Compared with the reinforcement learning and gradient descent methods mentioned above, evolutionary algorithms have the following advantages in architecture search: they exhibit high robustness, enabling them to handle complex search spaces without requiring them to be differentiable, thus making them suitable for a broader range of architecture search tasks. Moreover, they can achieve effective parallelism, which improves the search efficiency. However, there are some common problems in existing evolutionary NASs: for one thing, there is limited research into the specifics of the search space. For another, the traditional evolutionary algorithms focus primarily on inter-individual iterative evolution while neglecting the relationships between different dimensions or features within an individual, with very few relevant studies on this aspect. Currently, many researchers are addressing these problems from two perspectives: (1) expansive search spaces [11] and (2) evolutionary algorithms [12,13,14].

To address the aforementioned issues in evolutionary NAS, this paper proposes a novel multi-objective evolutionary NAS algorithm that enhances the exploration of the search space by considering both inter-individual and intra-individual perspectives. The proposed algorithm, named the elitist non-dominated sorting crisscross algorithm (Elitist NSCA), is a crisscross-based multi-objective neural architecture search algorithm. Firstly, the crisscross optimization (CSO) algorithm is improved to be suitable for the evolution operation for variable-length individuals. Secondly, the ideas from the residual block and dense connection are borrowed to construct a new search space. Thirdly, according to the performance characteristics of the reference proxy model, a specific mutation operator is proposed to avoid embedding the algorithm into the local optimal solution. Ultimately, a fast non-dominated sorting operator and CSO are fused to derive a new multi-objective evolutionary algorithm. In order to verify the performance of the proposed algorithm on high-dimensional data further, the algorithm is applied to image classification. The contributions of this paper are summarized as follows:

• The horizontal crossover (HC) and vertical crossover (VC) of the original CSO are improved to adapt to variable-length individuals in the NAS. Moreover, the improved CSO is combined with a fast non-dominated sorting operator to explore the performance of the elitist NSCA on multi-objective optimization problems.
• When designing the new search space, the classical residual block and dense connection are combined to obtain a powerful search space for neural network architectures, which has high flexibility and performance potential.
• According to the performance characteristics of the proxy model, a mutation operator is used to dynamically increase the number of pooling layers or initialize or delete a cell with a certain probability.
• Aiming at the problem of the low survival rate of the offspring in the late iterations of evolutionary algorithms, the population space is effectively vacated for the offspring using population pruning, the survival rate of the offspring is improved, and the population’s diversity is increased.

The rest of this paper is organized as follows: Section 2 introduces the related work. Section 3 introduces the elitist NSCA in detail, including the search space, the operators, and the improved elitist strategy. In Section 4, the proposed algorithm is compared with some state-of-the-art algorithms on the CIFAR and ImageNet dataset, and its stability and convergence are evaluated. Moreover, an ablation experiment is presented to analyze the impact of each component of the algorithm on the performance. In Section 5, the generalization of the algorithm is verified by using power line inspection pictures taken using an UAV. The conclusions of this paper are presented in Section 6.

2. Related Work

2.1. Crisscross Optimization

CSO [12] is an evolutionary algorithm which consists of HC and VC. HC refers to the selection of two individuals from a population at random to perform the crossover operations, and it focuses on sampling better positions in different search spaces (i.e., hypercubes and their respective peripheries). VC refers to the crossover operation between the dimensions of a individual, which is designed to facilitate the stagnant dimensions of the population to jump out of local optima.

Although CSO was proposed in 2014, its fast convergence characteristics and global search capability have attracted many researchers to conduct uninterrupted research since then [12]. Compared with evolutionary algorithms such as particle swarm optimization (PSO) and differential evolution (DE), which need a continuous search space, CSO is more suitable for solving discrete optimization problems and fits with the characteristics of neural networks’ search spaces. In addition, many innovative technologies have been combined with CSO to explore the excellent performance, such as multi-objective technology, attention mechanism technology, segment imbalance regression technology, and distributed technology. For multi-objective technology, Meng et al. [13] proposed a novel hybrid model using multi-objective crisscross optimization to enhance the stability of wind power predictions, employing multivariate variational mode decomposition for a synchronized time–frequency analysis of wind-related data and optimizing the deep extreme learning machine parameters to ensure accuracy and stability. For attention mechanism technology, many researchers [15,16,17,18] have used an attention mechanism to dynamically weight the input features, leading to an obvious improvement in the quality of the sample data and the prediction accuracy. For segment imbalance regression technology, a segment imbalance regression method with crisscross optimization has been proposed to proactively dig and utilize the imbalanced nature of the samples within the context of sample imbalance problems [17]. For distributed technology, Meng et al. [14] proposed distributed crisscross optimization to address the MAED problem through fully decentralized optimization, aiming to protect the data privacy, reduce the solving dimensions, and alleviate the heavy communication burden.

However, the research on CSO is limited to electric power, wherein the dimensionality of the data is low, meaning that the data features generally have only a dozen dimensions. In addition, CSO encodes the population in a single way, so it is the same as the traditional evolutionary algorithms in this respect. In order to fill the above gaps and explore the performance of CSO in high-dimensional data further, this paper improves CSO for its application to variable-length individuals and applies the algorithm to NAS.

2.2. Neural Architecture Search Based on Multi-Objective Evolutionary Algorithms

Multi-objective optimization has always been a research hotspot, in which is challenging to balance the different objectives. Therefore, researchers have proposed the Pareto front and various strategies to solve the multi-objective network architecture search problem. MOEA-PS [19] aims to balance between the precision and time cost by utilizing an adjacency list to represent the internal structure of deep neural networks, introducing a unique mechanism to guide the crossover and mutation, and leveraging a proxy model to stack the structural blocks, thereby efficiently generating deep neural networks. Lu et al. [20] proposed a surrogate-assisted multi-objective method for neural architecture search, effectively addressing the demands of high-resolution image processing and real-time inference for applications like autonomous driving. Ma et al. [21] proposed a classifier-based Pareto evolution approach, addressing the problems of the ranking disorder and the inefficiency of the predictions in surrogate-driven methods. Luong et al. [22] proposed an Enhanced Training-Free Multi-Objective Evolutionary Neural Architecture Search (E-TF-MOENAS) method which optimized multiple training-free performance metrics simultaneously to achieve comparable architecture search results to those of training-based methods but with significantly reduced computational costs. Bagherzadeh et al. [23] proposed an Empirical Mode Decomposition (EMD) algorithm enhanced by multi-objective optimization, which improved upon the traditional EMD algorithm by directly estimating the signal trend (instead of using envelopes). It utilized a Genetic Algorithm to optimize the decision parameters, thereby enhancing the analytical capability for nonlinear and non-stationary aircraft ice-related data. Zhu et al. [7] propose a method called Topology Complexity Neural Architecture Search (TCNAS) which evaluates the topological complexity of neural networks and combines it with the accuracy to guide the search for lightweight and efficient networks.

3. The Method

This paper proposes the elitist NSCA, that mainly consists of a variable-length coding strategy, the latest residual block, the dense connection, the mutation operator, and the improved elitist strategy.

3.1. An Overview

Figure 1 shows the overall architecture of the proposed algorithm, wherein the five steps of the algorithm are the following:

• Initializing a population with variable-length individuals;
• Optimizing the population by using improved crisscross optimization and the mutation operator;
• Updating the population using the improved elitist strategy;
• Repeating step 2 until the termination criterion is satisfied;
• Performing full training by using the optimal neural network architecture.

In the proposed elitist NSCA, multiple sets of strings of different lengths represent the different components of the CNN, which are then parsed into PyTorch 1.13.1 to calculate the fitness on a given dataset (“initialization” in Figure 1). Then, several heuristic strategies are used to optimize the population to maximize the search for the optimal architecture (“horizontal crossover”, “vertical crossover”, and “mutation” in Figure 1). Next, the parent and multiple newly generated populations are combined, the new population is screened through population pruning, and the offspring population with the optimal fitness is selected by the elitist strategy (“elitist strategy” in Figure 1). Finally, after obtaining the CNN with the optimal architecture, the algorithm is fully trained on the data and outputs the optimal precision.

3.2. The Search Space

The search space is the foundation of NAS. The individual architecture, as shown in “network architecture” under “initialization” in Figure 1, consists of “conv”, “search space”, “attention”, and “FC”. Compared with the intuitive presentation under “initialization” in Figure 1,

Table 1. The complete architecture of the elitist NSCA.

conv		3 × 3, u
search space	dense block	$\left[\begin{array}{c}{c}_1\times c_1,u_1\\ c_2\times c_2,u_2\end{array}\right]\times v_1$
	transition layer	1 × 1 conv
attention		Squeeze-and-Excitation
FC		dropout, softmax

NOTE: u and v represent the number of channels inside the residual block and the number of residual blocks, respectively; c represents the size of the convolution kernel; the square bracket represents a residual group which consists of multiple of the latest residual blocks.

provides an in-depth analysis of the individual architecture from a parameter perspective. The network architecture draws inspiration from the classic DenseNet, wherein “conv” represents the convolutional layer; “attention” denotes the attention mechanism, specifically Squeeze-and-Excitation attention [24]; and “FC” stands for the fully connected layer. Especially, the “search space” is the core part of the individual architecture, primarily composed of the transition layer and dense block. The transition layer is used to effectively control the number of channels within a reasonable range, which prevents the number of channels from exploding. The dense block uses the latest residual block as the basic cell, combining multiple residual blocks into a residual group (indicated by the square bracket in Table 1). Unlike the classic DenseNet, which simply densely links residual blocks, here, the decision on whether to connect them is made using the elitist NSCA (see Figure 2). When the residual blocks are not densely connected, they are simply stacked, similar to ResNet. By combining these components in different ways, individuals of varying lengths can be constructed, thus effectively leveraging the classic architectures of ResNet and DenseNet through evolutionary algorithms.

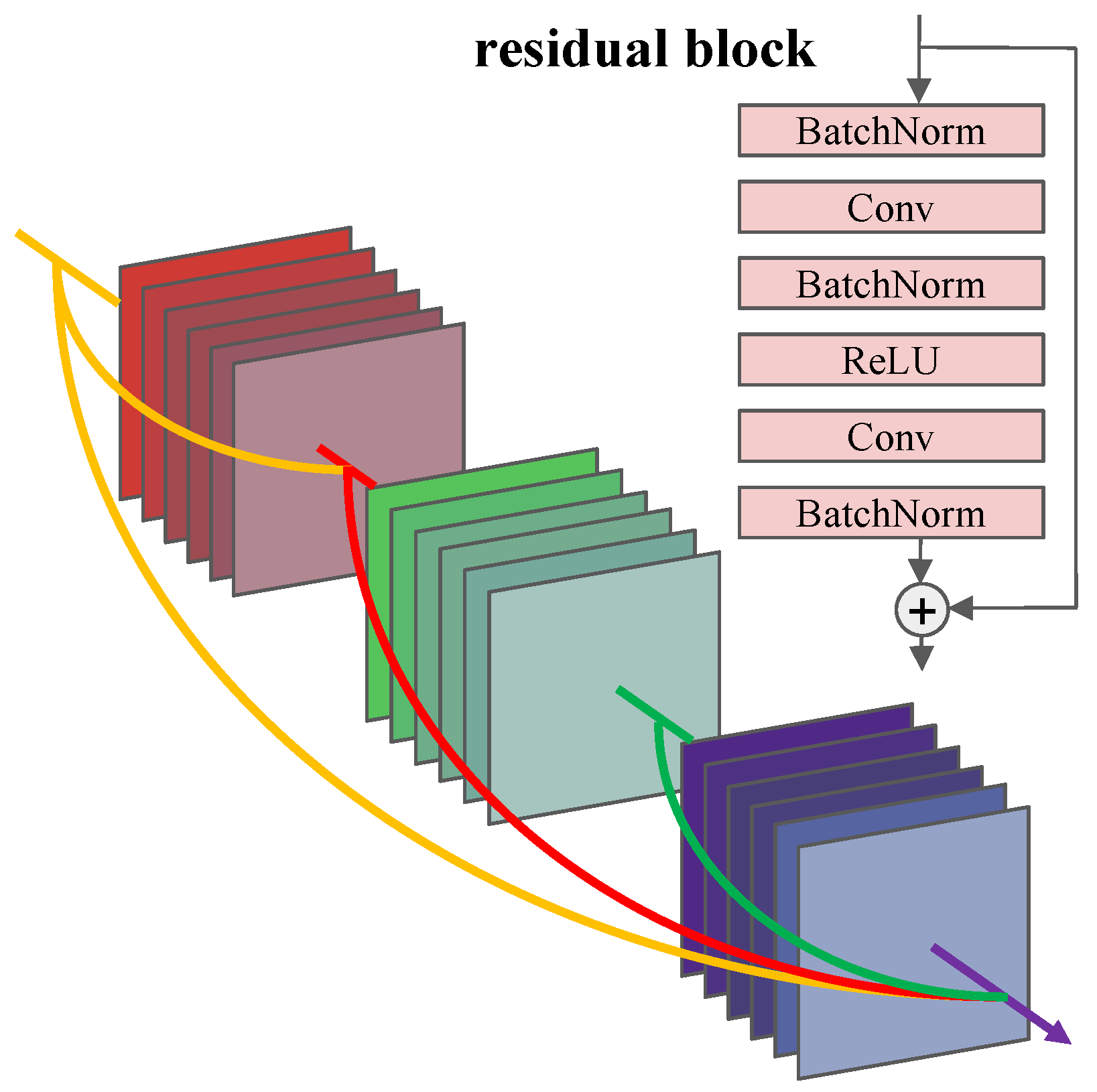
The residual block is a key component in ResNet, which effectively solves the vanishing gradient problem in neural networks and improves the feature transfer capabilities. Therefore, the residual block is defined as the basic cell in the search space. Typically, a 1 × 1 convolutional layer is incorporated into the skip connection of the residual block to handle situations where the number of output channels differs from the number of input channels. However, many researchers have found that the skip connection based on 1 × 1 convolution is not suitable for very deep network architectures. To address this limitation, a skip connection based on a zero-padded shortcut is proposed, which can avoid the overfitting problem even in deep network architectures. Referring to the residual block in [25], an evolutionary algorithm is employed to dynamically find the optimal parameters for the residual block and explore its optimal performance (see Figure 2).

The dense connection forms a densely connected structure by connecting the output of each previous layer with the input of the current layer. This design allows the features of each layer to be fused with the features of their previous layers. This connection effectively alleviates the vanishing gradient problem and enhances the feature reuse ability, which improves the expressive ability and generalization performance of neural networks. Therefore, the dense connections are optimized as optimization variables. The elitist NSCA decides whether to link the residual blocks or not, thereby increasing the flexibility of dense structures (see Figure 2).

3.3. Population Initialization

Population initialization is a crucial initial step in the elitist NSCA, where it generates multiple individuals through specific strategies to form the population. High-quality initialization not only increases the probability of the algorithm finding the global optimal solution but also effectively reduces the risk of it becoming trapped in the local optima. Specifically, the steps involved in population initialization are as follows:

• Parameter initialization: This involves setting hyperparameters such as the depth range of the network architecture, the maximum number of channels in the convolutional layers, and the population size.
• The initial population: Based on the predefined search space and different random parameters, a series of individuals is generated. Each individual is represented by a variable-length string that describes the structure of a CNN, thus constructing a virtual initial population.
• Individual fitness evaluation: The strings representing the different individuals are parsed to construct actual network architectures within PyTorch. The zero-cost proxy is used to predict their fitness, taking the synflow and the network parameters as the multi-objective fitness.

NAS is typically compute-intensive, as it requires the evaluation of multiple network architectures during the iteration process. To reduce the computational cost and time required, we use the zero-cost proxy to evaluate each network architecture instead of full training. The zero-cost proxy [26] uses only a small batch of training data to compute the score for a network architecture, which can significantly improve the efficiency while achieving a comparable accuracy in architecture ranking to that of the traditional algorithms.

We select synflow [27] as half of the fitness, with the other being the network parameters. Synflow is a novel data-agnostic pruning algorithm that overcomes layer collapse to identify the winning lottery tickets at initialization by computing the loss, which is simply the product of all of the parameters in the network. However, the difference between the maximum and minimum synflow across different network architectures can reach up to ${10}^{64}$. When normalizing the synflow, there are numerous outliers present in the data. Therefore, logarithmic transformation is applied to the synflow, with the formula as follows:

$$\begin{array}{c}\hfill \ln \left(S_p\left(\theta \right)\right)=\ln \left({\displaystyle \frac{\partial \mathcal{L}}{\partial \theta }}\odot \theta \right)\end{array}$$

(1)

where $\mathcal{L}$ is the loss function of the network parameters $\theta$, ${\mathit{S}}_p$ is the per-parameter saliency, and ⊙ is the Hadamard product. The same is true for the logarithmic transformation of the network parameters.

3.4. Crisscross

CSO consists of HC and VC. On the one hand, HC ensures that each pair of the parent individuals reproduces the offspring in the space of their own hypercube to a greater extent and additionally explores the periphery of each hypercube with a smaller probability. This reduces unsearchable blind spots and enhances the global search capability of CSO. On the other hand, VC operates by crossing between different dimensions of the same individual, allowing some stagnant dimensions to escape from the local minima. Once certain stagnant dimensions jump out of the local minima, they rapidly spread through the entire population via horizontal crossover. This is just because of the crisscross operation in both the horizontal and vertical directions, which permits CSO a unique global search ability in addressing multimodal problems with many local minima [12].

According to the search space shown in Table 1, the “Dense Block”, “Transition Layer”, and “Stack Block” are selected to construct the individuals of the population. The “attention” and “classifier” are added to the end of the network architecture. Specifically, the proposed algorithm optimizes three parts of the network architecture: (1) the hyperparameters of the “Dense Block”, “Transition Layer”, and “Stack Block”; (2) any combination of the “Dense Block”, “Transition Layer”, and “Stack Block”; and (3) the degree of the dense connection of the “Dense Block”.

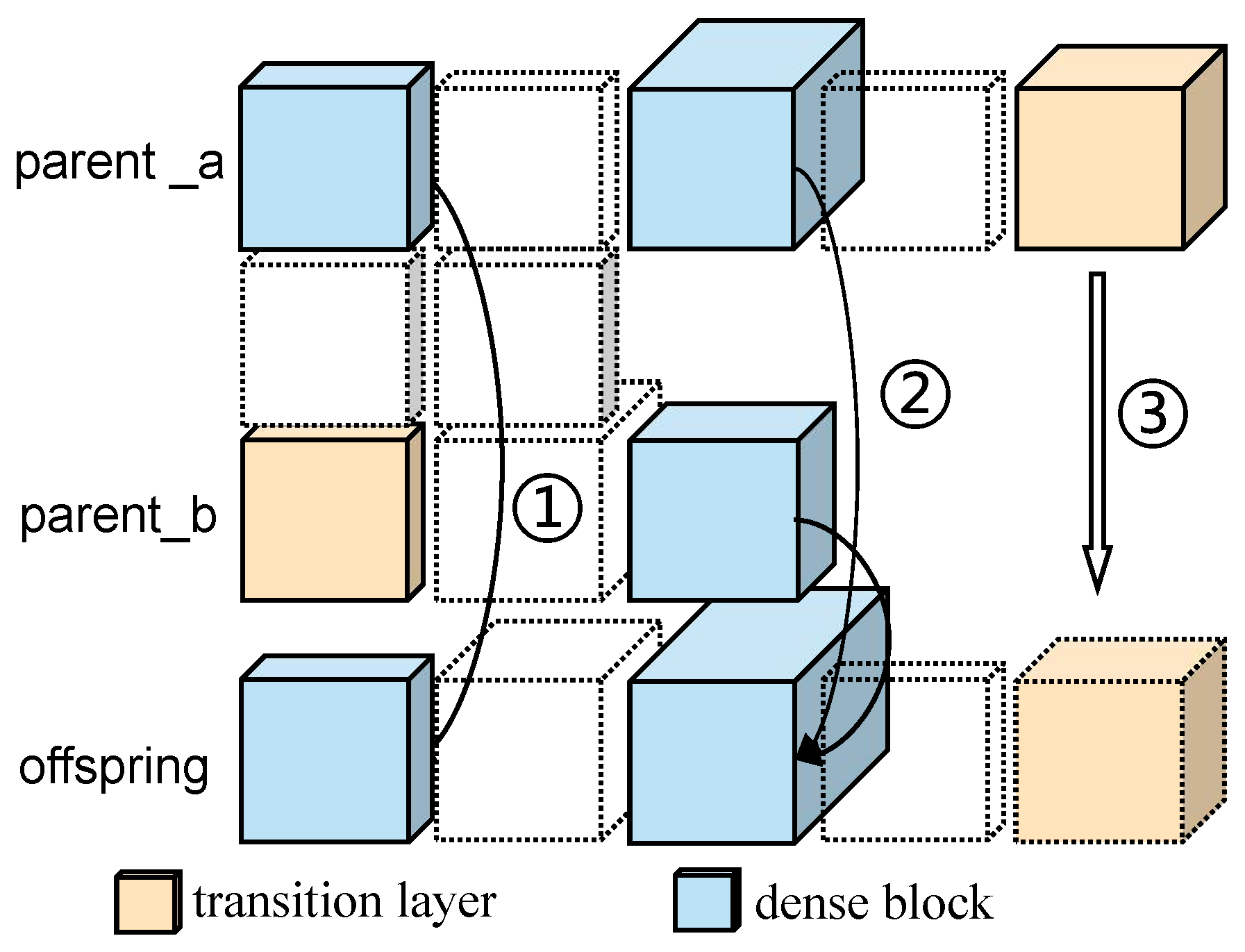
In HC, two individuals (e.g., parent_a and parent_b) are randomly selected from the population for crossover operations in the same dimension, as shown in Figure 3. Since individuals have different lengths and their dimensions have different types, simple arithmetic operations between individuals are not applicable. Therefore, we have made targeted improvements to HC, and its optimization can be divided into three scenarios. For scenario ➀, when two individuals contain a transition layer of the same dimension, the dimension from a randomly selected parent individual (parent_a) is incorporated into the offspring individual. For scenario ➁, when the same type of dimension of the two individuals (parent_a and parent_b) is a dense block, the dimension of the offspring individual is calculated using Formula (2):

$$\begin{array}{c}\hfill X_{i+1}=\mid \lfloor r{X}_i+(1-r)X_j+c(X_i-X_j)\rfloor \mid +\mathbb{B}C\end{array}$$

(2)

where r, $c\in [-1,1]$; $\mathbb{B}$ is a Boolean variable that can be set to either true or false; $X_i$ represents the hyperparameters, which include the number of channels within the residual block, the number of residual blocks, and the size of the convolution kernel; C is the remaining dimensions; and $\lfloor \rfloor$ represents the floor operation, as arithmetic calculations may result in decimal numbers. For scenario ➂, due to the different lengths of the individuals, Boolean variables are used to determine whether to transfer the remaining dimensions of an individual to the offspring individual.

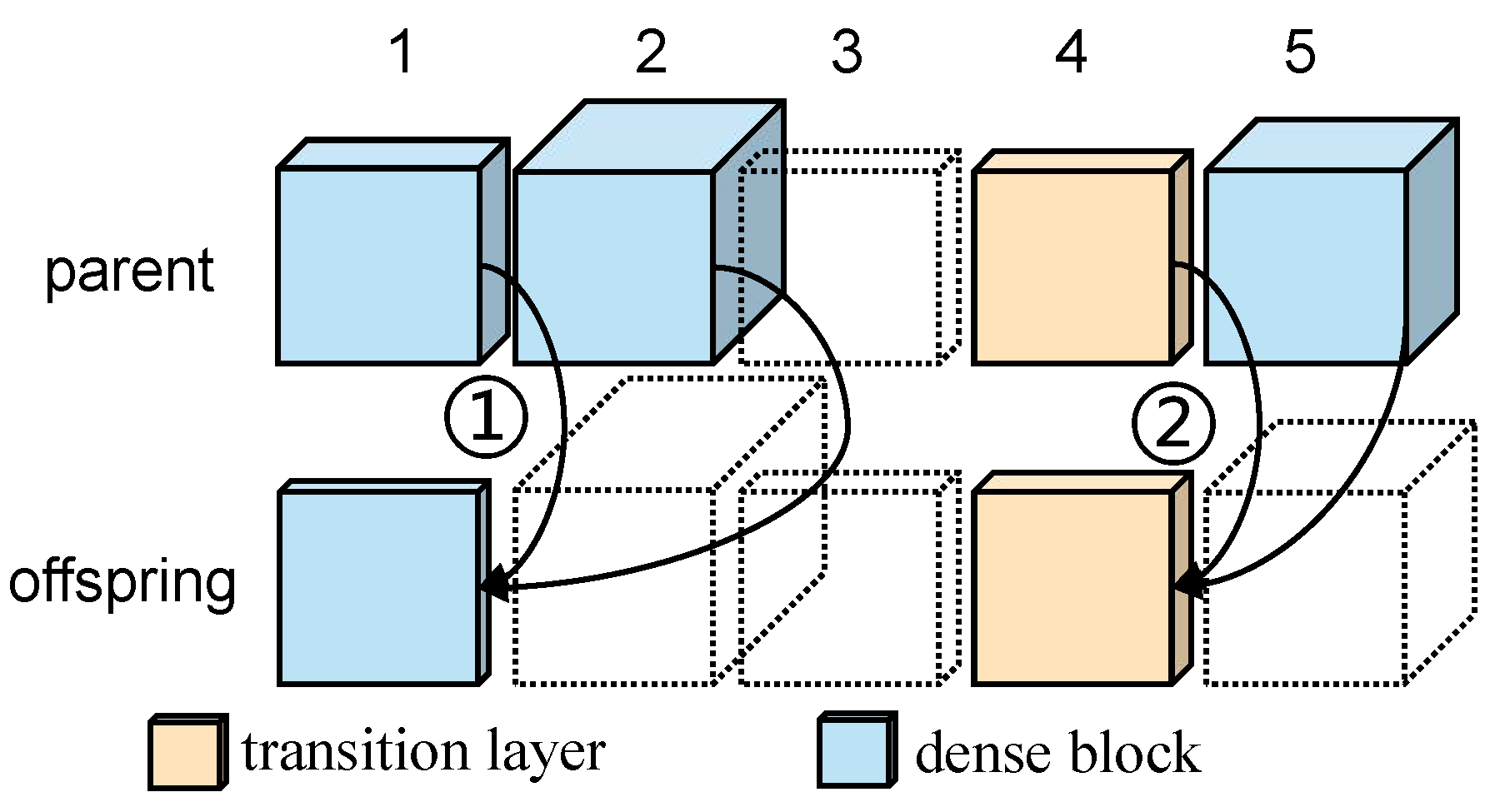
Similarly, the operations related to vertical crossover follow a similar pattern to that described above, as shown in Figure 4. In VC, an individual is randomly selected from the population, and crossover operations are performed on two different dimensions, which can be divided into two scenarios. For scenario ➀, we randomly select two dimensions (for example, 1 and 2) from the individual (parent). When the two dimensions are dense blocks, Formula (3) is used to calculate the dimension of the offspring:

$$\begin{array}{c}\hfill X_{i,no1+1}=\left|\lfloor r{X}_{i,no1}+(1-r)X_{i,no2}\rfloor \right|\end{array}$$

(3)

where $X_{i,no}$ is the $no$-th dimension of individual i, and the rest has the same meaning as above. For scenario ➁, when both dimensions (for example, 4 and 5) have a transition layer, a dimension is randomly selected to be incorporated into the offspring.

3.5. Mutation

There are some shortcomings to simply referencing the proxy model. On the one hand, the proxy model’s search results are more biased towards networks with only convolutional layers, which leads to many good components of the CNN being ignored. On the other hand, when all of the individuals in the population are highly similar, it is easy to embed local optimal solutions when searching through the crisscross optimization algorithm. At the same time, the deep network is prone to the problem of vanishing gradients, which reduces the classification accuracy. Therefore, three mutation operations are pertinently proposed with the following steps:

• Adding a pooling layer;
• Changing the number of residual blocks and the number of channels within them;
• Removing the residual block with a certain probability.

For the abovementioned mutation operations, the pooling layer has little impact on the classification accuracy, but it greatly reduces the number of network parameters and the computational complexity. However, due to the small size of the input images, the number of pooling layers is limited within a reasonable range (mutation operation 1). At the end of the iteration, all of the individuals are highly similar. Therefore, the number of residual blocks and the number of channels within them are changed. Through the evolutionary algorithm, differences in variants can quickly spread to the whole population, so the population can be rid of the local optimal solution (mutation operation 2). Moreover, the residual block is randomly deleted to control the network depth within a certain range and effectively reduce the problem of vanishing gradients in the network (mutation operation 3). The mutation is shown in Figure 1.

3.6. The Improved Elitist Strategy

When the zero-cost proxy [26] is used to predict the classification accuracy, several shortcomings are found. On the one hand, the difference between the maximum and minimum values of the synflow of different neural network architectures can reach the ten to the sixty-fourth power, and the number of network parameters also varies by 100 times. Therefore, there are many outliers (0 or 1) when normalization is applied. On the other hand, most of the individuals in the population are the same optimal individuals at the end of the iteration, resulting in the terrible diversity of the population and greatly reducing the survival of its offspring. 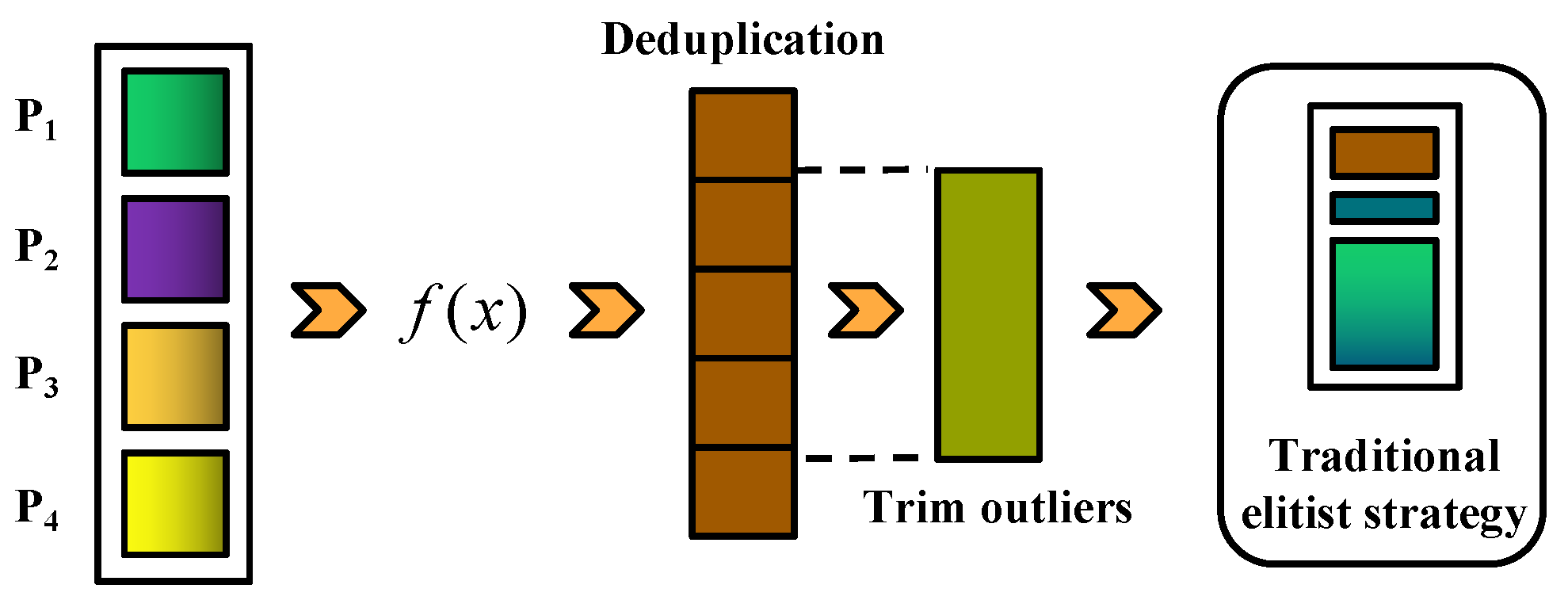Based on the above analysis, population pruning is proposed to improve the elitist strategy of NSGA-II [28], as shown in Figure 1. By calculating the natural logarithm of the synflow and the natural logarithm of the number of network parameters, the difference in the value of the synflow between different individuals in the population is significantly reduced. To reduce the influence of outliers further, the parent population is filtered to exclude more than 20% of individuals with the highest or lowest fitness, retaining the middle 80% of the individuals. This effectively filters out outlying individuals. For the problem of an excessive number of optimal individuals in the population at the end of the iteration, the deduplication operation is adopted: when generating the offspring population, only one duplicate individual is retained to ensure the uniqueness of each offspring individual and to free up space in the population for other offspring. In this way, the diversity of the population is maintained, but the original fast non-dominated sorting and the crowding distance are not affected.

$$\begin{array}{c}\hfill f\left(x\right)={\displaystyle \frac{\ln x-\min \left(\ln x\right)}{\max \left(\ln x\right)-\min \left(\ln x\right)}}\end{array}$$

(4)

where $x\in \left[synflow,networkparameter\right]$ is the fitness.

Figure 5 shows the procedure of the improved elitist strategy, wherein $\mathit{f}\left(\mathit{x}\right)$ is the operation of normalization after calculating the natural logarithm of fitness, as shown in Formula (4). Firstly, the offspring populations produced by multiple operators are aggregated. Compared with traditional elitist strategies, this operator expands the sampling space. Then, the proposed population pruning technique is introduced to improve the survival rate of the offspring population and increase the diversity of the population, aiming to avoid the algorithm from falling into local solutions and experiencing premature convergence. Finally, the original fast non-dominated sorting and the crowding distance from NSGA-II are used to obtain the Pareto front.

4. Experimental Results and Analysis

The present study aims to explore effective solutions for classification problems, particularly addressing the challenges encountered when processing high-dimensional data, such as images. Compared to regression problems, classification tasks demand not only a higher feature extraction capability and accuracy to distinguish between different classes but also pose greater requirements on the practical application performance and the reliability of the algorithms. To this end, we applied the elitist NSCA and tested it on a series of standard high-dimensional datasets to better validate the algorithm’s effectiveness and superiority in solving classification problems. Firstly, the performance of the proposed algorithm was compared with that of some state-of-the-art algorithms in terms of its classification accuracy, the number of network parameters, and its running time (GPU/days). Secondly, the evolutionary trajectories of the elitist NSCA were displayed to understand the procedure of the evolution of the population. Finally, ablation experiments were performed on the algorithm to analyze the performance impact of its components.

4.1. The Benchmark Datasets

Five benchmark datasets were used in the experiments, which were the MNIST, CIFAR-10 [29], CIFAR-100 [29], SVHN [30], and ImageNet-16-120 [31] datasets. The MNIST dataset contains 70,000 handwritten digit images with a spatial resolution of 28 × 28, in which 60,000 images are the training images and 10k are the test images. For the CIFAR-10 dataset, it comprises 10 classes of 32 × 32 RGB images, including 5000 training images and 1000 test images for each class. CIFAR-100 is similar to CIFAR-10, with 100 classes, with each including 500 training images and 100 test images. It can be seen that CIFAR-100 has more classes and fewer images in each class, making its classification more challenging. However, both of the above datasets are CIFAR, which are both non-complex datasets. SVHN is a widely used dataset for image recognition, consisting of over 600,000 digit images obtained from house number plates in Google Street View. It has 10 classes, with each representing a digit from 0 to 9. Additionally, SVHN has greater variation in the image backgrounds, lighting conditions, and image quality, making it a more realistic dataset for real-world scenarios. To explore the suitability of the elitist NSCA further, the proposed algorithm was tested on ImageNet-16-120, which is a subset of ImageNet consisting of 120 classes and about 150,000 16 × 16 RGB images. This subset can greatly reduce the computational cost while maintaining similar search results. Tiny-ImageNet is a modified subset of the original ImageNet containing color images in 200 classes. Each class has 500 training images, 50 validation images, and 50 testing images. The images are down-sampled to 64 × 64 pixels.

4.2. Parameter Settings

The hyperparameters involved in the elitist NSCA are divided into three scenarios. Firstly, in the search space, to verify the impact of image enhancement techniques on the model’s performance, random cropping and random rotation are applied in the preprocessing. Adjusting the cropping ratios to 10–30% and 80–100% of the original size reveals that moderate cropping enhances the model’s accuracy, while a cropping ratio approaching 80% leads to a decrease in accuracy, indicating that overly aggressive cropping may lose important information. For random rotations, setting the angles at 15°, 30°, and 45° demonstrates that this method effectively expands the dataset and increases its robustness. Secondly, in the search strategy, we conduct a detailed exploration of key hyperparameters such as the convolution kernel and channel numbers. For instance, experimenting with convolution kernel sizes across [1, 3, 5, 7] shows that the range [1, 5] offers the best performance in most cases; comparing the channel number ranges between [50, 200, 700] indicates that the latter improves the network’s expression capability without significantly increasing the computational costs. For the mutation operations, mutation rates of [0.1, 0.3, 0.5, 0.7] are set to maintain population diversity. For the filtered rates, filtered rates of [0.2, 0.4, 0.6, 0.8] are used to reduce the impact of outliers on the fitness of the individuals. Based on this and combined with ongoing exploration and analyses, an optimal configuration scheme is derived: a population size of 300, a maximum iteration count of 50, a mutation rate of 0.2, a filtered rate of 0.2, a convolution kernel range of [1, 5], and a channel number range of [50, 700]. Finally, the algorithm specifically employs the adversarial model perturbation (AMP) optimizer [32] and a cosine annealing learning rate scheduler (CosineAnnealingLR) to optimize the learning rate. The testing environment is described as follows: PyTorch 1.13.1 and an NVIDIA GeForce GTX 3080.

4.3. Comparison of the Precision

Table 2. Comparison results of the proposed algorithm with some state-of-the-art multi-objective algorithms (4 runs).

Dataset	Algorithms	Test Error (%)	#Param (M)	GPU/Day
MNIST	MOO-DNAS(s) [33]	0.54	3.3	1
	Elitist NSCA	0.35	0.49	0.56
CIFAR-10	T2MONAS [34]	9.15	0.15	-
	DisWOT [35]	6.45	-	0.01
	NASNet [36]	4.47	7.1	2000
	MnasNet [37]	3.85	3.5	1200
	MOGIG-Net [38]	4.67	0.9	-
	NSGANetV1-A0 [39]	4.67	0.2	27
	NSGANetV1-A1 [39]	3.49	0.5	27
	EG-DARTS+CutOut [40]	3.18	0.64	7
	CH-CNN [41]	5.6	0.837	10
	Elitist NSCA	3.45	0.85	0.76
CIFAR-100	T2MONAS [34]	33.41	0.14	-
	DisWOT [35]	25.79	-	0.11
	ENAS [42]	19.43	4.6	-
	MOGIG-Net [38]	24.71	0.7	-
	NSGANetV1-A0 [39]	25.17	0.2	27
	NSGANetV1-A1 [39]	19.23	0.7	27
	EG-DARTS+CutOut [40]	22	0.35	7
	CH-CNN [41]	24.1	1.64	19
	Elitist NSCA	19.15	1.52	0.68
SVHN	Progressive Self-supervised Multi-objective NAS [43]	2.82	0.51	5.79
	CGP-NASV2 [44]	2.7	2.21	16.25
	Elitist NSCA	2.65	0.73	0.63
ImageNet-16-120	T2MONAS [34]	59.92	0.21	-
	DisWOT [35]	52.7	-	0.23
	Elitist NSCA	48.12	1.32	0.86
Tiny-ImageNet	CIMNet [45]	64.5	8.9	-
	Elitist NSCA	66.9	6.98	0.75

NOTE: Reinforcement-learning-based algorithms (NASNet, MnasNet, and ENAS), gradient-based algorithms (EGDARTS+CutOut and MOO-DNAS(s)), and evolutionary-based algorithms (T2MONAS, DisWOT, MOGIG-Net, NSGANetV1-A0/A1, CH-CNN, Progressive Self-Supervised Multi-Objective NAS, CGP-NASV2, and CIMNet).

provides a comparison of the elitist NSCA with various types of multi-objective NAS algorithms in terms of the classification error rate, denoted by the test error (%); the network parameters, denoted by Param (M); and the search time, denoted by the GPU/day on the corresponding datasets. The experimental results show that the elitist NSCA can discover the optimal networks with fewer parameters and a lower classification error rate compared to reinforcement-learning-based algorithms such as NASNet, MnasNet, and ENAS. This is attributed to the deduplication among individuals during iterations and the inherent effect of evolutionary algorithms on the population, which effectively avoid local optima and enhance the robustness and generalization capability of the algorithm. Compared to gradient-based algorithms like EG-DARTS+CutOut and MOO-DNAS, the elitist NSCA performs excellently on CIFAR and MNIST, but its test error on CIFAR-10 is slightly higher than that of EG-DARTS+CutOut, by approximately 8.49%. However, its runtime is 89.14% of the latter’s, demonstrating a significant efficiency advantage. Since evolutionary algorithms do not rely on gradients, the elitist NSCA effectively enhances the global search capability and adaptability of the algorithm, improving the stability and reliability in complex environments. Compared to other evolutionary algorithms such as T²MONAS, DisWOT, MOGIG-Net, NSGANetV1-A0/A1, CH-CNN, Progressive Self-Supervised Multi-Objective NAS, CGP-NASV2, and CIMNet, the elitist NSCA reduces the classification test errors, particularly on ImageNet-16-120 and Tiny-ImageNet. By leveraging the zero-cost proxy, the elitist NSCA effectively overcomes the high computational cost associated with evolutionary algorithms and maintains efficient processing speeds across various datasets. This method outperforms most of the multi-objective NASs on benchmark tasks such as MNIST and CIFAR-10. Furthermore, it effectively tackles the challenges of complex multi-class classification in CIFAR-100 and demonstrates a robust performance for real-world scenarios like those in SVHN. Its superior performance was validated on large-scale image classification tasks, including ImageNet-16-120 and Tiny-ImageNet. Despite a certain degree of performance degradation when dealing with more complex datasets due to the need to learn more intricate features, the elitist NSCA still exhibits notable competitive advantages compared to the other algorithms.

During the search for the Pareto front, we use the “equal-weighted sum method” as the strategy for finding the Pareto-optimal solution. This method assigns equal weights to each objective based on their normalized fitness. To verify the effectiveness and stability of this approach, we conduct multiple independent experiments on various datasets. This methodology not only helps in providing a comprehensive evaluation of the algorithm’s performance but also ensures the reliability and universality of the results to a significant extent. The series of tests shows that the average test error is low, indicating that the adopted method possesses high stability and feasibility.

4.4. Evolutionary Trajectories

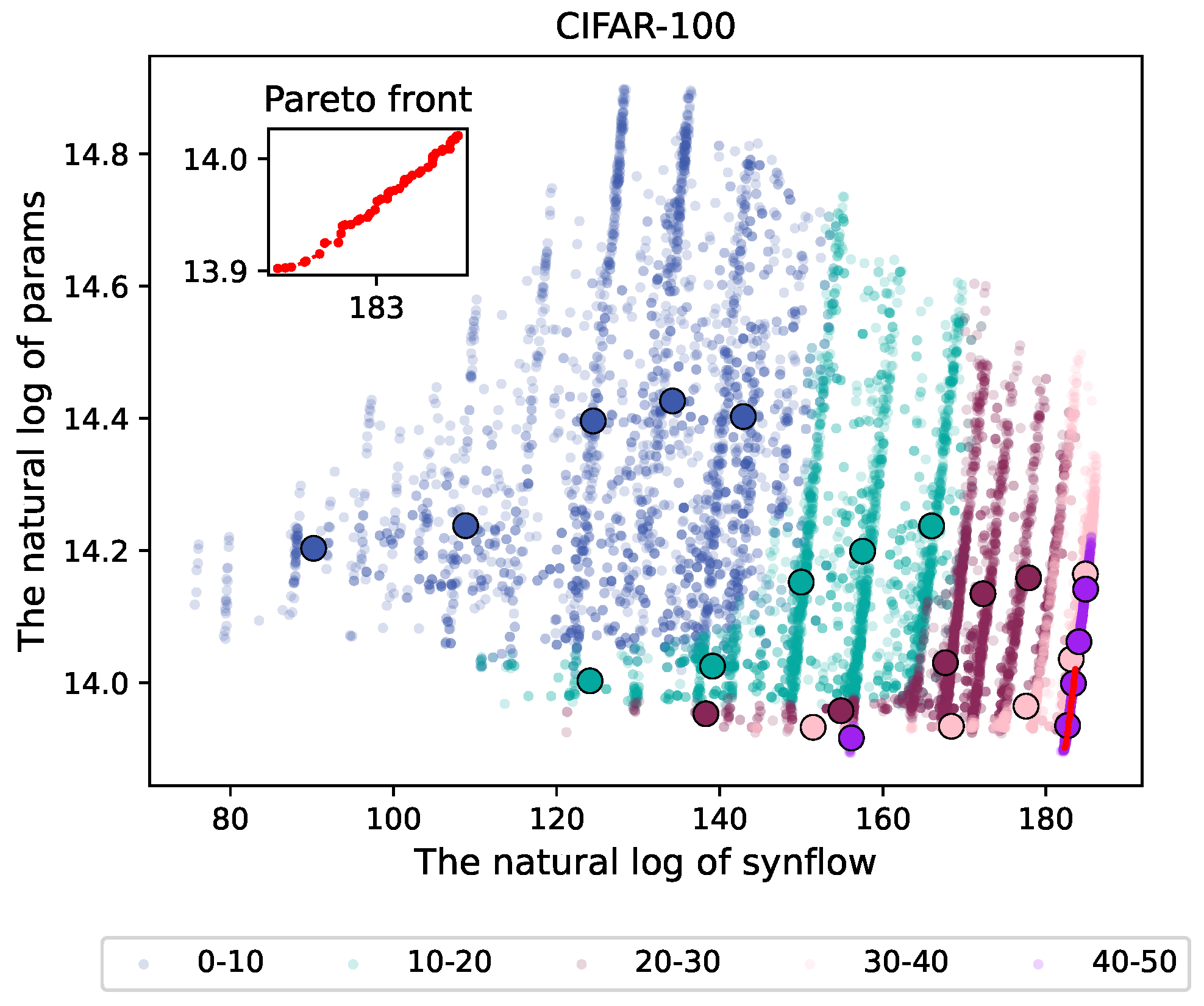
To demonstrate the correlation between or the trend in the network complexity and accuracy in neural architecture search using the proposed algorithm better, we present the fitness of different stages of the population in the form of scatter plots and combine this with k-means clustering to simplify them into a limited number of representative points. This approach clearly illustrates the changing trends. The network complexity is represented by the network parameters and the accuracy by the synflow, both of which are logarithmically transformed. Figure 6 shows the evolutionary trajectory of the proposed algorithm on CIFAR-100, wherein the blue portion represents the 0–10 generations. In this region, the majority of the individuals are dispersed, with a large number of network parameters and a small value for the synflow. With the progression of the iterations, the synflow’s value increases, and the number of network parameters decreases. The distribution of the population become more and more concentrated; i.e., the difference between individuals decreases. In the 40–50 generations, the population converges to a very small area. The set of red dots represents the Pareto front. This indicates that the proposed algorithm gradually converges to a steady state.

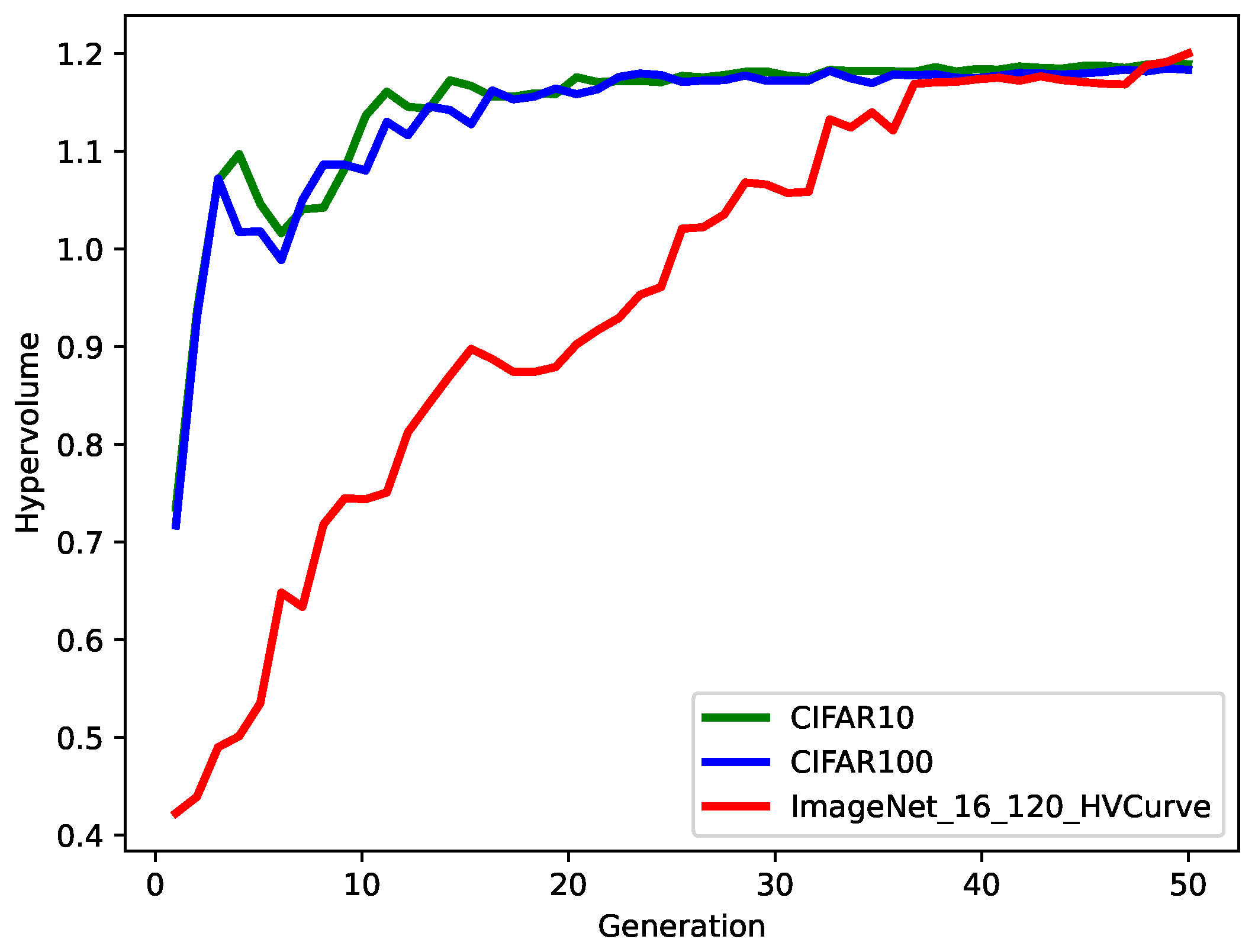
We record the set of Pareto fronts for each iteration to calculate the corresponding hypervolume of the elitist NSCA (see Figure 7). The result shows that the hypervolume presents an increasing trend with the progression of the iterations. This means that the elitist NSCA keeps searching for more high-quality solutions in the search procedure, meaning the set of Pareto fronts is constantly close to the ideal solution. The elitist NSCA converges at generation 20 and generation 40 for the CIFAR and ImageNet-16-120 datasets, respectively. This shows that the elitist NSCA can converge quickly for different datasets, which makes it suitable for different datasets and gives it good robustness.

4.5. The Ablation Study and Analysis

Comparison with some classical multi-objective algorithms: To demonstrate the effectiveness of the elitist NSCA further, it is compared with various multi-objective algorithms under the same search space. All of the search training settings and hyperparameters are identical to those used for the elitist NSCA. From

Table 3. Comparison with some classical multi-objective algorithms.

Algorithms	CIFAR-10/100 Test Error (%)	#Param (M)	GPU/Day	GD	IGD
NSGA-II	20.42/29.98	1.56/2.75	0.35/0.42	7.50/7.51	9.01/8.30
MOEA/D	6.76/22.45	1.05/3.45	3.60/3.65	2.66/6.50	2.81/7.01
Elitist NSCA	3.45/19.15	0.85/1.52	0.76/0.68	0.017/0.10	0.021/0.12

NOTE: The precision of the classification refers to the error rate; the true Pareto front is randomly distributed around [3.45/19.15, 0.85/1.52]; hence, the calculated GD and IGD will differ with different true Pareto fronts.

, it can be observed that the elitist NSCA achieves the highest accuracy. MOEA/D evolves only with neighboring individuals, which means its search procedure may remain incomplete by the end of the iteration, making it prone to falling into local optima. Since NSGA-II relies solely on crossover and mutation operators, its relatively simple mechanisms struggle to thoroughly explore the search space, resulting in lower accuracy; however, this also leads to a shorter search time compared to that of the elitist NSCA. The elitist NSCA outperforms both NSGA-II and MOEA/D in the two key metrics of GD (the generational distance [46]) and IGD (the inverse generational distance [46]), indicating that the solutions that it finds are not only closer to the true Pareto front but also provide broader coverage across the entire front. This means that the elitist NSCA can offer a more precise and evenly distributed set of solutions in multi-objective optimization, demonstrating its superior performance in maintaining the solution quality while enhancing the diversity and distribution.

Analysis of each component of the elitist NSCA: By increasing or decreasing the operators in the elitist NSCA (see

Table 4. Ablation experiments on CIFAR-10/CIFAR-100.

Algorithms	CIFAR-10/100 Test Error (%)	#Param (M)	GPU/Day
Elitist NSCA-A	4.42/21.37	3.92/5.45	0.48/0.52
Elitist NSCA-B	5.23/27.89	0.95/1.56	0.42/0.49
Elitist NSCA-C	6.69/25.35	1.12/2.03	1.16/1.23
Elitist NSCA-D	3.98/23.45	0.72/1.62	0.83/0.72

NOTE: The precision of the classification refers to the error rate.

), a comprehensive understanding of the influence of each operator on the performance of the algorithm is obtained. This helps determine key operators and provides a specific analysis for studying the algorithm in depth. Firstly, Elitist NSCA-A reduces the mutation operator: due to the lack of diversity of the population, the algorithm evolves slowly and easily falls into local optimal solutions, so the number of network parameters stays at the initial size. Secondly, Elitist NSCA-B reduces the attention mechanism: although it greatly reduces the computational cost and significantly improves the speed of the algorithm, it also leads to a decline in its classification accuracy. Thirdly, Elitist NSCA-C adds the crossover operator: the crossover operation between individuals makes the network architecture too deep, which causes a vanishing gradient and reduces the classification accuracy. Finally, Elitist NSCA-D reduces population pruning: as the proportion of duplicate individuals in the population becomes larger and larger, the computational cost of evolutionary search increases.

Comparison with different search spaces: The importance of the search space, which determines the boundary of all potential solutions to a problem, is beyond doubt. The proposed search space combines the latest residual block and the dense connection, which uses an evolutionary algorithm to decide whether to connect. By using the classical ResNet and DenseNet to compare the proposed search space, the proposed algorithm has the optimal classification accuracy (see

Table 5. Comparison among different search spaces.

Search Space	CIFAR-10	CIFAR-100	ImageNet-16-120
ResNet	5.78	24.08	49.5
DenseNet	4.03	23.81	44.13
Elitist NSCA	3.32	18.63	38.05

NOTE: The precision of the classification refers to the error rate.

).

5. Industrial Applications of UAV Image Classification

Traditional power line inspections primarily rely on human-operated UAVs to perform inspection tasks. However, manual inspections are prone to misjudgments and missed detections, which affect the reliability of the inspections. To address these issues, we employ the elitist NSCA to classify the images captured by UAVs, aiming to establish a crucial part of an automated power line inspection system. Figure 8 shows the dataset used in this study, which consists of 20,000 images with a resolution of 1920 × 2560 pixels, covering three main targets: switches, utility poles, and transformers.

Images captured by UAVs are characterized by their high resolution, which imposes higher requirements on subsequent research into the deployment of edge devices. To ensure that the image classification accuracy is not compromised while reducing the demand in terms of the computational resources, we introduced the methods of downsampling and mixed-precision training.

Table 6. Comparison of the elitist NSCA with the other baseline methods on the electric power dataset (4 runs).

Algorithms	Test Error (%)	#Param (M)	FLOPs (G)
DenseNet	$11.35\pm 0.42$	0.66	33.47
MOO-DNAS	$6.75\pm 0.75$	0.52	26.68
MnasNet	$7.75\pm 0.56$	0.82	43.91
Elitist NSCA	$4.22\pm 0.23$	0.28	14.61

compares the performance between the elitist NSCA and a traditional manually designed architecture (DenseNet), a gradient descent algorithm (MOO-DNAS), and a reinforcement learning algorithm (MnasNet). The experimental results show that using the elitist NSCA for NAS can significantly reduce the test error while maintaining a smaller number of network parameters. The optimized elitist NSCA has lower FLOPs (floating-point operations), meaning it requires fewer floating-point operations during image classification experiments on edge devices. This further demonstrates that the algorithm addresses the challenges posed by high-resolution UAV-captured images, achieving the dual objectives of minimizing the resource consumption and optimizing the performance.

Additionally, we conduct multiple independent experiments using four different random seeds on the same dataset. The experimental results demonstrate that the network architectures optimized using the elitist NSCA exhibit a superior performance, characterized by not only the lowest test error but also the smallest standard deviation. This experiment further validates the reliability and generalization capability of the algorithm.

6. Conclusions

This study proposes a novel neural architecture search technique using the elitist NSCA to address the challenge of finding the optimal network architecture designs under high-dimensional data. In this proposed method, we have designed an innovative search space and employed crisscross optimization based on a variable-length encoding strategy. Additionally, to enhance the population diversity, mutation operators are introduced, and the elitist strategy is improved to mitigate the interference of anomalous fitness in the results. Therefore, this study provides a new perspective and technical means for neural architecture search, not only promoting the development of deep learning model design but also offering robust support for more efficient and accurate image classification tasks. It holds significant importance in driving the field of artificial intelligence in a more automated and optimized direction.

In the future, we will focus on researching ways to improve the operational efficiency of the algorithm and strive to achieve real-time responses in resource-constrained environments. Although evolutionary algorithms are theoretically well suited to parallel processing, the current resource limitations have prevented us from fully leveraging their advantages. Additionally, we are considering deploying the model on edge devices to maintain a high performance even under restricted computational resources. Meanwhile, transfer learning will continue to serve as a key strategy for enhancing the model’s generalization capabilities and reducing the training costs.