Shape-Preserving C¹ and C² Reconstructions of Discontinuous Functions Using Spline Quasi-Interpolation

Abstract

This paper addresses fundamental challenges in numerical approximation methods, focusing on balancing accuracy with shape-preserving properties. We present novel approaches that combine traditional spline methods with modern numerical techniques, extending existing quasi-interpolation techniques based on B-splines. Our methods maintain computational efficiency while better handling discontinuities, achieving $C^1$ and $C^2$ reconstructions and preserving essential shape properties. We demonstrate theoretical frameworks showing optimal approximation order $O\left(h^{d+1}\right)$, $d=2,3$, with local reconstruction. Numerical experiments confirm significant improvements in accuracy and smoothness near discontinuities compared to existing methods, particularly in image processing and shock-capturing applications.

1. Introduction and Notations

Approximation methods used in scientific and engineering problems require not only the accurate representation of physical reality but also the preservation of certain properties of the data. In particular, shape-preserving properties such as monotonicity and convexity are often essential in applications ranging from chemistry to robotics. These properties ensure that the numerical approximations maintain physical meaningfulness and stability in practical applications.

Several monotonicity-preserving interpolatory methods based on cubic polynomials have been proposed in the literature [1,2,3,4,5,6,7]. These methods face a fundamental trade-off: the order of accuracy is typically compromised in regions where monotonicity constraints are enforced, while maintaining high-order accuracy often requires sacrificing monotonicity. As shown in [8], linear reconstruction operators can achieve at most second-order accuracy while preserving monotonicity, necessitating nonlinear techniques for higher-order accurate interpolants. This limitation has motivated extensive research into developing sophisticated nonlinear methods that can better balance accuracy and monotonicity preservation.

Spline functions have emerged as powerful tools across various applications due to their efficient description, smoothness properties, and ease of implementation. Traditional interpolation methods using splines require the solution of linear systems of equations, which makes them non-local in nature. To address this limitation, quasi-interpolation techniques based on B-splines were developed as local and more efficient alternatives, though they sacrifice strict interpolation conditions (see [9,10,11]). The advantages of quasi-interpolation methods include their computational efficiency, local nature, and ability to maintain high-order accuracy without solving global systems of equations.

We consider the increasing set of points ${\mathsf{\Xi }}_n=\{{\xi }_0=a,{\xi }_i,1\le i\le n-1,b={\xi }_n\}$ on $I:=[a,b]$, where $h_i={\xi }_i-{\xi }_{i-1}\in {\mathbb{R}}^{+}$, with $h={max}_i{\left\{h_i\right\}}_{i=1}^n$. From ${\left\{f_i\right\}}_{i=0}^n$, where $f_i=f\left(x_i\right)$, we want to obtain an approximant of $f\left(x\right)$.

Then, for a given degree d, we consider two nonuniform knot partitions ${\Delta }_n^x=\{x_{-d}=a-d{h}_1,\dots ,x_{-1}=a-h_1,x_0=a,x_i={\xi }_i,1\le i\le n-1,x_n=b,x_{n+1}=b+h_n,\dots ,$  $x_{n+d}=b+d{h}_n\}$, ${\Delta }_n^t=\{t_{-d}=a-{\displaystyle \frac{2d+1}{2}}{h}_1,\dots ,t_{-1}=a-{\displaystyle \frac{3}{2}}{h}_1,t_0=a-{\displaystyle \frac{1}{2}}{h}_1,t_i=({\xi }_i+{\xi }_{i-1})/2,1\le i\le n,$  $t_{n+1}=b+{\displaystyle \frac{1}{2}}{h}_n,t_{n+2}=b+{\displaystyle \frac{3}{2}}{h}_n,\dots ,t_{n+d+1}=b+{\displaystyle \frac{2d+1}{2}}{h}_n\}$ and the corresponding spaces of splines of degree d and smoothness $C^{d-1}$

$$S_d(I,{\Delta }_n^y)=\{s\in C^{d-1}\left(I\right):s{\mid }_{[y_i,y_{i+1})}\in {\mathsf{\Pi }}_d,i=0,1,\dots ,N\},$$

where ${\mathsf{\Pi }}_d$ is the space of polynomials of degree at most d, y can be x or t, and $N=n-1$ if $y=x$, otherwise $N=n$ if $y=t$. We consider the case of locally uniform partitions [12], and we recall that a sequence of partitions is locally uniform if, for some constant $A\ge 1$, ${\displaystyle \frac{h_i}{h_j}}\le A$ for all $1\le i\le n-1$ and $j=i\pm 1$.

In this space, we construct the normalized B-splines $B_i^{d,y}$ by the recursive formula (see, for instance [13]):

$$B_i^{0,y}\left(u\right)=\left\{\begin{array}{cc}1& \mathrm{i}\mathrm{f} u\in [y_i,y_{i+1})\hfill \\ 0& \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}\hfill \end{array}\right.$$

(1)

and, for $d\in \mathbb{N}$,

$$B_i^{d,y}\left(u\right)={\displaystyle \frac{u-y_i}{y_{i+d}-y_i}}{B}_i^{d-1,y}\left(u\right)-{\displaystyle \frac{u-y_{i+d+1}}{y_{i+d+1}-y_{i+1}}}{B}_{i+1}^{d-1,y}\left(u\right).$$

(2)

With this definition, we know that $B_i^{d,y}$ is a piecewise polynomial of degree d, it is positive in $(y_i,y_{i+d+1})$, and it is zero outside its support $supp{B}_j^{d,y}=[y_j,y_{j+d+1}]$. Moreover, the set of all B-splines forms a partition of unity and forms a basis for $S_d(I,{\Delta }_n^y)$, meaning that for any $S\in S_d(I,{\Delta }_n^y)$, there exist coefficients $\left(c_j\right)$, $c_j\in \mathbb{R}$, such that

$$S\left(x\right):=\sum _j{c}_j{B}_j^{d,y}\left(x\right).$$

This representation is particularly valuable because the support of each $B_j^{d,y}$ is compact, allowing local modifications of the spline by adjusting individual coefficients.

For example, given a function $f\in C^{d-1}\left(I\right)$, we can define a quasi-interpolating approximation $Ff$ to f in $S_d(I,{\Delta }_n^y)$ by [14,15]

$$Ff=\sum _i{\nu }_i\left(f\right)B_i^{d,y},$$

where, for each i, ${\nu }_i\left(f\right)$ is the linear functional, taken from [14],

$${\nu }_i\left(f\right)=\sum _{s=0}^{d-1}{(-1)}^{d-s}{\psi }^{(d-s)}\left({\tau }_i\right)f^{\left(s\right)}\left({\tau }_i\right),$$

(3)

where $\psi \left(u\right)=(y_{i+1}-u)\dots (y_{i+d}-u)/d!$, and for any ${\tau }_i\in (y_i,y_{i+d+1})$. The proposed quasi-interpolant is of differential type (i.e., with coefficient functionals ${\nu }_i\left(f\right)$ defined as linear combinations of values and derivatives of f), and in the following sections, we will propose some alternatives of point type, that means of type

$$Qf=\sum _i{\mu }_i\left(f\right)B_i^{d,y},$$

where ${\mu }_i\left(f\right)$ is a linear combination of values of f.

While traditional spline interpolation achieves optimal approximation order $O\left(h^{d+1}\right)$ and requires the solution of a global system of equations, quasi-interpolation techniques maintain this optimal approximation order and provide local reconstruction, though they sacrifice exact interpolation. However, when applied to functions with isolated discontinuities, classical quasi-interpolation methods can produce undesirable oscillations proportional to the jump magnitude, even for large values of n. This limitation is particularly problematic in applications such as image processing and shock-capturing schemes.

Recent research has focused on developing enhanced quasi-interpolation methods that can better handle discontinuities while maintaining high-order accuracy in smooth regions. Various approaches have been proposed, including the use of weighted essentially non-oscillatory techniques near discontinuities and adaptive stencil selection methods [16,17]. These developments have led to significant improvements in the handling of non-smooth data while preserving the computational efficiency of quasi-interpolation methods (see [18,19,20,21]).

In this paper, we propose new approaches that address these challenges by combining the advantages of traditional spline methods with modern numerical techniques. Our methods achieve improved accuracy and smoothness near discontinuities while maintaining the computational efficiency and local nature of quasi-interpolation methods.

Here, we list some notations used throughout the paper:

• QI stands for quasi-interpolation;
• WENO stands for weighted essentially non-oscillatory;
• We denote by $L^{d,m}$ a linear QI operator on the space of a spline of degree d, with coefficient functionals defined by using m points;
• We denote by $W^{d,m}$ the nonlinear QI operator obtained by applying WENO techniques to $L^{d,m}$;
• We denote by $A^{d,m}$ the monotone QI operator associated with $L^{d,m}$.

This paper is organized as follows: In Section 2, we revise the WENO techniques. In Section 3, we design $C^1$ QIs based on second-degree splines. First, in Section 3.1 we propose a new version of a classical QI, which only uses the data $\left\{f\left(x_i\right)\right\}$, and in Section 3.2 and Section 3.3, we develop nonlinear non-oscillatory $C^1$ QIs. In Section 4, we design $C^2$ QIs based on third degree splines. In Section 4.1, we define linear $C^2$ QIs, and in Section 4.2 and Section 4.3, we develop nonlinear non-oscillatory $C^2$ QIs. Moreover, in Section 5, we provide some numerical evidence concerning the accuracy, which confirms the theoretical results of the previous sections. Finally, in Section 6, we present some conclusions and possible future directions.

2. WENO Techniques

In this paper, we examine different approximations of ${\nu }_j\left(f\right)$, some of which are based on nonlinear approximations such as WENO techniques. This section explains how to apply WENO techniques in our context. For more detailed information on WENO techniques, see [16,17,22].

2.1. WENO with Positive Weights

Let us consider different approximations to ${\nu }_j\left(f\right)$ that satisfy:

$$\begin{array}{c}\hfill \mu \left(f\right)={\nu }_j\left(f\right)+O\left(h^p\right),{\mu }_1\left(f\right)={\nu }_j\left(f\right)+O\left(h^q\right) \mathrm{a}\mathrm{n}\mathrm{d} {\mu }_2\left(f\right)={\nu }_j\left(f\right)+O\left(h^q\right),\end{array}$$

where $p>q$, $p,q\in \mathbb{N}$. We assume that $\mu \left(f\right)$ is a linear combination of values around $f\left(x_j\right)$, and, at the same time, it is a linear combination of ${\mu }_1\left(f\right)$ and ${\mu }_2\left(f\right)$. That is, $\mu \left(f\right)={\gamma }_1{\mu }_1\left(f\right)+{\gamma }_2{\mu }_2\left(f\right)$. Since, in this case, $\mu \left(f\right)$ is a linear operator, the resulting $\mu \left(f\right)$ may produce oscillations when f has a jump discontinuity. The WENO technique provides an enhanced version of $\mu \left(f\right)$ that essentially eliminates oscillations, provided that ${\gamma }_i>0$, $i=1,2$. For negative coefficients, we introduce a suitable technique in the next subsection.

We define the following:

$$\begin{array}{c}\hfill {\alpha }_i\left(f\right):={\displaystyle \frac{{\gamma }_i}{{({\epsilon }_i+I_i\left(f\right))}^2}},{\omega }_i\left(f\right):={\displaystyle \frac{{\alpha }_i\left(f\right)}{{\sum }_{s=1}^2{\alpha }_s\left(f\right)}},i=1,2,\end{array}$$

where $I_i\left(f\right)\ge 0$ is a smoothness indicator, meaning that the smoother the data, the closer $I_i\left(f\right)$ is to zero, and the small positive number ${\epsilon }_i$ (possibly dependent on $h_i$) is in principle introduced to avoid null denominators. If ${\mu }_i\left(f\right)$, $i=1,2$, is obtained using s values $\left\{f\left(x_i\right)\right\}$ and $q_i\left(x\right)$ is the polynomial of degree $s-1$ that interpolate these values, Jiang and Shu in [16] propose using

$$I_i\left(f\right)=\sum _{k=1}^{s-1}{\int }_{t_{j+1}}^{t_{j+2}}{h}^{2k-1}{\left(q_i^{\left(k\right)}\left(x\right)\right)}^{2}dx$$

as the smoothness indicator of ${\mu }_i\left(f\right)$. Here, following [22], we set

$$I_i\left(f\right)=\sum _{k=1}^{s-1}{(t_{j+2}-t_{j+1})}^{2k}{\left(q_i^{\left(k\right)}\left(x_{j+1}\right)\right)}^2,$$

(4)

since the same results can be obtained and a compact formula can be derived, as is shown in [22]. The nonlinear analog of $\mu \left(f\right)$, denoted by ${\mu }^w\left(f\right)$, is:

$$\begin{array}{c}\hfill {\mu }^w\left(f\right):=\sum _{i=1}^2{\omega }_i\left(f\right){\mu }_i\left(f\right).\end{array}$$

If f is smooth, then ${\mu }^w\left(f\right)$ maintains the accuracy of $\mu \left(f\right)$:

$${\mu }^w\left(f\right)={\nu }_j\left(f\right)+O\left(h^p\right).$$

(5)

However, if f has a discontinuity in the interval where the data used by ${\mu }_1\left(f\right)$ lie, but it is smooth in the interval used to construct ${\mu }_2\left(f\right)$, then ${\mu }^w\left(f\right)$ is as precise as ${\mu }_2\left(f\right)$:

$${\mu }^w\left(f\right)={\nu }_j\left(f\right)+O\left(h^q\right).$$

(6)

The same holds if the discontinuity lies in the interval where the data used by ${\mu }_2\left(f\right)$ lie.

2.2. WENO with Negative Weights

WENO procedures cannot be directly applied to obtain stable schemes when negative linear weights are present. For handling negative weights, we use the techniques from [17]. For cases where $\mu \left(f\right)={\sum }_{i=1}^2{\gamma }_i{\mu }_i\left(f\right)$ with some ${\gamma }_i<0$, we define

$${\overline{\gamma }}_i^{+}:={\displaystyle \frac{1}{2}}({\gamma }_i+3|{\gamma }_i|),{\overline{\gamma }}_i^{-}:={\overline{\gamma }}_i^{+}-{\gamma }_i,i=1,2,$$

and their scaled versions

$${\sigma }^{\pm }:=\sum _{i=1}^2{\overline{\gamma }}_i^{\pm },{\gamma }_i^{\pm }:={\overline{\gamma }}_i^{\pm }/{\sigma }^{\pm },i=1,2.$$

We can then express $\mu \left(f\right)$

$$\mu \left(f\right)=\sum _{i=1}^2{\gamma }_i{\mu }_i\left(f\right)={\sigma }^{+}{\mu }^{+}\left(f\right)-{\sigma }^{-}{\mu }^{-}\left(f\right),$$

where ${\mu }^{+}\left(f\right)={\sum }_{i=1}^2{\gamma }_i^{+}{\mu }_i\left(f\right)$ and ${\mu }^{-}\left(f\right)={\sum }_{i=1}^2{\gamma }_i^{-}{\mu }_i\left(f\right)$. With ${\gamma }_i^{+},{\gamma }_i^{-}\ge 0$, $i=1,2$, we can apply the WENO strategy to ${\mu }^{+}\left(f\right),{\mu }^{-}\left(f\right)$, defining

$${\alpha }_i^{\pm }:={\displaystyle \frac{{\gamma }_i^{\pm }}{{({\epsilon }_i+I_i\left(f\right))}^2}},{\omega }_i^{\pm }:={\displaystyle \frac{{\alpha }_i^{\pm }}{{\sum }_{s=1}^k{\alpha }_s^{\pm }}},$$

and obtaining the nonlinear analog of $\mu \left(f\right)$:

$$\begin{array}{c}\hfill {\mu }^w\left(f\right):={\sigma }^{+}\sum _{i=1}^2{\omega }_i^{+}\left(f\right){\mu }_i\left(f\right)-{\sigma }^{-}\sum _{i=1}^2{\omega }_i^{-}\left(f\right){\mu }_i\left(f\right),\end{array}$$

which satisfies the accuracy properties (5) and (6).

3. Quadratic QI Approximants

3.1. Linear QI Based on 3 Points: $L^{2,3}$

In the literature, the authors assume that they know $f\left(x_i\right)$ or $f\left(t_i\right)$. In particular, in the quadratic case, they construct the B-spline with support $[x_i,x_{i+3}]$, what we call $B_i^{2,x}$, and they assume that $f\left(t_i\right)$ is known (see, e.g., [14,15,23], where different QIs of differential or point type are presented).

In this paper, we assume that we know $\left\{f\left(x_i\right)\right\}$; then, considering the B-splines $B_i^{2,t}$ given by (1) and (2) on the knot sequence ${\Delta }_n^t$ and with support $[t_i,t_{i+3}]$, we use

$$R^{2,3}f\left(z\right)=\sum _{i=-2}^n{\nu }_i^2\left(f\right)B_i^{2,t}\left(z\right),$$

where, by (3),

$${\nu }_i^2\left(f\right)=f\left(x_{i+1}\right)+{\displaystyle \frac{h_{i+2}-h_{i+1}}{4}}{f}^{\prime }\left(x_{i+1}\right)-{\displaystyle \frac{h_{i+1}{h}_{i+2}}{8}}{f}^{″}\left(x_{i+1}\right).$$

(7)

We define $p_i^2\left(x\right)$ as the polynomial of degree 2 that interpolates ${\left\{f_j\right\}}_{j=i}^{i+2}$. We approximate ${\nu }_i^2\left(f\right)$ with

$${\mu }_i^{2,3}\left(f\right):={\nu }_i^2\left(p_i^2\right)=a_i{f}_i+b_i{f}_{i+1}+c_i{f}_{i+2},$$

(8)

where

$$a_i=-{\displaystyle \frac{h_{i+2}^2}{4h_{i+1}(h_{i+1}+h_{i+2})}},b_i={\displaystyle \frac{h_{i+2}^2+3h_{i+1}{h}_{i+2}+h_{i+1}^2}{4h_{i+1}{h}_{i+2}}},c_i=-{\displaystyle \frac{h_{i+1}^2}{4h_{i+2}(h_{i+1}+h_{i+2})}},$$

obtaining ${\mu }_i^{2,3}\left(f\right)={\nu }_i^2\left(f\right)+O($$h^4)$, $i=0,\dots ,n-2$. To maintain the order of approximation in this section close to the boundaries using only information from ${\left\{f_i\right\}}_{i=0}^n$, we define ${\mu }_j^{2,3}\left(f\right):={\nu }_j^2\left(p_0^2\right)$, $j=-2,-1$, and ${\mu }_j^{2,3}\left(f\right):={\nu }_j^2\left(p_{n-2}^2\right)$, $j=n-1, n$, where $p_i^2\left(x\right)$ is the polynomial that interpolates ${\left\{f_j\right\}}_{j=i}^{i+2}$, obtaining:

$$\begin{array}{ccc}\hfill {\mu }_{-2}^{2,3}\left(f\right)& :=& {\nu }_{-2}^2\left(p_0^2\right)={\displaystyle \frac{32h_1{h}_2+60h_1^2}{16h_1(h_2+h_1)}}{f}_0-{\displaystyle \frac{16h_1{h}_2+28h_1^2}{16h_1{h}_2}}{f}_1+{\displaystyle \frac{7h_1^2}{4h_2(h_2+h_1)}}{f}_2,\hfill \\ \hfill {\mu }_{-1}^{2,3}\left(f\right)& :=& {\nu }_{-1}^2\left(p_0^2\right)={\displaystyle \frac{16h_1{h}_2+12h_1^2}{16h_1(h_2+h_1)}}{f}_0+{\displaystyle \frac{h_1}{4h_2}}{f}_1-{\displaystyle \frac{h_1^2}{4h_2(h_2+h_1)}}{f}_2,\hfill \\ \hfill {\mu }_{n-1}^{2,3}\left(f\right)& :=& {\nu }_{n-1}^2\left(p_{n-2}^2\right)={\displaystyle \frac{16h_n{h}_{n-1}+12h_n^2}{16h_n(h_{n-1}+h_n)}}{f}_n+{\displaystyle \frac{h_n}{4h_{n-1}}}{f}_{n-1}-{\displaystyle \frac{h_n^2}{4h_{n-1}(h_{n-1}+h_n)}}{f}_{n-2},\hfill \\ \hfill {\mu }_n^{2,3}\left(f\right)& :=& {\nu }_n^2\left(p_{n-2}^2\right)={\displaystyle \frac{32h_n{h}_{n-1}+60h_n^2}{16h_n(h_{n-1}+h_n)}}{f}_n-{\displaystyle \frac{16h_n{h}_{n-1}+28h_n^2}{16h_n{h}_{n-1}}}{f}_{n-1}+{\displaystyle \frac{7h_n^2}{4h_{n-1}(h_{n-1}+h_n)}}{f}_{n-2},\hfill \end{array}$$

and ${\mu }_i^{2,3}\left(f\right)={\nu }_i^2\left(f\right)+O($$h^4)$, $i=-2, -1, n-1, n$.

Now, we define

$$L^{2,3}f\left(z\right)=\sum _{i=-2}^n{\mu }_i^{2,3}\left(f\right)B_i^{2,t}\left(z\right)$$

and we have the following theorem, which can be stated thanks to the results presented in [9] (p. 154, Theorem 22). Indeed, the infinity norm of $L^{2,3}$ is bounded if the partition is locally uniform, because

$$\begin{array}{c}{\displaystyle \left|a_i\right|=\frac{h_{i+2}^2}{4h_{i+1}(h_{i+1}+h_{i+2})}\le \frac{h_{i+2}^2}{4h_{i+1}{h}_{i+2}}=\frac{h_{i+2}}{4h_{i+1}},}\hfill \\ {\displaystyle \left|b_i\right|=\frac{h_{i+2}^2+3h_{i+1}{h}_{i+2}+h_{i+1}^2}{4h_{i+1}{h}_{i+2}}=\frac{h_{i+2}^2}{4h_{i+1}{h}_{i+2}}+\frac{3h_{i+1}{h}_{i+2}}{4h_{i+1}{h}_{i+2}}+\frac{h_{i+1}^2}{4h_{i+1}{h}_{i+2}}=\frac{h_{i+2}}{4h_{i+1}}+\frac{3}{4}+\frac{h_{i+1}}{4h_{i+2}}}\hfill \end{array}$$

and $c_i$ is similar to $a_i$.

Theorem 1.

We have $L^{2,3}p=p$, $\forall p\in {\mathsf{\Pi }}_2$. In addition, if $f\in C^3\left(I\right)$, then

$$\underset{z\in I}{sup}|L^{2,3}f\left(z\right)-f\left(z\right)|=O\left(h^3\right).$$

While, if f has a jump in $(x_{i-1},x_i]$ and $f\in C^3([a,x_{i-1}]\cup [x_i,b])$, then

$$\underset{z\in (t_{i-2},t_{i+2})}{sup}|L^{2,3}f\left(z\right)-f\left(z\right)|=O\left(h^0\right)$$

(9)

and

$$\underset{z\in [a,t_{i-2}]\cup [t_{i+2},b]}{sup}|L^{2,3}f\left(z\right)-f\left(z\right)|=O\left(h^3\right).$$

(10)

Moreover, $L^{2,3}f\in C^1\left(I\right)$.

Proof. 

By Taylor series expansion, we have the following approximation of (7), ${\mu }_j^{2,3}\left(f\right)={\nu }_j^2\left(f\right)+f^{\left(3\right)}\left(\xi \right)O\left(h^3\right)$; thus, $L^{2,3}p=p$, $\forall p\in {\mathsf{\Pi }}_2$.

If the discontinuity is in $(x_{i-1},x_i]$ and $f\in C^3([a,x_{i-1}]\cup [x_i,b])$, we have ${\mu }_{i-2}^{2,3}\left(f\right)={\nu }_{i-2}^2\left(f\right)+O\left(h^0\right)$ and ${\mu }_{i-1}^{2,3}\left(f\right)={\nu }_{i-1}^2\left(f\right)+O\left(h^0\right)$, which affects $B_{i-2}^{2,t}$, with support $[t_{i-2},t_{i+1}]$ and $B_{i-1}^{2,t}$, with support $[t_{i-1},t_{i+2}]$, obtaining (9). We also have ${\mu }_j^{2,3}\left(f\right)={\nu }_j^2\left(f\right)+O\left(h^3\right)$, $\forall j\ne i-2,i-1$, which give us (10).

Moreover, the continuity of $L^{2,3}f$ follows from the continuity of f and the B-spline basis functions. □

3.2. Nonlinear QI: $W^{2,3}$

Note, also, that ${\mu }_i^{2,3}\left(f\right)$, in (8), can be written as

$$\begin{array}{ccc}\hfill {\mu }_i^{2,3}\left(f\right)& =& f_{i+1}+{\displaystyle \frac{h_{i+2}^2}{4(h_{i+2}+h_{i+1})}}{\displaystyle \frac{f_{i+1}-f_i}{h_{i+1}}}-{\displaystyle \frac{h_{i+1}^2}{4(h_{i+2}+h_{i+1})}}{\displaystyle \frac{f_{i+2}-f_{i+1}}{h_{i+2}}}\hfill \\ & =& f_{i+1}+{\gamma }_1{\nu }_1\left(f\right)+{\gamma }_2{\nu }_2\left(f\right),\hfill \end{array}$$

where

$$\begin{array}{c}{\displaystyle {\gamma }_1=\frac{h_{i+2}^2}{4(h_{i+2}+h_{i+1})},{\nu }_1\left(f\right)=\frac{f_{i+1}-f_i}{h_{i+1}},}\\ {\displaystyle {\gamma }_2=-\frac{h_{i+1}^2}{4(h_{i+2}+h_{i+1})},{\nu }_2\left(f\right)=\frac{f_{i+2}-f_{i+1}}{h_{i+2}}.}\end{array}$$

Since ${\gamma }_2<0$, we apply WENO with negative weights, obtaining:

$$\begin{array}{ccc}\hfill {\mu }_i^{2,3}\left(f\right)& =& f_{i+1}+(2{\gamma }_1-{\gamma }_2)\left({\displaystyle \frac{2{\gamma }_1}{2{\gamma }_1-{\gamma }_2}}{\nu }_1\left(f\right)+{\displaystyle \frac{-{\gamma }_2}{2{\gamma }_1-{\gamma }_2}}{\nu }_2\left(f\right)\right)\hfill \\ & & \phantom{f_{i+1}}+({\gamma }_1-2{\gamma }_2)\left({\displaystyle \frac{2{\gamma }_1}{{\gamma }_1-2{\gamma }_2}}{\nu }_1\left(f\right)+{\displaystyle \frac{-2{\gamma }_2}{{\gamma }_1-2{\gamma }_2}}{\nu }_2\left(f\right)\right)\hfill \end{array}$$

(11)

$$\begin{array}{ccc}\hfill & =& f_{i+1}+{\displaystyle \frac{2h_{i+2}^2+h_{i+1}^2}{4(h_{i+2}+h_{i+1})}}\left({\displaystyle \frac{2h_{i+2}^2}{h_{i+1}^2+2h_{i+2}^2}}{\displaystyle \frac{f_{i+1}-f_i}{h_{i+1}}}\right.\hfill \\ & & \phantom{f_{i+1}{f}_{i+1}}\left.+{\displaystyle \frac{h_{i+1}^2}{h_{i+1}^2+2h_{i+2}^2}}{\displaystyle \frac{f_{i+2}-f_{i+1}}{h_{i+2}}}\right)\hfill \\ \hfill & & \phantom{f_{i+1}}-{\displaystyle \frac{h_{i+2}^2+2h_{i+1}^2}{4(h_{i+2}+h_{i+1})}}\left({\displaystyle \frac{h_{i+2}^2}{h_{i+2}^2+2h_{i+1}^2}}{\displaystyle \frac{f_{i+1}-f_i}{h_{i+1}}}\right.\hfill \\ & & \phantom{f_{i+1}{f}_{i+1}}\left.+{\displaystyle \frac{2h_{i+1}^2}{h_{i+1}^2+2h_{i+1}^2}}{\displaystyle \frac{f_{i+2}-f_{i+1}}{h_{i+2}}}\right)\hfill \end{array}$$

(12)

We also apply the WENO technique to the parenthesis of (11) and (12). We define the smoothness indicators (4)

$$I{S}_i^{\ell }={\displaystyle \frac{{(h_{i+1}+h_{i+2})}^2}{4}}{\displaystyle \frac{{(f_{i+1}-f_i)}^2}{h_{i+1}^2}}\mathrm{a}\mathrm{n}\mathrm{d}I{S}_i^r={\displaystyle \frac{{(h_{i+1}+h_{i+2})}^2}{4}}{\displaystyle \frac{{(f_{i+2}-f_{i+1})}^2}{h_{i+2}^2}}.$$

Taking

$${\alpha }_i^{\ell }={\displaystyle \frac{2h_{i+2}^2}{h_{i+1}^2+2h_{i+2}^2}}{\displaystyle \frac{1}{{({\varepsilon }_i+I{S}_i^{\ell })}^2}},{\alpha }_i^r={\displaystyle \frac{h_{i+1}^2}{h_{i+1}^2+2h_{i+2}^2}}{\displaystyle \frac{1}{{({\varepsilon }_i+I{S}_i^r)}^2}},$$

$${\beta }_i^{\ell }={\displaystyle \frac{h_{i+2}^2}{h_{i+1}^2+2h_{i+2}^2}}{\displaystyle \frac{1}{{({\varepsilon }_i+I{S}_i^{\ell })}^2}},{\beta }_i^r={\displaystyle \frac{2h_{i+1}^2}{h_{i+1}^2+2h_{i+2}^2}}{\displaystyle \frac{1}{{({\varepsilon }_i+I{S}_i^r)}^2}},$$

where ${\varepsilon }_i={(h_{i+1}+h_{i+2})}^2/4$, and we define

$$\begin{array}{ccc}\hfill {\omega }_i^{2,3}\left(f\right)& =& f_{i+1}+{\displaystyle \frac{2h_{i+2}^2+h_{i+1}^2}{4(h_{i+2}+h_{i+1})}}\left({\displaystyle \frac{{\alpha }_i^{\ell }}{{\alpha }_i^{\ell }+{\alpha }_i^r}}{\displaystyle \frac{f_{i+1}-f_i}{h_{i+1}}}+{\displaystyle \frac{{\alpha }_i^r}{{\alpha }_i^{\ell }+{\alpha }_i^r}}{\displaystyle \frac{f_{i+2}-f_{i+1}}{h_{i+2}}}\right)\hfill \\ \hfill & & \phantom{f_{i+1}}-{\displaystyle \frac{h_{i+2}^2+2h_{i+1}^2}{4(h_{i+2}+h_{i+1})}}\left({\displaystyle \frac{{\beta }_i^{\ell }}{{\beta }_i^{\ell }+{\beta }_i^r}}{\displaystyle \frac{f_{i+1}-f_i}{h_{i+1}}}+{\displaystyle \frac{{\beta }_i^r}{{\beta }_i^{\ell }+{\beta }_i^r}}{\displaystyle \frac{f_{i+2}-f_{i+1}}{h_{i+2}}}\right)\hfill \end{array}$$

and

$$W^{2,3}f\left(z\right)=\sum _{i=-2}^n{\omega }_i^{2,3}\left(f\right)B_i^{2,t}\left(z\right),$$

for which have the following theorem.

Theorem 2.

We have $W^{2,3}p=p$, $\forall p\in {\mathsf{\Pi }}_1$. In addition, if $f\in C^3\left(I\right)$, then

$$\underset{z\in I}{sup}|W^{2,3}f\left(z\right)-f\left(z\right)|=O\left(h^3\right).$$

While, if f has a jump in $(x_{i-1},x_i]$ and $f\in C^3([a,x_{i-1}]\cup [x_i,b])$, then

$$\underset{z\in (t_{i-1},t_{i+1})}{sup}|W^{2,3}f\left(z\right)-f\left(z\right)|=O\left(h^0\right),$$

(13)

$$\underset{z\in [a,t_{i-1}]\cup [t_{i+1},b]}{sup}|W^{2,3}f\left(z\right)-f\left(z\right)|=O\left(h^2\right)$$

(14)

and

$$\underset{z\in [a,t_{i-2}]\cup [t_{i+2},b]}{sup}|W^{2,3}f\left(z\right)-f\left(z\right)|=O\left(h^3\right).$$

(15)

Moreover, $W^{2,3}f\in C^1\left(I\right)$.

Proof. 

With each of the pieces that form ${\mu }_i^{2,3}\left(f\right)$, we obtain ${\mu }_i^{2,3}\left(f\right)={\nu }_j^2\left(f\right)+f^{\left(2\right)}\left(\xi \right)O\left(h^2\right)$; then, we have $W^{2,3}p=p$, $\forall p\in {\mathsf{\Pi }}_1$.

If the discontinuity is in $(x_{i-1},x_i]$ and $f\in C^3([a,x_{i-1}]\cup [x_i,b])$, we have ${\mu }_{i-2}^{2,3}\left(f\right)={\nu }_{i-2}^2\left(f\right)+O\left(h^2\right)$ and ${\mu }_{i-1}^{2,3}\left(f\right)={\nu }_{i-1}^2\left(f\right)+O\left(h^2\right)$, which affect $B_{i-2}^{2,t}$, with support $[t_{i-2},t_{i+1}]$, and $B_{i-1}^{2,t}$, with support $[t_{i-1},t_{i+2}]$. Note that we are using information lying on the other side of the discontinuity; this is why we obtain (13) and (14). We also have ${\mu }_j^{2,3}\left(f\right)={\nu }_j^2\left(f\right)+O\left(h^3\right)$, $\forall j\ne i-2, i-1$, which give us (15).

Due to the fact that $W^{2,3}f\in S_2(I,{\Delta }_n^t)$, it is $C^1\left(I\right)$. □

3.3. Monotone QI: $A^{2,3}$

There are other ways to deal with the problem of trying to avoid the Gibbs phenomenon. We can also apply some of the techniques proposed in [1], and used in the context of derivative approximation for obtaining the Hermite polynomial, to (11) and (12). In fact, we can substitute the mean averages ${\gamma }_1{\nu }_1\left(f\right)+{\gamma }_2{\nu }_2\left(f\right)$ of the parenthesis by Broodlie’s formula [4], which is the one used in MATLAB 2023a to approximate the derivatives in the monotone PCHIP Hermite function. This formula have some disadvantages (for instance, the order of approximation is reduced in the case of using a nonuniform mesh). Here, we will use the formula presented in [1]

$$({\gamma }_1{\nu }_1\left(f\right)+{\gamma }_2{\nu }_2\left(f\right)){\displaystyle \frac{4{\nu }_1\left(f\right){\nu }_2\left(f\right)}{{({\nu }_1\left(f\right)+{\nu }_2\left(f\right))}^2}}$$

if ${\nu }_1\left(f\right){\nu }_2\left(f\right)>0$ or 0 when ${\nu }_1\left(f\right){\nu }_2\left(f\right)<0$, because, after analyzing different alternatives, it is the one with which we obtain the best results, from both the theoretical and the practical point of view.

In the context of Hermite interpolation, if a discontinuity is present and, for example, ${\nu }_1\left(f\right)<<{\nu }_2\left(f\right)$, then we have

$$({\gamma }_1{\nu }_1\left(f\right)+{\gamma }_2{\nu }_2\left(f\right)){\displaystyle \frac{4{\nu }_1\left(f\right){\nu }_2\left(f\right)}{{({\nu }_1\left(f\right)+{\nu }_2\left(f\right))}^2}}<<{\gamma }_1{\nu }_1\left(f\right)+{\gamma }_2{\nu }_2\left(f\right),$$

and we avoid the Gibbs phenomenon (see [1] for details). Here, we also reduce the oscillations with this approach.

In [1], it is proved that if ${\nu }_1\left(f\right)=O\left(1\right)$, ${\nu }_2\left(f\right)=O\left(1\right)$, $|{\nu }_1\left(f\right)-{\nu }_2\left(f\right)|=O\left(h^2\right)$ and ${\nu }_1\left(f\right){\nu }_2\left(f\right)>0$, then

$$\left|({\gamma }_1{\nu }_1\left(f\right)+{\gamma }_2{\nu }_2\left(f\right))-({\gamma }_1{\nu }_1\left(f\right)+{\gamma }_2{\nu }_2\left(f\right)){\displaystyle \frac{4{\nu }_1\left(f\right){\nu }_2\left(f\right)}{{({\nu }_1\left(f\right)+{\nu }_2\left(f\right))}^2}}\right|=O\left(h^4\right),$$

Hence, we maintain the order of approximation when the function is smooth and monotonous. On the other hand, let us point out that next to the discontinuity and when the function is not monotonous the approximation order decreases drastically.

Now, we define

$$\begin{array}{ccc}\hfill {\upsilon }_i^{2,3}\left(f\right)& =& f_{i+1}+{\displaystyle \frac{2h_{i+2}^2+h_{i+1}^2}{4(h_{i+2}+h_{i+1})}}\left({\displaystyle \frac{2h_{i+2}^2}{h_{i+1}^2+2h_{i+2}^2}}{\displaystyle \frac{f_{i+1}-f_i}{h_{i+1}}}+{\displaystyle \frac{h_{i+1}^2}{h_{i+1}^2+2h_{i+2}^2}}{\displaystyle \frac{f_{i+2}-f_{i+1}}{h_{i+2}}}\right)\hfill \\ & & \phantom{f_{i+1}-{\displaystyle \frac{h_{i+2}^2+2h_{i+1}^2}{4(h_{i+2}+h_{i+1})}}}{\displaystyle \frac{4\frac{f_{i+1}-f_i}{h_{i+1}}\frac{f_{i+2}-f_{i+1}}{h_{i+2}}}{{\left(\frac{f_{i+1}-f_i}{h_{i+1}}+\frac{f_{i+2}-f_{i+1}}{h_{i+2}}\right)}^2}}\hfill \\ \hfill & & \phantom{f_{i+1}}-{\displaystyle \frac{h_{i+2}^2+2h_{i+1}^2}{4(h_{i+2}+h_{i+1})}}\left({\displaystyle \frac{h_{i+2}^2}{h_{i+2}^2+2h_{i+1}^2}}{\displaystyle \frac{f_{i+1}-f_i}{h_{i+1}}}+{\displaystyle \frac{2h_{i+1}^2}{h_{i+1}^2+2h_{i+1}^2}}{\displaystyle \frac{f_{i+2}-f_{i+1}}{h_{i+2}}}\right)\hfill \\ & & \phantom{f_{i+1}-{\displaystyle \frac{h_{i+2}^2+2h_{i+1}^2}{4(h_{i+2}+h_{i+1})}}}{\displaystyle \frac{4\frac{f_{i+1}-f_i}{h_{i+1}}\frac{f_{i+2}-f_{i+1}}{h_{i+2}}}{{\left(\frac{f_{i+1}-f_i}{h_{i+1}}+\frac{f_{i+2}-f_{i+1}}{h_{i+2}}\right)}^2}}\hfill \end{array}$$

and

$$A^{2,3}f\left(z\right)=\sum _{i=-2}^n{\upsilon }_i^{2,3}\left(f\right)B_i^{2,t}\left(z\right).$$

We also emphasize that the evaluation of ${\upsilon }_i^{2,3}\left(f\right)$ is much more efficient, computationally speaking, than that of ${\omega }_i^{2,3}\left(f\right)$.

We present the following theorem.

Theorem 3.

If $f\in C^3\left(I\right)$, then

$$\underset{z\in I}{sup}|A^{2,3}f\left(z\right)-f\left(z\right)|=O\left(h^3\right).$$

In addition, if f has a jump in $(x_{i-1},x_i]$ and $f\in C^3([a,x_{i-1}]\cup [x_i,b])$, then

$$\underset{z\in (t_{i-1},t_{i+1})}{sup}|A^{2,3}f\left(z\right)-f\left(z\right)|=O\left(h^0\right),$$

(16)

$$\underset{z\in [a,t_{i-1}]\cup [t_{i+1},b]}{sup}|A^{2,3}f\left(z\right)-f\left(z\right)|=O\left(h^1\right)$$

(17)

and

$$\underset{z\in [a,t_{i-2}]\cup [t_{i+2},b]}{sup}|A^{2,3}f\left(z\right)-f\left(z\right)|=O\left(h^3\right).$$

(18)

Moreover, $A^{2,3}f\in C^1\left(I\right)$.

Proof. 

If the discontinuity is in $(x_{i-1},x_i]$ and $f\in C^3([a,x_{i-1}]\cup [x_i,b])$, we have ${\upsilon }_{i-2}^{2,3}\left(f\right)={\nu }_{i-2}^2\left(f\right)+O\left(h^1\right)$ and ${\upsilon }_{i-1}^{2,3}\left(f\right)={\nu }_{i-1}^2\left(f\right)+O\left(h^1\right)$, which affects $B_{i-2}^{2,t}$ with support $[t_{i-2},t_{i+1}]$ and $B_{i-1}^{2,t}$ with support $[t_{i-1},t_{i+2}]$. Note that we are using information lying on the other side of the discontinuity. This is why we obtain (16) and (17). We also have ${\upsilon }_j^{2,3}\left(f\right)={\nu }_j^2\left(f\right)+O\left(h^3\right)$, $\forall j\ne i-2,i-1$, which give us (18).

Due to the fact that $A^{2,3}f\in S_2(I,{\Delta }_n^t)$, it is $C^1\left(I\right)$. □

4. Cubic QI Approximants

4.1. Linear QI Based on 3 Points: $L^{3,3}$

If we consider the cubic case $d=3$, by (3), we can define the differential QI

$$Q^{3,3}f\left(x\right)=\sum _{i=-3}^{n-1}{\nu }_i^3\left(f\right)B_i^{3,x}\left(x\right)$$

with

$${\nu }_i^3\left(f\right)=f\left(x_{i+2}\right)+{\displaystyle \frac{h_{i+3}-h_{i+2}}{3}}{f}^{\prime }\left(x_{i+2}\right)-{\displaystyle \frac{h_{i+2}{h}_{i+3}}{6}}{f}^{″}\left(x_{i+2}\right),$$

(19)

or, by [24], we can define the point QI

$$L^{3,3}f\left(x\right)=\sum _{i=-3}^{n-1}{\mu }_i^{3,3}\left(f\right)B_i^{3,x}\left(x\right)$$

with

$${\mu }_i^{3,3}\left(f\right):=-{\displaystyle \frac{h_{i+3}^2}{3h_{i+2}(h_{i+3}+h_{i+2})}}f\left(x_{i+1}\right)+{\displaystyle \frac{{(h_{i+3}+h_{i+2})}^2}{3h_{i+2}{h}_{i+3}}}f\left(x_{i+2}\right)-{\displaystyle \frac{h_{i+2}^2}{3h_{i+3}(h_{i+3}+h_{i+2})}}f\left(x_{i+3}\right),$$

(20)

for $i=0,\dots ,n-4$. Note that if $p_i^s\left(x\right)$ is the polynomial that interpolates ${\left\{f_j\right\}}_{j=i}^{i+s}$, then ${\mu }_i^{3,3}\left(f\right)={\nu }_i^3\left(p_{i+1}^3\right)$. We also define ${\mu }_j^{3,3}\left(f\right)={\nu }_j^3\left(p_0^3\right)$, $j=-3,-2,-1$, and ${\mu }_j^{3,3}\left(f\right)={\nu }_j^3\left(p_{n-3}^2\right)$, $j=n-3,n-2,n-1$, obtaining

$$\begin{array}{ccc}\hfill {\mu }_{-3}^{3,3}\left(f\right)& :=& {\nu }_{-3}^3\left(p_0^3\right)={\displaystyle \frac{6h_1{h}_2{h}_3+6h_1{h}_2^2+11h_1^2{h}_3+22h_1^2{h}_2+18h_1^3}{3h_1(h_2+h_1)(h_3+h_2+h_1)}}{f}_0\hfill \\ & & -{\displaystyle \frac{3h_1{h}_2{h}_3+3h_1{h}_2^2+5h_1^2{h}_3+10h_1^2{h}_2+7h_1^3}{3h_1{h}_2(h_3+h_2))}}{f}_1\hfill \\ & & +{\displaystyle \frac{5h_1^2{h}_3+5h_1^2{h}_2+7h_1^3}{3h_2{h}_3(h_2+h_1)}}{f}_2-{\displaystyle \frac{5h_1^2{h}_2+7h_1^3}{3h_3(h_3+h_2)(h_3+h_2+h_1)}}{f}_3,\hfill \\ \hfill {\mu }_{-2}^{3,3}\left(f\right)& :=& {\nu }_{-2}^3\left(p_0^3\right)={\displaystyle \frac{3h_1{h}_2{h}_3+3h_1{h}_2^2+2h_1^2{h}_3+4h_1^2{h}_2}{3h_1(h_2+h_1)(h_3+h_2+h_1)}}{f}_0+{\displaystyle \frac{h_1^2{h}_3+2h_1^2{h}_2+2h_1^3}{3h_1{h}_2(h_3+h_2)}}{f}_1\hfill \\ & & -{\displaystyle \frac{h_1^2(h_3+h_2+2h_1)}{3h_2{h}_3(h_2+h_1)}}{f}_2+{\displaystyle \frac{h_1^2(h_2+2h_1)}{3h_3(h_3+h_2)(h_3+h_2+h_1)}}{f}_3,\hfill \\ \hfill {\mu }_{-1}^{3,3}\left(f\right)& :=& {\nu }_{-1}^3\left(p_0^3\right)=-{\displaystyle \frac{h_2^2}{3h_1(h_2+h_1)}}{f}_0+{\displaystyle \frac{{(h_2+h_1)}^2}{3h_1{h}_2}}{f}_1-{\displaystyle \frac{h_1^2}{3h_2(h_2+h_1)}}{f}_2,\hfill \\ \hfill {\mu }_{n-3}^{3,3}\left(f\right)& :=& {\nu }_{n-3}^3\left(p_{n-3}^2\right)=-{\displaystyle \frac{h_{n-1}^2}{3h_n(h_{n-1}+h_n)}}{f}_n+{\displaystyle \frac{{(h_{n-1}+h_n)}^2}{3h_n{h}_{n-1}}}{f}_{n-1}-{\displaystyle \frac{h_n^2}{3h_{n-1}(h_{n-1}+h_n)}}{f}_{n-2},\hfill \\ \\ \hfill {\mu }_{n-2}^{3,3}\left(f\right)& :=& {\nu }_{n-2}^3\left(p_{n-3}^2\right)={\displaystyle \frac{3h_n{h}_{n-1}{h}_{n-2}+3h_n{h}_{n-1}^2+2h_n^2{h}_{n-2}+4h_n^2{h}_{n-1}}{3h_n(h_{n-1}+h_n)(h_{n-2}+h_{n-1}+h_n)}}{f}_n\hfill \\ & & +{\displaystyle \frac{h_n^2{h}_{n-2}+2h_n^2{h}_{n-1}+2h_n^3}{3h_n{h}_{n-1}(h_{n_2}+h_{n-1})}}{f}_{n-1}\hfill \\ & & -{\displaystyle \frac{h_n^2(h_{n-2}+h_{n-1}+2h_n)}{3h_{n-1}{h}_{n-2}(h_{n-1}+h_n)}}{f}_{n-2}+{\displaystyle \frac{h_n^2(h_{n-1}+2h_n)}{3h_{n-2}(h_{n-2}+h_{n-1})(h_{n-2}+h_{n-1}+h_n)}}{f}_{n-3},\hfill \\ \hfill {\mu }_{n-1}^{3,3}\left(f\right)& :=& {\nu }_{n-1}^3\left(p_{n-3}^2\right)={\displaystyle \frac{6h_n{h}_{n-1}{h}_{n-2}+6h_n{h}_{n-1}^2+11h_n^2{h}_{n-2}+22h_n^2{h}_{n-1}+18h_n^3}{3h_n(h_{n-1}+h_n)(h_{n-2}+h_{n-1}+h_n)}}{f}_n\hfill \\ & & -{\displaystyle \frac{3h_n{h}_{n-1}{h}_{n-2}+3h_n{h}_{n-1}^2+5h_n^2{h}_{n-2}+10h_n^2{h}_{n-1}+7h_n^3}{3h_n{h}_{n-1}(h_{n-2}+h_{n-1})}}{f}_{n-1}\hfill \\ & & +{\displaystyle \frac{5h_n^2{h}_{n-2}+5h_n^2{h}_{n-1}+7h_n^3}{3h_{n-1}{h}_{n-2}(h_{n-1}+h_n)}}{f}_{n-2}-{\displaystyle \frac{5h_n^2{h}_{n-1}+7h_n^3}{3h_{n-2}(h_{n-2}+h_{n-1})(h_{n-2}+h_{n-1}+h_n)}}{f}_{n-3}.\hfill \end{array}$$

With this, we approximate (19), obtaining

$${\mu }_i^{3,3}\left(f\right)={\nu }_i^3\left(f\right)+O\left(h^4\right),i=-3,\dots ,n-1.$$

Now, we define

$$L^{3,3}f\left(z\right)=\sum _{i=-3}^{n-1}{\mu }_i^{3,3}\left(f\right)B_i^{3,x}\left(z\right)$$

and we can state the following theorem. Indeed, in this case, we have

$$\begin{array}{c}{\displaystyle \left|{\displaystyle -\frac{h_{i+3}^2}{3h_{i+2}(h_{i+3}+h_{i+2})}}\right|\le \frac{h_{i+3}}{3h_{i+2}},}\hfill \\ {\displaystyle \left|{\displaystyle \frac{{(h_{i+3}+h_{i+2})}^2}{3h_{i+2}{h}_{i+3}}}\right|=\frac{h_{i+3}}{3h_{i+2}}+\frac{2}{3}+\frac{h_{i+2}}{3h_{i+3}}}\hfill \end{array}$$

and the other coefficient is similar to the first one. Therefore, if the partition is locally uniform, the operator norm is bounded.

Theorem 4.

We have $L^{3,3}p=p$, $\forall p\in {\mathsf{\Pi }}_3$. In addition, if $f\in C^4\left(I\right)$, then

$$\underset{z\in I}{sup}|L^{3,3}f\left(z\right)-f\left(z\right)|=O\left(h^4\right).$$

In addition, if f has a jump in $(x_{i-1},x_i]$ and $f\in C^4\left([a,x_{i-1}]\cup [x_i,b]\right)$, then

$$\underset{z\in (x_{i-3},x_{i+2})}{sup}|L^{3,3}f\left(z\right)-f\left(z\right)|=O\left(h^0\right)$$

(21)

and

$$\underset{z\in [a,x_{i-3}]\cup [x_{i+2},b]}{sup}|L^{3,3}f\left(z\right)-f\left(z\right)|=O\left(h^4\right).$$

(22)

Moreover, $L^{3,3}f\in C^2\left(I\right)$.

Proof. 

By Taylor series expansion, ${\mu }_j^{3,3}\left(f\right)={\nu }_j^3\left(f\right)+f^{\left(4\right)}\left(\xi \right)O\left(h^4\right)$; thus, $L^{3,3}p=p$, $\forall p\in {\mathsf{\Pi }}_3$.

If the discontinuity is in $(x_{i-1},x_i]$ and $f\in C^4\left([a,x_{i-1}]\cup [x_i,b]\right)$, we have ${\mu }_{i-3}^{3,3}\left(f\right)={\nu }_{i-3}^3\left(f\right)+O\left(h^0\right)$ and ${\mu }_{i-2}^{3,3}\left(f\right)={\nu }_{i-2}^3\left(f\right)+O\left(h^0\right)$, which affects $B_{i-3}^{3,x}$ with support $[x_{i-3},x_{i+1}]$ and $B_{i-2}^{3,x}$ with support $[x_{i-2},x_{i+2}]$, obtaining (21). We also have ${\mu }_j^{3,3}\left(f\right)={\nu }_j^3\left(f\right)+O\left(h^3\right)$, $\forall j\ne i-3,i-2$, which give us (22).

Moreover, the continuity of $L^{3,3}f$ follows from the continuity of f and the B-spline basis functions. □

4.2. Nonlinear QI: $W^{3,3}$

Note, also, that ${\mu }_i^{3,3}\left(f\right)$, in (20), can be written as

$$\begin{array}{ccc}\hfill {\mu }_i^{3,3}\left(f\right)& =& f_{i+2}+{\displaystyle \frac{h_{i+3}^2}{3(h_{i+3}+h_{i+2})}}{\displaystyle \frac{f_{i+2}-f_{i+1}}{h_{i+2}}}-{\displaystyle \frac{h_{i+2}^2}{3(h_{i+3}+h_{i+2})}}{\displaystyle \frac{f_{i+3}-f_{i+2}}{h_{i+3}}}\hfill \\ & =& f_{i+2}+{\gamma }_1{\nu }_1\left(f\right)+{\gamma }_2{\nu }_2\left(f\right),\hfill \end{array}$$

where

$$\begin{array}{c}{\displaystyle {\gamma }_1=\frac{h_{i+3}^2}{3(h_{i+3}+h_{i+2})},{\nu }_1\left(f\right)=\frac{f_{i+2}-f_{i+1}}{h_{i+2}},}\\ {\displaystyle {\gamma }_2=-\frac{h_{i+2}^2}{3(h_{i+3}+h_{i+2})},{\nu }_2\left(f\right)=\frac{f_{i+3}-f_{i+2}}{h_{i+3}}.}\end{array}$$

Since ${\gamma }_2<0$, we apply WENO with negative weights, obtaining:

$$\begin{array}{ccc}\hfill {\mu }_i^{3,3}\left(f\right)& =& f_{i+2}+(2{\gamma }_1-{\gamma }_2)\left({\displaystyle \frac{2{\gamma }_1}{2{\gamma }_1-{\gamma }_2}}{\nu }_1\left(f\right)+{\displaystyle \frac{-{\gamma }_2}{2{\gamma }_1-{\gamma }_2}}{\nu }_2\left(f\right)\right)\hfill \\ & & \phantom{f_{i+1}}+({\gamma }_1-2{\gamma }_2)\left({\displaystyle \frac{2{\gamma }_1}{{\gamma }_1-2{\gamma }_2}}{\nu }_1+{\displaystyle \frac{-2{\gamma }_2}{{\gamma }_1-2{\gamma }_2}}{\nu }_2\right)\hfill \end{array}$$

(23)

$$\begin{array}{ccc}\hfill & =& f_{i+2}+{\displaystyle \frac{2h_{i+3}^2+h_{i+2}^2}{3(h_{i+3}+h_{i+2})}}\left({\displaystyle \frac{2h_{i+3}^2}{h_{i+2}^2+2h_{i+3}^2}}{\displaystyle \frac{f_{i+2}-f_{i+1}}{h_{i+2}}}\right.\hfill \\ & & \phantom{f_{i+1}{f}_{i+1}}\left.+{\displaystyle \frac{h_{i+2}^2}{h_{i+2}^2+2h_{i+3}^2}}{\displaystyle \frac{f_{i+3}-f_{i+2}}{h_{i+3}}}\right)\hfill \\ \hfill & & \phantom{f_{i+1}}-{\displaystyle \frac{h_{i+3}^2+2h_{i+2}^2}{3(h_{i+3}+h_{i+2})}}\left({\displaystyle \frac{h_{i+3}^2}{h_{i+3}^2+2h_{i+2}^2}}{\displaystyle \frac{f_{i+2}-f_{i+1}}{h_{i+2}}}\right.\hfill \\ & & \phantom{f_{i+1}{f}_{i+1}}\left.+{\displaystyle \frac{2h_{i+2}^2}{h_{i+3}^2+2h_{i+2}^2}}{\displaystyle \frac{f_{i+3}-f_{i+2}}{h_{i+3}}}\right)\hfill \end{array}$$

(24)

We also apply the WENO technique to the parenthesis of (23) and (24). We define the smoothness indicators (4)

$$I{S}_i^{\ell }={\displaystyle \frac{{(h_{i+3}+h_{i+2})}^2}{4}}{\displaystyle \frac{{(f_{i+2}-f_{i+1})}^2}{h_{i+2}^2}}\mathrm{a}\mathrm{n}\mathrm{d}I{S}_i^r={\displaystyle \frac{{(h_{i+3}+h_{i+2})}^2}{4}}{\displaystyle \frac{{(f_{i+3}-f_{i+2})}^2}{h_{i+3}^2}},$$

and

$${\alpha }_i^{\ell }={\displaystyle \frac{2h_{i+3}^2}{h_{i+2}^2+2h_{i+3}^2}}{\displaystyle \frac{1}{{({\epsilon }_i+I{S}_i^{\ell })}^2}},{\alpha }_i^r={\displaystyle \frac{h_{i+2}^2}{h_{i+2}^2+2h_{i+3}^2}}{\displaystyle \frac{1}{{({\epsilon }_i+I{S}_i^r)}^2}},$$

$${\beta }_i^{\ell }={\displaystyle \frac{h_{i+3}^2}{2h_{i+2}^2+h_{i+3}^2}}{\displaystyle \frac{1}{{({\epsilon }_i+I{S}_i^{\ell })}^2}},{\beta }_i^r={\displaystyle \frac{2h_{i+2}^2}{2h_{i+2}^2+h_{i+3}^2}}{\displaystyle \frac{1}{{({\epsilon }_i+I{S}_i^r)}^2}},$$

where ${\epsilon }_i={(h_{i+3}+h_{i+2})}^2/4$. Taking

$$\begin{array}{ccc}\hfill {\omega }_i^{3,3}\left(f\right)& =& f_{i+2}+{\displaystyle \frac{2h_{i+3}^2+h_{i+2}^2}{3(h_{i+3}+h_{i+2})}}\left({\displaystyle \frac{{\alpha }_i^{\ell }}{{\alpha }_i^{\ell }+{\alpha }_i^r}}{\displaystyle \frac{f_{i+2}-f_{i+1}}{h_{i+2}}}+{\displaystyle \frac{{\alpha }_i^r}{{\alpha }_i^{\ell }+{\alpha }_i^r}}{\displaystyle \frac{f_{i+3}-f_{i+2}}{h_{i+3}}}\right)\hfill \\ & & \phantom{f_{i+1}}-{\displaystyle \frac{h_{i+3}^2+2h_{i+2}^2}{3(h_{i+3}+h_{i+2})}}\left({\displaystyle \frac{{\beta }_i^{\ell }}{{\beta }_i^{\ell }+{\beta }_i^r}}{\displaystyle \frac{f_{i+2}-f_{i+1}}{h_{i+2}}}+{\displaystyle \frac{{\beta }_i^r}{{\beta }_i^{\ell }+{\beta }_i^r}}{\displaystyle \frac{f_{i+3}-f_{i+2}}{h_{i+3}}}\right),\hfill \end{array}$$

we define

$$W^{3,3}f\left(z\right)=\sum _{i=-3}^{n-1}{\omega }_i^{3,3}\left(f\right)B_i^{3,x}\left(z\right)$$

and we have the following theorem.

Theorem 5.

We have $W^{3,3}p=p$, $\forall p\in {\mathsf{\Pi }}_1$. In addition, if $f\in C^4\left(I\right)$, then

$$\underset{z\in I}{sup}|W^{3,3}f\left(z\right)-f\left(z\right)|=O\left(h^4\right).$$

In addition, if f has a jump in $(x_{i-1},x_i]$ and $f\in C^4\left([a,x_{i-1}]\cup [x_i,b]\right)$, then

$$\underset{z\in (x_{i-2},x_{i+1})}{sup}|W^{3,3}f\left(z\right)-f\left(z\right)|=O\left(h^0\right),$$

(25)

$$\underset{z\in [a,x_{i-2}]\cup [x_{i+1},b]}{sup}|W^{3,3}f\left(z\right)-f\left(z\right)|=O\left(h^2\right)$$

(26)

and

$$\underset{z\in [a,x_{i-3}]\cup [x_{i+2},b]}{sup}|W^{3,3}f\left(z\right)-f\left(z\right)|=O\left(h^4\right).$$

(27)

Moreover, $W^{3,3}f\in C^2\left(I\right)$.

Proof. 

With each of the pieces that form ${\mu }_i^{3,3}\left(f\right)$, we obtain ${\nu }_j^{3,3}\left(f\right)+f^{\left(2\right)}\left(\xi \right)O\left(h^2\right)$; then, we have $W^{3,3}p=p$, $\forall p\in {\mathsf{\Pi }}_1$.

If the discontinuity is in $(x_{i-1},x_i]$ and $f\in C^4\left([a,x_{i-1}]\cup [x_i,b]\right)$, we have ${\omega }_{i-3}^{3,3}\left(f\right)={\nu }_{i-3}^{3,3}\left(f\right)+O\left(h^2\right)$ and ${\omega }_{i-2}^{3,3}\left(f\right)={\nu }_{i-2}^{3,3}\left(f\right)+O\left(h^2\right)$, which affects to $B_{i-3}^{3,x}$ with support $[x_{i-3},x_{i+1}]$ and to $B_{i-2}^{3,x}$ with support $[x_{i-2},x_{i+2}]$, obtaining (25) and (26). We also have ${\mu }_j^{3,3}\left(f\right)={\nu }_j^{3,3}\left(f\right)+O\left(h^3\right)$, $\forall j\ne i-3,i-2$, which give us (27).

Due to the fact that $W^{2,3}f\in S_3(I,{\Delta }_n^x)$, it is $C^2\left(I\right)$. □

4.3. Monotone QI: $A^{3,3}$

As in the Section 3.3, we can also apply the technique of [1] to (23) and (24), that is, we substitute the mean averages ${\gamma }_1{\nu }_1\left(f\right)+{\gamma }_2{\nu }_2\left(f\right)$ of the parenthesis in the Formulas (23) and (24) by

$$({\gamma }_1{\nu }_1\left(f\right)+{\gamma }_2{\nu }_2\left(f\right)){\displaystyle \frac{4{\nu }_1\left(f\right){\nu }_2\left(f\right)}{{({\nu }_1\left(f\right)+{\nu }_2\left(f\right))}^2}}$$

if ${\nu }_1\left(f\right){\nu }_2\left(f\right)>0$ or by 0 when ${\nu }_1\left(f\right){\nu }_2\left(f\right)<0$. Therefore, we define

$$\begin{array}{ccc}\hfill {\upsilon }_i^{3,3}\left(f\right)& =& f_{i+2}+{\displaystyle \frac{2h_{i+3}^2+h_{i+2}^2}{3(h_{i+3}+h_{i+2})}}\left({\displaystyle \frac{2h_{i+3}^2}{h_{i+2}^2+2h_{i+3}^2}}{\displaystyle \frac{f_{i+2}-f_{i+1}}{h_{i+2}}}+{\displaystyle \frac{h_{i+2}^2}{h_{i+2}^2+2h_{i+3}^2}}{\displaystyle \frac{f_{i+3}-f_{i+2}}{h_{i+3}}}\right)\hfill \\ & & \phantom{f_{i+1}}·{\displaystyle \frac{4\frac{f_{i+2}-f_{i+1}}{h_{i+2}}\frac{f_{i+3}-f_{i+2}}{h_{i+3}}}{{\left(\frac{f_{i+2}-f_{i+1}}{h_{i+2}}+\frac{f_{i+3}-f_{i+2}}{h_{i+3}}\right)}^2}}\hfill \\ \hfill & & \phantom{f_{i+1}}-{\displaystyle \frac{h_{i+3}^2+2h_{i+2}^2}{3(h_{i+3}+h_{i+2})}}\left({\displaystyle \frac{h_{i+3}^2}{h_{i+3}^2+2h_{i+2}^2}}{\displaystyle \frac{f_{i+2}-f_{i+1}}{h_{i+2}}}+{\displaystyle \frac{2h_{i+2}^2}{h_{i+3}^2+2h_{i+2}^2}}{\displaystyle \frac{f_{i+3}-f_{i+2}}{h_{i+3}}}\right)\hfill \\ & & \phantom{f_{i+1}}·{\displaystyle \frac{4\frac{f_{i+2}-f_{i+1}}{h_{i+2}}\frac{f_{i+3}-f_{i+2}}{h_{i+3}}}{{\left(\frac{f_{i+2}-f_{i+1}}{h_{i+2}}+\frac{f_{i+3}-f_{i+2}}{h_{i+3}}\right)}^2}}\hfill \end{array}$$

and

$$A^{3,3}f\left(z\right)=\sum _{i=-3}^{n-1}{\upsilon }_i^{3,3}\left(f\right)B_i^{3,x}\left(z\right).$$

We have the following theorem.

Theorem 6.

If $f\in C^4\left(I\right)$, then

$$\underset{z\in I}{sup}|A^{3,3}f\left(z\right)-f\left(z\right)|=O\left(h^4\right).$$

In addition, if f has a jump in $(x_{i-1},x_i]$ and $f\in C^4\left([a,x_{i-1}]\cup [x_i,b]\right)$, then

$$\underset{z\in (x_{i-2},x_{i+1})}{sup}|A^{3,3}f\left(z\right)-f\left(z\right)|=O\left(h^0\right),$$

(28)

$$\underset{z\in [a,x_{i-2}]\cup [x_{i+1},b]}{sup}|A^{3,3}f\left(z\right)-f\left(z\right)|=O\left(h^1\right)$$

(29)

and

$$\underset{z\in [a,x_{i-3}]\cup [x_{i+2},b]}{sup}|A^{3,3}f\left(z\right)-f\left(z\right)|=O\left(h^4\right).$$

(30)

Moreover, $A^{3,3}f\in C^2\left(I\right)$.

Proof. 

If the discontinuity is in $(x_{i-1},x_i]$ and $f\in C^4\left([a,x_{i-1}]\cup [x_i,b]\right)$, we have ${\upsilon }_{i-3}^{3,3}\left(f\right)={\nu }_{i-3}^{3,3}\left(f\right)+O\left(h^1\right)$ and ${\upsilon }_{i-2}^{3,3}\left(f\right)={\nu }_{i-2}^{3,3}\left(f\right)+O\left(h^1\right)$, which affects $B_{i-3}^{3,x}$ with support $[x_{i-3},x_{i+1}]$ and $B_{i-2}^{3,x}$ with support $[x_{i-2},x_{i+2}]$, obtaining (28) and (29). We also have ${\mu }_j^{3,3}\left(f\right)={\nu }_j^{3,3}\left(f\right)+O\left(h^3\right)$, $\forall j\ne i-3,i-2$, which give us (30).

Due to the fact that $A^{3,3}f\in S_3(I,{\Delta }_n^t)$, it is $C^2\left(I\right)$. □

5. Numerical Experiments

In this section, we propose some numerical experiments confirming the theoretical results regarding the accuracy of the developed quasi-interpolants and showing significant improvements in accuracy and smoothness near discontinuities.

5.1. Approximation Properties

Now, we consider the piecewise smooth function

$$f\left(x\right)=\left\{\begin{array}{cc}{e}^x,& \mathrm{i}\mathrm{f} 0\le x<0.5,\\ 1+e^{x^2},& \mathrm{i}\mathrm{f} 0.5\le x\le 1,\end{array}\right.$$

and the discrete grid sets ${\mathrm{\Gamma }}_{N_k}:=\{y_j^k=j/N_k,0\le j\le N_k\}$ and ${\mathsf{\Xi }}_{N_k}:=\{x_j^k,0\le j\le N_k-1\}$, with $N_k=2^k$, $k=4,\dots ,9$, where

$$\begin{array}{ccc}\hfill x_{N_{k-1}-s}^k& =& 0.5-0.5{(s/N_{k-1})}^2,\mathrm{f}\mathrm{o}\mathrm{r} s=N_{k-1},N_{k-2},\dots ,1\hfill \\ \hfill x_{N_{k-1}+s-1}^k& =& 0.5+0.5{(s/N_{k-1})}^2,\mathrm{f}\mathrm{o}\mathrm{r} s=1,2,,\dots ,N_{k-1}.\hfill \end{array}$$

We recall that the sequence of partitions ${\mathsf{\Xi }}_{N_k}$ is locally uniform (see [25]). For each set of points, we construct the corresponding knots partitions ${\Delta }_{N_k}$ (as explained in Section 1), and, from ${\left\{f\left(z_j^k\right)\right\}}_{j=0}^{N_k}$, where $z_j^k=x_j^k$ or $z_j^k=y_j^k$, we construct the approximations $Qf$ for the different QI operators Q presented in this paper. Then, we evaluate the error

$$E^Q=\underset{u\in U}{max}|f\left(u\right)-Qf\left(u\right)|,$$

where U is a set of $2^4$ points in each subinterval $[z_i^k,z_{i+1}^k]$ of the interval $[c,1]$, and the possible values of c are related to the theoretical results given in Theorems 1–6. Moreover we compute the numerical convergence order $O^Q$, defined as the logarithm to base 2 of the ratio between two consecutive errors. In Table 1 and Table 2, we report, for each set of points, the numerical convergence order $O^Q$ for all the operators for the intervals $[z_{N_{k-1}+s}^k,1]$, where $s=0,1,2$. We can notice that the numerical results confirm the theoretical ones, given in Theorems 1–6. We note that when we use the nonuniform partition ${\mathsf{\Xi }}_{N_k}$ on the intervals $[t_{N_{k-1}+1},1]$ and $[x_{N_{k-1}+1},1]$ with the operators $W^{2,3}$, $A^{2,3}$, $W^{3,3}$, $A^{3,3}$, we obtain a higher order than expected with the Theorems 2, 3, 5 and 6.

Table 1. Errors and numerical convergence orders with ${\mathsf{\Gamma }}_{N_k}$ in the interval $[c,1]$.

	${\mathit{E}}^{{\mathit{L}}^{2,3}}$	${\mathit{O}}^{{\mathit{L}}^{2,3}}$	${\mathit{E}}^{{\mathit{W}}^{2,3}}$	${\mathit{O}}^{{\mathit{W}}^{2,3}}$	${\mathit{E}}^{{\mathit{A}}^{2,3}}$	${\mathit{O}}^{{\mathit{A}}^{2,3}}$
	4.478 × 10−2		8.104 × 10−2		6.198 × 10−2
	4.381 × 10−2	0.03	8.055 × 10−2	0.01	6.990 × 10−2	−0.17
$[t_{N_{k-1}},1]$	4.337 × 10−2	0.01	8.006 × 10−2	0.01	7.444 × 10−2	−0.09
	4.316 × 10−2	0.01	7.975 × 10−2	0.01	7.687 × 10−2	−0.05
	4.306 × 10−2	0.00	7.959 × 10−2	0.00	7.813 × 10−2	−0.02
	1.034 × 10−2		4.833 × 10−4		4.109 × 10−3
	1.012 × 10−2	0.03	6.583 × 10−5	2.88	2.250 × 10−3	0.87
$[t_{N_{k-1}+1},1]$	1.002 × 10−2	0.01	1.511 × 10−5	2.12	1.185 × 10−3	0.93
	9.972 × 10−3	0.01	3.699 × 10−6	2.03	6.090 × 10−4	0.96
	9.949 × 10−3	0.00	9.200 × 10−7	2.01	3.089 × 10−4	0.98
	9.754 × 10−5		4.833 × 10−4		6.097 × 10−5
	1.031 × 10−5	3.24	3.566 × 10−5	3.76	7.884 × 10−6	2.95
$[t_{N_{k-1}+2},1]$	1.164 × 10−6	3.15	2.848 × 10−6	3.65	1.009 × 10−6	2.97
	1.373 × 10−7	3.08	2.456 × 10−7	3.54	1.275 × 10−7	2.98
	1.665 × 10−8	3.04	2.351 × 10−8	3.39	1.604 × 10−8	2.99
	$E^{L^{3,3}}$	$O^{L^{3,3}}$	$E^{W^{3,3}}$	$O^{W^{3,3}}$	$E^{A^{3,3}}$	$O^{A^{3,3}}$
	5.425 × 10−2		1.082 × 10−1		8.798 × 10−2
	5.358 × 10−2	0.02	1.074 × 10−1	0.01	9.628 × 10−2	−0.13
$[x_{N_{k-1}},1]$	5.326 × 10−2	0.01	1.067 × 10−1	0.01	1.009 × 10−1	−0.07
	5.310 × 10−2	0.00	1.063 × 10−1	0.01	1.034 × 10−1	−0.03
	5.302 × 10−2	0.00	1.061 × 10−1	0.00	1.046 × 10−1	−0.02
	1.838 × 10−2		5.859 × 10−4		7.296 × 10−3
	1.799 × 10−2	0.03	1.141 × 10−4	2.36	3.999 × 10−3	0.87
$[x_{N_{k-1}+1},1]$	1.781 × 10−2	0.01	2.670 × 10−5	2.10	2.106 × 10−3	0.93
	1.773 × 10−2	0.01	6.566 × 10−6	2.02	1.083 × 10−3	0.96
	1.769 × 10−2	0.00	1.635 × 10−6	2.01	5.492 × 10−4	0.98
	5.357 × 10−5		5.319 × 10−4		7.219 × 10−6
	3.427 × 10−6	3.97	4.108 × 10−5	3.69	4.543 × 10−7	3.99
$[x_{N_{k-1}+2},1]$	2.198 × 10−7	3.96	2.592 × 10−6	3.99	3.049 × 10−8	3.90
	1.393 × 10−8	3.98	1.624 × 10−7	4.00	1.979 × 10−9	3.95
	8.775 × 10−10	3.99	1.016 × 10−8	4.00	1.261 × 10−10	3.97

Table 2. Errors and numerical convergence orders with ${\mathsf{\Xi }}_{N_k}$ in the interval $[c,1]$.

	${\mathit{E}}^{{\mathit{L}}^{2,3}}$	${\mathit{O}}^{{\mathit{L}}^{2,3}}$	${\mathit{E}}^{{\mathit{W}}^{2,3}}$	${\mathit{O}}^{{\mathit{W}}^{2,3}}$	${\mathit{E}}^{{\mathit{A}}^{2,3}}$	${\mathit{O}}^{{\mathit{A}}^{2,3}}$
	9.370 × 10−2		1.148 × 10−1		1.065 × 10−1
	9.385 × 10−2	−0.00	1.145 × 10−1	0.00	1.124 × 10−1	−0.08
$[t_{N_{k-1}},1]$	9.321 × 10−2	0.01	1.144 × 10−1	0.00	1.139 × 10−1	−0.02
	9.361 × 10−2	−0.01	1.144 × 10−1	0.00	1.142 × 10−1	−0.00
	9.373 × 10−2	−0.00	1.144 × 10−1	0.00	1.143 × 10−1	−0.00
	3.452 × 10−2		2.124 × 10−3		3.673 × 10−3
	3.440 × 10−2	0.00	1.503 × 10−4	3.82	9.309 × 10−4	1.98
$[t_{N_{k-1}+1},1]$	3.437 × 10−2	0.00	9.964 × 10−6	3.91	2.334 × 10−4	2.00
	3.436 × 10−2	0.00	8.014 × 10−7	3.64	5.839 × 10−5	2.00
	3.436 × 10−2	0.00	7.092 × 10−8	3.50	1.460 × 10−5	2.00
	2.332 × 10−4		2.124 × 10−3		2.746 × 10−4
	2.523 × 10−5	3.21	1.503 × 10−4	3.82	2.786 × 10−5	3.30
$[t_{N_{k-1}+2},1]$	2.851 × 10−6	3.15	9.964 × 10−6	3.91	3.014 × 10−6	3.21
	3.346 × 10−7	3.09	8.014 × 10−7	3.64	3.446 × 10−7	3.13
	4.033 × 10−8	3.05	7.092 × 10−8	3.50	4.095 × 10−8	3.07
	$E^{L^{3,3}}$	$O^{L^{3,3}}$	$E^{W^{3,3}}$	$O^{W^{3,3}}$	$E^{A^{3,3}}$	$O^{A^{3,3}}$
	9.512 × 10−2		1.435 × 10−1		1.348 × 10−1
	9.481 × 10−2	0.00	1.431 × 10−1	0.00	1.410 × 10−1	−0.06
$[x_{N_{k-1}},1]$	9.493 × 10−2	−0.00	1.430 × 10−1	0.00	1.425 × 10−1	−0.01
	9.496 × 10−2	−0.00	1.430 × 10−1	0.00	1.428 × 10−1	−0.00
	9.493 × 10−2	0.00	1.429 × 10−1	0.00	1.429 × 10−1	−0.00
	5.983 × 10−2		1.751 × 10−3		6.370 × 10−3
	5.963 × 10−2	0.00	1.894 × 10−4	3.21	1.614 × 10−3	1.98
$[x_{N_{k-1}+1},1]$	5.958 × 10−2	0.00	1.203 × 10−5	3.98	4.046 × 10−4	2.00
	5.956 × 10−2	0.00	7.517 × 10−7	4.00	1.012 × 10−4	2.00
	5.956 × 10−2	0.00	4.689 × 10−8	4.00	2.531 × 10−5	2.00
	2.172 × 10−4		1.751 × 10−3		2.639 × 10−4
	1.239 × 10−5	4.13	1.894 × 10−4	3.21	1.546 × 10−5	4.09
$[x_{N_{k-1}+2},1]$	7.500 × 10−7	4.05	1.203 × 10−5	3.98	9.531 × 10−7	4.02
	4.700 × 10−8	4.00	7.517 × 10−7	4.00	6.049 × 10−8	3.98
	3.021 × 10−9	3.96	4.689 × 10−8	4.00	3.851 × 10−9	3.97

5.2. Graphical Properties

5.2.1. Example 1: Data Reconstruction

In Figure 1, we can see the reconstruction proposed in the previous example, from 17 and 16 point values for the discretizations ${\mathrm{\Gamma }}_{N_k}$ and ${\mathsf{\Xi }}_{N_k}$ together with a close-up of the area where the discontinuity is.

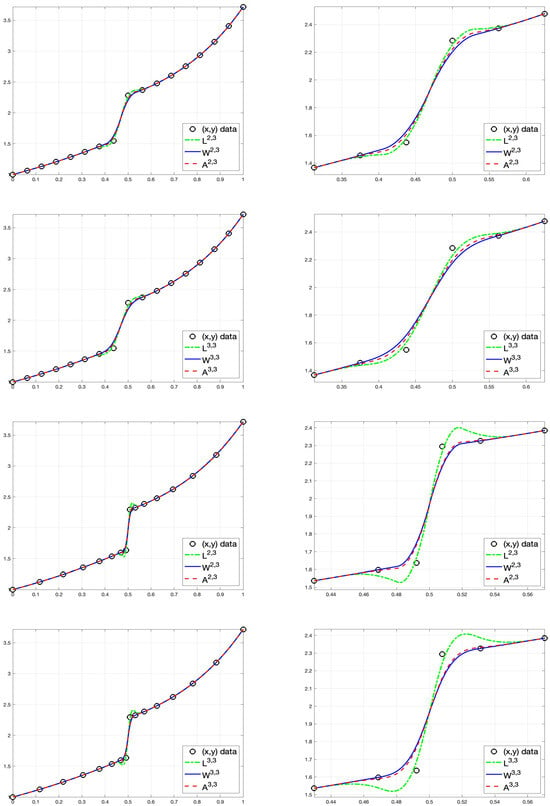
Figure 1. Different reconstructions from $f\left(x_i\right)$, denoted by ‘o’ in the pictures, obtained with the operators $L^{2,3}$, $W^{2,3}$, $A^{2,3}$, $L^{3,3}$, $W^{3,3}$, and $A^{3,3}$. Top (first and second row): uniform discretization; bottom (third and fourth row): nonuniform discretization; right: close-up of the left pictures.

We observe that with the $W^{2,3}$, $A^{2,3}$, $W^{3,3}$, $A^{3,3}$ operators, we always avoid the oscillations that appear with $L^{2,3}$, $L^{3,3}$. We also see that with the $A^{2,3}$ and $A^{3,3}$ operators, we obtain results closer to the original function.

5.2.2. Example 2: Geophysical Application

We present a numerical experiment demonstrating the application of quasi-interpolation operators to geophysical data with inherent discontinuities and nonuniform sampling. The dataset (Table 3) simulates electrical conductivity measurements across a two-layer soil structure, with measurements taken at varying depth intervals ranging from 0 to 5 m. The upper layer (0–2.0 m) exhibits conductivity values between 0.15 and 0.35 S/m, while the lower layer (2.001–5.0 m) shows higher values ranging from 0.85 to 1.0 S/m, representing a sharp geological boundary.

Table 3. Conductivity (cond.) measurements (in Siemmens/meter) taken at varying depth intervals (in meters) (Section 5.2.2).

depth	0	0.3	0.5	0.8	1.2	1.5	1.7	1.9	2.1	2.3	2.4	2.8	3.5	4.0	4.2	4.5	5.0
cond.	0.15	0.18	0.22	0.25	0.28	0.30	0.32	0.35	0.85	0.88	0.90	0.92	0.95	0.97	0.98	0.99	1.0

The nonuniform sampling strategy reflects real-world constraints, with intervals varying from 0.1 m to 0.7 m, allowing for higher resolution in regions of rapid change and more sparse sampling in areas of gradual variation. In Figure 2 we, can see the reconstructions obtained with the different operators presented in this paper. The results that we obtain with this approach not only preserve the sharp conductivity transition at the layer boundary but also maintain smooth approximation within each layer. Our implementation demonstrates the flexibility of quasi-interpolating splines in handling geophysical data with both discontinuities and varying sampling densities, making it particularly suitable for characterizing layered earth structures in geological and environmental studies.

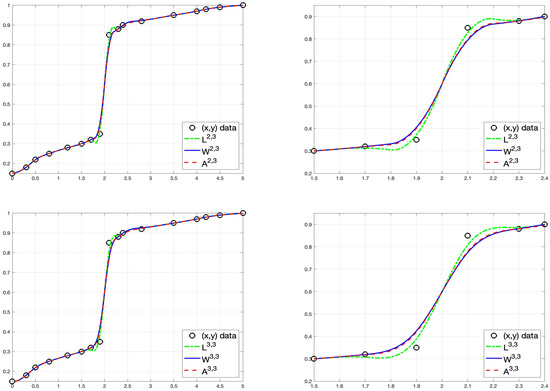
Figure 2. Different reconstructions from the data in Table 3, denoted by ‘o’ in the pictures, with the operators $L^{2,3}$, $W^{2,3}$, $A^{2,3}$, $L^{3,3}$, $W^{3,3}$, and $A^{2,3}$. Right: zoom of the left pictures.

6. Conclusions and Future Directions

Our research has successfully addressed the persistent tension between accuracy and shape preservation in numerical approximation methods. By developing novel quasi-interpolation techniques that integrate traditional B-spline methods with advanced WENO approaches, we have achieved both computational efficiency and improved handling of discontinuities. The numerical experiments conclusively demonstrate that our proposed methods maintain optimal approximation order $O\left(h^{d+1}\right)$$(d=2,3)$ while preserving essential shape properties like monotonicity. The $C^1$ and $C^2$ reconstructions show remarkable stability near discontinuities, significantly reducing the oscillations that plague conventional methods without sacrificing accuracy in smooth regions. Particularly noteworthy is the performance of our nonlinear quasi-interpolants in applications involving isolated discontinuities, where traditional approaches generate undesirable oscillations proportional to jump magnitude. Our methods achieve stable, non-oscillatory behavior while maintaining high-order accuracy in smooth regions, a critical advancement for image processing and shock-capturing schemes. The local nature of our reconstruction operators provides substantial computational advantages over traditional interpolation methods that require solving global systems of equations, making our approach particularly suitable for large-scale applications and adaptive schemes.

Several promising research directions emerge from this work, presenting opportunities to expand and enhance the applicability of our quasi-interpolation techniques. For instance, these methods can be naturally extended to multiresolution frameworks, allowing for adaptive representation at different scales and enabling more efficient handling of complex data structures with varying levels of detail. Additionally, exploring the application of these techniques in the context of conservation laws could lead to significant advancements in numerical schemes for hyperbolic partial differential equations, where preserving physical properties is crucial for stability and accuracy. Another compelling direction involves adapting our quasi-interpolation methods to work with different data representations. Specifically, we can investigate how to modify these techniques when, instead of having point values of the original function, we have cell averages or integral values. This adaptation would require reformulating the quasi-interpolation functionals to maintain the same level of accuracy and shape-preserving properties while working with this alternative data representation. The development of such methods would be particularly valuable in the context of image processing, where data is often naturally represented as pixel averages rather than point values. This extension would enable more accurate reconstruction of images from compressed data, improved edge detection algorithms, and enhanced restoration techniques for degraded images. Furthermore, combining these adapted methods with existing image processing frameworks could lead to new algorithms for image enhancement, segmentation, and feature extraction that preserve important structural properties while reducing artifacts and noise. This research direction could bridge the gap between traditional polynomial-based approximation methods and practical image processing applications, potentially yielding significant improvements in both computational efficiency and the visual quality of processed images.