A Framework for Breast Cancer Classification with Deep Features and Modified Grey Wolf Optimization
Abstract
1. Introduction
- Utilization of three distinct mammographic databases to evaluate the suggested approach thoroughly.
- The Haze-Removed Adaptive Technique (HRAT) improves contrast adjustment and image clarity.
- Designing a 32-layer CNN model for breast cancer mammographic data based on YOLO, U-Net, and ResNet.
- The modified Grey Wolf Optimization (mGWO) approach to extract highly discriminative features, minimize redundancy, and improve classification.
2. Literature Review
3. Materials and Methods
3.1. Mammogram Datasets
3.2. Haze-Removed Adaptive Technique (HRAT)
3.3. Data Augmentation
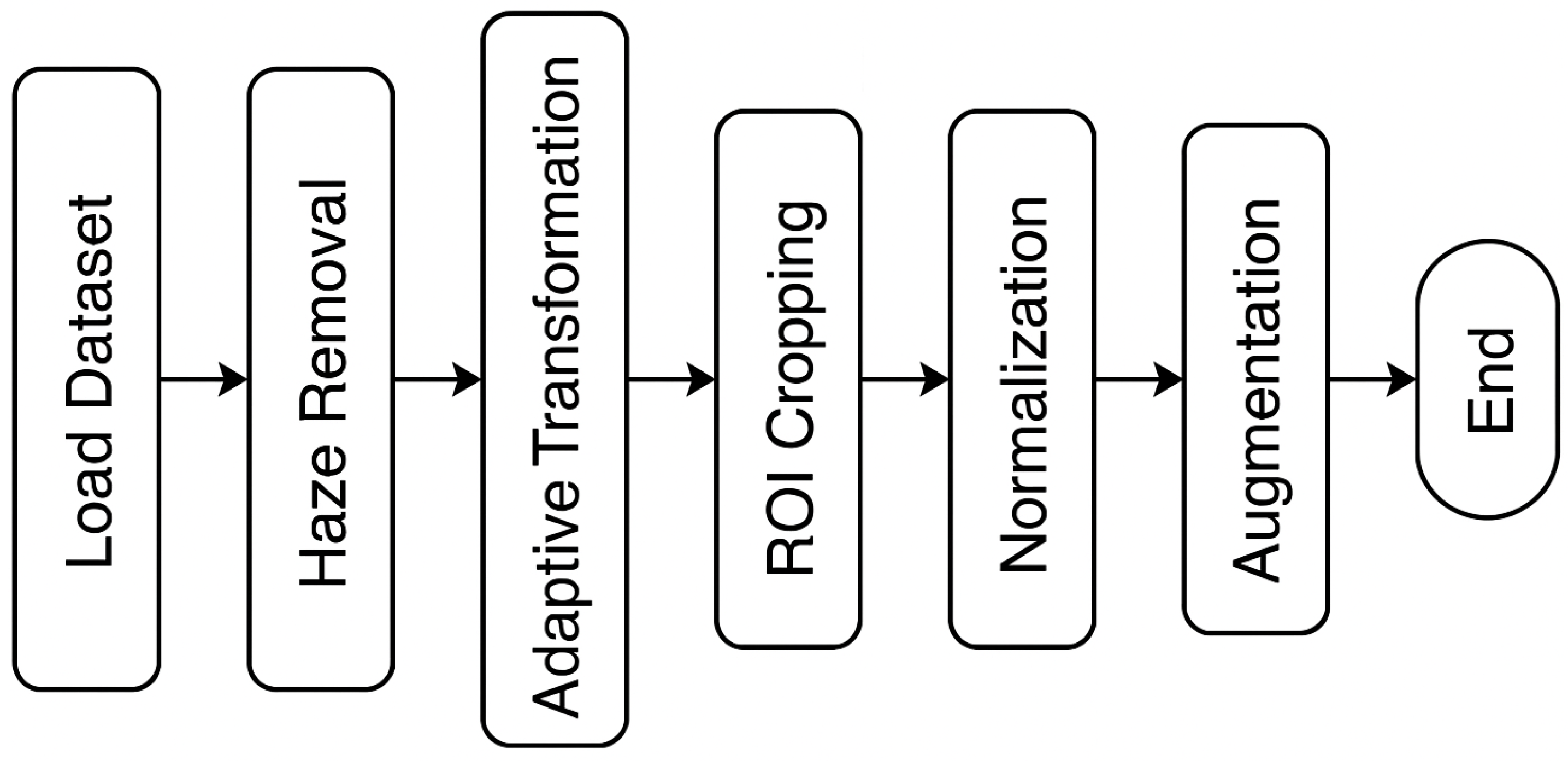
3.4. Preprocessing
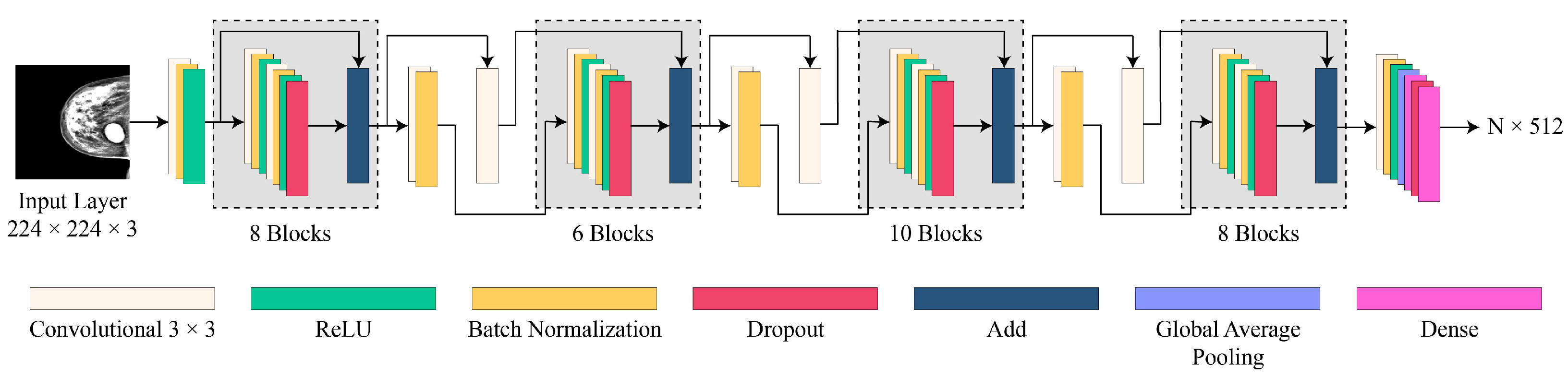
3.5. Proposed CNN Model Architecture
3.6. CNN Model Training
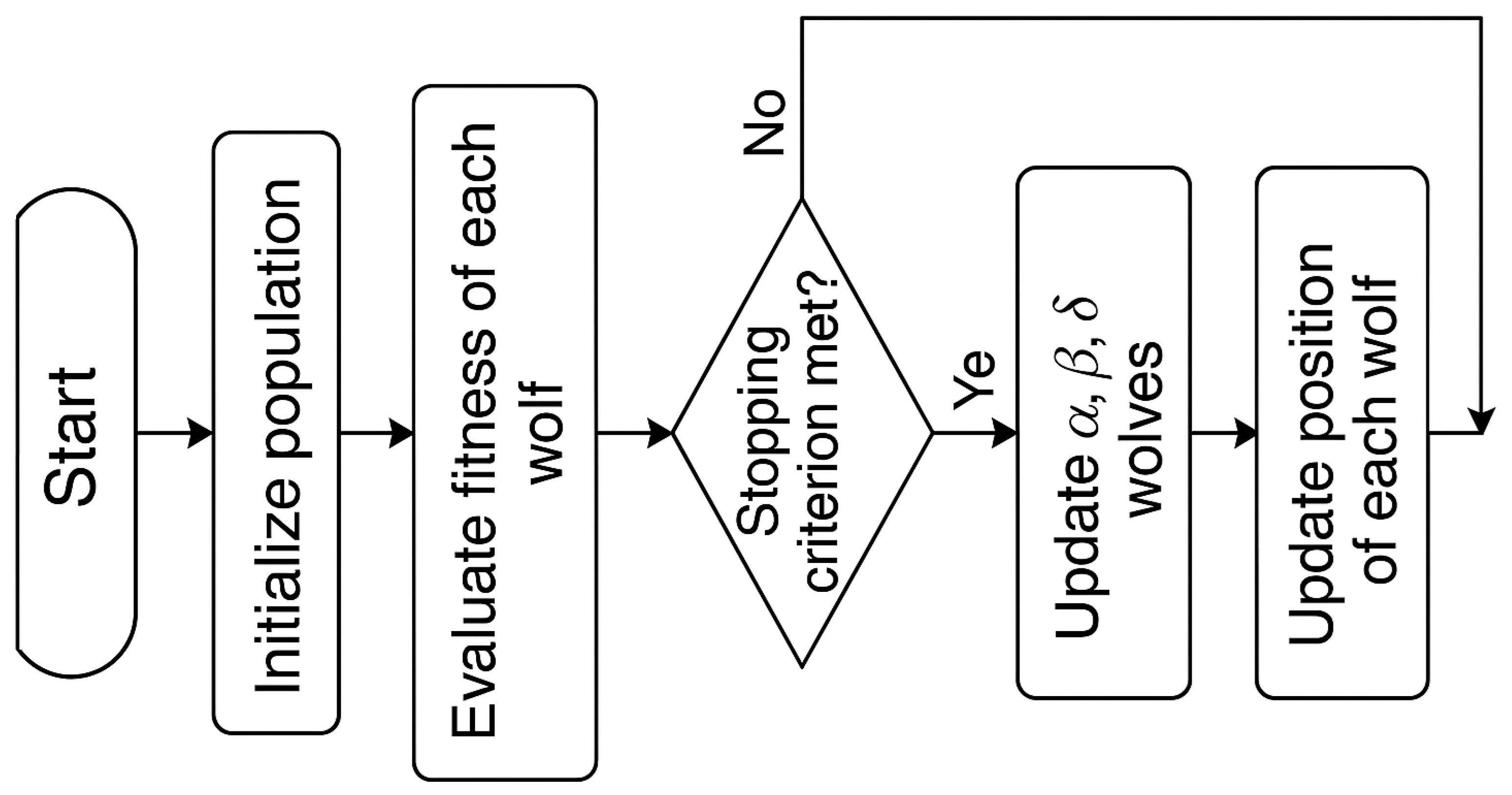
3.7. Modified Grey Wolf Optimization (mGWO) Algorithm
3.7.1. Encircling the Prey
3.7.2. Hunting of Prey
3.7.3. Attacking of Prey
3.7.4. Objective Function
3.8. Modifications in GWO
3.8.1. Modification I—Adaptive Dynamic Parameter Control for Exploration and Exploitation
3.8.2. Modification II—Chaos-Based Position Update for Better Global Search
3.8.3. Modification III—Opposition-Based Learning (OBL) for Faster Convergence
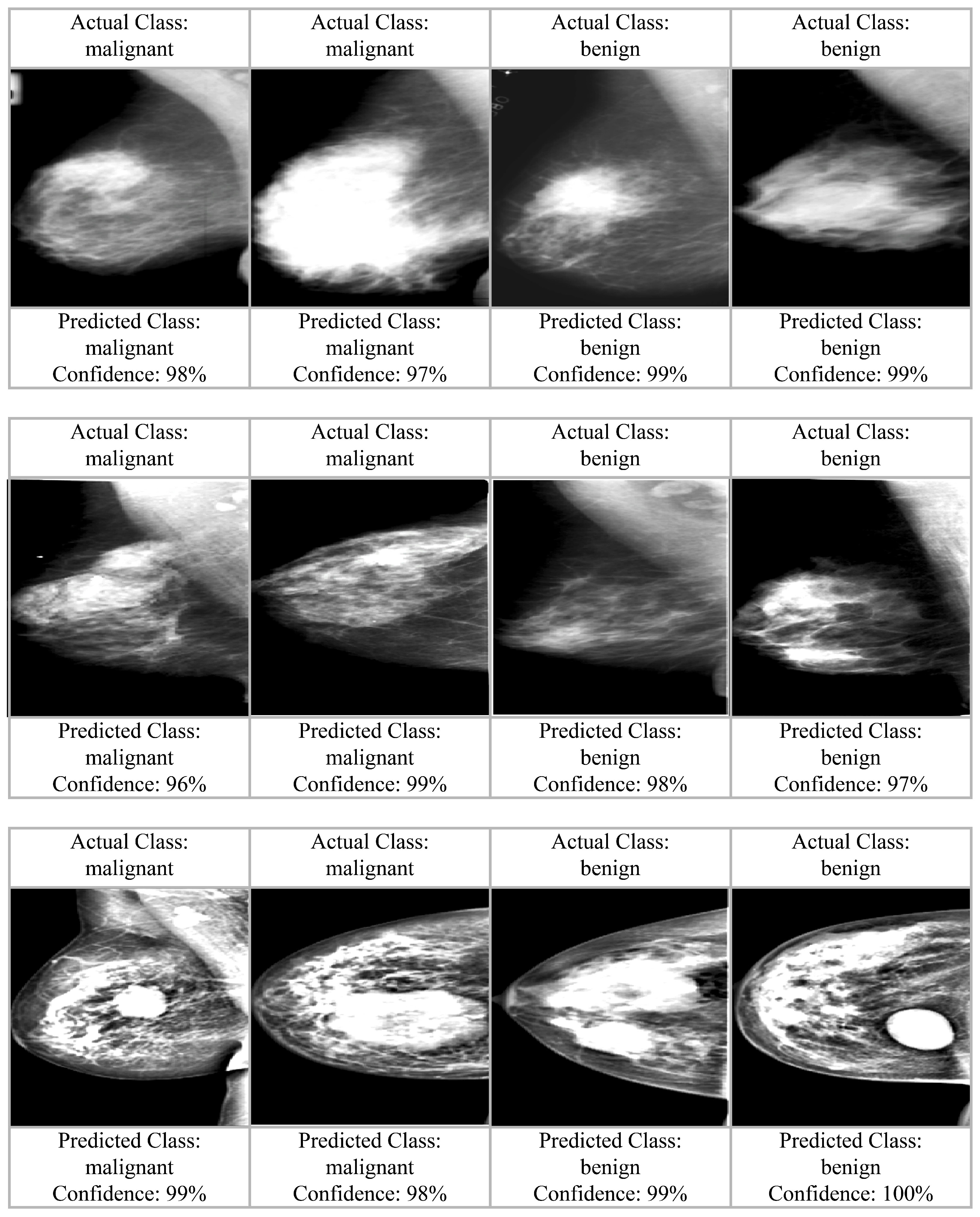
4. Experimental Results
4.1. Experimental Setup
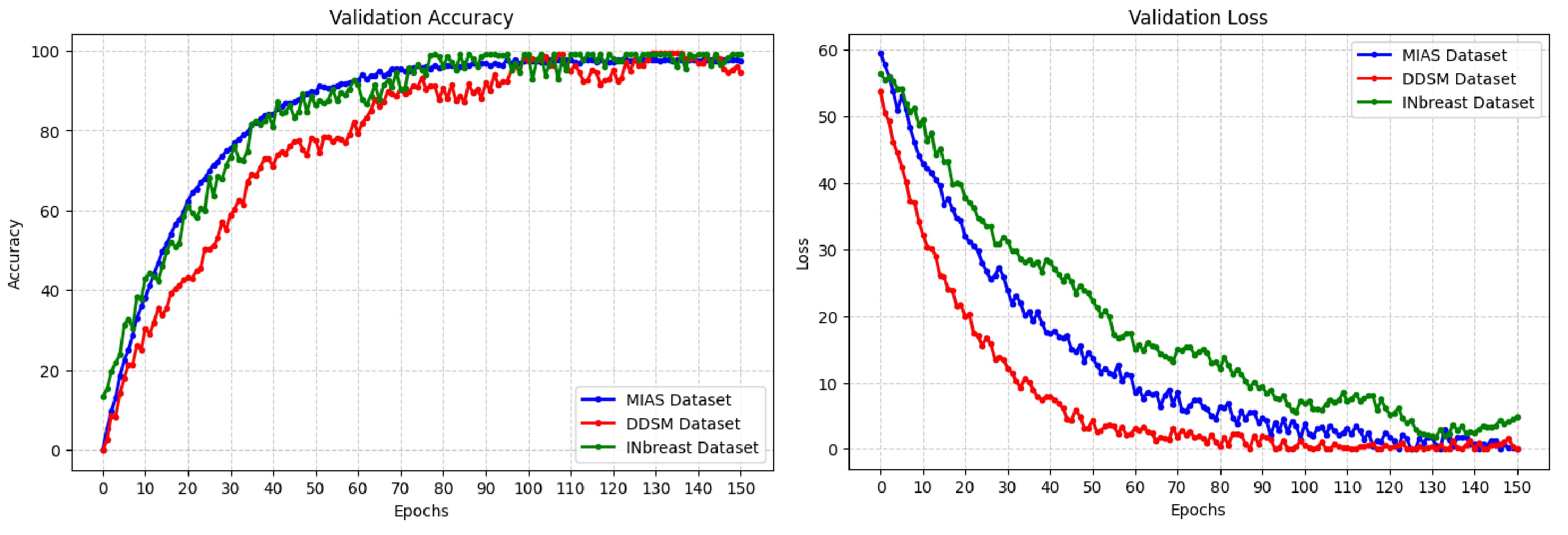
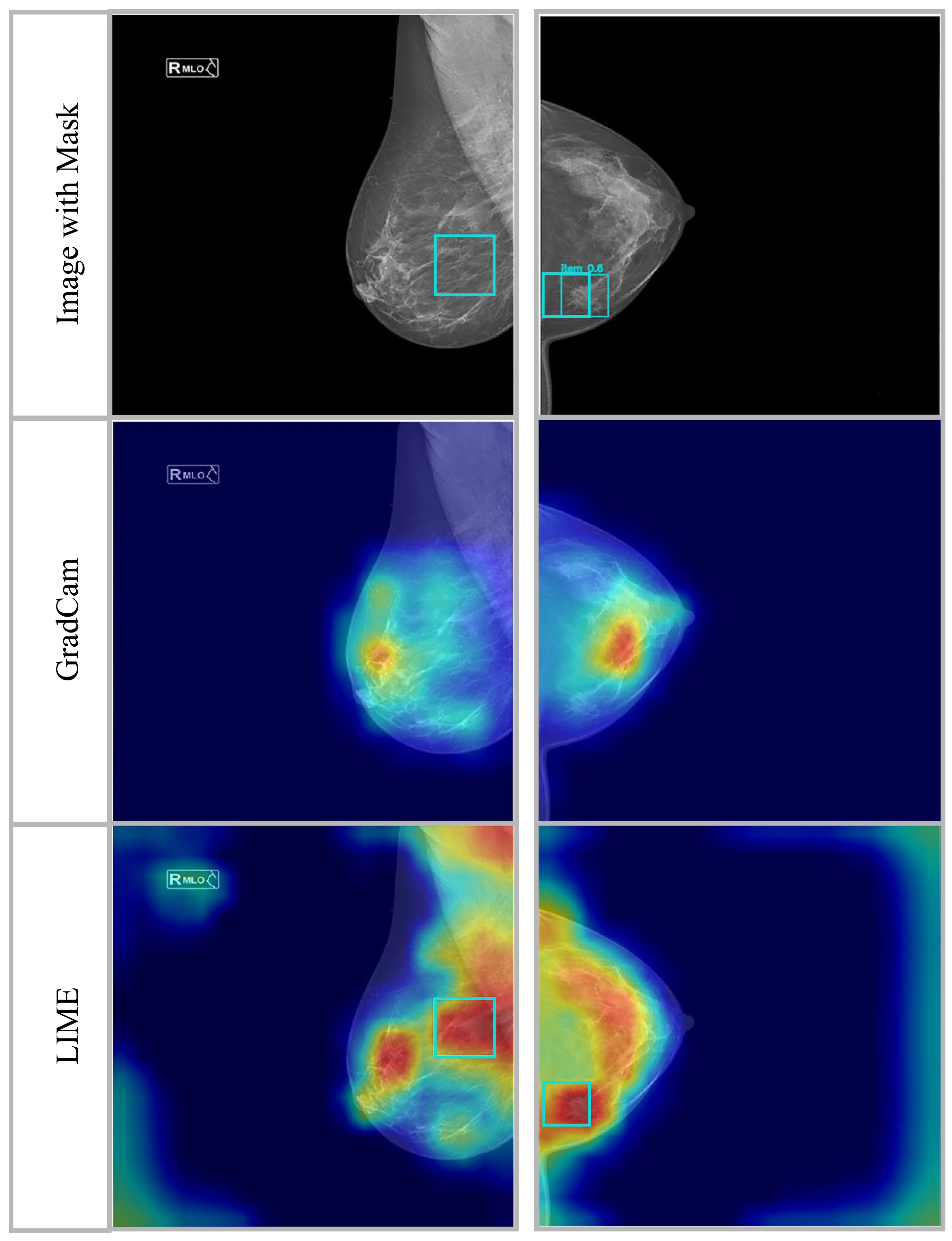
4.2. Results and Analysis
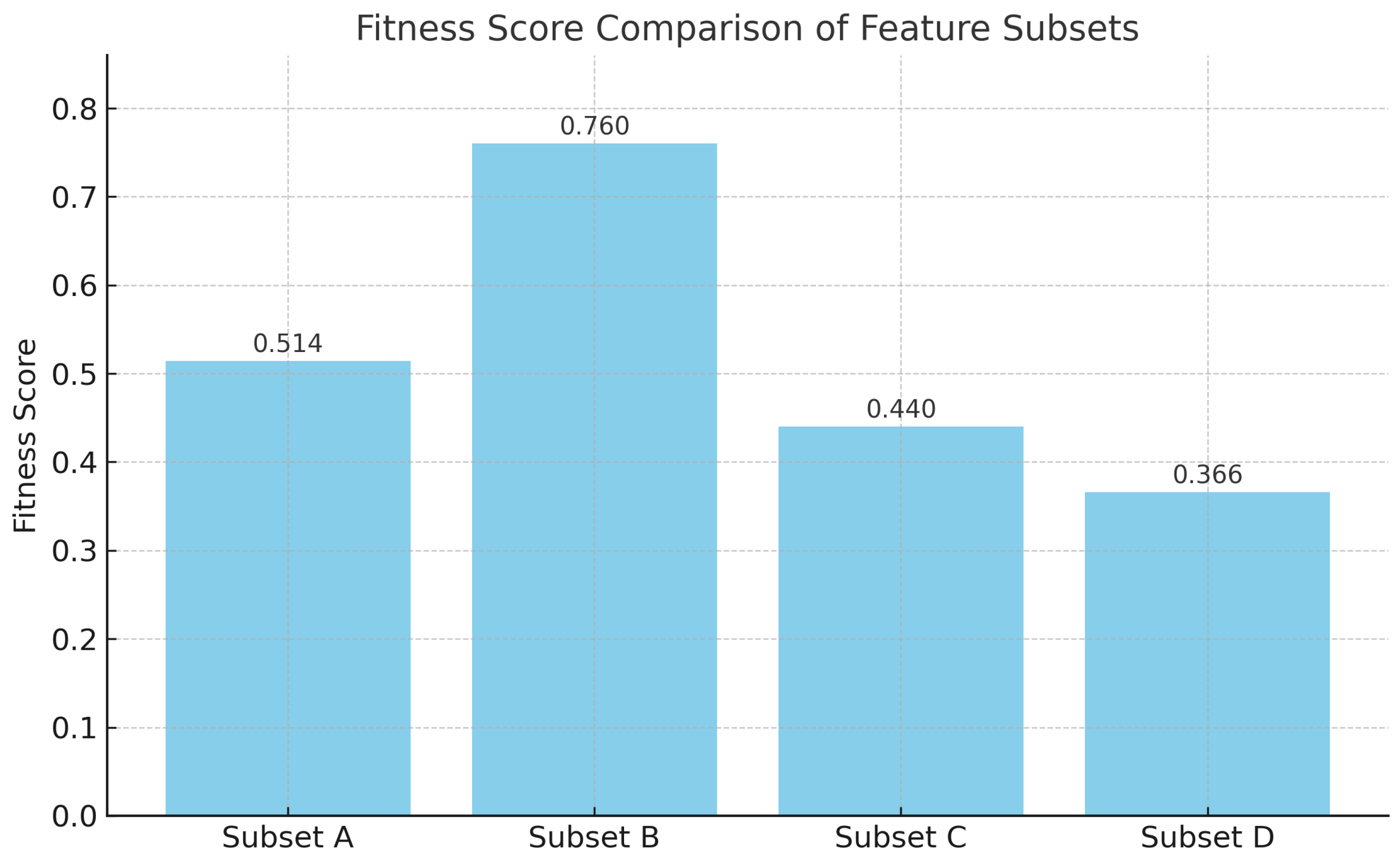
4.3. Ablation Studies
4.4. Comparison of mGWO with State-of-the-Art Optimization Algorithms
4.5. Comparative Analysis with State-of-the-Art Methods
5. Conclusions and Future Directions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ali Salman, R. Prevalence of women breast cancer. Cell. Mol. Biomed. Rep. 2023, 3, 185–196. [Google Scholar] [CrossRef]
- Trieu, P.D.; Mello-Thoms, C.R.; Barron, M.L.; Lewis, S.J. Look how far we have come: BREAST cancer detection education on the international stage. Front. Oncol. 2023, 12, 1023714. [Google Scholar] [CrossRef] [PubMed]
- Acs, B.; Leung, S.C.; Kidwell, K.M.; Arun, I.; Augulis, R.; Badve, S.S.; Bai, Y.; Bane, A.L.; Bartlett, J.M.; Bayani, J.; et al. Systematically higher Ki67 scores on core biopsy samples compared to corresponding resection specimen in breast cancer: A multi-operator and multi-institutional study. Mod. Pathol. 2022, 35, 1362–1369. [Google Scholar] [CrossRef] [PubMed]
- Sannasi Chakravarthy, S.; Rajaguru, H. SKMAT-U-Net architecture for breast mass segmentation. Int. J. Imaging Syst. Technol. 2022, 32, 1880–1888. [Google Scholar] [CrossRef]
- Nasir, I.M.; Alrasheedi, M.A.; Alreshidi, N.A. MFAN: Multi-feature attention network for breast cancer classification. Mathematics 2024, 12, 3639. [Google Scholar] [CrossRef]
- Sun, H.; Li, C.; Liu, B.; Liu, Z.; Wang, M.; Zheng, H.; Feng, D.D.; Wang, S. AUNet: Attention-guided dense-upsampling networks for breast mass segmentation in whole mammograms. Phys. Med. Biol. 2020, 65, 055005. [Google Scholar] [CrossRef]
- Sabour, S.; Frosst, N.; Hinton, G.E. Dynamic routing between capsules. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Suckling, J.; Parker, J.; Dance, D.; Astley, S.; Hutt, I.; Boggis, C.; Ricketts, I.; Stamatakis, E.; Cerneaz, N.; Kok, S.; et al. Mammographic Image Analysis Society (Mias) Satabase v1. 21. 2015. Available online: https://www.mammoimage.org/databases/ (accessed on 7 February 2025).
- Lee, R.S.; Gimenez, F.; Hoogi, A.; Miyake, K.K.; Gorovoy, M.; Rubin, D.L. A curated mammography data set for use in computer-aided detection and diagnosis research. Sci. Data 2017, 4, 170177. [Google Scholar] [CrossRef]
- Moreira, I.C.; Amaral, I.; Domingues, I.; Cardoso, A.; Cardoso, M.J.; Cardoso, J.S. Inbreast: Toward a full-field digital mammographic database. Acad. Radiol. 2012, 19, 236–248. [Google Scholar] [CrossRef]
- Nasir, I.M.; Raza, M.; Shah, J.H.; Khan, M.A.; Nam, Y.C.; Nam, Y. Improved shark smell optimization algorithm for human action recognition. Comput. Mater. Contin. 2023, 76, 2667–2684. [Google Scholar]
- Nasir, I.M.; Raza, M.; Ulyah, S.M.; Shah, J.H.; Fitriyani, N.L.; Syafrudin, M. ENGA: Elastic net-based genetic algorithm for human action recognition. Expert Syst. Appl. 2023, 227, 120311. [Google Scholar] [CrossRef]
- Nasir, I.M.; Raza, M.; Shah, J.H.; Wang, S.H.; Tariq, U.; Khan, M.A. HAREDNet: A deep learning based architecture for autonomous video surveillance by recognizing human actions. Comput. Electr. Eng. 2022, 99, 107805. [Google Scholar] [CrossRef]
- Wang, L.; Jiang, S.; Jiang, S. A feature selection method via analysis of relevance, redundancy, and interaction. Expert Syst. Appl. 2021, 183, 115365. [Google Scholar] [CrossRef]
- Tariq, J.; Alfalou, A.; Ijaz, A.; Ali, H.; Ashraf, I.; Rahman, H.; Armghan, A.; Mashood, I.; Rehman, S. Fast intra mode selection in HEVC using statistical model. Comput. Mater. Contin. 2022, 70, 3903–3918. [Google Scholar] [CrossRef]
- Shafipour, M.; Rashno, A.; Fadaei, S. Particle distance rank feature selection by particle swarm optimization. Expert Syst. Appl. 2021, 185, 115620. [Google Scholar] [CrossRef]
- Nasir, I.M.; Rashid, M.; Shah, J.H.; Sharif, M.; Awan, M.Y.; Alkinani, M.H. An optimized approach for breast cancer classification for histopathological images based on hybrid feature set. Curr. Med. Imaging Rev. 2021, 17, 136–147. [Google Scholar] [CrossRef]
- Samieinasab, M.; Torabzadeh, S.A.; Behnam, A.; Aghsami, A.; Jolai, F. Meta-Health Stack: A new approach for breast cancer prediction. Healthc. Anal. 2022, 2, 100010. [Google Scholar] [CrossRef]
- Mushtaq, I.; Umer, M.; Imran, M.; Nasir, I.M.; Muhammad, G.; Shorfuzzaman, M. Customer prioritization for medical supply chain during COVID-19 pandemic. Comput. Mater. Contin. 2021, 70, 59–72. [Google Scholar] [CrossRef]
- Nardin, S.; Mora, E.; Varughese, F.M.; D’Avanzo, F.; Vachanaram, A.R.; Rossi, V.; Saggia, C.; Rubinelli, S.; Gennari, A. Breast cancer survivorship, quality of life, and late toxicities. Front. Oncol. 2020, 10, 864. [Google Scholar] [CrossRef]
- Nasir, I.M.; Raza, M.; Shah, J.H.; Khan, M.A.; Rehman, A. Human action recognition using machine learning in uncontrolled environment. In Proceedings of the 2021 1st International Conference on Artificial Intelligence and Data Analytics (CAIDA), Riyadh, Saudi Arabia, 6–7 April 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 182–187. [Google Scholar]
- Nasir, I.; Bibi, A.; Shah, J.; Khan, M.; Sharif, M.; Iqbal, K.; Nam, Y.; Kadry, S. Deep learning-based classification of fruit diseases: An application for precision agriculture. Comput. Mater. Contin. 2020, 66, 1949–1962. [Google Scholar]
- Nasir, I.M.; Khan, M.A.; Yasmin, M.; Shah, J.H.; Gabryel, M.; Scherer, R.; Damaševičius, R. Pearson correlation-based feature selection for document classification using balanced training. Sensors 2020, 20, 6793. [Google Scholar] [CrossRef]
- Dar, R.A.; Rasool, M.; Assad, A. Breast cancer detection using deep learning: Datasets, methods, and challenges ahead. Comput. Biol. Med. 2022, 149, 106073. [Google Scholar]
- Nasir, I.M.; Khan, M.A.; Armghan, A.; Javed, M.Y. SCNN: A secure convolutional neural network using blockchain. In Proceedings of the 2020 2nd International Conference on Computer and Information Sciences (ICCIS), Sakaka, Saudi Arabia, 13–15 October 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–5. [Google Scholar]
- Khan, M.A.; Nasir, I.M.; Sharif, M.; Alhaisoni, M.; Kadry, S.; Bukhari, S.A.C.; Nam, Y. A blockchain based framework for stomach abnormalities recognition. Comput. Mater. Contin. 2021, 67, 141–158. [Google Scholar]
- Muduli, D.; Dash, R.; Majhi, B. Automated diagnosis of breast cancer using multi-modal datasets: A deep convolution neural network based approach. Biomed. Signal Process. Control 2022, 71, 102825. [Google Scholar] [CrossRef]
- El Houby, E.M.; Yassin, N.I. Malignant and nonmalignant classification of breast lesions in mammograms using convolutional neural networks. Biomed. Signal Process. Control 2021, 70, 102954. [Google Scholar] [CrossRef]
- Rahman, H.; Naik Bukht, T.F.; Ahmad, R.; Almadhor, A.; Javed, A.R. Efficient breast cancer diagnosis from complex mammographic images using deep convolutional neural network. Comput. Intell. Neurosci. 2023, 2023, 7717712. [Google Scholar] [CrossRef]
- Agarwal, R.; Diaz, O.; Yap, M.H.; Lladó, X.; Marti, R. Deep learning for mass detection in full field digital mammograms. Comput. Biol. Med. 2020, 121, 103774. [Google Scholar] [CrossRef]
- Al-Antari, M.A.; Han, S.M.; Kim, T.S. Evaluation of deep learning detection and classification towards computer-aided diagnosis of breast lesions in digital X-ray mammograms. Comput. Methods Programs Biomed. 2020, 196, 105584. [Google Scholar] [CrossRef]
- Prinzi, F.; Insalaco, M.; Orlando, A.; Gaglio, S.; Vitabile, S. A yolo-based model for breast cancer detection in mammograms. Cogn. Comput. 2024, 16, 107–120. [Google Scholar] [CrossRef]
- Baccouche, A.; Garcia-Zapirain, B.; Elmaghraby, A.S. An integrated framework for breast mass classification and diagnosis using stacked ensemble of residual neural networks. Sci. Rep. 2022, 12, 12259. [Google Scholar] [CrossRef]
- Falconí, L.; Pérez, M.; Aguilar, W.; Conci, A. Transfer learning and fine tuning in mammogram bi-rads classification. In Proceedings of the 2020 IEEE 33rd International Symposium on computer-based medical systems (CBMS), Rochester, MN, USA, 28–30 July 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 475–480. [Google Scholar]
- Kavitha, T.; Mathai, P.P.; Karthikeyan, C.; Ashok, M.; Kohar, R.; Avanija, J.; Neelakandan, S. Deep learning based capsule neural network model for breast cancer diagnosis using mammogram images. Interdiscip. Sci. Comput. Life Sci. 2021, 14, 113–129. [Google Scholar] [CrossRef]
- Nosheen, F.; Khan, S.; Sharif, M.; Kim, D.H.; Alkanhel, R.; AbdelSamee, N. Breakthrough in breast tumor detection and diagnosis: A noise-resilient, rotation-invariant framework. Multimed. Tools Appl. 2025, 1–27. Available online: https://link.springer.com/article/10.1007/s11042-024-20539-7 (accessed on 7 February 2025).
- Chakravarthy, S.; Nagarajan, B.; Kumar, V.V.; Mahesh, T.; Sivakami, R.; Annand, J.R. Breast tumor classification with enhanced transfer learning features and selection using chaotic map-based optimization. Int. J. Comput. Intell. Syst. 2024, 17, 18. [Google Scholar] [CrossRef]
- Aymaz, S. A new framework for early diagnosis of breast cancer using mammography images. Neural Comput. Appl. 2024, 36, 1665–1680. [Google Scholar] [CrossRef]
- Li, H.; Niu, J.; Li, D.; Zhang, C. Classification of breast mass in two-view mammograms via deep learning. IET Image Process. 2021, 15, 454–467. [Google Scholar] [CrossRef]
- Mashood Nasir, I.; Attique Khan, M.; Alhaisoni, M.; Saba, T.; Rehman, A.; Iqbal, T. A hybrid deep learning architecture for the classification of superhero fashion products: An application for medical-tech classification. Comput. Model. Eng. Sci. 2020, 124, 1017–1033. [Google Scholar] [CrossRef]
- Aly, G.H.; Marey, M.; El-Sayed, S.A.; Tolba, M.F. YOLO based breast masses detection and classification in full-field digital mammograms. Comput. Methods Programs Biomed. 2021, 200, 105823. [Google Scholar] [CrossRef]
- Huang, M.L.; Lin, T.Y. Considering breast density for the classification of benign and malignant mammograms. Biomed. Signal Process. Control 2021, 67, 102564. [Google Scholar] [CrossRef]
- Karnati, V.; Uliyar, M.; Dey, S. Fast non-local algorithm for image denoising. In Proceedings of the 2009 16th IEEE International Conference on Image Processing (ICIP), Cairo, Egypt, 7–10 November 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 3873–3876. [Google Scholar]
- Nyúl, L.G.; Udupa, J.K. On standardizing the MR image intensity scale. Magn. Reson. Med. 1999, 42, 1072–1081. [Google Scholar] [CrossRef]
- Faris, H.; Aljarah, I.; Al-Betar, M.A.; Mirjalili, S. Grey wolf optimizer: A review of recent variants and applications. Neural Comput. Appl. 2018, 30, 413–435. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Simonyan, K. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Szegedy, C.; Ioffe, S.; Vanhoucke, V.; Alemi, A. Inception-v4, inception-resnet and the impact of residual connections on learning. In Proceedings of the AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; Volume 31. [Google Scholar]
- Tan, M.; Le, Q. Efficientnet: Rethinking model scaling for convolutional neural networks. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; PMLR: New York, NY, USA, 2019; pp. 6105–6114. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; IEEE: Piscataway, NJ, USA, 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Dorigo, M.; Birattari, M.; Stutzle, T. Ant colony optimization. IEEE Comput. Intell. Mag. 2007, 1, 28–39. [Google Scholar] [CrossRef]
- Yang, X.S.; Hossein Gandomi, A. Bat algorithm: A novel approach for global engineering optimization. Eng. Comput. 2012, 29, 464–483. [Google Scholar] [CrossRef]
- Yang, X.S.; Deb, S. Cuckoo search via Lévy flights. In Proceedings of the 2009 World Congress on Nature & Biologically Inspired Computing (NaBIC), Coimbatore, India, 9–11 December 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 210–214. [Google Scholar]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
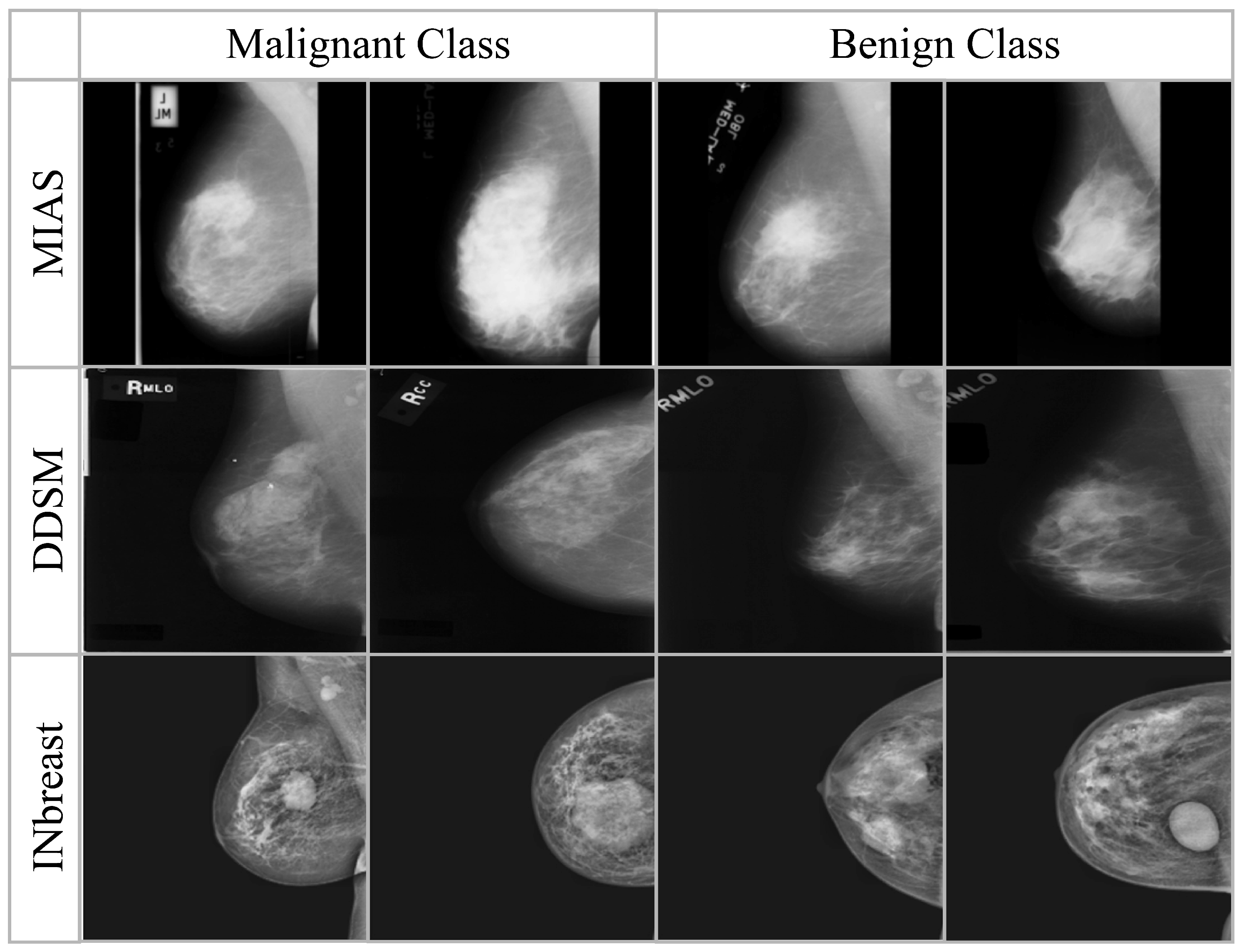
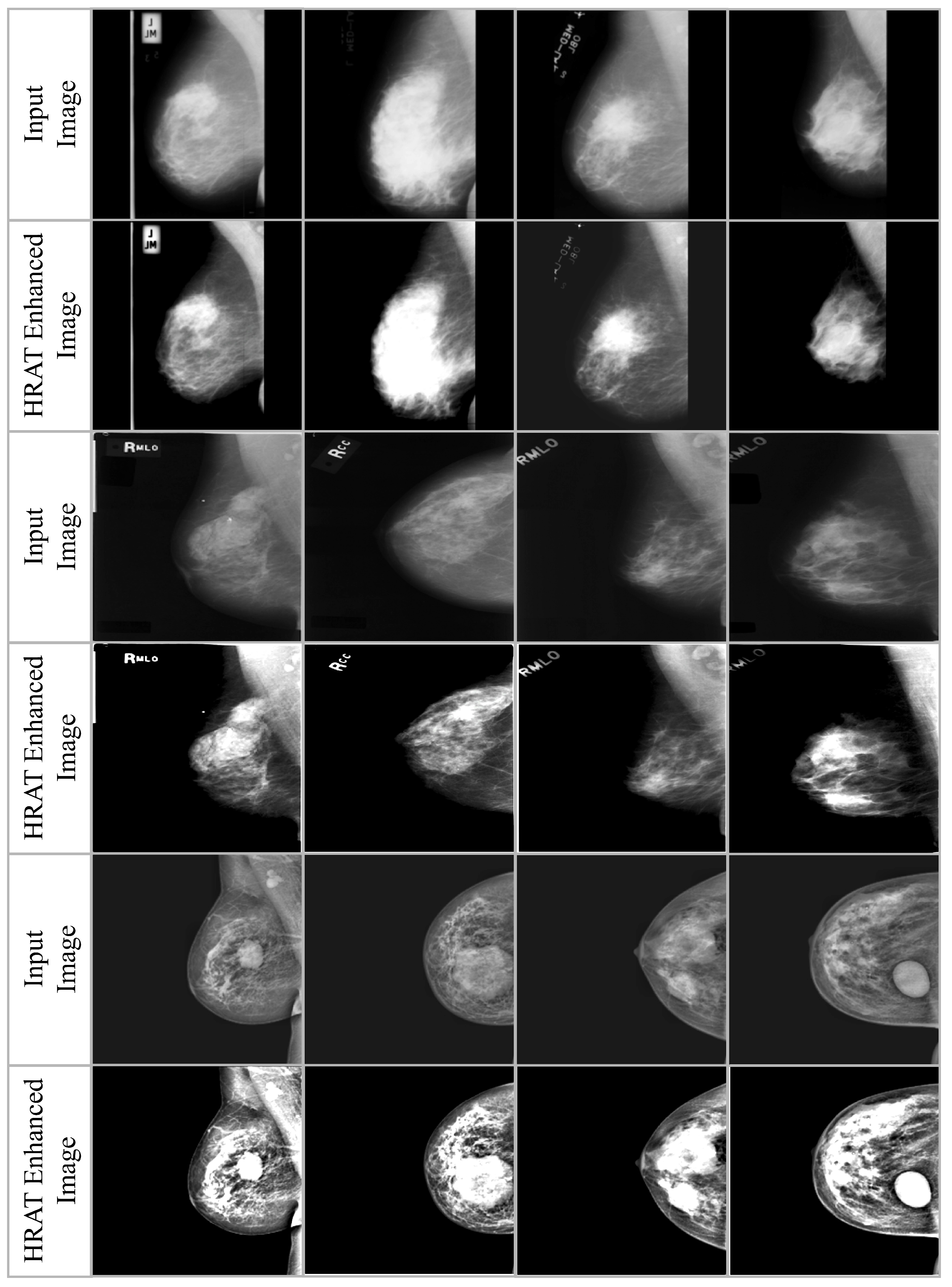



| Abbreviation | Definition | Abbreviation | Definition |
|---|---|---|---|
| AI | Artificial Intelligence | CAD | Computer-Aided Diagnosis |
| CNN | Convolutional Neural Network | DDSM | Digital Database for Screening Mammography |
| DL | Deep Learning | FN | False Negative |
| FP | False Positive | HRAT | Haze-Removed Adaptive Technique |
| INbreast | Full-Field Digital Mammogram Dataset | MIAS | Mammographic Image Analysis Society |
| ML | Machine Learning | mGWO | Modified Grey Wolf Optimization |
| NN | Neural Network | PSO | Particle Swarm Optimization |
| ROI | Region of Interest | TN | True Negative |
| TP | True Positive | YOLO | You Only Look Once |
| Method | Results (%) |
|---|---|
| A five-layer CNN model with data augmentation was used for automated breast cancer classification in mammograms and ultrasound images [27] | MIAS: 96.55 DDSM: 90.68 INbreast: 91.28 |
| CNN-based classification with preprocessing for mammogram image enhancement and lesion detection [28] | INbreast: 96.52 MIAS: 95.30 |
| Transfer learning with ResNet-50 trained on ImageNet [29] | INbreast: 93.00 |
| Faster R-CNN for detecting masses in FFDM mammograms [30] | Hologic: TPR 93.00 INbreast: 99.00 |
| YOLO for lesion detection, CNN/InceptionResNet-V2 for classification [31] | DDSM: 99.17 INbreast: 97.27 |
| YOLO-based breast cancer detection with transfer learning and Eigen-CAM for model explainability [32] | CBIS-DDSM: mAP 62.10 |
| Stacked ensemble of ResNet models with XGBoost for breast mass classification and BI-RADS diagnosis [33] | DDSM: 95.13 INbreast: 99.20 Private dataset: 95.88 |
| VGG16/VGG19 fine-tuned on mammogram datasets for lesion classification [34] | INbreast: 96.52 |
| CapsNet with adaptive fuzzy filtering and Kapur’s thresholding [35] | Mini-MIAS: 98.50 DDSM: 97.55 |
| ROI-based patch segmentation with noise-tolerant textural descriptors and SVM classification [36] | DDSM: 94.70 |
| EfficientNet-B4 with contrast enhancement, feature fusion, and chaotic-crow search optimization for classification [37] | INbreast: 98.45 DDSM: 96.17 |
| Breast region extraction, super-resolution enhancement, and feature-based classification for mammography [38] | MIAS: 97.14 |
| Two-view CNN-RNN model with ResNet and GRU for breast mass classification [39] | DDSM: 94.70 |
| Dataset | Training Images | Testing Images | Total Images | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Mal | Ben | Nor | Mal | Ben | Nor | Mal | Ben | Nor | |
| MIAS | 19 | 26 | 104 | 20 | 26 | 105 | 39 | 52 | 209 |
| DDMS | 318 | 278 | - | 319 | 279 | - | 637 | 557 | - |
| INbreast | 35 | 38 | - | 35 | 38 | - | 70 | 76 | - |
| Output Images | MIAS | DDSM | INbreast | |||
|---|---|---|---|---|---|---|
| Original | Augmented | Original | Augmented | Original | Augmented | |
| Malignant | 39 | 1170 | 637 | 19,110 | 70 | 2100 |
| Benign | 52 | 1560 | 557 | 16,710 | 76 | 2280 |
| Normal | 209 | 6270 | - | - | - | - |
| Parameters | Values |
|---|---|
| Iterations (n) | 100 or multiples of 100 s |
| Population | 5 or multiples of 5 s |
| Total Features | 65 |
| Total Instances | 646 |
| Upper Bound | 100 |
| Lower Bound | −100 |
| Control Parameter | Linear decrement from 2 to 0 |
| Hyperparameter | Value |
|---|---|
| L2 regularization | 0.0001 |
| Initial learning rate | 0.001 |
| Momentum | 0.7 |
| Total epochs | 150 |
| Batch size | 32 |
| Data split ratio | 50–50 |
| Iteration | Average Accuracy (%) | |||||
|---|---|---|---|---|---|---|
| 1 | 98.22 ± 0.95 | 99.27 ± 1.21 | 99.37 ± 1.18 | 96.75 ± 0.61 | 97.24 ± 0.83 | 98.16 ± 0.82 |
| 2 | 98.23 ± 1.04 | 97.63 ± 1.46 | 99.04 ± 1.32 | 97.85 ± 1.22 | 99.01 ± 1.08 | 98.35 ± 1.35 |
| 3 | 96.83 ± 1.01 | 97.89 ± 1.26 | 96.93 ± 0.59 | 96.77 ± 1.16 | 96.62 ± 1.46 | 96.99 ± 0.64 |
| 4 | 97.09 ± 1.21 | 95.89 ± 0.96 | 96.52 ± 1.16 | 96.39 ± 0.74 | 95.93 ± 1.24 | 96.36 ± 1.16 |
| 5 | 96.42 ± 1.31 | 99.16 ± 0.69 | 96.31 ± 1.06 | 97.93 ± 0.82 | 97.35 ± 1.14 | 97.42 ± 0.65 |
| 6 | 96.12 ± 1.32 | 98.33 ± 1.47 | 96.23 ± 1.18 | 97.44 ± 1.49 | 95.82 ± 0.83 | 96.78 ± 0.58 |
| 7 | 97.79 ± 1.23 | 96.48 ± 1.31 | 97.22 ± 1.33 | 97.68 ± 1.23 | 96.59 ± 1.41 | 97.15 ± 0.69 |
| 8 | 98.28 ± 1.17 | 97.11 ± 1.37 | 99.23 ± 0.56 | 95.86 ± 0.98 | 95.86 ± 1.06 | 97.27 ± 1.37 |
| 9 | 95.82 ± 0.59 | 97.08 ± 0.87 | 97.14 ± 1.35 | 96.88 ± 1.25 | 95.97 ± 1.22 | 96.58 ± 1.32 |
| 10 | 96.76 ± 0.55 | 96.86 ± 1.49 | 99.05 ± 0.96 | 96.63 ± 1.41 | 98.31 ± 1.02 | 97.52 ± 1.46 |
| Overall Result | 97.74 ± 1.04 | |||||
| Iteration | Average Accuracy (%) | |||||
|---|---|---|---|---|---|---|
| 1 | 98.33 ± 0.52 | 98.81 ± 0.33 | 98.19 ± 0.99 | 98.76 ± 0.37 | 98.47 ± 0.69 | 98.91 ± 0.07 |
| 2 | 98.40 ± 1.18 | 98.23 ± 0.27 | 98.14 ± 0.03 | 98.24 ± 0.19 | 98.87 ± 0.85 | 98.18 ± 0.98 |
| 3 | 98.89 ± 0.68 | 98.41 ± 0.06 | 98.35 ± 0.57 | 97.76 ± 0.43 | 98.13 ± 0.81 | 98.29 ± 0.29 |
| 4 | 98.34 ± 0.52 | 98.38 ± 0.09 | 98.36 ± 0.51 | 98.93 ± 0.08 | 98.37 ± 0.34 | 98.88 ± 0.79 |
| 5 | 97.90 ± 0.41 | 98.37 ± 0.68 | 98.85 ± 0.56 | 98.14 ± 0.57 | 98.43 ± 0.63 | 98.54 ± 0.47 |
| 6 | 98.08 ± 0.09 | 98.05 ± 0.22 | 98.17 ± 0.95 | 98.16 ± 0.36 | 98.32 ± 0.65 | 98.34 ± 0.86 |
| 7 | 98.39 ± 0.67 | 98.60 ± 0.10 | 97.83 ± 0.08 | 98.55 ± 0.07 | 98.02 ± 0.65 | 98.88 ± 0.72 |
| 8 | 98.57 ± 0.57 | 98.71 ± 0.07 | 98.73 ± 0.89 | 98.64 ± 0.75 | 98.56 ± 0.74 | 98.04 ± 0.65 |
| 9 | 98.22 ± 0.11 | 98.96 ± 0.88 | 98.16 ± 0.96 | 98.22 ± 0.38 | 98.16 ± 0.62 | 98.14 ± 0.52 |
| 10 | 98.71 ± 0.13 | 98.49 ± 0.78 | 98.27 ± 0.74 | 98.65 ± 0.73 | 98.87 ± 0.71 | 98.88 ± 0.73 |
| Overall Result | 99.37 ± 0.19 | |||||
| Iteration | Average Accuracy (%) | |||||
|---|---|---|---|---|---|---|
| 1 | 98.51 ± 1.07 | 98.51 ± 1.43 | 98.52 ± 0.85 | 97.25 ± 1.4 | 97.28 ± 0.67 | 98.73 ± 1.41 |
| 2 | 98.45 ± 0.89 | 98.16 ± 1.34 | 97.13 ± 1.01 | 98.85 ± 0.53 | 98.67 ± 1.38 | 98.45 ± 0.75 |
| 3 | 98.52 ± 0.84 | 98.77 ± 0.61 | 97.46 ± 0.75 | 97.96 ± 1.2 | 97.52 ± 1.31 | 97.25 ± 1.48 |
| 4 | 98.77 ± 1.41 | 97.42 ± 1.26 | 97.49 ± 0.96 | 97.02 ± 0.55 | 98.21 ± 0.58 | 97.98 ± 1.48 |
| 5 | 98.58 ± 1.22 | 97.01 ± 0.8 | 98.46 ± 0.77 | 98.54 ± 1.38 | 97.27 ± 1.37 | 97.56 ± 1.42 |
| 6 | 97.28 ± 0.78 | 97.42 ± 0.75 | 98.31 ± 0.53 | 98.01 ± 1.34 | 97.32 ± 0.62 | 97.66 ± 1.23 |
| 7 | 97.39 ± 1.09 | 97.35 ± 0.64 | 97.99 ± 0.88 | 97.91 ± 1.33 | 97.19 ± 1.47 | 97.17 ± 0.96 |
| 8 | 97.09 ± 0.58 | 97.69 ± 1.17 | 97.88 ± 0.95 | 97.72 ± 0.94 | 98.66 ± 0.93 | 98.81 ± 1.15 |
| 9 | 97.38 ± 0.96 | 97.92 ± 0.84 | 97.03 ± 0.61 | 97.18 ± 0.92 | 97.74 ± 0.67 | 97.45 ± 0.62 |
| 10 | 97.74 ± 0.55 | 97.44 ± 0.66 | 97.22 ± 0.52 | 97.09 ± 1.25 | 97.43 ± 0.83 | 97.18 ± 1.49 |
| Overall Result | 99.02 ± 0.19 | |||||
| Model | Accuracy (%) | Sensitivity (%) | Specificity (%) | Precision (%) | RSE (%) | F1 (%) | Kappa (%) |
|---|---|---|---|---|---|---|---|
| MIAS dataset | |||||||
| VGG19 | 92.54 ± 1.04 | 93.67 ± 1.68 | 92.14 ± 1.47 | 93.74 ± 1.75 | 93.42 ± 0.91 | 93.58 ± 1.32 | 92.15 ± 0.56 |
| ResNet50 | 95.02 ± 0.97 | 94.82 ± 0.64 | 93.69 ± 1.10 | 93.94 ± 1.06 | 93.74 ± 1.75 | 94.26 ± 1.27 | 94.21 ± 0.21 |
| InceptionResNet-V2 | 95.85 ± 1.14 | 94.22 ± 1.28 | 96.75 ± 0.24 | 96.46 ± 0.53 | 95.04 ± 0.99 | 94.06 ± 0.07 | 94.78 ± 0.79 |
| EfficientNet-B4 | 95.28 ± 0.67 | 92.56 ± 0.75 | 94.75 ± 0.82 | 95.11 ± 0.12 | 96.71 ± 0.97 | 95.86 ± 0.82 | 92.91 ± 1.19 |
| Proposed Model | 97.74 ± 1.04 | 98.02 ± 0.87 | 98.47 ± 0.97 | 98.79 ± 1.02 | 97.51 ± 0.76 | 94.94 ± 1.71 | 99.15 ± 0.84 |
| DDSM dataset | |||||||
| VGG19 | 92.33 ± 0.66 | 91.17 ± 0.18 | 90.59 ± 0.63 | 91.61 ± 0.75 | 91.72 ± 1.13 | 90.67 ± 0.78 | 91.95 ± 1.04 |
| ResNet50 | 92.07 ± 0.50 | 90.56 ± 0.79 | 94.38 ± 1.61 | 94.02 ± 1.03 | 94.64 ± 1.26 | 92.71 ± 0.58 | 92.97 ± 1.02 |
| InceptionResNet-V2 | 92.91 ± 0.92 | 92.57 ± 0.61 | 91.91 ± 0.92 | 92.47 ± 0.48 | 92.74 ± 0.89 | 91.41 ± 3.42 | 92.05 ± 0.74 |
| EfficientNet-B4 | 94.08 ± 1.45 | 93.87 ± 0.88 | 95.96 ± 0.03 | 92.82 ± 0.27 | 95.04 ± 0.86 | 94.75 ± 0.57 | 94.68 ± 1.26 |
| Proposed Model | 99.37 ± 0.19 | 97.98 ± 0.99 | 96.88 ± 1.89 | 98.36 ± 1.12 | 97.86 ± 1.87 | 99.05 ± 0.81 | 97.36 ± 0.31 |
| INbreast dataset | |||||||
| VGG19 | 90.34 ± 0.84 | 89.06 ± 1.13 | 88.97 ± 0.98 | 88.63 ± 1.04 | 88.22 ± 0.94 | 88.84 ± 0.74 | 88.15 ± 1.16 |
| ResNet50 | 89.21 ± 0.22 | 89.85 ± 2.86 | 91.42 ± 0.59 | 89.67 ± 1.61 | 89.78 ± 0.92 | 90.33 ± 0.74 | 89.27 ± 1.28 |
| InceptionResNet-V2 | 88.44 ± 0.45 | 88.96 ± 1.97 | 88.81 ± 0.94 | 88.48 ± 0.49 | 88.98 ± 2.99 | 88.97 ± 1.98 | 90.07 ± 0.92 |
| EfficientNet-B4 | 91.45 ± 0.46 | 93.15 ± 0.84 | 91.94 ± 0.95 | 91.77 ± 0.78 | 91.07 ± 2.08 | 92.75 ± 0.94 | 92.35 ± 0.82 |
| Proposed Model | 99.02 ± 0.19 | 99.86 ± 0.13 | 97.97 ± 1.98 | 98.08 ± 0.75 | 97.72 ± 1.41 | 98.16 ± 0.17 | 98.97 ± 0.75 |
| Model | Image Enhancement | Dataset | |||
|---|---|---|---|---|---|
| No | Yes | MIAS | DDSM | INbreast | |
| VGG19 | ✓ | × | 91.94 ± 1.47 | 90.83 ± 0.93 | 90.63 ± 1.52 |
| × | ✓ | 92.54 ± 1.04 | 92.33 ± 0.66 | 90.34 ± 0.84 | |
| ResNet50 | ✓ | × | 92.15 ± 0.57 | 91.11 ± 0.35 | 93.41 ± 0.63 |
| × | ✓ | 95.02 ± 0.97 | 92.07 ± 0.50 | 89.21 ± 0.22 | |
| InceptionResNet-V2 | ✓ | × | 90.68 ± 0.97 | 89.15 ± 0.24 | 84.22 ± 1.27 |
| × | ✓ | 95.85 ± 1.14 | 92.91 ± 0.92 | 88.44 ± 0.45 | |
| EfficientNet-B4 | ✓ | × | 89.98 ± 1.24 | 89.09 ± 0.17 | 86.41 ± 0.51 |
| × | ✓ | 95.28 ± 0.67 | 94.08 ± 1.45 | 91.45 ± 0.46 | |
| Proposed Model | ✓ | × | 93.55 ± 1.10 | 94.36 ± 1.21 | 93.86 ± 1.47 |
| × | ✓ | 97.74 ± 1.04 | 99.37 ± 0.19 | 99.02 ± 0.19 | |
| Model | Feature Optimization | MIAS Dataset | DDSM Dataset | INbreast Dataset | ||
|---|---|---|---|---|---|---|
| No | GWO | mGWO | ||||
| VGG19 | ✓ | × | × | 85.13 ± 0.93 | 87.76 ± 1.12 | 86.22 ± 1.23 |
| × | ✓ | × | 89.64 ± 1.48 | 89.02 ± 0.55 | 97.95 ± 1.34 | |
| × | × | ✓ | 87.54 ± 1.04 | 86.33 ± 0.66 | 88.34 ± 0.84 | |
| ResNet50 | ✓ | × | × | 86.60 ± 0.61 | 87.06 ± 1.42 | 86.99 ± 1.46 |
| × | ✓ | × | 90.24 ± 1.05 | 91.07 ± 0.53 | 91.23 ± 1.21 | |
| × | × | ✓ | 95.02 ± 0.97 | 92.07 ± 0.50 | 89.21 ± 0.22 | |
| InceptionResNet-V2 | ✓ | × | × | 87.15 ± 0.61 | 87.89 ± 0.08 | 88.16 ± 0.05 |
| × | ✓ | × | 92.16 ± 0.87 | 92.94 ± 0.05 | 91.69 ± 1.29 | |
| × | × | ✓ | 95.85 ± 1.14 | 92.91 ± 0.92 | 88.44 ± 0.45 | |
| EfficientNet-B4 | ✓ | × | × | 90.26 ± 1.24 | 89.77 ± 0.96 | 89.06 ± 1.24 |
| × | ✓ | × | 93.79 ± 0.81 | 92.12 ± 1.12 | 93.46 ± 0.72 | |
| × | × | ✓ | 95.28 ± 0.67 | 94.08 ± 1.45 | 91.45 ± 0.46 | |
| Proposed Model | ✓ | × | × | 92.05 ± 1.57 | 91.78 ± 1.44 | 90.51 ± 1.17 |
| × | ✓ | × | 93.92 ± 0.42 | 94.01 ± 0.92 | 94.34 ± 0.79 | |
| × | × | ✓ | 97.74 ± 1.04 | 99.37 ± 0.19 | 99.02 ± 0.19 | |
| Optimization Algorithm | MIAS Dataset | DDSM Dataset | INbreast Dataset |
|---|---|---|---|
| PSO | 82.58 ± 1.32 | 83.42 ± 1.39 | 83.63 ± 1.36 |
| ACO | 86.64 ± 0.57 | 89.41 ± 1.40 | 90.53 ± 1.29 |
| BA | 88.23 ± 0.51 | 91.71 ± 0.67 | 90.41 ± 1.07 |
| CSA | 81.69 ± 0.54 | 85.67 ± 1.30 | 84.46 ± 0.54 |
| WOA | 89.08 ± 1.28 | 91.18 ± 1.44 | 92.38 ± 1.17 |
| GWO | 93.92 ± 0.42 | 94.01 ± 0.92 | 94.34 ± 0.79 |
| mGWO | 97.74 ± 1.04 | 99.37 ± 0.19 | 99.02 ± 0.19 |
| Method | MIAS (%) | DDSM (%) | INbreast (%) |
|---|---|---|---|
| A five-layer CNN model [27] | 96.55 | 90.68 | 91.28 |
| CNN-based classification with preprocessing [28] | 95.30 | - | 96.52 |
| Transfer learning with ResNet-50 [29] | - | - | 93.00 |
| Faster R-CNN [30] | - | - | 99.00 |
| YOLO with InceptionResNet-V2 [31] | - | 99.17 | 97.27 |
| YOLO with transfer learning and Eigen-CAM [32] | 62.10 | - | - |
| Stacked ensemble of ResNet models with XGBoost [33] | - | 95.13 | 99.20 |
| VGG16/VGG19 fine-tuned [34] | - | - | 96.52 |
| CapsNet with adaptive fuzzy filtering [35] | 98.50 | 97.55 | - |
| ROI-based patch segmentation [36] | - | 94.70 | - |
| EfficientNet-B4 with contrast enhancement [37] | - | 96.17 | 98.45 |
| Breast region extraction and super-resolution enhancement [38] | 97.14 | - | - |
| Two-view CNN-RNN model with ResNet and GRU [39] | - | 94.70 | - |
| Proposed Model | 97.74 | 99.37 | 99.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
P.P, F.R.; Tehsin, S. A Framework for Breast Cancer Classification with Deep Features and Modified Grey Wolf Optimization. Mathematics 2025, 13, 1236. https://doi.org/10.3390/math13081236
P.P FR, Tehsin S. A Framework for Breast Cancer Classification with Deep Features and Modified Grey Wolf Optimization. Mathematics. 2025; 13(8):1236. https://doi.org/10.3390/math13081236
Chicago/Turabian StyleP.P, Fathimathul Rajeena, and Sara Tehsin. 2025. "A Framework for Breast Cancer Classification with Deep Features and Modified Grey Wolf Optimization" Mathematics 13, no. 8: 1236. https://doi.org/10.3390/math13081236
APA StyleP.P, F. R., & Tehsin, S. (2025). A Framework for Breast Cancer Classification with Deep Features and Modified Grey Wolf Optimization. Mathematics, 13(8), 1236. https://doi.org/10.3390/math13081236






