Invariant-Based Inverse Engineering for Balanced Displacement of a Cartpole System
Abstract
1. Introducton
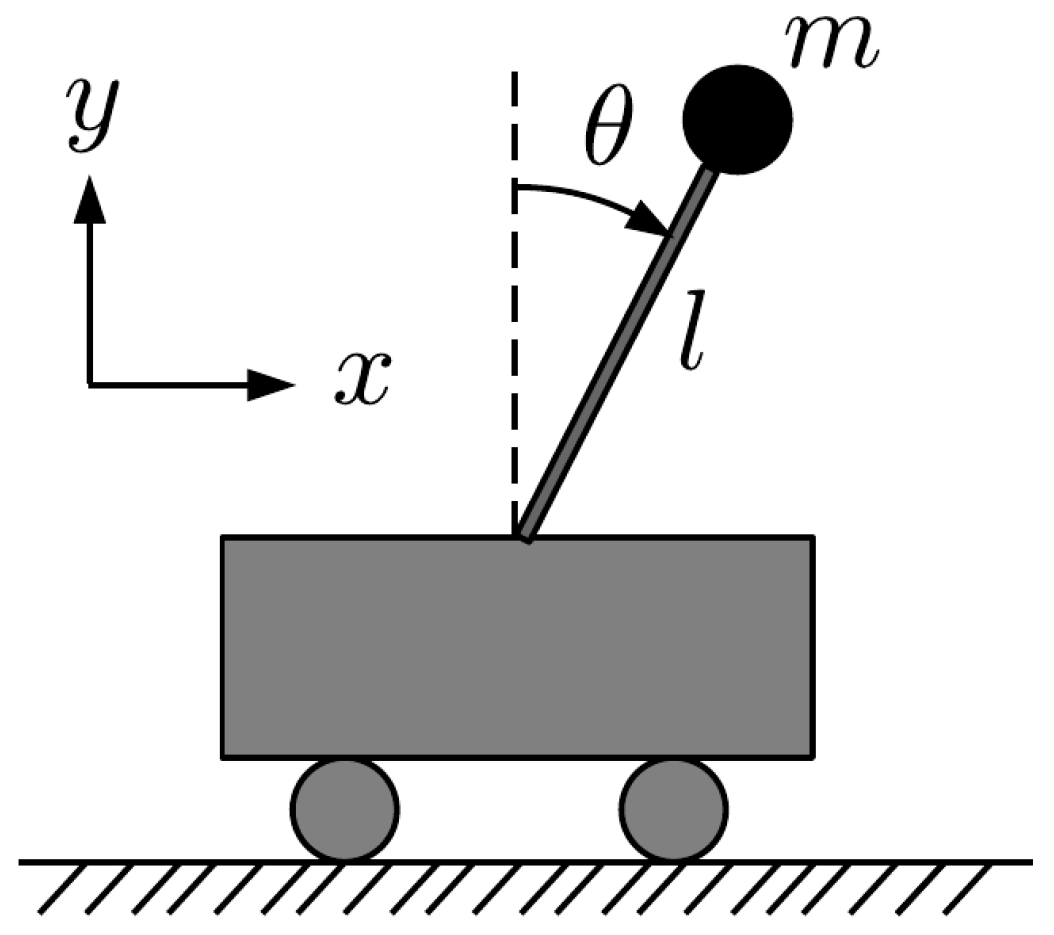
2. Physical Model and Basic Equations
3. Shortcuts to Adiabaticity
3.1. Dynamical Invariant
3.2. Shortcut to Adiabaticity
3.3. Inverse Engineering
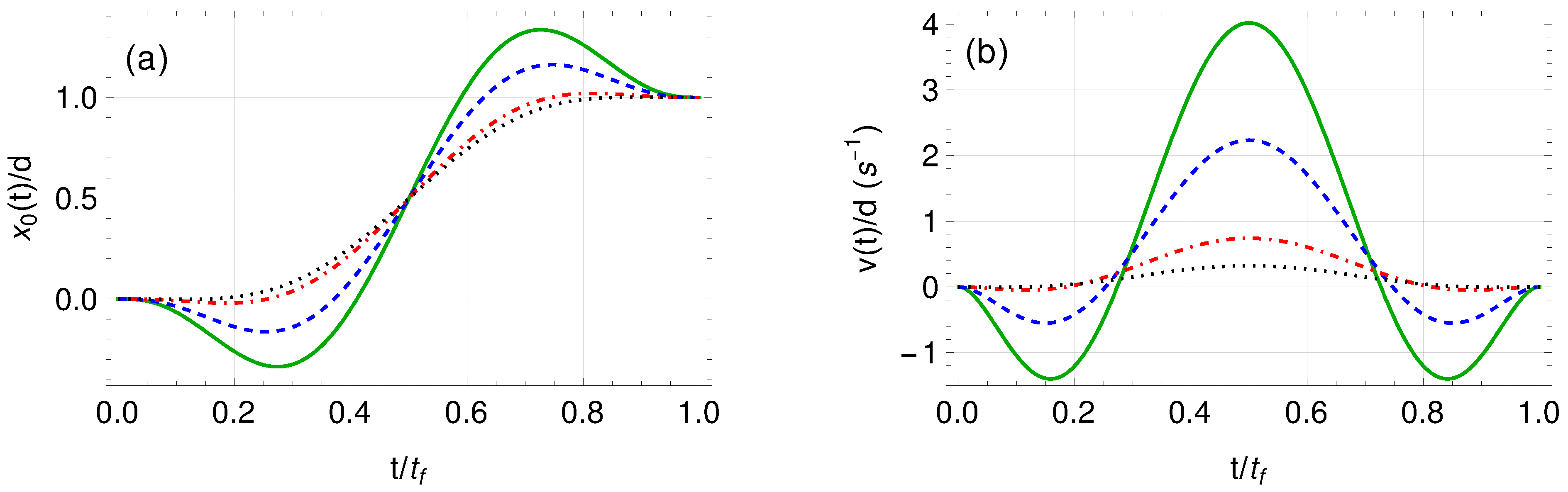
4. Numerical Results
Non-Linear Effects
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Spong, M.W. Underactuated mechanical systems. In Proceedings of the Control Problems in Robotics and Automation; Siciliano, B., Valavanis, K.P., Eds.; Springer: Berlin/Heidelberg, Germany, 1998; pp. 135–150. [Google Scholar]
- Liu, Y.; Yu, H. A survey of underactuated mechanical systems. IET Control. Theory Appl. 2013, 7, 921–935. [Google Scholar] [CrossRef]
- Nikpour, M.; Huang, L.; Al-Jumaily, A.M. Stability and Direction Control of a Two-Wheeled Robotic Wheelchair Through a Movable Mechanism. IEEE Access 2020, 8, 45221–45230. [Google Scholar] [CrossRef]
- Huang, Q.; Yokoi, K.; Kajita, S.; Kaneko, K.; Arai, H.; Koyachi, N.; Tanie, K. Planning walking patterns for a biped robot. IEEE Trans. Robot. Autom. 2001, 17, 280–289. [Google Scholar] [CrossRef]
- Chakraborty, K.; Mukherjee, R.R.; Mukherjee, S. Tuning of PID Controller of Inverted Pendulum using Genetic Algorithm. Int. J. Soft Comput. Eng. (IJSCE) 2013, 3, 2231. [Google Scholar]
- Prasad, L.B.; Tyagi, B.; Gupta, H.O. Optimal Control of Nonlinear Inverted Pendulum System Using PID Controller and LQR: Performance Analysis Without and With Disturbance Input. Int. J. Autom. Comput. 2015, 11, 661. [Google Scholar] [CrossRef]
- Mousa, M.E.; Hassan, M.A.E.; Moustafa Hassan, M.A. Stabilizing and Swinging-Up the Inverted Pendulum Using PI and PID Controllers Based on Reduced Linear Quadratic Regulator Tuned by PSO. Int. J. Syst. Dyn. Appl. (IJSDA) 2015, 4, 52–69. [Google Scholar] [CrossRef]
- Wang, Y. PD-Based Control of cartpole System on Inclined Plane with Variable Slope. J. Phys. Conf. Ser. 2022, 2216, 012064. [Google Scholar] [CrossRef]
- Yih, C.C. Sliding Mode Control for Swing-Up and Stabilization of the cartpole Underactuated System. Asian J. Control. 2013, 15, 1201–1214. [Google Scholar] [CrossRef]
- Aguilar-Ibáñez, C.; Mendoza-Mendoza, J.; Dávila, J. Stabilization of the cart pole system: By sliding mode control. Nonlinear Dyn. 2014, 78, 2769. [Google Scholar] [CrossRef]
- Li, T.-H.S.; Shieh, M.-Y. Switching-type fuzzy sliding mode control of a cart–pole system. Mechatronics 2000, 10, 91–109. [Google Scholar] [CrossRef]
- Roose, A.I.; Yahya, S.; Al-Rizzo, H. Fuzzy-logic control of an inverted pendulum on a cart. Comput. Electr. Eng. 2017, 61, 31–47. [Google Scholar]
- Geva, S.; Sitte, J. A cartpole experiment benchmark for trainable controllers. IEEE Control. Syst. Mag. 1993, 13, 40–51. [Google Scholar]
- Plank, J.S.; Rizzo, C.P.; White, C.A.; Schuman, C.D. The cartpole Application as a Benchmark for Neuromorphic Computing. J. Low Power Electron. Appl. 2025, 15, 5. [Google Scholar] [CrossRef]
- Wang, Z.T.; Ashida, Y.; Ueda, M. Deep Reinforcement Learning Control of Quantum cartpoles. Phys. Rev. Lett. 2020, 125, 100401. [Google Scholar] [CrossRef] [PubMed]
- Sakurai, J.J. Modern Quantum Mechanics, rev. ed.; Adison-Wesley: Reading, MA, USA, 1994. [Google Scholar]
- Torrontegui, E.; Ibáñez, S.; Martínez-Garaot, S.; Modugno, M.; del Campo, A.; Guéry-Odelin, D.; Ruschhaupt, A.; Chen, X.; Muga, J.G. Shortcuts to Adiabaticity. Adv. At. Mol. Opt. Phys. 2013, 62, 117–169. [Google Scholar]
- Guéry-Odelin, D.; Ruschhaupt, A.; Kiely, A.; Torrontegui, E.; Martínez-Garaot, S.; Muga, J.G. Shortcuts to adiabaticity: Concepts, methods, and applications. Rev. Mod. Phys. 2019, 91, 045001. [Google Scholar]
- Torrontegui, E.; Lizuain, I.; González-Resines, S.; Tobalina, A.; Ruschhaupt, A.; Kosloff, R.; Muga, J.G. Energy consumption for shortcuts to adiabaticity. Phys. Rev. A 2017, 96, 022133. [Google Scholar]
- González-Resines, S.; Guéry-Odelin, D.; Tobalina, A.; Lizuain, I.; Torrontegui, E.; Muga, J. Invariant-based inverse engineering of crane control parameters. Phys. Rev. Appl. 2017, 8, 054008. [Google Scholar] [CrossRef]
- Lizuain, I.; Tobalina, A.; Rodriguez-Prieto, A.; Muga, J.G. Invariant-Based Inverse Engineering for Fast and Robust Load Transport in a Double Pendulum Bridge Crane. Entropy 2020, 22, 350. [Google Scholar] [CrossRef]
- Sarandy, M.; Duzzioni, E.; Serrac, R. Quantum computation in continuous time using dynamic invariants. Phys. Lett. A 2011, 375, 3343–3347. [Google Scholar] [CrossRef]
- Palmero, M.; Martínez-Garaot, S.; Leibfried, D.; Wineland, D.J.; Muga, J. Fast phase gates with trapped ions. Phys. Rev. A 2017, 95, 022328. [Google Scholar]
- del Campo, A.; Rams, M.M.; Zurek, W.H. Assisted Finite-Rate Adiabatic Passage Across a Quantum Critical Point: Exact Solution for the Quantum Ising Model. Phys. Rev. Lett. 2012, 109, 115703. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, K. Shortcuts to adiabaticity for quantum annealing. Phys. Rev. A 2017, 95, 012309. [Google Scholar]
- Onofrio, R. Physics of our Days: Cooling and thermometry of atomic Fermi gases. Physics-Uspekhi 2017, 59, 1129. [Google Scholar] [CrossRef]
- Dann, R.; Tobalina, A.; Kosloff, R. Fast route to equilibration. Phys. Rev. A 2020, 101, 052102. [Google Scholar] [CrossRef]
- Torrontegui, E.; Ibáñez, S.; Chen, X.; Ruschhaupt, A.; Guéry-Odelin, D.; Muga, J.G. Fast atomic transport without vibrational heating. Phys. Rev. A 2011, 83, 013415. [Google Scholar]
- Bowler, R.; Gaebler, J.; Lin, Y.; Tan, T.R.; Hanneke, D.; Jost, J.D.; Home, J.; Leibfried, P.D.; Wineland, D.J. Coherent Diabatic Ion Transport and Separation in a Multizone Trap Array. Phys. Rev. Lett. 2012, 109, 080502. [Google Scholar]
- Chen, X.; Lizuain, I.; Ruschhaupt, A.; Guéry-Odelin, D.; Muga, J.G. Shortcut to Adiabatic Passage in Two- and Three-Level Atoms. Phys. Rev. Lett. 2010, 105, 123003. [Google Scholar]
- Bason, M.G.; Viteau, M.; Malossi, N.; Huillery, P.; Arimondo, E.; Ciampini, D.; Fazio, R.; Giovannetti, V.; Manella, R.; Morsch, O. High-fidelity quantum driving. Nat. Phys. 2012, 8, 147–152. [Google Scholar]
- Zhang, J.; Shim, J.H.; Niemeyer, I.; Taniguchi, T.; Teraji, T.; Abe, H.; Onoda, S.; Yamamoto, T.; Ohshima, T.; Isoya, J.; et al. Experimental Implementation of Assisted Quantum Adiabatic Passage in a Single Spin. Phys. Rev. Lett. 2013, 110, 240501. [Google Scholar]
- Zhou, B.B.; Baksic, A.; Ribeiro, H.; Yale, C.G.; Heremans, F.J.; Jerger, P.C.; Auer, A.; Burkard, G.; Clerk, A.A.; Awschalom, D.D. Accelerated quantum control using superadiabatic dynamics in a solid-state lambda system. Nat. Phys. 2017, 13, 330–334. [Google Scholar] [CrossRef]
- Torrontegui, E.; Chen, X.; Modugno, M.; Schmidt, S.; Ruschhaupt, A.; Muga, J. Fast transport of Bose–Einstein condensates. New J. Phys. 2012, 14, 013031. [Google Scholar] [CrossRef]
- Rohringer, W.; Fischer, D.; Steiner, F.; Mazets, I.E.; Schmiedmayer, J.; Trupke, M. Non-equilibrium scale invariance and shortcuts to adiabaticity in a one-dimensional Bose gas. Sci. Rep. 2015, 5, 9820. [Google Scholar] [CrossRef] [PubMed]
- Schaff, J.F.; Song, X.L.; Vignolo, P.; Labeyrie, G. Fast optimal transition between two equilibrium states. Phys. Rev. A 2010, 82, 033430. [Google Scholar] [CrossRef]
- Schaff, J.F.; Capuzzi, P.; Labeyrie, G.; Vignolo, P. Shortcuts to adiabaticity for trapped ultracold gases. New J. Phys. 2011, 13, 113017. [Google Scholar] [CrossRef]
- Torrontegui, E.; Martinez-Garaot, S.; Modugno, M.; Chen, X.; Muga, J.G. Engineering fast and stable splitting of matter waves. Phys. Rev. A 2013, 87, 033630. [Google Scholar] [CrossRef]
- Kiely, A.; Benseny, A.; Busch, T.; Ruschhaupt, A. Shaken not stirred: Creating exotic angular momentum states by shaking an optical lattice. J. Phys. B At. Mol. Opt. Phys. 2013, 49, 215003. [Google Scholar] [CrossRef]
- Mashuda, S.; Rice, S.A. Fast-Forward Assisted STIRAP. J. Phys. Chem. A 2015, 119, 3479–3487. [Google Scholar] [CrossRef]
- Tobalina, A.; Palmero, M.; Martínez-Garaot, S.; Muga, J.G. Fast atom transport and launching in a nonrigid trap. Sci. Rep. 2017, 7, 5753. [Google Scholar] [CrossRef]
- Ma, L.; Kong, Q. Optimal Shortcuts to Adiabatic Control by Lagrange Mechanics. Entropy 2023, 25, 719. [Google Scholar] [CrossRef]
- Abdel-Rahman, E.M.; Nayfeh, A.H.; Masoud, Z.N. Dynamics and Control of Cranes: A Review. Modal Anal. 2003, 9, 863–908. [Google Scholar]
- Damour, T.; Jaranowski, P.; Schäfer, G. Dynamical invariants for general relativistic two-body systems at the third post-Newtonian approximation. Phys. Rev. D 2000, 62, 044024. [Google Scholar] [CrossRef]
- Lewis, H.R.; Leach, P.G.L. Exact invariants for a class of time-dependent non-linear Hamiltonian-systems. J. Math. Phys. 1982, 23, 165–175. [Google Scholar]
- Fu, M. Control of the cartpole System: Model-based vs. Model-free Learning. IFAC-PapersOnLine 2023, 56, 11847–11852. [Google Scholar] [CrossRef]
- Ovalle, L.; Ríos, H.; Llama, M. Robust output-feedback control for the cart–pole system: A coupled super-twisting sliding-mode approach. IET Control. Theory Appl. 2019, 13, 269–278. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lizuain, I.; Tobalina, A.; Rodriguez-Prieto, A. Invariant-Based Inverse Engineering for Balanced Displacement of a Cartpole System. Mathematics 2025, 13, 1220. https://doi.org/10.3390/math13081220
Lizuain I, Tobalina A, Rodriguez-Prieto A. Invariant-Based Inverse Engineering for Balanced Displacement of a Cartpole System. Mathematics. 2025; 13(8):1220. https://doi.org/10.3390/math13081220
Chicago/Turabian StyleLizuain, Ion, Ander Tobalina, and Alvaro Rodriguez-Prieto. 2025. "Invariant-Based Inverse Engineering for Balanced Displacement of a Cartpole System" Mathematics 13, no. 8: 1220. https://doi.org/10.3390/math13081220
APA StyleLizuain, I., Tobalina, A., & Rodriguez-Prieto, A. (2025). Invariant-Based Inverse Engineering for Balanced Displacement of a Cartpole System. Mathematics, 13(8), 1220. https://doi.org/10.3390/math13081220






