GWO-FNN: Fuzzy Neural Network Optimized via Grey Wolf Optimization
Abstract
1. Introduction
- Adaptive learning: FNNs continuously update their parameters in response to new data, enabling them to maintain accuracy in dynamic environments.
- Rule-based interpretability: Through fuzzy logic, FNNs generate human-readable rules, enhancing transparency and facilitating expert-driven refinements.
- Hybrid reasoning: By combining neural network learning with fuzzy inference, FNNs balance computational efficiency with qualitative decision making.
1.1. Our Approach
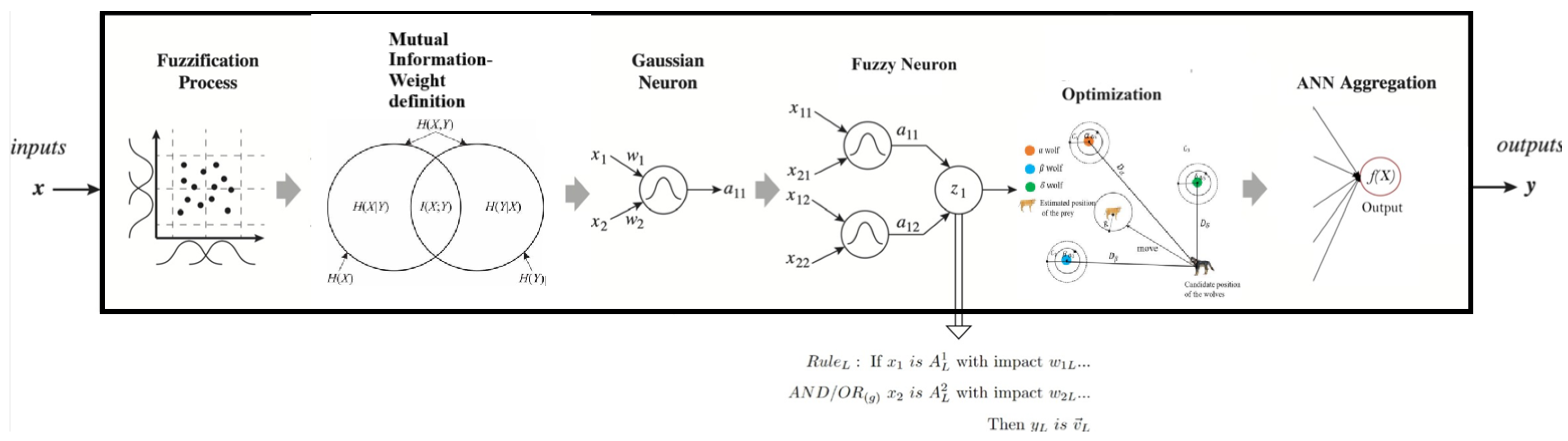
1.2. Model Architecture and Interpretability Enhancements
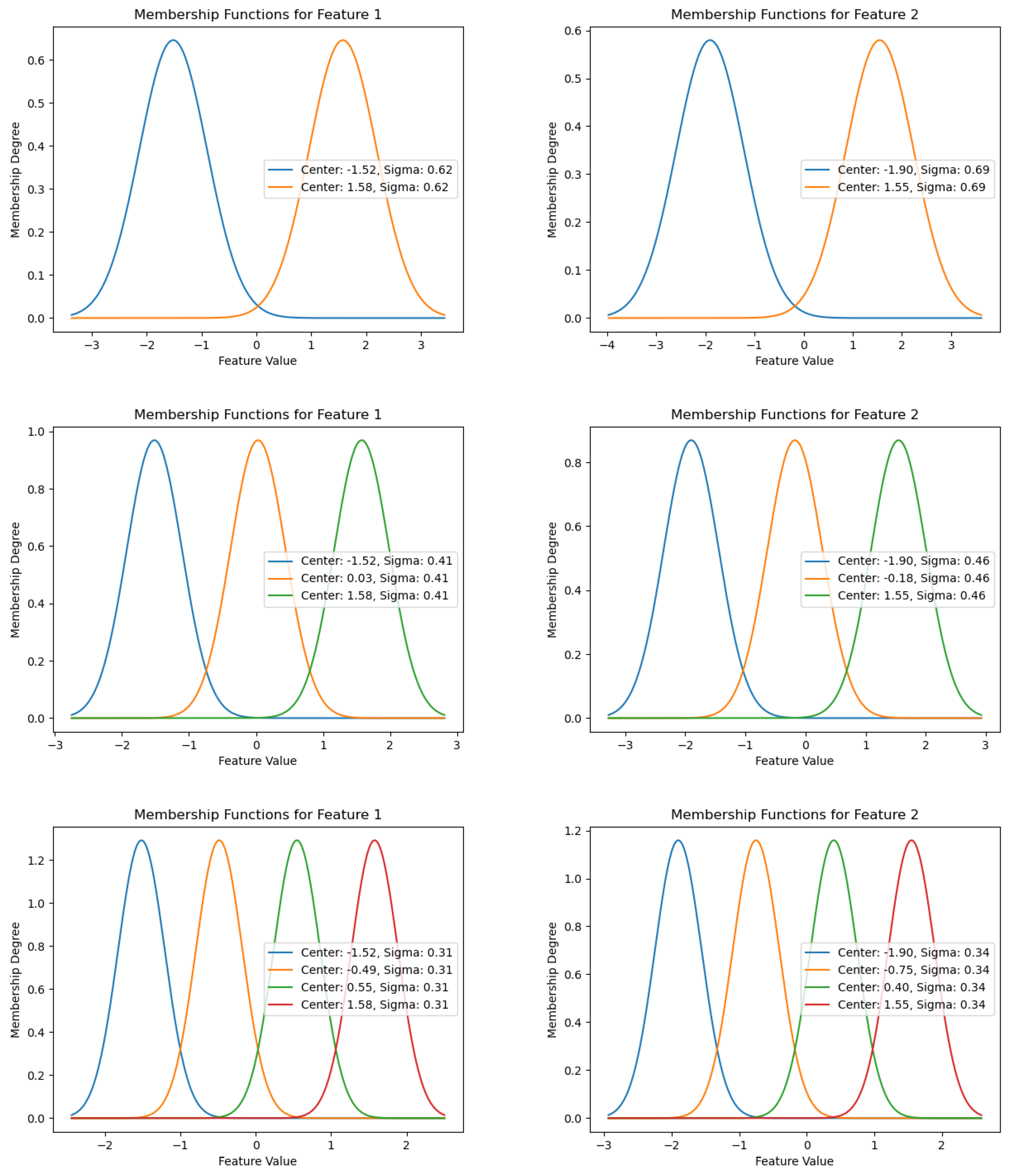
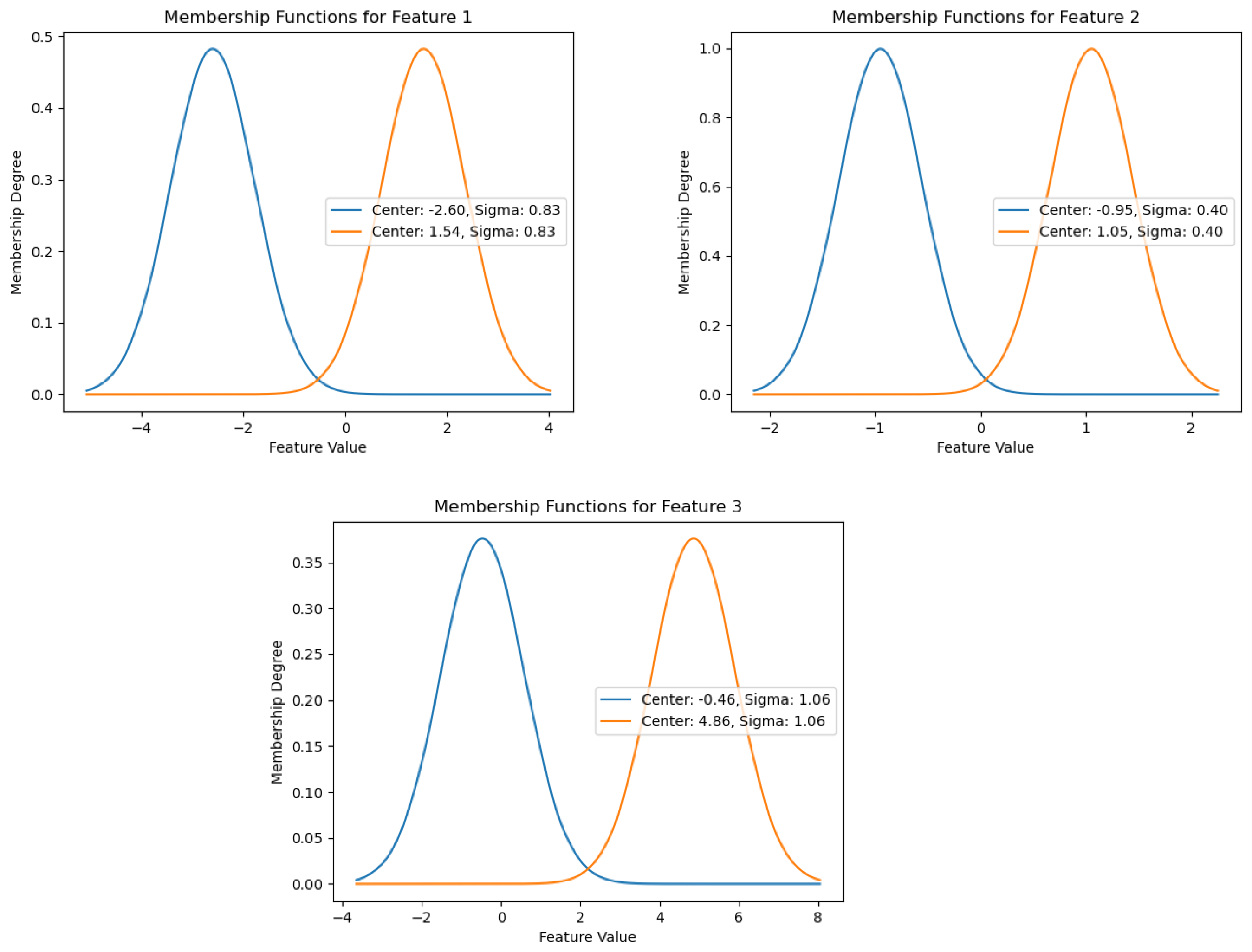
- Input layer (fuzzification process): This layer transforms numerical inputs into fuzzy values using membership functions (MFs), assigning each input a degree of membership in predefined fuzzy sets. The selection and parametrization of MFs are crucial for preserving the data structure and influencing model performance.
- Hidden layer (logical neurons and rule processing): The hidden layer comprises logical fuzzy neurons [16] that apply logical operations (e.g., AND, OR) to fuzzified inputs, leveraging fuzzy rules extracted from data or expert knowledge. Each neuron represents a distinct fuzzy rule, facilitating interpretable decision making. Optimizing these neurons ensures effective rule representation and enhances system robustness.
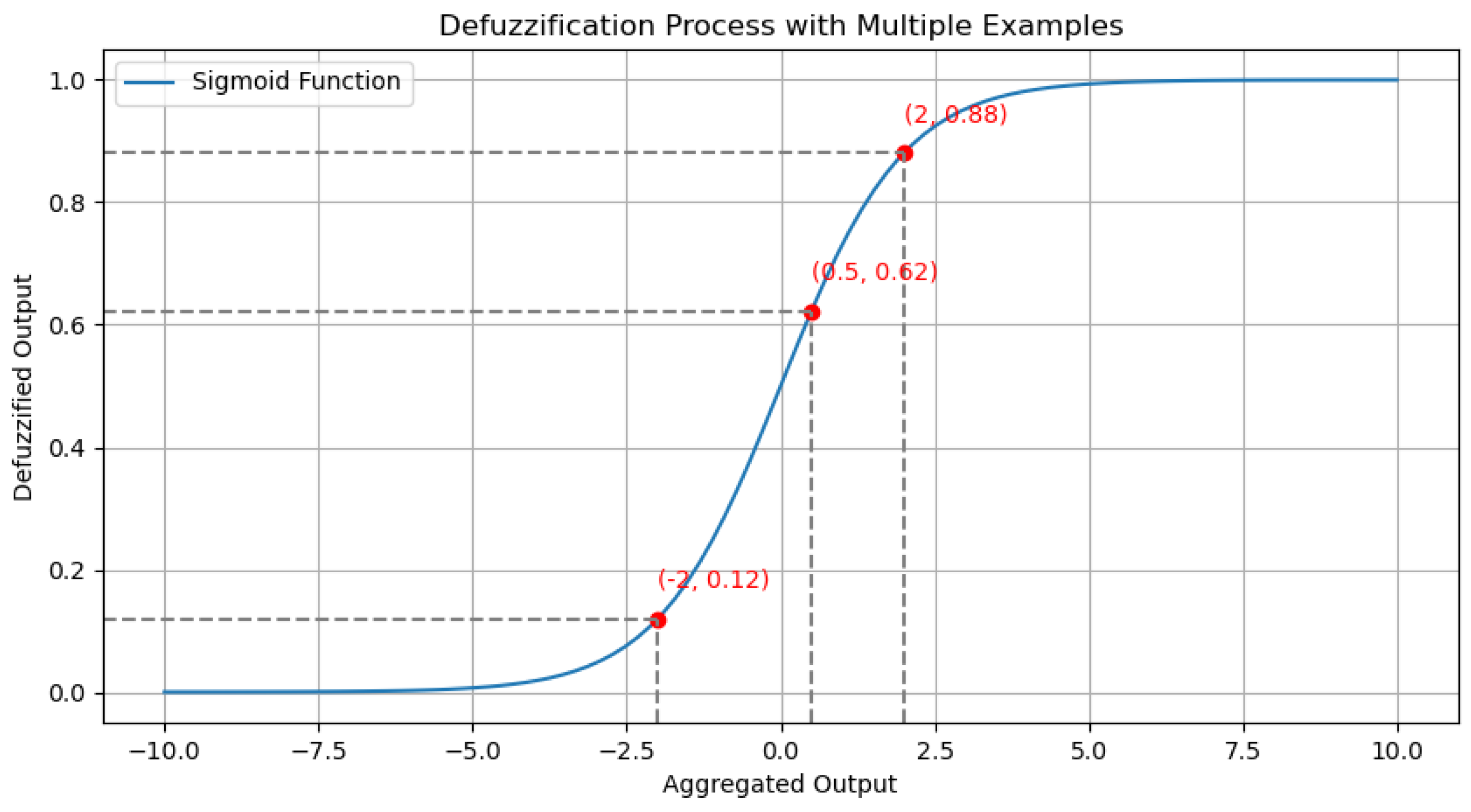
- Output layer (defuzzification and prediction): The final layer aggregates fuzzy outputs into crisp predictions or class labels. The Grey Wolf Optimizer (GWO) is employed to optimize rule consequent weights, improving class separability and prediction accuracy. Additionally, mutual information (MI) is incorporated in the input layer to assign higher initial weights to features with greater discriminative power, enhancing interpretability.
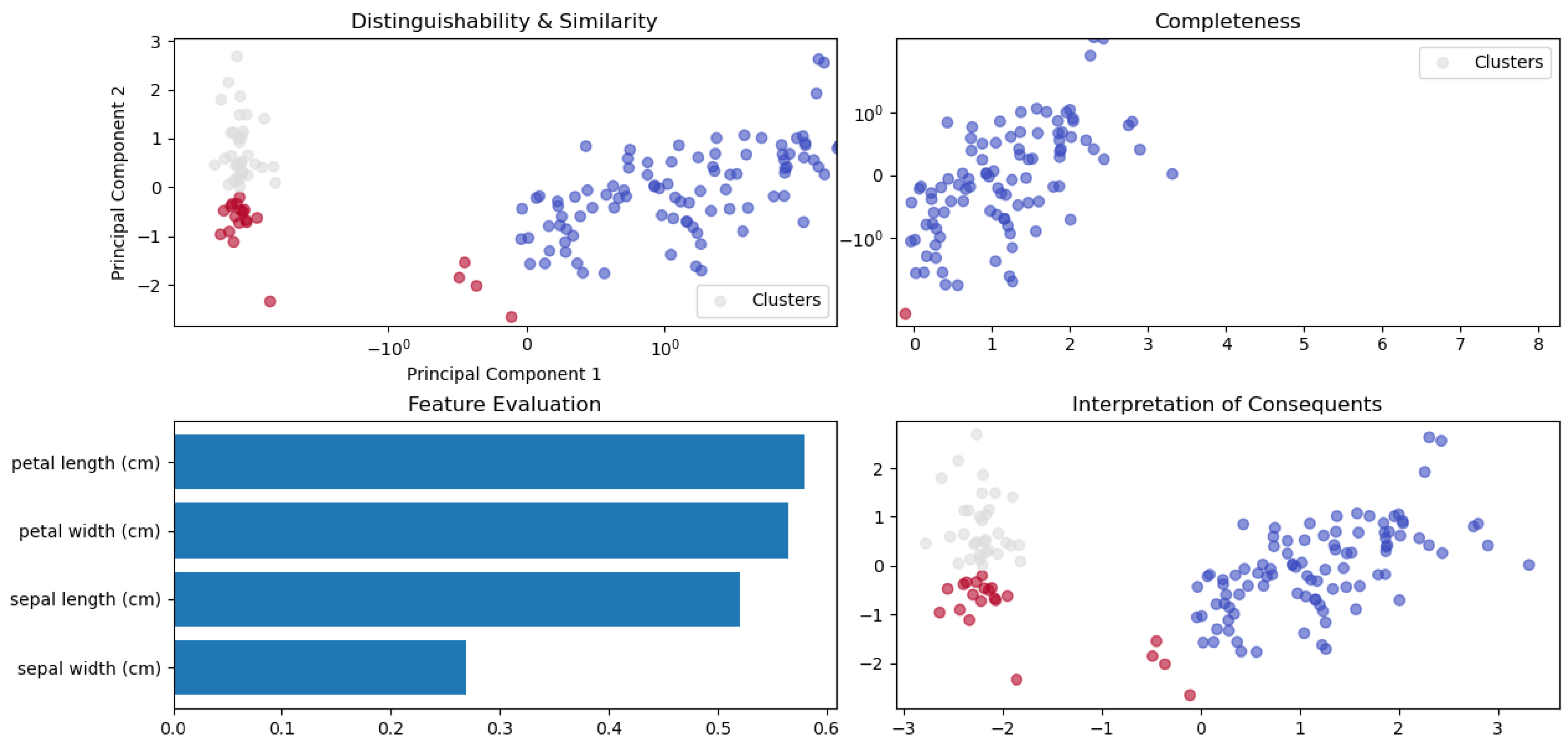
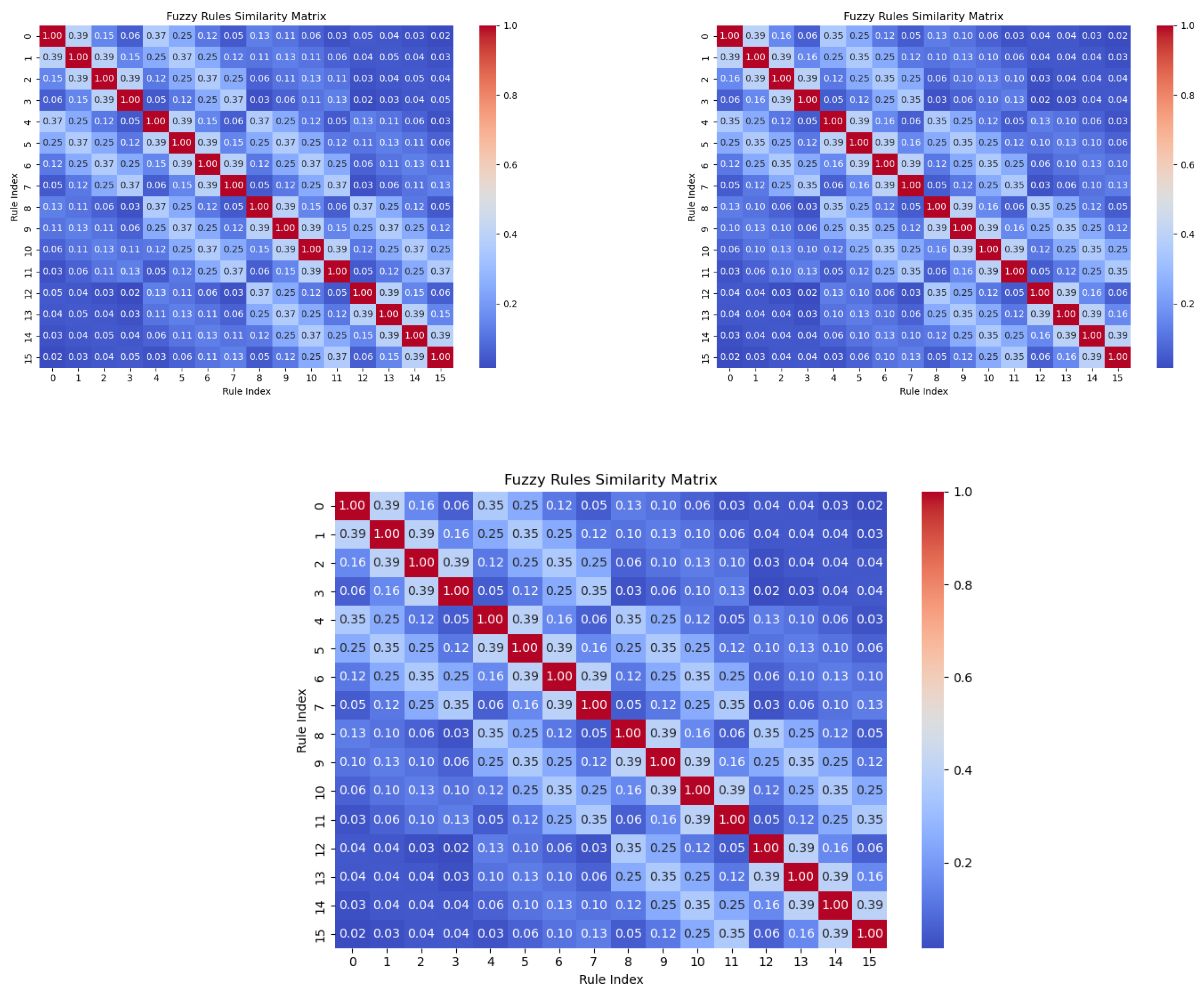
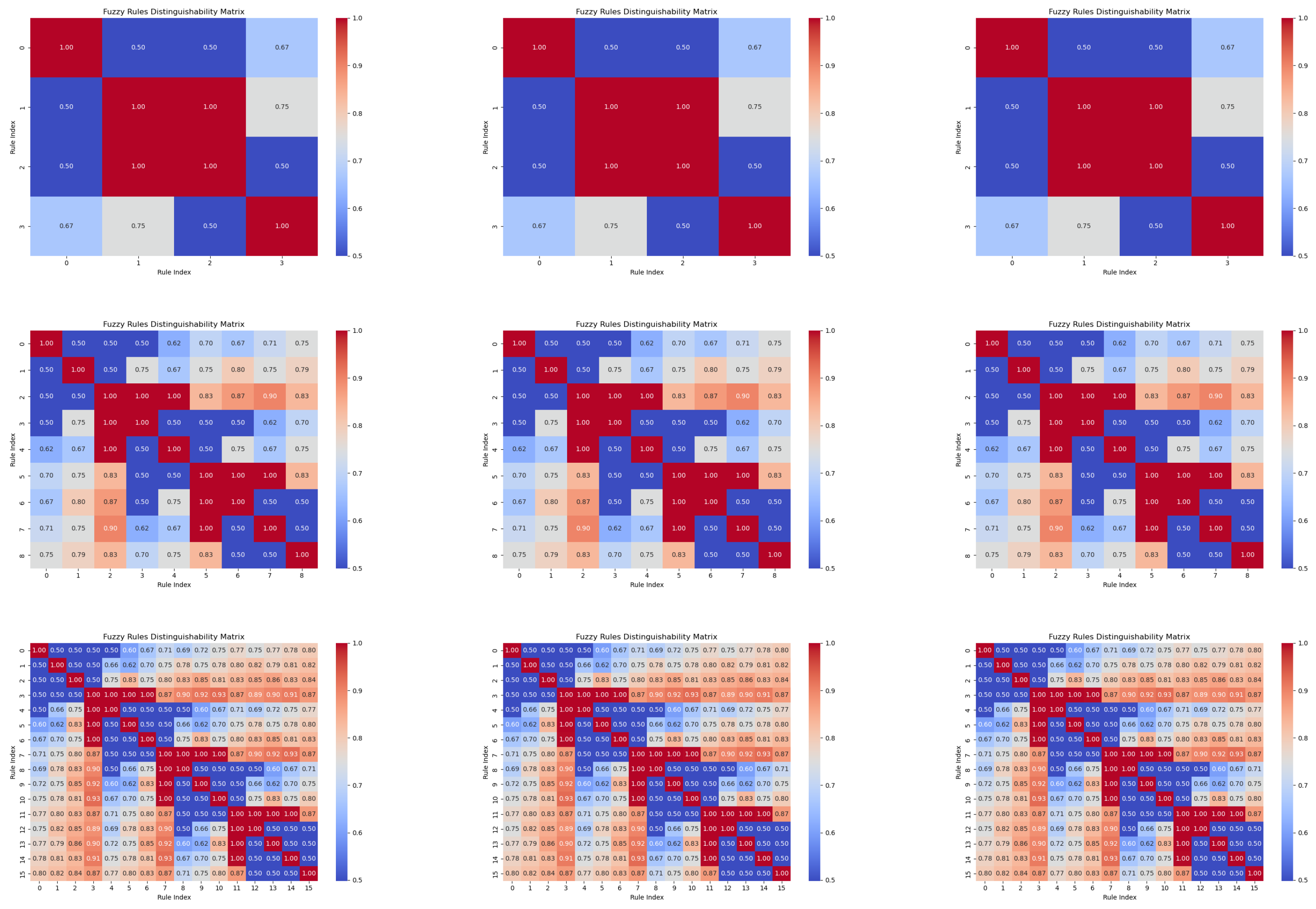
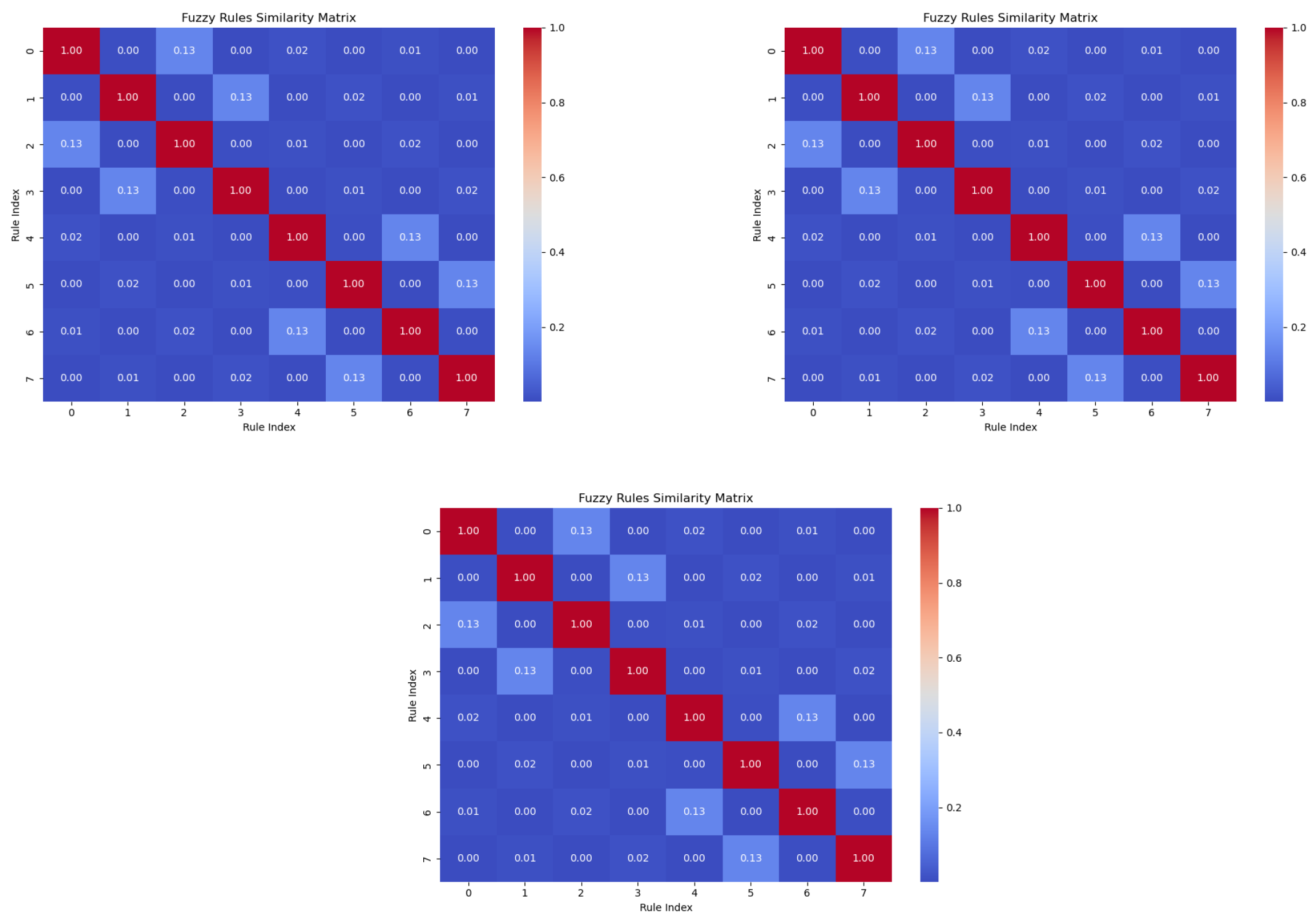
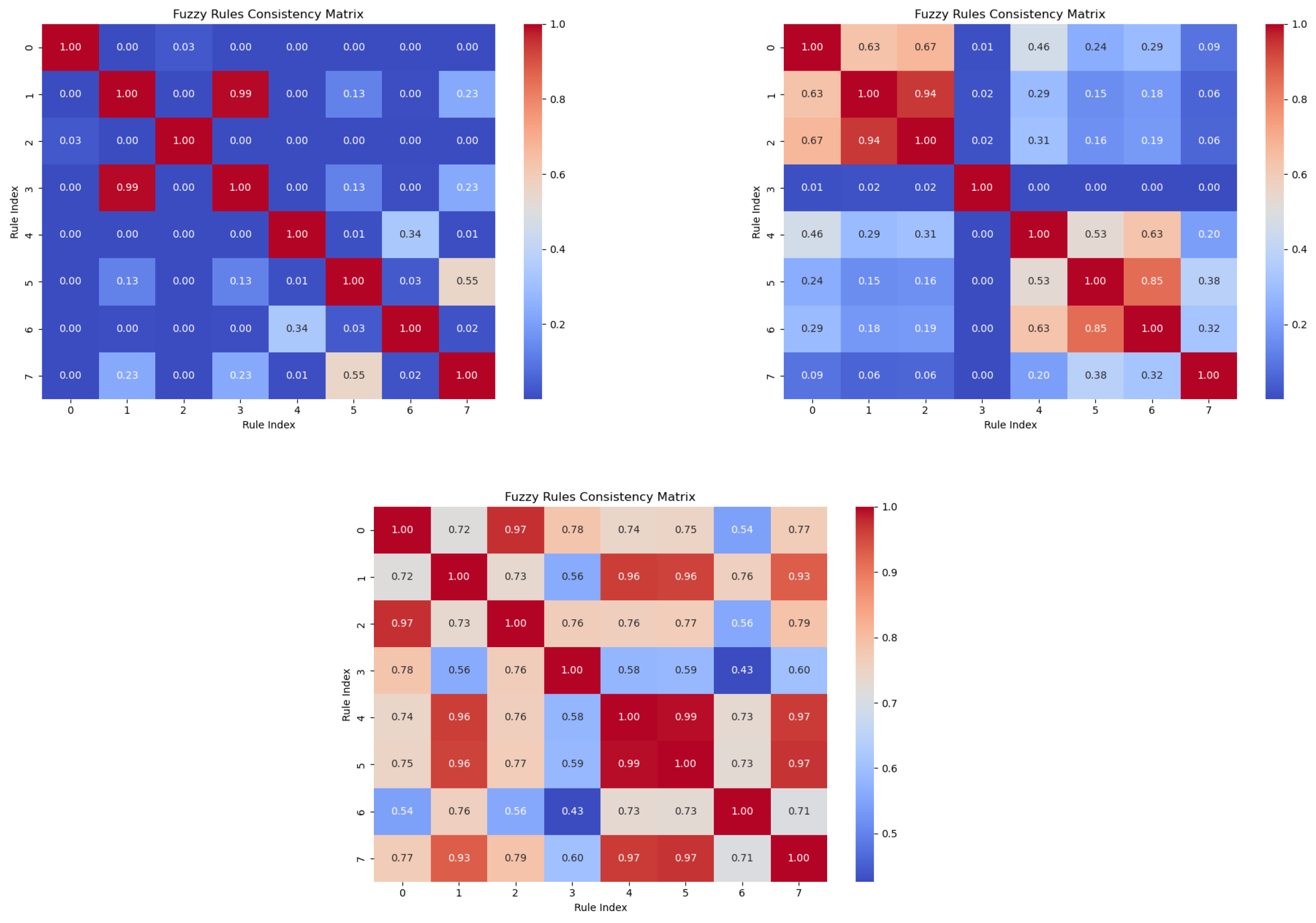
- Enhanced rule interpretability: The model incorporates advanced metrics, such as similarity, distinguishability, and rule activation levels, ensuring that each fuzzy rule uniquely contributes to decision making. Visualization of rule activations provides additional interpretability for users.
- Mutual information for input weight initialization: MI is used to assign higher initial weights to input features with greater discriminative power, aligning fuzzy rules with meaningful input dimensions and strengthening transparency.
- Grey Wolf Optimizer for rule-consequent optimization: The GWO is applied to optimize the consequent parameters of fuzzy rules, improving classification accuracy by refining rule outputs dynamically while maintaining interpretability.
- Adaptive learning through the GWO: GWO-based optimization enables dynamic tuning of rule consequent weights in the output layer, ensuring that the weights reflect the significance of each fuzzy rule, thereby enhancing system reliability and accuracy.
2. Literature Review
2.1. Fuzzy Systems and Fuzzy Logic Neurons
Fuzzy Sets and Developed Logic
2.2. Fuzzy Logic Operators
2.3. Fuzzy Logic Neurons
2.3.1. AndNeuron and OrNeuron
2.3.2. UniNeuron
2.3.3. Fuzzy Neural Networks
2.4. Innovations and Current Trends in Fuzzy Neural Networks
2.5. Advances in Interpretability of Fuzzy Neural Networks
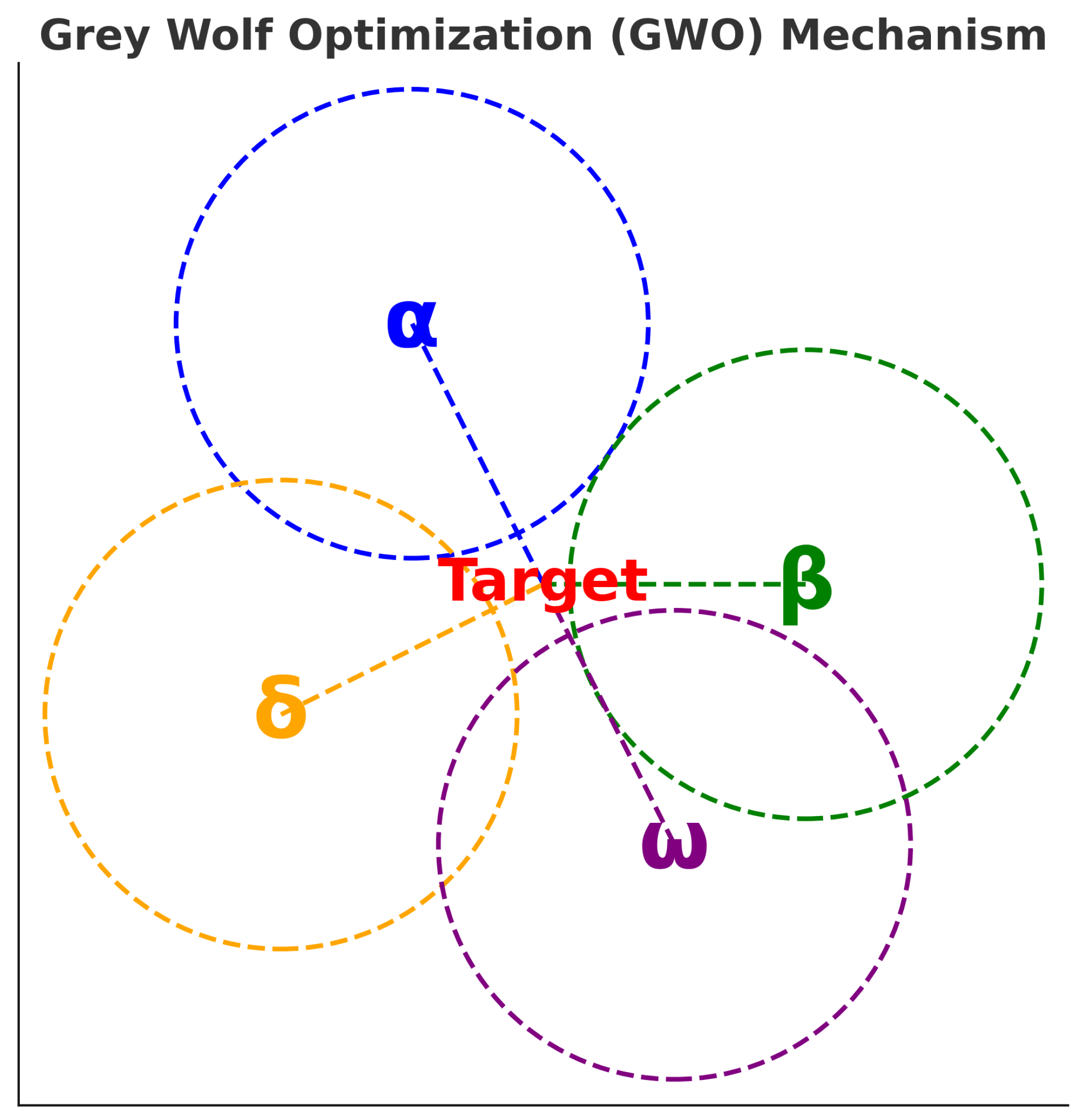
2.6. Grey Wolf Optimizer (GWO)
- t is the current iteration;
- represents the position of the prey;
- denotes the position vector of a gray wolf;
- and are coefficient vectors computed aswhere and are random vectors in , and is a parameter that decreases linearly from 2 to 0 over the course of iterations.
- Simple and easy to implement: It requires few hyper-parameters compared to other swarm-based optimizers.
- Balanced exploration and exploitation: The adaptive parameter helps transition smoothly from exploration to exploitation.
- Global optimization capability: It has been successfully applied to complex, multimodal optimization problems.
- Feature selection;
- Engineering design problems;
- Neural network training;
- Image processing and computer vision;
- Renewable energy optimization.
3. GWO-FNN: Architecture, Training, and Interpretable Tools
3.1. Optimization Methods Applied to Fuzzy Neural Networks
- Structural optimization: Pizzileo et al. [68] proposed an approach that simultaneously optimizes the number of inputs and rules, ensuring a balance between interpretability and accuracy.
- Multi-objective evolutionary algorithms: Gómez-Skarmeta et al. [69] introduced a multi-objective evolutionary algorithm that considers both accuracy and interpretability criteria to generate optimal fuzzy models.
- Gradient-based learning: Zhao et al. [70] developed a gradient descent approach that optimizes premise and consequent parameters simultaneously, improving both interpretability and accuracy.
- Genetic algorithms (GAs): Genetic optimization has been used to refine fuzzy rules and parameters [71].
- Fuzzy rough neural networks: Cao et al. [72] introduced evolutionary fuzzy rough networks that optimize both interpretability and predictive performance.
- Levenberg–Marquardt-optimized fuzzy models: Ebadzadeh and Salimi-Badr [73] implemented hierarchical Levenberg–Marquardt optimization for function approximation.
- Fuzzy GMDH neural network optimized by GWO: Heydari et al. [74] applied the GWO to optimize a fuzzy group method of data handling (GMDH) neural network for wind turbine power forecasting, leading to higher accuracy in energy predictions.
- Modified GWO for learning rate selection in fuzzy controllers: Le et al. [75] proposed a modified GWO to fine-tune learning rates in a multilayer fuzzy controller, improving both convergence and system stability.
- Fuzzy strategy GWO for multimodal problems: Qin et al. [76] developed a fuzzy strategy GWO (FSGWO) for multimodal optimization, demonstrating superior convergence over traditional GWOs.
- GWO in modular granular neural networks: Sánchez et al. [77] applied GWO to optimize modular neural networks for biometric recognition, achieving significant improvements in accuracy.
- Improved forecasting performance;
- Better interpretability–accuracy trade-offs;
- More efficient learning rate adaptation.
3.2. Fuzzy Neural Network Architecture: Structure of Variable Neurons and Activation Functions
3.3. First Layer: Grid-Based Fuzzification with Uniform Membership Functions
3.4. Second Layer: Fuzzy Rule Extraction
3.5. Third Layer: Neural Aggregation Output Layer
3.6. Training of the Third Layer with Grey Wolf Optimization (GWO)
- represents the best solution found so far (alpha wolf position);
- A is the adaptive control parameter, defined as , where a linearly decreases from 2 to 0 over a number of iterations;
- D represents the distance between the candidate solution and the leader, given by , where ;
- are random values in the range for stochastic behavior.
- N is the total number of training samples;
- is the actual class label for sample i;
- represents the network’s output after applying the Sigmoid activation function.
| Algorithm 1 Fuzzy Neural Network Training Process using Grey Wolf Optimizer (GWO) |
| Input: Dataset , target vector , number of wolves . Step 1: Initialize grid partition parameters and the number of membership functions (num_mfs) for each input feature. Step 2: Uniformly calculate centers () and standard deviations () for L fuzzy sets per input feature. Step 3: Apply Gaussian membership functions to construct L fuzzy neurons for each feature, as defined by Equation (23). Step 4: Generate fuzzy neuron outputs for each input sample using the Gaussian functions, forming . Step 5: Adapt target vector for binary classification tasks. Step 6: Initialize the Grey Wolf Optimizer (GWO) with wolves and set the stopping criteria. Step 7: Encode the consequent weights as the position of wolves in the search space. Step 8: Compute the fitness of each wolf based on classification accuracy. Step 9: Update the positions of the alpha (), beta (), and delta () wolves following the GWO update equations (Section 2.6). Step 10: Continue updating until the stopping criteria are met (e.g., max iterations or convergence). Step 11: Select the best solution (position of the wolf), which represents the optimized consequent weights . Output: FNN trained with optimized fuzzy rules. |
4. Advanced Interpretation of the Rules Extracted from the Evolving Neurons
Auxiliary Methods for Interpretability
- Heatmap visualization of logic neuron outputs: This technique provides a clear understanding of how different logical neurons contribute to the final classification decision. The intensity of each neuron’s activation is mapped to a color scale, revealing patterns in neuron activations across different samples.
- Three-dimensional projection of logical neuron outputs: By visualizing the response of fuzzy logic neurons in a three-dimensional space, we can analyze how input features influence decision making in a nonlinear fashion. This approach is particularly useful for understanding how different membership functions interact to generate final predictions.
5. Computational Complexity Analysis with Parameter Nomenclature
6. Experimental Evaluation
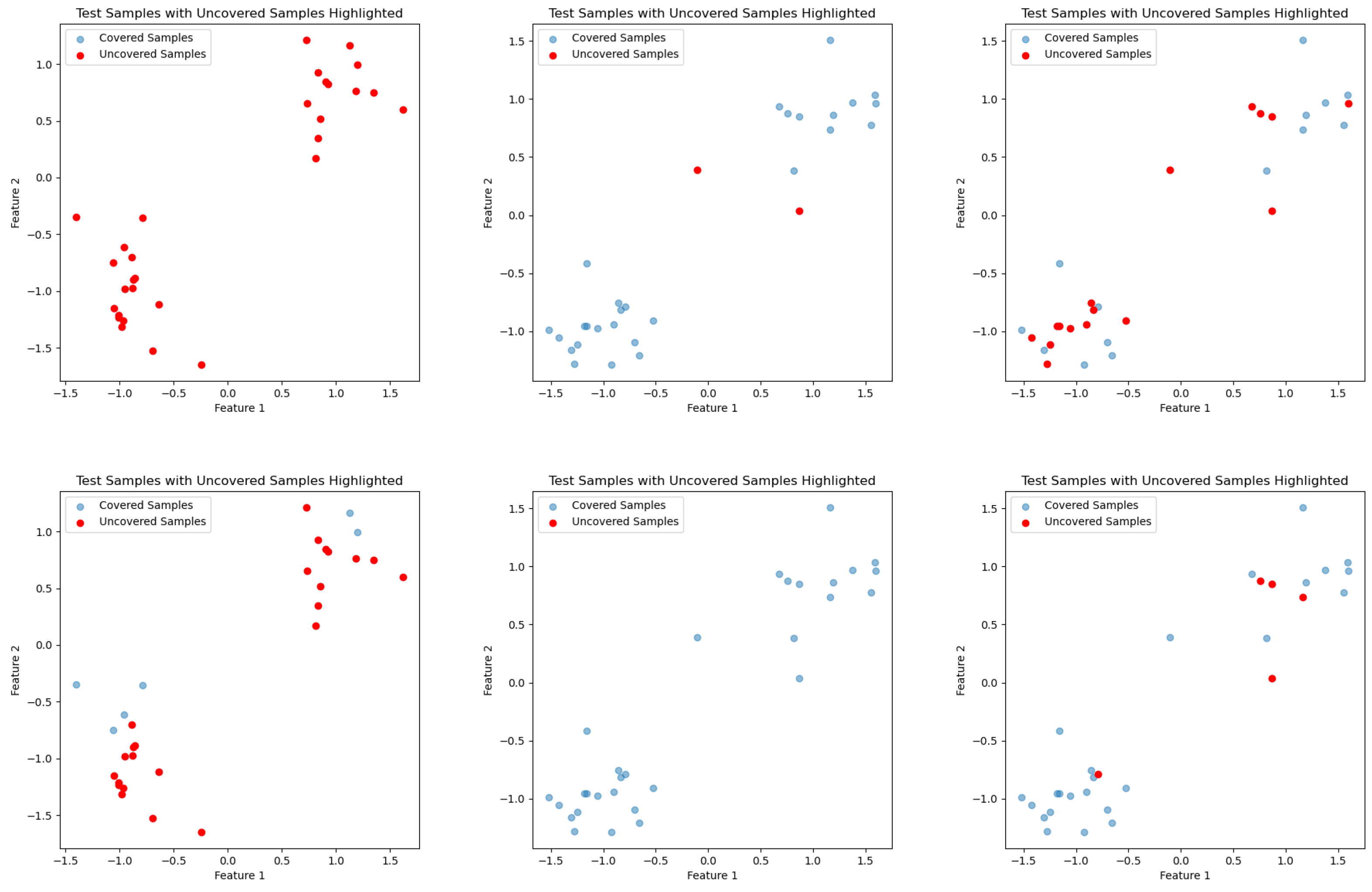
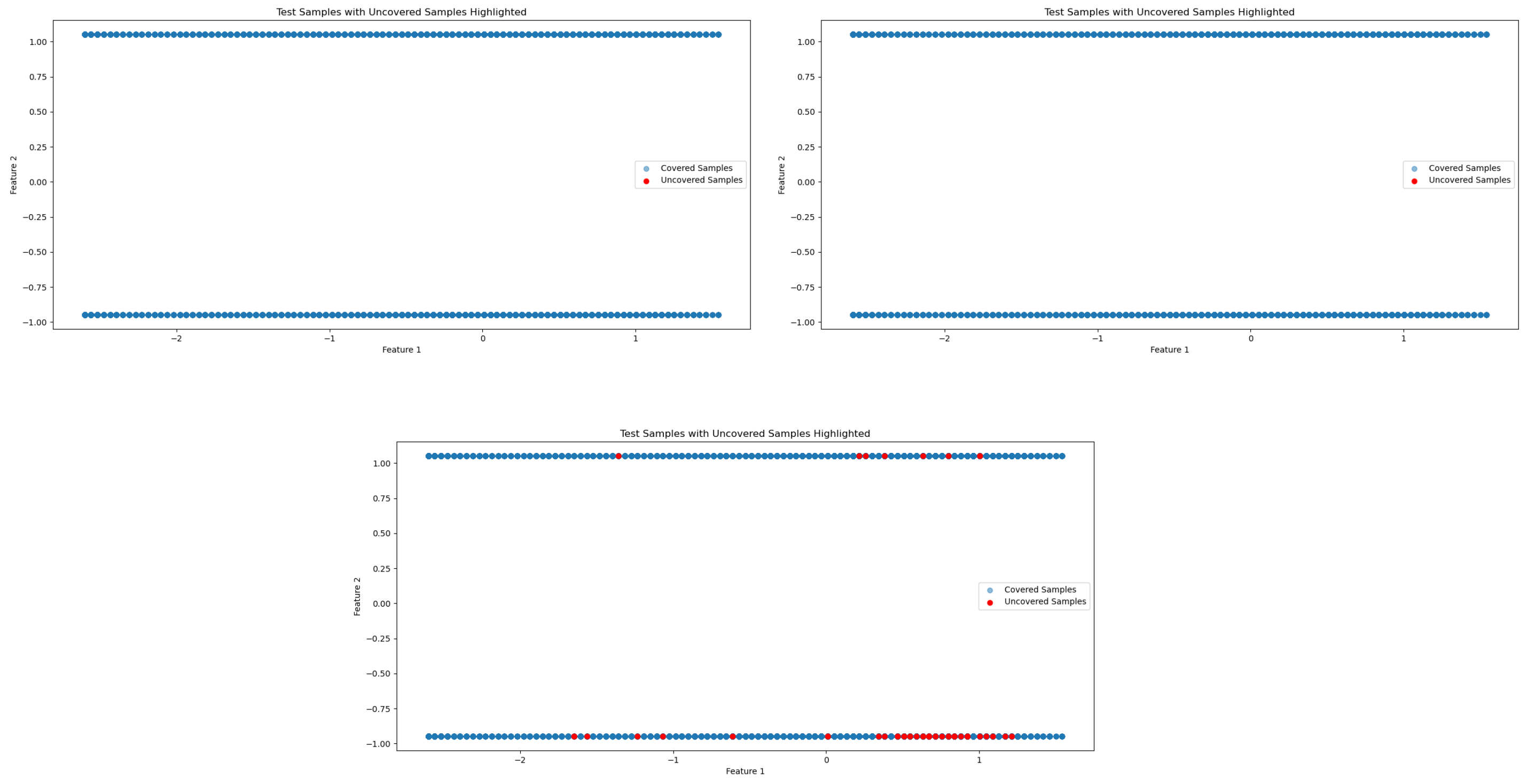
6.1. Understanding Interpretability Using Synthetic Data
6.2. Comparative Analysis with State-of-the-Art Models
- Accuracy: This is defined as the proportion of true results (both true positives and true negatives) among the total number of cases examined. It can be mathematically represented as .
- Precision: This metric reflects the proportion of true positive results in all positive predictions made by the model, given by .
- Recall: Also known as sensitivity, this measures the proportion of actual positives that are correctly identified, calculated as .
- F1 score: The F1 score is the harmonic mean of precision and recall, providing a balance between the two. It is computed as .
- GWO-FNN variants: We evaluated three versions of the proposed model—GWO-FNN with AndNeuron, OrNeuron, and UniNeuron logic configurations. Each variant utilized four membership functions per input dimension, selected based on preliminary experiments comparing different settings (mf = [2, 3, 4, 5]). The Adam optimizer was incorporated to enhance convergence during training.
- Baseline models: As benchmarks, we selected well-established classifiers. The Multilayer Perceptron (MLP) [87] was implemented with a single hidden layer containing 100 neurons to ensure sufficient learning capacity. The Random Forest Classifier [88] employed 100 decision trees to balance predictive accuracy and overfitting resistance. Lastly, the Gaussian Naive Bayes classifier [89] was used with default parameters, offering a probabilistic baseline.
6.3. Application to a Real-World Academic Dataset: Sepsis Dataset
Experimental Setup
- GWO-FNN models: We examine three distinct configurations of the GWO-FNN model—AndNeuron, OrNeuron, and UniNeuron variants—all enhanced with the Adam optimization algorithm and configured with four membership functions for each dimension, following insights from preliminary experiments with varying membership functions (mf = [2, 3, 4,5] and number of wolves = [10, 15, 20]).
- Benchmark models: We employ a suite of well-established models in our comparative analysis, including the following:
7. Discussion About the Tests
7.1. Analysis of Performance Metrics
7.2. State-of-the-Art Evaluation
7.3. Analysis of the Sepsis Identification Results
Analysis
- Impact of age: All models underscore the significant role of age in predicting sepsis outcomes. Rules with “Age” as a contributing factor often suggest that older age groups are associated with higher risks, reflecting a widely recognized clinical observation. The mathematical rigor behind this is apparent in the rules, where age’s impact scores directly correlate with the predicted outcomes, offering a quantitative basis for this age-related vulnerability.
- Influence of sex: While less pronounced than age, the variable “Sex” also features prominently across the models. The differentiation based on sex, albeit with varying degrees of impact across the models, hints at physiological or possibly social determinants influencing sepsis survival rates. This inclusion of sex as a variable enriches the models’ capacity to tailor predictions more closely to individual patient profiles.
- Number of episodes as a critical marker: Perhaps the most telling is the emphasis on the “Number of Episodes”. Models tend to associate a higher number of sepsis episodes with increased mortality risk, but the degree of impact and the manner in which this variable interacts with others (age and sex) vary. This variability offers nuanced insights into how recurrent sepsis episodes compound risk, a crucial consideration for clinicians.
- Similarities:
- 1.
- Consistent representation of risk factors: Despite the inherent differences in their formulation, the rules across models maintain a consistent representation of “Age” and “Number of Episodes” as critical risk factors. This consistency offers a unified view of these variables’ importance, facilitating a broader understanding of their impact on sepsis outcomes.
- 2.
- Logical structuring of antecedents and consequents: The models adhere to a logical structuring that maps specific combinations of antecedents (variables and their states) to consequents (predicted outcomes). This structuring aids in the interpretability of the rules by clearly delineating the conditions under which certain outcomes are expected, thereby providing insights into the decision-making process of the models.
- 3.
- Quantitative insights through impact scores: All models utilize impact scores to quantify the influence of each antecedent on the consequent, offering a measurable insight into the significance of each risk factor. This approach not only enhances the interpretability of the rules but also provides a basis for comparing the relative importance of different variables within the same rule, further enriching the models’ analytical depth.
- Interpretability through dimensional focus: Across all models, there is a clear emphasis on making the rules interpretable by focusing on clinically relevant dimensions such as “Age” and “Number of Episodes”. This focus not only aligns with clinical priorities but also enhances the models’ usability by providing clear, actionable insights into how key variables influence sepsis prognosis.
- Differences:
- 1.
- Conflicting outcomes from similar antecedents: An analysis reveals instances where identical or similar antecedents across different rules lead to divergent outcomes. For example, one rule might indicate a high risk of mortality with a specific configuration of “Age” and “Number of Episodes”, whereas another rule with the same antecedents suggests a survival outcome. This discrepancy can stem from the subtle nuances in how each model weighs the significance or impact of these features differently, reflecting the inherent complexity and variability in sepsis prognosis.
- 2.
- Variable interactions: The rules also differ in their portrayal of interactions between variables. In some models, “Age” and “Number of Episodes” might interact synergistically, amplifying each other’s effects. In contrast, other models might present these interactions as more independent, with each variable contributing to the outcome in a more isolated manner. This variation underscores different models’ interpretations of how sepsis risk factors interrelate.
- 3.
- Impact score variability: Even within models that use the same logical structure (AND/OR), the assigned impact scores for similar antecedents can vary significantly, leading to different conclusions. This aspect highlights the models’ flexibility but also introduces challenges in consistently interpreting the influence of specific risk factors on sepsis outcomes.
8. Conclusions
8.1. Key Contributions
8.2. Challenges and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ALMMo | Autonomous learning multi-model |
| ANFIS | Adaptive neuro-fuzzy inference system |
| ALS | Autonomous learning system |
Appendix A
| Symbol | Description |
|---|---|
| Input elements | |
| Predicted class label | |
| General fuzzy set values | |
| Fuzzy set for input variable at partition l | |
| Membership function of fuzzy set A | |
| Activation degree of fuzzy rule given input x | |
| c | Center of Gaussian membership function |
| Spread (standard deviation) of Gaussian membership function | |
| Gaussian membership function | |
| Membership degree of input in fuzzy set | |
| Center of the Gaussian neuron for fuzzy set | |
| Standard deviation of the Gaussian neuron for fuzzy set | |
| Mutual information (MI) between feature and class label y | |
| Joint probability distribution of feature and label y | |
| Marginal probabilities of feature and label y | |
| Initial weight based on mutual information | |
| Predefined range for MI-based weight normalization | |
| AND | Boolean AND operation (product) |
| OR | Boolean OR operation (probabilistic sum) |
| Fuzzy AND operation (t-norm) | |
| Fuzzy OR operation (t-conorm) | |
| T-norm operation (product) | |
| T-conorm operation (probabilistic sum) | |
| Uninorm function | |
| g | Identity element in the unit interval |
| Binary operator in | |
| Vector of fuzzy relevance values: | |
| Vector of weights: | |
| Output of the logical neuron | |
| Weight associated with fuzzy rule | |
| m | Total number of fuzzy rules |
| Weight assigned to feature i in fuzzy neuron l | |
| Optimized weight of rule consequent k | |
| L | Number of fuzzy neurons per feature |
| Position vector of a gray wolf | |
| Position of the prey | |
| Positions of the alpha, beta, and delta wolves | |
| Distance between wolf and prey | |
| Distances from wolves to the best solutions | |
| Coefficient vectors in the GWO | |
| Random vectors in [0, 1] | |
| Linearly decreasing parameter (from 2 to 0) | |
| t | Current iteration number |
| T | Maximum number of iterations |
| Weight vector of neuron k at iteration t | |
| Best solution found so far (alpha wolf position) at iteration t | |
| A | Adaptive control parameter in GWO |
| D | Distance between candidate solution and leader in GWO |
| C | Number of classes in classification task |
| Activation outputs of all neurons for input samples | |
| Target vector for binary classification | |
| Fitness function evaluating the quality of | |
| Actual class label for sample i | |
| Network’s output after applying Sigmoid activation | |
| Sigmoid activation function | |
| Exponential term in the Sigmoid function | |
| Threshold-based classification function | |
| Bias term (fixed at 1) | |
| Bias weight | |
| Weight in the aggregation step | |
| l | Number of aggregation neuron inputs |
| Output of neuron j before applying the Sigmoid function | |
| Fuzzy rule notation | |
| Output of the fuzzy rule consequent for rule L | |
| Singleton values for binary classification |
References
- Guidotti, R.; Monreale, A.; Ruggieri, S.; Turini, F.; Giannotti, F.; Pedreschi, D. A survey of methods for explaining black box models. ACM Comput. Surv. (CSUR) 2018, 51, 1–42. [Google Scholar] [CrossRef]
- de Campos Souza, P.V. Fuzzy neural networks and neuro-fuzzy networks: A review the main techniques and applications used in the literature. Appl. Soft Comput. 2020, 92, 106275. [Google Scholar] [CrossRef]
- Angelov, P.P.; Zhou, X. Evolving fuzzy-rule-based classifiers from data streams. IEEE Trans. Fuzzy Syst. 2008, 16, 1462–1475. [Google Scholar] [CrossRef]
- Škrjanc, I.; Iglesias, J.A.; Sanchis, A.; Leite, D.; Lughofer, E.; Gomide, F. Evolving fuzzy and neuro-fuzzy approaches in clustering, regression, identification, and classification: A survey. Inf. Sci. 2019, 490, 344–368. [Google Scholar] [CrossRef]
- Pedrycz, W. Fuzzy neural networks and neurocomputations. Fuzzy Sets Syst. 1993, 56, 1–28. [Google Scholar] [CrossRef]
- Wu, S.; Er, M.J.; Gao, Y. A fast approach for automatic generation of fuzzy rules by generalized dynamic fuzzy neural networks. IEEE Trans. Fuzzy Syst. 2001, 9, 578–594. [Google Scholar]
- Slawinski, T.; Krone, A.; Hammel, U.; Wiesmann, D.; Krause, P. A hybrid evolutionary search concept for data-based generation of relevant fuzzy rules in high dimensional spaces. In Proceedings of the FUZZ-IEEE’99. 1999 IEEE International Fuzzy Systems. Conference Proceedings (Cat. No.99CH36315), Seoul, Republic of Korea, 22–25 August 1999; Volume 3, pp. 1432–1437. [Google Scholar] [CrossRef]
- Mendel, J.M.; John, R.B. Type-2 fuzzy sets made simple. IEEE Trans. Fuzzy Syst. 2002, 10, 117–127. [Google Scholar] [CrossRef]
- Jang, J.S.; Sun, C.T. Neuro-fuzzy modeling and control. Proc. IEEE 1995, 83, 378–406. [Google Scholar] [CrossRef]
- Tan, J.C.M.; Cao, Q.; Quek, C. FE-RNN: A fuzzy embedded recurrent neural network for improving interpretability of underlying neural network. Inf. Sci. 2024, 663, 120276. [Google Scholar]
- Zhou, K.; Oh, S.K.; Qiu, J.; Pedrycz, W.; Seo, K.; Yoon, J.H. Design of Hierarchical Neural Networks Using Deep LSTM and Self-organizing Dynamical Fuzzy-Neural Network Architecture. IEEE Trans. on Fuzzy Syst. 2024, 32, 2915–2929. [Google Scholar] [CrossRef]
- Singh, B.; Doborjeh, M.; Doborjeh, Z.; Budhraja, S.; Tan, S.; Sumich, A.; Goh, W.; Lee, J.; Lai, E.; Kasabov, N. Constrained neuro fuzzy inference methodology for explainable personalised modelling with applications on gene expression data. Sci. Rep. 2023, 13, 456. [Google Scholar]
- Lughofer, E.; Pratama, M. Evolving multi-user fuzzy classifier system with advanced explainability and interpretability aspects. Inf. Fusion 2023, 91, 458–476. [Google Scholar]
- Pedrycz, W. Logic-based fuzzy neurocomputing with unineurons. IEEE Trans. Fuzzy Syst. 2006, 14, 860–873. [Google Scholar]
- Souza, P.V.C. Regularized Fuzzy Neural Networks for Pattern Classification Problems. Int. J. Appl. Eng. Res. 2018, 13, 2985–2991. [Google Scholar]
- Pedrycz, W.; Gomide, F. An Introduction to Fuzzy Sets: Analysis and Design; Mit Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Chicco, D.; Jurman, G. Survival prediction of patients with sepsis from age, sex, and septic episode number alone. Sci. Rep. 2020, 10, 17156. [Google Scholar]
- Pedrycz, W. Neurocomputations in relational systems. IEEE Trans. Pattern Anal. Mach. Intell. 1991, 13, 289–297. [Google Scholar]
- Klement, E.P.; Mesiar, R.; Pap, E. Triangular norms. Position paper III: Continuous t-norms. Fuzzy Sets Syst. 2004, 145, 439–454. [Google Scholar]
- Klement, E.P.; Mesiar, R.; Pap, E. Triangular Norms; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 8. [Google Scholar]
- Yager, R.R.; Rybalov, A. Uninorm aggregation operators. Fuzzy Sets Syst. 1996, 80, 111–120. [Google Scholar]
- Lemos, A.; Caminhas, W.; Gomide, F. A fast learning algorithm for uninorm-based fuzzy neural networks. In Proceedings of the Fuzzy Information Processing Society (NAFIPS), 2012 Annual Meeting of the North American, Berkeley, CA, USA, 6–8 August 2012; pp. 1–6. [Google Scholar]
- Klement, E.; Mesiar, R.; Pap, E. Triangular Norms; Kluwer Academic Publishers: Dordrecht, The Netherlands; Norwell, MA, USA; New York, NY, USA; London, UK, 2000. [Google Scholar]
- Zhou, H.; Liu, X. Characterizations of (U2,N)-implications generated by 2-uninorms and fuzzy negations from the point of view of material implication. Fuzzy Sets Syst. 2020, 378, 79–102. [Google Scholar]
- Lemos, A.; Caminhas, W.; Gomide, F. New uninorm-based neuron model and fuzzy neural networks. In Proceedings of the Fuzzy Information Processing Society (NAFIPS), 2010 Annual Meeting of the North American, Toronto, ON, Canada, 12–14 July 2010; pp. 1–6. [Google Scholar]
- Wang, Y.; Lu, H.; Qin, X.; Guo, J. Residual Gabor convolutional network and FV-Mix exponential level data augmentation strategy for finger vein recognition. Expert Syst. Appl. 2023, 223, 119874. [Google Scholar] [CrossRef]
- Yu, Y.F.; Zhong, G.; Zhou, Y.; Chen, L. FS-GAN: Fuzzy Self-guided structure retention generative adversarial network for medical image enhancement. Inf. Sci. 2023, 642, 119114. [Google Scholar] [CrossRef]
- Li, L.J.; Zhou, S.L.; Chao, F.; Chang, X.; Yang, L.; Yu, X.; Shang, C.; Shen, Q. Model compression optimized neural network controller for nonlinear systems. Knowl.-Based Syst. 2023, 265, 110311. [Google Scholar] [CrossRef]
- Khuat, T.T.; Gabrys, B. An online learning algorithm for a neuro-fuzzy classifier with mixed-attribute data. Appl. Soft Comput. 2023, 137, 110152. [Google Scholar] [CrossRef]
- Hao, Y.; Yang, W.; Yin, K. Novel wind speed forecasting model based on a deep learning combined strategy in urban energy systems. Expert Syst. Appl. 2023, 219, 119636. [Google Scholar] [CrossRef]
- Wang, L.; Li, H.; Hu, C.; Hu, J.; Wang, Q. Synchronization and settling-time estimation of fuzzy memristive neural networks with time-varying delays: Fixed-time and preassigned-time control. Fuzzy Sets Syst. 2023, 470, 108654. [Google Scholar] [CrossRef]
- Su, Y.; Yang, C.; Qiao, J. Self-organizing pipelined recurrent wavelet neural network for time series prediction. Expert Syst. Appl. 2023, 214, 119215. [Google Scholar] [CrossRef]
- Jan, N.; Gwak, J.; Pamucar, D.; MartÃnez, L. Hybrid integrated decision-making model for operating system based on complex intuitionistic fuzzy and soft information. Inf. Sci. 2023, 651, 119592. [Google Scholar] [CrossRef]
- Hwang, C.L. Cooperation of robot manipulators with motion constraint by real-time RNN-based finite-time fault-tolerant control. Neurocomputing 2023, 556, 126694. [Google Scholar] [CrossRef]
- Chen, Z.; Wu, K.; Wu, J.; Deng, C.; Wang, Y. Residual shrinkage transformer relation network for intelligent fault detection of industrial robot with zero-fault samples. Knowl.-Based Syst. 2023, 268, 110452. [Google Scholar] [CrossRef]
- Chen, J.; Mao, C.; Song, W.W. QoS prediction for web services in cloud environments based on swarm intelligence search. Knowl.-Based Syst. 2023, 259, 110081. [Google Scholar] [CrossRef]
- Dass, A.; Srivastava, S.; Kumar, R. A novel Lyapunov-stability-based recurrent-fuzzy system for the Identification and adaptive control of nonlinear systems. Appl. Soft Comput. 2023, 137, 110161. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, W.; Chen, X.M. Bibliometric methods in traffic flow prediction based on artificial intelligence. Expert Syst. Appl. 2023, 228, 120421. [Google Scholar] [CrossRef]
- Hu, Z.; Cheng, Y.; Xiong, H.; Zhang, X. Assembly makespan estimation using features extracted by a topic model. Knowl.-Based Syst. 2023, 276, 110738. [Google Scholar] [CrossRef]
- Gu, X. Self-adaptive fuzzy learning ensemble systems with dimensionality compression from data streams. Inf. Sci. 2023, 634, 382–399. [Google Scholar] [CrossRef]
- Javaheri, D.; Gorgin, S.; Lee, J.A.; Masdari, M. Fuzzy logic-based DDoS attacks and network traffic anomaly detection methods: Classification, overview, and future perspectives. Inf. Sci. 2023, 626, 315–338. [Google Scholar] [CrossRef]
- Kan, N.H.L.; Cao, Q.; Quek, C. Learning and processing framework using Fuzzy Deep Neural Network for trading and portfolio rebalancing. Appl. Soft Comput. 2024, 152, 111233. [Google Scholar] [CrossRef]
- Singh, D.J.; Verma, N.K. Interval Type-3Â T-S fuzzy system for nonlinear aerodynamic modeling. Appl. Soft Comput. 2024, 150, 111097. [Google Scholar] [CrossRef]
- Tavana, M.; Sorooshian, S. A systematic review of the soft computing methods shaping the future of the metaverse. Appl. Soft Comput. 2024, 150, 111098. [Google Scholar] [CrossRef]
- Zhao, T.; Zhu, Y.; Xie, X. Topology structure optimization of evolutionary hierarchical fuzzy systems. Expert Syst. Appl. 2024, 238, 121857. [Google Scholar] [CrossRef]
- Yan, A.; Wang, R.; Guo, J.; Tang, J. A knowledge transfer online stochastic configuration network-based prediction model for furnace temperature in a municipal solid waste incineration process. Expert Syst. Appl. 2024, 243, 122733. [Google Scholar] [CrossRef]
- Barhaghtalab, M.H.; Sepestanaki, M.A.; Mobayen, S.; Jalilvand, A.; Fekih, A.; Meigoli, V. Design of an adaptive fuzzy-neural inference system-based control approach for robotic manipulators. Appl. Soft Comput. 2023, 149, 110970. [Google Scholar] [CrossRef]
- Park, S.B.; Oh, S.K.; Kim, E.H.; Pedrycz, W. Rule-based fuzzy neural networks realized with the aid of linear function Prototype-driven fuzzy clustering and layer Reconstruction-based network design strategy. Expert Syst. Appl. 2023, 219, 119655. [Google Scholar] [CrossRef]
- Pham, P.; Nguyen, L.T.; Nguyen, N.T.; Kozma, R.; Vo, B. A hierarchical fused fuzzy deep neural network with heterogeneous network embedding for recommendation. Inf. Sci. 2023, 620, 105–124. [Google Scholar] [CrossRef]
- Cagcag Yolcu, O.; Yolcu, U. A novel intuitionistic fuzzy time series prediction model with cascaded structure for financial time series. Expert Syst. Appl. 2023, 215, 119336. [Google Scholar] [CrossRef]
- Azizi, F.; Hamid, M.; Salimi, B.; Rabbani, M. An intelligent framework to assess and improve operating room performance considering ergonomics. Expert Syst. Appl. 2023, 229, 120559. [Google Scholar] [CrossRef]
- Yu, D.; Fang, A.; Xu, Z. Topic research in fuzzy domain: Based on LDA topic modelling. Inf. Sci. 2023, 648, 119600. [Google Scholar] [CrossRef]
- Zheng, K.; Zhang, Q.; Peng, L.; Zeng, S. Adaptive memetic differential evolution-back propagation-fuzzy neural network algorithm for robot control. Inf. Sci. 2023, 637, 118940. [Google Scholar] [CrossRef]
- Stepin, I.; Suffian, M.; Catala, A.; Alonso-Moral, J.M. How to Build Self-Explaining Fuzzy Systems: From Interpretability to Explainability [AI-eXplained]. IEEE Comput. Intell. Mag. 2024, 19, 81–82. [Google Scholar] [CrossRef]
- Alonso, J.M.; Castiello, C.; Mencar, C. Interpretability of fuzzy systems: Current research trends and prospects. In Springer Handbook of Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2015; pp. 219–237. [Google Scholar]
- de Campos Souza, P.V.; Lughofer, E.; Rodrigues Batista, H. An explainable evolving fuzzy neural network to predict the k barriers for intrusion detection using a wireless sensor network. Sensors 2022, 22, 5446. [Google Scholar] [CrossRef]
- Jin, Y.; Cao, W.; Wu, M.; Yuan, Y.; Shi, Y. Simplification of ANFIS based on Importance-Confidence-Similarity Measures. Fuzzy Sets Syst. 2024, 481, 108887. [Google Scholar]
- Pratama, M.; Lu, J.; Lughofer, E.; Zhang, G.; Er, M.J. An incremental learning of concept drifts using evolving type-2 recurrent fuzzy neural networks. IEEE Trans. Fuzzy Syst. 2016, 25, 1175–1192. [Google Scholar]
- Li, Y.; Lin, Y.; Liu, J.; Weng, W.; Shi, Z.; Wu, S. Feature selection for multi-label learning based on kernelized fuzzy rough sets. Neurocomputing 2018, 318, 271–286. [Google Scholar]
- de Campos Souza, P.V.; Lughofer, E. EFNN-NullUni: An evolving fuzzy neural network based on null-uninorm. Fuzzy Sets Syst. 2022, 449, 1–31. [Google Scholar]
- Felizardo, L.K.; Lima Paiva, F.C.; de Vita Graves, C.; Matsumoto, E.Y.; Costa, A.H.R.; Del-Moral-Hernandez, E.; Brandimarte, P. Outperforming algorithmic trading reinforcement learning systems: A supervised approach to the cryptocurrency market. Expert Syst. Appl. 2022, 202, 117259. [Google Scholar] [CrossRef]
- Dong, L.; Jiang, F.; Li, X.; Wu, M. IRI: An intelligent resistivity inversion framework based on fuzzy wavelet neural network. Expert Syst. Appl. 2022, 202, 117066. [Google Scholar] [CrossRef]
- Hassani, S.; Dackermann, U.; Mousavi, M.; Li, J. A systematic review of data fusion techniques for optimized structural health monitoring. Inf. Fusion 2024, 103, 102136. [Google Scholar] [CrossRef]
- Qin, B.; lai Chung, F.; Nojima, Y.; Ishibuchi, H.; Wang, S. Fuzzy rule dropout with dynamic compensation for wide learning algorithm of TSK fuzzy classifier. Appl. Soft Comput. 2022, 127, 109410. [Google Scholar] [CrossRef]
- Liao, H.; He, Y.; Wu, X.; Wu, Z.; Bausys, R. Reimagining multi-criterion decision making by data-driven methods based on machine learning: A literature review. Inf. Fusion 2023, 100, 101970. [Google Scholar] [CrossRef]
- de Campos Souza, P.V.; Lughofer, E. EFNC-Exp: An evolving fuzzy neural classifier integrating expert rules and uncertainty. Fuzzy Sets Syst. 2023, 466, 108438. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Pizzileo, B.; Li, K.; Irwin, G.W.; Zhao, W. Improved Structure Optimization for Fuzzy-Neural Networks. IEEE Trans. Fuzzy Syst. 2012, 20, 1076–1089. [Google Scholar] [CrossRef]
- Gómez-Skarmeta, A.; Jiménez, F.; Sánchez, G. Improving interpretability in approximative fuzzy models via multiobjective evolutionary algorithms. Int. J. Intell. Syst. 2007, 22, 943–969. [Google Scholar] [CrossRef]
- Zhao, W.; Li, K.; Irwin, G. A New Gradient Descent Approach for Local Learning of Fuzzy Neural Models. IEEE Trans. Fuzzy Syst. 2013, 21, 30–44. [Google Scholar] [CrossRef]
- Oh, S.K.; Pedrycz, W.; Park, H.S. Genetically Optimized Fuzzy Polynomial Neural Networks. IEEE Trans. Fuzzy Syst. 2006, 14, 125–144. [Google Scholar] [CrossRef]
- Cao, B.; Zhao, J.; Lv, Z.; Gu, Y.; Yang, P.; Halgamuge, S. Multiobjective Evolution of Fuzzy Rough Neural Network via Distributed Parallelism for Stock Prediction. IEEE Trans. Fuzzy Syst. 2020, 28, 939–952. [Google Scholar] [CrossRef]
- Ebadzadeh, M.; Salimi-Badr, A. IC-FNN: A Novel Fuzzy Neural Network with Interpretable, Intuitive, and Correlated-Contours Fuzzy Rules for Function Approximation. IEEE Trans. Fuzzy Syst. 2018, 26, 1288–1302. [Google Scholar] [CrossRef]
- Heydari, A.; Nezhad, M.M.; Neshat, M.; Garcia, D.A.; Keynia, F.; Santoli, L.D.; Tjernberg, L.B. A Combined Fuzzy GMDH Neural Network and Grey Wolf Optimization Application for Wind Turbine Power Production Forecasting Considering SCADA Data. Energies 2021, 14, 3459. [Google Scholar] [CrossRef]
- Le, T.L.; Huynh, T.T.; Hong, S.H. A Modified Grey Wolf Optimizer for Optimum Parameters of Multilayer Type-2 Asymmetric Fuzzy Controller. IEEE Access 2020, 8, 121611–121629. [Google Scholar] [CrossRef]
- Qin, H.; Meng, T.; Cao, Y. Fuzzy Strategy Grey Wolf Optimizer for Complex Multimodal Optimization Problems. Sensors 2022, 22, 6420. [Google Scholar] [CrossRef]
- Sánchez, D.; Melin, P.; Castillo, O. A Grey Wolf Optimizer for Modular Granular Neural Networks for Human Recognition. Comput. Intell. Neurosci. 2017, 2017, 4180510. [Google Scholar] [CrossRef]
- de Campos Souza, P.V.; Silva, G.R.L.; Torres, L.C.B. Uninorm based regularized fuzzy neural networks. In Proceedings of the 2018 IEEE Conference on Evolving and Adaptive Intelligent Systems (EAIS), Rhodes, Greece, 25–27 May 2018; pp. 1–8. [Google Scholar]
- de Campos Souza, P.V.; de Oliveira, P.F.A. Regularized fuzzy neural networks based on nullneurons for problems of classification of patterns. In Proceedings of the 2018 IEEE Symposium on Computer Applications & Industrial Electronics (ISCAIE), Penang, Malaysia, 28–29 April 2018; pp. 25–30. [Google Scholar]
- Miller, G.A. The magical number seven, plus or minus two: Some limits on our capacity for processing information. Psychol. Rev. 1956, 63, 81. [Google Scholar] [CrossRef]
- Unwin, A.; Kleinman, K. The Iris Data Set: In Search of the Source of Virginica. Significance 2021, 18, 26–29. [Google Scholar] [CrossRef]
- Elter, M. Mammographic Mass. UCI Machine Learning Repository, 2007. Available online: https://archive.ics.uci.edu/dataset/161/mammographic+mass (accessed on 27 March 2025).
- Haberman, S. Haberman’s Survival. UCI Machine Learning Repository, 1999. Available online: https://archive.ics.uci.edu/dataset/43/haberman+s+survival (accessed on 27 March 2025).
- Yeh, I.C. Blood Transfusion Service Center. UCI Machine Learning Repository, 2008. Available online: https://archive.ics.uci.edu/dataset/176/blood+transfusion+service+center (accessed on 27 March 2025).
- Liver Disorders. UCI Machine Learning Repository, 1990. Available online: https://archive.ics.uci.edu/dataset/60/liver+disorders (accessed on 27 March 2025).
- Khozeimeh, F.; Jabbari Azad, F.; Mahboubi Oskouei, Y.; Jafari, M.; Tehranian, S.; Alizadehsani, R.; Layegh, P. Intralesional immunotherapy compared to cryotherapy in the treatment of warts. Int. J. Dermatol. 2017, 56, 474–478. [Google Scholar] [CrossRef] [PubMed]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Chan, T.F.; Golub, G.H.; LeVeque, R.J. Algorithms for computing the sample variance: Analysis and recommendations. Am. Stat. 1983, 37, 242–247. [Google Scholar] [CrossRef]
- St, L.; Wold, S. Analysis of variance (ANOVA). Chemom. Intell. Lab. Syst. 1989, 6, 259–272. [Google Scholar]
- Abdi, H.; Williams, L.J. Tukey’s honestly significant difference (HSD) test. Encycl. Res. Des. 2010, 3, 1–5. [Google Scholar]
- Razali, N.M.; Wah, Y.B. Power comparisons of shapiro-wilk, kolmogorov-smirnov, lilliefors and anderson-darling tests. J. Stat. Model. Anal. 2011, 2, 21–33. [Google Scholar]
- Gastwirth, J.L.; Gel, Y.R.; Miao, W. The Impact of Levene’s Test of Equality of Variances on Statistical Theory and Practice. Stat. Sci. 2009, 24, 343–360. [Google Scholar] [CrossRef]
- Kaya, U.; Yılmaz, A.; Aşar, S. Sepsis Prediction by Using a Hybrid Metaheuristic Algorithm: A Novel Approach for Optimizing Deep Neural Networks. Diagnostics 2023, 13, 2023. [Google Scholar] [CrossRef] [PubMed]
- Goh, K.H.; Wang, L.; Yeow, A.Y.K.; Poh, H.; Li, K.; Yeow, J.J.L.; Tan, G.Y.H. Artificial intelligence in sepsis early prediction and diagnosis using unstructured data in healthcare. Nat. Commun. 2021, 12, 711. [Google Scholar] [PubMed]
- Jones, L.C.; Dion, C.; Efron, P.A.; Price, C.C. Sepsis and cognitive assessment. J. Clin. Med. 2021, 10, 4269. [Google Scholar] [CrossRef]
- Xie, Y.; Li, B.; Li, Y.; Shi, F.; Chen, W.; Wu, W.; Zhang, W.; Fei, Y.; Zou, S.; Yao, C. Combining blood-based biomarkers to predict mortality of sepsis at arrival at the Emergency Department. Med Sci. Monit. Int. Med J. Exp. Clin. Res. 2021, 7, e929527-1–e929527-8. [Google Scholar]
- Gamboa-Antiñolo, F.M. Prognostic tools for elderly patients with sepsis: In search of new predictive models. Intern. Emerg. Med. 2021, 16, 1027–1030. [Google Scholar]
- Fonseca, F.S.; Torcate, A.S.; Silva, A.C.G.D.; Freire, V.H.W.; Farias, G.P.D.M.D.; Oliveira, J.F.L.D. Early prediction of generalized infection in intensive care units from clinical data: A committee-based machine learning approach. In Proceedings of the 2022 IEEE Latin American Conference on Computational Intelligence (LA-CCI), Montevideo, Uruguay, 23–25 November 2022; pp. 1–6. [Google Scholar]
- Samuel, S.V.; Viggeswarpu, S.; Chacko, B.; Belavendra, A. Predictors of outcome in older adults admitted with sepsis in a tertiary care center. J. Indian Acad. Geriatr. 2023, 19, 105–113. [Google Scholar]
- Shanthi, N.; A, A. A novel machine learning approach to predict sepsis at an early stage. In Proceedings of the 2022 International Conference on Computer Communication and Informatics (ICCCI), Coimbatore, India, 25–27 January 2022; pp. 1–7. [Google Scholar]
- John, G.H.; Langley, P. Estimating continuous distributions in Bayesian classifiers. In Proceedings of the Eleventh Conference on Uncertainty in Artificial Intelligence, Montreal, QC, Canada, 18–20 August 1995; pp. 338–345. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar]
- Walker, S.H.; Duncan, D.B. Estimation of the probability of an event as a function of several independent variables. Biometrika 1967, 54, 167–179. [Google Scholar] [CrossRef]

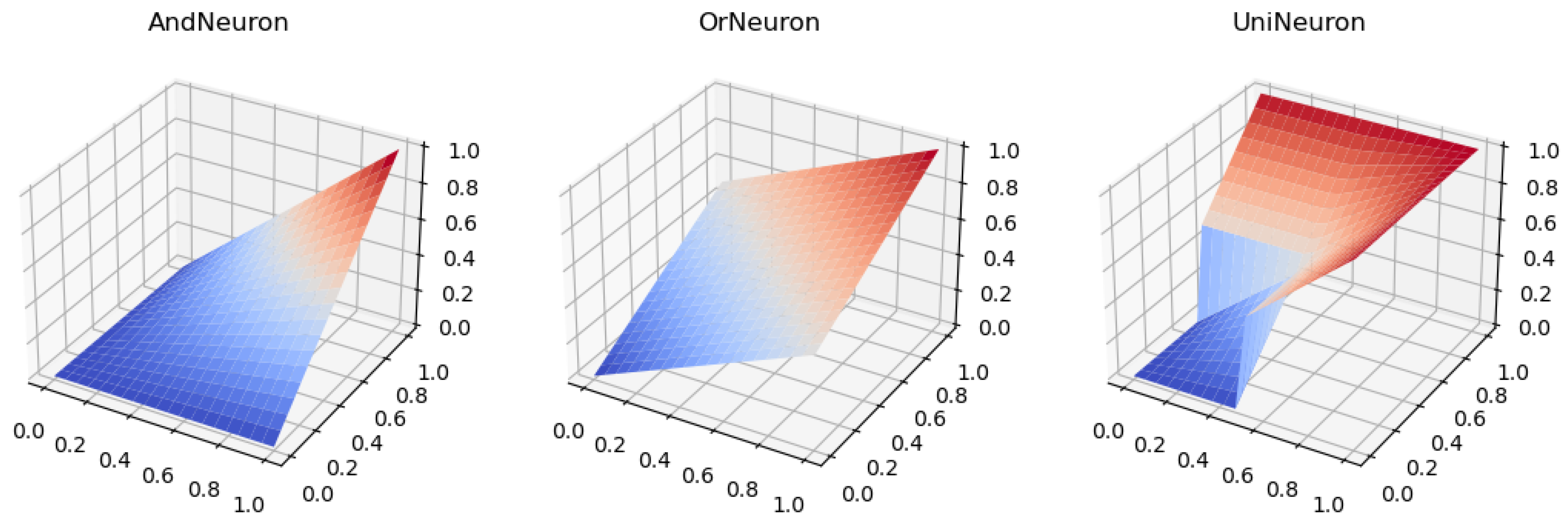
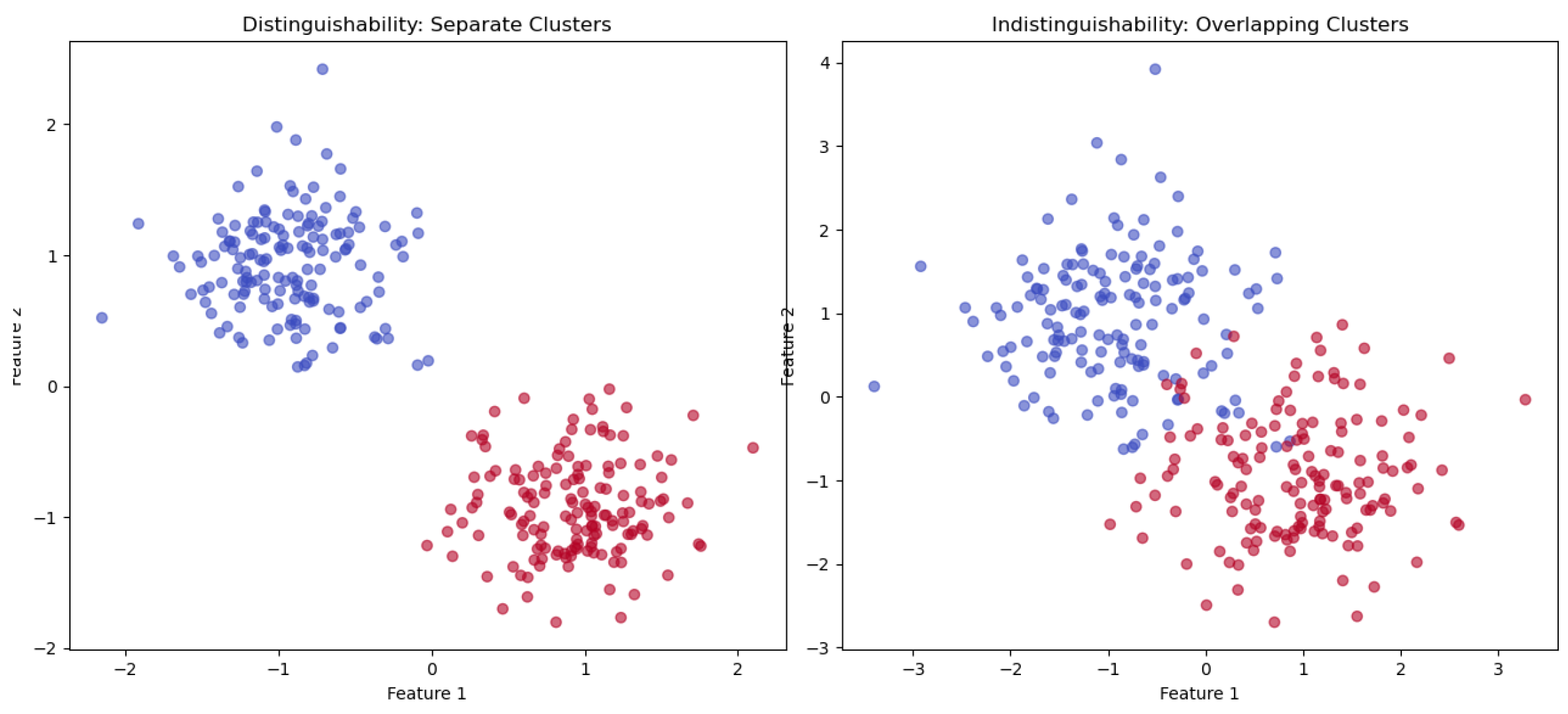

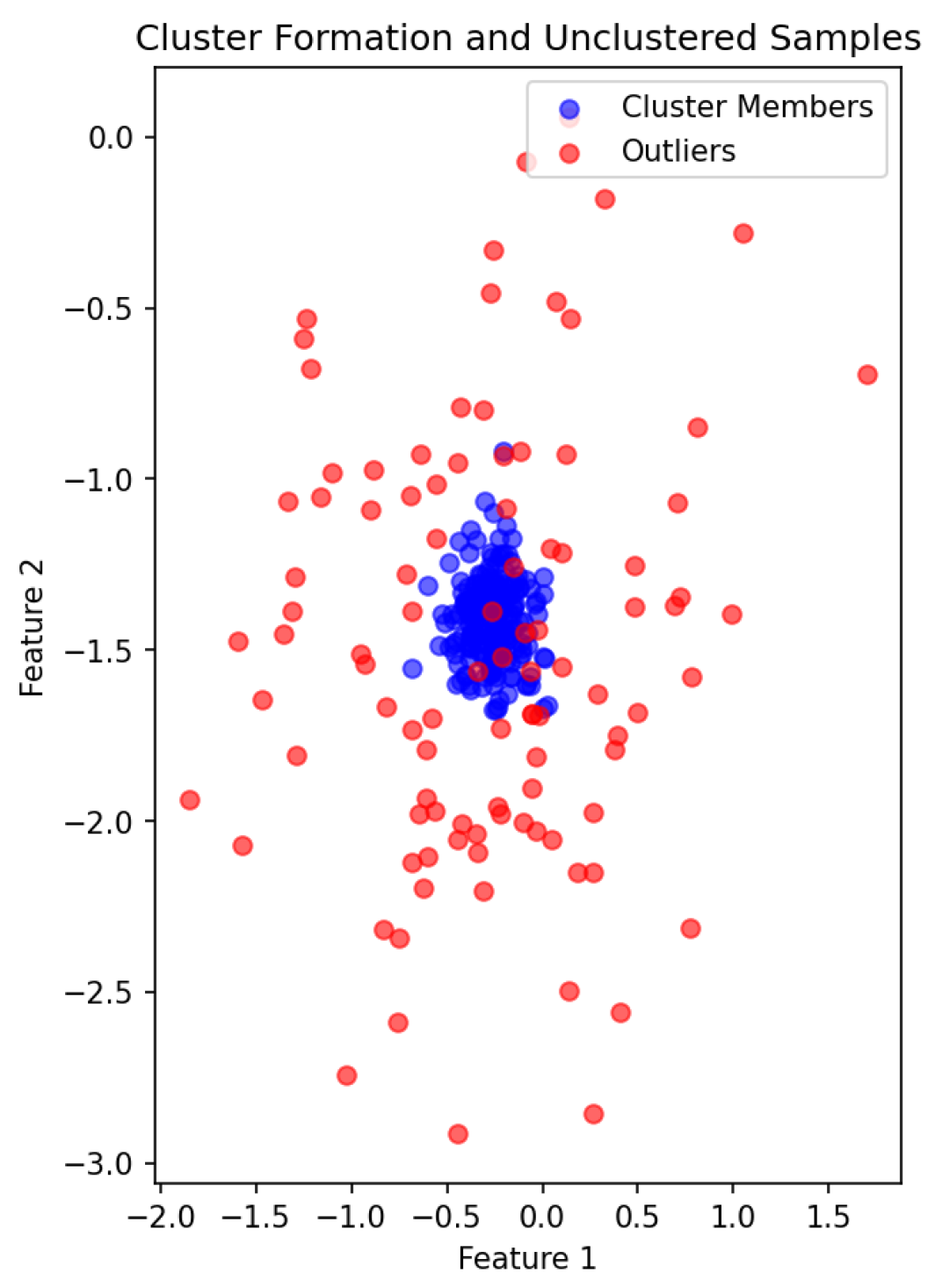
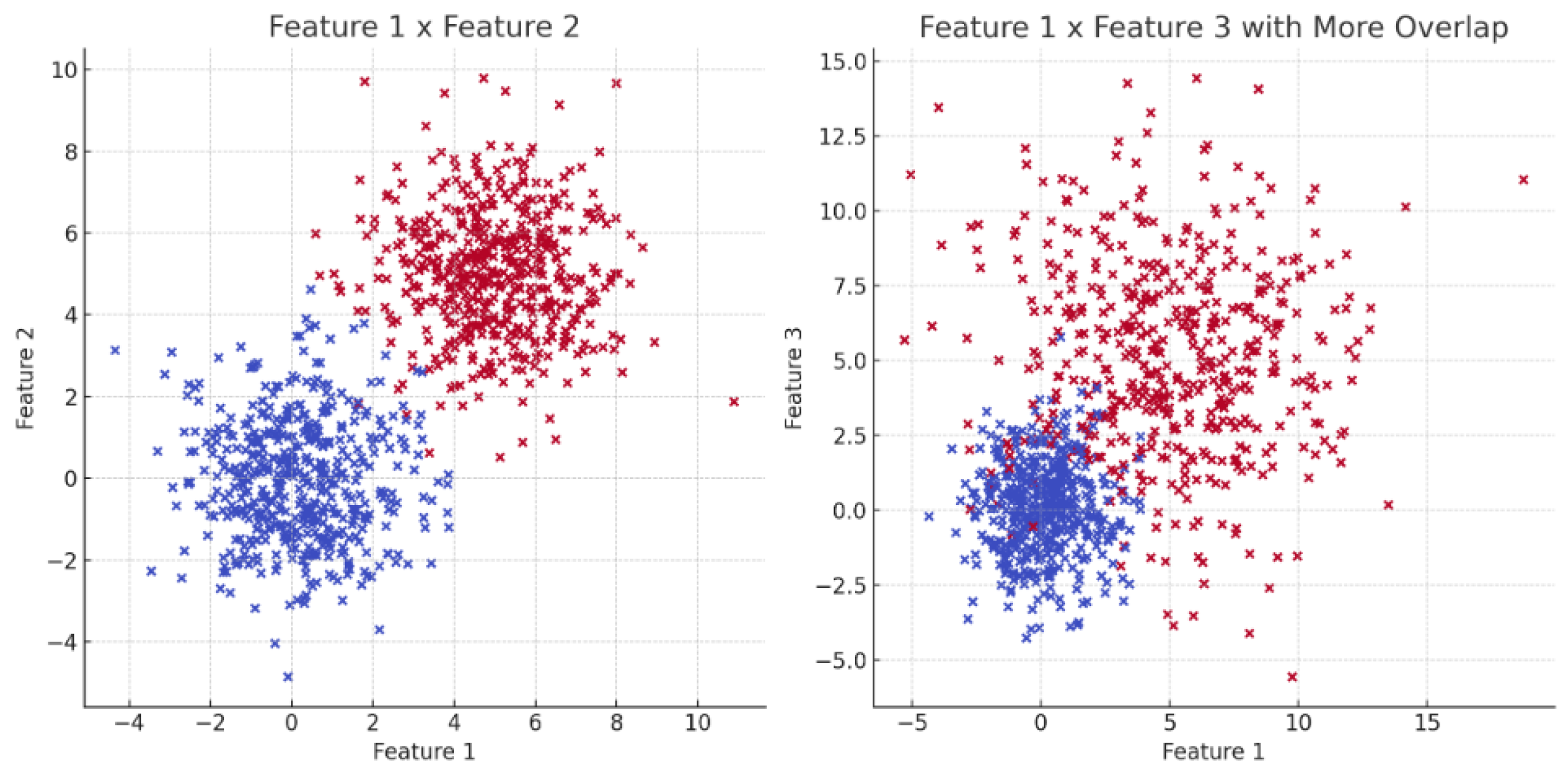





| Area of Application | Approach | Reference |
|---|---|---|
| Time-Series Prediction | Self-organizing PRWNN | [32] |
| Decision Making | Complex Intuitionist Fuzzy | [33] |
| Robotics | Real-time RNN-based Control | [34] |
| Fault Detection | Residual Shrinkage Transformer | [35] |
| Web Services | Swarm Intelligence Search | [36] |
| Nonlinear Systems Control | Recurrent-Fuzzy System | [37] |
| Traffic Flow Prediction | Bibliometric Analysis | [38] |
| Assembly Process | Topic Model-Based NN | [39] |
| Data Streams | Self-adaptive Fuzzy Learning | [40] |
| Cybersecurity | Fuzzy Logic-Based Detection | [41] |
| Ref. | Problem Area | Main Focus | Architecture | Training Technique |
|---|---|---|---|---|
| [47] | Robotic Manipulators | Adaptive control | ANFIS with PID | ANFIS estimator feedback |
| [48] | Regression Problems | Data analysis of complex regression | LFPFC with FCRM clustering | Estimated output-based LFPFC; distance-based LFPFC |
| [49] | Recommendation Systems | Data embedding with DL and FL | Hierarchical fused neural fuzzy and deep network | Fuzzy-driven HIN embedding |
| [50] | Financial Time Series | Linear and nonlinear modeling | Cascaded structure with intuitionist fuzzy model | Intuitionistic fuzzy C-means |
| [51] | Operating Room Performance | Ergonomics in ORs | ANN and DEA | Integrated algorithm using ANN |
| [52] | Fuzzy Research Analysis | Topic modeling | LDA topic models | Latent Dirichlet allocation (LDA) |
| [53] | Robot Control | Efficient and precise control | AMDE-BP-FNN | Adaptive and memetic differential evolution with BP |
| Dataset | Samples | Features |
|---|---|---|
| Iris Dataset [81] | 150 | 4 |
| Mammographic Masses [82] | 961 | 5 |
| Haberman’s Survival [83] | 306 | 3 |
| Blood Transfusion Service Center [84] | 748 | 4 |
| Liver Disorders [85] | 345 | 6 |
| Immunotherapy Dataset [86] | 90 | 7 |
| Cryotherapy Dataset [86] | 90 | 7 |
| Author | Technique | Achievement |
|---|---|---|
| [96] | Clinical Observations | Cognitive Decline Correlation |
| [97] | Multivariate Analysis | Mortality Prediction |
| [98] | Prognostic Analysis | New Model Proposal |
| [99] | Committee-based Machine Learning | Early Prediction of Generalized Infection |
| [100] | Predictive Analysis | Outcome Predictors in Older Adults |
| [101] | SVM, Extreme Gradient Boost | Early Sepsis Prediction |
| Variable Name | Description | Units/Missing Values |
|---|---|---|
| age_years | Age of the patient in years | years/no |
| sex_0male_1female | Gender of the patient. {0: male, 1: female} | no |
| episode_number | Number of prior sepsis episodes | no |
| hospital_outcome_1alive_0dead | Status after 9351 days. {1: alive, 0: dead} | no |
| Name | Mean | Median | Dispersion | Min. | Max. | Missing |
|---|---|---|---|---|---|---|
| Age | 62.74 | 68 | 0.38 | 0 | 100 | 0 (0%) |
| Episode Number | 1.35 | 1 | 0.56 | 1 | 5 | 0 (0%) |
| Hospital Outcome | 1 | - | 0.263 | - | - | 0 (0%) |
| Sex | 0 | - | 0.692 | - | - | 0 (0%) |
| Neuron Type | MFs | Accuracy | F1 Score | Recall | Precision |
|---|---|---|---|---|---|
| AndNeuron | 2 | 0.433 | 0.605 | 1.000 | 0.433 |
| AndNeuron | 3 | 0.667 | 0.722 | 1.000 | 0.565 |
| AndNeuron | 4 | 0.667 | 0.722 | 1.000 | 0.565 |
| OrNeuron | 2 | 1.000 | 1.000 | 1.000 | 1.000 |
| OrNeuron | 3 | 1.000 | 1.000 | 1.000 | 1.000 |
| OrNeuron | 4 | 1.000 | 1.000 | 1.000 | 1.000 |
| UniNeuron | 2 | 0.867 | 0.867 | 1.000 | 0.765 |
| UniNeuron | 3 | 0.667 | 0.615 | 0.615 | 0.615 |
| UniNeuron | 4 | 0.867 | 0.867 | 1.000 | 0.765 |
| Model | Accuracy | Precision | Recall | F1 Score |
|---|---|---|---|---|
| Dataset: Iris | ||||
| GWO-FNN AndNeuron | 1.00 (0.00) | 1.00 (0.00) | 1.00 (0.00) | 1.00 (0.00) |
| GWO-FNN OrNeuron | 1.00 (0.00) | 1.00 (0.00) | 1.00 (0.00) | 1.00 (0.00) |
| GWO-FNN UniNeuron | 1.00 (0.00) | 1.00 (0.00) | 1.00 (0.00) | 1.00 (0.00) |
| Random Forest | 1.00 (0.00) | 1.00 (0.00) | 1.00 (0.00) | 1.00 (0.00) |
| MLP | 1.00 (0.00) | 1.00 (0.00) | 1.00 (0.00) | 1.00 (0.00) |
| Naive Bayes | 1.00 (0.00) | 1.00 (0.00) | 1.00 (0.00) | 1.00 (0.00) |
| Dataset: Mammographic Masses | ||||
| GWO-FNN AndNeuron | 0.54 (0.01) | 1.00 (0.00) | 0.02 (0.01) | 0.04 (0.03) |
| GWO-FNN OrNeuron | 0.83 (0.01) | 0.76 (0.02) | 0.92 (0.00) | 0.83 (0.01) |
| GWO-FNN UniNeuron | 0.74 (0.02) | 0.73 (0.03) | 0.70 (0.02) | 0.72 (0.02) |
| Random Forest | 0.84 (0.00) | 0.83 (0.00) | 0.83 (0.00) | 0.83 (0.00) |
| MLP | 0.88 (0.00) | 0.87 (0.00) | 0.87 (0.00) | 0.87 (0.00) |
| Naive Bayes | 0.84 (0.00) | 0.79 (0.00) | 0.91 (0.00) | 0.84 (0.00) |
| Dataset: Haberman | ||||
| GWO-FNN AndNeuron | 1.00 (0.00) | 1.00 (0.00) | 1.00 (0.00) | 1.00 (0.00) |
| GWO-FNN OrNeuron | 1.00 (0.00) | 1.00 (0.00) | 1.00 (0.00) | 1.00 (0.00) |
| GWO-FNN UniNeuron | 1.00 (0.00) | 1.00 (0.00) | 1.00 (0.00) | 1.00 (0.00) |
| Random Forest | 1.00 (0.00) | 1.00 (0.00) | 1.00 (0.00) | 1.00 (0.00) |
| MLP | 1.00 (0.00) | 1.00 (0.00) | 1.00 (0.00) | 1.00 (0.00) |
| Naive Bayes | 1.00 (0.00) | 1.00 (0.00) | 1.00 (0.00) | 1.00 (0.00) |
| Dataset: Transfusion | ||||
| GWO-FNN AndNeuron | 0.78 (0.00) | 0.00 (0.00) | 0.00 (0.00) | 0.00 (0.00) |
| GWO-FNN OrNeuron | 0.77 (0.00) | 0.47 (0.01) | 0.25 (0.03) | 0.32 (0.02) |
| GWO-FNN UniNeuron | 0.76 (0.01) | 0.33 (0.01) | 0.08 (0.04) | 0.12 (0.05) |
| Random Forest | 0.68 (0.00) | 0.29 (0.01) | 0.28 (0.00) | 0.28 (0.00) |
| MLP | 0.78 (0.00) | 0.51 (0.01) | 0.31 (0.01) | 0.39 (0.01) |
| Naive Bayes | 0.78 (0.00) | 0.50 (0.00) | 0.16 (0.00) | 0.24 (0.00) |
| Dataset: Liver Data | ||||
| GWO-FNN AndNeuron | 1.00 (0.00) | 1.00 (0.00) | 1.00 (0.00) | 1.00 (0.00) |
| GWO-FNN OrNeuron | 1.00 (0.00) | 1.00 (0.00) | 1.00 (0.00) | 1.00 (0.00) |
| GWO-FNN UniNeuron | 1.00 (0.00) | 1.00 (0.00) | 1.00 (0.00) | 1.00 (0.00) |
| Random Forest | 1.00 (0.00) | 1.00 (0.00) | 1.00 (0.00) | 1.00 (0.00) |
| MLP | 1.00 (0.00) | 1.00 (0.00) | 1.00 (0.00) | 1.00 (0.00) |
| Naive Bayes | 1.00 (0.00) | 1.00 (0.00) | 1.00 (0.00) | 1.00 (0.00) |
| Dataset: Immunotherapy | ||||
| GWO-FNN AndNeuron | 0.78 (0.00) | 0.78 (0.00) | 1.00 (0.00) | 0.88 (0.00) |
| GWO-FNN OrNeuron | 0.74 (0.07) | 0.82 (0.02) | 0.86 (0.10) | 0.84 (0.05) |
| GWO-FNN UniNeuron | 0.80 (0.02) | 0.79 (0.02) | 1.00 (0.00) | 0.88 (0.01) |
| Random Forest | 0.80 (0.02) | 0.82 (0.02) | 0.95 (0.00) | 0.88 (0.01) |
| MLP | 0.72 (0.02) | 0.80 (0.02) | 0.86 (0.00) | 0.83 (0.01) |
| Naive Bayes | 0.59 (0.00) | 0.75 (0.00) | 0.71 (0.00) | 0.73 (0.00) |
| Dataset: Cryotherapy | ||||
| GWO-FNN AndNeuron | 1.00 (0.00) | 1.00 (0.00) | 1.00 (0.00) | 1.00 (0.00) |
| GWO-FNN OrNeuron | 1.00 (0.00) | 1.00 (0.00) | 1.00 (0.00) | 1.00 (0.00) |
| GWO-FNN UniNeuron | 1.00 (0.00) | 1.00 (0.00) | 1.00 (0.00) | 1.00 (0.00) |
| Random Forest | 1.00 (0.00) | 1.00 (0.00) | 1.00 (0.00) | 1.00 (0.00) |
| MLP | 1.00 (0.00) | 1.00 (0.00) | 1.00 (0.00) | 1.00 (0.00) |
| Naive Bayes | 1.00 (0.00) | 1.00 (0.00) | 1.00 (0.00) | 1.00 (0.00) |
| Source | sum_sq | df | F | PR (>F) |
|---|---|---|---|---|
| C(Model) | 0.083 | 5 | 78.682 | 2.038 × |
| C(Dataset) | 6.046 | 6 | 4797.360 | 0.000 × |
| C(Model):C(Dataset) | 1.055 | 30 | 167.438 | 2.708 × |
| Residual | 0.079 | 378 | NaN | NaN |
| Test | Statistics | p-Value |
|---|---|---|
| Shapiro–Wilk | 0.368 | 1.16 × |
| Levene’s | 0.953 | 0.447 |
| A | B | Mean (A) | Mean (B) | Diff | se | T | p-Tukey | Hedges |
|---|---|---|---|---|---|---|---|---|
| FNN AndNeuron | FNN OrNeuron | 0.870 | 0.913 | −0.043 | 0.022 | −1.930 | 0.385 | −0.305 |
| FNN AndNeuron | FNN UniNeuron | 0.870 | 0.903 | −0.033 | 0.022 | −1.505 | 0.661 | −0.231 |
| FNN AndNeuron | MLP | 0.870 | 0.902 | −0.031 | 0.022 | −1.424 | 0.713 | −0.212 |
| FNN AndNeuron | Naive Bayes | 0.870 | 0.888 | −0.018 | 0.022 | −0.796 | 0.968 | −0.111 |
| FNN AndNeuron | Random Forest | 0.870 | 0.904 | −0.034 | 0.022 | −1.520 | 0.651 | −0.230 |
| FNN OrNeuron | FNN UniNeuron | 0.913 | 0.903 | 0.010 | 0.022 | 0.425 | 0.998 | 0.087 |
| FNN OrNeuron | MLP | 0.913 | 0.902 | 0.011 | 0.022 | 0.507 | 0.996 | 0.098 |
| FNN OrNeuron | Naive Bayes | 0.913 | 0.888 | 0.025 | 0.022 | 1.134 | 0.867 | 0.197 |
| FNN OrNeuron | Random Forest | 0.913 | 0.904 | 0.009 | 0.022 | 0.410 | 0.999 | 0.081 |
| FNN UniNeuron | MLP | 0.903 | 0.902 | 0.001 | 0.022 | 0.081 | 1.000 | 0.015 |
| FNN UniNeuron | Naive Bayes | 0.903 | 0.888 | 0.015 | 0.022 | 0.709 | 0.981 | 0.119 |
| FNN UniNeuron | Random Forest | 0.903 | 0.904 | −0.001 | 0.022 | −0.015 | 1.000 | −0.003 |
| MLP | Naive Bayes | 0.902 | 0.888 | 0.014 | 0.022 | 0.628 | 0.989 | 0.101 |
| MLP | Random Forest | 0.902 | 0.904 | −0.002 | 0.022 | −0.096 | 1.000 | −0.017 |
| Naive Bayes | Random Forest | 0.888 | 0.904 | −0.016 | 0.022 | −0.724 | 0.979 | −0.119 |
| Model | Accuracy | Precision | Recall | F1 Score |
|---|---|---|---|---|
| FNN AndNeuron | 0.927 | 0.962 | 1.000 | 0.927 |
| FNN OrNeuron | 0.927 | 0.927 | 1.000 | 0.962 |
| FNN UniNeuron | 0.927 | 0.926 | 1.000 | 0.962 |
| Random Forest | 0.926 | 0.926 | 1.000 | 0.962 |
| MLP | 0.926 | 0.926 | 1.000 | 0.962 |
| Naive Bayes | 0.926 | 0.926 | 1.000 | 0.962 |
| SVM | 0.926 | 0.926 | 1.000 | 0.962 |
| Logistic Regression | 0.926 | 0.926 | 1.000 | 0.962 |
| Rule | Conseq. | Situation |
|---|---|---|
| IF Age is MF1 (0.51) AND Sex is MF1 (0.41) AND Ep. number is MF1 (0.37) | 12.84 | Alive |
| IF Age is MF1 (0.43) AND Sex is MF1 (0.21) AND Ep. number is MF2 (0.09) | 1.98 | Alive |
| IF Age is MF1 (0.58) AND Sex is MF2 (0.77) AND Ep. number is MF1 (0.45) | 15.42 | Alive |
| IF Age is MF1 (0.39) AND Sex is MF2 (0.63) AND Ep. number is MF2 (0.33) | 3.07 | Alive |
| IF Age is MF2 (0.19) AND Sex is MF1 (0.62) AND Ep. number is MF1 (0.55) | −4.11 | Deceased |
| IF Age is MF2 (0.48) AND Sex is MF1 (0.43) AND Ep. number is MF2 (0.86) | 0.71 | Alive |
| IF Age is MF2 (0.12) AND Sex is MF2 (0.91) AND Ep. number is MF1 (0.88) | −3.24 | Deceased |
| IF Age is MF2 (0.34) AND Sex is MF2 (0.68) AND Ep. number is MF2 (0.47) | 1.37 | Alive |
| Rule | Conseq. | Situation |
|---|---|---|
| IF Age is MF1 (0.33) OR Sex is MF1 (0.26) OR Ep. number is MF1 (0.18) | 1.17 | Alive |
| IF Age is MF1 (0.15) OR Sex is MF1 (0.64) OR Ep. number is MF2 (0.85) | 1.61 | Alive |
| IF Age is MF1 (0.23) OR Sex is MF2 (0.50) OR Ep. number is MF1 (0.77) | 1.45 | Alive |
| IF Age is MF1 (0.11) OR Sex is MF2 (0.90) OR Ep. number is MF2 (0.61) | 4.98 | Alive |
| IF Age is MF2 (0.44) OR Sex is MF1 (0.69) OR Ep. number is MF1 (0.72) | 0.38 | Alive |
| IF Age is MF2 (0.28) OR Sex is MF1 (0.52) OR Ep. number is MF2 (0.33) | −0.81 | Deceased |
| IF Age is MF2 (0.76) OR Sex is MF2 (0.38) OR Ep. number is MF1 (0.64) | −0.41 | Deceased |
| IF Age is MF2 (0.41) OR Sex is MF2 (0.51) OR Ep. number is MF2 (0.13) | −1.21 | Deceased |
| Rule | Conseq. | Situation |
|---|---|---|
| IF Age is MF1 (0.59) OR Sex is MF1 (0.39) OR Ep. number is MF1 (0.21) | 0.41 | Alive |
| IF Age is MF1 (0.37) AND Sex is MF1 (0.76) AND Ep. number is MF2 (0.84) | −0.11 | Deceased |
| IF Age is MF1 (0.16) AND Sex is MF2 (0.48) AND Ep. number is MF1 (0.87) | 0.19 | Alive |
| IF Age is MF1 (0.68) AND Sex is MF2 (0.79) AND Ep. number is MF2 (0.50) | 0.63 | Alive |
| IF Age is MF2 (0.62) OR Sex is MF1 (0.29) OR Ep. number is MF1 (0.47) | −0.07 | Imprecise |
| IF Age is MF2 (0.66) AND Sex is MF1 (0.37) AND Ep. number is MF2 (0.38) | −0.03 | Imprecise |
| IF Age is MF2 (0.36) OR Sex is MF2 (0.74) OR Ep. number is MF1 (0.91) | −0.41 | Deceased |
| IF Age is MF2 (0.11) AND Sex is MF2 (0.49) AND Ep. number is MF2 (0.73) | 0.05 | Imprecise |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
de Campos Souza, P.V.; Sayyadzadeh, I. GWO-FNN: Fuzzy Neural Network Optimized via Grey Wolf Optimization. Mathematics 2025, 13, 1156. https://doi.org/10.3390/math13071156
de Campos Souza PV, Sayyadzadeh I. GWO-FNN: Fuzzy Neural Network Optimized via Grey Wolf Optimization. Mathematics. 2025; 13(7):1156. https://doi.org/10.3390/math13071156
Chicago/Turabian Stylede Campos Souza, Paulo Vitor, and Iman Sayyadzadeh. 2025. "GWO-FNN: Fuzzy Neural Network Optimized via Grey Wolf Optimization" Mathematics 13, no. 7: 1156. https://doi.org/10.3390/math13071156
APA Stylede Campos Souza, P. V., & Sayyadzadeh, I. (2025). GWO-FNN: Fuzzy Neural Network Optimized via Grey Wolf Optimization. Mathematics, 13(7), 1156. https://doi.org/10.3390/math13071156







