Abstract
Financial stability analysis requires volatility modeling, especially in emerging nations where pension fund systems are very vulnerable to macrofinancial risks. In order to examine the volatility dynamics of Romania’s private pension system, this study uses daily net asset value (NAV) data from 2012 to 2024 to evaluate four GARCH-type models: standard GARCH (sGARCH), exponential GARCH (EGARCH), Glosten–Jagannathan–Runkle GARCH (GJR-GARCH), and component GARCH (C-GARCH). The analysis includes domestic and international equity indices (BET, STOXX), government bond yields (ROMGB 10Y, ROMANI 5Y), short-term interbank rates (ROBOR ON), and exchange rate fluctuations (RON/EUR). Current findings indicate that EGARCH captures asymmetric fluctuations in pension fund performance, where positive shocks generate larger increases in volatility than negative ones, highlighting an atypical asymmetry pattern. Furthermore, the stabilizing effects of government bonds are overshadowed by stock market behavior, which becomes the primary driver of risk. Fluctuations in exchange rates further increase volatility, especially in markets vulnerable to external disturbances. The findings offer empirical evidence for the necessity of more cautious risk management approaches and highlight the importance of regulatory oversight in maintaining market confidence. The study underscores the importance of customized allocation frameworks that reduce vulnerability to disruptive events while maintaining prospects for sustained growth. This new dataset contributes to enhancing the comprehension of pension fund volatility within the context of emerging markets. These insights can assist managers and policymakers seeking to fortify retirement outcomes.
Keywords:
emerging markets; pension fund risk; volatility modeling; volatility clustering; asymmetric conditional heteroskedasticity; leverage effects; macro-financial shock transmission; exchange rate pass-through; bond yield spillover; risk propagation MSC:
62M10; 62P05; 91G80; 91G70
1. Introduction
The stability of private pension funds is a key concern in both developed and emerging economies, as they play a crucial role in ensuring financial security for retirees [1], particularly as public pension systems face increasing demographic and economic pressures. Market volatility, driven by macroeconomic fluctuations, stock market performance, and bond yields, significantly affects pension fund valuations [2,3,4]. Understanding these dynamics is particularly important in emerging markets like Romania, where private pension portfolios are exposed to diverse financial risks. Given Romania’s growing integration into European financial markets, pension funds allocate substantial portions of their portfolios to government bonds, equities, and foreign currency assets, making them vulnerable to macroeconomic shocks, interest rate fluctuations, and geopolitical risks, such as post-pandemic economic recovery and the war in Ukraine.
A key measure of pension fund performance is the net asset value (NAV), which reflects the aggregated market valuation of pension fund assets per unit [5,6]. Changes in the NAV depend on the interplay of multiple economic factors, including equity market returns, bond yields, interest rate movements, and currency exchange rates. The volatility of the NAV can indicate the level of risk pension funds face, making it an essential component of financial stability and portfolio risk assessment [7].
While previous studies have examined pension fund risk exposures and market volatility [8,9,10], limited research specifically addresses the NAV volatility of Romania’s private pension system. Many existing studies focus on broad macroeconomic indicators, often overlooking the intricate financial linkages that drive NAV fluctuations. Traditional risk models often assume constant volatility, yet pension funds are exposed to time-varying and asymmetric financial shocks [11]. GARCH-type models provide a robust econometric framework for capturing volatility clustering, making them well-suited for pension fund risk analysis [12].
To address these gaps, this study investigates the volatility dynamics of Romania’s private pension system, focusing on the following key research questions:
- Which GARCH model provides the most accurate forecast for pension fund NAV volatility in Romania?
- To what extent do stock market fluctuations, bond yields, interbank interest rates, and exchange rate movements impact pension fund NAV volatility?
- Does NAV volatility in Romania’s private pension system exhibit asymmetric responses to positive and negative financial shocks?
- What are the implications of the identified volatility patterns for pension fund managers, regulators, and policymakers?
Based on prior research and economic theory, the study proposes the following hypotheses:
- H1: The EGARCH model outperforms other GARCH-type models in forecasting NAV volatility in Romania’s private pension system.
- H2: Macroeconomic and financial variables, specifically stock market indices (BET, STOXX), government bond yields (ROMGB 10Y, ROMANI 5Y), interbank interest rates (ROBOR ON), and exchange rate fluctuations (EUR/RON), significantly influence NAV volatility in Romania’s private pension system.
- H3: Pension fund NAV volatility exhibits asymmetric responses to financial shocks, where negative shocks increase volatility more than positive shocks of the same magnitude.
- H4: The volatility patterns observed during systemic events, such as the COVID-19 pandemic, emphasize the need for enhanced risk management and regulatory vigilance regarding systemic vulnerabilities.
To test these hypotheses, the study applies and compares four GARCH models to assess NAV volatility in Romania’s private pension system. Standard GARCH (sGARCH) serves as the baseline model, capturing volatility clustering and persistence but assuming a symmetric response to positive and negative market shocks [13]. Exponential GARCH (EGARCH) accounts for asymmetric volatility, making it particularly relevant given the stronger impact of market downturns on pension assets. Unlike standard GARCH, EGARCH allows for negative shocks to increase volatility more than positive shocks of the same magnitude. Glosten–Jagannathan–Runkle GARCH (GJR-GARCH) introduces leverage effects, distinguishing between positive and negative shocks by penalizing negative returns more heavily, thereby improving downside risk estimates. Component GARCH (C-GARCH) decomposes short-term fluctuations from long-term structural trends, making it suitable for analyzing persistent volatility risks and identifying how temporary shocks differ from enduring market trends.
By systematically evaluating these models’ performance, the study identifies the most robust approach for capturing time-varying volatility, leverage effects, and structural market shifts. The findings contribute to pension fund risk analysis, offering empirical insights that support enhanced portfolio resilience, regulatory frameworks, and long-term financial sustainability.
2. Literature Review
Volatility is one of the most important characteristics of the financial markets that determine the prices of assets, as well as the total risk of a portfolio and the overall investment stability. In the case of pension funds, volatility dynamics are quite different owing to the regulatory issues, the long-drawn investment periods, and the preference for fixed income assets [14]. Unlike hedge funds or mutual funds, pension funds aim to avoid volatility rather than emphasize high short-term returns; therefore, managing market risk is of significant interest. Previous studies have also established that pension fund NAV has different volatility behaviors compared to normal equity portfolios [15]. This paper goes further on this theoretical basis by exploring which macroeconomic and financial factors lead to NAV variations in Romania’s private pension system. The role of pension funds in stock markets has increased rapidly in the past, and their investment policies affect market efficiency and volatility. Thomas et al. [16] investigated the impact of pension fund equity allocations on stock market volatility across 28 OECD countries from the year 2000 to 2009. Employing random effects models and Prais–Winsten regressions, they observed a negative relationship between the two variables, which was statistically significant. Holzner et al. [17] continued this debate by exploring the link between public and private pension systems and macroeconomic volatility in 35 OECD countries between 1980 and 2018. The study also established that public pension expenditures were stabilizing, while private pension funds tended to increase financial instability, especially in the event of an economic downturn.
Pension funds are private assets that function within a risk-return investment framework, with their investments being in stocks, bonds, and other assets. In their work, Morina and Grima [18] investigated the macroeconomic impact of pension fund assets in transition and developing economies and developed countries during the years 2000–2020. The results of the study show that pension fund assets are beneficial for economic growth, but the magnitude of this effect depends on the quality of regulation and the level of financial market development. Transition economies have weak governance, and pension funds are more susceptible to financial turmoil and foreign shocks; therefore, sound policies and flexible investment plans are necessary for economic growth.
Paraschiv et al. [19] examined the pension system of Romania, discussing financial viability issues, risks, and imbalances in the system. They point out that the pillar I is under significant fiscal pressure owing to demographic changes and the increasing dependency rate and distinguish pillars II and III as being important for long-term financial health. The study also notes macroeconomic risks such as interest rate movements, market risks such as stock price volatility, and asset price risks such as inflation risk. It also points out that the Romanian pension funds are still rather dependent on government bonds and domestic equities and thus vulnerable to the shocks from the region. In this regard, the authors recommend the following measures: asset diversification, slow rise in the retirement age, and enhanced risk management and governance. Cristea and Siminica [20] highlight the critical role of macroeconomic variables in shaping the NAV of Romania’s private pension funds. Using multiple linear regression, their findings confirm that the RON/EUR exchange rate has the strongest positive correlation with NAV (0.832), while the BET-C index and benchmark interest rates exhibit inverse correlations. This suggests that pension fund performance is highly sensitive to currency fluctuations and stock market dynamics, emphasizing the need for adaptive investment strategies. Robu et al., [21] further examined the effect of pension market concentration on revenues, demonstrating that larger pension funds tend to generate higher returns due to economies of scale. Similarly, Cristea et al. [22] confirmed that fund size correlates with performance, emphasizing the importance of economies of scale in driving pension fund efficiency. Darmaz-Guzun [23] analyzed the investment behavior of Romania’s pillar II private pension funds, assessing their role in the capital market and the financial instruments they utilize. Using linear regression models on data from May 2008 to December 2017, the study found a significant correlation between the value of investments and the total assets of these funds, highlighting their impact on market dynamics.
Government bond yields, particularly ROMGB 10Y and ROMANI 5Y, provide stability to pension portfolios, and Seulean and Mos [24] highlight their role in ensuring long-term fund sustainability. However, Robu et al. [21] note that yield fluctuations can impact fund revenues, affecting overall financial stability. Short-term liquidity indicators, such as ROBOR ON, also play a key role, with Cristea et al. [25] demonstrating how interest rate shifts affect pension fund liquidity and asset allocation decisions. Chodorow-Reich [26] similarly emphasizes that monetary policy rate changes significantly impact institutional investors, including pension funds, influencing NAV volatility.
Exchange rate movements (EUR/RON) are another crucial determinant of pension fund performance. Cristea and Siminica [20] found that the RON/EUR exchange rate had the strongest positive correlation (0.832) with NAV, suggesting that currency fluctuations significantly affect fund valuations. Peksevim and Ercan [27] examined European pension funds and confirmed that exchange rate fluctuations influence financial stability, reinforcing similar findings from Romanian studies. Cristea et al. [25] further explored the impact of macroeconomic factors on NAV, concluding that currency exchange rate shifts and reference interest rates are among the most influential variables affecting pension fund performance. Dumiter et al. [28] extended this analysis to Central and Eastern European pension systems, demonstrating that macroeconomic stability is crucial for pension fund sustainability.
Research on pension fund management highlights key risks related to investment strategies, financial stability, and market exposure. Pension funds have increasingly shifted toward higher-risk portfolios, particularly equities and alternative assets like private equity, hedge funds, and real estate, to achieve higher returns [29,30,31]. While diversification reduces volatility, it also amplifies financial vulnerabilities, as market fluctuations impact fund valuations. Additionally, increased reliance on alternative assets introduces liquidity constraints, making it difficult to convert investments into cash during market downturns. Liquidity mismatches between long-term obligations and short-term assets further heighten systemic risks, emphasizing the need for strong risk management and regulatory oversight [32]. These findings are relevant for Romania’s pension system, where Pillar II and Pillar III funds are adopting similar investment. The increasing complexity of financial markets has driven the adoption of advanced econometric models to better assess and manage investment risk. Recent studies have particularly expanded the application of generalized autoregressive conditional heteroskedasticity (GARCH) models in analyzing pension fund volatility. Researchers have demonstrated their effectiveness in mitigating financial instability, with Doan et al. [33] showing how volatility targeting strategies help reduce investment risk for insurers and pension funds, particularly in equity, balanced, and target-date portfolios during periods of market stress like the COVID-19 pandemic. Similarly, Bukwimba [34] applied GARCH models to Tanzanian pension funds, highlighting the impact of volatility clustering on long-term stability and the importance of risk-adjusted returns.
Although the Financial Supervisory Authority of Romania [35] does not directly engage in econometric modeling, its monthly market surveillance reports offer valuable contextual insights into the volatility of Romanian financial markets. The December 2024 edition highlights how political instability, such as the annulled presidential election, and persistent macroeconomic imbalances, including elevated inflation and stagnant GDP growth, have contributed to sharp fluctuations in domestic asset prices and exchange rates. While not explicitly applying GARCH-family models, the FSA’s narrative reinforces key themes in volatility modeling literature, particularly the importance of incorporating macroeconomic shocks and policy uncertainty as exogenous factors influencing conditional variance.
While GARCH models have become a standard tool for modeling financial volatility, they are not without limitations. Traditional GARCH models assume symmetric volatility responses to positive and negative shocks, which may not fully capture financial market dynamics [36]. To address these shortcomings, researchers have explored various extensions. Exponential GARCH (EGARCH), introduced by Nelson [37], models asymmetric effects, capturing the tendency for negative market shocks to generate greater volatility than positive ones. Component GARCH (C-GARCH), developed by Engle and Lee [38], decomposes volatility into short-term and long-term components, allowing for a more structured representation of persistent financial risks. GJR-GARCH, proposed by Glosten et al. [39], extends the standard GARCH framework by incorporating leverage effects, acknowledging that negative shocks have a stronger impact on future volatility than positive shocks of the same magnitude. The sGARCH (standard GARCH) model, originally formulated by Bollerslev [36], serves as the foundational model for capturing volatility clustering, where periods of high volatility are likely to be followed by continued turbulence. This study applies sGARCH, EGARCH, GJR-GARCH, and C-GARCH models to examine the volatility dynamics of Romania’s private pension system. sGARCH establishes a baseline for volatility persistence, EGARCH captures asymmetry in market fluctuations, GJR-GARCH accounts for leverage effects, and C-GARCH differentiates between short- and long-term volatility components. Together, these models offer a robust analytical framework for evaluating financial risk and predicting NAV fluctuations, enhancing the understanding of volatility patterns in pension fund management. However, GARCH models remain widely used due to their interpretability and computational efficiency in large-scale financial applications.
Despite extensive research on pension fund risk management and market volatility, several gaps remain in the literature, particularly regarding systemic risks, liquidity constraints, and the integration of advanced risk models. While existing studies have analyzed the relationship between pension fund investments and financial market volatility, few focus specifically on the volatility of Romania’s private pension system, despite its importance for financial stability. Additionally, while GARCH models have been widely applied in risk assessment, most studies rely on standard GARCH frameworks, which may not fully capture the asymmetric effects of market shocks on net asset value volatility. More advanced econometric models could provide a more accurate representation of pension fund risk exposure by incorporating nonlinear volatility patterns and asymmetric market responses.
Another underexplored area is the impact of macroeconomic factors on pension fund volatility. Although macroeconomic fluctuations influence interest rates, inflation, and market returns, their specific effects on private pension fund stability remain insufficiently examined. Given the increasing integration of private pension funds into broader financial markets, understanding these dynamics is essential for developing robust risk management strategies.
By addressing these gaps, this study contributes to the literature by (i) providing the first detailed econometric analysis of NAV volatility in Romania’s private pension system; (ii) comparing multiple GARCH specifications to evaluate the importance of asymmetries and long-term volatility persistence; and (iii) assessing the impact of macroeconomic factors on pension fund NAV, offering policy-relevant insights for fund managers and regulators.
3. Methodology
3.1. Methodological Framework
This study analyzes and predicts the volatility of Romania’s private pension system by testing and comparing four generalized autoregressive conditional heteroskedasticity (GARCH) models: standard GARCH (sGARCH), exponential GARCH (EGARCH), Glosten–Jagannathan–Runkle GARCH (GJR-GARCH), and component GARCH (C-GARCH). The choice of GARCH-type models is driven by their capacity to capture volatility clustering, a recognized characteristic of financial time series [40]. The preliminary data analysis indicates that NAV fluctuations, characterized by high kurtosis and persistent volatility, align with the GARCH framework. EGARCH specifically addresses asymmetric shocks [37], whereas C-GARCH distinguishes between short-term fluctuations and long-term structural trends [38], rendering them especially pertinent for pension fund analysis.
Regulatory supervision, portfolio management, and financial risk assessment all heavily rely on volatility modeling. Understanding fluctuations in net asset value (NAV) is essential for pension funds, as these variations influence asset allocations, contribution policies, and risk mitigation strategies. GARCH models effectively model conditional heteroskedasticity, serving as a robust tool for measuring and predicting the risk dynamics of pension funds. Comparable methodologies have been extensively utilized in the financial econometrics literature [36,41].
This study aims to identify the model that best represents the relationship between NAV, a critical performance indicator for pension funds, and six financial variables that affect its variability. Six variables were extracted from financial data sourced from Bloomberg, including yields for ROMGB 10Y and ROMANI 5Y, ROBOR ON, the value for the BET Index, the STOXX Index, and FX EURRON. The NAV was calculated using the methodology established by the Financial Supervisory Authority (FSA). The six variables, detailed in a subsequent section, are summarized in Table 1. Additionally, the methodology for calculating the average NAV for the Romanian pension system will be detailed subsequentially.

Table 1.
Variable description.
Preliminary statistical tests were performed to confirm stationarity and prevent spurious regressions, thereby ensuring robustness. The augmented Dickey–Fuller (ADF), Phillips–Perron (PP), and Kwiatkowski–Phillips–Schmidt–Shin (KPSS) tests established that all variables exhibit stationarity at levels, thereby affirming their appropriateness for incorporation into the volatility modeling framework [42,43]. The results will be presented in a subsequent section.
Prior to being included in the GARCH framework, all financial variables were log-transformed in order to enhance model estimation and lessen heteroskedasticity. By stabilizing variance, this transformation brings the data distribution into line with conditional volatility modeling’s presumptions. Previous studies [36,44] emphasize the necessity of considering asymmetric return distributions in modeling pension fund volatility, given that extreme market movements significantly affect long-term pension sustainability.
GARCH model parameters are estimated using maximum likelihood estimation (MLE), which optimizes the likelihood of data observation under the postulated conditional distribution [36,45,46]. The likelihood function is numerically adjusted to find the appropriate parameters, ensuring volatility forecasts match observed variations. Conditional heteroskedasticity assumptions are used to estimate model parameters using the log-likelihood function in Equation (1).
where () is the conditional variance of pension fund returns, and () represents the observed NAV fluctuations.
Broyden–Fletcher–Goldfarb–Shanno (BFGS) or Newton–Raphson algorithms are used to maximize the log-likelihood function [46]. Recent volatility modeling advances show that adding exogenous macroeconomic variables like inflation and interest rate shocks to the variance equation improves GARCH model forecasts [47].
Predictive accuracy and information criteria determine model selection. The Akaike information criterion (AIC) (Equation (2)) and Bayesian information criterion (BIC) (Equation (3)) measure model parsimony, while root mean squared error (RMSE) and mean absolute error (MAE) (Equations (4) and (5)) estimate forecast precision [48]. Of note, complexity is penalized more in BIC [49].
where k is the number of estimated parameters.
RMSE is more sensitive to large errors, but MAE is more interpretable; therefore, both metrics are presented to show model correctness.
Three standard diagnostic tests are employed to validate model specification: the Ljung–Box test checks autocorrelation in standardized and squared residuals to ensure the model captures all temporal volatility dependencies [50]; the ARCH-LM test checks remaining ARCH effects to ensure the model adequately explains conditional variance [51]; and the sign bias test evaluates asymmetric volatility responses, confirming that negative shocks induce greater volatility than positive ones [52].
Pension fund volatility predictions may be improved by adding regime-switching volatility tests [53] or long-memory volatility measures [54] to model diagnostics.
We will conclude with a full review of the pension system volatility’s economic and financial drivers and market dangers. Understanding the relationship between macroeconomic data and pension fund volatility improves risk management for policymakers, fund managers, and regulators. Insights into the structural factors that influence long-term pension sustainability will be provided by our findings, which will underscore the necessity of adjusting financial policies to mitigate systemic risks in Romania’s private pension system. Market-based risk indicators like implied volatility measures and credit spreads should improve model prediction accuracy and regulatory decision-making [55].
The flowchart depicted in Figure 1 visually represents the sequential methodology for modeling pension fund volatility, from data acquisition and preprocessing to GARCH model selection, estimation, validation, and forecasting.
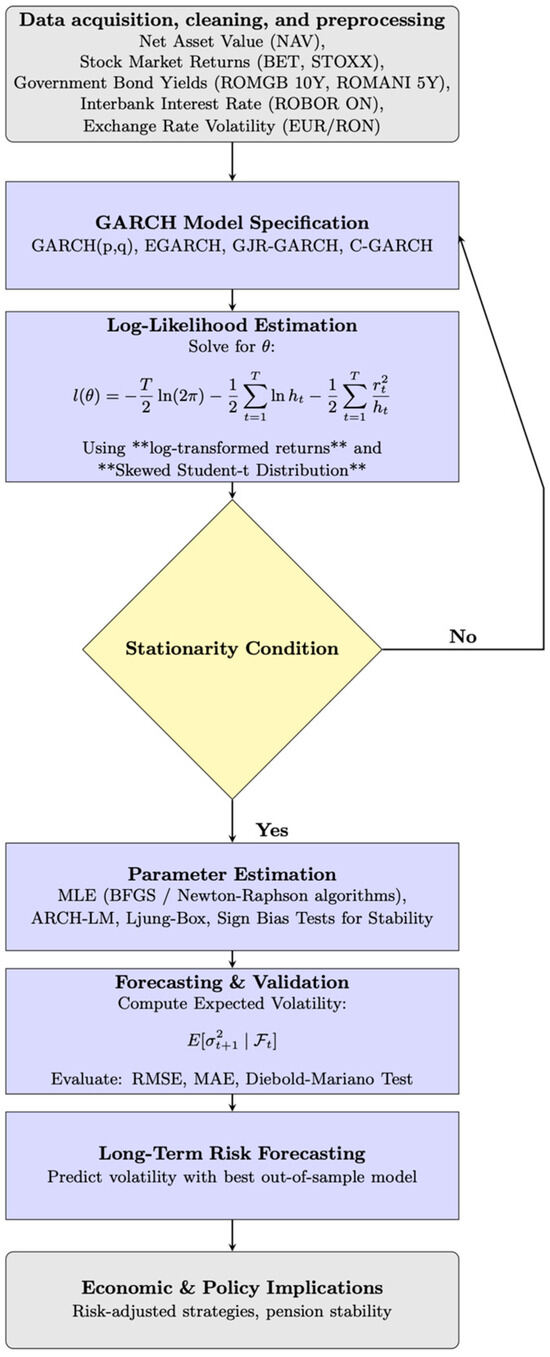
Figure 1.
Methodological pipeline for GARCH-based pension fund volatility modeling. Source: Constructed by the authors in Overleaf using the TikZ package. The log-likelihood function is implemented following the standard GARCH framework, and stationarity conditions are verified through diagnostic tests. The TikZ code used for this figure is available upon request. Note: The purple boxes denote the fundamental modeling and estimation phases of the methodology, encompassing GARCH specification, log-likelihood estimation, and parameter estimation. The yellow diamond signifies a critical decision node—the stationarity condition—that dictates whether the model advances to the subsequent level. The gray boxes represent border phases: the initial data gathering and preprocessing phase, and the concluding stage concerning economic and policy ramifications. The double asterisks (**) are deliberately employed to highlight two essential methodological elements in the log-likelihood estimation process: the usage of log-transformed returns and the implementation of the Skewed Student-t distribution. These were emphasized to attract visual focus on the fundamental assumptions underpinning the volatility modeling approach.
3.2. Data Sources and Variables
This study analyzes Romania’s private pension system volatility using daily measurements from 2012 to 2024. The selected period captures a mature and stable market environment while excluding the early consolidation era (2008–2011), when pension funds made substantial asset allocation and regulatory compliance changes. Deducting the 2008 global financial crisis from long-term volatility trends ensures that the study represents current market circumstances rather than extraordinary financial shocks.
The analysis period incorporates significant market events, including the COVID-19 pandemic. The extreme volatility of the 2020–2021 phase is captured endogenously through the conditional variance structure of the GARCH models, despite the absence of an explicit dummy variable. As seen in the dynamics of the NAV return, this enables the models to take into consideration sudden regime changes and the elevated uncertainty during the pandemic period.
Private pension funds in Romania must mitigate risk and diversify their portfolios under rigorous regulations. Government bonds, equities, short-term deposits, and foreign currency-denominated assets dominate investments due to regulatory restraints and market-driven asset allocation strategies. Financial variables are selected according to Norm No. 11/2011 and Norm No. 14/2015 set by the FSA [56,57], which specify asset class exposure restrictions. Since pension funds must disclose their portfolio structures periodically, NAV variations can be measured empirically.
Net asset value is a pension fund’s asset market value per unit. The key performance metric measures how bond yields, stock market movements, interest rates, and exchange rate volatility affect private pension assets. Norm No. 7/2010 of the Romanian Financial Supervisory Authority (FSA) mandates NAV calculation [58].
The FSA limits pension fund market share to 20% to prevent market concentration. When this level is exceeded, the surplus is dispersed proportionally among the remaining funds based on market shares. This strategy standardizes NAV calculations across the system, preserving regulatory risk diversification and market stability.
Table 1 shows six independent variables that capture macro-financial risk factors affecting NAV volatility. Bloomberg and the FSA provide these data for pension fund portfolios’ main investment categories.
The selected financial factors are consistent with volatility models and widely regarded as significant pension fund performance predictors [59]. Interest rate risk and long-term fixed-income trends can be accurately assessed using ROMGB 10Y and ROMANI 5Y since 60–70% of pension fund assets are government bonds.
Stock market indices are critical for quantifying NAV sensitivity to equities volatility since pension funds invest 20–25% domestically (BET) and 5–10% internationally (STOXX). The ROBOR ON rate affects fund deposit returns and reinvestment strategies due to short-term liquidity.
Finally, pension funds maintain 10–15% of their holdings in EUR, making EURRON a key foreign currency risk factor. RON depreciation raises foreign holdings’ market value, whereas appreciation lowers it, affecting NAV (Financial Supervisory Authority, 2024).
By incorporating these six explanatory factors into the GARCH framework, this study models Romania’s private pension system’s NAV volatility using data to capture domestic and international financial risks.
As a note, all financial time series, including NAV, market indices, and macro-financial variables, were log-transformed prior to analysis to stabilize variance and improve stationarity.
3.3. Mathematical Model Formulation
The following notations are used throughout the paper:
: Pension fund returns at time t
: Conditional variance of returns
: White noise error term, where
α, β, γ: Model parameters, representing volatility dynamics
: Expectation operator, denoting the expected value of a random variable X
Var [X]: Variance operator, capturing dispersion around
: Dummy variable, which equals 1 for negative shocks in GJR-GARCH and 0 otherwise
: Long-term volatility component, used in the C-GARCH model
3.3.1. sGARCH-MV
The standard GARCH (sGARCH) model, introduced by Bollerslev [36], extends Engle’s [51] ARCH framework by modeling conditional volatility as a function of both past squared residuals and previous volatility:
where is the conditional variance at time t, represents past squared shocks (ARCH effect), and captures volatility persistence (GARCH effect). This formulation effectively models volatility clustering and leptokurtic return distributions [60].
The multivariate extension (sGARCH-MV) incorporates exogenous financial variables , allowing macroeconomic factors to influence conditional variance [61,62]:
where represents the contribution of each explanatory variable, including bond yields, stock indices, and interbank rates [63].
3.3.2. EGARCH
The exponential GARCH (EGARCH) model [37] accounts for asymmetric volatility by applying a log transformation to the variance equation, removing the need for non-negativity constraints:
where γ captures the asymmetry in volatility responses. A negative γ indicates a leverage effect, meaning that negative shocks increase volatility more than positive ones. Conversely, a positive γ suggests that positive shocks lead to greater increases in volatility than negative shocks of the same size [64]. The term is standardized to ensure scale-invariant volatility modeling, making the shock impact comparable over time.
The multivariate EGARCH model extends this formulation by incorporating macro-financial variables:
This structure makes EGARCH particularly effective in modeling volatility persistence during financial downturns [65].
3.3.3. GJR-GARCH
The Glosten–Jagannathan–Runkle GARCH (GJR-GARCH) model [39] introduces leverage asymmetry, penalizing negative shocks more than positive ones. This is accomplished via a dummy variable, , which equals 1 if εt−1 < 0 and 0 otherwise:
where γ measures the additional impact of negative shocks on conditional variance. A positive and statistically significant γ confirms the presence of a leverage effect, meaning that volatility increases more after negative returns than after positive ones of equal size [66]. Unlike EGARCH, which models asymmetry through a signed shock term, GJR-GARCH explicitly captures the effect of negative shocks only via a dummy variable.
The multivariate GJR-GARCH model includes exogenous macroeconomic indicators:
This makes GJR-GARCH highly relevant for pension fund volatility, where market downturns create greater financial stress than upswings [67].
3.3.4. C-GARCH
The component GARCH (C-GARCH) model [38] decomposes volatility into short-term fluctuations and long-term structural components:
where represents long-term volatility, evolving as
and governs the persistence of long-term risk, whereas ϕ adjusts for deviations from expected volatility.
We offer formal proof confirming important statistical characteristics of the used GARCH-type models in order to guarantee the theoretical soundness of the volatility modeling framework. Appendix B provides mathematical derivations that illustrate the conditions necessary for stationarity, ergodicity, and volatility clustering, which are essential for the reliability of the estimated processes in capturing pension fund risk dynamics.
In all GARCH-type models estimated in this study, the conditional mean equation is provided as a constant. This choice is consistent with conventional practice in volatility modeling, where the primary attention lies on the second-moment dynamics. Diagnostic testing demonstrated that incorporating ARMA elements in the mean equation did not appreciably boost model performance or residual qualities, justifying the choice of a parsimonious constant-mean specification.
Moreover, the GARCH (1,1) structure is used to implement all of the volatility models in this study. This specification is a standard in financial econometrics and is highly respected for its capacity to capture volatility clustering with little parameterization [36,45]. Preliminary testing of alternate lag structures, such as GARCH (2,1) or GARCH (1,2), revealed no significant enhancements in model fit or forecast accuracy [41]. Conversely, GARCH (1,1) exhibited strong performance and convergence stability, especially within the EGARCH and C-GARCH frameworks, hence affirming its appropriateness for the pension NAV environment.
4. Results
4.1. Exploratory Data Analysis
This section provides an initial assessment of market trends and volatility dynamics through statistical analysis and key visual representations. The figures presented illustrate the evolution of NAV and government bond yields (ROMGB 10Y, ROMANI 5Y), offering insights into long-term trends and short-term fluctuations. Additional figures, including stock market indices (BET, STOXX) and the histogram of NAV log returns, are presented in Appendix A to streamline the mathematical analysis.
4.1.1. Market Trends and Volatility Dynamics
The average NAV evolution (Figure 2) exhibits a strong long-term growth trajectory, with an observable exponential trend, suggesting the compounding effect of reinvested earnings, capital appreciation, and consistent contributions. Despite the overall upward movement, temporary declines in 2018, 2020, and 2022 align with major financial disruptions, including the COVID-19 crisis, inflationary pressures, and geopolitical uncertainties [35]. However, NAV consistently recovered, demonstrating market resilience and robust portfolio management.
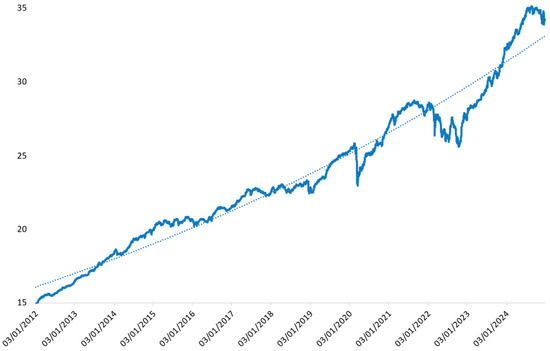
Figure 2.
Average net asset value (NAV) evolution (2012–2024). This chart illustrates the average daily NAV of Romania’s private pension funds, measured in RON per unit. Data were compiled by the authors using official records from the Financial Supervisory Authority (FSA). Note: The solid blue line represents the daily historical NAV data (2012–2024), while the dotted blue line depicts a simple linear trend fit, illustrating the overall upward trajectory in the NAV over time.
The government bond yield trends (Figure 3) further highlight volatility dynamics. The ROMGB 10Y yield declined from 7.36% in 2012 to 3.0% in 2020, reflecting lower interest rates and improved credit conditions. However, a sharp reversal in 2022 saw yields spike above 8.0% due to inflationary pressures and central bank policy shifts. Similarly, the ROMANI 5Y yield dropped from 6.05% to below 1.0% (2017–2021) before surging past 4.0% in 2022, mirroring global bond market trends. These fluctuations in bond yields are particularly relevant for pension funds, which allocate 60–70% of assets to fixed-income instruments [59]. While higher yields increase returns, they also reduce the market value of existing bonds, directly impacting NAV volatility.
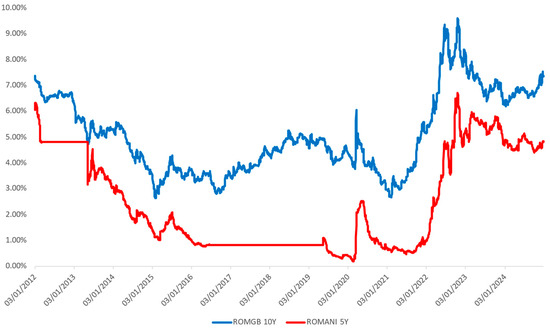
Figure 3.
Evolution of Romanian sovereign bond yields (2012–2024). The chart displays the yield trends for two major Romanian government securities: ROMGB 10Y (10-year domestic currency bonds) and ROMANI 5Y (5-year euro-denominated eurobonds). Yields are expressed as annual percentages. Source: Compiled by the authors using data from Bloomberg.
For completeness, the evolution of stock market indices (BET, STOXX) is provided in Appendix A, Figure A1. Additionally, a histogram of NAV log returns (Appendix A, Figure A2) illustrates its fat-tailed distribution, justifying the use of a skewed Student’s t-distribution in volatility modeling [68].
4.1.2. Descriptive Statistics
Table 2 presents descriptive statistics for the financial variables included in the study, providing insights into return distributions, volatility, and risk asymmetry.

Table 2.
Descriptive statistics.
The negative skewness of NAV (−1.89) suggests that sharp declines are more frequent than upward movements, reflecting asymmetric risk exposure. Additionally, high kurtosis (21.9) indicates a leptokurtic distribution, where extreme NAV fluctuations occur far more frequently than in a normal distribution. This reinforces the need for robust risk modeling, as pension funds are exposed to tail risks not captured under normality assumptions [68].
These descriptive statistics highlight the heterogeneous risk-return dynamics of pension fund investments, justifying the use of GARCH models to capture extreme market movements and volatility persistence [60].
4.1.3. Preliminary Statistical Tests for Model Selection
To ensure robustness, stationarity tests were conducted using augmented Dickey–Fuller (ADF), Phillips–Perron (PP), and Kwiatkowski–Phillips–Schmidt–Shin (KPSS) tests [69]. Table 3 summarizes the results.

Table 3.
Unit root test results.
4.1.4. Correlation Analysis
The correlation analysis provides insights into the relationships between NAV and key financial variables, as well as potential interdependencies among explanatory variables. NAV exhibits a strong positive correlation with the BET Index (80.75%) and a moderate correlation with the STOXX Index (54.97%), indicating that fluctuations in local and European stock markets influence pension fund performance. Conversely, government bond yields (ROMGB 10Y: −52.34%, ROMANI 5Y: −37.77%) are negatively correlated with NAV, reflecting the inverse relationship between interest rates and fixed-income asset valuation. The ROBOR ON rate (−6.63%) and EUR/RON exchange rate (−6.39%) show weaker relationships, suggesting that short-term interest rates and currency fluctuations have a more limited impact on pension fund NAV.
These findings reinforce the importance of including multiple asset classes in the volatility modeling process, as pension fund performance is affected by both domestic and international financial conditions. A detailed correlation matrix is provided in Appendix A, Table A1, where additional insights into variable interdependencies and potential collinearity risks are discussed.
4.2. Empirical Results of GARCH Models
This section presents the empirical findings from the estimation of four GARCH-type models: sGARCH, EGARCH, GJR-GARCH, and C-GARCH. All models are initially estimated using data from 2012 to 2022, which serves as the training period for model comparison and selection. The results allow for an evaluation of volatility persistence, asymmetric effects, and the influence of financial variables on NAV fluctuations. After identifying the best-performing model, it is re-estimated on the full dataset (2012–2024) to obtain final parameter estimates and generate forward-looking volatility forecasts.
4.2.1. Estimation Results and Volatility Dynamics
Table 4 provides the parameter estimates and significance levels for each model. The β coefficient (GARCH effect) is highly significant across all models, confirming that volatility persistence is a fundamental characteristic of pension fund NAV fluctuations. Notably, EGARCH exhibits the highest persistence (β = 0.9830), indicating that past volatility exerts a prolonged influence on future NAV fluctuations. In contrast, C-GARCH (β = 0.7007) shows lower persistence, reflecting its structure that separates long-term and short-term volatility components.

Table 4.
Parameter estimates of competing GARCH models (2012–2022).
The ARCH effect (α), which captures the sensitivity of volatility to recent shocks, is statistically significant across all models. In the EGARCH model, α is negative (−0.0604), indicating responsiveness to large return fluctuations. The asymmetry parameter γ is positive and significant (0.2082), indicating that volatility responds more strongly to positive shocks than to negative ones. Moreover, in the GJR-GARCH model, the asymmetry coefficient γ is also positive (0.0577) and statistically significant, reflecting an increase in volatility following negative shocks. While both models capture asymmetric effects, the estimated magnitude of asymmetry is higher in EGARCH than in GJR-GARCH.
These findings indicate that equity market fluctuations (BET, STOXX) significantly impact NAV volatility, with domestic stock market movements (γ1 ≈ 0.161) playing a larger role than European market trends (γ2 ≈ 0.041). Government bond yields (ROMGB 10Y, ROMANI 5Y) have a stabilizing effect, as rising yields reduce NAV volatility, consistent with bond investments acting as a hedge against market risk. Short-term interest rate fluctuations (ROBOR ON, γ5) exhibit a weak but significant effect, while exchange rate movements (EURRON, γ6) amplify NAV volatility, highlighting the currency risk exposure in pension fund portfolios.
4.2.2. Model Diagnostic Tests and Performance
To assess model adequacy, we employ Ljung–Box, ARCH-LM, and sign bias tests (Table 5).

Table 5.
Diagnostic test results for GARCH model validity.
The diagnostic tests reveal how well each GARCH model captures pension fund volatility. The Ljung–Box test shows considerable residual autocorrelation in all models (p < 0.01). EGARCH and sGARCH exhibit higher Ljung–Box Q-statistics, indicating some remaining autocorrelation in residuals despite effectively capturing volatility clustering. EGARCH, however, also models asymmetry and performs better in capturing the short-term shock dynamics observed in NAV behavior. C-GARCH, due to its decomposition into permanent and transitory volatility components, shows slightly reduced residual autocorrelation, aligning with its focus on long-term volatility trends. The ARCH-LM test shows that all models capture heteroskedasticity (p > 0.1), indicating no residual ARCH effects. In the sign bias Test, sGARCH demonstrates modest asymmetry (p ≤ 0.05), while EGARCH, GJR-GARCH, and C-GARCH accurately represent asymmetric volatility responses. This confirms that EGARCH is the best model for asymmetric pension fund volatility, C-GARCH is best for long-term risk forecasting, and sGARCH is limited by asymmetric market shocks.
4.3. Model Comparison and Forecasting Performance
To assess model efficiency, we compare Akaike (AIC), Bayesian (BIC), and Hannan–Quinn (HQIC) criteria, along with log-likelihood values (Table 6).

Table 6.
Information criteria and log-likelihood scores for model selection.
EGARCH achieves the highest log-likelihood (16053.83) and lowest AIC (−11.773), BIC (−11.745), and HQIC (−11.763), making it the most efficient model for NAV volatility forecasting.
Forecast accuracy is further evaluated using root mean squared error (RMSE) and mean absolute error (MAE) (Table 7).

Table 7.
Forecast accuracy comparison: RMSE and MAE metrics.
Root mean squared error (RMSE) and mean absolute error (MAE) reveal how well each GARCH model predicts NAV volatility. MAE measures average prediction error more evenly, while RMSE penalizes significant errors more harshly, making it beneficial for measuring the model’s ability to withstand extreme volatility fluctuations. The models differ slightly in forecast accuracy, but their predictive skills differ greatly.
EGARCH has the lowest RMSE (0.00243) and MAE (0.00172) of the investigated models, proving its superior predicting performance (Table 8). This reinforces its strong focus on asymmetric volatility effects, and it particularly underlines that positive financial shocks contribute more to NAV volatility than negative ones of the same magnitude.

Table 8.
Final estimation results of the EGARCH-MV model (2012–2024).
Figure 4 presents a comparison of model-fitted and predicted NAV volatility for the four GARCH-type models (sGARCH, EGARCH, GJR-GARCH, and C-GARCH) for the 2023–2024 validation period. The fitted volatility (solid blue line) denotes the in-sample conditional variance estimates derived from the actual NAV return series, whereas the predicted volatility (dashed red line) is produced by one-step-ahead forecasts from models developed until the conclusion of 2022. This method enables us to evaluate the explanatory and predictive capabilities of each model.
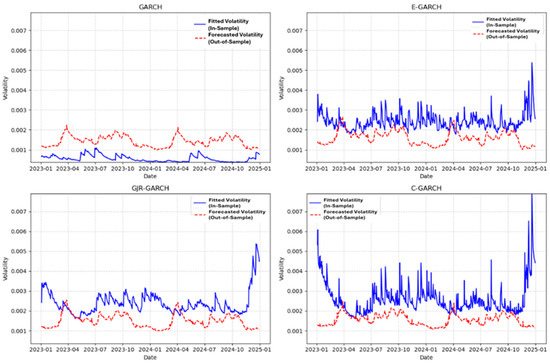
Figure 4.
Fitted vs. forecasted pension NAV volatility from GARCH-type models (2023–2024 validation period). Note: The blue line represents fitted conditional volatility, calculated using actual NAV return data for each respective model. The red dashed line displays one-step-ahead forecasted conditional variance, generated from models estimated up to 2022. The comparison assesses each model’s ability to replicate and anticipate volatility dynamics in Romania’s second-pillar pension system. Source: Authors’ representation; estimations performed in Python software, version 3.13.2.
The graphs demonstrate that EGARCH most successfully captures volatility clustering and extreme market swings, highlighting its robustness in predicting asymmetric reactions to market shocks. GJR-GARCH integrates asymmetry but often underestimates sustained volatility changes, indicating reduced responsiveness in extended high-risk scenarios. C-GARCH, which distinguishes between long-term and short-term volatility components, effectively identifies enduring risk trends but is less responsive to short-term fluctuations. The symmetric sGARCH model fails to account for asymmetries and demonstrates the least correlation with the changing volatility structure of pension fund net asset values.
The findings substantiate the assertion that EGARCH is the most efficacious model for projecting pension risk in real-world scenarios characterized by asymmetry and volatility in market conditions. The log-linear specification and leverage component provide superior modeling of non-normal return dynamics, particularly pertinent in emerging countries such as Romania, where market optimism and pro-cyclical portfolio habits can exacerbate volatility during upswings. C-GARCH is beneficial for trend analysis, whereas GJR-GARCH effectively addresses downside risk asymmetry.
4.4. Forecasting Pension Fund Volatility for 2025–2030
Given its superior performance in capturing volatility clustering and asymmetric risk dynamics, the EGARCH model is employed to forecast conditional NAV volatility over the period 2025–2030. This choice is justified by its strong statistical properties, particularly its ability to account for leverage effects and market shock asymmetries.
The full-sample estimation results (2012–2024) for the EGARCH model are detailed in Table 8, which provides robust statistical validation of its effectiveness in modeling pension fund risk.
The asymmetry parameter (γ = 0.1946) indicates that volatility reacts more strongly to positive shocks than to negative ones, an inversion of the typical leverage effect observed in many financial markets. This result suggests that even during periods of market optimism or rising asset prices, pension fund volatility may increase, highlighting the importance of maintaining risk-aware portfolio strategies regardless of market direction. The BET Index (γ1 = 0.1655) and STOXX Index (γ2 = 0.0402) significantly affect NAV volatility, elevating pension fund performance sensitivity to domestic and European equity markets. Government bonds stabilize volatility, as evidenced by the negative coefficients for ROMGB 10Y (γ3 = −0.0570) and ROMANI 5Y (γ4 = −0.0047), which match with the inverse link between bond rates and fixed-income valuations.
A negative ROBOR ON (γ5 = −0.0002) indicates that short-term interbank interest rate swings may lower NAV volatility, whereas a positive EURRON (γ6 = 0.0322) indicates currency exposure risks in pension fund portfolios.
The statistical diagnostics (presented in Appendix C, Table A2) demonstrate that the EGARCH model captures autocorrelation and volatility persistence while minimizing asymmetric effects and residual heteroskedasticity.
The projected NAV conditional volatility for 2025–2030, derived from the EGARCH model, is illustrated in Figure 5, offering critical insights into anticipated volatility patterns and forthcoming market situations.
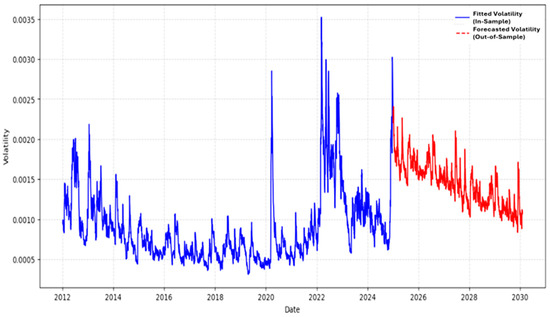
Figure 5.
Forecasted NAV volatility for Romania’s pension funds (2025–2030) using EGARCH-MV. Source: Authors’ representation; estimations performed in R software, version 4.4.2.
5. Discussion
The resilience of Romania’s private pension system is vital for sustaining financial security for retirees and guaranteeing consistency in long-term asset allocation strategies. This study assesses the volatility dynamics of pension fund net asset value, demonstrating substantial dependencies on macroeconomic variables, financial markets, and portfolio composition. These findings corroborate previous research, affirming that financial market shocks, sovereign yield variations, and exchange rate changes are key determinants of pension fund risk [59,70,71].
In line with H1, the comparative analysis of GARCH-type models indicates that EGARCH outperforms sGARCH, GJR-GARCH, and C-GARCH in modeling NAV volatility. EGARCH demonstrated the lowest forecast error (RMSE = 0.00243, MAE = 0.00172) and successfully captured volatility clustering and asymmetric dynamics. This supports previous findings in the literature that emphasize EGARCH’s strength in modeling non-linear volatility patterns, particularly in fund-level financial data [72].
The relationship between NAV volatility and macroeconomic-financial variables also strongly supports H2. The robust positive association between NAV volatility and stock market indices highlights the influence of equity market movements on pension fund risks. The BET Index (γ1 = 0.1655) and STOXX Index (γ2 = 0.0402) demonstrate the greatest explanatory capacity, corroborating earlier research indicating that pension fund performance is significantly influenced by stock market fluctuations [59]. Considering that Romanian pension funds invest 20–25% in domestic equities and 5–10% in international equities, the net asset value is significantly vulnerable to systemic market volatility.
Sovereign bonds, comprising 60–70% of Romanian pension fund holdings, serve as a stabilizing factor against net asset value volatility. The negative coefficients for ROMGB 10Y (γ3 = −0.0570) and ROMANI 5Y (γ4 ≈ −0.0047) affirm that elevated bond rates reduce NAV volatility, aligning with Ondieki [71], who recognized a stabilizing influence of government bond yields on pension fund fluctuations. Increasing yields enhance income potential for newly issued bonds, mitigating losses during equity-driven volatility cycles.
These results further underscore the vulnerability of pension fund stability to monetary policy fluctuations. The 2022 increase in bond rates, prompted by inflationary pressures and central bank policy tightening, unsettled fixed-income value, illustrating that although bonds reduce risk, they are not completely shielded from systemic market fluctuations. This highlights the necessity for adaptive portfolio rebalancing strategies that incorporate yield curve predictions and macroeconomic trend assessments.
The volatility of NAV is affected by currency changes, with the EUR/RON exchange rate (γ6 = 0.0322) exhibiting a positive correlation with NAV. This indicates that currency depreciation exacerbates pension fund volatility, especially in portfolios with 10–15% exposure to euro-denominated assets. These findings corroborate Aziz [73], who proved that fluctuations in exchange rates substantially influence investment fund volatility in emerging markets.
Although currency risk can be partially mitigated, the findings underscore the necessity for improved foreign exchange risk modeling in pension fund plans, especially with the rise of global market integration. The influence of RON depreciation on NAV is especially significant amid inflationary pressures, concerns of capital flight, and exposure to foreign debt, underscoring the need for currency hedging strategies and international asset diversification.
The findings demonstrate that short-term interest rates, as indicated by ROBOR ON (γ5 = −0.0002), exert a negligible influence on NAV volatility. This aligns with the findings of Otranto and Trudda [70], who determined that pension funds are comparatively shielded from short-term liquidity variations owing to their long-term investment perspective. Interbank interest rates affect credit market conditions and systemic liquidity, hence indirectly influencing asset valuations.
The minimal impact of ROBOR ON indicates that Romanian pension funds are not substantially influenced by short-term liquidity issues, distinguishing them from other financial entities like mutual funds or banks, which demonstrate heightened sensitivity to fluctuations in interbank rates. However, during phases of monetary tightening, the indirect impacts on capital costs and asset valuation necessitate ongoing observation.
A key contribution of this study lies in the detection of asymmetric volatility behavior, although not in the direction initially hypothesized in H3. While we expected to confirm the traditional leverage effect, where negative shocks increase volatility more, the EGARCH model instead revealed a positive and statistically significant asymmetry coefficient (γ = 0.1946), indicating that positive shocks, such as market rallies or favorable economic news, generate larger increases in NAV volatility than negative ones.
This phenomenon, often termed the inverse leverage effect, while less common, is not unprecedented. Recent studies across various financial contexts have documented similar results. For instance, Chen and Mu [74] document inverse leverage effects in several commodity contracts, where positive price shocks increase volatility more than negative ones. Similarly, Chen and Diaz [75] observe asymmetric volatility patterns in leveraged and inverse ETFs, where volatility reacts differently to positive versus negative returns, particularly during bullish market phases. A related study on the Tehran Stock Exchange by Tajdini et al. [76] introduced the concept of a reversed leverage effect bias, again supporting the notion that upward shocks can drive volatility more strongly than downward movements. A similar research conducted in the stock markets of Nigeria and Ghana [77] reveals that it is possible for the dynamics of volatility responses to differ even in emerging markets. In the case of Nigeria, researchers saw the typical leverage effect, meaning that negative shocks caused more volatility than positive ones. By contrast, the market in Ghana showed the opposite pattern, where positive shocks led to higher increases in volatility. This behavior is in line with the inverse leverage effect that we observed in our analysis. These differences across the countries are particularly interesting, meaning that emerging markets do not necessarily respond to shocks in the same way. We believe that structural, behavioral, and institutional factors determine how volatility will evolve in each context. This highlights the importance of employing risk models that acknowledge market-specific asymmetries, rather than assuming a universal approach, when modeling volatility dynamics in emerging financial systems.
In the Romanian context, several factors may help explain this atypical volatility pattern. Pension funds are relatively young, with many fund managers actively seeking to optimize performance and attract contributors. During market rallies, increased contributions and higher expected returns may encourage portfolio reallocation toward riskier, more volatile assets, such as equities or foreign currency instruments. This behavior may increase NAV fluctuations during optimistic periods, particularly in a market with lower liquidity and concentrated asset holdings, where price movements can be amplified by inflows or momentum-driven trading.
From a methodological standpoint, this finding also highlights how EGARCH and GJR-GARCH treat asymmetry differently. In EGARCH, the γ parameter reflects directional asymmetry, whether volatility reacts more strongly to positive or negative shocks. By contrast, GJR-GARCH captures asymmetry using a dummy variable that only activates for negative shocks; thus, a positive γ in GJR-GARCH still implies a traditional leverage effect. Both models detect asymmetry, but in opposite directions. This illustrates the importance of model selection in volatility analysis and emphasizes that asymmetric risk can arise in different forms.
Finally, with respect to H4, the study period includes the COVID-19 pandemic, a systemic shock that disrupted global markets. While systemic risk was not explicitly modeled, the GARCH framework, particularly EGARCH, successfully captured the heightened volatility and asymmetric responses associated with this period. This supports the hypothesis that systemic events are reflected in NAV volatility patterns, even if not directly measured. Nevertheless, we acknowledge that systemic risk, understood as contagion and interdependence across financial institutions, was not fully addressed. Future research should explore this through complementary methods such as financial stress indices, CoVaR, or regime-switching models to provide a more complete view of systemic risk exposure in pension systems.
Overall, the empirical findings support all four hypotheses, with important nuances: EGARCH is the most suitable model (H1); macroeconomic variables significantly influence NAV volatility (H2); asymmetry is present but takes the form of reverse leverage (H3); and systemic events like the COVID-19 pandemic impact volatility dynamics, even if systemic risk is not structurally modeled (H4). These results have practical implications for both investment strategy and regulatory oversight in Romania’s maturing pension landscape.
6. Conclusions
The stability of private pension systems is essential for long-term financial security; however, their vulnerability to financial market volatility is a significant issue. Although considerable research has investigated pension fund risks in developed markets, there is a scarcity of studies addressing NAV volatility in emerging economies. This research fills a gap by creating a distinctive high-frequency dataset that captures daily NAV fluctuations from 2012 to 2024, offering the first comprehensive volatility analysis in this domain. Unlike prior research that relies on aggregate or low-frequency data, this dataset captures pension fund fluctuations at a daily level, enabling a more precise estimation of risk dynamics. It includes essential financial variables, including domestic and international stock market indices, bond yields, interbank interest rates, and exchange rate movements. As such, new empirical insights into the causes influencing NAV volatility are provided by this study’s comprehensive evaluation of the variables influencing pension fund risk dynamics through the integration of these many macroeconomic indicators within an econometric framework.
A comparative analysis of four GARCH-type models—sGARCH, EGARCH, GJR-GARCH, and C-GARCH—indicates that pension fund volatility exhibits significant persistence and asymmetric reactions to financial shocks. The multivariate EGARCH model (EGARCH-MV) is identified as the most effective specification, effectively capturing volatility clustering and inverse leverage effects. The results indicate that pension funds exhibit significant sensitivity to fluctuations in the equity market, with the BET Index having the most pronounced effect on NAV volatility. Bond yields serve a stabilizing function, as increasing sovereign yields reduce NAV volatility, thereby alleviating stock market risks. Exchange rate fluctuations add a further dimension of uncertainty, as instances of local currency depreciation increase the volatility of net asset value (NAV). The results underscore the interrelation of macroeconomic factors and stress the necessity of risk-sensitive investment strategies that equilibrate equity exposure with fixed-income securities. The utilization of a high-frequency dataset improves the accuracy of volatility estimation, allowing for a detailed analysis of short-term market dynamics and their effects on pension fund stability.
This study offers a thorough analysis of the volatility within Romania’s private pension system; however, it is not without limitations. The GARCH-family models initially assume a parametric structure, which may inadequately represent nonlinear dependencies or structural breaks. Future research may investigate Markov-switching GARCH models or stochastic volatility models to evaluate regime-dependent volatility in pension funds. Second, although the EGARCH-MV model takes into account a number of macroeconomic factors, it does not specifically take into consideration modifications to the pension system’s regulations or policies. An extension could involve the integration of time-varying coefficient models, such as TVP-GARCH, to effectively capture evolving market dynamics. Third, the predictive performance of various machine learning-based volatility forecasting techniques, like attention-based transformers and LSTMs, in assessing pension fund risk might be assessed by comparing them to GARCH specifications.
Author Contributions
Conceptualization, C.T. and G.R.S.; methodology, C.T., A.G. and G.R.S.; software, G.R.S.; validation, C.T. and D.D.G.; formal analysis, G.R.S. and A.G.; investigation, G.R.S. and D.D.G.; resources, D.D.G. and G.R.S.; data curation, D.D.G. and G.R.S.; writing—original draft preparation, D.D.G. and G.R.S.; writing—review and editing, C.T. and A.G.; visualization, C.T., A.G. and G.R.S.; supervision, C.T.; project administration, A.G.; funding acquisition, A.G. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the EU’s NextGenerationEU instrument through the National Recovery and Resilience Plan of Romania—Pillar III-C9-I8, managed by the Ministry of Research, Innovation and Digitalization, within the project entitled “Non—Gaussian self—similar processes: enhancing mathematical tools and financial models for capturing complex market dynamics”, contract no. 760243/28 December 2023, code CF 194/31 July 2023.
Data Availability Statement
The data used in this study were collected from official sources. Financial variables, including the BET Index Return, STOXX Index Return, government and corporate bond yields, the ROBOR ON rate, and the RON/EUR exchange rate, were obtained via the Bloomberg Terminal. The net asset value (NAV) data for Romanian pension funds were sourced from the website of the Financial Supervisory Authority (ASF), under the “Pension Funds Statistical Data” section, available at: https://asfromania.ro/ro/a/1905/date-statistice-fonduri-de-pensii. (Accessed on 1 March 2025).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ADF | augmented Dickey–Fuller |
| ARCH | autoregressive conditional heteroskedasticity |
| ARMA | autoregressive moving average |
| ASF/FSA | Autoritatea de Supraveghere Financiară (Financial Supervisory Authority) |
| BET | Bucharest Exchange Trading Index |
| BFGS | Broyden–Fletcher–Goldfarb–Shanno optimization algorithm |
| BIC | Bayesian information criterion |
| C-GARCH | component GARCH |
| EGARCH | exponential GARCH |
| ETF | Exchange Traded Fund |
| EUR | euro |
| EURRON | exchange rate Euro-Ron |
| FX | foreign exchange |
| GARCH | generalized autoregressive conditional heteroskedasticity |
| GDP | gross domestic product |
| GJR-GARCH | Glosten–Jagannathan–Runkle GARCH |
| HQIC | Hannan–Quinn information criterion |
| IGARCH | integrated GARCH |
| KPSS | Kwiatkowski–Phillips–Schmidt–Shin test |
| LSTM | long short-term memory |
| MAE | mean absolute error |
| NAV | net asset value |
| OECD | Organisation for Economic Co-operation and Development |
| PP | Phillips–Perron |
| RMSE | root mean squared error |
| ROBOR | Romanian Interbank Offer Rate |
| ROMANI | Romanian Eurobond |
| ROMGB | Romanian Government Bond |
| sGARCH | standard GARCH |
| STOXX | Euro STOXX 50 Index |
| TGARCH | threshold GARCH |
| TVP-GARCH | time-varying parameter generalized autoregressive conditional heteroskedasticity |
| UK | United Kingdom |
| US | United States |
Appendix A. Supplementary Data Analysis
This appendix presents additional analyses supporting the main findings of the study. Figure A1 explores the evolution of stock market indices (BET and STOXX) and their volatility dynamics. Figure A2 examines the distributional properties of NAV returns, highlighting its fat-tailed behavior and the motivation for using a skewed Student-t distribution in GARCH modeling. Table A1 provides a detailed correlation matrix, offering insights into variable relationships and collinearity risks.
These supplementary analyses enhance the robustness of the study by providing a comprehensive view of market trends, risk distribution, and explanatory variable dependencies, which are essential for financial volatility modelling.
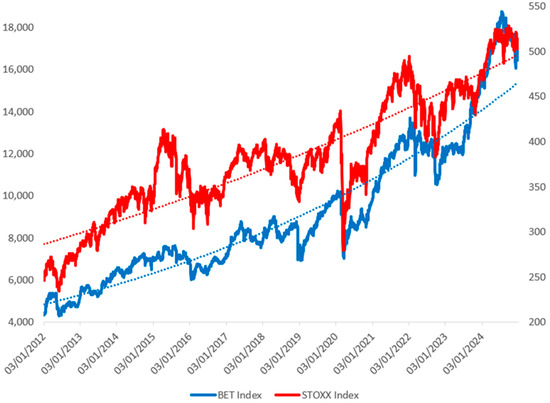
Figure A1.
Evolution of stock market indices (BET, STOXX). Depicts the daily returns of the BET Index (Romanian equities) and STOXX 50 Index (Eurozone blue-chip stocks). These indices serve as equity market proxies in the volatility model. BET shows higher sensitivity to local shocks, while STOXX provides international exposure context. Source: Compiled by the authors in R software, data sourced from Bloomberg. Note: The dotted lines represent trends estimated using an exponential trend model. An exponential trend reflects an accelerated increase or decrease in the value of a financial asset, and is frequently used to capture long-term developments in capital markets.
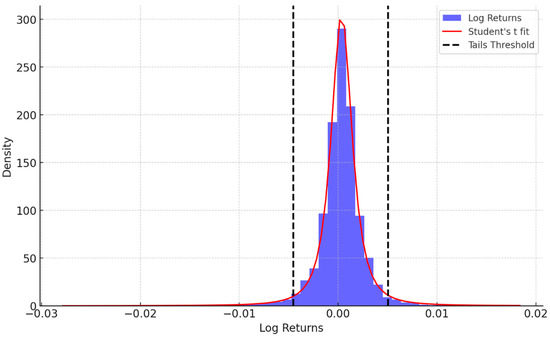
Figure A2.
Histogram of NAV Log Returns: Evidence of Leptokurtosis. The histogram illustrates the distribution of daily NAV log returns, revealing fat tails and negative skewness. This confirms the non-normal nature of pension fund returns and supports the use of GARCH-type models with skewed Student-t innovations. Source: Compiled by the authors in R software, data sourced from Bloomberg.

Table A1.
Correlation analysis heatmap.
Table A1.
Correlation analysis heatmap.
| Variable | NAV | BET Index | STOXX Index | ROMGB 10Y | ROMANI 5Y | ROBOR ON | EURRON |
|---|---|---|---|---|---|---|---|
| NAV | 100.00% | 80.75% | 54.97% | −52.34% | −37.77% | −6.63% | −6.39% |
| BET Index | 80.75% | 100.00% | 44.91% | −16.65% | −21.88% | −5.29% | −5.68% |
| STOXX Index | 54.97% | 44.91% | 100.00% | −17.61% | −25.03% | −3.27% | −13.56% |
| ROMGB 10Y | −52.34% | −16.65% | −17.61% | 100.00% | 35.0% | 5.4% | 12.5% |
| ROMANI 5Y | −37.77% | −21.88% | −25.03% | 35.01% | 100.00% | 0.00% | 0.06% |
| ROBOR ON | −6.63% | −5.29% | −3.27% | 5.43% | 0.78% | 100.00% | −5.56% |
| EURRON | −6.39% | −5.68% | −13.56% | 12.54% | 6.29% | −5.56% | 100.00% |
Source: Authors’ representation; estimations performed in R software.
Appendix B. Proof of Key Properties
Appendix B.1. Proof of Stationarity Condition
For stationarity in a GARCH (1,1) model, we require that the unconditional variance exists. From the expectation equation:
For the variance to be finite, we require α + β < 1. If α + β = 1, the process follows an Integrated GARCH (IGARCH) model, which has infinite variance and is non-stationary.
Appendix B.2. Proof of Ergodicity
A GARCH (1,1) process is ergodic if it has a unique stationary distribution. Ergodicity is ensured if the sum of the squared coefficients satisfies:
Appendix B.3. Proof of Volatility Clustering
Volatility clustering means that large changes in returns tend to be followed by large changes and small changes by small ones. In a GARCH model, conditional variance depends on past variances, hence implying periods of high volatility persist. This is evident from:
Since past shocks contribute to future variances, this confirms volatility clustering.
Appendix C. Statistical Validation

Table A2.
Statistical Diagnostics for the Final EGARCH-MV Model (2012–2024).
Table A2.
Statistical Diagnostics for the Final EGARCH-MV Model (2012–2024).
| EGARCH-MV | |
|---|---|
| Akaike (AIC) | −11.640 |
| Bayesian (BIC) | −11.616 |
| Ljung-Box (lag = 1, lag = 5) | 27.26 *** |
| 35.55 *** | |
| ARCH-LM (lag = 1, lag = 5) | 0.7693 |
| 3.0079 | |
| Sign Bias Test | 0.1424 |
This table presents diagnostic test results for the EGARCH-MV model estimated on the full dataset from 2012 to 2024. The low values of the Akaike (AIC) and Bayesian (BIC) information criteria confirm a strong model fit. The Ljung-Box test indicates some residual autocorrelation, while the ARCH-LM test suggests that the model successfully captures heteroskedasticity, with no significant ARCH effects remaining. Additionally, the Sign Bias test shows no evidence of unaccounted asymmetry. Significance levels: *** p ≤ 0.01. Source: Authors’ representation; estimations performed in R software, version 4.4.2.
References
- Sass, S.A. Will the Financial Fragility of Retirees Increase? Retire. Manag. J. 2018, 7, 41–45. [Google Scholar]
- Sánchez Serrano, A.; Peltonen, T. Pension Schemes in the European Union: Challenges and Implications from Macroeconomic and Financial Stability Perspectives; ESRB Occasional Paper Series No. 2020/17; European Systemic Risk Board (ESRB): Frankfurt am Main, Germany, July 2020. [Google Scholar]
- Head, S.J. Pension Fund Valuations and Market Values. Br. Actuar. J. 2000, 6, 55–141. [Google Scholar] [CrossRef]
- Franzoni, F.; Marín, J.M. Pension Plan Funding and Stock Market Efficiency. J. Financ. 2006, 61, 921–956. [Google Scholar] [CrossRef]
- Dyson, A.C.L.; Exley, C.J. Pension Fund Asset Valuation and Investment. Br. Actuar. J. 1995, 1, 471–557. [Google Scholar] [CrossRef]
- Fadun, O.S.; Oyerinde, M.T.; Isimoya, A.O. Analysis of Net Asset Value and the Performance of Pension Funds in Nigeria. Fuoye J. Manag. Innov. Entrep. 2024, 3, 286–298. [Google Scholar]
- Chen, Y. Funding Status of Defined Benefit Pension Plans and Idiosyncratic Return Volatility. J. Financ. Res. 2015, 38, 35–57. [Google Scholar] [CrossRef]
- Hue, B.; Jinks, A.; Spain, J.; Bora, M.; Siew, S. Investment Risk for Long-Term Investors: Risk Measurement Approaches—Considerations for Pension Funds and Insurers. Br. Actuar. J. 2019, 24, e16. [Google Scholar] [CrossRef]
- Doan, B.; Papageorgiou, N.; Reeves, J.J.; Sherris, M. Portfolio Management with Targeted Constant Market Volatility. Insur. Math. Econ. 2018, 83, 134–147. [Google Scholar] [CrossRef]
- Boon, L.-N.; Brière, M.; Rigot, S. Regulation and Pension Fund Risk-Taking. J. Int. Money Financ. 2018, 84, 23–41. [Google Scholar] [CrossRef]
- Triest, R.K.; Zhao, B. The Role of Economic, Fiscal, and Financial Shocks in the Evolution of Public Sector Pension Funding. In Proceedings of the Annual Conference on Taxation and Minutes of the Annual Meeting of the National Tax Association, Santa Fe, NM, USA, 13–15 November 2014; JSTOR: New York, NY, USA, 2014; pp. 1–25. [Google Scholar]
- Kim, H.Y.; Won, C.H. Forecasting the Volatility of Stock Price Index: A Hybrid Model Integrating LSTM with Multiple GARCH-Type Models. Expert Syst. Appl. 2018, 103, 25–37. [Google Scholar] [CrossRef]
- Jafari, G.R.; Bahraminasab, A.; Norouzzadeh, P. Why Does the Standard GARCH(1,1) Model Work Well? Int. J. Mod. Phys. C 2007, 18, 1223–1230. [Google Scholar]
- OECD. Pensions Market in Focus 2022; Pension Markets in Focus; OECD: Paris, France, 2022; ISBN 978-92-64-34788-5. [Google Scholar]
- Alda, M. The Relationship between Pension Funds and the Stock Market: Does the Aging Population of Europe Affect It? Int. Rev. Financ. Anal. 2017, 49, 83–97. [Google Scholar] [CrossRef]
- Thomas, A.; Spataro, L.; Mathew, N. Pension Funds and Stock Market Volatility: An Empirical Analysis of OECD Countries. Discussion Papers del Dipartimento di Economia e Management, Università di Pisa, Dipartimento di Economia e Management, Pisa, Italy, 2013; p. 33. [Google Scholar]
- Holzner, M.; Jestl, S.; Pichler, D. Public and Private Pension Systems and Macroeconomic Volatility in OECD Countries; wiiw Working Paper Series; The Vienna Institute for International Economic Studies (wiiw): Vienna, Austria, 2019; p. 48. [Google Scholar]
- Morina, F.; Grima, S. The Impact of Pension Fund Assets on Economic Growth in Transition Countries, Emerging Economies, and Developed Countries. Quant. Financ. Econ. 2022, 6, 459–504. [Google Scholar] [CrossRef]
- Paraschiv, C.; Smedoiu, A.; Codirlașu, A.; Purcărea, M. Sistemul de Pensii din România: Între Echitate, Sustenabilitate și Performanță [The Pension System in Romania: Between Equity, Sustainability, and Performance]; CFA Society Romania: Bucharest, Romania, 2025; Available online: https://generatiaindependenta.ro/wp-content/uploads/2025/01/INTEGRAL-SISTEMUL-DE-PENSII-2025.pdf (accessed on 12 February 2025).
- Cristea, M.; Marcu, N.; Dracea, R. Does the Dimension of Privately Managed Pension Funds Influence Their Performances? Statistical Study in Romania. Int. J. Math. Models Methods Appl. Sci. 2012, 6, 239–248. [Google Scholar]
- Robu, V.; Cişmaşu, I.D.; Sandu, M.I. The Effect of the Romanian Pension Market Concentration on the Magnitude of Pension Revenues. Theor. Appl. Econ. 2013, XX, 23–36. [Google Scholar]
- Cristea, M.; Siminica, M. Study on the Dynamics of Voluntary Private Pension Fund Assets in Romania. Afr. J. Bus. Manag. 2012, 6, 6347. [Google Scholar] [CrossRef]
- Darmaz-Guzun, A. Analysis of the Investments Made on the Romanian Capital Market by the Privately Managed Pension Funds—Pillar II. Theor. Appl. Econ. 2018, XXV, 49–60. [Google Scholar]
- Seulean, V.; Mos, L. Determinant Factors of the Investment Performance of Voluntary Pension Funds in Romania. Ann. Univ. Apulensis Ser. Oeconomica 2010, 12, 478–482. [Google Scholar]
- Cristea, M.; Siminica, M.; Dracea, R. Fluctuation in Pension Fund Assets Privately Managed under the Influence of Certain Factors: Statistical Study in Romania. Ann. Univ. Oradea Econ. Sci. Ser. 2011, 1, 476–486. [Google Scholar]
- Chodorow-Reich, G. Effects of Unconventional Monetary Policy on Financial Institutions. Eca 2014, 2014, 155–227. [Google Scholar] [CrossRef]
- Peksevim, S.; Ercan, M. Do Pension Funds Provide Financial Stability? Evidence from European Union Countries. J. Financ. Serv. Res. 2024, 66, 297–328. [Google Scholar] [CrossRef]
- Dumiter, F.C.; Jimon, Ș.; Balteș, N. Macroeconomic Impact of Pension System Upon Private Pension Funds Scheme. Empirical Evidence from Central and Eastern European Countries. Stud. Univ. „Vasile Goldis” Arad-Econ. Ser. 2021, 31, 1–19. [Google Scholar] [CrossRef]
- Aubry, J.-P. Public Pension Investment Update: Have Alternatives Helped or Hurt? Issue in Brief; Center for Retirement Research at Boston College: Chestnut Hill, MA, USA, 2022; p. 12. [Google Scholar]
- Giesecke, O.; Rauh, J. Trends in State and Local Pension Funds. Annu. Rev. Financ. Econ. 2023, 15, 221–238. [Google Scholar] [CrossRef]
- Dutton, B.B.; Wolfram, J.M. Revisiting Pension Asset Allocation; The Vanguard Group, Inc.: Malvern, PA, USA, 2022; p. 16. [Google Scholar]
- Jansen, K.A.E.; Klingler, S.; Ranaldo, A.; Duijm, P. Pension Liquidity Risk. SSRN J. 2023. [Google Scholar] [CrossRef]
- Doan, B.; Reeves, J.J.; Sherris, M. Portfolio Management for Insurers and Pension Funds and COVID-19: Targeting Volatility for Equity, Balanced, and Target-Date Funds with Leverage Constraints. Ann. Actuar. Sci. 2024, 18, 78–101. [Google Scholar] [CrossRef]
- Bukwimba, M.L. Pension Fund’s Risk Management Investment Portfolio in Tanzania. Int. J. Financ. Acc. 2022, 1, 1–20. [Google Scholar] [CrossRef]
- Autoritatea de Supraveghere Financiară (ASF). Financial Supervisory Authority of Romania. In Monthly Market Report; ASF Monthly Reports; ASF [FSA]: Bucharest, Romania, 2025; p. 23. [Google Scholar]
- Bollerslev, T. Generalized Autoregressive Conditional Heteroskedasticity. J. Econom. 1986, 31, 307–327. [Google Scholar] [CrossRef]
- Nelson, D.B. Conditional Heteroskedasticity in Asset Returns: A New Approach. Econometrica 1991, 59, 347. [Google Scholar] [CrossRef]
- Engle, R.F.; Lee, G.G.J. A Long-Run and Short-Run Component Model of Stock Return Volatility. In Cointigration, Causality, and forecating; Engle, R.F., White, H., Eds.; Oxford University Press: Oxford, UK, 1999; pp. 475–497. ISBN 978-0-19-829683-6. [Google Scholar]
- Glosten, L.R.; Jagannathan, R.; Runkle, D.E. On the Relation between the Expected Value and the Volatility of the Nominal Excess Return on Stocks. J. Financ. 1993, 48, 1779–1801. [Google Scholar] [CrossRef]
- Ding, Z.; Granger, C.W.J. Modeling Volatility Persistence of Speculative Returns: A New Approach. J. Econom. 1996, 73, 185–215. [Google Scholar] [CrossRef]
- Hansen, P.R.; Lunde, A. A Forecast Comparison of Volatility Models: Does Anything Beat a GARCH(1,1)? J. Appl. Econom. 2005, 20, 873–889. [Google Scholar] [CrossRef]
- Phillips, P.C.B.; Perron, P. Testing for a Unit Root in Time Series Regression. Biometrika 1988, 75, 335–346. [Google Scholar] [CrossRef]
- Kwiatkowski, D.; Phillips, P.C.B.; Schmidt, P.; Shin, Y. Testing the Null Hypothesis of Stationarity against the Alternative of a Unit Root. J. Econom. 1992, 54, 159–178. [Google Scholar] [CrossRef]
- Lee, S.W.; Hansen, B.E. Asymptotic Theory for the GARCH(1,1) Quasi-Maximum Likelihood Estimator. Econom. Theory 1994, 10, 29–52. [Google Scholar] [CrossRef]
- Hamilton, J.D. Time Series Analysis; Princeton University Press: Princeton, NJ, USA, 1994. [Google Scholar]
- Francq, C.; Zakoïan, J.M. GARCH Models: Structure, Statistical Inference and Financial Applications; Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
- Engle, R.F.; Ghysels, E.; Sohn, B. Stock Market Volatility and Macroeconomic Fundamentals. Rev. Econ. Stat. 2013, 95, 776–797. [Google Scholar] [CrossRef]
- Billah, B.; Hyndman, R.J.; Koehler, A.B. Empirical Information Criteria for Time Series Forecasting Model Selection. J. Stat. Comput. Simul. 2005, 75, 831–840. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the Dimension of a Model. Ann. Statist. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Davies, N.; Newbold, P. Some Power Studies of a Portmanteau Test of Time Series Model Specification. Biometrika 1979, 66, 153–155. [Google Scholar] [CrossRef]
- Engle, R.F. Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation. Econometrica 1982, 50, 987. [Google Scholar] [CrossRef]
- Engle, R.F.; Ng, V.K. Measuring and Testing the Impact of News on Volatility. J. Financ. 1993, 48, 1749–1778. [Google Scholar] [CrossRef]
- Hamilton, J.D. A New Approach to the Economic Analysis of Nonstationary Time Series and the Business Cycle. Econometrica 1989, 57, 357–384. [Google Scholar]
- Baillie, R.T.; Bollerslev, T.; Mikkelsen, H.O. Fractionally Integrated Generalized Autoregressive Conditional Heteroskedasticity. J. Econom. 1996, 74, 3–30. [Google Scholar] [CrossRef]
- Ammann, M.; Moerke, M. Credit Variance Risk Premiums. Euro Fin Manag. 2023, 29, 1304–1335. [Google Scholar] [CrossRef]
- Autoritatea de Supraveghere Financiară (ASF) (The Financial Supervisory Authority) Norma nr. 11/2011 Privind Investirea și Evaluarea Activelor Fondurilor de Pensii Private [Norm No. 11/2011 on the Investment and Evaluation of Assets of Private Pension Funds]. 2011. Available online: https://asfromania.ro/files/pensii/norme/N_ 11 _2011 _consolidata la 04.02.2020.pdf (accessed on 12 February 2025).
- Autoritatea de Supraveghere Financiară (ASF) (The Financial Supervisory Authority) Norma nr. 14/2015 Privind Reglementările Contabile Conforme cu Directivele Europene Aplicabile Sistemului de Pensii Private [Norm No. 14/2015 on Accounting Regulations in Compliance with European Directives Applicable to the Private Pension System]. 2015. Available online: https://static.anaf.ro/static/10/Anaf/legislatie/NormaASF_14_2015.pdf (accessed on 12 February 2025).
- Autoritatea de Supraveghere Financiară (ASF) (The Financial Supervisory Authority) Norma nr. 7/2010 Privind Ratele de Rentabilitate ale Fondurilor de Pensii Administrate Privat [Norm No. 7/2010 on the Rates of Return for Privately Managed Pension Funds]. 2010. Available online: https://asfromania.ro/files/pensii/NPII/N consolidata 7_2010 privind ratele de rentabilitate.pdf (accessed on 12 February 2025).
- Chovancova, B.; Hudcovsky, J.; University of Economics in Bratislava, Faculty of National Economy; Kotaskova, A.; Pan-European University in Bratislava, Faculty of Economics and Business. The Impact of Stocks and Bonds on Pension Fund Performance. J. Compet. 2019, 11, 22–35. [Google Scholar] [CrossRef]
- Ugurlu, E.; Thalassinos, E.; Muratoglu, Y. Modeling Volatility in the Stock Markets Using GARCH Models: European Emerging Economies and Turkey. Int. J. Econ. Bus. Adm. 2014, II, 72–87. [Google Scholar]
- Bauwens, L.; Laurent, S.; Rombouts, J.V.K. Multivariate GARCH Models: A Survey. J. Appl. Econom. 2006, 21, 79–109. [Google Scholar] [CrossRef]
- Engle, R.; Sheppard, K. Theoretical and Empirical Properties of Dynamic Conditional Correlation Multivariate GARCH; National Bureau of Economic Research: Cambridge, MA, USA, 2001; p. w8554. [Google Scholar]
- Larson, E. Volatility Forecasting Using GARCH Processes with Exogenous Variables. Master’s Thesis, KTH Royal Institute of Technology, School of Engineering Sciences, Stockholm, Sweden, 2023. [Google Scholar]
- Ferreira, N.B.; Menezes, R.; Mendes, D.A. Asymmetric Conditional Volatility in International Stock Markets. Phys. A Stat. Mech. Its Appl. 2007, 382, 73–80. [Google Scholar] [CrossRef][Green Version]
- Yi, J. Stock Return, Volume and Volatility in the EGARCH Model. J. Insur. Financ. 2020, 31, 115–136. [Google Scholar] [CrossRef]
- Zakoian, J.-M. Threshold Heteroskedastic Models. J. Econ. Dyn. Control 1994, 18, 931–955. [Google Scholar] [CrossRef]
- Rakshit, D.; Paul, R.; Yeasin, M.; Emam, W.; Tashkandy, Y.; Chesneau, C. Modeling Asymmetric Volatility: A News Impact Curve Approach. Mathematics 2023, 11, 2793. [Google Scholar] [CrossRef]
- Hu, W.; Kercheval, A.N. Portfolio Optimization for Student t and Skewed t Returns. Quant. Financ. 2010, 10, 91–105. [Google Scholar] [CrossRef]
- Binder, M.; Hsiao, C.; Pesaran, M.H. Estimation and Inference in Short Panel Vector Autoregressions with Unit Roots and Cointegration. Econ. Theory 2005, 21, 795–837. [Google Scholar] [CrossRef]
- Otranto, E.; Trudda, A. Classifying Italian Pension Funds via GARCH Distance. In Mathematical and Statistical Methods in Insurance and Finance; Perna, C., Sibillo, M., Eds.; Springer Milan: Milano, Italy, 2008; pp. 189–197. ISBN 978-88-470-0703-1. [Google Scholar]
- Ondieki, I. Modelling Volatility of Interest and Treasury Bill Rates Using ARCH/GARCH Family and Their Effect on Pension Fund. Master’s Thesis, University of Nairobi, Nairobi, Kenya, 2014. [Google Scholar]
- Petrova, M.; Todorov, T. Empirical Testing of Models of Autoregressive Conditional Heteroscedasticity Used for Prediction of the Volatility of Bulgarian Investment Funds. Risks 2023, 11, 197. [Google Scholar] [CrossRef]
- Abdul Aziz, N.S. On Modelling Volatility and Mortality for Pension Schemes. Doctoral Thesis, Department of Mathematical Sciences, University of Essex, Colchester, UK, 2020. [Google Scholar]
- Chen, Y.-F.; Mu, X. Asymmetric Volatility in Commodity Markets. J. Commod. Mark. 2021, 22, 100139. [Google Scholar] [CrossRef]
- Chen, J.H.; Diaz, J.F. Spillover and Asymmetric-Volatility Effects of Leveraged and Inverse Leveraged Exchange Traded Funds. J. Bus. Policy Res. 2012, 7, 1–10. [Google Scholar]
- Tajdini, S.; Jafari, F.; Lotfi Ghahroud, M. Unusual Behavior: Reversed Leverage Effect Bias. J. Math. Model. Financ. 2021, 1, 53–61. [Google Scholar]
- Aliyu, S.U.R. Does Inflation Have an Impact on Stock Returns and Volatility? Evidence from Nigeria and Ghana. Appl. Financ. Econ. 2012, 22, 427–435. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).