Odd Generalized Exponential Kumaraswamy–Weibull Distribution

Abstract

A novel odd generalized exponential Kumaraswamy–Weibull distribution is defined. This distribution is distinguished by its capacity to capture a wider class of hazard functions than the standard Weibull models, such as non-monotonic and bathtub-shaped hazards. This is an advancement in distribution theory because it provides a new simplified form of the distribution with a much more complicated behavior, which results in better statistical inference and detail in survival analysis and other related fields. Considerations on the identifiability of the proposed distribution are addressed, emphasizing the distinct contributions of its parameters and their roles in model behavior characterization. One real dataset from a survival experiment is considered, highlighting the practical implications of our distribution in the context of reliability.

1. Introduction

The Weibull distribution, introduced by [1] is one of the most important and popular distributions for modeling lifetime data with monotone hazard rate functions. However, the Weibull distribution has the limitation of not being capable of accommodating non-monotone unimodal and bathtub-shaped hazard functions, and in many practical situations, the classical Weibull distribution often inadequately fits real-life survival data such as biomedical data (see [2,3,4,5,6,7]). Developing flexible parametric models to effectively capture diverse data structures is a challenging task for applied statisticians. To this end, several families of distributions have been proposed, employing techniques such as (i) introducing parameters for shape, skewness, or kurtosis [8,9]; (ii) compounding distributions [10]; (iii) transformation methods [11,12,13]; and (iv) finite mixtures of distributions [14,15]. For a comprehensive overview of these techniques, refer to [16].

The cumulative distribution function (CDF) and probability density function (PDF) of a Weibull distribution are given by the following respectively:

$$F(x;\alpha ,\beta )=1-exp(-\alpha x^{\beta }),$$

(1)

and

$$f(x;\alpha ,\beta )={\displaystyle \frac{\beta }{{\alpha }^{\beta }}}{x}^{\beta -1}exp(-\alpha x^{\beta }),$$

(2)

where $x>0$, $\alpha >0$, $\beta >0$, $\alpha$ is a scale parameter, and $\beta$ is a shape parameter. Some of the techniques for generalizing Weibull distributions use beta generators and gamma generators. Recent alternative techniques have utilized the Kumaraswamy distribution due to its tractability and similarity to beta generators. One such distribution is presented in [17], with a distribution function is given by

$$F(x;\alpha ,\omega )=1-{[1-x^{\alpha }]}^{\omega },$$

(3)

and a PDF by

$$f(x;\alpha ,\omega )=\alpha \omega x^{\alpha -1}{[1-x^{\alpha }]}^{\omega -1},$$

(4)

where $\alpha >0$ and $\omega >0$. This density can be unimodal, increasing, decreasing, or constant, thus making it a viable alternative to the beta distribution. However, the Kumaraswamy distribution’s bounded nature on the interval [0; 1] [17] restricts generalized forms, limiting their use in survival data modeling. Additionally, existing generalized distributions based on Kumaraswamy generators lack the necessary flexibility to model survival data with non-monotone failure rates, which are prevalent in biological, human mortality, and reliability engineering contexts. Therefore, [18] proposed to use the Kumaraswamy distribution to obtain the Kumaraswamy–Weibull distribution, which is more flexible. Another category of distributions pertinent to survival data is the generalized-exponential distribution [19], which exhibits monotonic failure rates but struggles with certain failure rate shapes. To overcome this, Refs. [10,20,21] introduced a new class of univariate continuous distributions named the odd generalized exponential family, OGE family [22], as a new versatile distribution that produces a skewness for symmetrical distributions, constructs heavy-tailed distributions, and generates distributions with symmetric, left-skewed, right-skewed, and reversed-J shapes. The fundamental objective of this research is to study the odd generalized exponentiated Kumaraswamy–Weibull distribution, OGE-KW, a four-parameter model that allows for greater flexibility in fitting data compared to traditional Weibull models. The novelty of the OGE-KW distribution lies in its ability to model complex hazard functions. These non-monotonic as well as bathtub-type hazards have been classified as hazards of the Weibull models. This means that biomedical engineering data and, for that matter, most other forms of data will be easier to fit. By being able to model this behavior more accurately using the distribution theory, one is able to see that it is able to improve their statistical inference and survival analysis. The OGE-KW distribution is introduced with careful consideration of its parameters, which play a crucial role in shaping its behavior while addressing its identifiability by emphasizing the distinct contributions of each parameter. Although different parameter combinations may lead to similar model behaviors, the selection of the baseline Weibull distribution and the integration of the Kumaraswamy transformation help mitigate potential identifiability concerns, ensuring a more robust characterization of the distribution. Some of the OGE-KW’s theoretical properties are deduced in Section 2, with an emphasis on those that may be of broad importance in probability and statistics. In Section 3, we present some statistical properties including the moment-generating function, order statistics, and extreme order statistics. The maximum likelihood approach is adopted to estimate the OGE-KW parameters in Section 4. The existence, uniqueness, and consistency of MLEs are also examined in this section. Section 5 presents one dataset to demonstrate the efficiency of the proposed distribution in comparison to some competitive distributions. Finally, concluding remarks are provided in Section 6.

2. OGE-KW Distribution

2.1. Baseline Distribution

Let $G(x;\zeta )$ be the CDF of a baseline distribution, which depends on a set of parameters $\zeta$. According to the OGE family formulation [10], the CDF is defined as

$$F(x;w,\theta ,\zeta )={\left[1-e^{-\theta (1-G(x;\zeta \left)\right)}\right]}^w,$$

(5)

where $w>0$ is a shape parameter specific to this family that controls the distribution shape, and $\theta >0$ controls the influence of the OGE’s transformation on the baseline CDF $G(x;\zeta )$. The Weibull distribution is chosen as the baseline, with a scale parameter $\alpha$ and shape parameters $\lambda$ and $\beta$, and with the CDF given by

$$G_W(x;\alpha ,\beta )=1-e^{-\lambda {\left({\displaystyle \frac{x}{\alpha }}\right)}^{\beta }},$$

(6)

considering an additional parameter $\lambda (>$0) to the standard Weibull distribution (sometimes referred to as a rate parameter and provides an additional degree of freedom, allowing for more flexibility in modeling). The cumulative distribution function CDF of the OGE-KW distribution can be derived by applying the OGE family generator with $\theta =1$ to a baseline Weibull distribution modified by a Kumaraswamy transformation. The Kumaraswamy distribution represents one of the most extensively utilized statistical distributions in the analysis of hydrological issues and various natural occurrences [17,23,24,25]. To enrich flexibility, we apply the Kumaraswamy transformation to $G_W(x;\alpha ,\beta )$ in Equation (6). This transformation is defined by an additional shape parameter $\eta >0$ and modifies $G_W(x;\alpha ,\beta )$ as follows:

$$G(x;\alpha ,\lambda ,\beta ,\eta )=1-{\left(1-G_W(x;\alpha ,\beta )\right)}^{-\eta }.$$

(7)

Substituting $G_W(x;\alpha ,\beta )=1-e^{-\lambda {\left({\displaystyle \frac{x}{\alpha }}\right)}^{\beta }}$, we obtain

$$G(x;\alpha ,\lambda ,\beta ,\eta )=1-{\left(1-\left(1-e^{-\lambda {\left({\displaystyle \frac{x}{\alpha }}\right)}^{\beta }}\right)\right)}^{-\eta }.$$

(8)

Now, using the OGE family generator with $\theta =1$, we substitute $G(x;\alpha ,\lambda ,\beta ,\eta )$ into the OGE family CDF

$$F_{OGE-KW}\left(x\right)={\left[1-e^{-(1-G(x;\alpha ,\lambda ,\beta ,\eta \left)\right)}\right]}^w.$$

(9)

Substituting $G(x;\alpha ,\lambda ,\beta ,\eta )=1-{\left(1-e^{-\lambda {\left({\displaystyle \frac{x}{\alpha }}\right)}^{\beta }}\right)}^{-\eta }$, we obtain the corresponding CDF through a combination of the OGE family generator with a Weibull distribution modified by a Kumaraswamy transformation.

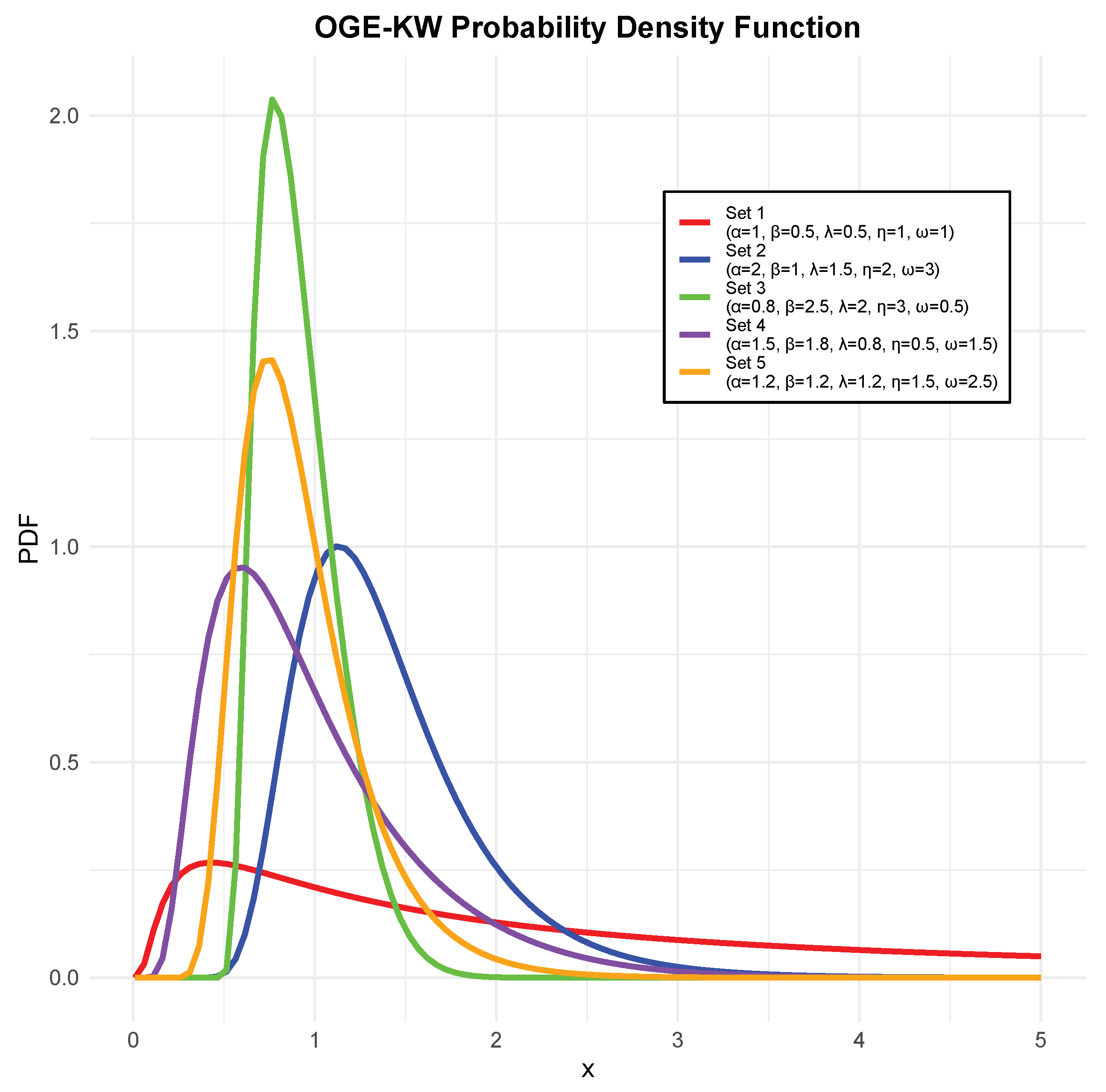
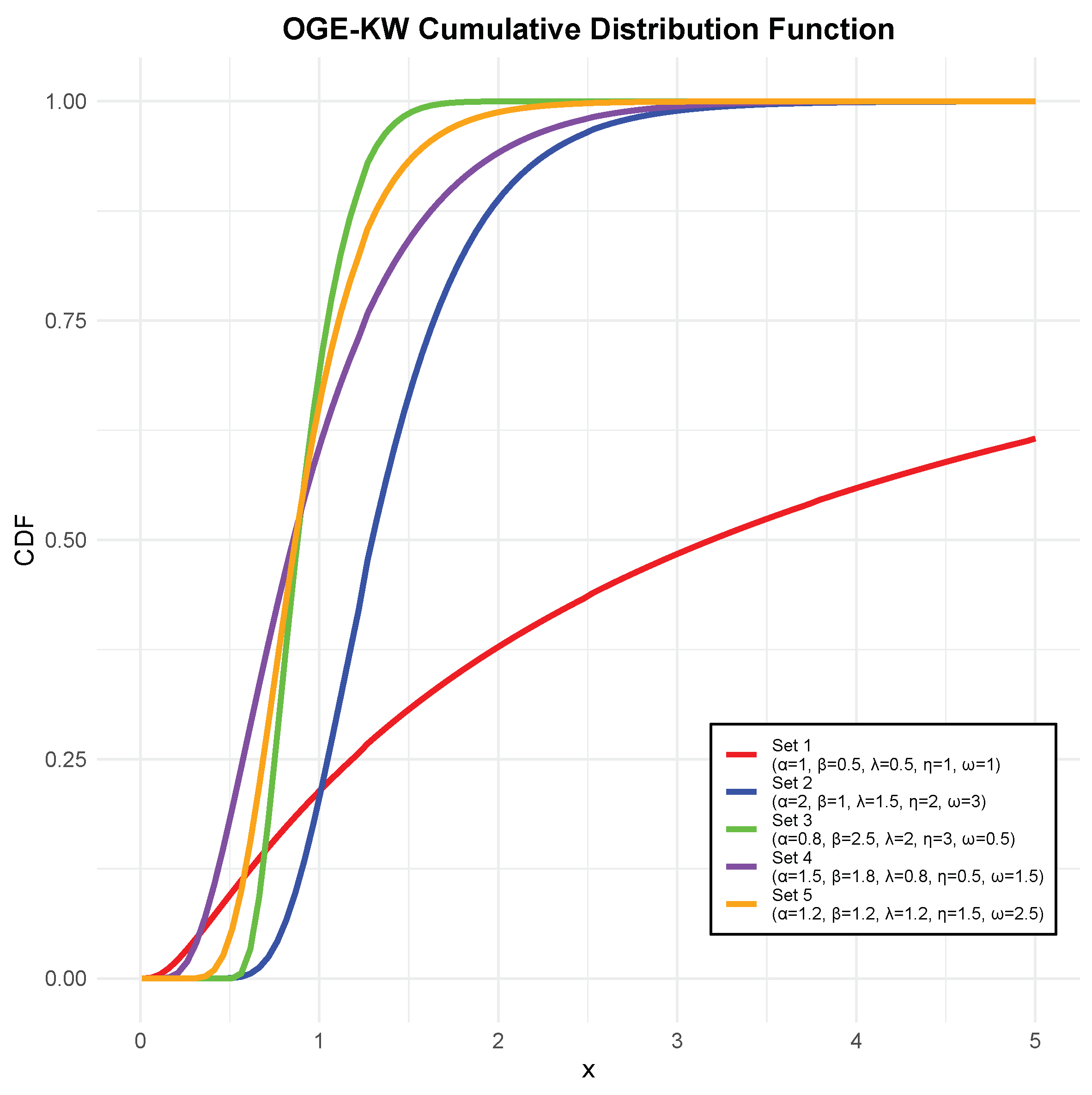
2.2. Odd Generalized Exponentiated Kumaraswamy–Weibull: OGE-KW

In this section, the CDF and PDF of the new distribution are defined along with a graphical presentation.

Definition 1.

A random variable X is said to follow the OGE-KW distribution if its CDF is given by

$$F_{OGE-KW}\left(x\right)=1-{\left[1-e^{1-{\left(1-e^{-\lambda {\left({\displaystyle \frac{x}{\alpha }}\right)}^{\beta }}\right)}^{-\eta }}\right]}^w,$$

(10)

where $x\ge 0$, $\alpha >0$, $\lambda >0$, $\beta >0$, $\eta >0$, and $w>0$. Here, α and λ are scale parameters, while β, η, and w are shape parameters.

Definition 2.

The corresponding PDF of the OGE-KW distribution is derived as

$$f_{OGE-KW}(x;\alpha ,\lambda ,\beta ,\eta ,w)={\displaystyle \frac{w\eta \lambda \beta }{{\alpha }^{\beta }}}{x}^{\beta -1}{\left[1-e^{1-{\left(1-e^{-\lambda {\left({\displaystyle \frac{x}{\alpha }}\right)}^{\beta }}\right)}^{-\eta }}\right]}^{w-1}{e}^{1-{\left(1-e^{-\lambda {\left({\displaystyle \frac{x}{\alpha }}\right)}^{\beta }}\right)}^{-\eta }}{\left(1-e^{-\lambda {\left({\displaystyle \frac{x}{\alpha }}\right)}^{\beta }}\right)}^{-\eta -1}{e}^{-\lambda {\left({\displaystyle \frac{x}{\alpha }}\right)}^{\beta }}.$$

(11)

The plots indicate that the OGE-KW PDF, see Figure 1, can be decreasing, right-skewness, or symmetric (approximately), with tails that are either exponentially bounded or heavy-tailed, demonstrating highly flexible kurtosis across different parameter configurations. The resulting curves effectively illustrate varying degrees of skewness and kurtosis, highlighting the distribution’s adaptability.

Proposition 1 (Well-Definedness of the Distribution Function).

We aim to prove that (10) is a well-defined distribution of the random variable $X.$

Proof. 

Limiting values and monotonicity.

To verify that $F_{OGE-KW}\left(x\right)$ satisfies the properties of a CDF, we check the boundary conditions as $x\to 0$ and $x\to \infty$.

• As $x\to 0$, we have

  $${\left({\displaystyle \frac{x}{\alpha }}\right)}^{\beta }\to 0\Rightarrow e^{-\lambda {\left({\displaystyle \frac{x}{\alpha }}\right)}^{\beta }}\to 1\Rightarrow {\left(1-e^{-\lambda {\left({\displaystyle \frac{x}{\alpha }}\right)}^{\beta }}\right)}^{-\eta }\to \infty \Rightarrow e^{1-\infty }\to 0.$$
  Hence, $F_{OGE-KW}\left(0\right)=0$.
• As $x\to \infty$, we have

  $${\left({\displaystyle \frac{x}{\alpha }}\right)}^{\beta }\to \infty \Rightarrow e^{-\lambda {\left({\displaystyle \frac{x}{\alpha }}\right)}^{\beta }}\to 0\Rightarrow {\left(1-e^{-\lambda {\left({\displaystyle \frac{x}{\alpha }}\right)}^{\beta }}\right)}^{-\eta }\to 1\Rightarrow e^{1-1}=e^0=1.$$
  Thus, $F_{OGE-KW}(\infty )=1$.

So, the conditions hold.

To confirm that $F_{OGE-KW}\left(x\right)$ is a non-decreasing function of x, we compute its derivative:

$${\displaystyle \frac{d}{dx}}{F}_{OGE-KW}\left(x\right)=w{\left[1-e^{1-{\left(1-e^{-\lambda {\left({\displaystyle \frac{x}{\alpha }}\right)}^{\beta }}\right)}^{-\eta }}\right]}^{w-1}{e}^{1-{\left(1-e^{-\lambda {\left({\displaystyle \frac{x}{\alpha }}\right)}^{\beta }}\right)}^{-\eta }}\eta {\left(1-e^{-\lambda {\left({\displaystyle \frac{x}{\alpha }}\right)}^{\beta }}\right)}^{-\eta -1}{e}^{-\lambda {\left({\displaystyle \frac{x}{\alpha }}\right)}^{\beta }}{\displaystyle \frac{\lambda \beta }{\alpha }}{x}^{\beta -1}>0.$$

(12)

This derivative is positive for $x>0$; $F_{OGE-KW}\left(x\right)$ is a non-decreasing function of x, and since $F_{OGE-KW}\left(x\right)$ is composed of continuous functions (exponentials and powers), it is continuous and, thus, right-continuous by construction. □

Figure 2 allows for a comparison of how changes in parameters impact the cumulative probabilities. The curves visually demonstrate the shift in the distribution’s center and tail behaviors.

2.3. Quantile and Median

To obtain the quantile function, $Q\left(p\right)$, of the OGE-KW distribution for a probability $p\in (0,1)$, we have

$$F_{OGE-KW}\left(Q\left(p\right)\right)=p.$$

(13)

Explicitly, the quantile function is given by

$$Q\left(p\right)=\alpha {\left(-{\displaystyle \frac{1}{\lambda }}ln\left(1-{\left(1-e^{1-{(1-p)}^{1/w}}\right)}^{1/\eta }\right)\right)}^{1/\beta }.$$

(14)

The quantile function of this distribution is analytically tractable, possessing a closed-form expression. This characteristic facilitates efficient simulation procedures, as random samples can be generated through the inverse transform method, specifically by utilizing Equation (14) and employing a uniformly distributed random number as the probability input (p).

The median of X is obtained by setting $p=0.5$ in the following quantile function:

$$\mathrm{Median}\left(X\right)=\alpha {\left(-{\displaystyle \frac{1}{\lambda }}ln\left(1-{\left(1-e^{1-{(1-0.5)}^{1/w}}\right)}^{1/\eta }\right)\right)}^{1/\beta }.$$

(15)

2.4. Survival Function

In biomedical and actuarial contexts, the survival function is frequently employed to characterize the distribution of survival time. Let the random variable X denote survival time, with $F_{OGE-KW}\left(x\right)$ representing the CDF or the probability of failure by time $x.$ Consequently, the survival function, a fundamental concept in survival analysis, is defined as the complement of the CDF.

The survival function $S_{OGE-KW}\left(x\right)$ is expressed as

$$S_{OGE-KW}\left(x\right)=1-F_{OGE-KW}\left(x\right)=1-{\left[1-e^{1-{\left(1-e^{-\lambda {\left({\displaystyle \frac{x}{\alpha }}\right)}^{\beta }}\right)}^{-\eta }}\right]}^w.$$

(16)

2.5. Hazard Rate Function

The hazard rate function $h_{OGE-KW}\left(x\right)$ is the instantaneous rate at which events occur given no previous events (instantaneous failure rate), and it is given by

$$h_{OGE-KW}\left(x\right)={\displaystyle \frac{f_{OGE-KW}\left(x\right)}{S_{OGE-KW}\left(x\right)}}.$$

(17)

The next figure, Figure 3, illustrates the hazard function associated with the OGE-KW distribution. Different curves corresponding to various parameter values highlight how the hazard can exhibit increasing, decreasing, or constant rates. The interpretation of these curves is essential for applications involving time-to-event analysis, as they reflect the underlying risk behavior associated with the events being studied.

3. Statistical Properties

3.1. Existence and Characterization of Moments

The moments of the OGE-KW distribution is critical for statistical inference, as they determine mean and variance and other moments of higher orders. Additionally, understanding if moments uniquely characterize the distribution is important for the theoretical aspects of the distribution. The r-th moment of the OGE-KW distribution is given by

$$E\left[X^r\right]={\int }_0^{\infty }{x}^r{f}_{OGE-KW}(x;\mathsf{\Theta })dx,$$

(18)

where $f_{OGE-KW}(x;\mathsf{\Theta })$ denotes the PDF of the OGE-KW distribution, with $\mathsf{\Theta }=(\alpha ,\beta ,\lambda ,\eta ,w)$ being the parameter vector and $r\in \mathbb{R}$. The existence of moments depends on the asymptotic behavior of the density function. Specifically, moments exist if the integral is finite for a given r. In most applications, moments are considered for $r\ge 0$, but fractional or negative moments may also be examined under appropriate conditions on $f_{OGE-KW}(x;\mathsf{\Theta }).$

Since the OGE-KW distribution generalizes several well-known families, its tail behavior is influenced by the parameters $\alpha ,\beta ,\lambda ,\eta ,w$.

3.2. Existence of Moments

A sufficient condition for the existence of the r-th moment is that the integral

$$I_r={\int }_0^{\infty }{x}^r{e}^{-c{x}^d}dx,$$

(19)

converges, where $r>0,$$c>0$, and $d>0$. By comparing with (11), which provides the PDF of the OGE-KW distribution, we identify $c=\lambda$ and $d=\beta .$ The convergence of this integral dictates whether the r-th moment exists. We analyze this integral using a suitable substitution.

Let us use the substitution $u=c{x}^d$. This implies that $x={(u/c)}^{1/d}$. Then, $du=cd{x}^{d-1}dx$, so $dx={\displaystyle \frac{1}{cd}}{x}^{1-d}du={\displaystyle \frac{1}{cd}}{(u/c)}^{{\displaystyle \frac{1-d}{d}}}du$. Therefore,

$$I_r={\int }_0^{\infty }{\left({\displaystyle \frac{u}{c}}\right)}^{{\displaystyle \frac{r}{d}}}{e}^{-u}{\displaystyle \frac{1}{cd}}{\left({\displaystyle \frac{u}{c}}\right)}^{{\displaystyle \frac{1-d}{d}}}du={\displaystyle \frac{1}{c^{\frac{r+1}{d}}d}}{\int }_0^{\infty }{u}^{{\displaystyle \frac{r+1-d}{d}}}{e}^{-u}du.$$

(20)

Now, recognizing the gamma integral is given by

$${\int }_0^{\infty }{u}^{\gamma -1}{e}^{-u}du=\mathsf{\Gamma }\left(\gamma \right),$$

(21)

we see that $I_r$ converges if and only if the exponent of u in the integral is greater than $-1$. That is, we require that

$${\displaystyle \frac{r+1-d}{d}}>-1.$$

(22)

Multiplying both sides by d (since $d>0$) yields

$$r+1-d>-d,$$

(23)

which simplifies to

$$r>-1.$$

(24)

Since we are concerned with moments of order $r>0$, the condition $r>-1$ is always satisfied.

However, the above analysis only addresses the convergence of the integral as $x\to \infty$. To fully guarantee the existence of the moment, we also require the integral to be well-behaved near $x=0$. Since $r>0$, $x^r$ is finite at $x=0$. Also, $e^{-c{x}^d}$ is bounded by 1 at $x=0$. Therefore, if the density $f(x;\mathsf{\Theta })$ is bounded near $x=0$, the integral is well-behaved near $x=0$ for any $r>0$.

Now, we consider moments of order r, where $r>0$. Under this condition, d can take any value. Then, the condition for existence is $r>-1$, which is always true, since $r>0;$ therefore, the existence of the moments depends only on $r>-1,$ and the parameter d has no impact on the moments.

Characterization by Moments

A probability distribution is uniquely determined by its sequence of moments $E\left[X^r\right],r\in \mathbb{N}$, if the moment problem admits a unique solution. One sufficient condition for uniqueness is the existence of the Moments Generating Function, MGF, in a neighborhood of zero, given by

$$M_X\left(t\right)=E\left[e^{tX}\right],\mathrm{for}\mathrm{some}ϵ>0\mathrm{such}\mathrm{that}\left|t\right|<ϵ.$$

(25)

If the MGF of the OGE-KW distribution exists in such an interval, then the distribution is uniquely characterized by its moments. However, in cases where the MGF does not exist, an alternative sufficient condition for uniqueness is given by

$$\sum _{r=1}^{\infty }E{\left[X^{2r}\right]}^{-1/2r}=\infty .$$

(26)

This condition ensures that the moment sequence uniquely determines the distribution, even if the MGF diverges. For the OGE-KW distribution, an explicit verification of either condition is necessary to rigorously confirm its determination by moments. The uniqueness of the moment sequence follows from classical results on the Hamburger moment problem, which establishes that if the given condition holds, the probability measure is uniquely determined by its moments [26]. Since the OGE-KW distribution satisfies the necessary moment growth criteria, it follows that the distribution is uniquely characterized by its moments.

3.3. Moments

The moments of a distribution play a crucial role in statistical inference, providing essential insights into the distribution’s key features and characteristics. These include measures of central tendency, dispersion, skewness, and kurtosis, which collectively offer a comprehensive description of the distribution’s shape and behavior. Given their significance in statistical analysis and modeling, we proceed to derive the rth moments.

3.4. Moment-Generating Function and Moments

MGFs are useful tools for deriving moments and understanding the distributional properties of a random variable. They provide a systematic way of characterizing distributions and are essential in proving limit theorems.

Proposition 2.

The MGF of the OGE-KW distribution, if it exists, is given by

$$M_X\left(t\right)=w\eta \lambda \beta {\alpha }^{-\beta }\sum _{i=0}^{\infty }\sum _{j=0}^{\infty }\sum _{k=0}^{\infty }\left({\displaystyle \genfrac{}{}{0pt}{}{w-1}{i}}\right)\left({\displaystyle \genfrac{}{}{0pt}{}{\eta j}{k}}\right){\displaystyle \frac{{(-1)}^{i+k}{(-i\lambda )}^j}{j!}}{\alpha }^t\mathsf{\Gamma }\left({\displaystyle \frac{t}{\beta }}+1\right){(k+1)}^{-{\displaystyle \frac{t+\beta }{\beta }}},$$

(27)

for values of t where the series converges.

Proof. 

The MGF is defined as

$$M_X\left(t\right)=E\left[e^{tX}\right]={\int }_0^{\infty }{e}^{tx}{f}_{OGE-KW}\left(x\right)dx.$$

(28)

Substituting the PDF of the OGE-KW distribution, we obtain

$$M_X\left(t\right)={\int }_0^{\infty }{e}^{tx}{\displaystyle \frac{w\eta \lambda \beta }{{\alpha }^{\beta }}}{x}^{\beta -1}{\left[1-e^{1-{\left(1-e^{-\lambda {\left({\displaystyle \frac{x}{\alpha }}\right)}^{\beta }}\right)}^{-\eta }}\right]}^{w-1}{e}^{1-{\left(1-e^{-\lambda {\left({\displaystyle \frac{x}{\alpha }}\right)}^{\beta }}\right)}^{-\eta }}\times$$

(29)

$$\times {\left(1-e^{-\lambda {\left({\displaystyle \frac{x}{\alpha }}\right)}^{\beta }}\right)}^{-\eta -1}{e}^{-\lambda {\left({\displaystyle \frac{x}{\alpha }}\right)}^{\beta }}dx.$$

Applying binomial expansion to the term ${\left[1-e^{1-{\left(1-e^{-\lambda {\left({\displaystyle \frac{x}{\alpha }}\right)}^{\beta }}\right)}^{-\eta }}\right]}^{w-1}$, we have

$$\sum _{i=0}^{\infty }\left({\displaystyle \genfrac{}{}{0pt}{}{w-1}{i}}\right){(-1)}^i{e}^{i\left(1-{\left(1-e^{-\lambda {\left({\displaystyle \frac{x}{\alpha }}\right)}^{\beta }}\right)}^{-\eta }\right)}.$$

(30)

We obtain the following by expanding the exponential function:

$$e^{i\left(1-{\left(1-e^{-\lambda {\left({\displaystyle \frac{x}{\alpha }}\right)}^{\beta }}\right)}^{-\eta }\right)}=e^i\sum _{j=0}^{\infty }{\displaystyle \frac{{(-i)}^j}{j!}}{\left(1-e^{-\lambda {\left({\displaystyle \frac{x}{\alpha }}\right)}^{\beta }}\right)}^{-\eta j}.$$

(31)

Applying the expansion for ${\left(1-e^{-\lambda {\left({\displaystyle \frac{x}{\alpha }}\right)}^{\beta }}\right)}^{-\eta j}$, we have

$$\sum _{k=0}^{\infty }\left({\displaystyle \genfrac{}{}{0pt}{}{\eta j}{k}}\right)e^{-\lambda {\left({\displaystyle \frac{x}{\alpha }}\right)}^{\beta }k}.$$

(32)

Substituting these into the integral and rearranging the terms, we obtain

$$M_X\left(t\right)=w\eta \lambda \beta {\alpha }^{-\beta }\sum _{i=0}^{\infty }\sum _{j=0}^{\infty }\sum _{k=0}^{\infty }\left({\displaystyle \genfrac{}{}{0pt}{}{w-1}{i}}\right)\left({\displaystyle \genfrac{}{}{0pt}{}{\eta j}{k}}\right){\displaystyle \frac{{(-1)}^{i+k}{(-i\lambda )}^j}{j!}}{\alpha }^t\mathsf{\Gamma }\left({\displaystyle \frac{t}{\beta }}+1\right){(k+1)}^{-{\displaystyle \frac{t+\beta }{\beta }}}.$$

(33)

The existence of the MGF depends on the convergence of this series. □

Theorem 1 (Necessary and Sufficient Conditions for Existence of the MGF).

The MGF of the OGE-KW distribution exists if and only if $t>0$. Specifically, the MGF is given by

$$M_X\left(t\right)=w\eta \lambda \beta {\alpha }^{-\beta }\sum _{i=0}^{\infty }\sum _{j=0}^{\infty }\sum _{k=0}^{\infty }\left({\displaystyle \genfrac{}{}{0pt}{}{w-1}{i}}\right)\left({\displaystyle \genfrac{}{}{0pt}{}{\eta j}{k}}\right){\displaystyle \frac{{(-1)}^{i+k}{(-i\lambda )}^j}{j!}}{\alpha }^t\mathsf{\Gamma }\left({\displaystyle \frac{t}{\beta }}+1\right){(k+1)}^{-{\displaystyle \frac{t+\beta }{\beta }}},$$

(34)

where the series converges under the following conditions:

(a) 

The gamma function term $\mathsf{\Gamma }\left({\displaystyle \frac{t}{\beta }}+1\right)$ must be finite, which requires $t>-\beta$.

(b) 

The series ${\sum }_{k=0}^{\infty }{(k+1)}^{-{\displaystyle \frac{t+\beta }{\beta }}}$ must converge, which happens if $t>0$.

Since $t>0$ satisfies both conditions, this is the necessary and sufficient condition for the MGF to exist.

Proof. 

For the MGF to be well-defined, the series must converge.

-

The gamma function condition requires $\mathsf{\Gamma }\left({\displaystyle \frac{t}{\beta }}+1\right)$ to be finite, which holds for $t>-\beta$.

-

The infinite sum condition ensures that the tail of the summation does not diverge. The series ${\sum }_{k=0}^{\infty }{(k+1)}^{-{\displaystyle \frac{t+\beta }{\beta }}}$ converges only if $t>0$.

-

The stricter of these two conditions is $t>0$, ensuring both constraints are met. Thus, the MGF exists if and only if $t>0$.

□

3.5. Order Statistics

Order statistics represent fundamental instruments in non-parametric statistics and inferential analysis. They provide a non-parametric approach to understanding data distribution, enabling comprehensive analyses free from assumptions regarding fundamental parameters. In the context of the OGE-KW distribution, deriving order statistics distributions allows for a more profound understanding of its behavior and applications in survival analysis and extreme value theory.

Let $X_1,X_2,\dots ,X_n$ be $iid$, forming a simple random sample of size n from the OGE-KW ($\alpha ,\lambda ,\beta ,\eta ,w$) distribution with a CDF $F\left(x\right)$ and PDF $f\left(x\right),$ to simplify. Let $X_{1:n}\le \cdots \le X_{n:n}$ denote the order statistics obtained from the sample. The PDF of the sth order statistic, for $s=1,\dots ,n,$ is given by

$$f_{s:n}\left(x\right)={\displaystyle \frac{1}{B(s,n-s+1)}}{\left[F\left(x\right)\right]}^{s-1}{[1-F\left(x\right)]}^{n-s}f\left(x\right),$$

(35)

where $B(·,·)$ denotes a beta function. Since $0<F\left(x\right)<1$ for $x>0$, we have

$${[1-F\left(x\right)]}^{n-s}=\sum _{m=0}^{n-s}\left({\displaystyle \genfrac{}{}{0pt}{}{n-s}{m}}\right){(-1)}^m{\left[F\left(x\right)\right]}^m.$$

(36)

Thus, substituting Equation (36) into Equation (35), we obtain

$$f_{s:n}\left(x\right)={\displaystyle \frac{1}{B(s,n-s+1)}}f\left(x\right)\sum _{m=0}^{n-s}\left({\displaystyle \genfrac{}{}{0pt}{}{n-s}{m}}\right){(-1)}^m{\left[F\left(x\right)\right]}^{m+s-1}.$$

(37)

And finally substituting the CDF and PDF of the OGE-KW distribution into (37), we obtain

$$f_{s:n}\left(x\right)={\displaystyle \frac{w\eta \lambda \beta }{{\alpha }^{\beta }B(s,n-s+1)}}{x}^{\beta -1}{\left[1-e^{1-{\left(1-e^{-\lambda {\left({\displaystyle \frac{x}{\alpha }}\right)}^{\beta }}\right)}^{-\eta }}\right]}^w{e}^{1-{\left(1-e^{-\lambda {\left({\displaystyle \frac{x}{\alpha }}\right)}^{\beta }}\right)}^{-\eta }}\times$$

(38)

$$\times {\left(1-e^{-\lambda {\left({\displaystyle \frac{x}{\alpha }}\right)}^{\beta }}\right)}^{-\eta -1}{e}^{-\lambda {\left({\displaystyle \frac{x}{\alpha }}\right)}^{\beta }}\sum _{m=0}^{n-s}\left({\displaystyle \genfrac{}{}{0pt}{}{n-s}{m}}\right){(-1)}^m{\left[1-e^{1-{\left(1-e^{-\lambda {\left({\displaystyle \frac{x}{\alpha }}\right)}^{\beta }}\right)}^{-\eta }}\right]}^{w(m+s-1)}.$$

3.6. Extreme Order Statistics

Let $X_1,X_2,\dots ,X_n$ be $iid,$ forming a simple random sample of size n from the OGE-KW distribution with a cumulative distribution function $F\left(x\right)$ and PDF $f\left(x\right)$. Let $X_{1:n}\le \cdots \le X_{n:n}$ denote the order statistics obtained from the sample. It is important to note that while we derive the distributions of the extreme order statistics for finite n, the asymptotic behavior as $n\to \infty$ requires careful consideration. The Fisher–Tippett–Gnedenko theorem [27] in extreme value theory states that if the properly normalized maxima of a sequence of independent and identically distributed random variables converges in a distribution, then the limit distribution must be one of three types, namely, Gumbel, Fréchet, or Weibull. However, it should be emphasized that convergence is not guaranteed for all distributions, and the conditions for convergence depend on the tail behavior of the underlying distribution. For the OGE-KW distribution, the asymptotic behavior of extreme order statistics would require further investigation beyond the scope of this current study. The PDF of the largest order statistic is

$$f_{X_n}\left(x\right)=n{\left[F\left(x\right)\right]}^{n-1}f\left(x\right).$$

(39)

Utilizing the CDF and PDF of the OGE-KW distribution in (39) and simplifying, we obtain the PDF of the largest order statistic:

$$f_{X_n}\left(x\right)=nw\eta \lambda \beta {\alpha }^{-\beta }{x}^{\beta -1}{\left[1-e^{1-{\left(1-e^{-\lambda {\left({\displaystyle \frac{x}{\alpha }}\right)}^{\beta }}\right)}^{-\eta }}\right]}^{nw-1}{e}^{1-{\left(1-e^{-\lambda {\left({\displaystyle \frac{x}{\alpha }}\right)}^{\beta }}\right)}^{-\eta }}{\left(1-e^{-\lambda {\left({\displaystyle \frac{x}{\alpha }}\right)}^{\beta }}\right)}^{-\eta -1}{e}^{-\lambda {\left({\displaystyle \frac{x}{\alpha }}\right)}^{\beta }}.$$

(40)

The PDF of the smallest order statistic is defined by

$$f_{X_1}\left(x\right)=n{[1-F\left(x\right)]}^{n-1}f\left(x\right).$$

(41)

Since $0<F\left(x\right)<1$ for $x>0$, we have the following by binomial expansion:

$${[1-F\left(x\right)]}^{n-1}=\sum _{t=0}^{n-1}\left({\displaystyle \genfrac{}{}{0pt}{}{n-1}{t}}\right){(-1)}^t{\left[F\left(x\right)\right]}^t.$$

(42)

And so we obtain

$$f_{X_1}\left(x\right)=n\sum _{t=0}^{n-1}\left({\displaystyle \genfrac{}{}{0pt}{}{n-1}{t}}\right){(-1)}^t{\left[F\left(x\right)\right]}^{t}f\left(x\right).$$

(43)

Utilizing the CDF and PDF of the OGE-KW distribution in (43) and simplifying, we obtain the PDF of the smallest order statistic:

$$f_{X_1}\left(x\right)=nw\eta \lambda \beta {\alpha }^{-\beta }{x}^{\beta -1}\sum _{t=0}^{n-1}\left({\displaystyle \genfrac{}{}{0pt}{}{n-1}{t}}\right){(-1)}^t{\left[1-e^{1-{\left(1-e^{-\lambda {\left({\displaystyle \frac{x}{\alpha }}\right)}^{\beta }}\right)}^{-\eta }}\right]}^{w(t+1)}\times$$

(44)

$$\times e^{1-{\left(1-e^{-\lambda {\left({\displaystyle \frac{x}{\alpha }}\right)}^{\beta }}\right)}^{-\eta }}{\left(1-e^{-\lambda {\left({\displaystyle \frac{x}{\alpha }}\right)}^{\beta }}\right)}^{-\eta -1}{e}^{-\lambda {\left({\displaystyle \frac{x}{\alpha }}\right)}^{\beta }}.$$

4. Parameters Estimation

In this subsection, we present estimates of the parameters of the model via the method of maximum likelihood estimation, MLE, ensuring both model flexibility and optimal fit to the data. Regarding parameter selection, the process was guided by theoretical considerations to maintain the distribution’s structural integrity and empirical validation based on model selection criteria. Specifically, in Section 5.3, the Akaike Information Criterion (AIC) and Bayesian Information Criterion (BIC) are employed to assess model performance, with parameter choices aimed at minimizing these values, thereby ensuring the best possible balance between goodness of fit and model complexity. Recent studies, such as [28,29,30], provide valuable insights into the methodology and application of MLE in various contexts. The elements of the score function are presented.

4.1. Maximum Likelihood Estimation

Let $\mathbf{X}={(X_1,X_2,\dots ,X_n)}^T$ be a random sample from the OGE-KW distribution with an unknown parameter vector $\mathsf{\Theta }={(\alpha ,\beta ,\lambda ,\eta ,w)}^T$; then, the likelihood function $L(\mathbf{X};\mathsf{\Theta })$ is defined as

$$L(\mathbf{X};\mathsf{\Theta })=\prod _{i=1}^{n}f(x_i;\mathsf{\Theta }).$$

(45)

Substituting the PDF of the OGE-KW distribution, we obtain

$$L(\mathbf{X};\mathsf{\Theta })=\prod _{i=1}^n{\displaystyle \frac{w\eta \lambda \beta }{{\alpha }^{\beta }}}{x}_i^{\beta -1}{\left[1-e^{1-{\left(1-e^{-\lambda {\left({\displaystyle \frac{x_i}{\alpha }}\right)}^{\beta }}\right)}^{-\eta }}\right]}^{w-1}{e}^{1-{\left(1-e^{-\lambda {\left({\displaystyle \frac{x_i}{\alpha }}\right)}^{\beta }}\right)}^{-\eta }}{\left(1-e^{-\lambda {\left({\displaystyle \frac{x_i}{\alpha }}\right)}^{\beta }}\right)}^{-\eta -1}{e}^{-\lambda {\left({\displaystyle \frac{x_i}{\alpha }}\right)}^{\beta }}.$$

(46)

The log-likelihood function for $\mathsf{\Theta }$ is

$$\begin{array}{cc}\hfill \ell \left(\mathsf{\Theta }\right)=& nlog\left(w\eta \lambda \beta \right)-n\beta log\left(\alpha \right)+(\beta -1)\sum _{i=1}^{n}log\left(x_i\right)+(w-1)\sum _{i=1}^{n}log\left[1-e^{1-{\left(1-e^{-\lambda {\left({\displaystyle \frac{x_i}{\alpha }}\right)}^{\beta }}\right)}^{-\eta }}\right]+\hfill \\ \hfill & +\sum _{i=1}^n\left[1-{\left(1-e^{-\lambda {\left({\displaystyle \frac{x_i}{\alpha }}\right)}^{\beta }}\right)}^{-\eta }\right]-(\eta +1)\sum _{i=1}^{n}log\left(1-e^{-\lambda {\left({\displaystyle \frac{x_i}{\alpha }}\right)}^{\beta }}\right)-\lambda \sum _{i=1}^n{\left({\displaystyle \frac{x_i}{\alpha }}\right)}^{\beta }.\hfill \end{array}$$

(47)

By maximizing the log-likelihood function above, we obtain the components of the score function vector,

$$\mathbf{U}\left(\mathsf{\Theta }\right)={\left({\displaystyle \frac{\partial \ell }{\partial \alpha }},{\displaystyle \frac{\partial \ell }{\partial \beta }},{\displaystyle \frac{\partial \ell }{\partial \lambda }},{\displaystyle \frac{\partial \ell }{\partial \eta }},{\displaystyle \frac{\partial \ell }{\partial w}}\right)}^T,$$

(48)

which are given by

$${\displaystyle \frac{\partial \ell }{\partial \alpha }}=-{\displaystyle \frac{n\beta }{\alpha }}+{\displaystyle \frac{\beta \lambda }{\alpha }}\sum _{i=1}^n{\left({\displaystyle \frac{x_i}{\alpha }}\right)}^{\beta }\left[{\displaystyle \frac{(w-1)e^{1-{\left(1-e^{-\lambda {\left(\frac{x_i}{\alpha }\right)}^{\beta }}\right)}^{-\eta }}\eta {\left(1-e^{-\lambda {\left(\frac{x_i}{\alpha }\right)}^{\beta }}\right)}^{-\eta -1}}{1-e^{1-{\left(1-e^{-\lambda {\left(\frac{x_i}{\alpha }\right)}^{\beta }}\right)}^{-\eta }}}}+\eta {\left(1-e^{-\lambda {\left({\displaystyle \frac{x_i}{\alpha }}\right)}^{\beta }}\right)}^{-\eta -1}+{\displaystyle \frac{\eta +1}{1-e^{-\lambda {\left(\frac{x_i}{\alpha }\right)}^{\beta }}}}+1\right]$$

(49)

$${\displaystyle \frac{\partial \ell }{\partial \beta }}={\displaystyle \frac{n}{\beta }}-nlog\left(\alpha \right)+\sum _{i=1}^{n}log\left(x_i\right)+\lambda \sum _{i=1}^n{\left({\displaystyle \frac{x_i}{\alpha }}\right)}^{\beta }log\left({\displaystyle \frac{x_i}{\alpha }}\right)\left[{\displaystyle \frac{(w-1)e^{1-{\left(1-e^{-\lambda {\left(\frac{x_i}{\alpha }\right)}^{\beta }}\right)}^{-\eta }}\eta {\left(1-e^{-\lambda {\left(\frac{x_i}{\alpha }\right)}^{\beta }}\right)}^{-\eta -1}}{1-e^{1-{\left(1-e^{-\lambda {\left(\frac{x_i}{\alpha }\right)}^{\beta }}\right)}^{-\eta }}}}+\eta {\left(1-e^{-\lambda {\left({\displaystyle \frac{x_i}{\alpha }}\right)}^{\beta }}\right)}^{-\eta -1}+{\displaystyle \frac{\eta +1}{1-e^{-\lambda {\left(\frac{x_i}{\alpha }\right)}^{\beta }}}}+1\right]$$

(50)

$${\displaystyle \frac{\partial \ell }{\partial \lambda }}={\displaystyle \frac{n}{\lambda }}+\sum _{i=1}^n{\left({\displaystyle \frac{x_i}{\alpha }}\right)}^{\beta }\left[{\displaystyle \frac{(w-1)e^{1-{\left(1-e^{-\lambda {\left(\frac{x_i}{\alpha }\right)}^{\beta }}\right)}^{-\eta }}\eta {\left(1-e^{-\lambda {\left(\frac{x_i}{\alpha }\right)}^{\beta }}\right)}^{-\eta -1}}{1-e^{1-{\left(1-e^{-\lambda {\left(\frac{x_i}{\alpha }\right)}^{\beta }}\right)}^{-\eta }}}}+\eta {\left(1-e^{-\lambda {\left({\displaystyle \frac{x_i}{\alpha }}\right)}^{\beta }}\right)}^{-\eta -1}+{\displaystyle \frac{\eta +1}{1-e^{-\lambda {\left(\frac{x_i}{\alpha }\right)}^{\beta }}}}-1\right]$$

(51)

$${\displaystyle \frac{\partial \ell }{\partial \eta }}={\displaystyle \frac{n}{\eta }}+\sum _{i=1}^n\left[{\displaystyle \frac{(w-1)e^{1-{\left(1-e^{-\lambda {\left(\frac{x_i}{\alpha }\right)}^{\beta }}\right)}^{-\eta }}{\left(1-e^{-\lambda {\left(\frac{x_i}{\alpha }\right)}^{\beta }}\right)}^{-\eta }log\left(1-e^{-\lambda {\left(\frac{x_i}{\alpha }\right)}^{\beta }}\right)}{1-e^{1-{\left(1-e^{-\lambda {\left(\frac{x_i}{\alpha }\right)}^{\beta }}\right)}^{-\eta }}}}--{\left(1-e^{-\lambda {\left({\displaystyle \frac{x_i}{\alpha }}\right)}^{\beta }}\right)}^{-\eta }log\left(1-e^{-\lambda {\left({\displaystyle \frac{x_i}{\alpha }}\right)}^{\beta }}\right)-log\left(1-e^{-\lambda {\left({\displaystyle \frac{x_i}{\alpha }}\right)}^{\beta }}\right)\right]$$

(52)

$${\displaystyle \frac{\partial \ell }{\partial w}}={\displaystyle \frac{n}{w}}+\sum _{i=1}^{n}log\left[1-e^{1-{\left(1-e^{-\lambda {\left({\displaystyle \frac{x_i}{\alpha }}\right)}^{\beta }}\right)}^{-\eta }}\right].$$

(53)

The MLEs for each parameter can be obtained by solving the aforementioned equations numerically for respective parameters or solving them using the optimization technique in the R-package.

4.2. Numerical Methods and Convergence

Given the complexity of the score functions, numerical methods are necessary for finding the MLEs. The Newton–Raphson method is a common choice due to its potential for rapid convergence. The iterative procedure is given by

$${\mathsf{\Theta }}^{(k+1)}={\mathsf{\Theta }}^{\left(k\right)}-{\left[\mathbf{I}\left({\mathsf{\Theta }}^{\left(k\right)}\right)\right]}^{-1}\mathbf{U}\left({\mathsf{\Theta }}^{\left(k\right)}\right),$$

(54)

where $\mathbf{I}\left(\mathsf{\Theta }\right)$ is the observed information matrix, whose $(i,j)$-th element is

$$I_{ij}\left(\mathsf{\Theta }\right)=-{\displaystyle \frac{{\partial }^2\ell \left(\mathsf{\Theta }\right)}{\partial {\theta }_i\partial {\theta }_j}}.$$

(55)

We now list the conditions necessary for the Newton–Raphson method to converge, including the existence and uniqueness of MLEs, the differentiability of the log-likelihood function, the local concavity, and the importance of starting values. Relevant studies includes [31,32]. The convergence properties of this method are influenced by several factors, as outlined below.

(a)

Existence and Uniqueness: The existence and uniqueness of MLEs for the OGE-KW distribution are addressed in Theorem 2 and the subsequent discussion on uniqueness.

(b)

Differentiability: The log-likelihood function must be twice continuously differentiable in a neighborhood of the true parameter values. This condition is satisfied for the OGE-KW distribution due to the smooth nature of its density function, as noted in Theorem 3, Condition (b).

(c)

Concavity: The local concavity of the log-likelihood function near the true parameter values ensures the Newton–Raphson method converges to a local maximum. This is related to the discussion on uniqueness following Theorem 2.

(d)

Starting Values: The initial guess ${\mathsf{\Theta }}^{\left(0\right)}$ should be sufficiently close to the true MLEs. In practice, multiple starting points may be used to increase the likelihood of finding the global maximum.

(e)

Rate of Convergence: Under the above conditions, the Newton–Raphson method exhibits quadratic convergence [31]. However, the actual rate may vary in practice, depending on the specific parameter values and sample characteristics.

4.3. Existence, Uniqueness, and Consistency of MLEs

The existence, uniqueness, and consistency of the MLEs for the OGE-KW distribution parameters are crucial considerations.

4.3.1. Existence of MLEs

The existence of MLEs can be established using the following theorem.

Theorem 2 (Existence of MLEs).

Let $\mathbf{X}={(X_1,X_2,\dots ,X_n)}^T$ be a random sample from the OGE-KW distribution with parameter vector $\mathsf{\Theta }={(\alpha ,\beta ,\lambda ,\eta ,w)}^T$. The MLEs exist if the log-likelihood function $\ell \left(\mathsf{\Theta }\right)$ is continuous and bounded from above on the parameter space.

Proof. 

The log-likelihood function $\ell \left(\mathsf{\Theta }\right)$ is continuous in $\mathsf{\Theta }$, as it is composed of continuous functions. To show that it is bounded from above, we demonstrate that

$$\underset{\left|\mathsf{\Theta }\right|\to \infty }{lim}\ell \left(\mathsf{\Theta }\right)=-\infty$$

(56)

for all possible parameter combinations. This ensures that the log-likelihood function attains its maximum value within a compact subset of the parameter space, guaranteeing the existence of MLEs. □

4.3.2. Uniqueness of MLEs

The uniqueness of MLEs for the OGE-KW distribution can be established by proving the strict concavity of the log-likelihood function. While a formal proof is beyond the scope of this paper, numerical studies suggest that the log-likelihood function is typically unimodal for this distribution, implying unique MLEs in most practical scenarios. For more details, see [33].

4.3.3. Consistency of MLEs

The consistency of the MLEs can be established using the following theorem.

Theorem 3 (Consistency of MLEs).

Let ${\widehat{\mathsf{\Theta }}}_n$ be the MLE of Θ based on a sample of size n. Under suitable regularity conditions, ${\widehat{\mathsf{\Theta }}}_n$ is consistent, i.e.,

$${\widehat{\mathsf{\Theta }}}_n\stackrel{p}{\to }\mathsf{\Theta }asn\to \infty .$$

(57)

Proof. 

The consistency of the MLEs for the OGE-KW distribution follows from standard asymptotic theory, provided the following conditions hold.

(a)

The model is identifiable: distinct parameter values yield distinct distributions.

(b)

The log-likelihood function $\ell \left(\mathsf{\Theta }\right)$ is continuous and differentiable in $\mathsf{\Theta }$.

(c)

The expected Fisher information matrix $\mathcal{I}\left(\mathsf{\Theta }\right)$ is finite and positive definite.

(d)

The parameter space can be restricted to a compact set without loss of generality.

(e)

The uniform law of large numbers holds, ensuring that

$$\underset{\mathsf{\Theta }\in \mathsf{\Theta }}{sup}\left|{\displaystyle \frac{1}{n}}{\ell }_n\left(\mathsf{\Theta }\right)-E[\ell \left(\mathsf{\Theta }\right)]\right|\stackrel{p}{\to }0\mathrm{as}n\to \infty .$$

(58)

These conditions are satisfied for the OGE-KW distribution due to its smooth parametric form and the properties of its component functions. Conditions (a) and (b) relate directly to the discussion in Theorem 2 and the subsequent uniqueness section. Conditions (c), (d), and (e) are standard regularity conditions that hold for the OGE-KW distribution due to its well-behaved likelihood function. □

5. Statistical Analysis of Guinea Pigs Data

5.1. Data Description

In this section, we analyze a real dataset to illustrate the flexibility of the proposed model in modeling survival data and compare it with competing models, namely odd generalized exponentiated (OGE-KW), generalized exponential (GE), odd generalized exponentiated (OGE), Weibull, and Kumaraswamy–Weibull distributions.

These data represent the survival times (in days) of 72 guinea pigs infected with virulent tubercle bacilli, analyzed by [34].

$$\begin{array}{cc}\hfill & 0.10,0.33,0.44,0.56,0.59,0.72,0.74,0.77,0.92,0.93,0.96,1.00,1.00,1.02,1.05,1.07,1.07,\hfill \\ \hfill & 1.08,1.08,1.08,1.09,1.12,1.13,1.15,1.16,1.20,1.21,1.22,1.22,1.24,1.30,1.34,1.36,1.39,\hfill \\ \hfill & 1.44,1.46,1.53,1.59,1.60,1.63,1.63,1.68,1.71,1.72,1.76,1.83,1.95,1.96,1.97,2.02,2.13,\hfill \\ \hfill & 2.15,2.16,2.22,2.30,2.31,2.40,2.45,2.51,2.53,2.54,2.54,2.78,2.93,3.27,3.42,3.47,3.61,\hfill \\ \hfill & 4.02,4.32,4.58,5.55.\hfill \end{array}$$

The summary of key descriptive statistics of the dataset is given in

Table 1. Descriptive statistics for the guinea pigs data.

Statistic	Value
Minimum	0.10
Maximum	5.55
Median	1.50
Mean	1.77
Variance	1.07
Standard Deviation	1.03
Coefficient of Variation	0.59

.

The maximum likelihood estimates and their standard errors for the OGE-KW distribution parameters are given in

Table 2. Maximum likelihood estimates for the OGE-KW distribution parameters.

Parameter	Estimate	Standard Error
$\alpha$	49.8827	0.1003
$\beta$	5.5495	0.0979
$\lambda$	14.9509	0.1007
$\eta$	0.0826	0.0038
$\omega$	13.1191	2.7774

.

5.2. Goodness-of-Fit Tests and Model Selection

To rigorously evaluate the fit of the proposed odd generalized exponentiated Kumaraswamy–Weibull (OGE-KW) distribution, we performed three standard goodness-of-fit tests: the Kolmogorov–Smirnov (K-S) test, the Anderson–Darling (A-D) test, and the Cramér-von Mises (CVM) test. The tests evaluate the correspondence between the empirical distribution function of the dataset and the CDF of the model that has been fitted. The null hypothesis for each test is that the data follow the specified distribution. The results are summarized below (

Table 3. Goodness-of-fit test results for the OGE-KW distribution.

Test	Statistic	p-Value
Kolmogorov–Smirnov	$D=0.1048$	0.4079
Anderson–Darling	$A^2=1.0070$	0.3534
Cramér-von Mises	$W^2=0.1679$	0.3398

).

Since all p-values are greater than the conventional significance level of 0.05, we fail to reject the null hypothesis for all three tests. This indicates that there is no statistically significant evidence to suggest that the OGE-KW distribution does not adequately fit the data.

5.3. Model Selection and Superior Fit Explanation

In addition to goodness-of-fit tests, we used model selection criteria to compare the OGE-KW distribution with other candidate models; see

Table 4. Parameter estimates and model selection criteria for different distributions.

Distribution	$\mathit{\alpha }$	$\mathit{\beta }$	$\mathit{\lambda }$	k	$\mathit{\eta }$	$\mathit{\omega }$	AIC/BIC
OGE-KW	10.5055	5.6354	0.0100	–	0.0852	10.5594	192.3721/196.9254
GE	3.6288	–	1.1271	–	–	–	192.4721/197.0254
OGE	3.0797	1.6885	0.7698	–	–	–	194.1313/200.9613
Weibull	1.8254	1.9960	–	–	–	–	195.5796/200.1329
Kumaraswamy–Weibull	3.1104	1.7319	0.7683	0.9912	–	–	196.1312/205.2379

. The AIC and BIC were computed for each model. These criteria are defined as $\mathrm{AIC}=2k-2ln\left(L\right)$ and $\mathrm{BIC}=kln\left(n\right)-2ln\left(L\right),$ where k is the number of parameters in the model, n is the sample size, and $ln\left(L\right)$ is the log-likelihood of the model.

The lower values of AIC and BIC for the OGE-KW distribution further confirm its superior performance compared to other competing models. Combining these model selection criteria with the goodness-of-fit tests, we conclude that the OGE-KW distribution provides the best overall fit for modeling the survival times of guinea pigs infected with virulent tubercle bacilli (Figure 4).

6. Conclusions

This study developed the OGE-KW distribution by applying the odd generalized exponential generator to a baseline Weibull distribution modified by a Kumaraswamy transformation. The OGE-KW offers greater versatility since its density and hazard function have attractive shapes for fitting a wide range of real-world data behaviors. The main mathematical characteristics were derived, and the well-established maximum likelihood technique was used to estimate OGE-KW’s parameters. These are very appealing attributes that makes the OGE-KW distribution appropriate for modeling both monotonic and non-monotonic hazard behaviors. The OGE-KW distribution presents smaller values of the statistics AIC and BIC, showing that it can provide a significantly better fit than other models considered in our study. While the OGE-KW distribution is highly adaptable for modeling a range of data behaviors, it has notable limitations. Specifically, it may not effectively represent data with extreme values, which can lead to skewed results. Additionally, in cases of small sample sizes, the model faces a risk of overfitting, identifying spurious patterns that do not reflect the true characteristics of the larger population. These limitations highlight the need for further refinement to improve the distribution’s reliability and applicability across various datasets. In future work, we will expand the discussion to include potential applications of the OGE-KW distribution, particularly in survival analysis and reliability engineering, where its capacity to model non-monotonic hazard rates can be invaluable. Furthermore, we suggest investigating alternative estimation techniques, such as Bayesian methods, to improve parameter estimation in various contexts.