Solution Methods for the Multiple-Choice Knapsack Problem and Their Applications

Abstract

The Knapsack Problem belongs to the best-studied classical problems in combinatorial optimization. The Multiple-choice Knapsack Problem (MCKP) represents a generalization of the problem, with various application fields such as industry, transportation, telecommunication, national defense, bioinformatics, finance, and life. We found a lack of survey papers on MCKP. This paper overviews MCKP and presents its variants, solution methods, and applications. Traditional operational research methods solving the knapsack problem, such as dynamic programming, greedy heuristics, and branch-and-bound algorithms, can be adapted to MCKP. Only a few algorithms appear to have solved the problem in recent years. We found various related problems during the literature study and explored the broad spectrum of application areas. We intend to inspire research into MCKP algorithms and motivate experts from different domains to apply MCKP.

1. Introduction

The Multiple-choice Knapsack Problem (MCKP) can be considered a commonly used generalization of the Knapsack Problem (KP) with numerous critical applications. A problem instance of the KP can be specified by a knapsack with a limited weight capacity and a set of items, each having a value and a weight. The aim is to put items into the knapsack with a total weight less than or equal to the knapsack capacity while maximizing the total value of the selected items. The most common type of KP is the 0–1 (or binary) KP when, at most, one sample can be chosen from each item. In MCKP, items are partitioned into r classes S₁,…, S_r and exactly one item is placed into the knapsack from each class. MCKP has proved useful for modeling resource allocation problems where the items can be selected from several options.

An important variant of MCKP, when no item may be selected from each class, frequently occurs in practice. The NP-complete 0–1 KP represents the special case of this variant, where each class has only one item. The variant can be easily reduced to MCKP by adding a dummy item with a weight and value of zero to each class. This implies the NP-completeness of MCKP, which justifies using approximation algorithms.

Different applications have inspired MCKP research in various areas, including finance, business management, engineering, manufacturing, logistics, communication technology, etc. Moreover, the problem is used to solve other problems in combinatorial optimization, e.g., non-linear KP, integer programming, etc.

The Multiple-choice Knapsack Problem (MCKP) has been studied for several decades; see e.g., [1,2,3,4,5] for some early papers. It is still a popular topic, although a decline can be observed in recent years (see Figure 1).

We aim to present versatile solution algorithms and a wide range of application areas of the problem. We examine where MCKP is applied and which algorithms are used to solve the problem. Our research methodology involves data acquisition and systematic literature evaluation. Several repositories were considered as sources of scientometric data for the current paper. We searched databases for the papers with the term “multiple-choice knapsack problem” published in 2024. Google Scholar, Web of Science (WoS), Scopus, and ScienceDirect returned 3090, 114, 249, and 356 hits, respectively. Google Scholar performed a full-text search, while the other repositories looked for the term in the publications’ title, abstract, and keywords. We selected Web of Science as the data source for our review to focus on the most relevant papers and keep the amount of included papers manageable.

Although MCKP is a generalization of the KP, it has several generalizations (e.g., Multidimensional Multiple-choice Knapsack Problem, MMKP). Our paper presents the problem models of the generalizations and variants of MCKP we found in the literature. However, their analysis is beyond the scope of our paper, and they are omitted from the review of the algorithms and applications of MCKP.

The main contributions of our review are as follows:

• The first comprehensive review of the MCKP after twenty years;
• Extensive list of the variants of the MCKP;
• Systematic collection of application areas of the MCKP;
• Highlighting research areas related to the MCKP that have not been studied or are weakly studied in the literature.

The remainder of this paper is organized as follows. In Section 2, the related reviews and books are discussed. Section 3 provides the formal model of MCKP. Section 4 lists the problem variants discussed in the literature. In Section 5, algorithms solving MCKP are provided. It includes the algorithms described or applied in the selected data source. Section 6 presents the applications of MCKP in combinatorial optimization. Section 7 reviews further applications by summarizing how specific papers apply MCKP to solve real-world problems. Section 8 discusses the review results. Section 9 outlines the paper, while Section 10 presents future research directions.

2. Related Work

As we have shown in the introduction, several thousand papers are available in the literature which deal with MCKP. Besides the basic version of the MCKP, it has several variants such as the linear, multidimensional, non-linear, multi-objective, and bounded versions. See Section 4 for a comprehensive list of the problem variants. We will see in Section 8 that the Multidimensional Multiple-choice Knapsack Problem is a widely used variant of the problem.

Several algorithms have been developed to solve the problem. Many of them are known from the solution methods of the Knapsack Problem (e.g., dynamic programming, greedy) but there are methods specific to the MCKP (e.g., Pisinger’s Minimal Algorithm, Bi-objective Approximate Solution Search Algorithm). See Section 5 for an overview of the solution methods for the MCKP. The dynamic programming method is the most popular algorithm to solve the MCKP.

Although MCKP is presented in numerous papers, we have found only a few review papers discussing it. To our knowledge, this is the first review paper whose entire content is dedicated to MCKP. Another unique feature of our paper is that it is application-oriented.

In 1998, Lin [6] provided a bibliographical survey on some generalizations of the knapsack problem. It summarizes the features of the solution methods and the computational experience as reported in the literature. The solution approaches developed for MCKP were included in the survey, along with other generalizations of the KP. Each algorithm was briefly summarized.

The 1990 book by Martello and Toth [7] on knapsack problems presents MCKP and summarizes the results in only four pages. The book by Pisinger and Toth [8] on knapsack problems includes a whole chapter on MCKP, and was published in 1998. The chapter explains the main concepts and terms related to MCKP and presents heuristics, relaxations, bounds, reductions, and other algorithmic techniques for the exact solution of MCKP. It also studies solutions for large-sized instances. Computational results compare the performance of the most effective algorithms published.

The book on knapsack problems by Kellerer et al. [9], published in 2004, also includes a chapter [10] dedicated to MCKP. It presents theoretical results, including dominance relations and upper bounds, some exact and heuristic solution methods, and computational results.

Cacchiani et al. [11] published a recent survey on knapsack problems in 2022. Their survey includes a short section on MCKP.

3. Problem Model

MCKP belongs to the category of integer programming problems. It can be formally defined as follows ($\mathbb{N},\mathbb{R}$ denote the natural and real numbers, respectively):

Inputs:

• The knapsack capacity: $c\in \mathbb{R}$
• The number of classes: $r\in \mathbb{N}$
• The number of items in each class: $n_i\in \mathbb{N}$ for 1 ≤ i ≤ r
• The value of each item: $v_{ij}\in \mathbb{R}$ for 1 ≤ i ≤ r, 1 ≤ j ≤ n_i
• The weight of each item: $w_{ij}\in \mathbb{R}$ for 1 ≤ i ≤ r, 1 ≤ j ≤ n_i

Output:

• The number of items in the selection: x_ij for 1 ≤ i ≤ r, 1 ≤ j ≤ n_i

Optimization goal:

• The total value of the selected items:

$$\mathrm{maximize} \sum _{i=1}^r\sum _{j=1}^{n_i}{v}_{ij}{x}_{ij}$$

(1)

Subject to

• The capacity constraint:

$$\sum _{i=1}^r\sum _{j=1}^{n_i}{w}_{ij}{x}_{ij}\le c$$

(2)

• Only one item is selected from each class:

$$\sum _{j=1}^{n_i}{x}_{ij}=1, 1 \le i \le r$$

(3)

• Binary condition (an item is either selected or not):

$$x_{ij}\in \left\{\mathrm{0,1}\right\}, 1 \le i \le r, 1 \le j \le n_i$$

(4)

MCKP can be formulated in an alternative way as well without using the variable x:

Optimization goal:

• The total value of the selected items:

$$\mathrm{maximize} \sum _{i=1}^r{v}_{i{j}_i}$$

(5)

Subject to

• The capacity constraint:

$$\sum _{i=1}^r{w}_{i{j}_i}\le c$$

(6)

• Index j_i denotes which item is selected from class i:

$$j_i\in \left\{\mathrm{1,2},\dots n_i\right\}, 1 \le i \le r$$

(7)

MCKP requires the selection of at least one item from each class. For this reason, it has a solution only if the sum of the smallest weight of each class is greater than or equal to the knapsack capacity:

$$\sum _{i=1}^r\underset{ 1 \le \mathit{j}\le n_i}{\min }{w}_{ij}\ge c$$

(8)

If the sum of the largest weights of each class is smaller than the knapsack capacity, the optimal solution can be found trivially: the item with the largest value should be selected from each class. The algorithmically interesting case is when the sum of the largest weights is smaller than the capacity:

$$\sum _{i=1}^r\underset{ 1 \le \mathit{j}\le n_i}{\max }{w}_{ij}\ge c$$

(9)

If an item has a larger weight than another item within the same class, it also should have a larger value. Otherwise, the item with a smaller value could always be replaced with another item in a selection. An item j is called dominated if there is another item k in the same class with a smaller or equal weight but larger value:

$${v_{ik}\ge v}_{ij} \mathrm{a}\mathrm{n}\mathrm{d} {w_{ik}\le w}_{ij}$$

(10)

The dominated items can be removed from the optimization problem instance. If the items are identical, one sample can be preserved from them.

In some applications, the problem is formulated to minimize item costs instead of maximizing item values.

MCKP can also be formulated alternatively using the differences in the subsequent items. Let us drop the dominated items and sort the other items in increasing order of their value and weight. Let us consider the differences in the values and weights of subsequent items:

$$\begin{gathered} {\overline{v}}_{i1}=v_{i1}, 1 \le i \le r \\ {\overline{v}}_{ij}=v_{ij+1}-v_{ij},\hspace{1em}1 \le i \le r, 1<j<n_i \end{gathered}$$

(11)

$$\begin{gathered} {\overline{w}}_{i1}=w_{i1}, 1 \le i \le r \\ {\overline{w}}_{ij}=w_{ij+1}-w_{ij},\hspace{1em}1 \le i \le r, 1<j<n_i \end{gathered}$$

(12)

In this case, the optimization goal, the knapsack constraint, and the binary condition can be the same as in Equations (1), (2), and (4). However, the condition of selecting one item (Equation (3)) can be replaced with the following constraint:

$${x_{ij+1}\le x}_{ij} 1 \le i \le r, 1\le j<n_i$$

(13)

The above constraint claims that an item can be selected only if the preceding item in the class is selected. By using this precedence constraint, MCKP can be formulated as a special case of the Precedence-constrained Knapsack Problem (PCKP), see Section 4.3.

The definition of the input size is required to calculate the computational complexity of the solution algorithms. Let n denote the total number of items ($n=\sum _{i=1}^r{n}_i$). The size of the input of the MCKP instance can be defined by Equation (14). It depends on the logarithm of the knapsack capacity, the number of classes, and the total number of items.

$$⌈\log c⌉+⌈\log r⌉+\sum _{i=1}^r⌈\log n_i⌉+\sum _{i=1}^r\sum _{j=1}^{n_i}⌈\log v_{ij}⌉+\sum _{i=1}^r\sum _{j=1}^{n_i}⌈\log w_{ij}⌉>⌈\log c⌉+r+n$$

(14)

4. Problem Variants

The literature contains a wide variety of MCKP generalizations. This section lists the variants presented in WoS publications. Although analysis of the problem variants is beyond the scope of our review, they are presented before the algorithms because some of them proved helpful in solving the base version of MCKP. Some generalizations can be reduced to the solution algorithms of MCKPs.

4.1. Linear Multiple-Choice Knapsack Problem (LMCKP)

The Linear Multiple-choice Knapsack Problem represents the linear relaxation of MCKP, i.e., where the binary condition Equation (4) for x_ij is replaced with linear constraints. In this way, the original Integer Programming (IP) problem can be transformed into a Linear Programming (LP) problem, which is much easier to solve. LMCKP may also be referred to as continuous MCKP in the literature.

• Linear constraints:

$${0 \le x}_{ij}\le 1,\hspace{1em}1 \le i \le r, 1 \le j \le n_i$$

(15)

Similarly to MCKP, the dominated items (Equation (10)) can be excluded from the solution in the case of LMCKP. Some further items can be skipped in the case of LMCKP because of dominance. LP dominance refers to the relationship between the ratios of the difference in values and the differences in the weights of the items within a class. An item j is called LP-dominated (or convex-dominated) by items k and l in class i in the following case:

$${v_{ik}\le v}_{i,j}\le v_{i,l} \mathrm{a}\mathrm{n}\mathrm{d} {w_{ik}\le w}_{i,j}\le w_{i,l},$$

(16)

and

$${\displaystyle \frac{v_{i,j}-v_{ik}}{w_{i,j}-w_{ik}}}\le {\displaystyle \frac{v_{i,l}-v_{ij}}{w_{i,l}-w_{ij}}}$$

(17)

If an item is LP-dominated, then an optimal LMCKP solution exists that does not include the item. We observe that if we skip dominated elements (Equation (10)), the values and the weights follow the same order. For this reason, the condition on the values can be omitted from Equation (16). Furthermore, if the LP-dominated items are deleted, the ratio of the increase in the value and the increase in the weight decreases within a class if the items are ordered in increasing order of their weights.

Although some applications are modeled with LMCKP [12], research on solution algorithms for LMCKP is highly motivated by finding a fast approximate solution or upper bound for MCKP. See Section 5.3 for more details on the solution algorithms.

4.2. Multidimensional Multiple-Choice Knapsack Problem (MMKP)

The Multidimensional Multiple-choice Knapsack Problem (MMKP) represents the most widely used generalization of the problem where several knapsacks are introduced. In the MMKP, the weight of an item can be represented by a vector whose elements contain the capacity requirements of the item from each knapsack. The capacity constraint in Equation (2) is replaced with the following constraints:

• The capacity constraints for each knapsack:

$$\sum _{i=1}^r\sum _{j=1}^{n_i}{w}_{ij}{x}_{ijk}\le c_k \hspace{1em}1\le k \le m$$

(18)

If the number of knapsacks is two (k = 2), we can refer to two-dimensional (2-D) MCKP [12].

MMKP is among the most complex knapsack problem variations [13]. It has a broad range of applications, especially in resource allocation, and several algorithms have been proposed in the literature to solve MMKP. There is a close relationship between MMKP and MCKP. The results of the MMKP can be applied to MCKP as well as its special case (e.g., [14]). A solution strategy for solving MMKP is to order the knapsacks and fill them individually by solving MCKP [15].

We observe that some papers apply the term Multiple-choice Knapsack Problem (MCKP) for MMKP as well (see, e.g., [15,16]). However, the two problems are different. MCKP always applies one knapsack; if there is more than one capacity constraint, we can refer to MMKP.

4.3. Precedence-Constrained Knapsack Problem (PCKP)

In the case of the Precedence-constrained Knapsack Problem [17], the precedence between the items is defined by a directed acyclic graph. Let the graph be denoted by G = (V, E), where V and E denote the vertices and edges, respectively. Equation (3) in the MCKP formulation is replaced with the following precedence constraint:

$${x_i\ge x}_j \left(i,j\right)\in E$$

(19)

As we mentioned in Section 3 MCKP can be formulated as a special case of the PCKP. In MCKP, the graph is a directed forest consisting of disjoint paths corresponding to classes.

4.4. Knapsack Problem with Conflicts

Similarly to the PCKP, the Knapsack Problem with Conflicts (KPC) also applies a graph to define additional constraints. However, the meaning of the graph is different. The items connected with an edge cannot be selected together. Equation (3) in the MCKP formulation is replaced with the following constraint:

$$x_i+x_j\le 1\left(i,j\right)\in E$$

(20)

MCKP can be considered a special KPC case where the conflict graph consists of pairwise disjoint cliques. Coniglio et al. [18] propose a branch-and-bound algorithm to solve the problem. They adopt MCKP in the proposed algorithm to derive upper bounds for pruning the branch-and-bound tree nodes. Several MCKP-based upper bounds are introduced. The MCKP-based lookup-table bound is calculated by using dynamic programming (see Section 5.2). A new partition-based upper bound is computed based on solving the dual of the LP relaxation of the MCKP formulation (Section 5.3).

4.5. Selective Multiple-Choice Knapsack Problem (SMCKP)

This is a practically relevant variant of the problem when no item may be selected from a class. Condition Equation (3) is replaced with the following one:

$$\sum _{j=1}^{n_i}{x}_{ij}\le 1, 1 \le i \le r$$

(21)

This variant can be easily reduced to the original case by adding a dummy item to the class whose weight and value are equal to zero. For this reason, the solution algorithms for MCKP can be applied to solve the problem. This variant is usually referred to as MCKP in the literature, but, sometimes, it is named Selective MCKP to distinguish it from the original problem [12]. It always has a feasible solution.

Algorithms have been developed especially for Selective MCKP. In MCKP, the question is which item to select from each class. In SMCKP, the question also concerns which classes to choose items from. Tsesmetzis et al. [12,19] propose an algorithm for SMCKP based on algorithms that solve the Knapsack Problem. First, classes are greedily selected with the best value and weight ratios. Then, the items of the remaining classes are examined in decreasing order of their values, and an item is selected if the capacity constraint is not violated. They applied the proposed algorithm for the profit maximization of web service providers.

4.6. Budgeting Problem with Bounded Multiple-Choice Constraints (BBMC)

The Budgeting Problem with Bounded Multiple-Choice Constraints allows the selection of more than one item from each class, and different relations bound the number of items. Condition Equation (3) is replaced with the following one:

The total number of item instances is bounded in each class by the “less than or equal to”, the “greater than or equal to”, or the equivalence relations:

$$\sum _{j=1}^{n_i}{x}_{ij}\le a_i i \in L$$

$$\sum _{j=1}^{n_i}{x}_{ij}\ge a_i i \in G$$

(22)

$$\sum _{j=1}^{n_i}{x}_{ij}=a_i i \in E$$

where a_i denotes the bound for the instances in class S_i and $L \cap G \cap E=\varnothing , L \cup G \cup E=\{S_1,\dots ,S_r\}$.

Despite its name, the problem has various applications, including manufacturing, logistics, and solving other combinatorial optimization problems. Pisinger [20] demonstrated that dynamic programming can transform the problem into an equivalent MCKP. The transformation leads to a drastic increase in the number of variables. For this reason, he proposed a more efficient algorithm based on Dantzig–Wolfe decomposition. The master problem solves a continuous MCKP, while the subproblems are optimized using a median search algorithm. The integer optimal solution is derived by applying the dynamic programming transformation to MCKP for an expanding core.

4.7. Multicriteria Multiple-Choice Knapsack Problem

In the Multicriteria Multiple-choice Knapsack Problem, instead of a single objective, there are several objectives to be optimized. The optimization goal in Equation (1) is replaced with the following expression:

• The optimization goal:

$$\mathrm{maximize} \sum _{i=1}^r\sum _{j=1}^{n_i}{v}_{ij1}{x}_{ij},\mathrm{maximize} \sum _{i=1}^r\sum _{j=1}^{n_i}{v}_{ij2}{x}_{ij},\dots ,\mathrm{maximize} \sum _{i=1}^r\sum _{j=1}^{n_i}{v}_{ijm}{x}_{ij},$$

(23)

In this case, the optimization goals are typically conflicting, and there is usually no clear optimum solution that simultaneously optimizes all objectives. Instead, we can speak about a solution set called the Pareto front. The Pareto optimal solutions form the Pareto front. A solution is described as Pareto optimal if none of the objectives can be improved without degrading another objective or violating any constraints.

Levin and Safinov [21] apply multicriteria MCKP to improve telecommunications networks. Using a two-stage heuristic scheme, their proposed method reduces the Multicriteria Multiple-choice Knapsack Problem to MCKP. In the first phase, multicriteria ranking is performed to estimate priorities, and then the obtained one-criterion MCKP is solved in the second phase.

Another way to reduce the multicriteria case to the original MCKP is to combine the multiple goals into one by applying their weighted sum. In this case, the MCKP solution provides one of the Pareto optimal solutions.

4.8. Multi-Objective, Multi-Dimensional, Multiple-Choice Knapsack Problem

The Multi-objective, Multi-dimensional, Multiple-choice Knapsack Problem extends the single objective of MMKP with further objectives, like the previous problem. Here the optimization goal in Equation (1) is replaced with multiple goals:

• The optimization goal:

$$\mathrm{maximize} \sum _{i=1}^r\sum _{j=1}^{n_i}{v}_{ij1}{x}_{ij},\mathrm{maximize} \sum _{i=1}^r\sum _{j=1}^{n_i}{v}_{ij2}{x}_{ij},\dots ,\mathrm{maximize} \sum _{i=1}^r\sum _{j=1}^{n_i}{v}_{ijm}{x}_{ij},$$

(24)

The capacity constraint in Equation (2) is replaced with several knapsack constraints:

• The capacity constraints for each knapsack:

$$\sum _{i=1}^r\sum _{j=1}^{n_i}{w}_{ij}{x}_{ijk}\le c_k \hspace{1em}1\le k \le m$$

(25)

The problem is applied to robotics [22].

4.9. $ϵ$-MCKP

This variant of the problem introduces an error $ϵ$ ≥ 0, and the sum of the weights of the selected items should be in the range $[c-ϵ, c+ϵ]$ (see [23]). The capacity constraint Equation (2) is replaced with the following inequalities:

$$\sum _{i=1}^r\sum _{j=1}^{n_i}{w}_{ij}{x}_{ij}\le c+ϵ$$

(26)

$$\sum _{i=1}^r\sum _{j=1}^{n_i}{w}_{ij}{x}_{ij}\ge c-ϵ$$

(27)

General ILP solvers or adapting the dynamic programming algorithm of the standard MCKP can solve the problem.

4.10. Fuzzy Multiple-Choice Knapsack Problem (FMCKP)

The item values $v_{ij}$, weights $w_{ij}$, and the knapsack capacity c are represented by fuzzy numbers which express their uncertainty. The fuzzy numbers can be defined by a pair (A, m), where A represents a set and m: A→ [0, 1] denotes a membership function. Furthermore, A is normalized and convex, while m achieves value 1 and is segmentally continuous. The triangular fuzzy numbers represent a common type of fuzzy number where the membership function is represented by three points connected with line segments. Either way, the optimization goal and the capacity constraint are the same, but they include fuzzy numbers.

Pareto optimal solutions can represent the results for fuzzy optimization. Several approximation algorithms are devised for FMCKP [24,25].

4.11. Fuzzy Multidimensional Multiple-Choice Knapsack Problem (FMMKP)

This is the fuzzy version of MMKP. In this case, the item values $v_{ij}$, weights $w_{ij}$, and the knapsack capacities c_k are represented by fuzzy numbers. For more information, see [26,27].

4.12. Bottleneck Multiple-Choice Knapsack Problem (BMCKP)

The Bottleneck Multiple-choice Knapsack Problem represents the min–max version of MCKP. The optimization goal in Equation (1) is replaced with the following expression:

$$\mathrm{minimize} \mathrm{z}=\underset{i,j}{\max }{v}_{ij}{x}_{ij}$$

(28)

Martello and Toth applied the above problem to solve the Bottleneck General Assignment Problem [28]. You can read about the application of MCKP to solve the General Assignment Problem in Section 6.4.

4.13. Generalized Multiple-Choice Knapsack Problem (GMCKP)

In the Generalized Multiple-choice Knapsack Problem, more than one item can be selected from each class. Equation (3) is replaced with the following expression:

• The total number of item instances is bounded in each class:

$$\sum _{j=1}^{n_i}{x}_{ij}\le a_i 1 \le i \le r$$

(29)

where a_i denotes the upper bound for the instances in class S_i.

4.14. Bounded Generalized Multiple-Choice Knapsack Problem (BGMCKP)

The Bounded Generalized Multiple-choice Knapsack Problem is a further generalization of GMCKP. It allows us to select a bounded number of instances from each item, and more than one item can be selected from each class [29]. The conditions Equations (3) and (4) are replaced with the following ones:

• The total number of item instances is bounded in each class:

$$\sum _{j=1}^{n_i}{x}_{ij}\le a_i 1 \le i \le r$$

(30)

where a_i denotes the upper bound for the instances in class S_i.

• A bounded number of instances can be selected from each item:

$$x_{ij}\in \left\{\mathrm{0,1}, \dots {, m}_{ij}\right\}, 1 \le i \le r, 1 \le j \le n_i$$

(31)

where m_ij denotes the upper bound for the instances of item j in class S_i.

4.15. Bi-Objective Linear Multiple-Choice Knapsack Problem (BLMCKP)

Besides the total value, other optimization goals may also be considered. For example, equity (or fairness) denotes balance in the weights allocated to the classes. It can be formulated as the difference between the weights allocated to any two classes. In this case, the optimization goal (Equation (1)) is extended with the minimization of the equity [30] as well.

• Minimize the equity denoted by f:

$$\min f$$

(32)

Some further constraints related to equity are added to the problem model:

• The auxiliary decision variables U and L are defined in such a way that the weight of the selected item in any class belongs to the interval [L, U]:

$$L\le \sum _{j=1}^{n_i}{w}_{ij}{x}_{ij}\le U$$

(33)

• Equity is the width of the interval [L, U]:

$$U-L \le f$$

(34)

Since the optimization goals of the problem include both the total value and the equity, it becomes a multi-objective optimization problem.

4.16. Hierarchical Generalization of MCKP

Mason and Blake [31] introduced a variant of MCKP that can be applied to items organized in a hierarchy. In this version, the classes are not disjoint; some items are members of more than one class. The problem is called hierarchical because the relationship between the items can be described as a hierarchy. Additional constraints can be added to the MCKP problem model to express sharing the items between classes:

• An item can belong to multiple classes:

$$x_{ij}=x_{kl}\in \left\{\mathrm{0,1}\right\}, i\in \left[1,r\right],k\in \left[1,r\right],i\ne k,j\in [1,n_i], l\in [1,n_k]$$

The problem was applied in multimedia, more precisely in rendering.

4.17. Non-Linear Multiple-Choice Knapsack Problem

In the non-linear case, the total value and weight are non-linear functions of the values and the weights of the items. The objective function (Equation (1)) and the knapsack constraints (Equation (2)) are defined in the following way in the non-linear separable MCKP:

• The total value of the selected items:

$$\mathrm{maximize} \sum _{i=1}^r\sum _{j=1}^{n_i}f\left(x_{ij}\right)$$

(35)

• The capacity constraint:

$$\sum _{i=1}^r\sum _{j=1}^{n_i}g\left(x_{ij}\right)\le c$$

(36)

where f(x) and g(x) are continuous and differentiable functions [32]. Although the problem is more complex than MCKP, several solution methods that utilize its unique structure have been developed. See Xu et al. [33] as an example of the application of the problem in vehicular crowd sensing.

4.18. Expanding Capacity Multiple-Choice Knapsack Problem (ECMCKP)

Sbihi [34] introduced the problem of the Expanding Capacity Multiple-choice Knapsack Problem (ECMCKP), which arises in budget planning over discrete periods. It can be considered as a special case of the MMKP. The classes correspond to the periods; there are as many knapsacks as the number of periods. The knapsack constraint (Equation (2)) is replaced with the following one:

$$\sum _{i=1}^p\sum _{j=1}^{n_i}{w}_{ij}{x}_{ij}\le c, 1 \le p \le r$$

(37)

A reactive Tabu search algorithm was developed to solve the problem.

4.19. Matroidal Knapsack

A matroid is defined by a pair of (N, F) where N denotes a finite set and F is a nonempty set of subsets of N with some unique properties (downward-closed property and augmentation property). F is called independent sets. The basis of a matroid is an independent set with the maximal number of items [35]. The problem of finding the maximum weight basis for a given matroid subject to a knapsack constraint is known as the Matroidal Knapsack (MK) problem [36]. MK applies a similar optimization goal and knapsack constraints to the Knapsack Problem. The naming convention is different: the item weight in MK corresponds to the item value in KP. The difference between the two problems is that while the knapsack problem performs optimization for any selection of the items, the matroidal knapsack restricts the choices to the matroid basis. MCKP can be considered a special MK case [37]. In this case, the independent sets of the matroid correspond to the set items consisting of at most one item from each group.

4.20. Fairness-Aware MCKP

The fairness-aware MCKP includes an extra constraint to provide fairness among classes:

$$\sum _{j=1}^{n_i}{w}_{ij}{x}_{ij}\le c\beta$$

(38)

β expresses the degree of fairness. Decreasing this parameter may ensure that each class occupies a similar amount of space in the knapsack.

The problem appears in the optimization of provisioning Deep Neural Networks (DNN) in a hybrid DNN deployment approach where the DNNs are located on mobile devices and edge nodes [38]. It can be solved by adapting MCKP solution methods to this variant.

4.21. MCKP with Setup

MCKP with setup is perhaps the most comprehensive variant of the original problem where the items can be processed in multiple periods, and a setup cost is also considered. This problem has been discussed in several recent papers [39,40]. In addition to the inputs used by MCKP, this version includes the following variables as well:

• The number of periods: $T\in \mathbb{N}$
• The setup cost of the classes: $f_{it}\in \mathbb{R}$ for 1 ≤ i ≤ r, 1 ≤ t ≤ T
• Capacity consumption of classes: $s_i\in \mathbb{R}$ for 1 ≤ i ≤ r

The value depends on the period as well:

• The value of each item: $v_{ijt}\in \mathbb{R}$ for 1 ≤ i ≤ r, 1 ≤ j ≤ n_i, 1 ≤ t ≤ T

The output has also changed:

• The number of items in the selection in period t: x_itj for 1 ≤ i ≤ r, 1 ≤ j ≤ n_i, 1 ≤ t ≤ T
• Indicator for whether class i is activated in period t:
• y_ij for 1 ≤ i ≤ r, 1 ≤ t ≤ T

Optimization goal:

• The total value of the selected items:

$$\mathrm{maximize} \sum _{t=1}^T\sum _{i=1}^r\sum _{j=1}^{n_i}{v}_{ijt}{x}_{ijt}+\sum _{t=1}^T\sum _{j=1}^{n_i}{f}_{it}{y}_{it}$$

(39)

Subject to

• The capacity constraint:

$$\sum _{t=1}^T\sum _{i=1}^r\left(\sum _{j=1}^{n_i}{w}_{ij}{x}_{ij}+s_i{y}_{it}\right)\le c$$

(40)

• Only items from active classes can be selected:

$$x_{ijt}\le y_{ij}, 1 \le i \le r, 1 \le j \le n_i, 1 \le t \le T$$

• At most one item is selected from each class:

$$\sum _{t=1}^T{x}_{ijt}\le 1,\hspace{1em}1 \le i \le r$$

(41)

• Binary condition (an item is either selected or not):

$$x_{ijt}\in \left\{\mathrm{0,1}\right\},\hspace{1em}1 \le i \le r, 1 \le j \le n_i, 1 \le t \le T$$

(42)

• Binary condition (a class is either activated or not):

$$y_{it}\in \left\{\mathrm{0,1}\right\}, 1 \le i \le r, 1 \le t \le T$$

(43)

4.22. Chance-Constrained MCKP

In Chance-constrained MCKP (CCMCKP), item weights are random variables [41]. The problem is motivated by real-world applications. In this case, the weights $w_{ij}$ are random variables. A new input variable is introduced:

• Confidence level: $P_0\in \left[\mathrm{0,1}\right]$

The capacity constraint Equation (2) changes to probability:

• The capacity constraint:

$$P\left(\sum _{i=1}^r\sum _{j=1}^{n_i}{w}_{ij}{x}_{ij}\le c\right)\ge P_0$$

(44)

5. Algorithms

The algorithms solving the binary Knapsack Problem (e.g., greedy and dynamic programming approaches) can also be adapted to MCKP. This section describes the algorithms presented or applied in the papers selected for our review.

5.1. Greedy

The greedy solution of the Knapsack Problem [42] offers a fast approach, although it usually fails to find the optimum. The KP’s greedy approximation algorithm iteratively selects the item for which the value and weight (v_i/w_i) ratio is the highest among the remaining items whose sizes do not exceed the available space in the knapsack.

The greedy method can be adapted to MCKP in several ways. A common approach starts with the initial solution where the first item is selected from each class. Then, the selection is greedily improved by replacing the items chosen from the classes with the next ones so that the capacity constraint is not violated. The measure of the goodness of a replacement of an item can be expressed by the ratio of the increase in the value and the increase in the weight, which is also called the slope [5,43]:

$$s_{ij}={\displaystyle \frac{v_{i,j}-v_{i,j-1}}{w_{i,j}-w_{i,j-1}}}1\le i\le r,2\le j\le n_i$$

(45)

The time complexity of the greedy algorithm is typically $O(n\log n)$. Although the greedy method usually fails to find the optimum value, it can produce a fast solution.

The term MCKP-greedy algorithm is often used in the literature for the greedy solution method of LP-relaxation (e.g., [10,44]). The greedy algorithms for LMCKP and MCKP (Section 5.3) are two different methods despite the similarities in their main improvement step. To distinguish them, we use the term MCKP greedy only if the method does not apply linear relaxation.

5.2. Dynamic Programming

Dynamic programming (DP), introduced by Bellman [45], is a widely used solution method for the Knapsack Problem [46]. This method can be adapted to MCKP as well (See e.g., [47,48]).

Dynamic programming solves a problem by reducing it recursively to subproblems. In the case of MCKP, the subproblem is about finding U(i,d), which denotes the maximum value that can be attained with a total weight less than or equal to d by selecting one item from each class S_l, S₂, … , S_i ($1 \le i \le r$, $0\le d \le c$). U(i,d) values are calculated with the help of a recursive formula from the optimal values of subproblems at the class $S_{i-1}$. They can be calculated either iteratively or recursively. The DP algorithm finds the exact optimum if each item’s weight is an integer. The recursive formula can also be created based on the item values.

The running time is $O\left(c·\sum _{i=1}^r{n}_i\right)=O(c·n)$, where n is the total number of items. Since c is exponential in the number of bits of the weights, the running time is exponential in the length of the input (see Section 3). MCKP can be solved using the dynamic programming method in pseudo-polynomial time. We observe that if all weights are polynomial in the number of items, DP leads to a polynomial solution of MCKP.

DP can be converted into a fully polynomial time approximation scheme (FPTAS) using scaling (Section 5.9). For more information on branch-and bound methods, see Sections 11.5 and 4.5 in the books by Kellerer et al. [10] and Pisinger and Toth [1], respectively.

5.3. Linear Relaxation

LMCKP (Section 4.1) has high relevance in solving MCKP as well. LMCKP has fast exact solution algorithms. It can be solved even in linear time. Rounding the solution of LMCKP provides an approximate solution for MCKP. It is suitable for finding an initial solution quickly (see e.g., Section 5.6). A rounded solution can be improved by using heuristic methods. Linear relaxation can provide an upper bound for MCKP with a short running time; therefore, it is used in branch-and-bound algorithms as well (Section 5.5).

Sinha and Zoltners [5] examined the properties of LMCKP and proposed a greedy algorithm to find its exact solution. The greedy approach is often used because of its simplicity. First, it removes the dominated and the LP-dominated items. The algorithm greedily selects items with the largest slope, which does not violate the resource constraint. The solution of the greedy method has some unique properties [5]: either all variables are integers (in this case the solution is optimal for MCKP as well), or the solution has two adjacent fractional variables in one so-called fractional class, and all other variables in the optimal solution are integers.

In the case of the greedy approach, most of the computational effort ($O\left(\sum _{i=1}^r{n}_i\log n_i\right)$ is used for sorting in the reduction phase to eliminate the dominated and LP-dominated items. The running time of the solution algorithms can be improved to linear time by using a partitioning technique without the initial reduction. Dyer [49] and Zemel [50] first independently devised a linear-time algorithm in 1984.

Dudziński and Wałukiewicz [51,52] proposed an algorithm by exploiting the relationship between the primal and dual feasible solutions in 1984. The initial reduction step makes its overall time complexity worse than linear. However, the reduced problem is solved in sublinear time, which supports its application in branch-and-bound methods where the algorithm solving LMCKP is called many times.

Sarin and Karwan [53] proposed the dual gradient method in 1989 to solve LMCKP, using dual simplex pivoting and pseudo pivoting. Pisinger [43] applies a primal approach in his minimal algorithm (Section 5.6 Pisinger’s Minimal Algorithm) to solve LMCKP in linear time, which is more straightforward to implement than the LP-dual approaches.

For more information, see Subchapter 11.2 in Kellerer et al.’s book [10] and Subsection 3.2 of the survey paper by Lin [6].

5.4. Lagrangian Relaxation

The Lagrangian relaxation of MCKP can be formulated by combining the optimization goal (Equation (1)) with the constraint (Equation (2)):

$$\mathrm{maximize} \sum _{i=1}^r\sum _{j=1}^{n_i}{(v}_{ij}{x}_{ij}-{\lambda (w}_{ij}{x}_{ij}-c))$$

(46)

where λ is the Lagrangian multiplier [54]. Replacing Equations (1) and (2) with Equation (38), the resulting problem does not contain any constraint and can be solved more quickly than the original problem. For any fixed non-negative Lagrangian multiplier, the optimal result to the Lagrangian relaxation serves as an upper bound for the optimum of the original problem. The algorithms for the relaxed Lagrangian often solve the dual problem, which is to minimize the value of the Lagrangian relaxation for the Lagrangian multiplier. Bisection and tangential approximation search techniques can be used to find the solution. The latter method terminates in a linear number of iterations.

5.5. Branch and Bound

A branch-and-bound algorithm systematically enumerates the candidate solutions by traversing a rooted tree where the branches represent subproblems and the leaves correspond to specific solutions. Before finding the exact optimum for a branch by an exhaustive search, a bound is calculated for the branch by a fast algorithm (e.g., linear relaxation, Lagrangian duality). If the upper bound of a branch is too small to achieve the largest solution value found so far, the branch is skipped from further processing. Branch-and-bound algorithms may have a long running time to find the exact solution, but they can produce a lower and upper bound if they terminate before the complete run.

Several branch-and-bound algorithms have been developed to solve MCKP, with the oldest ones published by Nauss [3] and Sinha and Zoltners [5]. Nauss applied Lagrangian-based relaxation in his algorithm. Sinha and Zoltners proposed a greedy algorithm to solve the linear relaxation of MCKP (Section 5.3) and incorporate it in a branch-and-bound procedure. They significantly reduced the running time compared to Nauss’ algorithm. Armstrong et al. [55] proposed an algorithm similar to Sinha and Zoltners’s but designed to solve large-scale MCKPs in 1983. They achieved a significant reduction in storage requirements.

Dyer, Kayal, and Walker et al. [56] proposed a dual simplex method-based branch-and-bound procedure in 1984. Glover and Klingman’s dual simplex method [57] is used to find the optimum solution of the linear relaxation of MCKP within a depth-first search procedure by applying different branching techniques. Dyer, Riha, and Walker [58] proposed a hybrid algorithm in 1995 which applies dynamic programming in a branch-and-bound method using a breadth-first search strategy and Lagrangian duality.

Nakagawa et al. [59] proposed a new calculation method for the upper bound of MCKP in 2001. The problem is converted into the LP relaxation of the KP by using a variable substitution. They gained an upper bound slightly tighter than the bound from the widely used LP relaxation of MCKP.

The worst-case complexity of a branch-and-bound algorithm is exponential because of the systematic enumeration. However, the average complexity of the algorithm is significantly lower due to the bounding process.

For more information on branch-and-bound methods, see Subchapters 11.4 and 4.4 in the books by Kellerer et al. [10] and Pisinger and Toth [2], respectively, and Subsection 3.3 of the survey paper by Lin [6].

5.6. Pisinger’s Minimal Algorithm

Pisinger’s Minimal Algorithm [43] proved to be efficient in practice, and it is a widely used algorithm for solving MCKP. It is a core-based branch-and-bound method combined with dynamic programming. It was devised for MCKP with integer item values and weights. First, it solves the linear relaxation of the problem through a partitioning algorithm to find an initial solution. LMCKP is solved in linear time by applying median search. Then, the algorithm exploits the observation that most of the variables in the LMCKP solution are equal to the optimal solution of the MCKP. It applies the concept of core, which denotes the classes that include the classes where the LP solutions differ from the optimal IP solutions with a significant probability. The algorithm starts with a core containing the fractional class of the initial solution. Then, dynamic programming adds new classes to the core if needed iteratively. The algorithm satisfies some minimality constraints because the core size, the number of classes enumerated, and the effort used for sorting and reduction are minimal. The time complexity of the algorithm is $O(n+c{\sum }_{N_i\in C}{n}_i)$, where C denotes the core.

5.7. Bi-Objective Approximate Solution Search Algorithm (BISSA)

The capacity constraint can be transformed into an optimization goal. The resulting bi-objective optimization problem both maximizes the total value and minimizes the total weight. The capacity constraint of MCKP defined by Equation (2) is replaced with a second objective in the bi-objective problem:

• Minimize the total weight of the selected items:

$$\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e} \sum _{i=1}^r\sum _{j=1}^{n_i}{w}_{ij}{x}_{ij}$$

(47)

The solutions to the modified problem and MCKP are closely related. The Pareto front representing its solution set contains optimal solutions of the original MCKP.

Bednarczuk et al. [60] proposed a heuristic approximation algorithm based on the bi-objective transformation of MCKP in 2018. The solution method relies on solving a series of linearly scalarized bi-objective problems. The linear scalarized version of the problem maximizes the following expression for 0 < λ < 1:

$$\max \lambda \sum _{i=1}^r\sum _{j=1}^{n_i}{v}_{ij}{x}_{ijk}+(1-\lambda )\sum _{i=1}^r\sum _{j=1}^{n_i}{(-w}_{ij}{x}_{ij})$$

(48)

There is a closed-form formula to solve the above problem explicitly. The bi-objective approximate solution search algorithm (BISSA) iteratively solves the linear scalarized problem with updated λ. Each iteration runs in linear time. However, the number of iterations is not determined in the paper. The algorithm finds an exact MCKP solution or provides a lower and upper bound. The original BISSA method was recently improved by using the Chebyshev scalarization instead of the linear scalarization [61].

5.8. Binary Search

Gens and Levner [62] presented an approximate binary search algorithm for finding an approximate solution for MCKP with running time O(n log m) in 1998. The ratio of the optimum value and the solution value obtained by the algorithm is at most 5. In the approximate binary search, when the optimum value lies within a search interval, the search interval can be iteratively reduced by applying a method that can determine for a given value x within the interval whether the optimum is smaller than $(1+{ϵ}_1)x$ or larger than $(1-{ϵ}_2)x$. He et al. [63] proposed an algorithm in 2016 which improves the approximation ratio to $3+{\left({\displaystyle \frac{1}{2}}\right)}^t$ and whose running time is O(n(t + log m)), where t is a positive integer.

5.9. Fully Polynomial Time Approximation Scheme (FPTAS)

An approximation scheme of a maximization problem is an algorithm which solves within a factor 1 − ε of the maximum for any ε > 0:

$$p \ge (1-\epsilon )p^{*}$$

(49)

where p* is the maximum of the problem and p is the solution value provided by the approximation scheme. The algorithm is called a fully polynomial time approximation scheme if it runs in polynomial time in the size of the problem input and 1/ε: O(nm/ε).

DP (Section 5.2) can be converted into a fully polynomial time approximation scheme (FPTAS) using scaling [64] in the following way. First, an appropriate scale factor is calculated for the given ε. The profit values are scaled by dividing them by the scale factor and then rounding the results down. The DP algorithm by profit runs with the scaled profit values to find the approximate solution. Bansal et al. [65] proposed an FPTAS in 2004, improving the other algorithms’ time bound.

For more information on FPTAS, see Subchapter 11.9 in Kellerer et al.’s book [10].

5.10. Integer Programming

Integer programming is a straightforward solution method of the formal MCKP model, but it is rarely used [66] because of the rich variety of other, more efficient methods.

5.11. Distributed Algorithms

Distributed algorithms are robust and efficient methods for optimizing large networks [67,68,69]. In this case, each network node makes decisions locally instead of globally, as in a centralized scheme. They are preferably used in wireless networks, cloud systems, and other parallel and distributed systems. Distributed algorithms are also popular in solving large-scale problems in a parallel way where parts of the algorithm run simultaneously on independent processors, with limited information about the status of computations in other processors. For this reason, their applications also include areas such as scientific computing, data mining, and machine learning.

Despite the broad range of potential applications, there is a lack of methods to solve MCKP in a distributed way. We found only one sample in our data source. Wang et al. [70] formulate the rate adaptation problem in multi-hop wireless networks as MCKP and provide a distributed cooperative method. Each network node runs the same algorithm. The algorithm consists of three components: information exchange algorithm, rate selection algorithm, and node cooperation algorithm. The information exchange algorithm collects information on all the links in the maximum interference range of a node. Each node uses the rate selection algorithm to calculate rates for the links based on the received information. This calculation uses a greedy MCKP method for the links within the maximum interference range of the node. The feasibility of this new rate setting is checked through the node cooperation algorithm. The convergence of the algorithm is proven in the paper.

5.12. Summary

In this subsection, we provide a comparison table of the MCKP algorithms (

Table 1. MCKP algorithms.

Algorithm	Time Complexity	Exact MCKP Optimum?	Special Condition
Dynamic Programming	$O(c·n)$	yes	$w_{ij}\in \mathbb{N}$
Greedy	$O(n\log n)$	no
Linear Relaxation	$O\left(n\right)$	no
Lagrangian relaxation	$O\left(n\right)$	no
Branch and Bound	$O\left(2^n\right)$	yes
Pisinger’s Minimal Algorithm	$O(n+c{\sum }_{N_i\in C}{n}_i)$	yes
Bi-objective Approximate Solution Search Algorithm (BISSA)	$O(n·iterations)$	no
Binary Search	O(n(t + log m))	no
Fully Polynomial Time Approximation Scheme (FPTAS)	O(nm/ε)	no
Integer Programming	$O\left(2^n\right)$	yes
Distributed Algorithms	O(n)	no

).

6. MCKP in Combinatorial Optimization

MCKP can also be applied to solve other combinatorial optimization problems. For example, some combinatorial optimization problems can be considered special cases. MCKP appears in solution approaches to some other combinatorial optimization problems, e.g., in non-linear KP, Integer Programming, Facility Location Problems, decomposition techniques, etc.

6.1. Knapsack Problems

We saw in Section 4 that MCKP has many variants and generalizations, and MCKP can help in solving them in several cases (e.g., Section 4.2, Multidimensional Multiple-choice Knapsack Problem (MMKP); Section 4.5, Selective Multiple-choice Knapsack Problem (SMCKP); Section 4.7, Multicriteria Multiple-choice Knapsack Problem, etc.).

MCKP proved useful in some variants of KP itself as well, such as the piecewise linear knapsack problems (PLKP). Kameshwaran and Narahari [71] applied MCKP to formulate the PLKP. When a general mixed integer linear programming (MILP) solver was used, the solution of the multiple-choice knapsack model of PLKP was the fastest among the various formulations of PLKP. A DP solution is proposed for PLKP based on the DP solution of MCKP. Computational experiments show that the proposed MCKP-based DP algorithm significantly reduces the solution time compared with other DP algorithms developed for PLKP.

Coniglio et al. [18] apply MCKP to the Knapsack Problem with Conflicts. A branch-and-bound method is proposed, using MCKP to derive upper bounds for pruning the branch-and-bound tree nodes.

6.2. Facility Location Problem

The P-Median Problem (PMP) [72] represents a special case of the facility location problem where the goal is to find locations for a fixed number of facilities on a network to minimize the total transportation cost between the facilities and clients. The P-Median Problem can be solved using a decomposition procedure where the subproblems can be represented as MCKP [73]. A three-stage exact method is proposed where MCKP is used several times. MCKP is used to calculate the lower and upper bounds for the initial PMP from the bounds of the sub-PMPs in the iterations of the algorithm. It is also used to calculate the optimal solution of the initial PMP from the optimal solution of the sub-PMPs in the final stage. Dynamic programming is applied to solve MCKP (Section 5.2).

Snyder and Daskin [74] proposed a novel robustness measure called stochastic p-robustness for optimization under uncertainty, which minimizes the expected cost while bounding the worst-case relative regret. The robustness measure was applied to various Facility Location Problems such as the k-Median Problem and the Fixed-charge Location Problem. The problems were solved using variable splitting, also known as Lagrangian decomposition. The Lagrangian subproblem was reduced to MCKP. The Lagrangian subproblems split into two problems, and one of them was reduced to MCKP. Armstrong’s algorithm was selected to produce a lower-bound solution for MCKP. The algorithm was stopped when it reached a 1% optimality gap.

6.3. Network Flow Problems

The problem of network design is constructing a flow network with minimum cost. Network nodes may generate and demand a commodity. The capacity of a node and an edge is called generating and transmission capacity, respectively. The cost of a node and an edge is a function of its capacity. The network design problem aims to find minimum-cost optimal built-in capacities subject to the constraint that all demands should be met in the flow network. The model can be applied to various application domains, from the interconnected power systems through flood control networks and the financial networks to cloud computing system design.

Agarwal [75] examined the multicommodity version of the network design problem. An algorithm is proposed starting from any given solution. The initial solution is gradually improved by solving a series of subproblems. The subproblem is defined over a subnetwork. The subproblem is formulated as MCKP.

In the case of the stochastic version of the problem, the demands at the nodes are random, and the needs are satisfied on a prescribed probability level (reliability constraint). Prékopa and Unuvar [76] apply MCKP, solving the single-commodity stochastic network design under a probabilistic constraint with discrete random variables. They used the concept of a p-efficient point to convert and relax the problem into an LP. The p-efficient points are generated by solving a multiple-choice knapsack problem.

Trofymchuk and Vasyanin study the problem of choosing the capacity of arcs from a given set under a constraint on the maximum flow delay time. It is an important task in multicommodity communication networks. FPTAS was applied to solve the problem in an experimental comparison (Section 5.9).

6.4. Generalized Assignment Problem

The multilevel generalized assignment problem (MGAP) is a variation of the generalized assignment problem, where the agents can execute tasks at different efficiency levels with different costs. Ceselli and Righini [77] present a branch-and-price algorithm to find the exact optimum for the MGAP. It is based on decomposing a master problem and a pricing subproblem. The master problem includes set-partitioning constraints while MCKP can represent the subproblem. MCKP was solved using a modified Pisinger’s minimal algorithm (Section 5.4). Since the original algorithm assumed integer item values and weights, it had to be adapted to manage the cases when they are real numbers. The adaptation applied the relaxation of the bounding tests.

7. Applications

Research on MCKP is motivated by practical applications. This section demonstrates the wide range of domains where MCKP can be applied. We found the WoS categories too general (e.g., Engineering, Electrical & Electronic) and did not apply them. We assigned an application area to the papers.

7.1. Biology

Optimization of resource allocation among multiple threats is a significant problem in land management, and it is essential to address the threats with feasible and effective actions. Moore et al. [66] propose an optimization framework for allocating conservation resources. They formulate the problem as MCKP where expected impact and cost are assigned to each action and the budget is limited. They apply the framework to manage the invasion of multiple introduced plant species in Australia.

7.2. Medical and Health Sciences

The effectiveness of treatment is proved by randomly selecting subjects to be exposed to therapy while the remaining subjects are exposed to a control condition. Randomization interference deals with the problem of how random assignment affects the outcome of the experiment. Feng et al. [78] apply MCKP to test the hypothesis that the mean of effects attributable to treatment is less than or equal to a specific constant. They implement the hybrid dynamic programming/branch-and-bound algorithm of Dyer, Riha, and Walker (Section 5.5) to give the solution of MCKP.

In a recent paper, Su and Li [79] also examine the effectiveness of treatments. They consider nonparametric randomization-based inference in stratified randomized experiments where the experiments are organized in multiple strata (participants are divided into subgroups by experimental conditions). They apply MCKP to compute the quantiles of individual treatment effects. MCKP is solved by dynamic programming (Section 5.2). Although dynamic programming can generally solve MCKP in pseudo-polynomial time, it can solve this problem in polynomial time since the sample size always bounds the weight capacities.

7.3. Management

Bai [80] applies MCKP to data quality management in information systems within an enterprise. An optimization problem is proposed in this framework to minimize the total cost of business control while keeping the risk below a threshold. The problem can be represented as a two-stage MCKP where the output of the local problems constitutes the input of the global problem. MCKP problems are solved by dynamic programming.

Lenstra and Voss [81] provided a quantitative model for the following problem related to the information security risk management problem: where a company should “spend its Information Security (IS) budget to limit as much as possible the damaging consequences of attacks”. They formulated the above problem as MCKP. They recommend applying Pisinger’s Minimal Algorithm and the LP-relaxation of the problem.

The Optimal Diversity Management Problem (ODMP) can arise in companies offering goods and services which can be customized with options for their clients. The problem is to select an optimal combination of options if many different demands must be satisfied with various subsets of options, but only a limited number of option combinations can be produced. This problem has high relevance in practice, e.g., in the automobile industry. ODMP can be formulated as a large-scale P-Median Problem (PMP) where MCKP can be used in a decomposition procedure [73] (see Section 6.2).

7.4. Marketing

In the case of pay-per-click advertising, the advertisers set a bid corresponding to the maximum amount of money per click. The aim of the advertiser is to maximize the revenue subject to a cumulative budget constraint. Nuara et al. [82] study the problem of optimal selection of the online joint bid and daily budget selection in pay-per-click advertising campaigns over multiple channels. They formulate the problem as a combinatorial semi-bandit problem, which is solved by applying a special case of MCKP for each day of the campaign. MCKP is solved by using dynamic programming (Section 5.2).

7.5. Transportation

Transportation programming is the process of selecting a set of projects to be funded by a transportation agency. Zhong and Young [83] apply MCKP to provide optimal solutions to this problem. The branch-and-bound method proposed by Dyer et al. [56] is used to solve MCKP (Section 5.5).

7.6. Mechanical Engineereing

Mohaddes et al. [84] applies MCKP to the simulation of fuel combustion in gas turbines used in aeronautical and space propulsion systems. It is a challenging task to simulate spray combustion with high fidelity within an affordable computational cost. A variety of models are available for spray combustion simulation with different accuracies and computational costs. The aim of the sub-model assignment problem is to dynamically assign sub-models throughout the combustor area to minimize the overall modelling error under the constraints on computational costs. The problem is formulated as MCKP, and it is solved using the minimal algorithm of Pisinger [43].

7.7. Architecture

Sharafi et al. [85] examine the problem of design optimization of rectilinear building frames. It can be modelled with a knapsack approach. The problem can be formulated as MCKP in the special case where all sub-rectangles within a bay must have one common dimension equal to the bay width.

7.8. Manufacturing

The tolerance allocation problem (TAP) occurs in mechanical assemblies with alternate manufacturing processes for the components. Balakrishnan [86] formulates TAP as MCKP and applies the branch-and-bound algorithm of Sinha and Zoltner [5] to rapidly solve large-scale problem instances (Section 5.5).

Schvartzman and Wellman [87] applied an auction mechanism to a market-based allocation problem arising in the manufacturing domain. They considered a scenario consisting of several manufacturing facilities with different capabilities to produce industrial parts. The facilities may exchange orders among themselves. This order allocation problem is solved as an auction problem which can preserve the private business information of the facilities. A dynamic programming approach is applied. An incremental algorithm is proposed where the solution method of MCKP is adapted to the dynamic auction context, where the auction is repeated periodically with small changes in the set of bids.

Kim et al. [88] examine the two-dimensional cutting stock problem in the paper industry. This problem has several optimization goals. The sheet products are produced in two main cutting stages. First, auxiliary rolls are cut from the so-called jumbo rolls produced from raw material pulp. Then, the sheets are cut from the auxiliary rolls. MCKP is applied to the second stage. It is solved by dynamic programming (Section 5.2).

Measurements are crucial for quality control in manufacturing systems. In semiconductor manufacturing, metrology tools are especially expensive. Dauzère-Pérès et al. [89] examine the problem of minimizing the production rate of defective wafer lots while considering metrology capacity. They apply MCKP to formulate the problem. Solving the linear relaxation of the problem and then applying various rounding heuristics is proposed to approximate the optimal solution of the problem (Section 5.3).

7.9. VLSI Design

In VLSI design, various input specification transformations can improve the layout and performance of a chip. De Leone et al. [90] examine the problem of which transformations and how many times should be applied to optimize the chip design. They formulate the problem as MCKP. The Lagrangian relaxation technique is used to find an approximate solution (Section 5.4).

Liu et al. [91] applied MCKP in data-reuse design of FPGA (Field-Programmable Gate Array)-based systems. It is a widely used technique in data processing applications. Finding the location of the data arrays can be formulated as MCKP where the aim is to minimize the total power consumption while the total occupied memory in the FPGA does not exceed the size of the on-chip RAM. The minimal algorithm of Pisinger was used to solve MCKP (Section 5.6).

7.10. Computer Hardware and Architecture

Effective power management can extend the battery life of mobile devices. Yang et al. [92] examine the problem of dynamic voltage scaling for CPUs. The supply voltage and the corresponding operating clock frequency can be dynamically adjusted according to the required system performance, effectively minimizing energy consumption. Dynamic programming (Section 5.2) is used to derive an Optimal Schedule for Realistic CPUs (OSRC) with minimal energy consumption by using actual power consumption specifications of realistic CPUs.

7.11. Wireless Networks

Data can be transmitted with different data rates over the links of a multi-hop wireless network. Reducing the data rate decreases both energy consumption and throughput. Wang et al. [70] study the rate adaptation problem in IEEE 802.11-based multi-hop networks. They formulate the rate adaptation as MCKP, where the total transmission power is minimized over data rates on the links while satisfying the throughput requirements of all the nodes in the network. They use the problem formulation to prove that the proposed rate adaptation problem is NP-complete. Instead of applying an algorithm of MCKP, they develop a distributed cooperative rate adaptation method to solve the problem (Section 5.11, Distributed Algorithms). Network nodes select transmission rates based on local information collected from neighboring nodes.

Cao et al. [28] propose a crowdsourcing-based framework for target tracking in a wireless sensor network (WSN). An auction-based mechanism is designed to allocate bandwidths in an energy-aware manner. The problem is formulated as MCKP, which is solved by the dynamic programming method (Section 5.2).

Some wireless communication standards enable the application of multiple antennas at both communication sides which can transmit multiple independent data streams. In the case of the channel-adaptive multiple-input multiple-output (CA-MIMO), several detection methods are available with different complexities and error rates for each data stream. Lai et al. [93] formulated the switching of detection methods as MCKP. In the problem model, one set of detection methods is selected for each subcarrier such that their overall complexity is minimized, and the just-acceptable error rate (JAER) constraint is satisfied. They applied the greedy algorithm for the linear relaxation of MCKP (Section 5.3) to solve the problem.

The IEEE 802.22 standard for wireless regional area networks exploits the locally unused spectrum bands. Since the spectrum is a scarce resource, it has high relevance to utilizing the holes in a wide spectrum used for other purposes (e.g., television broadcasting). Cognitive radio networks can be dynamically configured to select the best free channels for communication. Koufos et al. [94] proposed a formal model and algorithms for optimal allocation of cognitive users to sense spectrum bands. They formulated the distributed sensing problem as MCKP. They proposed to solve the problem by applying first the greedy method of the linear relaxation of MCKP (Section 5.3) and then by using some heuristics to improve the result. Ren et al. [95] also studied cognitive radio networks. They proposed novel diversity technology, called Channel Aggregation Diversity (CAD). The data transmission rate is maximized by converting a joint power-channel allocation problem to MCKP. Then, the optimal allocation policy is derived through dynamic programming (Section 5.2).

In wireless sensor networks (WSNs), the nodes closer to the base station have more network traffic load than the ones at the network periphery and they can deplete their energy faster than the other nodes. The overall lifetime of the network can be increased if the energy consumption is evenly distributed among the nodes. The Dynamic Transmission range Adjustment (DTA) algorithm selects a transmission level for each sensor node based on its residual energy. Tran-Quang et al. [96] formulate the DTA optimization problem as MCKP and present a dynamic programming method to solve the optimization problem.

Xu et al. [97] investigate coded caching in cache-enabled small-cell networks (SCNs), where each small base station (SBS) is equipped with a local cache. Coded caching is a technique to enhance cache efficiency by partitioning files into multiple segments and caching the different file segments in different SBSs. The problem is examined by applying different performance metrics. Coded cache placement problems with different optimization goals are formulated as MCKP, and solved by a greedy algorithm (Section 5.1) and linear relaxation (Section 5.3).

7.12. Parallel/Distributed Systems, Cloud and Edge Computing

Scheduling scientific workflows on the grid represents a complex multicriteria optimization problem. For example, the expected execution time and the cost of running activities on machines belong to typical optimization goals. Prodan and Wieczorek [98] propose a novel multicriteria scheduling algorithm. They model the problem as an extension of MCKP and propose a general bi-criteria scheduling heuristic called the dynamic constraint algorithm (DCA), based on dynamic programming.

Placing virtual machines (VMs) is about how to place the VMs assigned to users’ jobs on physical machines (PMs). It is used at the initialization of the system (static VM placement) and later it is performed when the VMs are migrated (dynamic VM placement). Al-Dulaimy et al. [99] formulated the problem as MCKP. The optimization goal of the VM placement is to minimize the energy consumption while the capacity constraint of the PMs is satisfied. Different algorithms are proposed for static and dynamic VM placement. Both algorithms follow the same strategy: the PMs are ordered in decreasing order of their capacity (in the static case) or utilization (in the dynamic case), and then the problem is solved for each PM by solving MCKP in a simple greedy manner.

Wang and Shi [100] propose scheduling algorithms to minimize cost while satisfying deadline constraints for a batch of MapReduce jobs in heterogeneous cloud platforms. MapReduce is a distributed execution framework for parallelizing large-scale data processing. It is used in clouds for Machine Learning, web analytics, scientific workflow systems, etc. The scheduling problem was converted into MCKP via a parallel transformation. The proposed algorithm proved to be efficient if the total budget and the deadline were polynomially bounded by the number of tasks and the number of stages, respectively, in the workflow, which is usually the case in practice.

Wang et al. [101] present a clustering-based cooperative computation offloading framework including mobile and static edge servers and a cloud server in an Intelligent Transportation System. The computation offloading framework enables roadside users to request computation resources to exploit the unused capacities of the onboard computers of the moving vehicles. The paper formulated the so-called “Less than or Equal to” Generalized Assignment Problem for the offloading. The offline problem is solved by using the Bound-and-Bound-based Optimal algorithm, which is a variant of the traditional branch-and-bound algorithm. The upper bound at each branch node is computed by transforming the allocation subproblem into MCKP, and the branching process is conducted by following a greedy solution. MCKP is solved by applying a branch-and-bound algorithm (Section 5.5).

Chanyour et al. [102] also examine the multitask offloading problem in Mobile Edge Computing. They formulate the general Multitask Offloading Decision and Channels Allocation (MODCA) optimization problem where the main goal is to minimize the overall energy consumption under several constraints. The multitask offloading decision is transformed into MCKP. MCKP is solved by using several methods for evaluation purposes (Pisinger’s minimal algorithm, BISSA, and dynamic programming; see Section 5.2, Section 5.6, and Section 5.7, respectively), and the results are compared with each other. According to the simulation results, the BISSA method is the best for a small number of mobile devices, but its performance remains acceptable for larger mobile device numbers.

Alidaee et al. [103] are concerned with scheduling several tasks on a set of parallel machines. The objective is to choose a subset of machines to perform all jobs while minimizing the sum of several costs (machine holding costs, total machine time costs, and total tardiness costs). The problem is transformed to MCKP. Dynamic programming is applied to solve the problem (Section 5.2, Dynamic Programming).

Wang et al. [104] examine the optimization versions of the workflow scheduling problem in clouds. They transform the scheduling problem into MCKP via parallel transformation, in the case where the optimization goal is to minimize the total cost of the workflow with fixed computation deadline.

Data-intensive, scalable computing frameworks have high relevance in distributed systems. In a recent paper, Michiardi et al. [105] study the problem of improving the efficiency of systems with SQL-like querying capabilities. Multi-query optimization (MQO) is about finding similarities among a set of queries to avoid redundant work during query execution. The optimization problem of selecting the best sharing plans is formulated as MCKP, and it is solved efficiently through dynamic programming (Section 5.2). The prototype is implemented for Apache SparkSQL Catalyst optimizer.

7.13. Web and Information Systems

Many web-based systems follow a tiered application architecture where processing a request requires contribution of multiple tiers (e.g., web servers, application servers, and database servers). Chaudhury et al. [106] examine the so-called server allocation problem for tiered systems, which is about minimizing the system cost while satisfying the total response-time requirement. The method proposed in the paper converts the original problem first into MCKP and then solves it by using dynamic programming in pseudo-polynomial time and standard scaling techniques to obtain a FPTAS (Section 5.9).

7.14. Telecommunications

Agarwal applied the multicommodity network design problem (Section 6.3) to telecommunication networks. The original problem was solved by solving a series of subproblems which are formulated as MCKPs. MCKP is solved by dynamic programming (Section 5.2).

7.15. Multimedia

Multimedia contents can be adapted to the actual usage context by applying scalable coding. An image sequence can be encoded at various target bit rates: a smaller bit rate results in poorer quality but less resource usage. Batra [107] applies knapsack problems to video coding. Mathematical formulations are presented for modelling object-based scalability in an MPEG-4-based system. MCKP is used to model authoring or multiplexing of scalable objects (e.g., encoding objects at various target bit rates). The LP relaxation of MCKP is solved by using the LP-dual approach (Section 5.3). The application of Lagrangian relaxation is also examined and the author shows that it does not improve the duality gap compared with the LP relaxation.

Further, 360-degree videos form an essential element of virtual reality (VR) and augmented reality (AR) systems. Mobile Edge Computing (MEC) can support streaming by providing extra storage and computing capabilities for caching and transcoding. Yu et al. [108] consider the joint caching and transcoding problem for tile-based 360-degree video for balancing the trade-offs between MEC storage and computation resource consumption. The combinatorial multi-armed bandit (CMAB) theory is applied to solve the problem. The optimization problem for a single period can be transformed into MCKP, which is solved by a fully polynomial time approximation scheme (FPTAS) (Section 5.9).

Various image compression algorithms are available to compress images. The multimode image compression algorithms adaptively select one from a set of encoding modes to encode a block of a given image. Lee et al. [109] formulate the problem of encoding mode selection for a lossy compression method as MCKP. They solve the problem by applying the greedy method for the linear relaxation of the problem (Section 5.3).

Poularakis et al. [110] examine the problem of caching video encoding layers to minimize the delivery delay in the network. The problem can be reduced to MCKP in polynomial time. MCKP is solved by using FPTAS (Section 5.9).

Application of point clouds is spreading in 3D visualization, including Virtual Reality and Augmented Reality. They require large amounts of data, and their streaming is challenging task. Wang et al. [111] examine the rate adaptation problem of point clouds. Their optimization target is to maximize the user’s Quality of Experience under limited bandwidth. The problem can be modelled by using MCKP. MCKP is reformulated as a submodular function maximization problem. Since the size of the problem instance is huge, they propose a greedy approximation algorithm (Section 5.1) to solve MCKP.

7.16. Software Design and Development

Das [44] examines the problems of function inlining and cloning in compiler optimization. A novel unified model is proposed to handle the above problems as MCKP. The greedy approach of the linear relaxation (Section 5.3) is adapted to solve MCKP.

7.17. Machine Learning

Classification is a standard technique of machine learning. Fischer et al. [112] analyze optimal rejection strategies for classifiers with input space partitioning, e.g., prototype-based classifiers, support vector machines, or decision trees, and they formulate this problem as MCKP. A dynamic programming method is devised to find the exact optimum for local thresholds. DP can solve MCKP in pseudo-polynomial time in general (see Section 5.2). However, it can find the optimum in polynomial time in this special case since the weights are polynomial with respect to the number of data points. Furthermore, a linear-time (without pre-processing) greedy approximation algorithm is proposed, which can be used for large training sets to find a near-optimum threshold.

7.18. Military

Bae et al. [113] consider a problem of finding a reconnaissance route for an unmanned combat vehicle (UCV) in a terrain. The problem of selecting partial routes from the set of candidates can be regarded as MCKP. DP is used to solve the problem (Section 5.2).

8. Discussion

First, we examine the distribution of the number of papers on MCKP and its different variants in the literature (Figure 2). We consider the problems presented in Section 4. The statistics are based on our selected data source, i.e., the WoS search results on the term “multiple-choice knapsack problem”.

The most widely used variant of the problem is the Multidimensional Multiple-choice Knapsack Problem (MMKP). The order of the words “multidimensional” and “multiple-choice” is often exchanged in the name of this problem. For this reason, we searched for the naming variant “multiple-choice multidimensional knapsack problem” of the MMKP as well. The search results were added to the number of references to the MMKP.

Several papers refer to LMCKP. This problem usually appears in the context of solving MCKP as its linear relaxation. The number of papers dealing with PCKP, whose special case is MCKP, is also large. Although there are many other variants of MCKP, none of them seems to be widely used. Three papers refer to MCKP with setup. The number of papers dealing with the other MCKP variants is only one or two in our data source.

We drop the papers on the variants of MCKP in further investigations, and we will focus on MCKP. The only exception is LMCKP, which is intensively applied in the solutions of MCKP. For this reason, the papers proposing new algorithms for LMCKP are also included in the examination of MCKP methods.

Now, let us examine the topics of the remaining papers. Only one of the papers [6] is a survey paper in our data source. Although there are more surveys in the literature (Section 2), they are book chapters or not indexed by WoS.

We can classify the paper topics into two main groups according to their relation to MCKP. Some papers focus on proposing new solution methods to MCKP, while other papers only apply MCKP algorithms to solve a practical problem. Figure 3 shows how the proportion of papers presenting new or enhanced algorithms decreases over time compared to the papers containing the applications of MCKP. The papers are grouped according to the decade of their publication date. We can see the first papers exclusively aimed at developing new algorithms and proposed new solution methods. It shows that the algorithms were extensively studied in the early papers. We found 15 papers in our data source which are oriented towards researching MCKP algorithms, and almost half of them were published before 1990. Later, the ratio of the papers focusing on MCKP algorithms quickly decreased, and the application-oriented papers spread intensively after 2000. Nowadays, we can find only a small number of papers presenting new algorithms.

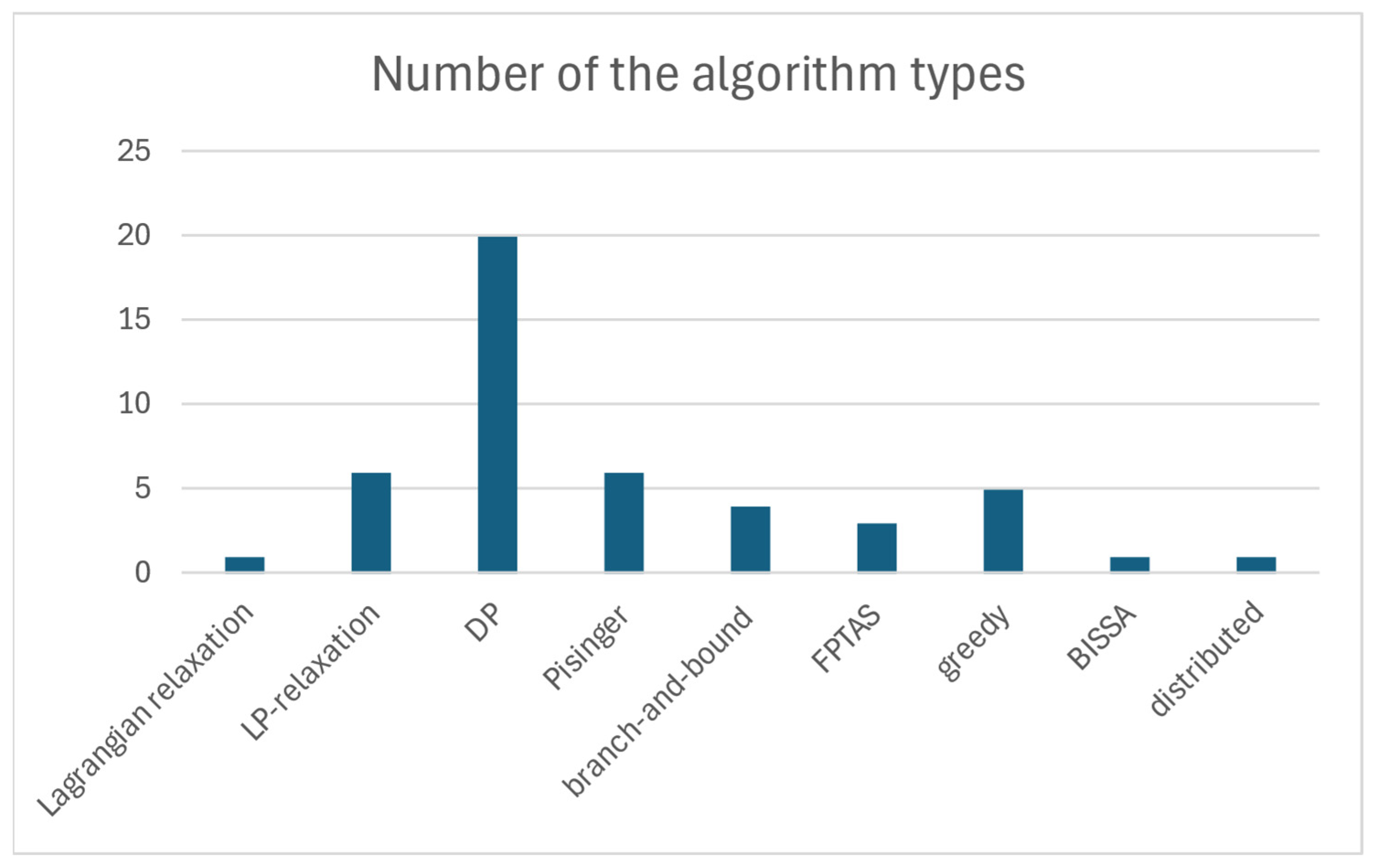
From now on, we restrict the analysis to application-oriented papers. Figure 4 presents the distribution of the different algorithms applied to solve MCKP. We can see that dynamic programming is clearly the most popular solution method. Pisinges’s minimal algorithm, LP relaxation, greedy algorithm, branch-and-bound algorithm, bi-objective approximate solution search algorithm (BISSA), and fully polynomial time approximation scheme are also used in several papers (their number is between three and six). Lagrangian relaxation, Integer Programming, and a distributed algorithm are applied only in one paper. One more algorithm is found in our literature review (Section 5), namely, the binary search, which has no application in our selected data source.

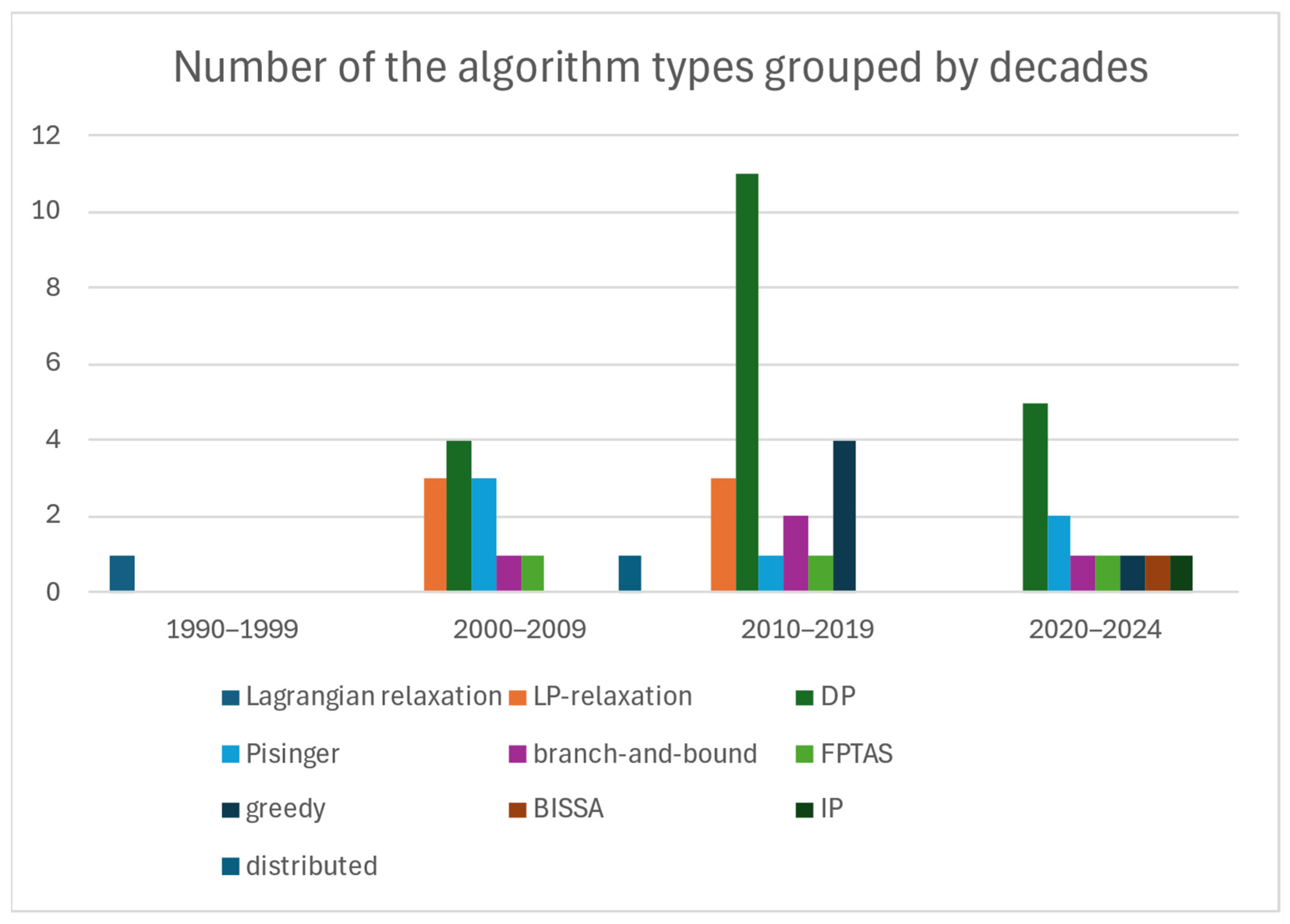
Let us examine how the application of different solution algorithms has changed over time. The algorithms are grouped by decades in Figure 5 to show the dynamic changes in their applications. Lagrangian relaxation was applied only in one early paper. Most of the application-oriented papers appeared after 2000. Since that time, the DP method has proved to be the most popular in each period.

We have found that the traditional algorithms (greedy, dynamic programming, linear programming, Pisinger’s minimal algorithm, branch-and-bound) are mostly applied in the literature; these were already known by 1995. The reason behind this could be that the problem can be well managed with classical approaches and suitable results can be achieved with the known methods. MCKP algorithms were developed intensively between 1975 and 1995 and only slight improvements to them can be observed since that time. Only a few papers applied algorithms developed after 1995 (the year of publication of Pisinger’s minimal algorithm), such as bi-objective approximate solution search algorithm (BISSA) (Section 5.2), improved FPTAS (Section 5.9), and distributed algorithm (Section 5.11).

Although the greedy method is a very simple and straightforward method, it was mainly used only in the 2010s. This could be explained by the fact that, although the greedy method is easy to implement, the quality of the result is worse than that of the results provided by other standard methods.

MCKP is applied to model and solve problems coming from various applications. Figure 6 presents the distribution of application areas of MCKP based on Section 7. Although some papers may belong to several application domains, we always assigned only their main application domain to them. The application areas where MCKP is most often used include parallel and distributed systems, cloud computing, and wireless networks. These domains are intensively studied in the literature, and they include several optimization problems under resource constraints. MCKP is also preferably applied in solving other combinatorial optimization problems (e.g., other knapsack problems, facility location problems, network flows, generalized assignment problem; see Section 6). Manufacturing, multimedia, management, web and information systems, and medical applications represent domains where MCKP has been applied several times. It is also applied in areas such as biology, transportation, military, machine learning, or VLSI design. Although most of the application areas belong to computer science, MCKP can be applied to other areas as well, such as biology, medical sciences, and manufacturing.

Let us examine the recent application areas. Figure 7 shows the areas where MCKP has been applied in the last five years. We can see that the following application areas are the most popular: parallel and distributed systems, and cloud computing. Biology, marketing, and mechanical engineering represent new application areas for MCKP.

9. Conclusions

We have provided an overview of the applications of the Multiple-Choice Knapsack problem. It has a wide area of application domains, primarily in engineering and technology, but also in biology, and medical and health sciences. The problem is used particularly often in parallel and distributed systems, cloud computing, and wireless networks, where it can be applied to job scheduling or resource allocation under resource constraints. Our aim is to help researchers in various domains to identify problems where MCKP can be applied to find an efficient solution.

The problem has several generalizations. The linear version of the problem has high relevance in solving MCKP. Since LMCKP can be solved very efficiently, it is preferably used to find an initial solution or an upper bound for MCKP. The Multidimensional Multiple-choice Knapsack Problem (MMKP) is the most often applied variant of MCKP in the literature. It can be applied when the selection of items should satisfy several resource constraints, which is often the case in practical applications. It would be worth dedicating a review paper to the MMKP as well.

Sometimes the names of the variants are incorrectly used in the literature and the term MCKP can be used for its variants (see Section 4.2). We hope that the presented review of the variants of MCKP will contribute to the correct usage of the term.

MCKP belongs to the category of basic problems in combinatorial optimization which can help solve other combinatorial optimization problems such as the Facility Location Problem, Single-commodity Network Design, or Generalized Assignment Problem. MCKP often appears as a subproblem after applying decomposition techniques.

We found that, although MCKP is intensively used even nowadays, the classical solution algorithms (e.g., greedy, dynamic programming, branch-and-bound methods) are mainly applied, which are almost thirty years old. Only a few algorithms were proposed after 1995, but they did not spread in the applications.

10. Future Directions

Most of the algorithms for MCKP were developed several decades ago. It would be useful to revise them according to the current requirements coming from real-world problems.

The vast majority of the algorithms in the literature were developed for the case when all parameters of MCKP are known in one central unit, where the optimization runs. However, this is not always the case in practice. There is a need to develop methods in large networks, which can solve MCKP in a distributed manner; see, for example, the rate adaptation algorithm for multi-hop networks in [70]. In this case, each network node makes decisions locally instead of globally, as in a centralized scheme. Although there are several distributed methods for KP (see e.g., [114]), we see a lack of MCKP algorithms in distributed computing. Although distributed algorithms pose new challenges compared to the centralized algorithms, such as communication and cooperation between nodes, managing network latency, proving convergence, etc., distributed methods can be adapted to solve MCKP as well.

In self-organizing systems, decisions of the nodes of the networks rely only on local information. They have high relevance in computer science as well and their advantageous features include robustness and adaptivity. Their structure can converge to an optimal state. It would be also interesting to examine how MCKP can be solved in self-organizing systems.

Uncertainty about the input values may pose a challenge in MCKP. How to manage this problem is also an interesting research direction. In the literature, the fuzzy and chance-constrained versions of the problem (see Section 4) have attempted to handle the uncertainty.

If the items may arrive at different times, and the items must be selected without knowledge of the future items, the problem can be modelled as an online problem. This is a typical problem, e.g., in serving requests with different value and resource needs. The online version of MCKP could be also the subject of future research. The problem is well studied in the case of the KP [115], but not MCKP. The offline version “knowing the future” can be solved by using the MCKP algorithm. A typical task in online problems is to compare the online version with the offline version, and to calculate a lower bound on the competitive ratio of the online algorithm, i.e., on the ratio of the total value achieved by the online algorithm and the total value of the optimal offline algorithm.

The sizes of the problem instances are increasing in several application areas (e.g., machine learning, multimedia), which brings new challenges. Although MCKP is NP-complete, it may have special cases which can be solved in polynomial time. Discovering MCKP subcases which have efficient solution algorithms could be also a subject of future research.

The versatile application possibilities of MCKP in the literature may inspire researchers to explore new application areas.