Synchronization in Fractional-Order Delayed Non-Autonomous Neural Networks
Abstract
1. Introduction
2. Preliminaries and System Description
3. Main Conclusions and Their Proof
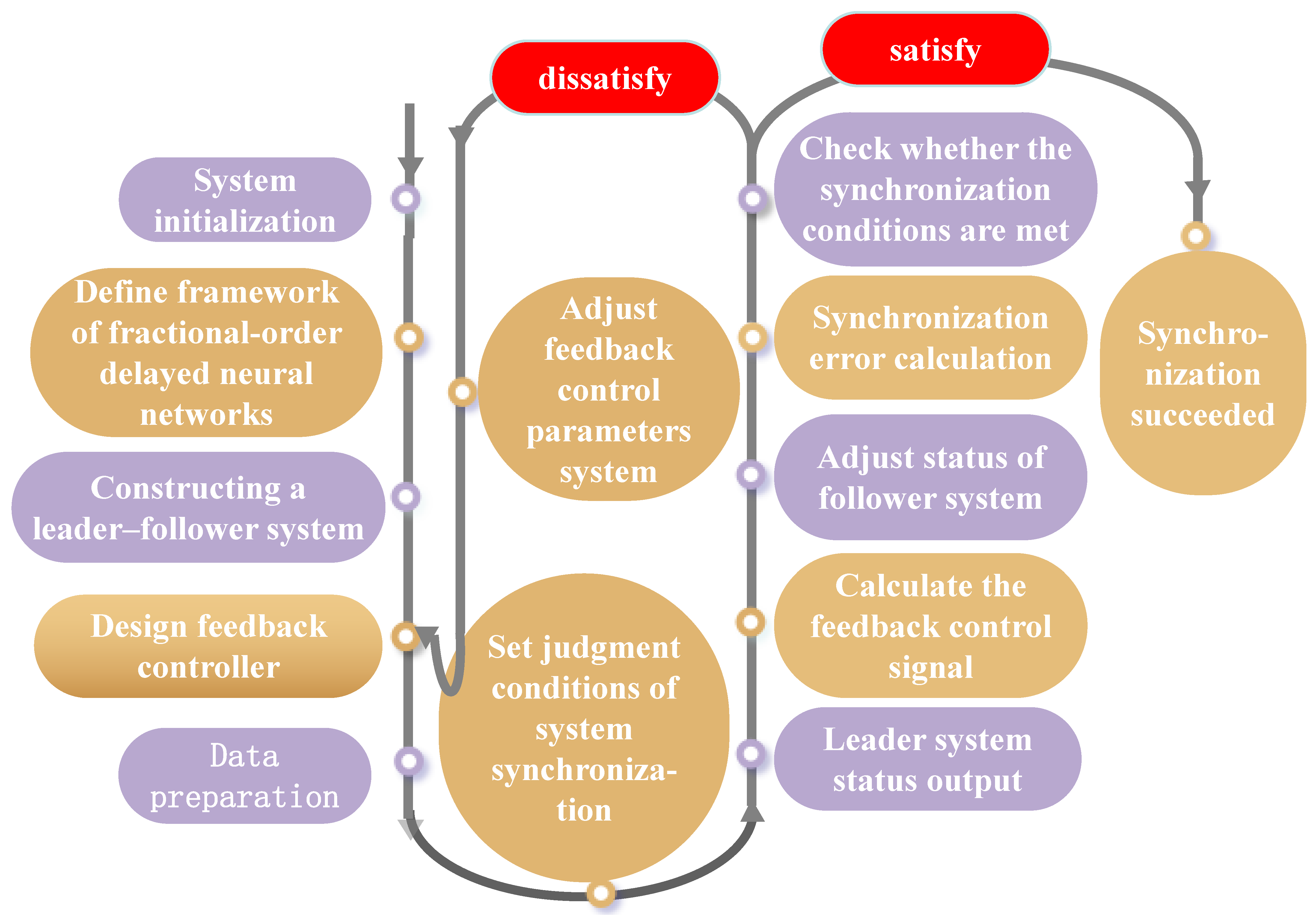
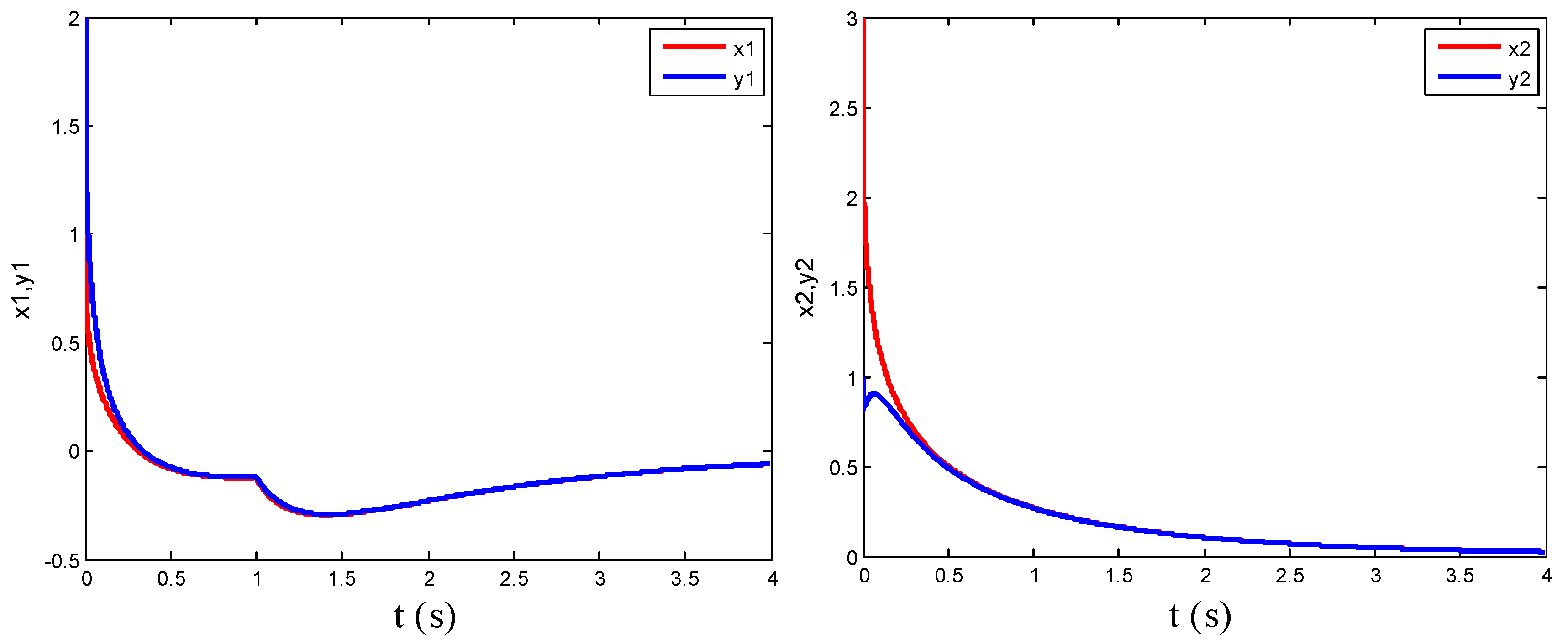
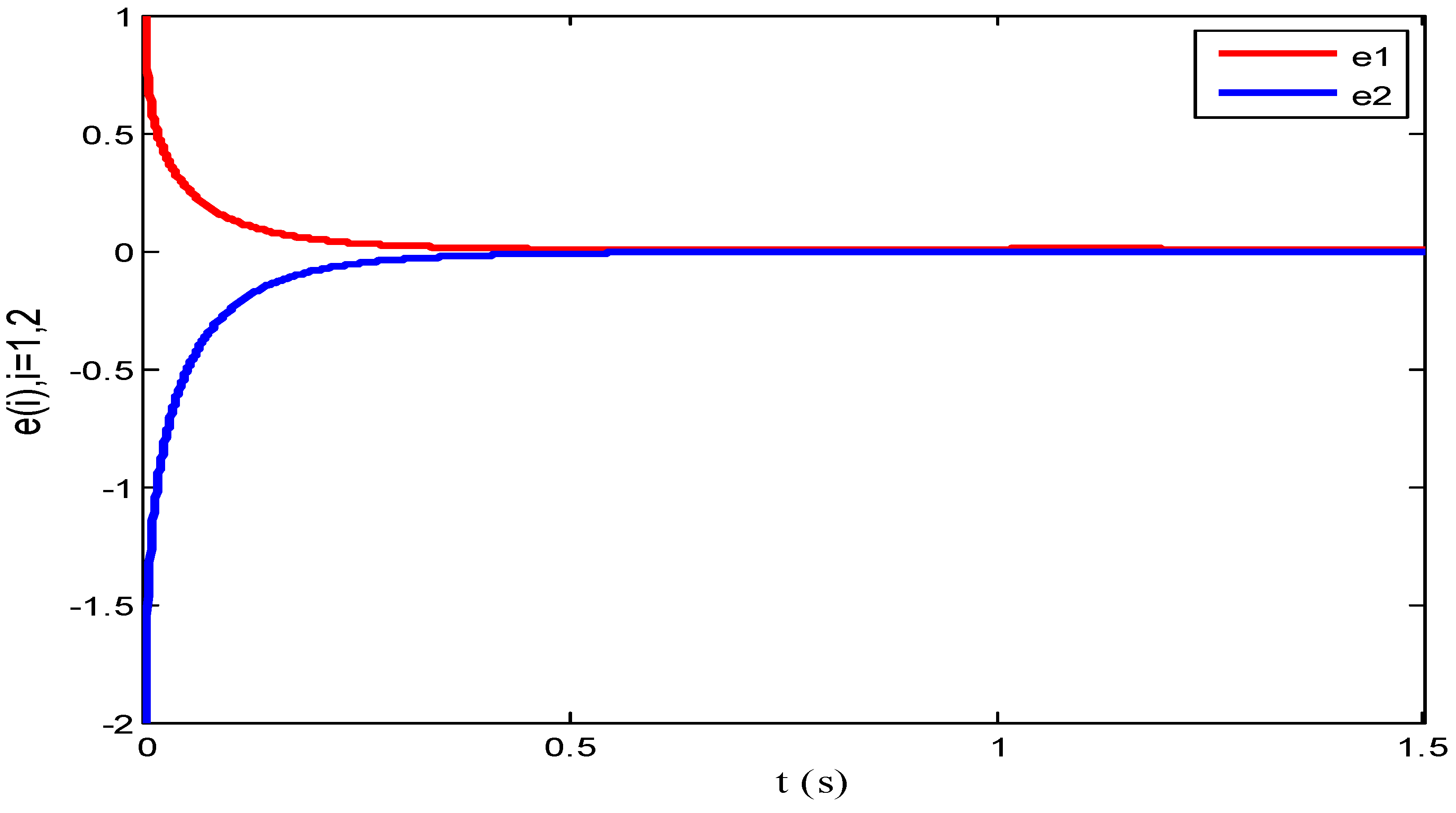
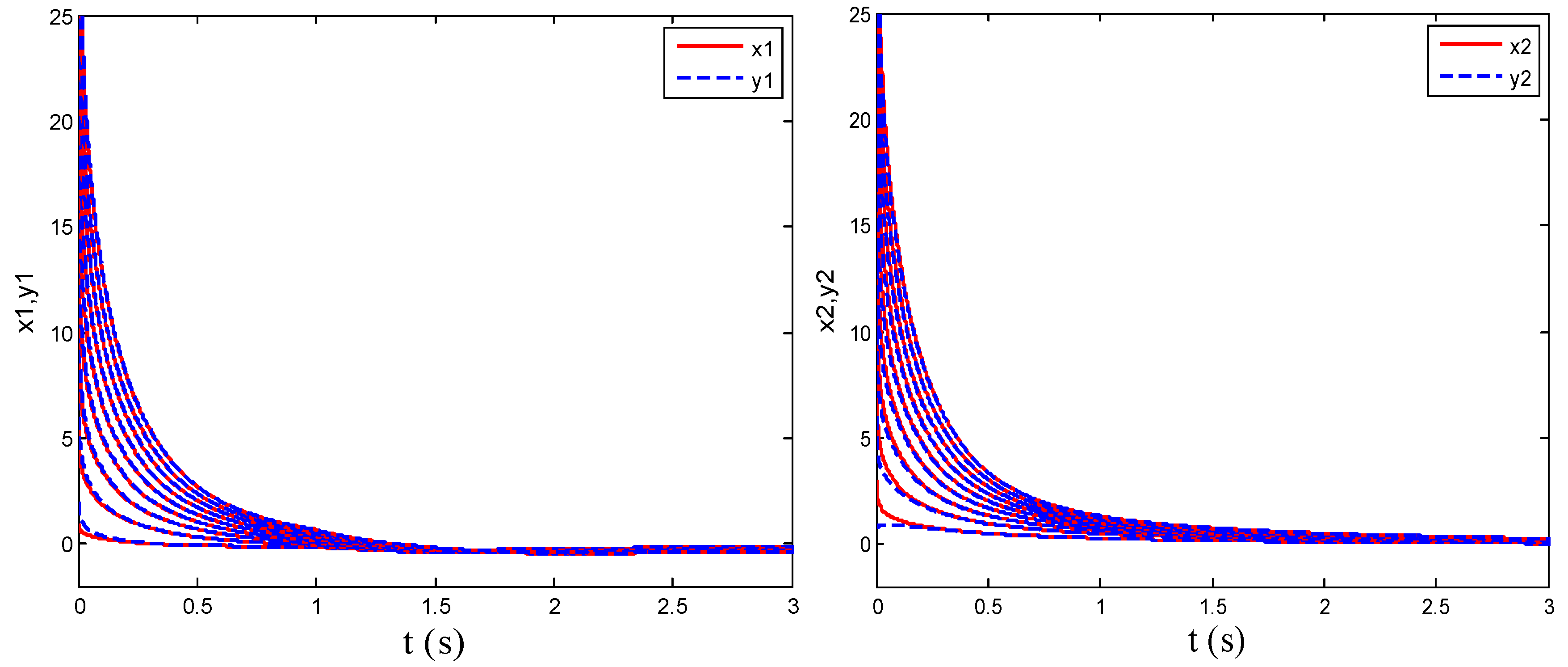
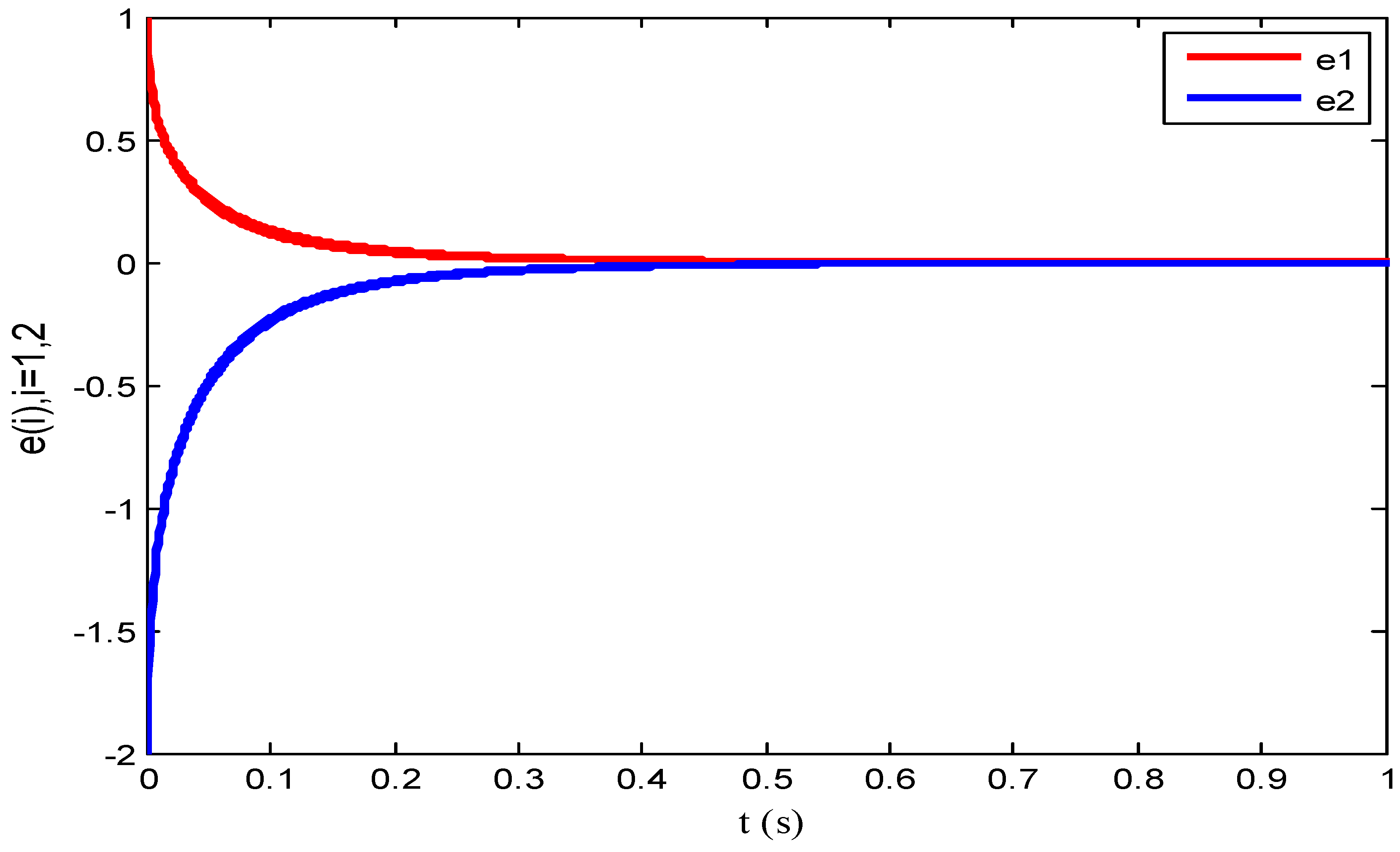
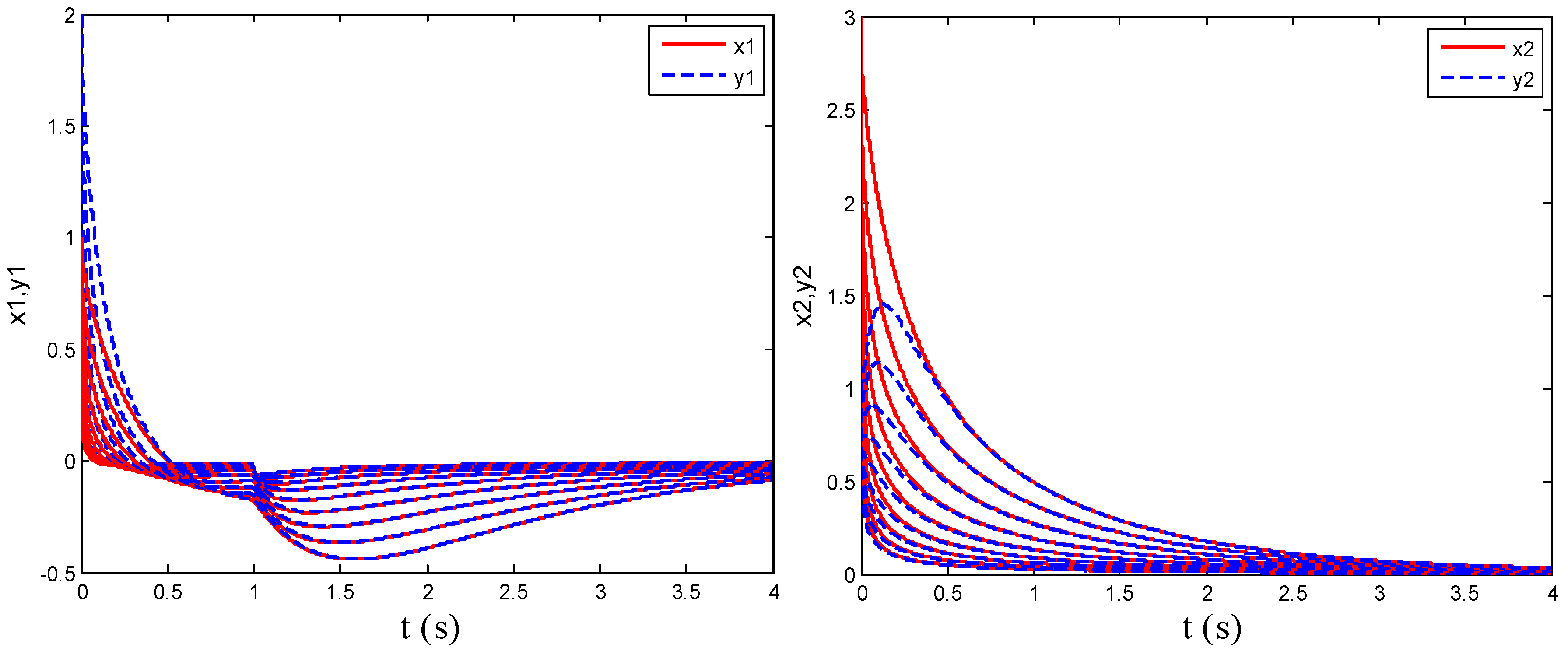
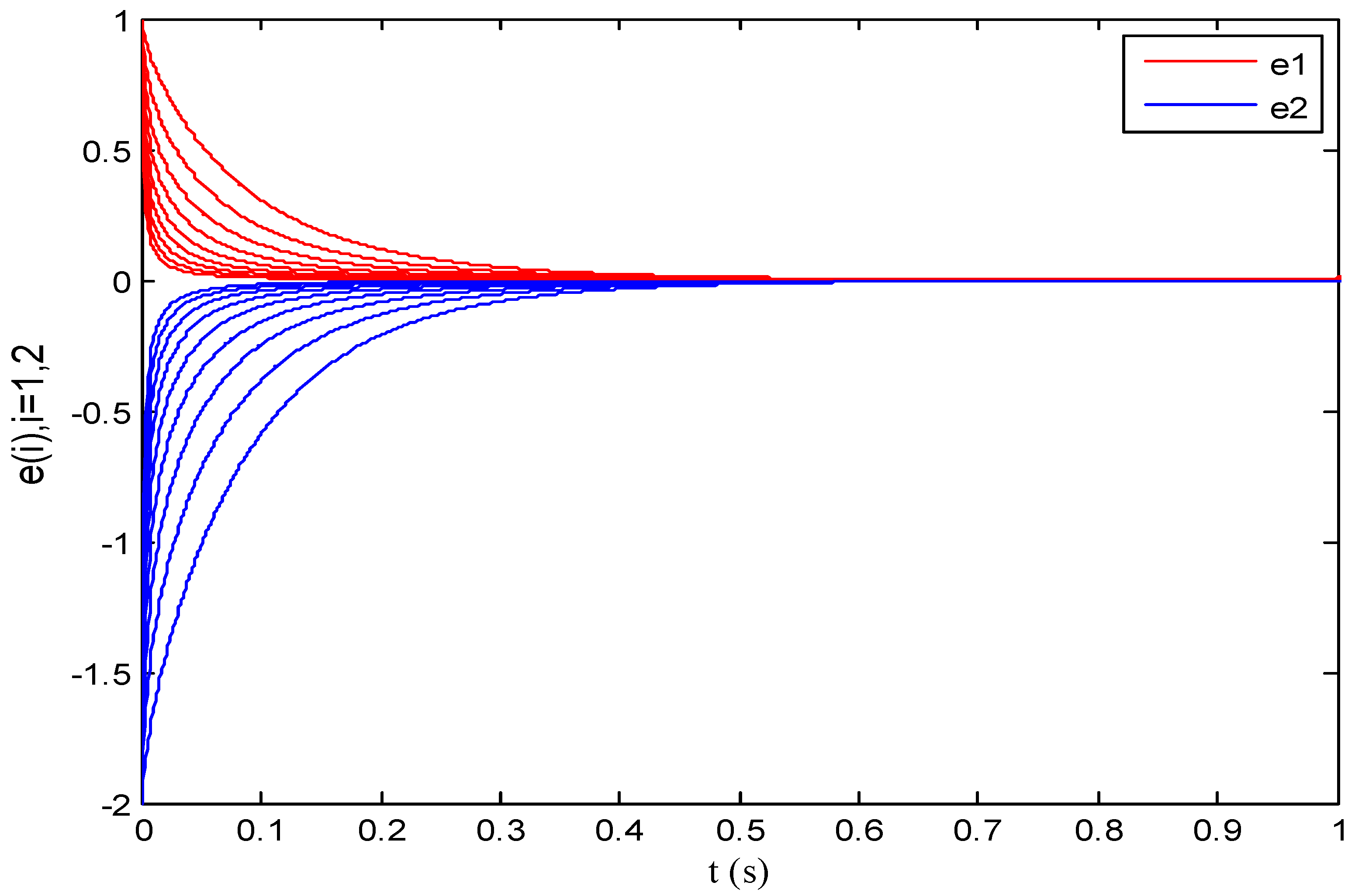
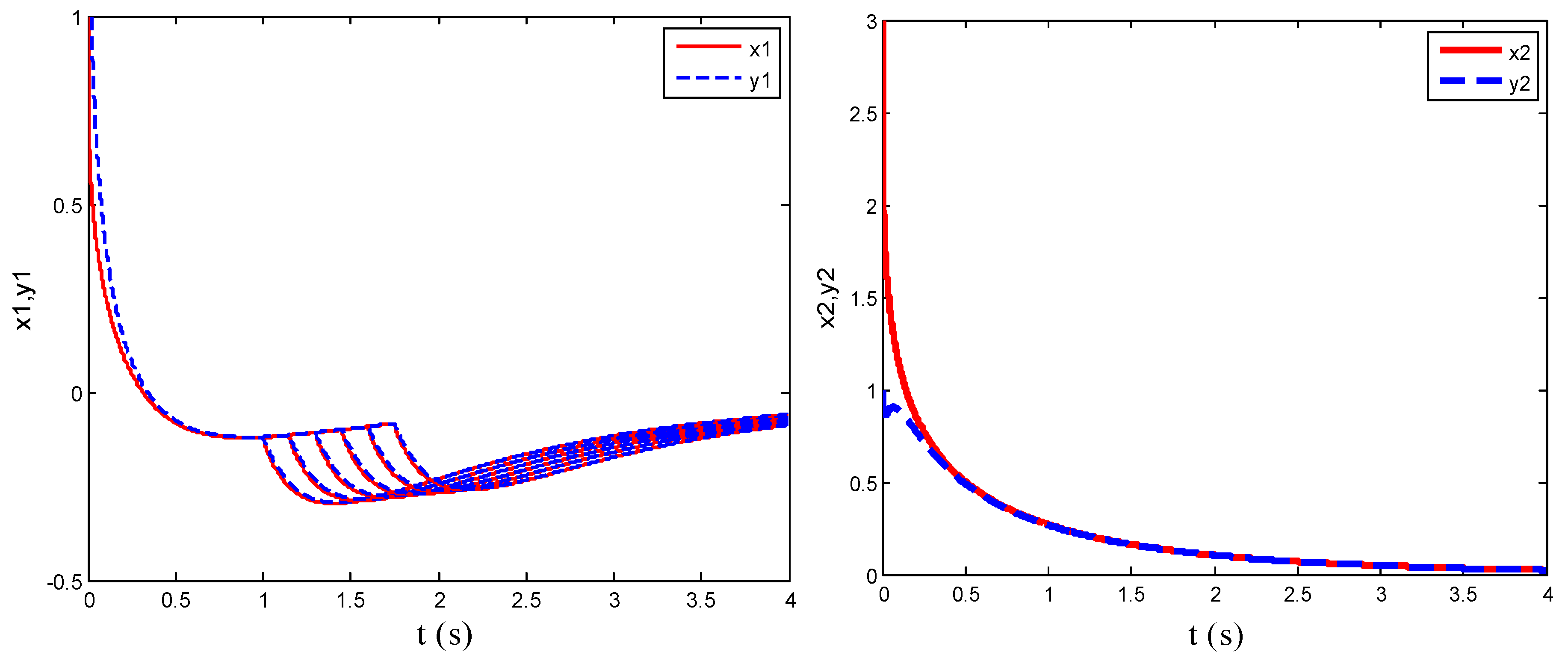
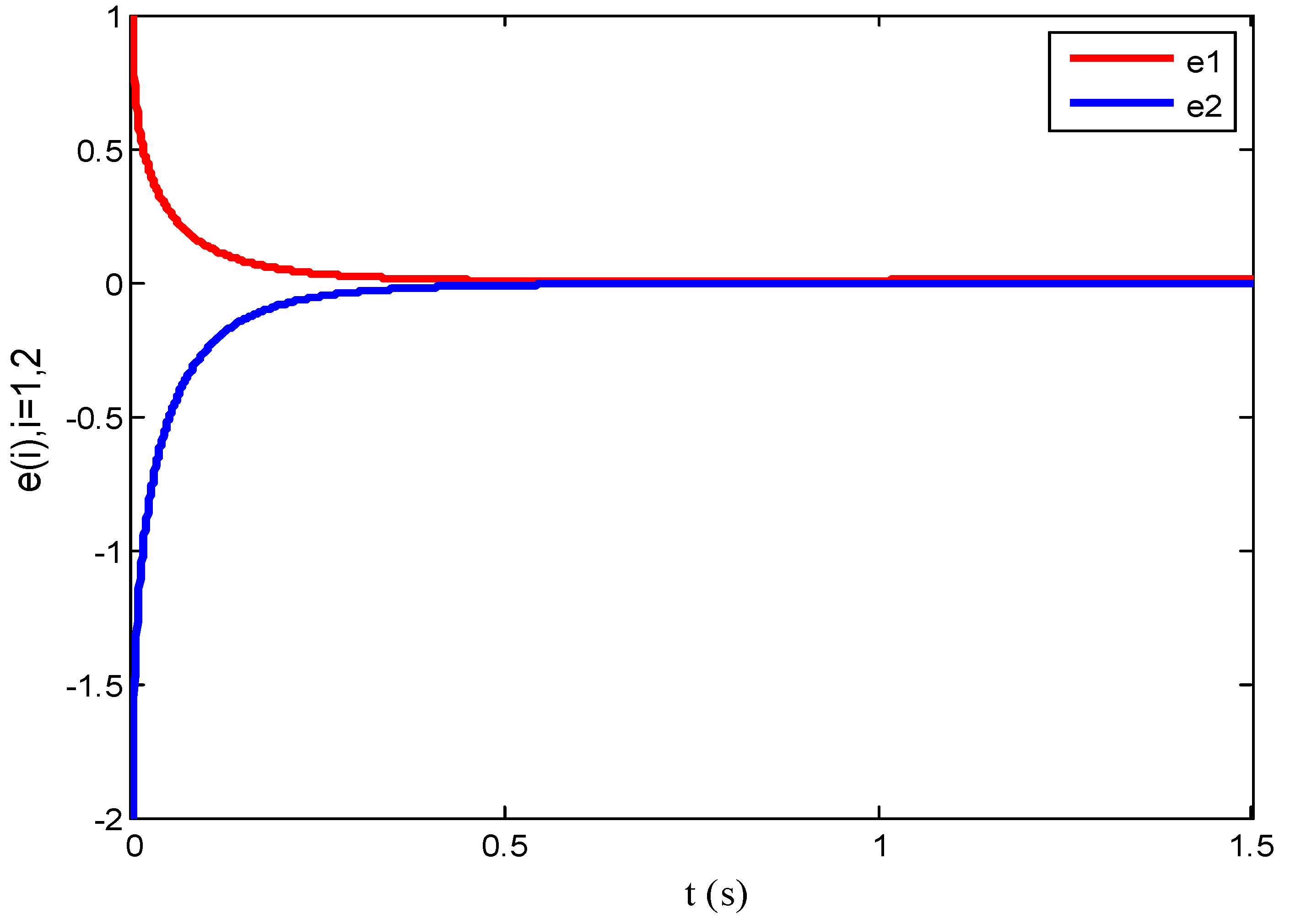
4. Numerical Simulation
5. Summary and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Song, Q. Synchronization analysis of coupled connected neural networks with mixed time delays. Neurocomputing 2009, 72, 3907–3914. [Google Scholar] [CrossRef]
- Bao, H.; Park, J.H.; Cao, J. Adaptive synchronization of fractional-order memristor-based neural networks with time delay. Nonlinear Dyn. 2015, 82, 1343–1354. [Google Scholar] [CrossRef]
- Velmurugan, G.; Rakkiyappan, R.; Cao, J. Finite-time synchronization of fractional-order memristor-based neural networks with time delays. Neural Netw. 2016, 73, 36–46. [Google Scholar] [CrossRef] [PubMed]
- Gu, Y.; Yu, Y.; Wang, H. Synchronization for fractional-order time-delayed memristor-based neural networks with parameter uncertainty. J. Frankl. Inst. 2016, 353, 3657–3684. [Google Scholar] [CrossRef]
- Stamova, I.; Stamov, G. Mittag-Leffler synchronization of fractional neural networks with time-varying delays and reaction–diffusion terms using impulsive and linear controllers. Neural Netw. 2017, 96, 22–32. [Google Scholar] [CrossRef] [PubMed]
- Hu, H.-P.; Wang, J.-K.; Xie, F.-L. Dynamics analysis of a new fractional-order hopfield neural network with delay and its generalized projective synchronization. Entropy 2019, 21, 1. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Cao, J.; Wu, R.; Alsaedi, A.; Alsaadi, F.E. Projective synchronization of fractional-order delayed neural networks based on the comparison principle. Adv. Differ. Equ. 2018, 2018, 73. [Google Scholar] [CrossRef]
- Yu, J.; Hu, C.; Jiang, H.; Fan, X. Projective synchronization for fractional neural networks. Neural Netw. 2014, 49, 87–95. [Google Scholar] [CrossRef] [PubMed]
- Hu, T.; Zhang, X.; Zhong, S. Global asymptotic synchronization of nonidentical fractional-order neural networks. Neurocomputing 2018, 313, 39–46. [Google Scholar] [CrossRef]
- Wang, H.; Yu, Y.; Wen, G.; Zhang, S. Stability analysis of fractional-order neural networks with time delay. Neural Process. Lett. 2015, 42, 479–500. [Google Scholar] [CrossRef]
- Peng, X.; Wu, H.; Song, K.; Shi, J. Global synchronization in finite time for fractional-order neural networks with discontinuous activations and time delays. Neural Netw. 2017, 94, 46–54. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Yang, Y.; Wang, F. Synchronization analysis of fractional-order neural networks with time-varying delays via discontinuous neuron activations. Neurocomputing 2018, 275, 40–49. [Google Scholar] [CrossRef]
- Yang, X.; Li, C.; Huang, T.; Song, Q.; Huang, J. Synchronization of fractional-order memristor-based complex-valued neural networks with uncertain parameters and time delays. Chaos Solitons Fractals 2018, 110, 105–123. [Google Scholar] [CrossRef]
- Wang, C.; Yang, Q.; Zhuo, Y.; Li, R. Synchronization analysis of a fractional-order non-autonomous neural network with time delay. Phys. A Stat. Mech. Its Appl. 2020, 549, 124176. [Google Scholar] [CrossRef]
- Wang, C.; Lei, Z.; Jia, L.; Du, Y.; Zhang, Q.; Liu, J. Projective synchronization of a nonautonomous delayed neural networks with Caputo derivative. Int. J. Biomath. 2024, 17, 2350069. [Google Scholar] [CrossRef]
- Pldlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Anatoly, A.K.; Hari, M.S.; Juan, J.T. Theory and Applications of Fractional Differential Equations; Elsevier Science Ltd.: New York, NY, USA, 2006. [Google Scholar]
- Duarte-Mermoud, M.A.; Aguila-Camacho, N.; Gallegos, J.A.; Castro-Linares, R. Using general quadratic Lyapunov functions to prove Lyapunov uniform stability for fractional order systems. Commun. Nonlinear Sci. Numer. Simul. 2015, 22, 650–659. [Google Scholar] [CrossRef]
- Chen, B.; Chen, J. Razumikhin-type stability theorems for functional fractional-order differential systems and applications. Appl. Math. Comput. 2015, 254, 63–69. [Google Scholar] [CrossRef]
- Dass, A.; Srivastava, S.; Kumar, R. A novel Lyapunov-stability-based recurrent-fuzzy system for the Identification and adaptive control of nonlinear systems. Appl. Soft Comput. 2023, 137, 110161. [Google Scholar] [CrossRef]
- Man, Z.; Wu, H.R.; Liu, S.; Yu, X. A new adaptive backpropagation algorithm based on lyapunov stability theory for neural networks. IEEE Trans. Neural Netw. 2006, 17, 1580–1591. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, D.; Wang, C.; Jiang, T. Synchronization in Fractional-Order Delayed Non-Autonomous Neural Networks. Mathematics 2025, 13, 1048. https://doi.org/10.3390/math13071048
Wu D, Wang C, Jiang T. Synchronization in Fractional-Order Delayed Non-Autonomous Neural Networks. Mathematics. 2025; 13(7):1048. https://doi.org/10.3390/math13071048
Chicago/Turabian StyleWu, Dingping, Changyou Wang, and Tao Jiang. 2025. "Synchronization in Fractional-Order Delayed Non-Autonomous Neural Networks" Mathematics 13, no. 7: 1048. https://doi.org/10.3390/math13071048
APA StyleWu, D., Wang, C., & Jiang, T. (2025). Synchronization in Fractional-Order Delayed Non-Autonomous Neural Networks. Mathematics, 13(7), 1048. https://doi.org/10.3390/math13071048





