Abstract
The growing sophistication of cyber-attacks demands encryption processes that go beyond the confines of conventional cryptographic methods. Traditional cryptographic systems based on numerical algorithms or standard graph theory are still open to structural and computational attacks, particularly in light of advances in computation power. Fuzzy logic’s in-built ability to manage uncertainty together with the representation ability of fuzzy hypergraphs for describing complex interrelations offers an exciting avenue in the direction of developing highly evolved and secure cryptosystems. This paper lays out a new framework for cryptography using fuzzy hypergraph networks in which a hidden value is converted into a complex structure of dual fuzzy hypergraphs that remains completely connected. This technique not only increases the complexity of the encryption process, but also significantly enhances security, thus making it highly resistant to modern-day cryptographic attacks and appropriate for high security application. This approach improves security through enhanced entropy and the introduction of intricate multi-path data exchange through simulated nodes, rendering it highly resistant to contemporary cryptographic attacks. It ensures effective key distribution, accelerated encryption–decryption processes, and enhanced fault tolerance through dynamic path switching and redundancy. The adaptability of the framework to high-security, large-scale applications further enhances its robustness and performance.
MSC:
05C07; 05C62; 05C69; 05C75; 05C90
1. Introduction
The exponential growth of computing power and the looming danger represented by quantum computing have uncovered major weaknesses in traditional encryption schemes. Secure communication is particularly crucial in sensitive areas, such as military operations, where mistakes would have catastrophic consequences. While current encryption algorithms are secure against typical attacks, they occasionally lack enough complexity to defend against advanced cryptanalysis and quantum attacks.
Challenging methods to construct cryptography systems with enhanced security attributes include fuzzy logic and hypergraph theory. Fuzzy hypergraphs have an increased amount of structural richness compared to traditional graphs based on their ability to represent multi-relational information [1]. Fuzzy logic, in contrast, provides versatility and resilience when handling ambiguous or imprecise data, thereby making it perfectly suited for use in the real world. Blending these two paradigms can provide an encryption model that is robust, adaptive, and resistant to changing threats [2].
Most of the present-day cryptographic methods draw upon conventional graph-based methods, which are more straightforward in form and consequently simpler to read and breach [3,4,5,6]. Besides this, contemporary encryption mechanisms fail to utilize concealing information strategies, like adding dummy nodes and edges, to raise complexity and deter investigation. Hibaoui et al.’s [7] method is best suited for dynamic and scattered networks, such as Ad-hoc mobile and Peer-to-Peer systems, since it offers resilience against a wide range of threats and preserves identity and location privacy. It employs hyperedges for stability at each hop to effectively manage network churn. Franklin et al. [8] addressed secure communication in multicast and distributed systems by bridging private channels and full information settings; concentrating on the viability and effectiveness of private message exchange, it uses combinatorial approaches to guarantee information-theoretic security against an infinite number of attackers. Somu et al. [9] provided weights and decrease complexity, using the MDHP method and the Fuzzy hypergraph-Based Computational Model to rank cloud service providers. Ranshous et al. [10] used structural graph characteristics to categorize exchange-owned bitcoin addresses in directed hypergraphs to find laundering tendencies. Pius et al. [11] developed a cryptographic technique to encrypt sensitive data in order to address data privacy in fuzzy graph theory. Miner More et al. [12] represented a hypergraph with parties as vertices and secrets as edges to characterize interdependencies in a multiparty system. To describe these interdependencies and generalize nondeducibility, it presented a multi-argument independence relation. Morimae et al. [13] investigated applications in quantum computational supremacy demonstrations employing fuzzy hypergraph states, and verified blind quantum computing. Deveci et al. [14] studied communication volumes and message counts using directed fuzzy hypergraphs by concurrently optimizing numerous communication metrics. Wang et al. [15] investigated the usage of meaningful shares for binary, grayscale, and color secret pictures, made possible by the paper’s matrix extension approach for building more broad (k,n)-visual secret-sharing schemes. Zhou et al. [16] described the possible secret key rate and public discussion rate for multiterminal sources represented by minimally linked fuzzy hypergraphs. Li et al. [17] investigated the security needs in fog computing while maintaining secrecy and integrity; the study suggests a key management strategy based on fuzzy hypergraphs. Wang et al. [18] provided a more succinct derivation for matrix extension by extending the Extended Visual Cryptography Scheme to secure multiple color pictures with meaningful shares. Christen et al. [19] investigated combining type theory, lambda calculus, and graph-based source code analysis. Hossein et al. [20] introduced new lower constraints for pixel expansion based on minimal qualified sets and induced the matching of hypergraphs; the research explored the optimal pixel expansion in visual cryptography methods. The study emphasized resource optimization and illustrated how useful it was in practical situations such as communication networks. The authors offered a framework that improved decision-making in uncertain situations by fusing fuzzy logic with domination theory. They emphasized the framework’s versatility in network analysis and multi-agent systems. In their exploration of total magic labeling in graph networks, Meenakshi et al. [21] studied hypergraph modeling in social networks. Also, the authors [22,23] suggested novel uses for these labeled structures and cryptography in order to maximize the graph features, especially in networks that demand high levels of efficiency and connectedness. The study presented a mathematical framework and outlined its applications in network security.
Shao et al. [24] enhanced decision-making procedures by employing graphical models to present new ideas in vague graphs and utilized them in medical diagnosis. Shi et al. [25] explored the energy ideas of image fuzzy graphs as a key, and demonstrated how these ideas could be implemented in practical cases, highlighting efficiency in computations. They also examined interval-valued quadripartitioned neutrosophic graphs and demonstrated how these can be implemented in real-life decision-making problems [26]. In a pioneering study of imprecise graphs, Rashmanlou et al. [27] examined their structural properties and applications in vague environments in their research on complex Pythagorean fuzzy graphs.
Banerjee et al. [28] researched the ability of quantum blockchain technology using weighted hypergraph states to provide greater security and a quantum-based distributed consensus protocol. Their research shows the potential of the use of hypergraph structures in quantum information processing. Singh and Uçar [29] studied the parallel efficient implementation of a perfect hashing technique for hypergraphs that improves computational performance considerably in applications involving large-scale hypergraphs, especially in parallel and distributed environments. Orts et al. [30] concentrated on enhancing the application of quantum blockchain with hypergraphs, overcoming major performance and scalability issues by presenting innovative hypergraph methods. Ramya et al. [31] explored a secure authentication protocol for IoT settings based on hypergraph-based hashing mechanisms, providing better security between edge devices and overcoming communication attacks through strong cryptographic practices. Romdhini et al. [32] studied the signless Laplacian energy of interval-valued fuzzy graphs based on mathematical properties and application perspectives in network optimization. Kosari et al. [33] explored the domination structures of vague graphs in the application contexts of medical diagnosis and decision-making processes. Rao et al. [34] proposed new intuitionistic fuzzy trees definitions, with an investigation into their theoretical models and applications within computational intelligence. The hypergraph structure facilitated more flexible and secure authentication compared to traditional graph-based models. The approach enhanced resistance to impersonation and replay attacks, ensuring secure communication between devices. Wu Qiwu et al. [35] proposed a security model using hypergraph structures to represent and manage security mechanisms across multiple layers in optical networks. The hypergraph-based model enabled secure transmission by incorporating complex multi-domain interconnections, reducing vulnerability to network-layer attacks. Masud et al. [36] presented a novel cryptographic approach that integrated hypergraph structures into encryption and decryption processes. By using hypergraph connections to represent encrypted data, the model ensured high security and resistance to data breaches. The approach demonstrated improved computational efficiency and resistance to quantum attacks. Together, these studies add to the development of fuzzy and vague graph theory, providing new insights into their structural properties and real-world applications in optimization, medicine, and computational modeling. Alkasasbeh et al. [37] studied the radio numbers of friendship communication networks, focusing on optimal labeling strategies to minimize interference and improve signal clarity. They established new bounds and properties for radio labeling in such networks. Together, these works illustrate the increasing significance of hypergraphs in fields like blockchain, IoT, and parallel computing, providing a basis for future research on secure and efficient data structures.
The proposed study provides an alternative encryption algorithm based on fuzzy hypergraph theory and prime calculation to address the vulnerabilities of prevailing cryptographic frameworks that are structurally susceptible to computational-based attacks based on advancements in computation capacity as well as the development of quantum computing.
The new approach provides security with complex hypergraph-based key distribution and anticipatory loops of encryption and decryption, ensuring secure transfer under malicious attack. As compared to the conventional encryption algorithms based on numbers and the conventional graph models, the new approach is founded on the structural complexity and uncertainty management property of fuzzy hypergraphs, which introduces layers of complexity with fuzzy transformations, dual fuzzy hypergraph transformations, and fuzzy hypergraph constructions. Among the key innovations is the introduction of advanced obfuscation techniques that make the system completely resistant to conventional and quantum attacks through the introduction of more entropy and structural randomness. The encryption mechanism constructs a complex network of hyperedges and common nodes with multiple paths and redundancy, enhancing data security with multi-path data exchange. This approach offers greater data integrity and confidentiality by virtue of the dynamic path adjustment and rerouting in the event of network failure, thereby improving fault tolerance and system strength. The adaptability of the framework to accommodate large-scale, high-security applications like secure communication in financial services, healthcare, cloud computing, IoT, and blockchain is a reflection of its flexibility. The study fills a critical gap in state-of-the-art cryptographic schemes, which are plagued by rigid key exchange mechanisms and predictable structural designs, by introducing a dynamic and multi-level encryption framework capable of resisting traditional and quantum attacks. The increased complexity and unpredictability of the fuzzy hypergraph-based scheme represent a quantum leap in encryption technology, with a scalable, resilient, and highly secure solution for modern communication systems.
2. Encryption and Decryption of the Fuzzy Hypergraph Network
The invention proposed offers a new encryption method for securely encrypting and transmitting confidential data using fuzzy hypergraph theory. Utilizing the structural complexity of fuzzy hypergraphs, the malleability of fuzzy theory, and the attributes of prime numbers, the essence is to conceal the original secret key such that the receiver will be able to decrypt the information through pre-determined metadata and mathematical operations.
The study achieves the following:
- The formation of fuzzy hypergraph and its dual;
- The generation of a secret key;
- The encryption algorithm;
- A decryption function.
The secret key is first chosen to be a very large prime number, and then split into smaller primes to provide greater security and modularity. To normalize and prepare these primes for further processing, they are subsequently transformed into triangular fuzzy numbers. By taking these fuzzy elements as nodes and their sums to form hyperedges, a fuzzy hypergraph is formed. To transmit it, the resulting fuzzy hypergraph is translated into its dual form, ensuring that the encrypted data cannot be read unless the corresponding decryption key is present, even in the case that it is intercepted. To enhance security further, additional fake nodes and edges are inserted, making the network more complex and hiding the data structure. In the decryption process, the receiver translates fuzzy weights back to their original nodes based on the provided key. Applying the provided key, the receiver decrypts the information by stripping dummy elements, reversing the transformations to recover the original primes, and mapping fuzzy weights back to their corresponding nodes and edges. Adding these primes results in the original secret key, ensuring secure communication and data integrity.
2.1. Encryption Process
The encryption process involves numerous steps aimed at transforming the original secret key into a complex, masked form that can only be accessed by the receiver who knows the metadata and secret decryption method.
2.1.1. Selection of Secret Key
The secret key, a large prime number (e.g., 10427), is selected at the beginning of the process. Prime numbers are a good place to begin in cryptographic techniques since they are difficult to factorize. The security of the system relies on the secrecy and unpredictability of this key.
2.1.2. Splitting the Secret Key into Smaller Primes
The secret key is broken into smaller prime numbers once it has been selected. The original secret key comprises as many as possible of these smaller primes taken together. The key 10427, for example, may be broken into primes such as 1007, 1003, 1013, and so on. Because there is no evident relationship between the different primes and the original key, this splitting operation makes the encryption even more difficult.
2.1.3. Conversion of Primes into Fuzzy Numbers
Fuzzy numbers are ideal for concealing the original values because they are a form of representation that allows some level of approximation or uncertainty. In this case, a triangle fuzzy function is used, with a spread defined by a pre-set fuzzy logic range and a peak at the original prime number. To ensure that the entire sum of the fuzzy components is consistent with its reference to the original secret key, the fuzzy numbers are normalized with respect to the original key. This is a critical phase that ensures the key is concealed and difficult to extract without the decryption key in case a portion of it gets intercepted or deciphered.
2.1.4. Fuzzy Hypergraph Construction
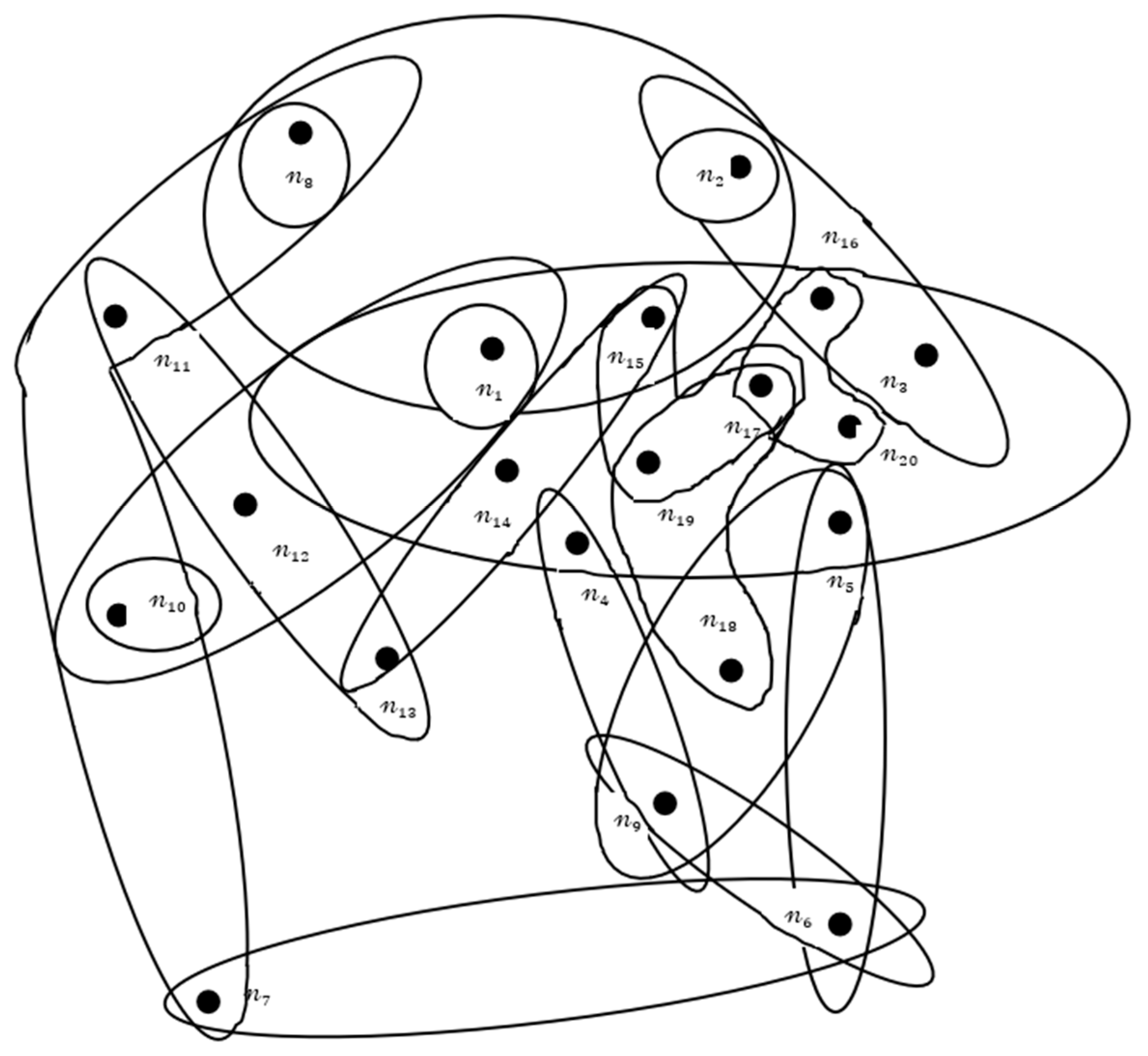
The nodes of a fuzzy hypergraph are subsequently created by further partitioning the fuzzy integers into smaller components. A fuzzy hypergraph is a graph extension whose edges, or hyperedges, may connect any number of nodes, not pairs. The hyperedges are produced by summing the fuzzy components of the nodes they connect, and the fuzzy numbers and components are distributed between these nodes. The larger the number of nodes and hyperedges, the more complex the fuzzy hypergraph is, as represented in Figure 1.
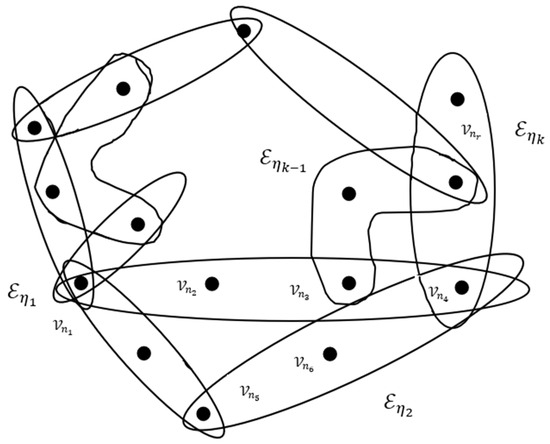
Figure 1.
Fuzzy hypergraph.
2.1.5. Dual Representation of the Fuzzy Hypergraph
The fuzzy hypergraph is transformed into its dual representation after it has been fully constructed. The dual of a fuzzy hypergraph is another fuzzy hypergraph wherein the roles of nodes and edges are swapped. The encoded message is transmitted along with the dual representation, which now comprises the scrambled and obscured data. Unless one knows the exact structure of the fuzzy hypergraph and the transformation process, an intruder will find it extremely hard to decrypt the secret key even if they are able to intercept the communication.
2.1.6. Introduction of Simulation Nodes and Hyperedges
The structure of the dual fuzzy hypergraph is rendered complicated through the inclusion of simulated edges and nodes placed randomly. The imaginary edges and nodes are designed to mislead any unauthorized party trying to decrypt the information. They enhance the complexity of the problem, making it significantly more difficult to determine the correct structure of the fuzzy hypergraph.
2.2. Transmission
The dual fuzzy hypergraph, the encrypted message, is then securely delivered to the recipient. The dual fuzzy hypergraph is sent along with metadata, which include important information such as:
- Total nodes and edges of the fuzzy hypergraph;
- A key is given for the purpose of searching the nodes and hyperedges of the dual fuzzy hypergraph;
- Additional information needed to decode the structure of the fuzzy hypergraph and reverse the encryption process.
The receiver needs these metadata in order to recognize and rebuild the original key accurately from the dual fuzzy hypergraph. Because the fuzzy hypergraph is dual in nature, containing real and imposter parts combined, the information acts as a guide that will allow the receiver to differentiate between the two and use only the relevant pieces.
2.3. Decryption Process
Via the decryption process, the recipient may use the metadata, the dual fuzzy hypergraph, and the set key to trace back the encryption steps and obtain the original secret key.
2.3.1. Receipt of the Dual Fuzzy Hypergraph and Metadata
The receiver starts the decryption process immediately upon receiving the dual fuzzy hypergraph and encrypted metadata. They receive essential details regarding the fuzzy hypergraph structure, such as the number of edges and nodes and the obscuring parameters, via the metadata. The recipient can hence realize the size and complexity of the fuzzy hypergraph and choose the best approach for accessing the original information.
2.3.2. Mapping Fuzzy Weights to Nodes and Edges
The recipient begins by allocating the fuzzy numbers (weights) to the nodes and edges of the dual fuzzy hypergraph using the given key. The recipient must accurately determine what nodes and edges represent the original secret elements, since the fuzzy hypergraph is dual. The fuzzy weights of the nodes and edges are added together and compared to their original counterparts in the original fuzzy hypergraph to do this.
2.3.3. Filtering Simulated Nodes and Edges
The information is utilized to filter the dummy nodes and edges that were added to conceal the original structure. The recipient is able to determine which nodes and edges are genuine and which are not based on the information. This step is necessary in order to recover the fuzzy hypergraph’s original structure, since it ensures that the original key is rebuilt utilizing only authorized nodes and edges.
2.3.4. Reversing the Fuzzy Transformation
The recipient reverses the fuzzy number transformation when they know which nodes and edges are applicable. By applying the inverse of the triangle fuzzy function used in encryption, this can be achieved. The fuzzy numbers are inverted back to the original prime numbers using the inverse function.
2.3.5. Reconstructing the Original Secret Key
Finally, the receiver reconstructs the original secret key by summing the retrieved prime numbers. The key is successfully protected against transmission by partitioning it into smaller primes, applying fuzzy transformations, and using the fuzzy hypergraph to obscure the structure. The only individual who can reverse the transformations and recover the secret is the receiving party possessing the correct key and metadata.
The following components constitute the key:
- The prime decomposition key is required for the recipient to reverse this process and reconstruct the original number, because the secret message is represented as a large prime number that is broken down into smaller primes corresponding to the nodes, a logical condition that helps in finding the simulated nodes and hyperedges in the constructed network based on their degree;
- Simulated nodes have degree ≤ 1, while genuine nodes have degree 2.
- Using the transposition found in the dual fuzzy hypergraph’s components, one can rebuild the original fuzzy hypergraph.
3. Encryption and Decryption Algorithm
3.1. Encryption Algorithm (Algorithm 1)
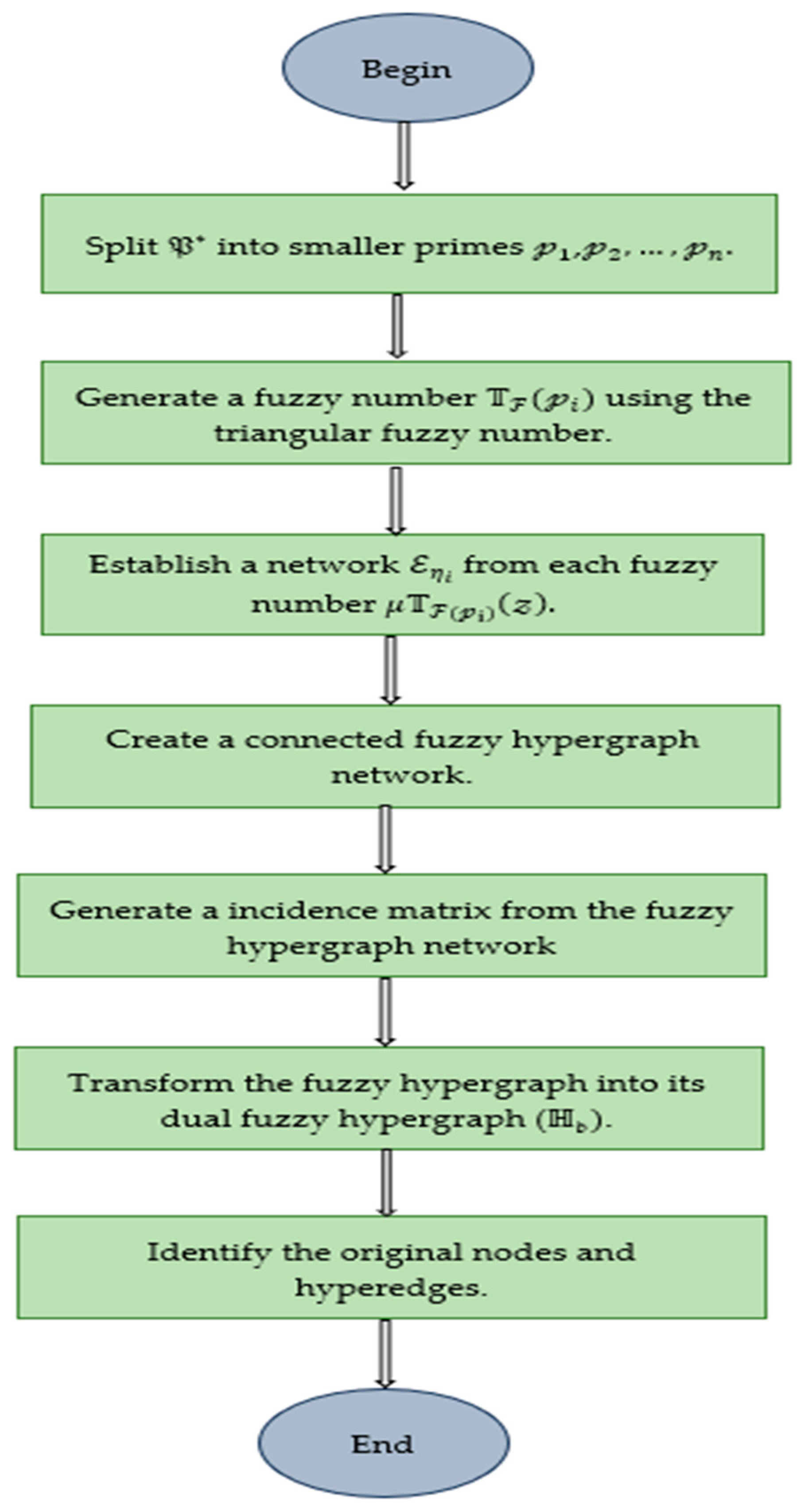
In cryptographic systems, Encryption Algorithm is responsible for protecting sensitive data by converting plaintext into an unread ciphertext. This preserves data confidentiality so that it becomes inaccessible to users who are not authorized. The flowchart of the Encryption Algorithm is represented in Figure 2.
| Algorithm 1. Encryption Algorithm |
| Input: Secret key (a large prime number). Output: The dual fuzzy hypergraph and metadata are prepared for transmission. Begin Step-1: Split into smaller primes ,, such that +. Step-2: For each prime generate a fuzzy number using the triangular fuzzy number conversion. Step-3: Each fuzzy number is splitted as nodes of a hyperedge in a fuzzy hypergraph (. Step-4: Establish a network from each fuzzy number Step-5: Develop a connected network with nodes values as with respective hyperedges . Step-6: Create a fuzzy hypergraph network, where the values of the nodes in the shared network can be interpreted as a contribution to each network it belongs to. Step-7: Generate an incidence matrix from the fuzzy hypergraph network, representing the relationships between nodes and hyperedges. Step-8: Transform the fuzzy hypergraph into its dual fuzzy hypergraph (. Step-9: Add simulated nodes and hyperedges to the dual fuzzy hypergraph to make the structure more complex and obscure. Step-10: Identify the original nodes and hyperedges . End |
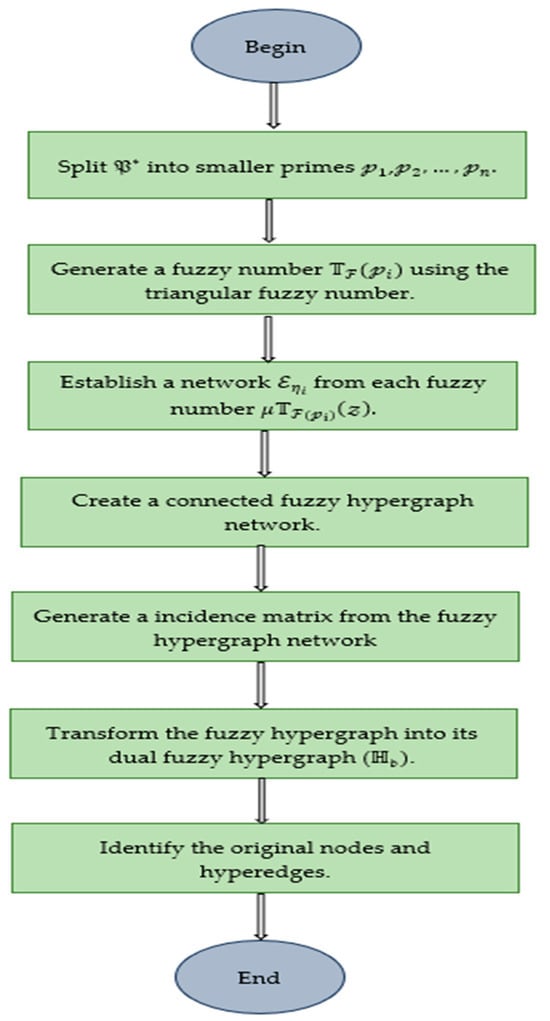
Figure 2.
Flowchart representation of encryption algorithm.
3.2. Decryption Algorithm (Algorithm 2)
The Decryption process then reverses this transformation, restoring the original plaintext.
| Algorithm 2. Decryption Algorithm |
| Input: The dual fuzzy hypergraph and decryption key. Output: Reconstructed secret key Begin Step-1: Use the decryption key to map fuzzy weights in the dual fuzzy hypergraph back to their corresponding nodes and edges in the original fuzzy hypergraph. Step-2: Remove simulated nodes and edges based on the provided metadata. Step-3: Invent a connected network with node values of with respective hyperedges . Step-4: Obtain the dual hypergraph network, where the values of the nodes in the shared network can be interpreted as a contribution to each network it belongs to. Step-5: Transform the dual fuzzy hypergraph into its fuzzy hypergraph (. Step-6: Reverse the normalization of fuzzy numbers to recover the original values of . Step-7: From the recovered fuzzy numbers, extract the original primes , . Step-8: Convert the fuzzy numbers back into their prime values. Step-9: Sum the extracted primes to reconstruct the original secret key + . Step-10: The original secret key is obtained. End |
4. Pseudo Code for Fuzzy Hypergraph-Based Encryption and Decryption (Algorithm 3)
Fuzzy hypergraphs are applied within the system to enhance the encryption and decryption processes. The pseudo code depicts important operations such as hypergraph creation, master key generation, encryption conversion, and decryption reconstruction and offers line-by-line algorithmic description of the operations. This approach can be used in secure communication and data security as it applies the concept of hypergraph structures for augmenting security, complexity, and resistance against attacks.
| Algorithm 3. Pseudo Code for Fuzzy Hypergraph-Based Encryption and Decryption |
| Input: Secret key (a large prime number), decryption key Output: Dual fuzzy hypergraph for encryption and reconstructed secret key for decryption --- Encryption Phase --- Initialize primes list = [] while > 0: Find the largest prime ≤ Add to primes list = − for each in primes list: Convert into a fuzzy number using triangular fuzzy conversion Add to fuzzy list Initialize fuzzy hypergraph for each fuzzy number in fuzzy list: Split into nodes Add nodes as a hyperedge in Initialize dual fuzzy hypergraph for each hyperedge in : Create a corresponding node in Connect nodes in based on overlapping hyperedges in for i = 1 to k: Add a simulated node n simulated to Connect simulated nodes with random existing nodes to form simulated hyperedges --- Transmission of and metadata --- --- Decryption Phase --- Initialize original fuzzy hypergraph for each node in : Use the decryption key to identify its corresponding hyperedge in for each node or edge in : if marked as dummy in metadata: Remove it from for each fuzzy number in : Convert back to its original prime Initialize primes list = [] for each in : Add to primes list = sum(primes list) Output: Reconstructed secret key |
5. Illustration
Consider a prime number = 10427, chosen as the secret key to represent the mission-critical information.
5.1. Implementation of Encryption Algorithm
Input: Secret key = 10427.
Output: The dual fuzzy hypergraph and metadata are prepared for transmission.
Begin
Step 1: Split the secret key into smaller primes as = 1007, , such that + . These smaller primes ensure security and are less susceptible to cryptanalysis.
Step 2: For each prime generate a fuzzy number using the triangular fuzzy number conversion.
The triangular fuzzy number, , is used to represent the degree of membership of a value in the fuzzy set. It is defined piecewise as
where is the lower bound of the fuzzy interval, is the peak or the most likely value of the fuzzy interval, and is the upper bound of the fuzzy interval.
This function represents how much of a value belongs to the fuzzy set . The closer is to , the higher its membership value will be, and the further is from , the lower its membership value.
Each prime number is transformed into a triangular fuzzy number based on one of the above triangular fuzzy formulae.
For instance, the prime number = 1007 is converted to 0.96,
Here, the range is <957, 1007, 1057>, = 957, = 1007, and , such that
Also, = 0.80, = 0.90, = 0.94 and so on.
Step 3: Each fuzzy number is split into nodes of a hyperedge in a fuzzy hypergraph (.
The network of the fuzzy hypergraphs is interconnected that they play their roles in the mission of encrypting and transferring the messages.
Let be the first network with nodes, be the second network with nodes, with nodes, and so on, and each networks is thus constructed.
The nodes of the first network are represented as , , and . In network , the weight of each hyperedge is distributed among the nodes according to their various roles, with these contributions determining their vertex membership values such as 0.25, 0.20, 0.36 and 0.15.
In the second network , the nodes are represented as . Here, the weight of the hyperedge is allocated among the nodes based on their distinct contributions, and these contributions define their vertex membership values as 0.15, .
Similarly, for the network , the weight of each hyperedge is assigned to the nodes based on their unique roles, and these roles determine their vertex membership values, such that has .
This is continued for ‘n’ distinct networks, where the allocation of hyperedge weights to the nodes is based on the specific roles and contributions of each node, thus determining the vertex membership values of each network, such that .
Step 4: The values of the nodes in the shared network can be interpreted as a contribution to each network it belongs to. When is shared across multiple hyperedges, its value is split or subtracted to ensure accurate membership representation in each individual network.
If is the shared node appearing in ‘n’ networks, say , ,… , then the value in each hyperedge is defines as
where is the number of nodes currently contained in the network, excluding the shared nodes . The shared value is evenly distributed across the hyperedges to reduce redundancy and avoid double counting.
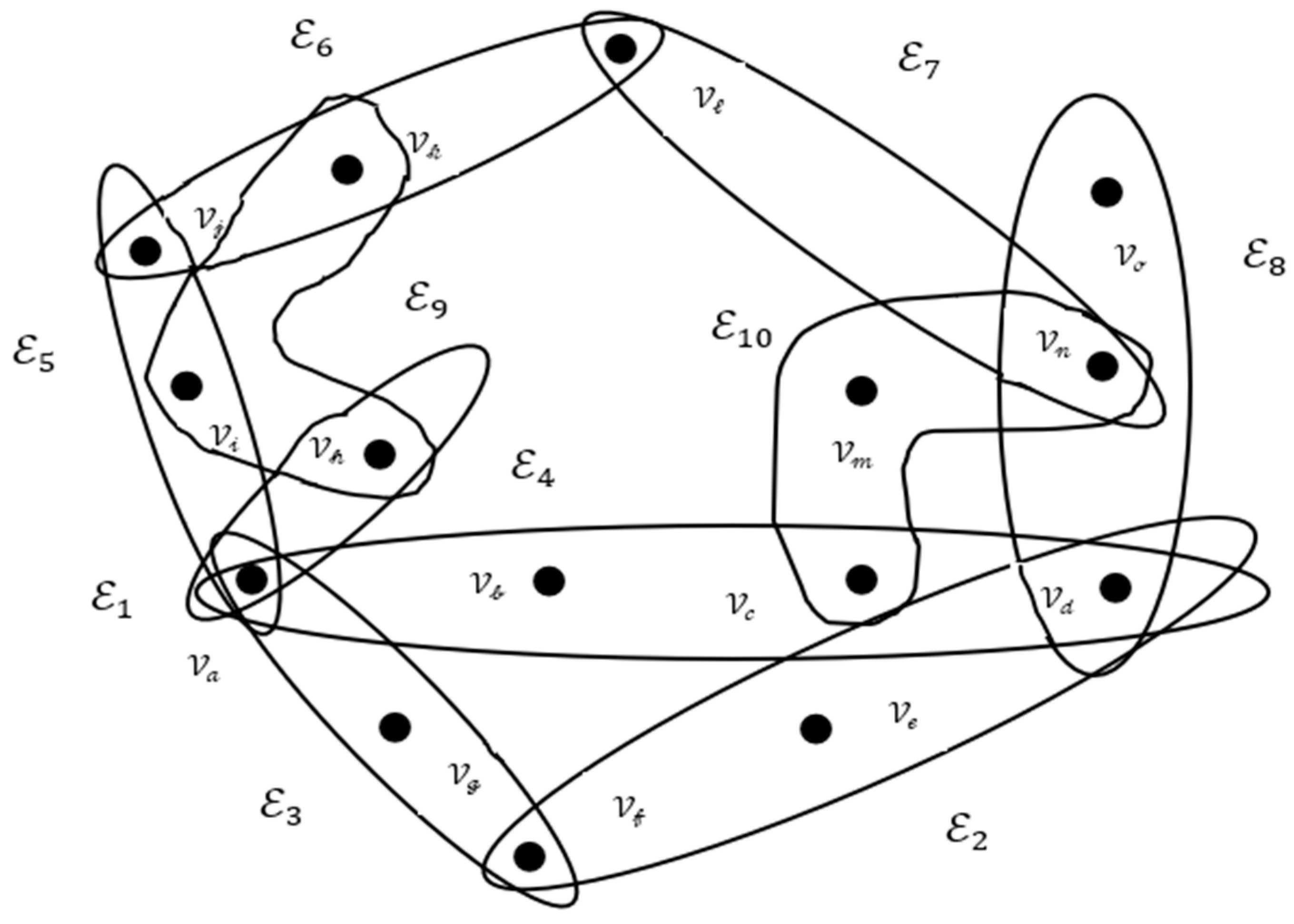
The sum of these nodes creates the hyperedges , ,… , ensuring data integrity (as mentioned in Figure 3) as follows.
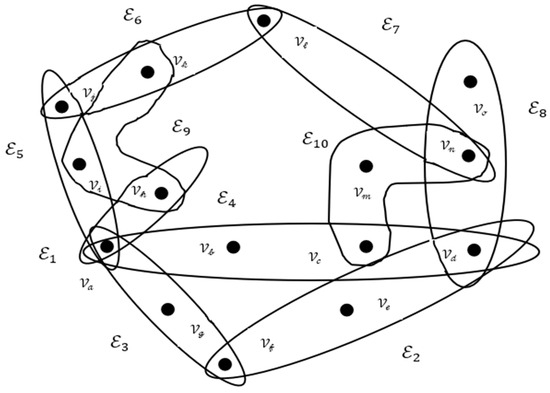
Figure 3.
Fuzzy hypergraph .
The membership values of the nodes and hyperedges are represented in the Table 1.

Table 1.
Fuzzy membership values of nodes and hyperedges.
The above table is a fuzzy hypergraph whose nodes are related with hyperedges , ,… . Every node possesses some membership value between 0 and 1 describing its level of belonging in the fuzzy hypergraph, whereas every hyperedge possesses some strength value describing the level of connectivity between the nodes. High membership values represent the high involvement of nodes, and high hyperedge strengths represent strong relationships between nodes. The table describes a structured fuzzy hypergraph in which nodes and hyperedges are dynamically interconnected to create a complex network with different connectivity and contribution levels in the network.
Step 5: An incidence matrix is derived from the fuzzy hypergraph network, representing the relationships between nodes and hyperedges. The matrix serves as a crucial tool for analyzing the network’s structure, and it is defined as
The incidence matrix of the above fuzzy hypergraph is as follows:
Step 6: Transform the fuzzy hypergraph into its dual fuzzy hypergraph (.
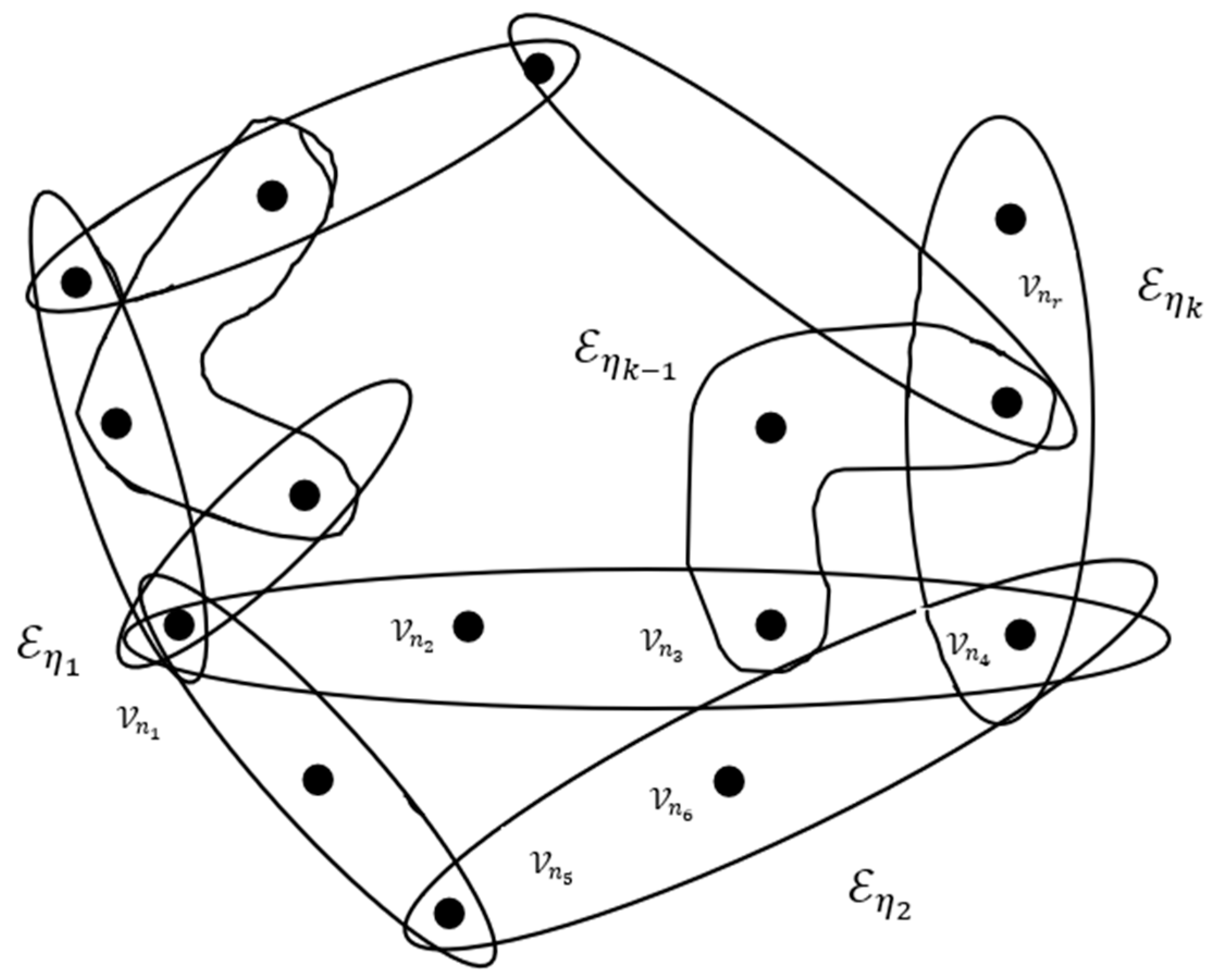
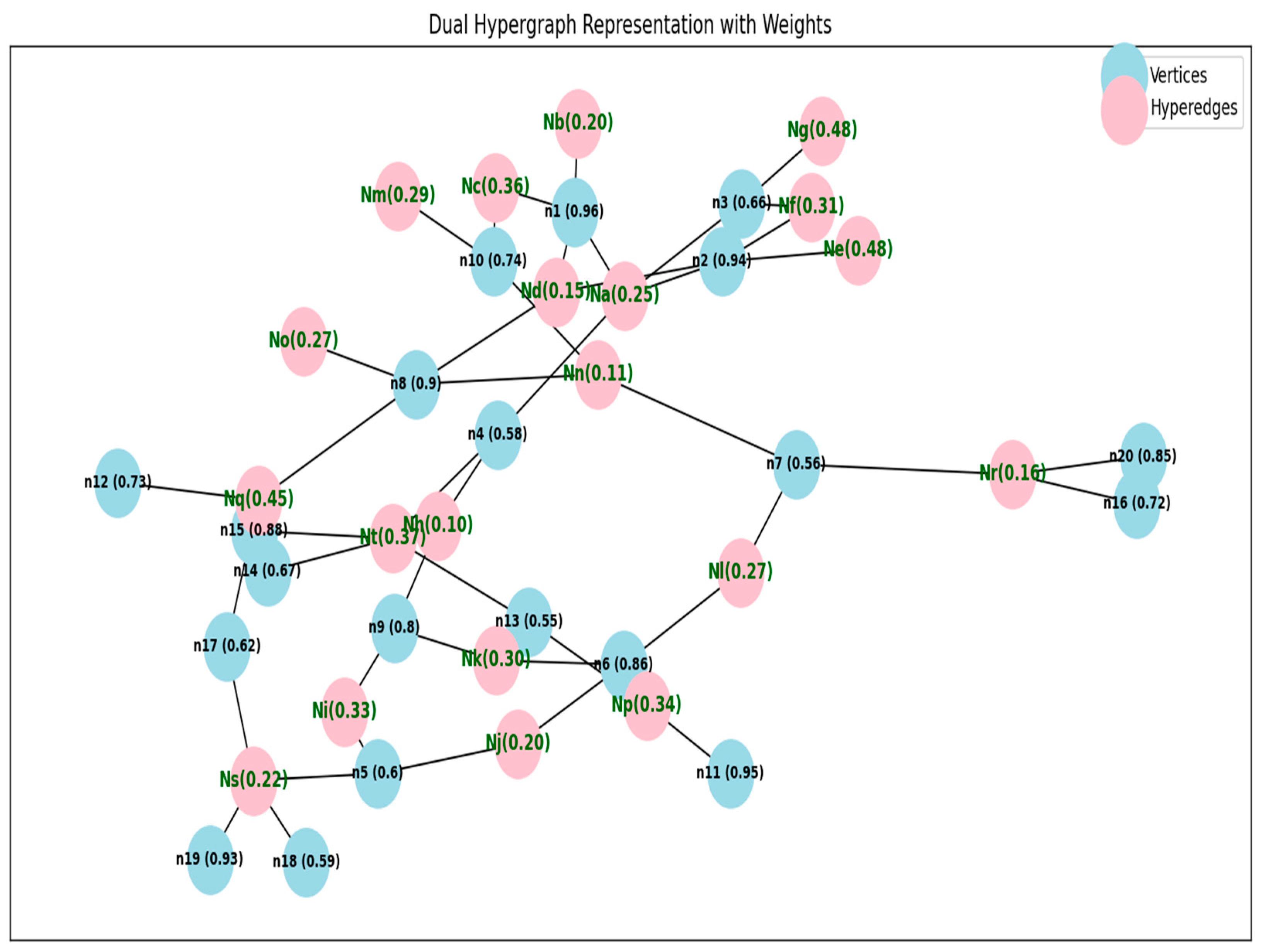
To transform a fuzzy hypergraph into its dual, compute the transpose of the incidence matrix, where the roles of nodes and edges are swapped. The dual representation, as shown in Figure 4, now containing the scrambled and obfuscated information, is transmitted as the encrypted message. The nodes are represented as and hyperedges as Simulated nodes and edges are added to the network to make is more complex. The nodes and hyperedges are swapped, with , , , …, swapped to and , ,… to
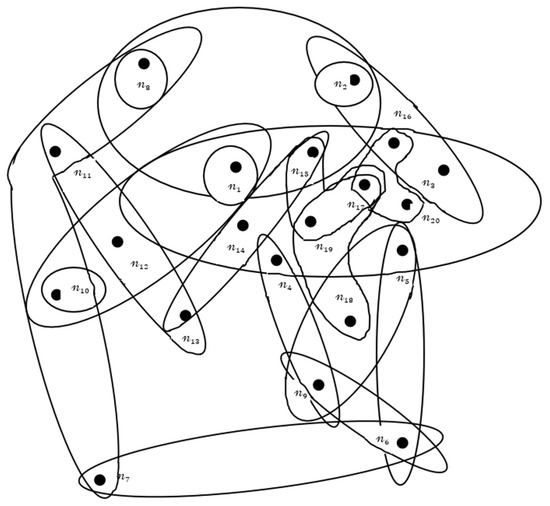
Figure 4.
Dual fuzzy hypergraph .
Step 7: The recipient is required to identify the original nodes and hyperedges by aggregating the hyperedges of each network such that .
End.
5.2. Implementation of Decryption Algorithm
Input: The dual fuzzy hypergraph and decryption key.
Output: Reconstructed secret key
Begin
Step-1: By using the decryption key to map fuzzy weights in the dual fuzzy hypergraph back to their corresponding nodes and edges in the original fuzzy hypergraph.
In this step, the decryption key is used to interpret the hyperedge fuzzy weights of the dual fuzzy hypergraph, effectively reversing the encryption process. These weights are mapped back to their corresponding nodes and edges in the original fuzzy hypergraph, restoring the original network structure and relationships.
Step-2: Remove simulated nodes and hyperedges , based on the provided metadata.
Step-3: Reverse the normalization of fuzzy numbers to recover the original values of . Each fuzzy number corresponds to a specific prime component of the original secret key.
Step-4: From the recovered fuzzy numbers extract the original primes ,.
Step-5: Convert the fuzzy numbers back into their prime values , . These primes were the ones used to split the original secret key during encryption.
Step-6: Sum the extracted primes to rebuild the original secret key, such that . This key is identical to the secret key used during encryption.
Step-7: The original secret key is received.
End
6. Performance Analysis and Comparative Study
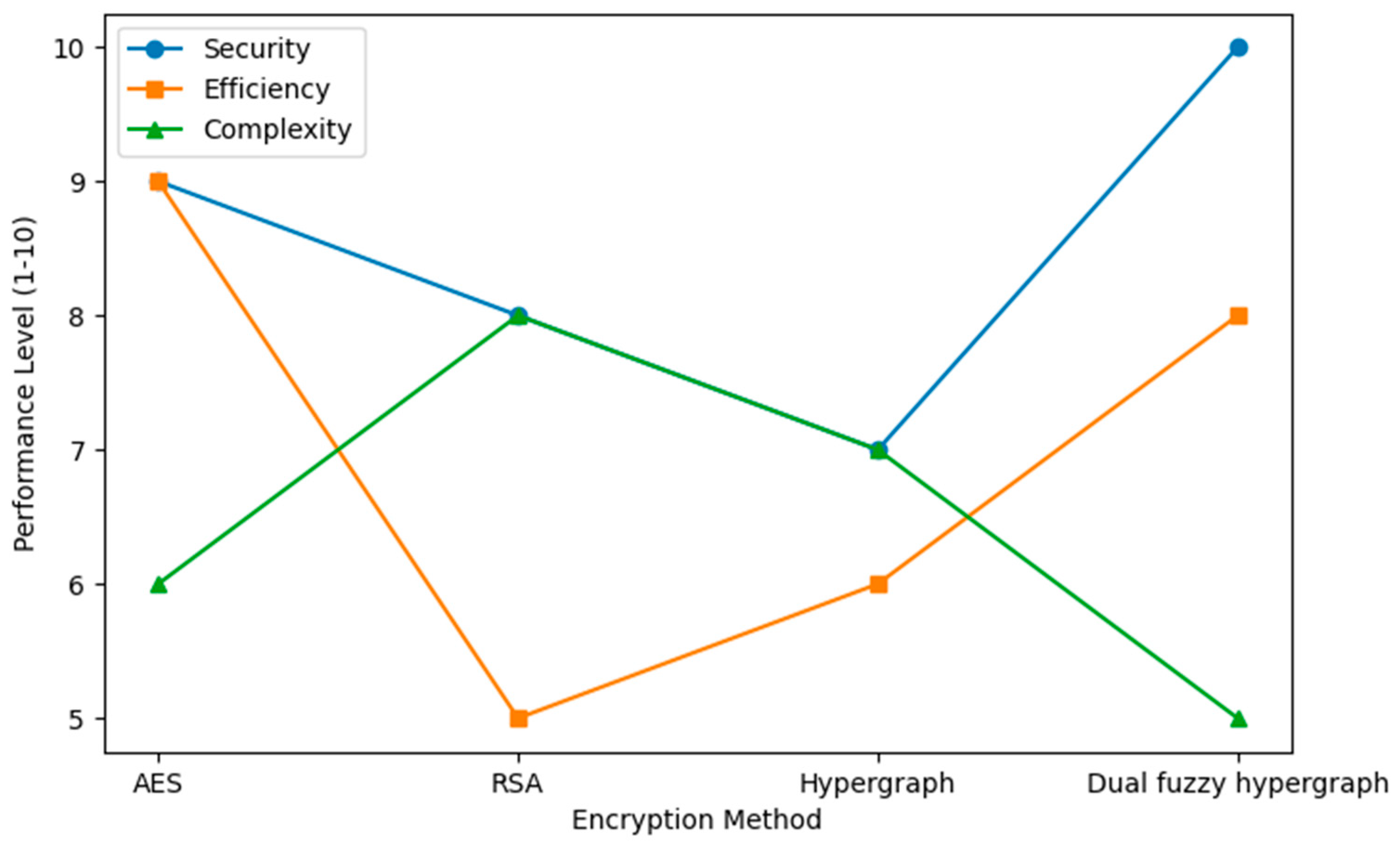
The graph below, in Figure 5, offers a detailed comparison of different encryption methods based on their efficiency, security level, and computational complexity. The compared algorithms are Advanced Encryption Standard (AES), Data Encryption Standard (DES), Rivest–Shamir–Adleman (RSA), and the suggested fuzzy hypergraph-based encryption scheme. The comparison reveals the merits and demerits of each method and how the suggested technique provides the best balance between security and performance.
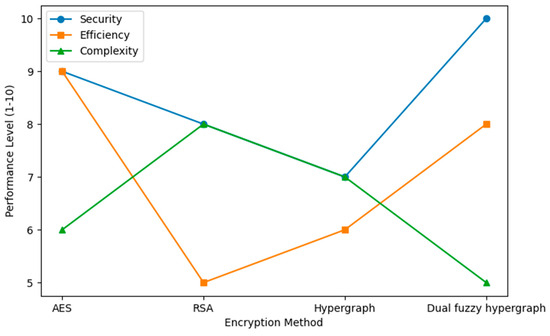
Figure 5.
Comparison of encryption techniques.
AES is the most common symmetric algorithm of encryption because it is fast and efficient. It uses a block cipher design with repeated rounds of encryption to provide high-speed encryption and decryption, even for very large data sets. Its high rate of computation makes it suitable for real-time communications and high-security storage systems. Nonetheless, although AES is efficient, it can be made susceptible to some cryptographic attacks if key length or randomness during key generation are compromised. In the same way, DES, a legacy symmetric key algorithm, shows high-speed processing, but is much less secure than AES because of its reduced key length (56 bits). This makes it prone to brute-force attacks, which reduces its use in contemporary cryptographic systems.
RSA, on the other hand, is a popular asymmetric encryption algorithm that has superior security due to its dependence on the complexity of large prime factorization. Unlike symmetric encryption, RSA uses a public and private key pair for decryption and encryption to offer secure communication even when networks are not trusted. The only drawback of RSA is its high computational cost. The time taken to decrypt and encrypt increases exponentially with the key size, making it impossible for large-scale uses or situations that require real-time processing. The tremendous overhead of using RSA makes it less efficient compared to symmetric key encryption.
The fuzzy hypergraph-based encryption model suggested here introduces a new approach that maps the data into a dual hypergraph representation. Every node and hyperedge is translated using fuzzy weights, with multiple layers of encryption. Simulated nodes and hyperedges are also introduced to further obscure the structure, significantly increasing security. Decryption involves reconstructing the original dual hypergraph, removing the virtual nodes, and re-establishing the original fuzzy values. This multi-step process of decryption makes it extremely difficult for the attacker to convert the encrypted message back into its readable form without knowing the decryption key. The decryption and encryption period of the fuzzy hypergraph model is a fraction of a nanosecond slower than that of symmetric techniques, but is offset by the more enhanced security. The model strongly protects against most previously known vulnerabilities via an amalgamation of graph theory, cryptography, and fuzzy logic. The dual hypergraph visualization of nodes and hyperedges provides an added layer of complexity, reducing the risk of structural attacks. Additionally, the fuzzy weights mapping adds another layer of randomness, further securely encrypting the communication.
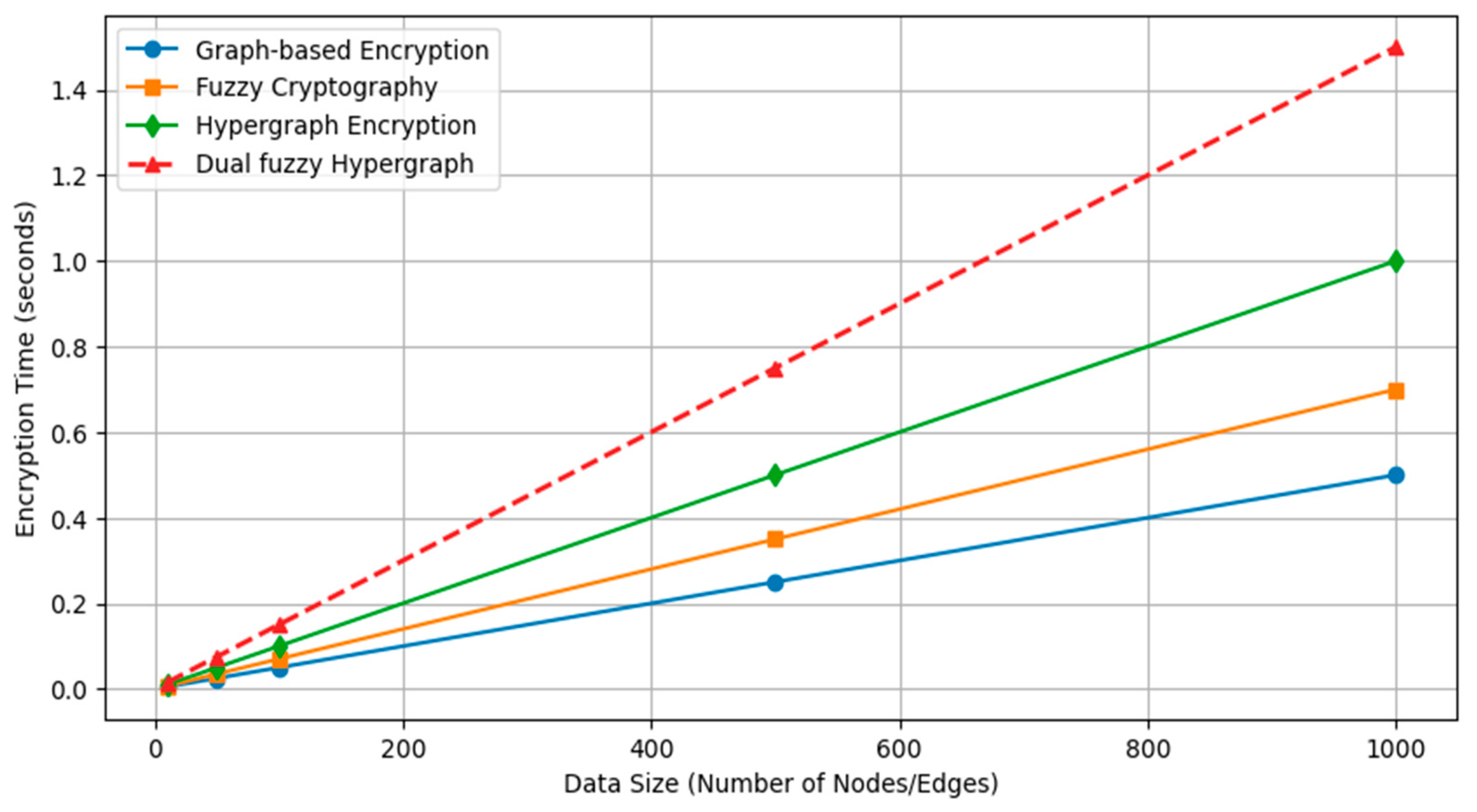
This balance between computation and security makes the fuzzy hypergraph-based encryption scheme a promising alternative for traditional cryptographic protocols. Its implementation, represented in Figure 6, is particularly well-suited in environments that prize data confidentiality and integrity, such as military communication, cloud data security, and secure transmission of sensitive healthcare information. With its capacity to repair the deficiency of existing techniques, the new model sets a standard in modern cryptanalysis, uniting hypergraph theory, fuzzy logic, and encryption in a novel and secure platform.
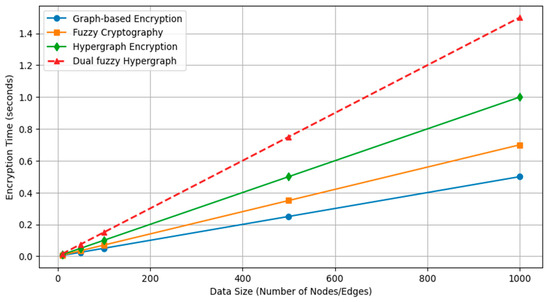
Figure 6.
Performance analysis.
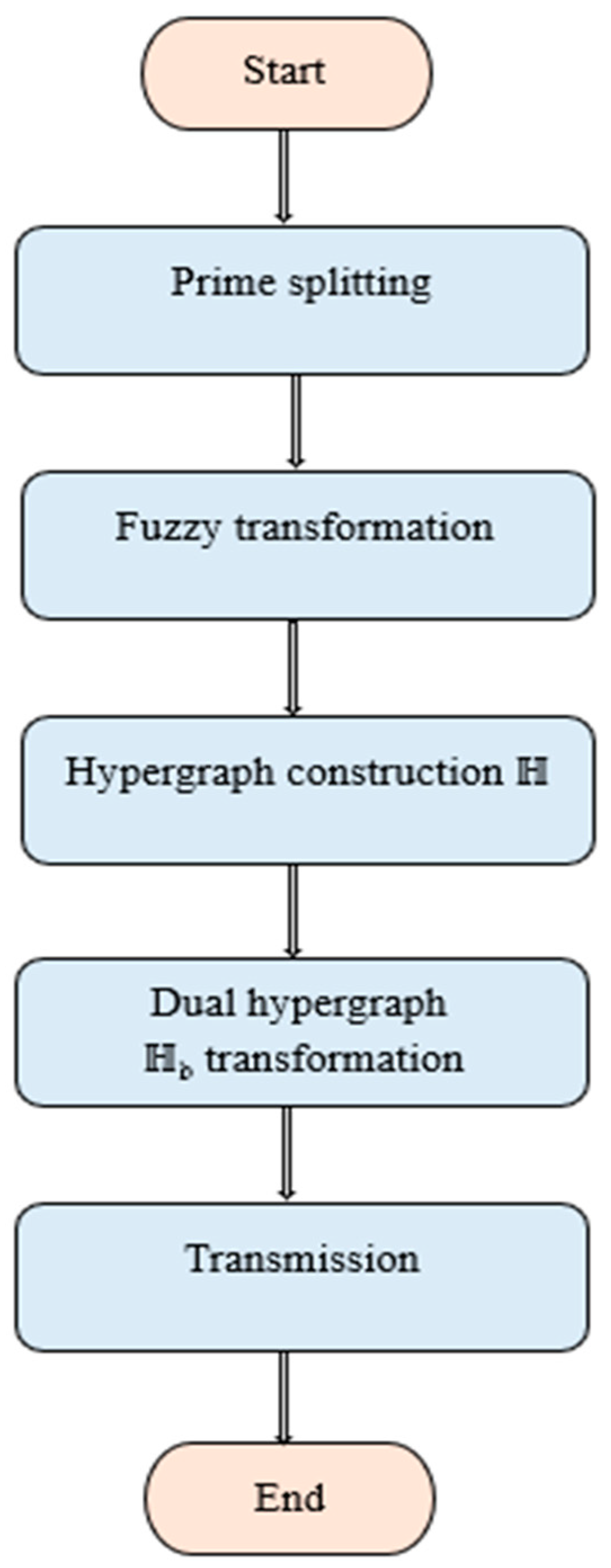
The investigation of quantum-resistant fuzzy hypergraph transformations offers a promising path towards improving the security of cryptography against impending quantum computing attacks. Conventional encryption technologies, based on mathematical problems such as integer factorization and discrete logarithms, are placed at risk by quantum algorithms. Fuzzy hypergraph-based encryption adds complexity by incorporating both fuzzy logic and hypergraph transformations, making it more quantum-resistant. The conversion of a hypergraph into its dual, as well as the addition of simulated nodes and edges, raises the bar on reconstructing the original data in the absence of the proper decryption key. Additionally, the combinatorial complexity of hypergraphs and the vagueness created by fuzzy logic make the attack surface for quantum computers more complex, thus strengthening security. The flowchart how the cryptanalysis being carried out is represented in Figure 7. Focusing future research efforts here could help in advancing new methods for fuzzy transformation, optimizing bi-level hypergraph forms, and making the treatment of simulated objects more delicate so as to enhance patterns of concealment, ending in enhancing the resistance of encryption schemes to both conventional and quantum attacks.
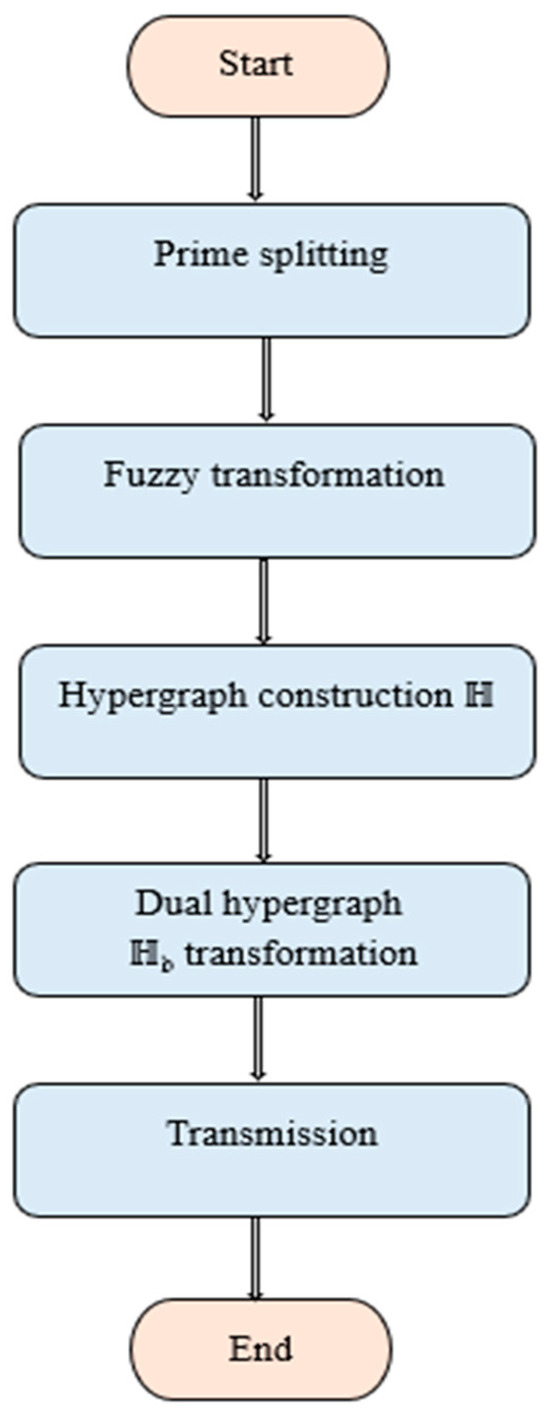
Figure 7.
Flowchart representation of the fuzzy hypergraph cryptanalysis.
7. Applications
Sensitive Message Transmission in the Military
To transmit sensitive data securely, such as mission orders or battlefield coordinates, we can use fuzzy graph theory and fuzzy hypergraph transformations to achieve strong encryption and thus prevent interception.
Fuzzy hypergraph cryptography ensures the safe transportation of sensitive battlefield information, e.g., the deployment of units, mission coordinates, and reconnaissance data, even when the situation changes and is insecure. For instance, a recon unit in a hostile area needs critical battlefield coordinates to be transported from a command post. To improve modularity and safety, the coordinates are first encrypted in a very large prime number that serves as the secret key. The number is then decomposed into smaller primes. Triangular fuzzy numbers are created from the primes, adding yet another degree of complexity and resilience.
To create a network representation of the encrypted data, a fuzzy hypergraph is built in which fuzzy numbers are vertices and their sums are hyperedges. The fuzzy hypergraph is also transformed into its dual, in which vertices turn into hyperedges and hyperedges turn into vertices. The integrity of the communication is ensured by sending this dual fuzzy hypergraph and a securely shared key to the reconnaissance unit.
(command center) is the central hub for all communications and decisions. (tactical updates) provides real-time battlefield updates. (logistics coordination) manages supply chains and troop movements. (medical evacuation) coordinates medical support for injured personnel. (intelligence sharing) shares classified intelligence reports. (mission execution) focuses on actual mission deployment and status. (cyber defense) monitors cybersecurity threats. (reconnaissance) provides information from the field. (air support coordination) manages airstrike and support operations, and (diplomatic liaison) communicates with allied forces and handles negotiations.
Upon being provided with the key, the reconnaissance unit returns the original fuzzy hypergraph to its original state by identifying and eliminating the phantom nodes and edges. The unit decomposes the fuzzy numbers into their prime factors and reverses the conversions. The device can decrypt the battlefield coordinates transmitted by summing the primes to reassemble the original secret key.
This approach has a number of advantages. It is essentially difficult for attackers to decipher the message, even when intercepted, by virtue of the extremely obfuscated structure formed as a result of using dummy elements and double fuzzy hypergraph transforms. The inherent combinatorial complexity of fuzzy hypergraphs renders the method resistant to advanced cryptanalysis attacks, including those by quantum computers. In addition, the distributed structure of the fuzzy hypergraph supports dynamic adaptation, ensuring secure communication even if nodes or edges are attacked.
The fuzzy logic of the transformation process ensures resistance to ambiguities and changes, which are characteristic of dynamic military actions. In addition, the scalability of the system allows large volumes of mission data to be encrypted without compromising security or effectiveness.
Critical information is kept private and safe when transmitted. The dummy and dual fuzzy hypergraph elements render the information useless without the decryption key, even if the enemy forces succeed in intercepting the message. With the proper key, the reconnaissance unit can successfully decrypt the message, ensuring that mission-critical information reaches the destination without any delay or compromise. Since it provides unparalleled security, flexibility, and reliability in the most challenging operating environments, fuzzy hypergraph-based encryption is a critical weapon for military communications.
In the financial sector, this method can be utilized in safe online payments, and by banking platforms for encrypting sensitive financial information and securing it from cyber-attacks. The new approach enhances the security of blockchain networks and cryptocurrency wallets through the addition of dynamic key generation and redundancy via fuzzy hypergraphs.
In communication networks, this approach enhances the security of 5G and IoT networks by proposing multi-path encryption using shared nodes in hypergraphs. It offers secure communication in cloud-based applications by utilizing fuzzy hypergraphs to develop a highly connected and fault-tolerant encryption layer, ensuring secure end-to-end encryption for instant messaging platforms.
In smart cities and infrastructure, it safeguards sensitive information from traffic volume, utility meters, and public services using adaptive encryption techniques that improve strength against cyber-attacks on city infrastructure. It also provides secure communication among smart devices and control centers in smart cities.
Also, in cloud computing and data centers, it ensures that user data will not be accessed by unauthorized users or leaked out by encrypting data on multiple virtual nodes, which ensures the safe migration and backup of encrypted data on multiple cloud servers.
Figure 8 shows how the required encrypted message is obtained using python programming.
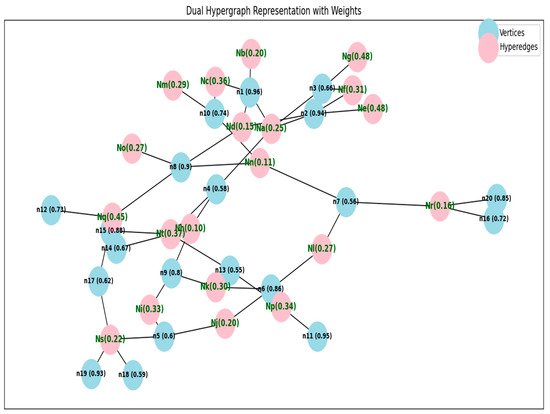
Figure 8.
Encrypted dual fuzzy hypergraph.
8. Conclusions
This research introduces a novel fuzzy hypergraph-based encryption model integrating cryptographic techniques and fuzzy hypergraph theory to address existing security challenges. Utilizing the fuzzy approach to handle ambiguity and fuzzy hypergraph structural complexity, the proposed scheme shows superior security characteristics. The method exhibits flexibility in accommodating different security requirements, and shows resistance to sophisticated cryptanalysis procedures. Additionally, the technology shows potential for quantum resistance, and hence is a suitable option for cryptographic systems that will be resilient for years to come. Because of such features, it is especially suitable for securing sensitive infrastructures, such as essential communications networks and military command. In an era when growing interconnectivity and changing cybersecurity threats are raising new challenges, this research makes valuable contributions to the cryptography field. It is a foreword to further research on fuzzy hypergraph-based cryptographic models, and promotes the further development of more secure communication technologies and their application in high-security environments.
Author Contributions
Conceptualization, A.M. and O.M.; methodology, A.M. and O.M.; validation, A.M., O.M., L.M., A.K. and S.S.; formal analysis, A.M., L.M., A.K. and S.S.; investigation, A.M.; data curation, A.M.; writing—original draft preparation, O.M. and A.M.; writing—review and editing, S.S., L.M., A.K. and O.M.; visualization, S.S., L.M., A.K. and A.M.; supervision, A.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Berge, C. Graphs and Hypergraphs; North-Holland Pub.: Amsterdam, The Netherlands, 1973; Volume 6. [Google Scholar]
- Berge, C. Hypergraphs: Combinatorics of Finite Sets; Elsevier: Amsterdam, The Netherlands, 1984; Volume 45. [Google Scholar]
- Aharoni, R.; Berger, E.; Kotlar, D.; Ziv, R. Degree conditions for matchability in 3-partite hypergraphs. J. Graph Theory 2018, 87, 61–71. [Google Scholar]
- Peng, H.; Qian, C.; Zhao, D.; Zhong, M.; Han, J.; Wang, W. Targeting attack hypergraph networks. Chaos Interdiscip. J. Nonlinear Sci. 2022, 32, 073121. [Google Scholar]
- Bretto, A. Hypergraph theory. In An Introduction. Mathematical Engineering; Springer: Cham, Switzerland, 2013; Volume 1. [Google Scholar]
- Qu, C.; Tao, M.; Yuan, R. A hypergraph-based blockchain model and application in internet of things-enabled smart homes. Sensors 2018, 18, 2784. [Google Scholar] [CrossRef] [PubMed]
- El Hibaoui, A.; Vallet, L. Fuzzy hypergraph model for anonymous communications. In Proceedings of the 2012 International Conference on Multimedia Computing and Systems, Tangiers, Morocco, 10–12 May 2012; pp. 888–894. [Google Scholar]
- Franklin, M.; Moti, Y. Secure hypergraphs: Privacy from partial broadcast. SIAM J. Discrete Math. 2004, 18, 437–450. [Google Scholar]
- Somu, N.; Kirthivasan, K.; VS, S.S. A computational model for ranking cloud service providers using hypergraph based techniques. Future Gener. Comput. Syst. 2017, 68, 14–30. [Google Scholar]
- Ranshous, S.; Joslyn, C.A.; Kreyling, S.; Nowak, K.; Samatova, N.F.; West, C.L.; Winters, S. Exchange pattern mining in the bitcoin transaction directed hypergraph. In Financial Cryptography and Data Security: FC 2017 International Workshops, WAHC, BITCOIN, VOTING, WTSC, and TA, Sliema, Malta, 7 April 2017, Revised Selected Papers 21; Springer: Cham, Switzerland, 2017; pp. 248–263. [Google Scholar]
- Pius, A.; Kirubaharan, D.R. Application of cryptography in data privacy using fuzzy graph theory. J. Discrete Math. Sci. Cryptogr. 2021, 24, 2389–2401. [Google Scholar] [CrossRef]
- Miner More, S.; Naumov, P. Hypergraphs of multiparty secrets. In Computational Logic in Multi-Agent Systems: 11th International Workshop, CLIMA XI, Lisbon, Portugal, 16–17 August 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 15–32. [Google Scholar]
- Morimae, T.; Yuki, T.; Masahito, H. Verification of fuzzy hypergraph states. Phys. Rev. A 2017, 96, 062321. [Google Scholar] [CrossRef]
- Deveci, M.; Kaya, K.; Uçar, B.; Çatalyürek, Ü.V. Fuzzy hypergraph partitioning for multiple communication cost metrics: Model and methods. J. Parallel Distrib. Comput. 2015, 77, 69–83. [Google Scholar]
- Wang, D.; Yi, F.; Li, X. On general construction for extended visual cryptography schemes. Pattern Recognit. 2009, 42, 3071–3082. [Google Scholar]
- Zhou, Q.; Chan, C. Secret key generation for minimally connected fuzzy hypergraphical sources. IEEE Trans. Inf. Theory 2020, 66, 4226–4244. [Google Scholar]
- Zhi, L.; Liu, Y.; Liu, D.; Li, C.; Cui, W.; Hu, G. A key management scheme based on fuzzy hypergraph for fog computing. China Commun. 2018, 15, 158–170. [Google Scholar]
- Wang, D.; Yi, F.; Li, X.; Luo, P.; Dai, Y. On the analysis and generalization of extended visual cryptography schemes. arXiv 2006. [Google Scholar] [CrossRef]
- Christen, N. Fuzzy hypergraph-based type theory for software development in a Cyber-Physical context. In Advances in Ubiquitous Computing; Academic Press: Cambridge, MA, USA, 2020; pp. 45–138. [Google Scholar]
- Hajiabolhassan, H.; Cheraghi, A. Bounds for visual cryptography schemes. Discrete Appl. Math. 2010, 158, 659–665. [Google Scholar] [CrossRef]
- Meenakshi, A.; Mythreyi, O. Mathematical Modeling of Social Networks using hypergraphs. In Proceedings of the 2023 First International Conference on Advances in Electrical, Electronics and Computational Intelligence (ICAEECI), Tamil Nadu, India, 19–20 October 2023; IEEE, 2023; pp. 1–6. [Google Scholar]
- Annamalai, M.; Dhanushiya, S.; Mythreyi, O.; Mishra, J.S. Enhancing Multicriteria Decision-Making through Cryptographic Security Systems. In Multi-Criteria Decision-Making and Optimum Design with Machine Learning; CRC Press: Boca Raton, FL, USA, 2024; pp. 224–232. [Google Scholar]
- Meenakshi, A.; Kannan, A.; Cep, R.; Elangovan, M. Efficient Graph Network Using Total Magic Labeling and Its Applications. Mathematics 2023, 11, 4132. [Google Scholar] [CrossRef]
- Shao, Z.; Kosari, S.; Shoaib, M.; Rashmanlou, H. Certain concepts of vague graphs with applications to medical diagnosis. Front. Phys. 2020, 8, 357. [Google Scholar] [CrossRef]
- Shi, X.; Kosari, S.; Talebi, A.A.; Sadati, S.H.; Rashmanlou, H. Investigation of the main energies of picture fuzzy graph and its applications. Inter. J. Comput. Intell. Syst. 2022, 15, 31. [Google Scholar] [CrossRef]
- Shi, X.; Kosari, S.; Rashmanlou, H.; Broumi, S.; Satham Hussain, S. Properties of interval-valued quadripartitioned neutrosophic graphs with real-life application. J. Intell. Fuzzy Syst. 2023, 44, 7683–7697. [Google Scholar] [CrossRef]
- Shoaib, M.; Kosari, S.; Rashmanlou, H.; Malik, M.A.; Rao, Y.; Talebi, Y.; Mofidnakhaei, F. Notion of Complex Pythagorean Fuzzy Graph with Properties and Application. J. Mult. -Valued Logic Soft Comput. 2020, 34, 553–586. [Google Scholar]
- Banerjee, S.; Mukherjee, A.; Panigrahi, P.K. Quantum blockchain using weighted hypergraph states. Phys. Rev. Res. 2020, 2, 013322. [Google Scholar] [CrossRef]
- Singh, S.; Uçar, B. An efficient parallel implementation of a perfect hashing method for hypergraphs. In Proceedings of the 2022 IEEE International Parallel and Distributed Processing Symposium Workshops (IPDPSW), Lyon, France, 30 May–3 June 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 265–274. [Google Scholar]
- Orts, F.; Paulavičius, R.; Filatovas, E. Improving the implementation of quantum blockchain based on hypergraphs. Quantum Inf. Process. 2023, 22, 330. [Google Scholar] [CrossRef]
- Ramya, S.; Mohan, K.; Krithivasan, K.; Doraipandian, M. A Secure Authentication Scheme between Edge Devices Using Hypergraph Hashing Technique in Iot Environment. In Proceedings of the International Conference on Applications and Techniques in Information Security, Tamil Nadu, India, 22–24 November 2024; Springer Nature: Singapore, 2024; pp. 269–287. [Google Scholar]
- Romdhini, M.U.; Al-Sharqi, F.; Nawawi, A.; Al-Quran, A.; Rashmanlou, H. Signless Laplacian energy of interval-valued fuzzy graph and its applications. Sains Malays. 2023, 52, 2127–2137. [Google Scholar] [CrossRef]
- Kosari, S.; Shao, Z.; Rao, Y.; Liu, X.; Cai, R.; Rashmanlou, H. Some Types of Domination in Vague Graphs with Application in Medicine. J. Mult.-Valued Logic Soft Comput. 2023, 41, pp.203. [Google Scholar]
- Rao, Y.; Kosari, S.; Shao, Z.; Talebi, A.A.; Mahdavi, A.; Rashmanlou, H. New concepts of intuitionistic fuzzy trees with applications. Inter. J. Comput. Intell. Syst. 2021, 14, 1–12. [Google Scholar] [CrossRef]
- Wu, Q.; Lu, J. A secure model based on hypergraph in multilayer and multi-domain intelligent optical network. In Proceedings of the Wireless Communications, Networking and Applications: Proceedings of WCNA, Shenzhen, China, 27–28 December 2014; Springer: New Delhi, India, 2016; pp. 35–40. [Google Scholar]
- Masud, K.I.; Hasan, M.R.; Hoque, M.M.; Nath, U.D.; Rahman, M.O. A new approach of cryptography for data encryption and decryption. In Proceedings of the 2022 5th International Conference on Computing and Informatics (ICCI), Cairo, Egypt, 9–10 March 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 234–239. [Google Scholar]
- Alkasasbeh, A.H.; Badr, E.; Attiya, H.; Shabana, H.M. Shabana. Radio number for friendship communication networks. Mathematics 2023, 11, 4232. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).