An Artificial Neural Network Method for Simulating Soliton Propagation Based on the Rosenau-KdV-RLW Equation on Unbounded Domains

Abstract

The simulation of wave propagation, such as soliton propagation, based on the Rosenau-KdV-RLW equation on unbounded domains requires a bounded computational domain. Therefore, a special boundary treatment, such as an absorbing boundary condition (ABC) or a perfectly matched layer (PML), is necessary to minimize the reflections of outgoing waves at the boundary, preventing interference with the simulation’s accuracy. However, the presence of higher-order partial derivatives, such as $u_{xxt}$ and $u_{xxxxt}$ in the Rosenau-KdV-RLW equation, raises challenges in deriving accurate artificial boundary conditions. To address this issue, we propose an artificial neural network (ANN) method that enables soliton propagation through the computational domain without imposing artificial boundary conditions. This method randomly selects training points from the bounded computational space-time domain, and the loss function is designed based solely on the initial conditions and the Rosenau-KdV-RLW equation itself, without any boundary conditions. We analyze the convergence of the ANN solution theoretically. This new ANN method is tested in three examples. The results indicate that the present ANN method effectively simulates soliton propagation based on the Rosenau-KdV-RLW equation in unbounded domains or over extended periods.

1. Introduction

Nonlinear waves are important phenomena in applied sciences, and the behavior of waves are usually described by various mathematical models. The KdV equation, $u_t+u_{xxx}+u{u}_x=0$ [1], is one of most famous nonlinear evolution equations that is used to describe the various physical properties of waves, such as acoustic waves in a harmonic crystal and ion-acoustic waves in plasmas. One of the shortcomings of the KdV equation is the description of the wave–wave and wave–wall interactions. To overcome the deficiency of the KdV equation, Rosenau proposed an equation known as the Rosenau KdV equation, $u_t+u_{xxxxt}+u_x+u{u}_x=0$ [2,3]. Moreover, the term $-u_{xxt}$ was added to further investigate the nonlinear behavior of waves named the Rosenau-regularized long wave (Rosenau-RLW) equation, $u_t-u_{xxt}+u_{xxxxt}+u_x+u{u}_x=0$ [4,5]. On the other hand, the Rosenau-KdV-RLW equation combines the Rosenau KdV equation and the Rosenau-RLW equation as

$$u_t+{{au}_x+b{\left(u^p\right)}_x-cu}_{xxt}+d{u}_{xxx}+u_{xxxxt}=0,$$

(1)

where a, b, c, and d are non-negative real constants, and $p\ge 2$ is a positive integer. The Rosenau-KdV-RLW equation and its various generalizations have been used for modeling nonlinear wave phenomena [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83].

Numerous numerical schemes have been developed to simulate shock waves, solitary waves, and similar phenomena based on the Rosenau-KdV-RLW equation as seen in the literature. However, these schemes typically simulate soliton propagation within a bounded computational domain, such as $[\alpha ,\beta ]$, but avoid reaching the boundary in order to prevent wave reflection as it destroys the soliton. When using the common numerical schemes to simulate soliton propagation over extended periods, it is unavoidable for the soliton to reach the boundary, necessitating the imposition of artificial boundary conditions—like absorbing boundary conditions (ABC) or perfectly matched layers (PML)—to minimize reflections. However, the presence of higher-order partial derivatives, such as $u_{xxt}$ and $u_{xxxxt}$, raises challenges in the derivation of effective artificial boundary conditions for the Rosenau-KdV-RLW equation in order to achieve accurate and stable numerical schemes. To our knowledge, no ABC or PML schemes have been successfully developed for incorporation with the Rosenau-KdV-RLW equation.

Thus, the objective of this article is to propose an artificial neural network (ANN) method that allows for soliton propagation within a bounded computational domain without the need for artificial boundary conditions. This is because in the ANN method, one could randomly select training points from the bounded computational space-time domain, and the loss function designed is based on only the initial condition and the Rosenau-KdV-RLW equation itself. In particular, for those training points on the boundary, the Rosenau-KdV-RLW equation is used as a replacement for the boundary condition in the loss function. This is the advantage of the ANN method over the common numerical schemes.

The remainder of this article is organized as follows: In Section 2, we introduce the new ANN method for solving the Rosenau-KdV-RLW equation. In Section 3, we theoretically analyze the convergence of the ANN solution to the exact solution when the loss function is small. Section 4 presents tests of the new method on three cases. Finally, we conclude in Section 5.

2. Artificial Neural Network Method

Suppose that we choose a finite computational domain for the solution of the Rosenau-KdV-RLW in Equation (1) as follows:

$$\begin{array}{cc}\hfill & u_t+a{u}_x+b{\left(u^p\right)}_x-c{u}_{xxt}+d{u}_{xxx}+u_{xxxxt}=0,\alpha \le x\le \beta ,0\le t\le T,\hfill \\ \hfill & u(x,0)=\varphi \left(x\right),\alpha \le x\le \beta .\hfill \end{array}$$

(2)

Because of the finite interval $[\alpha ,\beta ]$, Equation (2) requires some boundary conditions in order to obtain the solution. Thus, artificial boundary conditions such as ABC or PML should be given for common numerical schemes. In this study, we develop an ANN method for solving Equation (2) to avoid this trouble. The recently developed physics-informed neural network (PINN) has become popular for solving partial differential equations [84,85,86]. In particular, there are several ANN solutions proposed for the Rosenau-KdV equation [87,88,89,90,91,92]. In the PINN method, the output of a deep neural network is considered to be the solution of the PDE that is to be solved. This neural network, along with the PDE, forms the structure for the PINN method, as shown in Figure 1, where the loss function is used to optimize the weights and biases in the neural network solution.

To solve the Rosenau-KdV-RLW equation using an ANN method based on the PINN, we first construct a neural network architecture, as shown in Figure 1, where the ANN structure has n hidden layers and m perceptrons. Each connection between neurons (perceptrons) in adjacent layers is associated with a weight. In our case, these weights are initialized using a Glorot uniform distribution. Each neuron j in layer l (except for the input layer) has an associated bias $b_j^{\left(l\right)}$ and a set of weights $w_{ij}^{\left(l\right)}$ connecting it to the neurons in the previous layer $(l-1)$. The biases in our case are initialized to zeros. After the input layer, each neuron in the hidden layers and the output layer applies an activation function to the weighted sum of its inputs plus the bias. Common activation functions include ReLU (Rectified Linear Unit), Sigmoid, and Tanh. The output $z_j^{\left(l\right)}$ of neuron j in layer l is calculated as follows:

$$z_j^{\left(l\right)}=\sigma \left(\sum _{i=1}^{n^{(l-1)}}{w}_{ij}^{\left(l\right)}{a}_i^{(l-1)}+b_j^{\left(l\right)}\right),$$

(3)

where $\sigma$ is the activation function, $w_{ij}^{\left(l\right)}$ are the weights, $a_i^{(l-1)}$ are the outputs of neurons in the previous layer, and $b_j^{\left(l\right)}$ is the bias. In this study, we employ the hyperbolic tangent function as follows:

$$\sigma \left(z\right)=tanh\left(z\right)={\displaystyle \frac{e^z-e^{-z}}{e^z+e^{-z}}}.$$

(4)

Between the input and output layers, there are one or more hidden layers. Each hidden layer consists of neurons that take inputs from the previous layer, apply weights and biases, and pass the result through an activation function. The number of hidden layers and the number of neurons in each hidden layer are hyperparameters that are adjusted based on empirical methods.

The next process is known as feedforward propagation. During the feedforward process, the input data are passed through the network layer by layer, with each layer’s neurons performing the weighted sum of inputs and activation function calculations. The output of each layer becomes the input to the next layer until the final layer (output layer) is reached. This involves repeated application of the activation function to the weighted sum of inputs and biases. The final layer of the network is the output layer. We express the ANN solution as follows:

$$U(x,t;\theta )=\sum _{j=1}^m{w}_j^{\left(n\right)}{z}_j^{(n-1)},$$

(5)

where n is the number of hidden layers with a width of m neurons, and 

$$\theta =\{w_{11}^{\left(1\right)},w_{12}^{\left(1\right)},b_1^{\left(1\right)},\cdots ,w_N^{\left(M\right)}\}$$

are all the weights and biases.

Here, we define our loss function as follows:

$$\mathrm{Loss}={\mathrm{Loss}}_{\mathrm{PDE}}+{\mathrm{Loss}}_{\mathrm{IC}},$$

(6)

$$\begin{array}{cc}\hfill {\mathrm{Loss}}_{\mathrm{PDE}}& ={\displaystyle \frac{1}{n_1}}\sum _{i=1}^{n_1}(U_t(x_i,t_i;\theta )+a{U}_x(x_i,t_i;\theta )\hfill \\ \hfill & +b{\left(U(x_i,t_i;\theta )\right)}_x^p-c{U}_{xx}(x_i,t_i;\theta )\hfill \\ \hfill & +d{U}_{xxx}(x_i,t_i;\theta )+U_{xxxxt}(x_i,t_i;\theta ){)}^2\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill {\mathrm{Loss}}_{\mathrm{IC}}& ={\displaystyle \frac{1}{n_2}}\sum _{i=1}^{n_2}{\left(U(x_i,0;\theta )-\varphi \left(x_i\right)\right)}^2\hfill \\ \hfill & +{\displaystyle \frac{1}{n_2}}\sum _{i=1}^{n_2}{\left(U_x(x_i,0;\theta )-{\varphi }_x\left(x_i\right)\right)}^2\hfill \\ \hfill & +{\displaystyle \frac{1}{n_2}}\sum _{i=1}^{n_2}{\left(U_{xx}(x_i,0;\theta )-{\varphi }_{xx}\left(x_i\right)\right)}^2\hfill \end{array}$$

(8)

where $(x_i,t_i)$ is the training point, $n_1$ is the number of training points from the domain $D_1=\{\alpha \le x\le \beta ,0<t\le T\}$, and $n_2$ is the number of training points from domain $D_2=\{\alpha \le x\le \beta ,t=0\}$.

As seen from Equations (6)–(8), only the PDE and initial conditions are included in the loss function. It should be pointed out that we add

$${\displaystyle \frac{1}{n_2}}\sum _{i=1}^{n_2}{[U_x(x_i,0)-{\varphi }_x\left(x_i\right)]}^2+{\displaystyle \frac{1}{n_2}}\sum _{i=1}^{n_2}{[U_{xx}(x_i,0)-{\varphi }_{xx}\left(x_i\right)]}^2$$

to the loss function in order to analyze the convergence in the next section. Furthermore, the loss function does not need an artificial boundary condition for the computational domain. This is because we have used the PDE as a replacement for the boundary condition in the loss function.

Our neural network programming is executed using Python and JAX [93], Google’s open source Python library that supports in-house artificial intelligence and machine learning. Other libraries utilized include Flax [94] and Optax [95]. Flax is a high-performance neural network library and ecosystem for JAX designed for flexibility, allowing for the creation of neural networks with more fine-grained control than other libraries. Optax is a gradient processing and optimization library for JAX.

We use Optax’s Adam optimizer to update the weights and biases (parameters) based on the value of the loss function, as outlined in Algorithm 1. JAX’s automatic differentiation (autodiff) simplifies the computation of higher-order derivatives, since the functions that compute these derivatives are themselves differentiable. To evaluate our loss functions, we utilize JAX’s autodiff capabilities with the jacfwd, hessian, and vmap functions. The jacfwd function computes the Jacobian of a function, while hessian computes the Hessian. The vmap function allows us to vectorize our input, eliminating the need to create batches when handling large amounts of data.

Algorithm 1: Adam optimizer from Optax

For the initial condition portion of our loss function, we use jacfwd and hessian below to calculate the first- and second-order derivatives of $u(x,t)$ with respect to x, as seen in lines 6 and 12 of Listing 1. We then repeat this process in lines 18 and 24 to obtain the first- and second-order derivatives of $\varphi \left(x\right)$ with respect to x. This allows us to compute the mean squared error (MSE) of $u(x,t)-\varphi \left(x\right)$, $u_x(x,t)-{\varphi }_x\left(x\right)$, and $u_{xx}(x,t)-{\varphi }_{xx}\left(x\right)$, which are later used to minimize our overall loss. We employ vmap to create functions (lines 8, 14, 20, and 26) that vectorize our input data $(t,x)$ for each of the above functions. The nesting of functions is necessary for combining vectorization with the autodiff functions. This could have been made more concise if we had created a single line with nested Python Lambda functions.

It is important to note that higher-order derivatives are present in the PDE. To incorporate the loss function related only to the PDE, we create Listing 2 and use jacfwd to obtain $u_t$ and $u_x$ (lines 4 and 10). For the term $u_{xxx}$ and other higher-order derivatives, we chain together jacfwd and hessian calls (see lines 22, 28, and 34 in Listing 2).

Listing 1: Loss function related to the initial conditions using jacfwd, hessian, and vmap functions.

1   from jax import jacfwd, hessian, vmap 2 3   u = make_prediction(t_0, x_0) 4 5   def get_u_x(get_u, t, x): 6     u_x = jacfwd(get_u, 1)(t, x) 7     return u_x 8   u_x_vmap = vmap(get_u_x, in_axes=(None, 0, 0)) 9   u_x = u_x_vmap(make_prediction, t_0, x_0).reshape(-1,1) 10 11   def get_u_xx(get_u, t, x): 12     u_xx = hessian(get_u, 1)(t, x) 13     return u_xx 14   u_xx_vmap = vmap(get_u_xx, in_axes=(None, 0, 0)) 15   u_xx = u_xx_vmap(make_prediction, t_0, x_0).reshape(-1,1) 16 17   def get_phi_x(get_phi, x): 18     phi_x = jacfwd(get_phi, 0)(x) 19     return phi_x 20   phi_x_vmap = vmap(get_phi_x, in_axes=(None,0)) 21   phi_x = phi_x_vmap(initial_cond1, x_0).reshape(-1,1) 22 23   def get_phi_xx(get_phi, x): 24     phi_xx = hessian(get_phi, 0)(x) 25     return phi_xx 26   phi_xx_vmap = vmap(get_phi_xx, in_axes=(None,0)) 27   phi_xx = phi_xx_vmap(initial_cond1, x_0).reshape(-1,1) 28 29   mse_0_loss = MSE(u, u_0) 30   mse_0_loss_dP_x = MSE(phi_x, u_x) 31   mse_0_loss_dP_xx = MSE(phi_xx, u_xx) 32 33   Loss_Data = mse_0_loss + mse_0_loss_dP_x + mse_0_loss_dP_xx

Listing 2: Loss function related to the PDE using jacfwd, hessian, and vmap functions.

1   from jax import jacfwd, hessian, vmap 2 3   def get_u_t(get_u, t, x): 4       u_t = jacfwd(get_u, 0)(t, x) 5       return u_t 6   u_t_vmap = vmap(get_u_t, in_axes=(None, 0, 0)) 7   u_t = u_t_vmap(make_prediction, t_c, x_c).reshape(-1,1) 8 9   def get_u_x(get_u, t, x): 10     u_x = jacfwd(get_u, 1)(t, x) 11     return u_x 12   u_x_vmap = vmap(get_u_x, in_axes=(None, 0, 0)) 13   u_x = u_x_vmap(make_prediction, t_c, x_c).reshape(-1,1) 14 15   def get_u_x_power(get_u, t, x, p): 16     u_xpower = jacfwd(get_u, 1)(t, x, p) 17     return u_xpower 18   u_x_power_vmap = vmap(get_u_x_power, in_axes=(None, 0, 0, None)) 19   u_x_power = u_x_power_vmap(make_prediction_squared, t_c, x_c, p).reshape(-1,1) 20 21   def get_u_xxx(get_u, t, x): 22       u_xxx = jacfwd(hessian(get_u, 1), 1)(t, x) 23       return u_xxx 24   u_xxx_vmap = vmap(get_u_xxx, in_axes=(None, 0, 0)) 25   u_xxx = u_xxx_vmap(make_prediction, t_c, x_c).reshape(-1,1) 26 27   def get_u_xxt(get_u, t, x): 28       u_xxt = jacfwd(hessian(get_u, 1), 0)(t, x) 29       return u_xxt 30   u_xxt_vmap = vmap(get_u_xxt, in_axes=(None, 0, 0)) 31   u_xxt = u_xxt_vmap(make_prediction, t_c, x_c).reshape(-1,1) 32 33   def get_u_xxxxt(get_u, t, x): 34       u_xxxxt = jacfwd(hessian(hessian(get_u, 1), 1), 0)(t, x) 35       return u_xxxxt 36   u_xxxxt_vmap = vmap(get_u_xxxxt, in_axes=(None, 0, 0)) 37   u_xxxxt = u_xxxxt_vmap(make_prediction, t_c, x_c).reshape(-1,1) 38 39   residual = u_t + a*u_x + b*u_x_power - c*u_xxt + d*u_xxx + u_xxxxt 40   Loss_Physics = MSE(residual)

3. Convergence

To analyze the convergence of the ANN solution to the exact solution, we assume that $L(U;\theta )<ϵ$, where $ϵ$ is small, and $U(x,t)\equiv U(x,t;\theta )$ satisfies

$$\begin{array}{ccc}\hfill & U_t+a{U}_x+b{\left(U^P\right)}_x-c{U}_{xxt}+d{U}_{xxx}+U_{xxxxt}=f,\hfill & \hfill \alpha \le x\le \beta ,0<t<T,\\ \hfill & U(x,0)-u(x,0)=g,\hfill & \hfill \alpha \le x\le \beta ,\end{array}$$

where $f(x,t)$ and $g\left(x\right)$ are continuous functions such that ${\left|f\right|}^2\le c_1ϵ$ and ${\left|g\right|}^2\le c_2ϵ$ for constants $c_1$ and $c_2$ in the closed domain $D=\{\alpha \le x\le \beta ,0\le t\le T\}$. This assumption is reasonable because if there is a point $(x_0,t_0)$ such that either of the two functions $\{f,g\}$ is very large, then, by the continuity of that function, there is a small neighborhood around the point $(x_0,t_0)$ in which the function is also large. Since training points are randomly selected, some of the training points may fall into this small region. Thus, the function at these training points becomes very large in absolute value, which may indicate that the loss function $L(U;\theta )\le ϵ$ is not satisfied. Let $E(x,t)=U(x,t)-u(x,t)$, where $u(x,t)$ is the exact solution of Equation (1) in $D=\{\alpha \le x\le \beta ,0\le t\le T\}$. One may see that $E(x,t)$ satisfies

$$\begin{array}{cc}\hfill & E_t+a{E}_x+b{\left(U^P\right)}_x-b{\left(u^P\right)}_x-c{E}_{xxt}+d{E}_{xxx}+E_{xxxxt}=f,\alpha \le x\le \beta ,0<t<T,\hfill \\ \hfill & E(x,0)=g,\alpha \le x\le \beta .\hfill \end{array}$$

(9)

We now make a compact extension in $E(x,t)$ to $E(x,t)\in C_0^{4,1}((-\infty ,\infty )\times [0,T])$ as

$$E(x,t)=\left\{\begin{array}{cc}E(x,t),\hfill & \alpha \le x\le \beta ,0\le t\le T,\hfill \\ 0,\hfill & -\infty <x\le {\alpha }_0,{\beta }_0\le x<\infty ,0\le t\le T,\hfill \end{array}\right.$$

where $C_0^{4,1}$ refers to the continuity of the fourth-order derivative with respect to x and the first-order derivative to t. Here, ${\alpha }_0<\alpha$ and ${\beta }_0>\beta$ are any constants such that the interval $[\alpha ,\beta ]$ is inside $[{\alpha }_0,{\beta }_0]$. Similarly, we make the corresponding compact extensions for $U,u,f,$ and g as E in $[{\alpha }_0,{\beta }_0]$ so that Equation (9) can be extended to

$$\begin{array}{cc}\hfill E_t+a{E}_x+b{\left(U^P\right)}_x-b{\left(u^P\right)}_x-c{E}_{xxt}+d{E}_{xxx}+E_{xxxxt}=f,-\infty <x<+\infty ,& 0<t<T,\hfill \end{array}$$

(10a)

$$\begin{array}{c}\hfill E(x,0)=g,-\infty <x<+\infty .\end{array}$$

(10b)

Multiplying Equation (10a) by $E(x,t)$ and integrating x over the interval $(-\infty ,\infty$), we obtain

$$\begin{array}{c}\hfill {\int }_{-\infty }^{+\infty }{E}_t·Edx-c{\int }_{-\infty }^{+\infty }{E}_{xxt}·Edx+{\int }_{-\infty }^{+\infty }{E}_{xxxxt}·Edx=-a{\int }_{-\infty }^{+\infty }{E}_x·Edx\\ \hfill -b{\int }_{-\infty }^{+\infty }[{\left(U^P\right)}_x-{\left(u^p\right)}_x]·Edx-d{\int }_{-\infty }^{+\infty }{E}_{xxx}·Edx+{\int }_{-\infty }^{+\infty }f·Edx.\end{array}$$

(11)

We now choose an interval $[{\alpha }_1,{\beta }_1]\supset [{\alpha }_0,{\beta }_0]$ such that $E({\alpha }_1,t)=E({\beta }_1,t)=E_x({\alpha }_1,t)=E_x({\beta }_1,t)=0$. It can be seen that

$${\int }_{-\infty }^{+\infty }{E}_t·Edx={\int }_{{\alpha }_1}^{{\beta }_1}{E}_t·Edx={\displaystyle \frac{1}{2}}{\displaystyle \frac{d}{dt}}{\int }_{{\alpha }_1}^{{\beta }_1}{E}^{2}dx.$$

(12)

Using the integration by parts, we have

$${\int }_{-\infty }^{+\infty }{E}_{xxt}·Edx={\int }_{{\alpha }_1}^{{\beta }_1}{E}_{xxt}·Edx=(E·E_{xt}){|}_{{\alpha }_1}^{{\beta }_1}-{\int }_{{\alpha }_1}^{{\beta }_1}{E}_{xt}dE={\displaystyle \frac{1}{2}}{\displaystyle \frac{d}{dt}}{\int }_{{\alpha }_1}^{{\beta }_1}{E}_x^{2}dx,$$

(13)

$$\begin{array}{cc}\hfill {\int }_{-\infty }^{+\infty }{E}_{xxxxt}·Edx& =(E·E_{xxxt}){|}_{{\alpha }_1}^{{\beta }_1}-{\int }_{{\alpha }_1}^{{\beta }_1}{E}_{xxxt}dE\hfill \\ \hfill & =-(E_x·E_{xxt}){|}_{{\alpha }_1}^{{\beta }_1}+{\int }_{{\alpha }_1}^{{\beta }_1}{E}_{xxt}·E_{xx}dx={\displaystyle \frac{1}{2}}{\displaystyle \frac{d}{dt}}{\int }_{{\alpha }_1}^{{\beta }_1}{E}_{xx}^{2}dx\hfill \end{array}$$

(14)

$${\int }_{-\infty }^{+\infty }E·E_{x}dx={\int }_{{\alpha }_1}^{{\beta }_1}E·E_{x}dx={\displaystyle \frac{1}{2}}{E}^2{|}_{{\alpha }_1}^{{\beta }_1}=0,$$

(15)

$${\int }_{-\infty }^{+\infty }{E}_{xxx}·Edx=(E·E_{xx}-{\displaystyle \frac{1}{2}}{E}_x^2){|}_{{\alpha }_1}^{{\beta }_1}=0,$$

(16)

$$\begin{array}{cc}\hfill {\int }_{-\infty }^{+\infty }[{\left(U^P\right)}_x-{\left(u^P\right)}_x]·Edx& ={\int }_{{\alpha }_1}^{{\beta }_1}[{\left(U^P\right)}_x-{\left(u^P\right)}_x]·Edx\hfill \\ \hfill & =[\left(U^P\right)-\left(u^P\right)]·E{|}_{{\alpha }_1}^{{\beta }_1}-{\int }_{{\alpha }_1}^{{\beta }_1}[U^P-u^P]·E_{x}dx\hfill \\ \hfill & =-{\int }_{{\alpha }_1}^{{\beta }_1}\sum _{k=1}^{P-1}(U^{P-k}·u^k)E·E_{x}dx\hfill \\ \hfill & \le M{\int }_{{\alpha }_1}^{{\beta }_1}|E·E_x|dx\hfill \\ \hfill & \le {\displaystyle \frac{M}{2}}\left({\int }_{{\alpha }_1}^{{\beta }_1}{E}^{2}dx+{\int }_{{\alpha }_1}^{{\beta }_1}{\left(E_x\right)}^2\right)dx,\hfill \end{array}$$

(17)

where M is a positive constant such that $M=\underset{{\alpha }_1\le x\le {\beta }_1,0\le t\le T}{max}{\sum }_{k=1}^{P-1}{\left|U\right|}^{P-k}·{\left|u\right|}^k$. It should be pointed out that such M exists because of the continuity of $U(x,t)$ and $u(x,t)$ in the closed domain $D=\{{\alpha }_1\le x\le {\beta }_1,0\le t\le T\}$. Furthermore, using the Young inequality, we have

$${\int }_{-\infty }^{+\infty }f·Edx={\int }_{{\alpha }_1}^{{\beta }_1}f·Edx\le {\int }_{{\alpha }_1}^{{\beta }_1}\left|f\right|·\left|E\right|dx\le {\displaystyle \frac{1}{2}}{\int }_{{\alpha }_1}^{{\beta }_1}{\left|f\right|}^{2}dx+{\displaystyle \frac{1}{2}}{\int }_{{\alpha }_1}^{{\beta }_1}{E}^{2}dx.$$

(18)

Substituting the above results into Equation (11) gives

$$\begin{array}{cc}\hfill & {\displaystyle \frac{d}{dt}}{\int }_{{\alpha }_1}^{{\beta }_1}[E^2(x,t)+c{E}_x^2(x,t)+E_{xx}^2(x,t)]dx\hfill \\ \hfill & \le r{\int }_{{\alpha }_1}^{{\beta }_1}[E^2(x,t)+c{E}_x^2(x,t)]dx+{\int }_{{\alpha }_1}^{{\beta }_1}{f}^{2}dx,0\le t\le T,\hfill \end{array}$$

(19)

where $r=max(bM+1,(bM+1)/c)$, with the initial condition

$${\int }_{{\alpha }_1}^{{\beta }_1}{E}^2(x,0)dx={\int }_{{\alpha }_1}^{{\beta }_1}{g}^2\left(x\right)dx.$$

(20)

Solving Equation (19) gives

$$\begin{array}{cc}\hfill & {\int }_{{\alpha }_1}^{{\beta }_1}[E^2(x,t)+c{E}_x^2(x,t)+E_{xx}^2(x,t)]dx\hfill \\ \hfill & \le e^{rT}[{\int }_0^t{e}^{-rs}{\int }_{{\alpha }_1}^{{\beta }_1}{f}^{2}dxds+{\int }_{{\alpha }_1}^{{\beta }_1}[E^2(x,0)+c{E}_x^2(x,0)+E_{xx}^2(x,0)]dx]\hfill \\ \hfill & \le 2e^{rT}\left[\underset{0\le t\le T}{max}{\int }_{{\alpha }_1}^{{\beta }_1}{f}^{2}dx+{\int }_{{\alpha }_1}^{{\beta }_1}[E^2(x,0)+c{E}_x^2(x,0)+E_{xx}^2(x,0)]dx\right].\hfill \end{array}$$

(21)

Hence, we integrate Equation (21) with respect to t over $[0,T]$. This gives

$$\begin{array}{cc}\hfill & {\int }_0^T{\int }_{{\alpha }_1}^{{\beta }_1}[E^2(x,t)+c{E}_x^2(x,t)+E_{xx}^2(x,t)]dxdt\hfill \\ \hfill & \le 4e^{rT}\left\{\underset{0\le t\le T}{max}{\int }_{{\alpha }_1}^{{\beta }_1}{f}^{2}dx+{\int }_{{\alpha }_1}^{{\beta }_1}[E^2(x,0)+c{E}_x^2(x,0)+E_{xx}^2(x,0)dx]\right\}.\hfill \end{array}$$

(22)

Note that $E,f,E_x,$ and $E_{xx}$ are all continuous functions and $[{\alpha }_1,{\beta }_1]$ is any interval such that interval $[\alpha ,\beta ]$ is inside $[{\alpha }_1,{\beta }_1]$. We let ${\alpha }_1\to \alpha$ and ${\beta }_1\to \beta$ in Equation (22). This gives

$$\begin{array}{cc}\hfill & {\int }_0^T{\int }_{\alpha }^{\beta }[E^2(x,t)+c{E}_x^2(x,t)+E_{xx}^2(x,t)]dxdt\hfill \\ \hfill & \le 4e^{rT}\left\{\underset{0\le t\le T}{max}{\int }_{\alpha }^{\beta }{f}^{2}dx+{\int }_{\alpha }^{\beta }[E^2(x,0)+c{E}_x^2(x,0)+E_{xx}^2(x,0)]dx\right\}\hfill \\ \hfill & \le 4e^{rt}(\beta -\alpha )[c_1ϵ+c_2ϵ].\hfill \end{array}$$

(23)

Here, we have used the assumption of $|E_x{(x,0)|}^2\le c_2ϵ$ and $|E_{xx}^2(x,0)|\le c_2ϵ$, since we have imposed them in the loss function. This indicates that the neural network solution in $[\alpha ,\beta ]$ is convergent to the exact solution in $[\alpha ,\beta ]$ and the smaller $ϵ$ is, the more accurate the ANN solution can be.

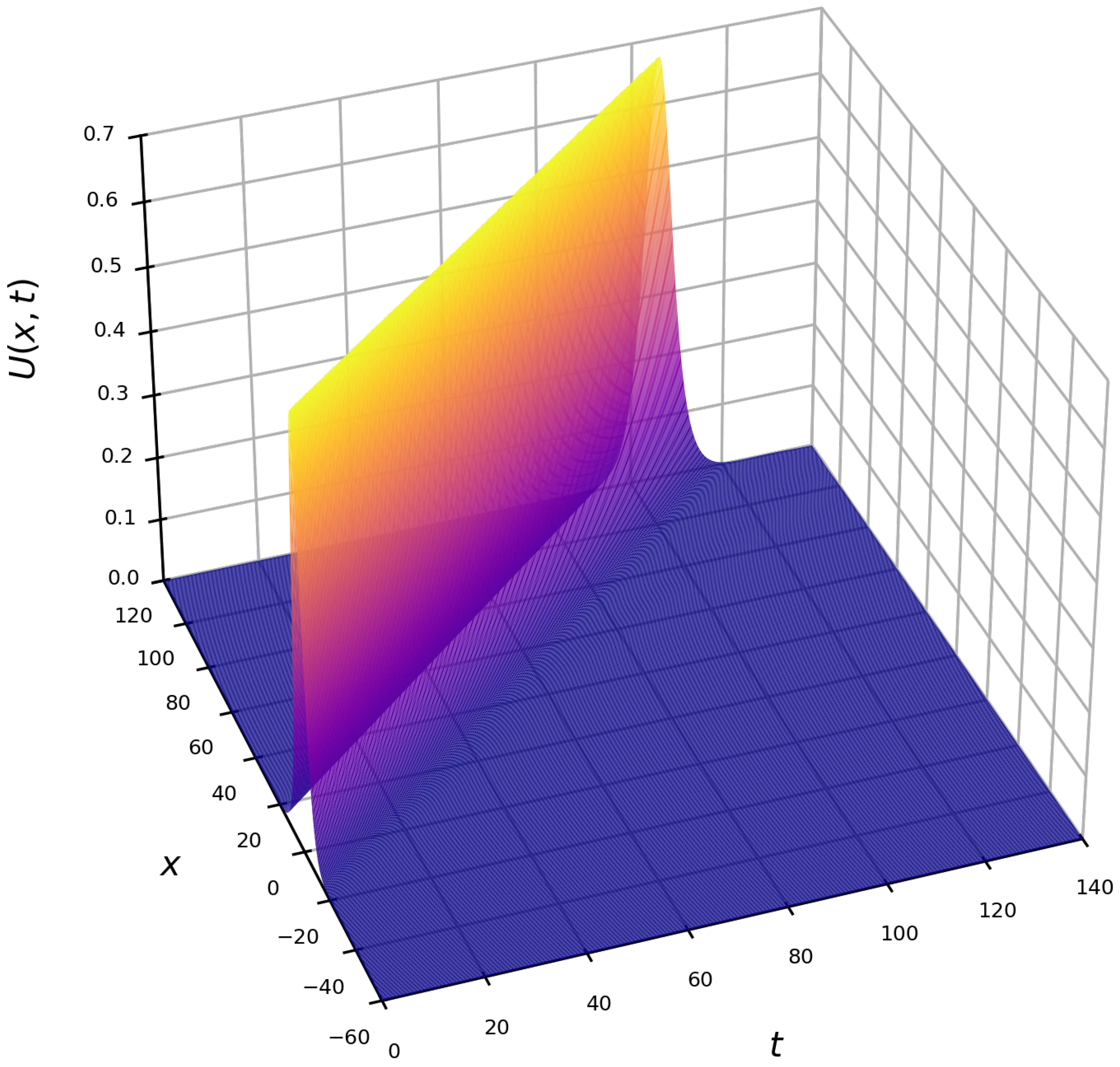
4. Numerical Experiments

To test the applicability of the present ANN method, we consider three examples for which we have exact solutions available. All models were trained using Optax’s Adam optimizer, a variant of Stochastic Gradient Descent that includes scaling adaptation through learning rate annealing. This technique systematically reduces the learning rate over time, and we set the parameters ${\beta }_1=0.9$ and ${\beta }_2=0.99$ for Algorithm 1. It should be pointed out that the default values for the $\beta$ variables in the Adam optimizer are typically set to ${\beta }_1=0.9$ and ${\beta }_2=0.999$. These values are widely used in practice because they work well in many common machine learning and deep learning tasks. ${\beta }_1=0.9$ controls the decay rate of the moving average of the first moment (mean of gradients). A value close to 1 (like 0.9) means that the optimizer remembers gradients over a long period but still gives some weight to more recent gradients. ${\beta }_2=0.999$ controls the decay rate of the second moment (uncentered variance of gradients). This is important for adapting the learning rate to the variance in gradients. A value like $0.999$ allows the optimizer to average out the gradients’ variance over time while still adapting quickly. These values allow the optimizer to use sufficient historical information (through the exponential moving averages) while adapting the learning rate to the gradient’s scale, especially for noisy gradients. Since these defaults are consistent across popular machine learning frameworks and research papers, it is common to see them used in practice. This consistency also facilitates benchmarking and comparing results across different studies and implementations.

The computational resources used for these experiments were performed on a shared HPC cluster node using a single NVIDIA A100 GPU with 80 GB of GPU memory. The training times for each of the experiments performed took between 2 and 3.5 h. Note that the number of collocation points directly impacts the accuracy of the model. More points generally allow the network to capture the solution to the differential equations and other physics-based constraints, such as boundary and initial conditions. For complex problems, more points are necessary to ensure that the loss function adequately represents the nuances of the underlying physics. Too few points may lead to underfitting, where the network fails to learn the physics across the entire domain. On the other hand, too many collocation points can lead to overfitting, reducing the model’s ability to generalize to unseen data. Due to the complexity of the problem’s underlying physics, a large number of collocation points (40,000) were selected, based on our experience with designing physics-informed neural networks. This number was chosen to strike a balance, ensuring the network trains effectively while avoiding overburdening the hardware (GPU) and minimizing unnecessary overhead during training.

4.1. Example 1

Consider the Rosenau-KdV-RLW equation in Equation (1) with $a=1,b=0.5,c=0,$ $d=1$ and $p=2$ as follows [6,63]:

$$u_t+u_x+0.5{\left(u^2\right)}_x+u_{xxx}+u_{xxxxt}=0,$$

(24)

subject to the initial condition

$$u(x,0)=\varphi \left(x\right)=35\left({\displaystyle \frac{\sqrt{313}}{212}}-{\displaystyle \frac{1}{24}}\right){sech}^4\left({\displaystyle \frac{1}{24}}\sqrt{-26+2\sqrt{313}}x\right),$$

(25)

where the exact soliton solution is

$$u(x,t)=35\left({\displaystyle \frac{\sqrt{313}}{212}}-{\displaystyle \frac{1}{24}}\right){sech}^4\left\{{\displaystyle \frac{1}{24}}\sqrt{-26+2\sqrt{313}}\left[x-\left({\displaystyle \frac{1}{2}}+{\displaystyle \frac{\sqrt{313}}{26}}\right)t\right]\right\}.$$

(26)

In our computation, we chose a domain over the spatial interval $[-70\le x\le 100]$ and the time interval $[0\le t\le T]$. We set $D_1=\{-70\le x\le 100,0<t\le 120\}$ and $D_2=\{-70\le x\le 100,t=0\}$. From $D_1$, we randomly picked 40,000 points from both the spatial and time domains, combining them into a set of $(x,t)$ coordinates as our training points. For $D_2$, we randomly selected 400 training points. Figure 2 shows a snapshot of the training points.

For the ANN configuration, we designed an input layer with 2 neurons corresponding to the x and t coordinates, five hidden layers with 50 neurons each, and one output layer with 1 neuron. This architecture was selected based on multiple trials, as shown in

Table 1. Neural network architecture trials.

Layers/Neurons	Total Loss	Max. Abs. Error
3 Layers of 50 Neurons	$2.011\times {10}^{-9}$	$2.336\times {10}^{-3}$
3 Layers of 100 Neurons	$9.379\times {10}^{-10}$	$1.474\times {10}^{-3}$
5 Layers of 50 Neurons 1	$6.494\times {10}^{-11}$	$3.999\times {10}^{-4}$

¹ Architecture selected.

. The model was then trained for 100,000 iterations, achieving a final loss of $6.494\times {10}^{-11}$.

Figure 3 shows the soliton propagation at various times $T=0,20,40,60,80,85,90$. Note that we added a vertical line at the boundary $x=100$ in the figure. From the figure, one may see that the soliton propagates through the computational interval $[-70,100]$ without reflection. In particular, we plotted the soliton at $T=90$, which has passed the boundary, demonstrating that the ANN method can still predict the soliton accurately.

To study stability, we used three separate training runs where the only changes were the initial seed values used in the Glorot uniform distribution used to assign the initial weights of our ANN. Otherwise, all training points used were created using the same seed values to ensure reproducibility. A low standard deviation indicates that the model consistently converges to similar solutions, thus showing the stability of our model. Furthermore, note that using differing initial seed values also shows that our model is not overly sensitive to the initialization or hyperparameters, thus showing that this ANN is reliable in finding good solutions. We calculated the mean and standard deviation of the three network predictions and plotted the results. As shown in the inset of Figure 3, the standard deviation among the predictions was negligible ($6.344\times {10}^{-6}$).

It should be pointed out out that the ANN method can still predict the soliton accurately, this is probably because predictions within the trained domain result from interpolation between known training points and the underlying physics. Outside this domain, the network has not seen the data during training, but as a universal function approximator (a feed-forward neural network with a single hidden layer that can approximate any continuous function on a compact subset of ${\mathbb{R}}^n$, given an appropriate activation function), it can extrapolate. If the network is well trained and the PDE solution is smooth, predictions just outside the trained region should be continuous and reasonable. However, predictions become more unreliable as the distance from the trained region increases.

Figure 4 presents a 3D plot of soliton propagation, while Figure 5 illustrates the absolute error between the ANN solution and the exact solution. The maximum absolute error between our ANN solutions and the exact solutions is $3.999\times {10}^{-4}$, and the error in the $L_2$-norm is $5.22\times {10}^{-5}$.

4.2. Example 2

Consider the Rosenau-KdV-RLW equation in Equation (1) with $a=1,b=1,c=1$, $d=0$, and $p=4$ as follows [6,63]:

$$u_t+u_x+{\left(u^4\right)}_x-u_{xxt}+u_{xxxxt}=0,$$

(27)

subject to the initial condition

$$u(x,0)=\varphi \left(x\right)=exp\left[{\displaystyle \frac{1}{p-1}}ln{\displaystyle \frac{(p+1)(3p+1)(p+3)}{2(p^2+3)(p^2+4p+7)}}\right]{sech}^{{\displaystyle \frac{4}{p-1}}}\left(k_{1}x\right),$$

(28)

where the exact soliton solution is

$$u(x,t)=exp\left[{\displaystyle \frac{1}{p-1}}ln{\displaystyle \frac{(p+1)(3p+1)(p+3)}{2(p^2+3)(p^2+4p+7)}}\right]{sech}^{{\displaystyle \frac{4}{p-1}}}\left[k_1(x-k_{2}t)\right],$$

(29)

and

$$k_1={\displaystyle \frac{p-1}{\sqrt{4p^2+8p+20}}},k_2={\displaystyle \frac{p^4+4p^3+14p^2+20p+25}{p^4+4p^3+10p^2+12p+21}}.$$

(30)

In our computation, we chose a domain over the spatial interval $[-60\le x\le 120]$ and the time interval $[0\le t\le T]$. We set $D_1=\{-60\le x\le 120,0<t\le 140\}$ and $D_2=\{-60\le x\le 120,t=0\}$. From $D_1$, we randomly picked $40,000$ points from both the spatial domain and the time domains and combined them into a set of $(x,t)$ coordinates as our training points. For $D_2$, we randomly picked 400 training points. We used the same ANN configuration as that for Example 1. The model was then trained using Optax’s Adam optimizer for $100,000$ iterations with a final loss of $5.49\times {10}^{-10}$.

Figure 6 illustrates the soliton propagation at various times $T=0,30,60,90,100,110$. A vertical line has been added at the boundary $x=120$. From the figure, it can be seen that the soliton propagates through the computational interval $[-60,120]$ without reflection. Notably, we plotted the soliton at $T=110$, which has passed the boundary, demonstrating that the ANN method can still accurately predict the soliton.

Figure 7 presents a 3D plot of soliton propagation, while Figure 8 displays the absolute error between the ANN solution and the exact solution. The maximum absolute error between our predicted solutions and the exact solutions is $3.57\times {10}^{-3}$, and the error in the $L_2$-norm is $4.12\times {10}^{-4}$.

4.3. Example 3

Consider the Rosenau-KdV-RLW equation in Equation (1) with $a=1,b=0.5,c=1$, $d=1$ and $p=2$ as follows [6]:

$$u_t+u_x+0.5{\left(u^2\right)}_x-u_{xxt}+u_{xxx}+u_{xxxxt}=0,$$

(31)

subject to the initial condition

$$u(x,0)=\varphi \left(x\right)=-{\displaystyle \frac{5}{456}}(25-13\sqrt{457}){sech}^4\left(k_{3}x\right),$$

(32)

where the exact soliton solution is

$$u(x,t)=-{\displaystyle \frac{5}{456}}(25-13\sqrt{457}){sech}^4\left[k_3(x-k_{4}t)\right],$$

(33)

and

$$k_3=\sqrt{{\displaystyle \frac{-13+\sqrt{457}}{288}}},k_4={\displaystyle \frac{241+13\sqrt{457}}{266}}.$$

(34)

In our computation, we chose a domain over the spatial interval $[-40\le x\le 100]$ and the time interval $[0\le t\le T]$. We set $D_1=\{-40\le x\le 100,0<t\le 120\}$ and $D_2=\{-40\le x\le 100,t=0\}$. From $D_1$, we randomly picked 40,000 points from both the spatial domain and the time domains and combined them into a set of $(x,t)$ coordinates as our training points. For $D_2$, we randomly picked 400 training points. We used the same ANN configuration as that for Example 1. The model was then trained using Optax’s Adam optimizer for 100,000 iterations with a final loss of $8.918\times {10}^{-9}$.

Figure 9 illustrates the soliton propagation at various times $T=0,20,40,45,50,55$. A vertical line has been added at the boundary $x=100$. From the figure, it can be seen that the soliton propagates through the computational interval $[-40,100]$ without reflection. Notably, we plotted the soliton at $T=55$, which has passed the boundary, demonstrating that the ANN method can still accurately predict the soliton.

Figure 10 presents a 3D plot of soliton propagation, while Figure 11 displays the absolute error between the ANN solution and the exact solution. The maximum absolute error between our predicted solutions and the exact solutions is $3.178\times {10}^{-3}$ and the error in the $L_2$-norm is $5.07\times {10}^{-4}$.

5. Conclusions

In this work, we have proposed an Artificial Neural Network (ANN) method for simulating soliton propagation based on the Rosenau-KdV-RLW equation in an unbounded domain, while the computational domain is chosen to be bounded. Unlike common numerical schemes that need ABC and PML, our ANN method can simulate the soliton propagation based on the Rosenau-KdV-RLW equation through the computational domain without using artificial boundary conditions. This is because the loss function is designed based on only the initial condition and the Rosenau-KdV-RLW equation itself and particularly for the training points on the boundary, the Rosenau-KdV-RLW equation is used as a replacement for the boundary condition in the loss function. This is the advantage of the ANN method over the common numerical schemes.

We have theoretically analyzed the convergence of the ANN solution to the exact solution. It shows that the smaller the loss function is, the more accurate the solution could be. The effectiveness of the proposed ANN method has been demonstrated through three test examples. The results indicate that the present ANN method is capable of accurately simulating soliton propagation based on the Rosenau-KdV-RLW equation in unbounded domains and/or over extended time periods.

The present study considers only 1D cases of the Rosenau-KdV-RLW equation. We will test the ANN method for the case where the exact solution of the Rosenau-KdV-RLW equation is unknown. We will further extend this research to multi-dimensional cases with soliton propagation and other wave propagations.