Simulation of Antiplane Piezoelectricity Problems with Multiple Inclusions by the Meshless Method of Fundamental Solution with the LOOCV Algorithm for Determining Sources
Abstract
1. Introduction
2. Problem Statement of Antiplane Piezoelectricity Problem and Formulation of MFS Using LOOCV Algorithm
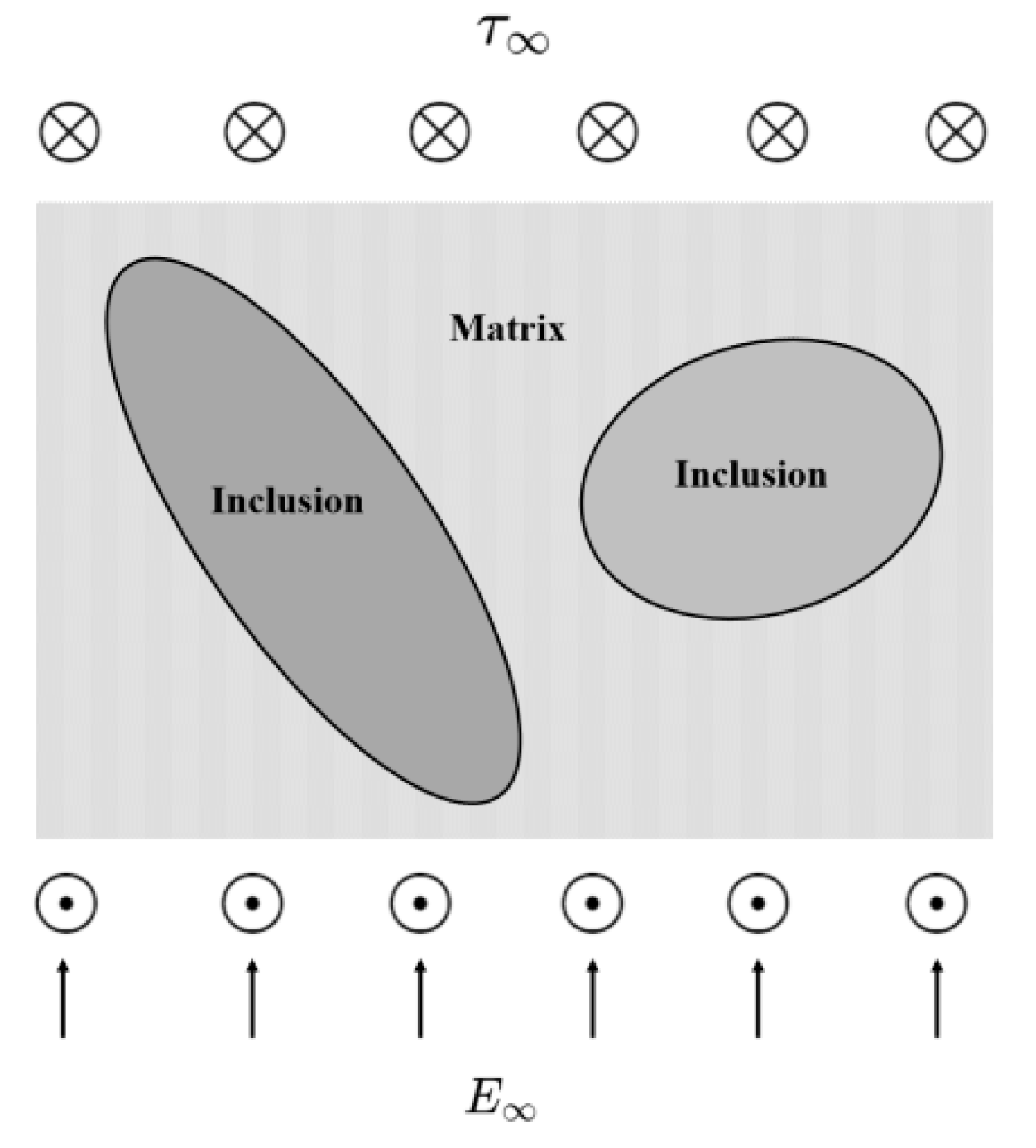
2.1. Antiplane Piezoelectricity Problem
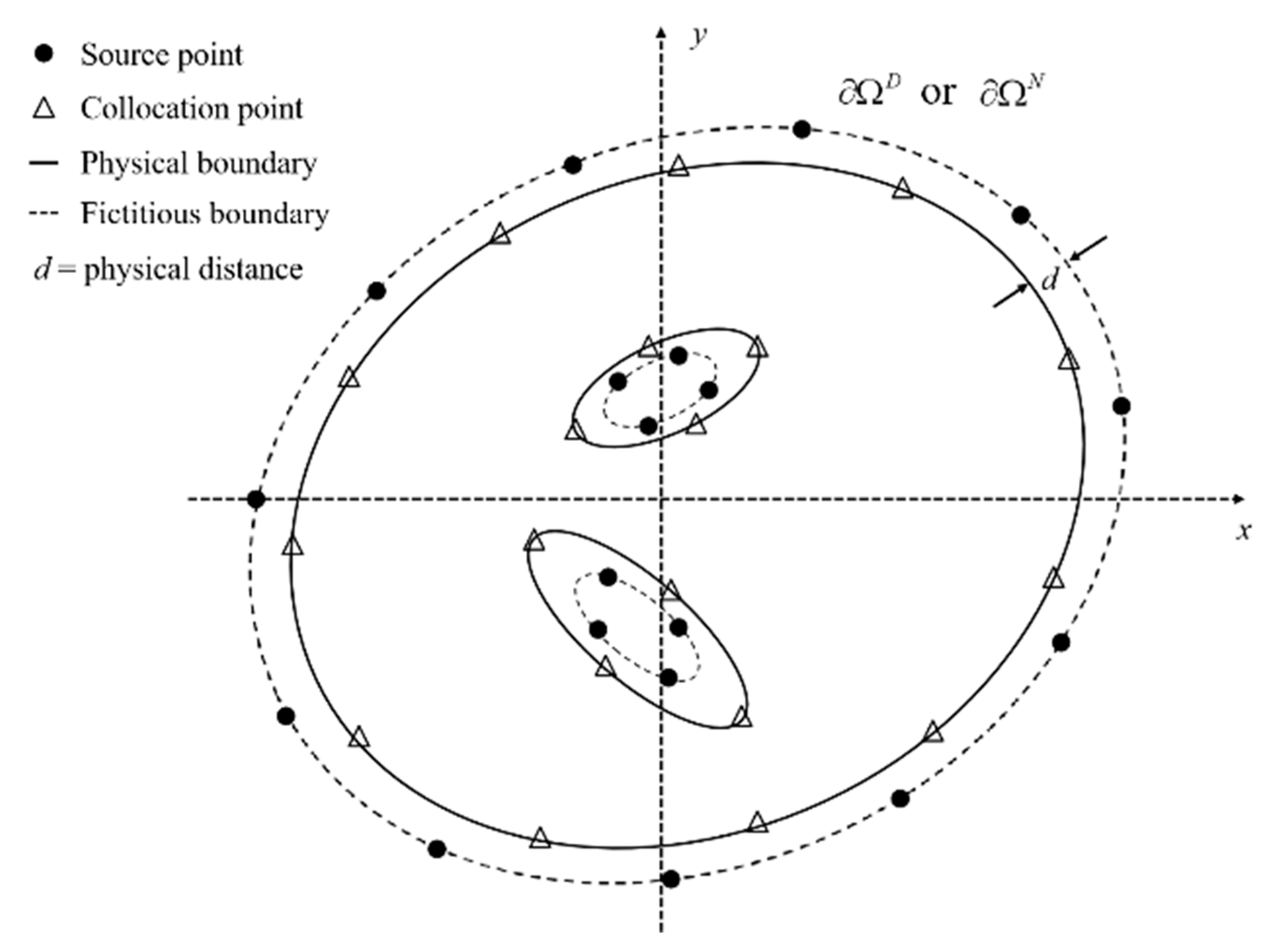
2.2. Method of Fundamental Solutions
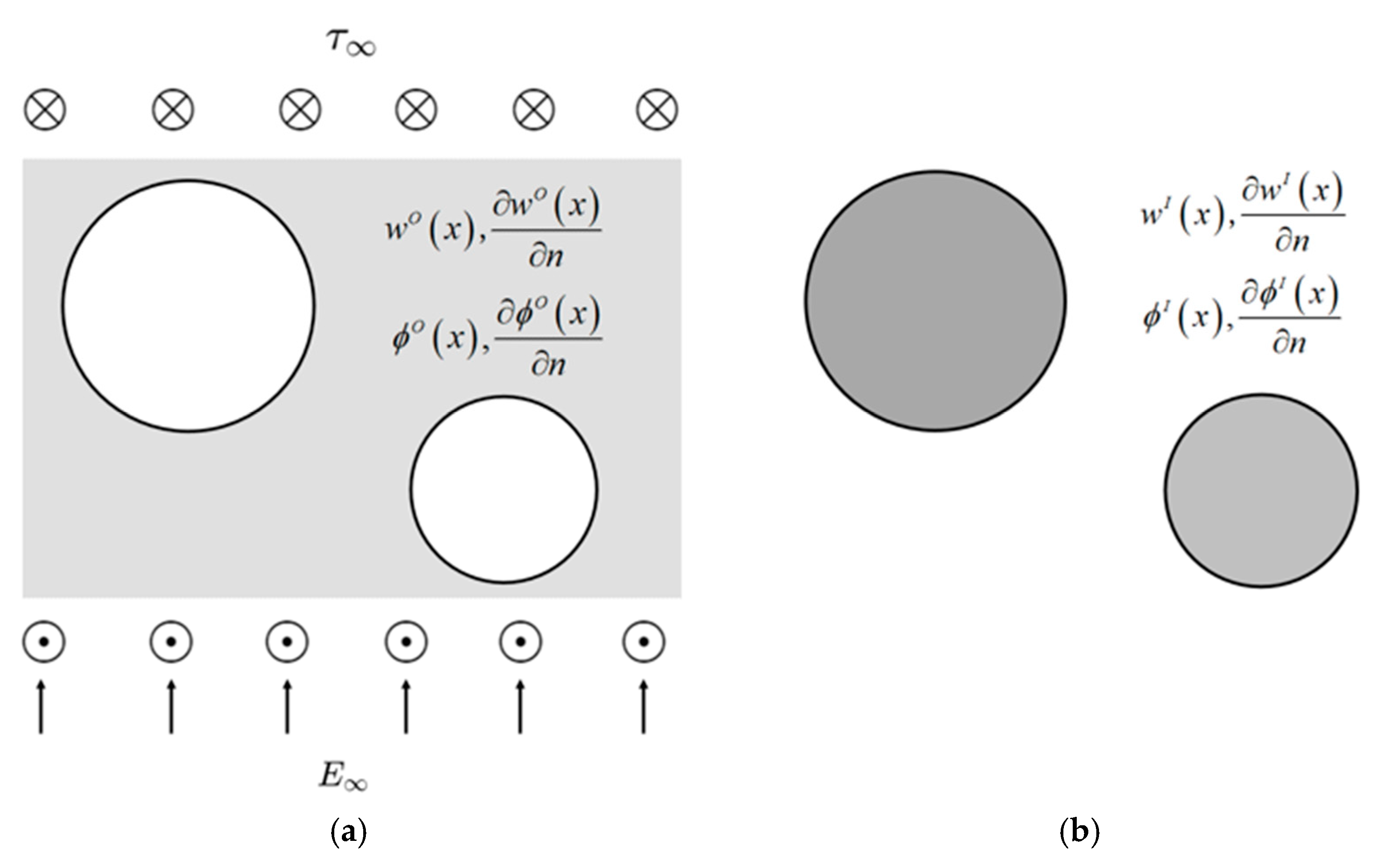
2.3. Derivation of Influence Matrices for Piezoelectricity Problems
2.4. LOOCV Algorithm
3. Numerical Results and Discussion
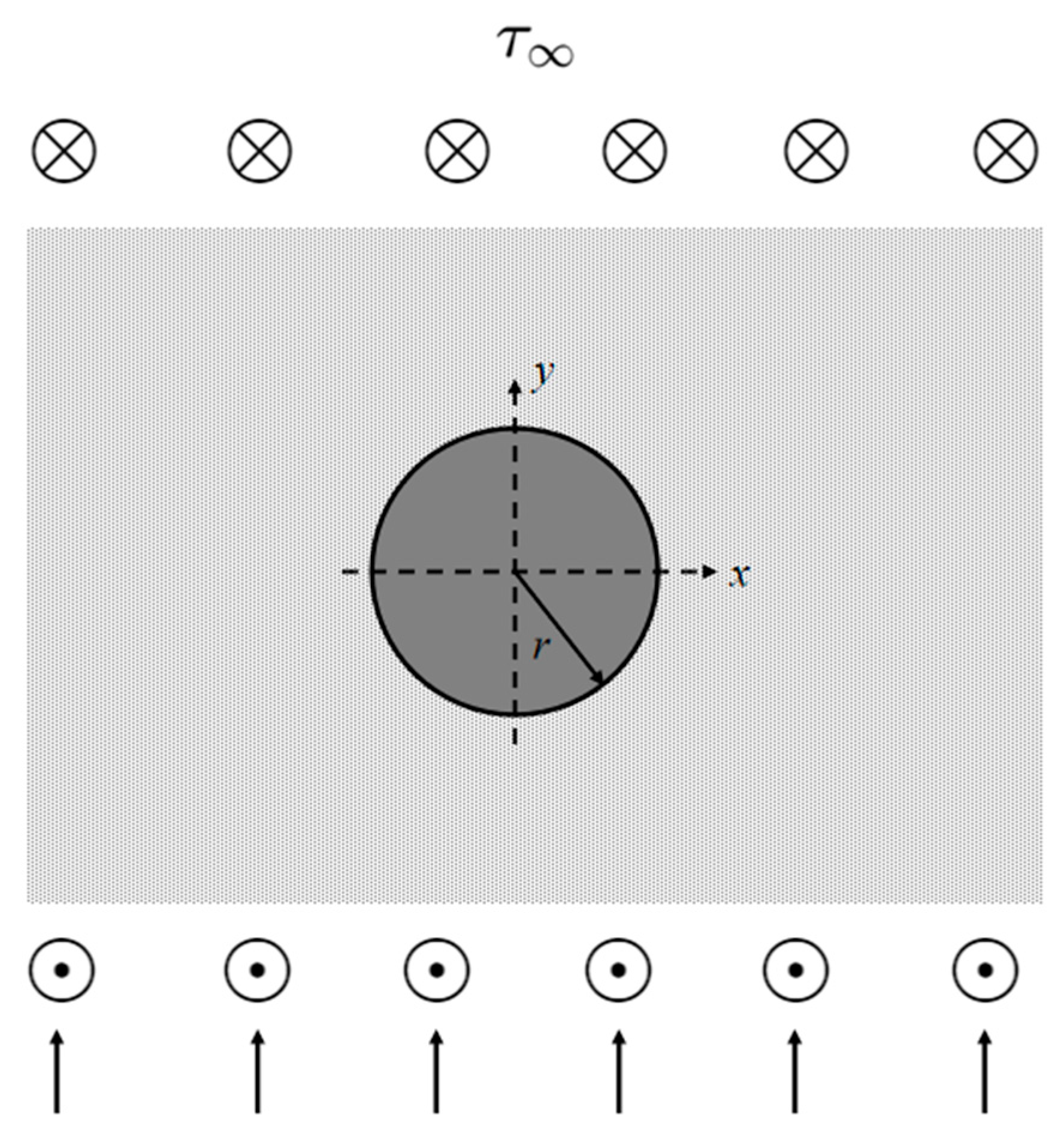
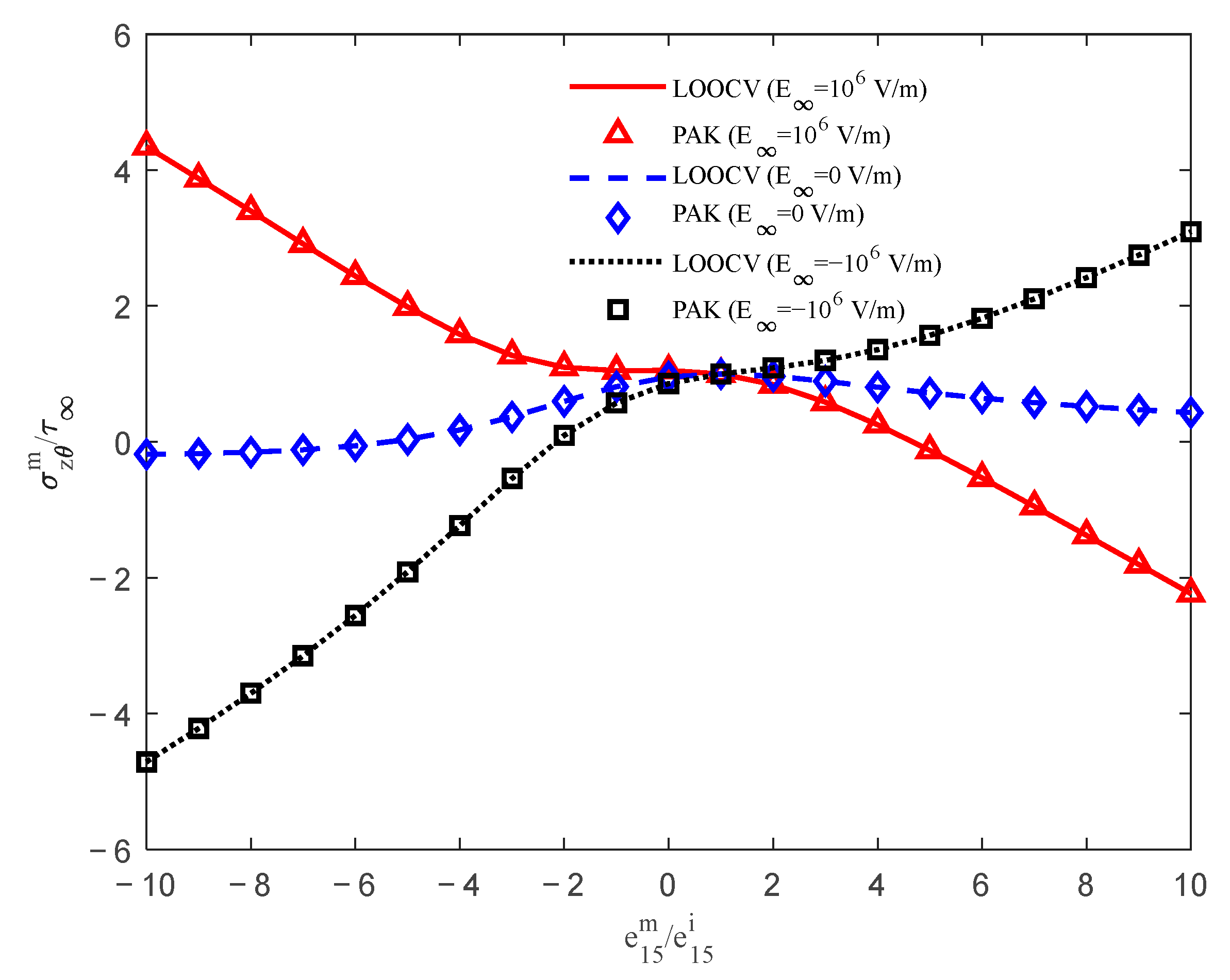
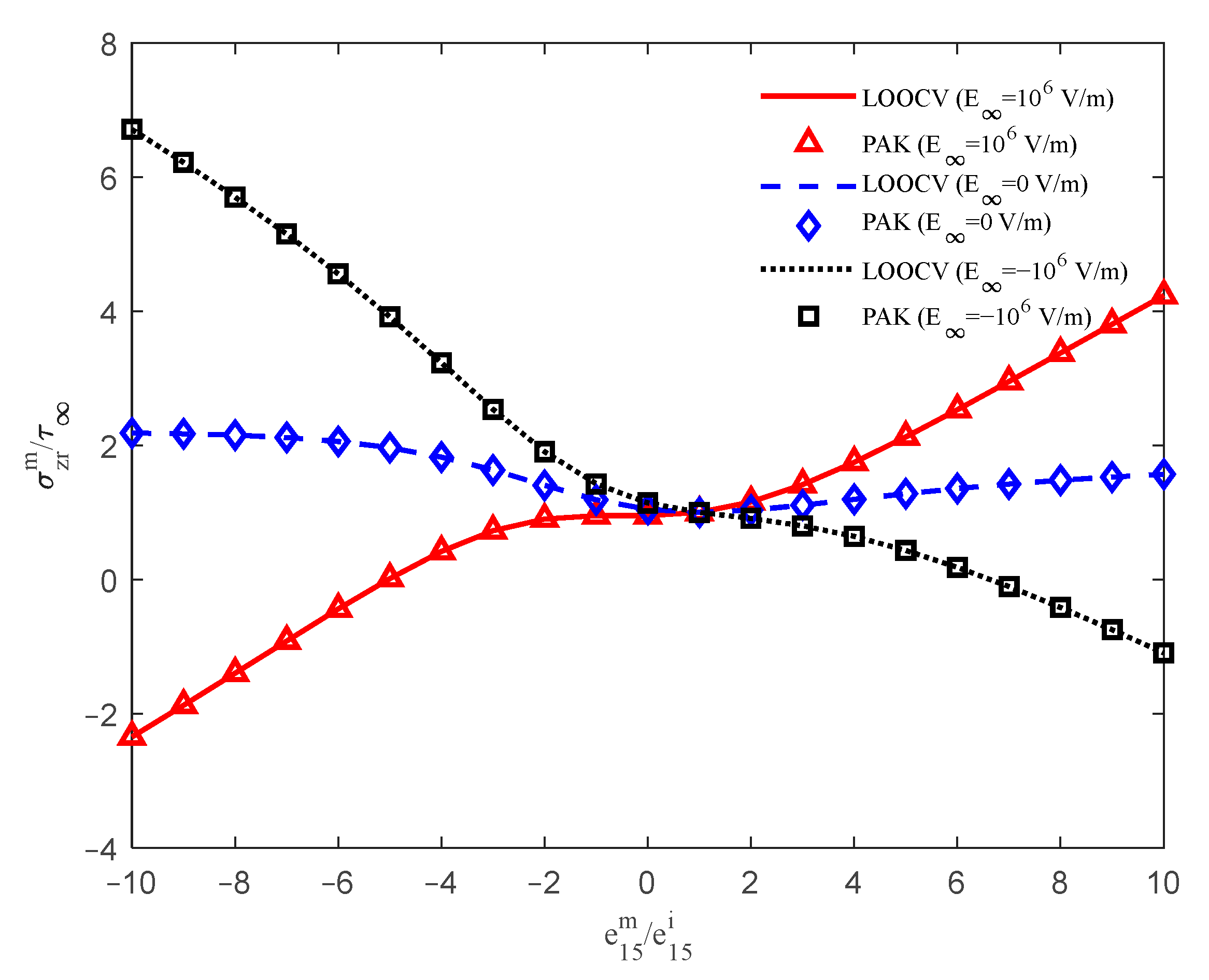
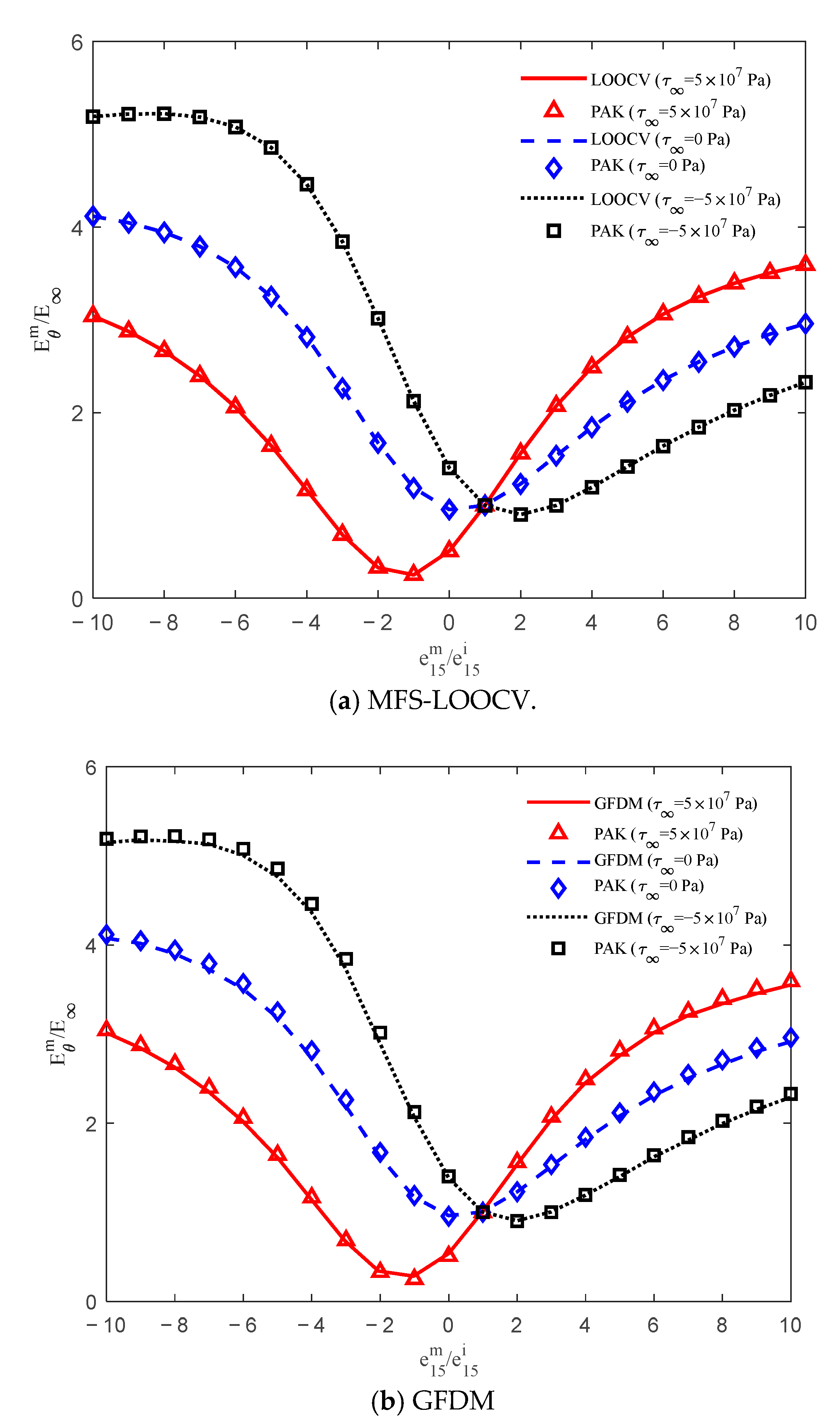
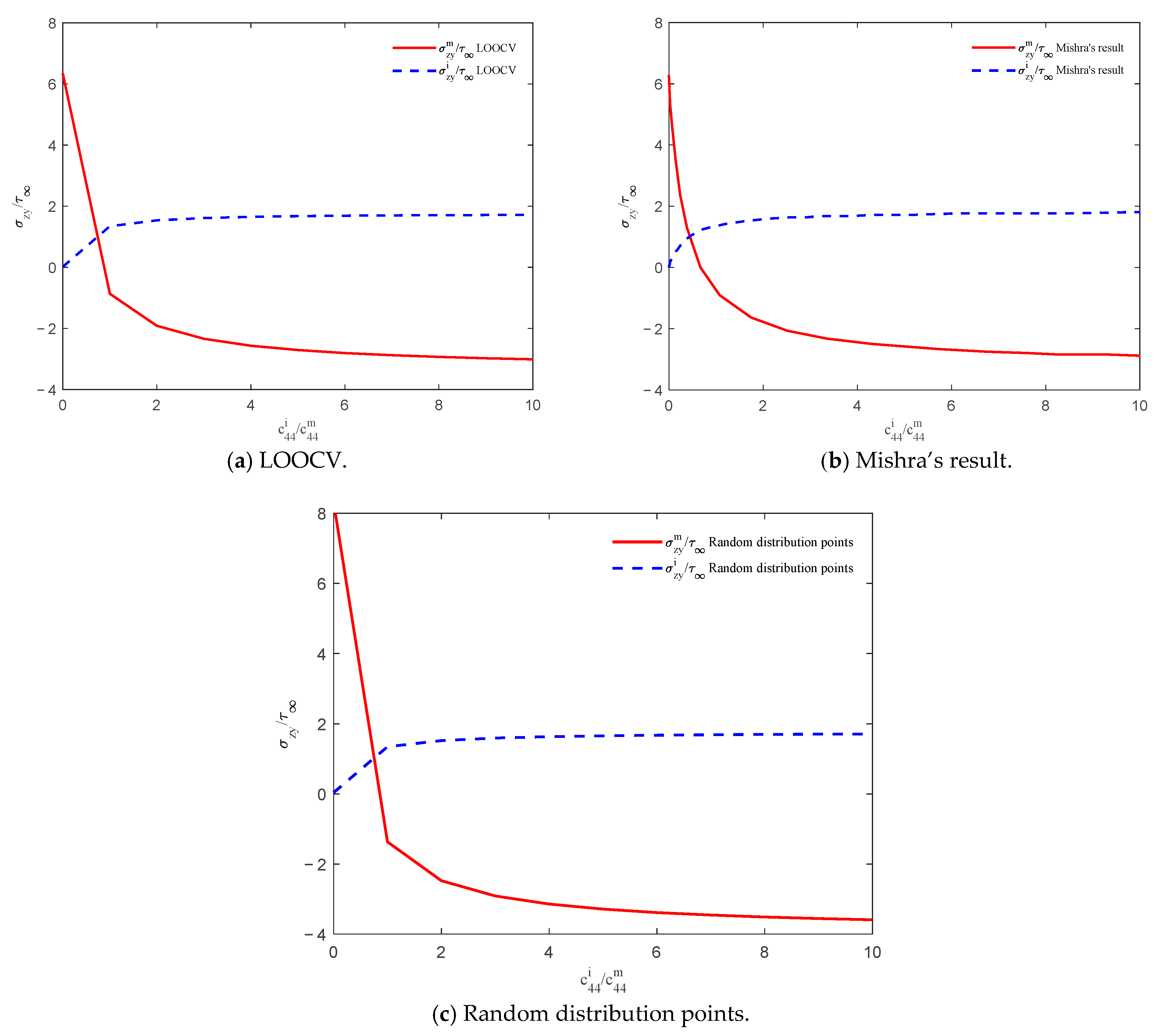
3.1. Case 1: Single Circular Piezoelectric Inclusion
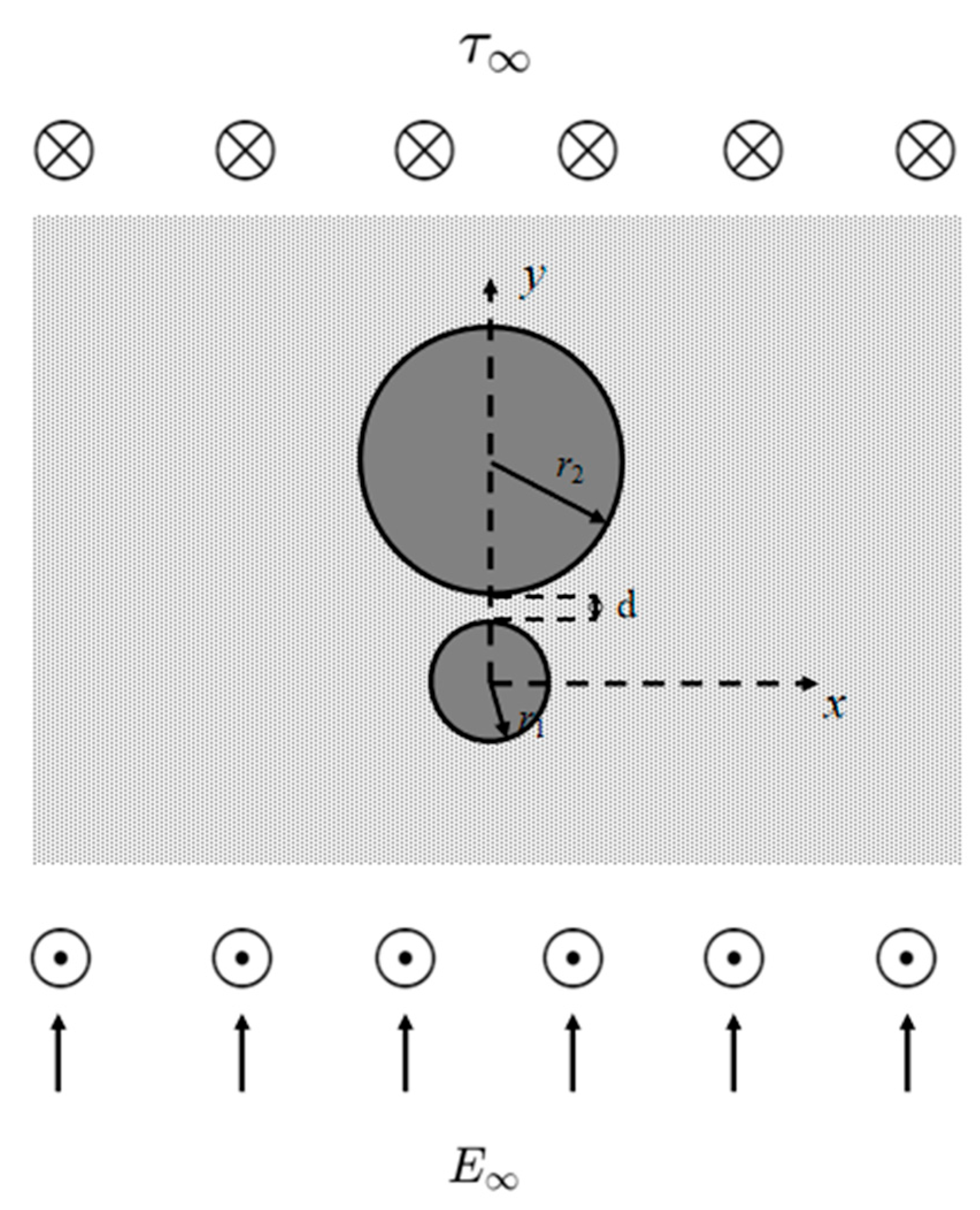
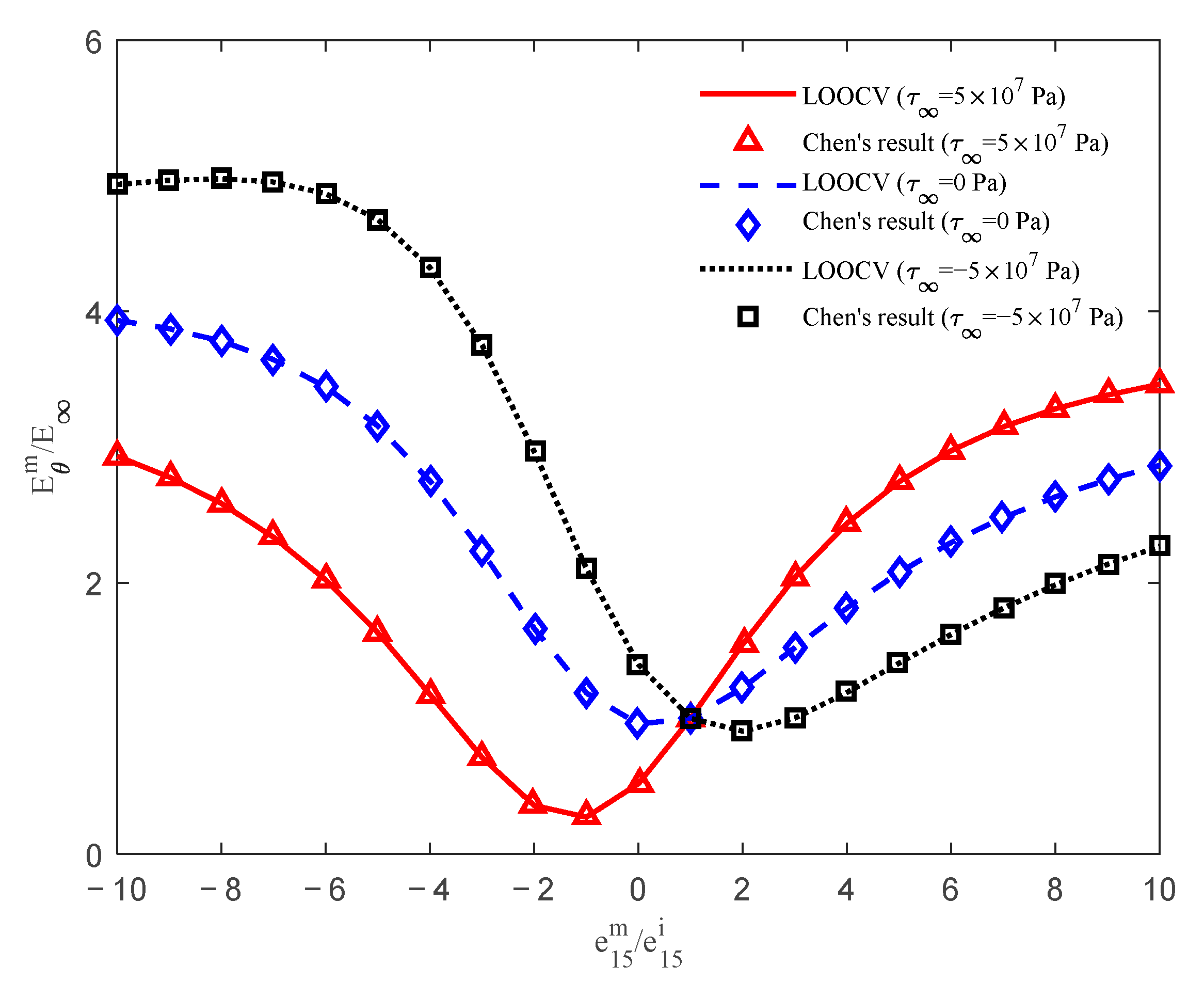
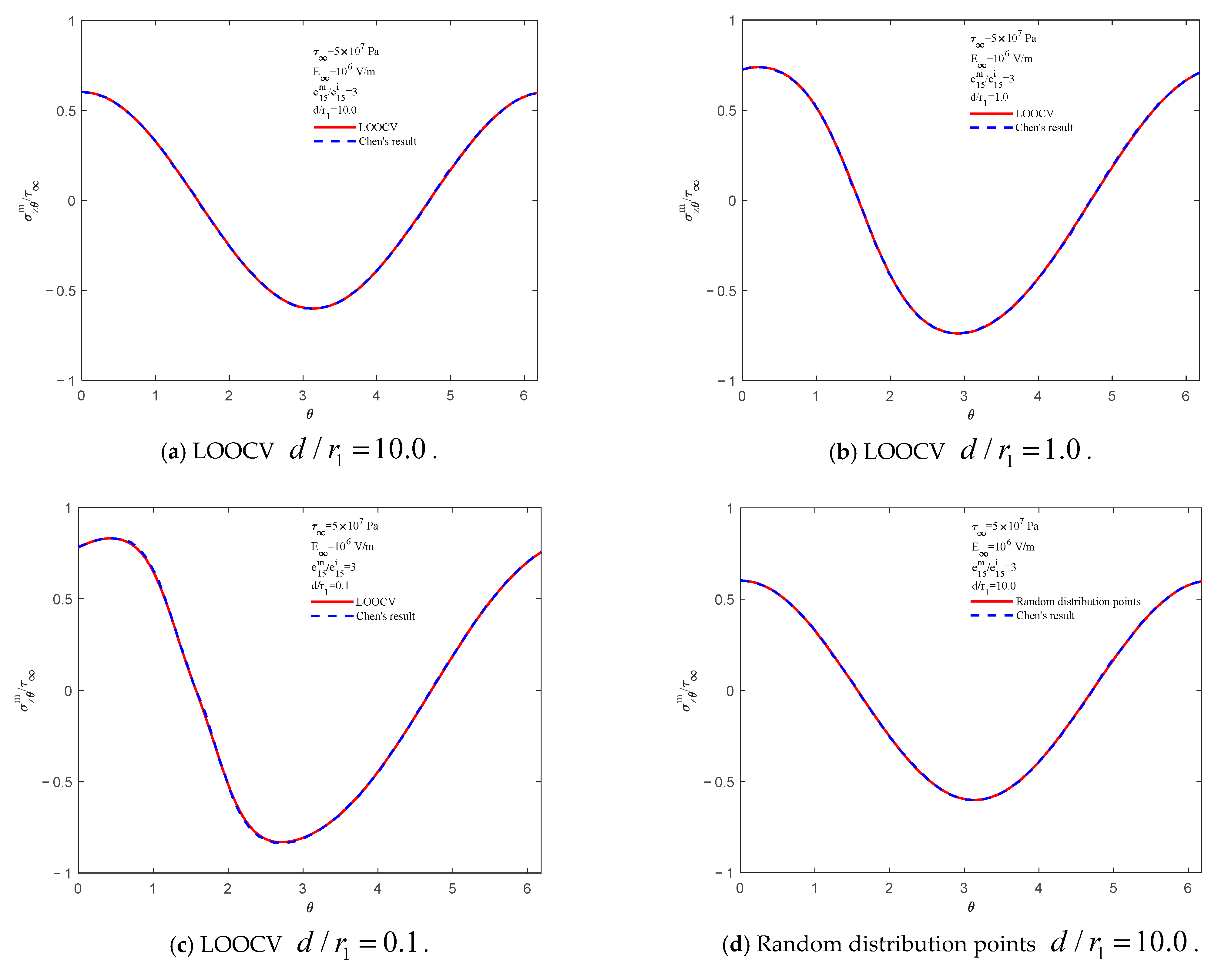
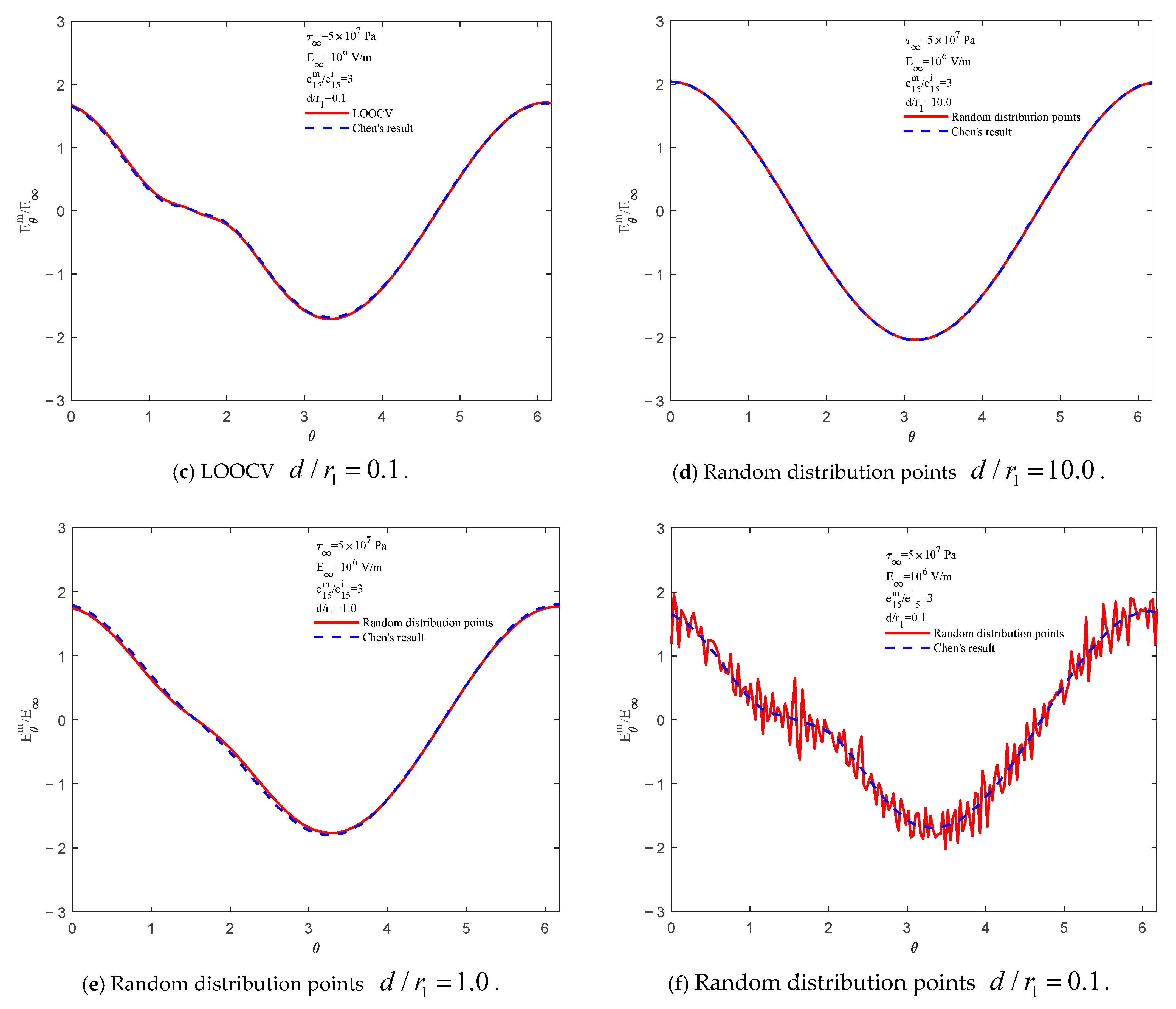
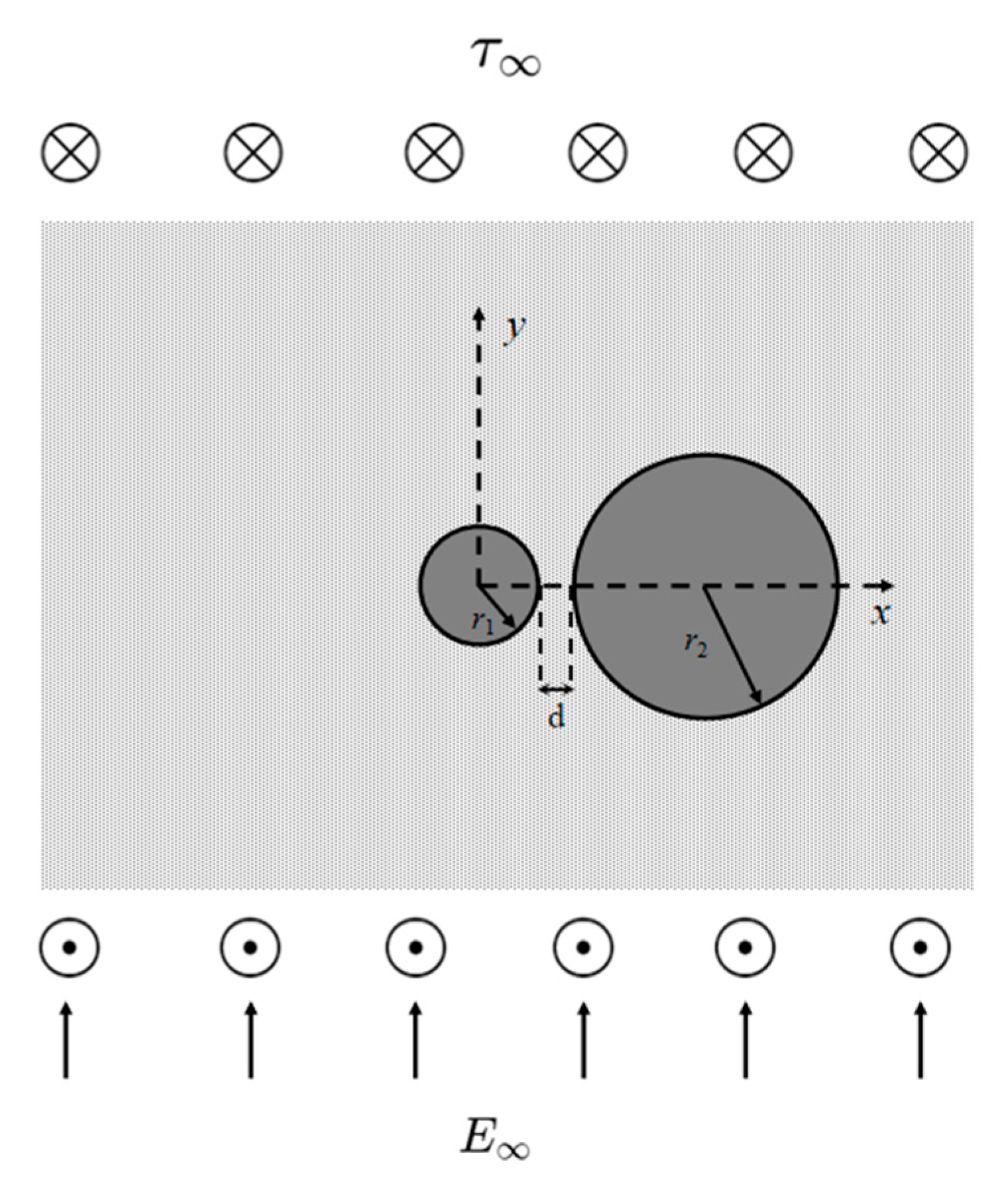
3.2. Case 2: Two Circular Piezoelectric Inclusions
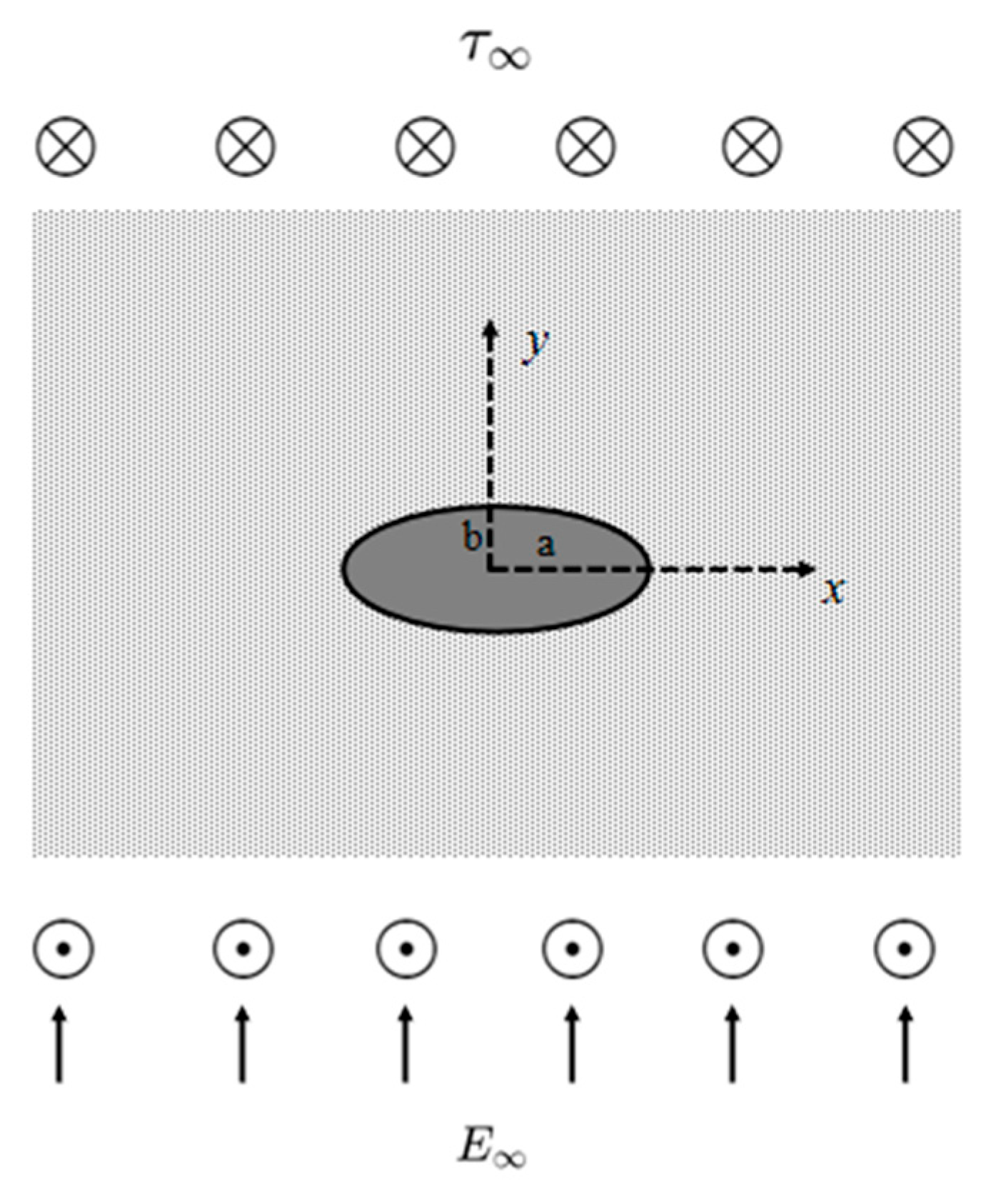
3.3. Case 3: Single Elliptical Piezoelectric Inclusion
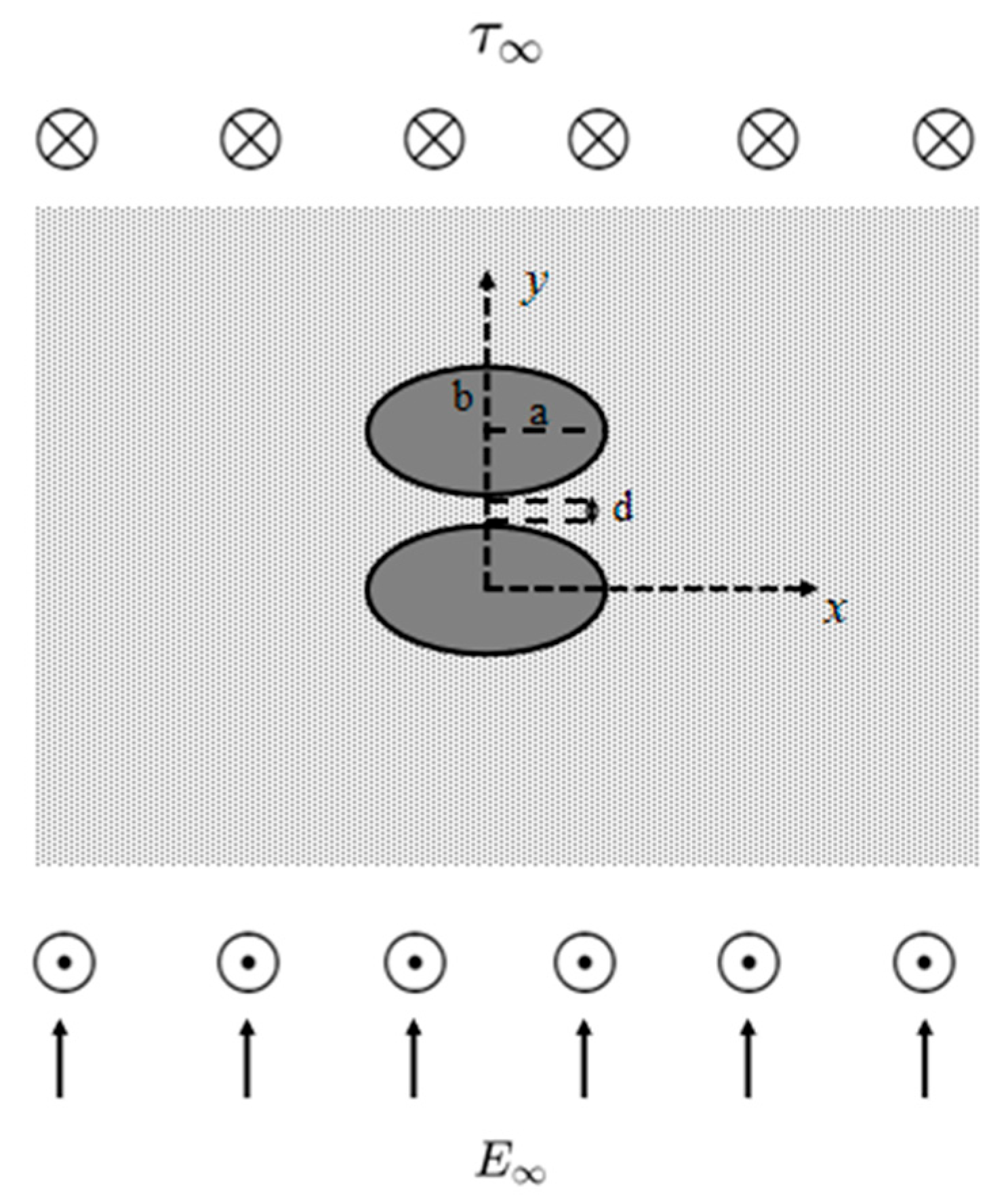
3.4. Case 4: Two Elliptical Piezoelectric Inclusions
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bleustein, J.L. A new surface wave in piezoelectric materials. Appl. Phys. Lett. 1968, 13, 412–413. [Google Scholar] [CrossRef]
- Pak, Y.E. Circular inclusion problem in antiplane piezoelectricity. Int. J. Solids Struct. 1992, 29, 2403–2419. [Google Scholar] [CrossRef]
- Honein, T.; Honein, B.V.; Honein, E.; Herrmann, G. On the interaction of two piezoelectric fibers embedded in an intelligent material. J. Intell. Mater. Syst. Struct. 1995, 6, 229–236. [Google Scholar] [CrossRef]
- Chao, C.K.; Chang, K.J. Interacting circular inclusions in antiplanepiezoelectricity. Int. J. Solids Struct. 1999, 36, 3349–3373. [Google Scholar] [CrossRef]
- Wu, L.; Chen, J.; Meng, Q. Two piezoelectric circular cylindrical inclusions in the infinite piezoelectric medium. Int. J. Eng. Sci. 2000, 38, 879–892. [Google Scholar] [CrossRef]
- Chen, J.T.; Wu, A.C. Null-field approach for piezoelectricity problems with arbitrary circular inclusions. Eng. Anal. Bound. Elem. 2006, 30, 971–993. [Google Scholar] [CrossRef]
- Chen, K.H.; Kao, J.H.; Chen, J.T. Regularized meshless method for antiplane piezoelectricity problems with multiple inclusions. Comput. Mater. Contin. 2009, 9, 253. [Google Scholar]
- Yu, H.; Lin, J. Simulation of antiplane piezoelectricity problems with multiple inclusions using the generalized finite difference method. Eur. J. Mech.-A/Solids 2022, 94, 104615. [Google Scholar] [CrossRef]
- Pak, Y.E. Elliptical inclusion problem in antiplane piezoelectricity: Implications for fracture mechanics. Int. J. Eng. Sci. 2010, 48, 209–222. [Google Scholar] [CrossRef]
- Mishra, D.; Park, C.Y.; Yoo, S.H.; Pak, Y.E. Closed-form solution for elliptical inclusion problem in antiplane piezoelectricity with far-field loading at an arbitrary angle. Eur. J. Mech.-A/Solids 2013, 40, 186–197. [Google Scholar] [CrossRef]
- Lee, Y.T.; Chen, J.T.; Kuo, S.R. Null-field integral approach for the piezoelectricity problems with multiple elliptical inhomogeneities. Eng. Anal. Bound. Elem. 2014, 39, 111–120. [Google Scholar] [CrossRef]
- Kupradze, V.D.; Aleksidze, M.A. The method of functional equations for the approximate solution of certain boundary value problems. USSR Comput. Math. Math. Phys. 1964, 4, 82–126. [Google Scholar] [CrossRef]
- Liu, C.S.; Kuo, C.L. Pseudo and anisotropic MFS for Laplace equation and optimal sources using maximal projection method with a substitution function. Eng. Anal. Bound. Elem. 2024, 158, 313–320. [Google Scholar] [CrossRef]
- Grabski, J.K. On the sources placement in the method of fundamental solutions for time-dependent heat conduction problems. Comput. Math. Appl. 2021, 88, 33–51. [Google Scholar] [CrossRef]
- Grabski, J.K.; Mrozek, A. Identification of elastoplastic properties of rods from torsion test using meshless methods and a metaheuristic. Comput. Math. Appl. 2021, 92, 149–158. [Google Scholar] [CrossRef]
- Ling, L.; Schaback, R. An improved subspace selection algorithm for meshless collocation methods. Int. J. Numer. Methods Eng. 2009, 80, 1623–1639. [Google Scholar] [CrossRef]
- Tsai, C.C.; Lin, Y.C.; Young, D.L.; Atluri, S.N. Investigations on the accuracy and condition number for the method of fundamental solutions. Comput. Model. Eng. Sci. 2006, 16, 103. [Google Scholar]
- Liu, C.S. An equilibrated method of fundamental solutions to choose the best source points for the Laplace equation. Eng. Anal. Bound. Elem. 2012, 36, 1235–1245. [Google Scholar] [CrossRef]
- Wang, F.; Liu, C.S.; Qu, W. Optimal sources in the MFS by minimizing a new merit function: Energy gap functional. Appl. Math. Lett. 2018, 86, 229–235. [Google Scholar] [CrossRef]
- Lin, S.R.; Young, D.L.; Chen, C.S. Ghost-point based radial basis function collocation methods with variable shape parameters. Eng. Anal. Bound. Elem. 2021, 130, 40–48. [Google Scholar] [CrossRef]
- Zhang, L.P.; Li, Z.C.; Huang, H.T.; Lee, M.G. New locations of source nodes for method of fundamental solutions solving Laplaces equation; pseudo radial-lines. Eng. Anal. Bound. Elem. 2022, 136, 93–115. [Google Scholar] [CrossRef]
- Chen, C.S.; Noorizadegan, A.; Young, D.L.; Chen, C.S. On the selection of a better radial basis function and its shape parameter in interpolation problems. Appl. Math. Comput. 2023, 442, 127713. [Google Scholar] [CrossRef]
- Rippa, S. An algorithm for selecting a good value for the parameter c in radial basis function interpolation. Adv. Comput. Math. 1999, 11, 193–210. [Google Scholar] [CrossRef]
- Fasshauer, G.E.; Zhang, J.G. On choosing optimal shape parameters for RBF approximation. Numer. Algorithms 2007, 45, 345–368. [Google Scholar] [CrossRef]
- Chen, C.S.; Karageorghis, A.; Li, Y. On choosing the location of the sources in the MFS. Numer. Algorithms 2016, 72, 107–130. [Google Scholar] [CrossRef]






| nb | 26 | 32 | 38 | 44 | 50 |
|---|---|---|---|---|---|
| 1.30 × 10−3 | 2.43 × 10−4 | 4.52 × 10−5 | 8.36 × 10−6 | 1.54 × 10−6 | |
| 2.71 × 10−4 | 4.69 × 10−5 | 8.35 × 10−6 | 1.51 × 10−6 | 2.76 × 10−7 | |
| 9.75 × 10−4 | 1.81 × 10−4 | 3.36 × 10−5 | 6.21 × 10−6 | 1.15 × 10−6 | |
| 1.11 × 10−3 | 2.07 × 10−4 | 3.85 × 10−5 | 7.12 × 10−6 | 1.31 × 10−6 |
| 0 | 0.1 | 0.01 | 0.001 | |
|---|---|---|---|---|
| 8.01 × 10−12 | 4.29 × 10−2 | 4.25 × 10−3 | 9.39 × 10−3 | |
| 1.62 × 10−12 | 1.41 × 10−2 | 3.19 × 10−3 | 4.73 × 10−4 | |
| 2.51 × 10−11 | 3.80 × 10−2 | 4.24 × 10−3 | 7.08 × 10−4 | |
| 6.11 × 10−14 | 7.65 × 10−2 | 5.57 × 10−3 | 8.81 × 10−4 |
| Meshless Method | Basis Function | Node Distribution | Method to Avoid Singularity | Strengths | Weakness |
|---|---|---|---|---|---|
| Method of fundamental solution [12] | Fundamental solution | Source nodes and collocation points | Source nodes are placed away from the boundary | High-dimensional complex geometry problems | Dense matrix |
| Regularized meshless method [7] | Double layer potentials | Boundary nodes only | Subtracting and adding-back technique | High accuracy | Difficult for irregular domain problems |
| Generalized finite difference method [8] | Taylor series | Nodes on the boundary and in the domain | No singularity | Sparse matrix | Sensitive to the placement of the nodes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Lin, J.; Wang, F.; Gu, Y. Simulation of Antiplane Piezoelectricity Problems with Multiple Inclusions by the Meshless Method of Fundamental Solution with the LOOCV Algorithm for Determining Sources. Mathematics 2025, 13, 920. https://doi.org/10.3390/math13060920
Zhang J, Lin J, Wang F, Gu Y. Simulation of Antiplane Piezoelectricity Problems with Multiple Inclusions by the Meshless Method of Fundamental Solution with the LOOCV Algorithm for Determining Sources. Mathematics. 2025; 13(6):920. https://doi.org/10.3390/math13060920
Chicago/Turabian StyleZhang, Jingyi, Ji Lin, Fajie Wang, and Yan Gu. 2025. "Simulation of Antiplane Piezoelectricity Problems with Multiple Inclusions by the Meshless Method of Fundamental Solution with the LOOCV Algorithm for Determining Sources" Mathematics 13, no. 6: 920. https://doi.org/10.3390/math13060920
APA StyleZhang, J., Lin, J., Wang, F., & Gu, Y. (2025). Simulation of Antiplane Piezoelectricity Problems with Multiple Inclusions by the Meshless Method of Fundamental Solution with the LOOCV Algorithm for Determining Sources. Mathematics, 13(6), 920. https://doi.org/10.3390/math13060920









