Multiscale Simulation of 2D Heat Transfer in Composite Media Based on Global–Local Enrichment Functions
Abstract
1. Introduction
2. XFEM Model of Temperature Fields
2.1. Mathematical Formulation of XFEM
2.2. Governing Equations and Discretization
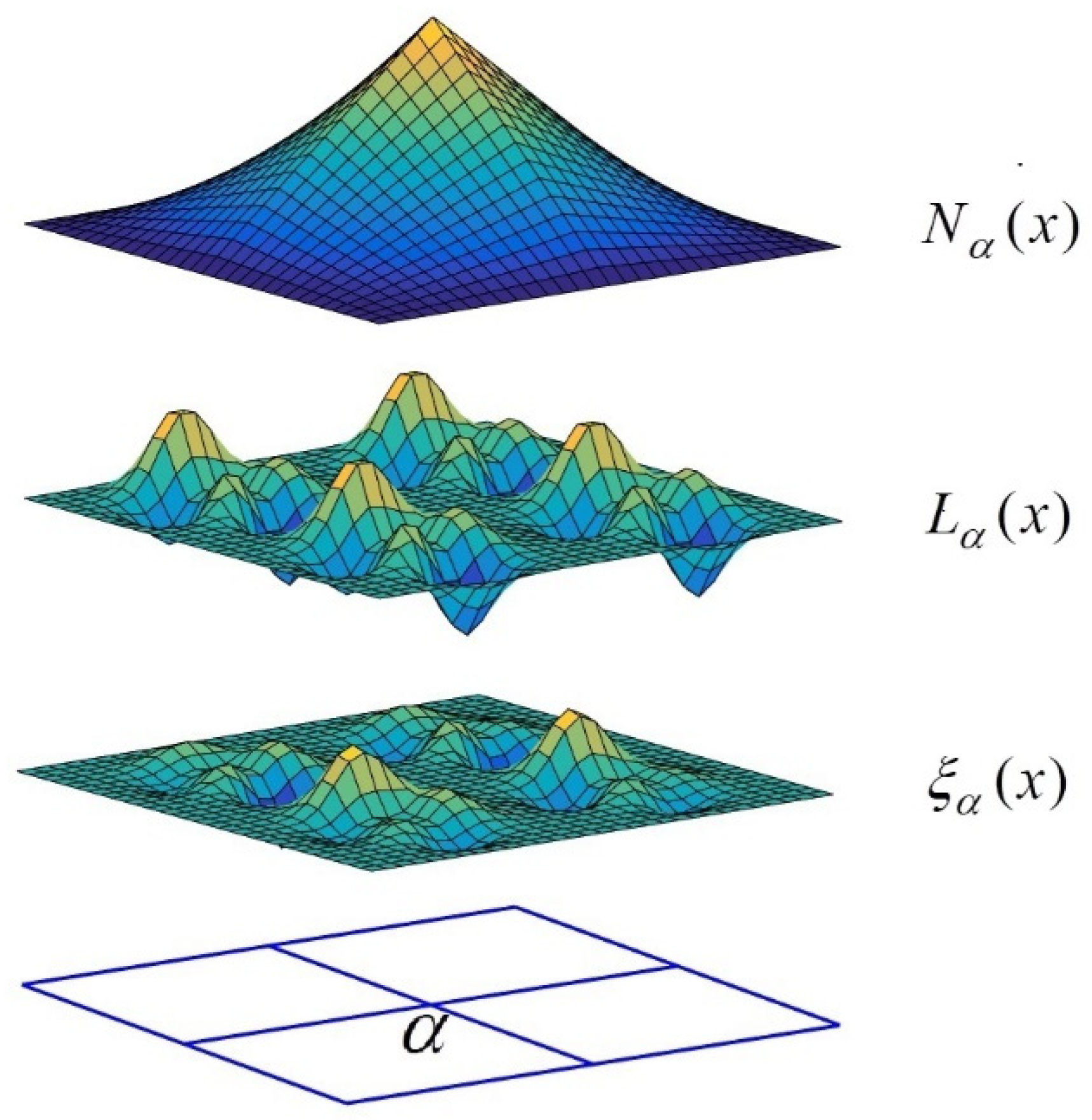
3. Framework and Implementation of GFEMgl
3.1. Implementation of GFEMgl
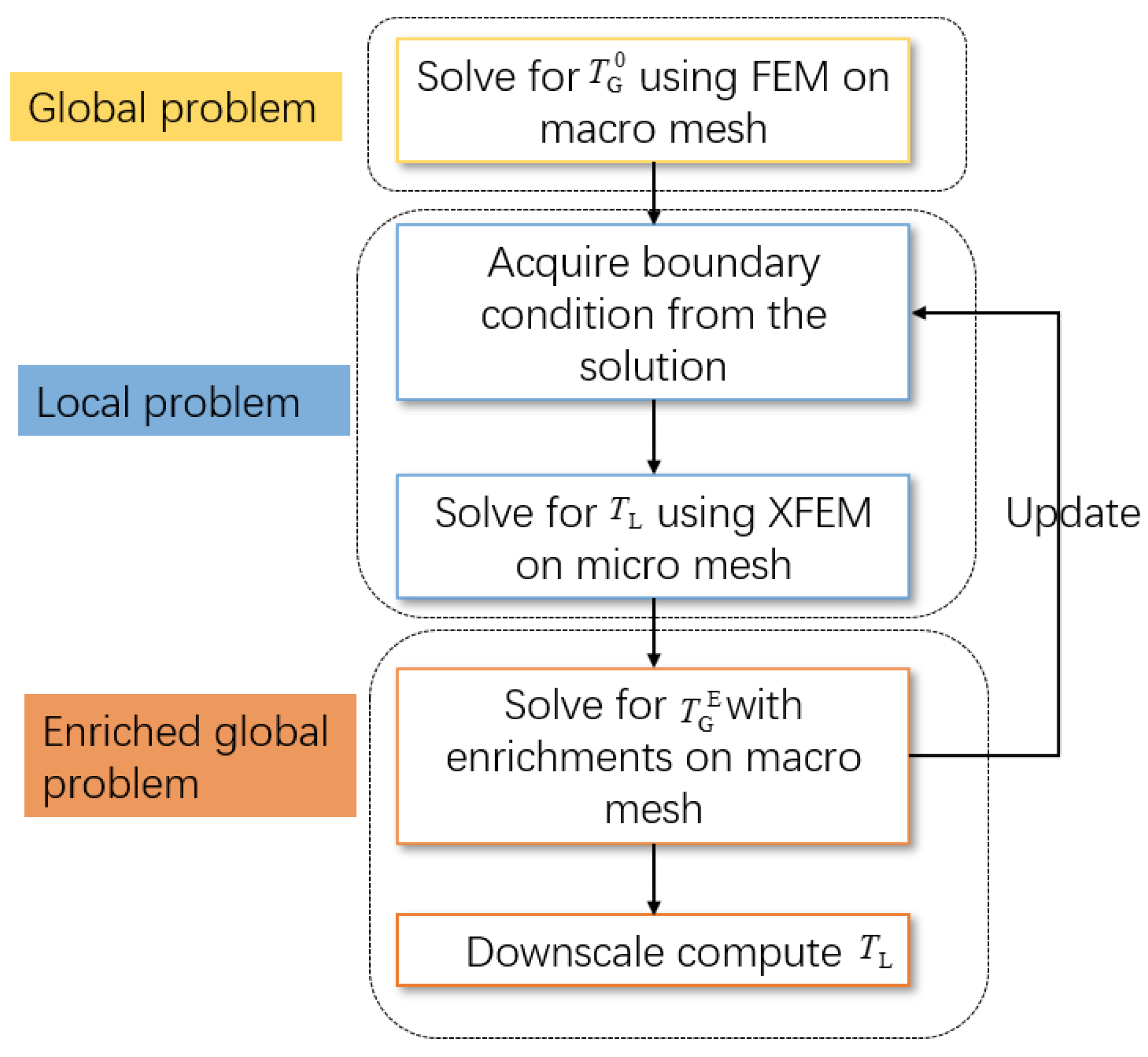
3.2. Computational Steps for Multiscale Simulation
4. Numerical Cases and Discussion
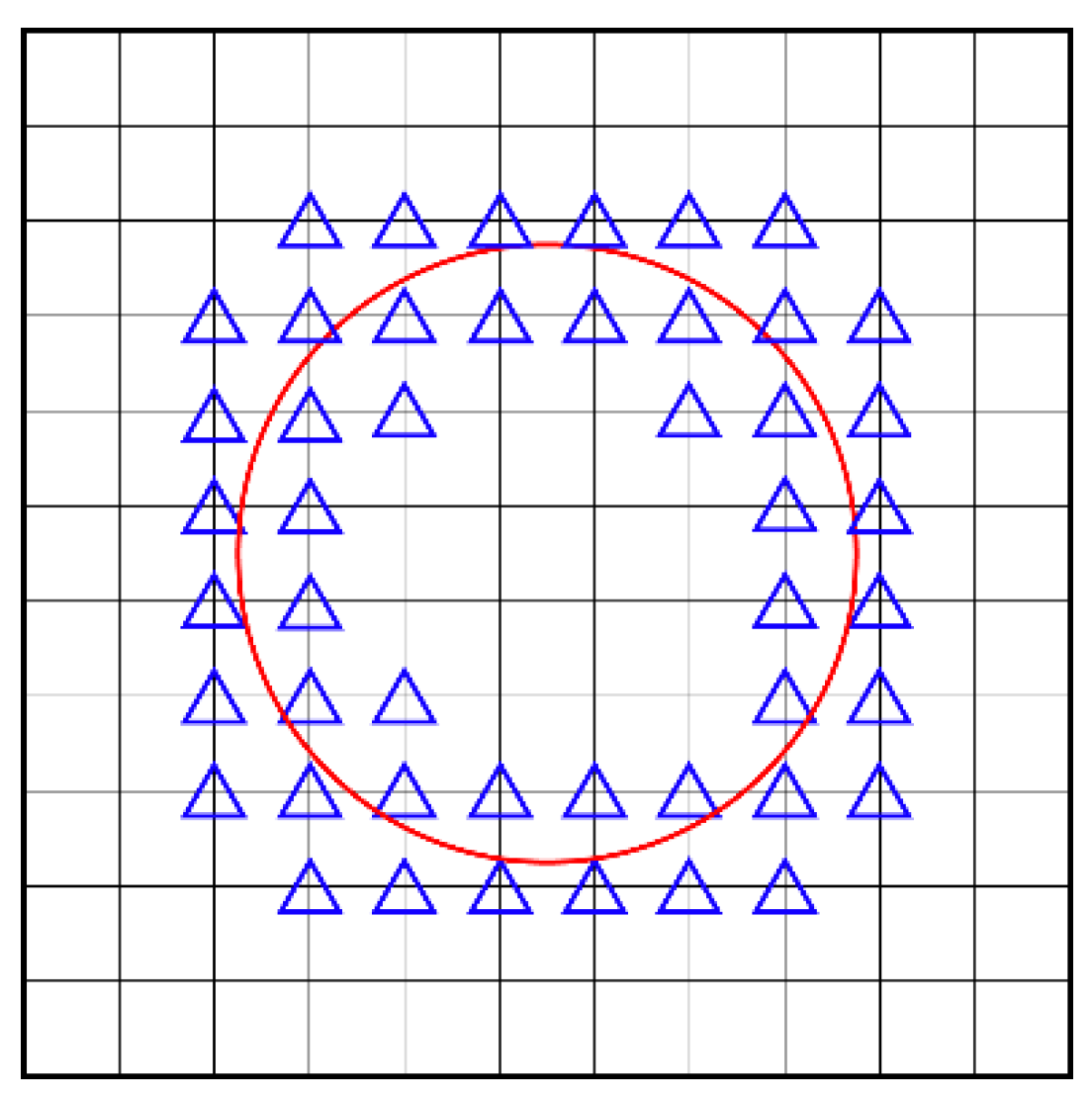
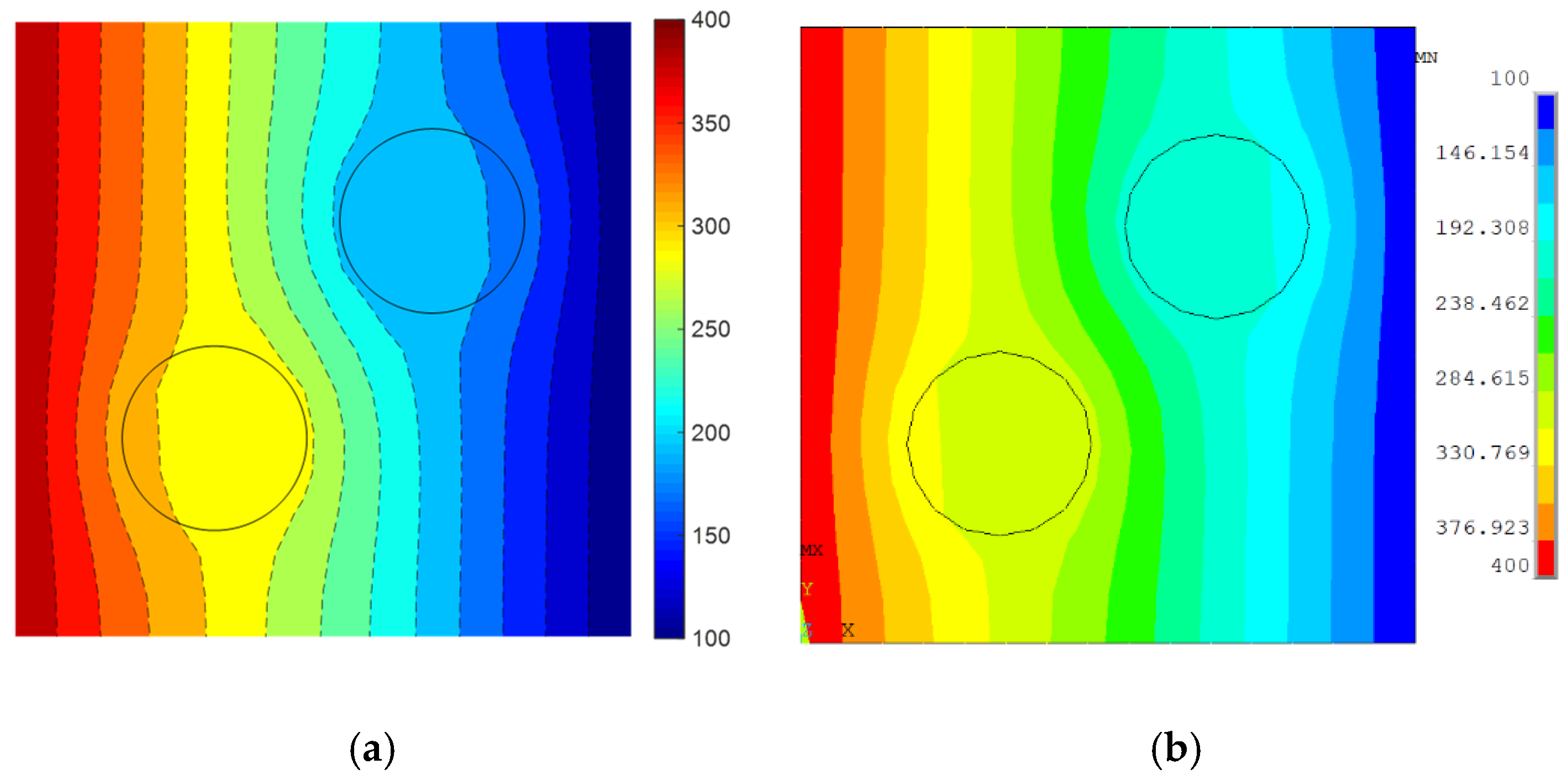
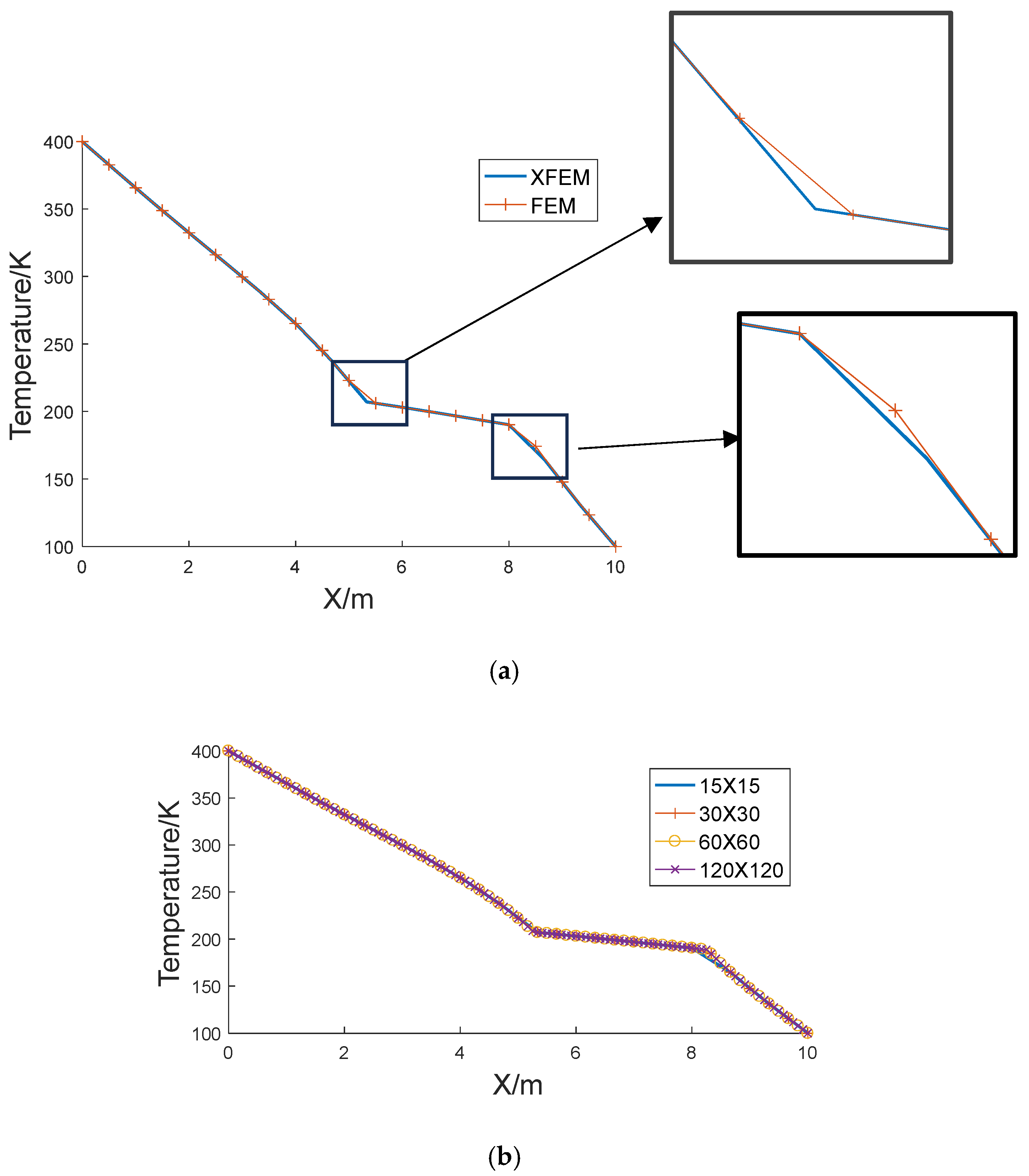
4.1. XFEM Simulation of Two Inclusions/Voids
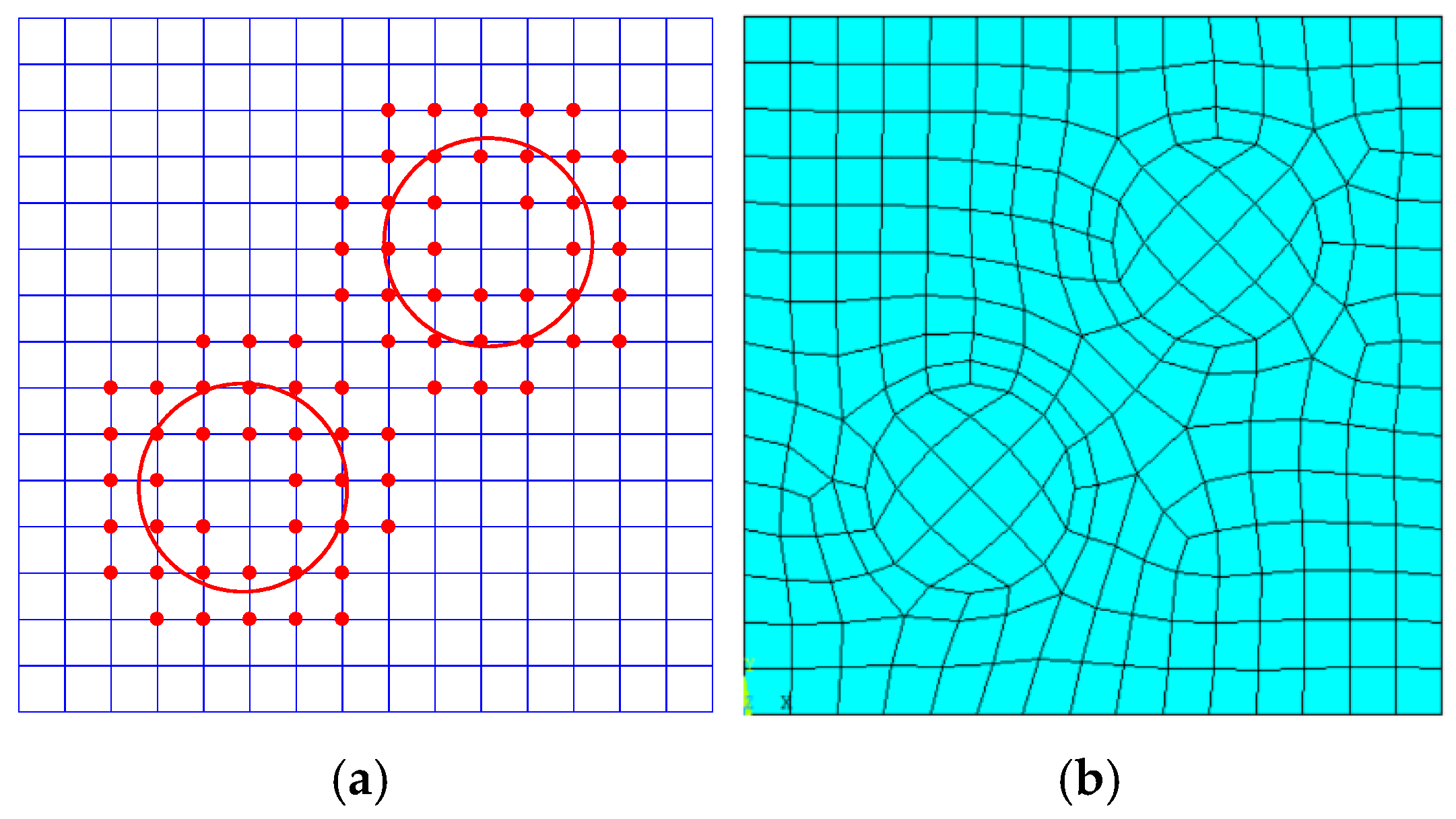
4.2. GFEMgl Simulation of RVEs with Inclusions
4.3. Influence of Volume Fraction of Inclusions on ETC
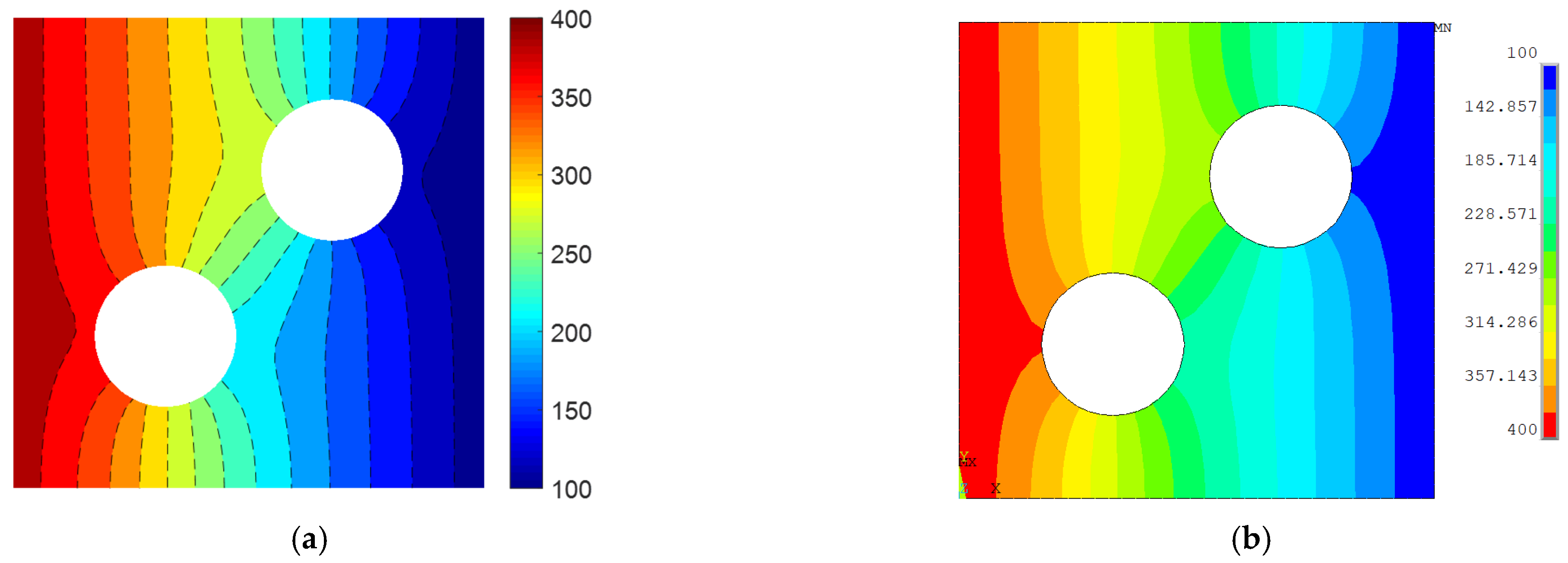
4.4. GFEMgl Simulation of RVEs with Voids
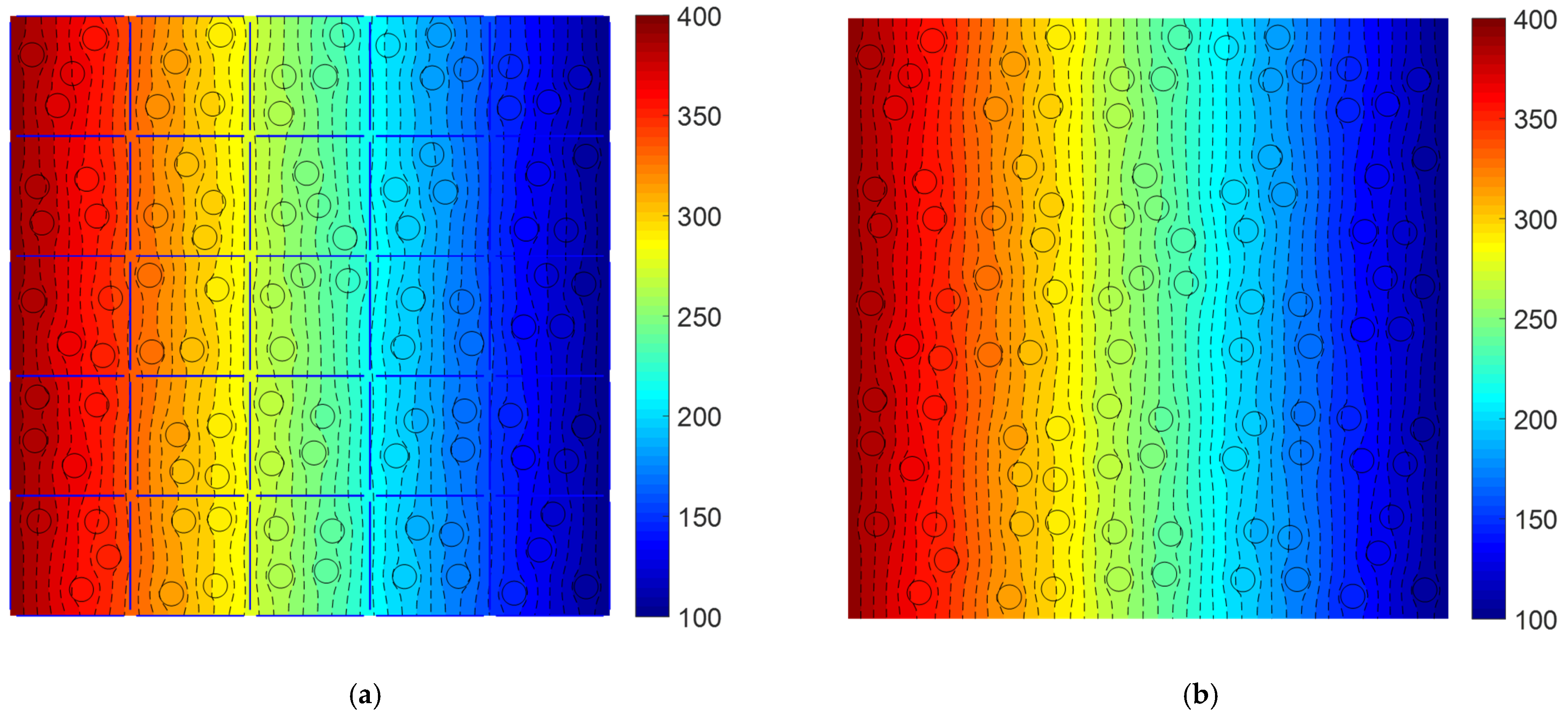
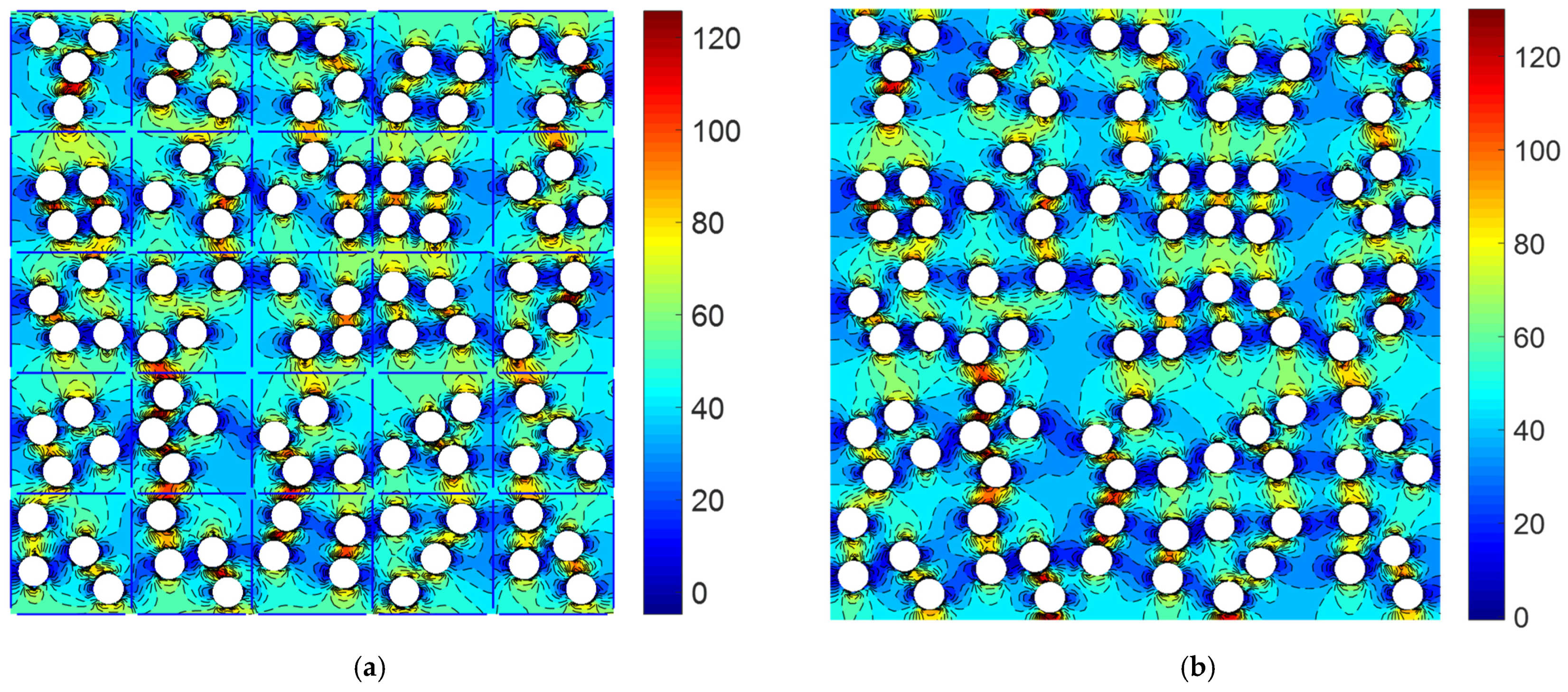
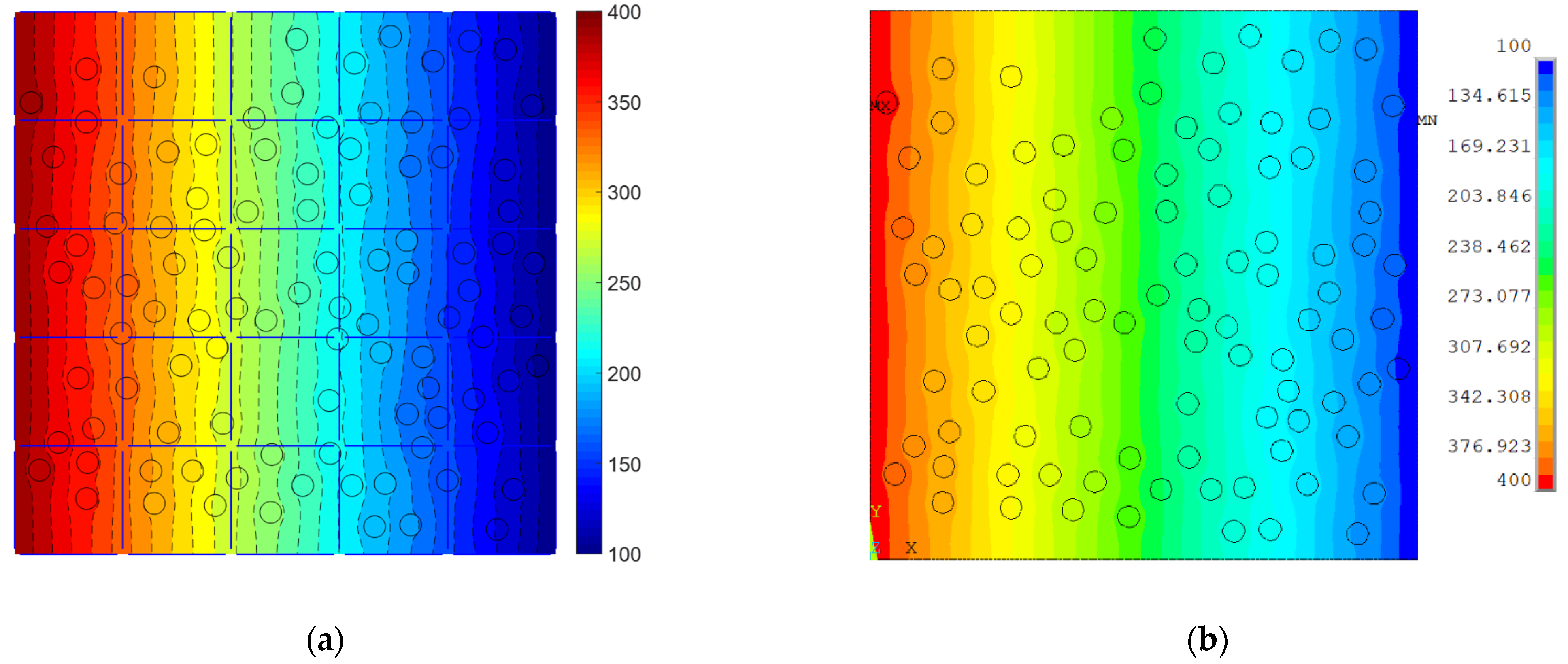
4.5. An RVE with 100 Randomly Distributed Inclusions
5. Conclusions
- The results of XFEM simulations of a plate with inclusions or voids agree well with those of FEM simulations in terms of temperature and thermal flux. The XFEM enables simulation to be conducted on a structured mesh, while maintaining high accuracy.
- The results produced by the proposed multiscale method are in favorable agreement with those produced by the standard single-scale XFEM, and the results fit in the bounds produced by the P-S model. However, the proposed method is more computationally efficient than the standard XFEM for composites with numerous heterogeneities.
- The randomness of the inclusion distribution does not notably affect the overall thermal property of a composite.
- ETC has an approximately linear relationship with the volume fraction of composites containing inclusions; however, ETC has a nonlinear relationship with the porosity of porous composites. The numerical ETC results obtained with the proposed method are closer to those produced by the Schultz model than to those produced by the Maxwell model.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kaur, I.; Mahajan, R.L.; Singh, P. Generalized correlation for effective thermal conductivity of high porosity architectured materials and metal foams. Int. J. Heat Mass Transf. 2023, 200, 123512. [Google Scholar]
- Wang, J.; Carson, J.K.; North, M.F.; Cleland, D.J. A new approach to modelling the effective thermal conductivity of heterogeneous materials. Int. J. Heat Mass Transf. 2006, 49, 3075–3083. [Google Scholar]
- Kiradjiev, K.B.; Halvorsen, S.A.; Van Gorder, R.A.; Howison, S.D. Maxwell-type models for the effective thermal conductivity of a porous material with radiative transfer in the voids. Int. J. Therm. Sci. 2019, 145, 106009. [Google Scholar]
- Zerhouni, O.; Tarantino, M.G.; Danas, K. Numerically-aided 3D printed random isotropic porous materials approaching the Hashin-Shtrikman bounds. Compos. Part B Eng. 2019, 156, 344–354. [Google Scholar]
- Back, S.Y.; Mori, T.; Rhyee, J.-S. Thermoelectric properties and effective medium theory analysis on the (GeTe)1-x(InTe)x composites. J. Alloys Compd. 2024, 1002, 175316. [Google Scholar]
- Bi, J.; Zhang, M.; Chen, W.; Lu, J.; Lai, Y. A new model to determine the thermal conductivity of fine-grained soils. Int. J. Heat Mass Transf. 2018, 123, 407–417. [Google Scholar] [CrossRef]
- Ranut, P. On the effective thermal conductivity of aluminum metal foams: Review and improvement of the available empirical and analytical models. Appl. Therm. Eng. 2016, 101, 496–524. [Google Scholar]
- Cook, R.D.; Malkus, D.S.; Plesha, M.E.; Witt, R.J. Concepts and Applications of Finite Element Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2002. [Google Scholar]
- Mendes, M.A.A.; Ray, S.; Trimis, D. A simple and efficient method for the evaluation of effective thermal conductivity of open-cell foam-like structures. Int. J. Heat Mass Transf. 2013, 66, 412–422. [Google Scholar]
- Yang, M.; Li, X. Optimum convergence parameters of lattice Boltzmann method for predicting effective thermal conductivity. Comput. Methods Appl. Mech. Eng. 2022, 394, 114891. [Google Scholar]
- Shen, Y.-L.; Abdo, M.G.; Van Rooyen, I.J. Numerical Study of Effective Thermal Conductivity for Periodic Closed-Cell Porous Media. Transp. Porous Media 2022, 143, 245–269. [Google Scholar]
- Li, Z.; Yang, Y.; Gariboldi, E.; Li, Y. Computational models of effective thermal conductivity for periodic porous media for all volume fractions and conductivity ratios. Appl. Energy 2023, 349, 121633. [Google Scholar] [CrossRef]
- Sukumar, N.; Chopp, D.L.; Moës, N.; Belytschko, T. Modeling holes and inclusions by level sets in the extended finite-element method. Comput. Methods Appl. Mech. Eng. 2001, 190, 6183–6200. [Google Scholar] [CrossRef]
- Moës, N.; Belytschko, T. Extended finite element method for cohesive crack growth. Eng. Fract. Mech. 2002, 69, 813–833. [Google Scholar] [CrossRef]
- Moës, N.; Cloirec, M.; Cartraud, P.; Remacle, J.F. A computational approach to handle complex microstructure geometries. Comput. Methods Appl. Mech. Eng. 2003, 192, 3163–3177. [Google Scholar] [CrossRef]
- Heidari-Rarani, M.; Sayedain, M. Finite element modeling strategies for 2D and 3D delamination propagation in composite DCB specimens using VCCT, CZM and XFEM approaches. Theor. Appl. Fract. Mech. 2019, 103, 102246. [Google Scholar] [CrossRef]
- Yu, T.T.; Gong, Z.W. Numerical simulation of temperature field in heterogeneous material with the XFEM. Arch. Civ. Mech. Eng. 2013, 13, 199–208. [Google Scholar] [CrossRef]
- Zamani, A.; Eslami, M.R. Implementation of the extended finite element method for dynamic thermoelastic fracture initiation. Int. J. Solids Struct. 2010, 47, 1392–1404. [Google Scholar] [CrossRef]
- Mora, D.F.; Niffenegger, M. A new simulation approach for crack initiation, propagation and arrest in hollow cylinders under thermal shock based on XFEM. Nucl. Eng. Des. 2022, 386, 111582. [Google Scholar] [CrossRef]
- Svenning, E.; Fagerström, M.; Larsson, F. On computational homogenization of microscale crack propagation. Int. J. Numer. Methods Eng. 2016, 108, 76–90. [Google Scholar] [CrossRef]
- Song, J.-H.; Yoon, Y.-C. Multiscale failure analysis with coarse-grained micro cracks and damage. Theor. Appl. Fract. Mech. 2014, 72, 100–109. [Google Scholar] [CrossRef]
- Aduloju, S.C.; Truster, T.J. A variational multiscale discontinuous Galerkin formulation for both implicit and explicit dynamic modeling of interfacial fracture. Comput. Methods Appl. Mech. Eng. 2019, 343, 602–630. [Google Scholar]
- Mergheim, J. A variational multiscale method to model crack propagation at finite strains. Int. J. Numer. Methods Eng. 2009, 80, 269–289. [Google Scholar]
- Wu, J.; Zhang, H.; Zheng, Y. A concurrent multiscale method for simulation of crack propagation. Acta Mech. Solida Sin. 2015, 28, 235–251. [Google Scholar]
- Patil, R.U.; Mishra, B.K.; Singh, I.V. A multiscale framework based on phase field method and XFEM to simulate fracture in highly heterogeneous materials. Theor. Appl. Fract. Mech. 2019, 100, 390–415. [Google Scholar] [CrossRef]
- Zhang, H.W.; Wu, J.K.; Lv, J. A new multiscale computational method for elasto-plastic analysis of heterogeneous materials. Comput. Mech. 2011, 49, 149–169. [Google Scholar]
- Liu, G.; Guo, J.; Bao, Y. A New Multiscale XFEM with Projection Method for Interaction between Macrocrack and Microcracks. Eng. Fract. Mech. 2023, 285, 109286. [Google Scholar] [CrossRef]
- Deng, H.; Yan, B.; Okabe, T. Fatigue crack propagation simulation method using XFEM with variable-node element. Eng. Fract. Mech. 2022, 269, 108533. [Google Scholar]
- Ding, J.; Yu, T.; Bui, T.Q. Modeling strong/weak discontinuities by local mesh refinement variable-node XFEM with object-oriented implementation. Theor. Appl. Fract. Mech. 2020, 106, 102434. [Google Scholar] [CrossRef]
- Teng, Z.H.; Liao, D.M.; Wu, S.C.; Sun, F.; Chen, T.; Zhang, Z.B. An adaptively refined XFEM for the dynamic fracture problems with micro-defects. Theor. Appl. Fract. Mech. 2019, 103, 102255. [Google Scholar]
- Duarte, C.A.; Kim, D.J. Analysis and applications of a generalized finite element method with global–local enrichment functions. Comput. Methods Appl. Mech. Eng. 2008, 197, 487–504. [Google Scholar]
- Wang, X.; Chung, E.; Fu, S.; Huang, Z. Mixed GMsFEM for linear poroelasticity problems in heterogeneous porous media. J. Comput. Appl. Math. 2021, 390, 102255. [Google Scholar]
- Pereira, J.P.A.; Kim, D.J.; Duarte, C.A. A two-scale approach for the analysis of propagating three-dimensional fractures. Comput. Mech. 2011, 49, 99–121. [Google Scholar]
- Plews, J.; Duarte, C.A.; Eason, T. An improved nonintrusive global–local approach for sharp thermal gradients in a standard FEA platform. Int. J. Numer. Methods Eng. 2012, 91, 426–449. [Google Scholar]
- He, L.; Valocchi, A.J.; Duarte, C.A. An adaptive global–local generalized FEM for multiscale advection–diffusion problems. Comput. Methods Appl. Mech. Eng. 2024, 418, 116548. [Google Scholar]
- Kim, J.; Simone, A.; Duarte, C.A. Mesh refinement strategies without mapping of non-linear solutions for the generalized and standard FEM analysis of 3-D cohesive fractures. Int. J. Numer. Methods Eng. 2015, 109, 235–258. [Google Scholar]
- Plews, J.A.; Duarte, C.A. A two-scale generalized finite element approach for modeling localized thermoplasticity. Int. J. Numer. Methods Eng. 2016, 108, 1123–1158. [Google Scholar]





| Radii of Inclusions | Total Number of Inclusions | |||||
|---|---|---|---|---|---|---|
| r = 1.0 m | r = 1.25 m | r = 1.5 m | 100 | 125 | 150 | |
| (%) | 12.6 | 19.6 | 28.3 | 12.6 | 15.7 | 18.9 |
| The present method | 12.19 | 13.82 | 16.27 | 12.19 | 12.85 | 13.58 |
| Standard XFEM | 12.18 | 13.71 | 16.21 | 12.19 | 12.78 | 13.49 |
| S bound | 21.31 | 27.77 | 35.44 | 21.31 | 24.14 | 26.97 |
| P bound | 11.28 | 12.15 | 13.41 | 11.28 | 11.65 | 12.04 |
| Radii of Voids | Total Number of Voids | |||||
|---|---|---|---|---|---|---|
| r = 1.0 m | r = 1.25 m | r = 1.5 m | 100 | 125 | 150 | |
| (%) | 12.6 | 19.6 | 28.3 | 12.6 | 15.7 | 18.9 |
| The present method | 7.221 | 6.084 | 4.963 | 7.221 | 6.633 | 6.118 |
| Standard XFEM | 7.172 | 6.038 | 4.910 | 7.172 | 6.593 | 6.023 |
| Maxwell model | 7.767 | 6.718 | 5.592 | 7.767 | 7.285 | 6.828 |
| Schultz model | 7.644 | 6.459 | 5.145 | 7.644 | 7.105 | 6.585 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, G.; Guo, J.; Bao, Y.; Ping, H. Multiscale Simulation of 2D Heat Transfer in Composite Media Based on Global–Local Enrichment Functions. Mathematics 2025, 13, 1027. https://doi.org/10.3390/math13071027
Liu G, Guo J, Bao Y, Ping H. Multiscale Simulation of 2D Heat Transfer in Composite Media Based on Global–Local Enrichment Functions. Mathematics. 2025; 13(7):1027. https://doi.org/10.3390/math13071027
Chicago/Turabian StyleLiu, Guangzhong, Jiamin Guo, Yan Bao, and Huan Ping. 2025. "Multiscale Simulation of 2D Heat Transfer in Composite Media Based on Global–Local Enrichment Functions" Mathematics 13, no. 7: 1027. https://doi.org/10.3390/math13071027
APA StyleLiu, G., Guo, J., Bao, Y., & Ping, H. (2025). Multiscale Simulation of 2D Heat Transfer in Composite Media Based on Global–Local Enrichment Functions. Mathematics, 13(7), 1027. https://doi.org/10.3390/math13071027







