Abstract
Complex dynamics and nonlinear systems play a critical role in industrial processes, where complex interactions, high uncertainty, and external disturbances can significantly impact efficiency, stability, and safety. In sectors such as mining, manufacturing, and energy networks, even small perturbations can lead to unexpected system behaviors, operational inefficiencies, or cascading failures. Understanding and controlling these dynamics is essential for developing robust, adaptive, and resilient industrial systems. This study conducts a systematic literature review covering 2015–2025 in Scopus and Web of Science, initially retrieving 2628 (Scopus) and 343 (WoS) articles. After automated filtering (Python) and applying inclusion/exclusion criteria, a refined dataset of 2900 references was obtained, from which 89 highly relevant studies were selected. The literature was categorized into six key areas: (i) heat transfer with magnetized fluids, (ii) nonlinear control, (iii) big-data-driven optimization, (iv) energy transition via SOEC, (v) fault detection in control valves, and (vi) stochastic modeling with semi-Markov switching. Findings highlight the convergence of robust control, machine learning, IoT, and Industry 4.0 methodologies in tackling industrial challenges. Cybersecurity and sustainability also emerge as critical factors in developing resilient models, alongside barriers such as limited data availability, platform heterogeneity, and interoperability gaps. Future research should integrate multiscale analysis, deterministic chaos, and deep learning to enhance the adaptability, security, and efficiency of industrial operations in high-complexity environments.
Keywords:
chaotic dynamics; robust control; industrial cybersecurity; Mining 4.0; magnetohydrodynamics; machine learning; energy transition; stochastic modeling MSC:
93A30; 93C10
1. Introduction
Modern industry is characterized by increasing complexity in its processes, involving highly nonlinear phenomena, dynamic interactions across multiple scales, and significant sensitivity to external perturbations [1,2]. This complexity is particularly critical in areas such as heat and energy management, fluid transport, and machinery automation. However, it becomes even more relevant in the mining industry, where geological variability and stringent safety and performance requirements demand robust and scalable control methodologies [3,4]. In this context, the study of nonlinear systems and highly sensitive behaviors, such as deterministic chaos, has become fundamental for anticipating and controlling potentially unstable dynamics [5,6].
The recent literature has documented a remarkable evolution in nonlinear control techniques and chaotic system modeling. The adoption of machine learning—encompassing deep learning, invertible neural networks, and Bayesian methods—the application of semi-Markov switching models, and new approaches to high-complexity cryptography demonstrate research directions that have gained traction in recent years [7,8]. Simultaneously, the energy transition, driven by hydrogen technologies and solid oxide electrolysis cells (SOEC), underscores the need for adaptive models suited to highly variable processes with stringent network security requirements [9]. These demands are even more pressing in the mining industry, where production optimization, risk reduction, and the adoption of Mining 4.0—real-time monitoring and the IoT—are strategic priorities [10,11].
While recent advances have significantly enhanced nonlinear control and mining intelligence, foundational theories remain essential for understanding and improving these methodologies. Classical works, such as those by Slotine and Li [12] on nonlinear feedback control and Khalil [13] on Lyapunov-based adaptive control, have provided the theoretical basis for modern robust control techniques. These contributions continue to influence emerging trends, including data-driven predictive control and hybrid AI–physics models, which address the challenges posed by industrial complexity and uncertainty. Therefore, this review not only synthesizes contemporary research (2015–2025) but also acknowledges the relevance of seminal studies that shaped the field, ensuring a comprehensive perspective on the evolution of nonlinear control in industrial applications.
In light of the growing complexity of modern industrial processes, this paper presents a systematic review that integrates robust control, high-sensitivity dynamics, nonlinear modeling, and data analysis in complex industrial environments, with a particular emphasis on mining applications and advanced process industries. The primary objective is to identify emerging research directions, assess their potential for industrial adoption, and highlight challenges—such as data quality, cybersecurity, and sustainability—that constrain their implementation. To achieve this, an automated literature retrieval and analysis procedure was carried out using Scopus and Web of Science, where filtering criteria were based on keyword relevance, and thematic clustering analysis was performed to categorize the literature into distinct domains.
Additionally, the adoption of systematic and machine learning-based tools has been reported to enhance the scope and precision of bibliographic exploration in areas characterized by significant complexity. By integrating automated text analysis, advanced bibliometric methods, and data-driven insights, recent investigations have demonstrated improved accuracy and depth in the literature categorization and synthesis, thus reinforcing the methodological rigor of reviews on intricate industrial processes [14,15].
This review is guided by several key research questions. One central inquiry focuses on the models and control techniques proposed to handle highly nonlinear and chaotic behaviors in mining and related sectors, including manufacturing and energy [1,2]. Another essential aspect concerns how uncertainty and robustness have been addressed in the presence of external disturbances, such as noise, actuator failures, valve saturation, and cyberattacks [7,8,10]. Additionally, the extent to which chaos-based cryptographic and cybersecurity strategies have been incorporated into Industry 4.0 and Industry 5.0 paradigms is examined [5,6]. Finally, this study investigates the remaining technical, organizational, and regulatory challenges that may hinder the adoption of these methodologies in mining operations and other complex industrial environments [3,4,9].
To address these questions, a comprehensive bibliographic search was conducted using Scopus and Web of Science, resulting in a dataset of 2628 articles from Scopus and 343 from WoS. After automated filtering using Python version 3.7 and the application of inclusion and exclusion criteria, 2900 consolidated references were obtained. From this dataset, 89 highly relevant studies were selected for in-depth analysis. A content analysis supported by k-means clustering grouped the literature into six major thematic areas, covering magnetohydrodynamics (MHD) and heat transfer with magnetized fluids [16], nonlinear control in high-complexity systems, big data-driven optimization, energy transition through SOEC cells and hydrogen applications, fault detection in control valves (stiction), and stochastic models with semi-Markovian switching.
The findings highlight several critical insights. The integration of robust control methods with machine learning has proven essential for managing nonlinearities and severe disturbances. Additionally, cybersecurity has emerged as a growing concern, with chaos-based cryptography and system synchronization offering promising solutions for protecting industrial networks [5,6]. The mining industry, in particular, has seen an expansion of applications in Mining 4.0, where geological variability and strict safety requirements demand scalable and reliable solutions [4]. Moreover, the ongoing energy transition, propelled by green hydrogen and SOEC technologies, introduces additional challenges in managing industrial networks and infrastructures, necessitating more resilient and adaptive control strategies [9].
The structure and development of this research are presented progressively in the following sections. First, Section 2 describes the systematic search and filtering methodology, emphasizing the traceability of selection criteria and the clustering analysis strategy. Next, Section 3 explores advanced nonlinear dynamics, which underpin many of the employed methods. Subsequently, Section 4 presents the main thematic findings, addressing key research directions and industrial applications. Section 5 then discusses technological convergence and the multidisciplinary perspectives that emerge from combining robust control, nonlinear modeling, and cybersecurity. Following this, Section 6 provides insights into future opportunities, highlighting the importance of resilience and sustainability in industrial innovation. In Section 7, the practical implications and remaining challenges for industrial adoption are examined. Finally, Section 8 synthesizes the main conclusions, emphasizing how advances in nonlinear modeling, machine learning, and cryptography can drive competitive and secure transformations in mining and other industrial sectors.
2. Review Methodology
This section details the search, filtering, and analysis strategy for the literature related to nonlinear dynamics and high-complexity phenomena in industrial environments, with a particular emphasis on applications and empirical validations within the mining industry and related processes. The procedure included consulting the Scopus and Web of Science (WoS) databases, defining inclusion/exclusion criteria, and using a Python script to automate filtering, clustering analysis, and bibliography generation.
2.1. Information Sources and Search Strategy
Two bibliographic sources of significant academic relevance were employed:
- Scopus, recognized for its multidisciplinary coverage and robust indexing of scientific articles.
- Web of Science (WoS), included for its high degree of indexing in engineering and applied sciences disciplines.
The search was limited to the period 2015–2025 (applying PUBYEAR > 2014 AND PUBYEAR < 2026) and focused exclusively on articles (DOCTYPE = “ar”) written in English.
The search strategy combined terms related to the following:
- Nonlinear and chaotic dynamics: (“chaotic systems” OR “chaotic dynamics” OR “deterministic chaos” OR “nonlinear systems”).
- Industry and process optimization: (“industry” OR “process control” OR “process optimization” OR “control systems”).
- Mining and industrial scope: (“mining” OR “mineral processing” OR “mining industry” OR “ore processing”).
- Applications and case studies: (“case study” OR “applications” OR “industrial case” OR “real-world application”).
The search algorithm in Scopus was as follows:
(TITLE-ABS-KEY(“chaotic systems” OR “chaotic dynamics” OR “deterministic chaos” OR “nonlinear systems”)
AND TITLE-ABS-KEY(“industry” OR “process control” OR “process optimization” OR “control systems”)
AND TITLE-ABS-KEY(“mining” OR “mineral processing” OR “mining industry” OR “ore processing”)
OR TITLE-ABS-KEY(“case study” OR “applications” OR “industrial case” OR “real-world application”))
AND PUBYEAR > 2014 AND PUBYEAR < 2026
AND (LIMIT-TO(DOCTYPE,“ar”))
AND (LIMIT-TO(LANGUAGE,“English”))
In Web of Science, the most cited articles in the specified period were additionally prioritized to ensure a minimum degree of relevance and methodological quality in the studies.
A supplementary step involved reviewing recent studies that employed systematic and machine learning-assisted techniques to enhance the scope and precision of the literature exploration [17]. These approaches—focused on automated text analysis, advanced bibliometric methods, and data-driven insights—have proven effective in extracting, categorizing, and synthesizing domain-specific knowledge, thereby reinforcing the robustness of the present methodology.
2.2. Document Extraction
The total number of retrieved references was as follows:
- Scopus: 2628 studies, stored in CSV format (01_scopus.csv).
- Web of Science: 343 studies, downloaded in Excel format (02_Wos.xls), filtered to include those with the highest impact (most cited).
After obtaining both datasets, they were integrated into a Python environment for automated metadata cleaning and processing.
2.3. Inclusion and Exclusion Criteria
To refine the final selection of documents, the following criteria were established:
- Inclusion:
- –
- Articles published in English between 2015 and 2025.
- –
- Studies including terms related to nonlinear systems or chaotic dynamics, with direct mention of or application in industrial processes.
- –
- Research based on real case studies or experimental validations, preferably in mining or advanced manufacturing.
- Exclusion:
- –
- Documents in languages other than English.
- –
- Records without available title or abstract (incomplete).
- –
- Duplicates between databases.
- –
- Sources not corresponding to original articles (e.g., nonindexed conference proceedings, theses, or patents).
2.4. Automated Cleaning and Filtering Process
To systematize the analysis and ensure traceability at each stage, a script was implemented in Python that integrates specialized libraries for text analysis, machine learning, and cluster generation. The pseudocode and main stages are illustrated in Figure 1. The key libraries used include the following:
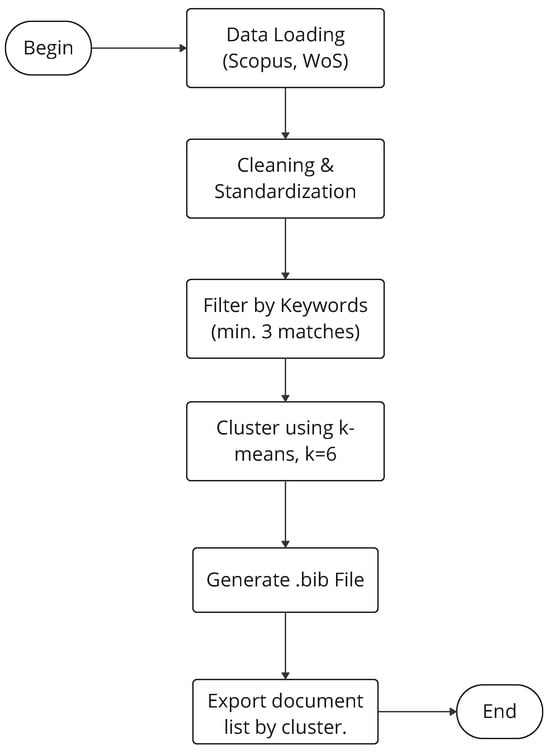
Figure 1.
Simplified flowchart of the cleaning and data analysis process using Python.
- Pandas, numpy for data manipulation.
- Scikit-learn for TF-IDF vectorization (TfidfVectorizer) and k-means clustering analysis.
- Transformers (BART-Large-CNN model) for generating thematic summaries in each cluster.
- Wordcloud for creating word clouds based on the abstracts.
- Matplotlib and seaborn for visualizing the distribution of documents across the resulting clusters.
The complete script details how documents were grouped into six thematic clusters and bibliographic references were generated in .bib format. The main steps are summarized below:
- Data loading (Scopus, WoS): Reading of scopus.csv (2628 records) and wos.xls (343 records) using pandas, combining them into a single DataFrame.
- Cleaning and standardization: Column names were unified (Title, Abstract, Year, etc.), and duplicate or incomplete records were removed.
- Filtering by keywords (minimum of three matches): A threshold of at least three keyword matches was set (e.g., “chaotic systems”, “nonlinear systems”, “mining”). Articles with fewer than three matches were excluded.
- Clustering using k-means (): TF-IDF (TfidfVectorizer) was applied to the concatenation of Title and Abstract, followed by k-means clustering (). For each cluster, the BART-Large-CNN model was used to generate short titles or labels.
- Generating .bib file: A bibliography file in .bib format (@article{}) was created, summarizing the articles in BibTeX format.
- Exporting document lists by cluster: Separate .docx files were generated, each containing a list of articles corresponding to a specific cluster.
As a final result, the identified articles underwent a critical evaluation that confirmed their relevance and the methodological soundness required for this review. This process ensures the reproducibility and reliability of the findings, in line with best practices for literature reviews focused on high-complexity processes and industrial applications, with a distinctive emphasis on mining and advanced manufacturing.
3. Nonlinear Dynamics in Complex Systems: Foundations and Applications
Nonlinear systems play a crucial role in industrial applications, where complex dynamics, uncertainties, and external disturbances challenge conventional control strategies. This section reviews the mathematical foundations and control methodologies for highly complex nonlinear systems, emphasizing their stability, adaptability, and robustness. The discussion includes strict feedback transformations, Lyapunov-based stability analysis, and predictive/adaptive control techniques. These methods are widely applied in industrial automation, robotics, energy systems, and aerospace engineering, where precise and resilient control is essential for optimizing performance and ensuring operational safety.
3.1. Highly Complex Nonlinear Systems
Highly complex nonlinear systems exhibit differential equations whose dynamics cannot be described by linear superposition. These systems frequently arise in engineering, physics, and industrial applications, where strong nonlinearities and uncertainties play a critical role. Several mathematical tools are employed to analyze and control such systems, including strict feedback transformations, Lyapunov stability theory, and predictive/adaptive control.
3.1.1. Strict Feedback Transformations
Many nonlinear systems can be transformed into a strict feedback form, which facilitates the design of robust controllers. A general nonlinear system can be expressed as
In Equations (1)–(4), , for , denotes the i-th state variable of the system at time t. The control input is . The functions and are assumed to be sufficiently smooth (e.g., continuously differentiable) to ensure existence and uniqueness of solutions under standard conditions.
This structure allows the application of backstepping control, which recursively stabilizes each state variable by explicitly designing virtual control inputs and Lyapunov functions at each step.
3.1.2. Lyapunov Stability Theory
Lyapunov’s direct method is widely applied to determine system stability. A nonlinear system is defined as
where is the state vector and is a locally Lipschitz function.
A continuously differentiable function is chosen as a candidate Lyapunov function if it satisfies the following:
- , (positive definiteness).
- (negative semi-definiteness).
If and for , then is said to be positive definite. If, in addition, for all , the system is asymptotically stable. If for all x, the system is stable in the sense of Lyapunov (but not necessarily asymptotically).
The Lyapunov stability theory has been extensively employed in the development of robust control strategies for complex systems. Early formulations of nonlinear feedback control, as proposed by Slotine and Li [12], and adaptive control methods introduced by Khalil [13] have significantly shaped modern stability analysis. These principles have been applied in various engineering fields, including industrial automation and mining intelligence, where robust control techniques are essential for managing nonlinearities and external disturbances. Additionally, research on self-sustained Macro ElectroMechanical Systems (MaEMS) has demonstrated the presence of chaos and bifurcations through Lyapunov exponent analysis, highlighting the necessity of stability considerations in nonlinear systems [18]. In parallel, studies on safety supervision in coal mining have revealed that periodic fluctuations and equilibrium conditions can be effectively analyzed using evolutionary game models, emphasizing the impact of stability theory in regulatory and industrial dynamics [19]. The integration of Lyapunov-based control with machine learning techniques has further enabled the development of advanced predictive models, allowing the mitigation of uncertainties and external perturbations in dynamic industrial environments.
3.1.3. Predictive and Adaptive Control
Predictive and adaptive control methods are employed to handle system complexity and uncertainty. Model predictive control (MPC) is a popular approach that optimizes control actions by solving a finite-horizon optimization problem:
subject to the system dynamics:
In Equations (6) and (7), is the state at step k, is the control input, N is the prediction horizon, and are user-defined weighting matrices, and is the discrete-time or discretized continuous-time system model.
Adaptive control, on the other hand, updates control parameters in real time based on observed uncertainties. The standard adaptive law can be written as
where is the vector of estimated parameters, the adaptation gain, the regressor (or state) vector, and the tracking error. This law typically arises from Lyapunov-based stability arguments ensuring parameter convergence under mild conditions.
3.1.4. Applications
These methods are applied in various industrial domains, including the following:
- Robotics: Motion control of robotic arms with dynamic uncertainties.
- Energy systems: Power grid stability and load frequency control.
- Aerospace: Flight trajectory optimization under external disturbances.
- Manufacturing: Fault-tolerant control in automated production lines.
3.2. Mathematical Modeling of Chaotic Dynamics
Chaotic dynamics are observed in nonlinear systems where small variations in initial conditions lead to exponentially divergent trajectories. This phenomenon is often described using differential equations, particularly in mechanical, electrical, and biological systems. Two fundamental approaches for modeling chaos include the Duffing oscillator and chaotic attractor synchronization.
3.2.1. Duffing Oscillator
The Duffing oscillator is a second-order nonlinear differential equation used to describe systems exhibiting chaotic behavior under periodic forcing. It is given by
In Equation (9), is the displacement, and are the first and second time derivatives of , respectively, is the damping coefficient, define linear and nonlinear stiffness terms, is the amplitude of external forcing, and is the driving frequency.
For certain parameter values, the system exhibits chaotic motion, characterized by a strange attractor and a sensitive dependence on initial conditions. This behavior is crucial in analyzing structural vibrations, fluid dynamics, and nonlinear circuits.
The phase-space representation of the Duffing oscillator reveals periodic, quasi-periodic, or chaotic trajectories, depending on system parameters. Chaos is typically identified using Lyapunov exponents, which quantify the rate of divergence of nearby trajectories:
A positive Lyapunov exponent () is a key indicator of chaos, implying exponential divergence of neighboring trajectories.
3.2.2. Synchronization of Chaotic Attractors
In many practical applications, chaotic synchronization is used for secure communications, neural modeling, and encrypted signal transmission. Consider two chaotic systems, a master system and a slave system, described by
In Equations (11) and (12), are the master and slave state vectors, respectively, and is a control term designed to drive toward . The nonlinear function is assumed to be continuous or differentiable, depending on the synchronization method.
The synchronization error is defined as
If an appropriate control law u is designed such that
then the two systems achieve asymptotic synchronization.
Various methods are used to enforce synchronization, including the following:
- Linear and nonlinear feedback control: Stabilizing the synchronization error by adjusting system parameters.
- Adaptive control: Dynamically updating parameters based on observed synchronization deviations.
- Sliding mode control: Ensuring robustness against system uncertainties.
- Phase-locking techniques: Aligning the phases of chaotic oscillators in coupled circuits.
3.2.3. Applications
Chaotic dynamics and synchronization methods are widely applied in the following areas:
- Secure communications: Encoding messages in chaotic signals to prevent unauthorized access.
- Biological systems: Modeling neuronal activity and heart rhythm irregularities.
- Mechanical systems: Studying chaotic vibrations in aerospace structures.
- Nonlinear circuits: Designing chaotic electronic oscillators for cryptographic applications.
3.3. Stochastic Functional Differential Equations
Stochastic functional differential equations (SFDEs) extend traditional differential equations by incorporating time delays and stochastic processes. These systems are widely used in control theory, robotics, finance, and biological modeling, where uncertainties and memory effects play a crucial role. Two important applications include switching systems with memory-dependent transitions and semi-Markov models.
3.3.1. Switching Systems with Memory-Dependent Transitions
Many real-world systems undergo random switching between different operating modes, influenced by historical states rather than instantaneous transitions. These systems are described by stochastic differential Equations (SDEs) with switching mechanisms:
Here, is the system state, (for some finite M) is a mode-switching variable, is an m-dimensional standard Wiener process, and are sufficiently smooth nonlinear drift and diffusion functions. The notation indicates the segment (or history) of up to time t, capturing memory effects.
The switching process follows a probability law dependent on the past system states. Unlike Markov jump systems, where transitions depend only on the present state, memory-dependent transitions obey history-sensitive probability distributions:
where is the rate of transition from mode i to mode j, explicitly depending on past states . This formulation accounts for memory-dependent phenomena often encountered in robotics, distributed control, and fault-tolerant systems.
3.3.2. Semi-Markov Models
Semi-Markov processes generalize Markov jump systems by allowing arbitrary sojourn time distributions instead of exponential waiting times. The system switches between states according to
where is the cumulative distribution function describing the probability that the system remains in mode i for at most h time units before transitioning to mode j.
Unlike Markovian models, where
semi-Markov models allow generalized distributions (e.g., Weibull, log-normal, or power-law), improving the realism of industrial, financial, and energy systems.
3.3.3. Applications
SFDEs and semi-Markov models are applied in various domains:
- Distributed control systems, including robotic networks and self-adaptive industrial processes.
- Cybersecurity, where they model attack patterns in stochastic cyber–physical systems.
- Energy networks, analyzing demand response strategies in smart grids with uncertain switching.
- Biological systems, representing neuronal signal transmission with random synaptic delays.
3.4. Nonlinear Control Methods
Nonlinear control methods are essential for handling uncertainties in industrial systems and enhancing resilience against disturbances. Unlike linear control strategies, these approaches explicitly account for system nonlinearities, providing robustness and adaptability in dynamic environments. Three widely used nonlinear control techniques include sliding mode control, nonlinear feedback control, and event-triggered control.
3.4.1. Sliding Mode Control
Sliding mode control (SMC) is a robust control technique designed to force system trajectories onto a predefined surface in the state space, known as the sliding surface. The system dynamics are given by
where , , and , are sufficiently smooth.
The sliding surface is defined as
where is a design matrix that defines the manifold on which the system states should converge ().
The control law is designed as
where is the equivalent control computed to satisfy on the sliding surface, and is the switching (discontinuous) term with gain . The function acts componentwise and enforces motion toward the sliding surface.
SMC provides robustness against modeling uncertainties and external perturbations. However, it introduces the chattering phenomenon due to high-frequency switching, which can be mitigated using boundary layer smoothing techniques or higher-order SMC formulations.
3.4.2. Nonlinear Feedback Control
Nonlinear feedback control extends Lyapunov stability principles to multigroup complex systems. The system dynamics can be expressed as
where is a state-dependent input matrix that is assumed to be invertible or of full column rank in the region of interest. A control law u is designed via a Lyapunov function that satisfies , ensuring stability.
For feedback linearization, the input is chosen as
where is a new (virtual) control input, designed for the linearized error dynamics. Such techniques are employed in robotics, aerospace, and industrial automation to handle nonlinearities explicitly.
3.4.3. Event-Triggered Control
Event-triggered control is designed to optimize energy consumption and reduce communication load in industrial networks. Unlike traditional periodic control, where updates occur at fixed intervals, event-triggered control updates the control input only when a triggering condition is met. The system follows
where are the event times at which the control is updated, is the control input applied over , and .
A common triggering mechanism is
where is the deviation between the current and the last updated control state, and is a threshold parameter. The objective is to balance control performance with reduced communication/computation overhead.
3.4.4. Applications
Nonlinear control methods are widely applied in the following areas:
- Robotics, where sliding mode control is used for motion planning under uncertainties.
- Power systems, where event-triggered control optimizes energy dispatch in smart grids.
- Aerospace, where nonlinear feedback control stabilizes aircraft and spacecraft under extreme conditions.
- Industrial automation, where adaptive nonlinear controllers improve precision in manufacturing.
3.5. Inverse Modeling and Nonlinear Optimization
Inverse modeling and nonlinear optimization are essential techniques for estimating parameters, predicting system behaviors, and solving control problems in complex dynamical systems. Unlike traditional forward models, inverse modeling aims to determine the system inputs or parameters given observed outputs. Two key methodologies include invertible neural networks and Bayesian optimization.
3.5.1. Invertible Neural Networks
Invertible neural networks (cINNs) provide a powerful framework for solving inverse problems by learning both direct and inverse mappings of a physical system simultaneously. A general system can be represented as
where is the input (e.g., parameters or boundary conditions), is the observed output, and is an unknown or partially known forward mapping.
Instead of solving the inverse explicitly, a cINN parameterizes a bijective function that allows bidirectional mappings:
where is a latent variable capturing model uncertainty or noise. The bijectivity of h ensures that the inverse mapping is uniquely defined, enabling robust parameter estimation in robotics, geophysics, medical imaging, and more.
3.5.2. Bayesian Optimization
Bayesian optimization is a probabilistic approach used to optimize functions that are expensive to evaluate or that exhibit high uncertainty. Given an unknown objective function , the optimization problem is
A surrogate probabilistic model, often a Gaussian process, is used to approximate and guide exploration:
where is the set of evaluated points, is the mean function, and is the covariance kernel. At each iteration, an acquisition function (e.g., Expected Improvement or Upper Confidence Bound) is maximized to select the next candidate point.
Bayesian optimization is widely used in the following:
- Hyperparameter tuning for machine learning models.
- Industrial process optimization.
- Reinforcement learning and robotics.
3.6. Applications in Big Data and Machine Learning
The increasing availability of large-scale datasets has led to significant advancements in data-driven modeling. Machine learning techniques are integrated with physics-based models to enhance predictions, optimize complex systems, and discover hidden patterns. Two major approaches in this domain include clustering algorithms and hybrid AI–physics models.
3.6.1. Clustering Algorithms and Sparse Regression
Clustering algorithms and sparse regression techniques enable the identification of patterns and dynamic behaviors in high-dimensional systems. Given a dataset X, clustering partitions data into K groups such that
where for are data points, assigns each data point to a cluster, and is the centroid of the assigned cluster. Methods such as k-means, hierarchical clustering, or density-based clustering can be applied depending on the data structure.
3.6.2. Hybrid AI and Physics-Based Models
Hybrid models combine artificial intelligence techniques with physics-based equations to improve system performance and interpretability. Given a physical system governed by
where is the state, the input, and uncertain or unknown parameters, a data-driven approximation can be included to capture unmodeled dynamics:
Here, is often realized via neural networks or other machine learning architectures with trainable parameters . This approach fuses domain knowledge (physics) with empirical insights (AI).
This framework is applied in the following areas:
- Digital twin technology for real-time monitoring of industrial processes.
- Neural PDE solvers for fluid and structural simulations.
- Predictive analytics in smart manufacturing and energy systems.
4. Thematic Clustering for Literature Analysis
To systematically analyze the extensive body of research on nonlinear systems and high-complexity phenomena, a structured thematic clustering approach was applied. After filtering the literature based on relevance and methodological rigor, the retained articles primarily focused on nonlinear dynamics, optimization techniques, and cybersecurity applications, with a strong emphasis on case studies in the mining sector. Using an automated clustering process, these studies were categorized into six thematic clusters, as illustrated in Figure 2. This classification provided a foundation for an in-depth exploration of key trends, methodologies, and interdisciplinary linkages within each domain.
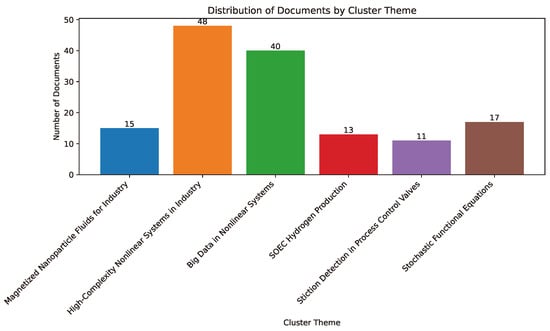
Figure 2.
Document distribution by thematic cluster in the automated analysis (k-means, n = 6).
Given the complexity and interconnectivity of research in nonlinear systems, process optimization, and industrial cybersecurity, an organized approach is essential to synthesizing findings from diverse sources. Thematic clustering offers a structured framework for categorizing studies based on their methodological foundations, theoretical perspectives, and applied contributions. This classification not only highlights underlying patterns and emerging trends but also reveals interdisciplinary synergies that might otherwise remain obscured in fragmented reviews.
Beyond simply grouping similar studies, thematic clustering plays a crucial role in advancing both academic and industrial perspectives. It facilitates the identification of research gaps, aids in the consolidation of methodologies, and enables a more nuanced contextualization of findings within broader scientific and technological landscapes. Specifically, from an academic standpoint, thematic clustering supports a more systemic approach to literature synthesis by enabling the following:
- Identification of knowledge gaps: Categorizing studies by thematic areas—such as nonlinear systems, optimization strategies, and cybersecurity—helps pinpoint underexplored topics and methodological deficiencies.
- Consolidation of methods: By analyzing studies that apply similar theoretical models or computational techniques (e.g., predictive control supported by machine learning algorithms), thematic clustering facilitates the identification of recurring methodological patterns.
- Contextualized discussion: Each cluster reveals the historical and conceptual evolution of its respective domain, ensuring a coherent literature review that avoids redundancy while enhancing the depth of the analysis.
Beyond its academic significance, thematic clustering also plays a crucial role in industrial applications, where structured analysis facilitates decision-making and technological advancements:
- Focusing solutions: Companies interested in industrial cybersecurity, for example, can focus on the specific cluster that analyzes cryptographic strategies based on high nonlinear complexity, reducing research time and ensuring a more targeted approach to their business problem.
- Transferring knowledge between sectors: Topic classification reveals ways to extrapolate methods from one domain (e.g., bioconvection or aerospace control) to others (e.g., the mining industry), highlighting similarities in the challenges of robustness, scalability, and security in processes.
- Assessing technological maturity: A better thematic arrangement helps identify which clusters present standardized protocols, production-ready tools, or long-term development needs, facilitating strategic decision-making in innovation.
In summary, classifying studies into clusters addresses the need to manage the complexity present in fields with high scientific and industrial dynamism. This structured framework not only facilitates the comparison and critique of different methodologies but also helps findings—and their possible applications—to emerge more clearly, fostering transdisciplinary dialogue and the adoption of innovative solutions.
4.1. Use of Algorithms and Cost Functions to Define the Number of Clusters
The selection of the number of clusters in the k-means method plays a crucial role in text mining and document classification, as an inadequate choice of k can lead to redundant groupings or, conversely, to overly broad macrogroups [15,17]. To ensure an optimal segmentation, a combination of quantitative and qualitative methods was used to determine , as detailed below:
- Elbow Method: The first indicator for determining a suitable k was obtained by plotting the Within-Cluster Sum of Squares (WCSS) against different values of k. A clear breakpoint or elbow was identified in the curve, indicating a significant decrease in intra-cluster inertia [1,2]. In our experiments, this breakpoint was observed around or , suggesting an optimal range between five and seven clusters. A qualitative inspection of the emerging topics confirmed that provided a well-balanced trade-off between granularity and coherence.
- Silhouette analysis: To complement the insights from the Elbow Method, we computed the silhouette index, which measures cluster separability. A higher silhouette score indicates well-defined clusters with minimal overlap. For , the silhouette index decreased, suggesting that some distinct topics were merged, while for , there was no significant improvement, and some well-formed clusters became fragmented. Therefore, the choice of maximized the silhouette index while preserving cluster cohesion.
- Thematic validity and expert review: Beyond numerical metrics, an expert validation process was conducted by manually reviewing the titles and abstracts of each cluster following the approach used in recent studies [14,15]. The six-cluster configuration clearly distinguished subtopics such as magnetized fluids, robust nonlinear control, stochastic switching, and big data and machine learning. Increasing the number of clusters beyond six diluted the coherence of certain groups, while reducing it to fewer than six resulted in the merging of distinct research areas (e.g., conflating chaotic cryptography with nonlinear predictive control).
- Data density considerations: The dataset, after automated and manual filtering, comprised approximately 2900 references with corresponding metadata (titles, abstracts, and keywords). After applying TF-IDF and frequency analysis, dimensionality reduction via SVD and PCA revealed cluster densities naturally concentrated in six distinct regions. This observation further supported the decision to set , minimizing the risk of merging thematically distinct studies [5,20].
- Replicability and transparency: From a systematic literature review (SLR) perspective, the selection of k was documented in Python scripts, including cross-validation results (see Section 2). This aligns with best practices for ensuring reproducibility in text mining and bibliometric studies [15,17].
In conclusion, the determination of was not based solely on statistical criteria but combined quantitative analyses—the Elbow Method and silhouette analysis—and qualitative expert review to ensure relevance and coherence in thematic segmentation. This hybrid approach resulted in a robust classification, capturing the underlying structure of the dataset while avoiding both oversegmentation and excessive topic merging.
4.2. Cluster 1: Advances in Magnetized Nanoparticle Fluids for Heat and Mass Transfer in Industrial Applications
It has been observed that magnetized nanoparticle fluids, governed by magnetohydrodynamic principles and Darcy–Forchheimer effects, provide significant improvements in heat and mass transfer within industrial processes. This cluster is closely aligned with the theoretical framework on advanced nonlinear system dynamics since the associated fluid models are inherently nontrivial and subject to uncertainties and strong coupling effects. In particular, the methods of robust control, Lyapunov-based stability analysis, and predictive optimization, as outlined in this theoretical review, have been applied to ensure reliable operation and energy efficiency. Consequently, a deeper understanding of these techniques has been found to be crucial for improving simulation accuracy, enhancing process resilience, and guiding the design of magnetized fluid solutions in real-world industrial contexts.
The research problem addressed in Cluster 1 focuses on the study and application of magnetized nanoparticle fluids to enhance heat and mass transfer processes in various industrial settings. The growing interest in this topic is justified by the need to achieve energy efficiency, ensure more precise control of thermohydrodynamic variables, and ultimately optimize critical operations such as cooling, thermal storage, and reactive fluid management in process plants.
4.2.1. MHD Effects, Forchheimer Influence, and Bioconvection
A notable reference is the work of Yang et al. [16], which analyzes the influence of ferromagnetic nanoparticles in an MHD (magnetohydrodynamic) flow through a double porous medium, considering parameters of chemical reaction and activation energy. The results highlight that a ternary hybrid ferrofluid exhibits a superior heat transfer rate compared to conventional hybrid fluids, providing benefits in sectors such as manufacturing industries and high-density electronics cooling. In a similar vein, Zhao et al. [21] examine bioconvection combined with an unstable flow under the influence of a magnetic field and first-order reactions, confirming that the Soret and Schmidt parameters can modulate temperature and concentration in microfluidic devices and production systems requiring fine control of advection–diffusion processes.
A common characteristic of these studies is the explicit consideration of Darcy–Forchheimer effects, which capture additional dissipation in porous environments where permeability is non-negligible. This allows for the extrapolation of models to highly complex industrial cases, such as filtering media pipelines, geothermal fluid containment tanks, and well injection systems [22]. The use of robust numerical methods (e.g., shooting technique or nonlinear preconditioning approaches) enables the resolution of coupled momentum, energy, and concentration equations with more reliable convergence.
4.2.2. Industrial Applications and Computational Optimization
The relevance of nanoparticle magnetization extends beyond theoretical research, playing a key role in the operation and maintenance of energy systems, particularly where high-temperature gradients exist. Hinkelman et al. [23] propose a rapid and precise thermodynamic model for steam and water applicable to district heating systems, aiming to eliminate costly algebraic loops and accelerate the simulation of large-scale urban heat networks. Likewise, Laudani et al. [24] emphasize the need for highly agile parameter-tuning schemes for photovoltaic device characterization, a finding that has also been extended to the calibration of cooling models in the manufacturing industry.
In environments where fluid properties vary significantly with temperature and where medium- to long-term prediction is required, hybrid LSTM–CNN methodologies have been successfully applied to predictive control. Kang et al. [25] demonstrate that combining deep learning architectures with ARX (AutoRegressive eXogenous) models improves accuracy in water tank level control, suggesting that these methods could be scaled to thermal regulation of magnetized fluids, thereby optimizing cooling and heat transport processes. Regarding operational uncertainty, Xie [26] explain the relevance of gray forecasting methods, which can capture internal dynamics even with limited data—an attractive strategy in the mining and petrochemical industries, where measurements are often sparse or noisy.
4.2.3. Impact on the Mining and Energy Industries
The adoption of magnetized nanoparticle fluids can lead to significant improvements in heat dissipation in mining operations (e.g., in underground ventilation circuits or comminution equipment cooling). Additionally, controlled chemical reactivity in magnetized fluids opens possibilities for optimizing leaching and flotation processes, which could result in lower reagent consumption and higher metallurgical recovery. Notably, MHD techniques and machine learning methods provide a solid foundation for ensuring operational robustness in response to variations in ore grade or temperature fluctuations in processing plants [22].
From the perspective of the energy transition, these studies pave the way for developing more efficient thermal storage strategies at both the urban and industrial scales. The ability to simulate and control large heat networks with high temporal fidelity—assisted by predictive control and optimization algorithms—is essential for the progressive decarbonization of the economy. This scenario is reinforced by the findings of Hinkelman et al. [23], who report drastic reductions in simulation times when using appropriate methodologies for modeling steam and water, indicating that integration with magnetized fluid technologies can be highly scalable.
4.2.4. Final Reflections on the Cluster
In summary, the studies associated with Cluster 1 highlight the high transformative potential of magnetized fluids, integrated with MHD theories, chemical reactions, and machine learning techniques, to significantly enhance heat and mass transfer in industrial systems. The use of functionalized nanomaterials and the adoption of robust numerical methodologies (Darcy–Forchheimer and shooting technique, among others) have improved the stability and speed of calculations, while predictive approaches (LSTM–CNN and gray forecasting) offer broader insights into uncertainty management and operational optimization.
From a practical standpoint, these contributions foster multidisciplinary applications, ranging from cooling large computational or power equipment in manufacturing industries to configuring heat circuits in the mining and petrochemical industries. Looking ahead, the convergence of these studies with intelligent control technologies and IoT infrastructures expands opportunities for automation and resilience in critical processes, enhancing energy security and reducing costs along the industrial value chain.
4.3. Cluster 2: High-Complexity Nonlinear Systems in Industry
The study of high-complexity nonlinear systems has gained significant attention in industrial applications due to the challenges associated with stability, robustness, and control precision. In this context, advanced mathematical techniques have been developed to transform nonlinear dynamics into structured forms, enabling more effective stabilization strategies. Various methodologies, including adaptive control, nonlinear feedback mechanisms, and predictive control approaches, have been explored to mitigate the uncertainties inherent in these systems. As a result, substantial improvements have been observed in areas such as process automation, cybersecurity, and energy optimization. This cluster focuses on the methodological advancements and industrial applications of nonlinear control strategies, providing insights into their practical implementation across multiple sectors.
4.3.1. Adaptive Control and Nonlinear Feedback
One of the most prominent areas of research is the development of adaptive controllers based on Lyapunov theory and their extension to nonlinear feedback mechanisms. In this regard, Adıgüzel [27] propose a discrete-time adaptive controller constructed using the concept of positive semi-definite Lyapunov functions, applied to a Duffing oscillator with high nonlinear sensitivity. Meanwhile, Yang et al. [22] and Nguyen et al. [2] introduce sliding mode control schemes and extended observers to compensate for uncertainties in highly complex systems, such as the rotary inverted pendulum and hypersensitive multigroup systems. These methods frequently rely on transformations that convert the original dynamics into strict feedback structures, reducing computational complexity [7,28]. Several studies have reported the ability of these algorithms to manage external disturbances and extreme nonlinearities, with applications in electromechanical systems [29,30,31] and robustness improvements for diesel engines and gas turbines [32,33].
4.3.2. Synchronization Schemes and Industrial Cybersecurity
The synchronization of highly complex nonlinear dynamics has been particularly relevant in the field of industrial cybersecurity and signal encryption [5,34]. In scenarios such as Industry 4.0 and 5.0, where cooperation between plants, machines, and network nodes is fundamental, multigroup synchronization with uncertainties remains a crucial research topic [22,35]. The application of sliding mode control in its specified-time or predefined-time versions [22,35] allows synchronization to be achieved within bounded time intervals regardless of initial states or perturbations. This perspective becomes essential for secure authentication and multilevel synchronization of processes in distributed systems and supply chains [7,29,34].
4.3.3. Predictive Control and Machine Learning Techniques
The rise of deep learning and cloud computing has accelerated the application of nonlinear predictive control [36,37]. On the on hand, Osorio et al. [38] and Chen et al. [7] introduce reference governors and event-triggered algorithms to efficiently manage state and input constraints. On the other hand, Nguyen et al. [39] and Lin and Le [40] integrate adaptive fuzzy neural networks with sliding mode controllers for systems with severe nonlinearities, while Chen et al. [7] and Aulisa et al. [41] explore gray prediction methodologies and online data analysis for parameter tuning and delay compensation. These solutions aim to address common industrial challenges, such as trajectory tracking in robotics, efficient motor management, and optimization in chemical plants [42,43,44].
4.3.4. Nonlinear Systems with Saturations and Intermittent Failures
A key challenge in industrial implementation involves saturated actuators, intermittent failures, and time delays [45,46,47]. For instance, Zhao and Yang [29] and Wang et al. [48] address deception attacks and fault-tolerant control in systems with nonmeasurable feedback, where the absence of state measurements exacerbates complexity. The importance of adaptive backstepping, state estimators, and variable transformation for accommodating such limitations without compromising stability is emphasized in [28,46,49]. Furthermore, the role of robust observers and predictive techniques [30,50] is highlighted as essential for real-time control under multiple failure modes, with illustrative applications in internal combustion engines, pH control in chemical reactors, and power circuit optimization [42,51,52].
4.3.5. Multidomain Applications and Industrial Perspective
The robustness of these nonlinear control methods spans diverse fields such as aviation [50], mining and transportation [31], mobile robotics [30,53], and the automotive industry [32,54]. Specifically, in smart mining, sliding mode and robust predictive control schemes help regulate conveyor belts and comminution equipment subject to overloads and stochastic disturbances [2,34]. In diesel engine management, strict feedback transformations enable precise control of fuel injection rates, reducing emissions and improving efficiency [32,54]. Additionally, in civil engineering, nonlinear feedback techniques have proven effective for seismic control of weakened buildings [49,52], while the chemical industry has benefited from adaptive controllers for pH regulation and exothermic reaction management [37,42].
4.3.6. Cluster Conclusions
The literature associated with Cluster 2 confirms the theoretical robustness and practical versatility of methods aimed at high-complexity nonlinear systems in industry. Research efforts have focused on the following areas:
- Robust control designs (sliding mode, finite-time, predefined-time, adaptive backstepping) applicable to electric machines, autonomous vehicles, and critical infrastructures.
- Synchronization methodologies and advanced encryption that, together with Industry 4.0/5.0, enhance cybersecurity and resilience against external attacks.
- The incorporation of machine learning techniques (fuzzy logic, LSTM, gray forecasting) to address the uncertain and nonlinear nature of various industrial systems, providing faster and more robust estimations.
- The resolution of real-world constraints such as saturations, intermittent failures, and delays, facilitated by model predictive control and distributed observers.
Collectively, these contributions demonstrate the increasing maturity of nonlinear control methodologies, with a high potential for transferability to industrial automation, mining, robotics, and the energy sector. As cybersecurity and resource optimization continue to be refined, the theoretical solidity presented translates into tangible solutions for the stabilization, synchronization, and robustness of highly complex processes in modern industry.
4.4. Cluster 3: Big Data Analysis and Nonlinear Modeling with External Perturbations
4.4.1. Relevance of Nonlinear Models and Big Data
Several studies highlight the difficulty of processing large volumes of information for nonlinear systems, where high dimensionality and external perturbations complicate identification and optimization. To mitigate these challenges, a hybrid approach combining coarse-graining techniques (e.g., k-means or centroidal clustering) and sparse regression has been proposed to describe state dynamics in real time [1]. This approach enables the design of flow control strategies and the monitoring of vortex shedding phenomena with high accuracy, providing significant results in scenarios with strong nonlinearity—such as the Lorenz system or flexible plates immersed in flow.
The application of machine learning—both supervised and unsupervised—serves to detect patterns, estimate parameters, and infer the internal structure of complex systems. For instance, Fañanás-Anaya et al. [55] propose recurrent neural network (RNN) architectures with self-attention mechanisms to capture nonlinear relationships over long prediction horizons. Similarly, Flores-Tlacuahuac and Fuentes-Cortés [10] employ data-driven Bayesian optimization to solve dynamic product transition problems without requiring an in-depth physicochemical model. These proposals illustrate the trend of leveraging both historical data and hybrid modeling (physics + AI) to enhance the efficiency and reliability of industrial processes.
4.4.2. Inverse Modeling and Estimation Under Uncertainty
Some research emphasizes the need to simultaneously identify both the direct and inverse models of nonlinear systems, which is essential for applications such as adaptive inverse control, active noise cancellation, or nonlinear actuator compensation. In this regard, Chen et al. [7] propose the use of conditional invertible neural networks (cINNs) to determine both the direct function and its inverse in a single step, reducing computational complexity. On the other hand, Bayesian approaches, as in Flores-Tlacuahuac and Fuentes-Cortés [10], facilitate the incorporation of external uncertainties, measurement noise, and parametric variations. These methodologies not only enhance controller robustness but also facilitate their application in the chemical and petrochemical industries, where noisy experimental data is the norm [20,56].
4.4.3. High-Complexity Signals, Encryption, and Real-Time Analysis
The processing of signals with high nonlinear complexity and the need to ensure cybersecurity have driven studies integrating advanced encryption methods within the framework of big data [5,6]. For example, Demirkol et al. [5] design hybrid encryption algorithms (based on memristors and DNA encoding) for the real-time protection of medical data, demonstrating how the unpredictable nature of these signals enhances robustness against cyberattacks. Similarly, Vignesh et al. [57] and Nguyen et al. [58] explore multiple attractors, hypersensitive synchronization, and the relationship between fractal analysis and zero theory to deepen the modeling and control of complex patterns in neural networks and physical systems. These studies confirm the industrial interest in algorithms capable of detecting, compressing, and encrypting large data flows with speed and security in fields such as telemedicine, process supervision, and inspection robotics [59,60,61].
4.4.4. Predictive Control, Observers, and External Perturbations
The fusion of model predictive control (MPC) and big data analytics methodologies has gained traction, especially for nonlinear systems subject to external perturbations [62,63,64]. In Fiedler et al. [62], the do-mpc platform is described, aiming to provide transparency and reproducibility (FAIR principles) in the development of nonlinear and robust MPC, ensuring interoperability with neural networks and industrial communication protocols (OPC UA). This technological–scientific unification facilitates the validation and real-time scaling of complex models, essential in sectors such as advanced manufacturing, smart grids, and Industry 4.0. Additionally, Lin et al. [20] and Shenoy et al. [65] highlight the importance of fuzzy observers in estimating unmeasured variables in highly nonlinear systems, such as adaptive control of dual-axis drilling systems or precise liquid-level measurements in containers.
In the same vein, Arya and Nair [1] emphasize the usefulness of cluster regression to classify dynamic behaviors and subsequently formulate specific control strategies for each group. This data-driven decomposition, combined with sparse or partial modeling, accelerates predictive algorithms and optimizes solutions in contexts where external perturbations can drastically alter operational regimes [7,66].
4.4.5. Applications in Mining, Energy, and Manufacturing
The approach of nonlinear modeling with external perturbations finds an ideal setting in mining and energy processes. In Ou and Chen [67], for instance, a digital sensor is developed to measure the wear of transport chutes, integrating in situ measurements with simulations based on the Discrete Element Method, improving wear prediction by leveraging large volumes of operational data. Similarly, Tripathi et al. [59] analyze speed recovery in hydrostatic transmissions of heavy drilling machines, proposing a real-time control strategy robust to load jumps and inherent nonlinearities. On the other hand, in chemical process plants, Flores-Tlacuahuac and Fuentes-Cortés [10] explore smooth dynamic transitions with minimal energy cost, while Pazmiño et al. [68] implement fractional PID controllers with heuristics (ACO, GWO, FPA) to compensate for delays and saturations in interconnected tanks.
4.4.6. Cluster Conclusions
In summary, the contributions of Cluster 3 highlight the complementarity between big data analysis and nonlinear modeling, emphasizing highly scalable and robust methodologies for handling external perturbations. The following key areas stand out:
- Clustering and sparse regression approaches for classifying complex dynamics and synthesizing specialized controllers [1].
- The use of invertible neural networks (cINNs) and gray forecasting algorithms for simultaneous direct and inverse system identification [7,26].
- The integration of cryptographic techniques with high nonlinear complexity, employing memristors, hidden attractors, and secure encryption algorithms [5,6].
- Robust predictive control and observer strategies that exploit the statistical and dynamic nature of data to manage saturations, failures, and uncertain environments [62,63,65].
The empirical validation of these studies, through simulations and field testing (e.g., industrial sensing, FPGA platforms, cyber–physical systems), confirms the applicability and effectiveness of these methods for Industry 4.0/5.0. Consequently, the convergence of large-scale data processing, nonlinear modeling, and intelligent control technologies is solidified as the preferred approach for optimizing high-complexity processes and ensuring operational resilience in the presence of various perturbations.
4.5. Cluster 4: SOEC, Hydrogen, and Energy Transition
Solid oxide electrolysis cells (SOEC) have emerged as a strategic technology for green hydrogen production due to their scalability—from small-capacity units to large-scale facilities—and their potential for direct integration with renewable energy sources or emission-free electrical systems [9]. Within the global context of energy transition, hydrogen is increasingly recognized as a key decarbonization vector for high-impact industries, including refineries, steel production, and heavy transport. At the same time, growing social and regulatory pressure is driving the phase-out of fossil fuels [4,69]. Cluster 4 examines 13 studies focusing on (i) the optimal management of SOEC under variable demand, (ii) hydrogen policy planning and infrastructure development, and (iii) the necessity of ensuring a just transition in mining regions heavily dependent on coal or petroleum industries.
4.5.1. Optimal Control and Participation in Demand Response
A key contribution in this area is the application of artificial intelligence to the control and operation of SOEC within smart grids, enabling highly precise demand response (DR) [9]. The proposed approach employs deep reinforcement learning (e.g., TD3) to ensure maximum efficiency in hydrogen production, dynamically adjusting to the power dispatch requested by the grid. These algorithms have proven effective in handling the inherent nonlinearity and nonconvexity of the thermoelectrochemical phenomena present in SOEC. The adaptability of such control schemes is crucial for integrating intermittent renewable energy sources and ancillary services into the energy market.
4.5.2. Just Transition in the Extractive Industry
The transition toward a cleaner energy model, in which hydrogen plays a leading role, also requires the economic restructuring of regions highly dependent on coal or petroleum, posing significant social and economic challenges. Jonek-Kowalska [70] examine the situation of Polish cities reliant on coal mining, highlighting their socioeconomic vulnerability once extraction sites close and the urgency of state policies promoting alternative development, workforce training, and the attraction of new clean industries. These findings align with Germany’s experience, where coal phase-out required coordinated institutional action [4]. This reinforces the concept of just transition, which integrates climate policies and economic compensation mechanisms to prevent social collapse in mining-dependent regions [71,72].
4.5.3. Policy Support and Infrastructure Planning
As governments and the private sector intensify efforts to develop clean hydrogen production, Zhang et al. [73] emphasize the need to optimize policy incentives, considering regional heterogeneity, production capacity, and the evolving demand landscape. Similarly, Crown et al. [74] highlight the advantages of constrained optimization methods for designing high-impact policies in both healthcare services and energy resource management. The potential for green hydrogen to be directly connected to renewable plants (solar, wind)—or even emerging technologies such as direct lithium extraction for batteries and energy storage [75,76]—requires significant expansion of transportation infrastructure (pipelines, cryogenic systems, or green ammonia solutions) and improvements in electrolyzer efficiency [59].
4.5.4. Environmental Demands and New Business Models
With the acceleration of decarbonization plans and growing societal pressure, low-carbon hydrogen offers opportunities to reshape the industrial energy mix in sectors such as steelmaking, petrochemicals, and heavy transportation [69]. The possibility of utilizing waste heat and surplus electricity during off-peak hours allows SOEC to function as grid-flexibility assets, enhancing stability and generating economic value [9]. However, adopting this model requires rethinking business models and value chains, particularly in regions where employment has historically depended on fossil fuel industries [4,70].
4.5.5. Emerging Trends and Perspectives
Several key research directions are emerging:
- Scaling up SOEC: Strategies for large-scale design and integration with smart grids, with a focus on predictive control and deep learning algorithms to maximize efficiency and flexibility [9].
- Just transition and social cohesion: The implementation of active economic restructuring policies in mining cities, including investment in workforce training, financial support, and incentives for nonpolluting industries [4,70].
- Hybrid applications: Synergies between green hydrogen production and energy storage technologies, including sodium [76] and lithium [75] batteries, as well as the digital transformation of industrial plants [59,73].
- Environmental sustainability and circularity: Advances in processes aimed at minimizing pollution and excessive resource consumption (water, land) in hydrogen production, such as zero-liquid discharge systems and significant reductions in residual emissions [71,72].
4.5.6. Cluster Conclusions
In summary, Cluster 4 highlights a broad spectrum of challenges and opportunities associated with hydrogen as a key energy transition vector, emphasizing the role of SOEC in decarbonization and grid resilience. However, widespread adoption requires not only scientific and technological advancements (in cell performance, materials, and digitalization) but also economic and social policies that ensure a just transition and strengthen local value chains. The coordination of these factors will determine the success of the hydrogen industry and its ability to catalyze large-scale energy transformation.
4.6. Cluster 5: Detection and Management of Stiction in Control Valves of Process Industries
Stiction in control valves, understood as the static friction that prevents free stem movement, represents one of the most persistent failures in process control loops, directly affecting product quality, operational safety, and energy efficiency [3,77]. This phenomenon can cause undesired loop oscillations, compromising plant stability and increasing maintenance costs. Cluster 5 gathers 16 studies focused on both the early detection of stiction and its management and compensation through nonlinear modeling techniques, machine learning, statistical methods, and advanced control algorithms.
4.6.1. Importance of Early Diagnosis and Analysis Phases
The timely detection of stiction is crucial, as 20–30% of industrial control loops experience oscillations due to valve failures [3,11]. The phase-space reconstruction method proposed by Guan et al. [3] is based on dynamic systems theory to identify characteristic patterns of static friction in the reconstructed trajectories of the controlled output. This approach, which uses statistical indices and recurrence plot (RP) distributions, demonstrates significant potential compared to traditional methods that require more restrictive assumptions. Complementarily, Rahimi and Saadat [78] and Khayyam et al. [79] highlight the advantage of combining phase-space reconstruction with classification algorithms (e.g., ensemble learning or fuzzy methods) to enhance fault identification and diagnosis.
4.6.2. Multivariate Tools and Functional Analysis
In multivariable systems—typical in petrochemical plants, refineries, or mining facilities—multivariate approaches have been employed to simultaneously detect stiction and other faults [77]. For instance, multivariate functional principal component analysis (MFPCA) methods allow latent features to be extracted from high-dimensional data, simplifying fault condition classification [11,77]. This perspective aligns with the application of machine learning on large-scale data (big data), enhancing both scalability and detection accuracy [80,81]. Additionally, the increasing digital transformation of industrial plants—progressively oriented toward Industry 4.0 and 5.0—enables real-time data collection and continuous analysis [11,82], facilitating constant monitoring and early detection.
4.6.3. Intelligent Classification and Predictive Control
Once stiction is identified, the next step is its compensation or intelligent management. Recent studies integrate an inverse valve model with robust predictive control to counteract the effects of static friction [9,83]. Other approaches utilize adaptive observers and backstepping techniques, correcting real-time discrepancies caused by the valve [2,3] in Cluster 2. Furthermore, ensemble learning has been highlighted for multifault classification in hydraulic valves [78], incorporating classification methods (kNN, random forest, decision trees) with cross-validation techniques (k-fold, leave-one-out). These strategies can be coupled with industrial controllers (PID or MPC) to minimize instability, maintain setpoints, and reduce maintenance costs.
4.6.4. Challenges in Complex Environments and Future Perspectives
In process industries, stiction coexists with other nonlinear phenomena, such as chemical reactions, fouling in heat exchangers, or instabilities in reactors [24,84] in Cluster 1 and Cluster 2. Therefore, holistic approaches are required that consider uncertainties and potential external disturbances (noise, leaks, etc.). The integration of data-driven models with operator expertise and fuzzy logic adds robustness, particularly in cases where instrumentation limitations result in sparse data [2,80] in Cluster 2 and Cluster 3.
Additionally, Ravi and Ravi [85] and Yang et al. [82] propose federated learning algorithms and edge computing to reduce latencies and ensure data confidentiality in distributed sensor networks. This set of strategies enables the automation of predictive maintenance, estimation of component lifespan, and prioritization of plant safety.
4.6.5. Conclusions and Future Directions
The detection and management of stiction in control valves remain a critical challenge in the process industry, impacting sectors such as petrochemicals, mining, food processing, and pharmaceuticals. Recent advancements indicate that the combination of phase-space-based methods, multivariate analysis, machine learning, and robust observers enables both early detection and automatic compensation. Future research directions include the following:
- Greater integration with big data and IoT: Adoption of advanced data analytics techniques for real-time data collection and processing, enabling self-tuning in industrial controllers [9,11,81].
- Explainable deep learning: Incorporation of interpretable models (XAI) to clarify the origins of stiction and provide more transparent corrective actions for operations [78,83].
- Secure cyber–physical systems: Strengthening data protection and reliability against potential cyberattacks by integrating security protocols into valve monitoring [5,82].
Ultimately, Cluster 5 underscores the importance of addressing stiction through the convergence of empirical expertise, nonlinear modeling, advanced statistics, and machine learning. As Industry 4.0 evolves, intelligent fault management in control loops is emerging as a key factor in competitiveness and sustainability.
4.7. Cluster 6: Stochastic Functional Differential Equations with Past-Dependent Switching
Systems with past-dependent random switching represent an extended class of hybrid models where the switching process evolves over time according to stochastic transition rules that may depend on previous states, even across an extended time horizon [2,8,29,86]. This type of configuration appears in collaborative robotics, distributed sensor control, power networks, and various industrial scenarios. In particular, semi-Markovian models with infinite states or semi-Markov switching provide greater realism compared to classical Markov jump systems as they do not constrain mode durations to simple exponential distributions [2,87].
4.7.1. General Perspective and Stability Challenges
Unlike traditional Markovian systems, past dependence generates more complex dynamics. The presence of delay or memory leads stochastic functional differential equations (SFDEs) with random switching to require a more elaborate study of stability, robust control, and filtering [2,88,89]. Some of the main challenges include the following:
- The infinite-dimensional state space, where past trajectories influence present dynamics.
- System uncertainty, as random switching may introduce modes with partially unknown transition rates [2,29].
- The impact of failures or cyberattacks, which alter system modes in a nontrivial manner [8,90].
To address these difficulties, methodologies based on Lyapunov–Krasovskii theory, the design of fuzzy filters, and the looped functional technique (extended memory functionals) have been developed [2,88,89]. These approaches allow for representing the delayed nature of the dynamics and time-dependent switching.
4.7.2. Applications in Industrial Networks, Distributed Control, and Cyber–Physical Systems
The semi-Markovian nature, with infinite states and delays (either in switching times or in state equations), aligns well with industrial contexts where multiple agents operate with stochastic delays and nontrivial transitions. Examples include the following:
- Autonomous vehicle and robotic fleet control: Each robot may exhibit different dynamic modes depending on network availability or external disturbances (weather, node failures). Additionally, mode duration does not necessarily follow an exponential distribution [2,91].
- Power systems and renewable energy: Uncertainty increases when network power levels fluctuate, and electronic switches (inverters, FACTS devices) enter or exit service based on prior states [29,92].
- Industrial value chains and Industry 4.0 manufacturing: The integration with Industry 4.0 increases the need for systems that manage delays and secure mode transitions against cyberattacks [8,90], similar to the stiction detection and network failure analysis discussed in Cluster 5 [3].
4.7.3. Switching and Cyberattacks
An emerging topic is cyberattacks, such as Denial-of-Service (DoS) or False Data Injection (FDI), which can force operational mode changes or partially corrupt exchanged information [8,90]. These malicious actions directly influence switching mechanisms and complicate the analysis of stochastic stability. Tan et al. [8], for example, describe a dynamic-memory event-triggered sliding mode approach that robustly preserves stability under DoS and FDI attacks using a fuzzy filter and a memory-based triggering mechanism.
4.7.4. Optimal Control and Nonlinear Optimization Algorithms
Past-dependent switching not only affects stability but also complicates control optimization. In Panigrahi and Nayak [86], optimization problems (nonlinear and involving epistemic uncertainties) are formulated and converted into conjugate gradient descent schemes with Armijo line search. These methods contribute to controller design by balancing fast convergence and robustness in systems with multiple modes and delays.
Beyond theoretical contributions, real applications emerge in mining industries and petrochemical processes, where stochastic switching with delay models random variations in boilers or changes in ore quality, similar to the nonlinear processes with perturbations presented in Cluster 2 [1,7]. The integration of machine learning—for example, neural networks to estimate delayed dynamics and switching patterns—could enhance predictability and control robustness [2,90].
4.7.5. Modern Control and Stability Methodologies
Sliding mode strategies and robust fuzzy control are essential for handling nonlinearity and combined uncertainty [8,87,89]. On the one hand, sliding mode control ensures system invariance against disturbances and actuator failures, a crucial aspect in cybersecurity studies [8,29], also discussed in Cluster 2. On the other hand, robust fuzzy control facilitates the approximation of switching functions, reducing modeling complexity in line with Takagi–Sugeno (T-S) fuzzy theory [87,89].
4.7.6. Conclusions and Future Directions
Cluster 6 highlights the significance of stochastic models with past dependence for describing realistic scenarios where mode switching does not follow a basic Markovian distribution but instead depends on historical trajectories [2,8]. Key contributions and challenges identified include the following:
- Managing computational complexity: Systems with numerous modes and delays require efficient numerical and theoretical approaches [2,86].
- Incorporating cybersecurity and actuator failures: Approaches addressing fault tolerance and resilience against external attacks [8,87,90].
- Synergy with machine learning and global optimization: The prediction of switching modes and identification of delayed dynamics can benefit from neural networks and metaheuristic methods [86,90].
- Expanded industrial applicability: IoT environments, plants with stochastic demand, cyber–physical systems, and smart energy networks where robust and secure control is essential.
In summary, the literature suggests that SFDEs with past-dependent switching and stochastic perturbations accurately capture the complexity of various industrial and transportation scenarios. As stability methods and robust control techniques advance, increasingly unified solutions are expected to address uncertainty, delays, and non-Markovian switching, with significant potential to enhance the security and efficiency of modern control systems.
5. Technological Convergence and Multidisciplinary Perspectives
Throughout the reviewed clusters, a space of convergence emerges, unifying research on nonlinear dynamics, data-driven optimization, and industrial cybersecurity. This is reflected in the diversity of advanced methodologies, ranging from fluid magnetization for heat transfer [16] and fault detection in valves [3] to cryptographic encryption supported by complex attractors [5,6] and semi-Markovian stochastic switching in control networks [2,8]. As the mining industry, advanced manufacturing, and global logistics adopt hybrid models, which integrate physical theory with machine learning, the ability to comprehensively address challenges such as thermal management (e.g., magnetized fluids in high-heat-load plants), secure automation (e.g., nonlinear cryptography for SCADA networks), and process optimization (via robust algorithms resilient to uncertainty and fluctuations) is expanding.
The findings described within each cluster confirm the strategic importance of researching and developing cross-disciplinary solutions:
- Intelligent heat and energy management: Both the mining and petrochemical industries benefit from advances in magnetohydrodynamics and thermal control [16], with direct applications in machinery cooling and thermal storage.
- Robust control and real-time supervision: The rise of highly sensitive systems (induction motors, gas turbines) and the presence of stochastic disturbances have driven adaptive and predictive methodologies capable of stabilizing complex dynamics [2,10].
- Industrial cybersecurity and resilience: The adoption of Mining 4.0 and smart grids underscores the need for cryptography based on highly complex behaviors [5,6] as well as synchronization mechanisms and secure switching [8].
- Energy transition and sustainability: The development of green hydrogen via SOEC [9], along with the transformation of coal-dependent regions into clean economy models [4,70], necessitates advanced algorithms for control, planning, and environmental impact reduction.
These thematic axes are becoming increasingly interconnected, revealing that academic and industrial leadership will rely on collaborative models where physics, statistics, computer science, and engineering converge in integrated approaches to automation and decision-making.
5.1. Relevant Applications in Key Sectors
5.1.1. Automotive and Aerospace Industry
The use of robust observers and nonlinear predictive control in engine regulation [32,54] has shown significant advances in reducing emissions and improving efficiency. In aviation, Lyapunov methodologies and adaptive control enhance the stability of aircraft subjected to dynamic disturbances [50].
5.1.2. Industrial Robotics, Mechatronics, and Civil Engineering
Robotics and mechatronics leverage sliding mode controllers and learning techniques to optimize trajectories and compensate for nonlinearities [30,40]. Meanwhile, civil engineering integrates nonlinear feedback for structural control in buildings vulnerable to earthquakes, validating the effectiveness of these methods in environments with high uncertainty [52].
5.1.3. Petrochemical and Manufacturing Processes
Studies on stiction detection [3] and the use of machine learning in distributed control loops [5,77,80] have demonstrated their potential to reduce downtime and improve operational reliability. Additionally, the management of energy networks and big data analysis in manufacturing have created opportunities for real-time optimization of chemical plants and refineries.
5.1.4. Energy Transition and Power Grids
Renewable energy, hydrogen production, and the adoption of SOEC [9] illustrate the value of merging nonlinear control techniques, big data analytics, and Bayesian optimization, promoting cleaner operation and greater reliability in smart power grids [23,62].
5.1.5. Mining Industry
Geological complexity and high operational risks make the mining sector an ideal case study for applying the reviewed methodologies [7,31]. From hybrid models (AI + physics) to anticipate critical failures to robust encryption techniques protecting geological and plant data [5], mining is emerging as a natural laboratory to validate advanced control approaches, nonlinear cryptography, and big data management [2].
5.2. Toward an Intelligent and Sustainable Industry
Given the diversity of applications, the contributions of each cluster converge on a common objective: addressing the increasing complexity and uncertainty of industrial processes through holistic approaches that integrate nonlinearity, artificial intelligence, and cybersecurity. Thus, disruptive innovation is not only about solving specific problems, such as cooling or encryption, but also about articulating a systemic vision where resilience, energy efficiency, and global competitiveness coexist harmoniously.
- Multidisciplinary perspective: Nanotechnology, control engineering, data mining, and cryptography converge to generate high-impact solutions that can be scaled across different productive sectors.
- Gradual and validated adoption: The transition from conceptual testing to industrial application requires pilot programs, standardization, and interinstitutional collaboration between academia, government, and industry, accelerating technology transfer.
- Balance between technology and policy: Advances in energy transition, such as SOEC and green hydrogen, along with the implementation of intelligent and cybersecure networks, require appropriate regulatory frameworks and socioeconomic transition plans, especially in mining regions.
In summary, the research lines and technological solutions described throughout the clusters establish a solid path toward Industry 4.0 and 5.0, where complexity management, predictive maintenance, and data security form a fundamental triangle for sustainable industrial transformation.
5.3. Projection Toward Smart Mining
The adoption of advanced methodologies for nonlinear control, large-scale data analytics, and cybersecurity—described in each of the clusters—has a particularly transformative potential in smart mining. This term refers to the convergence of mining process automation, the intensive use of digital technologies (IoT, SCADA), and the global optimization of the value chain under strict efficiency, safety, and sustainability criteria.
5.3.1. Automation and Advanced Control
The inherent complexity of mining—including drilling, blasting, loading, transportation, comminution, and separation—requires robust control schemes capable of responding to abrupt variations in ore quality, deposit geology, and demand fluctuations. In this context, stochastic switching functional differential equations [2,8] and hybrid models (physics + AI) [7,10] are particularly suitable for describing and stabilizing processes subject to extreme uncertainty and difficult-to-predict disturbances.
5.3.2. Predictive Maintenance and Intelligent Systems
The need to mitigate critical failures (e.g., stiction in valves, conveyor belt ruptures, breakdowns in comminution equipment) is reinforced by early detection methodologies and recurrence analysis [3] as well as deep learning approaches (e.g., LSTM–CNN–ARX) in predicting anomalous behaviors [25]. By combining the IoT, online monitoring, and robust optimization algorithms [1], the mining industry can anticipate potential failures and schedule timely interventions, maximizing equipment availability and reducing operational downtime.
5.3.3. Industrial Cybersecurity and Protection of Critical Data
The digitalization of mining and the use of SCADA networks in remote operations increase the risks of cyberattacks, which could compromise operational continuity or the confidentiality of topographic and reserve data. The incorporation of complex encryption—based on nonlinear behaviors and highly sensitive attractors—[5,6] strengthens the protection of digital infrastructure, preventing intrusions or intentional manipulations of control and monitoring systems.
5.3.4. Sustainability and Energy Transition
The convergence of clean technologies, water management, and energy efficiency represents a priority challenge for the future of mining. Magnetized fluids [16], SOEC cells [9], and smart grids enable the reduction of environmental impact while facilitating the integration of renewable energy into intensive processes (e.g., grinding, flotation). Likewise, the transition of traditional mining regions toward more sustainable models requires a systemic approach, integrating training programs, regulatory standards, and advanced control methodologies [4,70].
5.3.5. Toward Mining 4.0/5.0
The term Mining 4.0 refers to the incorporation of the IoT, automation, and large-scale data analysis at every stage of the production cycle. Several of the methods analyzed in the clusters (optimization under large data volumes, semi-Markov switching, industrial cryptography) constitute fundamental pillars for achieving the necessary connectivity and resilience. In this regard, the future Mining 5.0 is envisioned as a more sophisticated cyber–physical environment, capable of self-organizing and adapting intelligently to business fluctuations and geological conditions.
5.3.6. Implementation Challenges and Opportunities
- Scalability and standardization: Transitioning from conventional mining to smart mining requires investment in digital infrastructure, strengthening communication protocols (OPC UA, MQTT), and establishing interoperability guidelines that facilitate the widespread adoption of nonlinear and cryptographic algorithms.
- Cultural change and talent development: The adoption of AI tools and advanced control systems requires trained personnel, not only in mining operations but also in data analytics, robotics, and cybersecurity.
- Validation and real-scale pilot projects: To consolidate the transition toward Mining 4.0/5.0, it is essential to develop pilot projects that demonstrate return on investment and technical feasibility in concrete operations, encouraging public–private collaboration.
In conclusion, the qualitative leap toward smart mining leverages the integration of nonlinear models, machine learning, cybersecurity, and clean technologies. This transformation not only enhances profitability but also strengthens the sustainability and competitiveness of mining in an increasingly complex global environment that demands responsible solutions.
6. Final Perspectives and Research Opportunities
This review of studies ranging from the thermodynamics of magnetized fluids to stochastic switching and cybersecurity based on nonlinear methods highlights the relevance of the synergy between control theory, advanced modeling, and artificial intelligence in addressing the challenges of an evolving smart industry. The following research directions present high-potential areas for those seeking to contribute in an innovative and multidisciplinary manner, both in smart mining and in other productive and service sectors:
- Deepening hybrid models: The fusion of physical methods (e.g., MHD, chemical reactions, fluid mechanics) with deep learning and Bayesian optimization approaches is emerging as one of the most promising trends [10,16]. In mining, this could lead to more precise geometallurgical models and the integration of optimized chemical reactors based on efficiency and sustainability criteria.
- Scaling cybersecurity solutions: The increasing digitalization of remote plants and SCADA networks in the mining or petrochemical sectors underscores the importance of cryptography based on nonlinear behaviors [5,6] as well as the implementation of robust synchronization mechanisms to prevent attacks such as Denial-of-Service or false data injections [8]. Strengthening this area will provide a solid defense for critical industrial infrastructure.
- Energy transition and industrial reconversion: Technologies such as SOEC and green hydrogen [4,9] offer clean production pathways, particularly relevant in regions heavily dependent on fossil fuels. The development of robust predictive control models and dynamic planning—potentially supported by AI—could accelerate the adoption of these solutions and their integration into smart grids, enhancing decarbonization and industrial competitiveness.
- Gradual validation and standardization: To transfer these methodologies to real-world environments, it is essential to establish protocols and guidelines that unify simulation, implementation, and performance evaluation criteria across different industries. This process will strengthen confidence among the productive sector, regulatory bodies, and the scientific community, fostering the adoption of disruptive technologies with reduced risk.
Consequently, the convergence of nonlinear dynamics, industrial cybersecurity, and advanced optimization opens a wide range of opportunities for researchers aiming to contribute to the development of the smart industry—whether in mining, energy, manufacturing, or services—under unprecedented levels of autonomy, resilience, and sustainability. The invitation is clear: explore these emerging and vital topics, promoting collaborative and interdisciplinary approaches as well as continuous dialogue with industry stakeholders and regulatory frameworks. In this way, complexity becomes the driving force behind global competitiveness and sustainability, setting a path where smart mining and other high-impact industries move toward a safer, more profitable, and adaptive future.
7. Discussion
The analyzed studies confirm the growing relevance of modeling and monitoring methods in highly complex nonlinear systems, providing promising solutions in sectors that require robustness, scalability, and adaptability [6,27,35]. Compared to traditional approaches, there has been a substantial evolution in identification and control algorithms: the adoption of hybrid approaches—combining physical–mathematical techniques with deep learning—has significantly improved precision in managing complex dynamics and noise typical of industrial environments [1,7,25]. Additionally, the use of machine learning and semi-Markov switching theory and the integration of fuzzy logic [2,8,29] have enhanced fault detection and controller resilience against external disturbances or cyberattacks [3,5].
However, limitations persist that restrict the extensive application of these technologies. Among them, the scarcity of high-quality data in operational scenarios stands out as a factor that reduces the effectiveness of supervised approaches and emphasizes the need for robustness in parameter estimation [10,26]. Similarly, the complexity of implementing nonlinear models in plants with distributed systems and large data volumes can lead to computational overhead and challenges in standardizing interfaces [16]. The heterogeneity of platforms (field equipment, communication protocols, industrial networks) is another significant hurdle, particularly when harmonization with industrial cybersecurity measures is required [5,34]. Additionally, the lack of unified guidelines integrating control algorithms and data analytics hinders widespread adoption, requiring consensus among manufacturers, users, and regulatory bodies [4,70].
Despite these challenges, the practical implications of these advances are significant. From resource extraction and processing to energy management in urban heat networks and manufacturing upgrades, these are all areas where fault anticipation and resource optimization translate into reduced downtime, lower costs, and greater sustainability [11,23]. The validation of models in near-industrial-scale test environments confirms their technical feasibility and the high potential returns derived from adopting the IoT, digital twins, and remote control systems [7,93].
Regarding future opportunities, multiscale approaches appear particularly relevant, integrating microscopic dynamics (chemical reactions, quantum effects in fluids) with macroscopic industrial processes. Additionally, studying the interaction between nonlinearity and human decision-making—where operator intervention modulates system trajectories—could clarify emerging patterns under high uncertainty conditions [8,20]. Furthermore, technology transfer would be accelerated by adopting interoperability standards and formal cybersecurity assurance methodologies in control systems [5]. Finally, the development of visualization and explainability methods—facilitating the interpretation of complex information for both specialists and business stakeholders—would enhance the incorporation of these solutions into industry, increasing their socioeconomic impact and encouraging continuous innovation.
7.1. Industrial Applications and Scope of the Reviewed Methods
The discussed methods (nonlinear control, chaotic modeling, machine learning mechanisms, etc.) have demonstrated their effectiveness across different industries, from petrochemicals to aviation and mining [2,4,25]. To provide an integrated view of how these methodologies can be transferred between sectors, Table 1 presents a summary of their scope and key challenges in various fields, as well as their potential adaptability to other industries, including mining and the operation of chemical and energy plants.

Table 1.
Examples of industries, applied methodologies, and possibilities for cross-sector adaptation.
As noted in Table 1, nonlinear control, stochastic modeling, and machine learning exhibit significant transferability potential when industrial processes involve complex interactions or high uncertainty. For instance, semi-Markov switching systems in electrical networks [8] can be analogously applied to mining operations, where ore variability and equipment availability are influenced by stochastic factors (changes in ore grade, conveyor belt failures, etc.) [2]. Similarly, event-triggered control techniques and high-complexity cryptography [5,34] are highly useful in large-scale mining SCADA environments, strengthening the security of geological and operational data.
Likewise, the integration of digital twins and deep learning—already common in advanced manufacturing [25]—could optimize comminution and flotation in the mining industry, provided there is a robust IoT infrastructure and appropriate interoperability protocols [11]. Ultimately, the success of this technology transfer depends on plant flexibility and effective collaboration between academia and the industrial sector, accelerating the migration of cutting-edge methods from one domain to another [4,70].
7.2. Comparison Between Discrete Difference Equations and Continuous-Time Differential Equations
In many studies, authors prefer discrete difference equations over continuous-time differential equations for simulation experiments. This preference is not arbitrary but is motivated by theoretical and practical considerations within control theory and advanced mathematical modeling. The key reasons supporting this approach are as follows:
- Digital implementation and sampling: In most industrial control applications and computational simulations, data acquisition and system actuation occur in digital form. State variables are updated at periodic sampling intervals (e.g., every seconds), necessitating the transformation of continuous models (ordinary differential equations, ODEs) into discrete models (difference equations). Discretization methods, such as Tustin, Euler, or discrete Runge–Kutta, ensure that simulations and subsequent digital controller implementations closely reflect real-world system dynamics.
- Computational robustness and numerical stability: Continuous-time differential equations often require solving large-scale or nonlinear systems, which can present convergence and stability challenges in digital environments. Discrete formulations allow the use of well-established numerical algorithms that offer controlled truncation error at each step, improving computational efficiency and stability. This makes difference equations more suitable for discrete event-driven systems and reduces sensitivity to numerical precision limitations in computing.
- Sampling-based systems and digital control theory: Modern industrial controllers—such as those embedded in microprocessors—operate using digitized signals. As a result, digital control theory and the synthesis of predictive (MPC) or adaptive controllers are more naturally formulated in the discrete domain. This not only simplifies implementation but also enables the use of multihorizon optimization techniques that can be computed in real time, which would be significantly more complex in a strictly continuous-time framework.
- Integration of stochastic effects and disturbances: Many real-world systems experience switching dynamics, time delays, and stochastic perturbations. Difference equations facilitate the implementation of statistical estimation methods such as discrete Kalman filters and adaptive estimators. Additionally, discrete-time formulations are well suited for integrating machine learning techniques, particularly for time series data, which are naturally represented in discrete sequences, enhancing compatibility with recurrent neural networks and predictive models.
- Flexibility in multiscale and event-driven applications: Industrial simulations often involve processes occurring at multiple time scales or with asynchronous interactions, such as sensor networks or event-based actuation systems. In these cases, using difference equations within different model submodules—each with its own sampling rate—provides a modular and scalable approach that would be computationally expensive or impractical to handle using a single continuous-time formalism.
Ultimately, the use of discrete difference equations instead of continuous-time differential equations is not merely a matter of convenience. It ensures better numerical error control, aligns more naturally with digital instrumentation, and facilitates integration with estimation and optimization techniques. This approach bridges the gap between dynamic systems theory and practical industrial applications, particularly in sectors such as mining and smart manufacturing, where digitalization and distributed control are becoming increasingly essential for improving efficiency, reliability, and scalability.
7.3. Hyperparameter Selection Strategies in Intelligent Models
The selection of hyperparameters plays a crucial role in ensuring optimal and consistent performance in complex nonlinear scenarios. In advanced mathematical modeling and machine learning, various strategies have been developed to efficiently explore and optimize hyperparameter configurations. The most widely adopted methods in the literature are outlined below:
- Grid search: This method systematically explores a predefined set of values for each hyperparameter. While simple and easily reproducible, grid search can be computationally expensive, especially when dealing with high-dimensional hyperparameter spaces. In industrial applications involving deep neural networks or complex nonlinear models, exhaustive search often becomes impractical without large-scale computing infrastructure.
- Random search: Instead of systematically exploring all possible combinations, random search samples hyperparameter values from predefined probability distributions (e.g., uniform, logarithmic). Studies have shown that compared to grid search, fewer random evaluations often yield comparable or even better results, particularly when only a subset of hyperparameters significantly impacts model performance. This approach is valuable in robust models where the relative importance of each hyperparameter is unknown.
- Bayesian optimization: This method builds a probabilistic model (e.g., Gaussian process regression or kernel-based regression) to approximate the cost function over the hyperparameter space. An acquisition function (e.g., Expected Improvement, Upper Confidence Bound) guides the search by balancing exploration and exploitation. The Bayesian model is updated iteratively after each evaluation. This approach is particularly useful in scenarios where each experiment is computationally expensive—such as tuning a nonlinear controller in a physical plant—where minimizing the number of evaluations is critical.
- Multiobjective optimization: In many industrial applications, hyperparameter selection must optimize multiple objectives beyond model accuracy, such as inference time or energy consumption. Methods like Pareto frontier techniques or multiobjective evolutionary algorithms (e.g., NSGA-II, SPEA2) simultaneously explore various performance metrics, identifying optimal trade-off solutions that balance different criteria.
- Cross-validation and performance metrics: A standard practice in hyperparameter tuning is splitting data into training and validation subsets (k-fold cross validation), computing performance metrics (e.g., MSE, MAE, F1-score), and selecting the configuration that optimizes these measures. In adaptive control or highly variable systems, robustness is also assessed through additional indicators such as error variance or control energy consumption. Configurations that achieve a balance between reference tracking and resource efficiency are generally preferred.
- Dynamic recalibration and adaptive learning curves: In time-varying environments (e.g., flotation processes or diesel engines with gradual component aging), some studies adopt dynamic hyperparameter recalibration techniques. This is achieved through online learning or adaptive control methods, where hyperparameters are iteratively adjusted based on real-time plant performance.
The choice of hyperparameter tuning strategy depends on model complexity, computational resource availability, and the precision or robustness requirements set by the industrial application. Bayesian optimization and multiobjective evolutionary strategies have gained relevance in scenarios requiring high optimization levels with limited experimental costs, whereas random search and grid search remain practical options when search space size and computational cost are manageable. In all cases, rigorous cross validation and careful monitoring of performance and robustness metrics form the backbone of effective hyperparameter tuning in both industrial and academic contexts.
7.4. Recurrent Neural Network-Based Modeling and Control
Recurrent neural networks (RNNs), including variants such as Long Short-Term Memory (LSTM) and Gated Recurrent Unit (GRU), have gained increasing relevance in the recent literature for addressing nonlinear and high-dimensional control problems [14,15,17]. These models offer powerful tools for learning complex dynamics and optimizing advanced control strategies. Below, we outline the main approaches and motivations for their growing adoption in industrial applications:
- Temporal dynamics representation and historical dependency: RNNs retain past information through feedback loops in their architecture, making them highly effective in modeling processes with strong historical dependencies [25,55]. In complex control applications—such as internal combustion engines, chemical processes, or robotic systems—the temporal evolution and influence of previous states are critical for accurately estimating system dynamics. This provides a richer approximation than purely static models or sliding-window approaches.
- Robust learning of nonlinear models: When the system structure is unknown or highly complex (e.g., chaotic behavior in Duffing-type oscillators [27] or synchronization of uncertain systems [22,35]), RNNs can approximate the underlying dynamics without requiring an exact physical model. As a result, RNN-based modeling is increasingly integrated with adaptive or predictive control methods to enhance robustness against disturbances and nonlinearities.
- Predictive control and intelligent feedback: In modern control systems, RNNs have been utilized to develop state observers and real-time model predictive control (MPC) algorithms [7,36]. Similarly, in applications requiring robust closed-loop control—such as inverted rotation [2] or magnetohydrodynamic (MHD) fluid dynamics [16]—recurrent networks learn the underlying dynamics and compensate for modeling errors in real time, significantly reducing sensitivity to parameter uncertainties.
- Regularization strategies and stability considerations: A critical challenge in using RNNs for control is ensuring stability and mitigating issues such as gradient explosion or vanishing gradients. To address this, regularization techniques (e.g., weight decay) and architectures such as LSTM/GRU have been proposed to limit error accumulation over long simulation horizons. These approaches improve numerical convergence and practical implementation in industrial environments with stringent reliability requirements [28,38].
- Integration with global optimization and cybernetics: There is increasing interest in combining RNNs with global optimization algorithms (e.g., Bayesian optimization [10], Differential Evolution) to fine-tune neural architectures and optimize control solutions with multiobjective criteria; see Section 7.3. This has led to the development of self-tuning control systems with high adaptability to regime changes in manufacturing plants and Mining 4.0 applications [3,20].
- Industrial applications: RNNs have demonstrated effectiveness in real-time state estimation for fault detection (e.g., stiction in control valves [3], multifault classification [77]), security in chaotic cryptosystems [5,6], and even fluid-level and flow-rate prediction [25]. In the energy sector, integrating RNNs with robust control strategies can improve the efficiency of solid oxide electrolysis cells (SOEC) [9]. In mining, RNN-based models are emerging as promising tools for optimizing comminution and flotation processes by capturing the multiscale behavior of mineral processing [11,71].
In summary, recurrent neural networks have established themselves as a powerful alternative for capturing and controlling nonlinear systems with historical dependencies, complementing or even replacing complex physical–mathematical models. Their adoption is driven by deep learning capabilities and the increasing availability of distributed computing infrastructure, aligning with paradigms such as Mining 4.0 and Industrial IoT. However, large-scale deployment still requires further research in stability verification and cybersecurity integration given the critical role of these systems in industrial environments.
7.5. Pruning and Growing Techniques for Neural Network Optimization
Structural optimization of neural models is a crucial aspect of deep learning, particularly in industrial applications where computational efficiency and generalization performance must be balanced [17,20]. Two fundamental approaches to structural optimization are pruning (removing redundant components) and growing (progressively increasing network complexity). Below, we outline the main strategies associated with each method:
- Static pruning based on magnitude: This method evaluates the absolute weight of each synapse (or neuron) after training and removes those with the smallest magnitudes. Commonly referred to as magnitude-based pruning, this approach reduces network complexity while maintaining performance levels. Fañanás-Anaya et al. [55] and Arya and Nair [1] highlight that in industrial scenarios with large and noisy datasets, static pruning significantly improves inference time while preserving acceptable accuracy.
- Iterative pruning with weight feedback: This approach alternates between training and pruning over multiple cycles. The process consists of the following steps:
- Training the network until a convergence criterion is met.
- Removing synapses or neurons with weights below an adaptive threshold.
- Retraining the network to reallocate weights and mitigate capacity loss.
The final result is a lightweight model with comparable approximation capabilities to the original. Compared to static pruning, this method allows for a more gradual and robust refinement in highly nonlinear settings. According to Nguyen et al. [2] and Kang et al. [25], iterative pruning is particularly effective for recurrent neural networks (RNNs). - Structural pruning at the channel or block level: In large convolutional networks (CNNs) and deep RNN architectures, pruning can be extended beyond individual weights to entire channels or layers that contribute minimally to the model’s output. This architectural approach, often combined with quantization techniques, facilitates the deployment of models on embedded or low-power systems, which is critical in IoT and industrial applications [34,90].
- Growing strategies (network expansion): Unlike pruning, growing techniques start with small or minimal architectures and progressively add neurons or layers as needed. Common methods include the following:
- –
- Cascade Correlation: A method that sequentially adds hidden neurons to maximize residual correlation with the error [94].
- –
- Growth by sensitivity analysis: An approach that evaluates gradient sensitivity and error propagation to determine when additional capacity is needed [83,95].
The objective is to allow the network to grow until it reaches the optimal complexity for the problem without overfitting. In control and filtering applications for mining and industrial environments, this technique provides flexibility to adapt to sudden changes in plant dynamics [11,35]. - Multiobjective optimization perspective: In industrial applications, neural model optimization often requires balancing accuracy, execution time, and energy consumption while ensuring robustness against disturbances. Consequently, pruning and growing strategies are frequently optimized using multiobjective criteria [10,37]. Techniques such as evolutionary algorithms (genetic algorithms) and Bayesian optimization are commonly applied to determine when to prune nodes or expand layers, seeking an optimal trade-off between computational efficiency and estimation/control performance.
- Applications and limitations: While pruning significantly reduces computational cost, aggressive pruning can impair the network’s ability to capture complex dynamics (e.g., chaotic attractors [6] or multigroup synchronization [22]). A more moderated approach, incorporating dynamic thresholds and weight feedback, provides finer control over the final model. On the other hand, excessive network growth without proper stopping criteria may lead to overfitting and an over-reliance on historical data, requiring rigorous cross-validation techniques [14,15].
In conclusion, the coordinated use of pruning and growing techniques has proven effective in tailoring neural network complexity to industrial problem requirements, optimizing resource utilization while preserving (or even enhancing) generalization capabilities. The key to successful application lies in adapting these mechanisms dynamically, incorporating knowledge of problem structure (nonlinearity, network topology, robustness constraints), and carefully evaluating performance indicators in terms of both accuracy and computational cost.
7.6. Adaptability Statistics and Added Value in Mining
Beyond qualitative analysis, it is useful to quantify the adaptability of these approaches to the mining environment and the value they can provide, addressing the specific needs of this industry. Table 2 presents qualitative assessments based on three main criteria: (1) data requirements (high, medium, low), (2) implementation complexity (considering computational and engineering efforts), and (3) potential value in the mining industry (low, medium, high), weighing the ability to reduce costs, anticipate failures, and improve efficiency.

Table 2.
Qualitative statistics on the adaptability and value of various approaches in the mining industry.
In light of Table 2, several high-level implications emerge:
- Relationship between data requirements and implementation complexity: The mining industry, due to the multiplicity of processes (crushing, grinding, flotation, leaching), often presents partial or noisy data. Therefore, solutions that require lower data density (e.g., [2,5]) may be advantageous. However, when pursuing significant optimization benefits [10,25], it is essential to strengthen data acquisition infrastructure and ensure data quality.
- High return on investment (ROI): Methods such as stiction detection [3] or high-complexity cryptography [5] offer substantial ROI by either minimizing critical failures or preventing cyberattacks. This return is even higher in operations where downtime severely impacts productivity (e.g., unplanned shutdowns in furnaces or flotation cells).
- Scalability and adaptability: The effectiveness of approaches such as MHD with nanofluids [16] or stochastic switching [2] depends on the mining site’s ability to handle specialized fluids or implement switched controllers. While pilots in mid-scale projects serve as a reasonable starting point, large-scale mines could benefit from a progressive deployment in key subsystems.
- Need for academic–industrial collaboration: Studies suggest that co-creating knowledge—focused on machine learning, cybersecurity, and complex fluid analysis—[4,11] would accelerate the adoption of technological solutions. Establishing partnerships between universities, technology providers, and mining operators will reduce the integration gap and strengthen R&D efforts aimed at concrete results.
In summary, the analyzed methodologies offer a wide potential for adjustment to the mining industry, enabling cost reductions in maintenance and production optimization and even strengthening digital security. The critical point lies in balancing investment in data infrastructure with the benefits derived from optimization, creating a robust and sustainable digital ecosystem.
8. Conclusions
8.1. General Overview
The findings presented in this review highlight the necessity of nonlinear approaches—including hybrid models based on machine learning, semi-Markov switching processes, and robust control theory—to address the increasing complexity of industrial processes. In mining, in particular, geological variability, the need for critical failure anticipation, and the growing relevance of cybersecurity make complex dynamics and advanced control methods fundamental for ensuring efficiency, reliability, and optimal resource utilization [2,3,16]. Comparative analyses and adaptability metrics confirm that hybrid techniques—combining artificial intelligence, mathematical modeling, and cybersecurity tools—offer scalable solutions in control, monitoring, and data protection [5,6]. Such integration enables early fault detection (e.g., stiction in valves), energy optimization (use of nanofluids or SOEC cells), and secure data encryption, laying the foundation for an intelligent industrial ecosystem [10,11].
8.2. Key Contributions
- Holistic approach to mining (maturity: high; urgency: medium–high). The convergence of heterogeneous geological resources, nonlinear physicochemical processes, and potential cyberattacks requires an integrated approach—encompassing geomechanics, thermohydrodynamics, and SCADA monitoring—to enhance resilience in critical scenarios [2,7]. While large-scale instrumentation and modeling frameworks exist, further standardization and cross-institutional collaboration are needed for scalability.
- Hybrid techniques (AI + control theory) (maturity: medium–high; urgency: high). Solutions that combine deep learning algorithms (e.g., LSTM–CNN) with ARX models or Bayesian methods have proven effective in noisy and data-intensive industrial environments [10,25]. The urgency of these techniques lies in the current demand for predictive maintenance and dynamic asset planning (mills, flotation cells, pumping systems), offering immediate implementation opportunities.
- Cybersecurity and nonlinear cryptography (maturity: medium; urgency: very high). The rise of memristors, digital twins, and high-complexity encryption schemes enables secure data protection in distributed and IoT networks. Recent studies [5,6] suggest that these strategies significantly increase the difficulty of external attacks, reinforcing information confidentiality and availability. Given the rapid digitalization of industrial operations, its urgency is paramount.
- Thermal management and energy transition (maturity: medium; urgency: medium). The integration of magnetized nanofluids [16] and SOEC modeling [9,23] provides energy optimization benefits aligned with sustainability policies and circular economy principles. Although preliminary successes exist, further research is required to strengthen operational stability and large-scale feasibility.
- Multiscale approaches and Industry 5.0 (maturity: incipient; urgency: medium). The convergence of nonlinear models, big data, and AI facilitates multiscale scenarios (from fracture microscopy to transport logistics), optimizing the efficiency of the value chain. If current research trends continue, Mining 5.0 could evolve into a cyber–physical environment capable of real-time adaptation [4,70], although it is still in its early stages of prototyping and extended validation.
8.3. Recommendations Based on Maturity and Urgency
- Strengthening data infrastructure (maturity: high; urgency: high). Ensuring data quality and standardization [3,5] is a necessary step for enabling AI-based predictive systems. Investing in standardized sensor networks and unified protocols will yield tangible short-term benefits.
- Pilot projects and progressive validation (maturity: medium–high; urgency: high). To facilitate technological transition, proof-of-concept trials in critical subsystems (e.g., crushing or transport) are recommended, with impact evaluation (return on investment, failure reduction, safety) before full-scale adoption [2,10].
- Multidisciplinary collaboration (maturity: high; urgency: medium). Complex problems—such as physicochemical interactions or large-scale simulations—demand the convergence of research centers specialized in nonlinear control, high-performance computing, and geosciences, alongside direct industrial participation [4,11].
- Cybersecurity and digital twins (maturity: medium; urgency: very high). Given the increasing exposure of mining operations to cyberattacks, the adoption of digital twins and advanced encryption architectures [5] should be prioritized. Protecting geological data confidentiality and operational continuity is essential for competitiveness and security.
- Chaos theory and human decision-making (maturity: incipient; urgency: medium). Analyzing the interaction between chaotic dynamics and human intervention in industrial processes—where operator actions can alter nonlinear trajectories—requires interdisciplinary methodologies combining technical and cognitive aspects [8,20]. Although its immediate applicability is limited, its relevance will grow as industrial autonomy increases.
In summary, the integration of nonlinear models and high-level algorithms in mining—and other industrial sectors—advances toward safer, more efficient, and sustainable processes. Areas of highest urgency (e.g., cybersecurity, predictive maintenance, and data robustness) can be addressed in the short term, while proposals with lower maturity (e.g., chaos and human decision-making) require further experimental validation and governmental or institutional support for adoption. These perspectives invite the academic and industrial communities to strengthen joint initiatives that formalize and consolidate the evolution of Mining 5.0 and, more broadly, an intelligent industry aligned with global competitiveness and long-term socioenvironmental commitments.
Funding
The authors gratefully acknowledge the financial support received from the research project through Grant PID2023-150003OB-I00, funded by MICIU/AEI/10.13039/501100011033.
Data Availability Statement
No new data were created in this study. All relevant data are included in the article.
Acknowledgments
The authors express their gratitude to the institutions and funding bodies that supported this research. Special thanks to the Pontificia Universidad Católica de Valparaíso (PUCV) for its continuous academic support, particularly through the Doctorate in Intelligent Industry program.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Arya, N.; Nair, A.G. Cluster regression model for flow control. Phys. Fluids 2024, 36, 113607. [Google Scholar] [CrossRef]
- Nguyen, T.V.A.; Dao, Q.T.; Bui, N.T. Optimized fuzzy logic and sliding mode control for stability and disturbance rejection in rotary inverted pendulum. Sci. Rep. 2024, 14, 31116. [Google Scholar] [CrossRef]
- Guan, A.Q.; Xiang, F.N.; Li, Z.Y.; Liu, C.R.; Lin, Z.H.; Jin, Z.J.; Qian, J.Y. Stiction detection and recurrence analysis for control valves by phase space reconstruction method. Adv. Eng. Inform. 2025, 63, 102949. [Google Scholar] [CrossRef]
- Oei, P.Y.; Brauers, H.; Herpich, P. Lessons from Germany’s hard coal mining phase-out: Policies and transition from 1950 to 2018. Clim. Policy 2020, 20, 963–979. [Google Scholar] [CrossRef]
- Demirkol, A.S.; Sahin, M.E.; Karakaya, B.; Ulutas, H.; Ascoli, A.; Tetzlaff, R. Real time hybrid medical image encryption algorithm combining memristor-based chaos with DNA coding. Chaos Solitons Fractals 2024, 183, 114923. [Google Scholar] [CrossRef]
- Matouk, A.; Botros, M. Hidden chaotic attractors and self-excited chaotic attractors in a novel circuit system via Grünwald–Letnikov, Caputo-Fabrizio and Atangana-Baleanu fractional operators. Alex. Eng. J. 2025, 116, 525–534. [Google Scholar] [CrossRef]
- Chen, T.; Zhang, X.; Wang, C.; Feng, X.; Lv, J.; Deng, J.; You, S.; Chen, X. Identification of nonlinear system model and inverse model based on conditional invertible neural network. Eng. Res. Express 2024, 6, 035228. [Google Scholar] [CrossRef]
- Tan, Y.; Liu, J.; Xie, X.; Tian, E.; Liu, J. Dynamic-Memory Event-Triggered Sliding-Mode Secure Control for Nonlinear Semi-Markov Jump Systems with Stochastic Cyber Attacks. IEEE Trans. Autom. Sci. Eng. 2024, 22, 202–214. [Google Scholar] [CrossRef]
- Zhang, W.; Peng, J.; Luo, Y.; Liu, W.; Westover, T.L.; Casteel, M.J. Optimal Control of SOEC-based Hydrogen Production Systems for Demand Response Using Deep Reinforcement Learning in Smart Grids. IEEE Trans. Energy Convers. 2024, 1–16. [Google Scholar] [CrossRef]
- Flores-Tlacuahuac, A.; Fuentes-Cortés, L.F. A data-driven Bayesian approach for optimal dynamic product transitions. AIChE J. 2024, 70, e18428. [Google Scholar] [CrossRef]
- Ge, Z.; Song, Z.; Ding, S.X.; Huang, B. Data Mining and Analytics in the Process Industry: The Role of Machine Learning. IEEE Access 2017, 5, 20590–20616. [Google Scholar] [CrossRef]
- Slotine, J.J.E.; Li, W. Applied Nonlinear Control; Prentice Hall: Englewood Cliffs, NJ, USA, 1991. [Google Scholar]
- Khalil, H.K. Nonlinear Systems, 3rd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- García, J.; Leiva-Araos, A.; Diaz-Saavedra, E.; Moraga, P.; Pinto, H.; Yepes, V. Relevance of Machine Learning Techniques in Water Infrastructure Integrity and Quality: A Review Powered by Natural Language Processing. Appl. Sci. 2023, 13, 12497. [Google Scholar] [CrossRef]
- Sánchez-Garrido, A.J.; Navarro, I.J.; García, J.; Yepes, V. A systematic literature review on modern methods of construction in building: An integrated approach using machine learning. J. Build. Eng. 2023, 73, 106725. [Google Scholar] [CrossRef]
- Yang, H.; Li, R.; Yang, C. Bio-convection of ternary magnetized nanoparticles thermal conductivity in chemical reaction and activation energy flow with Darcy Forchheimer permeable across a double porous medium. Numer. Heat Transf. Part A Appl. 2024, 1–26. [Google Scholar] [CrossRef]
- Garcia, J.; Villavicencio, G.; Altimiras, F.; Crawford, B.; Soto, R.; Minatogawa, V.; Franco, M.; Martínez-Muñoz, D.; Yepes, V. Machine learning techniques applied to construction: A hybrid bibliometric analysis of advances and future directions. Autom. Constr. 2022, 142, 104532. [Google Scholar] [CrossRef]
- Kwuimy, C.K.; Nana, B.; Woafo, P. Experimental bifurcations and chaos in a modified self-sustained macro electromechanical system. J. Sound Vib. 2010, 329, 3137–3148. [Google Scholar] [CrossRef]
- Liu, D.; Xiao, X.; Li, H.; Wang, W. Historical evolution and benefit–cost explanation of periodical fluctuation in coal mine safety supervision: An evolutionary game analysis framework. Eur. J. Oper. Res. 2015, 243, 974–984. [Google Scholar] [CrossRef]
- Lin, F.C.; Chen, C.S.; Lin, C.J. Adaptive fuzzy observer and control in servo drivers for two-axis drilling machine. Int. J. Adv. Manuf. Technol. 2024, 132, 3105–3122. [Google Scholar] [CrossRef]
- Zhao, Q.; Xu, H.; Tao, L. Unsteady Bioconvection Squeezing Flow in a Horizontal Channel with Chemical Reaction and Magnetic Field Effects. Math. Probl. Eng. 2017, 2017, 2541413. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, C.; Zhang, H.; Ma, P.; Li, X.; Zhang, S. Specified time dual-group synchronization of uncertain complex chaotic systems. Phys. Scr. 2024, 99, 105268. [Google Scholar] [CrossRef]
- Hinkelman, K.; Anbarasu, S.; Wetter, M.; Gautier, A.; Zuo, W. A fast and accurate modeling approach for water and steam thermodynamics with practical applications in district heating system simulation. Energy 2022, 254, 124227. [Google Scholar] [CrossRef]
- Laudani, A.; Lozito, G.; Mancilla-David, F.; Riganti-Fulginei, F.; Salvini, A. An improved method for SRC parameter estimation for the CEC PV module model. Sol. Energy 2015, 120, 525–535. [Google Scholar] [CrossRef]
- Kang, T.; Peng, H.; Peng, X. LSTM-CNN Network-Based State-Dependent ARX Modeling and Predictive Control with Application to Water Tank System. Actuators 2023, 12, 274. [Google Scholar] [CrossRef]
- Xie, N. A summary of grey forecasting models. Grey-Syst.-Theory Appl. 2022, 12, 703–722. [Google Scholar] [CrossRef]
- Adıgüzel, F. Positive semi-definite Lyapunov function-based adaptive control for nonlinear discrete-time systems with application to chaotic Duffing oscillator. Nonlinear Dyn. 2024, 112, 21273–21289. [Google Scholar] [CrossRef]
- Zhu, Q.; Zhang, J.; Zhang, W. Non-Predictive Model-Free Control of Nonlinear Systems with Unknown Input Time Delay. Entropy 2023, 25, 1076. [Google Scholar] [CrossRef]
- Zhao, J.; Yang, G.H. Observer-Based Finite-Time Fuzzy Adaptive Resilient Control for Uncertain Nonlinear Systems Against Deception Attacks and Unknown Dead Zones. IEEE Trans. Autom. Sci. Eng. 2024, 1–11. [Google Scholar] [CrossRef]
- Xue, W.; Zhou, B.; Chen, F.; Taghavifar, H.; Mohammadzadeh, A.; Ghaderpour, E. A Constrained Fuzzy Control for Robotic Systems. IEEE Access 2024, 12, 7298–7309. [Google Scholar] [CrossRef]
- Bai, G.; Meng, Y.; Gu, Q.; Luo, W.; Liu, L. Relative navigation control of articulated vehicle based on LTV-MPC. Int. J. Heavy Veh. Syst. 2021, 28, 34–54. [Google Scholar] [CrossRef]
- Sankar, G.S.; Shekhar, R.C.; Manzie, C.; Sano, T.; Nakada, H. Fast Calibration of a Robust Model Predictive Controller for Diesel Engine Airpath. IEEE Trans. Control Syst. Technol. 2020, 28, 1505–1519. [Google Scholar] [CrossRef]
- Bonfiglio, A.; Cacciacarne, S.; Invernizzi, M.; Lanzarotto, D.; Palmieri, A.; Procopio, R. A Sliding Mode Control Approach for Gas Turbine Power Generators. IEEE Trans. Energy Convers. 2019, 34, 921–932. [Google Scholar] [CrossRef]
- Manikandan, K.P.; Saravanan, A.; Kadirvel, A.; Subramanian, D.V.; Jaganathan, A. Industry 5.0 based on Hybrid and Nonlinear Systems in Robustness. Int. J. Intell. Syst. Appl. Eng. 2024, 12, 223–230. [Google Scholar]
- Zhang, H.; Ding, Z.; Wang, L. Predefined-time multi-switch combination-combination synchronization of fractional-order chaotic systems with time delays. Phys. Scr. 2024, 99, 105223. [Google Scholar] [CrossRef]
- Soleymani, M.; Rahmani, M.; Bigdeli, N. Robust Tube-Based Reference Tracking Nonlinear Model Predictive Control for Wind Turbines. IEEE Trans. Autom. Sci. Eng. 2024, 22, 2854–2866. [Google Scholar] [CrossRef]
- Chakrabarty, A.; Buzzard, G.T.; Zak, S.H. Output-tracking quantized explicit nonlinear model predictive control using multiclass support vector machines. IEEE Trans. Ind. Electron. 2017, 64, 4130–4138. [Google Scholar] [CrossRef]
- Osorio, J.; Santillo, M.; Seeds, J.B.; Jankovic, M.; Ossareh, H.R. A novel Reference Governor approach for constraint management of nonlinear systems. Automatica 2022, 146, 110554. [Google Scholar] [CrossRef]
- Nguyen, S.D.; Vo, H.D.; Seo, T.I. Nonlinear adaptive control based on fuzzy sliding mode technique and fuzzy-based compensator. ISA Trans. 2017, 70, 309–321. [Google Scholar] [CrossRef]
- Lin, C.M.; Le, T.L. WCMAC-based control system design for nonlinear systems using PSO. J. Intell. Fuzzy Syst. 2017, 33, 807–818. [Google Scholar] [CrossRef]
- Aulisa, E.; Burns, J.A.; Gilliam, D.S. Approximate tracking for distributed parameter systems using only sensed data. Syst. Control Lett. 2023, 173, 105477. [Google Scholar] [CrossRef]
- Zou, Z.; Zhao, D.; Liu, X.; Guo, Y.; Guan, C.; Feng, W.; Guo, N. Pole-placement self-tuning control of nonlinear Hammerstein system and its application to pH process control. Chin. J. Chem. Eng. 2015, 23, 1364–1368. [Google Scholar] [CrossRef]
- Gao, C.; Liu, X.P.; Wang, H.Q.; Zhao, N.N.; Wu, L.B. Adaptive neural funnel control for a class of pure-feedback nonlinear systems with event-trigger strategy. Int. J. Syst. Sci. 2020, 51, 2307–2325. [Google Scholar] [CrossRef]
- Fateh, R.; Darif, A.; Safi, S. The influence of Gaussian kernel width on indoor and outdoor radio channels identification from binary output measurements. Int. J. Inf. Commun. Technol. 2023, 23, 327–345. [Google Scholar] [CrossRef]
- Wu, S.; Li, X. Finite-Time Stabilization of Nonlinear Systems with Actuator Saturation. IEEE Trans. Autom. Sci. Eng. 2024, 1–8. [Google Scholar] [CrossRef]
- Nai, Y.; Yang, Q. Adaptive neural output feedback fault tolerant control for a class of uncertain nonlinear systems with intermittent actuator faults. Neurocomputing 2020, 377, 145–158. [Google Scholar] [CrossRef]
- Liu, W.; Lu, J.; Xu, S.; Li, Y.; Zhang, Z. Sampled-data controller design and stability analysis for nonlinear systems with input saturation and disturbances. Appl. Math. Comput. 2019, 360, 14–27. [Google Scholar] [CrossRef]
- Wang, M.X.; Zhu, S.L.; Liu, S.M.; Du, Y.; Han, Y.Q. Design of Adaptive Finite-Time Fault-Tolerant Controller for Stochastic Nonlinear Systems with Multiple Faults. IEEE Trans. Autom. Sci. Eng. 2023, 20, 2492–2502. [Google Scholar] [CrossRef]
- Braun, S.; Albrecht, S.; Lucia, S. Adaptiv robuste, nichtlineare modellprädiktive Regelung mit Angriffsidentifikation. At-Autom. 2022, 70, 367–377. [Google Scholar] [CrossRef]
- Chen, J.; Xie, S.; Meng, W.; Yang, Q. Hierarchy of Quadratic Lyapunov Functions for Linear Time-Varying and Related Systems. J. Guid. Control. Dyn. 2024, 47, 597–608. [Google Scholar] [CrossRef]
- Tao, H.f.; Paszke, W.; Rogers, E.; Gałkowski, K.; Yang, H.z. Modified Newton method based iterative learning control design for discrete nonlinear systems with constraints. Syst. Control Lett. 2018, 118, 35–43. [Google Scholar] [CrossRef]
- Shmerling, A.; Gerdts, M. A Design Methodology for the Seismic Retrofitting of Existing Frame Structures Post-Earthquake Incident Using Nonlinear Control Systems. Buildings 2022, 12, 1886. [Google Scholar] [CrossRef]
- Ajayi, O.; Babahaji, M.; Aghdam, A. A Multi-Spectral Approach to Fuzzy Quantum Modelling of Nonlinear Systems. IEEE J. Radio Freq. Identif. 2021, 5, 254–260. [Google Scholar] [CrossRef]
- Fedor, P.; Perdukova, D.; Bober, P.; Fedor, M. New stable non-vector control structure for induction motor drive. Appl. Sci. 2021, 11, 6518. [Google Scholar] [CrossRef]
- Fañanás-Anaya, J.; López-Nicolás, G.; Sagüés, C. Dynamical system simulation with attention and recurrent neural networks. Neural Comput. Appl. 2024, 37, 2711–2731. [Google Scholar] [CrossRef]
- Morandi, S.; Nimmegeers, P.; Schwind, M.; Di Pretoro, A.; Manenti, F.; Logist, F. A roadmap for in silico development and evaluation of industrial NMPC applications: A practical case study. Comput. Chem. Eng. 2021, 150, 107278. [Google Scholar] [CrossRef]
- Vignesh, D.; Ma, J.; Banerjee, S. Multi-scroll and coexisting attractors in a Hopfield neural network under electromagnetic induction and external stimuli. Neurocomputing 2024, 564, 126961. [Google Scholar] [CrossRef]
- Nguyen, D.H.; Nguyen, N.N.; Ta, T.T.; Yin, G. Chaotic dynamics and zero distribution: Implications and applications in control theory for Yitang Zhang’s Landau Siegel zero theorem. Eur. Phys. J. Plus 2024, 139, 217. [Google Scholar] [CrossRef]
- Tripathi, J.P.; Hasan, M.E.; Ghoshal, S.K. Real-time model inversion control for speed recovery of hydrostatic drive used in the rotary head of a blasthole drilling machine. J. Braz. Soc. Mech. Sci. Eng. 2022, 44, 47. [Google Scholar] [CrossRef]
- Lin, H.; Wang, C.; Cui, L.; Sun, Y.; Zhang, X.; Yao, W. Hyperchaotic Memristive Ring Neural Network and Its Application in Medical Image Encryption. Nonlinear Dyn. 2022, 110, 841–855. [Google Scholar] [CrossRef]
- Silva, S.S.d.; Cardoso, M.; Nardo, L.; Nepomuceno, E.; Hubner, M.; Arias-Garcia, J. A New Chaos-Based PRNG Hardware Architecture Using the HUB Fixed-Point Format. IEEE Trans. Instrum. Meas. 2023, 72, 2001208. [Google Scholar] [CrossRef]
- Fiedler, F.; Karg, B.; Lüken, L.; Brandner, D.; Heinlein, M.; Brabender, F.; Lucia, S. do-mpc: Towards FAIR nonlinear and robust model predictive control. Control Eng. Pract. 2023, 140, 105676. [Google Scholar] [CrossRef]
- Chen, Z.; Xue, W.; Li, N.; Lewis, F.L. Two-loop reinforcement learning algorithm for finite-horizon optimal control of continuous-time affine nonlinear systems. Int. J. Robust Nonlinear Control 2022, 32, 393–420. [Google Scholar] [CrossRef]
- Li, H.; Shi, Y. Event-triggered robust model predictive control of continuous-time nonlinear systems. Automatica 2014, 50, 1507–1513. [Google Scholar] [CrossRef]
- Shenoy, V.; Shenoy, P.; Venkata, S.K. Accurate Liquid Level Measurement with Minimal Error: A Chaotic Observer Approach. Computation 2024, 12, 29. [Google Scholar] [CrossRef]
- Pukach, P.Y.; Kuzio, I.; Nytrebych, Z.; Ilkiv, V. Analytical methods for determining the effect of the dynamic process on the nonlinear flexural vibrations and the strength of compressed shaft. Nauk. Visnyk Natsionalnoho Hirnychoho Universytetu 2017, 5, 69–76. [Google Scholar]
- Ou, T.; Chen, W. On accurate prediction of transfer chute wear using a digital wear sensor and discrete element modelling. Powder Technol. 2022, 407, 117680. [Google Scholar] [CrossRef]
- Pazmiño, R.; Pavon, W.; Armstrong, M.; Simani, S. Performance Evaluation of Fractional Proportional–Integral–Derivative Controllers Tuned by Heuristic Algorithms for Nonlinear Interconnected Tanks. Algorithms 2024, 17, 306. [Google Scholar] [CrossRef]
- Hashemi, R.; Nassar, N.N.; Pereira Almao, P. Nanoparticle technology for heavy oil in-situ upgrading and recovery enhancement: Opportunities and challenges. Appl. Energy 2014, 133, 374–387. [Google Scholar] [CrossRef]
- Jonek-Kowalska, I. Demonstrating the need for a just transition: Socioeconomic diagnosis of polish cities living on hard coal mining. Resour. Policy 2024, 89, 104576. [Google Scholar] [CrossRef]
- Arabi, M.; Gholamian, M.R. Resilient closed-loop supply chain network design considering quality uncertainty: A case study of stone quarries. Resour. Policy 2023, 80, 103290. [Google Scholar] [CrossRef]
- Bao, Q.; Nie, W.; Liu, C.; Zhang, H.; Wang, H.; Jin, H.; Yan, J.; Liu, Q. The preparation of a novel hydrogel based on crosslinked polymers for suppressing coal dusts. J. Clean. Prod. 2020, 249, 119343. [Google Scholar] [CrossRef]
- Zhang, Q.; Chen, W.; Ling, W. Policy optimization of hydrogen energy industry considering government policy preference in China. Sustain. Prod. Consum. 2022, 33, 890–902. [Google Scholar] [CrossRef]
- Crown, W.; Buyukkaramikli, N.; Sir, M.Y.; Thokala, P.; Morton, A.; Marshall, D.A.; Tosh, J.C.; Ijzerman, M.J.; Padula, W.V.; Pasupathy, K.S. Application of Constrained Optimization Methods in Health Services Research: Report 2 of the ISPOR Optimization Methods Emerging Good Practices Task Force. Value Health 2018, 21, 1019–1028. [Google Scholar] [CrossRef]
- Farahbakhsh, J.; Arshadi, F.; Mofidi, Z.; Mohseni-Dargah, M.; Kök, C.; Assefi, M.; Soozanipour, A.; Zargar, M.; Asadnia, M.; Boroumand, Y.; et al. Direct lithium extraction: A new paradigm for lithium production and resource utilization. Desalination 2024, 575, 117249. [Google Scholar] [CrossRef]
- Tapia-Ruiz, N.; Armstrong, A.R.; Alptekin, H.; Amores, M.A.; Au, H.; Barker, J.; Boston, R.; Brant, W.R.; Brittain, J.M.; Chen, Y.; et al. 2021 roadmap for sodium-ion batteries. J. -Phys.-Energy 2021, 3, 031503. [Google Scholar] [CrossRef]
- Yildirim, C.; Franco-Pereira, A.M.; Lillo, R.E. Condition monitoring and multi-fault classification of hydraulic systems using multivariate functional data analysis. Heliyon 2025, 11, e41251. [Google Scholar] [CrossRef]
- Rahimi, A.; Saadat, A. Fault isolation of reaction wheels onboard three-axis controlled in-orbit satellite using ensemble machine learning. Aerosp. Syst. 2020, 3, 119–126. [Google Scholar] [CrossRef]
- Khayyam, H.; Jamali, A.; Bab-Hadiashar, A.; Esch, T.; Ramakrishna, S.; Jalili, M.; Naebe, M. A Novel Hybrid Machine Learning Algorithm for Limited and Big Data Modeling with Application in Industry 4.0. IEEE Access 2020, 8, 111381–111393. [Google Scholar] [CrossRef]
- Li, Y.; Ma, J.; Zhang, Y. Image retrieval from remote sensing big data: A survey. Inf. Fusion 2021, 67, 94–115. [Google Scholar] [CrossRef]
- Zhou, X.; Liang, W.; Wang, K.I.K.; Yang, L.T. Deep Correlation Mining Based on Hierarchical Hybrid Networks for Heterogeneous Big Data Recommendations. IEEE Trans. Comput. Soc. Syst. 2021, 8, 171–178. [Google Scholar] [CrossRef]
- Yang, H.; Alphones, A.; Xiong, Z.; Niyato, D.; Zhao, J.; Wu, K. Artificial-Intelligence-Enabled Intelligent 6G Networks. IEEE Netw. 2020, 34, 272–280. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, L.; Yu, K.; Min, G.; Al-Dubai, A.Y.; Zomaya, A.Y. Machine learning for synergistic network pharmacology: A comprehensive overview. Brief. Bioinform. 2023, 24, bbad120. [Google Scholar] [CrossRef]
- Chen, H.; Xu, B.; Wang, Y.; Li, W.; He, D.; Zhang, Y.; Zhang, X.; Xing, X. Emerging Natural Hemp Seed Proteins and Their Functions for Nutraceutical Applications. Food Sci. Hum. Wellness 2023, 12, 929–941. [Google Scholar] [CrossRef]
- Ravi, K.; Ravi, V. A survey on opinion mining and sentiment analysis: Tasks, approaches and applications. Knowl.-Based Syst. 2015, 89, 14–46. [Google Scholar] [CrossRef]
- Panigrahi, P.K.; Nayak, S. Conjugate gradient with Armijo line search approach to investigate imprecisely defined unconstrained optimisation problem. Int. J. Comput. Sci. Eng. 2024, 27, 458–471. [Google Scholar] [CrossRef]
- Echreshavi, Z.; Farbood, M.; Shasadeghi, M.; Mobayen, S. Reliable fuzzy control of uncertain nonlinear networked systems under actuator faults. ISA Trans. 2023, 141, 157–166. [Google Scholar] [CrossRef] [PubMed]
- Lian, Z.; He, Y.; Shi, P.; Wu, M. A New Filter Design Method for a Class of Fuzzy Systems with Time Delays. IEEE Trans. Syst. Man, Cybern. Syst. 2021, 51, 6477–6487. [Google Scholar] [CrossRef]
- Sun, X.; Zhang, H.; Han, J.; Wang, Y. Non-fragile control for interval type-2 TSK fuzzy logic control systems with time-delay. J. Frankl. Inst. 2017, 354, 7997–8014. [Google Scholar] [CrossRef]
- Zhao, W.; Weyer, E.; Yin, G.; Dong, D.; Zhang, Y.; Shen, T. Adaptive Regulation of Block-Oriented Nonlinear Systems Using Binary Sensors with Applications to Automotive Engine Control. IEEE Trans. Autom. Control 2023, 68, 1369–1382. [Google Scholar] [CrossRef]
- Wang, W.; Mosse, D.; Papadopoulos, A.V. Packet priority assignment for wireless control systems of multiple physical systems. J. Syst. Archit. 2020, 107, 101708. [Google Scholar] [CrossRef]
- Abdul-Aziz, Q.; Hashemi, H.H. Innovating aircraft control systems with the use of artificial intelligence and electronics. Adv. Control Appl. Eng. Ind. Syst. 2022, 4, e111. [Google Scholar] [CrossRef]
- Zinage, V.; Bakolas, E. Neural Koopman Lyapunov control. Neurocomputing 2023, 527, 174–183. [Google Scholar] [CrossRef]
- Zhang, S.; Li, X.; Zong, M.; Zhu, X.; Cheng, D. Learning k for kNN Classification. ACM Trans. Intell. Syst. Technol. 2017, 8, 1–19. [Google Scholar] [CrossRef]
- Hassanzadeh, A.; Safari, M.; Hoang, D.H.; Khoshdast, H.; Albijanic, B.; Kowalczuk, P.B. Technological Assessments on Recent Developments in Fine and Coarse Particle Flotation Systems. Miner. Eng. 2022, 180, 107509. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).