Abstract
Generalized closeness is a recently defined centrality measure. Decay stability, based on generalized closeness, has been previously studied, leading to several conjectures on the decay stability of certain graph classes. In this work, we disprove two of these conjectures by showing that the Cartesian and strong products of paths are not decay stable.
MSC:
05C76; 05C07; 05C12
1. Introduction
Centrality has been an interesting notion in graph theory since its beginnings. A significant increase in interest in centrality measures occurred in the late 1940s and early 1950s in the social sciences [1]. A more interdisciplinary approach emerged in the late 1990s and the early 2000s in the terminology used within the field of Network Science [2]. Since the 2000s, centrality metrics have grown in significance in communication networks, particularly with regard to efficient information transmission, fault tolerance, and vulnerability against attacks (see a recent comprehensive survey for more details [3]).
In ref. [4], closeness, also referred to as closeness centrality, is defined as a measure of centrality of a node within a connected graph or network, expressed as follows:
where represents the distance between two vertices and . Hence, a node’s centrality corresponds to its proximity to all other nodes. For instance, in an information network, closeness serves as an effective metric to estimate the speed at which information travels through a particular node to others. In social network analysis, closeness can identify individuals who are strategically positioned to impact the entire network in the shortest amount of time.
Dangalchev [5] introduces an alternative definition that is applicable to disconnected graphs and facilitates the development of convenient formulas for graph operations. In this work, we focus on simple undirected graphs, which are graphs without multiple edges or loops. In [5], the point closeness of a vertex is defined as follows:
with The closeness of the graph is subsequently defined as follows:
Dangalchev emphasizes that, in contrast to (1), the graph closeness based on (2) can also be used for disconnected graphs because if , then
As discussed in [6], numerous graph-theoretic parameters depend on distance, including vertex and edge betweenness, average vertex and edge betweenness, normalized average vertex and edge betweenness, closeness, and vertex residual closeness. The primary objective of closeness and residual closeness is to assess the vulnerability of a graph, even when actions result in its disconnection. It has been demonstrated in [5,7] that residual closeness serves as a more sensitive measure of vulnerability compared to other established metrics. The closeness of various graph classes has been explored in [5,8,9]. Several noteworthy results regarding the closeness of graph transformations—specifically in relation to vertex residual closeness, normalized vertex residual closeness, and closeness centrality—have been presented in [6,10].
The base in the definition of closeness (2) can be substituted with any constant , resulting in a generalized definition of closeness as
Closeness centrality seems to be a very natural concept, as it has been reinvented and studied independently under different names several times.
For example, Tsakas [11] studied decay centrality, the notion equivalent to generalized closeness (3). He demonstrated a strong connection between decay centrality and two widely studied, computationally simpler measures: degree centrality and closeness centrality. Among other things, he observed that, for sufficiently low values of , the nodes that maximize (3) are those of maximal degree, and on the other hand, for sufficiently large , the nodes that maximize closeness also maximize decay centrality (3).
We would like to highlight that the definition of generalized closeness was also presented in [12], where the author introduces the study of generalized closeness. Among other observations, it is argued that selecting the appropriate base for closeness depends on the characteristics of the network being investigated. Consequently, considering closeness with an arbitrary base could lead to several intriguing research questions. We wish to note that, also, as observed in [13], we clearly have , where H is the Hosoya–Wiener polynomial [14,15], a well-known notion in mathematical chemistry.
The rest of this paper is organized as follows. In Section 2, we discuss generalized closeness in relation to distance degree sequences and define a new relation on the set of nodes. Using this relation, we derive a criterion for decay-stable graphs (Theorems 1 and 2). In Section 3, we study the decay stability of two graph structures, Cartesian products of paths, and strong products of paths. Two conjectures of [16] are disproved by providing counter-examples. In the last section, ideas for future work are given. In particular, we briefly comment on another conjecture of [16], which is likely correct.
2. Decay-Stability
Let . The centrality index defines the ranking of G in the following way [16]: if is a permutation of such that
is a non-increasing sequence, then -ranking of G is
Distinct overlined blocks contain distinct values of index (in decreasing order), and the values within a block are the same. Of course, this ranking of the index depends on .
The generalized closeness of a vertex v is a polynomial of degree (eccentricity), and its coefficients are equal to terms of the distance degree sequence , the sequence , where is the number of vertices of the distance i from the vertex v. Obviously, , , and
Taking polynomials for all , their roots in are called decay thresholds of G. Graphs where the ranking does not change for different values of are called decay-stable graphs. Otherwise, we call the graph decay-unstable. In the following sections, we are interested in graphs that are decay-stable.
Proposition 1.
Let and , . If for each j, , it holds that
then, for any
If there exists j such that , then .
Proof.
It is observed that (4) implies . First, we assume that . From equality (4) and using , we obtain
Also, we note that, for any , , which implies that
and the equality holds exactly when for all i. Hence,
as needed. Finally, if for some j, then, in case , the sum above is strictly positive. Hence, .
In the remaining case, , we have
using Inequality (5). This completes the proof. □
In Proposition 1, we recalled the results of Proposition 2.2. from [16], but we wish to note, however, that the last part of the proof in [16] is false, although the claim is correct. For example, in the graph from Figure 1, we have and . Although , , and , the distance degree sequences for the vertices 2 and 3 have the same length, . The authors in [16] erroneously claimed that, in this case, .
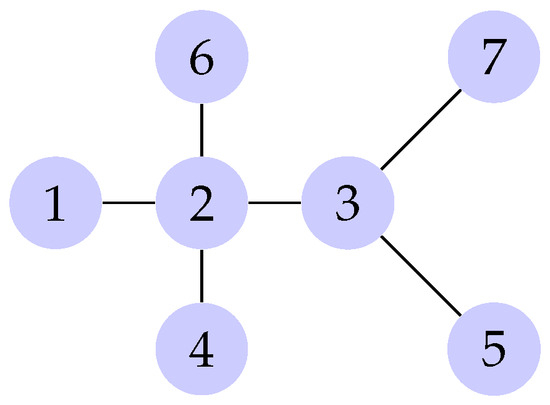
Figure 1.
An example of a tree with vertices, numbers on vertices are random.
We now define a new relation on the set of vertices :
Definition 1.
Let , and . Then, whenever Inequality (4) holds for all .
It is obvious that this relation is reflexive, antisymmetric, and transitive, so it defines a partial order on the set .
Recall that a partial order ⪰ defines a linear (total) order if for each or holds.
Theorem 1.
A graph G is decay-stable if and only if the relation ⪰ defines a linear (total) order on the set .
Proof.
First, we assume that graph G is decay-stable. Then, for all and for all . Thus, either for all , or for all . That means or .
Conversely, let ⪰ define a linear order on . Then, for each or . Let . Then, Inequality (4) holds for each , where . Following Proposition 1, then, for all , It follows that G is decay-stable. □
The immediate corollary to the last theorem is the following, already observed in [16].
Corollary 1
([16]). Any distance-degree regular graph is decay-stable.
The next result is more general. As we find the statement quite important, we state it as a theorem.
Theorem 2.
Let . If for two vertices , we have
then G is decay-unstable.
Proof.
Let and , and , . From , we have , and hence,
On the other hand, as ,
Therefore, neither nor , and through Theorem 1, G is not decay-stable. □
3. Decay Stability of Products of Paths
We now discuss two conjectures of [16] on the decay stability of certain graphs, namely Cartesian and strong products of paths. The following was previously proven.
Theorem 3
([16]). If graph G is decay-stable, then, for any positive integer n, the Cartesian product is also decay-stable.
Corollary 2
([16]). All graphs of diameter 2 are decay-stable, and all regular graphs of diameter 3 are decay-stable.
In [16], the following two conjectures were also given.
Conjecture 1
([16]). For all positive integers , the l-dimensional grid is decay-stable.
Conjecture 2
([16]). The strong product is decay-stable for all positive integers k and l.
Here, we provide counter-examples to both conjectures.
Definition 2.
The Cartesian product of two graphs is defined as a graph with vertex set , where two vertices and are adjacent precisely if and , or and .
Recall that the l-dimensional grid is Cartesian product of paths .
For a path and its vertices and , , it is obvious that
a sequence of length , where number 2 occurs exactly -times (never in the case of ). Thus,
It is obvious that the path is decay-stable since, from Definition 1 and Theorem 1, it follows that for its vertices , we have a linear order
The next two examples prove that Conjecture 1 is wrong.
Example 1.
Take a grid and its vertices and . Then,
Observe that , but . Thus, neither nor . Hence, the Cartesian product of two paths is decay-unstable.
Example 2.
Take a grid and its vertices and . Then,
and, obviously, the Cartesian product is decay-unstable.
On the positive side, we can show that is decay-stable for any It is obvious that, for the vertices on the corners, , or , as shown in the following:
which is a sequence of length k, where number 2 occurs exactly -times. For the vertices , we have
where number 2 occurs exactly -times. For a typical vertex inside the grid, given by or the distance degree sequence is the following:
Here, the number 4 appears exactly -times. The number 3 appears at position j either once or not at all, in the special case where k is odd and . The same condition applies to the number 1, which appears at the end of the sequence. The number 2 appears exactly -times. Thus, for odd k, we have a linear order
Similarly, for even k, we have
It is not hard to see that Cartesian products and are decay-stable. Summarizing the observations and the examples above, we can write the following proposition.
Proposition 2.
The Cartesian product of two paths , , is decay-unstable.
Definition 3.
In the strong product of graphs, , two distinct vertices and , are adjacent if and only if: and v is adjacent to , or and u is adjacent to , or u is adjacent to and v is adjacent to .
Similarly to the above discussion about Cartesian products, we can prove the following statement.
Proposition 3.
The strong product of two paths , , is decay-unstable.
It is obvious that the strong products , , and are decay-stable.
Example 3.
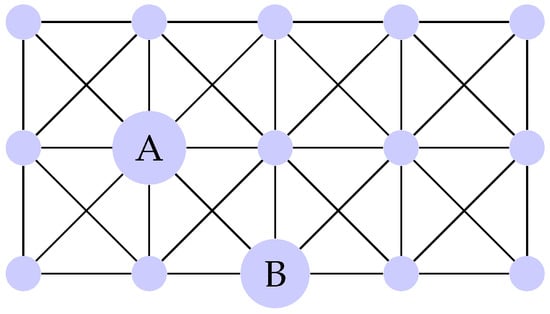

Figure 2.
Graph , with vertices A and B from Example 3.
4. Conclusions and Future Work
In this paper, we have shown that two conjectures stated in [16] are not valid by providing several examples. On the positive side, we prove that the conjecture holds for an infinite set of Cartesian products. Thus, it may be an interesting research task to characterize the subsets of decay stable Cartesian and strong products of paths.
The authors of our main reference also put forward another conjecture
Conjecture 3
([16]). Almost all trees are not decay-stable.
In our opinion, this is likely to be true. We only briefly explain the main ideas here. However, a formal proof with all details does not seem to be simple, and we leave it as a challenge for future work.
In short, the main idea of a possible proof of conjecture for random recursive trees (RRTs) is as follows. Theorem 2 implies that, on decay-stable trees, the degrees of vertices must form a non-increasing sequence from the center (or centers) to the leaves. As this is a strong condition that is probably not valid for the majority of trees, this alone provides some evidence that Conjecture 3 is true. However, a formal proof that almost all trees are not decay-stable is perhaps not trivial. In particular, it depends on the model of random trees chosen.
Recall that Eslava [17] proves that, in RRT, the distributions of the depths of the vertices that attain the maximum degree are asymptotically normal and independent. Furthermore, the number of such vertices converges to a mixture of Poisson random variables conditioned to be strictly positive. Here, the depth is the distance from the root, that is, any vertex from which the tree generation starts. So, in the case where the root is, at the same time, the center, the observation implies, with high probability, that there exists a vertex of large degree that is not a center; hence, the conjecture may follow.
One of the reviewers has asked some interesting questions that, in our opinion, open challenging avenues of future research.
The method for identifying decay-stable trees presented here is computationally efficient. Clearly, we only need to compute all distances in the graph, for example, by n breadth-first searches, and then compare the pairs of distance degree sequences; hence, the time needed is, at most, . (It is not clear how efficient methods were used for testing decay stability in previous work; ref. [16] just reported that they used the Maple computer algebra system.) However, it is not obvious how we should efficiently generate decay-stable graphs. Even an algorithm for the construction of all decay-stable trees is not known. Challenge: An algorithm for the construction of decay-stable graphs (trees) should be designed.
We have given examples of Cartesian and strong products that are not decay-stable. On the other hand, the majority of such products may be decay-stable. Challenge: the decay-stable (Cartesian or strong) products should be characterized.
Finally, for decay-unstable graphs, it is interesting to know if there is a critical range for the parameter where decay stability changes most abruptly. Can it be seen from certain properties of the partial order relation defined in this paper?
Author Contributions
Conceptualization, D.R.P. and J.Ž.; Methodology, D.R.P. and J.Ž.; Writing—original draft, D.R.P. and J.Ž.; Writing—review & editing, D.R.P. and J.Ž. All authors have read and agreed to the published version of the manuscript.
Funding
The research was partially funded by the Slovenian Research and Innovation Agency (ARIS) through project P2-0248 and through the annual work program of Rudolfovo.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
The authors wish to sincerely thank the two anonymous reviewers for their careful reading of the manuscript and their constructive comments.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Katz, L. A new status index derived from sociometric analysis. Psychometrika 1953, 18, 39–43. [Google Scholar] [CrossRef]
- NRC. Network Science; The National Academies Press: Washington, DC, USA, 2005; Available online: https://www.nap.edu/catalog/11516/network-science (accessed on 4 November 2024).
- Wan, Z.; Mahajan, Y.; Kang, B.W.; Moore, T.J.; Cho, J.H. A Survey on Centrality Metrics and Their Network Resilience Analysis. IEEE Access 2021, 9, 104773–104819. [Google Scholar] [CrossRef]
- Latora, V.; Marchiori, M. Efficient behavior of small-world networks. Phys. Rev. Lett. 2001, 87, 198701. [Google Scholar] [CrossRef] [PubMed]
- Dangalchev, C. Residual closeness in networks. Physica A 2006, 365, 556–564. [Google Scholar] [CrossRef]
- Turacı, T.; Ökten, M. Vulnerability of Mycielski Graphs via Residual Closeness. Ars Comb. 2015, 118, 419–427. [Google Scholar]
- Aytaç, A.; Odabaş, Z.N. Residual Closeness of Wheels and Related Networks. Int. J. Found. Comput. Sci. 2011, 22, 1229–1240. [Google Scholar] [CrossRef]
- Dangalchev, C. Residual Closeness of Generalized Thorn Graphs. Fundam. Inform. 2018, 162, 1–15. [Google Scholar] [CrossRef]
- Odabaş, Z.N.; Aytaç, A. Residual Closeness in Cycles and Related Networks. Fundam. Inform. 2013, 124, 297–307. [Google Scholar] [CrossRef]
- Turacı, T.; Aytaç, V. Residual Closeness Of Splitting Networks. Ars Comb. 2017, 130, 17–27. [Google Scholar]
- Tsakas, N. On Decay Centrality. 4 January 2017. Available online: https://ssrn.com/abstract=2767012 (accessed on 20 December 2024).
- Dangalchev, C. Residual Closeness and Generalized Closeness. Int. J. Found. Comput. Sci. 2011, 22, 1939–1948. [Google Scholar] [CrossRef]
- Rupnik Poklukar, D.; Žerovnik, J. Reliability Hosoya-Wiener Polynomial of Double Weighted Trees. Fundam. Inform. 2016, 147, 447–456. [Google Scholar] [CrossRef]
- Hosoya, H. On some counting polynomials in chemistry. Discret. Appl. Math. 1988, 19, 239–257. [Google Scholar] [CrossRef]
- Sagan, B.E.; Yeh, Y.-N.; Zhang, P. The Wiener polynomial of a graph. Int. J. Quantum Chem. 1996, 60, 959–969. [Google Scholar] [CrossRef]
- Coroničova Hurajova, J.; Gago, S.; Madaras, T. On decay centrality in graphs. Math. Scand. 2018, 123, 39–50. [Google Scholar] [CrossRef]
- Eslava, L. Depth of vertices with high degree in random recursive trees. ALEA Lat. Am. J. Probab. Math. Stat. 2022, 19, 839–857. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).