1. Introduction
Initial–boundary-value problems for pseudoparabolic equations, also known as Sobolev-type equations [
1], characterized by the presence of mixed space and time derivatives in the highest-order terms, are widely studied in the literature due to their significant applications. For instance, they can be found in the multiphase flow problem in porous media [
2], filtration [
3], electrical conduction phenomenon in heterogeneous media [
4], two-phase porous media flows, homogeneous fluid flow in fissured rocks and the transport problems of humidity in soil [
5,
6], heat or mass transfer in a stably stratified turbulent shear flow [
7], heat transfer in a heterogeneous medium or moisture transport in soils [
8], solvent uptake in polymeric solids [
9], etc. The pseudoparabolic Benjamin–Bona–Mahony equation is applicable to the study of long waves and shallow water waves, as well as drift waves in plasma or the Rossby waves in rotating fluids. Let us note that Schrödinger-type equations can describe the propagation of optical waves that include amplification, deformation, and prolongation; see, e.g., [
10].
The well-posedness of a one-dimensional (1D) pseudoparabolic model is proved in [
7] and the qualitative solutions behavior is also investigated. Some qualitative properties, especially the long-term dynamics of the solutions of a 1D pseudoparabolic equation, are studied in [
9]. In [
11], authors investigate solutions of a pseudoparabolic model over the halfstrip with two types of boundary conditions. The existence, uniqueness, and regularity of the solution is discussed in [
12] for a pseidoparabolic problem. In [
13], the authors consider a class of pseudoparabolic problems with integral boundary conditions. Using energy inequality, they prove the existence, uniqueness, and stability of the solution. The authors of [
14] prove the local existence and uniqueness of a weak solutions of a fractional pseudoparabolic equation with singular potential. The comparison principle and new existence and nonexistence results for solutions of a nonlinear source initial–boundary-value problem for the generalized Boussinesque equation are established in [
15].
The well-posedness for two pseudo-parabolic problems, connected by transmission condition through interfaces, is established in [
4]. A local existence and uniqueness of a weak solution of a system of pseudoparabolic equations with Robin–Dirichlet conditions is proved in [
16]. The weak solvability of a nonlinearly coupled system of parabolic and pseudoparabolic equations is discussed in [
17].
Pseudoparabolic models are investigated numerically, for example in [
2,
5,
6,
8,
18]. Two-dimensional (2D) nonlinear pseudoparabolic equations with Dirichlet boundary conditions are approximated by spectral schemes in space and robust schemes in time. A three-layer finite-difference scheme and a higher-order difference method for an initial–boundary-value problem for a 1D pseudoparabolic equation with time delay in the second spatial derivative, is constructed in [
5,
6]. An implicit finite-difference scheme for a third-order linear pseudoparabolic equation with nonlocal integral conditions is investigated in [
18]. A two-grid finite-element method is presented in [
19] to solve 2D nonlinear pseudoparabolic integro-differential equations. Differential and difference boundary-value problems for a third-order pseudoparabolic equation with variable coefficients and Caputo fractional derivative is studied in [
8]. The authors establish results for uniqueness of the solution and stability regarding to the initial data and the right-hand side, as well as the convergence of the discrete solution to the exact one. A three-layer alternating-direction implicit scheme is studied in [
20], for solving a nonlocal boundary-value problem for a 2D pseudoparabolic equation.
The solution of inverse problems is crucial in physics and engineering, as it enables the reconstruction of parameters, coefficients, source terms, boundary conditions, and initial data essential for system analysis and optimization. For instance, determining the filtration parameters, in solving environmental monitoring problems, in thermal engineering, identifying heat fluxes helps prevent overheating, while in material science, determining stress distributions ensures structural integrity. These solutions provide valuable insights into system behavior that are often unattainable through direct measurements alone or for quantities that cannot be directly measured; see, e.g., [
21,
22,
23,
24].
Inverse problems are ill-posed and it is challenging to solve them even numerically [
24,
25,
26,
27,
28,
29].
Inverse problems for parabolic diffusion, sub-diffusion, and similar classes of equations have been extensively investigated. In contrast, inverse problems for pseudoparabolic equations and their fractional counterparts have received comparatively less attention. Notable contributions in this area include a concise review presented in [
30], which outlines key developments and provides results on the existence and uniqueness of solutions for time-fractional pseudoparabolic equations. For additional foundational studies, see, for example [
9,
22,
31,
32,
33,
34,
35,
36].
The solvability of the inverse problem of finding a solution and a time-dependent coefficient in a pseudohyperbolic equation known as the Klein–Gordon equation for given integral overspecified data is studied in [
37]. The existence, uniqueness, and regularity of the solution of the inverse problem for recovering the diffusion and the leading coefficient in 2D and multi-dimensional linear pseudoparabolic equations of filtration are investigated in [
35,
36]. The results for the existence, uniqueness, stability of a strong generalized solution and a numerical investigation of the inverse problem for recovering space-dependent source terms in pseudoparabolic equations with memory is proposed in [
31]. In [
22], the Galerkin method is applied to prove the existence of the solution for the inverse coefficient problem for a third-order pseudoparabolic equation. A finite-difference method is also developed to solve the problem numerically. An inverse problem for identifying the space-dependent coefficient of the source term in a pseudoparabolic equation is studied in [
32]. The authors prove the unique solvability of the problem and the stability of the solutions. The inverse problem is solved, utilizing cubic B-spline functions and reformulating the problem as a nonlinear least-squares optimization of the Tikhonov regularization functional. The existence and uniqueness of the solution and an implicit finite-difference scheme are constructed in [
38] to solve an inverse source quasi-linear pseudoparabolic problem with periodic boundary conditions. In [
39], the authors consider an inverse problem for determining an unknown time-dependent potential coefficient in a linear pseudoparabolic equation. They prove the uniqueness and the Lipschitz conditional stability of the problem and develop an iterative algorithm to solve it. Inverse problems for a time-fractional pseudoparabolic equations are studied in [
30,
40]. The results for the existence and uniqueness of the solution are provided.
Boundary-condition-identification inverse problems for parabolic equations are solved in many papers. The semigroup approach is proposed in [
41] to investigate the inverse problems with unknown boundary condition in a linear parabolic equation. The uniqueness and stability results for a parabolic-boundary-condition inverse problem with an overdetermined value of the solution at a fixed point on the boundary are derived in [
42]. An implicit finite-difference scheme and a decomposition method to solve the boundary-condition inverse problem is used in [
43].
In [
44], an inverse problem for identifying Dirichlet conditions in 2D heat equations on disjoint rectangles is solved numerically. The results for the well-posedness of the direct and the inverse problems are established. The numerical approach is based on the reduction of the 2D inverse problem to a direct-heat 1D one, using integral observation and interface conditions. The existence and uniqueness of the solution of an inverse problem for the determination of the time-dependent coefficient in the boundary source for Caputo time-fractional diffusion equation is studied in [
45]. To solve the problem, a meshless method based on radial basis functions is developed. The inverse problem of the identification of non-linear boundary conditions for the time-fractional diffusion equation is solved in [
46]. The existence and uniqueness of the restored function is discussed. For the numerical solution of the problem, a regularization technique is applied.
Studies that investigate inverse problems for identifying boundary conditions for pseudoparabolic equation are limited. The solvability of the inverse problems for identifying the time-dependent boundary coefficient in a Dirichlet and Robins boundary condition from integral observation is investigated in [
33]. The existence and uniqueness results for a time-dependent boundary-coefficient inverse problem in a 2D pseudoparabolic equation from integral observation are obtained in [
34]. In [
47] is considered an inverse problem for recovering the time-dependent boundary condition in a 2D linear pseudoparabolic equation with Dirichlet–Neumann boundary conditions, from integral measurements. The well-posedness of the direct and inverse problems is discussed. By reformulating the inverse problem as a 1D direct problem and applying a substitution to address the resulting nonlocality, a numerical approach is developed. In contrast to the present study, in [
47] a different equation is considered—with constant coefficients and a pseudoparabolic part (a mixed third-order derivative) with respect to the time variable and only with respect to one of the spatial variables. Moreover, the Dirichlet boundary condition is reconstructed and the integral measurements are in the whole domain. The nature of this problem allows for its reduction to the 1D case. Consequently, the approach for solving the boundary-identification inverse problem in [
47] is completely different from those developed in the present investigation.
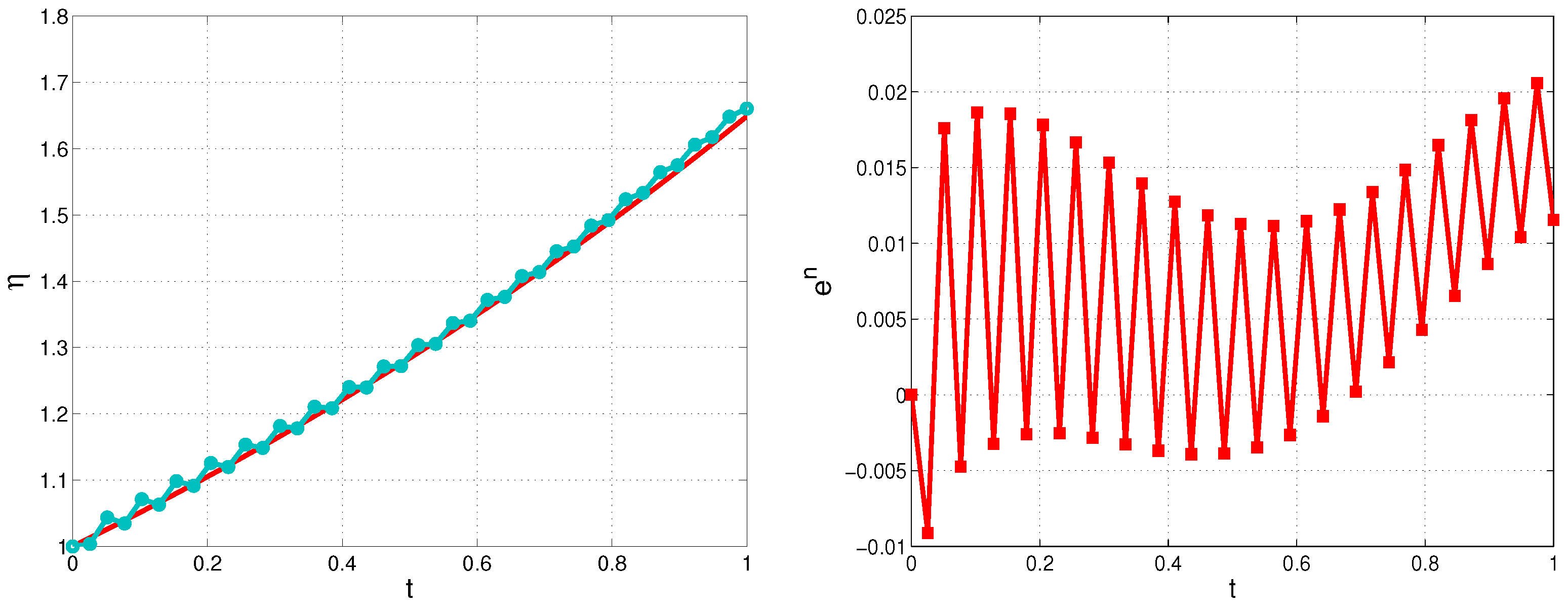
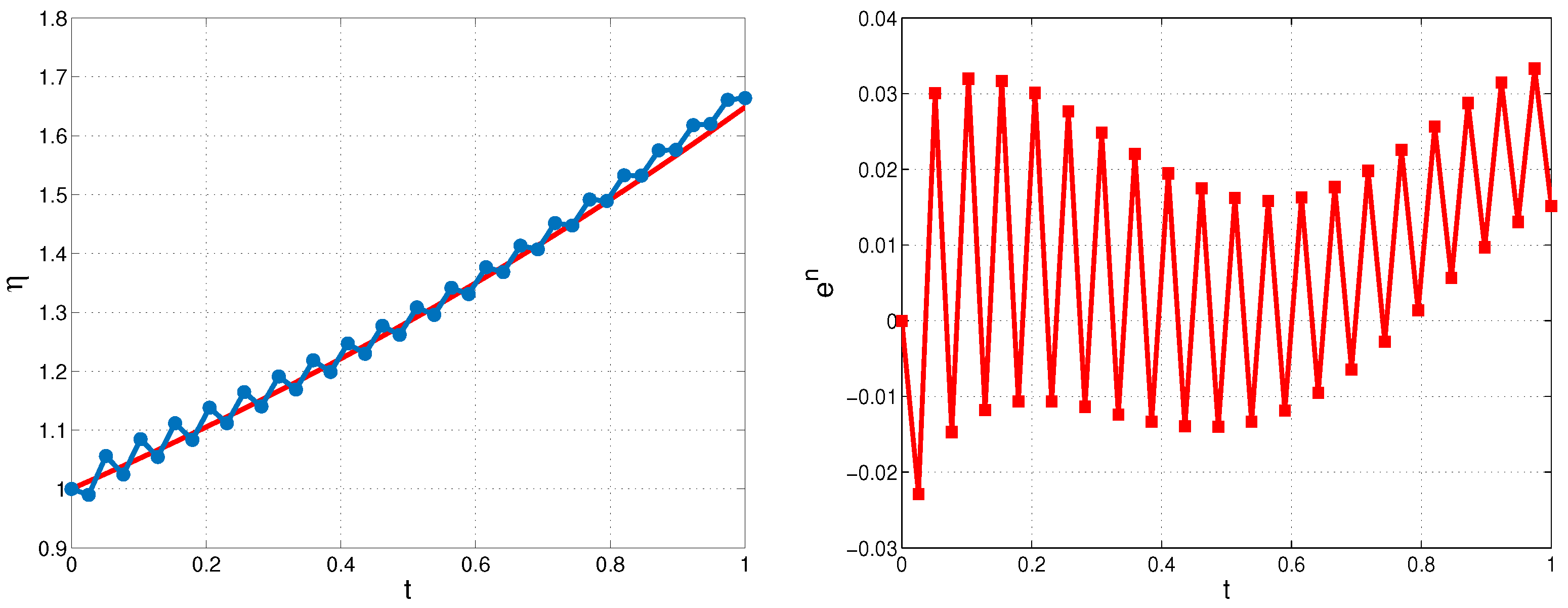
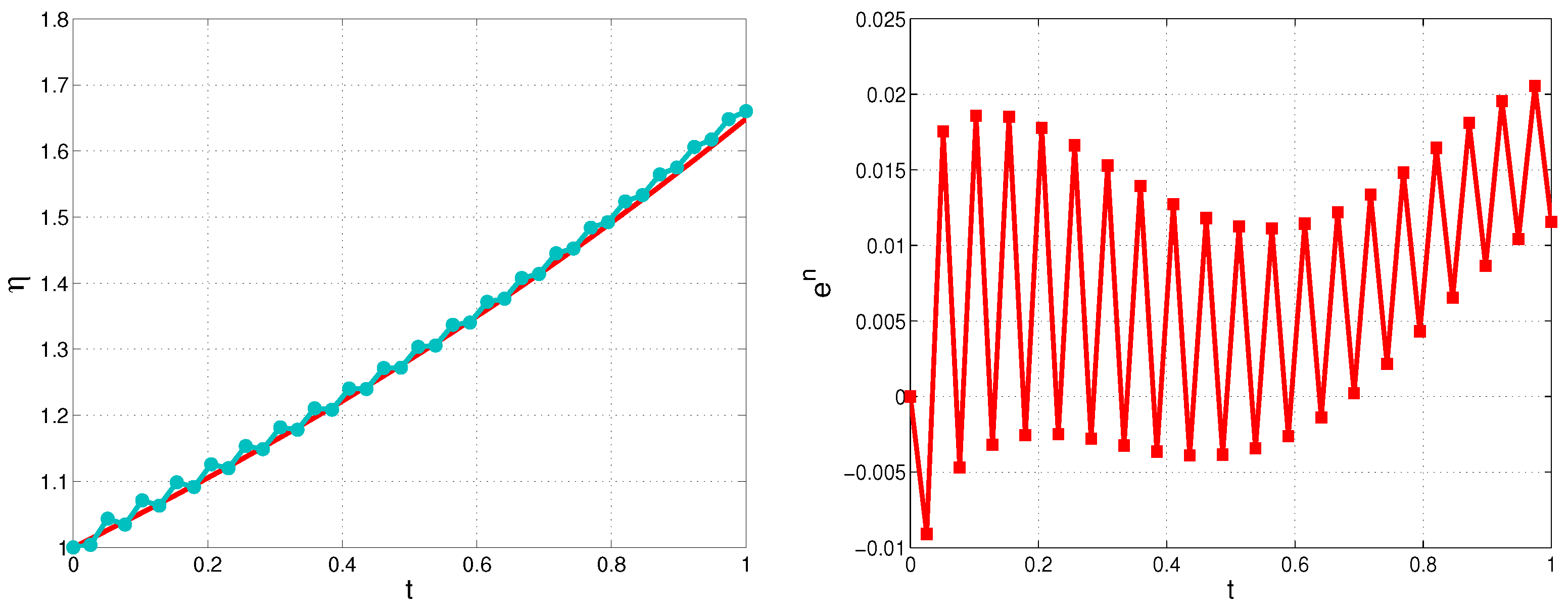
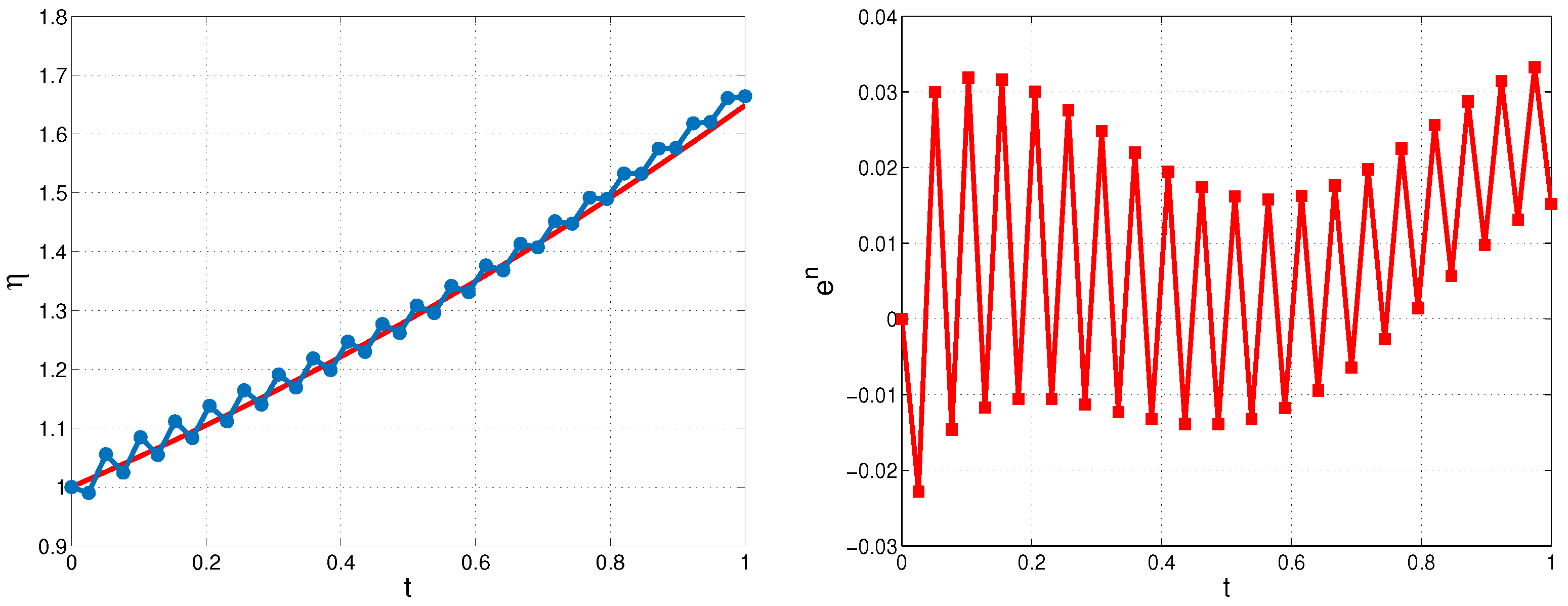
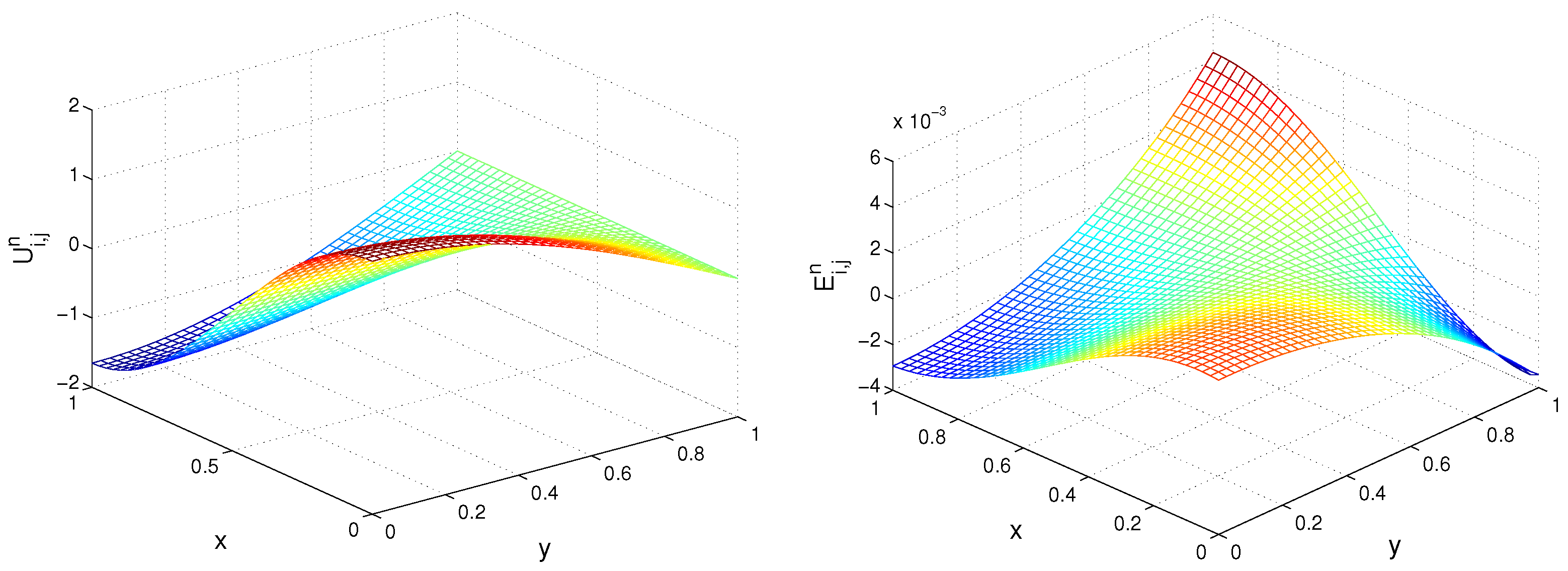
This study investigates the numerical solution of an inverse problem for a variable-coefficient pseudoparabolic equation, with a particular emphasis on reconstructing the boundary flux from integral solution measurements on the same boundary. The measured concentration of a substance’s filtration on a specified portion of the domain boundary, coupled with the corresponding medium properties, serves as supplementary information to facilitate the solution of the inverse problem.
We develop a new approach to reformulate ill-posed inverse problem to a well-posed but nonlocal direct one, and then we construct a fully implicit second order in space finite-difference approximation to solve the problem.
The remaining part of this paper is organized as follows. In the next section, we formulate direct and inverse problems. In
Section 3, we establish the well-posedness of the direct problem. The reformulation of the inverse problem as a direct one is described in
Section 4. Numerical methods for solving direct and inverse problems are developed in
Section 5. The results from numerical test examples are proposed and discussed in
Section 6. The paper is finalized with some concluding remarks.
2. The Direct and Inverse Problems
In this section, we introduce direct and inverse problems for a two-dimensional pseudoparabolic equation.
Let
,
,
and
, where
a,
b and
T are positive real numbers. We consider the pseudoparabolic equation for unknown function
,
with the initial and boundary conditions:
where
,
c,
r are given smooth functions of their arguments and
where
,
,
,
,
,
are positive constants.
The boundary condition (
4) represents a flux across the boundary
. In this context,
denotes the material’s conductivity at the boundary, and
signifies an external source or sink affecting the system at the boundary. The term
corresponds to the gradient of the state variable
u in the
y-direction at the boundary, representing the standard diffusive flux. The additional term
introduces a time-dependent component to the flux, characteristic of pseudoparabolic equations. This term accounts for memory effects or hereditary properties in the medium, indicating that the flux at a given time depends not only on the current state but also on the rate of change in the state over time, see e.g., [
16] and reference therein.
Thus, we will call the formulated problem (
1)–(
4) the direct problem.
In the inverse problem, the pair
is unknown. We consider
in the form
where the function
is known, while
, the time-dependent amplitude of the heat flux, must to be determined from the nonlocal inversion input
The function represents the average temperature with weight w on the upper boundary of the rectangle .
The following typical physical examples for the weighted function are very common:
•
Integral observation (IO). When
then
is the average temperature at time
t in the interval
.
• Point observation (PO). If , is the Dirac-delta function, then is the temperature at the point .