Ricci Semi-Symmetric Robertson–Walker Spacetime in f(R)-Gravity

Abstract

We investigated the properties of Ricci semi-symmetric Robertson–Walker spacetimes within the framework of $f(\mathcal{R})$-gravity theory. Initially, we established that Ricci semi-symmetric Robertson–Walker spacetimes are locally isometric to either Minkowski or de Sitter spacetimes. We then focused on the 4-dimensional formulation of these spacetimes in $f(\mathcal{R})$-gravity, deriving expressions for the isotropic pressure p and energy density $\sigma$. To further develop our understanding, we explored various energy conditions to constrain the functional form of $f(\mathcal{R})$. We analyzed several models, namely $f(\mathcal{R})=\mathcal{R}-\alpha (1-e^{-{\displaystyle \frac{\mathcal{R}}{\alpha }}})$, $f(\mathcal{R})=\mathcal{R}-\beta tanh\mathcal{R}$, and $f(\mathcal{R})=\mathcal{R}-log(m\mathcal{R})$, where $\alpha$, $\beta$, and m are constants. Our findings suggest that the equations of state parameters for these models are compatible with the universe’s accelerating expansion, indicating an equation of state parameter $\omega =-1$. Moreover, while these models satisfy the null, weak, and dominant energy conditions reflective of the observed accelerated expansion, our analysis reveals that they violate the strong energy condition.

1. Introduction

The geometry of generalized Robertson–Walker (GRW) spacetimes has emerged as a vital and dynamic area of research, bridging the fields of mathematics and theoretical physics. A GRW spacetime is characterized as a warped product manifold, where its foundational structure comprises a one-dimensional base manifold. In cosmological physics, the Friedmann–Lemaitre–Robertson–Walker (FLRW) metrics serve as elementary models for describing the expansion of the universe, acknowledging the pioneering contributions of several scientists in the evolution of modern cosmological theories. Recent advances in the study of Lorentzian manifolds have unveiled numerous intriguing decomposition theorems that deepen our understanding of spacetime geometry. Notably, in [1], a groundbreaking decomposition of Lorentzian manifolds was introduced, demonstrating a novel connection between their geometric properties and the foundational principles of General Relativity. This work significantly enhances our understanding of how Lorentzian manifolds relate to the more specialized FLRW spacetimes, revealing the potential for these structures to inform our understanding of cosmic evolution. A Lorentzian manifold can be modeled as a GRW spacetime if it satisfies a specific criterion: the presence of a time-like concircular vector field. However, this condition is relaxed when an additional condition [2] is taken into account, thus permitting a wider range of spacetime geometries to be classified as GRW. Specifically, a Lorentzian manifold M attains the GRW spacetime if it possesses a unit time-like torse-forming vector field $u^{♯b}$, which serves as an eigenvector of the Ricci tensor ${\mathrm{Ric}}_{ab}$. In the presence of a unit time-like torse-forming vector field, it suggests the existence of a scalar function $\phi$ on M such that

$$\begin{array}{c}\hfill {\nabla }_a{u}_b^{♯}=\phi (g_{ab}+u_a^{♯}{u}_b^{♯}),u^{♯a}{u}_a^{♯}=-1.\end{array}$$

(1)

In [3], it has been shown that the Ricci tensor of a GRW spacetime is characterized by

$$\begin{array}{c}\hfill {\mathrm{Ric}}_{ab}={\displaystyle \frac{\mathcal{R}-\psi }{n-1}}{g}_{ab}+{\displaystyle \frac{\mathcal{R}-n\psi }{n-1}}{u}_a^{♯}{u}_b^{♯}+(n-2)u^{♯k}{u}^{♯l}{\mathcal{C}}_{kabl},\end{array}$$

where ${\mathcal{C}}_{kabl}$ is the Weyl conformal curvature tensor and $\mathcal{R}$ is the scalar curvature. A conformally flat GRW spacetime is known as classical Robertson–Walker (RW) spacetime, allowing the Ricci curvature form to change as follows:

$$\begin{array}{c}\hfill {\mathrm{Ric}}_{ab}={\displaystyle \frac{\mathcal{R}-\psi }{n-1}}{g}_{ab}+{\displaystyle \frac{\mathcal{R}-n\psi }{n-1}}{u}_a^{♯}{u}_b^{♯}.\end{array}$$

(2)

At this point, we recall that the Ricci tensor for homogeneous and isotropic spacetime has the form

$$\begin{array}{c}\hfill {\mathrm{Ric}}_{ab}=\alpha g_{ab}+\beta u_a^{♯}{u}_b^{♯}.\end{array}$$

(3)

By virtue of (2) and (3), one can conclude that an $RW$-spacetime is a perfect fluid spacetime, where

$$\begin{array}{c}\hfill \alpha ={\displaystyle \frac{\mathcal{R}-\psi }{n-1}},\beta ={\displaystyle \frac{\mathcal{R}-n\psi }{n-1}}.\end{array}$$

For more information regarding perfect fluid spacetimes and the characterization of $GRW$- and $RW$-spacetimes, readers are encouraged to see the references [2,4,5,6]. An algebraic curvature condition for a spacetime to be classified as a perfect fluid spacetime is described in [7]. In differential geometry, manifolds that meet this algebraic curvature criterion are known as quasi-Einstein manifolds [8].

The quest to understand the dynamics of our universe, particularly during its late-time inflationary phase, has led some researchers to modify the action principle of Einstein’s field equations (EFEs), recognizing that the standard theory of gravity may not offer a complete explanation. A significant contribution to this field is found in Buchdahl’s proposal [9], which introduces a modified gravity theory by replacing the Ricci scalar $\mathcal{R}$ in the Einstein–Hilbert action with an arbitrary function $f(\mathcal{R})$. This innovative modification yields a new action principle that challenges conventional views of astrophysical phenomena. While the choice of functions $f(\mathcal{R})$ is indeed constrained by a range of observational data and scalar–tensor theoretical results, researchers can adopt a phenomenological approach that assumes specific forms for $f(\mathcal{R})$, allowing for empirical testing against existing criteria. A diverse array of models and functional forms has emerged in the literature, with notable contributions from studies such as [10,11,12,13,14,15]. These explorations have demonstrated that certain astrophysical structures, including massive neutron stars, resist explanations grounded in GR but can be effectively described through the higher-order curvilinear features of $f(\mathcal{R})$-gravity. Supporting evidence for these claims can be found in references [16,17,18,19,20], which highlight the notable advantages of investigating modified gravity theories. The equations of motion derived from $f(\mathcal{R})$-gravity reflect increased complexity, offering solutions that can diverge significantly from those predicted by traditional GR.

Energy conditions (ECs) play a crucial role in establishing the positivity of the energy–momentum tensor, serving as fundamental criteria for various theories of gravity. However, the introduction of $f(\mathcal{R})$-gravity models has posed significant challenges in effectively constraining their model parameters. By applying different energy conditions, researchers can derive potential constraints on the parameters governing the $f(\mathcal{R})$ framework [21]. Originally articulated within the confines of GR [22], these conditions have since been adapted for $f(\mathcal{R})$-gravity by defining effective pressure and energy density, facilitating a more nuanced understanding of these modified theories. As evident from the preceding literature, it is imperative to dedicate more attention to $f(\mathcal{R})$-gravity, which remains largely unexplored. Motivated by these gaps, the present study focuses on the Ricci semi-symmetric Robertson–Walker (RW) spacetime in the context of $f(\mathcal{R})$-gravity. Our objective is to shed light on the unanswered questions that arise within this realm, specifically through an examination of the null, weak, strong, and dominant energy conditions applicable to various $f(\mathcal{R})$-gravity models.

2. $\mathbf{RW}$-Spacetime

The scalar curvature of $RW$ spacetime, the eigenvalue of the Ricci tensor corresponding to $u^{♯}$, and the divergence of the one-form $u^{♯}$ can be easily deduced as follows:

$$\begin{array}{c}\hfill \mathcal{R}=n\alpha -\beta ,\psi =\alpha -\beta ,\end{array}$$

(4)

$$\begin{array}{c}\hfill {\nabla }^b{u}_b^{♯}=(n-1)\phi ,\mathrm{respectively}.\end{array}$$

(5)

An $RW$-spacetime is a conformally flat $GRW$-spacetime which holds significant interest in the standard theory of gravity [23] governed by Einstein’s field equations (EFEs):

$$\begin{array}{c}\hfill {\mathrm{Ric}}_{ab}-{\displaystyle \frac{\mathcal{R}}{2}}{g}_{ab}=k^2{T}_{ab},\end{array}$$

where $T_{ab}$ denotes the energy–momentum tensor and k is a gravitational constant. Thus,

$$\begin{array}{c}\hfill \left(\alpha -{\displaystyle \frac{\mathcal{R}}{2}}\right)g_{ab}+\beta u_a^{♯}{u}_b^{♯}=k^2{T}_{ab}.\end{array}$$

(6)

The energy momentum tensor for homogeneous and isotropic spacetime is defined by the symmetric tensor:

$$\begin{array}{c}\hfill T_{ab}=p{g}_{ab}+(p+\sigma )u_a^{♯}{u}_b^{♯},\end{array}$$

(7)

where p and $\sigma$ indicate isotropic pressure and energy density. Banerjee et al. [24] employed isotropic pressure to provide a detailed analysis of the characteristics of wormholes and energy conditions in the context of $f(\mathcal{R},\mathcal{T})$ gravity. The authors of reference [25] explored bouncing cosmology with higher-order curvature in modified gravity by using isotropic pressure. Gadbail et al. [26] studied the corrections to the Lagrangian for bouncing cosmology in $f(\mathcal{Q})$ gravity, using the energy–momentum tensor for homogeneous and isotropic spacetime. Extensive studies of isotropic pressure have been conducted in various cosmological and astrophysical phenomena [27,28,29,30,31,32,33,34,35]. Upon comparing (6) and (7), one can easily find that

$$\begin{array}{c}\hfill k^{2}p=\alpha -{\displaystyle \frac{\mathcal{R}}{2}}={\displaystyle \frac{\mathcal{R}-\psi }{n-1}}-{\displaystyle \frac{\mathcal{R}}{2}}={\displaystyle \frac{(3-n)\mathcal{R}-2\psi }{2(n-1)}},\\ \hfill k^2(p+\sigma )=\beta ={\displaystyle \frac{\mathcal{R}-n\psi }{n-1}},\\ \hfill k^2\sigma ={\displaystyle \frac{\mathcal{R}-n\psi }{n-1}}-{\displaystyle \frac{(3-n)\mathcal{R}-2\psi }{2(n-1)}}={\displaystyle \frac{\mathcal{R}-2\psi }{2}}.\end{array}$$

3. Characterization of Ricci Semi-Symmetric $\mathbf{RW}$-Spacetime

In this section, we investigate some geometric behaviors of $RW$-spacetime within the background of curvature condition on the Ricci tensor. A spacetime is said to be Ricci semi-symmetric [23] if it satisfies

$$\begin{array}{c}\hfill {\nabla }_l{\nabla }_k{\mathrm{Ric}}_{ab}-{\nabla }_k{\nabla }_l{\mathrm{Ric}}_{ab}=0.\end{array}$$

Taking the covariant derivative of (2) twice gives

$$\begin{array}{cc}\hfill {\nabla }_l{\nabla }_k{\mathrm{Ric}}_{ab}-{\nabla }_k{\nabla }_l{\mathrm{Ric}}_{ab}& ={\nabla }_l{\nabla }_k(\alpha g_{ab}+\beta u_a^{♯}{u}_b^{♯})-{\nabla }_k{\nabla }_l(\alpha g_{ab}+\beta u_a^{♯}{u}_b^{♯}),\hfill \\ \hfill & =\beta \left(u_a^{♯}({\nabla }_l{\nabla }_k-{\nabla }_k{\nabla }_l)u_b^{♯}+u_b^{♯}({\nabla }_l{\nabla }_k-{\nabla }_k{\nabla }_l)u_a^{♯}\right).\hfill \end{array}$$

We can easily conclude from the previous equation that an RW spacetime is Ricci semi-symmetric if and only if either $\beta =0$ or ${\nabla }_l{\nabla }_k{u}_b^{♯}={\nabla }_k{\nabla }_l{u}_b^{♯}$. Remarkably, if $\beta =0$ in (3), then this implies that an RW spacetime is Einstein, that is, ${\mathrm{Ric}}_{ab}={\displaystyle \frac{\mathcal{R}}{n}}{g}_{ab}$. Conversely, if the spacetime is Einstein, then

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\mathcal{R}}{n}}=(\alpha -n\alpha +\mathcal{R}).\hfill \end{array}$$

The aforementioned equation yields $\alpha ={\displaystyle \frac{\mathcal{R}}{n}}$, which, when considered in (4), gives $\beta =0$. The second condition is equivalent to $u_h^{♯}{\mathrm{Ric}}_{abk}^h=0$. Hence, we conclude the following.

Theorem 1. 

An $RW$-spacetime M is Ricci semi-symmetric if and only if M is Einstein or $u_h^{♯}{\mathit{Ric}}_{abk}^h=0$.

The Ricci semi-symmetric $RW$-spacetime is Einstein, provided that $\beta =0$. In this case, the Ricci tensor and energy–momentum tensor are, respectively, transformed into

$$\begin{array}{cc}\hfill & {\mathrm{Ric}}_{ab}={\displaystyle \frac{\mathcal{R}}{n}}{g}_{ab},\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill & T_{ab}=-{\displaystyle \frac{1}{k^2}}\left({\displaystyle \frac{n-2}{2n}}\right)\mathcal{R}{g}_{ab}.\hfill \end{array}$$

(9)

In this situation, one can find

$$\begin{array}{c}\hfill p=-{\displaystyle \frac{1}{k^2}}\left({\displaystyle \frac{n-2}{2n}}\right)\mathcal{R},\end{array}$$

(10)

$$\begin{array}{c}\hfill \sigma ={\displaystyle \frac{1}{k^2}}\left({\displaystyle \frac{n-2}{2n}}\right)\mathcal{R}.\end{array}$$

(11)

By virtue of the previous equation, one can obtain $p+\sigma =0$, which indicates that a perfect fluid is referred to as dark energy matter.

Remark 1. 

Let M be a Ricci semi-symmetric $RW$-spacetime. Then, perfect fluid spacetime is referred to as the dark matter era.

Since the energy density cannot be negative, it follows from (10) that $\mathcal{R}\ge 0$, that is, $\mathcal{R}=0$ or $\mathcal{R}>0$:

• When $\mathcal{R}=0$, then (8), which results in ${\mathrm{Ric}}_{ab}=0$, signifies that the spacetime is flat, and thus locally isometric to Minkowski spacetime [36].
• When $\mathcal{R}>0$, this condition leads to a spacetime characterized by a constant positive curvature, specifically classifying it as a de Sitter spacetime [36].

Therefore, we state the following.

Theorem 2. 

A Ricci semi-symmetric $RW$-spacetime is either locally isometric to Minkowski spacetime or a de Sitter spacetime.

4. Ricci Semi-Symmetric $\mathbf{RW}$-Spacetime Obeying $\mathbf{f}(\mathcal{R})$-Gravity

In this study, we delve into the implications of $f(\mathcal{R})$-gravity within the context of Ricci semi-symmetric $RW$-spacetime, which is characterized by a specific geometric structure that allows for cosmological models consistent with modern observations. This examination is prompted by the recognition that $f(\mathcal{R})$ theories can extend our understanding of gravitational phenomena beyond that provided by GR.

To initiate our analysis, we consider a modified form of the Einstein–Hilbert action represented by the following integral:

$$\begin{array}{c}\hfill H={\displaystyle \frac{1}{{\kappa }^2}}\int \{f(\mathcal{R})+{\mathcal{L}}_m\}\sqrt{-g}{d}^{4}x,\end{array}$$

(12)

where ${\mathcal{L}}_m$ corresponds to the Lagrangian matter density of scalar field and ${\kappa }^2$ is a coupling constant that relates the gravitational phenomenon to the energy–momentum tensor. The stress–energy tensor of the matter is calculated using the following expression:

$$\begin{array}{c}\hfill T_{ab}=-{\displaystyle \frac{2}{\sqrt{-g}}}{\displaystyle \frac{\delta (\sqrt{-g}{\mathcal{L}}_m)}{\delta g^{ab}}}.\end{array}$$

(13)

By varying the modified action H with respect to the metric, we arrive at the field equations for $f(\mathcal{R})$-gravity as

$$\begin{array}{c}\hfill f_{\mathcal{R}}(\mathcal{R}){\mathrm{Ric}}_{ab}-{\displaystyle \frac{1}{2}}f(\mathcal{R})g_{ab}+(g_{ab}\square -{\nabla }_a{\nabla }_b)f_{\mathcal{R}}(\mathcal{R})={\kappa }^2{T}_{ab},\end{array}$$

(14)

where □ denotes the d’Alembert operator. An interesting facet of this framework is the ability to simplify the field equations by substituting $f(\mathcal{R})$ with $\mathcal{R}$. We know that $\mathcal{R}$ is constant on Ricci semi-symmetric $RW$-spacetime, so the equation can be restructured to express the relationship more clearly, as follows:

$$\begin{array}{c}\hfill {\mathrm{Ric}}_{ab}-{\displaystyle \frac{\mathcal{R}}{2}}{g}_{ab}={\displaystyle \frac{{\kappa }^2}{f_{\mathcal{R}}(\mathcal{R})}}{T}_{ab}^{eff},\end{array}$$

(15)

with $T_{ab}^{eff}=T_{ab}+{\displaystyle \frac{f(\mathcal{R})-\mathcal{R}{f}_{\mathcal{R}}(\mathcal{R})}{2{\kappa }^2}}{g}_{ab}$. Due to Theorem 1, we obtain $Ri{c}_{ab}={\displaystyle \frac{\mathcal{R}}{4}}{g}_{ab}$. For a constant $\mathcal{R}$, the above field equation becomes

$$\begin{array}{c}\hfill -{\displaystyle \frac{\mathcal{R}}{2}}{g}_{ab}=\left[{\displaystyle \frac{{\kappa }^2}{f_{\mathcal{R}}(\mathcal{R})}}p+{\displaystyle \frac{f(\mathcal{R})-\mathcal{R}{f}_{\mathcal{R}}(\mathcal{R})}{2f_{\mathcal{R}}(\mathcal{R})}}\right]g_{ab}+{\displaystyle \frac{{\kappa }^2}{f_{\mathcal{R}}(\mathcal{R})}}(p+\sigma )u_a^{♯}{u}_b^{♯}.\end{array}$$

(16)

Combining a and b in the previous equation, one can obtain

$$\begin{array}{c}\hfill \mathcal{R}={\displaystyle \frac{3{\kappa }^{2}p}{f_{\mathcal{R}}(\mathcal{R})}}-{\displaystyle \frac{{\kappa }^2\sigma }{f_{\mathcal{R}}(\mathcal{R})}}+{\displaystyle \frac{2f(\mathcal{R})}{f_{\mathcal{R}}(\mathcal{R})}}.\end{array}$$

(17)

Once again, transvecting (16) by ${(u^{♯})}^b$ and after some computation, we obtain

$$\begin{array}{c}\hfill \mathcal{R}={\displaystyle \frac{2f(\mathcal{R})}{f_{\mathcal{R}}(\mathcal{R})}}-{\displaystyle \frac{4{\kappa }^2\sigma }{f_{\mathcal{R}}(\mathcal{R})}}.\end{array}$$

(18)

Combining (17) together with (18) gives

$$\begin{array}{c}\hfill p={\displaystyle \frac{\mathcal{R}{f}_{\mathcal{R}}(\mathcal{R})}{4{\kappa }^2}}-{\displaystyle \frac{f(\mathcal{R})}{2{\kappa }^2}},\mathrm{and}\sigma ={\displaystyle \frac{f(\mathcal{R})}{2{\kappa }^2}}-{\displaystyle \frac{\mathcal{R}{f}_{\mathcal{R}}(\mathcal{R})}{4{\kappa }^2}}.\end{array}$$

(19)

Hence, we state the following.

Theorem 3. 

In Ricci semi-symmetric $RW$-spacetime, isotropic pressure p and energy density σ are given by the expression (19).

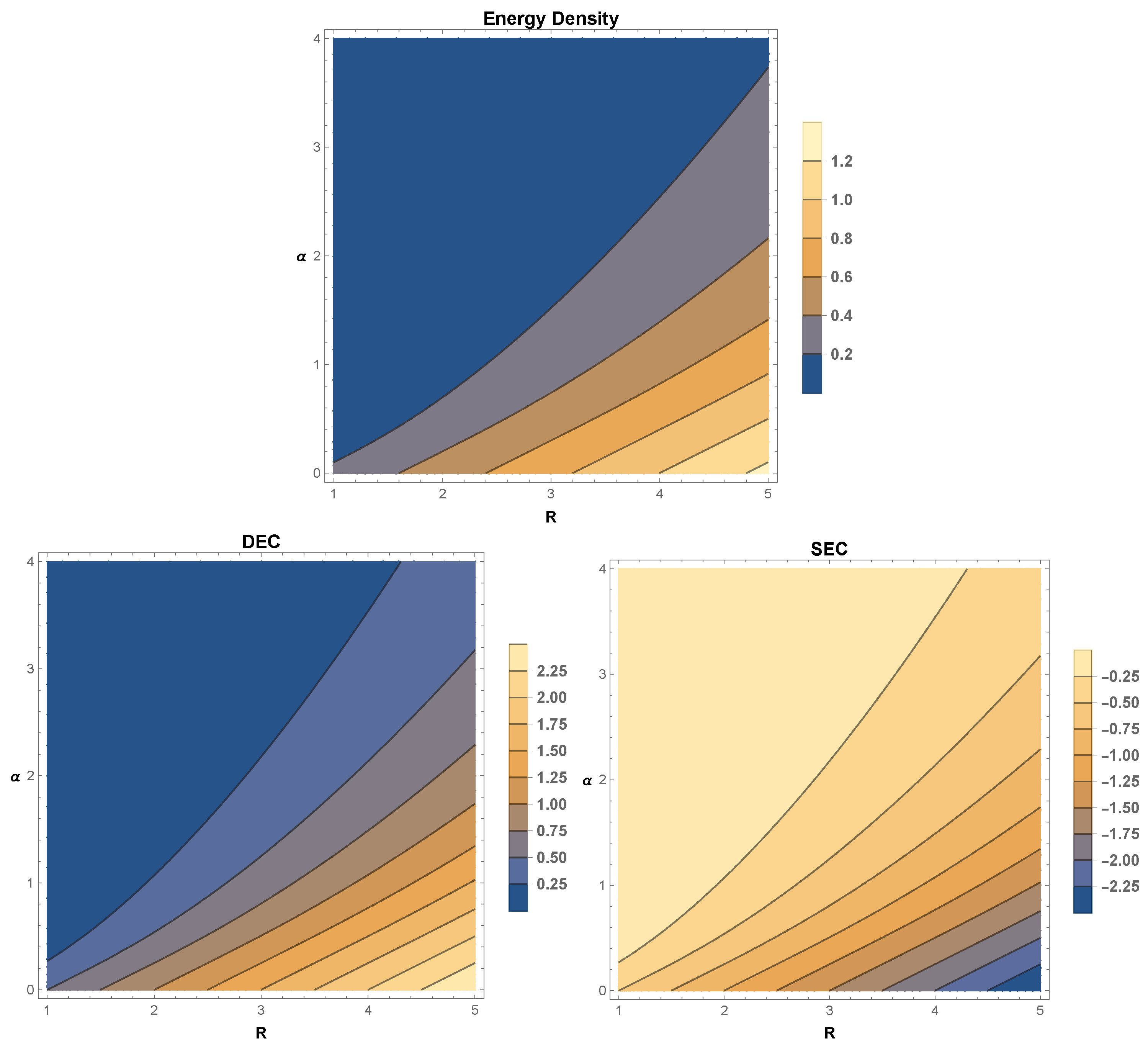
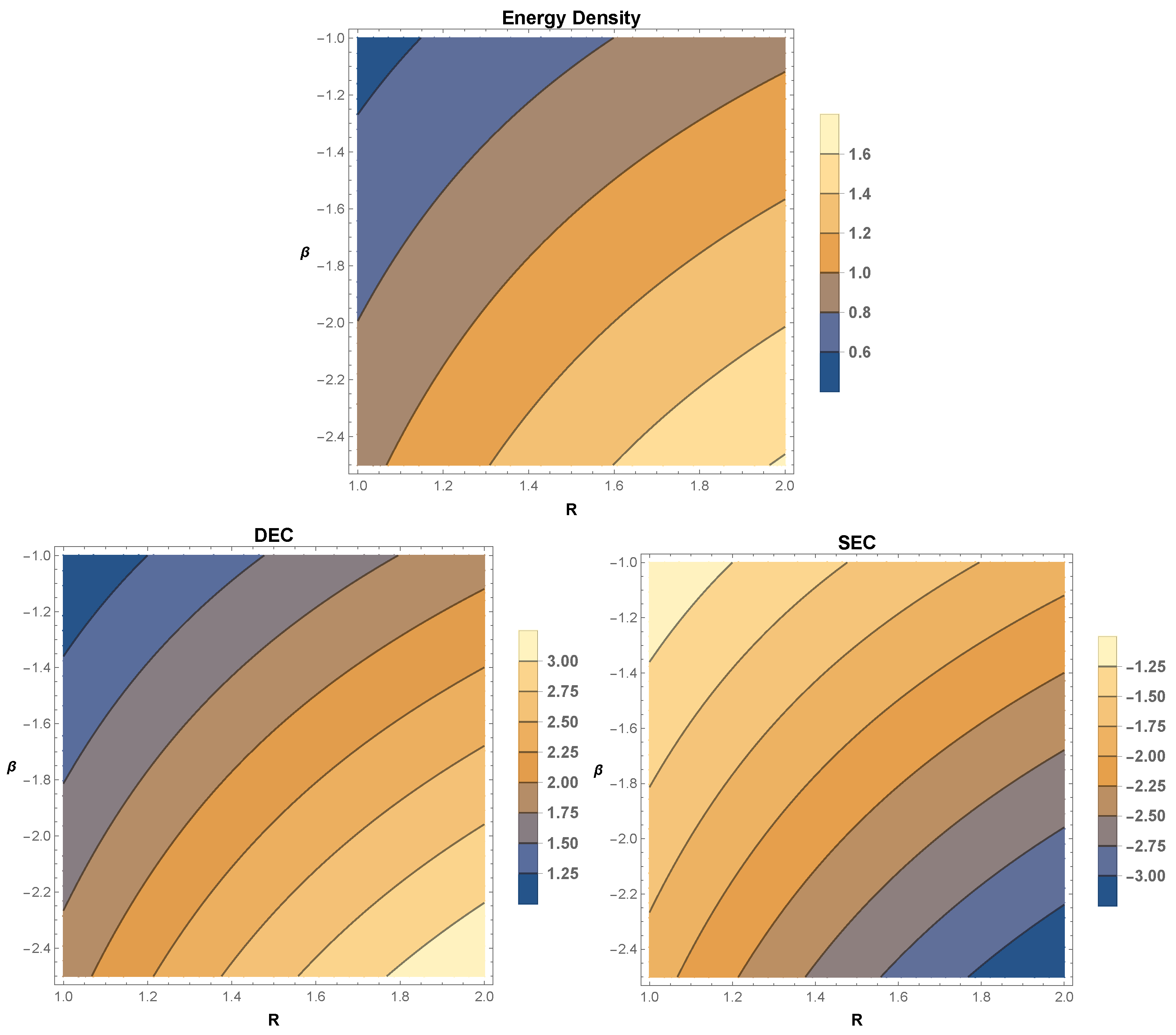
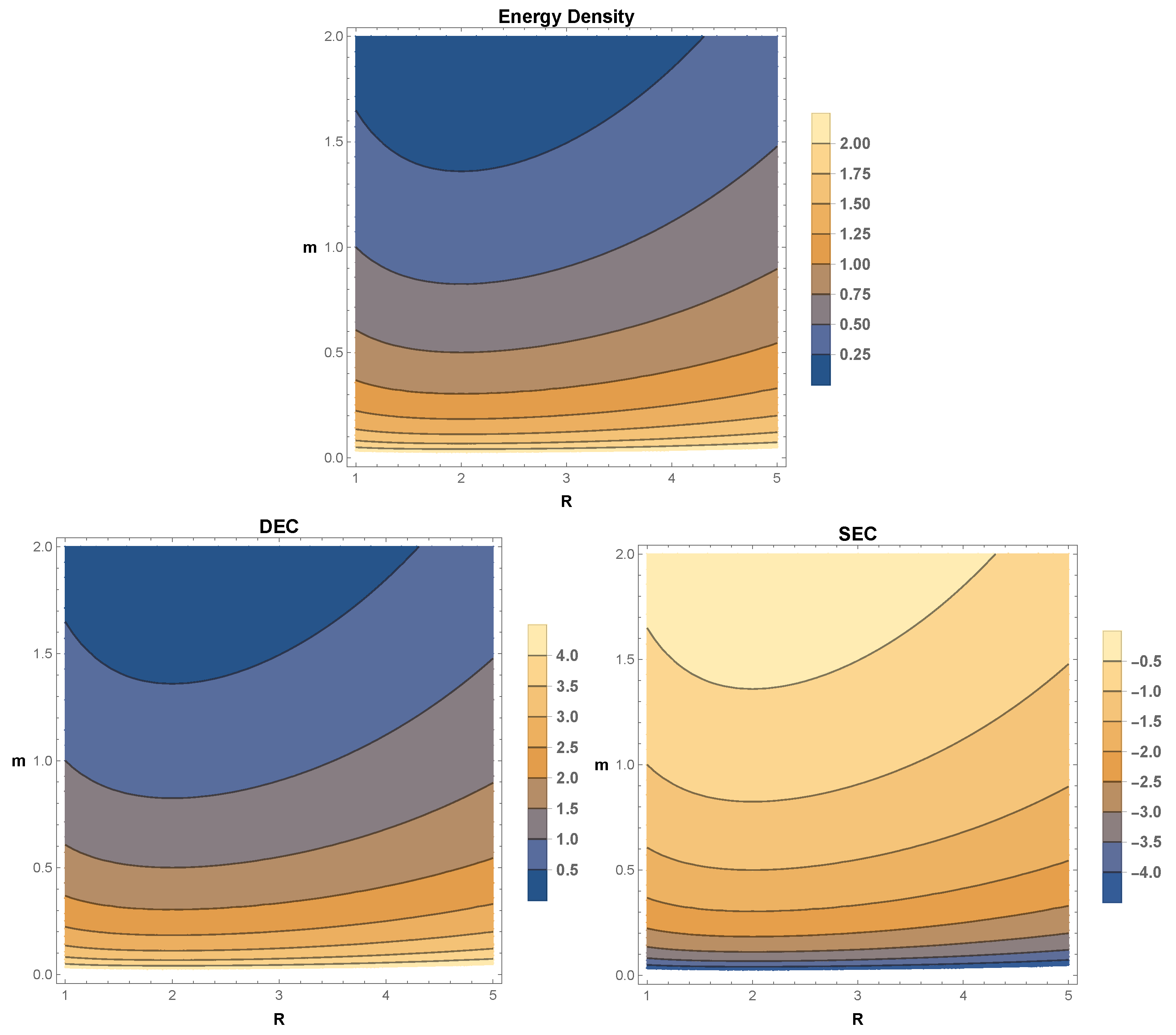
5. Energy Conditions

In the context of GR, ECs are widely regarded as crucial tools for exploring the properties of compact objects in various modified-gravity theories, as highlighted in references [37,38,39]. ECs serve as invaluable tools for assessing the self-stability of cosmological models, typically derived from the widely recognized Raychaudhuri equation [40,41]. Additionally, its helps us to elucidate the geometrical characteristics of spacetime curvature, such as space-like, time-like, and light-like behaviors, while also shedding light on the nature of dreadful singularities [42,43]. The expressions of the Raychaudhuri equations are

$$\begin{array}{c}\hfill {\displaystyle \frac{d\mathrm{\Theta }}{d\tau }}=-{\displaystyle \frac{1}{3}}{\mathrm{\Theta }}^2-{\sigma }_{ab}{\sigma }^{ab}+{\omega }_{ab}{\omega }^{ab}-Ri{c}_{ab}{u}^a{u}^b,\end{array}$$

(20)

$$\begin{array}{c}\hfill {\displaystyle \frac{d\mathrm{\Theta }}{d\tau }}=-{\displaystyle \frac{1}{2}}{\mathrm{\Theta }}^2-{\sigma }_{ab}{\sigma }^{ab}+{\omega }_{ab}{\omega }^{ab}-Ri{c}_{ab}{n}^a{n}^b.\end{array}$$

(21)

Here, $\mathrm{\Theta }$ refers to the expansion rate, $n^a$ is the null vector, and ${\sigma }^{ab}$ and ${\omega }^{ab}$ are the shear and rotation associated with the vector field $u^a$, respectively. For gravitational attraction, the conditions given by (20) and (21) are satisfied as follows:

$$\begin{array}{c}\hfill Ri{c}_{ab}{u}^a{u}^b\ge 0,Ri{c}_{ab}{n}^a{n}^b\ge 0.\end{array}$$

We use (19) to deduce some relevant energy conditions for the present scenario:

• Null energy condition (NEC): if $\sigma +p\ge 0$.
• Strong energy condition (SEC): if $\sigma +3p\ge 0$ with $\mathcal{R}{f}_{\mathcal{R}}(\mathcal{R})-f_{\mathcal{R}}(\mathcal{R})\ge 0$.
• Weak energy condition (WEC): if $\sigma \ge 0$, $\sigma +p\ge 0$ with $-\mathcal{R}{f}_{\mathcal{R}}(\mathcal{R})+f_{\mathcal{R}}(\mathcal{R})\ge 0$.
• Dominant energy condition (DEC): if $\sigma \ge 0$, $\parallel p\parallel \le \sigma$.

We will now explore the ECs for particular functions of the Ricci scalar $\mathcal{R}$ within this framework in the subsequent section.

6. Features of $\mathbf{f}(\mathcal{R})$-Gravity Models

In this section, we explore a specific class of $f(\mathcal{R})$-modified-gravity models by detailing the functional form of f. Generally, the field equations are influenced by the tensor $T_{ab}$, which incorporates the physical properties of the matter field. Consequently, in $f(\mathcal{R})$-gravity, each choice of the function f can lead to a variety of theoretical models, depending on the specific nature of the matter source considered. Some of the early $f(\mathcal{R})$ models, including the Starobinsky [44] and Carroll [11] models, accounted for cosmic inflation without the need for scalar fields and explained late-time acceleration purely as a gravitational phenomenon, without invoking dark energy. Although these models have their limitations, they played a significant role in popularizing $f(\mathcal{R})$ models overall. They also highlighted the complexity involved in identifying a viable and stable $f(\mathcal{R})$ model. For an in-depth review of $f(\mathcal{R})$-gravity theory, refer to [45]. Sotiriou et al. [37] described the $f(\mathcal{R})$ theory as a form of toy theory and provided a detailed explanation of this toy model in their research. Additionally, numerous researchers have examined various toy models in their studies [46,47,48]. We will analyze three different toy models to investigate energy conditions in the following subsections.

6.1. Model-1: $f(\mathcal{R})=\mathcal{R}-\alpha (1-e^{-{\displaystyle \frac{\mathcal{R}}{\alpha }}})$

In this context, we consider $f(\mathcal{R})$ to be an exponential function characterized by the free parameter $\alpha$. Consequently, the expressions for energy density and pressure can be formulated as

$$\begin{array}{c}\hfill \sigma ={\displaystyle \frac{1}{4{\kappa }^2}}\left(-2\alpha +e^{-{\displaystyle \frac{\mathcal{R}}{\alpha }}}(2\alpha +\mathcal{R})+\mathcal{R}\right),\end{array}$$

(22)

$$\begin{array}{c}\hfill p={\displaystyle \frac{1}{4{\kappa }^2}}\left(2\alpha -e^{-{\displaystyle \frac{\mathcal{R}}{\alpha }}}(2\alpha +\mathcal{R})-\mathcal{R}\right).\end{array}$$

(23)

Utilizing (22) and (23), one can examine the energy conditions within this framework. Figure 1 illustrates the profiles of various energy conditions within the context of cosmological evolution. The analysis reveals that the energy density remains strictly positive throughout the universe’s evolution for parameters, where $\mathcal{R}>1$ and $\alpha >0$. This figure further demonstrates that elevated values of $\mathcal{R}$ correspond to higher energy density levels, implying that the universe possessed substantial energy density during its early stages of development. It is noteworthy that the NEC is a subset of the WEC, thereby confirming the satisfaction of both conditions. The profiles for the DEC are also depicted in Figure 1, indicating positivity throughout. However, a violation of the SEC is observed, which suggests that the universe is experiencing a phase of late-time acceleration [49,50]. Throughout this analysis, the EoS parameter $\omega =-1$. The EoS parameter is viewed as a viable metric for assessing our models in relation to the $\mathrm{\Lambda }CDM$ cosmological model. Remarkably, this nature is consistent with the $\mathrm{\Lambda }CDM$ theoretical framework for dark energy and is further validated by recent experimental findings [51]. In [13], the author elaborated on a significant observation regarding this result.

Moreover, the present analysis demonstrates that the condition $\omega =-1$ characterizes late-time cosmic acceleration. Utilizing this parameter in the context of the SEC, it is observed that $\rho +3\omega \rho$ remains negative. In order to explain cosmic acceleration in a homogeneous and isotropic universe, it is necessary for the late universe to display substantial negative pressure. Consequently, these findings confirm that our model indicates that the universe is undergoing an accelerated expansion phase [49,52,53,54].

6.2. Model-2: $f(\mathcal{R})=\mathcal{R}-\beta tanh\mathcal{R}$

In this part, we consider a model $f(\mathcal{R})=\mathcal{R}-\beta tanh\mathcal{R}$. Tsujikawa [55], Appleby, and Battye [56] described this type of $f(\mathcal{R})$-gravity model. We can express the pressure and energy density in terms of this model as

$$\begin{array}{c}\hfill p={\displaystyle \frac{1}{2{\kappa }^2}}\beta tanh(\mathcal{R})-{\displaystyle \frac{1}{4{\kappa }^2}}\mathcal{R}\left(\beta {\mathrm{sech}}^2(\mathcal{R})+1\right),\end{array}$$

(24)

$$\begin{array}{c}\hfill \sigma ={\displaystyle \frac{1}{4{\kappa }^2}}\left(-2\beta tanh(\mathcal{R})+\beta \mathcal{R}{\mathrm{sech}}^2(\mathcal{R})+\mathcal{R}\right).\end{array}$$

(25)

By analyzing the behavior of t he pressure and energy density as expressed in (24) and (25), we can deduce the EoS parameter $\omega$ in this scenario. Upon performing the necessary calculations, we find that $\omega =-1$ for any $\beta$. This result implies that the universe is primarily driven by a cosmological constant, which is consistent with the widely accepted $\mathrm{\Lambda }CDM$ theory [51]. In Figure 2, we present the profiles of energy density and energy conditions to visually illustrate their characteristics. The graphs demonstrate that while both the energy density and DEC criteria are satisfied, the SEC is not met. Additionally, as $\sigma +p$ approaches zero in this analysis, it becomes clear that both the WEC and NEC are fulfilled.

6.3. Model-3: $f(\mathcal{R})=\mathcal{R}-log(m\mathcal{R})$

We consider $f(\mathcal{R})$ as a logarithmic function of the Ricci scalar with the free parameter $m>0$. This model is characterized by the following expressions for energy density and pressure:

$$\begin{array}{c}\hfill \sigma ={\displaystyle \frac{1}{4}}(\mathcal{R}+1-2log(m\mathcal{R})),\end{array}$$

(26)

$$\begin{array}{c}\hfill p={\displaystyle \frac{1}{4}}(2log(m\mathcal{R})-\mathcal{R}-1)\end{array}$$

(27)

In this scenario, the EoS is equal to 1 for all values of m, suggesting that the universe is primarily governed by a cosmological constant, aligning with the widely accepted $\mathrm{\Lambda }CDM$ model. Since WEC combines NEC and positive density, and NEC is always zero in this context, we can observe behaviors related to SEC, DEC, and the density parameter. Figure 3 presents the profiles of energy density, as well as the DEC and SEC. An analysis of these graphs indicates that while both the energy density and DEC criteria are satisfied, the SEC criterion is not. Furthermore, as $p+\sigma$ approaches zero in this construction, it is evident that both the WEC and NEC are also satisfied.

7. Discussion

This work has provided a comprehensive exploration of Ricci semi-symmetric Robertson–Walker spacetime within the framework of $f(\mathcal{R})$-gravity. By employing both analytical techniques and graphical analyses, we have effectively demonstrated the stability of several cosmological toy models, which were framed by carefully chosen functional forms of $f(\mathcal{R})$. Specifically, we investigated models defined by $f(\mathcal{R})=\mathcal{R}-\alpha (1-e^{-{\displaystyle \frac{\mathcal{R}}{\alpha }}})$, $f(\mathcal{R})=\mathcal{R}-\beta tanh\mathcal{R}$ and $f(\mathcal{R})=\mathcal{R}-log(m\mathcal{R})$, all of which allowed for a rich understanding of the underlying cosmological dynamics. In [13,57], the author employed these models to investigate the energy conditions, demonstrating its relevance and effectiveness in their analysis. Motivated by their findings, we adopted a similar model for our research, seeking to advance the understanding of this area.

Our study not only examined the expression and implications of energy conditions within these models but also highlighted their stability properties. In particular, for model-1, we found that the energy density remains positive across a range of parameters ($\mathcal{R}\ge 1$ and $\alpha >0$) in Figure 1 and that the dominant, null, and weak energy conditions are satisfied, while the SEC is violated. This behavior aligns well with the observed accelerated expansion of the universe, supporting the notion that such models can represent a dark energy era, characterized by an equation of state parameter $\omega$ that approaches $-1$, consistent with predictions from the $\mathrm{\Lambda }CDM$ model. Further, recent data from the Planck collaboration and the $\mathrm{\Lambda }CDM$ model suggest that the equation of the state parameter is roughly $\omega \simeq -1$ [51]. This behavior indicates that the universe is experiencing a negative pressure regime, which plays a key role in its ongoing accelerated expansion. Therefore, the $\omega$ parameter serves as an effective basis for comparing our models with the $\mathrm{\Lambda }CDM$ framework. Moreover, we have confirmed that similar results hold for model-2 and model-3, further validating our findings. These insights reinforce the potential of $f(\mathcal{R})$-gravity theories to provide viable alternatives to standard cosmological models. Comparable results have been documented in the literature [13,57,58,59], reinforcing the conclusions of the present study.

To relate the proposed $f(R)$ mathematical models to cosmological observational data, we will first determine the scale factor $a(t)$ and subsequently calculate the Hubble parameter $H(t)=a^{\prime }/a$ based on the modified Friedmann equations. Next, we will utilize the relation $H=-z^{\prime }/z+1$ to express cosmic time t as a function of the redshift parameter z. This will enable us to derive the Hubble parameter $H(z)$ in terms of redshift, forming our model equation. We plan to fit this $H(z)$ using observational data from cosmic chronometers (CCs), baryon acoustic oscillations (BAOs), and Type Ia supernovae (SNeIa) in the near future. Through this method, we aim to test the viability of the proposed $f(R)$ model in explaining the universe’s expansion history and ensuring its consistency with various cosmological observations.