Abstract
Modular arithmetic is used to apply generalized C-coloured checkerboard patterns to gridded rectangles, ensuring that colours cycle both horizontally and vertically. This paper yields methods for counting the number of squares of each colour, which is a nontrivial combinatorial problem in discrete geometry. The main theorem provides a closed-form expression for a sum of floor functions, representing the count of squares for each colour. Two proofs are presented: a heuristic, constructive approach dividing the problem into sub-cases, and a purely mathematical derivation that transforms the floor sum into a closed-form solution, computable in operations, independent of and C. Numerical counts are validated using a brute-force procedure in MATLAB (Version 9.14, R2023a).
Keywords:
tiling theory; modular arithmetic; checkerboard patterns; combinatorial enumeration; floor sums; MATLAB MSC:
05B45; 05A15; 11B75
1. Introduction and Motivation
A key problem in polyomino tiling theory is to tile a finite subset of the plane, called the target region, using a given set of polyominoes. Polyominoes are polyforms composed of edge-connected unit squares. A black and grey checkerboard colouring of the polyominoes and target region is necessary for an integer linear programming (ILP) approach that improves the scalability of the tiling method [1]. This method requires us to determine the number of black and grey squares in the target region. For a rectangular target region, a simple formula provides these counts [2]. The general formula for the number of black squares (b) and grey squares (g) in an checkerboard rectangle is given by
where p, the “parity” of the checkerboard region, is the difference between the number of black and grey squares. For a rectangle, if is even and if is odd. Another checkerboard pattern for the rectangle is obtained by swapping the colours (when is odd, the checkerboard variant with a black square in the top-left corner has parity , while the variant with a grey square in the top-left corner has parity ). For example, the checkerboard coloured rectangle in Figure 1 contains 59 black squares and 58 grey squares.

Figure 1.
A 2-colour checkerboard pattern applied to the rectangle with 59 black squares and 58 grey squares.
This paper generalizes the enumeration problem of counting the squares of each colour to a C-coloured checkerboard rectangle, which is a nontrivial problem in combinatorial and discrete mathematics. We use modular arithmetic to generate the checkerboard pattern, ensuring that the coloured squares cycle both vertically and horizontally (see Section 2 for a rigorous development). Our approach reformulates the combinatorial geometry problem [3] as an equivalent number-theoretic problem involving a sum of floor functions.
Enumeration problems in discrete geometry have been widely studied in combinatorics. Classical topics include counting lattice points in polytopes, tiling problems with constraints, and enumeration in structured partitions of the plane. Grünbaum and Shephard’s comprehensive work [4] systematically classifies plane tilings and their symmetry properties, establishing fundamental results for periodic and aperiodic tilings. Stanley’s text [5] develops key techniques for enumerative combinatorics, including generating functions and the transfer-matrix method, which provide powerful tools for counting discrete structures. Ziegler [6] presents a thorough treatment of polytope theory, covering face lattices, shellability, and enumeration of faces, which connects to various problems in discrete geometry.
Modular arithmetic methods, such as those used in divisor sums and residue class enumeration, also play an important role in combinatorial number theory [7]. However, the specific problem of counting cyclically coloured squares in finite grids, as formulated in this paper, does not appear to have been studied before.
We introduce our enumeration problem with an illustrative example. Applying six colours cyclically to a rectangle produces six distinct variants. Given any one variant, the remaining five variants are generated by cyclically shifting the colours. The variant with a black square in the top-left corner is shown in Figure 2.
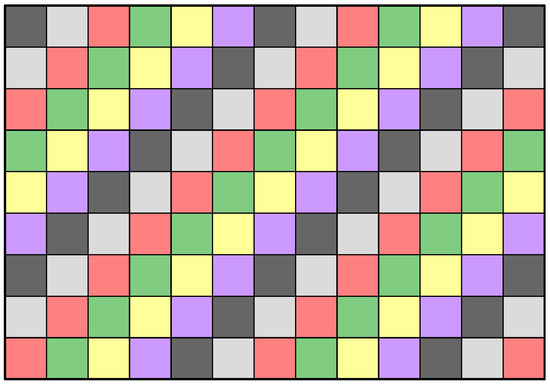
Figure 2.
A 6-colour checkerboard pattern applied to the rectangle with 20 black, grey, and red squares, and 19 green, yellow, and blue squares.
This paper is part of an ongoing research project that generalizes the ILP approach in [1] for polyomino tiling problems. Additional details are given in Appendix B.
Starting from a modular arithmetic formulation of the colouring procedure, the main goal of this paper is to derive a closed-form solution for enumerating coloured squares in a generalized C-coloured checkerboard rectangle. Colours are represented by indices . Our approach yields the following expression for the colour counts:
where the notation represents the largest integer less than or equal to z (the “floor function”). Thus, to find a closed-form solution for the colour counts, we derive closed-form solutions to the sum of floor functions of the form:
Research on sums involving floor functions is a popular area of study. Foundational work on floor and ceiling sums is found in the book “Concrete Mathematics” by Graham, Knuth, and Patashnik [8], which provides an in-depth treatment of these sums, such as finding an expression for
and their applications in various mathematical contexts. Further research has produced closed-form solutions for a variety of other floor sum forms [9,10,11,12,13,14].
It is worth noting that an alternative graph-theoretic perspective exists for addressing similar counting problems by considering the grid as a planar graph whose unit squares correspond to its faces. Classical results on face colourability demonstrate that an Eulerian planar graph is two-face colourable [15], whereas extending such results to three or more colours requires more sophisticated techniques. Although group-theoretic methods (cf. Pólya’s Enumeration Theorem [16]) can theoretically be applied to study such cyclic colourings, our approach using modular arithmetic provides a direct computational method that yields closed-form solutions while avoiding the complexities of advanced graph invariants and group actions.
The rest of this paper is structured as follows. In Section 2, we describe the rigorous mathematical procedure needed to apply a generalized C-coloured checkerboard pattern to rectangular grids. Section 3 presents a constructive proof for counting coloured squares, including an example and corollaries for specific cases. In Section 4, we introduce two lemmata for the sum of floor functions, which are needed for the main theorem. Section 5 provides the main result: a closed-form solution for counting coloured squares in rectangular grids. Finally, Section 6 concludes the paper, summarizing our findings and suggesting directions for future work. In the appendices, we list the MATLAB code used to validate the theoretical counts and give additional details concerning the relevance of the current paper to integer linear programming.
2. Modular Arithmetic Approach to Colouring Grids
To develop a systematic approach for applying a generalized C-coloured checkerboard pattern to rectangular grids, we first establish the mathematical framework using modular arithmetic.
Definition 1.
The gridded rectangle is the union of unit squares forming an rectangle, given by
Our goal is to develop a consistent and systematic procedure for colouring the squares of , using an arbitrary, but finite, number of colours.
Definition 2.
The finite grid is a subset of given by
The first step in the colouring procedure is to define a function given by
which maps every point in a square to its top right-hand corner with coordinates . Here, the notation represents the smallest integer greater than or equal to z (the “ceiling function”). Thus, each square in is uniquely identified with integer coordinates .
Definition 3.
A colour index is a unique integer from the set assigned to each of the C colours ().
Colours are assigned to the squares of using a cyclic permutation , an element of the symmetric group [17], ensuring that the colour indices cycle left-to-right and bottom-to-top.
A simple formula for generating the colour indices of the squares in the rectangle is as follows:
We have a “” in this formula so the indices increment from 1 to C instead of 0 to , which is more intuitive when counting colours.
There are C possible coloured variants of , obtained by cycling the colour indices. To obtain a mathematical expression for these checkerboard-coloured variants, indexed by k, we generalize the function in (3) via
Observe that when (4) reverts to (3). As we will represent coloured rectangles using matrices, we wish the colour indices to cycle left-to-right and top-to-bottom. To flip the order of colour indices vertically we apply a change in variable in the ordinate of the function via
This effectively changes the coordinates from in the Cartesian system to in the matrix system (we could have only used the matrix coordinates, but an initial introduction of the Cartesian coordinates allows the colouring procedure to be rigorously defined).
In practical computations coloured rectangles are stored as matrices. This leads to the following definition.
Definition 4.
The k-th colour matrix associated with a colouring of the rectangle , denoted by , is defined by
where and .
Remark 1.
For counting coloured squares it is sufficient to select a single one of the C variants of . We choose the variant with a colour index “1” in the top left-hand corner of the rectangle. The remaining variants are obtained by cycling the colour indices of the squares.
Definition 5.
Using Definitions 4 and 5 we determine the specific colour matrix we use by identifying which of the k-coloured variants satisfies the requirements of Definition 5.
Proposition 1.
The C-coloured checkerboard coloured rectangle is represented by the colour matrix , where
Proof.
Remark 2.
In the sequel, unless stated otherwise, the term “C-coloured checkerboard rectangle” refers to the -th coloured variant, i.e., we assume (see Remark 1).
3. A Constructive Proof for Counting Coloured Squares
We provide a constructive proof with heuristic elements for counting how many coloured squares of each colour are in a C-coloured checkerboard rectangle. The proof of this result was outlined on the mathematics stream of StackExchange [18], a public question-and-answer website. As this result is unpublished and the user requested that they remain anonymous, we provide a rigorous theorem and proof below.
Theorem 1.
Consider a C-coloured checkerboard rectangle, where , . We assume . Using the Euclidean Division Lemma ([7], Theorem 2.1), let a and b, , be the unique remainders when m and n are divided by C, i.e., and . We assume the top-left square has colour index “1”. If then the number of squares of each colour is given by . If, however, , then the number of coloured squares with index is given by the function:
where
Proof.
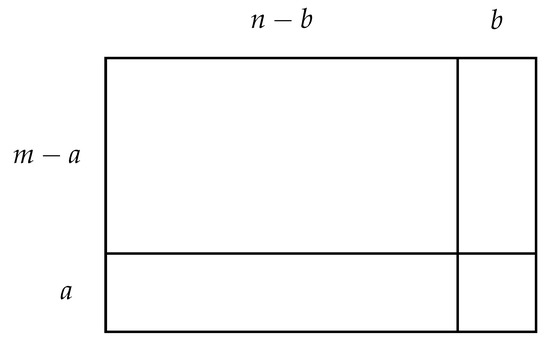
Partition the rectangle into four smaller rectangles, with dimensions , , , and , illustrated in Figure 4. Now due to the division lemma, and , thus . However, , thus . As a consequence, if at least one side of the rectangle is divisible by C (i.e., or ) the number of squares of each colour in the rectangle is exactly .

Figure 4.
Using the Euclidean Division Lemma to partition the rectangle into four smaller rectangles.
The rest of this proof is for the case when C does not divide m or n, i.e., . In this case, we need an expression for how many squares of each colour are in the “remainder” rectangle, which we then add to the counts for each colour.
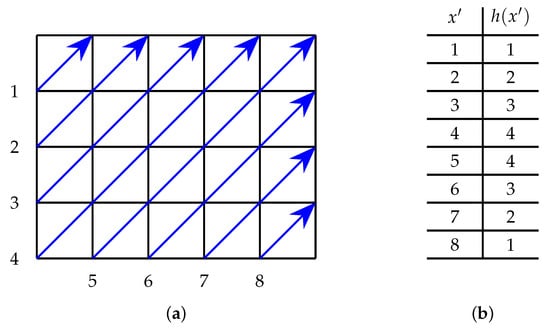
To derive an expression for colour counts in the rectangle, we count indices for each colour diagonally (south-west to north-east) starting from the index in the top-left corner of the rectangle. Let denote a variable that counts how far along half the perimeter we have traversed as we count the diagonal indices in the rectangle, so . An example of this counting procedure is illustrated in Figure 5. Observe that the general pattern for the index counts in a diagonal is , until , which occurs when the diagonal includes the lower left corner of the rectangle if , or the upper left corner of the rectangle if (and if , the diagonal includes both corners). For , the index counts in a diagonal remain a constant value of .

Figure 5.
Index counts: (a) indices for the diagonally coloured squares of an rectangle where and ; (b) index counts yielding the number of diagonal squares associated with .
Then for , the index counts decrease until . The general form is , , so we deduce that in this interval. Note that if then we are no longer within the rectangle and so the diagonal count is zero. Thus, to summarize, the diagonal counts can be split into four intervals:
The endpoints are chosen so that each index belongs to just one interval.
We now need total counts for the indices representing colour, and so we need to determine if a colour with index x can belong to more than one interval. To answer this we consider when where . Note that if , i.e., it is easily verified from the assumptions on and x, that , and so we have left the region of the rectangle, and so we need only consider the case . Notice that if we must have . Observe that , so we are in the first interval. Furthermore, as it follows immediately that and we assume , this yields , i.e., colours with index x in the first interval are repeated in the third interval, with counts and so the total (combined) contribution for x in the first interval satisfying is
Thus, putting this all together, the contributions for each colour with index x in the rectangle satisfy the following:
Adding these contributions to N (see (9)) yields the desired result. □
Example 2.
The case leads to Corollary 1, which is also stated in [2] in a slightly different form.
Corollary 1.
Consider a 2-coloured checkerboard rectangle, . Let denote the number of squares with colour index . Then is given by the function
where is the Kronecker delta function, which equals 1 if and 0 otherwise.
Proof.
The case leads to Corollary 2.
Corollary 2.
Consider a 3-coloured checkerboard rectangle, , with and . Let denote the number of squares with colour index . Then is given by
where is the Kronecker delta function, which equals 1 if and 0 otherwise.
Proof.
First observe that the values of a and b are restricted to 0, 1, or 2. We know that if or , i.e., then for , and 3. Thus, the possible values of a and b that we need to consider are (i) when , i.e., ; (ii) when either and , or when and , i.e., ; and (iii) when , i.e., when . Furthermore, as x can take three values this yields nine sub-cases to consider. Tedious but elementary calculations using (8) yields the following results:
which is easily verified to be equivalent to (13). □
A similar approach yields expressions for the colour counts in the cases. However, the number of sub-cases in the counts increases rapidly with increasing C. Determining the number of sub-cases is essentially the “multiplication table problem of Erdos” (the number of distinct products for is given by sequence A027424 from the On-line Encyclopedia of Integer Sequences (OEIS) [19]).
Remark 3.
Theorem 1 has several drawbacks. Firstly, the proof splits the problem into several sub-cases, resulting in a piecewise-defined solution. Secondly, the arguments includes heuristic elements due to intuitive geometric reasoning. Finally, the conditions of the theorem exclude the possibility that m or n equals 1, as it assumes , which was necessary for the partitioning and diagonal counting methods used in the proof. For these reasons, the remainder of the paper is devoted to deriving a purely mathematical solution for the colour counts that avoids these limitations.
4. Two Lemmata for the Sum of Floor Functions
The following two lemmata are necessary for proving a theorem given in Section 5.
Lemma 1.
Given and the sum
can be expressed in the following closed-form
where
Brief proof overview: The key observation is that the increasing sequence of floor values exhibits a periodic pattern. We begin by determining how often the initial and final values occur within the finite sequence. In between, the floor values increase steadily before decreasing, effectively forming an arithmetic progression. By partitioning the sequence into three segments—beginning, middle, and end—we sum the contributions of each part separately. This structured breakdown ultimately leads to the closed-form expression presented in Lemma 1.
Proof.
The approach here is similar to the proof of a related result for Lemma 1 in [10]. The infinite sequence
follows a predictable pattern, repeating every c terms, where the integers in each complete group of c terms are one more than the integers in the previous group. The terms in this increasing sequence are represented by
As we have a finite (truncated) series of terms
in the sum, the first and last group of integers in this series repeat a total of n times, where . We identify the contributions to S from the first term, the middle terms, and the last term in the sequence. To this end we need to identify the first and last terms of this sequence and the number of times they occur. The first and last integers in the finite series are given by
respectively. For example, with , , and , the terms of the sequence are
i.e., and occur two and one time, respectively.
To find the number of times the first term appears, we determine the smallest i such that
Solving for i:
Therefore, the number of times appears is
and the contribution from the first term is . To find the number of times the last term appears we determine the largest i such that
Solving for i:
Therefore, the number of times appears is
and the contribution from the last term is . Now consider the middle terms. The number of middle terms is . However, each integer is repeated c times, so we have an arithmetic series repeated c times. The number of terms in each arithmetic series is therefore
where and are defined as above.
The sum of an arithmetic series with first term , common difference d, and n terms is
For our problem,
Therefore, the sum of the middle terms is
Adding the contributions from the first term, middle terms, and last term yields
Simplifying this expression using SymPy, a Python (version 3.11.8) library for symbolic mathematics [20], yields the expression (15), as required. □
Lemma 2.
Given and the sum
can be expressed in the following closed-form:
where
Brief proof overview: We apply a change of variable that reverses the order of summation, thereby transforming the original decreasing sequence into an equivalent form that mirrors the increasing sequence considered in Lemma 1. This reformulation allows us to directly apply the formula in Lemma 1, yielding the desired closed-form expression.
Proof.
The groups of c integers in the sum exhibit a similar pattern to those in Lemma 1, but form a decreasing sequence. Instead of deriving the closed-form solution from first principles we simplify the proof by applying a change of variable to reverse the order of summation. This transformation converts the sum into the same form as the sum in (14), allowing us to directly apply the closed-form solution given in (15). Let then corresponds to and corresponds to . Substituting j into the sum (16) yields
where . As the sum is now in the form (14), applying (15) yields
where
as required. □
5. A Closed-Form Solution for Counting Squares in Rectangular Grids
We present the main result, which is a closed-form solution for the colour counts in . The proof of the theorem is based on Lemmata 1 and 2 and the following lemma regarding how many elements of a given colour index are in particular row of the colour matrix A.
Lemma 3.
Consider a colour matrix associated with a C-coloured checkerboard rectangle . The number of elements in the i-th row with a colour index is given by
Proof.
We use the following rules of congruences, which can be found in any elementary text on number theory, e.g., [7]:
- (i)
- ,
- (ii)
- ,
- (iii)
- ,
where a, b, c, and d are integers, and . Suppose , i.e., the -th entry of the colour matrix A has the colour index x. We consider i fixed and j freely varying across its range. From Proposition 1 we have
For a fixed row i we wish to find how many integers j satisfy this equation. The rules of congruences yield
Furthermore, we need to find how many integers t there are such that . As , we have
So we need to count the number of integers in the closed interval from to . Using the fact that the number of integers in the interval is , for all real and ([8], p. 74), the number of integers is given by
Using the identity for all real ([8], p. 68) the result follows. □
Example 3.
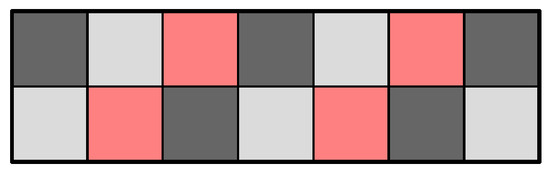
Consider the colour matrix
associated with the 3-coloured checkerboard rectangle illustrated in Figure 6. From (18), the number of squares in the i-th row of A with colour index x, where , is given by
For example:

Figure 6.
A 3-coloured checkerboard pattern applied to the rectangle, where the colour indices 1, 2, and 3 represent the colours black, grey, and red, respectively.
The following theorem is the main result of this paper.
Theorem 2.
Consider a C-coloured checkerboard rectangle , where , . The number of squares with colour index is given by the function
Proof.
Example 4.
Consider the colour matrix
associated with the 5-coloured checkerboard rectangle illustrated in Figure 7.
Using the closed-form solution (2) yields
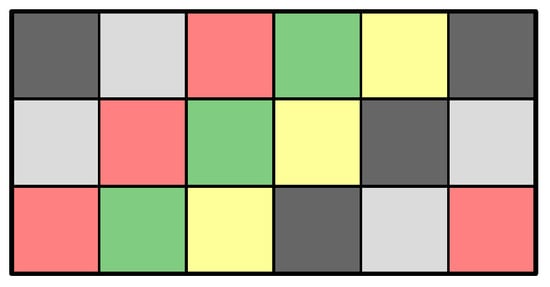
Figure 7.
A 5-coloured checkerboard pattern applied to the rectangle, where the colour indices 1, 2, 3, 4, and 5 represent the colours black, grey, red, green, and yellow, respectively.
Finally, we derive a formula for obtaining the colour counts for the general k-th checkerboard coloured variant, as the counts in Theorem 2 are for the -th variant (see Equation (4) and Proposition 1). To obtain the colour counts for a general variant, observe that, as the colour indices cycle up, the colour counts shift forward cyclically, yielding:
We illustrate this pattern in the following example:
Example 5.
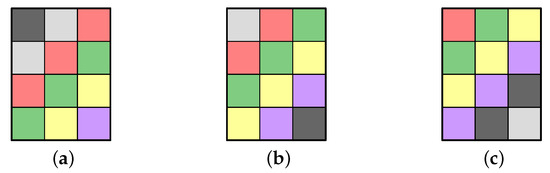

Consider three different 6-coloured checkerboard rectangles for , , and (see Figure 8). The colours used are black, grey, red, green, yellow, and blue, represented by the colour indices 1, 2, 3, 4, 5, and 6, respectively. Each time the colours cycle up by one colour, represented diagrammatically by
the variants increment, i.e., the k-th variant becomes the -th variant, and the corresponding colour counts shift forward cyclically, as shown in Table 1.

Figure 8.
Three 6-coloured checkerboard rectangles. The colour indices 1, 2, 3, 4, 5, and 6 represent the colours black, grey, red, green, yellow, and blue, respectively. (a) -th variant, (b) -th variant, (c) -st variant.

Table 1.
The table shows the colour counts for variants with colour indices .
Proposition 2 provides the generalized form of this example.
Proposition 2.
Proof.
We use proof by induction. Let be the statement that (21) is true for . Consider :
for , as required. Assume that is true. Now observe that , i.e., as r increments by one unit the corresponding colour counts shift forward by one unit because the modular arithmetic ensures that the values wrap around cyclically. Thus, holds for all . □
Remark 4.
It is instructive to contrast the computational work required to enumerate colour counts for different approaches. A brute-force method iterates over each square in the rectangle, computing the colour indices with the formula (see Proposition 1) in operations. The sum in Equation (20) is computed in operations. In contrast the formula in Theorem 2 needs operations, i.e., a fixed number of arithmetic operations, independent of and C. Thus from a computational perspective the formula in Theorem 2 is simpler than a brute-force approach or the sum in Equation (20).
Remark 5.
We used MATLAB (Version 9.14, R2023a) to numerically verify the closed-form solutions in Theorems 1 and 2 (details omitted). We compared the theoretical colour counts with numerical counts obtained via brute-force enumeration using MATLAB (see Appendix A). Many cases were checked for various values of m, n, and C.
6. Conclusions and Future Work
This paper derived closed-form solutions for counting coloured squares in rectangular grids with a generalized C-coloured checkerboard pattern. The colour indices were represented by a colour matrix , given by
The enumeration problem of counting the number of squares of each colour was converted into an equivalent problem involving sums of floor functions, where each sum has the form
We presented a method for finding a closed-form solution for the floor sums, which then led to a closed-form solution for the counts of coloured squares.
We also provided a MATLAB function using a brute-force method to numerically validate the theoretical counts (see Appendix A).
Future work could focus on deriving closed-form solutions for the counts of coloured squares in C-coloured checkerboard shapes other than rectangles, such as “Aztec diamond shapes”, “parallelogram shapes”, or “diamond shapes” (see the families of polyomino shapes in Table A1 of [2]).
Alternatively we could investigate counting coloured squares in more general C-coloured patterns applied to rectangles. For example, consider the modular arithmetic formulation of the “generalized” colour matrix defined by
and s and t are integers. For example, using colours applied to the rectangle with and yields the pattern in Figure 9, which is quite different from the coloured checkerboard patterns. Unlike the basic checkerboard arrangement, where the colour index increments are the same in both the horizontal and vertical directions, this generalized pattern employs different constant shifts across rows and down columns. These distinct step sizes yield a more intricate design, illustrating the flexibility of the modular arithmetic approach beyond simple cyclic patterns.

Figure 9.
A 4-coloured pattern applied to the rectangle using a “generalized” modular arithmetic formulation. The colours black, grey, red, and green are represented by the indices 1, 2, 3, and 4, respectively.
The methods in this paper convert this more general counting problem into an equivalent formulation involving the sum of floor functions, where each sum is of the form
Finding a closed-form solution to this sum is more challenging than the corresponding sum in (22) and will require additional strategies. Moreover, exploring these patterns could uncover interesting links between mathematics and art, as the aesthetically pleasing design in Figure 9 demonstrates.
Future work may also explore concrete applications of our enumeration techniques in computer graphics and discrete geometry. For instance, although Efros and Leung’s [21] non-parametric texture synthesis method relies on neighbourhood sampling to generate new textures, our closed-form expressions could be employed to analyze and constrain the underlying tiling configurations, thereby enhancing the efficiency of synthesis algorithms. Moreover, in discrete geometry, where similar counting problems arise in lattice point enumeration [5], our results may provide new insights into the combinatorial structure of geometric configurations.
Another promising research direction involves exploring the connections between cyclically coloured rectangular grids and graph labeling problems. In our work, we use modular arithmetic to derive closed-form expressions for counting coloured squares—a technique that mirrors modular-based labeling approaches in graph theory. For instance, Alkasasbeh et al. [22] recently applied similar ideas to the radio labeling of friendship communication networks, demonstrating that modular constraints can be used to obtain efficient bounds and algorithms for frequency assignment problems. Investigating these links further could yield new insights into colouring algorithms in both discrete geometry and graph theory, thereby enhancing our understanding and opening up practical applications in computer graphics and theoretical computer science.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding authors.
Acknowledgments
We gratefully acknowledge Rajesh Pereira (University of Guelph, Canada) for helpful suggestions on the Proof of Lemma 1. Laurence Garvie (Arizona State University, USA) provided valuable feedback on English language editing, and Allan Willms (University of Guelph, Canada) contributed useful corrections. We are also grateful to the anonymous referees for their careful corrections and valuable suggestions that improved this paper.
Conflicts of Interest
The authors declare no conflicts of interest.
Key Symbols and Notation
The following symbols and notation are used in this manuscript:
| C | Number of colours in the checkerboard pattern |
| Gridded rectangle (a polyomino) | |
| Finite grid as a subset of | |
| Integer Cartesian coordinates of a grid square | |
| Colour index function for the k-th checkerboard variant | |
| Matrix coordinates of the colour matrix | |
| Colour matrix representing the C-coloured checkerboard rectangle | |
| C-coloured checkerboard rectangle | |
| x | Colour index in the range |
| Function giving the number of squares of colour index x (see Theorem 1) | |
| Number of elements with colour index x in the i-th row of A (see Lemma 3) | |
| Closed-form function for the number of squares of colour index x (see Theorem 2) | |
| Colour count function for the k-th checkerboard variant (see Proposition 2) |
Appendix A. MATLAB Code for Colouring Rectangles
The following MATLAB code defines a function that generates and visualizes a colour matrix for an m-by-n rectangle using the -th coloured variant. It uses modular arithmetic to assign colours from the set to the rectangle’s cells and plots the result using predefined RGB colour mappings.

Appendix B. Application to an ILP-Based Tiling Method
Although our results are primarily theoretical, they are directly relevant to our ongoing research that aims to generalize an ILP techniques for tiling problems [1]. The method first imposes a fixed C-colour checkerboard pattern on the target region and then enumerates the distinct checkerboard-coloured polyominoes (called chrominoes) associated with each polyomino. In the initial ILP model, one variable is introduced per chromino, with constraints ensuring that the total counts of coloured squares in the target region match the sum of the corresponding coloured squares from the selected chrominoes. This step reduces the search space by eliminating infeasible chromino sets before considering tile placements. Solving this model yields a feasible set of chrominoes that may form a tiling.
Next, a second ILP model is built, assigning a variable to each valid placement of these chrominoes in the target region. It ensures that every chromino is placed in a way that fully covers the region while preserving the checkerboard colouring and satisfying the prescribed counts from the first model. Since the first model filters out many infeasible chromino sets, it reduces the number of placement variables required in the second model. This is useful because the general problem of determining whether a region can be tiled with polyominoes is -complete [23] and becomes computationally expensive as the problem size grows. By reducing the overall ILP size one can often achieve faster solve times with optimizers like CPLEX [24] or Gurobi [25], though the extent of these performance gains depends on the number of colours C, the problem structure, and solver heuristics.
References
- Garvie, M.R.; Burkardt, J. A Parallelizable Integer Linear Programming Approach for Tiling Finite Regions of the Plane with Polyominoes. Algorithms 2022, 15, 164. [Google Scholar] [CrossRef]
- Garvie, M.R.; Burkardt, J. A New Algorithm Based on Colouring Arguments for Identifying Impossible Polyomino Tiling Problems. Algorithms 2022, 15, 65. [Google Scholar] [CrossRef]
- Pach, J.; Agarwal, P.K. Combinatorial Geometry; Wiley-Interscience: New York, NY, USA, 1995. [Google Scholar] [CrossRef]
- Grünbaum, B.; Shephard, G. Tilings and Patterns; W.H. Freeman and Company: New York, NY, USA, 1987; Chapter 9. [Google Scholar]
- Stanley, R.P. Enumerative Combinatorics, 2nd ed.; Cambridge University Press: New York, NY, USA, 2011; Volume 1. [Google Scholar] [CrossRef]
- Ziegler, G. Lectures on Polytopes, 7th ed.; Graduate Texts in Mathematics; Springer: New York, NY, USA, 1995; Volume 152. [Google Scholar] [CrossRef]
- Burton, D. Elementary Number Theory, 7th ed.; McGraw-Hill: New York, NY, USA, 2011. [Google Scholar]
- Graham, R.L.; Knuth, D.E.; Patashnik, O. Concrete Mathematics: A Foundation for Computer Science, 2nd ed.; Addison-Wesley: Reading, MA, USA, 1994. [Google Scholar]
- Griffiths, M. More Sums Involving the Floor Function. Math. Gaz. 2002, 86, 285–287. [Google Scholar] [CrossRef]
- Palatsanga, W.; Pongsriiam, P.; Khemaratchatakumthorn, T.; Subwattanachai, K.; Khuntijit, N.; Kitnaka, N. Remarks on certain sums involving floor function. Sci. Asia 2021, 47, 640–644. [Google Scholar] [CrossRef]
- Podrug, L.; Svrtan, D. Some refinements of formulae involving floor and ceiling functions. Math. Commun. 2023, 28, 303–316. [Google Scholar]
- Bordellès, O. On certain sums of number theory. Int. J. Number Theory 2022, 18, 2053–2074. [Google Scholar] [CrossRef]
- Stucky, J. The fractional sum of small arithmetic functions. J. Number Theory 2022, 238, 731–739. [Google Scholar] [CrossRef]
- Zhang, W. On general sums involving the floor function with applications to k-free numbers. Lith. Math. J. 2023, 63, 547–556. [Google Scholar] [CrossRef]
- West, D.B. Introduction to Graph Theory; Prentice Hall: Urbana, IL, USA, 2001; Volume 2. [Google Scholar]
- Pólya, G. Kombinatorische Anzahlbestimmungen für Gruppen, Graphen und chemische Verbindungen. Acta Math. 1937, 68, 145–254. [Google Scholar]
- Ledermann, W.; Weir, A.J. Introduction to Group Theory, 2nd ed.; Longman Mathematical Series; Addison Wesley Longman Ltd.: New York, NY, USA, 1996. [Google Scholar] [CrossRef]
- Garvie, M.R. How Many Squares of Each Colour Are in a Generalized C-Coloured m × n Rectangle? Mathematics Stack Exchange. 2022. Available online: https://math.stackexchange.com/questions/4439271/how-many-squares-of-each-colour-are-in-a-generalized-checkerboard-c-coloured (accessed on 1 March 2025).
- OEIS Foundation Inc. Sequence A027424. Available online: https://oeis.org/A027424 (accessed on 1 March 2025).
- Meurer, A. SymPy: Symbolic Computing in Python, Version 1.8. 2024. Available online: https://www.sympy.org/en/index.html (accessed on 1 March 2025).
- Efros, A.A.; Leung, T.K. Texture Synthesis by Non-parametric Sampling. In Proceedings of the Seventh IEEE International Conference on Computer Vision, Corfu, Greece, 20–27 September 1999; pp. 1033–1038. [Google Scholar] [CrossRef]
- Alkasasbeh, A.H.; Badr, E.; Attiya, H.; Shabana, H.M. Radio Number for Friendship Communication Networks. Mathematics 2023, 11, 4232. [Google Scholar] [CrossRef]
- Demaine, E.; Demaine, M. Jigsaw Puzzles, Edge Matching, and Polyomino Packing: Connections and Complexity. Graphs Comb. 2007, 23, 195–208. [Google Scholar] [CrossRef]
- IBM ILOG. IBM ILOG CPLEX Optimization Studio. 2025. Available online: https://www.ibm.com/products/ilog-cplex-optimization-studio (accessed on 1 March 2025).
- Gurobi Optimization, LLC. GUROBI 12.0. 2024. Available online: https://www.gurobi.com/ (accessed on 1 March 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
