Evaluation Model for Indoor Comprehensive Environmental Comfort Based on the Utility Function Method
Abstract
1. Introduction
2. Methods
2.1. Field Survey
2.1.1. Survey Location
2.1.2. Subjective Questionnaire
2.1.3. Objective Measurements
2.2. Indoor Comprehensive Environmental Comfort Evaluation Method
2.2.1. Multi-Factor Comprehensive Evaluation Method
2.2.2. Principles for Determining Utility Function
- (1)
- y is related to x and only to x;
- (2)
- y is independent of the measurement units of x;
- (3)
- y = f (x) has a relatively clear range of values or critical points;
- (4)
- The results of y = f (x) are intuitive and have clear physical meanings;
- (5)
- Within the same indicator system, for different x values, different forms of y = f (x) may be used;
- (6)
- The range of values for y = f (x) should meet the requirements of the composite model;
- (7)
- The type and form of y = f (x) should be selected based on the impact of changes in x on the evaluation object;
- (8)
- Under the premise that the direction, concavity, and other characteristics of y = f (x) are clear, its form should be simplified as much as possible.
2.2.3. Weight Calculation Method
- a.
- Weight calculation using AHP [38]
- (1)
- Matrix construction. Based on the evaluations of the experts for each indicator, the importance of pairwise indicators is compared using a 1–9 scale [39] to construct an n × n judgment matrix A.where aij (i, j = 1, 2, 3, … n) is the relative importance of pairwise indicator comparisons, , .
- (2)
- Calculate weights.
- (3)
- Consistency test.where CI is the consistency indicator, RI is the average random consistency indicator, and CR is the consistency ratio (if CR is less than 0.1, it is considered that the judgment matrix A has passed the consistency).
- (4)
- Weight determination. The eigenvectors corresponding to the maximum eigenvalues are normalized to obtain the weights of each evaluation indicator.
- b.
- Weight calculation using EWM [40]
- (1)
- Matrix construction. Assuming that there are m samples and n indicators, an n × m evaluation matrix A is constructed based on the expert scores for each indicator.where (i = 1, 2, 3,…, m; j = 1, 2, 3,…, n) represents the original scores of the i-th evaluation object on the j-th evaluation criterion.
- (2)
- Data standardization. Different evaluation indicators have distinct dimensions and units. To eliminate the influence of differing dimensions and units on evaluation results, data standardization is necessary. The standardization method is as follows:where rij represents the standardized value of the j-th indicator for the i-th sample.
- (3)
- Entropy value calculation.where ej is the entropy value of the j-th indicator, and pij is the proportion of the i-th sample under the j-th indicator.
- (4)
- Entropy weight determination.where ωj is the weight of the j-th indicator, and dj is the differentiation coefficient of the j-th indicator.
- c.
- Combined weight calculation [41]
2.2.4. Model Synthesis Method
2.3. Key Environmental Factors Analysis Method
2.3.1. Multi-Factor Analysis Method
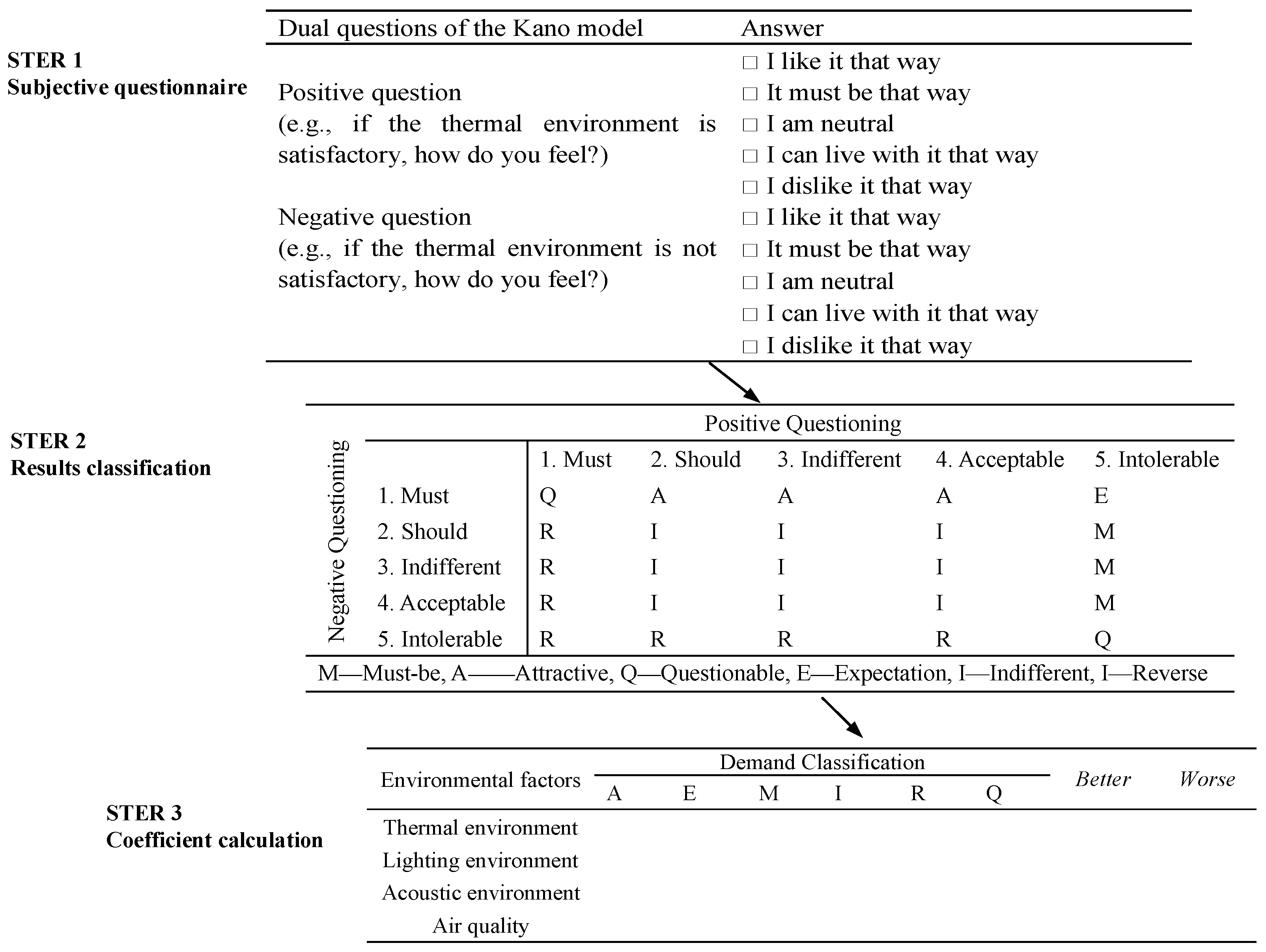
2.3.2. Overview of the Kano Model
3. Results and Analysis
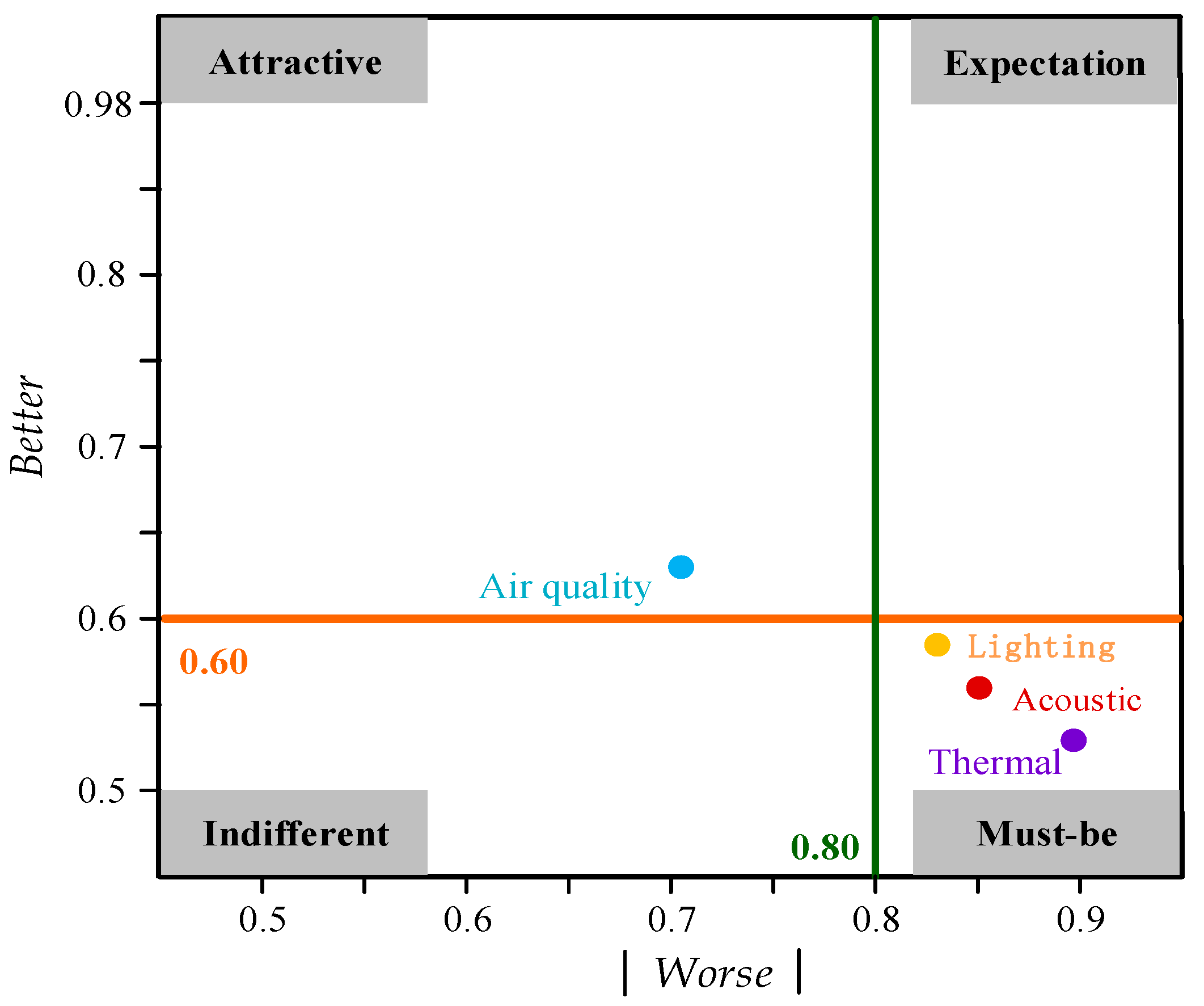
3.1. Key Environmental Factors
3.2. Individual Environmental Comfort
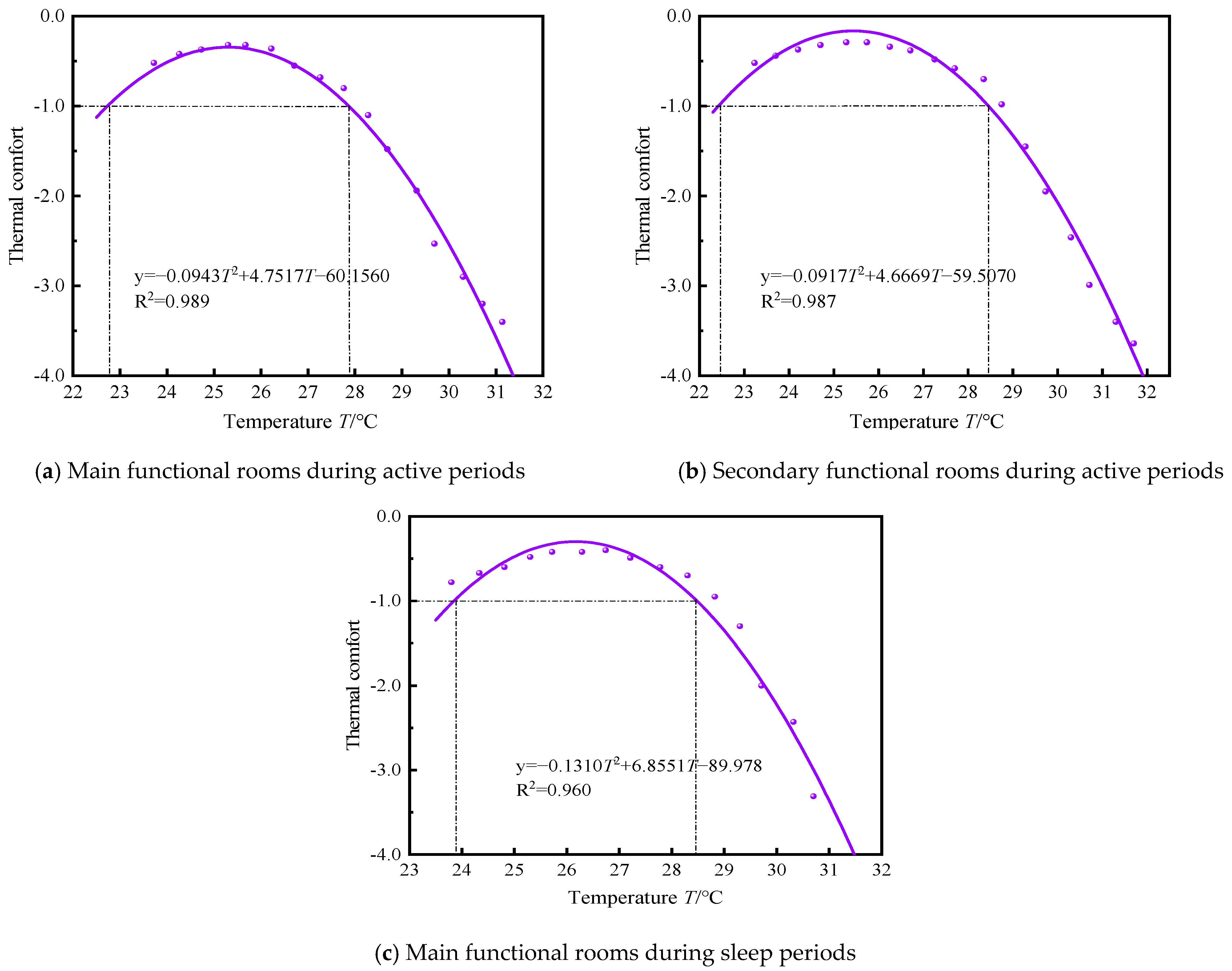
3.2.1. Thermal Environment
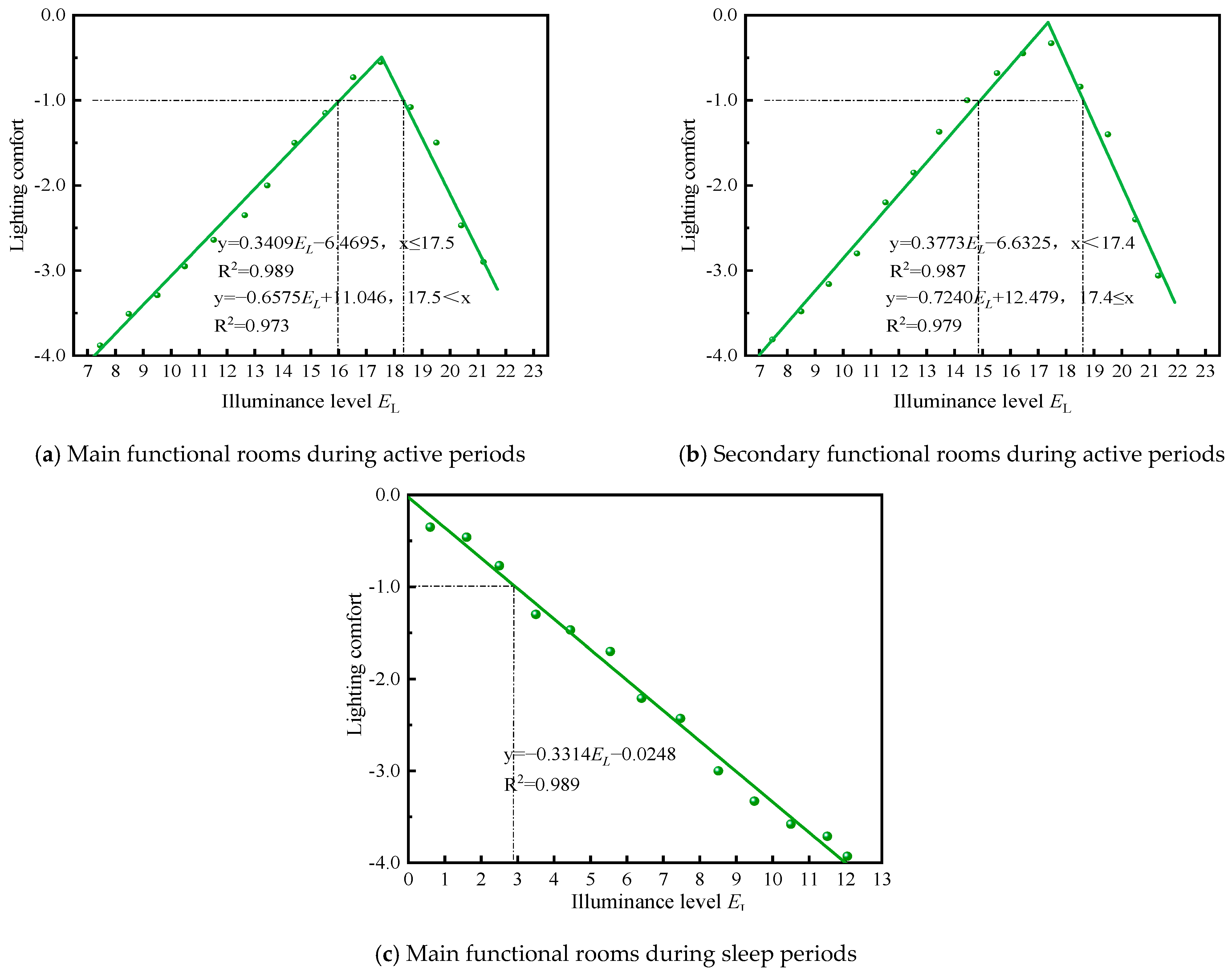
3.2.2. Luminous Environment
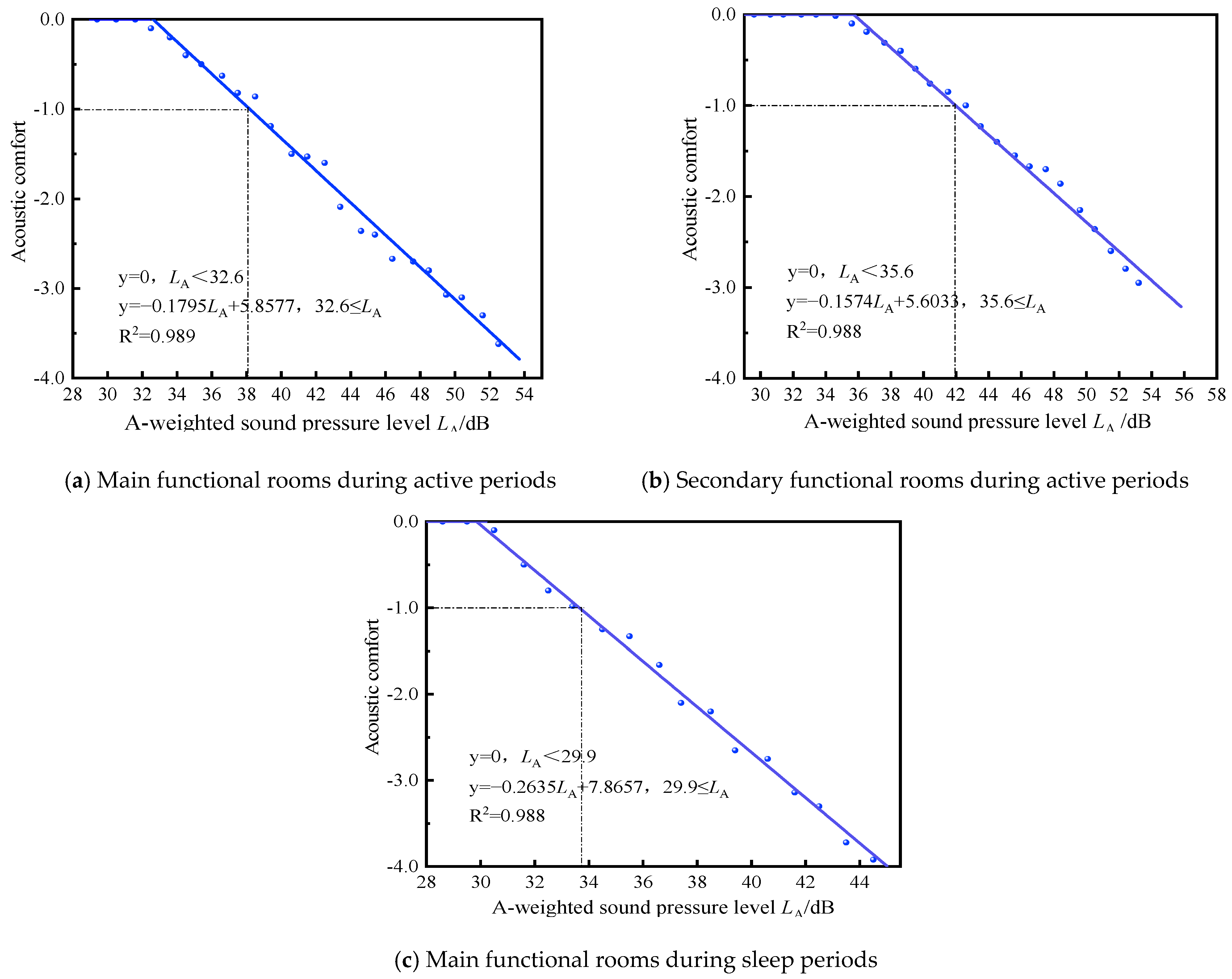
3.2.3. Acoustic Environment
3.3. Weight of Individual Environmental Comfort
3.4. Evaluation Model for Comprehensive Environmental Comfort
4. Discussion
4.1. Comparison with Previous Results of the Kano Model
4.2. Comparison with Previous Comprehensive Evaluation Models
4.3. Application of the Comprehensive Comfort Evaluation Model
5. Conclusions
- (1)
- Based on the subjective evaluation characteristics of indoor environmental comfort and the principles of multi-factor comprehensive evaluation, a comprehensive environmental comfort evaluation method utilizing the utility function approach was proposed.
- (2)
- Through a quantitative analysis using the Kano model, the thermal, light, and acoustic environments were identified as the key factors affecting comprehensive indoor environmental comfort, while air quality was a non-key factor.
- (3)
- The weights of different individual environmental comfort factors in the comprehensive environmental comfort varied, with differences further influenced by room attributes and usage time periods.
- (4)
- Quantitative relationships between comfort and temperature, illuminance, and noise levels were established, and the weights of individual environmental factors were determined, based on the perspective of categorizing functional rooms and usage time periods.
- (5)
- A quantitative evaluation model for indoor comprehensive environmental comfort that considered the one-vote veto characteristics and differentiated demands was proposed based on the penalty substitution synthesis method.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Abdel-Salam, M.M.M. Indoor exposure of elderly to air pollutants in residential buildings in Alexandria, Egypt. Build. Environ. 2019, 7, 109221. [Google Scholar] [CrossRef]
- Indraganti, M.; Boussaa, D. An adaptive relationship of thermal comfort for the Gulf Cooperation Council (GCC) Countries: The case of offices in Qatar. Energy Build. 2018, 159, 201–212. [Google Scholar] [CrossRef]
- Rajan, K.; Rijal, H.B.; Shukuya, M.; Yoshida, K. An in-situ study on occupants’ behaviors for adaptive thermal comfort in a Japanese HEMS condominium. Build. Eng. 2018, 19, 402–411. [Google Scholar]
- Rijal, H.B. Thermal adaptation of buildings and people for energy saving in extreme cold climate of Nepal. Build. Environ. 2021, 230, 110551. [Google Scholar] [CrossRef]
- Fan, X.N.; Zhao, Q.; Sang, G.C.; Zhu, Y.Y. Numerical Study on the Suitability of Passive Solar Heating Technology Based on Differentiated Thermal Comfort Demand. Comput. Model. Eng. Sci. 2022, 132, 627–660. [Google Scholar] [CrossRef]
- Mohd Husini, E.; Arabi, F.; Ossen Dilshan, R.; Kandar, M.Z.; Mat Lajis, N. Daylight in Office Buildings in Malaysia: A Pilot Study on Occupants’ Satisfaction and Luminous Environment. Spaces Flows Int. Urban Extra Urban Stud. 2008, 3, 662–677. [Google Scholar] [CrossRef]
- Zhu, C.H.; Li, N.P.; Re, D.; Guan, J. Uncertainty in indoor air quality and grey system method. Build. Environ. 2007, 42, 1711–1717. [Google Scholar] [CrossRef]
- Mui, K.W.; Wong, L.T. A method of assessing the acceptability of noise levels in air conditioned offices. Build. Serv. Eng. Res. Technol. 2006, 27, 249–254. [Google Scholar] [CrossRef]
- Liu, H.M.; He, H.; Qin, J.J. Does background sounds distort concentration and verbal reasoning performance in open-plan office. Appl. Acoust. 2021, 172, 107577. [Google Scholar] [CrossRef]
- Washita, G.; Kimura, K.; Tanabe, S.; Yoshizawa, S.; Ikeda, K. Indoor air quality assessment based on human olfactory sensation. J. Archit. Plan. Environ. 1990, 410, 9–19. [Google Scholar]
- Li, W.M.; Lee, S.C.; Chan, L.Y. Indoor air quality at nine shopping malls in Hong Kong. Sci. Total Environ. 2001, 273, 27–40. [Google Scholar] [CrossRef]
- Djamila, H.; Chu, C.M.; Kumaresan, S. Field study of thermal comfort in residential buildings in the equatorial hot-humid climate of Malaysia. Build. Environ. 2013, 62, 133–142. [Google Scholar] [CrossRef]
- Yu, W.; Li, B.Z.; Yao, R.M.; Wang, D.; Li, K.T. A study of thermal comfort in residential buildings on the Tibetan Plateau, China. Build. Environ. 2017, 119, 71–86. [Google Scholar] [CrossRef]
- Guo, T.M.; Hu, S.T.; Liu, T.M. Research on the influence factors of indoor light environment comfort within asymptomatic altitude reaction. Build. Sci. 2016, 32, 39–44. [Google Scholar]
- de Boer, J.B.F. Indoor Lighting; Light Industry Press: Beijing, China, 1989. [Google Scholar]
- Fanger, P.O. Theral Comfort; Krieger Publishing Company: Malabar, FL, USA, 1982. [Google Scholar]
- Clausen, G. A comparative study of discomfort caused by indoor air pollution, thermal load and noise. Indoor Air. 2021, 3, 255–262. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, Q.W.; Fan, F.; Shen, S.Z. A comprehensive comfort assessment method for indoor environmental quality in university open-plan offices in severe cold regions. Build. Environ. 2021, 197, 107845. [Google Scholar] [CrossRef]
- Guo, T.M.; Hu, S.T.; Liu, G.D. Evaluation model of specific indoor environment overall comfort based on effective-function method. Energies 2017, 10, 1634. [Google Scholar] [CrossRef]
- Fassio, F.; Fanchiotti, A.; De Lieto Vollaro, R. Linear, non-linear and alternative algorithms in the correlation of IEQ factors with global comfort: A case study. Sustainablity 2014, 6, 8113–8127. [Google Scholar] [CrossRef]
- Mihai, T.; Iordache, V. Determining the indoor environment quality for an educational building. Energy Proc. 2016, 85, 566–574. [Google Scholar] [CrossRef]
- Yang, D.; Mak, C.M. Relationships between indoor environmental quality and environmental factors in university classrooms. Build. Environ. 2020, 186, 107331. [Google Scholar] [CrossRef]
- Li, S.M. Study on Environmental Quality Evaluation Model of Office Building. Master’s Thesis, Guangzhou University, Guangzhou, China, 2018. [Google Scholar]
- Ncube, M.; Riffat, S. Developing an indoor environment quality tool for assessment of mechanically ventilated office buildings in the UK—A preliminary study. Build. Environ. 2012, 53, 26–33. [Google Scholar] [CrossRef]
- Lai, A.C.K.; Mui, K.W.; Wong, L.T.; Law, L.Y. An evaluation model for indoor environmental quality (IEQ) acceptance in residential buildings. Energy Build. 2009, 41, 930–936. [Google Scholar] [CrossRef]
- Wei, N.; Guo, Y.; Feng, X.Y.; Cao, X.Y.; Su, L.J. Study on the thermal environment of rural residential buildings in winter in the Guanzhong region of Shaanxi. Ecol. Econ. 2023, 1, 79–90. [Google Scholar]
- Ji, T.T.; Zhang, T.; Fukuda, H. Thermal Comfort Research on the Rural Elderly in the Guanzhong Region: A Comparative Analysis Based on Age Stratification of Residential Environments. Sustainability 2024, 16, 6101. [Google Scholar] [CrossRef]
- ISO 7726; Thermal Environmental Conditions for Human Occupancy. International Standardization Organization: Geneva, Switzerland, 1985.
- Liu, Y.S.; Yang, C.H.; Huang, K.K.; Liu, Y.P. A multi-factor selection and fusion method through the CNN-LSTM network for dynamic Price forecasting. J. Jpn. Soc. Qual. Control 2023, 11, 1132. [Google Scholar] [CrossRef]
- Fan, C.H.; Chen, Y.; Zhang, L.; Wu, W.J.; Ling, B.; Tian, S.J. Using fuzzy comprehensive evaluation to assess the competency of full-time water conservancy emergency rescue teams. Mathematics 2021, 10, 2111. [Google Scholar] [CrossRef]
- Zheng, G.Z.; Li, K.; Bu, W.T.; Wang, Y.J. Fuzzy comprehensive evaluation of human physiological state in indoor high temperature environments. Build. Environ. 2019, 150, 108–118. [Google Scholar] [CrossRef]
- Pazouki, M.; Rezaie, K.; Bozorgi Amiri, A. A fuzzy robust multi-objective optimization model for building energy retrofit considering utility function: A university building case study. Energy Build. 2021, 241, 110933. [Google Scholar] [CrossRef]
- Tong, H.P.; Krishna Kumar, T.; Huang, Y.X. Multivariate Statistical Analysis and Data Analysis; Wiley Online Library: Hoboken, NJ, USA, 2011. [Google Scholar]
- Li, J.P.; Xie, B.C. Multivariate Statistical Analysis; China Renmin University Press: Beijing, China, 2008. [Google Scholar]
- Liu, S.F.J.; Yang, Y.; Liu, S. Grey System: Thinking, Methods, and Models with Applications; Wiley Online Library: Hoboken, NJ, USA, 2015. [Google Scholar]
- Baymani, M.; Effati, S.; Niazmand, H.; Kerayechian, A. Kerayechian Artificial neural network method for solving the Navier–Stokes equations. Neural Comput. Appl. 2014, 26, 765–773. [Google Scholar] [CrossRef]
- Sun, X.D.; Li, Z.; Chen, F.M. Research on multiple attribute synthetical evaluation methods based on artificial neural network. J. Zhengzhou Univ. Light Ind. Nat. Sci. 2003, 18, 11–14. [Google Scholar]
- Liu, L.L.; Dou, Y.M.; Qiao, J.G. Evaluation method of highway plant slope based on rough set theory and analytic hierarchy process: A case study in Taihang mountain, Hebei, China. Mathematics 2022, 10, 1264. [Google Scholar] [CrossRef]
- Fan, X.N.; Guo, Y.; Zhao, Q.; Zhu, Y.Y. Structural optimization and application research of alkali-activated slag ceramsite compound insulation block based on finite element method. Mathematics 2021, 9, 2488. [Google Scholar] [CrossRef]
- Wang, Q.; Liu, Y.F.; Zhang, X.D.; Fu, H.C.; Niu, C.C. Study on an AHP-Entropy-ANFIS model for the prediction of the unfrozen water content of sodium-bicarbonate-type salinization frozen soil. Mathematics 2020, 8, 1209. [Google Scholar] [CrossRef]
- Liu, J.; Yu, S.H.; Chu, J.J. The comfort evaluation in civil aircraft cabin based on objective and subjective weighting method. J. Graph. 2017, 38, 192–197. [Google Scholar]
- Kano, N.; Seraku, N.; Takahashi, F. Attractive quality and must-be quality. J. Jpn. Soc. Qual. Control 1984, 14, 39–48. [Google Scholar]
- Kim, J.; de Dear, R. Nonlinear relationships between individual IEQ factors and overall workspace satisfaction. Build. Environ. 2012, 49, 33–40. [Google Scholar] [CrossRef]
- Zhang, Y.C. Research on Interaction Effect of Thermal, Light and Acoustic Environment on Human Comfort in Waiting Area of High-Speed Railway Station; Beijing Jiaotong University: Beijing, China, 2021. [Google Scholar]
- Geng, Y.; Yu, J.; Lin, B.; Wang, Z.; Huang, Y. Impact of individual IEQ factors on passengers’ overall satisfaction in Chinese airport terminals. Build. Environ. 2017, 12, 241–249. [Google Scholar] [CrossRef]
- Timko, M. An experiment in continuous analysis. J. Manag. Qual. Cent. 1993, 2, 17–20. [Google Scholar]
- GB 50034-2024; Standard for Lighting Design of Buildings. MOHURD, China Architecture & Building Press: Beijing, China, 2013.
- Wu, S.H.; Adil Khan, M. Refinements of majorization inequality involving convex functions via Taylor’s theorem with mean value form of the remainder. Mathematics 2019, 7, 663. [Google Scholar] [CrossRef]
- Kim, J.; de Dear, R. Impact of different building ventilation modes on occupant expectations of the main IEQ factors. Build. Environ. 2012, 57, 184–193. [Google Scholar] [CrossRef]
- Cao, B.; Qin, Q.; Zhu, Y.; Li, H.; Hu, H.; Deng, G. Development of a multivariate regression model for overall satisfaction in public buildings based on field studies in Beijing and Shanghai. Build. Environ. 2012, 47, 394–399. [Google Scholar] [CrossRef]

| Classification | Background | Percentage (%) |
|---|---|---|
| Gender | Male | 47.1 |
| Female | 52.9 | |
| Age | 18~35 | 14.2 |
| 36~55 | 29.5 | |
| 56~75 | 56.3 | |
| Educational level | Junior high school or lower | 57.8 |
| High school | 32.2 | |
| Associate degree | 7.1 | |
| Bachelor’s degree or higher | 2.9 |
| Measurement Parameters | Measurement Instruments | Type | Range | Accuracy |
|---|---|---|---|---|
| Temperature | Temperature and humidity recorder | SW-572 | −20~60 °C | ±0.3 °C |
| Noise level | Sound level meter | AWA6291 | 25~140 dB(A) | ±1% |
| CO2 concentration | CO2 detector | SW-723 | 0~9999 ppm | ±(40 + 3%) ppm |
| Illuminance | Illuminance meter | JTG01 | 0.1~100,000 lx | ±4% |
| Environmental Factors | Demand Classification | Better | Worse | |||||
|---|---|---|---|---|---|---|---|---|
| A | E | M | I | R | Q | |||
| Thermal environment | 368 | 332 | 86 | 3 | 0 | 5 | 0.53 | −0.89 |
| Lighting environment | 322 | 327 | 135 | 4 | 0 | 6 | 0.58 | −0.83 |
| Acoustic environment | 339 | 327 | 115 | 4 | 0 | 9 | 0.56 | −0.85 |
| Air quality | 210 | 320 | 199 | 58 | 0 | 7 | 0.66 | −0.67 |
| Illuminance Value | Illuminance Level | Illuminance Value | Illuminance Level |
|---|---|---|---|
| 0~0.25 | 0~1 | 75~100 | 12~13 |
| 0.25~0.5 | 1~2 | 100~150 | 13~14 |
| 0.5~1 | 2~3 | 150~200 | 14~15 |
| 1~2 | 3~4 | 200~300 | 15~16 |
| 2~3 | 4~5 | 300~500 | 16~17 |
| 3~5 | 5~6 | 500~750 | 17~18 |
| 5~10 | 6~7 | 750~1000 | 18~19 |
| 10~15 | 7~8 | 1000~1500 | 19~20 |
| 15~20 | 8~9 | 1500~2000 | 20~21 |
| 20~30 | 9~10 | 2000~3000 | 21~22 |
| 30~50 | 10~11 | 3000~5000 | 22~23 |
| 50~75 | 11~12 | —— | —— |
| Evaluation Indicators | Subjective Weights | ||
|---|---|---|---|
| Main Functional Rooms During Active Periods | Secondary Functional Rooms During Active Periods | Main Functional Rooms During Sleep Periods | |
| Thermal comfort | 40.9% | 45.6% | 34.0% |
| Lighting comfort | 31.7% | 33.5% | 28.8% |
| Acoustic comfort | 27.4% | 20.9% | 37.2% |
| Verification Indicators | Consistency Verification Indicators | ||
|---|---|---|---|
| Main Functional Rooms During Active Periods | Secondary Functional Rooms During Active Periods | Main Functional Rooms During Sleep Periods | |
| CI | 0.0010 | 0.0120 | 0.0002 |
| CR | 0.0017 | 0.0207 | 0.0003 |
| Evaluation Indicators | Objective Weights | ||
|---|---|---|---|
| Main Functional Rooms During Active Periods | Secondary Functional Rooms During Active Periods | Main Functional Rooms During Sleep Periods | |
| Thermal comfort | 42.3% | 45.0% | 33.8% |
| Lighting comfort | 31.7% | 36.7% | 30.9% |
| Acoustic comfort | 26.0% | 18.3% | 35.3% |
| Evaluation Indicators | Combined Weights | ||
|---|---|---|---|
| Main Functional Rooms During Active Periods | Secondary Functional Rooms During Active Periods | Main Functional Rooms During Sleep Periods | |
| Thermal comfort | 41.6% | 45.3% | 33.9% |
| Lighting comfort | 31.7% | 35.1% | 29.9% |
| Acoustic comfort | 26.7% | 19.6% | 36.2% |
| Correction Term | Different Types of Rooms | |||
|---|---|---|---|---|
| Main Functional Rooms During Active Periods | Secondary Functional Rooms During Active Periods | Main Functional Rooms During Sleep Periods | ||
| δ(X) | Winter | 0.3120x2 − 1.0863x | 0.2655x2 − 0.9491x | 0.3497x2 − 1.3080x |
| Summer | 0.3288x2 − 1.2290x | 0.2737x2 − 1.0744x | 0.3501x2 − 1.3706x | |
| Environmental Factors | ||||
|---|---|---|---|---|
| Thermal | Indoor Air Quality | Luminous | Acoustic | |
| Kim and de Dear [49] | ✓ | / | / | ✓ |
| Zhang [49] | ✓ | / | / | / |
| This study | ✓ | / | ✓ | ✓ |
| Studies | Research Object | Evaluation Method | Weight Method | Evaluation Model |
|---|---|---|---|---|
| Cao et al. [50] | Office, teaching building, library | Multivariate linear regression | Regression coefficient | |
| Ncube and Riffat [24] | Office | Multivariate linear regression | Regression coefficient | |
| Li [23] | Office | Multivariate linear regression | Regression coefficient | |
| Fassi et al. [20] | Classroom | Multivariate linear regression | Regression coefficient | |
| Yang and Mark [22] | Classroom | Multivariate logistic regression | Regression coefficient | |
| Lai et al. [25] | High-rise residential | Multivariate logistic regression | Regression coefficient | |
| Catalina and Iordache [21] | Classroom | Multivariate linear regression | Regression coefficient |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, X.; Zhu, Y. Evaluation Model for Indoor Comprehensive Environmental Comfort Based on the Utility Function Method. Mathematics 2025, 13, 1000. https://doi.org/10.3390/math13061000
Fan X, Zhu Y. Evaluation Model for Indoor Comprehensive Environmental Comfort Based on the Utility Function Method. Mathematics. 2025; 13(6):1000. https://doi.org/10.3390/math13061000
Chicago/Turabian StyleFan, Xiaona, and Yiyun Zhu. 2025. "Evaluation Model for Indoor Comprehensive Environmental Comfort Based on the Utility Function Method" Mathematics 13, no. 6: 1000. https://doi.org/10.3390/math13061000
APA StyleFan, X., & Zhu, Y. (2025). Evaluation Model for Indoor Comprehensive Environmental Comfort Based on the Utility Function Method. Mathematics, 13(6), 1000. https://doi.org/10.3390/math13061000






