Abstract
This study presents a comprehensive evaluation of the quick invariant signature (QIS), dynamic time warping (DTW), and a novel hybrid QIS + DTW approach for time series analysis. QIS, a translation and rotation invariant shape descriptor, and DTW, a widely used alignment technique, were tested individually and in combination across various datasets, including ECG5000, seismic data, and synthetic signals. Our hybrid method was designed to embed the structural representation of the QIS with the temporal alignment capabilities of DTW. This hybrid method achieved a performance of up to 93% classification accuracy on ECG5000, outperforming DTW alone (86%) and a standard MLP classifier in noisy or low-data conditions. These findings confirm that integrating structural invariance (QIS) with temporal alignment (DTW) yields superior robustness to noise and time compression artifacts. We recommend adopting hybrid QIS + DTW, particularly for applications in biomedical signal monitoring and earthquake detection, where real-time analysis and minimal labeled data are critical. The proposed hybrid approach does not require extensive training, making it suitable for resource-constrained scenarios.
Keywords:
time series analysis; affine invariance; hybrid QIS + DTW; time series classification; structural invariance; noise robustness in time series MSC:
62M10
1. Introduction
Time series analysis is fundamental in a wide range of disciplines, including biomedical signal processing, finance, climate modeling, and engineering. The ability to accurately classify, compare, and analyze time-dependent data is crucial for applications such as ECG-based cardiac diagnosis [1], seismic activity detection, and financial market trend forecasting. Traditional methods for time series similarity assessment primarily rely on distance metrics, with dynamic time warping, or DTW [2], being one of the most widely used techniques. DTW provides an effective means of aligning two sequences by minimizing temporal discrepancies through nonlinear warping. While DTW remains a widely adopted technique, it has notable limitations: it lacks explicit structural awareness, is sensitive to global distortions, and has a high computational cost for large datasets [3].
To address these challenges, researchers have explored alternative approaches, including deep learning-based time series classification [4], shapelet-based methods [5], and symbolic representations [6]. Wavelet transformations [7] have also been used to show frequency variations.
However, deep learning techniques require extensive labeled training data, suffer from interpretability issues, and often fail to generalize well outside their training distributions. Similarly, shapelet-based methods involve heuristic-driven feature extraction, making them less adaptable to unstructured time series data. Given these constraints, there is a need for a method that can robustly extract meaningful features from time series while remaining computationally efficient and adaptable across different domains. CNN or transformers were deliberately left out of this work because they require huge computational resources and large labeled datasets. These requirements are not always available, especially when dealing with rare cases, such as unusual cardiology instances or scenarios requiring near-real-time analysis.
Time series data in biomedical (ECG), seismic, or financial domains often contain significant noise, amplitude distortion, and temporal misalignment. While DTW excels at aligning signals, it overlooks global shape invariances; conversely, shape descriptors like QIS lack explicit time alignment. Merging these techniques addresses a critical need in real-world applications: robust classification even under limited labeled data, noise, or compression. By unifying QIS’s shape-based invariance with DTW’s alignment, our approach promises efficient and interpretable solutions for practitioners who cannot afford lengthy training or extensive datasets.
QIS [8] was originally developed for pattern recognition in binary images, where it efficiently encodes geometric relationships between significant points in a way that is invariant to translation and rotation. These properties make QIS a strong candidate for time series analysis, particularly for datasets with structural patterns that persist despite minor deformations, time shifts, or variations in amplitude. Unlike DTW, which strictly aligns sequences, QIS captures the overall structure of a signal by computing pairwise relationships between the key points (such as peaks and troughs) and encoding them into a compact signature. This allows QIS to distinguish between time series not solely based on their sequential alignment, but also by recognizing shape-based patterns.
Despite its advantages, QIS has not been extensively applied in time series analysis, and its effectiveness in practical applications remains underexplored. Previous research has demonstrated the value of shape-based descriptors in fields such as biomedical signal classification, where morphological differences in ECG signals are crucial for diagnosing cardiac conditions. This motivates our investigation into whether QIS can provide a viable alternative to existing time series similarity measures, particularly in scenarios where capturing geometric structure is as important as temporal alignment.
In this study, we introduce a hybrid QIS + DTW approach that integrates QIS’s structural representation with DTW’s alignment capabilities. Although DTW provides flexible temporal alignment, it does not inherently capture the global shape of signals. QIS, on the other hand, encodes structural information that is invariant under translation and rotation. Merging these approaches yields a more robust similarity measure, unifying local alignment with shape-based discrimination.
Our contributions are as follows:
- We developed a novel adaptation of QIS for time series analysis, including the implementation of Toric QIS, which accounts for periodic boundary conditions in cyclic signals.
- We introduced a hybrid similarity measure that optimally balances QIS and DTW, using an empirically tuned weighting factor to enhance classification performance.
- We evaluated our approach on real-world time series datasets, including ECG5000 from the UCR archive and seismic activity records, demonstrating improved robustness and interpretability compared to the existing methods.
- We conducted a comparative analysis against DTW, FastDTW, shapelet-based learning, and MLP classifiers, providing empirical evidence of QIS’s advantages in low-data and high-variability settings.
The remainder of this paper is structured as follows: Section 2 discusses related work in time series similarity, highlighting the strengths and limitations of the existing approaches. Section 3 details the methodology behind the QIS and its adaptation to time series, including the hybrid QIS + DTW framework. Section 4 presents our experimental setup, datasets, and evaluation metrics. Section 5 discusses our findings, including performance comparisons, noise robustness analysis, and computational efficiency. Finally, Section 6 concludes with insights into the applicability of the QIS for real-world time series analysis and potential future research directions.
2. Literature Review
2.1. Overview of Time Series Similarity Measures
Time series similarity measurement is a crucial problem across various domains, including finance, healthcare, and geophysics. The ability to accurately compare time-dependent signals has implications for predictive analytics, anomaly detection, and classification tasks. Over time, numerous methodologies have been developed, broadly categorized into distance-based approaches, feature-based approaches, and deep learning-based methods. While each category offers distinct advantages, they also present limitations, necessitating hybrid solutions that can integrate the strengths of multiple techniques.
2.1.1. Distance-Based Approaches
One of the most fundamental approaches to measuring time series similarity is Euclidean distance, which calculates the pointwise difference between two sequences. While straightforward and computationally efficient, Euclidean distance fails to account for temporal distortions and phase shifts, limiting its applicability in real-world scenarios.
To address these shortcomings, dynamic time warping (DTW) was introduced as a more flexible alternative that allows for nonlinear alignment between sequences [2]. DTW has been widely utilized in fields such as speech recognition, gesture analysis, and bioinformatics due to its robustness against time distortions. However, DTW suffers from high computational complexity, making it less practical for large-scale datasets. Various optimizations have been proposed, such as FastDTW [3], which approximates DTW with reduced computational costs but at the expense of some accuracy. Despite these improvements, DTW-based methods remain constrained by their reliance on alignment-based comparisons, which do not inherently capture structural relationships within time series data.
2.1.2. Feature-Based Approaches
Feature-based methods seek to extract meaningful characteristics from time series rather than rely solely on direct alignment. One of the most prominent techniques in this category is the shapelet transform [5], which identifies discriminative subsequences that contribute to classification tasks. Shapelet-based methods have demonstrated high classification accuracy in various applications, particularly in biomedical signal analysis. However, they require computationally expensive feature selection processes, limiting their scalability.
Another significant feature-based technique is symbolic aggregate approximation (SAX) [6], which converts time series into symbolic representations to facilitate efficient indexing and retrieval. While SAX improves computational efficiency, it may lead to the loss of fine-grained structural details due to its discretization process. Similarly, wavelet-based approaches [7] decompose time series into frequency components, capturing both local and global variations. These methods have been particularly valuable in domains where frequency information plays a critical role, such as financial forecasting and biomedical signal processing.
While feature-based approaches offer advantages in capturing time series characteristics, they often struggle with adaptability across different domains. The extracted features may not generalize well across datasets with diverse structural properties, highlighting the need for more versatile methods that integrate multiple perspectives.
2.1.3. Deep Learning-Based Methods
The emergence of deep learning has led to the development of data-driven approaches for time series similarity measurement. Convolutional neural networks (CNNs) have been employed to automate feature extraction, demonstrating notable success in time series classification tasks [4]. More recently, long short-term memory (LSTM) networks [9] and transformer models [10,11] have been used to model complex temporal dependencies, enabling improved sequence learning capabilities.
Despite their advantages, deep learning-based approaches present notable challenges. These models require large labeled datasets and substantial computational resources, making them impractical in low-data environments. Furthermore, deep learning models often function as “black boxes,” lacking interpretability, which can be a significant drawback in critical applications such as healthcare and finance. The computational burden associated with deep learning further underscores the necessity of hybrid approaches that can balance accuracy, efficiency, and interpretability.
Recent studies have also significantly advanced the field of time series classification using deep learning techniques. For example, ref. [12] provided a thorough review of deep learning models—including CNNs, RNNs, and hybrid architectures—and introduced InceptionTime, a CNN-based approach that captures multi-scale temporal features efficiently. These works underline the impressive performance that such models can achieve on benchmark datasets, especially when ample labeled data and computational resources are available.
In parallel, transformer-based methods are emerging as a robust alternative for handling complex temporal dependencies. Ref. [13] developed the temporal fusion transformer (TFT), which leverages attention mechanisms to provide both high forecasting accuracy and interpretability. Similarly, ref. [14] demonstrated that transformers can be effectively applied to time series classification tasks, offering competitive results by efficiently modeling long-range dependencies. These approaches contribute to a growing body of literature that emphasizes the potential of attention-based architectures in time series analysis.
The CNN- and transformer-based studies were deliberately left out of our evaluation because they need large labeled datasets and significant computational power. Therefore, they remain unusable for rare cases with low data volume or when fast analytics or ad-hoc results are required.
2.2. Quick Invariant Signature (QIS) in Time Series Analysis
The QIS was originally developed as a geometric pattern recognition technique for binary images [8]. The idea behind this algorithm was to encode the image based on the frequency of appearance of similar segments. Segments with the same length and slope are gathered in one bin. The QIS captures the structural relationships between the key points in a time series; this perspective is quite novel in similarity measurement. By encoding geometric properties such as shape and global orientation in a manner invariant to affine transformations, the QIS provides robustness against minor deformations, noise, and temporal shifts while maintaining computational efficiency.
Prior research explored alternative structural representations for time series, such as wavelet-based decompositions in biomedical signal processing [7] and contour-based descriptors in speech analysis [15]. However, these methods fail to fully capture translation and rotation invariance, which are inherent properties of the QIS. Despite its potential, the QIS has never been applied to time series analysis, representing an opportunity for further exploration and refinement.
2.3. Related Work on Hybrid Approaches
Given the inherent limitations of individual similarity measurement techniques, hybrid approaches have been increasingly explored in recent literature. Several studies have investigated hybrid models, which combine temporal alignment with automated feature extraction to improve classification accuracy in domains such as continuous wavelet transform (CWT) with CNNs and long short-term memory (LSTM) networks to classify ECG signals [16]. Similarly, approaches that integrate statistical and shape-based descriptors have demonstrated effectiveness in industrial anomaly detection [17].
Our proposed hybrid QIS + DTW approach follows this paradigm by leveraging the complementary strengths of the QIS and DTW. By integrating the QIS’s structural encoding with DTW’s alignment capabilities, we aimed to enhance the robustness and accuracy of time series similarity measurements while maintaining computational efficiency.
2.4. Research Gaps and Contributions
Despite significant advancements in time series similarity measurements, several key challenges remain unaddressed. First, the existing methods lack structure-aware similarity measures as they either focus on sequence alignment (DTW) or automated feature extraction (CNNs) without explicitly capturing shape-based relationships. Second, deep learning models remain computationally intensive, requiring substantial labeled data and processing power. Third, the current methods struggle in low-data environments, particularly in fields such as medical diagnostics and rare event detection, where data scarcity is a fundamental issue.
To address these gaps, our study introduced a novel hybrid QIS + DTW approach, which is characterized by the following:
- Incorporates the QIS for shape-based feature extraction, capturing structural relationships in time series data.
- Utilizes DTW for sequence alignment, ensuring robustness to time shifts and distortions.
- Combines both methods into a weighted hybrid similarity measure, balancing structural and alignment-based information.
- Evaluates performance across multiple real-world datasets, including ECG and seismic signals, demonstrating its effectiveness in diverse scenarios.
By integrating structural awareness with alignment flexibility, this research contributes a computationally efficient and interpretable solution for time series similarity measurements, offering a valuable alternative to traditional alignment-based and feature-driven approaches.
For a deeper view of existing methods and their complexity, please refer to the Supplementary Materials.
3. Materials and Methods
In this section, we outline the theoretical foundations, computational implementations, and enhancements introduced in our approach. We begin with a detailed explanation of the QIS, discuss DTW as a baseline method, and introduce our novel hybrid QIS + DTW framework. Finally, we present the datasets, preprocessing techniques, and evaluation metrics used for benchmarking.
All the analytics were implemented in Python 3 using standard available modules. No other tools or software were used.
3.1. Quick Invariant Signature (QIS) for Time Series Analysis
3.1.1. Background and Motivation
The QIS was developed as a shape outline recognition technique for binary images. The contours were encoded focusing on extracting geometric properties that remain invariant under transformations such as translation, rotation, and scaling. Unlike pixel-based image processing methods, the QIS encodes the relative relationships between active points in the image or the signal, forming a compact, distinctive signature.
Applying the QIS to time series requires reinterpreting a time series as a geometric structure, where the key points (e.g., peaks and troughs) act as structural features analogous to image contours. This method offers an advantage over traditional alignment techniques (such as DTW) as it allows for direct comparison of shape and structure while ignoring minor shifts and noise.
3.1.2. Extraction of the QIS from a Time Series
To transform a raw time series into a QIS representation, we employed the following step-by-step process:
- Step 1: preprocessing the time series.
- Each time series was first normalized to ensure scale invariance. We applied Z-score normalization, as shown in Equation (1).
- Step 2: identifying the key active points (peaks and troughs).
- We extracted structural points by detecting local maxima and minima using a peak detection algorithm (e.g., scipy.signal.find_peaks).
- Only prominent peaks and troughs (above a defined threshold) were retained.
- Step 3: computing geometric relationships.
- For every pair of active points , we computed two structural features:
- ○
- Slope (): represents the angle between two points, capturing the relative orientation. The slope computation is shown in Equation (2).
- ○
- Length (): measures the Euclidean distance between points, reflecting their spatial separation. The Euclidean distance computation is shown in Equation (3).
In practice, this explicit calculation is avoided as the core of the QIS process circumvents combinatorial and geometric computations to ensure computational efficiency. The fact that geometric invariance within a grid can be presented in a finite number of possibilities allows the QIS extraction to run in the complexity, where is the number of the key points. Although this sounds strange, referring to the original publication, the combinatory process is not necessary to collect the signature as the equivalent segments follow specific numeric rules.
- Step 4: quantizing the signature.
The QIS, although initially based on a combination of all active points in a grid, introduces simple accumulation algorithms and avoids the combinatory problem by formally clustering the possible segments within a given grid. Let us say that our active key points obtained from the time series are , and using the algorithms defined in the original publication of the QIS, a sparse vector of length is created, containing in each position the number of segments sharing the same slope and length. The vector, called a signature, is an invariant representation of the time series based on the key points. Then, given two points p and q where the subscript i is the flattened position of the point in an array and subscripts r and c refer to their index, the row, and the column in the grid, respectively, the algorithm below will find the similarity bin index (SGN) of a pair of points.
The complete details regarding the extraction of the invariant signature and the proof of its consistency can be found in the original published work. There are many different types of signatures, such as translation, cylindrical, toroidal, or scale invariant. One can also transform the image into a log-polar coordinate and extract the rotation invariant signature by using toroidal translation in the new space.
- GET-SGN-TT(p, q, n)
There are 4 bins returned by the process, because a toroidal shift modifies a given segment into at most 4 possible segments (Figure 1):
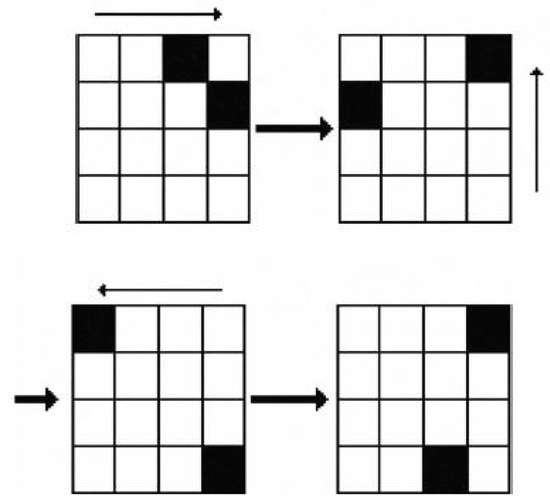
Figure 1.
Toroidal shifts Each border shift wraps around the image.
- Step 5: handling periodic time series with toric QIS.
- Many real-world time series, such as biomedical signals and seasonal data, exhibit cyclic properties.
- We introduced an adaptation of the toric QIS with the following features:
- ○
- Wraparound connections formed for the points near the boundaries of the time series.
- ○
- The first and last points (with no limit) were treated as neighbors to preserve continuity.
3.2. Dynamic Time Warping (DTW) as a Baseline
3.2.1. DTW Fundamentals
Dynamic time warping (DTW) is a widely used method for measuring time series similarity, allowing sequences to be nonlinearly aligned. It computes a warping path that minimizes the distance between two sequences, accommodating temporal distortions.
3.2.2. DTW Algorithm
Given two time series and , the DTW distance is computed as follows:
- 1.
- Define a cost matrix where each entry represents the distance between points and , as shown in Equation (4).
- 2.
- Compute the cumulative cost matrix recursively as shown in Equation (5).
- 3.
- The optimal warping path is found by backtracking from .
DTW works well for alignment, but lacks structural awareness, motivating a hybrid QIS + DTW approach.
3.3. Hybrid QIS + DTW: Integrating Structure with Alignment
3.3.1. Motivation for Hybridization
DTW provides alignment capabilities, but does not preserve geometric structure, while the QIS encodes geometric information, yet disregards time alignment. By integrating these two methods in a hybrid QIS + DTW approach, both alignment and geometric structure are retained, thereby the strength of each technique is embedded.
3.3.2. Computing Hybrid Similarity
We introduce a weighted hybrid score, , that combines QIS similarity and DTW distance as shown in Equation (6).
where α = 0.7 was empirically optimized to balance the QIS and DTW. A high indicates a strong match between two time series.
The sensitivity analysis using toroidal QIS on the ECG5000 dataset, evaluating accuracy, F1-score, precision, and recall for different α values (ranging from 0.5 to 0.9 in increments of 0.05), demonstrated that α = 0.7 yields the best performance, as detailed in Table 1.

Table 1.
Sensitivity analysis for different α values on the ECG5000 dataset
3.4. Datasets Used
We evaluated our approach on real-world and synthetic datasets as follows.
3.4.1. ECG5000 Dataset
The dataset comprises 5000 heartbeat signals from the UCR archive, categorized into five classes: normal, supraventricular, ventricular, fusion, and unknown. The proposed QIS + DTW method was applied to identify abnormal heartbeats within these signals.
This dataset contains 5000 instances distributed over 5 classes, with a length of 140 for each time series. The class distribution is as follows: Class 1 (normal), ~2919; Class 2 (R-on-T PVC), ~176; Class 3 (PVC), ~154; Class 4 (fusion), ~15; Class 5 (unclassified), ~1736.
3.4.2. Seismic Dataset
The dataset involves seismic waveform data distinguishing earthquake vs. non-earthquake events. The dataset is then used to evaluate how QIS + DTW generalizes to geophysical signals. This dataset contains 895 instances of length 512, each distributed over a binary classification.
3.4.3. Synthetic Sinusoidal Data
The dataset contains generated waveforms with controlled noise. The goal of using this dataset was to test the robustness of the QIS + DTW approach to controlled distortions.
3.5. Evaluation Metrics
We defined precision, recall, and F1-score as follows:
Here, TP, FP, and FN denote true positives, false positives, and false negatives, respectively. We reported the F1-score due to its balanced emphasis on both precision and recall. Precision measures the proportion of correct predictions among the total number of predicted positive cases.
We assessed each method based on the following metrics:
- Classification accuracy: measures correct predictions.
- Precision and recall: measure model reliability.
- F1-score: balances precision and recall.
- Noise robustness: tests method stability under noise injection.
- Computational efficiency: measures runtime performance.
4. Results
In this section, we present the evaluation results of each method on the datasets described in Section 3.4. We detail how these methods were applied to a pairwise similarity-based classification task.
4.1. Dynamic Time Warping (DTW) and FastDTW
For each method in this group, we first computed the DTW distance between every pair of test samples. Next, we compared this distance to a predefined threshold. If the distance was below the threshold, the pair was classified as class “1;” otherwise, it was classified as class “0.” Finally, the predicted labels were compared with the true class labels using the evaluation metrics mentioned.
4.2. Shapelet-Based and MLP Classifiers
Each model in this category was first fitted on the training set. Next, the model was used to predict the class of each test time series. Finally, the model was evaluated using the evaluation metrics.
4.3. Hybrid QIS + DTW
This method was used and evaluated based on the following steps:
- For each sample in the test set, toric QIS signatures were extracted.
- For each pair of points , the DTW distance between the points was computed.
- For each pair of test samples, the QIS method was applied to compute the cosine similarity between their toric QIS signatures extracted in Step 1.
- The hybrid similarity score (HS) was computed based on the proposed Equation (6).
- For each pair of test samples, if HS > 0.85, they were marked as the same class (1); otherwise, they were detected as a different class (0).
- Finally, the predicted labels were compared against the true class labels using the evaluation metrics.
4.4. Comparative Performance on Datasets
To evaluate the effectiveness of the QIS, DTW, and the hybrid QIS + DTW method, they were applied to the datasets stated in Section 3.4, and the performance of the methods was evaluated based on the metrics mentioned in Section 3.5. The following sections describe the obtained evaluation results.
4.4.1. Performance on the ECG5000 Dataset
The experimental setup consisted of an 80–20 train–test split, where 80% of the data were used for training, and 20%—for testing. Prior to model training, Z-score normalization was applied as a preprocessing step to standardize the features. Table 2 presents the evaluation results of applying the methods to the ECG5000 dataset.

Table 2.
Evaluation results of applying the methods to the ECG5000 dataset.
Table 2 shows that the Hybrid QIS + DTW method outperformed both DTW and FastDTW in terms of accuracy. While the shapelet-based and MLP classifiers achieved superior performance, they required a large amount of labeled data for effective training. In contrast, QIS + DTW was computationally more efficient and did not require any training, making it a computationally lightweight alternative.
4.4.2. Performance on the Seismic Dataset
We extended our experiments to seismic activity classification, using real-world earthquake time series data. Correspondingly, the dataset was split into the training and test sets, where 80% of the data were used for training and 20%—for testing. As a preprocessing step, Z-score normalization was applied to standardize the dataset. Table 3 shows the evaluation results of applying the methods to the seismic dataset.

Table 3.
Evaluation results of applying the methods to the seismic dataset.
Table 3 shows that QIS + DTW resulted in greater robustness compared to DTW alone, particularly in handling variations in the data. While the MLP classifier achieved the highest performance, it required extensive training and significant computational resources. Notably, QIS + DTW remained effective even in the presence of noisy seismic patterns, making it a reliable alternative in scenarios with limited labeled data or high data variability.
As shown in Table 2, hybrid QIS + DTW yields a 93% accuracy—notably higher than DTW (86%) and slightly below MLP’s 94%. In Table 3, again, we see that hybrid QIS + DTW achieves an accuracy of 90% on seismic data, surpassing standard DTW by approximately 7%. This performance gap highlights the benefit of adding shape-based invariance through the QIS, especially under seismic wave distortions.
The fact that any neural network-based learning model could eventually slightly outperform the proposed hybrid method is countered by the necessity for these models to train on large and clearly labeled datasets beforehand. Large datasets are not always available.
4.4.3. Noise Robustness Analysis
We introduced controlled Gaussian noise (5%, 10%, 20%) to the synthetic sinusoidal dataset in order to test the stability of different methods, where .
The observations shown in Table 4 indicate that DTW experiences significant accuracy degradation when subjected to noise. In contrast, hybrid QIS + DTW demonstrates greater robustness, maintaining more stable performance even in noisy conditions.

Table 4.
Evaluation results of the DTW and hybrid QIS + DTW methods against different noise levels.
4.4.4. Performance on Compressed Time Series
To simulate real-world distortions, we applied the DTW and hybrid QIS + DTW methods on the time-compressed signals.
Table 5 demonstrates that the QIS effectively preserved structural information even after compression, ensuring the integrity of the original data. In contrast, DTW alone was prone to excessive distortion effects, which negatively impacted its performance and reliability.

Table 5.
Evaluation results of the DTW and hybrid QIS + DTW methods on compressed time series.
5. Discussion
5.1. Why Hybrid QIS + DTW Is Effective
The hybrid QIS + DTW method combines the best of 2 robust methods: the QIS extracts meaningful structural representations of time series where shift or cyclic effects are not an issue, while DTW ensures temporal alignment. The method provides several advantages:
- Unlike standalone DTW, which relies on point-to-point alignment, the QIS extracts shape-based features, improving generalization to similar but temporally shifted patterns. This combines structure and alignment.
- The QIS reduces sensitivity to minor distortions in the signal, making the approach more resilient to variations such as background noise in ECG data.
- Unlike MLP and other deep learning models that require large amounts of labeled data, QIS + DTW can work effectively without extensive supervised training.
- Compared to deep learning-based approaches, which require multiple layers of feature extraction and extensive training, QIS + DTW remains efficient while delivering comparable results. This allows for real-time applications.
- The method has shown promising results in biomedical signal processing (ECG classification), seismic activity detection, and synthetic signal analysis, proving its broad applicability.
The essence of the QIS lies in the fact that it embeds any affine transformation within the structure of the extracted signature and, therefore, allows models to align without the burden of shifting. In other words, combinatory alignment problems are solved. The original work on invariance signature extraction images [8] demonstrates that the assumed combinatory property does not apply within the attention grid of the signal. Embedding this invariance into any problem dealing with alignments can effectively enhance the performance of the models.
5.2. Limitations
The QIS presumes that the structure of the shape can be defined by using the histogram representation of the equivalent segments. This representation, though efficient and invariant to affine transformations, could introduce slight biases into time series analyses. The effect of grouping into bins of similar segments reduces the individual importance of each segment. Although in practice this effect is not visible, it might be of interest in the future refinement of the algorithm.
5.3. Future Work
Extending QIS + DTW to multivariate time series data would allow the approach to handle datasets with multiple correlated signals. Another promising direction is the integration of the QIS with convolutional neural networks (CNNs), combining CNNs’ powerful feature extraction capabilities with the interpretability offered by QIS-based shape descriptors. Finally, developing an adaptive weighting strategy to dynamically balance the QIS and DTW based on dataset characteristics could further improve performance across diverse applications.
6. Conclusions
In this study, we presented an evaluation of the QIS, DTW, and the hybrid QIS + DTW method for time series classification. Our results on the ECG5000 and seismic datasets demonstrate that hybrid QIS + DTW consistently outperforms traditional DTW, showing advantages in noise robustness and time compression stability. While deep learning models such as MLP achieve higher performance in fully supervised settings, QIS + DTW remains a powerful alternative in low-data environments and applications requiring interpretability. The findings highlight that incorporating structural representations alongside traditional alignment techniques significantly enhances time series classification. Future research will focus on optimizing computational efficiency, extending QIS + DTW to multivariate datasets, and exploring new hybrid models integrating deep learning components.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/math13060999/s1, Table S1: Comparison in tabular format of existing methods.
Author Contributions
Conceptualization, H.R.S.; Methodology, H.R.K.; Validation, M.K.; Writing—review & editing, A.P. and E.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- de Chazal, P.; O’Dwyer, M.; Reilly, R.B. Automatic classification of heartbeats using ECG morphology and heartbeat interval features. IEEE Trans. Biomed. Eng. 2004, 51, 1196–1206. [Google Scholar] [CrossRef] [PubMed]
- Sakoe, H.; Chiba, S. Dynamic programming algorithm optimization for spoken word recognition. IEEE Trans. Acoust. Speech Signal Process. 1978, 26, 43–49. [Google Scholar] [CrossRef]
- Salvador, S.; Chan, P. Toward accurate dynamic time warping in linear time and space. Intell. Data Anal. 2007, 11, 561–580. [Google Scholar] [CrossRef]
- Wang, Z.; Yan, W.; Oates, T. Time series classification from scratch with deep neural networks: A strong baseline. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; IEEE: Piscataway, NJ, USA; pp. 1578–1585. [Google Scholar]
- Ye, L.; Keogh, E. Time series shapelets: A new primitive for data mining. In Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Paris, France, 28 June 28–1 July 2009; pp. 947–956. [Google Scholar]
- Lin, J.; Keogh, E.; Lonardi, S.; Chiu, B. A symbolic representation of time series, with implications for streaming algorithms. Proc. ACM SIGMOD Workshop 2003, 2–11. [Google Scholar] [CrossRef]
- Mallat, S. A Wavelet Tour of Signal Processing; Elsevier: Amsterdam, The Netherlands, 1999. [Google Scholar]
- Shahbazkia, H.; dos Anjos, A. Quick invariant signature extraction from binary images. In Proceedings of the IEEE International Symposium on Signal Processing and Information Technology (ISSPIT), Ajman, United Arab Emirates, 14–17 December 2009; pp. 172–177. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Fawaz, H.I.; Forestier, G.; Weber, J.; Idoumghar, L.; Müller, P.-A. Deep learning for time series classification: A review. Data Min. Knowl. Discov. 2018, 33, 917–963. [Google Scholar] [CrossRef]
- Fawaz, H.I.; Lucas, B.; Forestier, G.; Pelletier, N.; Schmidt, D.F.; Weber, J.; Müller, P.-A. InceptionTime: Finding AlexNet for time series classification. In Proceedings of the 2019 IEEE International Conference on Big Data (Big Data), Los Angeles, CA, USA, 9–12 December 2019; IEEE: Piscataway, NJ, USA; pp. 1–10. [Google Scholar]
- Lim, B.; Arik, S.O.; Loeff, N.; Pfister, T. Temporal fusion transformers for interpretable multi-horizon time series forecasting. Int. J. Forecast. 2020, 37, 1748–1764. [Google Scholar] [CrossRef]
- Zerveas, C.; Jayaraman, S.; Patel, D.; Wang, L.; Anandkumar, A. Transformers for time series classification. In Proceedings of the International Conference on Learning Representations (ICLR), Virtual, 3–7 May 2021. [Google Scholar]
- Akkermans, V.; Rodet, X.; Jaillet, F. Sparse approximation of sound signals using learned dictionaries and continuous relaxation. In Proceedings of the 2009 IEEE International Conference on Acoustics, Speech and Signal Processing, Taipei, Taiwan, 19–24 April 2009; IEEE: Piscataway, NJ, USA; pp. 1–4. [Google Scholar]
- Madan, P.; Singh, V.; Singh, D.P.; Diwakar, M.; Pant, B.; Kishor, A. A Hybrid Deep Learning Approach for ECG-Based Arrhythmia Classification. Bioengineering 2022, 9, 152. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Saeedi, S.; Giusti, A. Anomaly Detection for Industrial Inspection using Convolutional Neural Networks. In Proceedings of the 17th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISAPP), Virtual, 6–8 February 2022; pp. 107–114. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).