Bifurcation, Quasi-Periodic, Chaotic Pattern, and Soliton Solutions to Dual-Mode Gardner Equation

Abstract

This study aims to investigate various dynamical aspects of the dual-mode Gardner equation derived from an ideal fluid model. By applying a specific wave transformation, the model is reduced to a planar dynamical system, which corresponds to a conservative Hamiltonian system with one degree of freedom. Using Hamiltonian concepts, phase portraits are introduced and briefly discussed. Additionally, the conditions for the existence of periodic, super-periodic, and solitary solutions are summarized in tabular form. These solutions are explicitly constructed, with some graphically represented through their $2D$ and $3D$ profiles. Furthermore, the influence of specific physical parameters on these solutions is analyzed, highlighting their effects on amplitude and width. By introducing a more general periodic external influence into the model, quasi-periodic and chaotic behavior are explored. This is achieved through the presentation of $2D$ and $3D$ phase portraits, along with time-series analyses. To further examine chaotic patterns, the Poincaré surface of section and sensitivity analysis are employed. Numerical simulations reveal that variations in frequency and amplitude significantly alter the dynamical characteristics of the system.

1. Introduction

In mechanical engineering, nonlinear partial differential equations (PDEs) are crucial because they describe intricate processes, such as heat transfer, fluid flow, material stress, and deformation. Nonlinear PDEs are generally more difficult to solve and, due to their complexity, typically require numerical or approximate methods, in contrast to linear PDEs, which often have analytical solutions [1,2]. Finding exact solutions to such equations is important because it allows us to understand and explain many complex phenomena modeled by these equations. As a result, researchers are motivated to explore new methods or refine existing ones. Various powerful methods have been proposed and successfully applied in several works, such as the inverse scattering transform [3], Hirota’s bilinear operators [4,5], the Bäcklund–Darboux transform [6,7,8], the homotopy perturbation method [9], projective Riccati equations [10], the sub-ODE method [11,12], Lie symmetry [13,14,15,16,17,18], the auxiliary equation technique [19,20], the Kudryshov technique [21], Painlevé analysis [22,23], and bifurcation analysis [24,25,26,27,28,29].

Surface waves in shallow water have been extensively studied due to their distinctive characteristics. These waves are commonly described using mathematical models, with the Korteweg–de Vries (KdV) equation being one of the fundamental formulations. The KdV equation is particularly notable for its well-defined solutions and plays a crucial role in analyzing the dynamics of shallow-water waves [30]. Its origin is linked to its development as a nonlinear wave equation governing unidirectional wave propagation [30]. This equation was derived through an asymptotic expansion of the fundamental wave motion within the shallow-water Euler equations, closely related to the study of small-amplitude waves on a free surface. It encompasses two significant parameters, $\alpha$ and $\beta$, which define the wave size relative to the water depth and the square of the water depth relative to the wavelength, respectively. Thus, the KdV equation incorporates two essential elements: linear dispersion, which explains the spreading and transformation of waves, and nonlinear steepening, where waves grow taller in shallow water [31]. This equation is crucial for understanding the behavior of solitary waves in these contexts and for examining the characteristics of periodic waves, which aids in our comprehension of the consistent patterns and oscillations observed in various wave phenomena. Now, here is the key point: this equation behaves differently when $\alpha$ and $\beta$ have significantly different values. In other words, when the wave size differs from the water depth, it significantly affects how these waves move and behave. Equations that account for higher-order effects, such as higher-order KdV equations, follow the same principle [31]. The derivation of this equation originates from the (2 + 1)-dimensional Gardner equation [32], which illustrates the relationship between the sizes of $\alpha$ and $\beta$: $\beta ={\alpha }^2$ and $\gamma ={\alpha }^3$, where $\gamma$ is the transverse wavelength parameter.

It is important to highlight that in our research, we are focusing on a specific case with a flat bottom, which requires setting the bottom variation parameter $\delta$ equal to zero. This choice is particularly significant because it simplifies our calculations. Our study focuses on the Gardner equation, which was originally derived in a previous work [33]:

$$G_t+G_x+{\displaystyle \frac{3}{2}}\alpha G{G}_x-{\displaystyle \frac{3}{8}}{\alpha }^2{G}^2{G}_x+{\displaystyle \frac{\beta }{6}}(1-3\tau )G_{xxx}=0.$$

(1)

Equation (1) is essential to the analysis and is employed to examine the behavior of a specific non-dimensional parameter: the Bond number $\tau =T/\rho g{H}^2$, $\beta =H^2/L^2$, and $\alpha =a/H$, where $H,g,a,T,\rho$, and L define the average upstream depth, gravity acceleration, wave amplitude, surface tension coefficient, water density, and wave length, respectively. These non-dimensional factors are crucial to our investigation because they enable us to understand the behavior of the system under consideration. The Korsunsky approach [34] is applied to transform Equation (1) into a novel dual-mode model, as presented in [35]. Thus, we obtain the following dual-mode model for the Gardner equation:

$$G_{tt}-s^2{G}_{xx}+\left({\displaystyle \frac{\partial }{\partial t}}-s\eta {\displaystyle \frac{\partial }{\partial x}}\right)\left({\displaystyle \frac{3}{2}}\alpha G{G}_x-{\displaystyle \frac{3}{8}}{\alpha }^2{G}^2{G}_x\right)+\left({\displaystyle \frac{\partial }{\partial t}}-s\mu {\displaystyle \frac{\partial }{\partial x}}\right)\left({\displaystyle \frac{\beta (1-3\tau )}{6}}{G}_{xxx}+G_x\right)=0,$$

(2)

where $G(x,t)$ represents a field function defined over the domain $(x,t)\in {\mathbb{R}}^2$. Here, $\eta$ and $\mu$ denote the nonlinearity parameter and dispersion, respectively, and are restricted by $\left|\eta \right|\le 1$ and $\left|\mu \right|\le 1$, while s characterizes the phase velocity. The dual-mode Gardner equation generalizes both the KdV equation and the modified KdV (mKdV) equation by incorporating both quadratic and cubic nonlinear terms. It is widely used to model the propagation of nonlinear waves in various physical systems, especially in fields such as fluid dynamics and plasma physics [36,37]. It is worth mentioning that the Korsunsky approach has been extended to the KdV equation by several scholars to investigate dual-mode equations. For instance, the dual-mode modified KdV and higher order KdV equations were studied in [38], the dual-mode Kuramoto–Sivashinsky equation was investigated in [39,40], and the dual-mode Sharma–Tasso–Olver equation and the dual-mode fourth-order Burgers equation were considered in [41]. Soliton solutions of Equation (2) were constructed utilizing the tan/cot and tanh/coth methods in [35]. Lie symmetry analysis has been applied to Equation (2), and some solutions have been obtained using the power series method [42].

The primary objectives of this work are to apply the qualitative theory of planar systems to determine and systematically tabulate the existence conditions for certain bounded solutions to Equation (2) and to explicitly construct some of these solutions. Additionally, we analyze the influence of specific physical parameters on these solutions. Furthermore, by incorporating external periodic effects into the model, we investigate the emergence of quasi-periodic and chaotic behavior in wave phenomena.

This work is organized as follows. In Section 2, we apply a specific wave transformation to convert Equation (2) into a dynamical system that is equivalent to a Hamiltonian system with one degree of freedom. Section 3 focuses on the bifurcation analysis of the traveling wave system, including the tabulation of the existence conditions for periodic, super-periodic, and solitary solutions, along with a brief description of the phase portrait. In Section 4, we construct specific solutions categorized as periodic, super-periodic, and solitary. Section 5 presents graphical representations of some solutions in both $2D$ and $3D$ formats, as well as an analysis of the influence of certain physical parameters on these solutions. In Section 6, we examine quasi-periodic and chaotic behavior by introducing an external periodic perturbation term. A sensitivity analysis for different initial conditions is conducted, and Poincaré section and bifurcation diagrams are used to identify chaotic patterns in the model. Finally, Section 7 summarizes the key findings of this study.

2. Traveling Wave System

Let us assume that the solution to Equation (2) is expressed as follows:

$$G(x,t)=\mathcal{M}\left(\xi \right),\xi =\kappa (x-\sigma t),$$

(3)

where $\xi$ is the wave variable, $\kappa$ represents the wave number, and $\sigma$ denotes the wave speed. The solution form (3) stands for the traveling wave solution to Equation (2). By substituting Equation (3) into Equation (2), we obtain

$$\begin{array}{cc}\hfill & ({\sigma }^2-s^2){\kappa }^2{\mathcal{M}}^{″}-\kappa (\alpha +s\eta ){\left({\displaystyle \frac{3}{2}}\alpha \kappa \mathcal{M}{\mathcal{M}}^{\prime }-{\displaystyle \frac{3}{8}}{\alpha }^2\kappa {\mathcal{M}}^2{\mathcal{M}}^{\prime }\right)}^{\prime }-\kappa (\sigma +s\mu )\hfill \\ \hfill & \times {\left({\displaystyle \frac{\beta {\kappa }^3(1-3\tau )}{6}}{\mathcal{M}}^{‴}+\kappa {\mathcal{M}}^{\prime }\right)}^{\prime }=0,\hfill \end{array}$$

(4)

where ’ indicates the derivatives with respect to $\xi$. By integrating Equation (4) twice with respect to $\xi$ and setting the integration constants to zero, we derive

$${\mathcal{M}}^{″}+{\gamma }_1\mathcal{M}+{\gamma }_2{\mathcal{M}}^2+{\gamma }_3{\mathcal{M}}^3=0,$$

(5)

where ${\gamma }_i,i=1,2,3$ are newly introduced constants for simplicity, replacing the original ones, and are given by

$${\gamma }_1={\displaystyle \frac{6[\sigma -{\sigma }^2+s\mu +s^2]}{{\kappa }^2\beta (1-3\tau )(\sigma +s\mu )}},{\gamma }_2={\displaystyle \frac{9\alpha (\sigma +s\eta )}{2{\kappa }^2\beta (\sigma +s\mu )(1-3\tau )}},{\gamma }_3=-{\displaystyle \frac{3{\alpha }^2(\sigma +s\eta )}{4\beta {\kappa }^2(\sigma +s\mu )(1-3\tau )}}.$$

(6)

Let ${\kappa }^2\beta (1-3\tau )(\sigma +s\mu )\ne 0$ and let ${\mathcal{M}}^{\prime }=\mathcal{N}$. Then, the second-order differential Equation (5) is written as follows:

$$\begin{array}{cc}{\mathcal{M}}^{\prime }\hfill & =\mathcal{N},\hfill \end{array}$$

(7a)

$$\begin{array}{cc}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} {\mathcal{N}}^{\prime }\hfill & =-\mathcal{M}({\gamma }_1+{\gamma }_2\mathcal{M}+{\gamma }_3{\mathcal{M}}^2).\hfill \end{array}$$

(7b)

The system in Equation (7a,b) is referred to as the traveling wave system. It is conservative because $\mathrm{div}({\mathcal{M}}^{\prime },{\mathcal{N}}^{\prime })=0$, and it is Hamiltonian because it can be derived from the Hamiltonian function

$$H={\displaystyle \frac{1}{2}}{\mathcal{N}}^2+\mathcal{U}\left(\mathcal{M}\right),$$

(8)

using Hamilton’s canonical equations [43], where $\mathcal{U}\left(\mathcal{M}\right)$ is the three-parameter potential function given by

$$\mathcal{U}\left(\mathcal{M}\right)={\displaystyle \frac{{\gamma }_1}{2}}{\mathcal{M}}^2+{\displaystyle \frac{{\gamma }_2}{3}}{\mathcal{M}}^3+{\displaystyle \frac{{\gamma }_3}{4}}{\mathcal{M}}^4.$$

(9)

The Hamiltonian function itself is a constant of motion for the system in Equation (7a,b), as it does not explicitly depend on $\xi$ [43]. Hence, we have

$${\displaystyle \frac{1}{2}}{\mathcal{N}}^2+\mathcal{U}\left(\mathcal{M}\right)=q,$$

(10)

where q is a free parameter that will play a key role in the subsequent analysis, as we demonstrate later. Substituting Equation (7a) into the conserved quantity (10) and separating the variables, we obtain the following differential form:

$${\displaystyle \frac{\mathrm{d}\mathcal{M}}{\sqrt{F_q(\mathcal{M};q)}}}=\pm \sqrt{2}\mathrm{d}\xi ,$$

(11)

where $F_q(\mathcal{M};q)$ is a quartic polynomial taking the form

$$F_q(\mathcal{M};q)=q-\mathcal{U}\left(\mathcal{M}\right)=q-{\displaystyle \frac{{\gamma }_1}{2}}{\mathcal{M}}^2-{\displaystyle \frac{{\gamma }_2}{3}}{\mathcal{M}}^3-{\displaystyle \frac{{\gamma }_3}{4}}{\mathcal{M}}^4.$$

(12)

Since one of the main objectives is to construct all possible solutions to Equation (2), determining the range of the parameters ${\gamma }_1,{\gamma }_2,{\gamma }_3$, and q is essential for integrating the differential form (11). The qualitative theory for planar integrable systems is applied to identify this range. Furthermore, this approach is significant because it does not only provide the required parameter ranges but also determines the type of solutions before solving them by linking them with phase trajectories. This enables us to isolate bounded solutions, which are physically meaningful, and to construct only real (non-complex) solutions by introducing the concept of intervals for real wave propagation.

3. Bifurcation and Phase Portrait

The dynamical behavior and qualitative analysis of Equation (2) are explored using Hamiltonian concepts [43,44]. The significance of the bifurcation study is encapsulated in the following lemma, which is crucial, as it illustrates the relationship between the phase trajectories and the types of solutions.

Lemma 1 

([45,46]). Assume that $\mathcal{M}\left(\xi \right)$ is a solution to Equation (2) for all $-\infty <\xi <\infty$ with ${lim}_{\xi \to \infty }\mathcal{M}\left(\xi \right)={\nu }_1$ and ${lim}_{\xi \to -\infty }\mathcal{M}\left(\xi \right)={\nu }_2$. Hence, Equation (2) possesses the following:

 (a)

A solitary solution corresponding to a homoclinic trajectory when ${\nu }_1={\nu }_2$.

 (b)

A kink (or anti-kink) solution corresponding to a heteroclinic trajectory when ${\nu }_1\ne {\nu }_2$.

 (c)

A periodic solution corresponding to the periodic phase trajectory.

On the other hand, unbounded phase trajectories are linked to unbounded solutions, which are physically undesirable in real-world problems. Consequently, the bifurcation study allows us to disregard such solutions associated with these trajectories. Hence, the bifurcation analysis is necessary for determining the range of the parameters ${\gamma }_1,{\gamma }_2,{\gamma }_3,$ and q in order to integrate both sides of the differential form in Equation (11). Additionally, it is essential to find the conditions on these parameters that lead to periodic, homoclinic, heteroclinic, and unbounded trajectories.

The phase portrait of the system in Equation (7a,b) can vary depending on the number of equilibrium points and the number of separatrix layers it covers [47]. To systematize the distinct trajectories in the phase portrait, we denote the periodic trajectory, heteroclinic trajectory, homoclinic trajectory, and super-nonlinear periodic trajectory as $P{T}_{p,r}$, $HE{T}_{p,r}$, $H{T}_{p,r}$, and $SNP{T}_{p,r}$, where p represents the number of stable equilibrium points covered by the trajectory and r denotes the number of separatrix layers covered by the trajectory [48].

Let us first introduce the following theorem, which will be useful for the subsequent analysis.

Theorem 1 

((Lagrange Theorem) [44]). For a conservative system, if the potential energy has a strict minimum at some positions, then these positions are stable equilibrium points.

Let us assume $\Delta ={\gamma }_2^2-4{\gamma }_1{\gamma }_3$ and define $\mathcal{Q}({\mathcal{M}}_0,0)$ as the equilibrium point of the system in Equation (7a,b), where ${\mathcal{M}}_0$ is a critical point of the potential function in Equation (9), i.e., a solution to the equation

$${\displaystyle \frac{\mathrm{d}\mathcal{U}}{\mathrm{d}\mathcal{M}}}{|}_{\mathcal{Q}}={\mathcal{M}}_0({\gamma }_1+{\gamma }_2{\mathcal{M}}_0+{\gamma }_3{\mathcal{M}}_0^2)=0.$$

(13)

The number of equilibrium points depends on the value of $\Delta$, which can be negative, zero, or positive. We examine each case individually:

1.

If $\Delta <0$, which is equivalent to $-2\sqrt{{\gamma }_1{\gamma }_3}<{\gamma }_2<2\sqrt{{\gamma }_1{\gamma }_3}$, then Equation (13) has a unique solution, ${\mathcal{M}}_0=0$. Consequently, the system in Equation (7a,b) has a single equilibrium point, ${\mathcal{Q}}_0=(0,0)$. To classify the nature of this point, we apply Theorem 1. Direct calculations yield ${\displaystyle \frac{{\mathrm{d}}^2\mathcal{U}}{\mathrm{d}{\mathcal{M}}^2}}{|}_{{\mathcal{Q}}_0}={\gamma }_1$. The point ${\mathcal{Q}}_0$ is classified as either a center point if ${\gamma }_1>0({\gamma }_3>0)$ or a saddle point if ${\gamma }_1<0({\gamma }_3<0)$. The value of the parameter q at the equilibrium point ${\mathcal{Q}}_0$ is calculated, resulting in $q=q_0=0$. Figure 1 illustrates the phase portrait of the system (7a,b) for $\Delta <0$, representing the scenario in which the system has a single equilibrium point. We conclude that when $({\gamma }_1,{\gamma }_2,{\gamma }_3)\in {\mathbb{R}}^{+}\times ]-2\sqrt{{\gamma }_1{\gamma }_3},2\sqrt{{\gamma }_1{\gamma }_3}[\times {\mathbb{R}}^{+}$, all phase trajectories of the system are bounded and periodic, and are classified as $P{T}_{1,0}$ for all $q\in ]0,\infty [$, as depicted in Figure 1a. Conversely, when $({\gamma }_1,{\gamma }_2,{\gamma }_3)\in {\mathbb{R}}^{-}\times ]-2\sqrt{{\gamma }_1{\gamma }_3},2\sqrt{{\gamma }_1{\gamma }_3}[\times {\mathbb{R}}^{-}$, all phase trajectories of the system (7a,b) are unbounded for all possible values of $q\in \mathbb{R}$.

2.

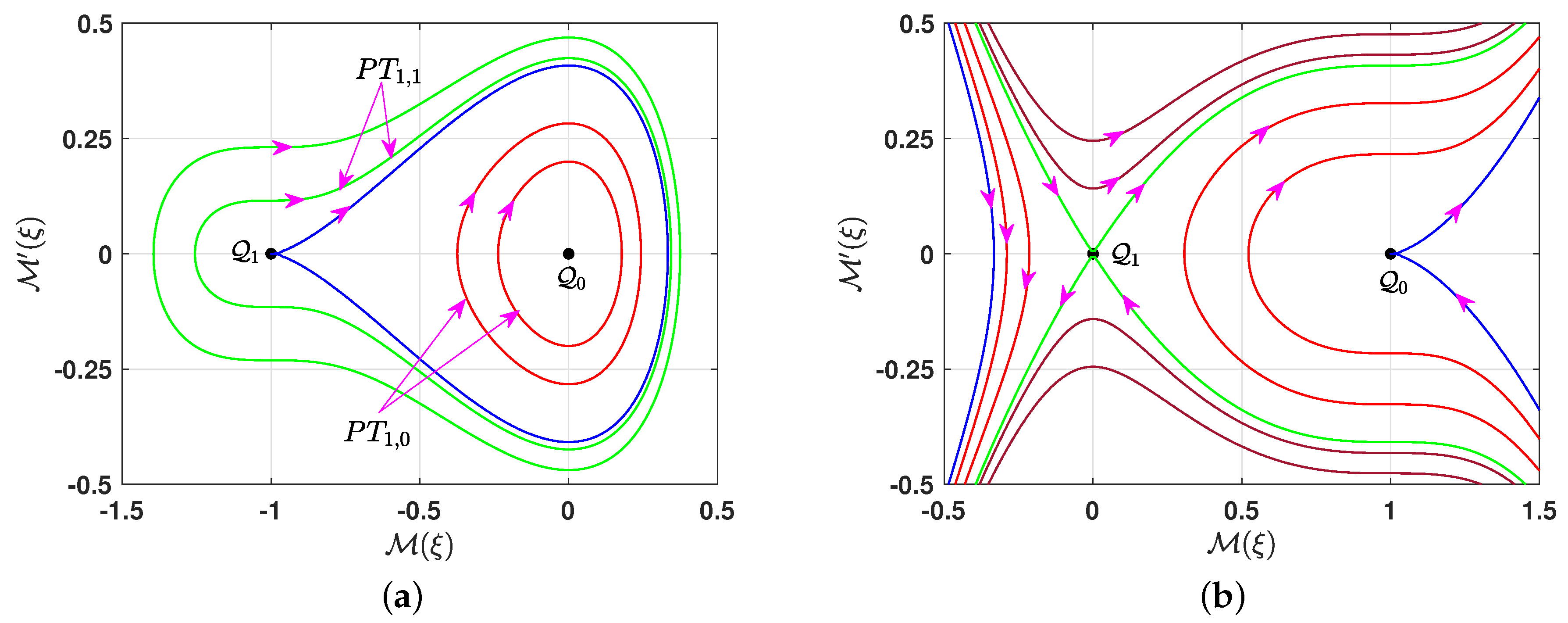
When $\Delta =0$, this condition corresponds to ${\gamma }_2=\pm 2\sqrt{{\gamma }_1{\gamma }_3}$, where ${\gamma }_1{\gamma }_3>0$. In this case, Equation (13) yields two solutions: ${\mathcal{M}}_0=0$ and $-{\displaystyle \frac{{\gamma }_2}{2{\gamma }_3}}$. As a result, the system (7a,b) possesses two equilibrium points: ${\mathcal{Q}}_0=(0,0)$ and ${\mathcal{Q}}_1(-{\displaystyle \frac{{\gamma }_2}{2{\gamma }_3}},0)$. Theorem 1 is applied to classify these points. Direct calculations yield

$${\displaystyle \frac{{\mathrm{d}}^2\mathcal{U}}{\mathrm{d}{\mathcal{M}}^2}}{{|}_{{\mathcal{Q}}_0}={\gamma }_1,{\displaystyle \frac{{\mathrm{d}}^2\mathcal{U}}{\mathrm{d}{\mathcal{M}}^2}}|}_{{\mathcal{Q}}_1}=0.$$

Hence, the equilibrium point ${\mathcal{Q}}_1$ is a cusp point, and ${\mathcal{Q}}_0$ is a center point if ${\gamma }_1>0 ({\gamma }_3>0)$ or a saddle point if ${\gamma }_1<0 ({\gamma }_3<0)$. The phase portrait for the system (7a,b) in this case is shown in Figure 2. We compute the value of the parameter q at the following equilibrium points: $q_0=H(0,0)=0$ and $q_1=H(-{\displaystyle \frac{{\gamma }_2}{2{\gamma }_3}},0)={\displaystyle \frac{{\gamma }_1^2}{12{\gamma }_3}}$. We briefly describe the phase portrait in this case. When $({\gamma }_1,{\gamma }_2,{\gamma }_3)\in {\mathbb{R}}^{+}\times \{\pm 2\sqrt{{\gamma }_1{\gamma }_3}\}\times {\mathbb{R}}^{+}$, all phase trajectories are bounded and periodic, varying according to the values of the parameter q, as shown in Figure 2a. There are two families of periodic trajectories: one characterized by $P{T}_{1,1}$ for $q\in ]q_1,\infty [$ in green, and the other by $P{T}_{1,0}$ for $q\in ]0,q_1[$ in red. Additionally, the blue trajectory passing through the cusp point ${\mathcal{Q}}_1$ typically exhibits periodic behavior, especially near the equilibrium point. On the other hand, if $({\gamma }_1,{\gamma }_2,{\gamma }_3)\in {\mathbb{R}}^{-}\times \{\pm 2\sqrt{{\gamma }_1{\gamma }_3}\}\times {\mathbb{R}}^{-}$, all phase trajectories of the system (7a,b) are unbounded, as shown in Figure 2b.

3.

If $\Delta >0$, which is equivalent to ${\gamma }_2^2>4{\gamma }_1{\gamma }_3$, then Equation (13) has three real solutions, ${\mathcal{M}}_0=0,{\displaystyle \frac{1}{2{\gamma }_3}}\left[-{\gamma }_2\pm \sqrt{{\gamma }_2^2-4{\gamma }_1{\gamma }_3}\right]$. Consequently, the system (7a,b) has three equilibrium points: ${\mathcal{Q}}_0=(0,0)$ and ${\mathcal{Q}}_{2,3}=\left({\displaystyle \frac{1}{2{\gamma }_3}}\left[-{\gamma }_2\pm \sqrt{{\gamma }_2^2-4{\gamma }_1{\gamma }_3}\right],0\right)$. The Lagrange Theorem 1 is employed to classify the equilibrium points; hence, we have

$${\displaystyle \frac{{\mathrm{d}}^2\mathcal{U}}{\mathrm{d}{\mathcal{M}}^2}}{{|}_{{\mathcal{Q}}_0}={\gamma }_1,{\displaystyle \frac{{\mathrm{d}}^2\mathcal{U}}{\mathrm{d}{\mathcal{M}}^2}}|}_{{\mathcal{Q}}_{2,3}}={\displaystyle \frac{\sqrt{{\gamma }_2^2-4{\gamma }_1{\gamma }_3}}{2{\gamma }_3}}\left[\sqrt{{\gamma }_2^2-4{\gamma }_1{\gamma }_3}\mp {\gamma }_2\right].$$

Also, we compute the value of q at the following points:

$$q_0=H\left({\mathcal{Q}}_0\right)=0,q_{2,3}=H\left({\mathcal{Q}}_{2,3}\right)=\pm {\displaystyle \frac{{\left({\gamma }_2\mp \sqrt{{\gamma }_2^2-4{\gamma }_2{\gamma }_3}\right)}^2}{96{\gamma }_3^3}}\left[{\gamma }_2\sqrt{{\gamma }_2^2-4{\gamma }_2{\gamma }_3}-6{\gamma }_1{\gamma }_3-{\gamma }_2^2\right],$$

(14)

which are sufficient to give a short description of the phase portrait. Let us now consider the next two cases, in which ${\gamma }_1{\gamma }_3$ is either positive or negative:

• Case A: If ${\gamma }_1{\gamma }_3>0$, the condition $\Delta >0$ yields ${\gamma }_2>2\sqrt{{\gamma }_1{\gamma }_3}$ or ${\gamma }_2<-2\sqrt{{\gamma }_1{\gamma }_3}$:

  (a)

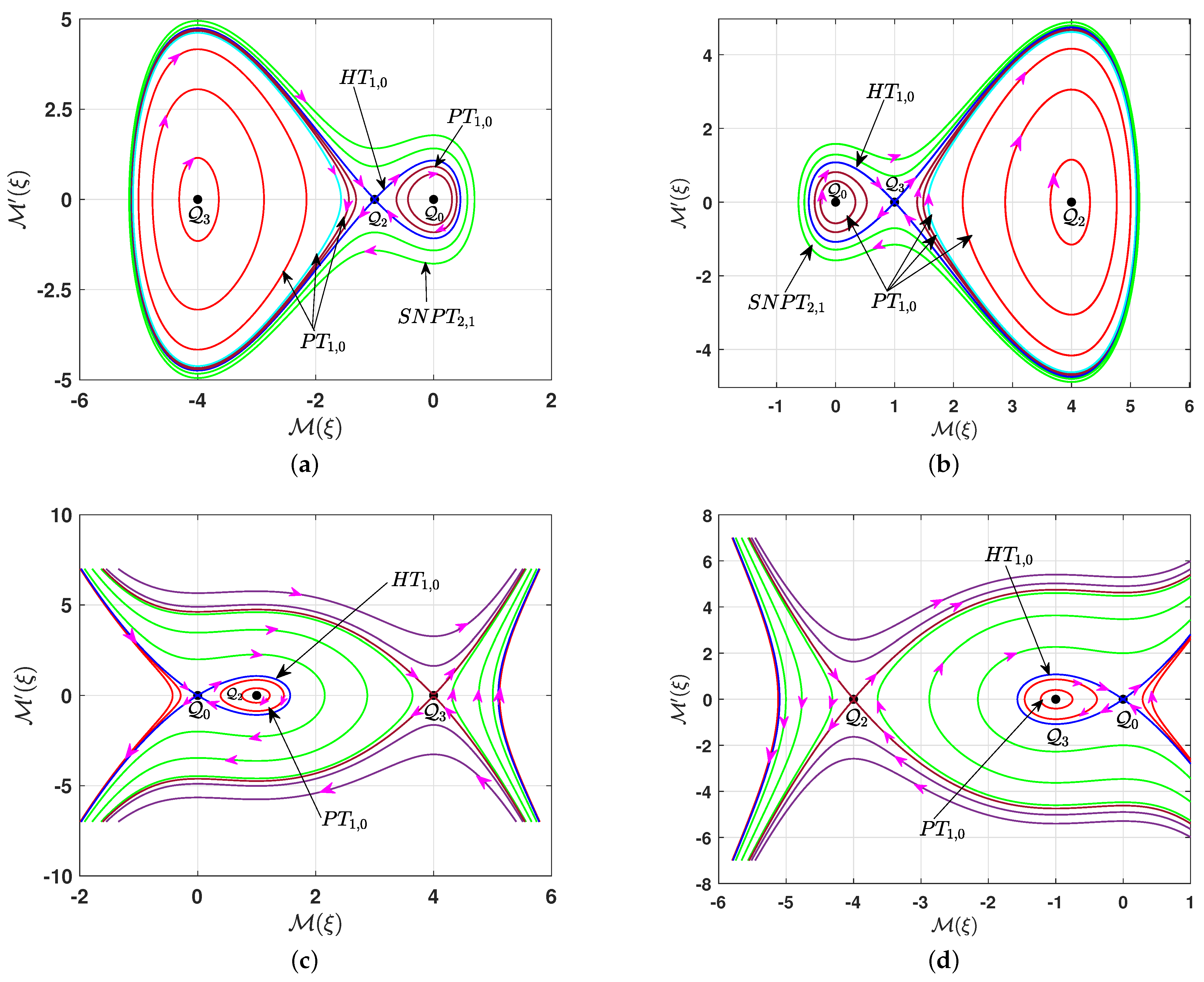
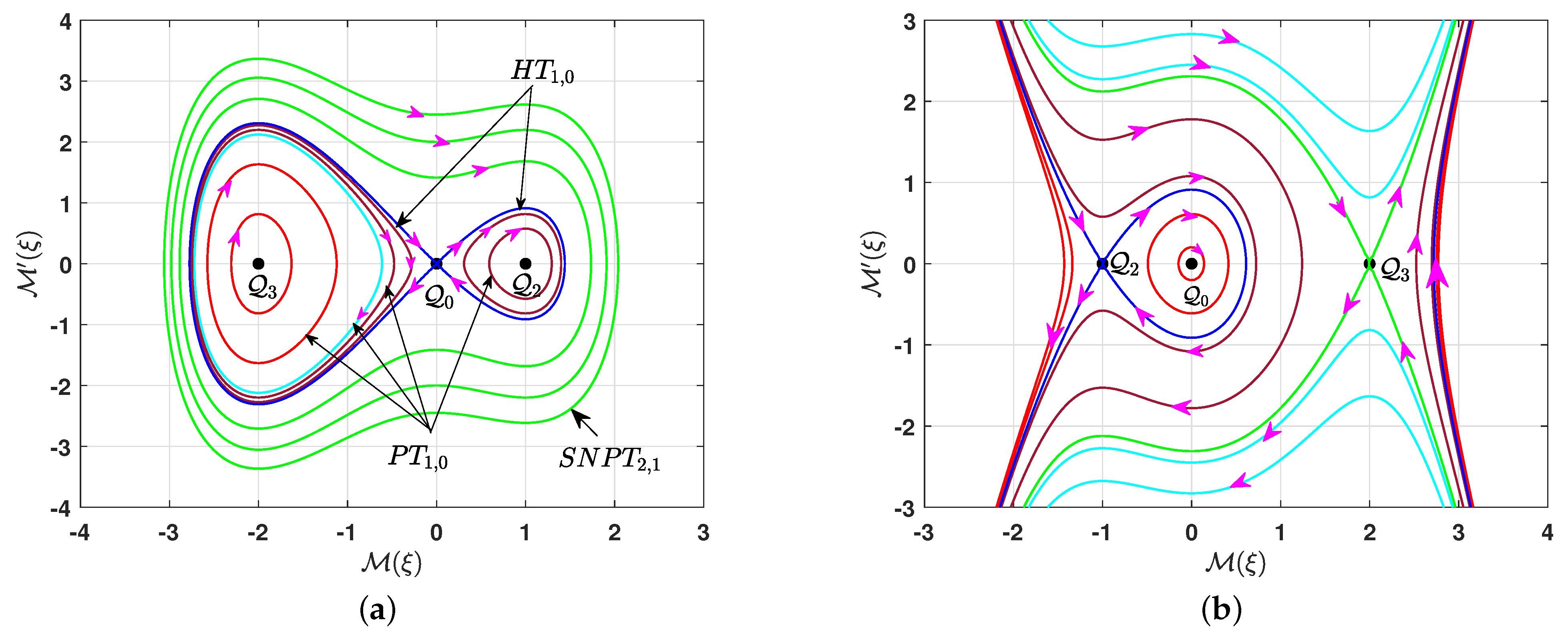
  If ${\gamma }_1>0,{\gamma }_3>0$, and ${\gamma }_2>2\sqrt{{\gamma }_1{\gamma }_3}$, the equilibrium point ${\mathcal{Q}}_0$ is a center point, while ${\mathcal{Q}}_2$ is a saddle point and ${\mathcal{Q}}_3$ is a center point. Figure 3a depicts the phase portrait for the system (7a,b) in this case. It consists of several types of bounded trajectories, depending on the values of the parameter q. There is a family of super-periodic trajectories in green, characterized by $SNP{T}_{2,1}$ for $q\in ]q_2,\infty [$, two brown families of periodic trajectories around the center point ${\mathcal{Q}}_0$, characterized by $P{T}_{1,0}$ for $q\in ]0,q_2[$, a family of red periodic trajectories around the center point ${\mathcal{Q}}_3$, characterized by $P{T}_{1,0}$ for $q\in ]q_3,0[$, and a single cyan periodic trajectory for $q=q_0$. Additionally, there are two homoclinic trajectories in blue for $q=q_2$, which is characterized by $H{T}_{1,0}$.

  (b)

  On the other hand, if ${\gamma }_1>0,{\gamma }_3>0$, and ${\gamma }_2<-2\sqrt{{\gamma }_1{\gamma }_3}$, then ${\mathcal{Q}}_0$ is a center point, ${\mathcal{Q}}_2$ is a center point, and ${\mathcal{Q}}_3$ is a saddle point. The phase portrait for this case is shown in Figure 3b. All the trajectories are bounded and categorized into different types based on the value of the parameter q. A similar phase description can be provided as in (a).

  (c)

  If ${\gamma }_1<0,{\gamma }_3<0$, and ${\gamma }_2>2\sqrt{{\gamma }_1{\gamma }_3}$, the equilibrium point ${\mathcal{Q}}_0$ is a saddle point, while ${\mathcal{Q}}_2$ is a center point and ${\mathcal{Q}}_3$ is a saddle point. The phase portrait for this case is illustrated in Figure 3c. All the phase trajectories are unbounded, except for the family of periodic red trajectories for $q\in ]q_3,0[$, which is characterized by $P{T}_{1,0}$. This family is enclosed within a homoclinic trajectory in blue for $q=0$, which is characterized by $H{T}_{1,0}$.

  (d)

  If ${\gamma }_1<0,{\gamma }_3<0$, and ${\gamma }_2<-2\sqrt{{\gamma }_1{\gamma }_3}$, the equilibrium point ${\mathcal{Q}}_0$ is a saddle point, while ${\mathcal{Q}}_2$ is a saddle point and ${\mathcal{Q}}_3$ is a center point. The phase portrait for this case is shown in Figure 3d. A similar phase description can be provided as in (c).

• Case B: If ${\gamma }_1{\gamma }_2<0$, then the condition ${\gamma }_2^2>4{\gamma }_1{\gamma }_3$ holds automatically. Thus, we proceed to consider the following possible cases:

  (a)

  If ${\gamma }_1<0,{\gamma }_3>0$, and ${\gamma }_2$ is a nonzero real number, the equilibrium point ${\mathcal{Q}}_0$ is a saddle point while ${\mathcal{Q}}_2$ and ${\mathcal{Q}}_3$ are center points. The phase portrait for the system (7a,b) corresponding to this case is illustrated in Figure 4a. All the phase trajectories are bounded, and their type depends on the value of the parameter q. There is a family of periodic red trajectories around the center point ${\mathcal{Q}}_3$ for $q\in ]q_3,q_2[$, and two periodic families of brown trajectories surrounding the two center points ${\mathcal{Q}}_2$ and ${\mathcal{Q}}_3$ for $q\in ]q_2,0[$, situated within the two homoclinic orbits (blue) at $q=0$. Additionally, there is a single periodic trajectory (cyan) for $q=q_2$. All these periodic trajectories are characterized by $P{T}_{1,0}$. Furthermore, for $q\in ]0,\infty [$, there is a green family of super-periodic trajectories characterized by $SNP{T}_{2,1}$.

  (b)

  If ${\gamma }_1>0,{\gamma }_3<0$, and ${\gamma }_2$ is a nonzero real number, the equilibrium point ${\mathcal{Q}}_0$ is a center point while both equilibrium points ${\mathcal{Q}}_{2,3}$ are saddle points. The phase portrait for this case is depicted in Figure 4b. All the phase trajectories are unbounded, except for a family of red periodic trajectories around the center point ${\mathcal{Q}}_0$ when $q\in ]0,q_2[$. This family lies within the homoclinic orbit (blue) at $q=q_2$.

4. Solutions

According to Lemma 1, the nature of the solution depends on the characteristics of the trajectories. Therefore, it is more appropriate to compile and tabulate the conditions that result in periodic, super-periodic, and solitary solutions. Unbounded solutions are excluded, as they are physically unacceptable. Hereafter, we compute the solutions corresponding to similar trajectories where the leading term of the polynomial (12) has the same sign.

4.1. Periodic Solutions

This subsection constructs periodic solutions to Equation (2), utilizing the parameter restrictions summarized in

Table 1. Conditions for the existence of periodic solutions to Equation (2).

Case	${\mathit{\gamma }}_1$	${\mathit{\gamma }}_3$	${\mathit{\gamma }}_2$	q	Figure/Trajectory Color
1.	+	+	$]-2\sqrt{{\gamma }_1{\gamma }_3},2\sqrt{{\gamma }_1{\gamma }_3}[$	$]0,\infty [$	Figure 1a/red
2.			$\pm 2\sqrt{{\gamma }_1{\gamma }_3}$	$]q_1,\infty [$	Figure 2a/green
3.				$]0,q_1[$	Figure 2a/red
4.			$]2\sqrt{{\gamma }_1{\gamma }_3},\infty [$	$]0,q_2[$	Figure 3a/brown
5.				$]q_3,0[$	Figure 3a/red
6.				0	Figure 3a/cyan
7.			$]-\infty ,-2\sqrt{{\gamma }_1{\gamma }_3}[$	$]q_2,0[$	Figure 3b/red
8.				$]0,q_3[$	Figure 3b/brown
9.				0	Figure 3b/cyan
10.	−	−	$]2\sqrt{{\gamma }_1{\gamma }_3},\infty [$	$]q_3,0[$	Figure 3c/red
11.			$]-\infty ,-2\sqrt{{\gamma }_1{\gamma }_3}[$	$q_3,0[$	Figure 3d/red
12.	−	+	$+/-$	$]q_3,q_2[$	Figure 4a/red
13.				$]q_2,q_0[$	Figure 4a/brown
14.				$q_2$	Figure 4a/cyan
15.	+	−	$+/-$	$]0,q_2[$	Figure 4b/red

. Thus, we have the following:

(a) 

The parameter conditions in Case 1 indicate that the polynomial (12) has two real roots, denoted as $p_1,p_2$, where $p_1<p_2$, and two complex conjugate roots, denoted as $p_3,p_3^{*}$, where * denotes the complex conjugate. Thus, it can be expressed as $F_q=-{\displaystyle \frac{{\gamma }_3}{4}}(\mathcal{M}-p_1)(p_2-\mathcal{M})(\mathcal{M}-p_3)(\mathcal{M}-p_3^{*})$. The interval for the real solution is $\mathcal{M}\in ]p_1,p_2[$. Assuming $\mathcal{M}\left(0\right)=p_1$, integrating both sides of Equation (11) yields a new solution to Equation (2) of the form

$$G(x,t)=\mathcal{M}\left(\xi \right)={\displaystyle \frac{1}{A_1-B_1}}\left[A_1{p}_1-B_1{p}_2-{\displaystyle \frac{2A_1{B}_1(p_1-p_2)}{A_1+B_1+(A_1-B_1)\mathrm{cn}(\frac{\sqrt{2{\gamma }_3{A}_1{B}_1}}{2}\kappa (x-\sigma t),k_1)}}\right],$$

(15)

where $A_1^2={(p_2-\mathrm{Re}{p}_3)}^2+\mathrm{Im}{p}_3$, $B_1^2={(p_1-\mathrm{Re}{p}_3)}^2+{\mathrm{Im}}^2{p}_3$, and $k_1^2={\displaystyle \frac{{(p_2-p_1)}^2-{(A_1-B_1)}^2}{4A_1{B}_1}}$. The solution (15) is periodic, with a period given by ${\displaystyle \frac{8}{\sqrt{2{\gamma }_3{A}_1{B}_1}}}K\left(k_1\right)$, where $K\left(k_1\right)$ denotes the complete elliptic integral of the first kind [49].

The solutions corresponding to Case 2, Case 3, Case 5, Case 7, and Case 12 in Table 1 are identical to the solution (15), differing only in their arguments. This difference arises because the roots of the polynomial change with the parameter constraints, while the sign of the leading order of the polynomial remains fixed.

(B) 

The parameter conditions in Case 4, Case 8, and Case 13 indicate that the polynomial (12) has four real zeros, denoted as $p_i$ for $i=4,5,6,7$, satisfying $p_4<p_5<p_6<p_7$. Thus, it is written as $F_q=-{\displaystyle \frac{{\gamma }_3}{4}}(\mathcal{M}-p_4)(p_5-\mathcal{M})(\mathcal{M}-p_6)(\mathcal{M}-p_7)$. The intervals of the real solutions are $\mathcal{M}\in ]p_4,p_5[\cup ]p_6,p_7[$. For $\mathcal{M}\in ]p_4,p_5[$, we assume $\mathcal{M}\left(0\right)=p_4$ and integrate both sides of Equation (11). Consequently, we obtain a novel periodic solution to Equation (2) of the form

$$G(x,t)=\mathcal{M}\left(\xi \right)=p_7+{\displaystyle \frac{(p_7-p_5)(p_7-p_4)}{p_5-p_7+{\mathrm{sn}}^2(\frac{1}{4}\sqrt{2{\gamma }_3(p_7-p_5)(p_6-p_4)}\kappa (x-\sigma t),k_2)}},$$

(16)

where $k_2^2={\displaystyle \frac{(p_7-p_6)(p_5-p_4)}{(p_7-p_5)(p_6-p_4)}}$. The period of the solution (16) is ${\displaystyle \frac{8K\left(k_2\right)}{\sqrt{2{\gamma }_3(p_7-p_5)(p_6-p_4)}}}$, where $K\left(k_2\right)$ is a complete elliptic integral of the first kind [49]. The solution (16) corresponds to the left family of periodic trajectories, as illustrated in Figure 3a,b. On the other hand, if $\mathcal{M}\in ]p_6,p_7[$, we assume that $\mathcal{M}\left(0\right)=p_7$. Consequently, integrating both sides of Equation (11) yields

$$G(x,t)=M\left(\xi \right)=p_4-{\displaystyle \frac{(p_7-p_4)(p_6-p_4)}{p_4-p_6+(p_6-p_7){\mathrm{sn}}^2(\frac{1}{4}\sqrt{{\gamma }_3(p_7-p_5)(p_6-p_4)}\kappa (x-\sigma t),k_2)}},$$

(17)

which is a new periodic solution to Equation (2) with period ${\displaystyle \frac{8K\left(k_2\right)}{\sqrt{{\gamma }_3(p_7-p_5)(p_6-p_4)}}}$. The solution (17) corresponds to the right family of periodic trajectories, as shown in Figure 3a,b.

Note that for fixed values of the parameters ${\gamma }_1,{\gamma }_2,{\gamma }_3$, and q, two distinct solutions arise, depending on the differences in the intervals of real solutions. Hence, employing such intervals is crucial.

(c) 

The parameter conditions in Case 6 and Case 9 indicate that the polynomial (12) has one double root at the origin and two simple roots given by $p_{8,9}={\displaystyle \frac{1}{3{\gamma }_3}}\left[-2{\gamma }_2\mp \sqrt{4{\gamma }_2^2-18{\gamma }_1{\gamma }_3}\right]$. In Case 6, these roots satisfy $p_7<p_8<0$, while in Case 9, $p_9>p_8>0$. The polynomial (12) can be expressed as $F_q={\displaystyle \frac{{\gamma }_3}{4}}{\mathcal{M}}^2(\mathcal{M}-p_8)(p_9-\mathcal{M})$. The interval of real propagation is $\mathcal{M}\in ]p_8,p_9[$ for Case 6 and $\mathcal{M}\in ]p_9,p_8[$ for Case 9. Postulating $\mathcal{M}\left(0\right)=p_8$ in both cases and integrating both sides of Equation (11), we obtain

$$G(x,t)=M\left(\xi \right)={\displaystyle \frac{6{\gamma }_1}{\sqrt{4{\gamma }_2^2-18{\gamma }_1{\gamma }_3}\cos \left(2\sqrt{{\gamma }_1}\kappa (x-\sigma t)\right)-2{\gamma }_2}}.$$

(18)

The solution (18) represents a novel solution to Equation (2).

(d) 

Cases 10, 11, and 15 justify the existence of four real zeros of the polynomial, namely $r_i,i=1,2,3,4$, with $r_1<r_2<r_3<r_4$. It is worth mentioning that the values of these roots vary from case to case due to their dependence on the polynomial coefficients. The polynomial (12) is expressed as $F_q={\displaystyle \frac{-{\gamma }_3}{4}}(\mathcal{M}-r_1)(\mathcal{M}-r_2)(\mathcal{M}-r_3)(\mathcal{M}-r_4)$. The intervals of the real solutions are given by $M\in ]-\infty ,r_1[\cup ]r_2,r_3[\cup ]r_4,\infty [$. We restrict ourselves to $M\in ]r_2,r_3[$, as this interval corresponds to periodic trajectories, whereas the other intervals describe unbounded trajectories. Integrating both sides of Equation (11) under the assumption (11) that $\mathcal{M}\left(0\right)=r_2$ yields

$$G(x,t)=M\left(\xi \right)=r_2+{\displaystyle \frac{(r_3-r_2)(r_4-r_2)}{(r_4-r_2)+(r_3-r_4){\mathrm{sn}}^2(\frac{1}{2}\sqrt{-2{\gamma }_3(r_4-r_2)(r_3-r_1)}\kappa (x-\sigma t),k_3)}},$$

(19)

where $k_3=\sqrt{{\displaystyle \frac{(r_4-r_3)(r_2-r_1)}{(r_4-r_2)(r_3-r_1)}}}$. The solution (19) characterizes a new solution to Equation (2), with a period given by ${\displaystyle \frac{4K\left(k_3\right)}{\sqrt{-2{\gamma }_3(r_4-r_2)(r_3-r_1)}}}$.

4.2. Super-Periodic Solutions

A super-periodic nonlinear wave, a novel type of nonlinear wave, is characterized by the nontrivial topology of its phase portraits, which exhibit greater complexity than simple periodic waves. These waves correspond to phase-plane orbits or trajectories that involve at least two stable equilibrium points (centers) and a separatrix layer. Super-periodic wave solutions arise in various physical phenomena, including fluid dynamics, optics, and plasma physics, where they play a crucial role in describing and predicting the evolution of wave patterns in complex systems. For further details on these solutions, see, for example, [50,51].

The conditions for the existence of super-periodic solutions to Equation (2) are summarized in

Table 2. Conditions for the existence of super-periodic solutions to Equation (2).

Case	${\mathit{\gamma }}_1$	${\mathit{\gamma }}_3$	${\mathit{\gamma }}_2$	q	Figure/Trajectory Color
1.	+	+	$]2\sqrt{{\gamma }_1{\gamma }_3},\infty [$	$]q_2,\infty [$	Figure 3a/green
2.			$]-\infty ,-2\sqrt{{\gamma }_1{\gamma }_3}[$	$]q_3,\infty [$	Figure 3b/green
3.	−	+	$+/-$	$]0,\infty [$	Figure 4a/green

. This section focuses on constructing these solutions.

All cases in Table 2 demonstrate that the polynomial (12) has two real roots, $r_5$ and $r_6$, with $r_5<r_6$, and two complex conjugate roots, $r_7$ and $r_7^{*}$. Consequently, the polynomial (12) can be expressed as $F_q={\displaystyle \frac{{\gamma }_3}{4}}(\mathcal{M}-r_5)(r_6-\mathcal{M})(\mathcal{M}-r_7)(\mathcal{M}-r_7^{*})$. The interval of the real solutions is $\mathcal{M}\in ]r_5,r_6[$. Integrating both sides of Equation (11) under the assumption that $\mathcal{M}\left(0\right)=r_5$ yields

$$G(x,t)=\mathcal{M}\left(\xi \right)={\displaystyle \frac{1}{A_2-B_2}}\left[A_2{r}_5-B_2{r}_6-{\displaystyle \frac{2A_2{B}_2(r_5-r_6)}{A_2+B_2+(A_2-B_2)\mathrm{cn}(\frac{\sqrt{2{\gamma }_3{A}_2{B}_2}}{2}\kappa (x-\sigma t),k_4)}}\right],$$

(20)

where $A_2^2={(r_6-\mathrm{Re}{r}_7)}^2+{\mathrm{Im}}^2{r}_7$, $B_2^2={(r_5-\mathrm{Re}{r}_7)}^2+{\mathrm{Im}}^2{r}_7$, and $k_4^2={\displaystyle \frac{{(r_6-r_5)}^2-{(A_2-B_2)}^2}{4A_2{B}_2}}$. Solution (20) characterizes a novel super-periodic solution to Equation (2).

4.3. Solitary Solutions

This subsection focuses on deriving the solitary wave solution to Equation (2), incorporating the parameter conditions specified in

Table 3. Conditions for the existence of solitary solutions to Equation (2).

Case	${\mathit{\gamma }}_1$	${\mathit{\gamma }}_3$	${\mathit{\gamma }}_2$	q	Figure/Trajectory Color
1.	+	+	$]-\infty ,-2\sqrt{{\gamma }_1{\gamma }_3}[$	$q_3$	Figure 3b/blue
2.			$]2\sqrt{{\gamma }_1{\gamma }_3},\infty [$	$q_2$	Figure 3a/blue
3.	−	−	$]2\sqrt{{\gamma }_1{\gamma }_3},\infty [$	0	Figure 3c/blue
4.			$]-\infty ,-2\sqrt{{\gamma }_1{\gamma }_3}[$	0	Figure 3d/blue
5.	−	+	$+/-$	0	Figure 4a/blue
6.	+	−	$+/-$	$q_2$	Figure 4a/blue

. For brevity, only selected cases are considered, as the calculations for the remaining cases follow a similar approach.

First, we examine Case 1 in Table 3. In this case, the polynomial (12) has one double root, denoted by ${\omega }_2$, which corresponds to the $\mathcal{M}$-coordinate of the saddle point ${\mathcal{Q}}_3$. The other roots, ${\omega }_1,{\omega }_3$, are simple. This implies that $F_q$ can be expressed as $F_q={\displaystyle \frac{{\gamma }_3}{4}}{(\mathcal{M}-{\omega }_2)}^2({\omega }_1-\mathcal{M})(\mathcal{M}-{\omega }_3)$, where ${\omega }_1<0<{\omega }_2<{\omega }_3$. The roots ${\omega }_1$ and ${\omega }_2$ are given by

$${\omega }_{1,3}={\displaystyle \frac{1}{3{\gamma }_3}}\left[\mp 3\sqrt{{\gamma }_2^2-4{\gamma }_1{\gamma }_3}\mp {\gamma }_2+2\sqrt{{\gamma }_2^2+3{\gamma }_2\sqrt{{\gamma }_2^2-4{\gamma }_1{\gamma }_3}}\right].$$

The intervals for the real solutions are $\mathcal{M}\in ]{\omega }_2,{\omega }_3[\cup ]{\omega }_1,{\omega }_2[$. The first interval, $]{\omega }_2,{\omega }_3[$, corresponds to the left homoclinic trajectory, while the second interval, $]{\omega }_1,{\omega }_2[$, corresponds to the right homoclinic trajectory, as illustrated by the blue curves in Figure 3b. Let us construct the solution corresponding to each interval individually:

 (a)

Let $\mathcal{M}\in ]{\omega }_2,{\omega }_3[$ and assume $\mathcal{M}\left(0\right)={\omega }_3$. Integrating both sides of Equation (11) yields

$$G(x,t)=\mathcal{M}\left(\xi \right)={\omega }_2-{\displaystyle \frac{2({\omega }_2-{\omega }_3)({\omega }_1-{\omega }_2)}{{\omega }_1-2{\omega }_2+{\omega }_3+({\omega }_1-{\omega }_3)\cosh \left(\frac{1}{2}\sqrt{2{\gamma }_3({\omega }_2-{\omega }_1)({\omega }_3-{\omega }_2)}\kappa (x-\sigma t)\right)}},$$

(21)

which is a new solitary solution to Equation (2).

 (b)

Let $\mathcal{M}\in ]{\omega }_1,{\omega }_2[$ and assume $\mathcal{M}\left(0\right)={\omega }_1$. Integrating both sides of Equation (11) yields

$$G(x,t)=\mathcal{M}\left(\xi \right)={\omega }_2+{\displaystyle \frac{2({\omega }_2-{\omega }_3)({\omega }_1-{\omega }_2)}{-{\omega }_1+2{\omega }_2-{\omega }_3+({\omega }_1-{\omega }_3)\cosh \left(\frac{1}{2}\sqrt{2{\gamma }_3({\omega }_2-{\omega }_1)({\omega }_3-{\omega }_2)}\kappa (x-\sigma t)\right)}},$$

(22)

which is a new solitary solution to Equation (2).

Using similar calculations, we can construct the solution for Case 2 in Table 3.

Case 3 and Case 4 indicate that the polynomial (12) has a double root at the origin and two distinct simple roots, ${\rho }_1,{\rho }_2$. For Case 3, these roots satisfy $0<{\rho }_1<{\rho }_2$, whereas for Case 4, they satisfy ${\rho }_2<{\rho }_1<0$. Accordingly, the polynomial (12) can be expressed as $F_q={\displaystyle \frac{-{\gamma }_3}{4}}{\mathcal{M}}^2(\mathcal{M}-{\rho }_1)(\mathcal{M}-{\rho }_2)$. The intervals of real wave propagation are $\mathcal{M}\in ]{\rho }_2,0[$ for Case 3 and $\mathcal{M}\in ]0,{\rho }_2[$ for Case 4. By integrating both sides of Equation (11) under the assumption that $\mathcal{M}\left(0\right)={\rho }_2$, we obtain the solution

$$G(x,t)=\mathcal{M}\left(\xi \right)={\displaystyle \frac{2r_1{r}_2}{r_1+r_2+(r_2-r_1)\cosh \left(\frac{\sqrt{-2{\gamma }_3{\rho }_1{\rho }_2}}{2}\kappa (x-\sigma t)\right)}},$$

(23)

which characterizes a novel solitary solution to Equation (2).

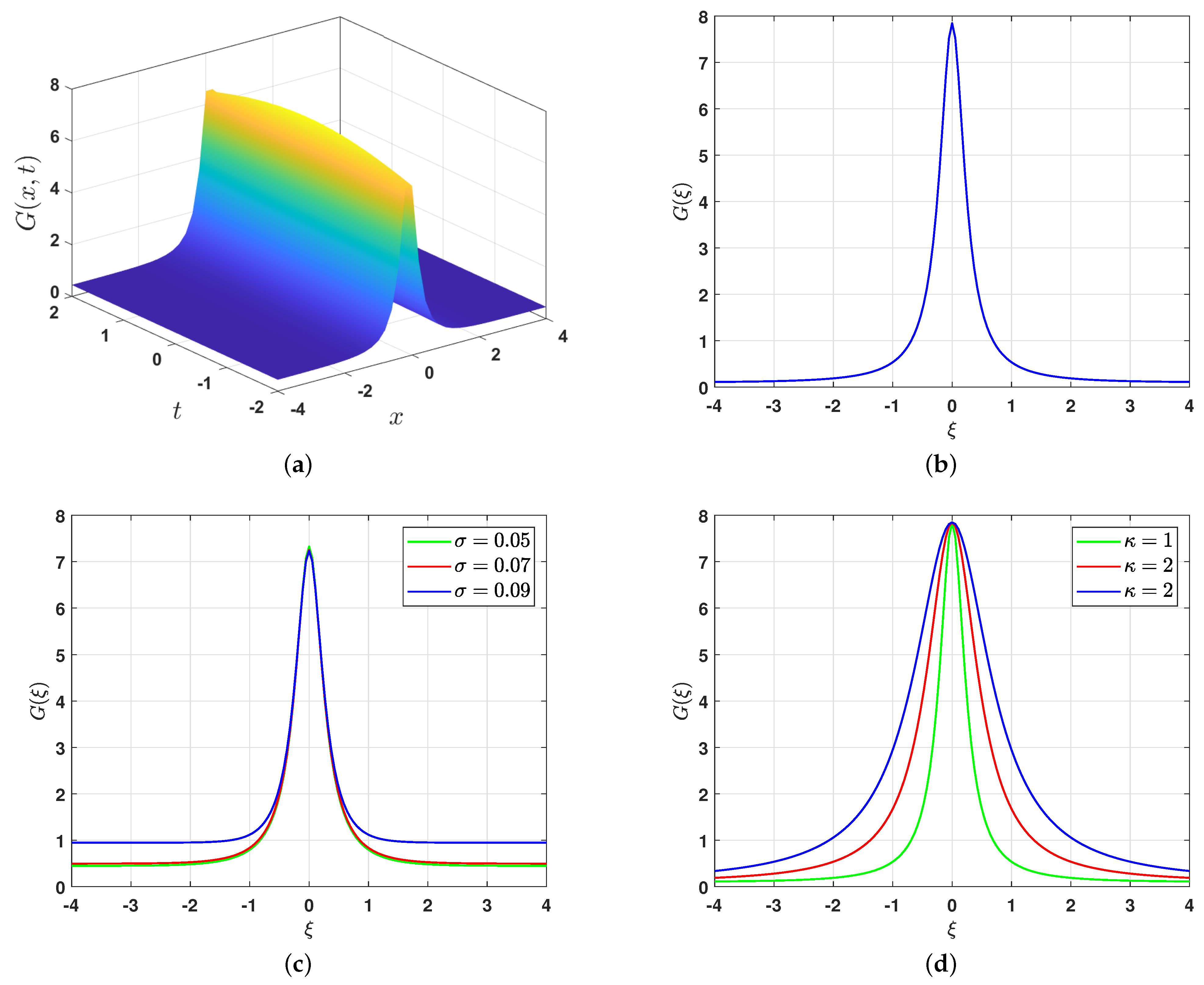
5. Physical Interpretation

This section focuses on graphically presenting some of the obtained solutions using $3D$ and $2D$ representations, as well as exploring the effects of the wave velocity $\sigma$ and wave number $\kappa$ on the periodic, super-periodic, and solitary solutions.

We allow the parameters to take the values $\mu =0.8$, $\eta =0.85$, $\beta =2$, $\tau =0.4$, $\alpha =1$, $s=-0.8$, $\sigma =0.05$, and $\kappa =1$. Consequently, Equation (6) yields ${\gamma }_1=1.207627119$, ${\gamma }_2=-12.01271186$, and ${\gamma }_3=2.002118644$. It is evident that ${\gamma }_1>0$, ${\gamma }_3>0$, and ${\gamma }_2<-2\sqrt{{\gamma }_1{\gamma }_3}=-3.109863514$. The phase portrait for the system (7a,b) is shown in Figure 3a. The values of the parameter q at the equilibrium points ${\mathcal{Q}}_0=0$, ${\mathcal{Q}}_2=(0.1022723737,0)$, and ${\mathcal{Q}}_3=(5.897727624,0)$ are $q_0=0$, $q_2=-194.8578173$, and $q_3=0.002086970512$, respectively. As mentioned above, the type of solution depends on the values of q, which also determine the nature of the trajectory.

If we select $q=0.001043485256\in ]0,0.002086970512[$, then the system (7a,b) has two families of periodic orbits, shown in brown. The corresponding solution can be determined by calculating the roots $p_i$, for $i=4,5,6,7$, of the polynomial (12). These roots are $p_4=-0.03721316573$, $p_5=0.05102437429$, $p_6=0.1399328644$, and $p_7=0.846255925$. Consequently, the solution (16) becomes

$$G(x,t)=7.846255925+{\displaystyle \frac{61.45346699}{-7.795231551-\mathrm{sn}{\left(0.04156857488t-0.8313714975x,0.7017300579\right)}^2}}.$$

(24)

Figure 5a and Figure 5b present the $3D$ and $2D$ representations of the solution (24), respectively, illustrating its periodicity. Additionally, we examine the influence of the wave velocity $\sigma$ and wave number $\kappa$ on the periodic solution (16) by fixing the values of all parameters while allowing only $\sigma$ or $\kappa$ to vary. Figure 5c demonstrates the impact of $\sigma$ on the periodic solution (16), showing that as $\sigma$ increases, the amplitude of the solution grows while its width decreases. Similarly, Figure 5d illustrates the effect of the wave number $\kappa$ on the periodic solution (16). It is evident that as $\kappa$ increases, the amplitude of the solution remains unchanged, while its width expands.

If we select $q=3.002086971\in ]0.002086970512,\infty [$, the system (7a,b) exhibits a family of super-periodic trajectories, shown in green in Figure 3b. Consequently, Equation (2) admits a solution of the form (20). To derive this solution, we calculate the roots of the polynomial (12), which are $r_5=-0.8356228633$, $r_6=7.858855170$, $r_7=0.4883838458-0.8214639844\mathrm{i}$, and $r_7^{*}=0.4883838458+0.8214639844\mathrm{i}$. Hence, the solution (20) is expressed as

$$G(x,t)=-3.148234177+{\displaystyle \frac{34.30114829}{8.974246415+5.857968607\mathrm{cn}\left(3.401112529\kappa \left(-0.05t+x\right),0.8930547131\right)}}.$$

(25)

Figure 6a,b present the $3D$ and $2D$ representations of the super-periodic solution (20), respectively. Figure 6c demonstrates that the effect of the wave velocity $\sigma$ on the solution (20) is minimal for both amplitude and width. Figure 6d illustrates the influence of the wave number $\kappa$ on the solution (20), showing that as $\kappa$ increases, the amplitude of the solution remains nearly constant, while its width increases.

If we choose $q=q_3=0.1572351228$, the system (7a,b) has two homoclinic trajectories, as shown in Figure 3b. Hence, Equation (2) has a solitary solution of the form (21) or (22), depending on the possible intervals of the real solutions. To find these solutions, we first find the roots of the polynomial (12). These roots are ${\omega }_1=-0.2162195553,{\omega }_2=0.4455920452$, and ${\omega }_3=7.325035462$. Hence, the solution (21) takes the form

$$G(x,t)=0.4455920452-{\displaystyle \frac{9.105790916}{-7.541255017cosh\left(2.133751500\kappa \left(-0.05t+x\right)\right)+6.217631816}}.$$

(26)

Figure 7 provides a graphical representation of the solution (21). Specifically, Figure 7a,b show the $3D$ and $2D$ depictions of the solution, respectively. It is evident that this solution is symmetric about the vertical line $\xi =0$, as illustrated in Figure 7b. Figure 7c demonstrates that the variation in the wave velocity has a minimal effect on the amplitude and width of the solution. Finally, Figure 7d highlights the influence of the wave number $\kappa$ on the solution (21). As the wave number $\kappa$ increases, the amplitude of the solution remains approximately constant, while its width expands.

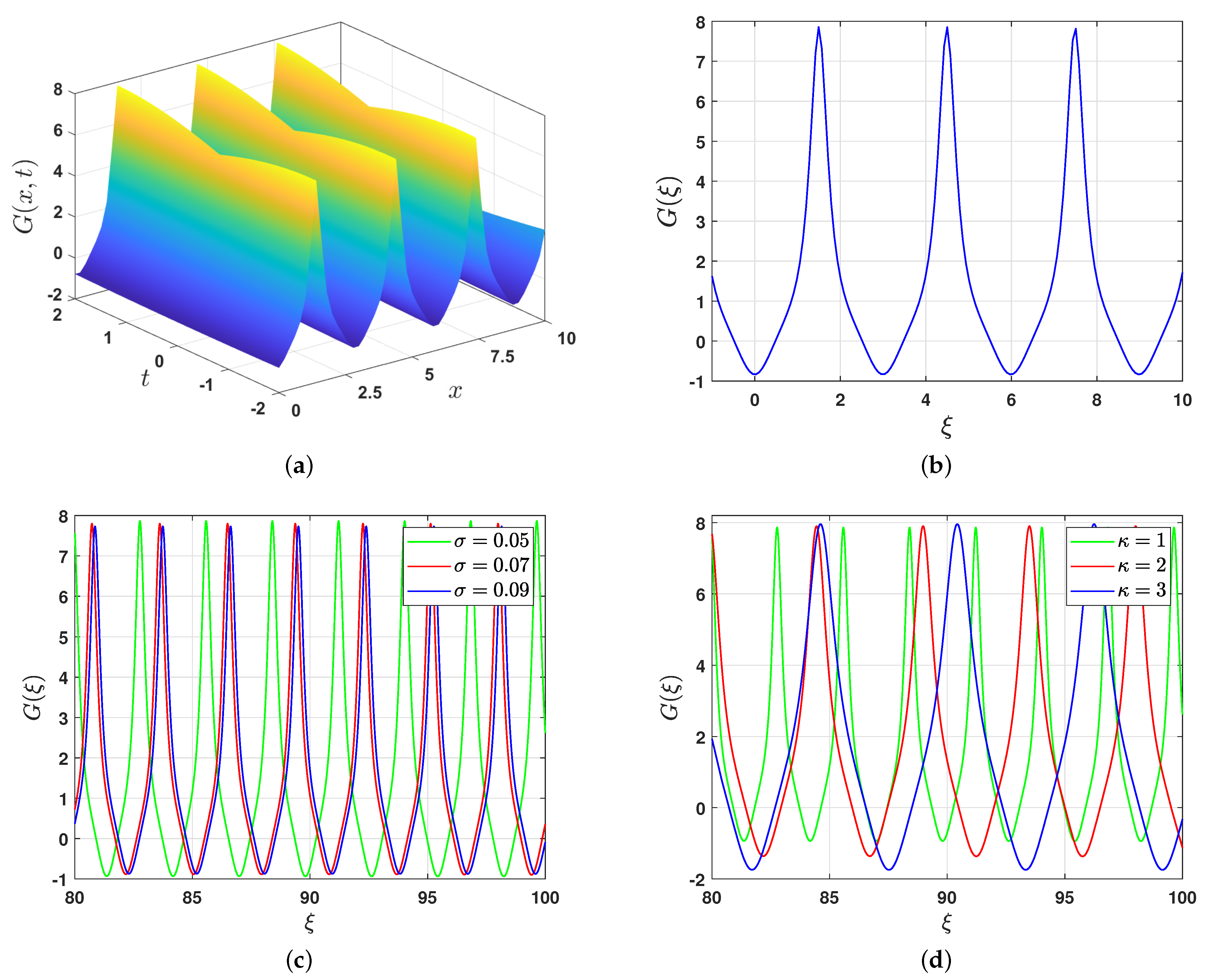
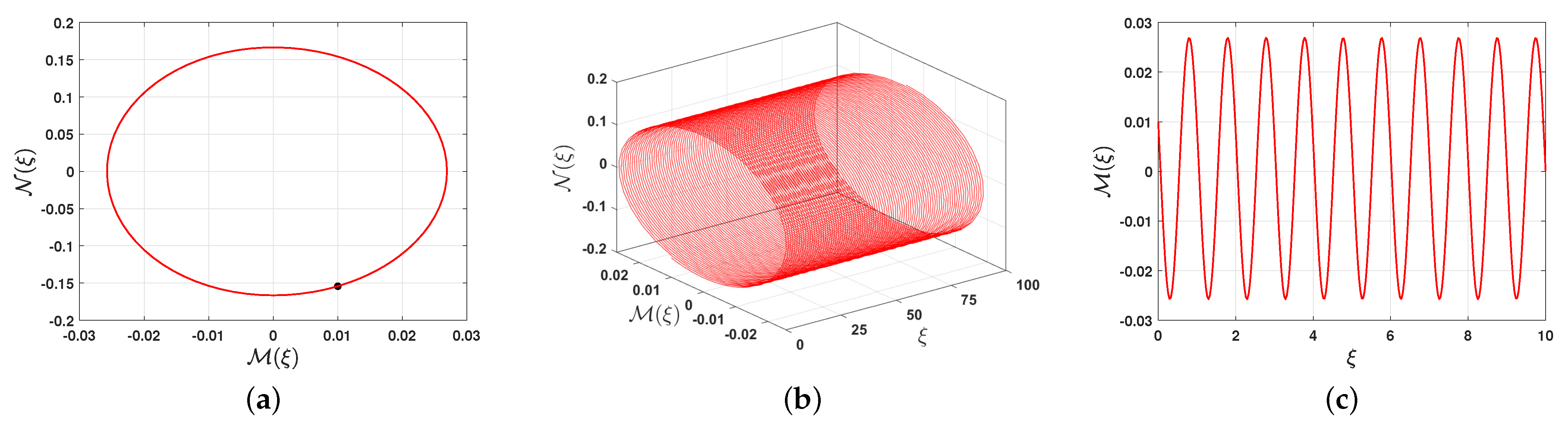
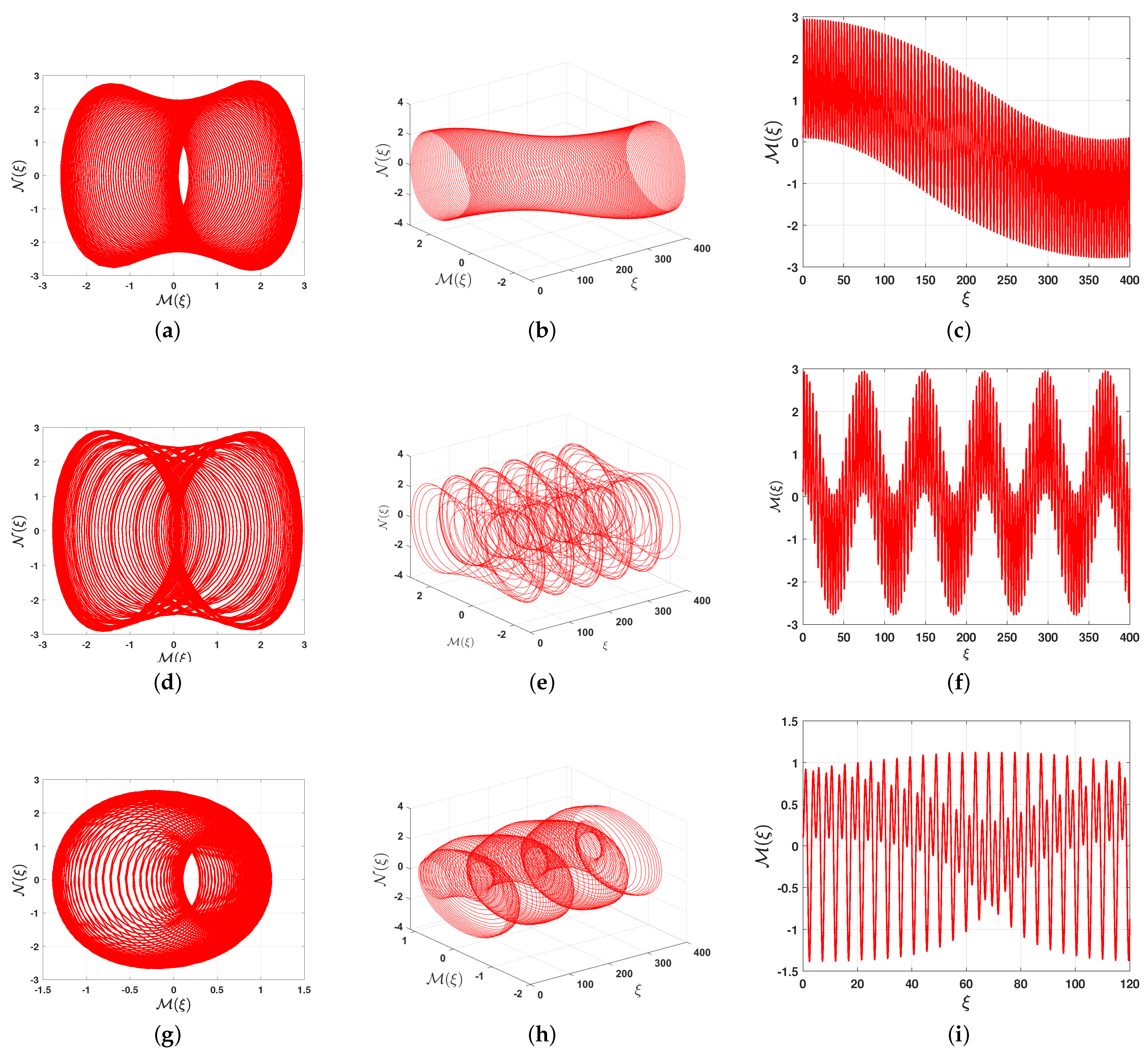
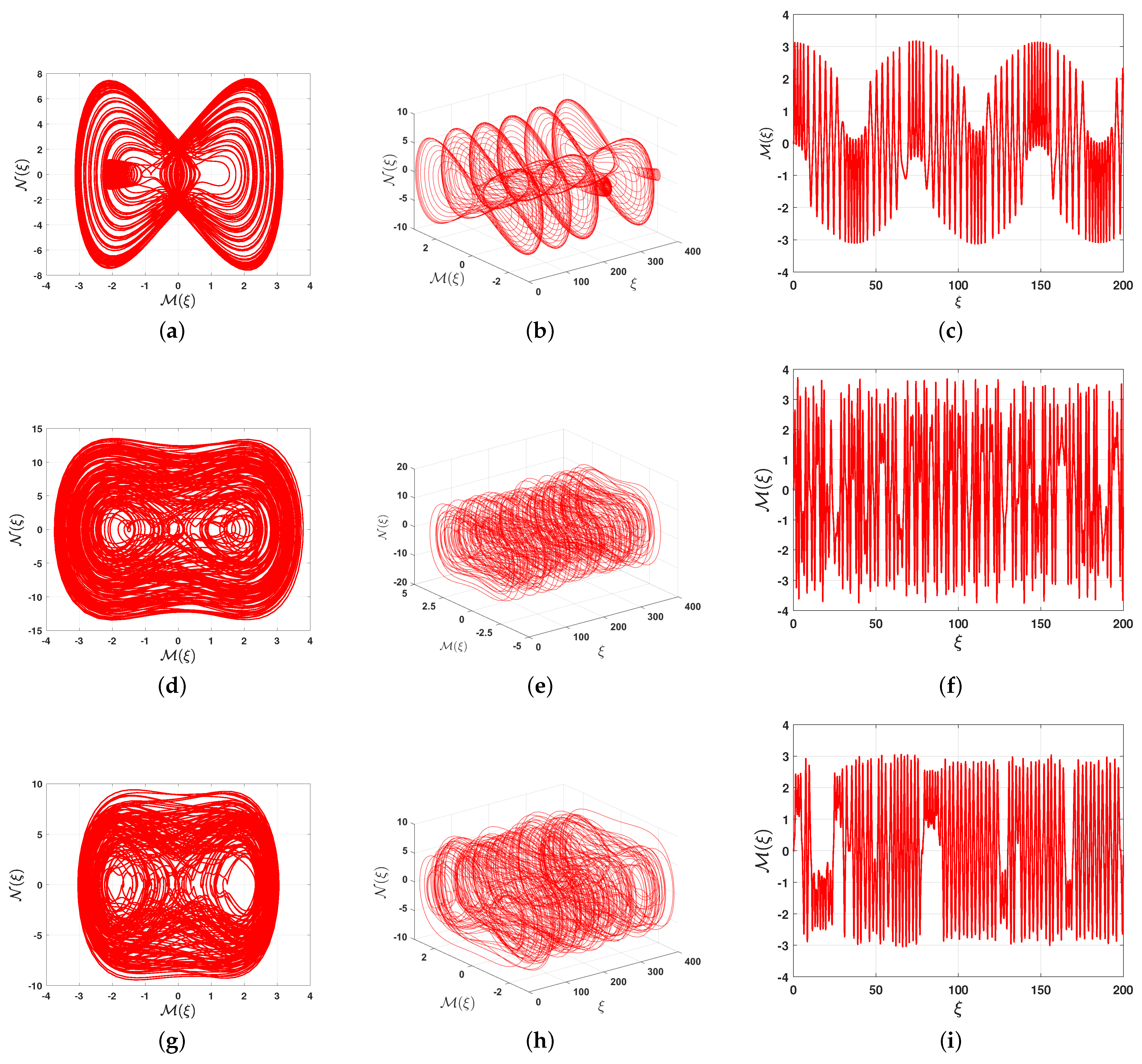
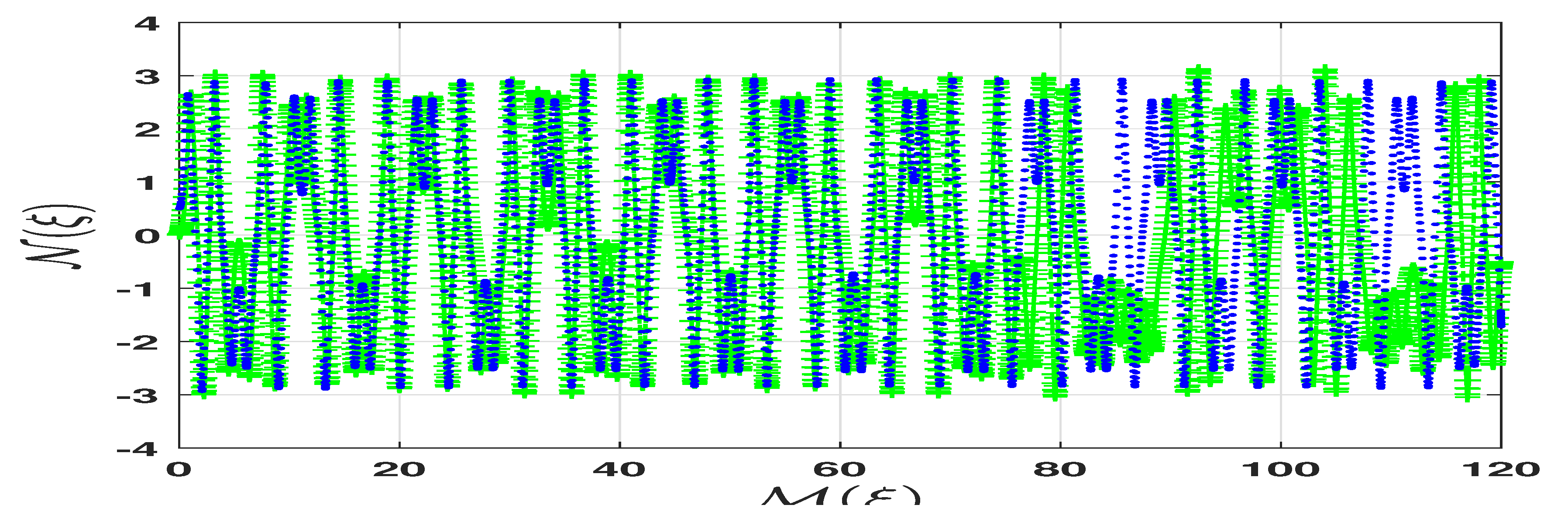
6. Quasi-Periodic Behavior

This section investigates the autoresonance behavior of a non-autonomous system in which the oscillator self-regulates under the influence of a variable periodic force. The perturbed version of the traveling wave system corresponding to Equation (2) emerges as a result of external effects. These effects are characterized by the inclusion of specific forces, represented as ${\displaystyle \frac{1}{{\kappa }^2}}{Q}_{xx}\left(\kappa (x-\sigma t)\right)$. It has the form

$$\begin{array}{cc}\hfill & G_{tt}-s^2{G}_{xx}+\left({\displaystyle \frac{\partial }{\partial t}}-s\eta {\displaystyle \frac{\partial }{\partial x}}\right)\left({\displaystyle \frac{3}{2}}\alpha G{G}_x-{\displaystyle \frac{3}{8}}{\alpha }^2{G}^2{G}_x\right)+\left({\displaystyle \frac{\partial }{\partial t}}-s\mu {\displaystyle \frac{\partial }{\partial x}}\right)\left({\displaystyle \frac{\beta (1-3\tau )}{6}}{G}_{xxx}+G_x\right)\hfill \\ \hfill & ={\displaystyle \frac{1}{{\kappa }^2}}{Q}_{xx}\left(\kappa (x-\sigma t)\right).\hfill \end{array}$$

(27)

By substituting (3) into Equation (27), we derive a perturbed system that corresponds to the unperturbed system (7a,b) of the form

$$\begin{array}{cc}\hfill {\mathcal{M}}^{\prime }& =\mathcal{N},\hfill \\ \hfill {\mathcal{N}}^{\prime }& =-\mathcal{M}({\gamma }_1+{\gamma }_2\mathcal{M}+{\gamma }_3{\mathcal{M}}^2)+\rho \mathrm{cn}(\Omega \xi ,k),\hfill \end{array}$$

(28)

where $\mathrm{cn}(u,k)$ is the Jacobi elliptic function [49]. The parameters ${\gamma }_i$ are defined by (6), and the external periodic force is chosen as $Q=\rho \mathrm{cn}(\Omega \xi ,k)$, where $\rho$ represents the strength of the external periodic force and $\Omega$ denotes its frequency. This choice is significant because it can degenerate into trigonometric or hyperbolic functions as k approaches 0 or 1, respectively.

The unperturbed system (7a,b) is studied with the following parameter values: $\mu =0.8$, $\eta =0.85$, $\beta =2$, $\tau =0.4$, $\sigma =0.05$, $s=-0.063$, $\alpha =1$, and $\kappa =1$. These parameters are equivalent to ${\gamma }_1=40.0875$, ${\gamma }_2=-99.84375$, and ${\gamma }_3=16.640625$. We choose the initial conditions $\mathcal{M}\left(0\right)=-0.1542242022$ and ${\mathcal{M}}^{\prime }\left(0\right)=0.01$, which results in $q=-0.1542184004$, where q lies within the interval $]0,0.002086970512[$. This case corresponds to Case 8 in Table 1. Hence, the unperturbed system (7a,b) exhibits periodic behavior, as demonstrated in Figure 8a,b. Additionally, Figure 8c shows the plot of $\mathcal{M}\left(\xi \right)$ versus $\xi$, which further confirms the system’s periodic behavior.

The inclusion of the free parameters ${\gamma }_1,{\gamma }_2$, and ${\gamma }_3$, in addition to the three parameters $\rho$, $\Omega$, and k associated with the perturbed term, adds complexity to understanding the periodic and chaotic dynamical behavior of the dual-mode Gardner model. This problem is addressed through the adoption of comprehensive and diverse strategies. This involves the presentation of 2D and 3D phase portraits, time series, and an examination of the influence of parameters through two distinct events. The investigation systematically varies the frequency (or strength) of the external force while keeping the other parameters fixed.

First, we assume the following parameter values: $\mu =0.8$, $\eta =0.85$, $\beta =31.940745$, $\tau =0.4$, $\sigma =0.05$, $s=-0.05885733$, $\alpha =18$, $\kappa =1$, $k=0.5$, and, consequently, ${\gamma }_1=-1.25$, ${\gamma }_2=1.25$, and ${\gamma }_3=-0.375$. In this section, we fix the strength of the external periodic effect at $\rho =4$ and allow the frequency $\Omega$ to vary while keeping the initial condition $(\mathcal{M}\left(0\right),{\mathcal{M}}^{\prime }\left(0\right))=(0.1,0)$ fixed. For $\Omega =0.01$, Figure 9a and Figure 9b, which depict the $2D$ and $3D$ phase portraits of the perturbed system (28), show a quasi-periodic wave phenomenon, as confirmed by Figure 9c, which illustrates the solution $\mathcal{M}$ as a function of $\xi$. As the frequency increases to $\Omega =0.1$, the quasi-periodic behavior remains, as shown in Figure 9d–f. Moreover, chaotic behavior is absent even for $\Omega =3.1$, as confirmed by the $2D$ and $3D$ phase portraits in Figure 9g,h and the time-series representation depicted in Figure 9i. This is consistently observed due to the in commensurability of the frequency ratio.

Second, we select suitable values for the physical parameters, fixing one of the parameters ${\gamma }_i$ ($i=1,2,3$) while allowing all other parameters to vary. Specifically, we assume $\mu =0.8$, $\eta =0.85$, $\beta =-3.77656$, $\tau =0.4$, $\sigma =0.05$, $s=-0.05885788$, $\alpha =18$, $\rho =9$, and $\kappa =1$. As a result, we have ${\gamma }_1=10.5$, ${\gamma }_2=1.25$, and ${\gamma }_3=-0.375$. We present the 2D and 3D phase portraits, along with the time-series representation, for different values of the frequency $\Omega$ and a fixed initial condition $(\mathcal{M}\left(0\right),{\mathcal{M}}^{\prime }\left(0\right))=(-0.02,0)$. For $\Omega =0.1$, the 2D and 3D phase portraits displayed in Figure 10a–c clearly show that the perturbed system (28) still exhibits quasi-periodic behavior. As the frequency increases to $\Omega =3.1$, the system dynamics shift to chaotic behavior, as shown in Figure 10d–f. Moreover, as the frequency further increases to $\Omega =9.1$, even more pronounced chaotic behavior is observed, as illustrated in Figure 10g–i.

We introduce the Poincaré surface of section using the same parameter values as those in Figure 10, which lead to chaotic dynamics. The Poincaré surface of section shown in Figure 11 is irregular. In other words, it is dispersed and fails to form any recognizable pattern. This behavior arises because the perturbed dynamical system (28) exhibits chaotic dynamics.

One can investigate the sensitivity of quasi-periodic waves by slightly altering the initial conditions. To explore this sensitivity, we consider two different initial conditions. The first set includes $(0.01,0)$ in green with a plus sign marker and $(0.02,0)$ in blue with a dot marker, as shown in Figure 12. The second set includes $(0.01,0)$ in green with a plus sign marker and $(0.5,0)$ in blue with a dot marker, as shown in Figure 13. Both figures compare the solutions of the system (28) for various initial conditions. The perturbed dynamical system (28) is sensitive to changes in the initial conditions due to its chaotic nature, which depends on the parameter values. Based on the observations and comparisons in Figure 12 and Figure 13, we conclude that the quasi-periodic chaotic behavior of the perturbed system is evident in its sensitivity to the initial conditions when specific parameter values are tested.

7. Conclusions

This study focuses on examining certain qualitative aspects of a dual-mode model for the Gardner equation derived from an ideal fluid. A wave transformation is applied to Equation (2), converting it into a dynamical system that corresponds to a Hamiltonian system with one degree of freedom. Consequently, finding a solution to Equation (2) is equivalent to solving the one- dimensional motion of a particle under the influence of a three-parameter potential function (9). This equivalence is significant as it allows for the determination of the real wave propagation intervals, which correspond to the possible real motions in Hamiltonian mechanics. Additionally, a bifurcation analysis is conducted on the traveling wave systems, highlighting its significance for several reasons, which are outlined below:

 (a)

This approach enables us to classify the solutions before explicitly determining them by linking the solution types to the phase trajectories, as stated in Lemma 1. In other words, it provides the existence conditions for periodic, super-periodic, and solitary solutions, as shown in Table 1, Table 2, and Table 3, respectively.

 (b)

This approach allows us to construct real (non-complex) solutions by considering the intervals of real wave propagation. Moreover, the significance of these intervals cannot be overlooked, as different intervals of real wave propagation yield different solutions. In other words, even under the same parameter conditions, distinct solutions arise due to variations in the intervals of real wave propagation.

 (c)

This approach allows us to isolate unbounded solutions, which are less relevant in real-world applications. However, it is worth mentioning that these solutions can be computed using the same procedures as bounded solutions.

Although bifurcation analysis offers several advantages, as discussed earlier, it also has certain limitations in its application. For its effective use, the reduced traveling wave system must be conservative and Hamiltonian, with only one or two degrees of freedom. While this approach is theoretically applicable to Hamiltonian systems with higher degrees of freedom, practically implementing it in such cases remains highly challenging.

Taking into account the bifurcation conditions on the parameters, we construct new solutions to Equation (2), classifying them into periodic, super-periodic, and solitary solutions. These solutions are graphically illustrated through their $2D$ and $3D$ representations. Additionally, we analyze the influence of the wave number and wave velocity on some of these solutions, revealing their effects on amplitude and width variations. Finally, we introduce a periodic perturbation term to Equation (2), leading to the perturbed dynamical system (28). In the absence of this term, the unperturbed dynamical system (7a,b) is integrable, and consequently, it exhibits regular behavior. However, the inclusion of the perturbation alters the dynamical behavior, leading to quasi-periodic and chaotic dynamics. To analyze these effects, we present $2D$ and $3D$ phase diagrams, along with time-series representations. Furthermore, a sensitivity analysis is conducted for different initial conditions, and Poincaré maps are used to identify chaotic patterns in the model.

Now, let us compare the findings of this paper with those from the relevant literature. In [35], the authors utilized the tan/cot and tanh/coth methods to derive solutions, all of which were expressed in terms of tan, cot, tanh, and coth functions. In contrast, our solutions are constructed using Jacobi elliptic functions, rendering them entirely novel. Furthermore, in [42], the authors conducted a symmetry analysis and examined the conservation laws of model (2), as well as investigated its dynamical behavior under a cosine-perturbed term. Our work extends this perturbation to the Jacobi elliptic function $\mathrm{cn}(u,k)$, which reduces to the cosine-perturbed term when $k=0$.