Domain Adaptation Based on Human Feedback for Enhancing Image Denoising in Generative Models

Abstract

How can human feedback be effectively integrated into generative models? This study addresses this question by proposing a method to enhance image denoising and achieve domain adaptation using human feedback. Deep generative models, while achieving remarkable performance in image denoising within training domains, often fail to generalize to unseen domains. To overcome this limitation, we introduce a novel approach that fine-tunes a denoising model using human feedback without requiring labeled target data. Our experiments demonstrate a significant improvement in denoising performance. For example, on the Fashion-MNIST test set, the peak signal-to-noise ratio (PSNR) increased by 94%, with an average improvement of 1.61 ± 2.78 dB and a maximum increase of 18.21 dB. Additionally, the proposed method effectively prevents catastrophic forgetting, as evidenced by the consistent performance on the original MNIST domain. By leveraging a reward model trained on human preferences, we show that the quality of denoised images can be significantly improved, even when applied to unseen target data. This work highlights the potential of human feedback for efficient domain adaptation in generative models, presenting a scalable and data-efficient solution for enhancing performance in diverse domains.

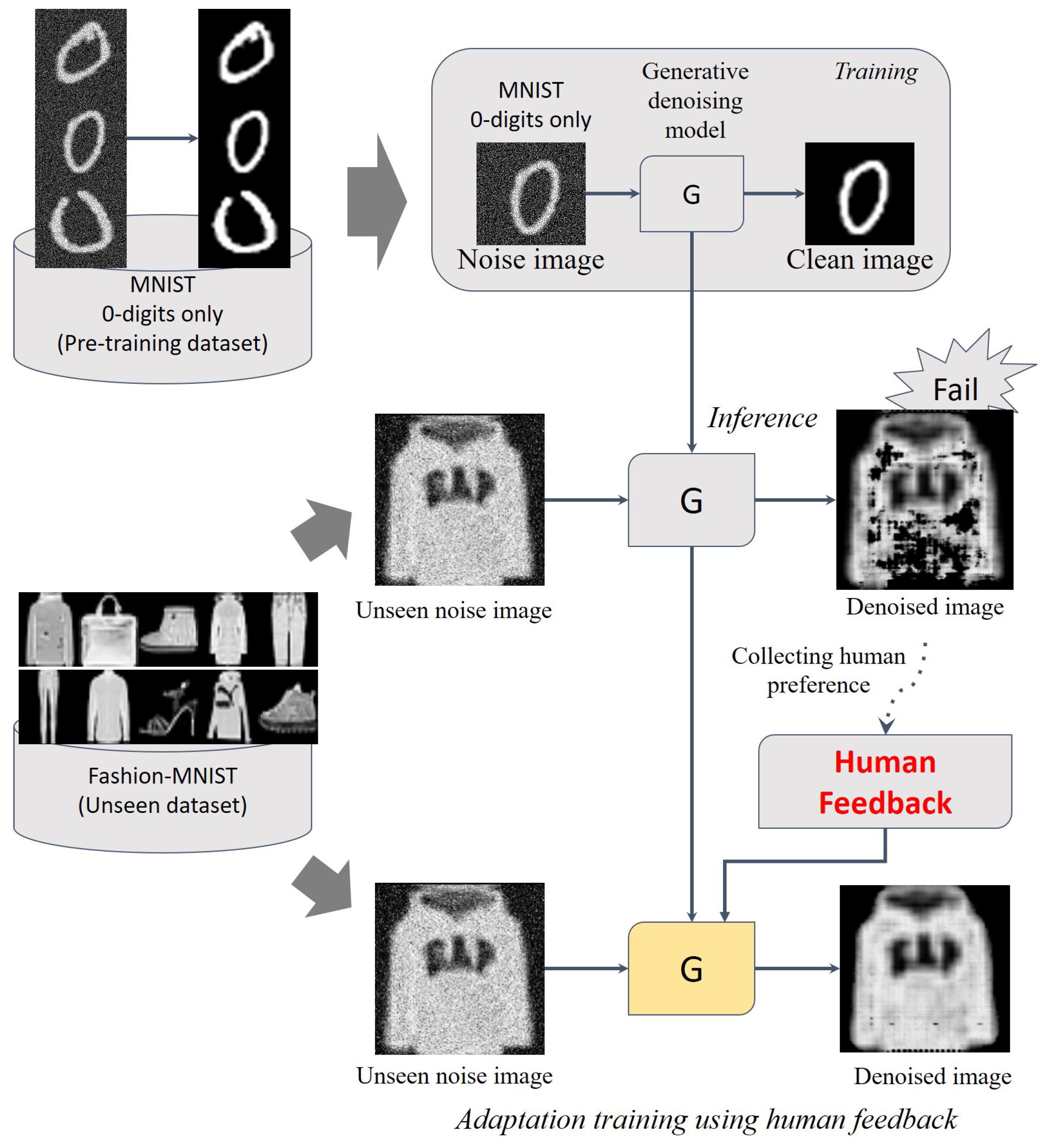
1. Introduction

Deep generative models have achieved remarkable success in image generation tasks [1,2,3]. In particular, generative adversarial networks (GANs) are widely known as a fundamental theory that demonstrates how to generate realistic images. Recently, GANs are also utilized for specific purposes such as image denoising [4,5,6], super-resolution [7,8], and style transfer [9,10,11,12]. These objectives involve training GANs using supervised learning with paired data sets aiming to learn the target distribution, which has been shown to yield successful results.

However, despite the impressive performance of these models within their training domain, they often encounter challenges when applied to unseen domains, resulting in subpar outputs. In the context of GANs based on image-to-image generation [13], which aim to preserve the original intrinsic characteristics while learning the target distribution, both successful and unsuccessful cases can emerge during testing on unseen domains. For example, when presented with ten samples from an unseen domain, seven of them may yield successful translations, while the remaining three produce unsatisfactory results. This raises the question: should we simply discard these three failed samples, or is there a way to enhance and improve them to achieve better outcomes? Obtaining ground-truth data for the unseen domain could facilitate domain-specific training; however, in many practical scenarios, acquiring target data for unseen domains poses significant challenges. As an alternative, applying domain adaptation methods [14,15,16,17,18,19,20,21] can mitigate this issue, but even domain-adapted models may still yield failed results based on human preferences.

Our objective diverges from conventional domain adaptation approaches. As demonstrated in [14,19], domain adaptation focuses on training methods that aim to minimize the distinguishability between the source and target domain distributions in the latent space. This macro-level approach seeks to minimize the overall gap between source and target domains. However, at a micro-level, there remain opportunities for improvement in the generated results. Therefore, our goal is to address and rectify instances of failure within the output produced by the trained model.

Similarly, during the training of ChatGPT [22], it excels at generating high-quality language responses through extensive pre-training on vast data sets. Nevertheless, upon human evaluation, the generated sentences may exhibit a dichotomy: some appear naturally flowing, while others seem less fluent. To bridge this gap, ChatGPT [22] leverages human feedback [23] to enhance its ability to produce more seamlessly natural sentences. Furthermore, in the domain of aligning text-to-image models [24], the introduction of human feedback has demonstrated significant improvements in model performance. However, research on model refinement through human feedback in GANs is still scarce, and through our paper, we aim to showcase the potential of model refinement through the profound influence of human feedback.

Recently, drawing inspiration from the success of reinforcement learning human feedback [25] in language domains, we present an innovative approach for unseen domain adaptation based on human feedback. Analogous to how children learn from the feedback provided by their parents, we adopt a similar strategy. For instance, if a child learns how to remove noise from the background of a single image, they can subsequently apply denoising techniques to new images. While the quality of the denoised image may vary, receiving feedback from a parent can lead to improvement. Even if we cannot surpass our previous achievements, we can still imitate and learn from them. This approach shows promise in addressing the challenges of unsupervised unseen domain adaptation and opens new possibilities for model enhancement through the profound influence of human feedback. As we explore this innovative avenue, our aim is to make significant contributions to the field of AI and foster advancements in human-guided domain adaptation research.

To achieve this, we introduce a deep feedback network that utilizes human feedback to the adaptation of an unlabeled target domain. As illustrated in Figure 1, to replicate restricted learning circumstances, we conduct experiments on the denoising problem. Initially, we train the model using a restrictive training approach, focusing solely on denoising the digit ‘0’ within the MNIST data set. Subsequently, we evaluate the model’s performance on the Fashion-MNIST data set, which represents an unseen domain. It becomes evident that the pre-trained model, trained on MNIST, produces unintended results when applied to the unseen domain. To adapt to the unseen domain, we introduce a training method based on human feedback. Human feedback assesses the model’s results in the unseen domain as either ‘Good’ or ‘Bad’. The model is then fine-tuned using the gradient of these assessments. This approach shows promising potential for efficiently fine-tuning the model using feedback from generators trained in other domains.

We can summarize our main contributions as follows

• We propose an adaptation method for the domain of image-based generative models through human feedback.
• We perform domain adaptation while maintaining the quality of the generated image using an optional loss function with a reward model using human feedback.
• We show that the model can be adapted by human feedback, even in the absence of labeled target data.

2. Methods

Our overall process consists of three steps. First, the denoising model is pre-trained in the basis domain, serving as the fundamental ability for denoising. Next, the reward model is trained using human feedback. To train the reward model, humans manually annotate denoised images as either $Good$ or $Bad$. Finally, the basis generator is re-trained using the reward model. Even if the generator produces denoised images of low quality, it will be trained to prioritize good results based on the provided human feedback.

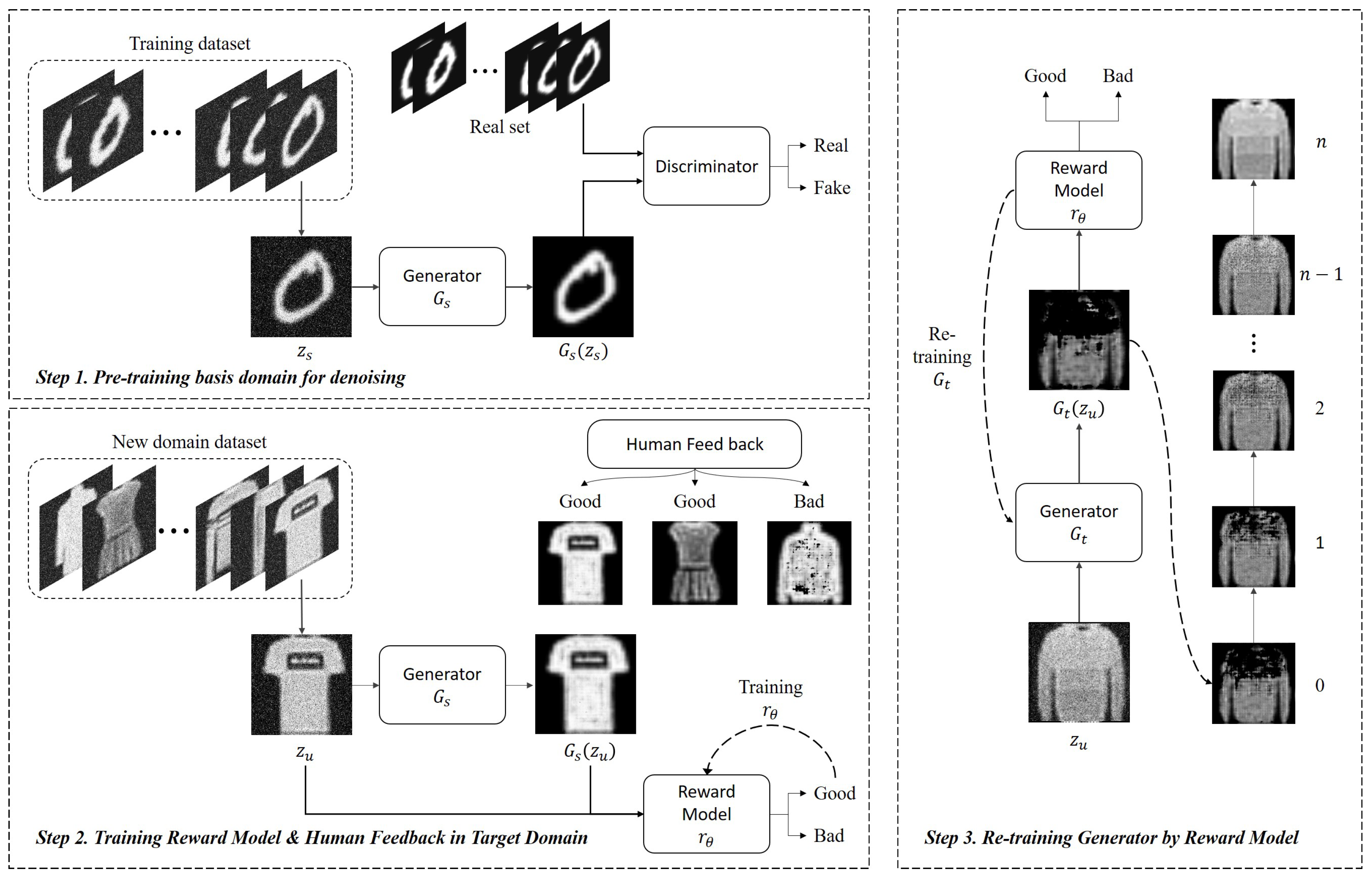
2.1. Pre-Training Basis Domain for Denoising

In this step, we focused on creating an intentional class-biased generator. The model is trained to acquire the fundamental ability of denoising using simple images, as shown in Step 1 of Figure 2. The architecture of the model consists of generative adversarial networks (GANs). We employed the pix2pix [26] model as our baseline, which relies on paired training. To train the model, a paired data set is required, consisting of both clean and noisy images. For our paired training data set, we used only 0 digits in the MNIST data set. To create a pair, 0-digit images were selected and combined with synthesized noise. Consider the synthesized noise of image z, which is a 2D image represented as $z\in R^{m\times n}$. It is composed of both the original image and noise, denoted as x and n, respectively:

$$z=x+n.$$

(1)

We assume that the clean image is selected from the source domain. Therefore, the synthesized noise image z and the original image x are treated as paired data. For convenience notation, the source and unseen domain data are denoted as $z_s$ and $z_u$, respectively.

The generator is trained to produce samples of good quality from input noise variables $p_n$. To train the model on the source domain, the final loss is defined as follows:

$$L_{ste{p}_1}(G_s,D)=L_{GAN}(G_s,D)+L_{pixel-wise}\left(G_s\right)$$

(2)

where the samples $G_s\left(z_s\right)$ are obtained when $z_s\sim p_n$ follows a distribution that represents good quality in the source domain. In other words, The generator $G_s$ is trained to learn the mapping from the noise image z to the clean image x, denoted as $G_s:z_s\to x$. The objective of the generator is to estimate the distribution of x, denoted as $G_s\left(z_s\right)\approx x$. To achieve this, the GAN consists of an adversarial discriminator D, which distinguishes between ‘Real’ and ‘Fake’ images. ‘Real’ refers to the original image x, while ’Fake’ corresponds to the generated image $G_s\left(z_s\right)$ produced by the generator. Both the generator $G_s$ and the discriminator D are trained adversarially. The objective function can be expressed as follows:

$$\begin{array}{cc}\underset{G_s}{\min }\underset{D}{\max }{L}_{GAN}(G_s,D)={\mathbb{E}}_{z_s,x}[logD(z_s,x)]+\hfill & \\ & \hfill {\mathbb{E}}_{z_s\sim p_n\left(z_s\right)}[log(1-D(z_s,G_s\left(z_s\right)))].\end{array}$$

(3)

where $G_s\left(z_s\right)$ represents the generation of a clean image from a noisy image $z_s$. The discriminator D is responsible for classifying between the real and fake distributions. In order to induce a mistake in $D,G_s$ aims to minimize Equation (3). On the other hand, D maximizes the objective function to distinguish between real and generated images.

In our study, we tackle the problem of denoising while preserving the underlying morphological structures. Traditional GAN [1] frameworks approximate the target distribution during training. However, in the context of image processing, the generated images may inadvertently alter the essential morphological characteristics of the originals [26,27,28]. To mitigate this issue and ensure the preservation of morphological structures, an auxiliary loss term is incorporated into the objective function:

$$L_{pixel-wise}\left(G_s\right)={\mathbb{E}}_{z_s,x}[\parallel x-G_s\left(z_s\right){\parallel }_1].$$

(4)

Similar to the [26] approach, the auxiliary loss employs the $L1$ distance between the target image x and the generated image $G_s\left(z_s\right)$.

2.2. Human Feedback and Training Reward Model

The integration of human feedback has demonstrated high adaptability across various domains [24,25,29]. This valuable information is used to train a reward model, which acts as a substitute for human assessment and enhances the model’s performance. In this section, we provide a detailed description of how human feedback is gathered. In the previous section, we presented the basic denoising GAN model using pix2pix [26], which we referred to as the supervised denoising model (SDM). Human feedback is obtained through manual assessments of the SDM results from unseen domain samples $z_u$. The assessments are categorized as ‘Good’ if the image was clean and ‘Bad’ if the image contained noise or collapse (see Step 2 in Figure 2).

The assessments ‘Good’ and ‘Bad’ are utilized as ground truth labels ($y_r=0,1$) to train the reward model. The reward model, denoted as $r_{\theta }$, follows the same architecture as the discriminator in the SDM. The loss function for $r_{\theta }$ is as follows:

$$\begin{array}{c}{L}_{reward}(\widehat{G_s},r_{\theta })=\underset{r_{\theta }}{\min }{\mathbb{E}}_{z_u\sim p_n\left(z_u\right)}-[y_{r}log{r}_{\theta }(\widehat{G_s}\left(z_u\right),z_u)\hfill \\ \hfill \hspace{1em}& \hfill +(1-y_r)log(1-r_{\theta }(\widehat{G_s}\left(z_u\right),z_u)\left)\right].\end{array}$$

(5)

where $\widehat{G_s}$ is a frozen denoising generator model using the source domain. During the training of the reward model, $\widehat{G_s}$ remains untrainable and is solely used to generate denoised images. $r_{\theta }$ assesses these denoised images and is trained using $y_r$ labels. Notably, the reward model can be trained to capture human preferences, as the $y_r$ labels are collected through human feedback.

2.3. Objective

In this section, we present the final formulation of the loss function, which consists of auxiliary terms. Each auxiliary term includes reward loss, consistency loss, and regularization loss, used to train $G_t$. Here, $G_t$ represents the adapted model, which is fine-tuned from $G_s$ in the unseen domain. Thus, the architecture and initial parameters of $G_t$ are the same as those of $G_s$.

• Reward Loss $L_r$: The primary objective of generator $G_t$ is to generate denoised images that are assessed by the reward model as ‘$Good$’ (0, indicating clean images). The minimization of $L_r$ aims to train generator $G_t$ to generate clean images. In other words, the reward loss $L_r$ trains $G_t$ to map from the distribution of ‘$Bad$’ quality images (distribution j) to the distribution of ‘$Good$’ quality images (distribution k), $G_t:j\to k$.

  $$L_r\left(G_t\right)={\mathbb{E}}_{z_u\sim p_n\left(z_u\right)}[-log(1-\widehat{r_{\theta }}(G_t\left(z_u\right),z_u)].$$

  (6)

  where $\widehat{r_{\theta }}$ is a reward model trained on human feedback that has fixed parameters. Thus, $\widehat{r_{\theta }}$ only assesses the quality of the generated image from $G_t$ and the input image $z_u$.

In this context, by fine-tuning $G_t$ from $G_s$ using $L_r$ loss, $G_t$ is able to closely approximate the $x\sim p_{data}$ distribution represented by $r_{\theta }$ in an unseen domain. However, relying solely on $L_r$ loss for training $G_t$ may lead to over-fitting and the risk of distorting the morphological information of the original images. To alleviate this problem, we describe ‘Regularization Loss’ and ‘Consistency Loss’ as follows.

• Consistency Loss $L_p$: As the model learns from new data, there is a potential issue of the performance of past good results deteriorating due to parameter updates. This is commonly referred to as the problem of catastrophic forgetting. To control this issue, it is necessary to compare the outcomes of the initial parameters with the current results. We present a novel compensatory term, denoted as $L_p$, which facilitates a comparison between the outputs of the initial frozen generator, $\widehat{G_s}$, and the target generator $G_t$. The primary objective of $L_p$ is to minimize the pixel-wise $L_1$ loss between the outcomes generated by $\widehat{G_s}$ and $G_t$, thereby ensuring that the current model preserves crucial insights acquired from the initial generator throughout the training procedure. By incorporating this approach, we effectively address the issue of neglecting important details and consequently witness a notable enhancement in the overall performance of the current model.

  $$L_p\left(G_t\right)={\mathbb{E}}_{z_u\sim p_n\left(z_u\right)}[\sigma (\widehat{r_{\theta }}(\widehat{G_s}\left(z_u\right),z_u))\parallel \widehat{G_s}\left(z_u\right)-G_t\left(z_u\right){\parallel }_1].$$

  (7)

  $$\sigma \left(r\right)=\left\{\begin{array}{cc}0\hfill & \mathrm{if}r\ge ϵ\hfill \\ 1\hfill & \mathrm{if}r<ϵ\hfill \end{array}\right.$$

  (8)

  where $\sigma$ is the step function, and r denotes the result of the reward. $ϵ$ is a threshold value ranging from 0 to 1.
• Regularization Loss $L_n$: We employ a regularization loss term to address the issues of over-fitting and mode collapse. In existing methods, the difference in cosine similarity of feature vectors in the latent space has been compared [21,30]. However, in our approach, we intuitively compare the outputs of the model from the past and the current training stages to suppress excessive variations caused by the model’s learning. $L_n$ calculates the pixel-wise $L_1$ loss between the results of the current generator and the ($n-i$)$th$ generator $\widehat{G_t}$. The generator $\widehat{G_t}$ copies weights from $G_t$ every N steps and then freezes them.

  $$L_n\left(G_t\right)={\mathbb{E}}_{z_u\sim p_n\left(z_u\right)}[\parallel \widehat{G_t}\left(z_u\right)-G_t\left(z_u\right){\parallel }_1].$$

  (9)

The final loss used to train $G_t$ is as follows:

$$\underset{G_t}{\min }L\left(G_t\right)=L_r\left(G_t\right)+\alpha L_p\left(G_t\right)+(1-\alpha )L_n\left(G_t\right).$$

(10)

where, $\alpha$ controls the relative balance of the two $L_p$ and $L_n$ losses. In the ablation study, we analyze the impact of each auxiliary loss on the final loss. Figure 3 represents the flow diagram of the more specific final objective loss functions we designed.

3. Experiments

3.1. Data Sets

We utilized two data sets in our experiments: MNIST [31] and Fashion-MNIST [32]. MNIST is a grayscale image data set consisting of 10 classes representing digits from 0 to 9. Each MNIST image has dimensions of 28 × 28 pixels. The data set comprises a training set of 60,000 images and a test set of 10,000 images.

In the experiments, the MNIST data set serves as the source domain for training the initial denoising generator. Specifically, only the ‘0’ digit is used for restrictive training on the source domain. The training set consists of 6000 samples, and the validation set contains 1000 samples. The MNIST images are resized to a size of 256 × 256 pixels using bicubic interpolation. To train the initial denoising generator, a pair of data points is required, consisting of clean and noisy images. The original MNIST data set is used as the clean image counterpart, while the noisy images are created by introducing artifact noise in the form of salt-and-pepper noise combined with Gaussian noise. The salt-and-pepper noise was applied with equal proportions of salt and pepper pixels at 50%, while the Gaussian noise was added with a mean of 0 and a standard deviation of 0.05, perturbing the pixel intensity values. This approach ensures a controlled and reproducible noise level, typical for evaluating image denoising models [33].

Fashion-MNIST is a data set consisting of images representing 10 types of fashion items. It also includes a training set of 60,000 images and a test set of 10,000 images. Fashion-MNIST is employed to evaluate the model’s performance and train adaptive learning. The images in Fashion-MNIST are resized to 256 × 256 pixels and similarly augmented with noise, as conducted with the MNIST data set.

3.2. Training Setting

• Pre-training for denoising: “pix2pix” [26] is employed as the baseline model in this experiment. The main objective of most GANs is to establish a mapping $G:Z\to X$. “pix2pix” demonstrated the training approach for pixel-wise mapping between input and output images. Consequently, the generator of “pix2pix" can effectively learn the transformation from the noise space Z to the clean space X. In this experiment, we trained a denoising model, denoted as $G_s$, using the MNIST data set. $G_s$ was specifically trained using a set of 1000 image pairs consisting of clean digits and their corresponding noisy versions. The clean images used in the training process were specifically selected to represent the digit ‘0’. For optimization, we employed the Adam solver [34] with a batch size of 10, a learning rate of 0.0002, and momentum parameters ${\beta }_1=0.5$ and ${\beta }_2=0.999$. The denoising model was trained for 200 epochs.
• Inference and human feedback: In this paper, our proposed method demonstrates the adaptability of a pre-trained model to a target domain through human feedback. To gather human feedback, the pre-trained generate model $G_s$ is used to infer results in the target domain, which are then manually assessed by human evaluators. In our experiments, we employ Fashion-MNIST as the target domain data set, and we collect human feedback for the 10,000 test images in this data set.
• Training for reward model by human feedback: The reward model, denoted as $r_{\theta }$, is utilized in the auxiliary loss term. The architecture of the reward model is designed to be the same as the discriminator of the “pix2pix" model. The hyperparameters used for training $r_{\theta }$ remain consistent with the pre-training setting.
• Adaptive training by human feedback: Note that the adaptive training process implements Equation (10), utilizing the same set of hyperparameters as mentioned above. It is important to note that $G_t$ has trainable parameters, whereas $\widehat{G_s},\widehat{G_t},$ and $\widehat{r_{\theta }}$ are untrainable parameters. The constant $ϵ$ in Equation (8) is set to 0.2, and the constant $\alpha$ in Equation (10) is set to 0.9. In the ablation study, we examine the influence of $L_p$ and $L_n$ as $\alpha$ is varied.

3.3. Evaluation

We evaluate the quality of the denoised images using the metrics of PSNR (peak signal-to-noise ratio) and SSIM (structural similarity index measure). PSNR is a widely used metric for evaluating denoising models. It measures the quality of the denoised image by comparing it to the original (clean) image. Higher PSNR values indicate better denoising performance. PSNR can be calculated using the mean squared error (MSE) between the denoised image and the original image. SSIM is another popular metric that quantifies the similarity between the denoised image and the original image. It takes into account not only pixel-level differences but also structural information, such as luminance, contrast, and structure. Higher SSIM values indicate better preservation of structural details.

3.4. Results of Domain Adaptive Denoising by Human Feedback

• Comparison of evaluation metrics: In this section, we examine the results of domain adaptive denoising. Our intuition is that, even when presented with unseen data from a target domain, if we provide human feedback to a supervised learning model, the model can adapt to the data effectively. Note that our human feedback is not ground-truth for a denoised image; it shows human preference, consisting of ‘$Good$’ and ‘$Bad$.’ In

  Table 1. Result of fine tuning using human feedback. Each row corresponds to the outcomes under different conditions of the loss function. The first row represents our proposed results. The second row shows results without $L_p$ loss, the third row shows results without $L_n$ loss, and the fourth row shows results using only $L_r$ loss. The fifth row presents results from the model trained on the source domain, and the last row displays the baseline results between noisy and clean images.

  	MNIST Test (10k)		Fashion-MNIST Test (10k)		Fashion-MNIST Train (60k)
  	PSNR	SSIM	PSNR	SSIM	PSNR	SSIM
  Gt(z) vs. x	29.36 ± 0.92	0.95 ± 0.01	25.68 ± 3.91	0.84 ± 0.11	25.75 ± 3.86	0.84 ± 0.10
  $G_t\left(z\right)$ vs. x/wo $L_p$ loss	24.20 ± 0.65	0.66 ± 0.08	25.00 ± 2.44	0.68 ± 0.10	25.07 ± 2.37	0.69 ± 0.10
  $G_t\left(z\right)$ vs. x/wo $L_n$ loss	29.10 ± 0.98	0.95 ± 0.01	25.30 ± 4.35	0.83 ± 0.12	25.41 ± 4.25	0.83 ± 0.12
  $G_t\left(z\right)$ vs. x/only $L_r$ loss	20.66 ± 0.69	0.82 ± 0.03	17.97 ± 2.15	0.58 ± 0.13	18.03 ± 2.14	0.58 ± 0.12
  $G_s\left(z\right)$ vs. x	29.26 ± 1.04	0.94 ± 0.01	24.18 ± 5.57	0.80 ± 0.16	24.27 ± 5.52	0.80 ± 0.16
  Baseline source (z vs. x)	14.72 ± 0.06	0.12 ± 0.01	13.23 ± 0.13	0.07 ± 0.13	13.23 ± 0.13	0.07 ± 0.02

  , ‘$G_s\left(z\right)$ vs. x’ represents the denoising results of the model before adaptive learning using human feedback. ‘$G_t\left(z\right)$ vs. x’ shows the denoising outcomes of the adapted model based on human feedback. The results obtained from the MNIST data set indicate the performance in the pre-trained domain, while the results from the Fashion-MNIST data set reflect the performance on unseen data. Therefore, we can observe the adaptation progress between the initial model $G_s$ and the updated model $G_t$. In our experiments, both $G_s$ and $G_t$ demonstrated a significant improvement in PSNR measured on the Fashion-MNIST test set, with an overall increase of 94% over the entire 10K data set. The statistical analysis of the PSNR improvement revealed a mean increase of 1.61 ± 2.78 dB (MAX: 18.21, MIN: 0.0001). Figure 4a shows the images with the most significant increase in PSNR, along with the corresponding metrics between each generator output image and the ground truth image. In addition, for the remaining 6% of cases, there was a decrease in PSNR values, with the statistical analysis showing a mean decrease of 0.12 ± 0.18 dB (MAX: 2.75, MIN: 0.0001) (See Figure 4b). Figure 5 shows the boxplot of PSNR for each generator $G_s$ and $G_t$ on the experimental data set. The $G_t$ images from the same data set exhibit higher PSNR values, indicating improved image quality after adaptation. Particularly noteworthy is that after adaptation, the PSNR and SSIM values of the MNIST test set (10K) from the $G_t$ generator, corresponding to the source domain, show little to no variation or even slight improvement (see Figure 5a). This demonstrates the prevention of the catastrophic forgetting issue for the source domain even after adaptation to the target domain. Furthermore, we apply the $G_t$ model tuned on the Fashion-MNIST test set with the reward model to the Fashion-MNIST training set (60k). This demonstrates that when the reward model is trained in a new domain, it can effectively work without requiring additional training.
• Visual evaluation: Figure 4 illustrates the improvement in denoising and restoration, particularly in addressing image collapse. Notably, $G_s$ trained on the ‘0’ digits of MNIST, exhibits instances where the results suffer from image collapse in several images, indicating a lack of adaptation. However, our approach effectively enhances the image quality by leveraging human feedback, as demonstrated by the results obtained with $G_t$.

3.5. Ablation Study

To validate the effectiveness of each loss term of our method, we conduct comprehensive ablation studies for the loss term.

• Effect of $L_p$ term: The $Lp$ term compares the image quality between $G_s$ and $G_t$ and is the loss function between images that are well evaluated by human feedback based on the reward function. We examine the effect of the $L_p$ loss on the quality of the output. Typically, the constant alpha of $L_p$ is fixed at 0.9. To evaluate the effect of excluding the $L_p$ term, we vary the alpha value to 0, resulting in the loss equation becoming $L\left(G_t\right)=L_r\left(G_t\right)+L_n\left(G_t\right)$. Performing the adaptation without an $L_p$ term exhibits low quantitative performance, as demonstrated in the second row of Table 1. Additionally, Figure 6d,e depict the anomaly texture created in the image for reference.
• Effect of $L_n$ term: $L_n$ represents the $L_1$ loss between the ($n-2$)th and (n)th iterations of G($\widehat{G_t}$ and $G_t$). In terms of quantitative evaluation, it demonstrates comparable performance (Table 1, first and third row). However, in qualitative assessment, it becomes evident that there are limitations in generating the desired image to a satisfactory degree. (See Figure 6d–f). We also examine the effect of $L_n$ loss on the output quality. The role of $L_n$ is to restrict significant parameter changes from the previous model. Given that the function of $L_n$ is to restrict parameter updates between the previous and current models, it becomes apparent that there are limitations in generating the desired image to a satisfactory extent in qualitative evaluation, leading to potential issues such as collapse.
• Effect of $L_r$ term: $L_r$ represents the cross-entropy loss used to distinguish between ‘$Good$’ and ‘$Bad$’ cases. In the experiments where $L_p$ and $L_n$ are ablated, the adaptation relies solely on $L_r$, resulting in parameter updates exclusively driven by human feedback. Consequently, in the absence of pixel-wise losses, such as $L_p$ and $L_n$, it is evident that image details and shapes are not preserved, as illustrated in Figure 6d–g.

4. Discussion and Conclusions

In this paper, we propose a novel method based on human feedback to address the domain adaptation problem of denoising generative models, particularly focusing on the condition of an unlabeled target domain. Unlike conventional approaches that aim to enhance a generative model’s overall performance on the entire test data set, our method leverages human feedback to directly improve the quality of failed images in denoising tasks. While many existing approaches require a large amount of labeled data and may discard failed images, our approach fine-tunes the model based on human feedback, similar to the process used in ChatGPT [22] to select generated sentences of ‘Good’ quality. This novel utilization of human feedback represents a promising avenue for enhancing generative models.

A comparison with existing domain adaptation techniques highlights the distinct features of the proposed approach. Conventional domain adaptation methods primarily focus on minimizing the distributional gap between the source and target domains [14,15,16,17,18,19,20,21]. While these approaches effectively address macro-level domain shifts, they often lack the ability to correct fine-grained failure cases in individual images. In contrast, the proposed method introduces a micro-level adaptation strategy by incorporating human feedback to specifically target and improve failure cases within the target domain. This fine-grained approach to domain adaptation has not been extensively explored in prior studies and provides a novel perspective on improving model performance beyond conventional techniques.

To assess the effectiveness of the proposed method, a performance comparison was conducted using PSNR (peak signal-to-noise ratio) and SSIM (structural similarity index measure). The experimental results demonstrate a 94% improvement in PSNR in the target domain, indicating a substantial enhancement in performance compared to traditional domain adaptation techniques. This quantitative evaluation confirms the effectiveness of leveraging human feedback for fine-tuning generative models and highlights its potential in practical applications.

The originality of this study lies in its novel integration of human feedback into generative AI for domain adaptation. Rather than relying on large labeled datasets, as is common in existing domain adaptation approaches, the proposed method utilizes subjective human evaluations to adapt the model efficiently and effectively. This strategy not only reduces the dependency on extensive labeled datasets but also enhances the adaptability of the model to real-world scenarios where failure cases require specific adjustments. By employing human-guided model fine-tuning, this study introduces an innovative approach to improving the robustness and flexibility of generative AI models.

We proposed a novel human-guided domain adaptation approach for image denoising and demonstrated its effectiveness on MNIST and Fashion-MNIST datasets. Notably, the PSNR improved by 94% on the Fashion-MNIST test set, with an average increase of 1.61 ± 2.78 dB and a maximum of 18.21 dB, while preserving performance on the original MNIST domain. These results highlight the potential of human feedback in enhancing model adaptability and performance across domains.

Domain adaptation poses challenges, particularly regarding the issue of catastrophic forgetting. However, through our proposed adaptation approach, which incorporates selective loss functions and an ablation study based on decisions from a reward model trained with human feedback, we successfully mitigated the challenging issue of catastrophic forgetting. Our results align with related studies, demonstrating the effectiveness of our approach.

Despite its success, the study has limitations, including the possibility of overfitting to specific noise types and challenges in applying the method to more complex datasets. Future research will address these limitations by testing on high-resolution datasets and exploring methods to standardize and optimize human feedback collection.

In the context of real-world applications, the unseen data domain adaptation of deep generative models has always been a crucial research topic. In this paper, we demonstrate the adaptation of a model trained on the source domain to the label-less target domain, guided by human feedback. Through ablation study, we analyzed the loss functions and provided compelling evidence for the direction of domain adaptation research, particularly in the realm of image generation.

Although the proposed method has been successfully applied to simple image datasets, such as MNIST and Fashion-MNIST, its performance may not be guaranteed when extended to more complex images (e.g., medical imaging or natural photographs). Additionally, if feedback is inconsistent across users, the model’s performance may deteriorate. To mitigate these issues, further exploration of feedback integration and standardization methods is required.

To improve the reliability and efficiency of human feedback in future work, we will explore several key strategies. Specifically, we aim to analyze the correlation between feedback reliability and performance improvement to develop an optimized feedback collection strategy that minimizes the amount of required feedback while maximizing its effectiveness. In addition, we will investigate cost-effective methods for large-scale feedback collection, such as utilizing crowdsourcing platforms or user-friendly interfaces, to enhance the practical feasibility of integrating human feedback into real-world applications. These efforts will be complemented by measures to ensure consistency and reliability, including the integration of multiple feedback sources and the establishment of clear evaluation criteria to minimize potential biases. To further reduce dependence on human feedback, we will also explore automated evaluation techniques, such as proxy model learning, which can either supplement or replace human input while preserving model adaptability and performance. These strategies will contribute to improving the scalability and robustness of the proposed approach, facilitating its application in more complex and diverse domains.

Furthermore, we will grapple with two things as follows: 1. Human preference: Our work also collects human feedback data by personal preference, similar to ChatGPT. Thus, the distribution of ‘Good’ quality can be different. This will be connected directly with the model’s performance. 2. Model performance is dependent on pre-training: We assume that the SDM is over a certain level. However, if SDM does not work in an unseen domain, we can not collect human feedback. Human feedback has to be collected in the ‘Good’ and ‘Bad’ categories.