On Ideals of Submonoids of Power Monoids
Abstract
1. Introduction
2. Some Results on Commutative Algebra
3. Some Properties of -Monoids
- it is non-cancellative, for example ;
- it is a reduced monoid;
- it is not torsion-free, for example ;
- is atomic and BF-monoid. Moreover, its submonoids are also BF-monoids.
- ;
- .
4. Monoid Ideals of a Fundamental Family of -Monoids
5. Computing the Monoid Ideals
| Algorithm 1: Computation of . |
Data: , the generating set of S. Result: , a generating set of the monoid ideal of S. begin 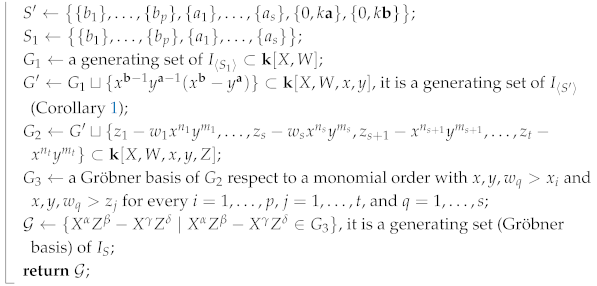 |
- ,
- .
6. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ruzsa, I.Z. Sumsets and structure. Combinatorial Number Theory and Additive Group Theory; 87–210 Advanced Courses in Mathematics CRM Barcelona; Birkhäuser Verlag: Basel, Switzerland, 2009. [Google Scholar]
- Nathanson, M.B. Additive Number Theory: Inverse Problems and the Geometry of Sumsets; Graduate Texts in Mathematics; Springer: Cham, Switzerland, 1996; Volume 165. [Google Scholar]
- Eliahou, S.; García-García, J.I.; Marín-Aragón, D.; Vigneron-Tenorio, A. The Buchweitz set of a numerical semigroup. Bull. Braz. Math. Soc. 2023, 54, 4. [Google Scholar] [CrossRef]
- Tao, T.; Vu, V. Additive Combinatorics: 105; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2006. [Google Scholar]
- Rosales, J.C.; García-Sánchez, P.A. Numerical Semigroups; Developments in Mathematics, 20; Springer: New York, NY, USA, 2009. [Google Scholar]
- Austin, A.A.; Tringali, S. On the arithmetic of power monoids and sumsets in cyclic groups. Pac. J. Math. 2021, 312, 279–308. [Google Scholar]
- Bienvenu, P.Y.; Geroldinger, A. On Algebraic Properties of Power Monoids of Numerical Monoids. 2023. Available online: https://arxiv.org/abs/2306.05530 (accessed on 16 December 2024).
- Rosales, J.C.; García-Sánchez, P.A.; García-García, J.I. Atomic commutative monoids and their elasticity. Semigroup Forum 2004, 68, 64–86. [Google Scholar] [CrossRef][Green Version]
- Gilmer, R. Commutative Semigroup Rings; Chicago Lectures in Mathematics; University of Chicago Press: Chicago, IL, USA, 1984. [Google Scholar]
- García-García, J.I.; Marín-Aragón, D.; Sánchez-R.-Navarro, A.; Vigneron-Tenorio, A. CommutativeMonoids, a Python Library for Computations in Finitely Generated Commutative Monoids. Available online: https://github.com/D-marina/CommutativeMonoids (accessed on 16 December 2024).
- Cox, D.A.; Little, J.; D. O’Shea, D. Ideals, Varieties, and Algorithms: An Introduction to Computational Algebraic Geometry and Commutative Algebra; Undergraduate Texts in Mathematics; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Herzog, J. Generators and relations of abelian semigroups and semigroup rings. Manuscripta Math. 1970, 3, 175–193. [Google Scholar] [CrossRef]
- Rosales, J.C.; García-Sánchez, P.A.; Urbano-Blanco, J.M. On presentations of commutative monoids. Int. J. Algebra Comput. 1999, 9, 539–553. [Google Scholar] [CrossRef]
- Philipp, A. A characterization of arithmetical invariants by the monoid of relations. Semigroup Forum 2010, 81, 424–434. [Google Scholar] [CrossRef]
- Rosales, J.C.; García-Sánchez, P.A. Finitely Generated Commutative Monoids; Nova Science Publishers, Inc.: New York, NY, USA, 1999. [Google Scholar]
- Pisón-Casares, P.; Vigneron-Tenorio, A. N-solutions to linear systems over Z. Linear Algebra Appl. 2004, 384, 135–154. [Google Scholar] [CrossRef]
- Fan, Y.; Tringali, S. Power monoids: A bridge between factorization theory and arithmetic combinatorics. J. Algebra 2018, 512, 252–294. [Google Scholar] [CrossRef]
- Baginski, P.; Chapman, C.; Crutchfield, K.G.; Wright, M. Elastic properties and prime elements. Results Math. 2006, 49, 187200. [Google Scholar] [CrossRef]
- Rosales, J.C.; García-Sánchez, P.A.; García-García, J.I. Presentations of finitely generated submonoids of finitely generated commutative monoids. Int. J. Algebra Comput. 2002, 12, 659–670. [Google Scholar] [CrossRef]
- Bruns, W.; Ichim, B.; Söger, C.; von der Ohe, U. Normaliz. Algorithms for Rational Cones and Affine Monoids. Available online: https://www.normaliz.uni-osnabrueck.de (accessed on 16 December 2024).
| i | Reduction of | |
|---|---|---|
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
García-García, J.I.; Marín-Aragón, D.; Vigneron-Tenorio, A. On Ideals of Submonoids of Power Monoids. Mathematics 2025, 13, 584. https://doi.org/10.3390/math13040584
García-García JI, Marín-Aragón D, Vigneron-Tenorio A. On Ideals of Submonoids of Power Monoids. Mathematics. 2025; 13(4):584. https://doi.org/10.3390/math13040584
Chicago/Turabian StyleGarcía-García, Juan Ignacio, Daniel Marín-Aragón, and Alberto Vigneron-Tenorio. 2025. "On Ideals of Submonoids of Power Monoids" Mathematics 13, no. 4: 584. https://doi.org/10.3390/math13040584
APA StyleGarcía-García, J. I., Marín-Aragón, D., & Vigneron-Tenorio, A. (2025). On Ideals of Submonoids of Power Monoids. Mathematics, 13(4), 584. https://doi.org/10.3390/math13040584






