A Possible Degree-Based D–S Evidence Theory Method for Ranking New Energy Vehicles Based on Online Customer Reviews and Probabilistic Linguistic Term Sets

Abstract

As people’s environment awareness increases and the “double carbon” policy is implemented, the new energy vehicle (NEV) becomes a popular form of transformation and more and more car manufacturers start to produce NEVs. Thus, how to choose an appropriate type of NEVs from many brands is an interesting topic for customers, which can be regarded as a multiple-attribute decision-making (MADM) problem because customers often concern several different factors such as the price, endurance mileage, appearance and so on. This paper proposes a possible degree-based D–S evidence theory method for helping customers select a proper type of NEVs in the probabilistic linguistic environment. In order to derive decision information reflecting customer demands, online customer reviews (OCRs) are crawled from multiple websites and converted into five-granularity probabilistic linguistic term sets (PLTSs). Afterwards, by maximizing deviation and minimizing the information uncertainty, a bi-objective programming model is built to determine attribute weights. Furthermore, a possible degree-based D–S evidence theory method in the PLTS environment is proposed to rank alternatives in each website. For fusing these ranking results, a 0–1 programming model is set up by maximizing the consensus between the comprehensive ranking and individual ones in each website. At length, a case study of selecting a type of NEVs is provided to show the application and validity of the proposed method.

1. Introduction

With the rapid development of our national economy and people’s living standards improving, cars have become a common transportation tool for many people. However, fuel vehicles emit a large amount of exhaust gas, which causes air pollution [1,2] and affects the air quality [3,4]. In order to control the environment pollution and decrease the carbon emission, the China government formulates a series of policy and reform measures including collecting green tax and recommending the new energy vehicles (NEVs). Supported by the new policy, more and more car manufacturers shift their focus from fuel vehicles to NEVs, such as Chuanqi, Changcheng and Jili. Meanwhile, some NEV manufactures, like BYD and Tesla, are booming. Thus, more and more brands of NEVs emerge in the market and make consumers puzzled for selecting an appropriate car. Generally, when consumers seek to purchase a NEV, they often evaluate and compare candidate vehicles in multiple ways consisting of price, outlook, interior, intelligence and so on. Therefore, the selection of an optimal NEV among a collection of candidates can be considered as a typical multi-attribute decision-making (MADM) problem.

As the social media and mobile devices are more and more popular, many customers prefer to share their reviews and opinions on social media platforms. These online reviews are very helpful for potential purchasers because they provide much valuable information including purchasing experiences and evaluations on many indices about NEVs. Generally, an online review comprises a total rating and the text description. Compared with the rating, the text description may express more abundant evaluations and more explicitly reflect opinions of a consumer regarding his/her car. The sentiment technique [5,6,7] is an effective tool for handling and transforming online reviews into proper decision making information such as intuitionistic fuzzy sets, hesitant intuitionistic sets and q-rung orthopair fuzzy numbers. Nevertheless, these forms only describe the proportions of positive and negatives, but are unable to express the strength of positive and negative sentiments. To make up for this limitation, this study converts the sentiment analysis results into five-granularity PLTSs which can indicate different sentiment orientations with probability and their strength.

After transforming online reviews into PLTSs, the decision matrix is formed. In the decision-making process, the attribute weights play an important role and are often determined by experts [8], minimizing similarity degree [9], maximizing deviation [10] or other optimization models [11] in most MADM methods. However, it is hard for experts to assign reasonable attribute weights and the assigned weights have some subjective randomness. Although the minimizing similarity degree method and the maximizing deviation method objectively derive attribute weights based on decision information, the former only considers the similarity of each attribute, and the latter only considers the differences between alternatives on each attribute, both of which ignore the uncertainty of the decision information obtained from the sentiment analysis results. Therefore, by combining the differences and uncertainty of decision information, this paper constructs a bi-objective programming model to acquire attribute weights objectively. Furthermore, to decrease the uncertainty and fuse the decision information from multiple aspects, alternatives are ranked with the D–S evidence theory method which has been widely used in distinct fuzzy environments [12,13,14] and different fields [15,16,17].

According to this background, this paper presents a possible degree-based D–S evidence theory method for resolving NEV selection problems with on online reviews. The innovations and contributions of this paper are outlined as follows:

(1)

This paper crawls online reviews from multiple websites and transforms them into five-granularity PLTSs. Compared with existing methods on online reviews which are from a single website and transformed into hesitant intuitionistic fuzzy sets and q-rung orthopair fuzzy numbers, the decision information concealed in the online reviews is more plentiful and more clearly express the sentiment orientations, including very positive, positive, neutral, negative and very negative sentiments.

(2)

Attribute weights are determined by building a bi-objective programming model based on the maximization deviation and the information entropy, by which the differences between alternatives and uncertainty of decision information on each attribute are both considered. However, in other studies, the attribute weights are assigned by experts subjectively or derived only depending on the maximization deviation. Thus, the attribute weights generated in this paper can more synthetically reflect the quality of the decision information and are more reliable.

(3)

A possible degree-based D–S theory method is proposed to rank alternatives. A dominant feature of this method is that it can quantitively measure and decrease uncertainty of decision information. Furthermore, it has a stronger distinguishing power compared with existing D–S theory methods.

The rest of this paper is arranged as follows: Section 2 conducts a brief literature review related to this study. Section 3 introduces some basic theories on the probabilistic linguistic term set and Dempster–Shafer theory methods. Section 4 develops a new sentiment analysis technique and proposes a possible degree-based D–S theory method in the PLTS context. Section 5 provides a case study of the proposed method to prove its practicability and rationality. Section 6 performs compares analyses this method with other methods from multiple perspectives. Section 7 summarizes the conclusions.

2. Literature Review

This section conducts literature reviews from two aspects, including decision methods for resolving NEV selection problems and MADM methods with online reviews in the probabilistic linguistic context.

2.1. Decision Methods for Resolving NEV Selection Problems

As the NEVs are more and more prevalent in the market, increasing NEV manufactures are arising. In this context, fruitful decision methods have been developed for evaluating and selecting NEVs. For example, Ziemba [18] investigated five NEV users to collect decision information in the form of real numbers. Then, attribute weights are assigned by experts and a New Easy Approach To Fuzzy PROMETHEE method is proposed to rank NEVs. By inviting experts to perform pairwise comparison, Huang et al. [19] set up preference relations with distributed linguistic term sets and furnished a TSOG-PSO approach to evaluate NEVs. According to the data from automobile manufactures, Dwivedi and Sharma [2] obtained attribute weights with Shannon entropy and ranked NEVs by the TOPSIS method. In these studies, the data do not come from NEV users or very few users, so the objectivity and comprehensiveness of data may be affected by the data source and the size.

In recent years, many NEV users post their experience and opinions on some social platforms such as autohome.com and xcar.com. A lot of potential users often look through such opinions before buying NEVs. More and more scholars are inclined to study how to evaluate and select best NEVs based on online reviews, and some novel decision methods have been raised depending on online reviews. Tian et al. [6] crawled online reviews from the “Autohome” platform and transformed them into hesitant intuitionistic fuzzy sets. Afterwards, combining subjective weights generated by best and worst method as well as objective weights derived by the maximization deviation, the comprehensive attribute weights were determined. At length, the extended ORESTE method was proposed to rank NEVs. Yang et al. [7] also collected comments based on the “Autohome” platform and then transformed them into q-rung orthopair fuzzy numbers. According to the cumulative prospect theory [20], candidate NEVs were ranked based on the attribute weights assigned by experts. Resorting to the “Dcar” platform, Liu et al. [21] mined online reviews and expressed them in the form of hesitant probabilistic fuzzy sets. Subsequently, the attribute weights were obtained based on the prospect values of alternatives and the TODIM-MULTIMOORA method was applied to sort NEVs.

The above research achievements gathered online reviews from a single website and transformed them into different fuzzy sets rather than linguistic term sets. In addition, the uncertainty of decision information is neglected while determining attribute weights. As users prefer to comment NEVs on different platforms and describe opinions in the form of natural languages, this paper crawls online reviews from multiple websites and converted them into five-granularity PLTSs, by which the decision information is abundant and retains the initial language format with the probability. Furthermore, the uncertainty of decision information is considered besides the deviations between evaluations on NEVs.

2.2. MADM Methods with Online Reviews in the PLTS Environment

Owing to the fact that the PLTSs can use linguistic terms associated with their probabilities to elaborate the comments in the form of languages as well as the frequency, it has been applied to resolve decision problems with online reviews in many fields and different MADM methods are presented [4,22,23,24,25]. For instance, Chen and Li [22] investigated the doctor ranking problems in the online consultation and proposed a Combined Compromise Solution method by transforming patients’ reviews into the three granularity PLTSs. By computing the sentiment scores with the sentiment analysis technique, Darko et al. [23] converted online reviews into five-granularity PLTSs and developed a PL-ELECTEE methodology for ranking mobile payment services. Similarly, Yang et al. [24] addressed the product selection problems and built an online product decision support system frame based on the regret theory. Zhao et al. [25] applied the TOPSIS method to resolve the hotel selection problems with online reviews. Wan et al. [26] puts forward an integrated method of prospect theory, DEMATEL (decision-making trial and evaluation laboratory) and QUALIFLEX (qualitative flexible) to resolve photovoltaic power station site selection problems.

Although the above-mentioned literature has transformed online reviews into PLTSs and successfully tackled lots of decision problems in many fields, only positive and negative sentiments are considered but the sentiment strength is ignored. Thus, the transformed decision information is unable to accurately indicate the opinions in the online reviews. For example, given two reviews, “the seat is comfortable” and “the seat is very comfortable”, though they are both positive sentiments, the strengths are obviously different and the latter is stronger. However, existing methods regarded them as the same strength. Moreover, the decision methods, such as TOPSIS, ELECTREE and the regret theory, are incapable of measuring and decreasing the uncertainty embodied in the decision information.

To fill the above-stated gaps, this paper studies the NEV selection problem based on online reviews. By considering noun, adjective, adverb and negation words, online reviews are directly converted into five-granularity PLTSs corresponding to different levels of sentiments, including very positive, positive, neutral, negative and very negative sentiments. Therefore, sentiment orientations and their strengths are both reflected. Furthermore, a possible degree-based D–S evidence theory method is proposed to quantitively measure and decrease the uncertainty of the decision information and derive reasonable decision results.

3. Preliminaries

This section reviews some definitions and methods to facilitate discussion in the sequel, such as the probabilistic linguistic term set, the D–S theory and existing D–S theory-based decision methods.

3.1. Probabilistic Linguistic Term Sets

Definition 1

[27]. Let $S=\left\{\left.s_{\alpha }\right|\alpha =-\eta ,\cdots ,-1,0,1,\cdots ,\eta \right\}$ be a linguistic term set (LTS). Then, a probabilistic linguistic term set (PLTS) is defined as

$$L(p)=\{\left.s_{\alpha }^{(l)}(p^{(l)})\right|s_{\alpha }^{(l)}\in S,p^{(l)}\ge 0,l=1,2,\cdots ,L_o,{\displaystyle \sum _{l=1}^{L_o}{p}^{(l)}\le 1}\}.$$

(1)

where $s_{\alpha }^{(l)}(p^{(l)})$ is a probabilistic linguistic element (PLE), representing the $l$th possible linguistic term $s_{\alpha }^{(l)}$ associated with the probability $p^{(l)}$, and $L_o$ is the number of all linguistic terms in $L(p)$.

Definition 2

[28]. Let $S=\left\{\left.s_{\alpha }\right|\alpha =-\eta ,\cdots ,-1,0,1,\cdots ,\eta \right\}$ be an LTS; the linguistic term $s_{\alpha }$ that expresses the equivalent information to the membership degree $\theta$ is obtained by a linguistic scale function $f$.

$$f: [s_{-\eta },s_{\eta }]\to [0,1],f(s_{\alpha })=(\alpha +\eta )/2\eta =\theta .$$

(2)

Further, the membership degree $\theta$ that expresses the equivalent information to the linguistic variable $s_{\alpha }$ is obtained as

$$f^{-1}: [0,1]\to [s_{-\eta },s_{\eta }],f^{-1}(\theta )=s_{2\eta ·\theta -\eta }=s_{\alpha }.$$

(3)

Definition 3

[29]. The probability of missing information is evenly distributed among all linguistic terms in the linguistic term set. In this case, the standard PLTS can be expressed as

$$\widehat{L}(p)=\{\left.s_{\alpha }^{\left(l\right)}({\widehat{p}}^{\left(l\right)})\right|s_{\alpha }^{(l)}\in S,{\widehat{p}}^{(l)}\ge 0,l=1,2,\cdots ,{\widehat{L}}_o,{\displaystyle \sum _{l=1}^{{\widehat{L}}_o}{\widehat{p}}^{(l)}=1}\}.$$

(4)

where ${\widehat{p}}^{(l)}=p^{(l)}+(1-{\displaystyle \sum _{l=1}^{{\widehat{L}}_o}{p}^{\left(l\right)}})/(2\eta +1)$.

Definition 4

[28]. Let $\widehat{L}(p)$, ${\widehat{L}}^1(p)$, ${\widehat{L}}^2(p)$ be three standard PLTSs; then, the basic operations of PLTSs are stipulated as

$${\widehat{L}}_1(p)\oplus {\widehat{L}}_2(p)={\cup }_{s^{\left(l_1\right)}\in {\widehat{L}}_1(p),s^{\left(l_2\right)}\in {\widehat{L}}_2(p)}\{f^{-1}[f(s^{\left(l_1\right)})+f(s^{\left(l_2\right)})-f(s^{\left(l_1\right)})f(s^{\left(l_2\right)})](p^{(l_1)}{p}^{(l_2)})\},$$

(5)

$$\lambda \widehat{L}(p)={\cup }_{s^{(l)}\in \widehat{L}(p)}\left\{f^{-1}\left(1-{(1-f(s^{(l)}))}^{\lambda }\right)p^{(l)}\right\}.$$

(6)

where $l_1=1,2,\cdots ,{\widehat{L}}_o^1$, $l_2=1,2,\cdots ,{\widehat{L}}_o^2$, $l=1,2,\cdots ,{\widehat{L}}_o$.

Definition 5

[30]. Let $\widehat{L}(p)$ be a standard PLTS; the score function for $\widehat{L}(p)$ in the probabilistic linguistic form is defined as

$$E(\widehat{L}(p))={\displaystyle \sum _{l=1}^{{\widehat{L}}_o}(f(s_{\alpha }^{(l)})\cdot {\widehat{p}}^{(l)}/{\displaystyle \sum _{l=1}^{{\widehat{L}}_o}{\widehat{p}}^{(l)}})}.$$

(7)

3.2. Dempster–Shafer Theory

The D–S evidence theory, proposed by Dempster [31] and improved by Shafer [32], fuses the evidence from multiple sources with different attributes and can explicitly measure the uncertainty in decision making.

Definition 6

[32]. Let $\Theta =\{A_1,A_2,\cdots ,A_{\mathrm{i}},\cdots A_m\}$ be a frame of discernment, a set of some collectively exhaustive and mutually exclusive hypotheses. A mass function, which is also called a basic probability assignment (BPA), is a mapping $m:2^{\Theta }\to [0,1]$, satisfying

$${\displaystyle \sum _{D\subseteq \Theta }m(D)=1}\mathrm{and} m(Ø)=0.$$

(8)

where $Ø$ is an empty set and $D$ is a subset of $\Theta$. $2^{\Theta }$, the power set of $\Theta$, consists of all subsets of $\Theta$. The probability mass $m(D)$ measures the belief exactly assigned to $D$ and represents how strongly the evidence supports $D$. The probability mass raised to $\Theta$, i.e., $m(\Theta )$, is called the ignorance degree. If $m(D)>0$, then $D$ is called a focal element, and all focal elements constitute a body of evidence.

Definition 7

[31]. Let $m_1$ and $m_2$ be two independent evidences defined on the same frame of discernment $\Theta$; the combination of $m_1$ and $m_2$, denoted by $m=m_1\oplus m_2$, is defined as

$$m(A)=\left\{\begin{array}{c}{\displaystyle \frac{1}{1-K}}{\displaystyle \sum _{\left.B,C\in 2^{\Theta }\right|B\cap C=A}{m}_1(B)m_2(C)},A\ne Ø\\ 0,A=Ø\end{array}\right.$$

(9)

where $K={\displaystyle \sum _{\begin{array}{l}B,C\in 2^{\Theta }\\ B\cap C=Ø\end{array}}{m}_1(B)m_2(C)}$, and $K$ represents the conflict coefficient between $m_1$ and $m_2$.

Definition 8

[13]. For a proposition $B\in 2^{\Theta }$, the confidence function $Bel:2^{\Theta }\to [0,1]$ and the plausibility function $Pl:2^{\Theta }\to [0,1]$ are, respectively, defined as

$$Bel(B)={\displaystyle \sum _{Ø\ne C\subseteq B}m(C)},$$

(10)

$$Pl(B)={\displaystyle \sum _{\mathrm{C}\cap \mathrm{B}\ne Ø}m\left(\mathrm{C}\right)}.$$

(11)

In the special case when $B=\left\{A_i\right\}$, Equations (10) and (11) can be simplified as

$$Bel(\{A_i\})=m(\{A_i\}),$$

(12)

$$Pl(\{A_i\})={\displaystyle \sum _{C\cap \left\{A_i\right\}\ne Ø}m(C)}.$$

(13)

where $Bel(B)$ and $Pl(B)$ are, respectively, the upper and lower bound functions of proposition $B$, satisfying $Bel(B)\le Pl(B)$. Because $Pl$ is the plausibility function and $Bel$ is the confidence function, they can also be called the upper and lower bounds of trust. Therefore, $[Bel(B),Pl(B)]$ can be used as the trust interval of proposition $B$.

3.3. Existing D–S Evidence Theory-Based Methods

Xiao [13] and Fei et al. [33] proposed different D–S evidence theory-based methods for ranking alternatives. Xiao [13] applied confidence values of alternatives to rank alternatives. In this case, when two alternatives with the same confidence values cannot be differentiated, please see Example 1. To make up for this defect, Fei et al. [33] suggested sorting alternatives based on the center of confidence and plausibility values. Unfortunately, although the distinguishing power of method [33] is stronger than that of method [13], it is unable to discriminate alternatives which have identical centers; please see Example 2.

Example 1.

Suppose $\Theta =\{A_1,A_2,A_3,A_4\}$ is an alternative set and the mass function values of alternatives are shown as Table 1.

Table 1. Mass function values in Example 1.

	${\mathit{m}}_{\mathit{j}}(\{{\mathit{A}}_1\})$	${\mathit{m}}_{\mathit{j}}(\{{\mathit{A}}_2\})$	${\mathit{m}}_{\mathit{j}}(\{{\mathit{A}}_3\})$	${\mathit{m}}_{\mathit{j}}(\{{\mathit{A}}_4\})$	${\mathit{m}}_{\mathit{j}}(\{{\mathit{A}}_1,{\mathit{A}}_2\})$	${\mathit{m}}_{\mathit{j}}(\{{\mathit{A}}_3,{\mathit{A}}_4\})$	${\mathit{m}}_{\mathit{j}}(\mathbf{\Theta })$
$C_1$	0.2031	0.0950	0.1901	0.1067	0.2016	0.1231	0.0804
$C_2$	0.1611	0.0934	0.2090	0.2208	0.1167	0.1092	0.0898

According to Equation (9), the comprehensive mass functions of alternatives $A_1$ and $A_3$ are obtained as $m(\{A_1\})=0.2522$ and $m(\{A_3\})=0.2522$. By virtue of Equation (10), one obtains $Bel(\{A_1\})=0.2522$ and $Bel(\{A_3\})=0.2522$. Thus, one has $Bel(\{A_1\})=Bel(\{A_3\})$. According to the method [13], it is concluded that $A_1$ is indifferent from $A_3$. In other words, the method [13] cannot distinguish which alternative is more preferred.

In light of Equation (11), one obtains $Pl(\{A_1\})=0.3744$ and $Pl(\{A_3\})=0.3372$. Hence, we have ${\displaystyle \frac{1}{2}}(Bel(A_1)+Pl(A_1))>{\displaystyle \frac{1}{2}}(Bel(A_3)+Pl(A_3))$. Employing the method [33], it obtains as $A_1$ is better than $A_3$. At this point, the distinguish power of the method [33] is stronger than that of the method [13]. However, there still exist some cases where the method [33] is unable to differentiate two alternatives; please see Example 2.

Example 2.

Suppose $\Theta =\{A_1,A_2,A_3,A_4\}$ is an alternative set and mass function values of some subsets are listed in Table 2.

Table 2. Mass function values in Example 2.

	${\mathit{m}}_{\mathit{j}}(\{{\mathit{A}}_1\})$	${\mathit{m}}_{\mathit{j}}(\{{\mathit{A}}_2\})$	${\mathit{m}}_{\mathit{j}}(\{{\mathit{A}}_3\})$	${\mathit{m}}_{\mathit{j}}(\{{\mathit{A}}_4\})$	${\mathit{m}}_{\mathit{j}}(\{{\mathit{A}}_1,{\mathit{A}}_2\})$	${\mathit{m}}_{\mathit{j}}(\{{\mathit{A}}_3,{\mathit{A}}_4\})$	${\mathit{m}}_{\mathit{j}}(\mathbf{\Theta })$
$C_1$	0.4131	0	0.1950	0.1469	0	0.1531	0.0919
$C_2$	0.2730	0	0.1751	0.2707	0	0.2192	0.0620

By Equations (9)–(11), we have ${\displaystyle \frac{1}{2}}(Bel(\{A_1\})+Pl(\{A_1\}))={\displaystyle \frac{1}{2}}(Bel(\{A_3\})+Pl(\{A_3\}))=0.3251$, and the distribution is shown in Figure 1. According to the method [33], the alternatives $A_1$ and $A_3$ cannot be distinguished.

Figure 1. The confidence and plausibility values of alternatives $A_1$ and $A_3$.

In a word, Example 1 and Example 2 demonstrate that the distinguishing powers of methods [13,33] are not strong enough. Therefore, it is necessary to improve these methods to strengthen their distinguishing powers.

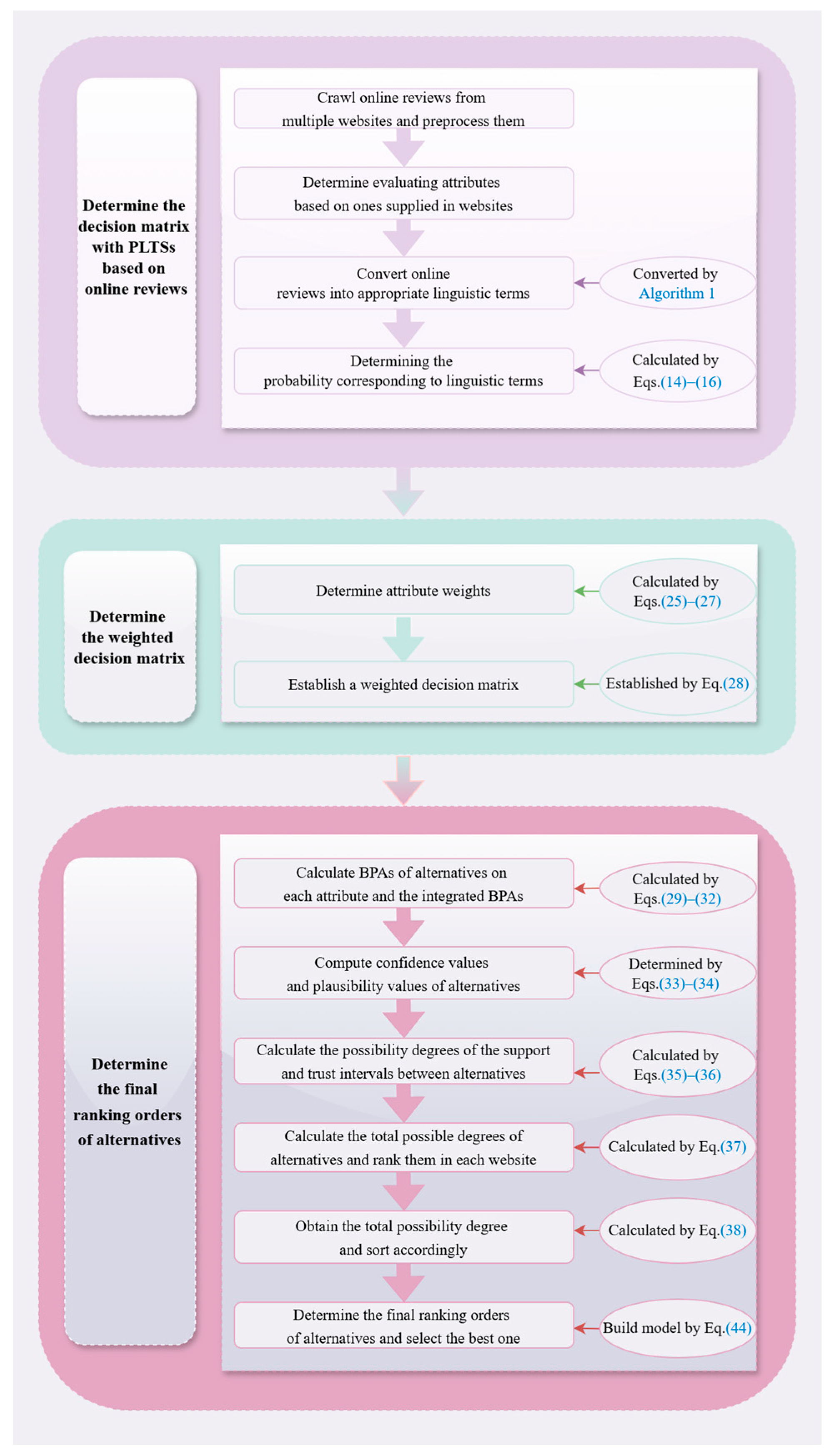
4. A Possible Degree-Based D–S Evidence Theory Method with Online Reviews in the PLTS Context

In this section, a possible degree-based D–S evidence theory method is proposed to resolve decision problems with online reviews in the PLTS environment. By sentiment analyses, online reviews crawled from multiple websites are transformed into five-granularity PLTSs. Thus, a decision matrix corresponding to each website is constructed. Subsequently, a bi-objective programming model is set up to determine attribute weights. Finally, by introducing a confidence–plausibility-based possibility degree, a possible degree-based D–S evidence theory method is presented to rank alternatives for each website. At length, a 0–1 programming model is constructed to obtain the final alternative ranking results.

4.1. Problem Description

Let $A=\{A_1,A_2,\cdots A_m\}$ be the set of candidate alternatives and the online reviews are crawled from $q$ popular websites. Suppose the attribute set is $C=\{C_1,C_2,\cdots C_n\}$ with weight vector ${\overline{\mathit{w}}}^{(k)}={({\overline{w}}_1^{(k)},{\overline{w}}_2^{(k)},\cdots ,{\overline{w}}_j^{(k)},\cdots ,{\overline{w}}_n^{(k)})}^T(k=1,2,\cdots ,q)$, where ${\overline{w}}_j^{(k)}$ indicates the weight of attributes for the $k$th website and satisfies ${\displaystyle \sum _{j=1}^n{\overline{w}}_j^{(k)}}=1$. The set $U_{ij}^{(k)}=\{u_{ij1}^{(k)},u_{ij2}^{(k)},\cdots ,u_{ij{\mathrm{\Pi }}_{ij}^{(k)}}^{(k)}\}$ represents the review of alternative $A_i$ on attribute $C_j$ from the $k$th website. $u_{ij\pi }^{(k)}$ is the $\pi$th review alternative $A_i$ on attribute $C_j$ from the $k$th website.

4.2. Determine the Decision Matrix with PLTSs Based on Online Reviews

This section collects online reviews on NEVs and transforms them into PLTSs with a five-granularity linguistic term set. Thus, the decision matrix with PLTSs is formed. In this process, three issues are involved: (1) data collection and preprocessing; (2) convert online reviews into appropriate linguistic terms; (3) determine probabilities corresponding to linguistic terms.

4.2.1. Data Collection and Preprocessing

Using the GooSeeker information collection tool, online reviews, which are posted with respect to the given attributes, are collected from $q$ popular websites, such as “autohome.com.cn”, “xcar.com.cn”, “pcauto.com.cn” accessed on 2 February, 2024. Afterwards, the collected data are preprocessed with Jieba in Python2021.1 software, including deleting duplicated reviews, useless words and word segmentation.

4.2.2. Convert Online Reviews into Appropriate Linguistic Terms by Sentiment Analyses

In order to transform preprocessed reviews into linguistic terms, it is necessary to conduct sentiment analyses. For different attributes, sentiment words are distinct and even the sentiment orientations for the same sentiment word are opposite. For example, the sentiment of the word “lower” is positive when it expresses the attribute “price”. However, its sentiment is negative when it describes the comfort degree. Therefore, to ensure the accuracy of the sentiment analysis results, this paper compiles different sentiment dictionary associated with attributes. According to the common CNKI sentimental vocabulary, attribute sentiment dictionaries are compiled by adding some words appearing more than 100 times in the reviews and dividing the sentiment words in the CNKI vocabulary into different attributes. For convenience, Table 3 lists some symbols appearing in this section.

Table 3. Main notations appearing in the sentimental analyses.

Notation	Explanation
$S=\{s_{-\eta },\cdots ,s_0,\cdots ,s_{\eta }\}$	The set of linguistic term. where $s_{\alpha }(\alpha =-\eta ,\cdots ,0,\cdots ,\eta )$.
$u_{ij\pi }^{(k)}$	The $\pi$th review from the $k$th website revaluating the $i$th alternative with respect to $j$th attribute.
$P_{ij\pi }^{*(k)}$	The number of positive sentiment words in the $\pi$th reviews for attribute $C_j$ of alternative $A_i$ for website $t_k$.
$N_{ij\pi }^{*(k)}$	The number of negative sentiment words in the $\pi$th reviews for attribute $C_j$ of alternative $A_i$ for website $t_k$.
$P{D}_{ij\pi }^{*(k)}$	The number of positive degree adverb words in the $\pi$th reviews for attribute $C_j$ of alternative $A_i$ for website $t_k$.
$N{D}_{ij\pi }^{*(k)}$	The number of negative degree adverb words in the $\pi$th reviews for attribute $C_j$ of alternative $A_i$ for website $t_k$.
${Ø}_{ij}^{(k)}$	The number of users who have missing evaluations the attribute $C_j$ of alternative $A_i$ for website $t_k$.

For a review $u_{ij\pi }^{(k)}$, it may include both positive and negative comments. Thus, it is natural to determine the sentiment orientation based on the numbers of positive and negative words. Let $S=\{s_{-2}=\mathrm{more} \mathrm{annoying},s_{-1}=\mathrm{annoying},s_0=\mathrm{general},s_1=\mathrm{like},s_2=\mathrm{more} \mathrm{like}\}$ be a linguistic term set. According to the compiled attribute dictionary, a statistic is conducted on the positive and negative sentiment words as well as positive and negative degree adverb words. If $P_{ij\pi }^{\ast (k)}>N_{ij\pi }^{\ast (k)}$ and $P{D}_{ij\pi }^{\ast (k)}>N{D}_{ij\pi }^{\ast (k)}$, it is deduced that the number of positive sentiment words is larger than that of negative sentiment words. Furthermore, the number of the positive degree words is greater than that of negative degree words. In this case, the review $u_{ij\pi }^{(k)}$ represents that the user is more satisfied with the $i$th alternative with respect to the $j$th attribute. Therefore, this review is assigned as “$s_2$”. For example, the $\pi$th review from $k$th website, evaluating the $i$th type of car on the $j$th attribute is “The screen is very large and clear, but the sound quality is bad”. In this review, the words “large” and “clear” are both positive sentiment words, but the word “bad” is a negative sentiment word. In addition, the word “very” is a positive degree word because it follows the positive sentiment word “big”. Thus, one derives $P_{ij\pi }^{*(k)}=2>N_{ij\pi }^{\ast (k)}=1$ and $P{D}_{ij\pi }^{\ast (k)}=1>N{D}_{ij\pi }^{\ast (k)}=0$, so this review is assigned as “$s_2$”. Similarly, if $P_{ij\pi }^{\ast (k)}>N_{ij\pi }^{\ast (k)}$ but $P{D}_{ij\pi }^{\ast (k)}=N{D}_{ij\pi }^{\ast (k)}$, this review is assigned as “$s_1$”. According to this idea, Algorithm 1 is designed to transform reviews into corresponding linguistic terms.

Algorithm 1. Transforming reviews into linguistic terms

Input: the preprocessed user reviews $U_{ij}^{(k)}=\{u_{ij1}^{(k)},u_{ij2}^{(k)},\cdots ,u_{ij{\mathrm{\Pi }}_{ij}^{(k)}}^{(k)}\},k=1,2,\cdots ,q,i=1,2,\cdots ,m,j=1,2,\cdots ,n,\pi =,1,2,\cdots {\mathrm{\Pi }}_{ij}^{(k)}$; positive word set $PV$, negative word set $NV$, degree adverb word set $DGV$ and deny word set $DNV$ of the new sentiment dictionary; linguistic term set $S=\{s_{-2},s_{-1},s_0,s_1,s_2\}$. Output: the sentimental orientation ${\gamma }_{ij\pi }^{(k)}$ of $u_{ij\pi }^{(k)}$. 1: for $k=1\to q$ do 2:  for $i=1\to m$ do 3:   for $j=1\to n$ do 4:    for $\pi =1\to {\mathrm{\Pi }}_{ij}^{(k)}$ do 5:    let $P_{ij\pi }^{\ast (k)}=0$,$N_{ij\pi }^{\ast (k)}=0$ do 6:     if $(u_{ij\pi }^{(k)}\cap PV)\ne Ø \wedge (u_{ij\pi }^{(k)}\cap DNV)=Ø$ then $P_{ij\pi }^{\ast (k)}\leftarrow |u_{ij\pi }^{(k)}\cap PV|$ 7:     else if $(u_{ij\pi }^{(k)}\cap NV)\ne Ø \wedge (u_{ij\pi }^{(k)}\cap DNV)=Ø$ then $N_{ij\pi }^{\ast (k)}\leftarrow |u_{ij\pi }^{(k)}\cap NV|$ 8:     else if $((u_{ij\pi }^{(k)}\cap PV)\ne Ø \vee (u_{ij\pi }^{(k)}\cap NV)\ne Ø) \wedge (DN=(u_{ij\pi }^{(k)}\cap DNV)\ne Ø)$ then 9:      if $\min (dis(PV,DN))\ge \min (dis(NV,DN))$ then $P_{ij\pi }^{\ast (k)}\leftarrow P_{ij\pi }^{\ast (k)}+2|u_{ij\pi }^{(k)}\cap DNV|$ 10:       else $N_{ij\pi }^{\ast (k)}\leftarrow N_{ij\pi }^{\ast (k)}+2|u_{ij\pi }^{(k)}\cap DNV|$ 11:       end if 12:      else $P_{ij\pi }^{\ast (k)}\leftarrow 0$,$N_{ij\pi }^{\ast (k)}\leftarrow 0$ 13:      end if 14:      let $P{D}_{ij\pi }^{\ast (k)}=0$,$N{D}_{ij\pi }^{\ast (k)}=0$ do 15:       if $(DG=(u_{ij\pi }^{(k)}\cap DGV)\ne Ø)\wedge \left(\min \right(dis(PV,DG))\ge \min (dis(NV,DG)))$ then $N{D}_{ij\pi }^{\ast (k)}\leftarrow |u_{ij\pi }^{(k)}\cap DGV|$ 16:       else if $(DG=(u_{ij\pi }^{(k)}\cap DGV)\ne Ø) \wedge \left(\min \right(dis(PV,DG))<\min (dis(NV,DG)))$ then$P{D}_{ij\pi }^{\ast (k)}\leftarrow |u_{ij\pi }^{(k)}\cap DGV|$ 17:       else $P{D}_{ij\pi }^{\ast (k)}\leftarrow 0$,$N{D}_{ij\pi }^{\ast (k)}\leftarrow 0$ 18:       end if 19:       if $(P_{ij\pi }^{\ast (k)}>N_{ij\pi }^{\ast (k)}) \wedge (P{D}_{ij\pi }^{\ast (k)}>N{D}_{ij\pi }^{\ast (k)})$ then ${\gamma }_{ij\pi }^{(k)}=s_2$ 20:       else if $((P_{ij\pi }^{\ast (k)}>N_{ij\pi }^{\ast (k)}) \wedge (P{D}_{ij\pi }^{\ast (k)}=N{D}_{ij\pi }^{\ast (k)})) \vee \left(\right(P_{ij\pi }^{\ast (k)}=N_{ij\pi }^{\ast (k)}) \wedge (P{D}_{ij\pi }^{\ast (k)}>N{D}_{ij\pi }^{\ast (k)}))$ then ${\gamma }_{ij\pi }^{(k)}=s_1$ 21:       else if $(P_{ij\pi }^{\ast (k)}=N_{ij\pi }^{\ast (k)}=0) \vee ((P_{ij\pi }^{\ast (k)}>N_{ij\pi }^{\ast (k)}) \wedge (P{D}_{ij\pi }^{\ast (k)}<N{D}_{ij\pi }^{\ast (k)})) \vee \left(\right(P_{ij\pi }^{\ast (k)}=N_{ij\pi }^{\ast (k)}) \wedge (P{D}_{ij\pi }^{\ast (k)}=N{D}_{ij\pi }^{\ast (k)}))$       $\vee ((P_{ij\pi }^{\ast (k)}<N_{ij\pi }^{\ast (k)}) \wedge (P{D}_{ij\pi }^{\ast (k)}>N{D}_{ij\pi }^{\ast (k)}))$ then ${\gamma }_{ij\pi }^{(k)}=s_0$ 22:       else if $((P_{ij\pi }^{\ast (k)}=N_{ij\pi }^{\ast (k)}) \wedge (P{D}_{ij\pi }^{\ast (k)}<N{D}_{ij\pi }^{\ast (k)}\left)\right) \vee \left(\right(P_{ij\pi }^{\ast (k)}<N_{ij\pi }^{\ast (k)}) \wedge (P{D}_{ij\pi }^{\ast (k)}=N{D}_{ij\pi }^{\ast (k)}))$ then ${\gamma }_{ij\pi }^{(k)}=s_{-1}$ 23:       else ${\gamma }_{ij\pi }^{(k)}=s_{-2}$ 24:       end if 25:      end for 26:     end for 27:    end for 28:   end for 29:  end for 30: end for

Note: $dis(PV,DG)$ is computed by the number of words between positive words and degree adverb words. Similarly, $dis(PV,DN)$$dis(NV,DG)$ and $dis(NV,DN)$ are calculated. Table 4 illustrates the calculation process. $\left|A\right|$ represents the number of elements in $A$.

Table 4. An example of calculating $dis(PV,DG)$.

Review	Classification of Words	The Examples of Degree Words	The Sentimental Orientation of Words
The space inside the car is quite spacious. As soon as you get into the car, you will feel very light and bright. Whether you sit in the front or the back, the useful space is very gelivable and very large. I, 1.78 m, can have such experiences, so it is no problems for other people. It is not crowded at all for three people sitting in the back.	Positive sentiment words: spacious, light and bright, gelivable, large. Negative sentiment words: problem, crowded Degree words: quite, very1, very2, very3.	$dis(PV,DG)$: $dis(PV,quite)$$dis(spacious,quite)=0$, $dis(light and bright,quite)=13$, $dis(gelivable,quite)=30$, $dis(large,quite)=33$	$\begin{array}{l}\min (dis(PV,quite))=0\\ <\\ \min (dis(NV,quite))=45\end{array}$ The degree adverb “quite” is regarded as a positive degree ($PD$) word
		$dis(NV,DG)$: $dis(NV,quite)$$dis(problem,quite)=45$,$dis(crowded,quite)=52$

To understand Algorithm 1 visually Table 4 and Table 5 provide some examples illustrating the process of transforming a review into a linguistic term.

Table 5. Classification illustrating the sentiment orientation of reviews.

Review Symbols	Review	The Sentiment Orientation of Word	Quantity Comparison	Review Orientation
$u_{4,1,5}^{(2)}$	The space inside the car is quite spacious. As soon as you get into the car, you will feel very light and bright. Whether you sit in the front or the back, the useful space is very gelivable and very large. I, 1.78 m, can have such experiences, so it is no problems for other people. It is not crowded at all for three people sitting in the back.	$P_{4,1,5}^{\ast (2)}$: spacious, light and bright, gelivable, large $N_{4,1,5}^{\ast (2)}$: problem, crowded $P{D}_{4,1,5}^{\ast (2)}$: quite, very1, very2, very3 $N{D}_{4,1,5}^{\ast (2)}$: at all $D{N}_{4,1,5}^{\ast (2)}$: no, not	$P_{4,1,5}^{\ast (2)}=8>N_{4,1,5}^{\ast (2)}=2$$P{D}_{4,1,5}^{\ast (2)}=4>N{D}_{4,1,5}^{\ast (2)}=1$	$s_2$(more like)
$u_{1,3,9}^{(1)}$	The technology configuration is average, but the screen resolution is okay. While surfing the internet, the configuration is not smooth enough, and it is stuck sometimes. But the navigation is more convenient than that of the mobile phone.	$P_{1,3,9}^{\ast (1)}$: is okay, smooth, convenient $N_{1,3,9}^{\ast (1)}$: stuck $D{N}_{1,3,9}^{\ast (1)}$: not	$P_{1,3,9}^{\ast (1)}=3=N_{1,3,9}^{\ast (1)}=3$$P{D}_{1,3,9}^{\ast (1)}=0=N{D}_{1,3,9}^{\ast (1)}=0$	$s_0$(general)
$u_{5,1,8}^{(3)}$	The space in the front row is good, but the back row is very crowded. It is hard for adults to sit in the back row. The trunk is so small that some gift boxes cannot be held during the Chinese New Year.	$P_{5,1,8}^{\ast (3)}$: good $N_{5,1,8}^{\ast (3)}$: crowded, so small, can’t be held $N{D}_{4,1,5}^{\ast (2)}$: very, hard	$P_{5,1,8}^{\ast (3)}=1<N_{5,1,8}^{\ast (3)}=3$$P{D}_{5,1,8}^{\ast (3)}=0<N{D}_{5,1,8}^{\ast (3)}=2$	$s_{-2}$(more annoying)

4.2.3. Determining the Probability Corresponding to Linguistic Terms

In the process of transforming the reviews into PLTSs, it is needed to determine the probability corresponding to the linguistic terms derived in Section 4.2.2. We denote by $T_i^{(k)}$ number of users evaluating the $i$th alternative in the $k$th website. Generally, users evaluate alternatives on all given attributes. However, sometimes, a few users may miss evaluations on alternatives with some attributes. Suppose ${\mathrm{\Pi }}_{ij}^{(k)}$ represents the number of reviews on the $i$th alternatives with respect to the $j$th attribute for the $k$th website, and ${Ø}_{ij}^{(k)}$ indicate the number of users who have missed evaluations on the $i$th alternative with the $j$th attribute for the $k$th website. Thus, we have $T_i^{(k)}={\mathrm{\Pi }}_{ij}^{(k)}+{Ø}_{ij}^{(k)}$. Furthermore, assume $G_{\alpha ij}^{(k)}$ is the number of reviews which come from the $k$th website and evaluate the $i$th alternative as $s_{\alpha }$ with respect to the $j$th attribute, and let ${\tilde{p}}_{\alpha ij}^{(k)}$ be the initial probability of the linguistic term $s_a$ which is one of a possible linguistic term transformed from all reviews $u_{ij\pi }^{(k)}$. ${\tilde{p}}_{Øij}^{(k)}$ means the proportion associated with missing information. Thus, the probabilities ${\tilde{p}}_{\alpha ij}^{(k)}$ and ${\tilde{p}}_{Øij}^{(k)}$ can be obtained as

$${\tilde{p}}_{\alpha ij}^{(k)}=G_{\alpha ij}^{(k)}/T_i^{(k)},$$

(14)

$${\tilde{p}}_{Øij}^{(k)}={Ø}_{ij}^{(k)}/T_i^{(k)}.$$

(15)

where $T_i^{(k)}$ represents the number of users under the $i$th alternative for the $k$th website.

Remark 1.

In the $k$ th website, if a user does not provide the evaluation on the $i$th alternative with the $j$th attribute, any linguistic term may be possible. Thus, the probability  ${\tilde{p}}_{Øij}^{(k)}$ can be equally divided to all possible linguistic terms.

According to Remark 1, the adjusted probability associated with possible linguistic term $s_a$, denoted by $p_{\alpha ij}^{(k)}$, can be derived as

$$p_{\alpha ij}^{(k)}={\tilde{p}}_{\alpha ij}^{(k)}+{\tilde{p}}_{Øij}^{(k)}/(2\eta +1).$$

(16)

where $\eta$ represents the cardinality of the given linguistic term set $S$.

The aim of Equation (16) is to divide the probability ${\tilde{p}}_{Øij}^{(k)}$ equally into all possible linguistic terms. Thus, obtained probabilistic linguistic terms are standardized PLTSs in which the sum of probabilities associated with all possible linguistic terms is equal to 1.

In virtue of the linguistic terms $s_{ij\pi }^{(k)}$ associated with probability $p_{\alpha ij}^{(k)}$, a decision matrix for the $k$th website, denoted by $D^{(k)}={[h_{ij}^{(k)}(p)]}_{m\times n}$ is constructed, where $h_{ij}^{(k)}(p)=\{s_{aij}^{(k)}(p_{\alpha ij}^{(k)})|\alpha =-2,-1,0,1,2\}$.

4.3. Determine Attribute Weights by Constructing a Bi-Objective Programming Model

Attribute weights play an important role while ranking alternatives. Therefore, how to determine attribute weights is a key issue. On the one hand, there exists uncertainty in the decision information expressed by PLTSs. Hence, the smaller the uncertainty of decision information with respect to an attribute, the weight of this attribute should be assigned a greater value. On the other hand, according to the principle of maximizing deviations between decision information, the more the deviations between attribute values associated with the same attribute, the bigger this attribute weight is. Keeping this idea in mind, by minimizing the uncertainty and maximizing deviations between alternatives, a bi-objective programming model is constructed to determine attribute weights objectively.

4.3.1. A Minimum Probabilistic Linguistic Entropy Model

According to the JS entropy proposed by [34], the uncertainty degree of attribute $C_j$, denoted by $H_{JS}^{(k)}(C_j)$, can be calculated as

$$H_{JS}^{(k)}(C_j)={\displaystyle \sum _{{\Theta }_{\tau j}\in 2^A}m({\Theta }_{\tau j})\log (|{\Theta }_{\tau j}|)}-{\displaystyle \sum _{A_{ij}^{(k)}\in A}Pl\_P_m(A_{ij}^{(k)})\log [Pl\_P_m(A_{ij}^{(k)})]}.$$

(17)

where ${\Theta }_{\tau j}$ represents $\tau$th element of the power set $2^A$ respect to $C_j$, and $\left|{\Theta }_{\tau j}\right|$ is the cardinality of the set ${\Theta }_{\tau j}$. As only the singleton set comprised of a single alternative is considered in this Section 5.2, it obtains $\left|{\Theta }_{\tau j}\right|=1$, so $\log (|{\Theta }_{\tau j}|)=0$. Therefore, the JS entropy in Equation (17) is degenerated into the Shannon entropy, i.e.,

$$H_{JS}^{(k)}(C_j)=-{\displaystyle \sum _{A_{ij}^{(k)}\in A}Pl\_P_m(A_{ij}^{(k)})\log [Pl\_P_m(A_{ij}^{(k)})]}.$$

(18)

where $A_{ij}^{(k)}$ is the $i$th alternative with respect to the $j$th attribute for the $k$th website, $Pl\_P_m(A_{ij}^{(k)})={\displaystyle \frac{Pl(A_{ij}^{(k)})}{{\displaystyle \sum _{i=1}^{m}Pl(A_{ij}^{(k)})}}}={\displaystyle \frac{E\left(h_{ij}^{(k)}(p)\right)}{{\displaystyle \sum _{i=1}^{m}E\left(h_{ij}^{(k)}(p)\right)}}}$, $E\left(h_{ij}^{(k)}(p)\right)={\displaystyle \sum _{l=1}^{L_o}\left(f_{ij}^{(k)}(s_{\alpha }^{(l)})\cdot p_{\alpha ij}^{(k)(l)}/{\displaystyle \sum _{l=1}^{L_o}{p}_{\alpha ij}^{(k)(l)}}\right)}$, and $Pl\_P_m(A_{ij}^{(k)})$ represents the plausibility transformation function of $A_{ij}^{(k)}$.

By normalizing $H_{JS}^{(k)}(C_j)$, the standard entropy of attribute $C_j$ for the kth website can be obtained, i.e.,

$${\overline{H}}_{JS}^{(k)}(C_j)={\displaystyle \frac{H_{JS}^{(k)}(C_j)}{{\displaystyle \sum _{j=1}^n{H}_{JS}^{(k)}(C_j)}}}.$$

(19)

Thus, the weighted uncertainty of decision information from the $k$th website can be expressed as

$${\tilde{H}}_{JS}^{(k)}={\displaystyle \sum _{j=1}^n{w}_j^{(k)}\cdot {\overline{H}}_{JS}^{(k)}(C_j)}.$$

(20)

where $w_j^{(k)}$ is the weight of attribute $C_j$ for the $k$th website.

As mentioned before, a smaller uncertainty with respect to an attribute means a bigger weight associated with this attribute. Hence, by minimum probabilistic linguistic entropy for the $k$th website, an optimal programming model is built as

$$\begin{array}{c}\min {\tilde{H}}_{JS}^{(k)}\\ s.t.\left\{\begin{array}{c}0<w_j^{(k)}<1\\ {\displaystyle \sum _{j=1}^n{w}_j^{(k)2}=1}\end{array}\right.\end{array}.$$

(21)

4.3.2. Construct a Bi-Objective Programming Model to Determine Attribute Weights

On the other hand, the total deviations between alternatives for the $k$th website, denoted by ${\sigma }^{(k)}(w)$, can be expressed as

$${\sigma }^{(k)}(w)={\displaystyle \sum _{j=1}^n{w}_j^{(k)}{\displaystyle \sum _{i=1}^m{\displaystyle \sum _{t=1}^m{\left(E\left(h_{ij}^{(k)}(p)\right)-E\left(h_{tj}^{(k)}(p)\right)\right)}^2}}}.$$

(22)

Maximizing the total deviations, the other optimal model is constructed as below:

$$\begin{array}{c}\max {\sigma }^{(k)}(w)\\ s.t.\left\{\begin{array}{c}0<w_j^{(k)}<1\\ {\displaystyle \sum _{j=1}^n{w}_j^{(k)2}=1}\end{array}\right.\end{array}.$$

(23)

Combining Equations (21) and (23), a bi-objective programming model is generated as

$$\begin{array}{c}\max {\sigma }^{(k)}(w)\\ \min {\tilde{H}}_{JS}^{(k)}\\ s.t.\left\{\begin{array}{c}0<w_j^{(k)}<1\\ {\displaystyle \sum _{j=1}^n{w}_j^{(k)2}=1}\end{array}\right.\end{array}.$$

(24)

By setting a balancing coefficient $\epsilon$, Equation (24) is transformed into a single-objective programming model and can be expressed as

$$\begin{array}{c}\min {\displaystyle \sum _{j=1}^n\left(\epsilon {\tilde{H}}_{JS}^{(k)}-(1-\epsilon ){\sigma }^{(k)}(w)\right)}\\ s.t.\left\{\begin{array}{c}0<w_j^{(k)}<1\\ {\displaystyle \sum _{j=1}^n{w}_j^{(k)2}=1}\end{array}\right.\end{array}$$

(25)

By solving Equation (25), $w_j^{(k)}$ are obtained. In order to avoid the interference of non-positive values, the obtained weights are improved as

$${\widehat{w}}_j^{(k)}=e^{w_j^{(k)}}.$$

(26)

By standardizing ${\widehat{w}}_j^{(k)}(j=1,2,\dots ,n)$, the standardized attribute weights are derived as

$${\overline{w}}_j^{(k)}={\displaystyle \frac{e^{w_j^{(k)}}}{{\displaystyle \sum _{j=1}^n{e}^{w_j^{(k)}}}}}.$$

(27)

Thereby, the weighted decision matrix is generated as

$$D^{w(k)}={[x_{ij}^{(k)}]}_{m\times n}={\overline{w}}_j^{(k)}\cdot D^{(k)}.$$

(28)

4.4. A Possible Degree-Based D–S Evidence Theory Method for Ranking Alternatives in the PLTS Context

In this section, a possible degree-based D–S evidence theory method is proposed to rank alternatives in the probabilistic linguistic environment. In this method, a new mass function is defined by fusing score values and the proposed entropy in Section 4.3.1. According to the defined mass function, a novel confidence function and a plausibility function of alternatives are introduced, respectively. Afterwards, a confidence–plausibility-based possible degree is recommended for deriving the ranking values of alternatives for the kth website. Finally, to derive the final rankings of alternatives, a 0–1 programming model is established for synthesizing the ranking results for different websites.

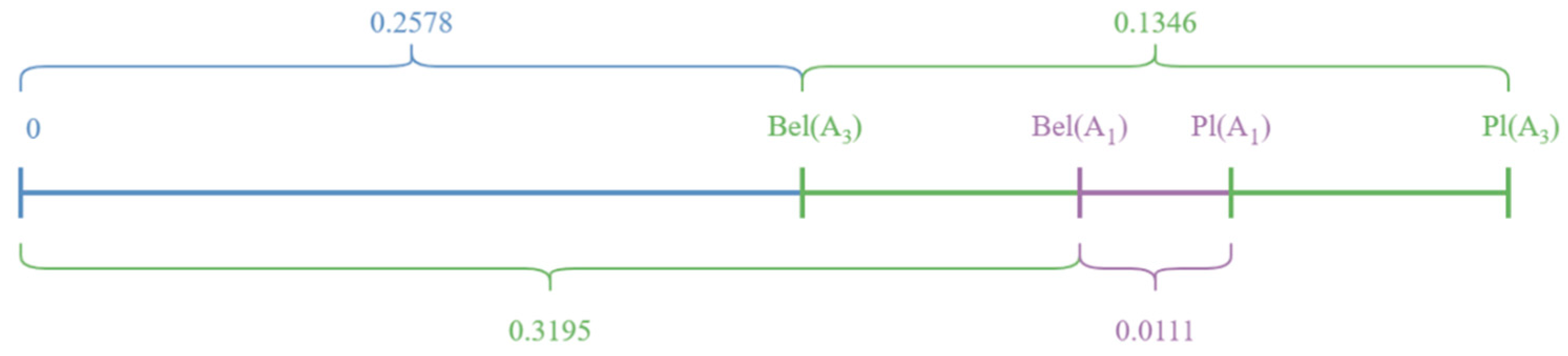
4.4.1. New Confidence and Plausibility Functions

According to the score function in Equation (7), the BPA of alternative $A_i$ with respect to the attribute $C_j$ for the $k$th website, denoted by $m_{C_j}^{(k)}(A_i)$ can be calculated as

$$m_{C_j}^{(k)}(Ø)=0,$$

(29)

$$m_{C_j}^{(k)}(A_i)=\overline{E}(x_{ij}^{(k)})\cdot (1-{\overline{H}}_{JS}^{(k)}(C_j)),$$

(30)

$$m_{C_j}^{(k)}(\Theta )=1-{\displaystyle \sum _{i=1}^m{m}_{C_j}^{(k)}(A_i)}.$$

(31)

where $\overline{E}(x_{ij}^{(k)})={\displaystyle \frac{E(x_{ij}^{(k)})}{{\displaystyle \sum _{t=1}^{m}E(x_{tj}^{(k)})}}}$, $E(x_{ij}^{(k)})={\displaystyle \sum _{l=1}^{L_o}\left(f(s_{\alpha ij}^{(k)(l)})\cdot p_{\alpha ij}^{(k)(l)}/{\displaystyle \sum _{l=1}^{L_o}{p}_{\alpha ij}^{(k)(l)}}\right)}$, $\Theta =\{A_1,A_2,\cdots ,A_m\}$.

Then, according to the Dempster’s combination rule (see Definition 7), the integrated BPAs of alternatives are generated by fusing BPAs with regards to all attributes. That is

$$m_C^{(k)}(A_i)=((m_{C_1}^{(k)}(A_i)\oplus m_{C_2}^{(k)}(A_i))\oplus \cdots )\oplus m_{C_n}^{(k)}(A_i).$$

(32)

According to Equations (12) and (13) in Section 3.2, the confidence and the plausibility functions of alternative $A_i$ with regard to $k$th website, denoted by $Be{l}^{(k)}(A_i)$ and $P{l}^{(k)}(A_i)$ can be designed as

$$Be{l}^{(k)}(A_i)=m_C^{(k)}(A_i),$$

(33)

$$P{l}^{(k)}(A_i)={\displaystyle \sum _{B\cap \left\{A_i\right\}\ne Ø}{m}_C^{(k)}(B)}.$$

(34)

To resolve the drawbacks in methods [13,33] mentioned in Section 3.3, this section proposes a possible degree ranking method by combining confidence and plausibility functions. According to the interval possibility degree [35,36], we define the possibility degrees of supporting interval and trust interval depicted in Figure 2.

Figure 2. Supporting interval and trust interval of an alternative.

4.4.2. A Confidence–Plausibility-Based Possible Degree for Ranking Alternatives for Each Website

Definition 9.

Let $Be{l}^{(k)}(A_i)$ and $Be{l}^{(k)}(A_t)$ be, respectively, the confidence values of alternatives $A_i$ and $A_t$ for the $k$th website; then, the supporting possibility degree of alternative $A_i$ prior to $A_t$, denoted by $C{P}^{(k)}\left(A_i\underset{\_}{\succ }{A}_t\right)$, is defined as

$$C{P}^{(k)}\left(A_i\underset{\_}{\succ }{A}_t\right)={\displaystyle \frac{1}{2}}\left(1+{\displaystyle \frac{\left|Be{l}^{(k)}\left(A_i\right)-0\right|-\left|0-Be{l}^{(k)}\left(A_t\right)\right|}{Be{l}^{(k)}\left(A_i\right)-0+Be{l}^{(k)}\left(A_t\right)-0}}\right)={\displaystyle \frac{1}{2}}\left(1+{\displaystyle \frac{Be{l}^{(k)}\left(A_i\right)-Be{l}^{(k)}\left(A_t\right)}{Be{l}^{(k)}\left(A_i\right)+Be{l}^{(k)}\left(A_t\right)}}\right).$$

(35)

Definition 10.

Suppose $T{A}_i^{(k)}=[Be{l}^{(k)}(A_i),P{l}^{(k)}(A_i)]$ and $T{A}_t^{(k)}=[Be{l}^{(k)}(A_t),P{l}^{(k)}(A_t)]$ are, respectively, the trust intervals of alternatives $A_i$ and $A_t$ for the $k$th website; then, the trust possibility degree of alternative $A_i$ prior to $A_t$, denoted by $T{P}^{(k)}\left(A_i\underset{\_}{\succ }{A}_t\right)$, can be defined as

$$T{P}^{(k)}\left(A_i\underset{\_}{\succ }{A}_t\right)={\displaystyle \frac{1}{2}}\left(1+{\displaystyle \frac{\left|P{l}^{(k)}(A_i)-Be{l}^{(k)}(A_t)\right|-\left|Be{l}^{(k)}(A_i)-P{l}^{(k)}(A_t)\right|}{P{l}^{(k)}(A_i)-Be{l}^{(k)}(A_i)+P{l}^{(k)}(A_t)-Be{l}^{(k)}(A_t)}}\right).$$

(36)

Fusing the possibility degrees $C{P}^{(k)}\left(A_i\underset{\_}{\succ }{A}_t\right)$ and $T{P}^{(k)}\left(A_i\underset{\_}{\succ }{A}_t\right)$ with a balance coefficient $v(0\le v\le 1)$, the comprehensive possibility degree of alternative $A_i$ prior to $A_t$ for the $k$th website is obtained as

$$P^{(k)}\left(A_i\underset{\_}{\succ }{A}_t\right)=vC{P}^{(k)}\left(A_i\underset{\_}{\succ }{A}_t\right)+(1-v)T{P}^{(k)}\left(A_i\underset{\_}{\succ }{A}_t\right).$$

(37)

Thereby, the total possibility degree of alternative $A_i$ prior to $A_t$ can be calculated as:

$$P^{(k)}(A_i)={\displaystyle \sum _{t=1}^m{P}^{(k)}\left(A_i\underset{\_}{\succ }{A}_t\right)}.$$

(38)

By virtue of Equation (38), all alternatives are sorted for the $k$th website.

Remark 2.

The confidence–plausibility-based possible degree ranking method absorbs the virtues of method [33] and has a stronger distinguishing power compared with method [13], which can be verified by Example 3 and Example 4.

Example 3.

Continuing Example 1, the calculation of the confidence and plausibility values of the alternatives is shown in Table 6.

Table 6. Confidence and plausibility values in Example 3.

	$\left\{{\mathit{A}}_1\right\}$	$\left\{{\mathit{A}}_2\right\}$	$\left\{{\mathit{A}}_3\right\}$	$\left\{{\mathit{A}}_4\right\}$	$\{{\mathit{A}}_1,{\mathit{A}}_2\}$	$\{{\mathit{A}}_3,{\mathit{A}}_4\}$	$\mathbf{\Theta }$
$Bel$	0.2522	0.1151	0.2522	0.1884	0.4744	0.5105	1
$Pl$	0.3745	0.2374	0.3373	0.2735	0.4896	0.5257

According to Equations (35)–(37), let $v=0.65$, then $P\left(A_1\underset{\_}{\succ }{A}_3\right)=0.53143>0.5$; thus, it generates $A_1\succ A_3$.

Example 4.

Continuing Example 2, according to Equations (35)–(37), let $v=0.65$; then, $P\left(A_1\underset{\_}{\succ }{A}_3\right)=0.53478>0.5$; thus, it generates $A_1\succ A_3$.

4.4.3. Build a 0–1 Programming Model for Obtaining the Final Alternative Ranking Orders

After deriving the rankings in each website with the confidence–plausibility-based possible degree ranking method, how to obtain the final alternative ranking orders is still an important issue. This section builds a 0–1 programming model to derive the final alternative ranking orders.

For the sake of convenience, suppose the ranking position of alternative $A_i$ for the $k$th website is $R_i^{(k)}$, and the final ranking of alternative $A_i$ is the $r$th position, denoted by $R_{ir}$. It is natural that the consensus degree between $R_i^{(k)}$ and $R_{ir}$ should be maximized as much as possible. The consensus degree index between $R_i^{(k)}$ and $R_{ir}$, denoted by $V_{ir}^{(k)}$, can be expressed as

$$V_{ir}^{(k)}=1-{\displaystyle \frac{\left|R_i^{(k)}-R_{ir}\right|}{m-1}}.$$

(39)

Among all websites, the total consensus degree of the $i$th alternative sorted in the $r$th position can be expressed as

$$V_{ir}={\displaystyle \sum _{k=1}^q{V}_{ir}^{(k)}}.$$

(40)

Thus, the consensus matrix $M$ can be constructed as

$$M={\left(V_{ir}\right)}_{m\times m}.$$

(41)

Suppose a 0–1 variable $y_{ir}$ as

$$y_{ir}=\left\{\begin{array}{l}1, \mathrm{the} \mathrm{final} \mathrm{ranking} \mathrm{of} A_i \mathrm{is} \mathrm{the} r-\mathrm{th} \mathrm{position} \\ 0, \mathrm{else}\end{array}\right..$$

(42)

In order to determine the final sorting of alternatives, a 0–1 programming model is constructed by maximizing consensus degrees, i.e.,

$$\begin{array}{l}\max z={\displaystyle \sum _{i=1}^m{\displaystyle \sum _{r=1}^m{y}_{ir}{V}_{ir}}}\\ s.t.\left\{\begin{array}{c}{V}_{ir}={\displaystyle \sum _{k=1}^q(1-\frac{\left|R_i^{(k)}-R_{ir}\right|}{m-1})}\\ {\displaystyle \sum _{i=1}^m{y}_{ir}}=1, r=1,2,\cdots ,m\\ {\displaystyle \sum _{r=1}^m{y}_{ir}}=1, i=1,2,\cdots ,m\\ y_{ir}=0 or 1, i,r=1,2,\cdots ,m\end{array}\right.\end{array}.$$

(43)

Let ${\chi }_{ir}^{(k)}=\left|R_i^{(k)}-R_{ir}\right|$, and Equation (43) can be easily transformed into a 0–1 linear programming model as

$$\begin{array}{l}\max z={\displaystyle \sum _{i=1}^m{\displaystyle \sum _{r=1}^m{y}_{ir}{\displaystyle \sum _{k=1}^q(1-\frac{{\chi }_{ir}^{(k)}}{m-1})}}}\\ s.t.\left\{\begin{array}{c}\begin{array}{l}{\chi }_{ir}^{(k)}\ge R_i^{(k)}-R_{ir} (i,r=1,2,\cdots ,m)\\ {\chi }_{ir}^{(k)}\ge R_{ir}-R_i^{(k)} (i,r=1,2,\cdots ,m)\end{array}\\ {\displaystyle \sum _{i=1}^m{y}_{ir}}=1 (r=1,2,\cdots ,m)\\ {\displaystyle \sum _{r=1}^m{y}_{ir}}=1 (i=1,2,\cdots ,m)\\ y_{ir}=0 or 1, (i,r=1,2,\cdots ,m)\end{array}\right.\end{array}.$$

(44)

Solving Equation (44), the collective ranking matrix $Y={(y_{ir})}_{m\times m}$ can be derived. Thus, the final ranking order of the alternatives can be easily obtained and the best alternative is determined.

4.5. The Structure of the Possible Degree-Based D–S Evidence Theory Method in the PLTS Context

Based on the above analysis, the decision process for the possible degree-based D–S evidence theory method in the PLTS context is summarized as below.

Step 1. Crawl online reviews from multiple websites and preprocess them.

Step 2. Determine evaluating attributes based on ones supplied in the websites.

Step 3. According to Algorithm 1, the linguistic terms $s_{\alpha }$ corresponding to each review are determined.

Step 4. Determine the probability $p_{\alpha ij}^{(k)}$ corresponding to linguistic terms $s_{\alpha }$ by Equations (14)–(16).

Step 5. Determine attribute weights by Equations (25)–(27).

Step 6. Establish a weighted decision matrix $D^{w(k)}$ by Equation (28).

Step 7. Calculate BPAs of alternatives on each attribute and the integrated BPAs by Equations (29)–(32).

Step 8. Compute confidence values and plausibility values of alternatives based on Equations (33) and (34).

Step 9. Calculate the possibility degrees of the support and trust intervals between alternatives by Equations (35) and (36).

Step 10. Calculate the total possible degrees of alternatives by Equation (37) and rank them in each website.

Step 11. Obtain the total possibility degree $P^{(k)}(A_i)$ by Equation (38), and sort accordingly.

Step 12. Determine the final ranking orders of alternatives by Equation (44) and select the best one.

The main steps of the method proposed are shown in Figure 3.

Figure 3. Procedure for proposed methodology.

5. A Case Study of Selecting New Energy Vehicles

In this section, we provide a case study of selecting new energy vehicles to demonstrate the application of the proposed method.

5.1. Description of the Problem

In recent years, in order to protect the environment and reduce carbon emissions, the Chinese government strongly advocates new energy vehicles gradually replacing oil-fueled vehicles and has promulgated some policies, such as exempting them from the purchase tax, freely offering the equipment for charging batteries and distributing financial subsidies for NEV manufacturers. With the strong support of these policies, more and more car manufacturers have shifted their focuses from oil-fueled vehicles to NEVs. Meanwhile, a lot of consumers are inclined to NEVs. In this case, it is difficult for consumers to select a satisfactory NEV from many brands of cars because they usually are not familiar with the professional car knowledge and structures. Hence, a car consumer often browses online reviews on some E-commerce platforms before buying a NEV, such as autohome.com.cn, xcar.com.cn and so on. Now, we seek five popular types of NEVs, including AIONS ($A_1$), Tesla Model Y ($A_2$), Great Wall Euler Good Cat ($A_3$), BYD Han ($A_4$) and BYD Qin ($A_5$). In what follows, we apply the proposed method to recommend the best popular type of NEVs based on online reviews from three platforms, i.e., autohome.com ($t_1$), xcar.com ($t_2$) and pcauto.com ($t_3$).

5.2. Solving Process by the Proposed Method

Step 1. Crawl and preprocess online reviews on each type of NEVs from websites.

Using the GooSeeker information collection tool, we crawled 200 user online reviews on each type of NEV mentioned above from the websites $t_1$, $t_2$ and $t_3$. The contents included in each review are shown in Figure 4. It is observed from Figure 4 that each review provides comments on each attribute given by this website. Some online reviews are listed in Table A1 in Appendix A. Subsequently, we preprocessed the crawled reviews, such as deleting duplicate reviews, segregating words, cleaning and filtering noises including emoticons and incorrect sentences. Due to the limit of space, we only show the preprocessed reviews of website $t_1$ on alternatives with respect to all attributes, please see Table 7.

Figure 4. Comments of a review in website $t_1$.

Table 7. Distribution of number of reviews.

Alternatives	${\mathit{C}}_1$	${\mathit{C}}_2$	${\mathit{C}}_3$	${\mathit{C}}_4$	${\mathit{C}}_5$	${\mathit{C}}_6$	${\mathit{C}}_7$
$A_1$	85	85	63	85	85	85	85
$A_2$	133	132	130	132	133	132	133
$A_3$	88	88	87	87	87	87	87
$A_4$	104	104	101	105	105	102	104
$A_5$	105	104	104	105	105	105	105

Step 2. Determine evaluating attributes.

According to Figure 4, each website provides different evaluating criteria. To entirely evaluate alternatives, we choose the criteria provided by the website which supplies the most criteria as evaluating attributes. The determined attributes are $C=\{C_1,C_2,C_3,C_4,C_5,C_6,C_7\}$, including the space ($C_1$), the comfort ($C_2$), the battery life ($C_3$), the appearance ($C_4$), the interior ($C_5$), the cost performance ($C_6$) and the intelligence ($C_7$).

Step 3. Transform preprocessed online reviews into linguistic terms.

By Algorithm 1 and the compiled sentimental dictionary, the preprocessed online reviews in Step 1 are transformed into proper linguistic terms. For the detailed transforming process, please see Table 5 in Section 4.2.2.

Step 4. Compute the probabilities associated with linguistic terms.

To facilitate computing probability, we count the number of reviews corresponding to each linguistic term and the number of users who miss evaluations on some attributes, i.e., $G_{\alpha ij}^{(1)}$ and ${Ø}_{ij}^{(1)}$. The statistical results are shown in Table A2 in Appendix A. According to Equations (14) and (15), the probability ${\tilde{p}}_{\alpha ij}^{(k)}$ and ${\tilde{p}}_{Øij}^{(k)}$ are calculated and shown as Table A3 in Appendix A. By virtue of Equation (16), the decision matrix $D^{(k)}={[h_{ij}^{(k)}(p)]}_{m\times n}$ with PLTSs is obtained and listed in Table 8; for details, please refer to Matrix A1 in Appendix A.

Table 8. The standardized PLTS.

Attribute	${\mathit{A}}_1$	${\mathit{A}}_2$	${\mathit{A}}_3$	${\mathit{A}}_4$	${\mathit{A}}_5$
$C_1$	$\begin{array}{l}\{s_{-2}(0.0235),s_{-1}(0.0353),\\ s_0(0.1529),s_1(0.2235),\\ s_2(0.5647)\}\end{array}$	$\begin{array}{l}\{s_{-2}(0.0239),s_{-1}(0.0687),\\ s_0(0.2552),s_1(0.1806),\\ s_2(0.4716)\}\end{array}$	$\begin{array}{l}\{s_{-2}(0.0114),s_{-1}(0.0682),\\ s_0(0.2045),s_1(0.1591),\\ s_2(0.5568)\}\end{array}$	$\begin{array}{l}\{s_{-2}(0.0210),s_{-1}(0.0400),\\ s_0(0.0876),s_1(0.1543),\\ s_2(0.6971)\}\end{array}$	$\begin{array}{l}\{s_{-2}(0.0095),s_{-1}(0.0095),\\ s_0(0.1238),s_1(0.2190),\\ s_2(0.6381)\}\end{array}$
$C_2$	$\begin{array}{l}\{s_{-1}(0.0471),s_0(0.1176),\\ s_1(0.1647),s_2(0.6706)\}\end{array}$	$\begin{array}{l}\{s_{-2}(0.0254),s_{-1}(0.0254),\\ s_0(0.1597),s_1(0.1821),\\ s_2(0.6075)\}\end{array}$	$\begin{array}{l}\{s_{-2}(0.0227),s_{-1}(0.0114),\\ s_0(0.0682),s_1(0.1705),\\ s_2(0.7273)\}\end{array}$	$\begin{array}{l}\{s_{-2}(0.0114),s_{-1}(0.0210),\\ s_0(0.0686),s_1(0.0971),\\ s_2(0.8019)\}\end{array}$	$\begin{array}{l}\{s_{-2}(0.0019),s_{-1}(0.0495),\\ s_0(0.0305),s_1(0.1638),\\ s_2(0.7543)\}\end{array}$
$C_3$	$\begin{array}{l}\{s_{-2}(0.0753),s_{-1}(0.0635),\\ s_0(0.1341),s_1(0.2282),\\ s_2(0.4988)\}\end{array}$	$\begin{array}{l}\{s_{-2}(0.0134),s_{-1}(0.0582),\\ s_0(0.2075),s_1(0.2000),\\ s_2(0.5209)\}\end{array}$	$\begin{array}{l}\{s_{-2}(0.0136),s_{-1}(0.0250),\\ s_0(0.1386),s_1(0.2182),\\ s_2(0.6045)\}\end{array}$	$\begin{array}{l}\{s_{-2}(0.0171),s_{-1}(0.0267),\\ s_0(0.1029),s_1(0.1505),\\ s_2(0.7029)\}\end{array}$	$\begin{array}{l}\{s_{-2}(0.0210),s_{-1}(0.0495),\\ s_0(0.0686),s_1(0.2019),\\ s_2(0.6590)\}\end{array}$
$C_4$	$\begin{array}{l}\{s_{-2}(0.0118),s_{-1}(0.0471),\\ s_0(0.0588),s_1(0.2000),\\ s_2(0.6824)\}\end{array}$	$\begin{array}{l}\{s_{-2}(0.0179),s_{-1}(0.0552),\\ s_0(0.1149),s_1(0.1896),\\ s_2(0.6224)\}\end{array}$	$\begin{array}{l}\{s_{-2}(0.0023),s_{-1}(0.0250),\\ s_0(0.1045),s_1(0.1500),\\ s_2(0.7182)\}\end{array}$	$\begin{array}{l}\{s_{-1}(0.0190),s_0(0.0857),\\ s_1(0.1143),s_2(0.7810)\}\end{array}$	$\begin{array}{l}\{s_{-2}(0.0190),s_{-1}(0.0095),\\ s_0(0.0762),s_1(0.2095),\\ s_2(0.6857)\}\end{array}$
$C_5$	$\begin{array}{l}\{s_{-1}(0.0471),s_0(0.0824),\\ s_1(0.1176),s_2(0.7529)\}\end{array}$	$\begin{array}{l}\{s_{-2}(0.0239),s_{-1}(0.0612),\\ s_0(0.1806),s_1(0.1881),\\ s_2(0.5463)\}\end{array}$	$\begin{array}{l}\{s_{-2}(0.0136),s_{-1}(0.0023),\\ s_0(0.0818),s_1(0.0932),\\ s_2(0.8091)\}\end{array}$	$\begin{array}{l}\{s_{-2}(0.0095),s_{-1}(0.0286),\\ s_0(0.0571),s_1(0.0857),\\ s_2(0.8190)\}\end{array}$	$\begin{array}{l}\{s_{-2}(0.0095),s_0(0.0857),\\ s_1(0.0857),s_2(0.8190)\}\end{array}$
$C_6$	$\begin{array}{l}\{s_{-2}(0.0353),s_{-1}(0.0706),\\ s_0(0.1647),s_1(0.1882),\\ s_2(0.5412)\}\end{array}$	$\begin{array}{l}\{s_{-2}(0.0254),s_{-1}(0.0776),\\ s_0(0.2194),s_1(0.2642),\\ s_2(0.4134)\}\end{array}$	$\begin{array}{l}\{s_{-2}(0.0250),s_{-1}(0.0250),\\ s_0(0.1500),s_1(0.2977),\\ s_2(0.5023)\}\end{array}$	$\begin{array}{l}\{s_{-2}(0.0057),s_{-1}(0.0248),\\ s_0(0.0914),s_1(0.2343),\\ s_2(0.6438)\}\end{array}$	$\begin{array}{l}\{s_{-2}(0.0286),s_{-1}(0.0190),\\ s_0(0.0857),s_1(0.1333),\\ s_2(0.7333)\}\end{array}$
$C_7$	$\begin{array}{l}\{s_{-1}(0.0588),s_0(0.2588),\\ s_1(0.2706),s_2(0.4118)\}\end{array}$	$\begin{array}{l}\{s_{-2}(0.0164),s_{-1}(0.0836),\\ s_0(0.2030),s_1(0.3149),\\ s_2(0.3821)\}\end{array}$	$\begin{array}{l}\{s_{-2}(0.0136),s_{-1}(0.0932),\\ s_0(0.1841),s_1(0.1727),\\ s_2(0.5364)\}\end{array}$	$\begin{array}{l}\{s_{-2}(0.0210),s_{-1}(0.1162),\\ s_0(0.2400),s_1(0.2305),\\ s_2(0.3924)\}\end{array}$	$\begin{array}{l}\{s_{-2}(0.0667),s_{-1}(0.0762),\\ s_0(0.1810),s_1(0.2190),\\ s_2(0.4571)\}\end{array}$

Step 5. Determine attribute weights.

According to Equations (17)–(19), the normalized uncertainty degrees of each attribute are calculated as ${\overline{H}}_{JS}^{(1)}(C_1)=0.1428$, ${\overline{H}}_{JS}^{(1)}(C_2)=0.1429$, ${\overline{H}}_{JS}^{(1)}(C_3)=0.1428$, ${\overline{H}}_{JS}^{(1)}(C_4)=0.1429$, ${\overline{H}}_{JS}^{(1)}(C_5)=0.1428$, ${\overline{H}}_{JS}^{(1)}(C_6)=0.1428$, ${\overline{H}}_{JS}^{(1)}(C_7)=0.1429$. Subsequently, the balancing coefficient $\epsilon$ in Equation (25) is set to 0.5 and solved. Using Equations (26) and (27), the normalized attribute weight vector ${\overline{w}}^{(1)}$ is ${\overline{w}}^{(1)}={(0.1502,0.1168,0.1550,0.1089,0.1741,0.1893,0.1057)}^T$.

Step 6. Derive the weighted decision matrix.

In light of Equation (28) and the operations of PLTSs in Definition 2, the weighted decision matrix $D^{w(k)}={[x_{ij}^{(k)}]}_{m\times n}$ is derived. Please see Matrix A2 in Appendix A.

Step 7. Calculate the BPAs of alternatives on each attribute and the integrated BPAs.

By Equations (29)–(31), the BPAs of alternatives are calculated and shown in Table 9. Furthermore, the integrated BPAs are generated by Equation (32) as $m_C^{(1)}(A_1)=0.1612$, $m_C^{(1)}(A_2)=0.1071$, $m_C^{(1)}(A_3)=0.2119$, $m_C^{(1)}(A_4)=0.2640$, $m_C^{(1)}(A_5)=0.2550$, $m_C^{(1)}(\Theta )=0.0008$.

Table 9. BPAs of the alternatives with respect to attributes.

Alternative	${\mathit{C}}_1$	${\mathit{C}}_2$	${\mathit{C}}_3$	${\mathit{C}}_4$	${\mathit{C}}_5$	${\mathit{C}}_6$	${\mathit{C}}_7$
$A_1$	0.1672	0.1628	0.1473	0.1683	0.1722	0.1635	0.1651
$A_2$	0.1432	0.1494	0.1536	0.1549	0.1330	0.1358	0.1557
$A_3$	0.1636	0.1749	0.1743	0.1757	0.1828	0.1587	0.2028
$A_4$	0.1976	0.1896	0.1958	0.1889	0.1843	0.1909	0.1565
$A_5$	0.1856	0.1805	0.1862	0.1694	0.1847	0.2084	0.1769
$\Theta$	0.1428	0.1429	0.1428	0.1429	0.1428	0.1428	0.1429

Step 8. Compute the confidence values and plausibility values of alternatives.

In virtue of Equations (33) and (34), the confidence values and the plausibility values of alternatives, i.e., $Be{l}^{(1)}(A_i)$ and $P{l}^{(1)}(A_i)$, are computed and shown in Table 10.

Table 10. The confidence values and plausibility values of alternatives.

Value	${\mathit{A}}_1$	${\mathit{A}}_2$	${\mathit{A}}_3$	${\mathit{A}}_4$	${\mathit{A}}_5$
$Be{l}^{(1)}(A_i)$	0.1612	0.1071	0.2119	0.2640	0.2550
$P{l}^{(1)}(A_i)$	0.1620	0.1078	0.2127	0.2648	0.2558

Step 9. Calculate the possibility degrees of the support and trust intervals between alternatives.

By Equations (35) and (36), the possibility degree matrices associated with the support interval and trust interval are obtained as

$$\begin{gathered} C{P}^{(1)}(A_i\underset{\_}{\succ }{A}_t)=\left[\begin{array}{ccccc}0.5000& 0.6009& 0.4320& 0.3792& 0.3874\\ 0.3991& 0.5000& 0.3356& 0.2886& 0.2957\\ 0.5680& 0.6644& 0.5000& 0.4453& 0.4539\\ 0.6208& 0.7114& 0.5547& 0.5000& 0.5087\\ 0.6126& 0.7043& 0.5461& 0.4913& 0.5000\end{array}\right] \\ T{P}^{(1)}(A_i\underset{\_}{\succ }{A}_t)=\left[\begin{array}{ccccc}0.5& 1& 0& 0& 0\\ 0& 0.5& 0& 0& 0\\ 1& 1& 0.5& 0& 0\\ 1& 1& 1& 0.5& 1\\ 1& 1& 1& 0& 0.5\end{array}\right] \end{gathered}$$

Step10. Calculate the total possible degree of each alternative and rank alternatives in each website.

Taking $v=0.65$, the comprehensive possible degree matrix is calculated by Equation (37) as

$$P^{(1)}(A_i\underset{\_}{\succ }{A}_t)=\left[\begin{array}{ccccc}0.5000& 0.7406& 0.2808& 0.2465& 0.2518\\ 0.2594& 0.5000& 0.2182& 0.1876& 0.1922\\ 0.7192& 0.7818& 0.5000& 0.2895& 0.2950\\ 0.7535& 0.8124& 0.7105& 0.5000& 0.6806\\ 0.7482& 0.8078& 0.7050& 0.3194& 0.5000\end{array}\right]$$

Then, the total possibility degrees of alternatives are derived by Equation (38) as $P^{(1)}(A_1)=2.0197$, $P^{(1)}(A_2)=1.3574$, $P^{(1)}(A_3)=2.5855$, $P^{(1)}(A_4)=3.4571$, $P^{(1)}(A_5)=3.0803$.

According to the total possibility degrees of alternatives, the ranking order of alternatives for the website $t_1$ is $A_4\succ A_5\succ A_3\succ A_1\succ A_2$.

Similarly, repeating Steps 1 to 9, the ranking orders of alternatives for websites $t_2$ and $t_3$ are, respectively, obtained as $A_4\succ A_1\succ A_3\succ A_5\succ A_2$ and $A_5\succ A_4\succ A_3\succ A_1\succ A_2$.

Step 11. Determine the final ranking orders of alternatives and select the best one.

According to the 0–1 programming model in Equation (44), the collective ranking matrix $Y={(y_{ir})}_{m\times m}$ is yielded as

$$Y=\left[\begin{array}{cccc}0& 0& 0& \begin{array}{cc}1& 0\end{array}\\ 0& 0& 0& \begin{array}{cc}0& 1\end{array}\\ 0& 0& 1& \begin{array}{cc}0& 0\end{array}\\ \begin{array}{c}1\\ 0\end{array}& \begin{array}{c}0\\ 1\end{array}& \begin{array}{c}0\\ 0\end{array}& \begin{array}{cc}\begin{array}{c}0\\ 0\end{array}& \begin{array}{c}0\\ 0\end{array}\end{array}\end{array}\right]$$

Hence, the final ranking order is $A_4\succ A_5\succ A_3\succ A_1\succ A_2$ and the best alternative is BYD Han.

6. Sensitivity Analysis and Comparative Analysis

To demonstrate the advantages of the proposed method, this section conducts the sensitivity analysis of the balancing coefficient $\epsilon$ in the single-objective model (i.e., Equation (25)) and comparative analyses with existing methods.

6.1. Sensitivity Analysis of the Balancing Coefficient $\epsilon$

In Section 5.2, we take $\epsilon =0.5$. This section performs the sentiment analysis of $\epsilon$. By taking the value of $\epsilon$ from 0 to 0.9, the results are obtained and shown in Table 11.

Table 11. Sensitivity analysis results of the balancing coefficient $\epsilon$.

Parameter Settings	Attribute Weights	Alternative Rankings
$\epsilon =0$	$\begin{array}{l}{\overline{\mathit{w}}}^{(1)}=(0.1493,0.1218,0.1532,\\ 0.1151,0.1683,0.1801,0.1123{)}^T\end{array}$	$A_4\succ A_5\succ A_3\succ A_1\succ A_2$
$\epsilon =0.1$	$\begin{array}{l}{\overline{\mathit{w}}}^{(1)}=(0.1500,0.1180,0.1546,\\ 0.1105,0.1726,0.1870,0.1073{)}^T\end{array}$	$A_4\succ A_5\succ A_3\succ A_1\succ A_2$
$\epsilon =0.2$	$\begin{array}{l}{\overline{\mathit{w}}}^{(1)}=(0.1508,0.1118,0.1566,\\ 0.1029,0.1798,0.1987,0.0993{)}^T\end{array}$	$A_4\succ A_5\succ A_3\succ A_1\succ A_2$
$\epsilon =0.3$	$\begin{array}{l}{\overline{\mathit{w}}}^{(1)}=(0.1514,0.1019,0.1591,\\ 0.0913,0.1911,0.2181,0.0871{)}^T\end{array}$	$A_4\succ A_5\succ A_3\succ A_1\succ A_2$
$\epsilon =0.4$	$\begin{array}{l}{\overline{\mathit{w}}}^{(1)}=(0.1514,0.0997,0.1596,\\ 0.0888,0.1935,0.2225,0.0845{)}^T\end{array}$	$A_4\succ A_5\succ A_3\succ A_1\succ A_2$
$\epsilon =0.5$	$\begin{array}{l}{\overline{\mathit{w}}}^{(1)}=(0.1502,0.1168,0.1550,\\ 0.1089,0.1741,0.1893,0.1057{)}^T\end{array}$	$A_4\succ A_5\succ A_3\succ A_1\succ A_2$
$\epsilon =0.6$	$\begin{array}{l}{\overline{\mathit{w}}}^{(1)}=(0.1476,0.1290,0.1501,\\ 0.1242,0.1597,0.1671,0.1222{)}^T\end{array}$	$A_4\succ A_5\succ A_3\succ A_1\succ A_2$
$\epsilon =0.7$	$\begin{array}{l}{\overline{\mathit{w}}}^{(1)}=(0.1457,0.1353,0.1470,\\ 0.1326,0.1521,0.1559,0.1314{)}^T\end{array}$	$A_4\succ A_5\succ A_3\succ A_1\succ A_2$
$\epsilon =0.8$	$\begin{array}{l}{\overline{\mathit{w}}}^{(1)}=(0.1444,0.1389,0.1451,\\ 0.1375,0.1477,0.1496,0.1369{)}^T\end{array}$	$A_4\succ A_5\succ A_3\succ A_1\succ A_2$
$\epsilon =0.9$	$\begin{array}{l}{\overline{\mathit{w}}}^{(1)}=(0.1435,0.1413,0.1438,\\ 0.1406,0.1448,0.1456,0.1404{)}^T\end{array}$	$A_4\succ A_5\succ A_3\succ A_1\succ A_2$

As shown in Table 11, although the attribute weights change slightly with varying the values of $\epsilon$, the ranking results of alternatives remain unchanged all the time. This indicates the robustness of the proposed method.

6.2. Comparative Analysis

This section conducts comparative analyses from two aspects: one is to compare with existing NEV selection methods based on online reviews, and the other is to compare with MADM methods in the PLTS environment.

6.2.1. Comparation with Existing Car Selection Methods Based on Online Reviews

Comparing the proposed method with existing car selection methods [6,7,21], the comparative results are listed in Table 12.

Table 12. The comparison results with existing NEV selection methods based on online reviews.

Methods	Expression Forms	Rank Methods	The Number of Websites
Yang’s method [7]	q-ROFS	Prospect theory	Single
Tian’s method [6]	HIFS	ORESTE	Single
Liu’s method [21]	HPFS	TODIM-MULTIMOORA	Single
The proposed method	PLTS	Possible degree-based D–S evidence theory	Multiple websites

According to Table 12, the proposed method has the following merits:

(1)

The proposed method crawls online reviews from multiple websites, while existing NEVs selection methods [6,7,21] obtained online reviews from only one website. As different consumers prefer distinct platforms and online reviews in a single platform is limited, it is advisable to derive online reviews from several websites. At this point, the evaluation information collected by the proposed method is more sufficient, which is helpful for determining reasonable decision results.

(2)

The evaluation information extracted from online reviews by the proposed method is more precise and reliable because it is represented as PLTSs with five-granularity linguistic terms. The method [7] applied q-rung orthopair fuzzy sets (q-ROFSs) to express evaluation information. However, q-ROFSs only express the proportions of positive and negative sentiments but failed to distinguish comments which are neutral sentiments or do not provide any evaluation. Although the method [6] can handle comments without any evaluations by hesitant intuitionistic fuzzy sets (HIFSs), it is unable to express the strength of positive and negative sentiments. Converting sentiment scores into memberships of alternatives, Ref. [21] delt with online reviews into hesitant probabilistic fuzzy sets (HPFSs). Compared with methods [6,7], the method [21] represented online reviews more smoothly. Nevertheless, the decision information may be distorted when online reviews are transformed into sentiment scores. The proposed method describes evaluation information by five-granularity PLTSs, including very positive, positive, neutral, negative and very negative linguistic terms, which can not only retain natural language forms of sentiment orientations in online reviews, but also reflex strengths of different sentiments with their proportions. Hence, evaluation information derived by the proposed method is more precise and reliable.

6.2.2. Comparison with MADM Methods in the PLTS Environment

To further show the merits of the proposed method, it is compared with existing MADM methods in the PLTS environment [37,38,39]. By applying these methods, the problems in MADM are solved step by step, and these problems are listed in Table 13.

Table 13. Comparison results of the proposed method and existing methods in the PLTS context.

Methods	Decision Information	Determination of Attribute Weights	Attribute Weights	Decision Methods	Alternatives Ranking Orders
Du’s method [37]	Provided by DMs	Given subjectively	$\begin{array}{l}{\overline{\mathit{w}}}^{(1)}=(0.1502,0.1168,0.1550,\\ 0.1089,0.1741,0.1893,0.1057{)}^T\end{array}$	Prospect theory	$\begin{array}{l}{A}_4\succ A_5\succ \\ A_1\succ A_3\succ A_2\end{array}$
Li’s method [38]	Provided by DMs	Maximizing deviation	$\begin{array}{l}{\overline{\mathit{w}}}^{(1)}=(0.1493,0.1218,0.1532,\\ 0.1151,0.1683,0.1801,0.1123{)}^T\end{array}$	Operator based on D–S evidence	$\begin{array}{l}{A}_4\succ A_5\succ \\ A_3\succ A_1\succ A_2\end{array}$
Liang’s method [39]	Online reviews	AHP and deviation	$\begin{array}{l}{\overline{\mathit{w}}}^{(1)}=(0.1349,0.1405,0.1300,\\ 0.1364,0.1582,0.1855,0.1145{)}^T\end{array}$	Fuzzy comprehensive evaluation	$\begin{array}{l}{A}_4\succ A_5\succ \\ A_3\succ A_1\succ A_2\end{array}$
The proposed method	Online reviews	Uncertainty degree and maximum deviation	$\begin{array}{l}{\overline{\mathit{w}}}^{(1)}=(0.1502,0.1168,0.1550,\\ 0.1089,0.1741,0.1893,0.1057{)}^T\end{array}$	Possible degree-based D–S evidence	$\begin{array}{l}{A}_4\succ A_5\succ \\ A_3\succ A_1\succ A_2\end{array}$

Compared with methods [37,38,39], it can be observed from Table 13 that the proposed method has following advantages:

(1)

The decision information in the proposed method is more reliable because it is extracted from user online reviews on products. However, decision information in methods [37,38] are provided by several DMs. Due to the limited knowledge and experiences of DMs, the provided decision information may be limited and unable to represent general evaluations of most users.

(2)

The attribute weights in the proposed method are obtained by minimizing the uncertainty degrees of attributes as well as maximizing deviations between alternatives with respect to attributes. The method [37] gave attribute weights subjectively, which may greatly impact on alternative ranking orders. For example, when the attribute weights are assigned as the ones obtained by the proposed method, alternatives are sorted as $A_4\succ A_5\succ A_1\succ A_3\succ A_2$. However, when attribute weights are given as $w=(0.1964,0.0845,0.1000,0.1805,0.1482,0.1849,0.1055)$, the ranking order is $A_5\succ A_4\succ A_1\succ A_3\succ A_2$ and the best alternative changes $A_5$ from $A_4$. Although method [38] objectively determined attribute weights by maximizing deviation and method [39] fused AHP and deviation, they both neglected the uncertainty degrees of attributes. As decision information is based on online reviews in which there exists much uncertainty, it is more reasonable to consider uncertainty besides deviations between alternatives while deriving attribute weights.

(3)

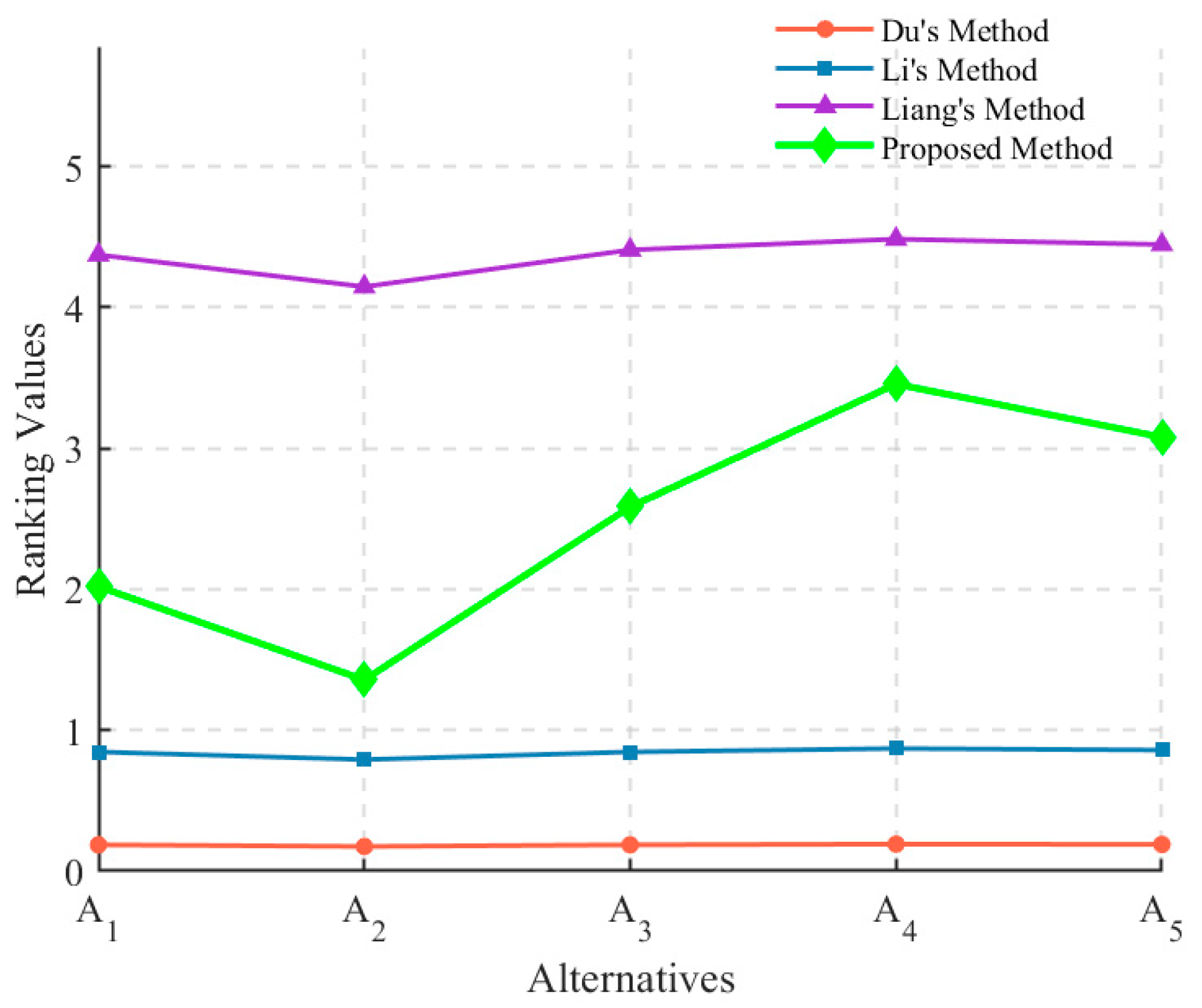
The proposed method is feasible and has a stronger distinguishing power while ranking alternatives. It can be seen from Table 13 the that alternative ranking order by the proposed method is similar with those derived by methods [37,38,39] and the best alternative is $A_4$. Furthermore, Observing Table 14, the Pearson correlation coefficients of alternative ranking orders are all greater than 0.9, which verifies the similarity of alternative ranking orders between the proposed method and existing ones. This illustrates the feasibility of the proposed method. Moreover, the distinguishing power of the proposed method is stronger, which can be described in Figure 5.

Table 14. Pearson correlation coefficients between methods.

	Du’s Method [37]	Li’s Method [38]	Liang’s Method [39]	The Proposed Method
Du’s method [37]	1.000	1.000	0.994	0.920
Li’s method [38]	1.000	1.000	0.995	0.918
Liang’s method [39]	0.994	0.995	1.000	0.927
The proposed method	0.920	0.918	0.927	1.000

Figure 5. Ranking order values of alternatives.

7. Conclusions

This paper addresses the NEV selection problems with online reviews and proposes a novel MADM method based on the sentiment analyses and the possible degree based D–S evidence theory in the PLTS environment. First, online customer reviews on NEVs are crawled from multiple websites and transformed into five granularity PLTSs with the sentiment analysis technique. The difference of this technique from existing ones is that it considers the degree adverb words and negation words besides sentiment words, so it retains the initial linguistic evaluations rather than computing sentiment scores. Afterwards, by maximizing the deviations between alternatives and minimizing the uncertainty, a bi-objective programming model is constructed to determine attribute weights objectively. Finally, a possible degree-based D–S evidence theory method in the PLTS context is proposed to rank the alternatives for each website. Then, a 0–1 programming model is built to fuse ranking orders in each website into a final one. Comparative analyses show the merits of the proposed method compared with existing ones.

Although the proposed method resolves the NEV selection problem and can be extended into other fields, such as hotel selection and education evaluation, it has some room for improvement. For example, the proposed method only considers the decision information in the online reviews without inviting experts into decision making. Although online reviews can provide abundant information, this type of information may not be professional enough. Therefore, in the future, we will fuse the online review with large-scale expert information [40] and develop a new methodology by considering the consensus between these two types of decision information.