An Efficient Iterative Scheme for Approximating the Fixed Point of a Function Endowed with Condition (B_γ,μ) Applied for Solving Infectious Disease Models

Abstract

The purpose of this paper is to construct a new fixed-point iterative scheme, called the Picard-like iterative scheme, for approximating the fixed point of a mapping that satisfies condition $(B_{\gamma ,\mu })$ in the setting of a uniformly convex Banach space. We prove that this novel iterative scheme converges faster than some existing iterative schemes in the literature. Moreover, $\mathcal{G}$-stability and almost $\mathcal{G}$-stability results are proven. Furthermore, we apply our results for approximating the solution of an integral equation that models the spread of some infectious diseases. Similarly, we also applied the results for approximating the solution of the boundary value problem by embedding Green’s function in our novel method. Our results extend and generalize other existing results in the literature.

1. Introduction

Let $\mathcal{D}$ be a subset of a uniformly convex Banach space X. A self mapping $\mathcal{G}:\mathcal{D}\to \mathcal{D}$ is a mapping satisfying condition (C) on the subset $\mathcal{D}$, if

$${\displaystyle \frac{1}{2}}\parallel x-\mathcal{G}x\parallel \le \parallel x-y\parallel \Rightarrow \parallel \mathcal{G}x-\mathcal{G}y\parallel \le \parallel x-y\parallel ,$$

for all $x,y\in \mathcal{D}$.

The mapping satisfying condition (C) was introduced by Suzuki [1] in 2008 as an extension and generalization of nonexpansive mappings. Furthermore, this class of nonlinear mappings is known to be weaker than mappings with nonexpansiveness and stronger than mappings with quasi-nonexpansiveness.

In 2011, García-Falset et al. [2] introduced a more general mapping than the Suzuki’s mappings satisfying condition (C). It was described as a mapping satisfying condition (E) or the García-Falset mapping on $\mathcal{D}$, and defined as

$$\parallel x-\mathcal{G}y\parallel \le \mu \parallel x-\mathcal{G}x\parallel +\parallel x-y\parallel$$

for all $x,y\in \mathcal{D}$ and $\mu \ge 1$. Patir et al. [3], in 2018, introduced a class of generalized two-parameter nonexpansive mapping known as mapping satisfying condition $(B_{\gamma ,\mu })$, and proved that it was wider than mappings satisfying condition (C) of Suzuki [1]. This class of mapping is defined as follows:

Definition 1

([3]). Let $\mathcal{D}$ be a subset of a uniformly convex Banach space, X. A mapping $\mathcal{G}:\mathcal{D}\to \mathcal{D}$ satisfies condition $(B_{\gamma ,\mu })$ if for any two elements $x,y\in \mathcal{D}$, one can choose a $\gamma \in [0,1]$ and some $\mu \in [0,{\displaystyle \frac{1}{2}}]$ with $2\mu \le \gamma$, such that

$$\gamma \parallel x-\mathcal{G}x\parallel \le \parallel x-y\parallel +\mu \parallel y-\mathcal{G}y\parallel$$

implies

$$\parallel \mathcal{G}x-\mathcal{G}y\parallel \le (1-\gamma )\parallel x-y\parallel +\mu (\parallel x-\mathcal{G}y\parallel +\parallel y-\mathcal{G}x\parallel ).$$

Natural processes form the basis of understanding the world around us, encompassing phenomena such as the motion of objects, heat transfer, fluid dynamics, and more. These processes, governed by principles of motion and change, provide insights into the laws of nature and are essential for scientific and technological advancements. To describe such phenomena quantitatively, we rely on mathematical tools, with differential equations playing a central role.

Differential equations, whether ordinary or partial, of an integer or fractional order, allow us to model these processes mathematically. The classification of these equations depends on the order of the differential coefficient and the number of independent variables involved. Such equations are often accompanied by initial conditions or boundary conditions, leading to either initial value problems (IVPs) or boundary value problems (BVPs).

Once a natural phenomenon is modeled using differential equations, the next critical step is to determine its solution using appropriate mathematical methods, unlocking deeper understanding and practical applications.

Fixed-point theory is an important tool for solving differential equations, particularly for proving the existence and uniqueness of solutions, including the approximation of the solution through the use of an iterative scheme (see for example [4,5,6] and other literature). This theory revolves around the concept of obtaining a point x called the fixed point, such that $\mathcal{G}x=x$ for any mapping $\mathcal{G}:\mathcal{D}\to \mathcal{D}$, where $\mathcal{D}\in X$.

Fixed-point theory has been applied for solving several problems including BVP, which involves the use of Green’s function (see [7,8,9,10,11] and the references therein).

The objective of this work is to construct an effective fixed-point iterative scheme that performs better than some existing iterative schemes for a mapping satisfying condition $(B_{\gamma ,\mu })$ in a way to generalize and extend them. We apply it for solving a third-order BVP via Green’s function with series of numerical examples and illustrations. Furthermore, we apply it for approximating the solution of an integral equation modeling the spread of certain infectious diseases with a periodic contact rate with seasonal variations.

The rest of this paper is arranged such that in Section 2, preliminary facts, definitions, and lemmas are presented. Section 3 contains the main results, which include weak and strong convergence theorems and where the stability/almost stability of the new iterative scheme are considered. In Section 4, the application of the new iterative scheme to an infectious disease model is considered. Section 5 applies a boundary value problem of the third order via Green’s function. Finally, Section 6 provides the conclusion.

2. Preliminaries

While fixed-point theory is very instrumental in proving the existence and uniqueness of solutions for differential equations transformed to an operator equation, it can also be used to approximate the solutions by using a fixed-point iterative scheme.

In 2018, Ullah and Arshad [12] introduced the M iterative scheme, as follows:

$$\left\{\begin{array}{c}{u}_0\in \mathcal{D}\hfill \\ w_n=(1-{\alpha }_n)u_n+{\alpha }_n\mathcal{G}{u}_n\hfill \\ v_n=\mathcal{G}{w}_n\hfill \\ u_{n+1}=\mathcal{G}{v}_n,n\in \mathbb{N},\hfill \end{array}\right.$$

(1)

where $\{{\alpha }_n\}$ is a real sequence in $[0,1]$. The scheme was used to prove weak and strong convergence theorems for Suzuki-generalized nonexpansive mapping in the framework of uniformly convex Banach spaces.

Gürsoy et al. [13], in 2014, introduced an iterative scheme called the Picard-S, defined as follows:

$$\left\{\begin{array}{c}{u}_0\in \mathcal{D}\hfill \\ w_n=(1-{\beta }_n)u_n+{\beta }_n\mathcal{G}{u}_n\hfill \\ v_n=(1-{\alpha }_n)\mathcal{G}{u}_n+{\alpha }_n\mathcal{G}{w}_n\hfill \\ u_{n+1}=\mathcal{G}{v}_n,n\in \mathbb{N}.\hfill \end{array}\right.$$

(2)

Abbas et al. (2022) [14] constructed the AA iterative scheme, which is defined as follows:

$$\left\{\begin{array}{c}{u}_0\in \mathcal{D}\hfill \\ x_n=(1-{\alpha }_n)u_n+{\alpha }_n\mathcal{G}{u}_n\hfill \\ w_n=\mathcal{G}[(1-{\beta }_n)x_n+{\beta }_n\mathcal{G}{x}_n]\hfill \\ v_n=\mathcal{G}[(1-{\gamma }_n)\mathcal{G}{x}_n+{\gamma }_n\mathcal{G}{w}_n]\hfill \\ u_{n+1}=\mathcal{G}{v}_n,n\in \mathbb{N}.\hfill \end{array}\right.$$

(3)

They used this iterative scheme to approximate the fixed point of $(b,\eta )$-enriched contraction mapping in the framework of Banach spaces and applied it for approximating the solution to a delay fractional differential equation.

In 2018, Ullah and Arshad [15] proposed a new iteration process called the $K^{\ast }$ iteration process, defined as:

$$\left\{\begin{array}{c}{u}_0\in \mathcal{D}\hfill \\ w_n=(1-{\beta }_n)u_n+{\beta }_n\mathcal{G}{u}_n\hfill \\ v_n=\mathcal{G}((1-{\alpha }_n)w_n+{\alpha }_n\mathcal{G}{w}_n)\hfill \\ u_{n+1}=\mathcal{G}{v}_n,n\in \mathbb{N}.\hfill \end{array}\right.$$

(4)

The authors used this iterative scheme to approximate the fixed point of a Suzuki-generalized nonexpansive mapping in the setting of uniformly convex Banach spaces.

Recently, in 2024, Ullah et al. [16] used the $K^{\ast }$ iteration process (4) to approximate the fixed point of mapping, satisfying condition $(B_{\gamma ,\mu })$ in the setting of Banach space.

Motiveted by the foregoing, we propose a new fixed-point iterative scheme called the Picard-like iterative scheme, as follows:

$$\left\{\begin{array}{c}{u}_0\in \mathcal{D}\hfill \\ x_n=\mathcal{G}[(1-{\alpha }_n)u_n+{\alpha }_n\mathcal{G}{u}_n]\hfill \\ w_n={\mathcal{G}}^2{x}_n\hfill \\ v_n={\mathcal{G}}^2{w}_n\hfill \\ u_{n+1}={\mathcal{G}}^2{v}_n,n\in \mathbb{N}.\hfill \end{array}\right.$$

(5)

Next, we consider some definitions and lemmas that will be useful in the sequel.

Definition 2

([17,18]). Let $\mathcal{D}$ be a nonempty closed convex subset of a Banach space X and $\{u_n\}$ be a bounded sequence in X. For each $u\in X$, we define

(a) 

asymptotic radius of $\{u_n\}$ at u as a functional, $\mathcal{R}(·,\{u_n\}):X\to {\mathbb{R}}_{+}$ defined by $\mathcal{R}(u,\{u_n\})=\underset{n\to \infty }{lim\; sup}\parallel u-u_n\parallel$,

(b) 

asymptotic radius of $\{u_n\}$ relative to the set $\mathcal{D}$ by

$$\mathcal{R}(\mathcal{D},\{u_n\})=inf\{\mathcal{R}(u,\{u_n\}):u\in \mathcal{D}\},\mathit{and}$$

(c) 

asymptotic center of $\{u_n\}$ relative to the set $\mathcal{X}$ by

$$\mathcal{A}(\mathcal{D},\{u_n\})=\{u\in X:\mathcal{R}(u,\{u_n\})=\mathcal{R}(\mathcal{D},\{u_n\})\}.$$

Definition 3

([18]). A Banach space X is said to satisfy the Opial condition [19] if, for each sequence $\{u_n\}$ in X, converging weakly to $u\in X$, we have

$$\underset{n\to \infty }{lim\; sup}\parallel u_n-u\parallel <\underset{n\to \infty }{lim\; sup}\parallel u_n-w\parallel ,$$

(6)

for all $w\in X$, such that $u\ne w$.

Definition 4

([20]). A mapping $\mathcal{G}:\mathcal{D}\to \mathcal{D}$ with $\mathcal{F}(\mathcal{G})\ne \varnothing$ is said to satisfy condition (I) if there exists a nondecreasing function $h:[0,\infty )\to [0,\infty )$ with $h(0)=0$, $h(s)>0$ for $s\in (0,\infty )$, such that $\parallel u-\mathcal{G}u\parallel \ge h(\rho (u,\mathcal{F}(\mathcal{G})))$ for all $u\in \mathcal{D}$, where $\rho (u,\mathcal{F}(\mathcal{G}))=inf\{\parallel u-\tau \parallel :\tau \in \mathcal{F}(\mathcal{G})\}$.

Definition 5

([21]). Let $\mathcal{G}:\mathcal{D}\to \mathcal{G}$ be an operator on a real Banach space X. Assume that $u_n\in \mathcal{B}$ and $u_{n+1}=f(\mathcal{G},u_n)$ defines an iterative scheme that generates a sequence ${\{u_n\}}_{n=0}^{\infty }$ in $\mathcal{D}$. Assume, furthermore, that ${\{u_n\}}_{n=0}^{\infty }$ converges strongly to ${\tau }^{\ast }\in \mathcal{F}(\mathcal{G})\ne \varnothing$, where $\mathcal{F}(\mathcal{G})$ is the set of all fixed points of $\mathcal{G}$. Assume that ${\{s_n\}}_{n=0}^{\infty }$ is an arbitrary bounded sequence in X and set ${ϵ}_n=\parallel s_{n+1}-f(\mathcal{G},s_n)\parallel$. Then,

1. 

the iterative scheme ${\{u_n\}}_{n=0}^{\infty }$ in a real Banach space X, defined by $u_{n+1}=f(\mathcal{G},u_n)$, is said to be $\mathcal{G}$-stable or stable with respect to $\mathcal{G}$ if $\underset{n\to \infty }{lim}{ϵ}_n=0$ implies $\underset{n\to \infty }{lim}\parallel p_n-{\tau }^{\ast }\parallel =0$

2. 

the iterative scheme ${\{u_n\}}_{n=0}^{\infty }$ defined by $u_{n+1}=f(\mathcal{G},u_n)$ is said to be almost $\mathcal{G}$-stable if ${\sum }_{n=0}^{\infty }{ϵ}_n<\infty$ implies that $\underset{n\to \infty }{lim}\parallel s_n-{\tau }^{\ast }\parallel =0$.

Lemma 1

([3]). Let $\mathcal{D}$ be a nonempty subset of a Banach space X with an Opial condition and $\mathcal{G}:\mathcal{D}\to \mathcal{D}$ is a mapping satisfying condition ($B_{\gamma ,\mu }$). If ${\tau }^{\ast }$ is a fixed point of $\mathcal{G}$, then for each $x\in \mathcal{D}$,

$$\parallel {\tau }^{\ast }-\mathcal{G}x\parallel \le \parallel {\tau }^{\ast }-x\parallel .$$

Lemma 2

([22]). Let X be a uniformly convex Banach space and ${\{{\alpha }_n\}}_{n=0}^{\infty }$ be any sequence of numbers, such that $0<a\le {\alpha }_n\le b<1$, $n\ge 1$, for $a,b\in \mathbb{R}$. Let ${\{u_n\}}_{n=0}^{\infty }$ and ${\{r_n\}}_{n=0}^{\infty }$ be sequences in X, such that $\underset{n\to \infty }{lim\; sup}\parallel u_n\parallel \le \lambda$, $\underset{n\to \infty }{lim\; sup}\parallel r_n\parallel \le \lambda$ and $\underset{n\to \infty }{lim\; sup}\parallel {\alpha }_n{u}_n+(1-{\alpha }_n)r_n\parallel =\lambda$ for some $\lambda \ge 0$. Then, $\underset{n\to \infty }{lim}\parallel u_n-r_n\parallel =0$.

Proposition 1

([3]). Let $\mathcal{D}$ be a nonempty subset of a Banach space X. Suppose that $\mathcal{G}:\mathcal{D}\to \mathcal{D}$ is a mapping satisfying condition $(B_{\gamma ,\mu })$ on $\mathcal{D}$. Then, for all $x,y\in \mathcal{D}$ and for $0\le \lambda \le 1$,

1. 

$\parallel \mathcal{G}x-{\mathcal{G}}^{2}x\parallel \le \parallel x-\mathcal{G}x\parallel$

2. 

at least one of the following holds:

(i) 

${\displaystyle \frac{\lambda }{2}}\parallel x-\mathcal{G}x\parallel \le \parallel x-y\parallel$

(ii) 

${\displaystyle \frac{\lambda }{2}}\parallel \mathcal{G}x-{\mathcal{G}}^{2}x\parallel \le \parallel \mathcal{G}x-y\parallel$.

The condition $(i)$ implies $\parallel \mathcal{G}x-\mathcal{G}y\parallel \le (1-{\displaystyle \frac{\lambda }{2}})\parallel x-y\parallel +\mu (\parallel x-\mathcal{G}y\parallel +\parallel y-\mathcal{G}x\parallel )$ and condition $(ii)$ implies $\parallel {\mathcal{G}}^{2}x-\mathcal{G}y\parallel \le (1-{\displaystyle \frac{\lambda }{2}})\parallel \mathcal{G}x-y\parallel +\mu (\parallel \mathcal{G}x-\mathcal{G}y\parallel +\parallel y-{\mathcal{G}}^{2}x\parallel )$.

3. 

$\parallel x-\mathcal{G}y\parallel \le (3-\lambda )\parallel x-\mathcal{G}x\parallel +(1-{\displaystyle \frac{\lambda }{2}})\parallel x-y\parallel +\mu (2\parallel x-\mathcal{G}x\parallel +\parallel x-\mathcal{G}y\parallel +\parallel y-\mathcal{G}x\parallel +2\parallel \mathcal{G}x-{\mathcal{G}}^{2}x\parallel )$

Lemma 3

([23]). If $\varpi \in [0,1]$ is a real number and ${\{{ϵ}_n\}}_{n=0}^{\infty }$ is a sequence of positive numbers, such that $\underset{n\to \infty }{lim}{ϵ}_n=0$, then for any sequence of positive numbers, ${\{s_n\}}_{n=0}^{\infty }$ satisfying $s_{n+1}\le \varpi s_n+{ϵ}_n,(n=0,1,2,\dots )$, such that $\underset{n\to \infty }{lim}{s}_n=0$.

Lemma 4

([24]). Let ${\{{\eta }_n\}}_{n=0}^{\infty }$ and ${\{{ϵ}_n\}}_{n=0}^{\infty }$ be sequences of nonnegative numbers and $\delta \in [0,1]$, such that

$${\eta }_{n+1}=\delta {\eta }_n+{ϵ}_{n}n\ge 0.$$

If ${\sum }_{n=0}^{\infty }{ϵ}_n<\infty$, then ${\sum }_{n=0}^{\infty }{\eta }_n<\infty$.

Lemma 5

([3]). Assume $\mathcal{D}$ is a nonempty subset of a Banach space X endowed with the Opial property. Assume $\mathcal{G}:\mathcal{D}\to \mathcal{D}$ is a mapping satisfying condition $(B_{\gamma ,\mu })$. If $\{u_n\}$ is a sequence in X, such that

1. 

$\{u_n\}$ converges weakly to τ,

2. 

$\underset{n\to \infty }{lim}\parallel \mathcal{G}{u}_n-u_n\parallel =0$,

then $\mathcal{G}\tau =\tau$.

Proposition 2

([25]). Assume that $\mathcal{D}$ is any nonempty closed subset of a Banach space and $\{u_n\}$ be any Fejer-monotone sequence in the set $\mathcal{D}$. Then, $\{u_n\}$ converges strongly to the point of $\mathcal{D}$, if and only if $\underset{n\to \infty }{lim}\rho (u_n,\mathcal{D})=0$.

3. Main Results

3.1. Weak and Strong Convergence Theorems

Before stating the main results of this section, it suffices to state and prove the following lemmas, which will be helpful for proving the main results.

Lemma 6.

Let $\mathcal{D}$ be a nonempty closed convex subset of a Banach space X and $\mathcal{G}:\mathcal{D}\to \mathcal{D}$ is a mapping satisfying condition $(B_{\gamma ,\mu })$ with $\mathcal{F}(\mathcal{G})\ne \varnothing$. Suppose $\{u_n\}$ is a sequence generated by the iterative scheme (5), then $\underset{n\to \infty }{lim}\parallel u_n-{\tau }^{\ast }\parallel$ exists for each ${\tau }^{\ast }\in \mathcal{F}(\mathcal{G})$.

Proof. 

Let ${\tau }^{\ast }\in \mathcal{F}(\mathcal{G})$ be a fixed point. By Lemma 1, and using (5), we have,

$$\begin{array}{cc}\hfill \parallel x_n-{\tau }^{\ast }\parallel & =\parallel \mathcal{G}[(1-{\alpha }_n)u_n+{\alpha }_n\mathcal{G}{u}_n]-{\tau }^{\ast }\parallel \hfill \\ & \le \parallel (1-{\alpha }_n)u_n+{\alpha }_n\mathcal{G}{u}_n-{\tau }^{\ast }\parallel \hfill \\ & \le (1-{\alpha }_n)\parallel u_n-{\tau }^{\ast }\parallel +{\alpha }_n\parallel \mathcal{G}{u}_n-{\tau }^{\ast }\parallel \hfill \\ & \le (1-{\alpha }_n)\parallel u_n-{\tau }^{\ast }\parallel +{\alpha }_n\parallel u_n-{\tau }^{\ast }\parallel \hfill \\ & =\parallel u_n-{\tau }^{\ast }\parallel .\hfill \end{array}$$

(7)

Using (5) and (7)

$$\begin{array}{cc}\hfill \parallel w_n-{\tau }^{\ast }\parallel & =\parallel \mathcal{G}\left[\mathcal{G}{x}_n\right]-{\tau }^{\ast }\parallel \hfill \\ & \le \parallel \mathcal{G}{x}_n-{\tau }^{\ast }\parallel \hfill \\ & \le \parallel x_n-{\tau }^{\ast }\parallel \hfill \\ & =\parallel u_n-{\tau }^{\ast }\parallel \hfill \end{array}$$

(8)

and

$$\begin{array}{cc}\hfill \parallel v_n-{\tau }^{\ast }\parallel & =\parallel \mathcal{G}\left[\mathcal{G}{w}_n\right]-{\tau }^{\ast }\parallel \hfill \\ & \le \parallel \mathcal{G}{w}_n-{\tau }^{\ast }\parallel \hfill \\ & \le \parallel w_n-{\tau }^{\ast }\parallel \hfill \end{array}$$

(9)

Combining (5), (8) and (9), we have

$$\begin{array}{cc}\hfill \parallel u_{n+1}-{\tau }^{\ast }\parallel & =\parallel \mathcal{G}\left[\mathcal{G}{v}_n\right]-{\tau }^{\ast }\parallel \hfill \\ & \le \parallel \mathcal{G}{v}_n-{\tau }^{\ast }\parallel \hfill \\ & \le \parallel v_n-{\tau }^{\ast }\parallel \hfill \\ & \le \parallel u_n-{\tau }^{\ast }\parallel .\hfill \end{array}$$

As we have shown that $\parallel u_{n+1}-{\tau }^{\ast }\parallel \le \parallel u_n-{\tau }^{\ast }\parallel$, it follows that $\{\parallel u_n-{\tau }^{\ast }\parallel \}$ is bounded and nonincreasing. Hence, for all ${\tau }^{\ast }\in \mathcal{F}(\mathcal{G})\ne \varnothing$, $\underset{n\to \infty }{lim}\parallel u_n-{\tau }^{\ast }\parallel$ exists, thereby completing the proof. □

Lemma 7.

Assume $\mathcal{D}$ is a nonempty closed convex subset of a uniformly convex Banach space X and $\mathcal{G}:\mathcal{D}\to \mathcal{D}$ is a mapping satisfying condition $(B_{\gamma ,\mu })$, if $\{u_n\}$ is a sequence generated by the iterative scheme (5). Then, $\mathcal{F}(\mathcal{G})\ne \varnothing$ if and only if $\{u_n\}$ is bounded and $\underset{n\to \infty }{lim}\parallel \mathcal{G}{u}_n-u_n\parallel =0$.

Proof. 

Suppose that $\mathcal{F}(\mathcal{G})\ne \varnothing$ and ${\tau }^{\ast }\in \mathcal{F}(\mathcal{G})$ is a fixed point. Then, by Lemma 6, we have that $\underset{n\to \infty }{lim}\parallel u_n-{\tau }^{\ast }\parallel$ exists and $\{u_n\}$ is bounded.

Let $\omega$ be a real value,

$$\underset{n\to \infty }{lim}\parallel u_n-{\tau }^{\ast }\parallel =\omega$$

(10)

From (7)–(9) as in the proof of Lemma 6, together with (10), we have

$$\underset{n\to \infty }{lim\; sup}\parallel x_n-{\tau }^{\ast }\parallel \le \underset{n\to \infty }{lim\; sup}\parallel u_n-{\tau }^{\ast }\parallel \le \omega ,$$

(11)

$$\underset{n\to \infty }{lim\; sup}\parallel w_n-{\tau }^{\ast }\parallel \le \underset{n\to \infty }{lim\; sup}\parallel u_n-{\tau }^{\ast }\parallel \le \omega .$$

(12)

and

$$\underset{n\to \infty }{lim\; sup}\parallel v_n-{\tau }^{\ast }\parallel \le \underset{n\to \infty }{lim\; sup}\parallel u_n-{\tau }^{\ast }\parallel \le \omega .$$

(13)

By Lemma 1, we have that

$$\parallel \mathcal{G}{u}_n-{\tau }^{\ast }\parallel \le \parallel u_n-{\tau }^{\ast }\parallel ,$$

(14)

and

$$\underset{n\to \infty }{lim\; sup}\parallel \mathcal{G}{u}_n-{\tau }^{\ast }\parallel \le \underset{n\to \infty }{lim\; sup}\parallel u_n-{\tau }^{\ast }\parallel =\omega .$$

(15)

Now,

$$\begin{array}{cc}\hfill \parallel u_{n+1}-{\tau }^{\ast }\parallel & =\parallel {\mathcal{G}}^2{v}_n-{\tau }^{\ast }\parallel \hfill \\ & \le \parallel \mathcal{G}{v}_n-{\tau }^{\ast }\parallel \hfill \\ & \le \parallel v_n-{\tau }^{\ast }\parallel \hfill \end{array}$$

(16)

Again from Lemma 1, together with (10), we have

$$\omega =\underset{n\to \infty }{lim\; inf}\parallel u_{n+1}-{\tau }^{\ast }\parallel \le \underset{n\to \infty }{lim\; inf}\parallel v_n-{\tau }^{\ast }\parallel .$$

(17)

It can immediately follow from (13) and (17) that

$$\omega =\underset{n\to \infty }{lim\; inf}\parallel v_n-{\tau }^{\ast }\parallel \le \underset{n\to \infty }{lim\; sup}\parallel v_n-{\tau }^{\ast }\parallel \le \omega$$

and we have

$$\underset{n\to \infty }{lim}\parallel v_n-{\tau }^{\ast }\parallel =\omega$$

(18)

From (18), we also have

$$\omega =\underset{n\to \infty }{lim\; inf}\parallel v_n-{\tau }^{\ast }\parallel \le \underset{n\to \infty }{lim\; inf}\parallel w_n-{\tau }^{\ast }\parallel ,$$

which follows that

$$\omega \le \underset{n\to \infty }{lim\; inf}\parallel w_n-{\tau }^{\ast }\parallel \le \underset{n\to \infty }{lim\; sup}\parallel w_n-{\tau }^{\ast }\parallel \le \omega .$$

$$\underset{n\to \infty }{lim}\parallel w_n-{\tau }^{\ast }\parallel =\omega$$

(19)

and

$$\begin{array}{cc}\hfill \parallel w_n-{\tau }^{\ast }\parallel & =\parallel {\mathcal{G}}^2{x}_n-{\tau }^{\ast }\parallel \hfill \\ & \le \parallel \mathcal{G}{x}_n-{\tau }^{\ast }\parallel \hfill \\ & \le \parallel x_n-{\tau }^{\ast }\parallel .\hfill \end{array}$$

That is,

$$\parallel w_n-{\tau }^{\ast }\parallel \le \parallel x_n-{\tau }^{\ast }\parallel$$

(20)

Taking lim inf on both sides, we have

$$\omega \le \underset{n\to \infty }{lim\; inf}\parallel w_n-{\tau }^{\ast }\parallel \le \underset{n\to \infty }{lim\; inf}\parallel x_n-{\tau }^{\ast }\parallel$$

(21)

Using (11) and (21), we have

$$\omega \le \underset{n\to \infty }{lim\; inf}\parallel w_n-{\tau }^{\ast }\parallel \le \underset{n\to \infty }{lim\; sup}\parallel x_n-{\tau }^{\ast }\parallel \le \omega$$

and

$$\underset{n\to \infty }{lim}\parallel x_n-{\tau }^{\ast }\parallel =\omega .$$

(22)

From (22)

$$\begin{array}{cc}\hfill \omega & =\underset{n\to \infty }{lim}\parallel x_n-{\tau }^{\ast }\parallel \hfill \\ & =\underset{n\to \infty }{lim}\parallel \mathcal{G}[(1-{\alpha }_n)u_n+{\alpha }_n\mathcal{G}{u}_n]-{\tau }^{\ast }\parallel \hfill \\ & \le \underset{n\to \infty }{lim}\parallel (1-{\alpha }_n)u_n+{\alpha }_n\mathcal{G}{u}_n-{\tau }^{\ast }\parallel \hfill \\ & \le \underset{n\to \infty }{lim}\parallel (1-{\alpha }_n)(u_n-{\tau }^{\ast })+{\alpha }_n(\mathcal{G}{u}_n-{\tau }^{\ast })\parallel .\hfill \end{array}$$

(23)

With (10), (15) and (23) in sight and applying Lemma 2, it is clear that $\underset{n\to \infty }{lim}\parallel \mathcal{G}{u}_n-u_n\parallel =0.$

• Conversely, assume that $\{u_n\}$ is bounded and $\underset{n\to \infty }{lim}\parallel \mathcal{G}{u}_n-u_n\parallel =0$. We can show that $\mathcal{F}(\mathcal{G})\ne \varnothing$. To do that, let ${\tau }^{\ast }\in \mathcal{A}(\mathcal{D},\{u_n\})$. Applying (3) of Proposition 1 for $\gamma ={\displaystyle \frac{\omega }{2}}$, $\omega \in [0,1]$,

$$\begin{array}{cc}\hfill \parallel u_n-\mathcal{G}{\tau }^{\ast }\parallel & \le (3-\omega )\parallel u_n-\mathcal{G}{u}_n\parallel +\left({\displaystyle \frac{1-\omega }{2}}\right)\parallel u_n-{\tau }^{\ast }\parallel +\mu (2\parallel u_n-\mathcal{G}{u}_n\parallel \hfill \\ & +\parallel u_n-\mathcal{G}{\tau }^{\ast }\parallel +\parallel {\tau }^{\ast }-\mathcal{G}{u}_n\parallel +2\parallel \mathcal{G}{u}_n-{\mathcal{G}}^2\parallel )\hfill \\ & \le (3-\omega )\parallel u_n-\mathcal{G}{u}_n\parallel +\left({\displaystyle \frac{1-\omega }{2}}\right)\parallel u_n-{\tau }^{\ast }\parallel +\mu (2\parallel u_n-\mathcal{G}{u}_n\parallel \hfill \\ & +\parallel u_n-\mathcal{G}{\tau }^{\ast }\parallel +\parallel u_n-{\tau }^{\ast }\parallel +\parallel u_n-\mathcal{G}{u}_n\parallel +2\parallel \mathcal{G}{u}_n-{\mathcal{G}}^2{u}_n\parallel ).\hfill \end{array}$$

Again, by condition (2) of Proposition 1, it follows that

$$(1-\mu )\underset{n\to \infty }{lim\; sup}\parallel u_n-\mathcal{G}{\tau }^{\ast }\parallel \le \left(1-{\displaystyle \frac{\omega }{2}}+\mu \right)\underset{n\to \infty }{lim\; sup}\parallel x_n-{\tau }^{\ast }\parallel$$

or

$$\underset{n\to \infty }{lim\; sup}\parallel u_n-\mathcal{G}{\tau }^{\ast }\parallel \le \left({\displaystyle \frac{1-\frac{\omega }{\mu }+\mu }{1-\mu }}\right)\underset{n\to \infty }{lim\; sup}\parallel x_n-{\tau }^{\ast }\parallel$$

As ${\displaystyle \frac{1-\frac{\omega }{\mu }+\mu }{1-\mu }}\le 1$, for $2\mu \le \gamma ={\displaystyle \frac{\omega }{2}}$, then

$$\underset{n\to \infty }{lim\; sup}\parallel u_n-\mathcal{G}{\tau }^{\ast }\parallel \le \underset{n\to \infty }{lim\; sup}\parallel u_n-{\tau }^{\ast }\parallel ,$$

it follows that

$$\mathcal{R}(\mathcal{G}{\tau }^{\ast },\{u_n\})\le \mathcal{R}({\tau }^{\ast },\{u_n\}).$$

That is, $\mathcal{G}{\tau }^{\ast }\in \mathcal{A}(\mathcal{D},\{u_n\})$. As the set $\mathcal{A}(\mathcal{D},\{u_n\})$ is singleton, then, it follows that $\mathcal{G}{\tau }^{\ast }={\tau }^{\ast }$. Hence, completing the proof. □

Theorem 1.

Suppose $\mathcal{D}$ is a nonempty closed subset of a uniformly convex Banach space X satisfying the Opial condition (6). Assume $\mathcal{G}:\mathcal{D}\to \mathcal{D}$ is a mapping satisfying condition $(B_{\gamma ,\mu })$ with $\mathcal{F}(\mathcal{G})\ne \varnothing$. Then, the sequence ${\{u_n\}}_{n=0}^{\infty }$ generated by the fixed-point iterative scheme (5) converges weakly to a fixed point, ${\tau }^{\ast }\in \mathcal{F}(\mathcal{G})$.

Proof. 

By Lemma 7, clearly, $\{u_n\}$ is bounded. As X is a uniformly convex Banach space, then it can obviously be reflexive. From the Eberlein theorem, there exists a convergent subsequence $\{u_{n_k}\}$ of $\{u_n\}$, such that $u_{n_k}\rightharpoonup {\tau }_1$ for some ${\tau }_1\in \mathcal{D}$ (where ⇀ denotes weak convergence).

From the hypothesis of Lemma 7 $\underset{k\to \infty }{lim}\parallel \mathcal{G}{u}_{n_k}-u_{n_k}\parallel =0$ and applying Lemma 5, we have that ${\tau }_1\in \mathcal{F}(\mathcal{G})$.

We want to show that ${\tau }_1$ is a weak limit of $\{u_n\}$. We assume that ${\tau }_1$ is the only weak limit of $\{u_n\}$, that is $\{u_n\}$ converges weakly to ${\tau }_1$.

Suppose in the contrary that the claim does not hold, then we can construct another subsequence $\{u_{n_l}\}$ of $\{u_n\}$ and further assume that it converges to another point ${\tau }_2\in \mathcal{D}$, such that ${\tau }_1\ne {\tau }_2$.

As in the previous claim, it follows that, ${\tau }_2\in \mathcal{F}(\mathcal{G})$. From Lemma 6 and using the Opial condition (6) for Banach space, we have

$$\begin{array}{cc}\hfill \underset{n\to \infty }{lim}\parallel u_n-{\tau }_1\parallel & =\underset{k\to \infty }{lim}\parallel u_{n_k}-{\tau }_1\parallel \hfill \\ & <\underset{k\to \infty }{lim}\parallel u_{n_k}-{\tau }_2\parallel \hfill \\ & =\underset{n\to \infty }{lim}\parallel u_n-{\tau }_2\parallel \hfill \\ & =\underset{l\to \infty }{lim}\parallel u_{n_l}-{\tau }_2\parallel \hfill \\ & <\underset{l\to \infty }{lim}\parallel u_{n_l}-{\tau }_1\parallel \hfill \\ & =\underset{n\to \infty }{lim}\parallel u_n-{\tau }_1\parallel \hfill \end{array}$$

Clearly, we obtain $\underset{n\to \infty }{lim}\parallel u_n-{\tau }_1\parallel <\underset{n\to \infty }{lim}\parallel u_n-{\tau }_1\parallel$, which is obviously a contradiction. Hence, ${\tau }_1={\tau }_2$ and the proof is complete. □

Theorem 2.

Assume $\mathcal{D}$ is a nonempty closed and convex subset of a uniformly convex Banach space X, and suppose that $\mathcal{G}:\mathcal{D}\to \mathcal{D}$ is a mapping satisfying condition $(B_{\gamma ,\mu })$ with $\mathcal{F}(\mathcal{G})\ne \varnothing$. If ${\{u_n\}}_{n=0}^{\infty }$ is a sequence generated by the iterative scheme (5). Then, ${\{u_n\}}_{n=0}^{\infty }$ converges strongly to a fixed point ${\tau }^{\ast }\in \mathcal{F}(\mathcal{G})$ provided that the mapping satisfies condition $(I)$.

Proof. 

For the fact that $\mathcal{G}$ satisfies condition $(I)$, we have that $\underset{n\to \infty }{lim}\rho (u_n,\mathcal{F}(\mathcal{G}))=0$.

We are to show that $\mathcal{F}(\mathcal{G})$ is closed. To do so, we assume that $\{t_n\}$ is an arbitrary sequence in $\mathcal{F}(\mathcal{G})$ and it converges to some point $t\in \mathcal{D}$. As $\gamma \parallel t_n-\mathcal{G}{t}_n\parallel \le \parallel t_n-t\parallel +\mu \parallel t-\mathcal{G}{t}_n\parallel ,$ by condition $(B_{\gamma ,\mu })$, we obtain

$$\begin{array}{cc}\hfill \parallel t_n-\mathcal{G}t\parallel & =\parallel \mathcal{G}{t}_n-\mathcal{G}t\parallel \hfill \\ & \le (1-\gamma )\parallel t_n-t\parallel +\mu (\parallel t_n-\mathcal{G}t\parallel +\parallel t-\mathcal{G}{t}_n\parallel )\hfill \\ & =(1-\gamma )\parallel t_n-t\parallel +\mu \parallel t_n-\mathcal{G}t\parallel +\mu \parallel t-\mathcal{G}{t}_n\parallel .\hfill \end{array}$$

This implies that as $2\mu <\gamma$, we have

$$\parallel t_n-\mathcal{G}t\parallel \le \left({\displaystyle \frac{1-\gamma +\mu }{1-\mu }}\right)\parallel t_n-t\parallel \le \parallel t_n-t\parallel .$$

Hence, $t_n\to \mathcal{G}t$. This follows that $\mathcal{G}t=t$ and, as such, $t\in \mathcal{F}(\mathcal{G})$. Therefore, $\mathcal{F}(\mathcal{G})$ is closed.

• By the hypothesis of Lemma 6, we have that $\{u_n\}$ is Fejer-monotone with respect to $\mathcal{F}(\mathcal{G})$. Again, from Proposition 2, $\{u_n\}$ converges strongly to a fixed point in $\mathcal{F}(\mathcal{G})$. □

Theorem 3.

Let $\mathcal{G}:\mathcal{D}\to \mathcal{D}$ be a mapping satisfying condition $(B_{\gamma ,\mu })$ defined on a nonempty closed convex subset $\mathcal{D}$ of a uniformly convex Banach space X, such that $\mathcal{F}(\mathcal{G})\ne \varnothing$. If $\{u_n\}$ is a sequence generated by (5), then $\{u_n\}$ converges to a fixed point of $\mathcal{G}$ if and only if $\underset{n\to \infty }{lim\; inf}\parallel u_n-\mathcal{F}(\mathcal{G})\parallel =0$.

Proof. 

If the sequence $\{u_n\}$ converges to a fixed point ${\tau }^{\ast }\in \mathcal{F}(\mathcal{G})$, then

$$\underset{n\to \infty }{lim\; inf}\parallel u_n-{\tau }^{\ast }\parallel =0$$

so that

$$\underset{n\to \infty }{lim\; inf}\parallel u_n-\mathcal{F}(\mathcal{G})\parallel =0.$$

Conversely, suppose that $\underset{n\to \infty }{lim\; inf}\parallel u_n-\mathcal{F}(\mathcal{G})\parallel =0.$ From Lemma 6, it is clear that

$$\parallel u_{n+1}-{\tau }^{\ast }\parallel \le \parallel u_n-{\tau }^{\ast }\parallel ,\mathrm{for}\mathrm{any}{\tau }^{\ast }\in \mathcal{F}(\mathcal{G})$$

and we have

$$\parallel u_{n+1}-\mathcal{F}(\mathcal{G})\parallel \le \parallel u_n-\mathcal{F}(\mathcal{G})\parallel .$$

It follows that $\parallel u_n-\mathcal{F}(\mathcal{G})\parallel$ forms a decreasing sequence that is bounded below by zero and it is guaranteed that $\underset{n\to \infty }{lim}\parallel u_n-\mathcal{F}(\mathcal{G})\parallel$ exists.

As $\underset{n\to \infty }{lim\; inf}\parallel u_n-\mathcal{F}(\mathcal{G})\parallel =0$, so is $\underset{n\to \infty }{lim}\parallel u_n-\mathcal{F}(\mathcal{G})\parallel =0$ as well.

Now, it is our aim to show that $\{u_n\}$ is a Cauchy sequence in $\mathcal{D}$. Given $ϵ>0$ as any arbitrary number, there exists $n_0\in \mathbb{N}$, such that for all $n\ge n_0$, we obtain

$$\rho (u_n,\mathcal{F}(\mathcal{G}))<{\displaystyle \frac{ϵ}{4}}.$$

In particular,

$$inf\{\rho (u_{n_0},{\tau }^{\ast }):{\tau }^{\ast }\in \mathcal{F}(\mathcal{G})\}<{\displaystyle \frac{ϵ}{4}},$$

so that there exists a ${\tau }^{\ast }\in \mathcal{F}(\mathcal{G})$ such that

$$\parallel u_{n_0}-{\tau }^{\ast }\parallel <{\displaystyle \frac{ϵ}{2}}.$$

Hence, for $m,n\ge n_0$, we obtain

$$\begin{array}{cc}\hfill \parallel u_{n+m}-u_n\parallel & \le \parallel u_{n+m}-{\tau }^{\ast }\parallel +\parallel u_n-{\tau }^{\ast }\parallel \hfill \\ & \le \parallel u_{n_0}-{\tau }^{\ast }\parallel +\parallel u_{n_0}-{\tau }^{\ast }\parallel \hfill \\ & =2\parallel u_{n_0}-{\tau }^{\ast }\parallel \hfill \\ & <2\left({\displaystyle \frac{ϵ}{2}}\right)=ϵ\hfill \end{array}$$

which shows that $\{u_n\}$ is a Cauchy sequence in $\mathcal{D}$.

As $\mathcal{D}$ is a closed subset of a Banach space X, $\mathcal{D}$ is also a Banach space and it follows that $\{u_n\}$ must converge to some point $u\in \mathcal{D}$.

As $\underset{n\to \infty }{lim}\rho (u_n,\mathcal{F}(\mathcal{G}))=0$, which gives $\rho (u,\mathcal{F}(\mathcal{G}))$. Therefore, $\mathcal{F}(\mathcal{G})$ is closed and so $u\in \mathcal{F}(\mathcal{G})$. □

3.2. Stability and Almost Stability Results

Theorem 4.

Let X be a Banach space. Suppose $\mathcal{G}:\mathcal{D}\to \mathcal{D}$ is a mapping satisfying condition $(B_{\gamma ,\mu })$ with fixed point ${\tau }^{\ast }\in \mathcal{F}(\mathcal{G})\ne \varnothing$. Furthermore, suppose that $\{u_n\}$ is a sequence generated by the iterative scheme (5) and converges to the fixed point ${\tau }^{\ast }$. Then, (5) is stable with respect to the mapping $\mathcal{G}$.

Proof. 

Let $\{s_n\}$ be an arbitrary sequence in $\mathcal{D}$ and let the sequence generated by the iterative scheme (5) be $u_{n+1}=f(\mathcal{G},u_n)$ and it converges to a unique fixed point ${\tau }^{\ast }$.

• Let ${ϵ}_n=\parallel s_{n+1}-f(\mathcal{G},s_n)\parallel$. We show that $\underset{n\to \infty }{lim}{ϵ}_n=0$ if and only if

$$\underset{n\to \infty }{lim}\parallel s_n-{\tau }^{\ast }\parallel =0.$$

Set

$$u_n=\mathcal{G}{s}_n.$$

Suppose $\underset{n\to \infty }{lim}{ϵ}_n=0$,

$$\begin{array}{cc}\hfill \parallel s_{n+1}-{\tau }^{\ast }\parallel & =\parallel s_{n+1}-f(\mathcal{G},s_n)+f(\mathcal{G},s_n)-{\tau }^{\ast }\parallel \hfill \\ & \le \parallel s_{n+1}-f(\mathcal{G},s_n)\parallel +\parallel f(\mathcal{G},s_n)-{\tau }^{\ast }\parallel \hfill \\ & ={ϵ}_n+\parallel f(\mathcal{G},s_n)-{\tau }^{\ast }\parallel \hfill \\ & \le {ϵ}_n+\parallel {\mathcal{G}}^2{v}_n-{\tau }^{\ast }\parallel \hfill \\ & \le {ϵ}_n+\parallel \mathcal{G}{v}_n-{\tau }^{\ast }\parallel \hfill \\ & \le {ϵ}_n+\parallel v_n-{\tau }^{\ast }\parallel ,\hfill \end{array}$$

(24)

but

$$\begin{array}{cc}\hfill \parallel v_n-{\tau }^{\ast }\parallel & =\parallel {\mathcal{G}}^2{w}_n-{\tau }^{\ast }\parallel \hfill \\ & \le \parallel \mathcal{G}{w}_n-{\tau }^{\ast }\parallel \hfill \\ & \le \parallel w_n-{\tau }^{\ast }\parallel ,\hfill \end{array}$$

(25)

and

$$\begin{array}{cc}\hfill \parallel w_n-{\tau }^{\ast }\parallel & =\parallel {\mathcal{G}}^2{x}_n-{\tau }^{\ast }\parallel \hfill \\ & \le \parallel \mathcal{G}{x}_n-{\tau }^{\ast }\parallel \hfill \\ & \le \parallel x_n-{\tau }^{\ast }\parallel ,\hfill \end{array}$$

(26)

moreover,

$$\begin{array}{cc}\hfill \parallel x_n-{\tau }^{\ast }\parallel & =\parallel \mathcal{G}[(1-{\alpha }_n)u_n+{\alpha }_n\mathcal{G}{u}_n]-{\tau }^{\ast }\parallel \hfill \\ & \le \parallel (1-{\alpha }_n)u_n+{\alpha }_n\mathcal{G}{u}_n-{\tau }^{\ast }\parallel \hfill \\ & \le (1-{\alpha }_n)\parallel u_n-{\tau }^{\ast }\parallel +{\alpha }_n\parallel \mathcal{G}{u}_n-{\tau }^{\ast }\parallel \hfill \\ & \le (1-{\alpha }_n)\parallel u_n-{\tau }^{\ast }\parallel +{\alpha }_n\parallel u_n-{\tau }^{\ast }\parallel \hfill \\ & =\parallel u_n-{\tau }^{\ast }\parallel \hfill \\ & =\parallel \mathcal{G}{s}_n-{\tau }^{\ast }\parallel \hfill \\ & \le \parallel s_n-{\tau }^{\ast }\parallel .\hfill \end{array}$$

(27)

Combining (25)–(27), we have

$$\parallel v_n-{\tau }^{\ast }\parallel \le \parallel s_n-{\tau }^{\ast }\parallel .$$

(28)

Putting (28) in (24)

$$\parallel s_{n+1}-{\tau }^{\ast }\parallel \le {ϵ}_n+\parallel s_n-{\tau }^{\ast }\parallel .$$

By Lemma 3, we have $\underset{n\to \infty }{lim}\parallel s_n-{\tau }^{\ast }\parallel =0$.

Conversely, suppose $\underset{n\to \infty }{lim}{s}_n-{\tau }^{\ast }\parallel =0$, then

$$\begin{array}{cc}\hfill {ϵ}_n& =\parallel s_{n+1}-f(\mathcal{G},s_n)\parallel \hfill \\ & \le \parallel s_{n+1}-{\tau }^{\ast }+{\tau }^{\ast }-f(\mathcal{G},s_n)\parallel \hfill \\ & \le \parallel s_{n+1}-{\tau }^{\ast }\parallel +\parallel {\tau }^{\ast }-f(\mathcal{G},s_n)\parallel \hfill \\ & \le \parallel s_{n+1}-{\tau }^{\ast }\parallel +\parallel {\tau }^{\ast }-{\mathcal{G}}^2{v}_n\parallel \hfill \\ & =\parallel s_{n+1}-{\tau }^{\ast }\parallel +\parallel {\mathcal{G}}^2{v}_n-{\tau }^{\ast }\parallel \hfill \\ & \le \parallel s_{n+1}-{\tau }^{\ast }\parallel +\parallel \mathcal{G}{v}_n-{\tau }^{\ast }\parallel \hfill \\ & \le \parallel s_{n+1}-{\tau }^{\ast }\parallel +\parallel v_n-{\tau }^{\ast }\parallel \hfill \\ & \le \parallel s_{n+1}-{\tau }^{\ast }\parallel +\parallel {\mathcal{G}}^2{w}_n-{\tau }^{\ast }\parallel \hfill \\ & \le \parallel s_{n+1}-{\tau }^{\ast }\parallel +\parallel \mathcal{G}{w}_n-{\tau }^{\ast }\parallel \hfill \\ & \le \parallel s_{n+1}-{\tau }^{\ast }\parallel +\parallel w_n-{\tau }^{\ast }\parallel \hfill \\ & \le \parallel s_{n+1}-{\tau }^{\ast }\parallel +\parallel {\mathcal{G}}^2{x}_n-{\tau }^{\ast }\parallel \hfill \\ & \le \parallel s_{n+1}-{\tau }^{\ast }\parallel +\parallel \mathcal{G}{x}_n-{\tau }^{\ast }\parallel \hfill \\ & \le \parallel s_{n+1}-{\tau }^{\ast }\parallel +\parallel x_n-{\tau }^{\ast }\parallel \hfill \\ & \le \parallel s_{n+1}-{\tau }^{\ast }\parallel +\parallel \mathcal{G}[(1-{\alpha }_n)u_n+{\alpha }_n\mathcal{G}{u}_n]-{\tau }^{\ast }\parallel \hfill \\ & \le \parallel s_{n+1}-{\tau }^{\ast }\parallel +\parallel (1-{\alpha }_n)u_n+{\alpha }_n\mathcal{G}{u}_n-{\tau }^{\ast }\parallel \hfill \\ & \le \parallel s_{n+1}-{\tau }^{\ast }\parallel +(1-{\alpha }_n)\parallel u_n-{\tau }^{\ast }\parallel +{\alpha }_n\parallel u_{-}{\tau }^{\ast }\parallel \hfill \\ & \le \parallel s_{n+1}-{\tau }^{\ast }\parallel +\parallel u_n-{\tau }^{\ast }\parallel \hfill \\ & \le \parallel s_{n+1}-{\tau }^{\ast }\parallel +\parallel s_n-{\tau }^{\ast }\parallel .\hfill \end{array}$$

Taking limit as $n\to \infty$ on both sides and taking cognizance that $\underset{n\to \infty }{lim}\parallel s_n-{\tau }^{\ast }\parallel =0$. Hence, the fixed-point iterative scheme is stable with respect to the mapping $\mathcal{G}$. □

Next is the almost $\mathcal{G}$-stability result.

Theorem 5.

Let X, $\mathcal{D}$ and $\mathcal{G}$ be the same as used in Theorem 4 with $\mathcal{G}$ being a mapping that satisfies condition $(B_{\gamma ,\mu })$ for $\mathcal{F}(\mathcal{G})\ne \varnothing$. Then the iterative scheme (5) is almost $\mathcal{G}$-stable.

Proof. 

Let $\{s_n\}$ be an approximate sequence of $\{u_n\}$ in $\mathcal{D}$. Assume that the iterative scheme (5) is represented as $u_{n+1}=f(\mathcal{G},u_n)$ and it converges to a fixed point ${\tau }^{\ast }$ and let ${ϵ}_n=\parallel s_{n+1}-f(\mathcal{G},s_n)\parallel$, $n\in \mathbb{N}$.

We are to prove that ${\sum }_{n=0}^{\infty }{ϵ}_n<\infty$ implies $\underset{n\to \infty }{lim}\parallel s_n-{\tau }^{\ast }\parallel =0$.

Let ${\sum }_{n=0}^{\infty }{ϵ}_n<\infty$, then by (5), we obtain:

$$\begin{array}{cc}\hfill \parallel s_{n+1}-{\tau }^{\ast }\parallel & =\parallel s_{n+1}-f(\mathcal{G},s_n)+f(\mathcal{G},s_n)-{\tau }^{\ast }\parallel \hfill \\ & \le \parallel s_{n+1}-f(\mathcal{G},s_n)\parallel +\parallel f(\mathcal{G},s_n)-{\tau }^{\ast }\parallel \hfill \\ & \le {ϵ}_n+\parallel f(\mathcal{G},s_n)-{\tau }^{\ast }\parallel \hfill \\ & \le {ϵ}_n+\parallel {\mathcal{G}}^2{v}_n-{\tau }^{\ast }\parallel \hfill \\ & \le {ϵ}_n+\parallel \mathcal{G}{v}_n-{\tau }^{\ast }\parallel \hfill \\ & \le {ϵ}_n+\parallel v_n-{\tau }^{\ast }\parallel \hfill \\ & \le {ϵ}_n+\parallel {\mathcal{G}}^2{w}_n-{\tau }^{\ast }\parallel \hfill \\ & \le {ϵ}_n+\parallel \mathcal{G}{w}_n-{\tau }^{\ast }\parallel \hfill \\ & \le {ϵ}_n+\parallel w_n-{\tau }^{\ast }\parallel \hfill \\ & \le {ϵ}_n+\parallel {\mathcal{G}}^2{x}_n-{\tau }^{\ast }\parallel \hfill \\ & \le {ϵ}_n+\parallel \mathcal{G}{x}_n-{\tau }^{\ast }\parallel \hfill \\ & \le {ϵ}_n+\parallel x_n-{\tau }^{\ast }\parallel \hfill \\ & \le {ϵ}_n+\parallel \mathcal{G}[(1-{\alpha }_n)u_n+{\alpha }_n\mathcal{G}{u}_n]-{\tau }^{\ast }\parallel \hfill \\ & \le {ϵ}_n+\parallel (1-{\alpha }_n)u_n+{\alpha }_n\mathcal{G}{u}_n-{\tau }^{\ast }\parallel \hfill \\ & \le {ϵ}_n+(1-{\alpha }_n)\parallel u_n-{\tau }^{\ast }\parallel +{\alpha }_n\parallel \mathcal{G}{u}_n-{\tau }^{\ast }\parallel \hfill \\ & \le {ϵ}_n(1-{\alpha }_n)\parallel u_n-{\tau }^{\ast }\parallel +{\alpha }_n\parallel u_n-{\tau }^{\ast }\parallel \hfill \\ & ={ϵ}_n+\parallel u_n-{\tau }^{\ast }\parallel \hfill \\ & \le {ϵ}_n+\parallel s_n-{\tau }^{\ast }\parallel .\hfill \end{array}$$

Set ${\eta }_n=\parallel s_n-{\tau }^{\ast }\parallel$, then ${\eta }_{n+1}<{\eta }_n+{ϵ}_n$.

As ${\sum }_{n=0}^{\infty }{ϵ}_n<\infty$, then by Lemma 4, we have ${\sum }_{n=0}^{\infty }{\eta }_n<\infty$. It follows that $\underset{n\to \infty }{lim}{\eta }_n=0$, that is, $\underset{n\to \infty }{lim}\parallel s_n-{\tau }^{\ast }\parallel =0$. Therefore, the proof is complete. □

3.3. Numerical Example

Here, we provide an example of a mapping that satisfies condition $(B_{\gamma ,\mu })$, specifically for when $\gamma =1$ and $\mu ={\displaystyle \frac{1}{2}}$. Furthermore, this example is used to compare the rate of convergence of our iterative scheme (5) with all of AA, K*, M, and Picard-S iterative schemes for ${\alpha }_n={\beta }_n={\gamma }_n={\displaystyle \frac{4}{5}}$.

Table 1. Comparison of speed of convergence of some iterative scheme for Example 1.

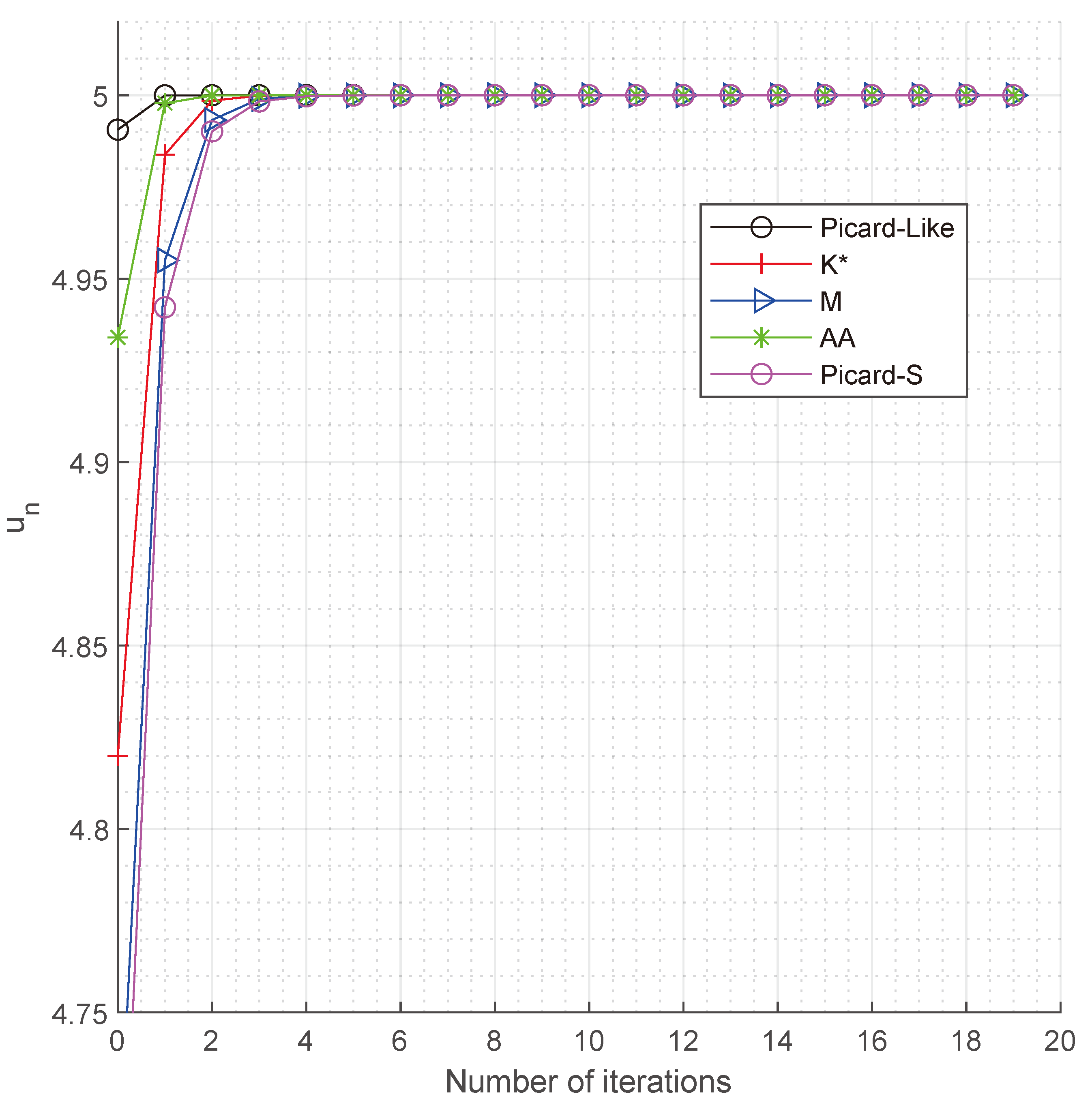
Step	Picard-like	${\mathit{K}}^{\ast }$	M	AA	Picard-S
1	4.9906	4.8200	4.7000	4.9340	4.6600
2	5.0000	4.9838	4.9550	4.9978	4.9422
3	5.0000	4.9985	4.9932	4.9999	4.9902
4	5.0000	4.9999	4.9990	5.0000	4.9983
5	5.0000	5.0000	4.9998	5.0000	4.9997
6	5.0000	5.0000	5.0000	5.0000	5.0000
7	5.0000	5.0000	5.0000	5.0000	5.0000
8	5.0000	5.0000	5.0000	5.0000	5.0000
9	5.0000	5.0000	5.0000	5.0000	5.0000
10	5.0000	5.0000	5.0000	5.0000	5.0000
11	5.0000	5.0000	5.0000	5.0000	5.0000
12	5.0000	5.0000	5.0000	5.0000	5.0000
13	5.0000	5.0000	5.0000	5.0000	5.0000
14	5.0000	5.0000	5.0000	5.0000	5.0000
15	5.0000	5.0000	5.0000	5.0000	5.0000
16	5.0000	5.0000	5.0000	5.0000	5.0000
17	5.0000	5.0000	5.0000	5.0000	5.0000
18	5.0000	5.0000	5.0000	5.0000	5.0000
19	5.0000	5.0000	5.0000	5.0000	5.0000
20	5.0000	5.0000	5.0000	5.0000	5.0000

and Figure 1 below shows a comparison of the rate of convergence of the mentioned iterative schemes with our new scheme in line with Example 1 below.

Example 1.

Define a mapping $\mathcal{G}:[5,7]\to [5,7]$ as follows

$$\mathcal{G}u=\left\{\begin{array}{c}{\displaystyle \frac{u+5}{2}},\mathrm{if}u\ne 7\hfill \\ 5,\mathrm{if}u=7.\hfill \end{array}\right.$$

We want to show that the mapping satisfies condition $(B_{\gamma ,\mu })$. If $\gamma =1$ and $\mu ={\displaystyle \frac{1}{2}}$, then our aim is to show that $\mathcal{G}$ satisfies condition $(B_{1,\frac{1}{2}})$.

Case A 

For $u,v\in [5,7)$, we obtain

$$\begin{array}{cc}\hfill (1-\gamma )|u-v|+\mu (|u-\mathcal{G}v|+|v-\mathcal{G}u|)& ={\displaystyle \frac{1}{2}}(|u-\mathcal{G}v|+|v-\mathcal{G}u|)\hfill \\ & ={\displaystyle \frac{1}{2}}\left(|u-({\displaystyle \frac{v+5}{2}})|+|v-({\displaystyle \frac{u+5}{2}})|\right)\hfill \\ & \ge {\displaystyle \frac{1}{2}}|{\displaystyle \frac{3u}{2}}-{\displaystyle \frac{3v}{2}}|\hfill \\ & ={\displaystyle \frac{3}{4}}|u-v|\hfill \\ & \ge {\displaystyle \frac{1}{2}}|u-v|\hfill \\ & =|\mathcal{G}u-\mathcal{G}v|\hfill \end{array}$$

Case B 

For $u\in [5,7]$ and $y=7$, we obtain

$$\begin{array}{cc}\hfill (1-\gamma )|u-v|+\mu (|u-\mathcal{G}v|+|v-\mathcal{G}u|)& ={\displaystyle \frac{1}{2}}(|u-\mathcal{G}v|+|v-\mathcal{G}u|)\hfill \\ & ={\displaystyle \frac{1}{2}}(|u-5|+|v-({\displaystyle \frac{u+5}{2}})|)\hfill \\ & ={\displaystyle \frac{1}{2}}|u-5|+{\displaystyle \frac{1}{2}}|v-({\displaystyle \frac{u+5}{2}})|\hfill \\ & \ge {\displaystyle \frac{1}{2}}|u-5|\hfill \\ & =|\mathcal{G}u-\mathcal{G}v|\hfill \end{array}$$

Case C 

For $u=v=7$, we obtain

$$(1-\gamma )|u-v|+\mu (|u-\mathcal{G}v|+|v-\mathcal{G}u|)\ge 0=|\mathcal{G}u-\mathcal{G}v|.$$

We can conclude that $\mathcal{G}$ satisfies condition $(B_{1,\frac{1}{2}})$.

4. Application to Infectious Diseases Model

Mathematical models for the transmission of infectious diseases are essential tools for understanding how diseases spread within populations and for designing effective intervention strategies. These models range from simple to highly complex, depending on the disease, population structure, and the level of detail required. Some of such models include; the SIR model, SEIR model, SIS model, stochastic model, and network models. In [26,27,28], the following nonlinear integral equation

$$u(t)={\int }_{t-\lambda }^{t}f(s,u(s))ds$$

(29)

was presented to represent a model for the spread of certain infectious diseases with a periodic contact rate that varies according to season, where $u(t)$ is the demography of the population infected (also known as the infective class) with the disease at time t, $f(t,u(t))$ is the new infective population per unit time (i.e., $f(t,0)=0$), and $\lambda$ is period of time an individual remains infectious and continue spreading the disease.

To analyze the existence of solution of (29), let $t\in [0,\eta ]$ and $X=([0,\eta ],\mathbb{R})$ be a Banach space with supremum norm

$$\parallel u\parallel =\underset{t\in [0,\eta ]}{sup}\{|u(t)|:u\in X\},$$

such that $\parallel u_1-u_2\parallel ={sup}_{t\in [0,\eta ]}\{|u_1(t)-u_2(t)|\}$.

To continue, we define an operator $\mathcal{G}:X\to X$ by

$$\mathcal{G}u(t)={\int }_{t-\lambda }^{t}f(s,u(s))ds.$$

(30)

Furthermore, f satisfies the following conditions:

(C₁) 

$f:\mathbb{R}\times {\mathbb{R}}_{+}\to {\mathbb{R}}_{+}$ is continuous,

(C₂) 

$f(t,s)=f(t+\eta ,s)$, $\forall t\in \mathbb{R},s\ge 0$,

(C₃) 

$|f(s,u_1(t))-f(s,u_2(t))|\le |u_1(t)-u_2(t)|$, $\forall u_1,u_2\in X$.

Remark 1.

The operator (30) clearly satisfies the $(B_{\gamma ,\mu })$ condition, as defined in Definition 1 for $x,y\in \mathcal{D}$, provided that $f(s,u)$ satisfies Lipschitz condition with respect to the second variable, u with a Lipschitz constant $L>0$ and $s\in [t-\lambda ,t]$. For the second part of the condition, one may choose $\gamma =1-L\lambda$ (for $L\lambda <1$) and $\mu ={\displaystyle \frac{\gamma }{2}}$.

Theorem 6.

Suppose conditions $(C_1)-(C_3)$ are satisfied. Let $\lambda \in [0,1]$, $\{{\alpha }_n\}\in (0,1)$ is a real sequence of the iterative scheme (5) such that ${\sum }_{n=0}^{\infty }{\alpha }_n=\infty$. The nonlinear integral equation model (29) has a solution ℓ and the iterative scheme (5) converges to a fixed point ℓ.

Proof. 

Recall $X=([0,\eta ],\mathbb{R})$ and $\parallel u\parallel ={sup}_{t\in [0,\eta ]}\{|u(t)|:u\in X\}$.

Let $\{u_n\}$ be a sequence generated by the iterative scheme (5) for the operator $\mathcal{G}:X\to X$ defined by (30), i.e.,

$$\mathcal{G}u(t)={\int }_{t-\lambda }^{t}f(s,u(s))ds.$$

It is our aim to show that $\{u_n\}$ converges to ℓ as $n\to \infty$.

From (5), (30) and condition $(C_1)-(C_3)$, we have

$$\begin{array}{cc}\hfill \parallel x_n-\ell \parallel & =\parallel \mathcal{G}[(1-{\alpha }_n)u_n+{\alpha }_n\mathcal{G}{u}_n]-\ell \parallel \hfill \\ & =\parallel \mathcal{G}[(1-{\alpha }_n)u_n+{\alpha }_n\mathcal{G}{u}_n]-\mathcal{G}\ell \parallel \hfill \\ & \le \parallel (1-{\alpha }_n)u_n+{\alpha }_n\mathcal{G}{u}_n-\ell \parallel \hfill \\ & \le (1-{\alpha }_n)\parallel u_n-\ell \parallel +{\alpha }_n\parallel \mathcal{G}{u}_n-\ell \parallel \hfill \\ & =(1-{\alpha }_n)\parallel u_n-\ell \parallel +{\alpha }_n\parallel \mathcal{G}{u}_n-\mathcal{G}\ell \parallel \hfill \\ & \le (1-{\alpha }_n)\parallel u_n-\ell \parallel +{\alpha }_n\underset{t\in [0,\eta ]}{sup}|\mathcal{G}{u}_n-\mathcal{G}\ell |\hfill \\ & \le (1-{\alpha }_n)\parallel u_n-\ell \parallel +{\alpha }_n\underset{t\in [0,\eta ]}{sup}|{\int }_{t-\lambda }^{t}f(s,u_n(s))ds-{\int }_{t-\lambda }^{t}f(s,\ell (s))ds|\hfill \\ & =(1-{\alpha }_n)\parallel u_n-\ell \parallel +{\alpha }_n\underset{t\in [0,\eta ]}{sup}\left|{\int }_{t-\lambda }^t\left(f(s,u_n(s))-f(s,\ell (s))\right)ds\right|\hfill \\ & =(1-{\alpha }_n)\parallel u_n-\ell \parallel +{\alpha }_n\underset{t\in [0,\eta ]}{sup}{\int }_{t-\lambda }^t|f(s,u_n(s))-f(s,\ell (s))|ds\hfill \\ & \le (1-{\alpha }_n)\parallel u_n-\ell \parallel +{\alpha }_n\underset{t\in [0,\eta ]}{sup}{\int }_{t-\lambda }^t|u_n(s)-\ell (s)|ds\hfill \\ & \le (1-{\alpha }_n)\parallel u_n-\ell \parallel +{\alpha }_n\lambda \parallel u_n-\ell \parallel \hfill \\ & =[1-(1-\lambda ){\alpha }_n]\parallel u_n-\ell \parallel \hfill \end{array}$$

(31)

using (5)

$$\begin{array}{cc}\hfill \parallel w_n-\ell \parallel & =\parallel {\mathcal{G}}^2{x}_n-\ell \parallel \hfill \\ & \le \parallel \mathcal{G}{x}_n-\ell \parallel \hfill \\ & =\parallel \mathcal{G}{x}_n-\mathcal{G}\ell \parallel \hfill \\ & \le \underset{t\in [0,\eta ]}{sup}|\mathcal{G}{x}_n(t)-\mathcal{G}\ell (t)|\hfill \\ & \le \underset{t\in [0,\eta ]}{sup}|{\int }_{t-\lambda }^{t}f(s,x_n(s))ds-{\int }_{t-\lambda }^{t}f(s,\ell (s))ds|\hfill \\ & =\underset{t\in [0,\eta ]}{sup}\left|{\int }_{t-\lambda }^t\left(f(s,x_n(s))-f(s,\ell (s))\right)ds\right|\hfill \\ & =\underset{t\in [0,\eta ]}{sup}{\int }_{t-\lambda }^t|f(s,x_n(s))-f(s,\ell (s))|ds\hfill \\ & \le \underset{t\in [0,\eta ]}{sup}{\int }_{t-\lambda }^t|x_n(s)-\ell (s)|ds\hfill \\ & \le \lambda \parallel x_n-\ell \parallel \hfill \end{array}$$

(32)

again, using (5)

$$\begin{array}{cc}\hfill \parallel v_n-\ell \parallel & =\parallel {\mathcal{G}}^2{w}_n-\ell \parallel \hfill \\ & \le \parallel \mathcal{G}{w}_n-\ell \parallel \hfill \\ & =\parallel \mathcal{G}{w}_n-\mathcal{G}\ell \parallel \hfill \\ & \le \underset{t\in [0,\eta ]}{sup}|\mathcal{G}{w}_n(t)-\mathcal{G}\ell (t)|\hfill \\ & \le \underset{t\in [0,\eta ]}{sup}|{\int }_{t-\lambda }^{t}f(s,w_n(s))ds-{\int }_{t-\lambda }^{t}f(s,\ell (s))ds|\hfill \\ & \le \underset{t\in [0,\eta ]}{sup}\left|{\int }_{t-\lambda }^t\left(f(s,w_n(s))-f(s,\ell (s))\right)ds\right|\hfill \\ & =\underset{t\in [0,\eta ]}{sup}{\int }_{t-\lambda }^t|f(s,w_n(s))-f(s,\ell (s))|ds\hfill \\ & \le \underset{t\in [0,\eta ]}{sup}{\int }_{t-\lambda }^t|w_n(s)-\ell (s)|ds\hfill \\ & \le \lambda \parallel w_n-\ell \parallel \hfill \end{array}$$

(33)

using (5)

$$\begin{array}{cc}\hfill \parallel u_{n+1}-\ell \parallel & =\parallel {\mathcal{G}}^2{v}_n-\ell \parallel \hfill \\ & \le \parallel \mathcal{G}{v}_n-\ell \parallel \hfill \\ & =\parallel \mathcal{G}{v}_n-\mathcal{G}\ell \parallel \hfill \\ & \le \underset{t\in [0,\eta ]}{sup}|\mathcal{G}{v}_n(t)-\mathcal{G}\ell (t)|\hfill \\ & \le \underset{t\in [0,\eta ]}{sup}|{\int }_{t-\lambda }^{t}f(s,v_n(s))ds-{\int }_{t-\lambda }^{t}f(s,\ell (s))ds|\hfill \\ & \le \underset{t\in [0,\eta ]}{sup}\left|{\int }_{t-\lambda }^t\left(f(s,v_n(s))-f(s,\ell (s))\right)ds\right|\hfill \\ & =\underset{t\in [0,\eta ]}{sup}{\int }_{t-\lambda }^t|f(s,v_n(s))-f(s,\ell (s))|ds\hfill \\ & \le \underset{t\in [0,\eta ]}{sup}{\int }_{t-\lambda }^t|v_n(s)-\ell (s)|ds\hfill \\ & \le \lambda \parallel v_n-\ell \parallel \hfill \end{array}$$

(34)

Combining (31)–(34), we have

$$\begin{array}{cc}\hfill \parallel u_{n+1}-\ell \parallel & ={\lambda }^3[1-(1-\lambda ){\alpha }_n]\parallel u_n-\ell \parallel \hfill \\ & \le [1-(1-\lambda ){\alpha }_n]\parallel u_n-\ell \parallel .\hfill \end{array}$$

By induction, we have

$$\parallel u_{n+1}-\ell \parallel \le \parallel u_0-\ell \parallel \prod _{k=0}^n[1-(1-\lambda ){\alpha }_k].$$

(35)

From basic analysis, we recall that $1-x\le e^{-x}$ for $x\in [0,1]$, so that

$$\parallel u_{n+1}-\ell \parallel \le \parallel u_0-\ell \parallel e^{-(1-\lambda ){\sum }_{k=0}^n{\alpha }_k}.$$

Taking limit as $n\to \infty$, we have that $\underset{n\to \infty }{lim}\parallel u_n-\ell \parallel =0$. Thereby. completing the proof. □

5. Application to Boundary Value Problem of Third Order via Green’s Function

5.1. Construction of Green’s Function

Consider a third-order boundary value problem (BVP);

$$g_1(t)h^{‴}(t)+q_2(t)h^{″}(t)+q_3(t)h^{\prime }(t)+q_4(t)h(t)=\Psi (t)$$

(36)

for $a\le t\le b$, with the following boundary conditions (BCs);

$$\begin{array}{cc}\hfill B_{{\lambda }_1}\left[h\right]& ={\zeta }_{1}h({\lambda }_1)+{\zeta }_2{h}^{\prime }({\lambda }_1)+{\zeta }_3{h}^{″}({\lambda }_1)=\zeta \hfill \\ \hfill B_{{\lambda }_2}\left[h\right]& ={\eta }_{1}h({\lambda }_2)+{\eta }_2{h}^{\prime }({\lambda }_2)+{\eta }_3{h}^{″}({\lambda }_2)=\eta \hfill \\ \hfill B_{{\lambda }_3}\left[h\right]& ={\xi }_{1}h({\lambda }_3)+{\xi }_2{h}^{\prime }({\lambda }_3)+{\xi }_3{h}^{″}({\lambda }_3)=\xi \hfill \end{array}$$

(37)

for ${\lambda }_3={\lambda }_2$ or ${\lambda }_3$ = ${\lambda }_1$. Equation (36) can be shortened to:

$$L\left[h\right]=\Psi (t)$$

where $L\left[h\right]$ is linear and the right-hand side can be written as $\Psi (t,h(t),h^{\prime }(t),h^{″}(t))$. The right-hand side could be linear or nonlinear. For the BCs, $\zeta ,\eta$ and $\xi$ are constants.

If the homogeneous part of (36) (i.e., $L\left[h\right]=0$) is solved, then three linearly independent complementary solutions $h_1,h_2$ and $h_3$ can be obtained and can subsequently be used to construct the Green’s function, which is a piecewise function defined as a linear combination of the linearly independent solutions $h_1,h_2$ and $h_3$; thus,

$$G(t,s)=\left\{\begin{array}{c}{k}_1{h}_1+k_2{h}_2+k_3{h}_3,a<t<s\hfill \\ l_1{h}_1+l_2{h}_2+l_3{h}_3,s<t<b\hfill \end{array}\right.$$

(38)

where $k_1,k_2,k_3,l_1,l_2,l_3$ are constants whose real values can be obtained using the following axioms;

(A₁) 

$G(t,s)$ satisfies the associated boundary conditions;

$$B_{{\lambda }_1}\left[G(t,s)\right]=B_{{\lambda }_2}\left[G(t,s)\right]=B_{{\lambda }_3}\left[G(t,s)\right]=0$$

(A₂) 

$G(t,s)$ is continuous at $t=s$, that is

$$k_1{h}_1(s)+k_2{h}_2(s)+k_3{h}_3(s)=l_1{h}_1(s)+l_2{h}_2(s)+l_3{h}_3(s)$$

(A₃) 

$G^{\prime }(t,s)$ is continuous at $t=s$, that is

$$k_1{h}_1^{\prime }(s)+k_2{h}_2^{\prime }(s)+k_3{h}_3^{\prime }(s)=l_1{h}_1^{\prime }(s)+l_2{h}_2^{\prime }(s)+l_3{h}_3^{\prime }(s)$$

(A₄) 

$G^{″}(t,t)$ has jump disconttinuity at $t=s$;

$$k_1{h}_1^{″}(s)+k_2{h}_2^{″}(s)+k_3{h}_3^{″}(s)+{\displaystyle \frac{1}{g(s)}}=l_1{h}_1^{″}(s)+l_2{h}_2^{″}(s)+l_3{h}_3^{″}(s).$$

If the Green function, $G(t,s)$ can solve the BVP, (36), then it will satisfy the equation,

$$-L[G(t,s)]=\delta (t-s)$$

(39)

subject to the homogeneous boundary conditions

$$B_{{\lambda }_1}\left[G(t,s)\right]=B_{{\lambda }_2}\left[G(t,s)\right]=B_{{\lambda }_3}\left[G(t,s)\right]=0,$$

where $\delta$ is the Kronecker Delta.

5.2. Picard-like-Green Iterative Scheme

To construct the New Picard-like-Green iterative scheme, we embed the Green’s function in the Picard-like fixed-point iterative scheme (5).

To do this, we begin by considering the following nonlinear boundary value problem

$$L\left[h\right]+N\left[h\right]=\Psi (t,h)$$

(40)

where $L\left[h\right]$ is linear in h, $N\left[h\right]$ is nonlinear in h, and $\Psi (t,h)$ is a function in h that could be either linear or nonlinear.

The general solution of (40) can be expressed as $h=h_c+h_p$, with $h_c$ being the complementary solution subject to the homogeneous part, $L\left[h\right]=0$ of (40) with regards to the boundary conditions mentioned in axiom $(A_1)$. Furthermore, $h_g$ is a particular solution of the nonhomogeneous part of (40).

Next, we define an integral operator in terms of Green’s function, $G(t,s)$ and the particular solution, $h_p$:

$$\mathcal{H}\left[h_p\right]={\int }_a^{b}G(t,s)L\left[h_p\right]ds.$$

(41)

Remark 2.

Observe that the operator $\mathcal{H}\left[h_p\right](t)={\int }_a^{b}G(t,s)L\left[h_p\right](s)ds$ of Equation (41) satisfies condition $(B_{\gamma ,\mu })$, provided that:

(a) 

the kernel, $G(t,s)$ which represents the Green function is bounded,

(b) 

L is a bounded linear operator, and

(c) 

one can choose $\gamma =1-\lambda$ and $\mu ={\displaystyle \frac{\gamma }{2}}$ for $\lambda =M\ell (b-a)<1$ where M is a bound for $G(t,s)$ (i.e., $|G(t,s)\le M|$) and $\parallel L\parallel \le \ell$, $\ell >0$.

For convenience, let $h_p$ be simply h, so that (41) becomes

$$\mathcal{H}\left[h\right]={\int }_a^{b}G(t,s)L\left[h\right]ds$$

Clearly, h is a fixed point if and only if h is the solution to Equation (40).

Let

$$h={\int }_a^{b}G(t,s)[\Psi (t,h)-N\left[h\right]]ds,$$

then

$$\begin{array}{cc}\hfill \mathcal{H}\left[h\right]& ={\int }_a^{b}G(t,s)[L\left[h\right]+N\left[h\right]-\Psi (t,h)-N\left[h\right]+\Psi (t,h)]ds\hfill \\ & \le {\int }_a^{b}G(t,s)[L\left[h\right]+N\left[h\right]-\Psi (t,h)]ds+{\int }_a^{b}G(t,s)[\Psi (t,h)-N\left[h\right]]ds\hfill \\ & =h+{\int }_a^{b}G(t,s)[L\left[h\right]+N\left[h\right]-\Psi (t,h)]ds.\hfill \end{array}$$

(42)

Applying the new iterative scheme (5), we obtain

$$\left\{\begin{array}{c}{u}_0\in \mathcal{D}\hfill \\ x_n=\mathcal{H}[(1-{\alpha }_n)u_n+{\alpha }_n\mathcal{H}{u}_n]\hfill \\ w_n={\mathcal{H}}^2{x}_n\hfill \\ v_n={\mathcal{H}}^2{w}_n\hfill \\ u_{n+1}={\mathcal{H}}^2{v}_n,n\in \mathbb{N}\hfill \end{array}\right.$$

(43)

wher $\{{\alpha }_n\}$ is a real sequence in $(0,1)$.

If (43) is expanded with regards to (42), we have

$$\begin{array}{cc}\hfill x_n& =[(1-{\alpha }_n)u_n+{\alpha }_n\mathcal{H}{u}_n]+{\int }_a^b\mathcal{G}(t,s)[L[(1-{\alpha }_n)u_n+{\alpha }_n\mathcal{H}{u}_n]\hfill \\ & +N[(1-{\alpha }_n)u_n+{\alpha }_n\mathcal{H}{u}_n]-\Psi (t,[(1-{\alpha }_n)u_n+{\alpha }_n\mathcal{H}{u}_n])]ds\hfill \\ & =\left[(1-{\alpha }_n)u_n+{\alpha }_n\{u_n+{\int }_a^{b}G(t,s)[L\left[u_n\right]+N\left[u_n\right]-\Psi (t,u_n)]ds\}\right]\hfill \\ & +{\int }_a^{b}G(t,s)\left[L\right[(1-{\alpha }_n)u_n+{\alpha }_n\{u_n+{\int }_a^{b}G(t,s)[L\left[u_n\right]+N\left[u_n\right]\hfill \\ & -\Psi (t,u_n)]ds\}]+N[(1-{\alpha }_n)u_n+{\alpha }_n\{u_n+{\int }_a^{b}G(t,s)[L\left[u_n\right]+N\left[u_n\right]-\Psi (t,u_n)]ds\}]\hfill \\ & -\Psi (t,[(1-{\alpha }_n)u_n+{\alpha }_n\{u_n+{\int }_a^{b}G(t,s)[L\left[u_n\right]+N\left[u_n\right]-\Psi (t,u_n)]ds\}])]ds\hfill \\ & =u_n+{\alpha }_n{\int }_a^{b}G(t,s)[L\left[u_n\right]+N\left[u_n\right]-\Psi (t,u_n)]ds\hfill \\ & +{\int }_a^{b}G(t,s)[L[u_n+{\alpha }_n{\int }_a^{b}G(t,s)[L\left[u_n\right]+N\left[u_n\right]-\Psi (t,u_n)]ds]\hfill \\ & +N[u_n+{\alpha }_n{\int }_a^{b}G(t,s)[L\left[u_n\right]+N\left[u_n\right]-\Psi (t,u_n)]ds]\hfill \\ & -\Psi (t,u_n+{\int }_a^{b}G(t,s)[L\left[u_n\right]+N\left[u_n\right]-\Psi (t,u_n)]ds)]ds\hfill \end{array}$$

$$\begin{array}{cc}\hfill w_n& =\mathcal{H}[x_n+{\int }_a^{b}G(t,s)[L\left[x_n\right]+N\left[x_n\right]-\Psi (t,x_n)]ds]\hfill \\ & =x_n+{\int }_a^{b}G(t,s)[L\left[x_n\right]+N\left[x_n\right]-\Psi (t,x_n)]ds\hfill \\ & +{\int }_a^{b}G(t,s)[L[x_n+{\int }_a^{b}G(t,s)[L\left[x_n\right]+N\left[x_n\right]-\Psi (t,x_n)]ds]\hfill \\ & +N[x_n+{\int }_a^{b}G(t,s)[L\left[x_n\right]+N\left[x_n\right]-\Psi (t,x_n)]ds]-\Psi (t,\mathcal{H}{x}_n)]ds\hfill \end{array}$$

$$\begin{array}{cc}\hfill v_n& =\mathcal{H}[w_n+{\int }_a^{b}G(t,s)[L\left[w_n\right]+N\left[w_n\right]-\Psi (t,w_n)]ds]\hfill \\ & =w_n+{\int }_a^{b}G(t,s)[L\left[w_n\right]+N\left[w_n\right]-\Psi (t,w_n)]ds\hfill \\ & +{\int }_a^{b}G(t,s)[L[w_n+{\int }_a^{b}G(t,s)[L\left[w_n\right]+N\left[w_n\right]-\Psi (t,w_n)]ds]\hfill \\ & +N[w_n+{\int }_a^{b}G(t,s)[L\left[w_n\right]+N\left[w_n\right]-\Psi (t,w_n)]ds]-\Psi (t,\mathcal{H}{w}_n)]ds\hfill \end{array}$$

$$\begin{array}{cc}\hfill u_{n+1}& =\mathcal{H}[v_n+{\int }_a^{b}G(t,s)[L\left[v_n\right]+N\left[v_n\right]-\Psi (t,v_n)]ds]\hfill \\ & =v_n+{\int }_a^{b}G(t,s)[L\left[v_n\right]+N\left[v_n\right]-\Psi (t,v_n)]ds\hfill \\ & +{\int }_a^{b}G(t,s)[L[v_n+{\int }_a^{b}G(t,s)[L\left[v_n\right]+N\left[v_n\right]-\Psi (t,v_n)]ds]\hfill \\ & +N[v_n+{\int }_a^{b}G(t,s)[L\left[v_n\right]+N\left[v_n\right]-\Psi (t,v_n)]ds]-\Psi (t,\mathcal{H}{v}_n)]ds\hfill \end{array}$$

This can summarily be written as:

$$\begin{array}{cc}\hfill x_n& =u_n+{\alpha }_n{\int }_a^{b}G(t,s)[L\left[u_n\right]+N\left[u_n\right]-\Psi (t,u_n)]ds\hfill \\ & +{\int }_a^{b}G(t,s)[L[u_n+{\alpha }_n{\int }_a^{b}G(t,s)[L\left[u_n\right]+N\left[u_n\right]-\Psi (t,u_n)]ds]\hfill \\ & +N[u_n+{\alpha }_n{\int }_a^{b}G(t,s)[L\left[u_n\right]+N\left[u_n\right]-\Psi (t,u_n)]ds]\hfill \\ & -\Psi (t,u_n+{\int }_a^{b}G(t,s)[L\left[u_n\right]+N\left[u_n\right]-\Psi (t,u_n)]ds)]ds\hfill \\ \hfill w_n& =x_n+{\int }_a^{b}G(t,s)[L\left[x_n\right]+N\left[x_n\right]-\Psi (t,x_n)]ds\hfill \\ & +{\int }_a^{b}G(t,s)[L[x_n+{\int }_a^{b}G(t,s)[L\left[x_n\right]+N\left[x_n\right]-\Psi (t,x_n)]ds]\hfill \\ & +N[x_n+{\int }_a^{b}G(t,s)[L\left[x_n\right]+N\left[x_n\right]-\Psi (t,x_n)]ds]-\Psi (t,\mathcal{H}{x}_n)]ds\hfill \\ \hfill v_n& =w_n+{\int }_a^{b}G(t,s)[L\left[w_n\right]+N\left[w_n\right]-\Psi (t,w_n)]ds\hfill \\ & +{\int }_a^{b}G(t,s)[L[w_n+{\int }_a^{b}G(t,s)[L\left[w_n\right]+N\left[w_n\right]-\Psi (t,w_n)]ds]\hfill \\ & +N[w_n+{\int }_a^{b}G(t,s)[L\left[w_n\right]+N\left[w_n\right]-\Psi (t,w_n)]ds]-\Psi (t,\mathcal{H}{w}_n)]ds\hfill \\ \hfill u_{n+1}& =v_n+{\int }_a^{b}G(t,s)[L\left[v_n\right]+N\left[v_n\right]-\Psi (t,v_n)]ds\hfill \\ & +{\int }_a^{b}G(t,s)[L[v_n+{\int }_a^{b}G(t,s)[L\left[v_n\right]+N\left[v_n\right]-\Psi (t,v_n)]ds]\hfill \\ & +N[v_n+{\int }_a^{b}G(t,s)[L\left[v_n\right]+N\left[v_n\right]-\Psi (t,v_n)]ds]-\Psi (t,\mathcal{H}{v}_n)]ds\hfill \end{array}$$

(44)

5.3. Convergence Analysis

We can now find the solution for the BVP via Green’s function by showing the convergence analysis of our iterative scheme, the Picard like-Green scheme (43). This can be achieved by considering the following third-order BVP;

$$-h^{‴}(t)=\Psi (t,h(t),h^{\prime }(t),h^{″}(t))$$

with BCs

$$h(1)={\mathcal{K}}_1,h^{″}(1)={\mathcal{K}}_2,h(2)={\mathcal{K}}_3.$$

We obtain the Green’s function by solving the homogeneous equation $h^{‴}(t)=0$. The Green’s function is given as follows:

$$G(t,s)=\left\{\begin{array}{c}{k}_1{t}^2+k_{2}t+k_3,1\le t\le s\le 2\hfill \\ l_1{t}^2+l_{2}t+l_3,1\le s\le t\le 2\hfill \end{array}\right.$$

(45)

The real values of $k_i,l_i$ ($i=1,2,3$) can be obtained by applying axioms $(A_1)-(A_4)$, so that (45) becomes

$$G(t,s)=\left\{\begin{array}{c}-{\displaystyle \frac{s^2}{2}}+2s-2+({\displaystyle \frac{s^2}{2}}-2s+2)t,1\le t\le s\le 2\hfill \\ -s^2+2s-2+({\displaystyle \frac{s^2}{2}}-s+2)t-{\displaystyle \frac{1}{2}}{t}^2,1\le s\le t\le 2.\hfill \end{array}\right.$$

(46)

Next, we redefine the Picard-like-Green iterative scheme (43) as

$$\left\{\begin{array}{c}{x}_n={\mathcal{G}}_G[(1-{\alpha }_n)u_n+{\alpha }_n{\mathcal{G}}_G{u}_n]\hfill \\ w_n={\mathcal{G}}_G^2{x}_n\hfill \\ v_n={\mathcal{G}}_G^2{w}_n\hfill \\ u_{n+1}={\mathcal{G}}_G^2{v}_n\hfill \end{array}\right.$$

(47)

where the operator ${\mathcal{G}}_G:C^2([1,2])\to C^2([1,2])$ is defined as

$${\mathcal{G}}_G=u+{\int }_1^{2}G(t,s)(u^{‴}-\Psi (s,u,u^{\prime },u^{″}))ds$$

(48)

The initial iterate, $u_0$ of (47) satisfies the equation $u_0^{″}=0$ with BCs; $u_0(1)={\mathcal{K}}_1$, $u_0^{″}(1)={\mathcal{K}}_2$ and $u_0(2)={\mathcal{K}}_3$.

If we apply integration by part three times to ${\int }_1^{2}G(t,s)u^{‴}(s)ds$, as it appears in (48) and keeping in mind that ${\int }_1^2{\displaystyle \frac{{\partial }^{3}G(t,s)}{\partial s^3}}u(s)ds={\int }_1^2\delta (x-s)u(s)ds$, we have that

$${\mathcal{G}}_G(u)=(2-t){\mathcal{K}}_1+{\displaystyle \frac{1}{2}}(t^2-3t+2){\mathcal{K}}_2+(t-1){\mathcal{K}}_3-{\int }_1^{2}G(t,s)\Psi (s,u,u^{\prime },u^{″})ds.$$

Furthermore, we want to show that the operator ${\mathcal{G}}_G$ is a contraction on the Banach space $C^2([1,2])$ with respect to the norm

$${\parallel u\parallel }_{C^2}=\sum _{i=0}^2\underset{s\in [1,2]}{sup}|u^{(i)}(s)|$$

under certain conditions on $\Psi$. Particularly, we prove that ${\mathcal{G}}_G$ is a Zamfirescu operator under certain conditions on $\Psi$.

Theorem 7.

Assume Ψ as in ${\mathcal{G}}_G$, satisfies the Lipschitz condition

$$|\Psi (s,u,u^{\prime },u^{″})-\Psi (s,m,m^{\prime },m^{″})|\le {\sigma }_1|u(s)-m(s)|+{\sigma }_2|u^{\prime }(s)-m^{\prime }(s)|+{\sigma }_3|u^{″}(s)-m^{″}(s)|$$

(49)

where ${\sigma }_1,{\sigma }_2$ and ${\sigma }_3$ are positive constants, such that

$${\displaystyle \frac{1}{8}}max\{{\sigma }_1,{\sigma }_2,{\sigma }_3\}\le 1.$$

The operator ${\mathcal{G}}_G$ is a contraction on the Banach space $C^2{([1,2],\parallel ·\parallel }_{C^2})$, and the sequence $\{u_n\}$ defined by (5) converges strongly to the fixed point of ${\mathcal{G}}_G$.

Proof. 

Let $u_1,u_2\in C^2([1,2])$, so that by (49), we have

$$\begin{array}{cc}\hfill |{\mathcal{G}}_G(u_1)-{\mathcal{G}}_G(u_2)|& =|{\int }_1^{2}G(t,s)\Psi (s,u_1,u_1^{\prime },u_1^{″})ds-{\int }_1^{2}G(t,s)\Psi (s,u_2,u_2^{\prime },u_2^{″})ds|\hfill \\ & =\left|{\int }_1^{2}G(t,s)[\Psi (s,u_1,u_1^{\prime },u_1^{″})-\Psi (s,u_2,u_2^{\prime },u_2^{″})]ds\right|\hfill \\ & \le {\int }_1^2|G(t,s)|\left|[\Psi (s,u_1,u_1^{\prime },u_1^{″})-\Psi (s,u_2,u_2^{\prime },u_2^{″})]\right|ds\hfill \\ & \le \left(\underset{[1,2]\times [1,2]}{sup}|G(t,s)|\right){\int }_1^2\left|[\Psi (s,u_1,u_1^{\prime },u_1^{″})-\Psi (s,u_2,u_2^{\prime },u_2^{″})]\right|ds\hfill \\ & =G({\displaystyle \frac{3}{4}},1){\int }_1^2\left|[\Psi (s,u_1,u_1^{\prime },u_1^{″})-\Psi (s,u_2,u_2^{\prime },u_2^{″})]\right|ds\hfill \\ & ={\displaystyle \frac{1}{8}}{\int }_1^2\left|[\Psi (s,u_1,u_1^{\prime },u_1^{″})-\Psi (s,u_2,u_2^{\prime },u_2^{″})]\right|ds\hfill \\ & \le {\displaystyle \frac{1}{8}}{\int }_1^2\left[{\sigma }_1|u_1(s)-u_2(s)|+{\sigma }_2|u_1^{\prime }(s)-u_2^{\prime }(s)|+{\sigma }_3|u_1^{″}(s)-u_2^{″}(s)|\right]ds\hfill \\ & \le {\displaystyle \frac{1}{8}}max\{{\sigma }_1,{\sigma }_2,{\sigma }_3\}{\int }_1^2\left(\sum _{i=1}^2|u_1^{(i)}(s)-u_2^{(i)}(s)|\right)ds\hfill \\ & \le {\displaystyle \frac{1}{8}}max\{{\sigma }_1,{\sigma }_2,{\sigma }_3\}{\parallel u_1-u_2\parallel }_{C^2}\hfill \\ & <\parallel u_1-u_2{\parallel }_{C^2}\hfill \end{array}$$

which shows that ${\mathcal{G}}_G$ is a contraction.

Again, we prove that the sequence $\{u_n\}$ generated by the Picard-like iterative scheme (5) converges strongly to the fixed point of the operator, ${\mathcal{G}}_G$.

As ${\mathcal{G}}_G$ is a contraction as shown above, it is guaranteed from the Banach contraction principle that there exists a unique fixed point, ${\tau }^{\ast }$ of ${\mathcal{G}}_G$ in the Banach space $C^2{([1,2],\parallel ·\parallel }_{C^2})$. Then, what is left is to show that $\underset{n\to \infty }{lim}=0$. From (47), we have

$$\begin{array}{cc}\hfill \parallel x_n-{\tau }^{\ast }\parallel & =\parallel {\mathcal{G}}_G[(1-{\alpha }_n)u_n+{\alpha }_n{\mathcal{G}}_G{u}_n]-{\tau }^{\ast }\parallel \hfill \\ & \le \delta \parallel (1-{\alpha }_n)u_n+{\alpha }_n{\mathcal{G}}_G{u}_n-{\tau }^{\ast }\parallel \hfill \\ & \le \delta (1-{\alpha }_n)\parallel u_n-{\tau }^{\ast }\parallel +\delta {\alpha }_n\parallel {\mathcal{G}}_G{u}_n-{\tau }^{\ast }\parallel \hfill \\ & \le \delta (1-{\alpha }_n)\parallel u_n-{\tau }^{\ast }\parallel +{\delta }^2{\alpha }_n\parallel u_n-{\tau }^{\ast }\parallel \hfill \\ & =[\delta (1-{\alpha }_n)+{\delta }^2{\alpha }_n]\parallel u_n-{\tau }^{\ast }\parallel \hfill \\ & =\delta [1-(1-\delta ){\alpha }_n]\parallel u_n-{\tau }^{\ast }\parallel \hfill \end{array}$$

(50)

$$\begin{array}{cc}\hfill \parallel w_n-{\tau }^{\ast }\parallel & =\parallel {\mathcal{G}}_G^2{x}_n-{\tau }^{\ast }\parallel \hfill \\ & \le \delta \parallel {\mathcal{G}}_G{x}_n-{\tau }^{\ast }\parallel \hfill \\ & \le {\delta }^2\parallel x_n-{\tau }^{\ast }\parallel \hfill \end{array}$$

(51)

$$\begin{array}{cc}\hfill \parallel v_n-{\tau }^{\ast }\parallel & =\parallel {\mathcal{G}}_G^2{w}_n-{\tau }^{\ast }\parallel \hfill \\ & \le \delta \parallel {\mathcal{G}}_G{w}_n-{\tau }^{\ast }\parallel \hfill \\ & \le {\delta }^2\parallel w_n-{\tau }^{\ast }\parallel \hfill \end{array}$$

(52)

$$\begin{array}{cc}\hfill \parallel u_{n+1}-{\tau }^{\ast }\parallel & =\parallel {\mathcal{G}}_G^2{v}_n-{\tau }^{\ast }\parallel \hfill \\ & \le \delta \parallel {\mathcal{G}}_G{v}_n-{\tau }^{\ast }\parallel \hfill \\ & \le {\delta }^2\parallel v_n-{\tau }^{\ast }\parallel .\hfill \end{array}$$

(53)

Combining (50) and (51), we have;

$$\parallel w_n-{\tau }^{\ast }\parallel \le {\delta }^3[1-(1-\delta ){\alpha }_n]\parallel u_n-{\tau }^{\ast }\parallel$$

(54)

Putting (54) in (52),

$$\parallel v_n-{\tau }^{\ast }\parallel \le {\delta }^5[1-(1-\delta ){\alpha }_n]\parallel u_n-{\tau }^{\ast }\parallel$$

(55)

Combining (53) and (55), we have

$$\parallel un+1-{\tau }^{\ast }\parallel \le {\delta }^7[1-(1-\delta ){\alpha }_n]\parallel u_n-{\tau }^{\ast }\parallel .$$

Inductively,

$$\begin{array}{cc}\hfill \parallel u_{n+1}-{\tau }^{\ast }\parallel & \le {\delta }^{7(n+1)}[1-(1-\delta ){\alpha }_n]\parallel u_0-{\tau }^{\ast }\parallel \hfill \\ & \le {\delta }^{7(n+1)}\parallel u_0-{\tau }^{\ast }\parallel \prod _{j=0}^n[1-(1-\delta ){\alpha }_j].\hfill \end{array}$$

From basic analysis, it is obvious that $1-x\le e^{-x}$ for $0<x<1$, so that

$$\begin{array}{cc}\hfill \parallel u_{n+1}-{\tau }^{\ast }\parallel & \le {\delta }^{7(n+1)}\parallel u_0-{\tau }^{\ast }\parallel \prod _{j=0}^n{e}^{-(1-\delta ){\alpha }_j}\hfill \\ & \le {\delta }^{7(n+1)}{\parallel u_0-{\tau }^{\ast }\parallel }^{n+1}{e}^{-(1-\delta ){\sum }_{j=0}^{\infty }{\alpha }_j}.\hfill \end{array}$$

Clearly, if ${\sum }_{j=0}^{\infty }=\infty$, such that $e^{-(1-\delta ){\sum }_{j=0}^{\infty }{\alpha }_j}\to 0$ as $n\to \infty$, then $\underset{n\to \infty }{lim}\parallel u_n-{\tau }^{\ast }\parallel =0$, which completes the proof. □

Example 2.

Consider the equation

$$u^{″}(t)+[u^{\prime }(t)+2t{u}^{″}(t)+{\displaystyle \frac{1}{3}}t{(u^{\prime }(t))}^2]e^{-{\displaystyle \frac{u}{4}}}=0$$

(56)

with BCs.

$$u(1)=0,u^{″}(1)=-1,u(2)=ln2.$$

The Green’s function corresponding to the homogeneous linear part of (56), that is $u^{‴}=0$ on the interval $[1,2]$ is

$$G(t,s)=\left\{\begin{array}{c}{\displaystyle \frac{1}{2}}{t}^2+(-{\displaystyle \frac{1}{2}}{s}^2+s-2)+s^2-2s+2,1\le s\le t\le 2.\hfill \\ (-{\displaystyle \frac{1}{2}}{s}^2+2s-2)t+({\displaystyle \frac{1}{2}}{s}^2-2s+2),1\le t\le s\le 2.\hfill \end{array}\right.$$

Applying the Picard-like-Green iterative scheme, as expressed in (44), we have the initial iterate as

$$u_0=-1-ln2+({\displaystyle \frac{3}{2}}+ln2)t-{\displaystyle \frac{1}{2}}{t}^2$$

and,

$$\begin{array}{cc}\hfill x_n& =(u_n+{\alpha }_n{\int }_1^t\left[{\displaystyle \frac{1}{2}}{t}^2+(-{\displaystyle \frac{1}{2}}{s}^2+s-2)+s^2-2s+2\right]\hfill \\ & \times \left[u_n^{‴}(s)+[u^{\prime }(s)+2s{u}_n^{″}(s)+{\displaystyle \frac{1}{2}}s{(u_n^{\prime }(s))}^2]e^{-{\displaystyle \frac{u_n(s)}{4}}}\right]ds\hfill \\ & +{\alpha }_n{\int }_t^2\left[(-{\displaystyle \frac{1}{2}}{s}^2+2s-2)t+({\displaystyle \frac{1}{2}}{s}^2-2s+2)\right]\hfill \\ & \times \left[u_n^{‴}(s)+[u_n^{\prime }(s)+2s{u}_n^{″}(s)+{\displaystyle \frac{1}{2}}s{(u_n^{\prime }(s))}^2]e^{-{\displaystyle \frac{u_n(s)}{4}}}\right]ds)\hfill \\ & +{\int }_1^t\left[{\displaystyle \frac{1}{2}}{t}^2+(-{\displaystyle \frac{1}{2}}{s}^2+s-2)+s^2-2s+2\right]\hfill \\ & \times [u_n+{\alpha }_n{\int }_1^t\left[{\displaystyle \frac{1}{2}}{t}^2+(-{\displaystyle \frac{1}{2}}{s}^2+s-2)+s^2-2s+2\right]\hfill \\ & \times \left[u_n^{‴}(s)+[u^{\prime }(s)+2s{u}_n^{″}(s)+{\displaystyle \frac{1}{2}}s{(u_n^{\prime }(s))}^2]e^{-{\displaystyle \frac{u_n(s)}{4}}}\right]ds\hfill \\ & +{\alpha }_n{\int }_t^2\left[(-{\displaystyle \frac{1}{2}}{s}^2+2s-2)t+({\displaystyle \frac{1}{2}}{s}^2-2s+2)\right]\hfill \\ & \times \left[u_n^{‴}(s)+[u_n^{\prime }(s)+2s{u}_n^{″}(s)+{\displaystyle \frac{1}{2}}s{(u_n^{\prime }(s))}^2]e^{-{\displaystyle \frac{u_n(s)}{4}}}\right]ds]ds\hfill \\ & +{\int }_t^2\left[(-{\displaystyle \frac{1}{2}}{s}^2+2s-2)t+({\displaystyle \frac{1}{2}}{s}^2-2s+2)\right]\hfill \\ & \times [u_n+{\alpha }_n{\int }_1^t\left[{\displaystyle \frac{1}{2}}{t}^2+(-{\displaystyle \frac{1}{2}}{s}^2+s-2)+s^2-2s+2\right]\hfill \\ & \times \left[u_n^{‴}(s)+[u^{\prime }(s)+2s{u}_n^{″}(s)+{\displaystyle \frac{1}{2}}s{(u_n^{\prime }(s))}^2]e^{-{\displaystyle \frac{u_n(s)}{4}}}\right]ds\hfill \\ & +{\alpha }_n{\int }_t^2\left[(-{\displaystyle \frac{1}{2}}{s}^2+2s-2)t+({\displaystyle \frac{1}{2}}{s}^2-2s+2)\right]\hfill \\ & \times \left[u_n^{‴}(s)+[u_n^{\prime }(s)+2s{u}_n^{″}(s)+{\displaystyle \frac{1}{2}}s{(u_n^{\prime }(s))}^2]e^{-{\displaystyle \frac{u_n(s)}{4}}}\right]ds]ds,\hfill \end{array}$$

$$\begin{array}{cc}\hfill w_n& =(x_n+{\alpha }_n{\int }_1^t\left[{\displaystyle \frac{1}{2}}{t}^2+(-{\displaystyle \frac{1}{2}}{s}^2+s-2)+s^2-2s+2\right]\hfill \\ & \times \left[x_n^{‴}(s)+[x^{\prime }(s)+2s{x}_n^{″}(s)+{\displaystyle \frac{1}{2}}s{(x_n^{\prime }(s))}^2]e^{-{\displaystyle \frac{x_n(s)}{4}}}\right]ds\hfill \\ & +{\alpha }_n{\int }_t^2\left[(-{\displaystyle \frac{1}{2}}{s}^2+2s-2)t+({\displaystyle \frac{1}{2}}{s}^2-2s+2)\right]\hfill \\ & \times \left[x_n^{‴}(s)+[x_n^{\prime }(s)+2s{x}_n^{″}(s)+{\displaystyle \frac{1}{2}}s{(x_n^{\prime }(s))}^2]e^{-{\displaystyle \frac{x_n(s)}{4}}}\right]ds)\hfill \\ & +{\int }_1^t\left[{\displaystyle \frac{1}{2}}{t}^2+(-{\displaystyle \frac{1}{2}}{s}^2+s-2)+s^2-2s+2\right]\hfill \\ & \times [x_n+{\alpha }_n{\int }_1^t\left[{\displaystyle \frac{1}{2}}{t}^2+(-{\displaystyle \frac{1}{2}}{s}^2+s-2)+s^2-2s+2\right]\hfill \\ & \times \left[x_n^{‴}(s)+[x^{\prime }(s)+2s{x}_n^{″}(s)+{\displaystyle \frac{1}{2}}s{(x_n^{\prime }(s))}^2]e^{-{\displaystyle \frac{x_n(s)}{4}}}\right]ds\hfill \\ & +{\alpha }_n{\int }_t^2\left[(-{\displaystyle \frac{1}{2}}{s}^2+2s-2)t+({\displaystyle \frac{1}{2}}{s}^2-2s+2)\right]\hfill \\ & \times \left[x_n^{‴}(s)+[x_n^{\prime }(s)+2s{x}_n^{″}(s)+{\displaystyle \frac{1}{2}}s{(x_n^{\prime }(s))}^2]e^{-{\displaystyle \frac{x_n(s)}{4}}}\right]ds]ds\hfill \\ & +{\int }_t^2\left[(-{\displaystyle \frac{1}{2}}{s}^2+2s-2)t+({\displaystyle \frac{1}{2}}{s}^2-2s+2)\right]\hfill \\ & \times [x_n+{\alpha }_n{\int }_1^t\left[{\displaystyle \frac{1}{2}}{t}^2+(-{\displaystyle \frac{1}{2}}{s}^2+s-2)+s^2-2s+2\right]\hfill \\ & \times \left[x_n^{‴}(s)+[x^{\prime }(s)+2s{x}_n^{″}(s)+{\displaystyle \frac{1}{2}}s{(x_n^{\prime }(s))}^2]e^{-{\displaystyle \frac{x_n(s)}{4}}}\right]ds\hfill \\ & +{\alpha }_n{\int }_t^2\left[(-{\displaystyle \frac{1}{2}}{s}^2+2s-2)t+({\displaystyle \frac{1}{2}}{s}^2-2s+2)\right]\hfill \\ & \times \left[x_n^{‴}(s)+[x_n^{\prime }(s)+2s{x}_n^{″}(s)+{\displaystyle \frac{1}{2}}s{(x_n^{\prime }(s))}^2]e^{-{\displaystyle \frac{x_n(s)}{4}}}\right]ds]ds,\hfill \end{array}$$

$$\begin{array}{cc}\hfill v_n& =(w_n+{\alpha }_n{\int }_1^t\left[{\displaystyle \frac{1}{2}}{t}^2+(-{\displaystyle \frac{1}{2}}{s}^2+s-2)+s^2-2s+2\right]\hfill \\ & \times \left[w_n^{‴}(s)+[w^{\prime }(s)+2s{w}_n^{″}(s)+{\displaystyle \frac{1}{2}}s{(w_n^{\prime }(s))}^2]e^{-{\displaystyle \frac{w_n(s)}{4}}}\right]ds\hfill \\ & +{\alpha }_n{\int }_t^2\left[(-{\displaystyle \frac{1}{2}}{s}^2+2s-2)t+({\displaystyle \frac{1}{2}}{s}^2-2s+2)\right]\hfill \\ & \times \left[w_n^{‴}(s)+[w_n^{\prime }(s)+2s{w}_n^{″}(s)+{\displaystyle \frac{1}{2}}s{(w_n^{\prime }(s))}^2]e^{-{\displaystyle \frac{w_n(s)}{4}}}\right]ds)\hfill \\ & +{\int }_1^t\left[{\displaystyle \frac{1}{2}}{t}^2+(-{\displaystyle \frac{1}{2}}{s}^2+s-2)+s^2-2s+2\right]\hfill \\ & \times [w_n+{\alpha }_n{\int }_1^t\left[{\displaystyle \frac{1}{2}}{t}^2+(-{\displaystyle \frac{1}{2}}{s}^2+s-2)+s^2-2s+2\right]\hfill \\ & \times \left[w_n^{‴}(s)+[w^{\prime }(s)+2s{w}_n^{″}(s)+{\displaystyle \frac{1}{2}}s{(w_n^{\prime }(s))}^2]e^{-{\displaystyle \frac{w_n(s)}{4}}}\right]ds\hfill \\ & +{\alpha }_n{\int }_t^2\left[(-{\displaystyle \frac{1}{2}}{s}^2+2s-2)t+({\displaystyle \frac{1}{2}}{s}^2-2s+2)\right]\hfill \\ & \times \left[w_n^{‴}(s)+[w_n^{\prime }(s)+2s{w}_n^{″}(s)+{\displaystyle \frac{1}{2}}s{(w_n^{\prime }(s))}^2]e^{-{\displaystyle \frac{w_n(s)}{4}}}\right]ds]ds\hfill \\ & +{\int }_t^2\left[(-{\displaystyle \frac{1}{2}}{s}^2+2s-2)t+({\displaystyle \frac{1}{2}}{s}^2-2s+2)\right]\hfill \\ & \times [w_n+{\alpha }_n{\int }_1^t\left[{\displaystyle \frac{1}{2}}{t}^2+(-{\displaystyle \frac{1}{2}}{s}^2+s-2)+s^2-2s+2\right]\hfill \\ & \times \left[w_n^{‴}(s)+[w^{\prime }(s)+2s{w}_n^{″}(s)+{\displaystyle \frac{1}{2}}s{(w_n^{\prime }(s))}^2]e^{-{\displaystyle \frac{w_n(s)}{4}}}\right]ds\hfill \\ & +{\alpha }_n{\int }_t^2\left[(-{\displaystyle \frac{1}{2}}{s}^2+2s-2)t+({\displaystyle \frac{1}{2}}{s}^2-2s+2)\right]\hfill \\ & \times \left[w_n^{‴}(s)+[w_n^{\prime }(s)+2s{w}_n^{″}(s)+{\displaystyle \frac{1}{2}}s{(w_n^{\prime }(s))}^2]e^{-{\displaystyle \frac{w_n(s)}{4}}}\right]ds]ds,\hfill \end{array}$$

$$\begin{array}{cc}\hfill u_{n+1}& =(v_n+{\alpha }_n{\int }_1^t\left[{\displaystyle \frac{1}{2}}{t}^2+(-{\displaystyle \frac{1}{2}}{s}^2+s-2)+s^2-2s+2\right]\hfill \\ & \times \left[v_n^{‴}(s)+[v^{\prime }(s)+2s{v}_n^{″}(s)+{\displaystyle \frac{1}{2}}s{(v_n^{\prime }(s))}^2]e^{-{\displaystyle \frac{v_n(s)}{4}}}\right]ds\hfill \\ & +{\alpha }_n{\int }_t^2\left[(-{\displaystyle \frac{1}{2}}{s}^2+2s-2)t+({\displaystyle \frac{1}{2}}{s}^2-2s+2)\right]\hfill \\ & \times \left[v_n^{‴}(s)+[v_n^{\prime }(s)+2s{v}_n^{″}(s)+{\displaystyle \frac{1}{2}}s{(v_n^{\prime }(s))}^2]e^{-{\displaystyle \frac{v_n(s)}{4}}}\right]ds)\hfill \\ & +{\int }_1^t\left[{\displaystyle \frac{1}{2}}{t}^2+(-{\displaystyle \frac{1}{2}}{s}^2+s-2)+s^2-2s+2\right]\hfill \\ & \times [v_n+{\alpha }_n{\int }_1^t\left[{\displaystyle \frac{1}{2}}{t}^2+(-{\displaystyle \frac{1}{2}}{s}^2+s-2)+s^2-2s+2\right]\hfill \\ & \times \left[v_n^{‴}(s)+[v^{\prime }(s)+2s{v}_n^{″}(s)+{\displaystyle \frac{1}{2}}s{(v_n^{\prime }(s))}^2]e^{-{\displaystyle \frac{v_n(s)}{4}}}\right]ds\hfill \\ & +{\alpha }_n{\int }_t^2\left[(-{\displaystyle \frac{1}{2}}{s}^2+2s-2)t+({\displaystyle \frac{1}{2}}{s}^2-2s+2)\right]\hfill \\ & \times \left[v_n^{‴}(s)+[v_n^{\prime }(s)+2s{v}_n^{″}(s)+{\displaystyle \frac{1}{2}}s{(v_n^{\prime }(s))}^2]e^{-{\displaystyle \frac{v_n(s)}{4}}}\right]ds]ds\hfill \\ & +{\int }_t^2\left[(-{\displaystyle \frac{1}{2}}{s}^2+2s-2)t+({\displaystyle \frac{1}{2}}{s}^2-2s+2)\right]\hfill \\ & \times [v_n+{\alpha }_n{\int }_1^t\left[{\displaystyle \frac{1}{2}}{t}^2+(-{\displaystyle \frac{1}{2}}{s}^2+s-2)+s^2-2s+2\right]\hfill \\ & \times \left[v_n^{‴}(s)+[v^{\prime }(s)+2s{v}_n^{″}(s)+{\displaystyle \frac{1}{2}}s{(v_n^{\prime }(s))}^2]e^{-{\displaystyle \frac{v_n(s)}{4}}}\right]ds\hfill \\ & +{\alpha }_n{\int }_t^2\left[(-{\displaystyle \frac{1}{2}}{s}^2+2s-2)t+({\displaystyle \frac{1}{2}}{s}^2-2s+2)\right]\hfill \\ & \times \left[v_n^{‴}(s)+[v_n^{\prime }(s)+2s{v}_n^{″}(s)+{\displaystyle \frac{1}{2}}s{(v_n^{\prime }(s))}^2]e^{-{\displaystyle \frac{v_n(s)}{4}}}\right]ds]ds.\hfill \end{array}$$

With the best choice of ${\alpha }_n\in (0,1)$, our new Picard-like-Green iterative scheme performs better than other existing Green’s-function-based iterative schemes such as Picard–Green [7], Mann–Green [8], Ishikawa–Green [9], Khan–Green [29], Picard–Ishikawa–Green [30], and many more in the literature.

6. Conclusions

In this paper, our new iterative scheme (5) approximates the fixed point of mapping satisfying the condition $(B_{\gamma ,\mu })$, as shown in the main results. The scheme converges faster than some selected schemes, already existing in the literature, as shown in Example 1 which is also presented numerically in Table 1 and Figure 1. Furthermore, the Picard-like-Green iterative scheme generalizes other Green’s-function-based scheme highlighted in the work. Finally, to show the applicability of our main results, it is applied to the approximation of the solution of infectious disease models.