Abstract
Evolutionary inferences from phylogenetic trees can be modeled stochastically using a range of mathematical frameworks. Among these, stochastic differential equations (SDEs) provide a particularly flexible and powerful approach to capturing the continuous-time dynamics of evolutionary processes. This review summarizes advances in stochastic modeling for trait evolution along a phylogenetic tree, with a focus on stochastic differential equations (SDEs), Gaussian and non-Gaussian processes, and time series models that can be expressed as special cases of general stochastic frameworks, depending on the questions being addressed or the types of data analyzed. We explore current developments and future research directions of stochastic modeling for phylogenetic comparative analysis in trait evolution.
Keywords:
stochastic differential equations; trait evolution; biological modeling; phylogenetic trees; measures of association MSC:
60H10; 92D15; 92B10; 62M10; 62H20
1. Introduction
Phylogenetics, the study of evolutionary relationships between species, addresses fundamental questions about life’s history and the mechanisms that shape biodiversity. The field faces challenges in scaling computational methods, modeling complex evolutionary processes, and integrating diverse data types, driving ongoing innovation in mathematics, methodology, and computation. One of the main challenges is the development of robust models of the evolution of traits that account for complex dynamics, including correlations, constraints, and varying rates [1,2,3]. Such models are crucial for studying adaptive evolution and the development of ecological and life-history traits [4]. These models allow researchers to infer evolutionary processes by accounting for shared ancestry, using stochastic approaches to describe trait dynamics. For example, understanding the rate heterogeneity in molecular evolution remains a fundamental challenge [5]. Understanding why some lineages or genes evolve faster than others and how to incorporate rate variation into phylogenetic inference, along with combining quantitative genetics and phylogenetic information [6], is critical for studying adaptive evolution and reconstructing ancient evolutionary events [7,8]. These advances have bridged phenotypic evolution, ecological adaptation, and genomic underpinnings by allowing researchers to account for evolutionary rate heterogeneity and, thus, gain deeper insights into the processes shaping trait variation over evolutionary timescales.
One of the current key challenges is ensuring the reliability and robustness of phylogenetic methods. Achieving this requires developing a more rigorous mathematical model and performing more realistic simulations and benchmarks to test methods under various evolutionary scenarios, as well as strategies to mitigate the effects of model mis-specification [4]. Solving these problems will deepen our understanding of evolution and provide powerful tools for studying the diversity of life.
In this review, we begin by exploring the mathematical perspective, utilizing stochastic differential equations as a comprehensive framework for studying the evolution of traits in biological systems [1]. We then examine recent advancements in models that integrate paleontological and field study data with phylogenetic comparative methods (PCMs), enabling more accurate reconstructions of ancestral states and correlated evolution while providing valuable insights into trait evolution over deep timescales [9,10]. This progression has ultimately led to the development of phylogenetic comparative methods, incorporating both likelihood-based and non-likelihood-based statistical models to detect correlated evolution and advance methodological approaches [11,12,13,14].
The next section delves into the stochastic framework, highlighting its role in modeling trait evolution and addressing the complexities of evolutionary processes.
2. Stochastic Frameworks in PCMs
Stochastic processes, a mathematical framework that captures randomness and variability, have emerged as a powerful tool to elucidate the dynamics of ecosystems. The mathematical elegance showcased delves into stochastic differential equations, Markov processes, and advanced statistical techniques. These methodologies, fine-tuned for the intricacies of biological systems, enable researchers to simulate and analyze the inherent randomness and variability in ecological processes. Through this lens, this review catalyzes breakthroughs in predicting population trends, assessing biodiversity, and unraveling the subtleties of evolutionary dynamics. From population dynamics to species interactions, we explore how stochastic models navigate inherent uncertainties, providing a nuanced understanding of complex biological phenomena.
2.1. The Stochastic Model for Trait Evolution
The use of stochastic differential equations (SDEs) in evolutionary modeling offers a versatile approach to describing the temporal evolution of traits in a group of related species evolving along the phylogenetic tree . SDEs are governed by the general equation in Equation (1):
where represents the state of the system at time t (e.g., a trait value or species richness), is the drift term parameterized by , capturing deterministic trends, is the diffusion term parameterized by , modeling stochastic variability, and is a Wiener process (standard Brownian motion).
Early PCMs were built on Brownian motion models [15], serving as neutral baselines. The introduction of the Ornstein–Uhlenbeck (OU) process incorporated stabilizing selection and adaptive peaks [7,16]; it serves as the cornerstone in PCMs for modeling stabilizing selection. Other models, such as the early burst model for studying adaptive radiation [17] and the phylogenetic mixed model, which offers a potentially unifying approach to quantitative genetic and phylogenetic analysis [6], are feasible extensions of the Brownian motion models of trait evolution. Table 1 presents the three most commonly applied models and their associated biological phenomena.

Table 1.
Brownian-based extension model equations. The nuisance parameter is the positive rate of evolution parameter . The Ornstein–Uhlenbeck (OU) model includes a positive force parameter and a real-valued optimum parameter . The early burst (EB) model incorporates a parameter r with a non-positive value.
A phylogenetic tree , as shown in Figure 1 (upper-left panel), with branch set is a graphical representation of the evolutionary relationships among species, where both the branching pattern and the lengths of the branches convey important evolutionary information. The branching structure reflects the hierarchical divergence of lineages over time, illustrating how species have radiated from common ancestors. Each branch length in the tree can be interpreted as a measure of evolutionary time or genetic change—effectively serving as a molecular clock [22].
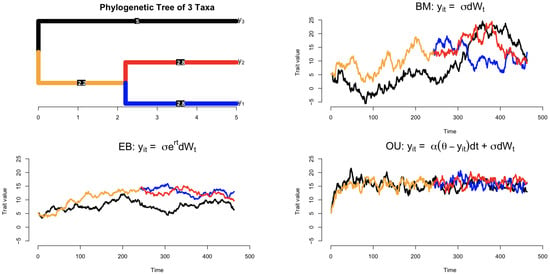
Figure 1.
Scheme for stochastic trait evolution along a rooted phylogenetic tree. Upper left: A phylogenetic tree of three taxa with branch lengths. The colors represent different lineages: Black: Lineage leading to Taxon . Red: Lineage leading to Taxon . Blue: Lineage leading to Taxon . Orange: The shared ancestral lineage before divergence. Upper right: Brownian motion trait evolution. The colored lines correspond to the evolutionary trajectory of traits for each taxon over time, showing random, unbounded changes. Lower left: Early burst trait evolution. The same color scheme applies, illustrating rapid initial trait changes (e.g., along the orange ancestral lineage) that slow down over time. Lower right: Ornstein–Uhlenbeck process trait evolution. Colored lines show the trait values stabilizing over time toward an optimal value (due to the attraction parameter ).
Longer branches indicate more extended periods of evolution or greater amounts of accumulated change, while shorter branches suggest more recent divergence or slower rates of evolution. This temporal scaling allows researchers to correlate trait evolution, as modeled by Brownian motion or Ornstein–Uhlenbeck processes, with specific periods in evolutionary history. By examining branch lengths, one can infer not only the chronological sequence of divergence events but also the relative depth of lineages in the tree, providing insights into how long a lineage has evolved independently. This dual encoding of time and hierarchical structure makes phylogenetic trees invaluable for studying evolutionary processes such as adaptive radiation, stabilizing selection, and other dynamics across deep time.
Figure 1 shows the trajectories for the Brownian motion–based Gaussian process model from Table 1, which depend on the phylogenetic tree . The plots illustrate deviations of trait evolution models (OU, EB) from the baseline Brownian motion (BM) model, assuming a rate parameter of and an ancestral state at the root of . For the Ornstein–Uhlenbeck (OU) model, key parameters include the strength of selection (force) and the adaptive optimum . A larger typically indicates a stronger force pulling traits back toward the optimum , leading to faster convergence to this mean-reverting state. In the early burst (EB) model, the radiation parameter signifies a strongly negative rate of evolutionary change. According to the literature, a more negative r results in pronounced adaptive radiation, as traits exhibit less change after divergence, thereby highlighting clearer adaptive phenomena. This combination of parameters showcases how each model diverges from the BM baseline over time, reflecting different evolutionary pressures and trajectories.
In the following section, we examine the interplay between natural selection and genetic drift and integrated OU processes and other Gaussian processes to account for adaptive constraints and micro-evolutionary assumptions.
2.2. Modeling Adaptation to Random Environment
A generalized OU model for the evolution of adaptive traits assumes the trait variable, , satisfying the SDE in Equation (2):
where is the strength of selection, is the optimal trait, and is the amplitude of noise.
Integrating with the factor , we have
where the optimal trait value is related to the covariate :
Bayesian approaches have proven particularly useful in estimating the parameters of such complex evolutionary models. For example, ref. [23] introduced flexible Bayesian methods to infer evolutionary parameters across a range of model formulations, and ref. [24] proposed Bayesian inference techniques for studying adaptive landscapes, providing nuanced insights into the shape and dynamics of evolutionary optima.
More recently, refs. [25,26] extended Brownian motion models to incorporate Ornstein–Uhlenbeck and early burst covariates, thereby accounting for both stabilizing selection [8] and adaptive radiation [8]. In particular, ref. [26] utilized approximate Bayesian computation (ABC) [27] to develop a flexible phylogenetic model of optimal adaptive trait evolution, allowing for diverse functional relationships between trait variables and their covariates (see also [28] for modeling trait-dependent speciation with ABC). Such advances in Bayesian inference frameworks continue to enrich our understanding of how traits evolve in response to varying evolutionary pressures.
2.3. Multivariate Normal Models
Multivariate normal models, particularly those founded on the Ornstein–Uhlenbeck (OU) process, offer a powerful framework for describing continuous trait evolution under stabilizing selection. In such models, each trait evolves stochastically toward an optimal value, and the joint distribution of the trait values at any time point is multivariate normal [29]. Consequently, one can fully characterize the process by its mean and covariance structures across the phylogeny.
Extending the standard univariate OU process to multiple traits requires matrix generalizations of the selection () and diffusion () parameters. Specifically, the SDE for a multivariate OU process is
where is the vector of traits at time t, (the drift matrix) describes how traits adapt towards their optima, represents time-varying optimal trait values (or selective regimes), and is the diffusion matrix controlling stochastic perturbations [30,31]. Often, is modeled as a step function along the phylogeny to capture shifts in selective regimes [21,29,30].
The solution to Equation (5) is given by
This formulation naturally accommodates correlation among traits and enables the study of complex patterns of phenotypic evolution under different adaptive landscapes [32].
Building on these foundational models, recent research has used BM and extended OU to model high-dimensional traits, often leveraging geometric morphometrics. Such approaches are particularly valuable for analyzing shape data, quantifying morphological integration, and identifying modules of functionally or developmentally correlated traits [11,12,33,34]. These techniques allow researchers to incorporate phylogenetic information into assessments of morphological variation, illuminating how ecological and selective pressures influence phenotypic diversification [35,36]. Overall, multivariate OU models continue to provide a robust and flexible framework for investigating the evolutionary processes that shape complex phenotypes in diverse taxa.
2.4. Non-Gaussian Processes
Beyond the classical Gaussian assumptions of Brownian and Ornstein–Uhlenbeck processes, there is growing interest in non-Gaussian processes.
2.4.1. Non-Negative Trait Model
To model the evolution of a non-negative adaptive trait , one may use the Cox–Ingersoll–Ross (CIR) process [37,38], which ensures that trait values remain non-negative. The SDE for the CIR-based trait evolution is
where is the strength of selection, is the optimal trait at time t, and is the diffusion parameter governing stochastic fluctuations. Multiplying both sides of Equation (7) by (and integrating) yields an explicit solution. Since appears in the diffusion term, is constrained to remain non-negative throughout its evolution.
2.4.2. Bounded Trait Model
For traits constrained to the interval —such as proportions or ratios in morphometric studies—ref. [39] introduced a bounded Brownian motion (BBM) model with two reflective boundaries. More generally, a Beta-like SDE can be written as [37]
where and play roles analogous to those in the CIR model, and . This specification is particularly useful for modeling proportional trait data (e.g., the ratio of tail length to body length in lizards or beak length to beak width in birds [40]).
Figure 2 presents the Gaussian processes ((a) Brownian motion and (b) Brownian motion with bounds) and non-Gaussian processes ((c) Cox-Ingersoll-Ross process and (d) Beta-like process) trajectories described in this section.
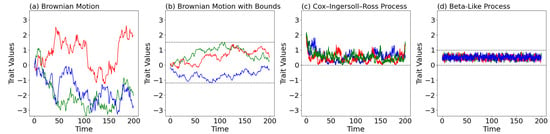
Figure 2.
Illustration of four different stochastic processes for trait evolution, each shown with three realizations, where each color represents an independent trajectory in the figure: (a) Brownian motion with and an overall scale of per time step, plotted with horizontal bounding lines. (b) Bounded Brownian-motion paths scaled by and marked by dashed boundary lines. (c) Cox–Ingersoll–Ross (CIR) process , which ensures non-negative trait values and exhibits mean-reverting behavior. (d) Beta-like process with reflective boundaries at 0 and 1, suitable for modeling traits confined to a fixed interval. Varying parameter choices and boundary constraints give rise to qualitatively different evolutionary dynamics.
Other contributions have examined fractional Brownian motion (FBM) [41] and Cauchy processes [42], which enable modeling of long-term dependencies and pulsed evolution, highlighting a promising direction, and which offer richer modeling frameworks for evolutionary biology and open new avenues for future research.
2.5. Phylogenetic Adaptive Regression and Rate of Evolution Model
One can model the time-varying optimal trait value as presented in Section 2.5.1:
where is a basis function expansion of the covariate , and where is a vector of regression coefficients. This approach accommodates flexible, potentially non-linear relationships between the covariate and the evolving trait optimum.
Additionally, as described in Section 2.5.2, the rate parameter in an evolutionary model can also be specified as a function of the covariate:
where is another set of basis functions, and where is a vector of coefficients. This formulation allows the intensity of stochastic fluctuations to adapt to the same (or different) covariate that drives the trait optimum.
By choosing appropriate basis functions for and , one can extend the optimal regression paradigm to encompass a wide variety of covariate effects and evolutionary dynamics, thereby offering a richer mathematical framework for phylogenetic adaptive trait evolution.
2.5.1. Optimal Regression Model
A simple polynomial representation of is given by
When follows a Brownian motion and , this reduces to an OUBM model, studied by [8]. Extensions to an OU process for yield the OUOU model [43]. More recently, ref. [44] introduced the OUBMPk and OUOUPk models, completing a family of phylogenetic adaptive trait-evolution frameworks.
Several alternative basis functions can also be used for the expansion in Equation (9). For instance, B-splines provide a smooth, piecewise-polynomial fit:
where are B-spline basis functions of order k, and where m is the number of basis terms.
2.5.2. Rate of Trait Evolution
To model rate of trait evolution as a function of the covariate, ref. [45] proposed an example where , with potentially following either Brownian motion or geometric Brownian motion. Ref. [26] further extended this model to cases where is generated by Ornstein–Uhlenbeck or early burst processes, thereby accounting for more complex evolutionary scenarios. One can also consider more general functional forms for . For instance: (quadratic), (polynomial), and (exponential). Although these formulations provide a richer representation of rate variation, the associated complexity can make exact moment-based derivations intractable, hence calling for a novel approach.
An potential extension involves modeling the optimum alongside a separate rate process; for instance:
where both (the optimal covariate) and (the rate covariate) follow their own stochastic dynamics [38]. In such a scenario, for instance, where and are Brownian motions, the target trait associated with the two covariates and evolve according to the system of stochastic differential equations as following
Since there is no closed-form likelihood for jointly using these more general processes , it is necessary to develop advanced statistical methods—such as approximate Bayesian computation (ABC) with efficient algorithms—to estimate parameters and perform inference, thereby facilitating the study of complex evolutionary dynamics. Figure 3 presents an overview of phylogenetic modeling of a trait evolution framework where the diagram illustrates the progression of models starting from Brownian motion (BM) with Gaussian increments, leading to Ornstein–Uhlenbeck (OU) with stabilizing selection, Cox–Ingersoll–Ross (CIR) with non-negative diffusion, and Beta distributions for bounded traits. These models converge into Joint Stochastic Modeling, which integrates phylogenetic optimality and rates of trait evolution for multivariate traits.
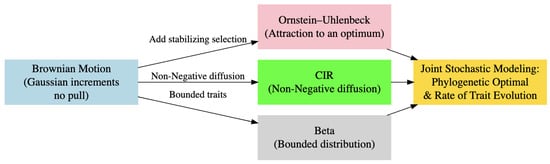
Figure 3.
Phylogenetic modeling framework: Models progress from Brownian motion (BM) to Joint Stochastic Modeling, integrating OU, CIR, and Beta distributions for trait evolution.
2.6. Joint Modeling Trait Evolution with DNA Data
Recent advances in phylogenetics have emphasized integrating DNA substitution models with trait evolution models [5,46]. Such approaches jointly analyze two types of data for n species: first, the molecular sequences , where each with represents the sequence data for species i (see Table 2 as an example); second, the real value phenotypic trait data .

Table 2.
Aligned coding sequences for three species () each with DNA sequence of length 10.
The transition rate matrix for the nucleotide substitution is shown in Equation (17):
where represents the transition rate from base x to base y, and the diagonal contains the term , which indicates that the rates sum to zero.
The transition probability matrix is evaluated as the exponential of the rate matrix [22] in Equation (18):
Accurate phylogenetic trees may be estimated using tools such as PASTA [47,48] for alignment refinement in large datasets, or ASTRAL [49] and BEST [50] for species-tree estimation under incomplete lineage sorting. These multilocus methods [51,52] improve the resolution and scalability of phylogenetic inference, enabling more precise exploration of correlations between molecular evolution and trait diversification. Alternatively, researchers may employ the pipeline by [53] to obtain phylogenetic trees and subsequently infer trait evolution. Figure 4 shows a six-taxa phylogenetic tree where the hierarchical structure highlights divergence events from the root to the terminal nodes, with time progressing upward. The divergence times vectors obtained from the tree and later used in the stochastic process modeling:
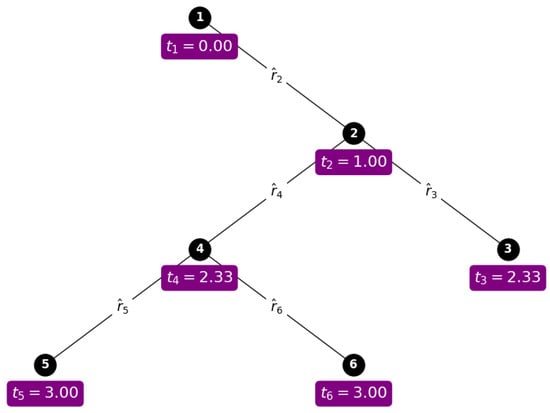
Figure 4.
Phylogenetic tree with divergence times: the nodes represent taxa, with their divergence times () shown in purple boxes, including values , , , , , and . Branch labels () indicate the rate parameters along corresponding branches.
Figure 5 illustrates the conceptual parallels in modeling evolutionary processes at both molecular and phenotypic scales. The JC model (shown in the left panel) serves as the foundational model for substitution modeling, with more complex models, such as K80, HKY, SYM, F81, and GTR, building upon this base [54]. Similarly, the BM (Brownian motion) model (depicted in the right panel) forms the basis for modeling trait evolution and can be extended to more advanced Gaussian-based models such as OU, EB [17], FBM [41] and LBD [10]. Parameters such as and for DNA models and H and for trait models represent additional components incorporated into these extended models, as indicated by the arrows in the figure.
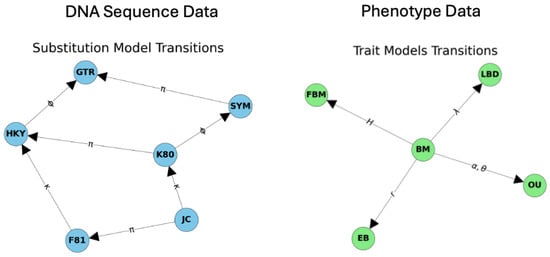
Figure 5.
Comparative framework for DNA sequence and phenotype data: Left: Transition map of substitution models, illustrating pathways between models such as JC, K80, HKY, SYM, F81, and GTR. Edges represent model transitions labeled with evolutionary parameters like , , and . Right: Transition map of trait evolution models, centered around the Brownian motion (BM) model. Transitions to other models (e.g., OU, EB, FBM, and LBD) are labeled with key parameters, such as , , r, H, and , representing extensions of the BM framework.
Figure 6 illustrates the integration of trait evolution models and molecular substitution models into a joint likelihood framework. This approach provides a foundation for deriving parameter estimates and performing model selection, ultimately enhancing phylogenetic inference and analysis [5]:

Figure 6.
Integrative phylogenetic framework.
For the joint modeling framework, the components of the substitution rate matrix and the trait vector are considered. One would adopt a continuous stochastic process, applying a logarithmic transformation to both substitution parameters and traits to stabilize the variance and account for known biological scaling laws. The novel trait vector is presented in Equation (19):
where is the vector of log-transformed rates, suitable for modeling as a multivariate continuous process.
We can evaluate only at the nodes of tree with divergence times , where is the branch length to node j, and where is its immediate ancestor. Let denote the value at node j. Given in Equation (19), the common likelihood, which integrates trait evolution models and molecular substitution models, is illustrated in Figure 6, given the set of values and the root value , as shown in Equation (20):
where describes the transition probability between nodes with [5].
In parallel, time series methodologies have emerged to model correlated evolutionary rates along phylogenetic trees. For example, ref. [55] introduced autoregressive (AR) and heteroskedastic (ARCH) models to account for rate heterogeneity in evolutionary processes, while [56] applied ARMA models to capture correlations in rates across ancestral and descendant branches. Autoregressive conditional heteroskedasticity (ARCH) has proven effective for analyzing correlated molecular rates along phylogenies [57], whereas ARMA-based approaches (PhyRateARMA) illuminate the interdependence of rates in ancestor–descendant lineages [56]. By integrating these time series frameworks with nucleotide sequence data, one can simultaneously estimate substitution counts, evolutionary rates, divergence times, and potentially even trait dynamics. Such joint modeling leverages cross-validation and other robust statistical techniques to ensure reliability and scalability, especially in the context of genome-scale datasets.
Overall, the convergence of molecular phylogenetics, trait evolution modeling, and time series methods offers exciting new perspectives on the processes that shape biodiversity. By jointly considering substitution rates and phenotypic data, these cutting-edge models capture the interplay between molecular evolution and trait diversification more realistically than ever before, facilitating deeper insights into the mechanisms driving evolutionary change.
2.7. Count-Based Trait Data
Significant advances in comparative phylogenetic methods have emerged through the development of phylogenetic regression for traits of different data types. In particular, ref. [58] introduced a phylogenetic logistic regression framework that accounts for shared ancestry among species when modeling binary dependent variables, thereby yielding more accurate inferences regarding evolutionary processes. A more generalized approach was proposed by [59], who utilized generalized estimating equations (GEEs) to incorporate a phylogenetic correlation matrix directly into the modeling process. This allows for the simultaneous analysis of discrete or continuous outcomes without the need to estimate ancestral states, and it can accommodate phylogenies with multichotomies.
For instance, when modeling count data from phylogenetically related species, observations are not independent. The generalized estimating equations (GEEs) framework allows us to account for these dependencies by incorporating a correlation structure into the model. For phylogenetic dependent trait data with a specific constraint (e.g., count type) and covariate trait data , where is a real-valued vector, we use a transformation matrix derived from the phylogenetic tree to represent interdependencies among species. For distributions belonging to the exponential family, the probability density function for an observation y in this family is given by
Using GEEs, we link the mean to the canonical parameter via a monotonic link function . The mean and variance functions are defined as
Let the linear predictor be . The relationships between the parameters imply that the gradient of the log-likelihood ℓ with respect to can be decomposed using the chain rule
Setting this derivative to zero gives the estimating equation for the regression parameters :
This equation provides the foundation for estimating in the context of phylogenetically correlated count data using GEEs. Building on this framework, ref. [60] developed a phylogenetic negative binomial regression model to handle overdispersed count data while incorporating lineage dependence, thus overcoming the limitations of traditional GLMs.
Future extensions of these methods to joint modeling of multivariate traits would be especially valuable. Such developments would enable researchers to capture the complex interplay among multiple traits within a phylogenetic framework, further enriching our understanding of trait evolution.
2.8. Phylogenetic Networks
Reticulate evolution, including hybridization and horizontal gene transfer, challenges the assumption of strictly bifurcating phylogenetic trees. As illustrated in Figure 7 [61], which includes gene transfer, consider the scenario where trait evolution incorporates gene flow (dashed arrow):
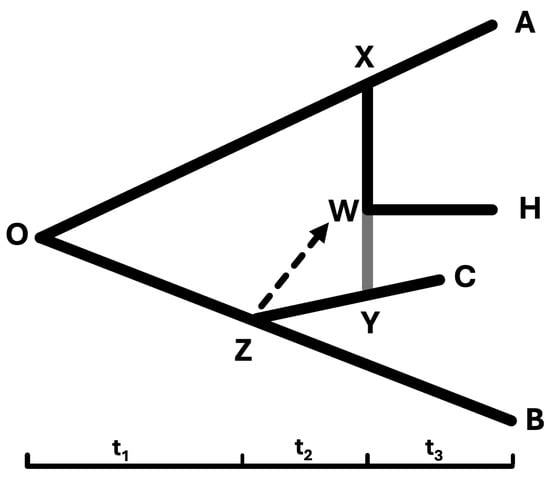
Figure 7.
A phylogenetic network where species Z splits at time into two lineages, one leading to species B and the other leading to species Y and its descendant C. Hybridization occurs at time , resulting in the formation of species W. Since species C is unsampled, Y and X are considered the immediate parents of W. Consequently, evolutionary changes from Z to Y are reflected in W, but not in B. Regraph from [61].
To model trait evolution with the stochastic process on a phylogenetic network, let the trait value at the root state O be . Assuming that species evolve under Brownian motion, the trait values for species Y and X are expressed as and , respectively, where and are error terms that follow a normal distribution with zero mean and variance . Under this model and with variables analyzed on a logarithmic scale in comparative studies, the hybrid species W, at the moment of hybridization, assumes the trait value , which is defined in Equation (25):
where follows a normal distribution with mean and variance . The parameter of positive value governs the possible bias in trait value as a result of hybridization and the parameter r represents the proportion of the hybrid trait value inherited from parent Y, while represents the proportion inherited from parent X. The parameter r is constrained between 0 and 1.
Statistical and computational frameworks that incorporate phylogenetic networks [62,63] address these complexities by representing evolutionary histories beyond tree-like structures. Recent efforts have further broadened the scope of phylogenetic comparative methods to accommodate non-ultrametric or network-based frameworks [25] and to integrate Gaussian models into networks [64]. In addition, ref. [65] developed a comparative framework facilitating phylogenetic regression for within-species comparisons. Ongoing research into network identifiability and circular orders of blobs in phylogenetic networks [66,67] is refining our capacity to pinpoint both local and global features of these complex evolutionary structures.
As these models continue to evolve, their application to various types of trait data promises further insights. For example, previous work has proposed a phylogenetic regression model that extends Gaussian-based continuous stochastic processes (e.g., Brownian motion, Ornstein–Uhlenbeck (OU), and early burst (EB) processes) as well as non-Gaussian processes (e.g., the CIR process and the Beta process) to network topologies. This approach uses maximum likelihood estimation and variance–covariance matrices derived from eNewick networks. These methods yield improved parameter accuracy and reveal significant trait correlations, thereby advancing comparative analyses in scenarios involving reticulation events. Extending this work to multivariate trait data promises to enhance our understanding of correlated trait evolution under reticulate processes.
3. Software
Advanced phylogenetic comparative methods have been significantly enriched by the development of the phytools R package (version 2.4-2), which offers functionalities for analyzing, visualizing, and simulating trait evolution on phylogenetic trees [68]. Work on adaptive radiation, particularly in Greater Antillean anoles, has provided insights into how ecological opportunities shape morphological evolution and diversification rates [69]. Parallel advances include the creation of multivariate Ornstein–Uhlenbeck models [31] and efficient likelihood evaluation tools (e.g., the PCMBase R package (version 1.2.14) [70,71]), which enable the study of complex trait evolution in large datasets [31]. Other noteworthy developments comprise mvSLOUCH R package (version 2.7.6) for multivariate OU-based models in large phylogenies [31,72], Blouch R package (version 1.0) for Bayesian linear OU comparative hypotheses [73], and ouxy R package (version 2.1) for simulating parametric diffusion processes along phylogenies [74].
Contributions to Bayesian phylogenetic analysis—via BEAST (version 10.5.0-beta5) [23] and enhancements to MrBayes (version 3.2) [75]—have also greatly expanded the scalability and flexibility of comparative phylogenetic methods. Concurrently, integrating geometric morphometrics with these approaches—particularly by using the geomorph R package (version 4.0.9) [33]—has facilitated research on shape data in evolutionary contexts, while new techniques for high-dimensional phylogenetic analysis have improved our understanding of morphological evolution and its relationship to species diversification [2]. The RRPP R package (version 2.0.4) has further advanced phenotypic evolution studies by enabling robust analyses of high-dimensional morphometric data [76], and collaborations involving phylogenetically aligned component analysis (PACA) continue to yield powerful tools for investigating morphological variation [33].
Additional contributions include the PHYLIP software (version Version 3.698) [77] suite, whose focus on maximum likelihood methods has profoundly influenced evolutionary biology research. Specialized tools such as AnnotationBustR R package (version 1.3.0) [78] and dietr R package (version 1.1.6) [79] have promoted new studies of adaptive radiation and trophic specialization by linking genetic and ecological data. Phylogenetic comparative methods have also been expanded to account for reticulate evolution through PhyloNet (version 3.8.2) [80], enabling reconstruction of hybridization and gene-flow events in evolutionary histories, with parallel implementations in Julia software (version 1.10) [62].
Finally, work on integrating multilocus data and hidden Markov models for detecting introgression has produced powerful frameworks for disentangling complex evolutionary relationships, further pushing the boundaries of phylogenetic comparative analysis. The history of life is analyzed within a phylogenetic context, using mathematical theories, statistical methods, and tools for phylogenetic tree analysis, comparative methods, and applications across disciplines. Readers can refer to [81] for more practical data analysis methods tailored to their specific research needs.
4. Prospective Research and Future Applications
The integration of increasingly sophisticated stochastic models into phylogenetic comparative methods (PCMs) holds significant promise for driving innovation across diverse research areas. In the context of global change biology, advanced models that link genomic data [5,82] to environmental variables can help predict how species and communities respond to rapid climate change. By leveraging machine learning algorithms alongside high-performance computing, researchers can efficiently process massive genomic and environmental datasets, enabling real-time assessment of evolutionary responses and potential adaptive trajectories.
Beyond environmental applications, PCMs enriched with causal inference frameworks can facilitate robust hypothesis testing in biomedical research, particularly when mapping disease-associated traits within large phylogenetic trees of pathogens. Coupling epidemiological models—such as noisy SIR frameworks [83,84]—and phylogenetic comparative approaches could transform our understanding of how infectious diseases evolve, spread, and adapt to new hosts [85].
Additionally, the future will likely see increased collaboration between evolutionary biologists, mathematicians, and computational scientists to develop novel stochastic processes that capture the irregularities and complexities of trait evolution. Such interdisciplinary efforts could also expand PCMs to analyze hybridization and reticulate evolution, pushing the boundaries of current models by embracing phylogenetic trees and networks. These advances would enhance our ability to model intricate evolutionary histories, illuminate the role of introgression events in speciation, and, ultimately, improve our understanding of biodiversity patterns.
There is an emerging need to refine software packages that implement cutting-edge models while maintaining user-friendly interfaces. Encouraging open-source development and transparent benchmarking of computational tools will foster accessible, reproducible research. With these efforts, PCMs will be poised not only to tackle pressing questions in evolutionary biology but also to extend their utility to fields such as conservation, synthetic biology, and even cultural evolution studies.
5. Conclusions
The continued refinement and integration of advanced stochastic processes, evolutionary models, and frameworks within phylogenetic comparative methods promises significant gains in understanding trait evolution. By bridging genomic, ecological, and environmental data and adopting more rigorous causal inference tools, these approaches stand to deepen theoretical insights and expand practical applications in areas ranging from conservation to emerging infectious diseases. Interdisciplinary collaboration, improved scalability for large datasets, and active engagement from mathematicians, computational scientists, and evolutionary biologists will foster ongoing innovations, ultimately strengthening both our theoretical foundation and our capacity to address pressing challenges in evolutionary biology research.
Funding
This research and APC were funded by the Ministry of Science and Technology, Taiwan (grant No. MOST-113-2118-M-035-001).
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
I would like to express my sincere gratitude to the editors and the three anonymous reviewers for their insightful feedback, which significantly improved the earlier version of this manuscript.
Conflicts of Interest
The author declares no conflicts of interest.
References
- O’Meara, B.C. Evolutionary inferences from phylogenies: A review of methods. Annu. Rev. Ecol. Evol. Syst. 2012, 43, 267–285. [Google Scholar] [CrossRef]
- Adams, D.C.; Berns, C.M.; Kozak, K.H.; Wiens, J.J. Are rates of species diversification correlated with rates of morphological evolution? Proc. R. Soc. B Biol. Sci. 2009, 276, 2729–2738. [Google Scholar] [CrossRef] [PubMed]
- Hassler, G.; Tolkoff, M.R.; Allen, W.L.; Ho, L.S.T.; Lemey, P.; Suchard, M.A. Inferring phenotypic trait evolution on large trees with many incomplete measurements. J. Am. Stat. Assoc. 2022, 117, 678–692. [Google Scholar] [CrossRef]
- Schwery, O.; Freyman, W.; Goldberg, E.E. adequaSSE: Model Adequacy Testing for Trait-Dependent Diversification Models. bioRxiv 2023. [Google Scholar] [CrossRef]
- Lartillot, N.; Poujol, R. A phylogenetic model for investigating correlated evolution of substitution rates and continuous phenotypic characters. Mol. Biol. Evol. 2011, 28, 729–744. [Google Scholar] [CrossRef] [PubMed]
- Housworth, E.A.; Martins, E.P.; Lynch, M. The phylogenetic mixed model. Am. Nat. 2004, 163, 84–96. [Google Scholar] [CrossRef]
- Beaulieu, J.M.; Jhwueng, D.C.; Boettiger, C.; O’Meara, B.C. Modeling stabilizing selection: Expanding the Ornstein–Uhlenbeck model of adaptive evolution. Evolution 2012, 66, 2369–2383. [Google Scholar] [CrossRef]
- Hansen, T.F.; Pienaar, J.; Orzack, S.H. A comparative method for studying adaptation to a randomly evolving environment. Evolution 2008, 62, 1965–1977. [Google Scholar] [CrossRef] [PubMed]
- Polly, P.D. Paleontology and the Comparative Method: Ancestral Node Reconstructions versus Observed Node Values. Am. Nat. 2001, 157, 596–609. [Google Scholar] [CrossRef] [PubMed]
- Pagel, M. Inferring the historical patterns of biological evolution. Nature 1999, 401, 877–884. [Google Scholar] [CrossRef] [PubMed]
- Adams, D.C. A generalized K statistic for estimating phylogenetic signal from shape and other high-dimensional multivariate data. Syst. Biol. 2014, 63, 685–697. [Google Scholar] [CrossRef] [PubMed]
- Adams, D.C.; Collyer, M.L. Extending phylogenetic regression models for comparing within-species patterns across the tree of life. Methods Ecol. Evol. 2024, 15, 2234–2246. [Google Scholar] [CrossRef]
- Blomberg, S.P.; Muniz, M.; Bui, M.N.; Janke, C. Multivariate Trait Evolution: Models for the Evolution of the Quantitative Genetic G-Matrix on Phylogenies. bioRxiv 2024. [Google Scholar] [CrossRef]
- Ho, L.S.T.; Dinh, V. When can we reconstruct the ancestral state? A unified theory. Theor. Popul. Biol. 2022, 148, 22–27. [Google Scholar] [CrossRef]
- Felsenstein, J. Phylogenies and the comparative method. Am. Nat. 1985, 125, 1–15. [Google Scholar] [CrossRef]
- Hansen, T.F. Stabilizing selection and the comparative analysis of adaptation. Evolution 1997, 51, 1341–1351. [Google Scholar] [CrossRef]
- Harmon, L.J.; Losos, J.B.; Jonathan Davies, T.; Gillespie, R.G.; Gittleman, J.L.; Bryan Jennings, W.; Kozak, K.H.; McPeek, M.A.; Moreno-Roark, F.; Near, T.J.; et al. Early bursts of body size and shape evolution are rare in comparative data. Evolution 2010, 64, 2385–2396. [Google Scholar] [CrossRef]
- O’Meara, B.C.; Ané, C.; Sanderson, M.J.; Wainwright, P.C. Testing for different rates of continuous trait evolution using likelihood. Evolution 2006, 60, 922–933. [Google Scholar] [PubMed]
- Martins, E.P.; Hansen, T.F. Phylogenies and the comparative method: A general approach to incorporating phylogenetic information into the analysis of interspecific data. Am. Nat. 1997, 149, 646–667. [Google Scholar] [CrossRef]
- Martins, E.P.; Diniz-Filho, J.A.F.; Housworth, E.A. Adaptive constraints and the phylogenetic comparative method: A computer simulation test. Evolution 2002, 56, 1–13. [Google Scholar]
- Butler, M.A.; King, A.A. Phylogenetic comparative analysis: A modeling approach for adaptive evolution. Am. Nat. 2004, 164, 683–695. [Google Scholar] [CrossRef]
- Felsenstein, J. Inferring Phylogenies; Sinauer Associates: Sunderland, MA, USA, 2004. [Google Scholar]
- Drummond, A.J.; Suchard, M.A.; Xie, D.; Rambaut, A. Bayesian phylogenetics with BEAUti and the BEAST 1.7. Mol. Biol. Evol. 2012, 29, 1969–1973. [Google Scholar] [CrossRef] [PubMed]
- Uyeda, J.C.; Harmon, L.J. A novel Bayesian method for inferring and interpreting the dynamics of adaptive landscapes from phylogenetic comparative data. Syst. Biol. 2014, 63, 902–918. [Google Scholar] [CrossRef] [PubMed]
- Jhwueng, D.C.; Wang, C.P. Phylogenetic Curved Optimal Regression for Adaptive Trait Evolution. Entropy 2021, 23, 218. [Google Scholar] [CrossRef] [PubMed]
- Jhwueng, D.C. Stochastic Modeling of Morphological Rate Evolution: Phylogenetic Regression with Approximate Bayesian Computation. 2024; submitted. [Google Scholar]
- Beaumont, M.A. Approximate bayesian computation. Annu. Rev. Stat. Its Appl. 2019, 6, 379–403. [Google Scholar] [CrossRef]
- Bartoszek, K.; Liò, P. Modelling trait dependent speciation with approximate Bayesian computation. arXiv 2018, arXiv:1812.03715. [Google Scholar] [CrossRef]
- Cressler, C.E.; Butler, M.A.; King, A.A. Detecting adaptive evolution in phylogenetic comparative analysis using the Ornstein–Uhlenbeck model. Syst. Biol. 2015, 64, 953–968. [Google Scholar] [CrossRef]
- Bartoszek, K.; Pienaar, J.; Mostad, P.; Andersson, S.; Hansen, T.F. A phylogenetic comparative method for studying multivariate adaptation. J. Theor. Biol. 2012, 314, 204–215. [Google Scholar] [CrossRef] [PubMed]
- Bartoszek, K.; Tredgett Clarke, J.; Fuentes-González, J.; Mitov, V.; Pienaar, J.; Piwczyński, M.; Puchałka, R.; Spalik, K.; Voje, K.L. Fast mvSLOUCH: Multivariate Ornstein–Uhlenbeck-based models of trait evolution on large phylogenies. Methods Ecol. Evol. 2024, 15, 1507–1515. [Google Scholar] [CrossRef]
- Martins, E.P. Phylogenies and the Comparative Method in Animal Behavior; Oxford University Press: Oxford, UK, 1996. [Google Scholar]
- Adams, D.C.; Otárola-Castillo, E. geomorph: An R package for the collection and analysis of geometric morphometric shape data. Methods Ecol. Evol. 2013, 4, 393–399. [Google Scholar] [CrossRef]
- Adams, D.C.; Collyer, M.L. Phylogenetic comparative methods and the evolution of multivariate phenotypes. Annu. Rev. Ecol. Evol. Syst. 2019, 50, 405–425. [Google Scholar] [CrossRef]
- Caumul, R.; Polly, P.D. Phylogenetic and environmental components of morphological variation: Skull, mandible, and molar shape in marmots (Marmota, Rodentia). Evolution 2005, 59, 2460–2472. [Google Scholar]
- Goswami, A.; Polly, P.D. Methods for studying morphological integration and modularity. Quant. Methods Paleobiol. 2010, 16, 213–243. [Google Scholar] [CrossRef]
- Blomberg, S.P.; Rathnayake, S.I.; Moreau, C.M. Beyond Brownian motion and the Ornstein-Uhlenbeck process: Stochastic diffusion models for the evolution of quantitative characters. Am. Nat. 2020, 195, 145–165. [Google Scholar] [CrossRef]
- Jhwueng, D.C. Modeling rate of adaptive trait evolution using Cox–Ingersoll–Ross Process: An approximate Bayesian computation approach. Comput. Stat. Data Anal. 2020, 145, 106924. [Google Scholar] [CrossRef]
- Boucher, F.C.; Démery, V. Inferring bounded evolution in phenotypic characters from phylogenetic comparative data. Syst. Biol. 2016, 65, 651–661. [Google Scholar] [CrossRef] [PubMed]
- Hansen, T.F. Three modes of evolution? Remarks on rates of evolution and time scaling. J. Evol. Biol. 2024, 37, 1523–1537. [Google Scholar] [CrossRef]
- Jhwueng, D.C.; Lin, M.H. On the Fractional Brownian Motion for Modeling and Simulating Phylogenetic Trait Evolution. 2024; in preparation. [Google Scholar]
- Bastide, P.; Didier, G. The Cauchy process on phylogenies: A tractable model for pulsed evolution. Syst. Biol. 2023, 72, 1296–1315. [Google Scholar] [CrossRef]
- Jhwueng, D.C.; Maroulas, V. Phylogenetic ornstein–uhlenbeck regression curves. Stat. Probab. Lett. 2014, 89, 110–117. [Google Scholar] [CrossRef][Green Version]
- Jhwueng, D.C.; Chang, C.H. Stochastic Modeling of Adaptive Trait Evolution in Phylogenetics: A Polynomial Regression and Approximate Bayesian Computation Approach. Mathematics 2025, 13, 170. [Google Scholar] [CrossRef]
- Hansen, T.F.; Bolstad, G.H.; Tsuboi, M. Analyzing disparity and rates of morphological evolution with model-based phylogenetic comparative methods. Syst. Biol. 2022, 71, 1054–1072. [Google Scholar] [CrossRef] [PubMed]
- Latrille, T.; Lartillot, N. An improved codon modeling approach for accurate estimation of the mutation bias. Mol. Biol. Evol. 2022, 39, msac005. [Google Scholar] [CrossRef]
- Mirarab, S.; Nguyen, N.; Guo, S.; Wang, L.S.; Kim, J.; Warnow, T. PASTA: Ultra-large multiple sequence alignment for nucleotide and amino-acid sequences. J. Comput. Biol. 2015, 22, 377–386. [Google Scholar] [CrossRef]
- Liu, K.; Raghavan, S.; Nelesen, S.; Linder, C.R.; Warnow, T. Rapid and accurate large-scale coestimation of sequence alignments and phylogenetic trees. Science 2009, 324, 1561–1564. [Google Scholar] [CrossRef] [PubMed]
- Mirarab, S.; Reaz, R.; Bayzid, M.S.; Zimmermann, T.; Swenson, M.S.; Warnow, T. ASTRAL: Genome-scale coalescent-based species tree estimation. Bioinformatics 2014, 30, i541–i548. [Google Scholar] [CrossRef] [PubMed]
- Liu, L. BEST: Bayesian estimation of species trees under the coalescent model. Bioinformatics 2008, 24, 2542–2543. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Yu, L.; Edwards, S.V. A maximum pseudo-likelihood approach for estimating species trees under the coalescent model. BMC Evol. Biol. 2010, 10, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Yu, L.; Pearl, D.K.; Edwards, S.V. Estimating species phylogenies using coalescence times among sequences. Syst. Biol. 2009, 58, 468–477. [Google Scholar] [CrossRef]
- Maitner, B.S.; Pearse, W.; Roehrdanz, P.; Enquist, B.J.; Sanderson, M.J. APPENDIX C. Re-scaling phylogenetic branches to reflect trait evolution. Univ. Ariz. Grad. Coll. 2020, 1001, 86. [Google Scholar]
- Yang, Z. Computational Molecular Evolution; OUP Oxford: Oxford, UK, 2006. [Google Scholar]
- Jhwueng, D.C. Estimating Absolute Rates of Molecular Evolution and Divergence Times Using an Autoregressive Conditional Heteroskedasticity Framework. 2024; submitted. [Google Scholar]
- Jhwueng, D.C. Modeling the Phylogenetic Rates of Continuous Trait Evolution: An Autoregressive–Moving-Average Model Approach. Mathematics 2025, 13, 111. [Google Scholar] [CrossRef]
- Jhwueng, D.C. Statistical Modeling and Analysis of Phylogenetic Trait Evolution Variability in Species Using Heteroskedasticity Models. 2024; submitted. [Google Scholar]
- Ives, A.R.; Garland Jr, T. Phylogenetic logistic regression for binary dependent variables. Syst. Biol. 2010, 59, 9–26. [Google Scholar] [CrossRef] [PubMed]
- Paradis, E.; Claude, J. Analysis of comparative data using generalized estimating equations. J. Theor. Biol. 2002, 218, 175–185. [Google Scholar] [CrossRef]
- Jhwueng, D.C.; Wu, C.Y. A Novel Phylogenetic Negative Binomial Regression Model for Count-Dependent Variables. Biology 2023, 12, 1148. [Google Scholar] [CrossRef] [PubMed]
- Jhwueng, D.C.; O’Meara, B.C. Trait evolution on phylogenetic networks. BioRxiv 2015, 023986. [Google Scholar]
- Solís-Lemus, C.; Bastide, P.; Ané, C. PhyloNetworks: A package for phylogenetic networks. Mol. Biol. Evol. 2017, 34, 3292–3298. [Google Scholar] [CrossRef]
- Bastide, P.; Ané, C.; Robin, S.; Mariadassou, M. Inference of adaptive shifts for multivariate correlated traits. Syst. Biol. 2018, 67, 662–680. [Google Scholar] [CrossRef]
- Bastide, P.; Solís-Lemus, C.; Kriebel, R.; Sparks, K.W.; Ané, C. Phylogenetic comparative methods on phylogenetic networks with reticulations. Syst. Biol. 2018, 67, 800–820. [Google Scholar] [CrossRef] [PubMed]
- Teo, B.; Rose, J.; Bastide, P.; Ané, C. Accounting for Within-Species Variation in Continuous Trait Evolution on a Phylogenetic Network. Bull. Soc. Syst. Biol. 2023, 2, 1–29. [Google Scholar] [CrossRef]
- Xu, J.; Ané, C. Identifiability of local and global features of phylogenetic networks from average distances. J. Math. Biol. 2023, 86, 12. [Google Scholar] [CrossRef] [PubMed]
- Rhodes, J.A.; Banos, H.; Xu, J.; Ané, C. Identifying circular orders for blobs in phylogenetic networks. Adv. Appl. Math. 2025, 163, 102804. [Google Scholar] [CrossRef]
- Revell, L.J. phytools: An R package for phylogenetic comparative biology (and other things). Methods Ecol. Evol. 2012, 3, 217–223. [Google Scholar] [CrossRef]
- Mahler, D.L.; Revell, L.J.; Glor, R.E.; Losos, J.B. Ecological opportunity and the rate of morphological evolution in the diversification of Greater Antillean anoles. Evolution 2010, 64, 2731–2745. [Google Scholar] [CrossRef] [PubMed]
- Mitov, M.V. Package PCMBase: Simulation and Likelihood Calculation of Phylogenetic Comparative Models Version 1.2.14 2024. Available online: https://CRAN.R-project.org/package=PCMBase (accessed on 20 December 2024).
- Mitov, V.; Bartoszek, K.; Asimomitis, G.; Stadler, T. Fast likelihood calculation for multivariate Gaussian phylogenetic models with shifts. Theor. Popul. Biol. 2020, 131, 66–78. [Google Scholar] [CrossRef] [PubMed]
- Bartoszek, K.; Fuentes-Gonz’alez, J.; Mitov, V.; Pienaar, J.; Piwczy’nski, M.; Puchalka, R.; Spalik, K.; Voje, K.L. Model Selection Performance in Phylogenetic Comparative Methods Under Multivariate Ornstein–Uhlenbeck Models of Trait Evolution. Syst. Biol. 2023, 72, 275–293. [Google Scholar] [CrossRef] [PubMed]
- Grabowski, M. Blouch: Bayesian Linear Ornstein-Uhlenbeck Models for Comparative Hypotheses. Syst. Biol. 2024, 73, 1038–1050. [Google Scholar] [CrossRef]
- Jhwueng, D.C. Building an adaptive trait simulator package to infer parametric diffusion model along phylogenetic tree. MethodsX 2020, 7, 100978. [Google Scholar] [CrossRef] [PubMed]
- Ronquist, F.; Teslenko, M.; van der Mark, P.; Ayres, D.L.; Darling, A.; Höhna, S.; Larget, B.; Liu, L.; Suchard, M.A.; Huelsenbeck, J.P. MrBayes 3.2: Efficient Bayesian phylogenetic inference and model choice across a large model space. Syst. Biol. 2012, 61, 539–542. [Google Scholar] [CrossRef] [PubMed]
- Adams, D.C.; Collyer, M.L. Phylogenetic ANOVA: Group-clade aggregation, biological challenges, and a refined permutation procedure. Evolution 2018, 72, 1204–1215. [Google Scholar] [CrossRef] [PubMed]
- Felsenstein, J. PHYLIP (Phylogeny Inference Package), Version 3.698; University of Washington: Seattle, WA, USA, 1993. [Google Scholar]
- Borstein, S.R.; O’Meara, B.C. AnnotationBustR: An R package to extract subsequences from GenBank annotations. PeerJ 2018, 6, e5179. [Google Scholar] [CrossRef]
- Borstein, S.R.; Hammer, M.P.; O’Meara, B.C.; McGee, M.D. The macroevolutionary dynamics of pharyngognathy in fishes fail to support the key innovation hypothesis. Nat. Commun. 2024, 15, 1–13. [Google Scholar] [CrossRef]
- Nakhleh, L.; Ringe, D.; Warnow, T. Perfect phylogenetic networks: A new methodology for reconstructing the evolutionary history of natural languages. Language 2005, 81, 382–420. [Google Scholar] [CrossRef]
- Gearty, W.; O’Meara, B.; Berv, J.; Ballen, G.A.; Ferreira, D.; Lapp, H.; Schmitz, L.; Smith, M.R.; Upham, N.S.; Nations, J.A. CRAN Task View: Phylogenetics. 2024. Available online: https://mirror.truenetwork.ru/CRAN/web/views/Phylogenetics.html (accessed on 22 December 2024).
- Card, D.C.; Jennings, W.B.; Edwards, S.V. Genome evolution and the future of phylogenomics of non-avian reptiles. Animals 2023, 13, 471. [Google Scholar] [CrossRef] [PubMed]
- Castillo-Chavez, C.; Brauer, F.; Feng, Z. Mathematical Models in Epidemiology; Springer: Berlin/Heidelberg, Germany, 2019; Volume 32. [Google Scholar]
- Allen, L.J. An Introduction to Stochastic Processes with Applications to Biology; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Britton, T.; Pardoux, E.; Ball, F.; Laredo, C.; Sirl, D.; Tran, V.C. Stochastic Epidemic Models with Inference; Springer: Berlin/Heidelberg, Germany, 2019; Volume 2255. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).