Shear-Induced Anisotropy Analysis of Rock-like Specimens Containing Different Inclination Angles of Non-Persistent Joints
Abstract
1. Introduction
2. Methodology
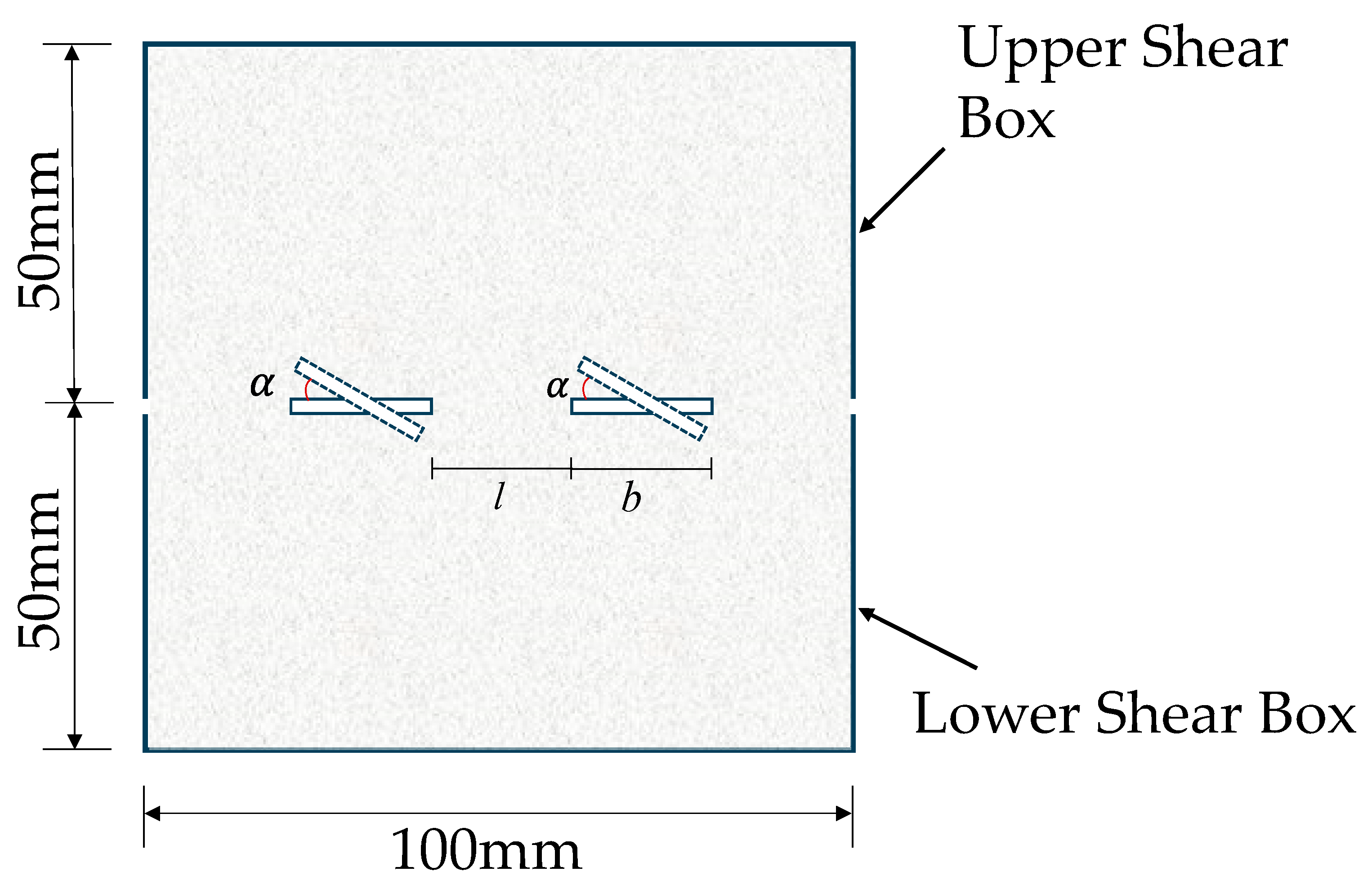
2.1. Laboratory Experiment
2.2. Numerical Experiment
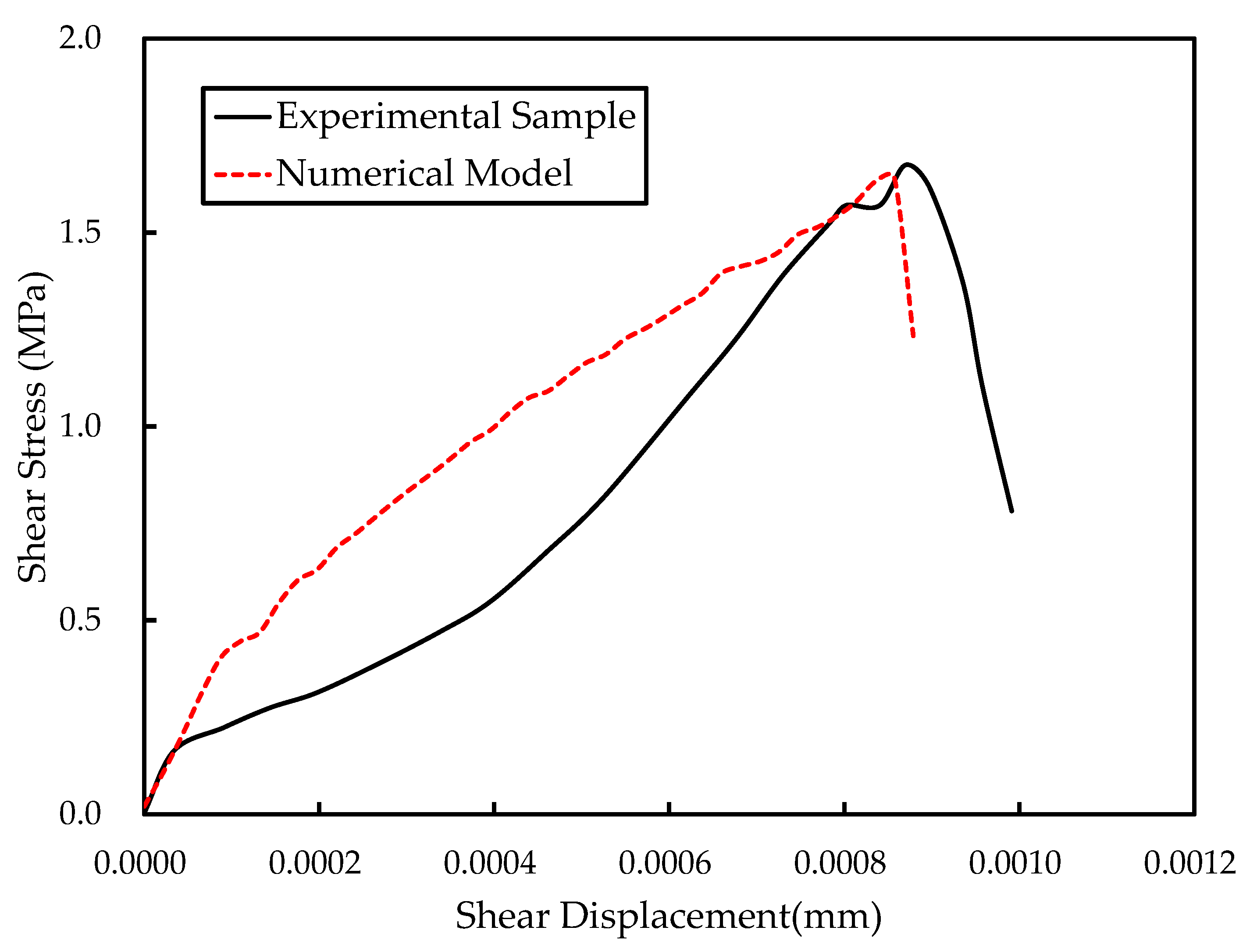
2.2.1. Model Generation and Calibration
2.2.2. Joint Arrangements for Numerical Analysis
3. Results of Numerical Simulation
3.1. Deformation and Failure Process
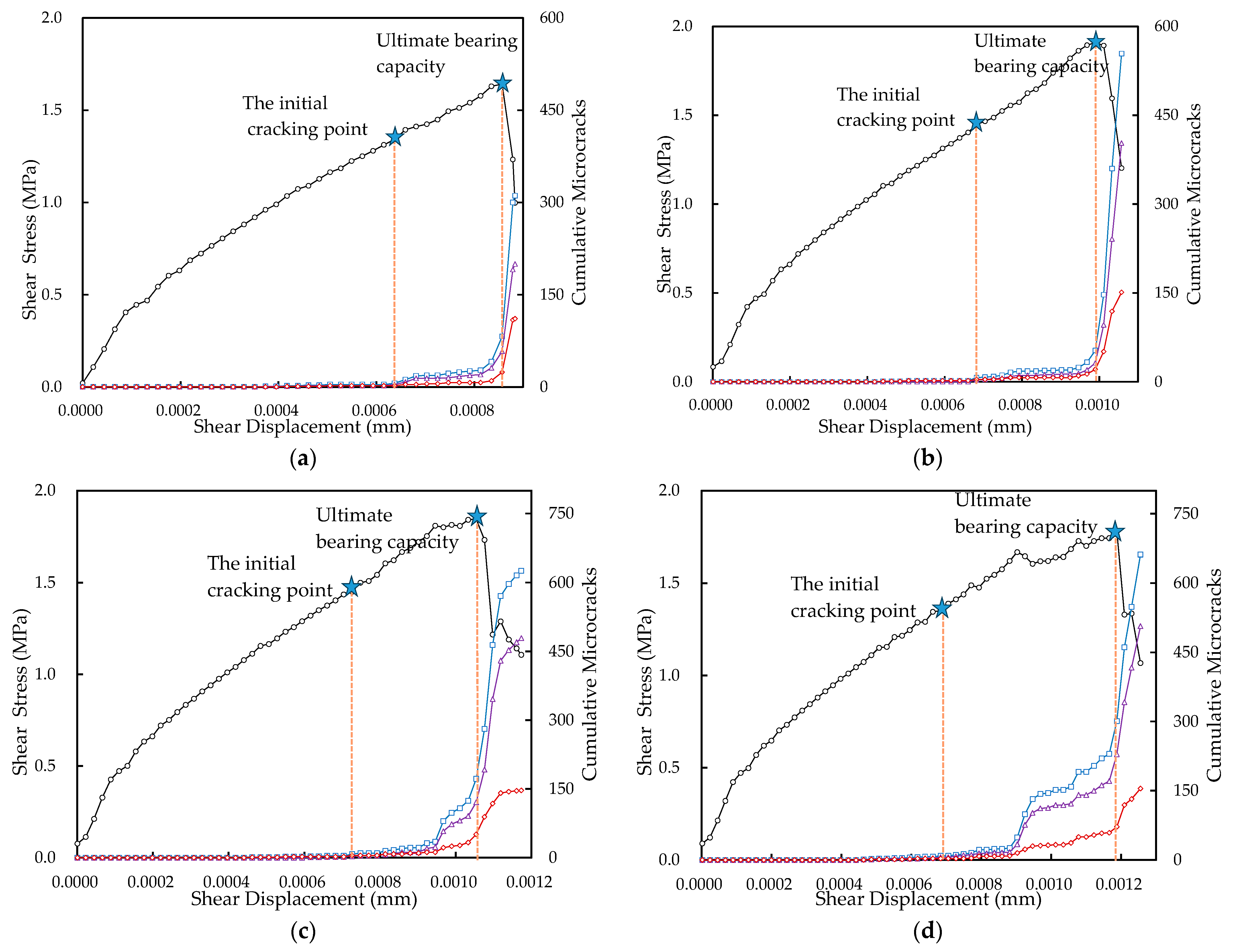
3.1.1. Strength Characteristics of Rock-like Samples Containing Different Joint Inclinations of Non-Persistent Joints
- (1)
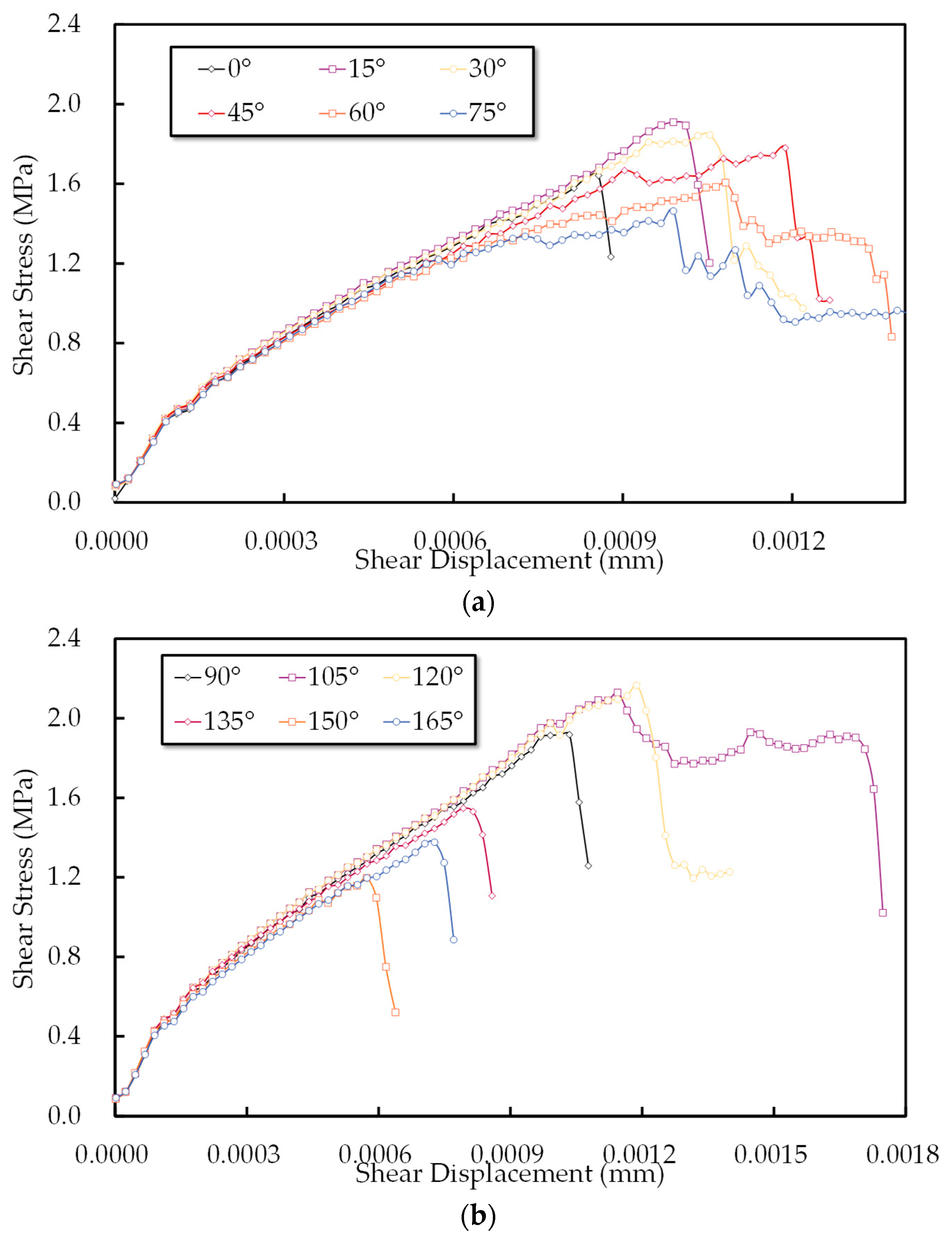
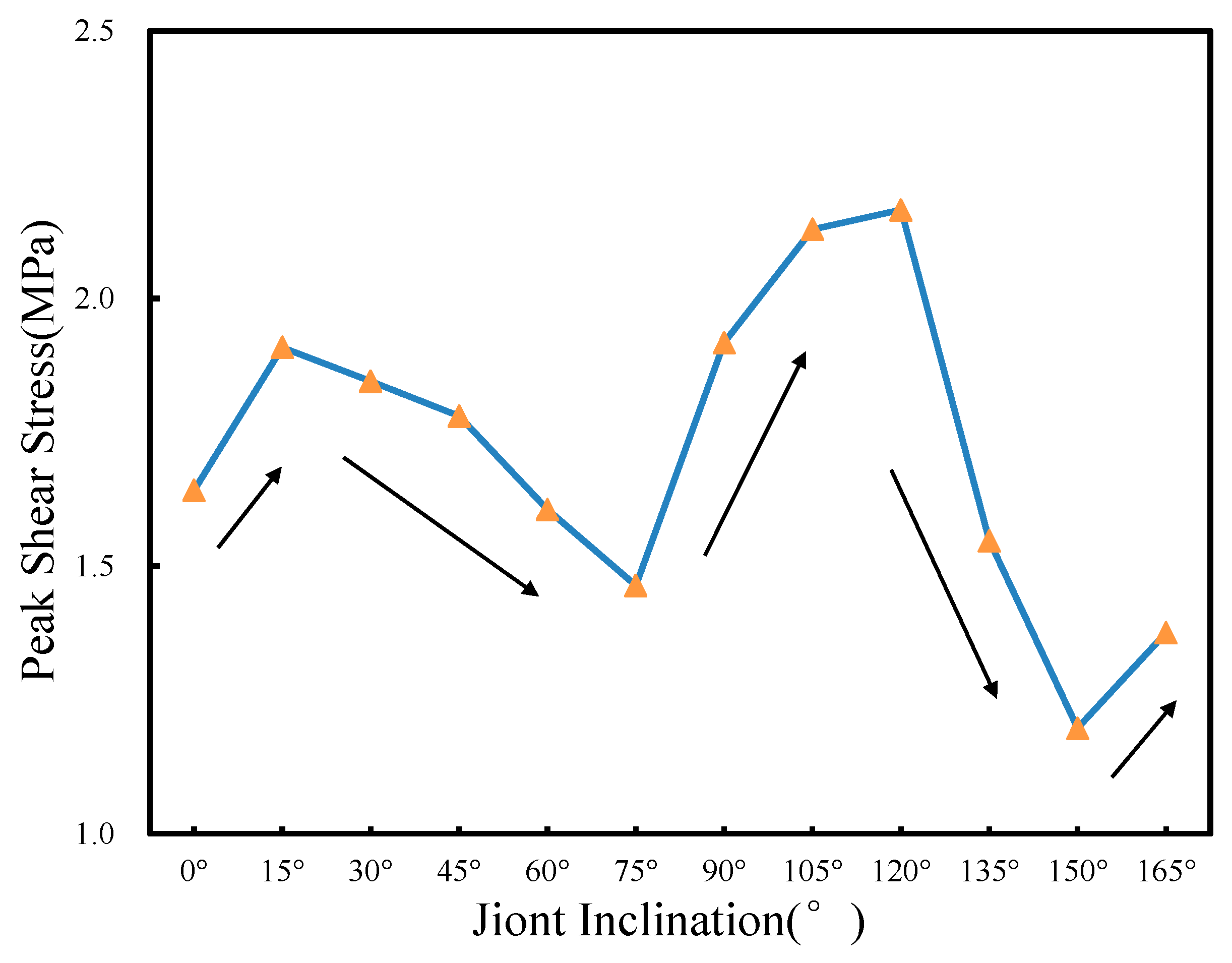
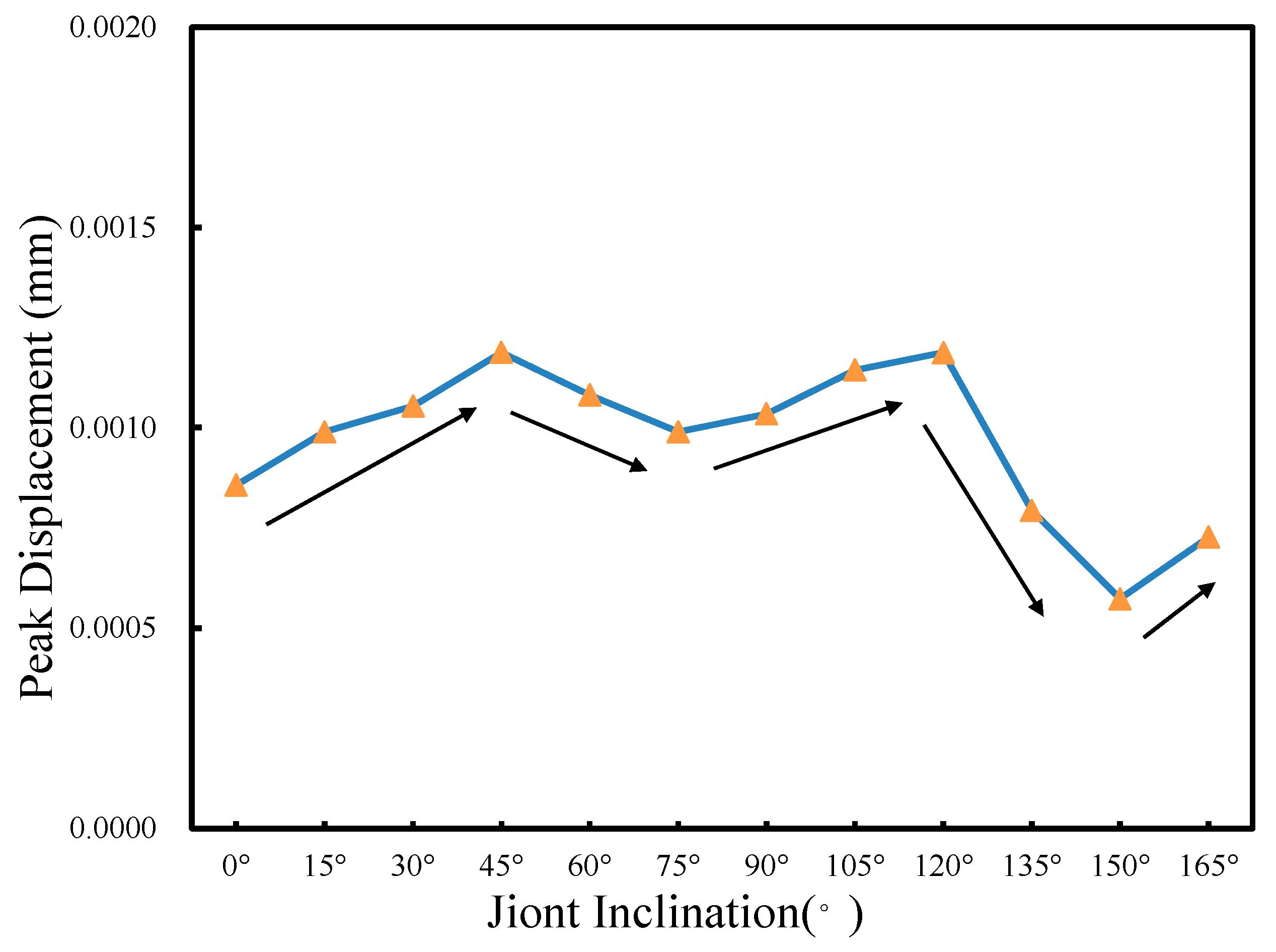
- Joint inclination has significant effects on peak shear stress and peak displacement. Under a constant normal load of 2.5 kN, the peak shear stress of 12 specimens with different joint inclination ranges from 1.20 MPa to 2.17 MPa, and the peak displacement ranges from 0.573 mm to 1.189 mm. Both of them show roughly the same trend of variation, showing an increase, then a decrease, then an increase and then a decrease and finally a slight increase. However, the opposite trend was observed in the specimens with joint inclinations of 30° and 45°; this due to the ductile failure of these specimens, which results in a larger peak displacement even with lower peak shear stress;
- (2)
- Joint inclination plays an important role in the deformability of jointed rock specimens. When the inclination of the joints is the same as the direction of load application, the existence of the joints will make the specimen slide along the joints easily, which makes the specimen’s deformability increase and, at the same time, due to the existence of friction between the joints, the specimen damage tends to be ductile;
- (3)
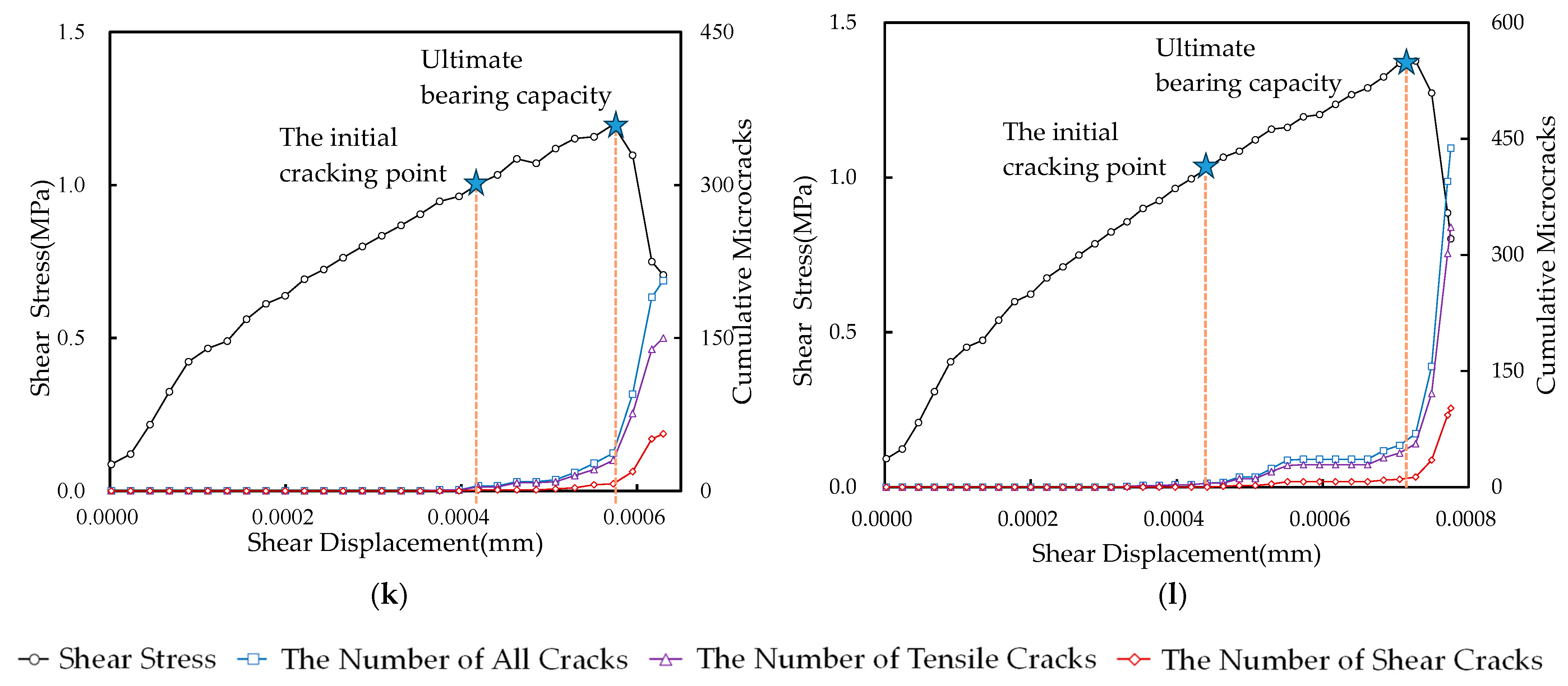
- Joint inclination has little effect on the shear bearing capacity and deformation capacity of the specimens in the early loading stage, and it can be noticed from Figure 4 that the stress–displacement curves of the specimens with different joint inclinations in the early loading stage are coincident.
3.1.2. Failure Patterns and Crack Evolution in Specimens
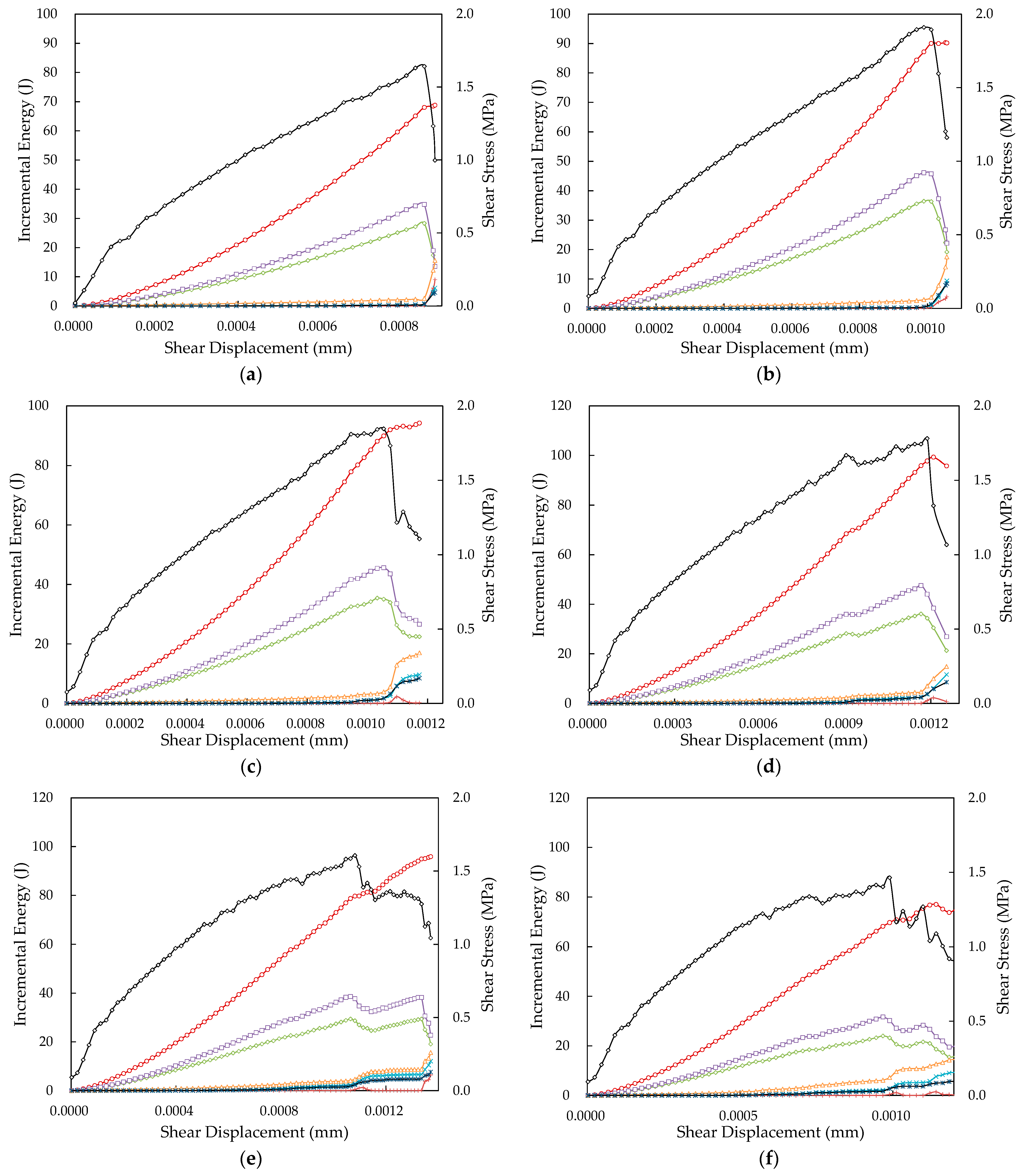
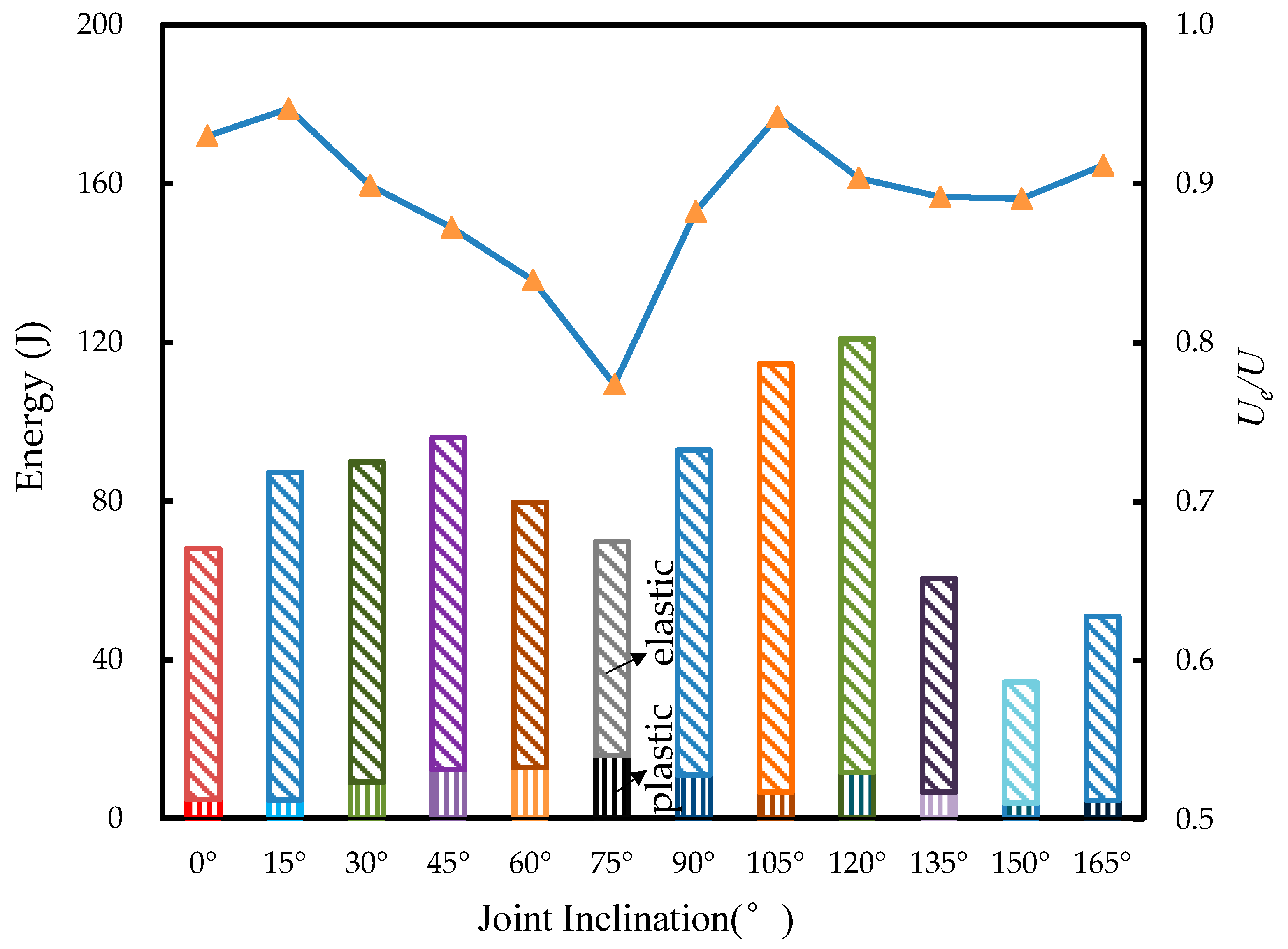
3.1.3. Energy Evolution
3.2. Micromechanism and Macroresponse
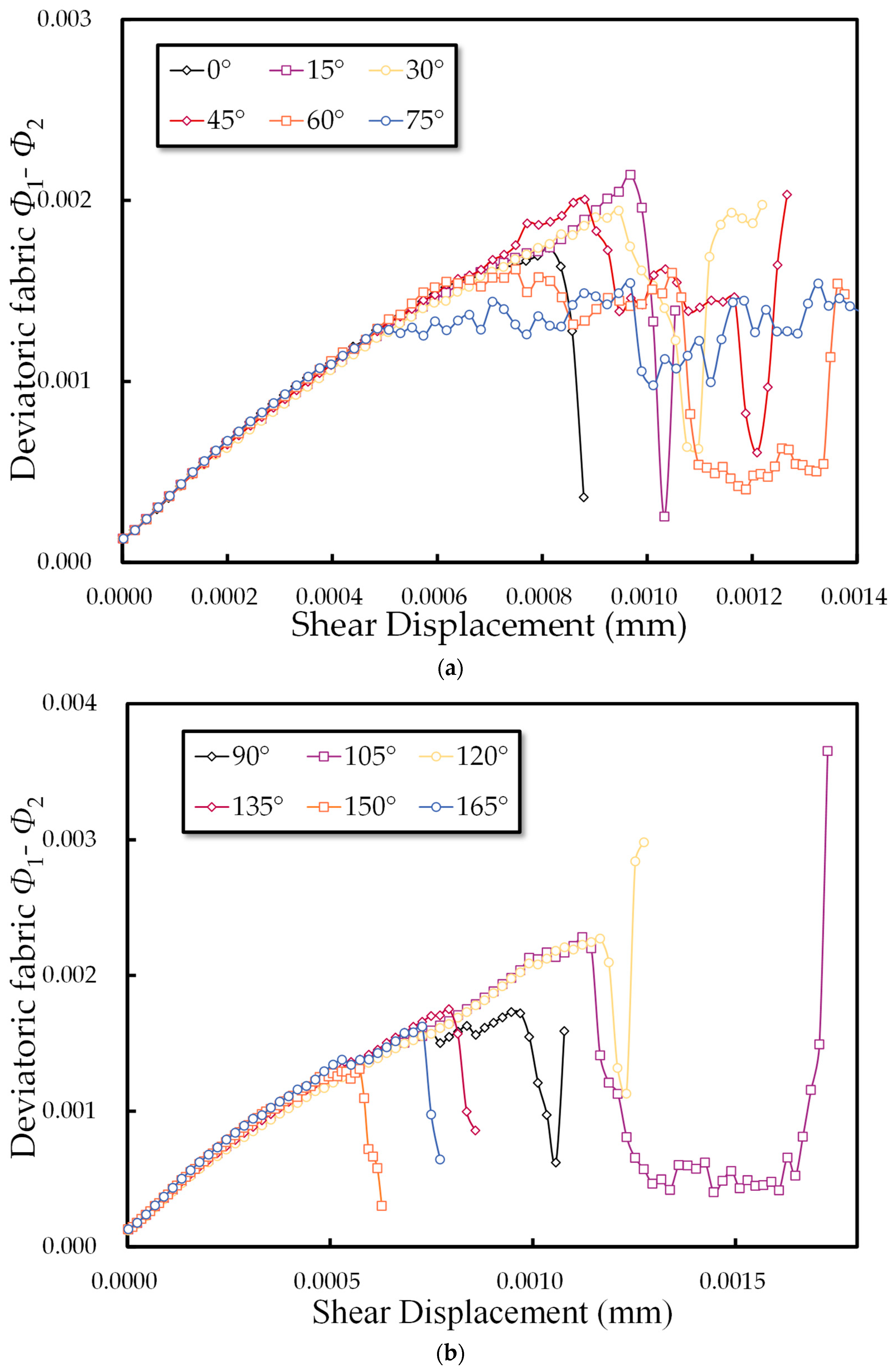
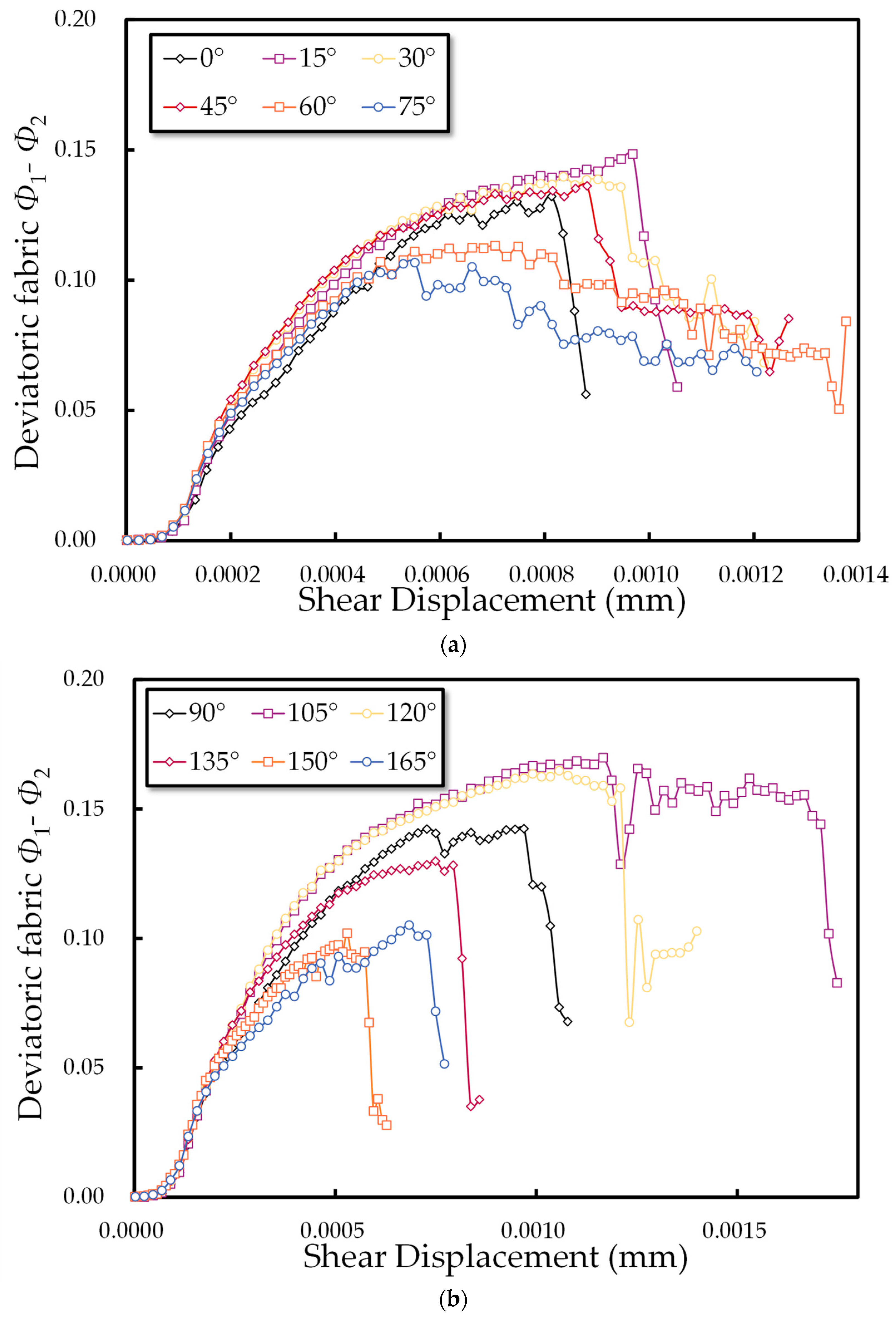
3.2.1. Evolution of Fabric
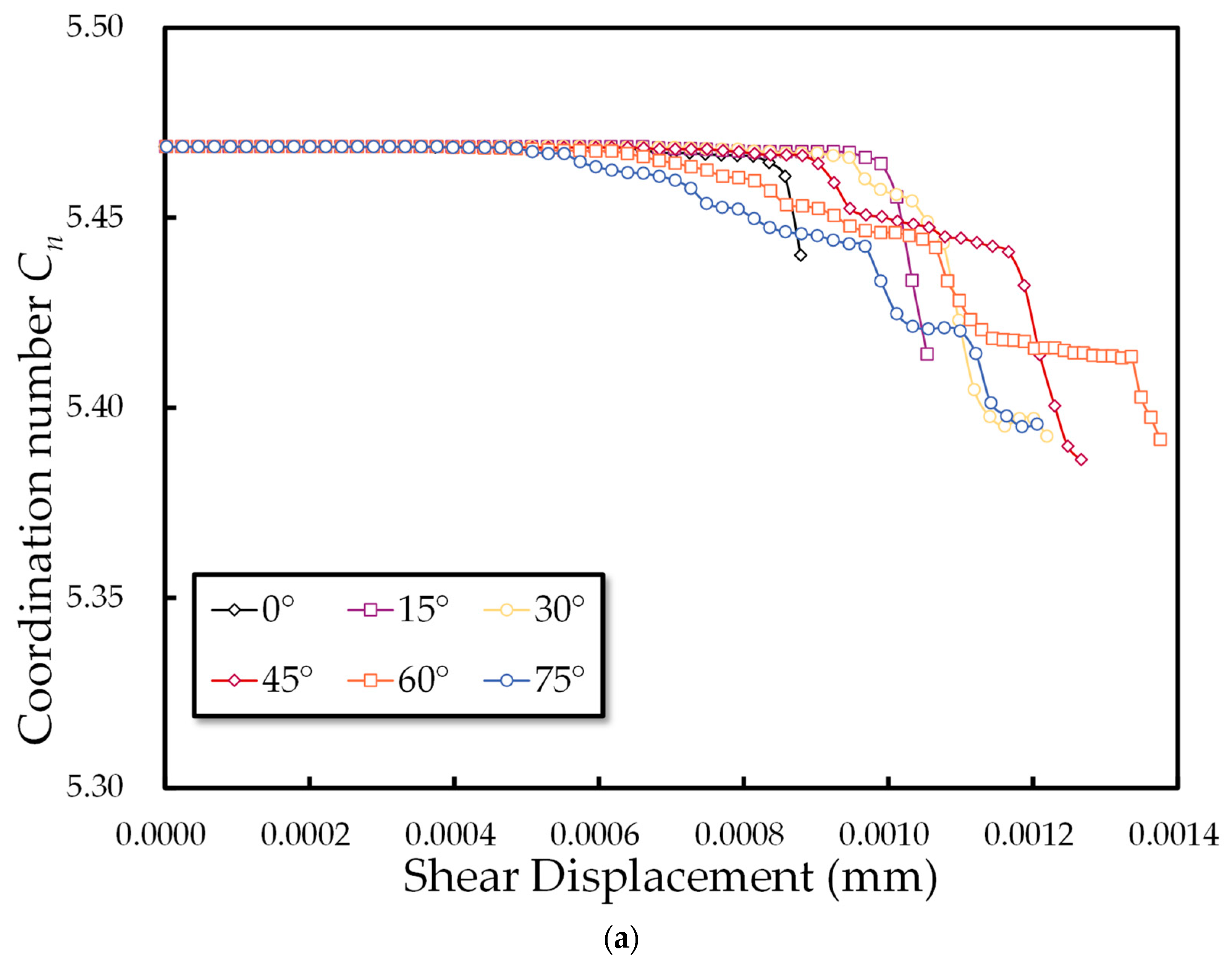
3.2.2. Evolution of Coordination Number
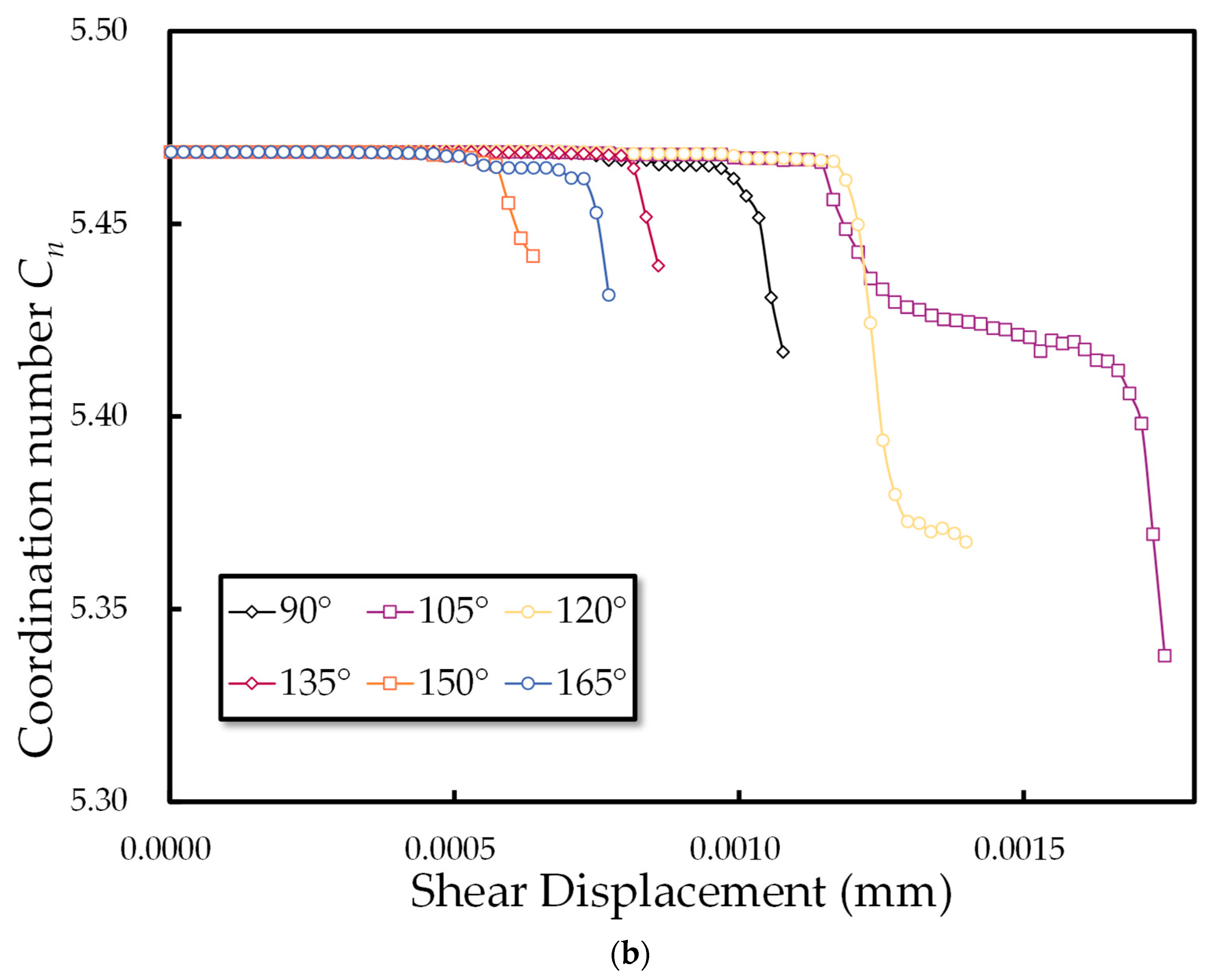
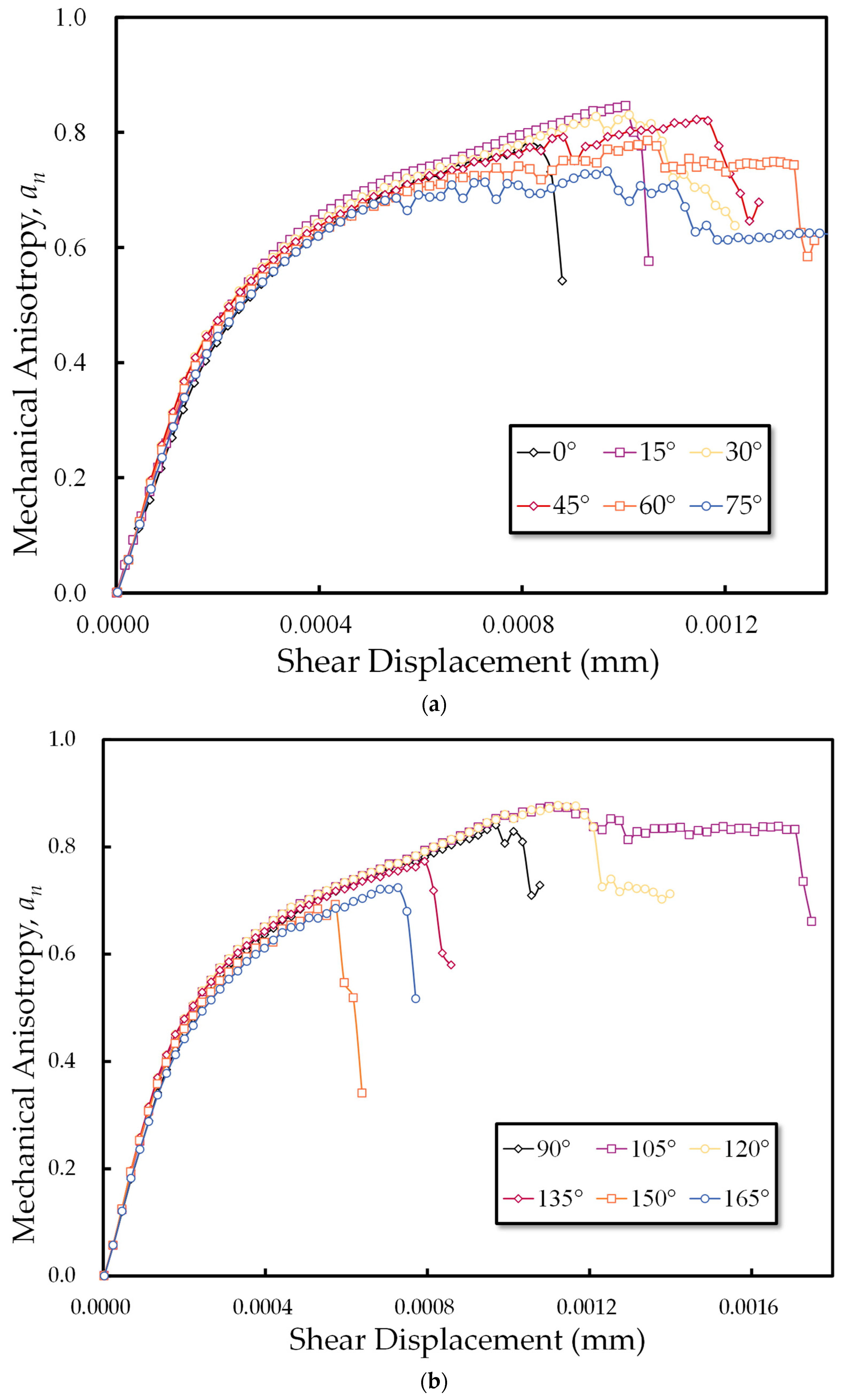
3.2.3. Introduction to Microstructure Anisotropy
3.2.4. The Evolution of the Anisotropy of Microstructure During the Numerical Experiment
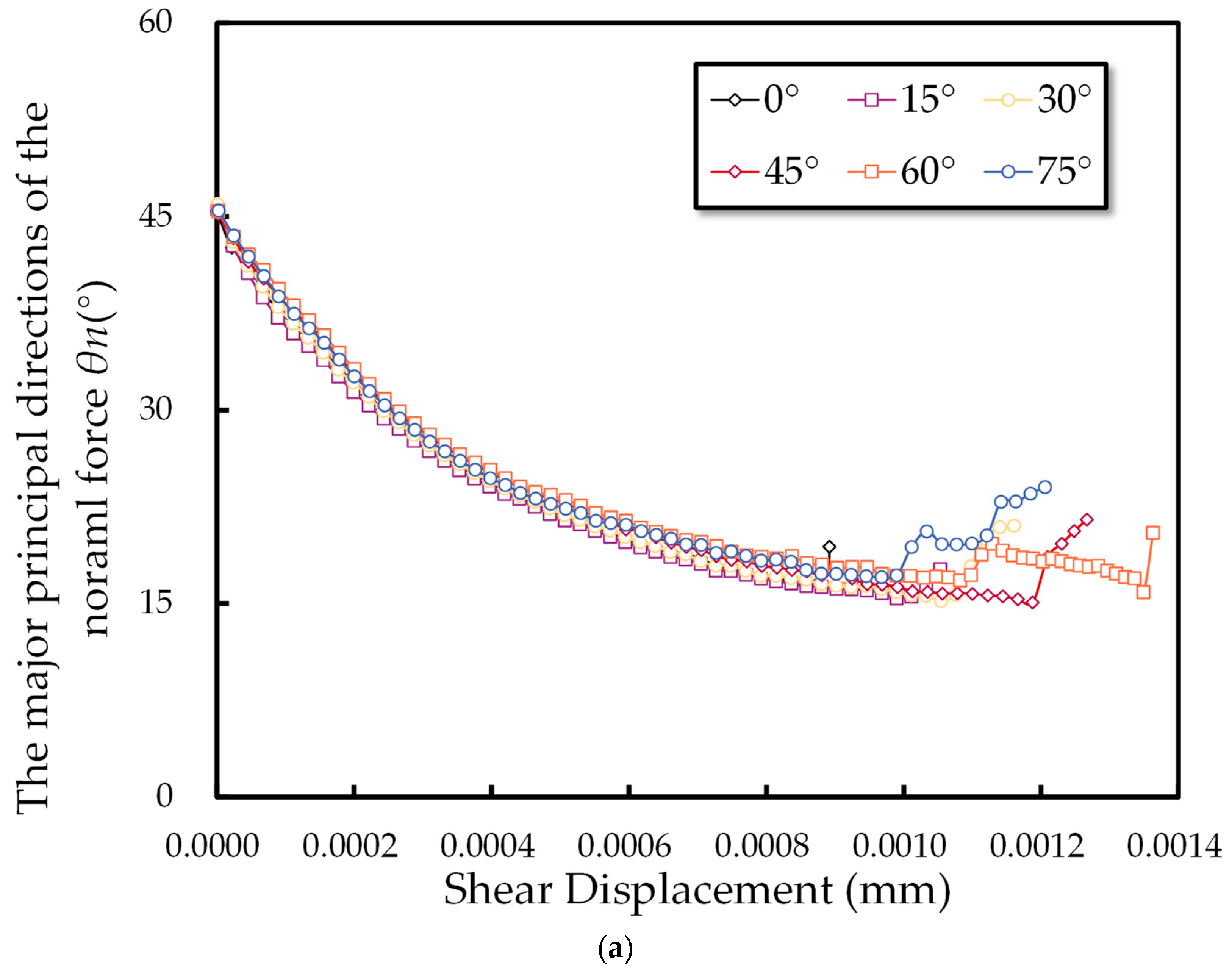
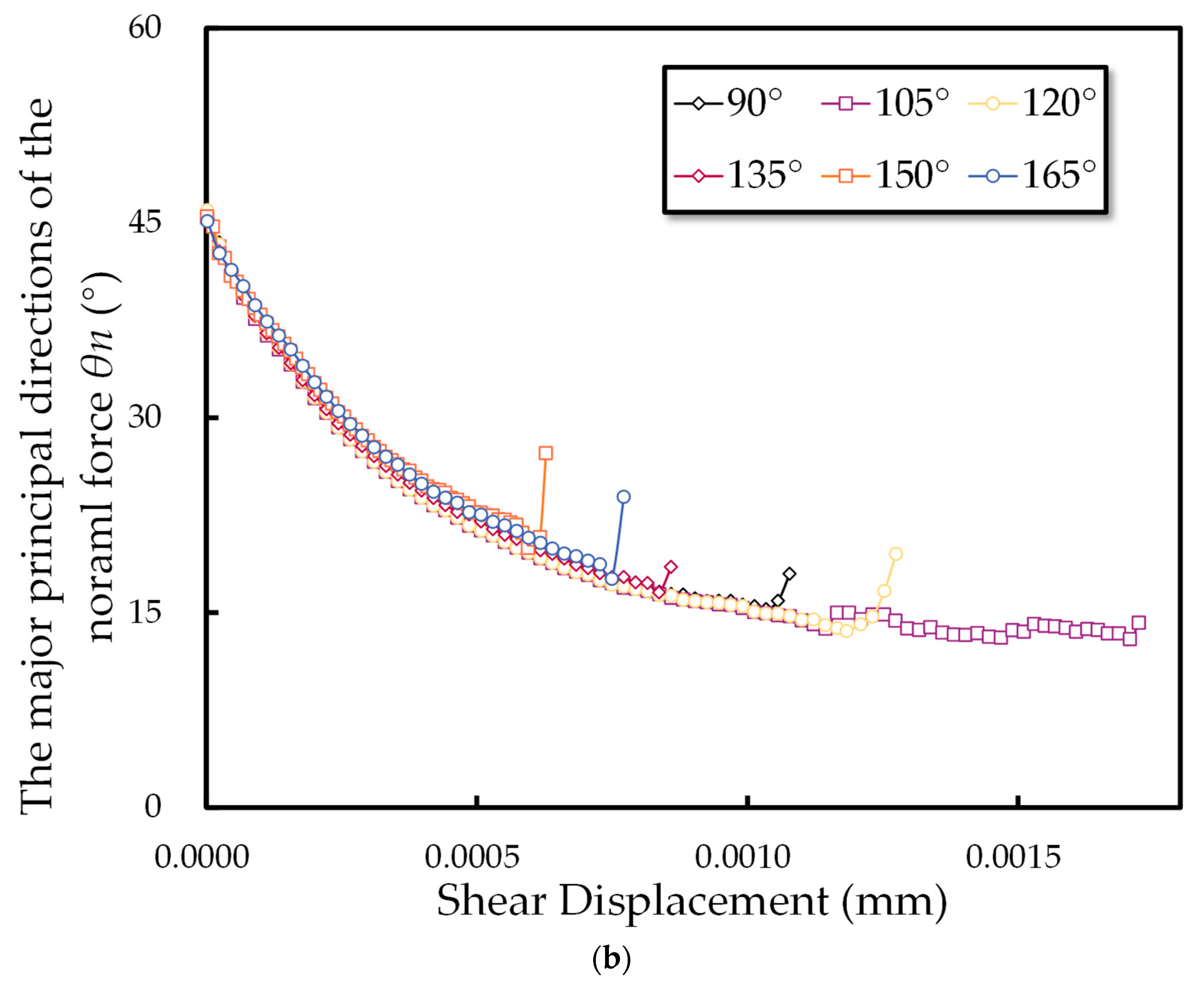
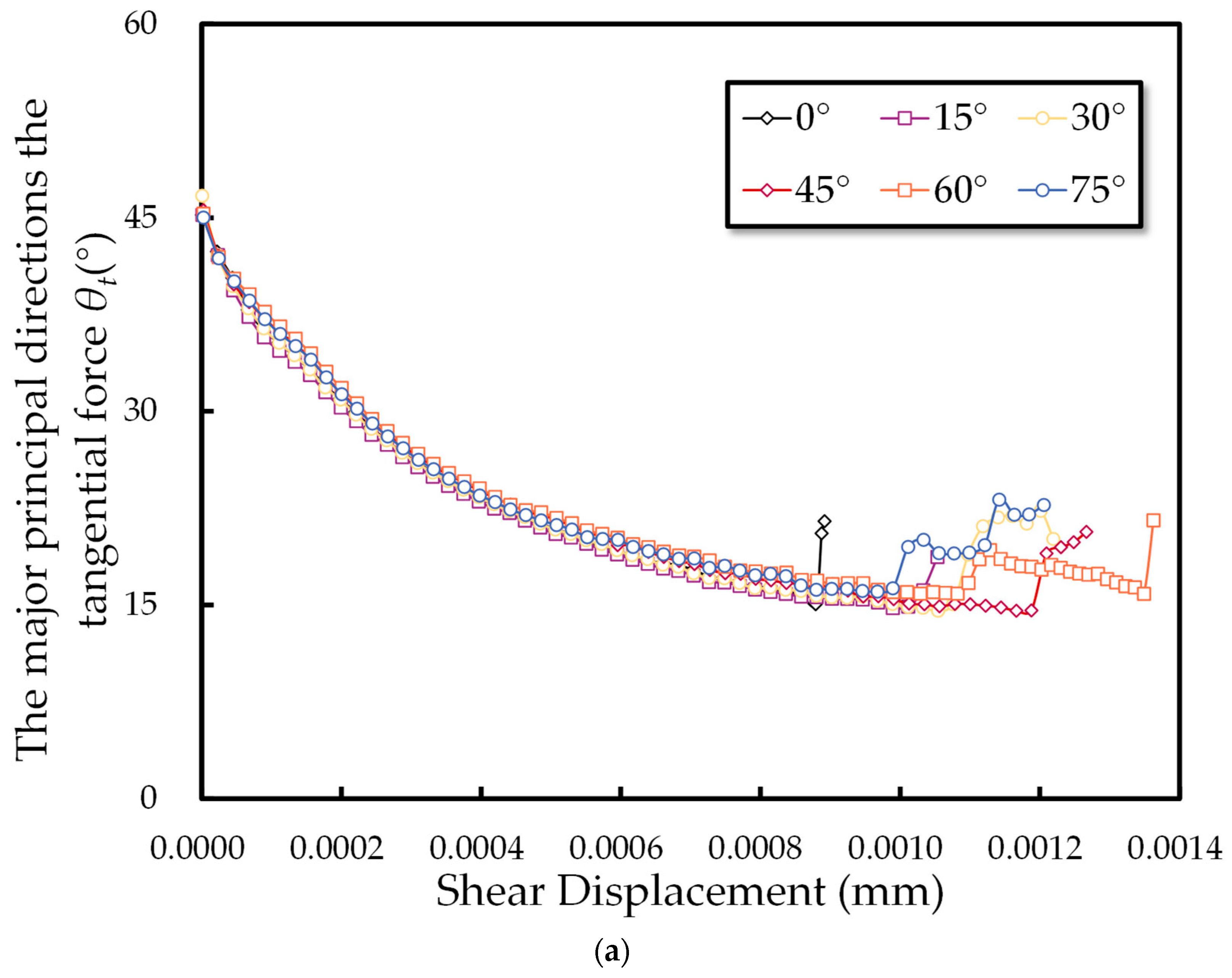
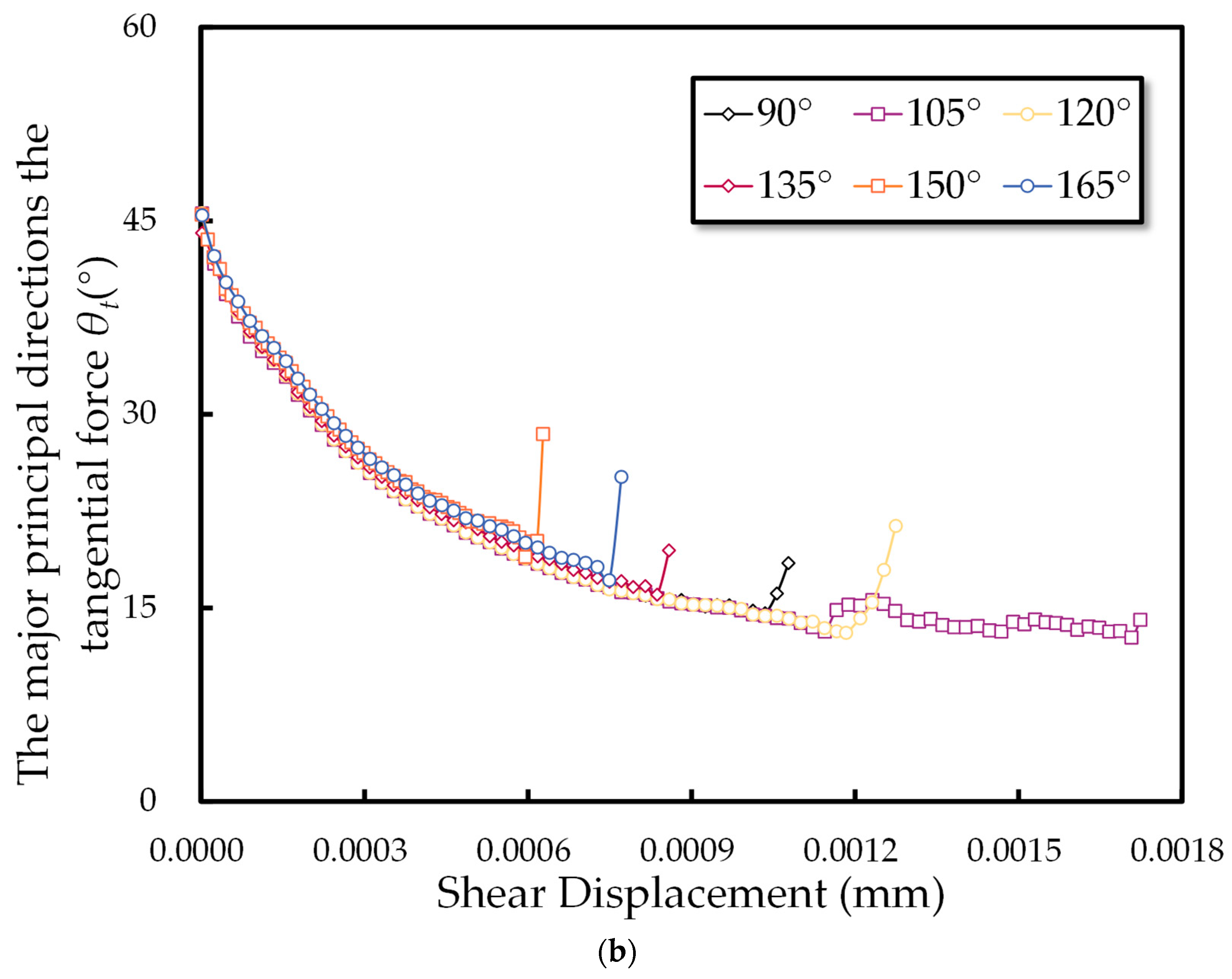
3.2.5. The Evolution of Major Principal Directions During the Numerical Experiment
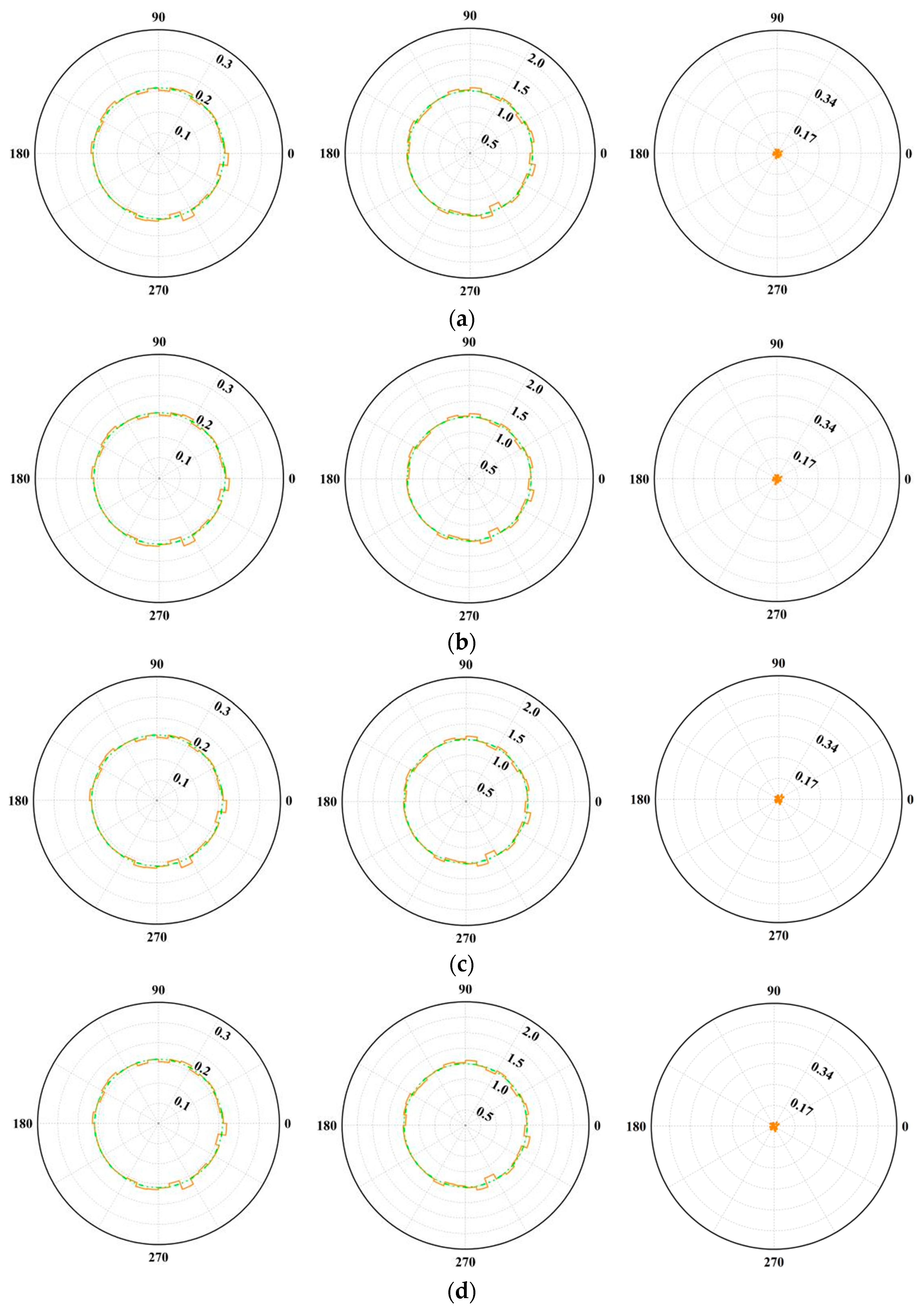
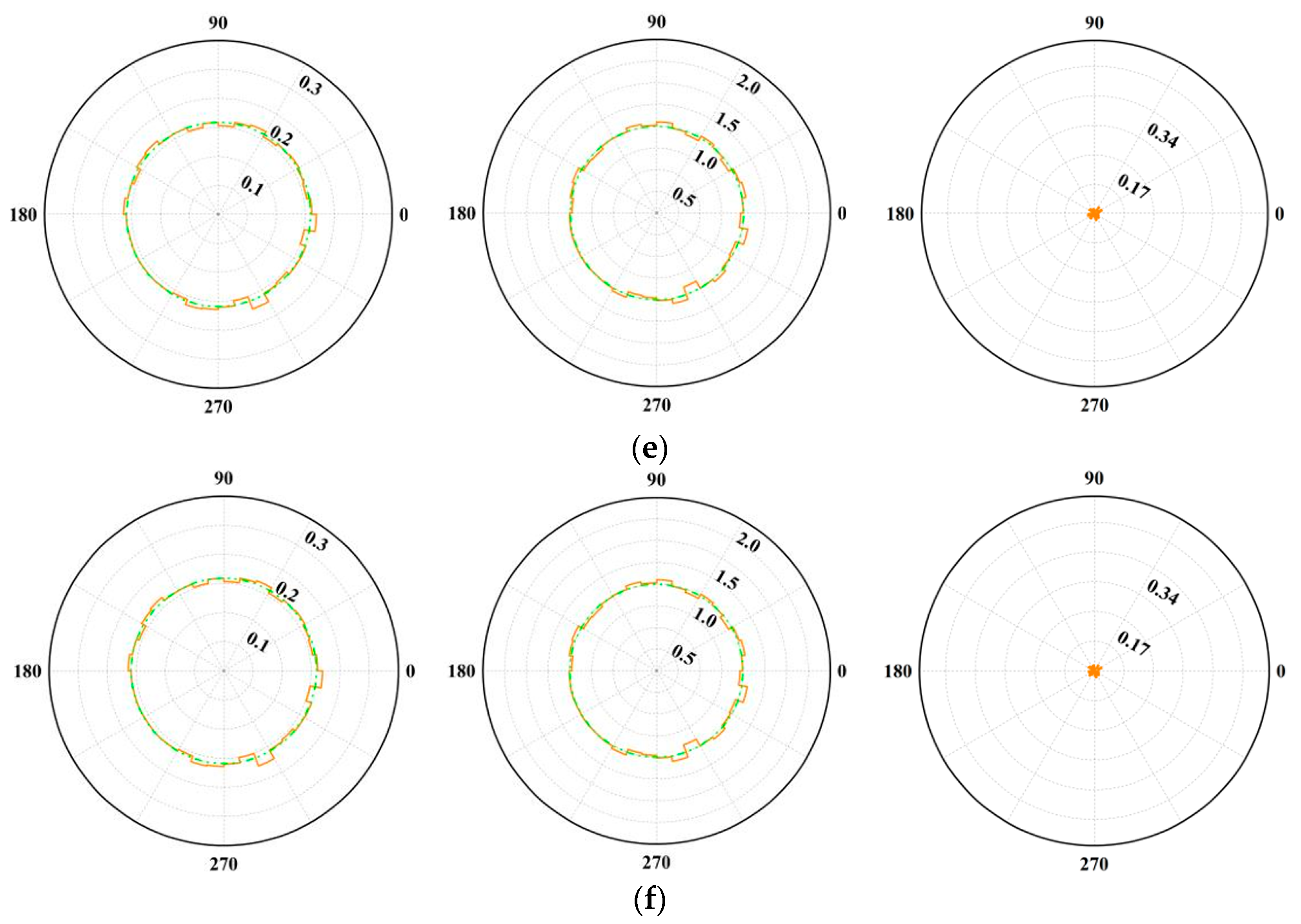
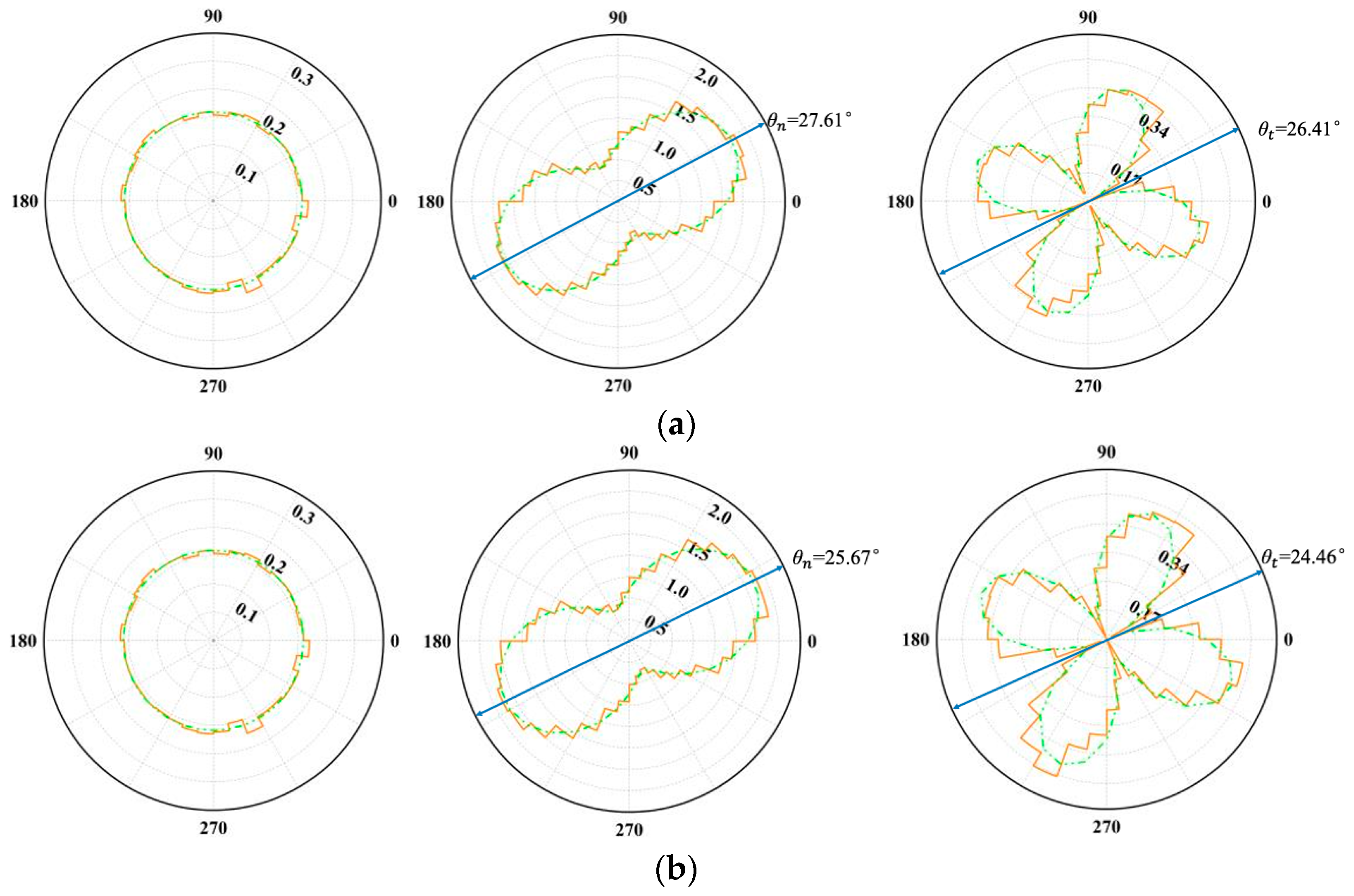
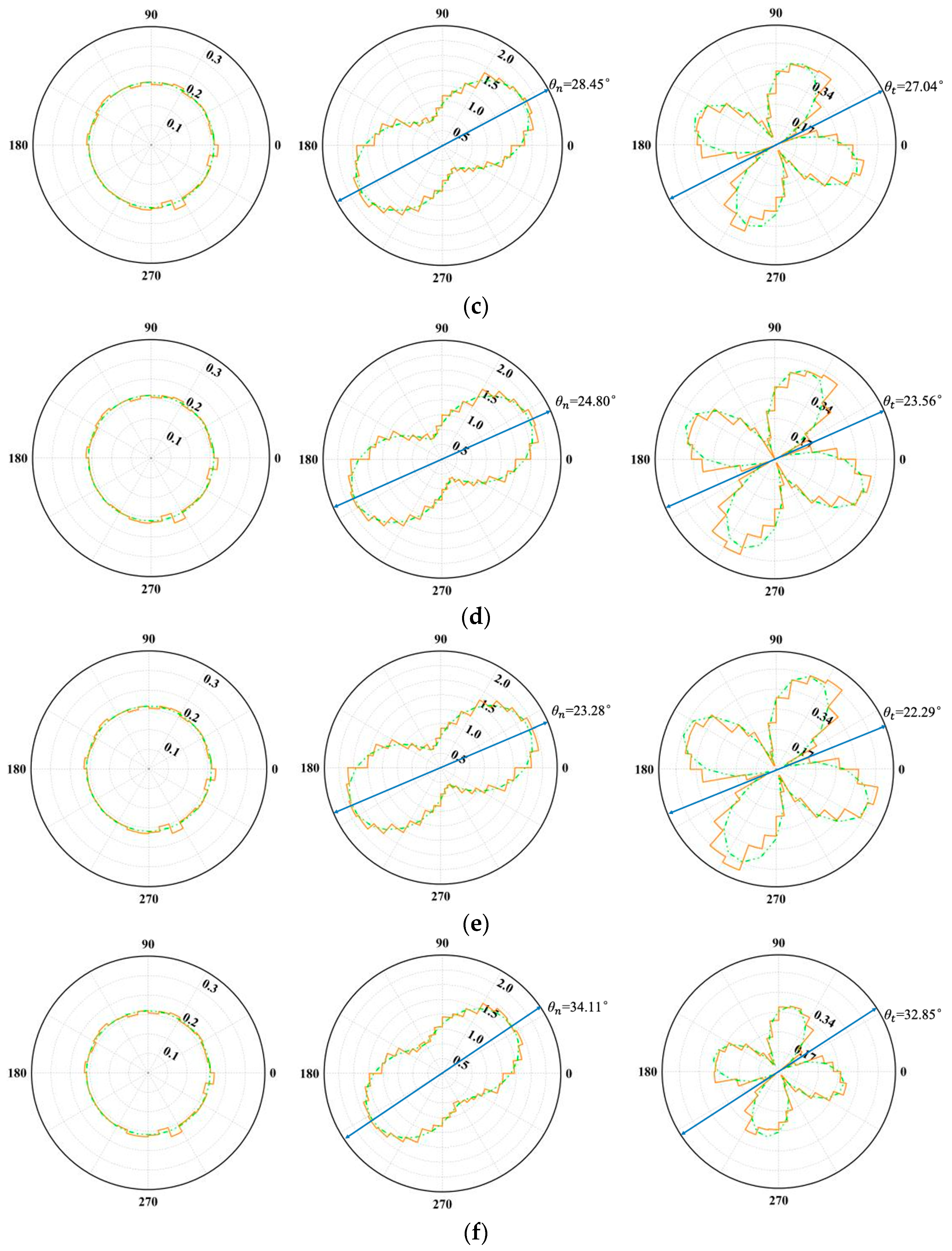
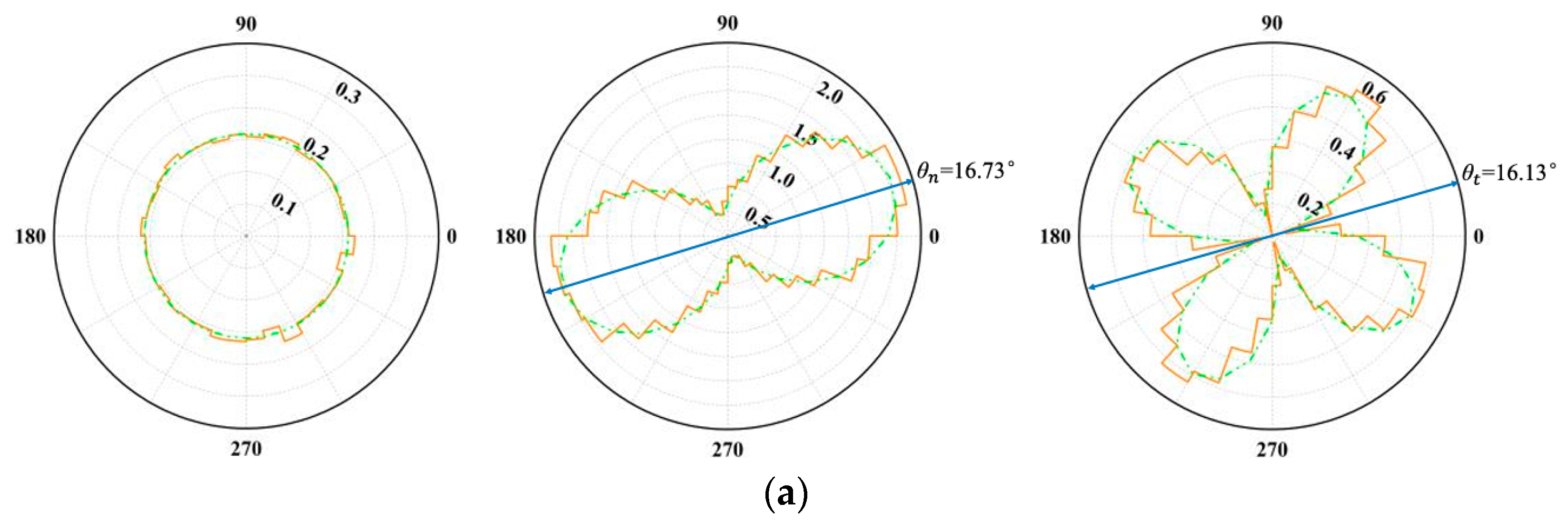
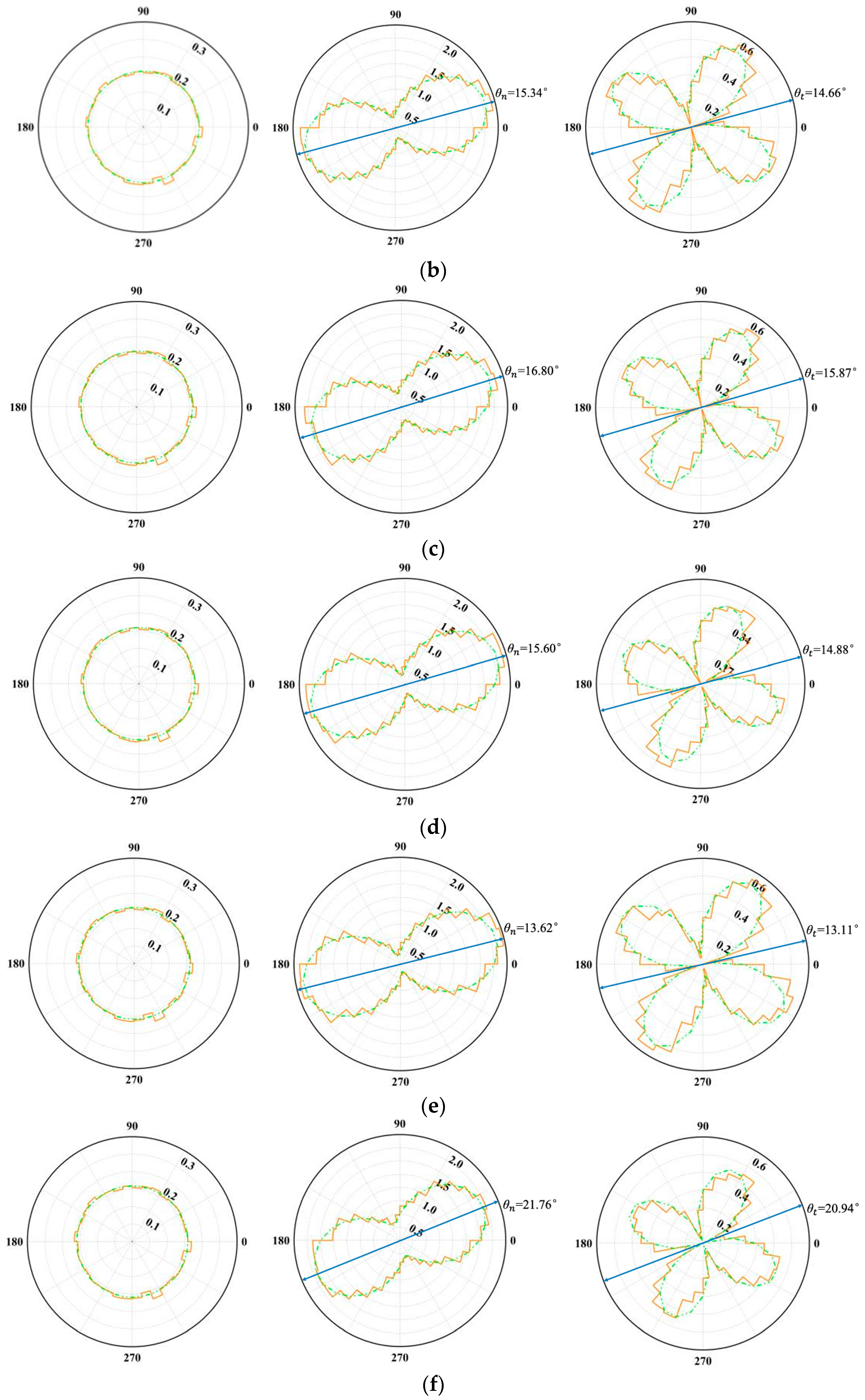
3.2.6. Anisotropic Distribution
4. Discussion
5. Conclusions
- (1)
- (2)
- Although fracture energy accounts for a minor proportion of the total input energy, it markedly alters the rock mass microstructure. Variations in joint inclination angles directly influence the formation and orientation of microcracks. These, in turn, have a decisive effect on peak displacement and the nature of failure brittle or ductile. Additionally, these angles impact the specimens’ capacity to store elastic energy, which is a crucial factor determining the peak shear stress of the rock-like specimens.
- (3)
- The progression of fabric and mechanical anisotropy at the microscopic level aligns with macroscopic deformation behaviors, as depicted in the shear stress–shear displacement curve. This correlation provides micromechanical substantiation and underscores the transition in rock mass failure modes with varying joint inclination angles. As the angle increases, the mode shifts from brittle to ductile, then reverts to brittle failure.
- (4)
- Changes in joint inclination angles not only influence the emergence of microcracks, impacting internal microstructure of the rock mass, but also significantly affect fabric and contact force anisotropy. Consistent with macroscopic deformation behavior, changes in fabric anisotropy and mechanical anisotropy provide micromechanical evidence; decreases in fabric anisotropy and contact anisotropy often signal specimen failure. Specimens displaying higher peaks in these anisotropies typically exhibit greater peak shear stress.
- (5)
- Polar histograms of the contact normal force often exhibit a “peanut-shaped” distribution, while those of the tangential force assume a four-lobed “petal-shaped” pattern. The approximation function presented in this study accurately captures these numerical measurement outcomes. Joint inclination plays a pivotal role in shaping these force distributions; specimens with higher peak shear stresses tend to show more pronounced, slender peanut shapes in a normal force distribution and more expansive petal shapes under tangential force, with the principal direction more closely aligned with the loading axis.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cheng, Y.; Wong, L.N.Y.; Zou, C. Experimental Study on the Formation of Faults from En-Echelon Fractures in Carrara Marble. Eng. Geol. 2015, 195, 312–326. [Google Scholar] [CrossRef]
- Huang, D.; Cen, D.; Ma, G.; Huang, R. Step-Path Failure of Rock Slopes with Intermittent Joints. Landslides 2015, 12, 911–926. [Google Scholar] [CrossRef]
- Zhang, K.; Chen, Y.; Fan, W.; Liu, X.; Luan, H.; Xie, J. Influence of Intermittent Artificial Crack Density on Shear Fracturing and Fractal Behavior of Rock Bridges: Experimental and Numerical Studies. Rock Mech. Rock Eng. 2020, 53, 553–568. [Google Scholar] [CrossRef]
- Shang, J.; West, L.J.; Hencher, S.R.; Zhao, Z. Geological Discontinuity Persistence: Implications and Quantification. Eng. Geol. 2018, 241, 41–54. [Google Scholar] [CrossRef]
- Lajtai, E.Z. Tensile Strength and Its Anisotropy Measured by Point and Line-Loading of Sandstone. Eng. Geol. 1980, 15, 163–171. [Google Scholar] [CrossRef]
- Gehle, C.; Kutter, H.K. Breakage and Shear Behaviour of Intermittent Rock Joints. Int. J. Rock Mech. Min. Sci. 2003, 40, 687–700. [Google Scholar] [CrossRef]
- Tang, P.; Chen, G.-Q.; Huang, R.-Q.; Zhu, J. Brittle Failure of Rockslides Linked to the Rock Bridge Length Effect. Landslides 2020, 17, 793–803. [Google Scholar] [CrossRef]
- Cao, R.H.; Yao, R.; Lin, H.; Lin, Q.B.; Meng, Q.; Li, T. Shear behaviour of 3D nonpersistent jointed rock-like specimens: Experiment and numerical simulation. Comput. Geotech. 2022, 148, 104858. [Google Scholar] [CrossRef]
- Nguyen, H.; Wang, J.; Bazilevs, Y. A smooth Crack-Band Model for anisotropic materials: Continuum theory and computations with the RKPM meshfree method. Int. J. Solids Struct. 2024, 288, 112618. [Google Scholar] [CrossRef]
- Zhang, Y.; Bažant, Z.P. Smooth Crack Band Model—A Computational Paragon Based on Unorthodox Continuum Homogenization. J. Appl. Mech. 2023, 90, 041007. [Google Scholar] [CrossRef]
- Gao, G.; Meguid, M.A.; Chouinard, L.E. On the Role of Pre-Existing Discontinuities on the Micromechanical Behavior of Confined Rock Samples: A Numerical Study. Acta Geotech. 2020, 15, 3483–3510. [Google Scholar] [CrossRef]
- Oda, M. Deformation Mechanism of Sand in Triaxial Compression Tests. Soils Found. 1972, 12, 45–63. [Google Scholar] [CrossRef] [PubMed]
- Oda, M.; Kazama, H.; Konishi, J. Effects of Induced Anisotropy on the Development of Shear Bands in Granular Materials. Mech. Mater. 1998, 28, 103–111. [Google Scholar] [CrossRef]
- Oda, M. Initial Fabrics and Their Relations to Mechanical Properties of Granular Material. Soils Found. 1972, 12, 17–36. [Google Scholar] [CrossRef]
- Oda, M. The Mechanism of Fabric Changes During Compressional Deformation of Sand. Soils Found. 1972, 12, 1–18. [Google Scholar] [CrossRef]
- Zhu, K.; Sun, G.; Shi, L. Shear-Induced Anisotropy Analysis of Rock Masses Containing Non-Coplanar Intermittent Joints. Arch. Appl. Mech. 2024, 94, 841–864. [Google Scholar] [CrossRef]
- Gao, G.; Meguid, M.A. Microscale Characterization of Fracture Growth in Increasingly Jointed Rock Samples. Rock Mech. Rock Eng. 2022, 55, 6033–6061. [Google Scholar] [CrossRef]
- Guo, N.; Zhao, J. The Signature of Shear-Induced Anisotropy in Granular Media. Comput. Geotech. 2013, 47, 1–15. [Google Scholar] [CrossRef]
- Tai, D.; Qi, S.; Zheng, B.; Wang, C.; Guo, S.; Luo, G. Shear Mechanical Properties and Energy Evolution of Rock-like Samples Containing Multiple Combinations of Non-Persistent Joints. J. Rock Mech. Geotech. Eng. 2022, 15, 1651–1670. [Google Scholar] [CrossRef]
- Qi, S.; Zheng, B.; Wu, F.; Huang, X.; Guo, S.; Zhan, Z.; Zou, Y.; Barla, G. A New Dynamic Direct Shear Testing Device on Rock Joints. Rock Mech. Rock Eng. 2020, 53, 4787–4798. [Google Scholar] [CrossRef]
- Sarfarazi, V.; Ghazvinian, A.; Schubert, W.; Blumel, M.; Nejati, H.R. Numerical Simulation of the Process of Fracture of Echelon Rock Joints. Rock Mech. Rock Eng. 2014, 47, 1355–1371. [Google Scholar] [CrossRef]
- Zhang, X.-P.; Wong, L.N.Y. Cracking Processes in Rock-Like Material Containing a Single Flaw Under Uniaxial Compression: A Numerical Study Based on Parallel Bonded-Particle Model Approach. Rock Mech. Rock Eng. 2011, 45, 711–737. [Google Scholar] [CrossRef]
- Xing, L.; Gong, W.; Li, B.; Zhao, C.; Tang, H.; Wang, L. Probabilistic Analysis of Earthquake-Induced Failure and Runout Behaviors of Rock Slopes with Discrete Fracture Network. Comput. Geotech. 2023, 159, 105487. [Google Scholar] [CrossRef]
- Chen, M.; Yang, S.-Q.; Ranjith, P.G.; Zhang, Y.-C. Cracking Behavior of Rock Containing Non-Persistent Joints with Various Joints Inclinations. Theor. Appl. Fract. Mech. 2020, 109, 102701. [Google Scholar] [CrossRef]
- Lin, Q.; Cao, P.; Liu, Y.; Cao, R.; Li, J. Mechanical Behaviour of a Jointed Rock Mass with a Circular Hole under Compression-Shear Loading: Experimental and Numerical Studies. Theor. Appl. Fract. Mech. 2021, 114, 102998. [Google Scholar] [CrossRef]
- Xie, H.; Li, L.; Peng, R.; Ju, Y. Energy Analysis and Criteria for Structural Failure of Rocks. J. Rock Mech. Geotech. Eng. 2009, 1, 11–20. [Google Scholar] [CrossRef]
- Luo, Y.; Wang, G.; Li, X.; Liu, T.; Mandal, A.K.; Xu, M.; Xu, K. Analysis of Energy Dissipation and Crack Evolution Law of Sandstone under Impact Load. Int. J. Rock Mech. Min. Sci. 2020, 132, 104359. [Google Scholar] [CrossRef]
- Satake, M. Fundamental Quantities in the Graph Approach to Granular Materials. In Studies in Applied Mechanics; Elsevier: Amsterdam, The Netherlands, 1983; Volume 7, pp. 9–19. ISBN 978-0-444-42192-0. [Google Scholar]
- Silbert, L.E.; Grest, G.S.; Landry, J.W. Statistics of the Contact Network in Frictional and Frictionless Granular Packings. Phys. Rev. E 2002, 66, 061303. [Google Scholar] [CrossRef] [PubMed]
- Oda, M. Co-Ordination Number and Its Relation to Shear Strength of Granular Material. Soils Found. 1977, 17, 29–42. [Google Scholar] [CrossRef] [PubMed]
- Li, X. Micro-Scale Investigation on the Quasi-Static Behavior of Granular Material. Ph.D. Thesis, The Hong Kong University of Science and Technology, Hong Kong, China, 2006. [Google Scholar]
- Li, X.; Yu, H.-S. On the Stress–Force–Fabric Relationship for Granular Materials. Int. J. Solids Struct. 2013, 50, 1285–1302. [Google Scholar] [CrossRef]
- Ken-Ichi, K. Distribution of Directional Data and Fabric Tensors. Int. J. Eng. Sci. 1984, 22, 149–164. [Google Scholar] [CrossRef]
- Li, X.; Yu, H.S. Tensorial Characterisation of Directional Data in Micromechanics. Int. J. Solids Struct. 2011, 48, 2167–2176. [Google Scholar] [CrossRef]
- Guo, N. Multiscale Characterization of the Shear Behavior of Granular Media. Ph.D. Thesis, The Hong Kong University of Science and Technology, Hong Kong, China, 2014; p. b1334193. [Google Scholar]
- Xu, W.; Ren, W.; Liu, Y.; Liu, C.; Cai, S. Micromechanical Behavior of Jointed Rock Masses under Uniaxial Compression Loading: A Numerical Study Based on the Discrete Element Method. Eur. J. Environ. Civil. Eng. 2022, 27, 3653–3678. [Google Scholar] [CrossRef]





| Fundamental Mechanical Parameters | Value |
|---|---|
| Density, (kg/m3) | 1.32 |
| Young’s modulus, E (GPa) | 5.78 |
| Uniaxial compressive strength, (MPa) | 9.22 |
| Cohesion, c (MPa) | 0.523 |
| Friction angle, (°) | 59 |
| Materials | Item | Micromechanical Properties |
|---|---|---|
| Rock | Ball–ball contact effective modulus () | 0.22 GPa |
| Ball stiffness ratio () | 1.1 | |
| Ball friction coefficient () | 0.3 | |
| Parallel-bond effective modulus () | 0.22 GPa | |
| Parallel-bond stiffness ratio () | 1.1 | |
| Parallel-bond tensile strength () | 2.8 MPa | |
| Parallel-bond cohesion () | 2.2 MPa | |
| Joint | Smooth-joint normal stiffness () | 1000 GPa/m |
| Smooth-joint shear stiffness () | 500 GPa/m | |
| Smooth-joint friction coefficient () | 0.2 | |
| Smooth-joint tensile strength () | 0 MPa | |
| Smooth-joint cohesion () | 0 MPa |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, K.; Wang, W.; Shi, L.; Sun, G. Shear-Induced Anisotropy Analysis of Rock-like Specimens Containing Different Inclination Angles of Non-Persistent Joints. Mathematics 2025, 13, 362. https://doi.org/10.3390/math13030362
Zhu K, Wang W, Shi L, Sun G. Shear-Induced Anisotropy Analysis of Rock-like Specimens Containing Different Inclination Angles of Non-Persistent Joints. Mathematics. 2025; 13(3):362. https://doi.org/10.3390/math13030362
Chicago/Turabian StyleZhu, Kaiyuan, Wei Wang, Lu Shi, and Guanhua Sun. 2025. "Shear-Induced Anisotropy Analysis of Rock-like Specimens Containing Different Inclination Angles of Non-Persistent Joints" Mathematics 13, no. 3: 362. https://doi.org/10.3390/math13030362
APA StyleZhu, K., Wang, W., Shi, L., & Sun, G. (2025). Shear-Induced Anisotropy Analysis of Rock-like Specimens Containing Different Inclination Angles of Non-Persistent Joints. Mathematics, 13(3), 362. https://doi.org/10.3390/math13030362





