Dynamic Event-Triggered, Fixed-Time Control for Heterogeneous Multi-Agent Systems with Hybrid DoS Attacks

Abstract

In this article, the fixed-time, quasi-consensus control problem for heterogeneous multi-agent systems (HMASs) under denial-of-service (DoS) attacks is investigated. Unlike most previous studies in this area, which focus on periodic (or single-type) DoS attacks with static event-triggered control, this paper ensures that HMASs achieve fixed-time quasi-consensus under aperiodic hybrid DoS attacks via dynamic event-triggered control. According to whether DoS attacks are known, two control protocols based on dynamic event-triggered conditions are given, which both ensure that HMASs achieve output quasi-consensus within a fixed time and exhibit less conservative triggering conditions than static event-triggered protocols. Moreover, the proof that the given dynamic event-triggered conditions can avoid Zeno-behavior is provided. Lastly, simulation examples are presented to support the obtained points.

1. Introduction

During the last few years, multi-agent systems (MASs) have been widely applied in practical fields, such as robotics [1], vehicle formation [2], and spacecraft [3]. As a foundational problem in MAS research, the issue of consensus, which aims to achieve state or output consensus for MASs, has attracted scholarly attention. Different from centralized systems, the control strategy of MASs depends on both the agent dynamics and communication networks. In ref. [4], a topology graph matrix was provided to describe the communications of MASs, and a control scheme based on this matrix was also proposed. However, this method is only applicable to multi-agent systems in which all agents share identical dynamics, i.e., homogeneous MASs. On this basis, considering the agent dynamics can be different in practical situations, a novel control scheme was investigated in [5], which can make heterogeneous multi-agent systems achieve consensus. Similar issues were also studied in [6,7]. Although these strategies provided can effectively control heterogeneous multi-agent systems (HMASs), only the basic state and output consensus issues were solved. Considering that the simple consensus control cannot meet different needs in practice, three cases were studied. Specifically, the containment control scheme making all agents asymptotically tend to the convex hull formed by leaders [8], the asynchronous control scheme making agent asymptotically have the dynamic characteristics completely opposite to the leader [9] and the quasi-consensus control scheme making the error between agent and leader converge to a bounded compact set [10] were all investigated.

The control schemes provided in the above-mentioned references always make MASs achieve asymptotic consensus. Nevertheless, letting MASs achieve consensus or quasi-consensus within a limited time is more in line with the actual demands of a control scheme. Motivated by this problem, how to design a consensus control strategy that makes MASs achieve finite-time consensus has attracted significant attention. In ref. [11], the network consensus problem was investigated, and a state-dependent sign function was used in a control approach that solves the finite-time consensus problem. Then, control strategies that solve the finite-time consensus issue for second-order [12], nonlinear [13] and non-holonomic chained-form [14] MASs were also investigated. For the purpose of further accelerating convergence, ref. [15] investigated the fast finite-time consensus control scheme, combing existing finite-time consensus control schemes and improved tracking algorithms. Although the control schemes provided in these references ensure MASs achieve consensus within finite time, these schemes’ convergence time depends on initial states, indicating that the convergence time cannot be estimated when the initial conditions are unknown. To overcome this limitation, fixed-time consensus control has been studied. In ref. [16], a control scheme based on hybrid-order system information was provided for achieving a fixed-time consensus that is invariant to initial conditions. Similar problems for first-order [17], second-order [18] and nonlinear stochastic [19] MASs were also investigated.

Considering that continuous controller updates and information transfer will cause communication congestion and energy loss, a series of discontinuous control schemes were investigated. Among these, the event-triggered control approach attracted wide attention due to its flexibility and reduced conservatism. In ref. [20], an event-triggered control scheme for linear MASs, which can make MASs achieve consensus and enables the triggering condition to exclude Zeno-behavior successfully, was provided. However, this control scheme can only solve the consensus issue of homogeneous MASs. In ref. [21], for the purpose of achieving consensus of HMASs based on event-triggered control, a triggering condition based on the agent system’s and its corresponding dynamic compensator’s information was designed. Although the event-triggered mechanisms provided in these two references can reduce the frequency of controller updates, continuous information transmission is inevitable, which may increase the communication costs. To solve this problem, a periodic event-triggered control approach for HMASs, which can avoid the continuous information transfer and controller update simultaneously, was provided in [22]. The event-triggered control schemes proposed in early references (including [20,21,22,23,24]) can only solve the asymptotic consensus problem. On this basis, ref. [25] provided a novel periodic event-triggered control scheme that enables MASs to solve the control problem within a fixed time.

The early research on the control of MASs (including the literature mentioned above) always overlooked the impact of cyber attacks on the systems. As information transfer of MASs is critical for achieving consensus, the threats posed by malicious cyber attacks disrupting communication networks cannot be neglected. In general, malicious cyber attacks fall into two categories: denial-of-service (DoS) attacks [26], which compromise service availability; and deception attacks [27], which inject false information. Among these, DoS attacks are more frequently launched by attackers because of their simple implementation and high destructive force. Since the communication networks of MASs can be changed or even broken by DoS attacks, providing proper control schemes under these conditions becomes a significant challenge, which has attracted considerable attention. In ref. [28], the consensus problem for MASs under a special case of DoS attacks, wherein it was assumed that the attacks were periodic, was investigated. Considering that aperiodic cyber attacks are more in line with reality, a novel control scheme for MASs with aperiodic DoS attacks was provided in ref. [29]. For the purpose of further reducing the communication burden, the event-triggered control scheme [30] and dynamic event-triggered control scheme [31] for MASs under DoS attacks have been considered, and the fixed-time consensus problem for MASs with different types of attacks was also considered in ref. [32].

Although the consensus issue for MASs under DoS attacks have been investigated for a while, obtaining important results, it is still difficult to design proper dynamic event-triggered control schemes that solve this issue.

• Since DoS attacks disrupt the message communication between agents, a controller may not be able to receive system information and complete controller updates, even though the triggering condition has been met. To solve this problem, most of the existing control strategies assume that the real-time information of DoS attacks are known and have to stop triggering when the systems are under DoS attacks, which is difficult to achieve and makes the control scheme even more conservative.
• Compared to the static event-triggered control strategy, the core advantage of the dynamic event-triggered control strategy lies in reducing the controller update frequency by decreasing the conservatism of the triggering condition. The key to this strategy lies in the design of the dynamic event-triggering condition. Currently, the most fundamental method is to add a non-negative dynamic term that approaches zero over time with respect to the static event-triggered condition. However, when the problem shifts from asymptotic consensus to fixed-time consensus in multi-agent systems (MASs), this traditional design faces a serious challenge: the dynamic term must not only remain non-negative to preserve the advantage of reduced conservatism, but it must also ensure that the system achieves consensus within a fixed time. These dual requirements make the design of the dynamic term particularly challenging. Consequently, although the dynamic event-triggered control strategy offers advantages in terms of reduced conservatism, the dual constraints in designing the dynamic event-triggering condition for fixed-time consensus scenarios have led to its limited adoption in existing research on fixed-time consensus problems for MASs.

Inspired by these problems, we have written this article.

This article investigates the fixed-time, quasi-consensus problem for HMASs under DoS attacks. Two dynamic event-triggered control schemes for HMASs under known and unknown DoS attacks are proposed. The main contributions are listed as follows.

• Based on whether the DoS attacks are known or not, two different dynamic compensators and the corresponding consensus criteria are provided, which can achieve the fixed-time consensus between dynamic compensators and leader systems regardless of whether the attacks are known. Moreover, one additional consensus criterion based on a special case, which can reduce the conservatism of the given control schemes successfully, is also provided.
• A new type of dynamic term is designed in this paper. On this basis, the dynamic event-triggered condition is constructed and a novel dynamic event-triggered control scheme is proposed. This scheme not only ensures HMASs achieve quasi-consensus within fixed time, but it also has lower conservatism than a static event-triggered control scheme, thereby reducing the update frequency of the controller.

The rest of this paper is arranged as follows. The preliminaries and problem formulation are provided in Section 2 and Section 3, respectively. The dynamic event-triggered control schemes for systems under known and unknown DoS attacks are provided in Section 4 and Section 5, respectively. The numerical examples are given in Section 6, and the conclusion is provided in Section 7.

2. Preliminaries

2.1. Notations

Take ${\mathbf{R}}^{m\times n}$ and ${\mathbf{R}}^n$ as the set of $m\times n$ real matrices and n-dimensional Euclidean space, respectively, where $\parallel ·\parallel$ is the Euclidean norm of vectors or 2-norm of matrices; $X>0$ ($X<0$) means that X is a symmetric positive (negative) definite matrix; ${\lambda }_{min}\left(X\right)$ and ${\lambda }_{max}\left(X\right)$ represent the minimum and maximum eigenvalues of X if $X>0$, respectively; $I_n$ represents the $n\times n$-dimensional identity matrix; $\mathrm{sign}(·)$ represents the symbolic function; $\mathrm{sign}\left(x\right)={(\mathrm{sign}\left(x_1\right), \mathrm{sign}\left(x_2\right),\dots ,\mathrm{sign}\left(x_n\right))}^T$ and $\mathrm{sign}{\left(x\right)}^2={(x_1^2\mathrm{sign}\left(x_1\right), x_2^2\mathrm{sign}\left(x_2\right),\dots ,x_n^2\mathrm{sign}\left(x_n\right))}^T$ for any $x={(x_1, x_2,\dots ,x_n)}^T\in {\mathbf{R}}^n$. $\lceil ·\rceil$ represent a function satisfying $\lceil x\rceil =inf\left\{x^{\ast }\right|x^{\ast }\ge x,x^{\ast }\in \mathbf{N}\}$ for any $x\ge 0$, where $\mathbf{N}$ is the set of natural numbers; and e represents the natural constant.

2.2. Topology Graph Knowledge of MASs

Consider that MASs consist of one leader and N agents. The communication networks of MASs can be described by a $n\times n$-dimensional topology matrix $H={\left[h_{ij}\right]}_{N\times N}$, where $h_{ij}$ represents the element of H located in the i-th row and j-th column, and i, $,j$ denote the index of the followers, i.e., i, $j\in \{1,2,\dots ,N\}$. To be specific, $h_{ii}={\sum }_{j=1}^N{a}_{ij}+b_i$ and $h_{ij}=-a_{ij}$ if $i\ne j$. Moreover, $a_{ij}$ satisfies $a_{ij}=a_{ji}>0$ if $i\ne j$ and there exists an undirected information channel between agents i and j; otherwise, $a_{ij}=0$. Additionally, $b_i>0$ if there exists a information channel from leader to agent i; otherwise, $b_i=0$. Agent i can receive information from leader if there exist a series of ${\varrho }_w\in \{1,2,\dots ,N\}$ for $w=1,2,\dots ,s$ such that $a_{i{\varrho }_1},a_{{\varrho }_1{\varrho }_2},\dots ,a_{{\varrho }_{s-1}{\varrho }_s},b_{{\varrho }_s}>0$. Moreover, the communication networks of MASs can be called connected if each agent can receive information from the leader.

Lemma 1 

([4]). $H>0$ if the communication networks are connected.

Assumption 1. 

The communication networks of MASs without attacks are connected.

2.3. DoS Attacks

The topology graph matrix of MASs under DoS attacks can be represented as $H^{\sigma \left(t\right)}={\left[h_{ij}\left(t\right)\right]}_{N\times N}$, where

• $\sigma \left(t\right)$: $[0,+\infty )\to \{0,1,2,\dots ,s\}$ is a switching signal representing active DoS attacks mode at time instant t, with s being the total number of DoS attacks modes.
• $H^0=H$ represents the topology matrix without DoS attacks.
• $H^w$ ($w=1,2,\dots ,s$) corresponds to the topology matrix under the w-th DoS attacks mode.
• $h_{ij}\left(t\right)={\sum }_{j=1}^N{a}_{ij}\left(t\right)+b_i\left(t\right)$ if $i=j$, $h_{ij}\left(t\right)=-a_{ij}\left(t\right)$; otherwise, $a_{ij}\left(t\right)$ ($b_i\left(t\right)$) means the same thing to $H^{\sigma \left(t\right)}$ as $a_{ij}$ ($b_i$) to H.

Meanwhile, based on [32], DoS attacks can be divided into two categories: connectivity-maintained attacks (CMA) and connectivity-broken attacks (CBA). Without loss of generality, the index of element of a DoS attack set can be rearranged such that the w-th DoS attack mode belongs to CMA for any $w\in \{1,2,\dots ,s^{\ast }\}$ with $s^{\ast }\le s$; otherwise, it belongs to CBA. Therefore, $H^w>0$ for any $w\in \{0,1,2,\dots ,s^{\ast }\}$.

Assumption 2. 

There are constants $\tau ,\underline{T},\overline{T}>0$ and a time sequence ${\left\{T_r\right\}}_{r=0}^{\infty }$ with $T_0=0$ such that

1. 

$\underline{T}\le T_r-T_{r-1}\le \overline{T}$ for any $r=1,2,\dots$

2. 

For any $w\in \{0,1,2,\dots ,s\}$, if $\sigma \left(t\right)=w$ for some $t\in [T_r,T_{r+1})$, there exists ${\overline{t}}_w,{\underline{t}}_w\in [T_r,T_{r+1})$ such that ${\underline{t}}_w\le t\le {\overline{t}}_w$, ${\overline{t}}_w-{\underline{t}}_w\ge \tau$ and $\sigma \left(t\right)=w$ for $t\in [{\underline{t}}_w,{\overline{t}}_w]$.

Lemma 2 

([17]). If ${\vartheta }_i\ge 0$ for $i=1,2,\dots ,s$, the following results can be obtained:

$$\begin{array}{c}\hfill \sum _{i=1}^s{\vartheta }_i^g\ge {(\sum _{i=1}^s{\vartheta }_i)}^g,0<g<1,\\ \hfill \sum _{i=1}^s{\vartheta }_i^g\ge s^{1-g}{(\sum _{i=1}^s{\vartheta }_i)}^g,g>1.\end{array}$$

Lemma 3 

([33] (Young’s Inequality)). For any $a,b\ge 0$, the following result can be obtained:

$$\begin{array}{c}\hfill ab\le {\displaystyle \frac{a^p}{p}}+{\displaystyle \frac{b^q}{q}},\end{array}$$

(1)

where $p,q>0$, which satisfy

$$\begin{array}{c}\hfill {\displaystyle \frac{1}{p}}+{\displaystyle \frac{1}{q}}=1.\end{array}$$

(2)

Based on Lemma 3, the next conclusion can be given.

Lemma 4. 

For any $a,b\ge 0$ and $\chi >0$, we have

$$\begin{array}{c}\hfill a^{2}b\le {\displaystyle \frac{2}{3}}{\chi }^{\frac{1}{2}}{a}^3+{\displaystyle \frac{1}{3}}{\chi }^{-1}{b}^3.\end{array}$$

(3)

Proof of Lemma 4. 

Take $\widehat{a}={\chi }^{\frac{1}{3}}{a}^2$, $\widehat{b}={\chi }^{-\frac{1}{3}}b$, $p={\displaystyle \frac{3}{2}}$$q=3$, which is based on Lemma 3. Then, we have

$$\begin{array}{ccc}\hfill a^{2}b& =& \widehat{a}\widehat{b}\hfill \\ & \le & {\displaystyle \frac{{\widehat{a}}^p}{p}}+{\displaystyle \frac{{\widehat{b}}^q}{q}}\hfill \\ & =& {\displaystyle \frac{2}{3}}{\chi }^{\frac{1}{2}}{a}^3+{\displaystyle \frac{1}{3}}{\chi }^{-1}{b}^3.\text{\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}(4)}\hfill \end{array}$$

□

3. Problem Formulation

Consider the HMASs that are given as follows:

$$\begin{array}{ccc}\hfill {\dot{x}}_i\left(t\right)& =& A_i{x}_i\left(t\right)+u_i\left(t\right)+{\omega }_i\left(t\right),\hfill \end{array}$$

(5)

$$\begin{array}{ccc}\hfill y_i\left(t\right)& =& C_i{x}_i\left(t\right),\hfill \end{array}$$

(6)

$$\begin{array}{ccc}\hfill {\dot{x}}_0\left(t\right)& =& A_0{x}_0\left(t\right),\hfill \end{array}$$

(7)

$$\begin{array}{ccc}\hfill y_0\left(t\right)& =& C_0{x}_0\left(t\right),\hfill \end{array}$$

(8)

where $x_i\left(t\right),u_i\left(t\right),{\omega }_i\left(t\right)\in {\mathbf{R}}^{n_i},y_i\left(t\right)\in {\mathbf{R}}^q$ represent the state, input, external disturbance, and output of agent i for $i=1,2,\dots ,N$, respectively; and $x_0\left(t\right)\in {\mathbf{R}}^{n_0},y_0\left(t\right)\in {\mathbf{R}}^q$ represent the state and output of the leader.

Assumption 3. 

There is a constant $\gamma >0$ such that $\parallel {\omega }_i\left(t\right)\parallel \le \gamma$ for any $t\ge 0$ and $i=1,2,\dots ,N$.

Assumption 4. 

There exists matrix ${\Pi }_i\in {\mathit{R}}^{n_i\times n_0}$ for $i=1,2,\dots ,N$ such that

$$\begin{array}{ccc}\hfill {\Pi }_i{A}_0& =& A_i{\Pi }_i,\hfill \\ \hfill C_i{\Pi }_i& =& C_0.\hfill \end{array}$$

Definition 1. 

The fixed-time quasi-consensus problem for Systems (5)–(8) is solved if there exist positive constants ${\varphi }_i,T_{max}^i>0$ for $i=1,2,\dots ,N$ such that $\parallel y_i\left(t\right)-y_0\left(t\right)\parallel \le {\varphi }_i$ for any $t\ge T_{max}^i$.

The purpose of this paper was to design a control scheme that makes Systems (5)–(8) solve the fixed-time quasi-consensus problem.

4. Event-Based Control Scheme Under Known DoS Attacks

Consider the case that the DoS attacks are known, which means that $\sigma \left(t\right)$ and $H^{\sigma \left(t\right)}$ can be known in advance.

4.1. Design of Dynamic Compensator

Although the control objective is to achieve the consensus of the outputs $y_i\left(t\right)$, the heterogeneity of HMASs prevents the direct design of a unified consensus protocol. For ensuring HMASs achieve output consensus, the dynamic compensator should be introduced to transform the heterogeneous dynamics into equivalent isomorphic forms, enabling the control scheme to be directly applied. The dynamic compensators for each follower agent are provided as follows:

$$\begin{array}{ccc}\hfill {\dot{z}}_i\left(t\right)& =& A_0{z}_i\left(t\right)-{\beta }^{\ast }{\phi }_{2i}\left(t\right)-{\alpha }_1\mathrm{sign}\left({\phi }_{2i}\left(t\right)\right)-{\alpha }_2\mathrm{sign}{\left({\phi }_{2i}\left(t\right)\right)}^2,\mathrm{if}\sigma \left(t\right)=0,\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill {\dot{z}}_i\left(t\right)& =& A_0{z}_i\left(t\right)-{\beta }^{\ast }\left(t\right){\phi }_{2i}\left(t\right)-{\alpha }_1\left(t\right)\mathrm{sign}\left({\phi }_{2i}\left(t\right)\right)-{\alpha }_2\left(t\right)\mathrm{sign}{\left({\phi }_{2i}\left(t\right)\right)}^2,\mathrm{if}\sigma \left(t\right)=1,2,\dots ,s^{\ast },\hfill \end{array}$$

(10)

$$\begin{array}{ccc}\hfill {\dot{z}}_i\left(t\right)& =& A_0{z}_i\left(t\right),\mathrm{otherwise},\hfill \end{array}$$

(11)

where $z_i\left(t\right)$ represents the state of dynamic compensator of agent i, and ${\phi }_{2i}\left(t\right)={\sum }_{j=1}^N{a}_{ij}\left(t\right)(z_i\left(t\right)-z_j\left(t\right))+b_i\left(t\right)(z_i\left(t\right)-x_0\left(t\right))$ and ${\beta }^{\ast },{\beta }^{\ast }\left(t\right),{\alpha }_1,{\alpha }_1\left(t\right),{\alpha }_2$, ${\alpha }_2\left(t\right)>0$ need to be calculated.

Proposition 1. 

Assume that Assumptions 1–4 hold. If there exists ${\beta }^{\ast }$, ${\beta }_w^{\ast }$, ${\alpha }_1$, ${\alpha }_{1w}^{\ast }$, ${\alpha }_2$, ${\alpha }_{2w}^{\ast }>0$ such that

$$\begin{array}{ccc}& & p_1>0,p_2>0,p_3>0,\hfill \end{array}$$

(12)

$$\begin{array}{ccc}& & p_{1w}^{\ast }>0,p_{2w}^{\ast }>0,p_{3w}^{\ast }>0,\hfill \end{array}$$

(13)

$$\begin{array}{ccc}& & {\beta }^{\ast }\left(t\right)={\beta }_w^{\ast },{\alpha }_1\left(t\right)={\alpha }_{1w}^{\ast },{\alpha }_2\left(t\right)={\alpha }_{2w}^{\ast },{\alpha }_3\left(t\right)={\alpha }_{3w}^{\ast },if\sigma \left(t\right)=w,w\in \{1,2,\dots ,s^{\ast }\},\hfill \end{array}$$

(14)

$$\begin{array}{ccc}& & {\tau }^{\ast }>0,\hfill \end{array}$$

(15)

then $\parallel z_i\left(t\right)-x_0\left(t\right)\parallel =0$ for any $t\ge T_{max}^{\ast }$, where

$$\begin{array}{ccc}\hfill p_1& =& 2{\alpha }_1\sqrt{{\lambda }_{min}\left(H\right)},\hfill \\ \hfill p_2& =& 2({\beta }^{\ast }{\lambda }_{min}\left(H\right)-\parallel A_0\parallel ),\hfill \\ \hfill p_3& =& 2{\alpha }_2{\left(N{n}_0\right)}^{-{\displaystyle \frac{1}{2}}}{\left({\lambda }_{min}\left(H\right)\right)}^{{\displaystyle \frac{3}{2}}},\hfill \\ \hfill p_{1w}^{\ast }& =& 2{\alpha }_{1w}^{\ast }\sqrt{{\lambda }_{min}\left(H^w\right)},\hfill \\ \hfill p_{2w}^{\ast }& =& 2({\beta }_w^{\ast }{\lambda }_{min}\left(H^w\right)-\parallel A_0\parallel ),\hfill \\ \hfill p_{3w}^{\ast }& =& 2{\alpha }_{2w}^{\ast }{\left(N{n}_0\right)}^{-{\displaystyle \frac{1}{2}}}{\left({\lambda }_{min}\left(H^w\right)\right)}^{{\displaystyle \frac{3}{2}}},\hfill \\ \hfill {\tau }^{\ast }& =& \{{\displaystyle \frac{1}{2}}(p_2{\tau }_1+min\left\{p_{2w}^{\ast }\right\}·{\tau }_2-max\{ln{\displaystyle \frac{{\lambda }_{max}\left(H\right)}{{\lambda }_{min}\left(H\right)}},ln{\displaystyle \frac{{\lambda }_{max}\left(H^w\right)}{{\lambda }_{min}\left(H^w\right)}}\}·\lceil {\displaystyle \frac{{\tau }_1^{\ast }+{\tau }_2^{\ast }}{\tau }}\rceil )-\parallel A_0\parallel {\tau }_3^{\ast },w\in \{1,2,\dots ,s^{\ast }\}\},\hfill \\ \hfill T_{max}^{\ast }& =& \overline{T}(1+\lceil {\displaystyle \frac{{\epsilon }_2^{\ast }}{p^{\ast }}}\rceil ),\hfill \\ \hfill {\epsilon }_2^{\ast }& =& max\{{\lambda }_{min}{\left(H\right)}^{-{\displaystyle \frac{1}{2}}}{e}^{\parallel A_0\parallel {\tau }_3^{\ast }}{\displaystyle \frac{p_2}{p_3(e^{\frac{1}{2}{p}_2\tau }-1)}},{\lambda }_{min}{\left(H^w\right)}^{-{\displaystyle \frac{1}{2}}}{e}^{\parallel A_0\parallel {\tau }_3^{\ast }}\sqrt{{\overline{\lambda }}_w}{\displaystyle \frac{p_{2w}^{\ast }}{p_{3w}^{\ast }(e^{\frac{1}{2}{p}_{2w}^{\ast }\tau }-1)}},w\in \{1,2,\dots ,s^{\ast }\}\},\hfill \\ \hfill p^{\ast }& =& min\{{\lambda }_{min}{\left(H\right)}^{-{\displaystyle \frac{1}{2}}}{p}_1{p}_2^{-1}(1-e^{-{\displaystyle \frac{1}{2}}{p}_2\tau }),{\lambda }_{min}{\left(H^w\right)}^{-{\displaystyle \frac{1}{2}}}{p}_{1w}^{\ast }{p}_{2w}^{\ast -1}(1-e^{-{\displaystyle \frac{1}{2}}{p}_{2w}^{\ast }\tau }),w\in \{1,2,\dots ,s^{\ast }\}\},\hfill \end{array}$$

and ${\tau }_1$, ${\tau }_2$ represent the minimum dwell time of $\sigma \left(t\right)=0$ and $\sigma \left(t\right)\in \{1,2,\dots ,s^{\ast }\}$ during $t\in [T_r,T_{r+1})$; and ${\tau }_1^{\ast }$, ${\tau }_2^{\ast }$ and ${\tau }_3^{\ast }$ represent the maximum dwell time of $\sigma \left(t\right)=0$, $\sigma \left(t\right)\in \{1,2,\dots ,s^{\ast }\}$ and $\sigma \left(t\right)\in \{s^{\ast }+1,s^{\ast }+2,\dots ,s\}$ during $t\in [T_r,T_{r+1})$.

Proof of Proposition 1. 

Set ${\epsilon }_{2i}\left(t\right)=z_i\left(t\right)-x_0\left(t\right)$ and ${\epsilon }_2\left(t\right)={({\epsilon }_{21}^T\left(t\right),{\epsilon }_{22}^T\left(t\right),\dots ,{\epsilon }_{2N}^T\left(t\right))}^T$. Then, we have $\parallel z_i\left(t\right)-x_0\left(t\right)\parallel =0$ if $\parallel {\epsilon }_2\left(t\right)\parallel$ = 0. Define $V_2\left(t\right)={\epsilon }_2^T\left(t\right)(H^{\sigma \left(t\right)}\otimes I_{n_0}){\epsilon }_2\left(t\right)$ as the Lyapunov function and ${\phi }_2\left(t\right)={({\phi }_{21}^T\left(t\right),{\phi }_{22}^T\left(t\right),\dots ,{\phi }_{2N}^T\left(t\right))}^T$. Then,

(i) Considering $\sigma \left(t\right)=0$, based on (7), (9) and the result of Lemma 2, we have

$$\begin{array}{ccc}\hfill {\dot{V}}_2\left(t\right)& =& 2{\epsilon }_2^T\left(t\right)(H\otimes I_{n_0})((I_N\otimes A_0){\epsilon }_2\left(t\right)-{\beta }^{\ast }{\phi }_2\left(t\right)-{\alpha }_1\mathrm{sign}\left({\phi }_2\left(t\right)\right)-{\alpha }_2\mathrm{sign}{\left({\phi }_2\left(t\right)\right)}^2)\hfill \\ & \le & 2\parallel A_0\parallel V_2\left(t\right)-2{\beta }^{\ast }\parallel {\phi }_2{\left(t\right)\parallel }^2-2{\alpha }_1\parallel {\phi }_2\left(t\right)\parallel -2{\alpha }_2{\left(N{n}_0\right)}^{-{\displaystyle \frac{1}{2}}}{\parallel {\phi }_2\left(t\right)\parallel }^3\hfill \\ & \le & -p_1{V}_2^{{\displaystyle \frac{1}{2}}}\left(t\right)-p_2{V}_2\left(t\right)-p_3{V}_2^{{\displaystyle \frac{3}{2}}}\left(t\right),\sigma \left(t\right)=0.\text{\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}(16)}\hfill \end{array}$$

Set $V_2^{\ast }\left(t\right)=V_2^{{\displaystyle \frac{1}{2}}}\left(t\right)$. Then, we have

$$\begin{array}{ccc}\hfill {\dot{V}}_2^{\ast }\left(t\right)& \le & -{\displaystyle \frac{1}{2}}(p_1+p_2{V}_2^{\ast }\left(t\right)+p_3{V}_2^{\ast 2}\left(t\right)),\hfill \end{array}$$

which means that

$$\begin{array}{ccc}\hfill V_2^{\ast }\left(t\right)& \le & max\{0,min\{V_{21}^{\ast }\left(t\right),V_{22}^{\ast }\left(t\right)\}\}\hfill \end{array}$$

(17)

if $\sigma \left(t_s\right)=0$ for $t_s\in [t_0,t)$, where

$$\begin{array}{ccc}\hfill V_{21}^{\ast }\left(t\right)& =& e^{-{\displaystyle \frac{1}{2}}{p}_2(t-t_0)}{V}_2^{\ast }\left(t_0\right)-p_1{p}_2^{-1}(1-e^{-{\displaystyle \frac{1}{2}}{p}_2(t-t_0)}),\hfill \\ \hfill V_{22}^{\ast }\left(t\right)& =& {\displaystyle \frac{p_2}{p_3(e^{\frac{1}{2}{p}_2(t-t_0)}-1)}}.\hfill \end{array}$$

According to the definitions of $V_2\left(t\right)$ and ${\epsilon }_2\left(t\right)$, we have

$$\begin{array}{c}\hfill {\lambda }_{max}{\left(H\right)}^{-{\displaystyle \frac{1}{2}}}{V}_2^{\ast }\left(t\right)\le \parallel {\epsilon }_2\left(t\right)\parallel \le {\lambda }_{min}{\left(H\right)}^{-{\displaystyle \frac{1}{2}}}{V}_2^{\ast }\left(t\right),\end{array}$$

(18)

which means that

$$\begin{array}{ccc}\hfill \parallel {\epsilon }_2\left(t\right)\parallel & \le & max\{0,min\{{\tilde{\epsilon }}_{201}\left(t\right),{\tilde{\epsilon }}_{202}\left(t\right)\}\},\hfill \end{array}$$

(19)

where

$$\begin{array}{ccc}\hfill {\tilde{\epsilon }}_{201}\left(t\right)& =& {\lambda }_{min}{\left(H\right)}^{-{\displaystyle \frac{1}{2}}}(e^{-{\displaystyle \frac{1}{2}}{p}_2(t-t_0)}{\lambda }_{max}{\left(H\right)}^{{\displaystyle \frac{1}{2}}}\parallel {\epsilon }_2\left(t_0\right)\parallel -p_1{p}_2^{-1}(1-e^{-{\displaystyle \frac{1}{2}}{p}_2(t-t_0)})),\hfill \\ \hfill {\tilde{\epsilon }}_{202}\left(t\right)& =& {\displaystyle \frac{{\lambda }_{min}{\left(H\right)}^{-\frac{1}{2}}{p}_2}{p_3(e^{\frac{1}{2}{p}_2(t-t_0)}-1)}}.\hfill \end{array}$$

(ii) Considering $\sigma \left(t\right)=w\in \{1,2,\dots ,s^{\ast }\}$, take $V_{2w}\left(t\right)={\epsilon }_2^T\left(t\right)(H^w\otimes I_{n_0}){\epsilon }_2\left(t\right)$, which is based on (7) and (10). Then, we have

$$\begin{array}{c}\hfill {\dot{V}}_{2w}\left(t\right)\le -p_{1w}^{\ast }{V}_{2w}^{{\displaystyle \frac{1}{2}}}\left(t\right)-p_{2w}^{\ast }{V}_{2w}\left(t\right)-p_{3w}^{\ast }{V}_{2w}^{{\displaystyle \frac{3}{2}}}\left(t\right).\end{array}$$

(20)

Set $V_{2w}^{\ast }\left(t\right)=V_{2w}^{{\displaystyle \frac{1}{2}}}\left(t\right)$. Then, we have

$$\begin{array}{ccc}\hfill V_{2w}^{\ast }\left(t\right)& \le & max\{0,min\{V_{2w1}^{\ast }\left(t\right),V_{2w2}^{\ast }\left(t\right)\}\}\hfill \end{array}$$

(21)

if $\sigma \left(t_s\right)=w\in \{1,2,\dots ,s^{\ast }\}$ for $t_s\in [t_0,t)$, where

$$\begin{array}{ccc}\hfill V_{2w1}^{\ast }\left(t\right)& =& e^{-{\displaystyle \frac{1}{2}}{p}_{2w}^{\ast }(t-t_0)}{V}_{2w}^{\ast }\left(t_0\right)-p_{1w}^{\ast }{p}_{2w}^{\ast -1}(1-e^{-{\displaystyle \frac{1}{2}}{p}_{2w}^{\ast }(t-t_0)}),\hfill \\ \hfill V_{2w2}^{\ast }\left(t\right)& =& {\displaystyle \frac{p_{2w}^{\ast }}{p_{3w}^{\ast }(e^{\frac{1}{2}{p}_{2w}^{\ast }(t-t_0)}-1)}}.\hfill \end{array}$$

By a similar analysis that yields result (19), we have

$$\begin{array}{ccc}\hfill \parallel {\epsilon }_2\left(t\right)\parallel & \le & max\{0,min\{{\tilde{\epsilon }}_{2w1}\left(t\right),{\tilde{\epsilon }}_{2w2}\left(t\right)\}\},\hfill \end{array}$$

(22)

where

$$\begin{array}{ccc}\hfill {\tilde{\epsilon }}_{2w1}\left(t\right)& =& {\lambda }_{min}{\left(H^w\right)}^{-{\displaystyle \frac{1}{2}}}(e^{-{\displaystyle \frac{1}{2}}{p}_{2w}^{\ast }(t-t_0)}{\lambda }_{max}{\left(H^w\right)}^{{\displaystyle \frac{1}{2}}}\parallel {\epsilon }_2\left(t_0\right)\parallel -p_{1w}^{\ast }{p}_{2w}^{\ast -1}(1-e^{-{\displaystyle \frac{1}{2}}{p}_{2w}^{\ast }(t-t_0)})),\hfill \\ \hfill {\tilde{\epsilon }}_{2w2}\left(t\right)& =& {\displaystyle \frac{{\lambda }_{min}{\left(H^w\right)}^{-\frac{1}{2}}{p}_{2w}^{\ast }}{p_{3w}^{\ast }(e^{\frac{1}{2}{p}_{2w}^{\ast }(t-t_0)}-1)}}.\hfill \end{array}$$

(iii) Considering $\sigma \left(t\right)=w\in \{s^{\ast }+1, s^{\ast }+2,\dots ,s\}$, which is based on (7) and (11), we have

$$\begin{array}{ccc}\hfill \parallel {\epsilon }_2\left(t\right)\parallel & \le & e^{\parallel A_0\parallel (t-t_0)}\parallel {\epsilon }_2\left(t_0\right)\parallel \hfill \end{array}$$

(23)

if $\sigma \left(t_s\right)=w\in \{s^{\ast }+1,s^{\ast }+2,\dots ,s\}$ for $t_s\in [t_0,t)$.

Based on the results of (i)–(iii) and Assumption 2, the following results can be given:

$$\begin{array}{ccc}\hfill \parallel {\epsilon }_2\left(T_1\right)\parallel & \le & {\epsilon }_2^{\ast },\hfill \end{array}$$

(24)

$$\begin{array}{ccc}\hfill \parallel {\epsilon }_2\left(T_{r+1}\right)\parallel & \le & max\{0,e^{-{\tau }^{\ast }}\parallel {\epsilon }_2\left(T_r\right)\parallel -p^{\ast }\}\hfill \\ & \le & max\{0,\parallel {\epsilon }_2\left(T_r\right)\parallel -p^{\ast }\},r=1,2,\dots .\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\left(25\right)\hfill \end{array}$$

Therefore, based on (17), (19), (22) and (23), we have $V_2^{\ast }\left(t\right)=0$ for any $t\ge T_{max}^{\ast }$. □

Since most possible cases have been considered, the estimation of $T_{max}^{\ast }$ given by Proposition 1 is particularly conservative. The less conservative estimation of $T_{max}^{\ast }$ can be obtained based on a specific case.

Consider that $\sigma \left(t\right)$ satisfies the next condition as follows:

$$\begin{array}{c}\hfill \sigma \left(t\right)=\left\{\begin{array}{ccc}0,& & t\in [rT,rT+{\tau }_{01}),\\ 1,& & t\in [rT+{\tau }_{01},rT+{\tau }_{01}+{\tau }_{021}),\\ 2,& & t\in [rT+{\tau }_{01}+{\tau }_{021},rT+{\tau }_{01}+{\tau }_{021}+{\tau }_{022}),\\ ⋮\\ s^{\ast },& & t\in [rT+{\tau }_{01}+\sum _{i=1}^{s\ast -1}{\tau }_{02i},rT+{\tau }_{01}+\sum _{i=1}^{s\ast }{\tau }_{02i}),\\ w,& w\in \{s^{\ast }+1,s^{\ast }+2,\dots ,s\},& t\in [rT+{\tau }_{01}+{\tau }_{02},rT+{\tau }_{01}+{\tau }_{02}+{\tau }_{03})\end{array}\right.\end{array}$$

(26)

for $r=0,1,2,\dots$, where ${\tau }_{01},{\tau }_{02i},{\tau }_{02},{\tau }_{03}>0$ are positive constants and satisfy ${\sum }_{i=1}^{s\ast }{\tau }_{02i}={\tau }_{02}$ and ${\tau }_{01}+{\tau }_{02}+{\tau }_{03}=T$.

In this case, the next conclusion can be obtained.

Corollary 1. 

Assume that Assumptions 1–4 hold and $\sigma \left(t\right)$ satisfies Condition (26) if there exist ${\beta }^{\ast }$, ${\beta }_w^{\ast }$, ${\alpha }_1$, ${\alpha }_{1w}^{\ast }$, ${\alpha }_2$, ${\alpha }_{2w}^{\ast }>0$ such that Conditions (12)–(14) and

$$\begin{array}{c}\hfill {\tau }^{\ast }>0.\end{array}$$

(27)

Then, $\parallel z_i\left(t\right)-x_0\left(t\right)\parallel =0$ for any $t\ge T_{max}^{\ast }$, where

$$\begin{array}{ccc}\hfill {\tau }^{\ast }& =& {\displaystyle \frac{1}{2}}(p_2{\tau }_{01}+\sum _{i=1}^{s^{\ast }}{p}_{2i}^{\ast }{\tau }_{02i}-ln{\displaystyle \frac{{\lambda }_{max}\left(H\right)}{{\lambda }_{min}\left(H\right)}}-\sum _{i=1}^{s^{\ast }}ln{\displaystyle \frac{{\lambda }_{max}\left(H^i\right)}{{\lambda }_{min}\left(H^i\right)}})-\parallel A_0\parallel {\tau }_{03},\hfill \\ \hfill T_{max}^{\ast }& =& \left\{\begin{array}{cc}{\tau }_{01},& \mathit{condition}\mathit{\left(}\mathit{a}\mathit{\right)}\mathit{is}\mathit{satisfied}\mathit{,}\\ {\tau }_{01}+\sum _{i=1}^w{\tau }_{02i},& \mathit{condition}\mathit{\left(}\mathit{a}\mathit{\right)}\mathit{is}\mathit{not}\mathit{satisfied}\mathit{and}\mathit{condition}\mathit{\left(}\mathit{b}\mathit{\right)}\mathit{is}\mathit{satisfied}\mathit{,}\\ (1+\lceil {\displaystyle \frac{ln{p}^{\ast }}{{\tau }^{\ast }}}\rceil )T,& \mathit{otherwise}\mathit{,}\end{array}\right.\hfill \\ & & p^{\ast }=1+{\displaystyle \frac{p_1^{\ast }(1-e^{-{\tau }^{\ast }})}{p_2^{\ast }}},\hfill \\ & & p_1^{\ast }=e^{\parallel A_0\parallel {\tau }_{03}}{e}^{-{\widehat{\tau }}_{s^{\ast }}^{\ast }}{\widehat{\epsilon }}_2^{\ast }-{\overline{p}}_{s^{\ast }}^{\ast },\hfill \\ & & p_2^{\ast }=max\{e^{\parallel A_0\parallel {\tau }_{03}}{\overline{p}}_w^{\ast },w\in \{1,2,\dots ,s^{\ast }\}\},\hfill \\ & & {\widehat{\tau }}_w^{\ast }={\displaystyle \frac{1}{2}}(\sum _{i=1}^w{p}_{2i}^{\ast }{\tau }_{02i}-\sum _{i=1}^{w}ln{\displaystyle \frac{{\lambda }_{max}\left(H^i\right)}{{\lambda }_{min}\left(H^i\right)}}),w\in \{1,2,\dots ,s^{\ast }\},\hfill \\ & & {\widehat{\epsilon }}_2^{\ast }={\displaystyle \frac{{\lambda }_{min}{\left(H\right)}^{-\frac{1}{2}}{p}_2}{p_3(e^{\frac{1}{2}{p}_2{\tau }_{01}}-1)}},\hfill \\ & & {\overline{p}}_w^{\ast }={\lambda }_{min}{\left(H^w\right)}^{-{\displaystyle \frac{1}{2}}}(p_{1w}^{\ast }{p}_{2w}^{\ast -1}(1-e^{-{\displaystyle \frac{1}{2}}{p}_{2w}^{\ast }{\tau }_{02w}})),w\in \{1,2,\dots ,s^{\ast }\}.\hfill \end{array}$$

Condition (a): there exists ${\tau }_{01}^{\ast }>0$ such that ${\tau }_{01}^{\ast }<{\tau }_{01}$ and

$$\begin{array}{c}\hfill {\displaystyle \frac{p_2{e}^{-\frac{1}{2}{p}_2{\tau }_{01}^{\ast }}}{p_3(e^{\frac{1}{2}{p}_2({\tau }_{01}-{\tau }_{01}^{\ast })}-1)}}-p_1{p}_2^{-1}(1-e^{-{\displaystyle \frac{1}{2}}{p}_2{\tau }_{01}^{\ast }})\le 0.\end{array}$$

Condition (b): there exists $w\in \{1,2,\dots ,s^{\ast }\}$ such that

$$\begin{array}{c}\hfill e^{-{\widehat{\tau }}_w^{\ast }}{\widehat{\epsilon }}_2^{\ast }-{\overline{p}}_w^{\ast }\le 0.\end{array}$$

The other symbols retain their meanings, as defined in Proposition 1.

Proof of Corollary 1. 

Based on the result of Proposition 1, we have

$$\begin{array}{ccc}\hfill \parallel {\epsilon }_2\left(t\right)\parallel & \le & max\{0,min\{{\epsilon }_{2r11}^{\ast }\left(t\right),{\epsilon }_{2r12}^{\ast }\left(t\right)\}\},t\in [0,{\tau }_{01}),\hfill \end{array}$$

(28)

$$\begin{array}{ccc}\hfill \parallel {\epsilon }_2({\tau }_{01}+{\tau }_{021})\parallel & \le & max\{0,e^{-{\widehat{\tau }}_1^{\ast }}{\widehat{\epsilon }}_2^{\ast }-{\overline{p}}_1^{\ast }\},\hfill \end{array}$$

(29)

$$\begin{array}{ccc}\hfill \parallel {\epsilon }_2({\tau }_{01}+\sum _{i=1}^w{\tau }_{02i})\parallel & \le & max\{0,e^{-{\widehat{\tau }}_w^{\ast }}{\widehat{\epsilon }}_2^{\ast }-{\overline{p}}_w^{\ast }\},\hfill \end{array}$$

(30)

$$\begin{array}{ccc}\hfill \parallel {\epsilon }_2\left(t\right)\parallel & \le & e^{\parallel A_0\parallel (t-rT-{\tau }_{01}-{\tau }_{02})}\parallel {\epsilon }_2(rT+{\tau }_{01}+{\tau }_{02})\parallel ,\hfill \\ & & t\in [rT+{\tau }_{01}+{\tau }_{02},rT+{\tau }_{01}+{\tau }_{02}+{\tau }_{03}),\hspace{1em}\hspace{1em}\hspace{1em}\left(31\right)\hfill \end{array}$$

where

$$\begin{array}{ccc}\hfill {\epsilon }_{2r11}^{\ast }\left(t\right)& =& {\lambda }_{min}{\left(H\right)}^{-{\displaystyle \frac{1}{2}}}(e^{-{\displaystyle \frac{1}{2}}{p}_{2}t}{\lambda }_{max}{\left(H\right)}^{{\displaystyle \frac{1}{2}}}\parallel {\epsilon }_2\left(rT\right)\parallel -p_1{p}_2^{-1}(1-e^{-{\displaystyle \frac{1}{2}}{p}_{2}t})),\hfill \\ \hfill {\epsilon }_{2r12}^{\ast }\left(t\right)& =& {\displaystyle \frac{{\lambda }_{min}{\left(H\right)}^{-\frac{1}{2}}{p}_2}{p_3(e^{\frac{1}{2}{p}_{2}t}-1)}}.\hfill \end{array}$$

Based on (28)–(31), if Condition (a) is satisfied, then $\parallel {\epsilon }_2^{\ast }\left(t\right)\parallel =0$ for any $t\ge {\tau }_{01}$; if Condition (a) is not satisfied and Condition (b) is satisfied, then $\parallel {\epsilon }_2^{\ast }\left(t\right)\parallel =0$ for any $t\ge {\tau }_{01}+{\sum }_{i=1}^w{\tau }_{02i}$; and if both Conditions (a) and (b) are not satisfied, then the next result can be obtained:

$$\begin{array}{c}\hfill \parallel {\epsilon }_2\left((r+1)T\right)\parallel \le max\{0,e^{-{\tau }^{\ast }}\parallel {\epsilon }_2\left(rT\right)\parallel -p_2^{\ast }\}.\end{array}$$

(32)

Moreover, it can be obtained that

$$\begin{array}{c}\hfill \parallel {\epsilon }_2\left(T\right)\parallel \le p_1^{\ast }.\end{array}$$

(33)

According to Conditions (32) and (33), we have

$$\begin{array}{ccc}\hfill {\epsilon }_2^{\ast }\left((r+1)T\right)& \le & max\{0,e^{-r{\tau }^{\ast }}{p}_1^{\ast }-\sum _{i=0}^{r-1}{e}^{-i{\tau }^{\ast }}{p}_2^{\ast }\}.\hfill \end{array}$$

(34)

Therefore, ${\epsilon }_2^{\ast }\left(t\right)=0$ for any $t\ge (1+\lceil {\displaystyle \frac{ln{p}^{\ast }}{{\tau }^{\ast }}}\rceil )T$. The proof is thus finished. □

4.2. Dynamic Event-Triggered Control Scheme

Based on dynamic Compensator (9)–(11), the controller and event-triggered condition for Systems (5)–(8) are given as follows:

$$\begin{array}{ccc}\hfill u_i\left(t\right)& =& -{\beta }_i{\phi }_{1i}\left(t_k^i\right)-{\alpha }_{1i}\mathrm{sign}\left({\phi }_{1i}\left(t_k^i\right)\right)-{\alpha }_{2i}\mathrm{sign}{\left({\phi }_{1i}\left(t_k^i\right)\right)}^2,t\in [t_k^i,t_{k+1}^i),\hfill \end{array}$$

(35)

$$\begin{array}{ccc}\hfill t_{k+1}^i& =& inf\left\{t\right|t>t_k^i,\parallel {\phi }_{1i}\left(t\right)-{\phi }_{1i}\left(t_k^i\right)\parallel >{\delta }_i(\parallel {\phi }_{1i}\left(t\right)\parallel +{\xi }_i)+{\eta }_i\left(t\right)\},\hfill \end{array}$$

(36)

where

$$\begin{array}{ccc}\hfill {\dot{\eta }}_i\left(t\right)& =& -{\mu }_1|{\eta }_i{\left(t\right)|}^{{\displaystyle \frac{1}{2}}}-{\mu }_2{\eta }_i\left(t\right)-{\mu }_3{\left|{\eta }_i\left(t\right)\right|}^{{\displaystyle \frac{3}{2}}}\hfill \\ & & -{\rho }_{1i}(\parallel {\phi }_{1i}\left(t\right)-{\phi }_{1i}(t_k^i)\parallel -{\delta }_i(\parallel {\phi }_{1i}\left(t\right)\parallel +{\xi }_i\left)\right)\hfill \\ & & -{\rho }_{2i}(\parallel {\phi }_{1i}\left(t\right)-{\phi }_{1i}(t_k^i){\parallel }^2-2({\delta }_i(\parallel {\phi }_{1i}\left(t\right)\parallel +{\xi }_i{\left)\right)}^2)\hfill \\ & & -{\rho }_{3i}(\parallel {\phi }_{1i}\left(t\right)-{\phi }_{1i}(t_k^i){\parallel }^3-4({\delta }_i(\parallel {\phi }_{1i}\left(t\right)\parallel +{\xi }_i{\left)\right)}^3)\hfill \\ & & +\widehat{\xi },t\in [t_k^i,t_{k+1}^i),\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}(37)\hfill \end{array}$$

and ${\phi }_{1i}\left(t\right)=x_i\left(t\right)-{\Pi }_i{z}_i\left(t\right)$, ${\mu }_1,{\mu }_2,{\mu }_3,\widehat{\xi }>0$ and ${\eta }_i\left(0\right)\ge 0$ for $i\in \{1,2,\dots ,N\}$. Moreover, ${\beta }_i,{\alpha }_{1i},{\alpha }_{2i},{\delta }_i,{\xi }_i,{\rho }_{1i},{\rho }_{2i},{\rho }_{3i}>0$ needs to be calculated.

Theorem 1. 

Assume that Assumptions 1–4 hold and dynamic Compensators (9)–(11) satisfy Conditions (12)–(15) (or Conditions (12)–(14) and (26) and (27)) if there exists ${\beta }_i,{\alpha }_{1i},{\alpha }_{2i},{\delta }_i,{\xi }_i,{\chi }_{1i},{\chi }_{2i}$, ${\rho }_{1i},{\rho }_{2i},{\rho }_{3i}>0$ for $i=1,2,\dots ,N$ such that

$$\begin{array}{ccc}& & p_{1i}>0,p_{2i}>0,p_{3i}>0,\hfill \end{array}$$

(38)

$$\begin{array}{ccc}& & {\rho }_{1i}=4{\alpha }_{1i},\hfill \end{array}$$

(39)

$$\begin{array}{ccc}& & {\rho }_{2i}=2{\beta }_i{\chi }_{1i}^{-1},\hfill \end{array}$$

(40)

$$\begin{array}{ccc}& & {\rho }_{3i}=2{\alpha }_{2i}(n_i^{-{\displaystyle \frac{1}{2}}}+2+{\displaystyle \frac{2}{3}}{\chi }_{2i}^{-1}).\hfill \end{array}$$

(41)

Then, Systems (5)–(8) with dynamic Compensators (9)–(11), Controller (35) and event-triggered Condition (36) satisfy the following condition: $\parallel y_i\left(t\right)-y_0\left(t\right)\parallel \le {\varphi }_i$ for $t\ge T_{max}^i$, where

$$\begin{array}{ccc}\hfill p_{1i}& =& min\{p_{1i1},{\mu }_1\},\hfill \\ \hfill p_{2i}& =& min\{p_{1i2},{\mu }_2\},\hfill \\ \hfill p_{3i}& =& {\displaystyle \frac{1}{\sqrt{2}}}·min\{p_{1i3},{\mu }_3\},\hfill \\ \hfill p_{1i1}& =& 2{\alpha }_{1i}-2\gamma -{\rho }_{1i}{\delta }_i,\hfill \\ \hfill p_{1i2}& =& 2{\beta }_i(1-{\chi }_{1i})-2\parallel A_i\parallel -4{\rho }_{2i}{\delta }_i^2,\hfill \\ \hfill p_{1i3}& =& 2{\alpha }_{2i}(2^{-2}{n}_i^{-{\displaystyle \frac{1}{2}}}-{\displaystyle \frac{4}{3}}{\chi }_{2i}^{{\displaystyle \frac{1}{2}}})-16{\rho }_{3i}{\delta }_i^3,\hfill \\ \hfill {\varphi }_i& =& \parallel C_i\parallel \sqrt{q_i^{\ast }},\hfill \\ \hfill q_i^{\ast }& =& min\{{({\displaystyle \frac{q_i}{p_{1i}(1-\theta )}})}^2,{\displaystyle \frac{q_i}{p_{2i}(1-\theta )}},{({\displaystyle \frac{q_i}{p_{3i}(1-\theta )}})}^{{\displaystyle \frac{2}{3}}}\},\hfill \\ \hfill q_i& =& {\rho }_{1i}{\delta }_i{\xi }_i+4{\rho }_{2i}{\delta }_i^2{\xi }_i^2+16{\rho }_{3i}{\delta }_i^3{\xi }_i^3+\widehat{\xi },\hfill \\ \hfill T_{max}^i& =& T_{max}^{\ast }+{\tilde{T}}_{max}^i,\hfill \\ \hfill {\tilde{T}}_{max}^i& =& {\displaystyle \frac{4ln(1+\frac{p_{2i}}{\sqrt{p_{1i}{p}_{3i}}})}{\theta p_{2i}}},\hfill \end{array}$$

and $\theta \in (0,1)$ and $T_{max}^{\ast }$ are obtained by Proposition 1 or Corollary 1.

Proof of Theorem 1. 

Based on the results of Proposition 1 and Corollary 1, $z_i\left(t\right)-x_0\left(t\right)=\mathbf{0}$ for any $t\ge T_{max}^{\ast }$ and $i=1,2,\dots ,N$. By Assumption 4, for $t\ge T_{max}^{\ast }$, $y_i\left(t\right)-y_0\left(t\right)=C_i{\phi }_i\left(t\right)$ and

$$\begin{array}{ccc}\hfill {\dot{\phi }}_{1i}\left(t\right)& =& A_i{\phi }_{1i}\left(t\right)+{\omega }_i\left(t\right)\hfill \\ & & -{\beta }_i{\phi }_{1i}\left(t_k^i\right)-{\alpha }_{1i}\mathrm{sign}\left({\phi }_{1i}\left(t_k^i\right)\right)-{\alpha }_{2i}\mathrm{sign}{\left({\phi }_{1i}\left(t_k^i\right)\right)}^2.\hspace{1em}\hspace{1em}\hspace{1em}(42)\hfill \end{array}$$

Set $V_{1i}\left(t\right)=V_{1i1}\left(t\right)+V_{1i2}\left(t\right)$, where

$$\begin{array}{ccc}\hfill V_{1i1}\left(t\right)& =& {\phi }_{1i}^T\left(t\right){\phi }_{1i}\left(t\right),\hfill \\ \hfill V_{1i2}\left(t\right)& =& {\eta }_i\left(t\right).\hfill \end{array}$$

Based on (36) and (37), we have

$$\begin{array}{ccc}\hfill {\dot{\eta }}_i\left(t\right)& \ge & -{\mu }_1|{\eta }_i{\left(t\right)|}^{\frac{1}{2}}-({\mu }_2+{\rho }_{1i}){\eta }_i\left(t\right)-{\mu }_3|{\eta }_i\left(t\right){|}^{\frac{3}{2}}-2{\rho }_{2i}{\eta }_i^2\left(t\right)-4{\rho }_{3i}{\left|{\eta }_i\left(t\right)\right|}^3+\widehat{\xi }.\hfill \end{array}$$

(43)

Since ${\eta }_i\left(0\right)\ge 0$, which is based on (43), we have ${\eta }_i\left(t\right)\ge 0$ for any $t\ge 0$, which means that $\parallel {\phi }_{1i}{\left(t\right)\parallel }^2\le V_{1i}\left(t\right)$ and $\parallel y_i\left(t\right)-y_0\left(t\right)\parallel \le \parallel C_i\parallel V_{1i}^{\frac{1}{2}}\left(t\right)$ for $t\ge T_{max}^{\ast }$.

• By taking the derivative of $V_{1i}\left(t\right)$, we have

$$\begin{array}{ccc}\hfill {\dot{V}}_{1i}\left(t\right)& \le & 2\gamma V_{1i1}^{\frac{1}{2}}\left(t\right)+2\parallel A_i\parallel V_{1i1}\left(t\right)\hfill \\ & & -2{\phi }_{1i}^T\left(t\right)({\beta }_i{\phi }_{1i}\left(t_k^i\right)+{\alpha }_{1i}\mathrm{sign}\left({\phi }_{1i}\left(t_k^i\right)\right)+{\alpha }_{2i}\mathrm{sign}{\left({\phi }_{1i}\left(t_k^i\right)\right)}^2)\hfill \\ & & -{\mu }_1{\eta }_i^{\frac{1}{2}}\left(t\right)-{\mu }_2{\eta }_i\left(t\right)-{\mu }_3{\eta }_i^{\frac{3}{2}}\left(t\right)+\widehat{\xi }\hfill \\ & & -{\rho }_{1i}(\parallel {\phi }_{1i}\left(t\right)-{\phi }_{1i}(t_k^i)\parallel -{\delta }_i(\parallel {\phi }_{1i}\left(t\right)\parallel +{\xi }_i\left)\right)\hfill \\ & & -{\rho }_{2i}(\parallel {\phi }_{1i}\left(t\right)-{\phi }_{1i}(t_k^i){\parallel }^2-2({\delta }_i(\parallel {\phi }_{1i}\left(t\right)\parallel +{\xi }_i{\left)\right)}^2)\hfill \\ & & -{\rho }_{3i}(\parallel {\phi }_{1i}\left(t\right)-{\phi }_{1i}(t_k^i){\parallel }^3-4({\delta }_i(\parallel {\phi }_{1i}\left(t\right)\parallel +{\xi }_i{\left)\right)}^3).\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}(44)\hfill \end{array}$$

Meanwhile, according to event-triggered Condition (36) and Lemma 2, we have

$$\begin{array}{ccc}\hfill -{\beta }_i{\phi }_{1i}^T\left(t\right){\phi }_{1i}\left(t_k^i\right)& =& -{\beta }_i{\parallel {\phi }_{1i}\left(t\right)\parallel }^2+{\beta }_i{\phi }_{1i}^T\left(t\right)({\phi }_{1i}\left(t\right)-{\phi }_{1i}(t_k^i))\hfill \\ & \le & -{\beta }_i(1-{\chi }_{1i})\parallel {\phi }_{1i}\left(t\right){\parallel }^2+{\beta }_i{\chi }_{1i}^{-1}{\parallel {\phi }_{1i}\left(t\right)-{\phi }_{1i}\left(t_k^i\right)\parallel }^2,\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}(45)\hfill \end{array}$$

$$\begin{array}{ccc}\hfill -{\alpha }_{1i}{\phi }_{1i}^T\left(t\right)\mathrm{sign}\left({\phi }_{1i}\left(t_k^i\right)\right)& =& -{\alpha }_{1i}{\phi }_{1i}^T\left(t_k^i\right)\mathrm{sign}\left({\phi }_{1i}\left(t_k^i\right)\right)\hfill \\ & & -{\alpha }_{1i}({\phi }_{1i}^T\left(t\right)-{\phi }_{1i}^T\left(t_k^i\right))\mathrm{sign}\left({\phi }_{1i}\left(t_k^i\right)\right)\hfill \\ & \le & -{\alpha }_{1i}\parallel {\phi }_{1i}\left(t_k^i\right)\parallel +{\alpha }_{1i}\parallel {\phi }_{1i}\left(t\right)-{\phi }_{1i}\left(t_k^i\right)\parallel \hfill \\ & \le & -{\alpha }_{1i}\parallel {\phi }_{1i}\left(t\right)\parallel +2{\alpha }_{1i}\parallel {\phi }_{1i}\left(t\right)-{\phi }_{1i}\left(t_k^i\right)\parallel ,\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\left(46\right)\hfill \end{array}$$

$$\begin{array}{ccc}\hfill -{\alpha }_{2i}{\phi }_{1i}^T\left(t\right)\mathrm{sign}{\left({\phi }_{1i}\left(t_k^i\right)\right)}^2& =& -{\alpha }_{2i}{\phi }_{1i}^T\left(t_k^i\right)\mathrm{sign}{\left({\phi }_{1i}\left(t_k^i\right)\right)}^2\hfill \\ & & -{\alpha }_{2i}({\phi }_{1i}^T\left(t\right)-{\phi }_{1i}^T\left(t_k^i\right))\mathrm{sign}{\left({\phi }_{1i}\left(t_k^i\right)\right)}^2\hfill \\ & \le & -{\alpha }_{2i}{n}_i^{-{\displaystyle \frac{1}{2}}}{\parallel {\phi }_{1i}\left(t_k^i\right)\parallel }^3\hfill \\ & & +{\alpha }_{2i}\parallel {\phi }_{1i}\left(t\right)-{\phi }_{1i}\left(t_k^i\right)\parallel \parallel {\phi }_{1i}\left(t_k^i\right){\parallel }^2\hfill \\ & \le & -{\alpha }_{2i}{n}_i^{-{\displaystyle \frac{1}{2}}}(2^{-2}\parallel {\phi }_{1i}{\left(t\right)\parallel }^3-\parallel {\phi }_{1i}\left(t\right)-{\phi }_{1i}\left(t_k^i\right){\parallel }^3)\hfill \\ & & +2{\alpha }_{2i}\parallel {\phi }_{1i}\left(t\right)-{\phi }_{1i}\left(t_k^i\right)\parallel (\parallel {\phi }_{1i}\left(t\right){\parallel }^2+\parallel {\phi }_{1i}\left(t\right)-{\phi }_{1i}\left(t_k^i\right){\parallel }^2)\hfill \\ & \le & -{\alpha }_{2i}{n}_i^{-{\displaystyle \frac{1}{2}}}(2^{-2}\parallel {\phi }_{1i}{\left(t\right)\parallel }^3-\parallel {\phi }_{1i}\left(t\right)-{\phi }_{1i}\left(t_k^i\right){\parallel }^3)\hfill \\ & & +2{\alpha }_{2i}{\parallel {\phi }_{1i}\left(t\right)-{\phi }_{1i}\left(t_k^i\right)\parallel }^3\hfill \\ & & +{\displaystyle \frac{4}{3}}{\alpha }_{2i}{\chi }_{2i}^{{\displaystyle \frac{1}{2}}}\parallel {\phi }_i{\left(t\right)\parallel }^3+{\displaystyle \frac{2}{3}}{\alpha }_{2i}{\chi }_{2i}^{-1}{\parallel {\phi }_{1i}\left(t\right)-{\phi }_{1i}\left(t_k^i\right)\parallel }^3.\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}(47)\hfill \end{array}$$

Therefore,

$$\begin{array}{ccc}\hfill {\dot{V}}_{1i}\left(t\right)& \le & -p_{1i1}{V}_{1i1}^{{\displaystyle \frac{1}{2}}}\left(t\right)-p_{2i1}{V}_{1i1}\left(t\right)-p_{3i1}{V}_{1i1}^{{\displaystyle \frac{3}{2}}}\left(t\right)\hfill \\ & & -{\mu }_1{V}_{1i2}^{{\displaystyle \frac{1}{2}}}\left(t\right)-{\mu }_2{V}_{1i2}\left(t\right)-{\mu }_3{V}_{1i2}^{{\displaystyle \frac{3}{2}}}\left(t\right)+q_i,t\ge T_{max}.\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}(48)\hfill \end{array}$$

By utilizing the result of Lemma 2, we have

$$\begin{array}{c}\hfill {\dot{V}}_{1i}\left(t\right)\le -p_{1i}{V}_{1i}^{{\displaystyle \frac{1}{2}}}\left(t\right)-p_{2i}{V}_{1i}\left(t\right)-p_{3i}{V}_{1i}^{{\displaystyle \frac{3}{2}}}\left(t\right)+q_i,t\ge T_{max}.\end{array}$$

(49)

Set $\theta \in (0,1)$. Then, we have

$$\begin{array}{ccc}\hfill {\dot{V}}_{1i}\left(t\right)& \le & -\theta (p_{1i}{V}_{1i}^{{\displaystyle \frac{1}{2}}}\left(t\right)+p_{2i}{V}_{1i}\left(t\right)+p_{3i}{V}_{1i}^{{\displaystyle \frac{3}{2}}}\left(t\right))\hfill \\ & & -(1-\theta )(p_{1i}{V}_{1i}^{{\displaystyle \frac{1}{2}}}\left(t\right)+p_{2i}{V}_{1i}\left(t\right)+p_{3i}{V}_{1i}^{{\displaystyle \frac{3}{2}}}\left(t\right))+q_i,t\ge T_{max}.\hspace{1em}\hspace{1em}(50)\hfill \end{array}$$

Hence,

$$\begin{array}{c}\hfill {\dot{V}}_{1i}\left(t\right)\le -\theta (p_{1i}{V}_{1i}^{{\displaystyle \frac{1}{2}}}\left(t\right)+p_{2i}{V}_{1i}\left(t\right)+p_{3i}{V}_{1i}^{{\displaystyle \frac{3}{2}}}\left(t\right)),t\ge T_{max}\end{array}$$

(51)

if $V_{1i}\left(t\right)$ satisfies $V_{1i}\left(t\right)\ge q_i^{\ast }$.

Then, by using the similar analysis given in Proposition 1 and Corollary 1, we have $V_{1i}\left(t\right)\le q_i^{\ast }$ for any $t\ge T_{max}^i$, which means that $\parallel y_i\left(t\right)-y_0\left(t\right)\parallel \le {\varphi }_i$ for any $t\ge T_{max}^i$. Hence, the proof is completed. □

Remark 1. 

Based on the conclusions of Proposition 1 and Theorem 1, the maximum dwell-time $T_{\max }^i$ and the size of the error bound ${\varphi }_i$ are mainly influenced by the parameters defined in (9), (10) and (35), (36), namely ${\beta }^{\ast }$, ${\alpha }_1$, ${\alpha }_2$, ${\beta }_w^{\ast }$ (which equals ${\beta }^{\ast }\left(t\right)$); ${\alpha }_{1w}^{\ast }$ (which equals ${\alpha }_1\left(t\right)$); ${\alpha }_{2w}^{\ast }$ (which equals ${\alpha }_2\left(t\right)$); and ${\beta }_i$, ${\alpha }_{1i}$, ${\alpha }_{2i}$, ${\delta }_i$ and ${\xi }_i$. Specifically, in most cases, the larger ${\beta }^{\ast }$, ${\alpha }_1$, ${\alpha }_2$, ${\beta }_w^{\ast }$, ${\alpha }_{1w}^{\ast }$, ${\alpha }_{2w}^{\ast }$, ${\beta }_i$, ${\alpha }_{1i}$ and ${\alpha }_{2i}$ are, the smaller $T_{\max }^i$ is; similarly, the smaller ${\delta }_i$ and ${\xi }_i$ are, the smaller ${\varphi }_i$ is.

Next, the proof that event-triggered Condition (36) can avoid Zeno-behavior is given as follows.

Proposition 2. 

If Conditions (12)–(15) (or Conditions (12)–(14) and (26), (27)) and Condition (38) are satisfied, then the event-triggered Condition (36) can avoid Zeno-behavior for any given initial values.

Proof of Proposition 2. 

Set ${\psi }_i\left(t\right)={\displaystyle \frac{\parallel {\phi }_{1i}\left(t\right)-{\phi }_{1i}\left(t_k^i\right)\parallel }{{\delta }_i(\parallel {\phi }_{1i}\left(t\right)\parallel +{\xi }_i)}}$. Then, based on Proposition 1, Corollary 1, Theorem 1 and ${\eta }_i\left(t\right)\ge 0$, we have ${\psi }_i\left(t_k^i\right)=0$, $t_{k+1}^i\ge inf\left\{t\right|t>t_k^i,{\psi }_i\left(t\right)>1\}$ and

$$\begin{array}{ccc}\hfill {\dot{\psi }}_i\left(t\right)& =& {\displaystyle \frac{\frac{(\parallel {\phi }_{1i}\left(t\right)\parallel +{\xi }_i){({\phi }_{1i}\left(t\right)-{\phi }_{1i}(t_k^i))}^T(A_i{\phi }_{1i}\left(t\right)+{\omega }_i\left(t\right)-{\beta }_i{\phi }_{1i}(t_k^i)-{\alpha }_{1i}\mathrm{sign}({\phi }_{1i}(t_k^i))-{\alpha }_{2i}\mathrm{sign}{\left({\phi }_{1i}\left(t_k^i\right)\right)}^2+{\phi }_{2i}^{\ast }\left(t\right))}{\parallel {\phi }_{1i}\left(t\right)-{\phi }_{1i}\left(t_k^i\right)\parallel }}{{\delta }_i(\parallel {\phi }_{1i}\left(t\right){\parallel +{\xi }_i)}^2}}\hfill \\ & & -{\displaystyle \frac{\frac{\parallel {\phi }_{1i}\left(t\right)-{\phi }_{1i}\left(t_k^i\right)\parallel {\phi }_{1i}^T\left(t\right)(A_i{\phi }_{1i}\left(t\right)+{\omega }_i\left(t\right)-{\beta }_i{\phi }_{1i}\left(t_k^i\right)-{\alpha }_{1i}\mathrm{sign}\left({\phi }_{1i}\left(t_k^i\right)\right)-{\alpha }_{2i}\mathrm{sign}{\left({\phi }_{1i}\left(t_k^i\right)\right)}^2+{\phi }_{2i}^{\ast }\left(t\right))}{\parallel {\phi }_{1i}\left(t\right)\parallel }}{{\delta }_i(\parallel {\phi }_{1i}\left(t\right){\parallel +{\xi }_i)}^2}},\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}(52)\hfill \end{array}$$

where

$$\begin{array}{ccc}\hfill {\phi }_{2i}^{\ast }\left(t\right)& =& {\Pi }_i({\beta }^{\ast }{\phi }_{2i}\left(t\right)+{\alpha }_1\mathrm{sign}\left({\phi }_{2i}\left(t\right)\right)+{\alpha }_2\mathrm{sign}{\left({\phi }_{2i}\left(t\right)\right)}^2),\hfill \\ & & \mathrm{if}\sigma \left(t\right)=0\mathrm{and}t<T_{max}^{\ast },\hfill \\ \hfill {\phi }_{2i}^{\ast }\left(t\right)& =& {\Pi }_i({\beta }_w^{\ast }{\phi }_{2i}\left(t\right)+{\alpha }_{1w}^{\ast }\mathrm{sign}\left({\phi }_{2i}\left(t\right)\right)+{\alpha }_{2w}^{\ast }\mathrm{sign}{\left({\phi }_{2i}\left(t\right)\right)}^2),\hfill \\ & & \mathrm{if}\sigma \left(t\right)=w\in \{1,2,\dots ,s^{\ast }\}\mathrm{and}t<T_{max}^{\ast },\hfill \\ \hfill {\phi }_{2i}^{\ast }\left(t\right)& =& 0,\mathrm{if}\sigma \left(t\right)=w\in \{s^{\ast }+1,s^{\ast }+2,\dots ,s\}\mathrm{or}t\ge T_{max}^{\ast }.\hfill \end{array}$$

Meanwhile, according to the results of Proposition 1, Corollary 1 and Theorem 1, we have $\parallel {\phi }_{1i}\left(t\right)\parallel \le {\varphi }_i$ and $\parallel {\phi }_{2i}\left(t\right)\parallel =0$ for any $t\ge T_{max}^i$. Hence, for any given initial values, there must exist positive constants ${\phi }_{1i}^{\ast }$ and ${\phi }_{2i}^{\ast }$ such that

$$\begin{array}{c}\hfill \parallel {\phi }_{1i}\left(t\right)\parallel \le {\phi }_{1i}^{\ast },\parallel {\phi }_{2i}\left(t\right)\parallel \le {\phi }_{2i}^{\ast }\end{array}$$

(53)

for any $t\ge 0$.

Then, set ${\phi }_{2imax}^{\ast }=max\{\parallel {\Pi }_i\parallel ({\beta }^{\ast }{\phi }_{2i}^{\ast }+{\alpha }_1+{\alpha }_2{\phi }_{2i}^{\ast 2}),\parallel {\Pi }_i\parallel ({\beta }_2^{\ast }{\phi }_{2i}^{\ast }+{\alpha }_{1w}^{\ast }+{\alpha }_{2w}^{\ast }{\phi }_{2i}^{\ast 2})\}$, which is based on (52) and (53). As such, we have

$$\begin{array}{ccc}\hfill {\dot{\psi }}_i\left(t\right)& \le & {\displaystyle \frac{\parallel A_i-{\beta }_i{I}_{n_i}\parallel \parallel {\phi }_{1i}\left(t\right)\parallel +\gamma +{\alpha }_{1i}+{\alpha }_{2i}{\phi }_{1i}^{\ast 2}+{\phi }_{2imax}^{\ast }+{\beta }_i\parallel {\phi }_{1i}\left(t\right)-{\phi }_{1i}\left(t_k^i\right)\parallel }{{\delta }_i(\parallel {\phi }_{1i}\left(t\right)\parallel +{\xi }_i)}}\hfill \\ & & +{\displaystyle \frac{{\beta }_i{\parallel {\phi }_{1i}\left(t\right)-{\phi }_{1i}\left(t_k^i\right)\parallel }^2}{{\delta }_i{(\parallel {\phi }_{1i}\left(t\right)\parallel +{\xi }_i)}^2}}\hfill \\ & & +{\displaystyle \frac{\parallel {\phi }_{1i}\left(t\right)-{\phi }_{1i}\left(t_k^i\right)\parallel (\parallel A_i-{\beta }_i{I}_{n_i}\parallel \parallel {\phi }_{1i}\left(t\right)\parallel +\gamma +{\alpha }_{1i}+{\alpha }_{2i}{\phi }_{1i}^{\ast 2}+{\phi }_{2imax}^{\ast })}{{\delta }_i(\parallel {\phi }_{1i}\left(t\right){\parallel +{\xi }_i)}^2}}\hfill \\ & \le & {\aleph }_{1i}{\psi }_i^2\left(t\right)+{\aleph }_{2i}{\psi }_i\left(t\right)+{\aleph }_{3i},\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \left(54\right)\hfill \end{array}$$

where

$$\begin{array}{ccc}\hfill {\aleph }_{1i}& =& {\delta }_i{\beta }_i,\hfill \\ \hfill {\aleph }_{2i}& =& {\beta }_i+{ϵ}_i,\hfill \\ \hfill {\aleph }_{3i}& =& {\delta }_i^{-1}{ϵ}_i,\hfill \\ \hfill {ϵ}_i& =& max\{\parallel A_i-{\beta }_i{I}_{n_i}\parallel ,{\xi }_i^{-1}(\gamma +{\alpha }_{1i}+{\alpha }_{2i}{\phi }_{1i}^{\ast 2}+{\phi }_{2imax}^{\ast })\}.\hfill \end{array}$$

Therefore,

$$\begin{array}{c}\hfill t_{k+1}^i-t_k^i\ge {\int }_0^1{\displaystyle \frac{1}{{\aleph }_{1i}{v}^2+{\aleph }_{2i}v+{\aleph }_{3i}}}\mathrm{d}v,\end{array}$$

(55)

where v is a dummy variable.

The proof is thus completed. □

Remark 2. 

Based on the conclusion of Proposition 2, the following event-triggered condition can avoid Zeno-behavior:

$$\begin{array}{ccc}\hfill t_{k+1}^i& =& inf\left\{t\right|t>t_k^i,\parallel {\phi }_{1i}\left(t\right)-{\phi }_{1i}\left(t_k^i\right)\parallel >{\delta }_i(\parallel {\phi }_{1i}\left(t\right)\parallel +{\xi }_i\left)\right\}.\hfill \end{array}$$

(56)

Since ${\eta }_i\left(t\right)\ge 0$, event-triggered Condition (36) is a sufficient condition for Condition (56), which means that the event-triggered condition can also avoid Zeno-behavior. Meanwhile, due to the existence of ${\eta }_i\left(t\right)$, the controller under Condition (36) generally exhibits a lower update frequency than under Condition (56).

5. Event-Based Control Scheme Under Unknown DoS Attacks

5.1. Design of Dynamic Compensator

Consider the case that DoS attacks are unknown, which means that $\sigma \left(t\right)$ and $H^{\sigma \left(t\right)}$ cannot be known in advance. Assume that it is known for each agent whether the topology graph is connected or not. Then, the dynamic compensators for Systems (5)–(8) are provided as follows:

$$\begin{array}{ccc}\hfill {\dot{z}}_i\left(t\right)& =& A_0{z}_i\left(t\right)-{\beta }^{\ast }{\phi }_{2i}\left(t\right)-{\alpha }_1\mathrm{sign}\left({\phi }_{2i}\left(t\right)\right)-{\alpha }_2\mathrm{sign}{\left({\phi }_{2i}\left(t\right)\right)}^2,\sigma \left(t\right)\in \{0,1,2,\dots ,s^{\ast }\},\hfill \end{array}$$

(57)

$$\begin{array}{ccc}\hfill {\dot{z}}_i\left(t\right)& =& A_0{z}_i\left(t\right),\mathrm{otherwise},\hfill \end{array}$$

(58)

where ${\beta }^{\ast },{\alpha }_1,{\alpha }_2>0$ need to be calculated and the other symbols have the same meanings as given before.

Proposition 3. 

Assume that Assumptions 1–4 hold, if there exist ${\beta }^{\ast }$, ${\alpha }_1$, ${\alpha }_2>0$ such that

$$\begin{array}{ccc}& & p_1>0,p_2>0,p_3>0,\hfill \end{array}$$

(59)

$$\begin{array}{ccc}& & {\widehat{p}}_1>0,{\widehat{p}}_2>0,{\widehat{p}}_3>0,\hfill \end{array}$$

(60)

$$\begin{array}{ccc}& & \tilde{\tau }>0.\hfill \end{array}$$

(61)

Then, $\parallel z_i\left(t\right)-x_0\left(t\right)\parallel =0$ for any $t\ge {\widehat{T}}_{max}$, where

$$\begin{array}{ccc}\hfill {\widehat{p}}_1& =& min\{2{\alpha }_1\sqrt{{\lambda }_{min}\left(H^w\right)},w\in \{1,2,\dots ,s^{\ast }\}\},\hfill \\ \hfill {\widehat{p}}_2& =& min\left\{2\right({\beta }^{\ast }{\lambda }_{min}\left(H^w\right)-\parallel A_0\parallel ),w\in \{1,2,\dots ,s^{\ast }\}\},\hfill \\ \hfill {\widehat{p}}_3& =& min\{2{\alpha }_2{\left(N{n}_0\right)}^{-{\displaystyle \frac{1}{2}}}{\left({\lambda }_{min}\left(H^w\right)\right)}^{{\displaystyle \frac{3}{2}}},w\in \{1,2,\dots ,s^{\ast }\}\},\hfill \\ \hfill \tilde{\tau }& =& {\displaystyle \frac{1}{2}}(p_2{\tau }_1+{\widehat{p}}_2{\tau }_2-max\{ln{\displaystyle \frac{{\lambda }_{max}\left(H\right)}{{\lambda }_{min}\left(H\right)}},ln{\displaystyle \frac{{\lambda }_{max}\left(H^w\right)}{{\lambda }_{min}\left(H^w\right)}}\}·\lceil {\displaystyle \frac{{\tau }_1^{\ast }+{\tau }_2^{\ast }}{\tau }}\rceil )-\parallel A_0\parallel {\tau }_3,w\in \{1,2,\dots ,s^{\ast }\}\},\hfill \\ \hfill {\widehat{T}}_{max}& =& \overline{T}(1+\lceil {\displaystyle \frac{{\widehat{\epsilon }}_2^{\ast }}{{\widehat{p}}^{\ast }}}\rceil ),\hfill \\ \hfill {\widehat{\epsilon }}_2^{\ast }& =& max\{{\lambda }_{min}{\left(H\right)}^{-{\displaystyle \frac{1}{2}}}{e}^{\parallel A_0\parallel {\tau }_3}{\displaystyle \frac{p_2}{p_3(e^{\frac{1}{2}{p}_2\tau }-1)}},{\lambda }_{min}{\left(H^w\right)}^{-{\displaystyle \frac{1}{2}}}{e}^{\parallel A_0\parallel {\tau }_3}{\displaystyle \frac{{\widehat{p}}_2}{{\widehat{p}}_3(e^{\frac{1}{2}{\widehat{p}}_2\tau }-1)}},w\in \{1,2,\dots ,s^{\ast }\}\},\hfill \\ \hfill {\widehat{p}}^{\ast }& =& min\{{\lambda }_{min}{\left(H\right)}^{-{\displaystyle \frac{1}{2}}}{p}_1{p}_2^{-1}(1-e^{-{\displaystyle \frac{1}{2}}{p}_2\tau }),{\lambda }_{min}{\left(H^w\right)}^{-{\displaystyle \frac{1}{2}}}{\widehat{p}}_1{\widehat{p}}_2^{-1}(1-e^{-{\displaystyle \frac{1}{2}}{\widehat{p}}_2\tau }),w\in \{1,2,\dots ,s^{\ast }\}\},\hfill \end{array}$$

and the other symbols have the same meanings as given before.

Proof of Proposition 3. 

Let $V_2\left(t\right)$ and ${\epsilon }_2\left(t\right)$ have the same meanings as given in Proposition 1. Then, it can be obtained that

$$\begin{array}{ccc}\hfill {\dot{V}}_2\left(t\right)& \le & -p_1{V}_2^{{\displaystyle \frac{1}{2}}}\left(t\right)-p_2{V}_2\left(t\right)-p_3{V}_2^{{\displaystyle \frac{3}{2}}}\left(t\right),\sigma \left(t\right)=0,\hfill \end{array}$$

(62)

$$\begin{array}{ccc}\hfill {\dot{V}}_2\left(t\right)& \le & -{\widehat{p}}_1{V}_2^{{\displaystyle \frac{1}{2}}}\left(t\right)-{\widehat{p}}_2{V}_2\left(t\right)-{\widehat{p}}_3{V}_2^{{\displaystyle \frac{3}{2}}}\left(t\right),\sigma \left(t\right)=1,2,\dots ,s^{\ast },\hfill \end{array}$$

(63)

$$\begin{array}{ccc}\hfill \parallel {\epsilon }_2\left(t\right)\parallel & \le & e^{\parallel A_0\parallel (t-t_0)}\parallel {\epsilon }_2\left(t_0\right)\parallel ,\mathrm{if}\sigma \left(t\right)=0\mathrm{for}[t_0,t),\hfill \end{array}$$

(64)

and

$$\begin{array}{ccc}& & {\lambda }_{max}{\left(H\right)}^{-{\displaystyle \frac{1}{2}}}{V}_2^{\ast }\left(t\right)\le \parallel {\epsilon }_2\left(t\right)\parallel \le {\lambda }_{min}{\left(H\right)}^{-{\displaystyle \frac{1}{2}}}{V}_2^{\ast }\left(t\right),\mathrm{if}\sigma \left(t\right)=0,\hfill \end{array}$$

(65)

$$\begin{array}{ccc}& & {\lambda }_{max}{\left(H^w\right)}^{-{\displaystyle \frac{1}{2}}}{V}_2^{\ast }\left(t\right)\le \parallel {\epsilon }_2\left(t\right)\parallel \le {\lambda }_{min}{\left(H^w\right)}^{-{\displaystyle \frac{1}{2}}}{V}_2^{\ast }\left(t\right),\mathrm{if}\sigma \left(t\right)=w,w\in \{1,2,\dots ,s^{\ast }\}.\hfill \end{array}$$

(66)

Then, by a similar analysis that yields Proposition 1, we have $\parallel z_i\left(t\right)-x_0\left(t\right)\parallel =0$ for any $t\ge {\widehat{T}}_{max}$. The proof is thus completed. □

5.2. Dynamic Event-Triggered Control Scheme

Chose (35) and (36) as the controller and event-triggered condition, respectively. Based on dynamic Compensator (57) and (58) and Theorem 1, the next conclusion can be given directly.

Theorem 2. 

Assume that Assumptions 1–4 hold and dynamic Compensators (57) and (58) satisfy Conditions (59)–(61) if there exist ${\beta }_i,{\alpha }_{1i},{\alpha }_{2i},{\delta }_i,{\xi }_i,{\chi }_{1i},{\chi }_{2i},{\rho }_{1i},{\rho }_{2i},{\rho }_{3i}>0$ for $i=1,2,\dots ,N$ such that Conditions (38)–(41). Then, Systems (5)–(8) with dynamic Compensators (57) and (58), Controller (35) and event-triggered Condition (36) satisfy the following condition: $\parallel y_i\left(t\right)-y_0\left(t\right)\parallel \le {\varphi }_i$ for any $t\ge T_{max}^i$, where

$$\begin{array}{c}\hfill T_{max}^i={\widehat{T}}_{max}+T_{{max}_i},\end{array}$$

and ${\widehat{T}}_{max}$ is obtained by Proposition 3 and the other symbols have the same meanings as given before.

Moreover, the next result can be given directly.

Proposition 4. 

If Conditions (59)–(61) and Condition (38) are satisfied, then the event-triggered Condition (36) can avoid Zeno-behavior for any given initial values.

6. Numerical Example

Consider Systems (5)–(8) as consisting of one leader and four agents, and the parameters are given as follows:

$$\begin{array}{ccc}& & A_0=\left(\begin{array}{cc}0.2& 0.3\\ -0.1& 0.15\end{array}\right),A_1=\left(\begin{array}{cc}-0.4& 0.3\\ -1.2& 0.75\end{array}\right),A_2=\left(\begin{array}{cc}0.3& 0.45\\ -0.1& 0.05\end{array}\right),\hfill \\ & & A_3=\left(\begin{array}{cc}-0.15& 0.45\\ -0.3& 0.5\end{array}\right),A_4=\left(\begin{array}{ccc}0.25& 0.25& 0.05\\ 0& 0.05& 0.1\\ -0.2& -0.25& 0.1\end{array}\right),\hfill \\ & & C_0=\left(\begin{array}{cc}1& 1\end{array}\right),C_1=\left(\begin{array}{cc}-1& 1\end{array}\right),C_2=\left(\begin{array}{cc}-1& -2\end{array}\right),\hfill \\ & & C_3=\left(\begin{array}{cc}-1& 2\end{array}\right),C_4=\left(\begin{array}{ccc}1.5& 0.5& 0.5\end{array}\right),\hfill \\ & & {\omega }_1\left(t\right)={(0.2sin\left(t\right)0.1cos\left(t\right))}^T,{\omega }_2\left(t\right)={(0.2cos\left(t\right)-0.2sin\left(t\right))}^T,\hfill \\ & & {\omega }_3\left(t\right)={(0.2sin\left(t\right)-0.2cos\left(t\right))}^T,{\omega }_4\left(t\right)={(0.15sin\left(t\right)0.1cos\left(t\right)0.1sin\left(t\right))}^T.\hfill \end{array}$$

Moreover, the topology graph of Systems (5)–(8) is such that

$$\begin{array}{ccc}& & H^{\sigma \left(t\right)}=H=\left(\begin{array}{cccc}0.8& -0.4& 0& 0\\ -0.4& 1.1& -0.4& 0\\ 0& -0.4& 1.1& -0.3\\ 0& 0& -0.3& 0.5\end{array}\right),\sigma \left(t\right)=0,\hfill \\ & & H^{\sigma \left(t\right)}=H^1=\left(\begin{array}{cccc}0.8& -0.4& 0& 0\\ -0.4& 1.1& -0.4& 0\\ 0& -0.4& 0.7& -0.3\\ 0& 0& -0.3& 0.5\end{array}\right),\sigma \left(t\right)=1,\hfill \\ & & H^{\sigma \left(t\right)}=H^2=\left(\begin{array}{cccc}0.8& -0.4& 0& 0\\ -0.4& 0.8& -0.4& 0\\ 0& -0.4& 1.1& -0.3\\ 0& 0& -0.3& 0.5\end{array}\right),\sigma \left(t\right)=2,\hfill \\ & & \sigma \left(t\right)=\left\{\begin{array}{cc}0,& t\in [rT,rT+1),\\ 1,& t\in [rT+1,rT+1.5),\\ 2,& t\in [rT+1.5,rT+2),\\ \mathrm{otherwise},& t\in [rT+2,(r+1\left)T\right),\end{array}\right.r=0,1,2,\dots ,T=4.\hfill \end{array}$$

Case (a): Consider the case that DoS attacks are known. In this case, based on Corollary 1 and Theorem 1, choose (9)–(11), (35) and (36) as the dynamic compensators, controller and event-triggered condition for systems with the following parameters:

$$\begin{array}{ccc}& & {\Pi }_1=\left(\begin{array}{cc}1& 0\\ 2& 1\end{array}\right),{\Pi }_2=\left(\begin{array}{cc}-1& 1\\ 0& -1\end{array}\right),{\Pi }_3=\left(\begin{array}{cc}1& -1\\ 1& 0\end{array}\right),{\Pi }_4=\left(\begin{array}{cc}1& 0\\ 0& 1\\ -1& 1\end{array}\right),\hfill \\ & & {\beta }^{\ast }=5,{\beta }_1^{\ast }=8,{\beta }_2^{\ast }=7,{\alpha }_1={\alpha }_2={\alpha }_{11}^{\ast }={\alpha }_{21}^{\ast }={\alpha }_{12}^{\ast }={\alpha }_{22}^{\ast }=1,\hfill \\ & & {\beta }_1=3,{\beta }_2=2.5,{\beta }_3=3.5,{\beta }_4=3,\hfill \\ & & {\alpha }_{ij}=1,i\in \{1,2\},j\in \{1,2,3,4\},\hfill \\ & & {\delta }_1={\delta }_4=0.02,{\delta }_2={\delta }_3=0.03,\hfill \\ & & {\xi }_1={\xi }_2={\xi }_3={\xi }_4=0.1,\widehat{\xi }=0.1,{\mu }_1={\mu }_2={\mu }_3=1,\hfill \\ & & {\chi }_{11}={\chi }_{12}={\chi }_{13}={\chi }_{14}=0.1,{\chi }_{21}={\chi }_{22}={\chi }_{23}={\chi }_{24}=0.01,\hfill \end{array}$$

where ${\rho }_{1i}$, ${\rho }_{2i}$ and ${\rho }_{3i}$ can be provided by calculating (39)–(41). According to Figure 1, Systems (5)–(8) have achieved quasi-consensus. By Figure 2 and Figure 3 and

Table 1. The comparison between dynamic and static periodical event-triggered conditions.

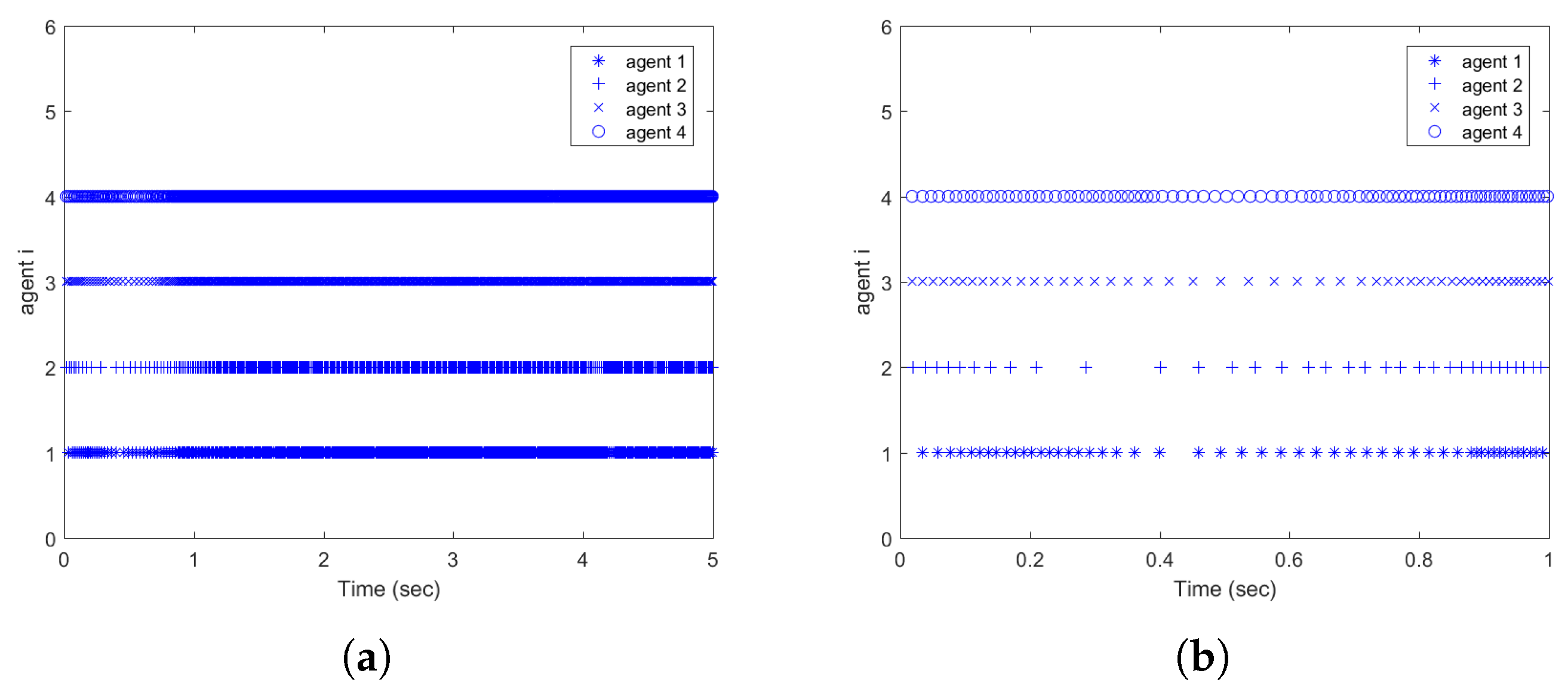
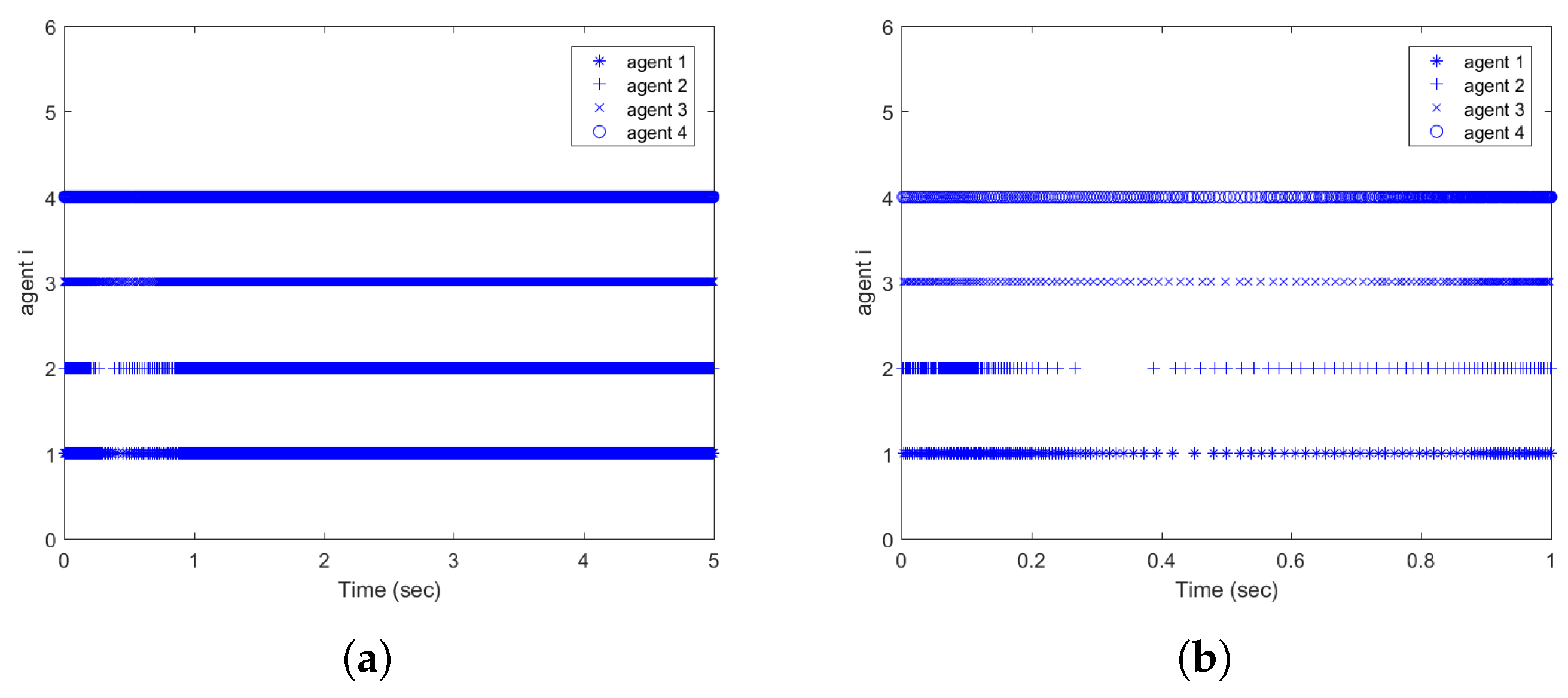
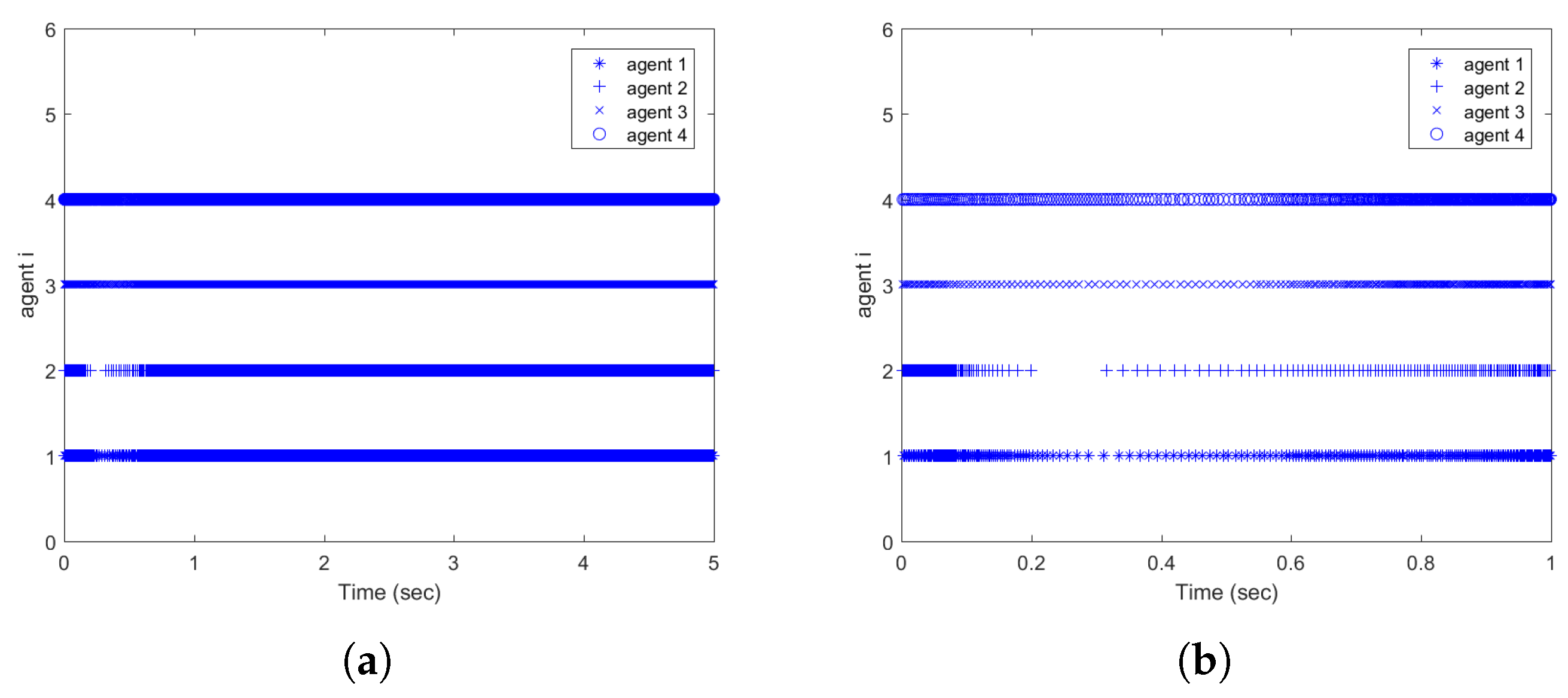
Triggering Condition	Condition (36)	Corresponding Static Event-Triggered Condition
Mean triggered times for case (a)	600	2465.5
Mean triggered times for case (b)	618.75	2559.5

, the event-triggered Condition (36) avoids Zeno-behavior and is less conservative than the static event-triggered condition (with a lower triggering frequency) in this example.

Case (b): Consider the case that the DoS attacks are unknown. In this case, based on Proposition 3 and Theorem 2, choose (57), (58), (35) and (36) as the dynamic compensators, controller and event-triggered condition for the systems with the following parameters:

$$\begin{array}{c}\hfill {\beta }^{\ast }=10,{\alpha }_1={\alpha }_2=1,\end{array}$$

where the values of the other parameters are the same as in the former example.

According to Figure 4, Systems (5)–(8) achieved quasi-consensus. As shown in Figure 5 and Figure 6 and Table 1, the event-triggered Condition (36) avoids Zeno-behavior and is less conservative than the static event-triggered condition (with a lower triggering frequency) in this example.

Based on the results of the numerical example, the following conclusions can be obtained: (i) By comparing Figure 1 with Figure 4, the convergence rate of the output errors under a control scheme for unknown DoS attacks is faster than those under a control scheme for known DoS attacks. (ii) By comparing Figure 2 and Figure 5, supported by Table 1, the controller update frequency under unknown DoS attacks is higher than under known DoS attacks. (iii) By comparing Figure 2 with Figure 3 and Figure 5 with Figure 6, as well as being supported by Table 1, the dynamic event-triggered control schemes given in this paper significantly reduce the controller update frequency.

Based on the results of Propositions 1 and 3, the control scheme for known DoS attacks adopts less conservative parameters compared to the control scheme for unknown DoS attacks, which leads to the slower convergence rate and lower controller update frequency (the results of (i) and (ii)). Moreover, (iii) demonstrates the superiority of the proposed dynamic event-triggered control schemes (significantly alleviating communication bandwidth demands).

A comparison between the control schemes proposed in this paper with existing representative works is shown in

Table 2. The comparison between the control schemes proposed in this paper with existing representative works.

Source of the Method	This Paper	Reference [9]	Reference [25]	Reference [31]
Heterogeneous Agent	Yes	Yes	Yes	No
Event-Triggered Mechanism	Dynamic	N/A	Static	Dynamic
Type of DoS Attacks	Aperiodic Unknown	N/A	Periodic Known	Aperiodic Unknown
Convergence Type	Fixed time	Asymptotic	Fixed time	Asymptotic

. Based on the comparison of Table 2, the advantage of the control schemes proposed in this paper lies in that they comprehensively possess all the advanced characteristics that are scattered in the existing literature. Specifically, unlike the methods presented in these references, this paper is the only one that simultaneously achieves the following: (1) control of heterogeneous agents, (2) a dynamic event-triggered mechanism, (3) resilience against aperiodic and unknown DoS attacks, and (4) fixed-time convergence. This integration results in a more comprehensive and capable solution.

7. Practical Significance and Challenges

The dynamic event-triggered control schemes for MASs under known and unknown DoS attacks provided in this paper have both theoretical value and practical significance, but they also face challenges in practical application. At the practical level, the following challenges apply: (1) The studies on HMASs under known and unknown DoS attacks have the potential to be applied to real-world scenarios, such as periodic maintenance and sudden interference, and they can provide a framework for designing cooperative control. (2) The designed dynamic event-triggered mechanism can significantly save communication resources and is suitable for platforms with limited bandwidth and energy, such as unmanned aerial vehicles and robots. (3) A fixed-time control scheme can provide a definite upper bound of the maximum dwell time, which is conducive to the prediction of the actual control results. The main challenges faced include the following: (1) The theoretical performance is relatively sensitive to the model accuracy. (2) The dynamic event-triggered mechanism increases real-time computing overhead and may exacerbate signal loss under extreme attacks. (3) Overly strict selection conditions for parameters may lead to conservative controller design. Our future work will focus on enhancing the robustness of the framework and advancing its implementation under physical constraints.

8. Conclusions

The fixed-time quasi-consensus problem of HMASs under DoS attacks was investigated in this paper. Based on the characteristics of CMA and CBA, Lyapunov stability theory and the method of solving fractional differentiation, considering whether the attacks are known, two dynamic compensators were designed, and the corresponding fixed-time consensus criteria were provided, which can ensure that the state of the dynamic compensator agrees with the state of the leader with in a fixed time. On this basis, the event-triggered control schemes were provided to solve the fixed-time consensus issue of HMASs under both known and unknown DoS attacks. Moreover, the proposed dynamic event-triggered condition not only avoids Zeno-behavior successfully but also exhibits lower conservatism than the static event-triggered condition. Finally, the results of the numerical example support the correctness of our theoretical conclusions. In the future, we would like to extend these conclusions to research on nonlinear MASs, stochastic MASs, time-varying MASs, etc.