A Multi-Scale Approach for the Piezoelectric Modal Analysis in Periodically Perforated Structures
Abstract
1. Introduction
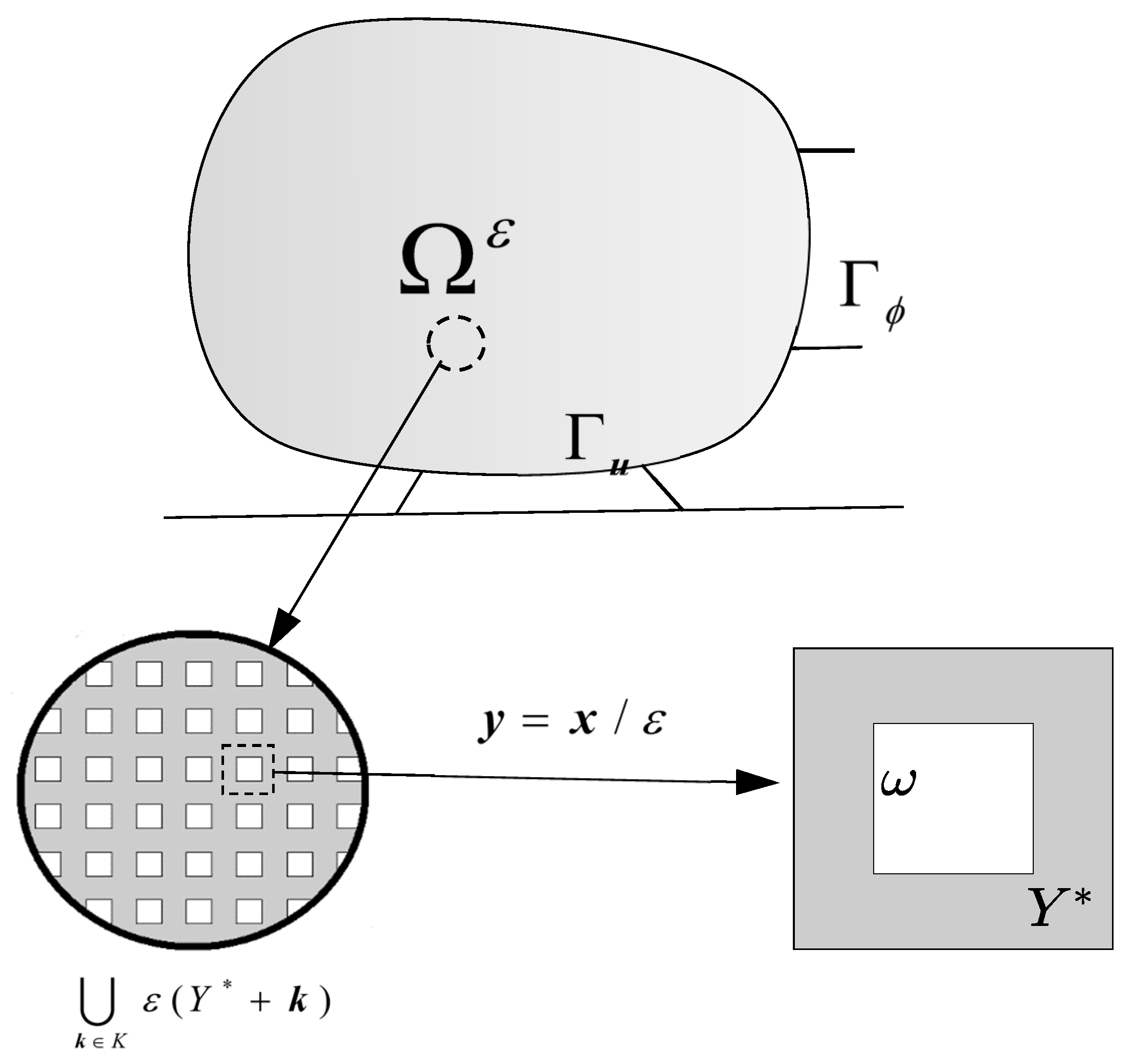
2. Piezoelectric Modal Problem for Cellular Structure
3. Two-Scale Asymptotic Homogenization and Second-Order Expansion
3.1. SOTS Expansions of the Eigenvalues and Eigenfunctions
3.2. Error Estimations of the Eigenvalue
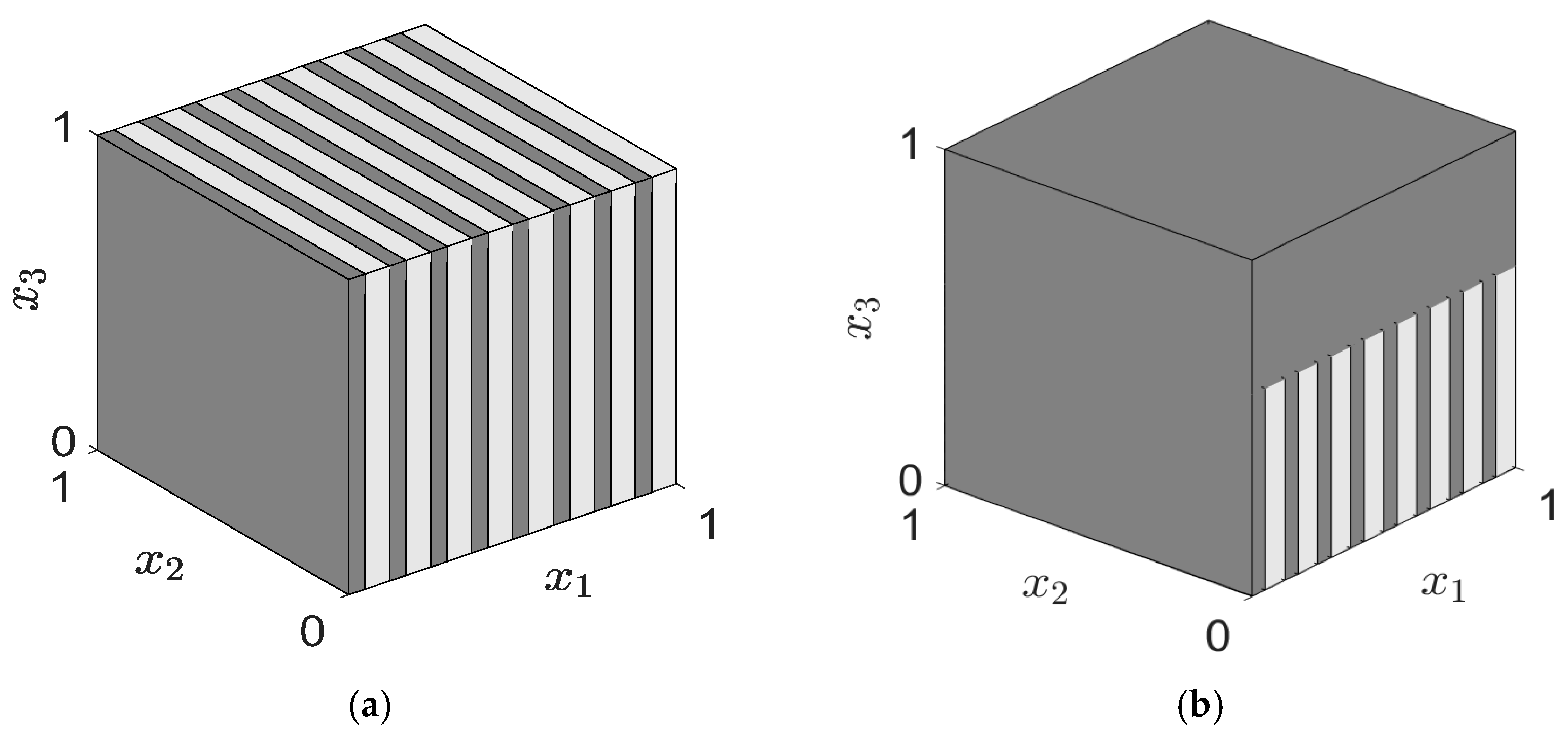
3.3. Layered Structures
4. SOTS Finite Element Algorithm
- Finite element computation of the cell functions:
- Configure the domain , determine the coefficients , , and for each constituent material, and construct the finite element mesh. Compute the first-order cell functions , , , and with the following weak forms:
- Compute the homogenized coefficients , , , and from the expressions in Equation (15).
- Compute the second-order cell functions , , , and with the following weak forms:
- Construct the finite element mesh on the homogeneous domain and perform the eigenvalue computations of Homogenized Problem (14) using the weak form:
- Assemble the FOTS and SOTS approximations of the eigenvector in Equation (28), and compute eigenvalue correctors and in Equation (25). Then, we obtain the approximations of the eigenvalues and
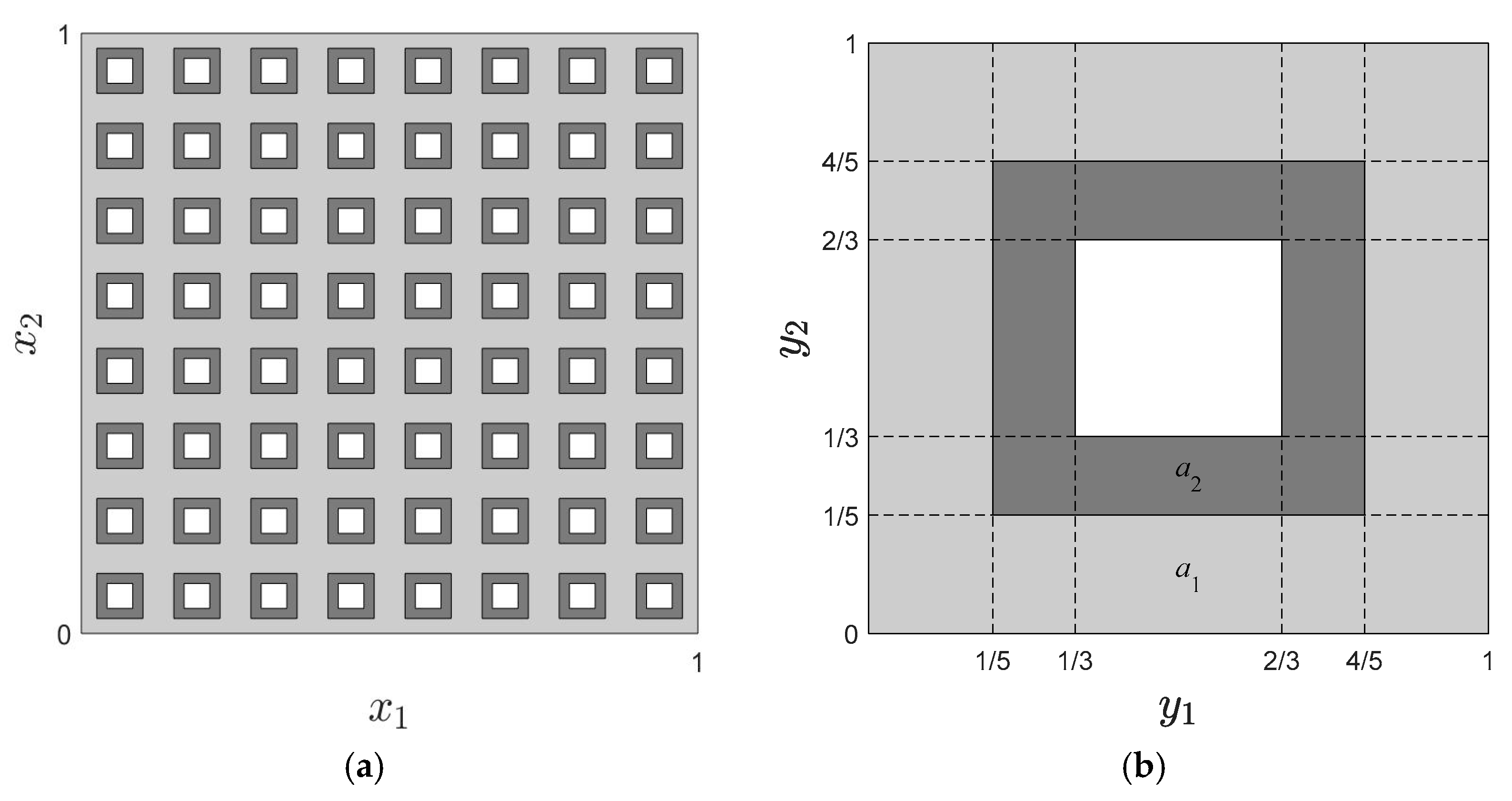
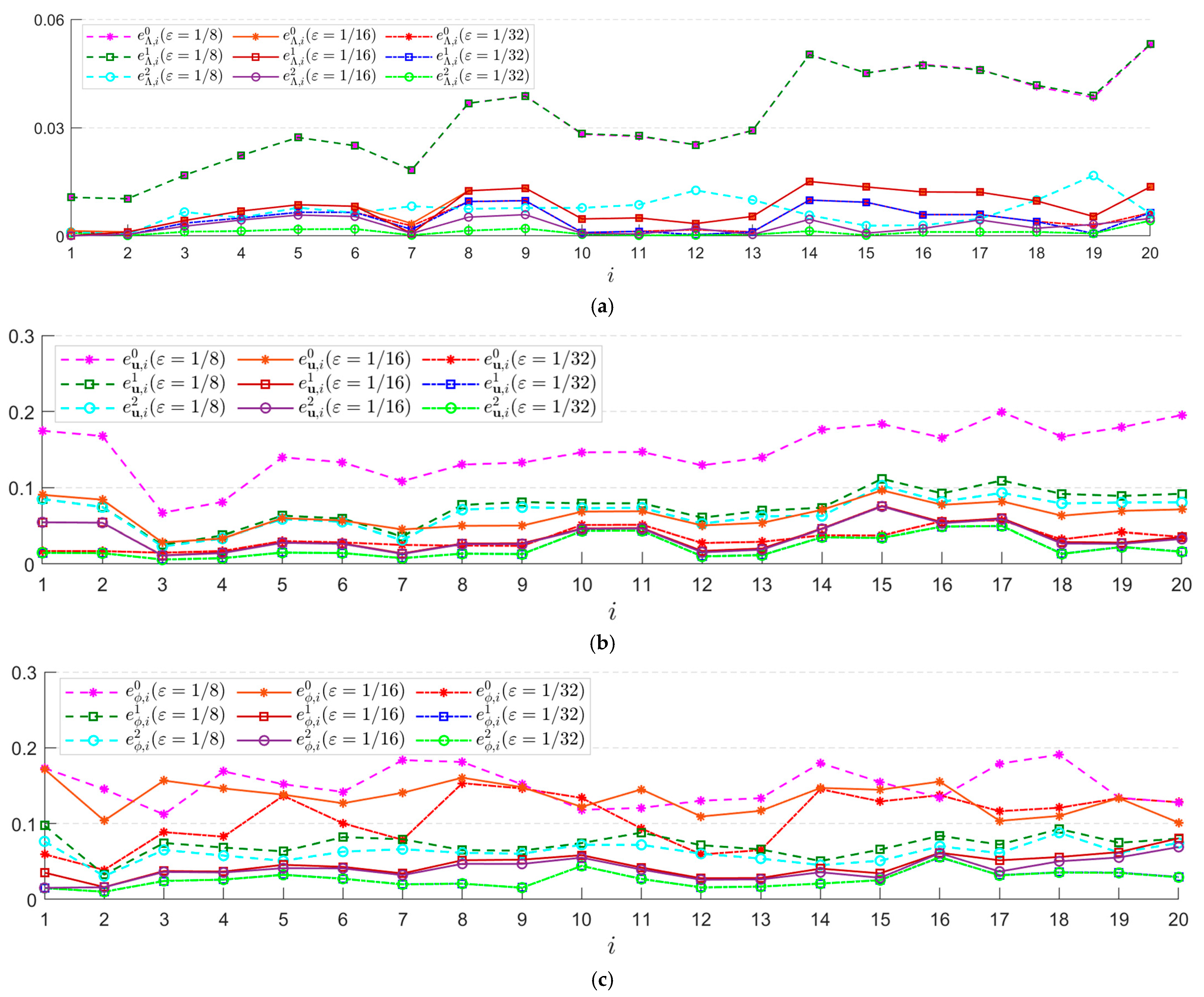
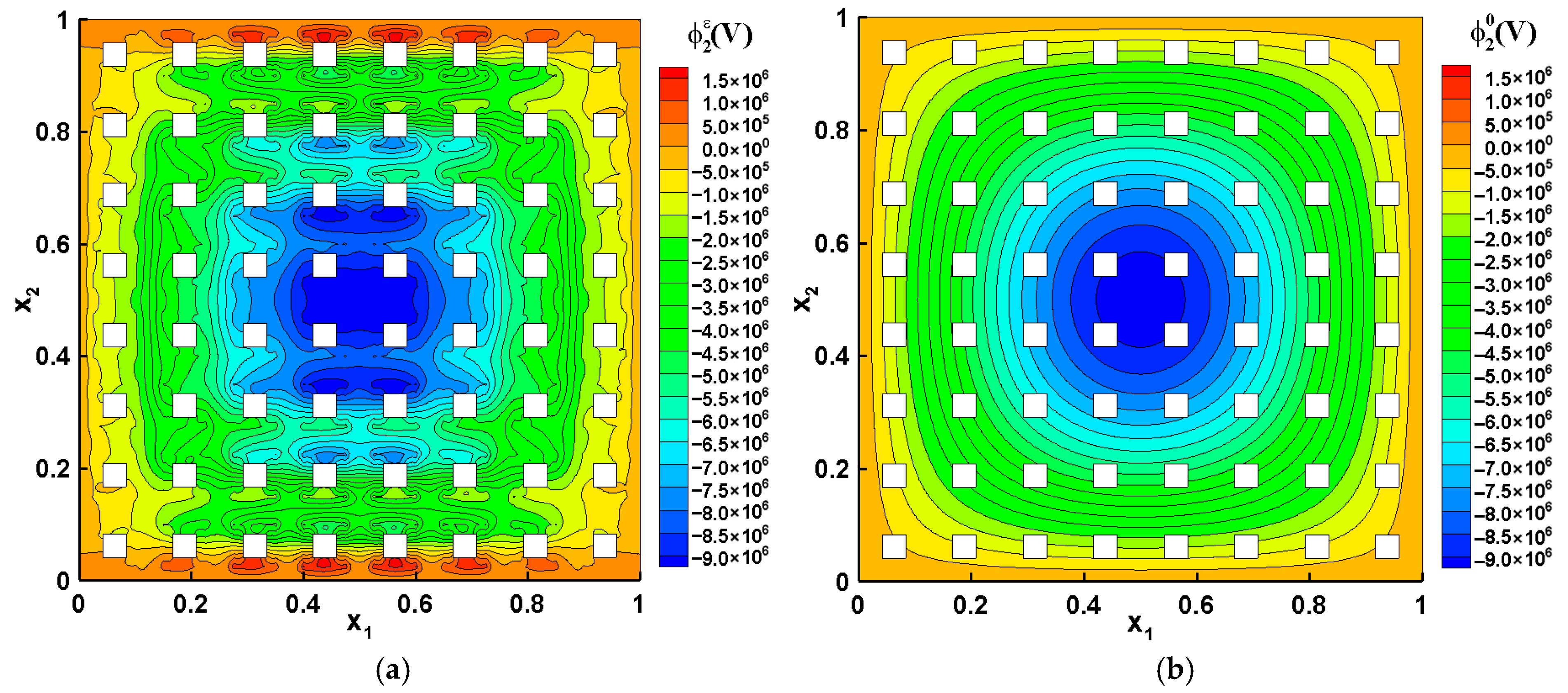
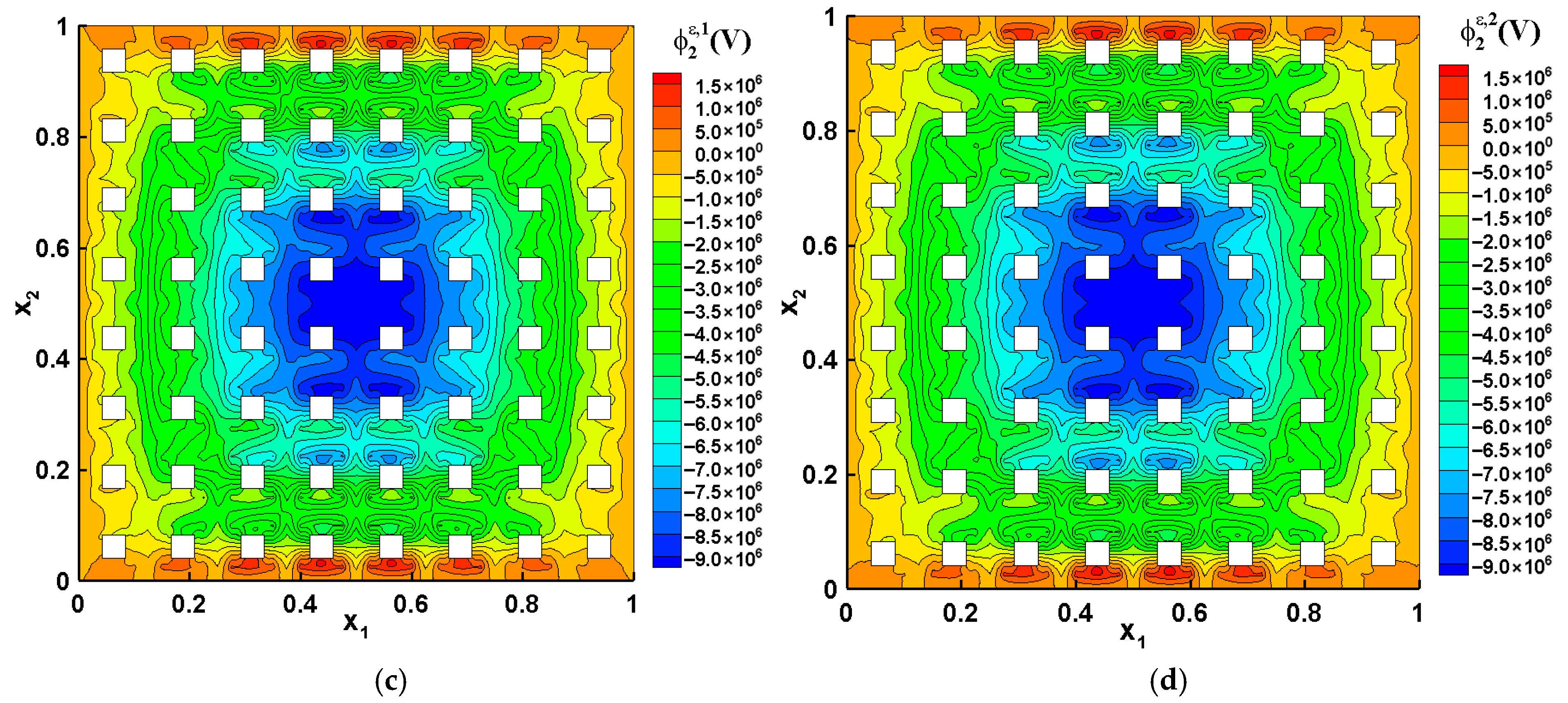
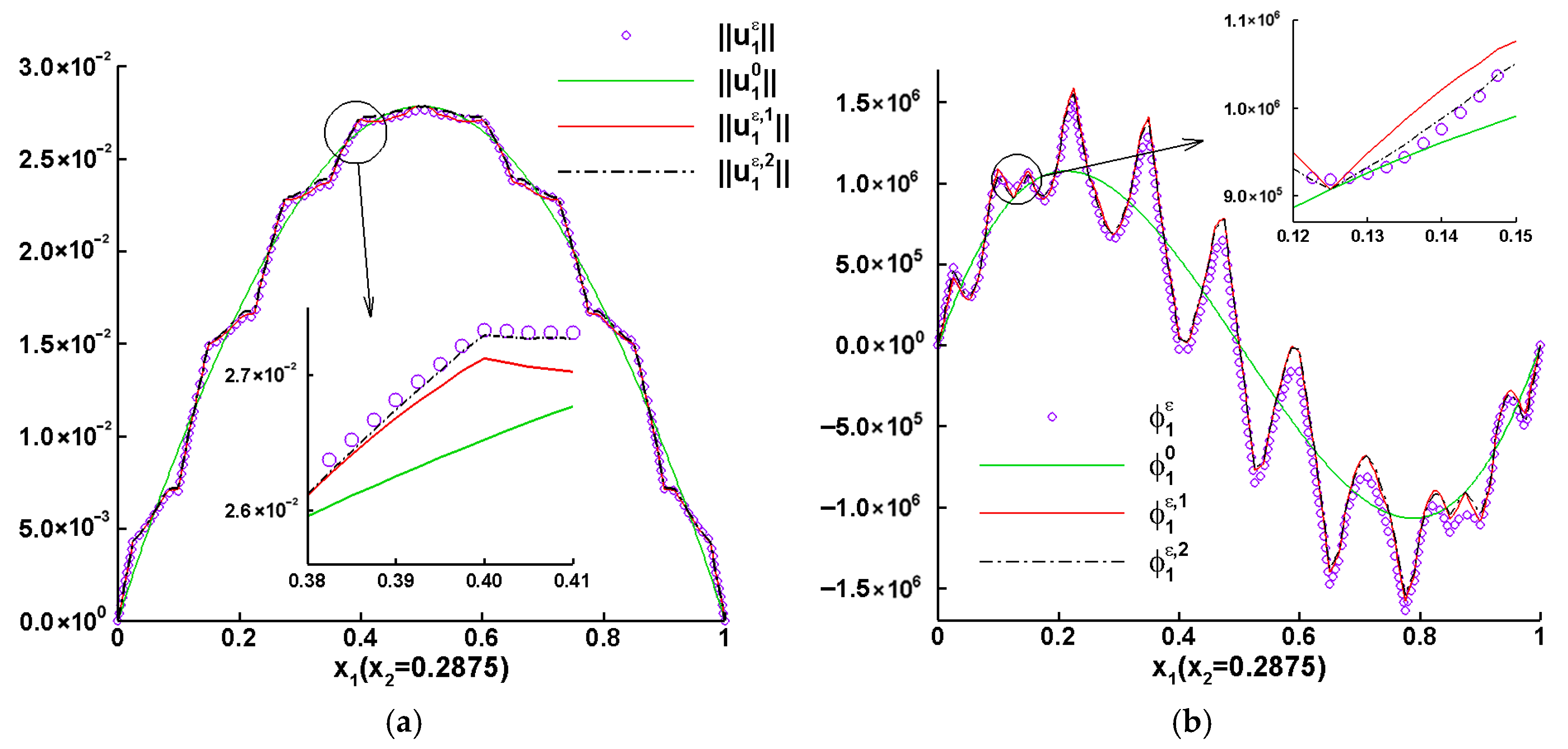
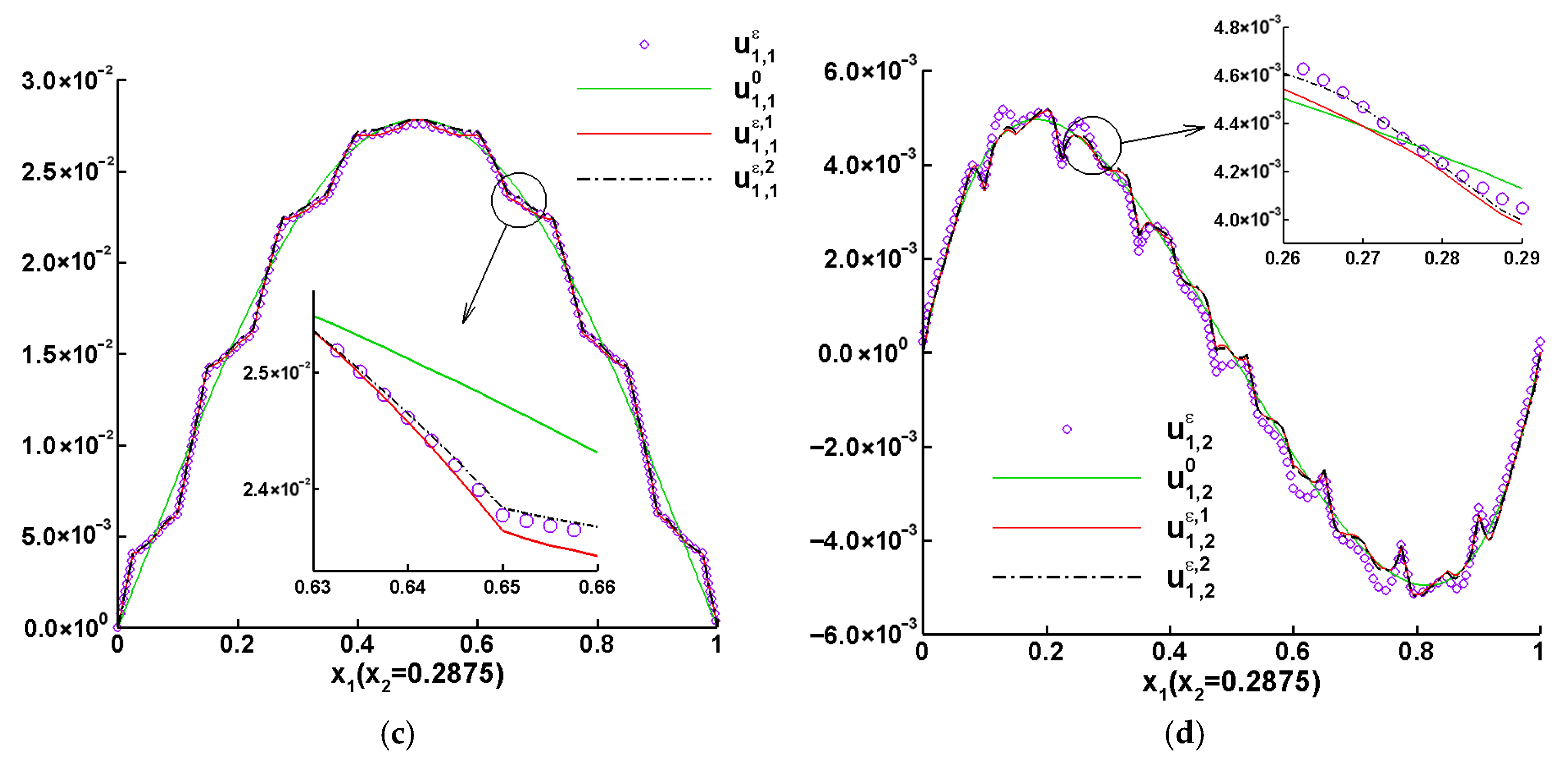
5. Numerical Example and Discussions
6. Conclusions and Future Expectations
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Error Estimation
Appendix B. Rank-2 Structure
References
- Montoya, A.; Ocampo, A.; March, C. Piezoelectric Transducers and Applications; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Yang, J. An Introduction to the Theory of Piezoelectricity; Springer: Cham, Switzerland, 2004. [Google Scholar]
- Fang, D.N.; Jiang, B.; Hwang, K.C. A model for predicting effective properties of piezocomposites with non-piezoelectric inclusions. J. Elast. Phys. Sci. Solids 2001, 62, 95–118. [Google Scholar] [CrossRef]
- Bensoussan, A.; Lions, J.L.; Papanicolaou, G. Asymptotic Analysis for Periodic Structures; North-Holland: Amsterdam, The Netherlands, 1978. [Google Scholar] [CrossRef]
- Cioranescu, D.; Donato, P. An Introduction to Homogenization; Oxford University Press: New York, NY, USA, 1999. [Google Scholar] [CrossRef]
- Allaire, G. Homogenization and two-scale convergence. SIAM J. Math. Anal. 1992, 23, 1482–1518. [Google Scholar] [CrossRef]
- Nguetseng, G. A general convergence result for a functional related to the theory of homogenization. SIAM J. Math. Anal. 1989, 20, 608–623. [Google Scholar] [CrossRef]
- Hou, T.Y.; Wu, X.H. A Multiscale Finite element method for elliptic problems in composite materials and porous media. J. Comput. Phys. 1997, 134, 169–189. [Google Scholar] [CrossRef]
- Silva, E.C.N.; Fonseca, J.S.O.; Kikuchi, N. Optimal design of periodic piezocomposites. Comput. Methods Appl. Mech. Eng. 1998, 159, 49–77. [Google Scholar] [CrossRef]
- Fonseca, J.S.O. Design of Microstructures of Periodic Composite Materials. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 1997. [Google Scholar]
- Cui, J.Z.; Cao, L.Q. Finite element method based on two-scale asymptotic analysis. Math. Numer. Sin. 1998, 20, 89–102. [Google Scholar] [CrossRef]
- Deng, M.X.; Feng, Y.P. Two-scale finite element method for piezoelectric problem in periodic structure. Appl. Math. Mech. 2011, 32, 1525–1540. [Google Scholar] [CrossRef]
- Ma, Q.; Wang, H.; Yang, Z.Q.; Li, Z.H.; Cui, J.Z. Second-order asymptotic analysis and computations of axially and spherically symmetric piezoelectric problems for composite structures. J. Sci. Comput. 2019, 81, 689–731. [Google Scholar] [CrossRef]
- Douanla, H. Two-scale convergence of Stekloff eigenvalue problems in perforated domains. Bound. Value Probl. 2010, 2010, 853717. [Google Scholar] [CrossRef]
- Allaire, G.; Capdeboscq, Y. Homogenization and localization for a 1-D eigenvalue problem in a periodic medium with an interface. Ann. Mat. Pura Appl. 2002, 181, 247–282. [Google Scholar] [CrossRef]
- Vanninathan, M. Homogenization of eigenvalue problems in perforated domains. Proc. Indian Acad. Sci. Math. Sci. 1981, 90, 239–271. [Google Scholar] [CrossRef]
- Nandakumar, A.K. Homogenization of eigenvalue problems of elasticity in perforated domains. Asymptot. Anal. 1994, 9, 337–358. [Google Scholar] [CrossRef]
- Kesavan, S. Homogenization of elliptic eigenvalue problems: Part 1. Appl. Math. Optim. 1979, 5, 153–167. [Google Scholar] [CrossRef]
- Kesavan, S. Homogenization of elliptic eigenvalue problems: Part 2. Appl. Math. Optim. 1979, 5, 197–216. [Google Scholar] [CrossRef]
- Ding, S.; Hu, Y.; Jian, B.; Zhang, Y.; Xia, R.; Hu, G. A semi-analytical solution to incipient sliding contact on viscoelastic layer-elastic substrate with imperfectly bonded interface. Appl. Math. Model. 2024, 125, 35–58. [Google Scholar] [CrossRef]
- Benveniste, Y. Universal relations in piezoelectric composites with eigenstress and polarization fields, Part II: Multiphase media—Effective behavior. J. Appl. Mech. 1993, 60, 270–275. [Google Scholar] [CrossRef]
- Wang, H.M.; Ding, H.J.; Chen, Y.M. Dynamic solution of a multilayered orthotropic piezoelectric hollow cylinder for axisymmetric plane strain problems. Int. J. Solids Struct. 2005, 42, 85–102. [Google Scholar] [CrossRef]
- Gu, G.Q.; Wei, E.B.; Xu, C. Effective elastic properties of piezoelectric composites with radially polarized cylinders. Phys. B 2009, 404, 4001–4006. [Google Scholar] [CrossRef]
- Adeff, S.E. Simulation of axisymmetric piezoelectric devices. Appl. Math. Comput. 1994, 65, 355–369. [Google Scholar] [CrossRef]
- Lotnyk, A.; Roddatis, V.; Braun, N.; Voß, L.; Bryja, H.; Kienle, L. Atomic-scale investigation of layered Cu7Te4 nanostructures featuring two and three tellurium layers. ACS Appl. Nano Mater. 2025, 8, 11621–11628. [Google Scholar] [CrossRef]
- Allik, H.; Hughes, T.J.R. Finite element method for piezoelectric vibration. Int. J. Numer. Methods Eng. 1970, 2, 151–157. [Google Scholar] [CrossRef]
- Iovane, G.; Nasedkin, A.V. Modal Analysis of Piezoelectric Bodies with Voids. I. Mathematical Approaches. Appl. Math. Model. 2010, 34, 60–71. [Google Scholar] [CrossRef]
- Iovane, G.; Nasedkin, A.V. Modal Analysis of Piezoelectric Bodies with Voids. II. Finite Element Simulation. Appl. Math. Model. 2010, 34, 47–59. [Google Scholar] [CrossRef]
- Rodríguez-Ramos, R.; Sabina, F.J.; Guinovart-Díaz, R.; Bravo-Castillero, J. Closed-form expressions for the effective coefficients of a fiber-reinforced composite with transversely isotropic constituents—I. Elastic and square symmetry. Mech. Mater. 2001, 33, 223–235. [Google Scholar] [CrossRef]
- Bravo-Castillero, J.; Otero, J.A.; Rodríguez-Ramos, R.; Bourgeat, A. Asymptotic homogenization of laminated piezocomposite materials. Int. J. Solids Struct. 1998, 35, 527–541. [Google Scholar] [CrossRef]
- Qin, Q.H. Material properties of piezoelectric composites by BEM and homogenization method. Compos. Struct. 2004, 66, 295–299. [Google Scholar] [CrossRef]
- Fantoni, F.; Bacigalupo, A.; Paggi, M. Multi-field asymptotic homogenization of thermo-piezoelectric materials with periodic microstructure. Int. J. Solids Struct. 2017, 120, 31–56. [Google Scholar] [CrossRef]
- Martínez-Ayuso, G.; Friswell, M.I.; Adhikari, S.; Khodaparast, H.H.; Berger, H. Homogenization of porous piezoelectric materials. Int. J. Solids Struct. 2017, 113–114, 218–229. [Google Scholar] [CrossRef]
- Lenglet, E.; Hladky-Hennion, A.C.; Debus, J.C. Numerical homogenization techniques applied to piezoelectric composites. J. Acoust. Soc. Am. 2003, 113, 826–833. [Google Scholar] [CrossRef]
- Berger, H.; Gabbert, U.; Köppe, H.; Rodríguez-Ramos, R.; Bravo-Castillero, J.; Guinovart-Diaz, R.; Otero, J.A.; Maugin, G.A. Finite element and asymptotic homogenization methods applied to smart composite materials. Comput. Mech. 2003, 33, 61–67. [Google Scholar] [CrossRef]
- Fu, C.; Wang, Z.; Jin, X.; Zhu, X.; Zhu, J. Effective piezoelectric coefficients of cement-based 2–2 type piezoelectric composites based on a multiscale homogenization model. Compos. Struct. 2018, 194, 170–177. [Google Scholar] [CrossRef]
- Yang, J.S.; Batra, R.C. Free vibrations of a piezoelectric body. J. Elast. 1994, 34, 239–254. [Google Scholar] [CrossRef]
- Ma, Q.; Li, Z.H.; Cui, J.Z. Multi-scale asymptotic analysis and computation of the elliptic eigenvalue problems in curvilinear coordinates. Comput. Methods Appl. Mech. Eng. 2018, 340, 340–365. [Google Scholar] [CrossRef]
- Ma, Q.; Cui, J.Z. A third-order multiscale analysis and computation for the elliptic problem in arbitrarily heterogeneous domains. Appl. Math. Lett. 2026, 174, 109806. [Google Scholar] [CrossRef]
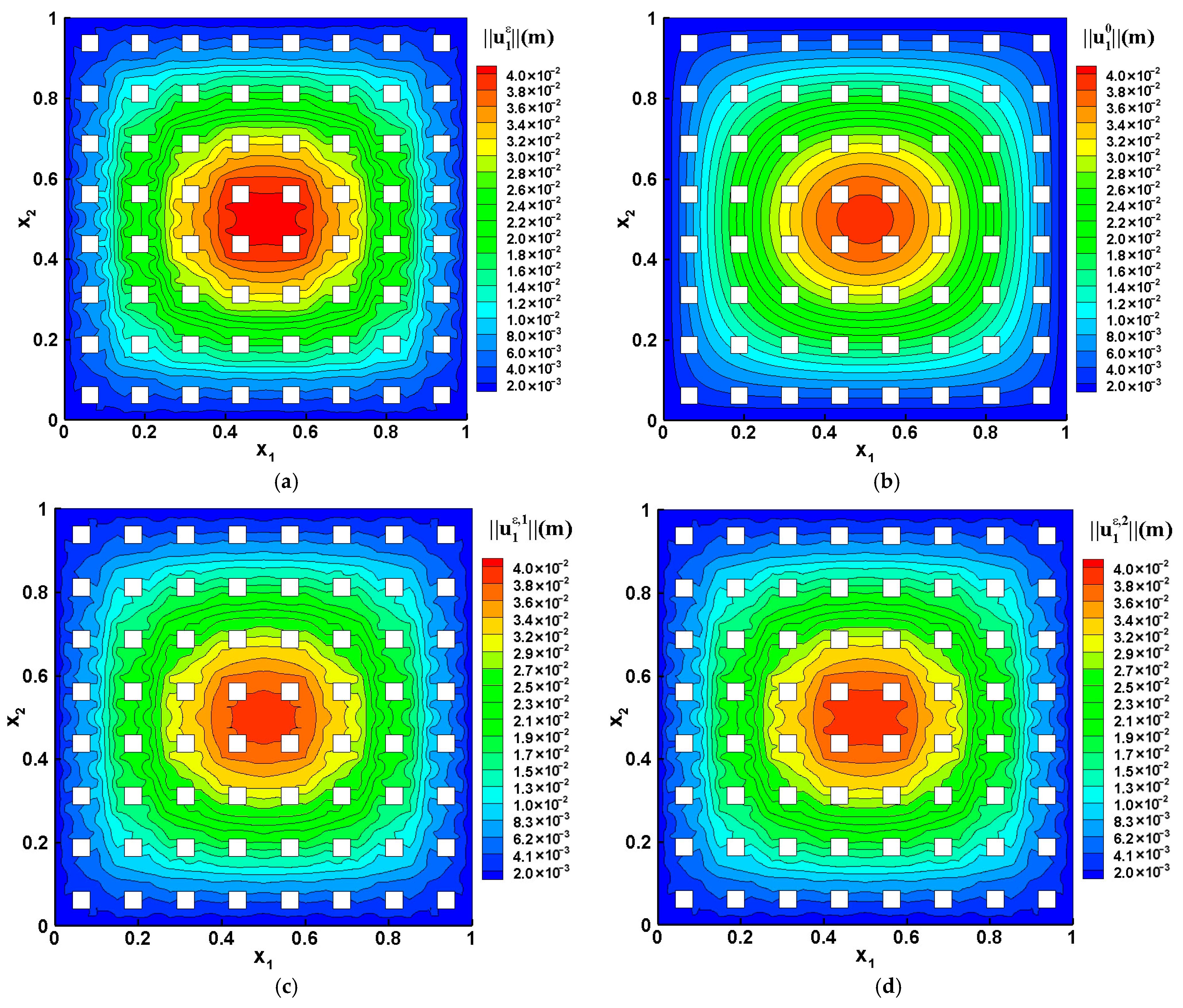
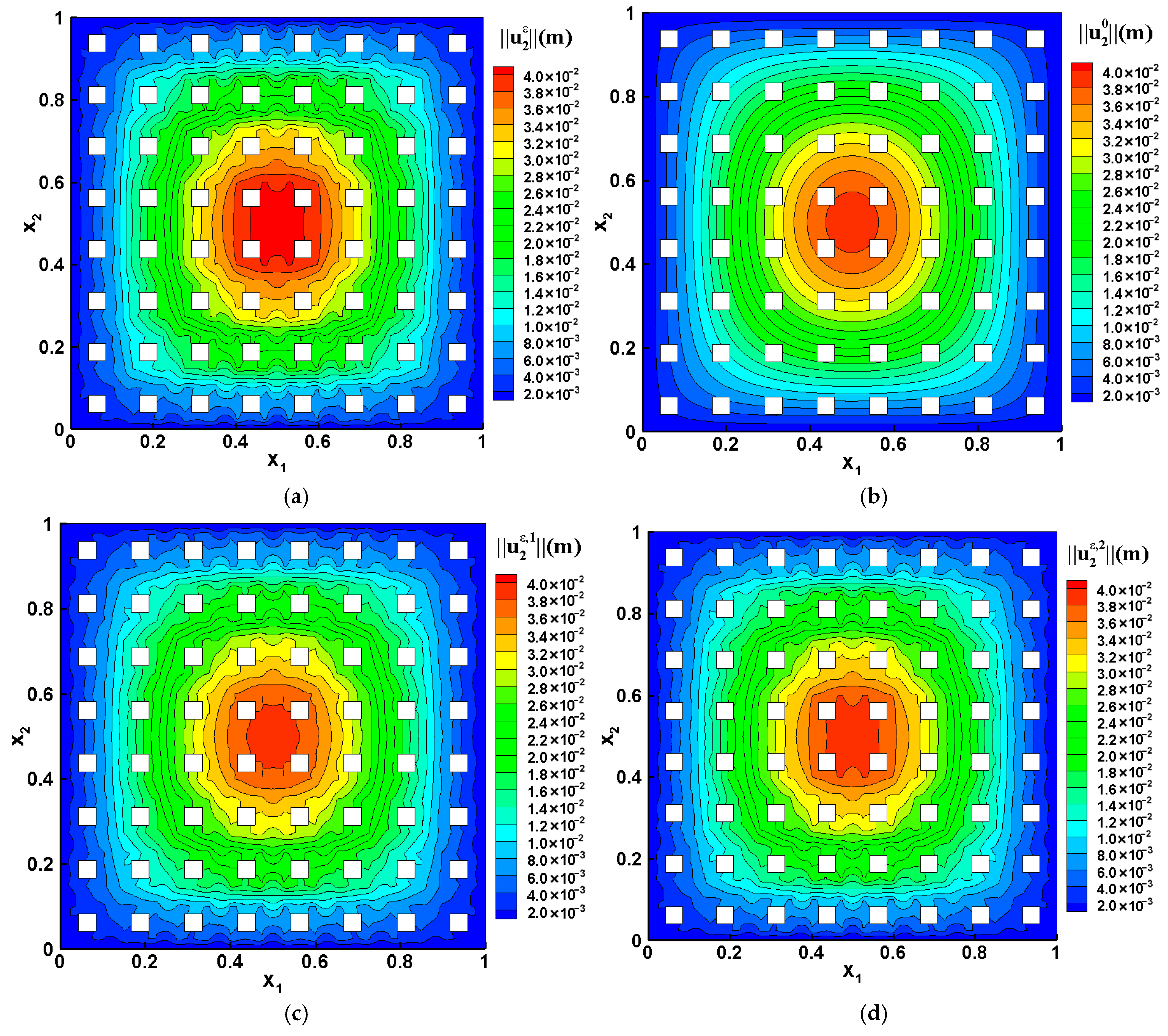
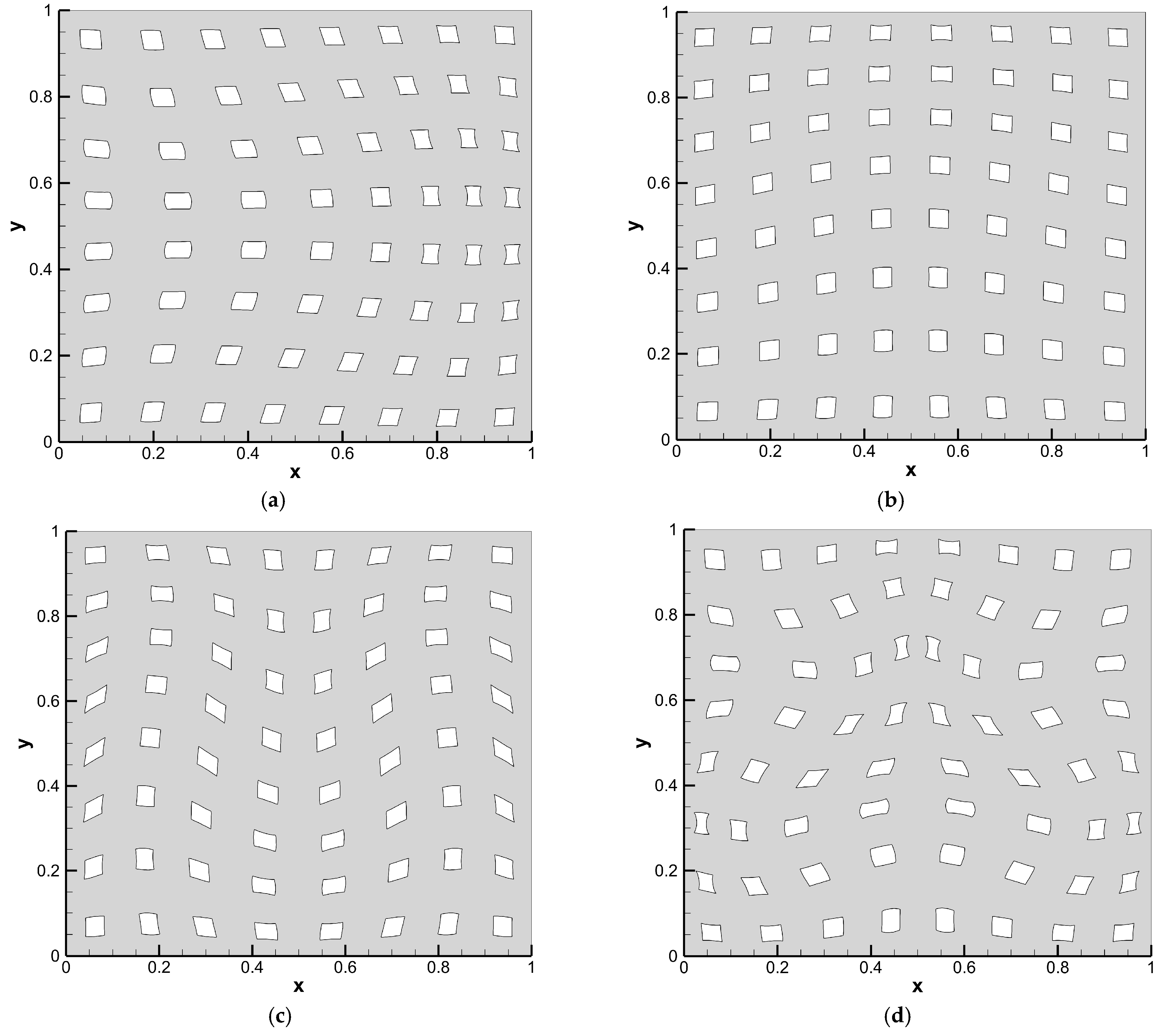
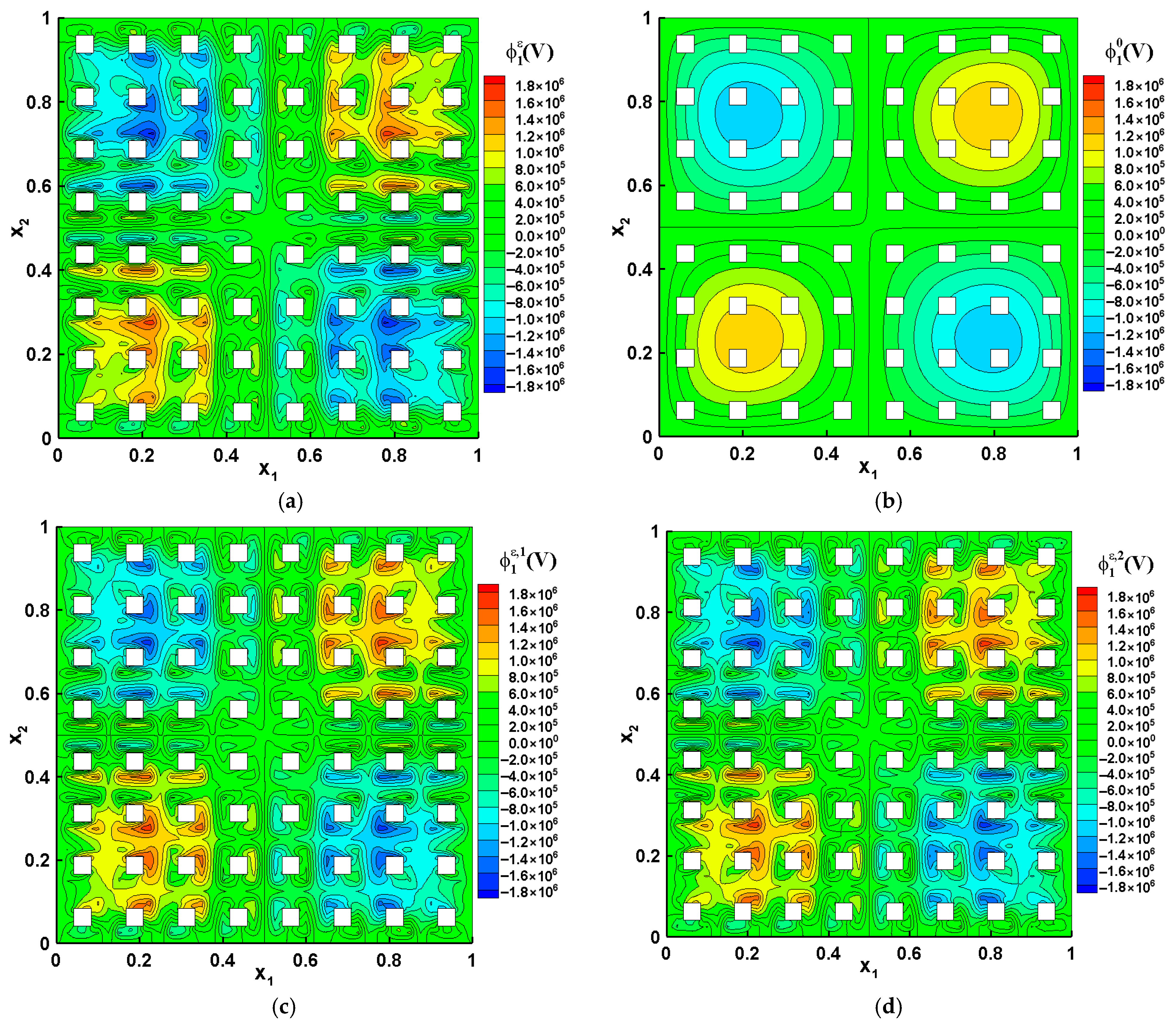
| Variable | Unit | Physical Meaning |
|---|---|---|
| m | Displacement | |
| V | Electric potential | |
| s−2 | Eigenvalue | |
| kg/m3 | Density | |
| C/m2 | Piezoelectric coefficient | |
| F/m | Dielectric coefficient | |
| Pa | Elastic stiffness | |
| C/m2 | Electric flux | |
| V/m | Electric field | |
| PA | Stress | |
| - | Linear strain |
| No. of Nodes | 78,193 | 311,649 | 1,244,353 | 1584 | 8192 |
| No. of Elements | 152,576 | 610,304 | 2,441,216 | 2956 | 16,641 |
| Mesh size | 5.8732 × 10−3 | 2.9366 × 10−3 | 1.4683 × 10−3 | 4.0020 × 10−2 | 2.2097 × 10−2 |
| CPU times(s) | 189.708 | 2386.555 | 10,969.14 | 4.494 | 7.042 |
| 1 | 5.2661 × 107 | 5.3223 × 107 | 5.3222 × 107 | 5.2717 × 107 | 1.0670 × 10−2 | 1.0661 × 10−2 | 1.0724 × 10−3 |
| 2 | 5.3939 × 107 | 5.4494 × 107 | 5.4493 × 107 | 5.3964 × 107 | 1.0286 × 10−2 | 1.0281 × 10−2 | 4.7619 × 10−4 |
| 3 | 5.7439 × 107 | 5.8404 × 107 | 5.8404 × 107 | 5.7817 × 107 | 1.6808 × 10−2 | 1.6811 × 10−2 | 6.5881 × 10−3 |
| 4 | 9.5413 × 107 | 9.7544 × 107 | 9.7542 × 107 | 9.5894 × 107 | 2.2329 × 10−2 | 2.2309 × 10−2 | 5.0331 × 10−3 |
| 5 | 1.0611 × 108 | 1.0901 × 108 | 1.0901 × 108 | 1.0694 × 108 | 2.7287 × 10−2 | 2.7271 × 10−2 | 7.7943 × 10−3 |
| 6 | 1.0691 × 108 | 1.0958 × 108 | 1.0958 × 108 | 1.0759 × 108 | 2.4994 × 10−2 | 2.4982 × 10−2 | 6.3768 × 10−3 |
| 7 | 1.4371 × 108 | 1.4633 × 108 | 1.4634 × 108 | 1.4253 × 108 | 1.8182 × 10−2 | 1.8281 × 10−2 | 8.2089 × 10−3 |
| 8 | 1.6295 × 108 | 1.6894 × 108 | 1.6894 × 108 | 1.6416 × 108 | 3.6780 × 10−2 | 3.6763 × 10−2 | 7.4778 × 10−3 |
| 9 | 1.7207 × 108 | 1.7875 × 108 | 1.7874 × 108 | 1.7340 × 108 | 3.8855 × 10−2 | 3.8756 × 10−2 | 7.7410 × 10−3 |
| 10 | 1.9365 × 108 | 1.9909 × 108 | 1.9912 × 108 | 1.9214 × 108 | 2.8139 × 10−2 | 2.8296 × 10−2 | 7.7486 × 10−3 |
| 11 | 1.9586 × 108 | 2.0125 × 108 | 2.0129 × 108 | 1.9418 × 108 | 2.7528 × 10−2 | 2.7706 × 10−2 | 8.6053 × 10−3 |
| 12 | 2.0096 × 108 | 2.0603 × 108 | 2.0602 × 108 | 1.9842 × 108 | 2.5264 × 10−2 | 2.5225 × 10−2 | 1.2594 × 10−2 |
| 13 | 2.0772 × 108 | 2.1380 × 108 | 2.1379 × 108 | 2.0566 × 108 | 2.9239 × 10−2 | 2.9189 × 10−2 | 9.9406 × 10−3 |
| 14 | 2.3611 × 108 | 2.4797 × 108 | 2.4798 × 108 | 2.3746 × 108 | 5.0248 × 10−2 | 5.0258 × 10−2 | 5.7048 × 10−3 |
| 15 | 2.3730 × 108 | 2.4801 × 108 | 2.4801 × 108 | 2.3797 × 108 | 4.5131 × 10−2 | 4.5128 × 10−2 | 2.8153 × 10−3 |
| 16 | 2.6545 × 108 | 2.7806 × 108 | 2.7801 × 108 | 2.6467 × 108 | 4.7519 × 10−2 | 4.7314 × 10−2 | 2.9231 × 10−3 |
| 17 | 2.6825 × 108 | 2.8063 × 108 | 2.8058 × 108 | 2.6698 × 108 | 4.6167 × 10−2 | 4.5985 × 10−2 | 4.7024 × 10−3 |
| 18 | 2.7455 × 108 | 2.8590 × 108 | 2.8601 × 108 | 2.7183 × 108 | 4.1308 × 10−2 | 4.1710 × 10−2 | 9.9075 × 10−3 |
| 19 | 2.9220 × 108 | 3.0341 × 108 | 3.0357 × 108 | 2.8732 × 108 | 3.8361 × 10−2 | 3.8907 × 10−2 | 1.6710 × 10−2 |
| 20 | 3.1367 × 108 | 3.3030 × 108 | 3.3034 × 108 | 3.1175 × 108 | 5.3010 × 10−2 | 5.3151 × 10−2 | 6.1318 × 10−3 |
| 1 | 5.3160 × 107 | 5.3086 × 107 | 5.3160 × 107 | 5.3160 × 107 | 1.3786 × 10−3 | 1.7089 × 10−5 | 1.7067 × 10−5 |
| 2 | 5.4399 × 107 | 5.4457 × 107 | 5.4457 × 107 | 5.4378 × 107 | 1.0743 × 10−3 | 1.0743 × 10−3 | 3.8148 × 10−4 |
| 3 | 5.8077 × 107 | 5.8322 × 107 | 5.8322 × 107 | 5.8232 × 107 | 4.2239 × 10−3 | 4.2237 × 10−3 | 2.6614 × 10−3 |
| 4 | 9.6716 × 107 | 9.7381 × 107 | 9.7381 × 107 | 9.7141 × 107 | 6.8773 × 10−3 | 6.8766 × 10−3 | 4.3961 × 10−3 |
| 5 | 1.0787 × 108 | 1.0880 × 108 | 1.0880 × 108 | 1.0849 × 108 | 8.6054 × 10−3 | 8.6043 × 10−3 | 5.7417 × 10−3 |
| 6 | 1.0850 × 108 | 1.0939 × 108 | 1.0939 × 108 | 1.0908 × 108 | 8.1857 × 10−3 | 8.1845 × 10−3 | 5.3671 × 10−3 |
| 7 | 1.4616 × 108 | 1.4566 × 108 | 1.4626 × 108 | 1.4626 × 108 | 3.4053 × 10−3 | 6.7067 × 10−4 | 6.6842 × 10−4 |
| 8 | 1.6648 × 108 | 1.6856 × 108 | 1.6856 × 108 | 1.6734 × 108 | 1.2495 × 10−2 | 1.2493 × 10−2 | 5.1830 × 10−3 |
| 9 | 1.7602 × 108 | 1.7835 × 108 | 1.7835 × 108 | 1.7705 × 108 | 1.3234 × 10−2 | 1.3231 × 10−2 | 5.8670 × 10−3 |
| 10 | 1.9796 × 108 | 1.9889 × 108 | 1.9889 × 108 | 1.9783 × 108 | 4.6836 × 10−3 | 4.6863 × 10−3 | 6.7044 × 10−4 |
| 11 | 2.0011 × 108 | 2.0110 × 108 | 2.0110 × 108 | 2.0001 × 108 | 4.9561 × 10−3 | 4.9593 × 10−3 | 5.0851 × 10−4 |
| 12 | 2.0514 × 108 | 2.0583 × 108 | 2.0583 × 108 | 2.0472 × 108 | 3.3922 × 10−3 | 3.3926 × 10−3 | 2.0393 × 10−3 |
| 13 | 2.1250 × 108 | 2.1364 × 108 | 2.1364 × 108 | 2.1242 × 108 | 5.3798 × 10−3 | 5.3795 × 10−3 | 3.6217 × 10−4 |
| 14 | 2.4376 × 108 | 2.4743 × 108 | 2.4743 × 108 | 2.4487 × 108 | 1.5069 × 10−2 | 1.5066 × 10−2 | 4.5500 × 10−3 |
| 15 | 2.4417 × 108 | 2.4748 × 108 | 2.4748 × 108 | 2.4435 × 108 | 1.3557 × 10−2 | 1.3554 × 10−2 | 7.3713 × 10−4 |
| 16 | 2.7426 × 108 | 2.7759 × 108 | 2.7759 × 108 | 2.7482 × 108 | 1.2153 × 10−2 | 1.2149 × 10−2 | 2.0420 × 10−3 |
| 17 | 2.7688 × 108 | 2.8023 × 108 | 2.8023 × 108 | 2.7810 × 108 | 1.2093 × 10−2 | 1.2090 × 10−2 | 4.4090 × 10−3 |
| 18 | 2.8280 × 108 | 2.8554 × 108 | 2.8554 × 108 | 2.8340 × 108 | 9.6712 × 10−3 | 9.6768 × 10−3 | 2.1110 × 10−3 |
| 19 | 3.0166 × 108 | 3.0328 × 108 | 3.0329 × 108 | 3.0071 × 108 | 5.3653 × 10−3 | 5.3745 × 10−3 | 3.1553 × 10−3 |
| 20 | 3.2539 × 108 | 3.2980 × 108 | 3.2980 × 108 | 3.2695 × 108 | 1.3563 × 10−2 | 1.3565 × 10−2 | 4.8052 × 10−3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, M.; Ye, S.; Ma, Q. A Multi-Scale Approach for the Piezoelectric Modal Analysis in Periodically Perforated Structures. Mathematics 2025, 13, 3967. https://doi.org/10.3390/math13243967
Zhang M, Ye S, Ma Q. A Multi-Scale Approach for the Piezoelectric Modal Analysis in Periodically Perforated Structures. Mathematics. 2025; 13(24):3967. https://doi.org/10.3390/math13243967
Chicago/Turabian StyleZhang, Mengyu, Shuyu Ye, and Qiang Ma. 2025. "A Multi-Scale Approach for the Piezoelectric Modal Analysis in Periodically Perforated Structures" Mathematics 13, no. 24: 3967. https://doi.org/10.3390/math13243967
APA StyleZhang, M., Ye, S., & Ma, Q. (2025). A Multi-Scale Approach for the Piezoelectric Modal Analysis in Periodically Perforated Structures. Mathematics, 13(24), 3967. https://doi.org/10.3390/math13243967








