Exploring Stability and Chaos in the Fractional-Order Arneodo System via Grünwald–Letnikov Scheme

Abstract

This paper investigates the dynamical properties of the fractional-order Arneodo system using a Grünwald–Letnikov-based numerical discretization. Fractional-order operators introduce memory and hereditary effects, enabling a more realistic description than classical integer-order models. The local stability of equilibrium points is examined through eigenvalue analysis of the Jacobian matrix, along with dissipativity conditions and the emergence of complex attractors. A comprehensive dynamical investigation is presented through phase portraits, time series, Lyapunov exponents, and bifurcation diagrams for varying fractional orders. Numerical findings demonstrate the emergence of new chaotic and hyperchaotic attractors. The results confirm that the fractional order strongly influences the system’s stability, sensitivity, and complexity. Our results confirm the relevance of fractional-order modeling in applications, such as secure communication, random number generation, and complex system analysis.

1. Introduction

Fractional differential equations are currently indispensable tools for describing chaotic dynamical systems across a wide range of disciplines. Given the rapid advancement of fractional calculus, considerable attention has been directed toward its study, and a wide variety of fractional-order extensions of classical chaotic models has been developed [1,2,3,4].

Fractional-order chaotic systems typically exhibit richer and more complex dynamical behavior than their integer-order counterparts. They also tend to be more sensitive to initial conditions and system parameters, which makes them very appropriate to model real-world complex processes. The ability of fractional-order models to embody memory effects and long-term dependencies has opened up promising applications for these systems in economics, engineering, meteorology, sociology, medicine, chemistry, and ecology [5,6,7,8]. The ability to capture history-dependent dynamics is one of the key advantages of fractional modeling.

Interestingly, nonlinear fractional-order systems can exhibit chaotic behavior even for a total system order of less than three, a result that departs from the classical integer-order theory, where continuous-time chaos typically requires a system order greater than three [9]. This unique property has motivated researchers to reformulate many well-known chaotic systems within the fractional framework. Some of these formulations involve Chua, Lorenz, Chen, Lü, unified chaotic, Rössler, and Liu systems [10,11,12,13,14,15,16]. These formulations correspond to several distinct fractional operators. The Caputo, Riemann–Liouville, Caputo–Fabrizio, and Atangana–Baleanu derivatives use different kernel functions—the power-law, exponential, or Mittag–Leffler—for generalizing the classical derivative. This has been demonstrated in recent studies that model complex chaotic behavior using these operators [17,18,19].

Among these, the Caputo derivative naturally incorporates memory and hereditary effects, making it particularly effective for accurately modeling complex dynamical processes [20,21]. In comparison with other kinds of operators, the numerical stability, accuracy, smoothness of solutions, and convergence properties of the Caputo derivative make it more desirable [22,23]. On account of these merits, it has been applied quite successfully in many fields of science, including epidemiology, for modeling dynamic systems while providing deeper insight into the dynamics than classical approaches [24,25].

The Figure 1 depicts the study of fractional-order Arneodo systems using the Grünwald–Letnikov scheme. In the left branch, dynamical analysis is performed with the stability of equilibria together with the evaluation of the eigenvalues; the middle one shows the main effects of fractional orders on numerical solutions and sensitivity to initial conditions; finally, the right part presents some numerical simulations: phase portraits, time series, Lyapunov exponents, and bifurcation diagrams. This structure, therefore, shows how fractional calculus combined with numerical methods effectively captures stability, sensitivity, and complex dynamical behaviors.

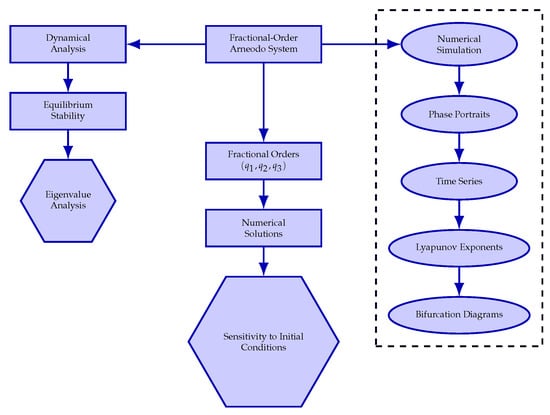
Figure 1. Dynamical analysis of the fractional-order Arneodo system.

The classical Arneodo system [26] is one of the well-known nonlinear chaotic systems, which has become a paradigm for studying complex oscillations and the bifurcation behavior of dynamical systems. Because its chaotic characteristics are well established, the Arneodo system is used to validate new numerical techniques, as described by

$$\begin{array}{cc}\hfill {\displaystyle \frac{du}{dt}}& =v,\hfill \\ \hfill {\displaystyle \frac{dv}{dt}}& =w,\hfill \\ \hfill {\displaystyle \frac{dw}{dt}}& =-au-bv-cw+d{u}^3,\hfill \end{array}$$

(1)

Following the parameter settings in [9], the system parameters are chosen as $a=-5.5$, $b=3.5$, $c=1$, and $d=-1$.

Parameters a, b, c, and d in system (1) determine a balance between linear restoring forces, damping, and nonlinear excitation. The linear stiffness of the system is controlled by a, viscous damping is represented by b, whereas c governs the decay rate of the third state variable. Finally, the parameter d scales the cubic nonlinear term $u^3$ that generates complex oscillatory behavior and chaos in the Arneodo model.

The fractional-order Arneodo system [27] incorporates memory effects and hereditary properties through the use of fractional-order derivatives, hence allowing a richer and more realistic description of real-world physical and biological processes. Studying fractional versions enables the investigation of enhancing system stability analysis, chaos prediction, and long-term behavior modeling using fractional calculus. Such models are used in secure communications, signal processing, biological modeling, neural dynamics, and control engineering, where chaotic behavior and memory effects play an essential role, as described by

$$\begin{array}{cc}\hfill {\displaystyle \frac{d^{q}u}{d{t}^q}}& =v,\hfill \\ \hfill {\displaystyle \frac{d^{q}v}{d{t}^q}}& =w,\hfill \\ \hfill {\displaystyle \frac{d^{q}w}{d{t}^q}}& =-au-bv-cw+d{u}^3,\hfill \end{array}$$

(2)

where $q=(q_1,q_2,q_3)$, $0<q_i\le 1$, denotes the fractional orders of the system.

The novelty in this paper is the introduction and analysis of a new fractional-order Arneodo system that shows previously unreported dynamical patterns and attractor geometries.

Next, the paper employs the Grünwald–Letnikov scheme to illustrate how the fractional order q influences stability, sensitivity, and the occurrence of chaos, including the appearance of new hyperchaotic regimes. Stability is checked by the eigenvalues of the Jacobian matrix, and the results clearly indicate the dependence of the memory effects on the increased complexity of the system’s dynamics; such results have important implications for encryption, random number generation, and the modeling of complex nonlinear processes. The contribution of this work can be summarized as follows:

We provide the first comprehensive investigation of the fractional-order Arneodo system using the Grünwald–Letnikov scheme and demonstrate how the fractional order q fundamentally reshapes the dynamics in this system. We demonstrate, by means of a detailed phase–space and time–series analysis, that the decrease in q significantly enhances memory effects, hence increasing dispersion and complexity of the chaotic attractor.

• In this presentation, we will provide the theoretical explanation of these transitions using a stability analysis supported by Jacobian eigenvalues.
• These results demonstrate that the fractional order q represents an effective control parameter for adjusting nonlinear behavior, making available potential paths towards applications of secure communication, random number generation, and hardware implementation with FPGA platforms.

The paper is organized as follows: Section 2 presents the fractional-order formulation and dynamical analysis framework; Section 3 describes the Grünwald–Letnikov numerical method; Section 4 presents the numerical solutions; Section 5, Section 6 and Section 7 analyze the system dynamics through Lyapunov exponents, and bifurcations; Section 8 discusses the obtained results and its implications; finally, the conclusions are provided in Section 9.

2. Fractional-Order Dynamical Analysis

In this section, we analyze the dynamical behavior of the fractional-order Arneodo-type system under variations in the fractional order q, initial conditions, and parameter values. The system parameters are fixed as

$$a=-5.5,b=3.5,c=1,d=-1.$$

2.1. Jacobian Matrix

The vector field of system (1) is

$$F(u,v,w)=\left(v,w,-au-bv-cw+d{u}^3\right),$$

and the Jacobian matrix is given by

$$J(u,v,w)=\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ -(a-3d{u}^2)& -b& -c\end{array}\right].$$

(3)

Equilibrium $E_0$

Setting the right-hand side of system (1) to zero yields

$$v=0,w=0,-au-c·0+d{u}^3=0.$$

Hence,

$$u(d{u}^2-a)=0.$$

Thus, the system admits the following equilibria:

$$E_0=(0,0,0),E_1=\left(\pm \sqrt{{\displaystyle \frac{a}{d}}},0,0\right).$$

Using the chosen parameters $a=-5.5$ and $d=-1$, we obtain

$$E_1=\left(\pm \sqrt{5.5},0,0\right)=(\pm 2.3452,0,0).$$

Jacobian at $E_0=(0,0,0)$:

$$J\left(E_0\right)=\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ 5.5& -3.5& -1\end{array}\right]$$

Characteristic polynomial at $E_0$:

$${\lambda }^3+{\lambda }^2+3.5\lambda -5.5=0$$

Eigenvalues at $E_0$:

$$\begin{array}{c}\hfill {\lambda }_1=1,{\lambda }_{2,3}=-1\pm {\displaystyle \frac{3\sqrt{2}}{2}}i.\end{array}$$

Jacobian at $E_1=(\pm 2.3452,0,0)$:

At these points,

$$-(a-3d{u}^2)=-(-5.5-3(-1)\left(u^2\right))=-(-5.5+3u^2).$$

Since $u^2=5.5$,

$$-(-5.5+3(5.5\left)\right)=-11.$$

Thus,

$$J\left(E_1\right)=\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ -11& -3.5& -1\end{array}\right]$$

Characteristic polynomial at $E_1$:

$${\lambda }^3+{\lambda }^2+3.5\lambda +11=0$$

Eigenvalues at $E_1$:

$$\begin{array}{c}\hfill {\lambda }_1=-2,{\lambda }_{2,3}={\displaystyle \frac{1}{2}}\pm {\displaystyle \frac{\sqrt{21}}{2}}i.\end{array}$$

2.2. Local Stability of Equilibria

(a)

Classical case $q=1$

For an integer-order system, an equilibrium is locally asymptotically stable if and only if all eigenvalues have negative real parts.

At $E_0$: one eigenvalue $=1>0$ → unstable saddle-focus.

At $E_1$: two eigenvalues have real part $0.5>0$ → unstable saddle-foci.

So for $q=1$, all equilibria are unstable.

(b)

Fractional order $0<q<1$

For the commensurate fractional-order system with $0<q<1$, an equilibrium point E is locally asymptotically stable if all eigenvalues $\lambda$ satisfy

$$|arg\left(\lambda \right)|>{\displaystyle \frac{q\pi }{2}}.$$

Stability of $E_0$:

Minimum argument:

$$|arg\left({\lambda }_1\right)|=0^{\circ },$$

giving no range of q that satisfies Matignon’s condition. Thus, $E_0$ is unstable for all $0<q<1$.

Stability of $E_1$:

Minimum argument:

$$|arg\left({\lambda }_2\right)|\approx {\mathrm{77.7.7.0}}^{\circ }\left(1.356\mathrm{rad}\right),$$

so the stability bound is

$$q<{\displaystyle \frac{2\times 1.356}{\pi }}\approx 0.863.$$

Hence, the equilibrium points $E_1$ are locally asymptotically stable for

$$0<q<0.863.$$

(c)

Incommensurate fractional orders

For the incommensurate case with different orders $q_1,q_2,q_3$, the linearized characteristic matrix is

$$\Delta \left(\lambda \right)=diag\left({\lambda }^{M{q}_1},{\lambda }^{M{q}_2},{\lambda }^{M{q}_3}\right)-J\left(E\right),$$

where M is the least common multiple of the denominators of $q_1,q_2,q_3$. The equilibrium is asymptotically stable if all eigenvalues ${\lambda }_i$ satisfy

$$|arg\left({\lambda }_i\right)|>{\displaystyle \frac{\pi }{2M}}.$$

Remark

The system exhibits transitions from stability to oscillatory instability and chaos as the fractional order q increases, consistent with the emergence of memory-driven complex dynamics.

2.3. Divergence of the Fractional-Order Arneodo System

The vector field of the system is described by

$$F=(F_1,F_2,F_3)=\left(v,w,-au-bv-cw+d{u}^3\right).$$

(4)

To determine the divergence, we compute

$$\nabla ·F=F_{1}u+F_{2}v+F_{3}w.$$

(5)

Since $F_1=v$, $F_2=w$, and $F_3=-au-bv-cw+d{u}^3$, we obtain

$$F_{1}u=0,F_{2}v=0,F_{3}w=-c.$$

(6)

Thus, the divergence becomes

$$\nabla ·F=-c,$$

(7)

which shows that the system is dissipative whenever $c>0$, since the phase–space volume contracts exponentially.

3. Grünwald–Letnikov Numerical Method

The GL approach is used because of its simplicity, numerical robustness, and suitability for the simulation of fractional-order dynamical systems. Despite the widespread use of the GL method, several alternative schemes outperform it for stiff or highly nonlinear systems. As an example, the tuned two-stage Runge–Kutta method M2sFRK introduced in [28] is significantly more efficient than GL. Another promising strategy can be found in [29], which provides additional numerical advantages and forms a strong basis for comparative studies.

Fractional calculus generalizes classical differentiation and integration to non-integer orders through the operator ${}_{a}D_t^r$, defined over the interval $[a,t]$. Several formulations exist, with the Riemann–Liouville (RL) and Grünwald–Letnikov (GL) definitions being among the most commonly adopted in modeling and numerical simulation [30,31]. The RL derivative is expressed as

$${}_{a}D_t^{r}f\left(t\right)={\displaystyle \frac{1}{\Gamma (n-r)}}{\displaystyle \frac{d^n}{d{t}^n}}{\int }_a^t{\displaystyle \frac{f\left(\tau \right)}{{(t-\tau )}^{r-n+1}}}d\tau ,$$

(8)

while the GL derivative is defined through a limit of backward finite differences:

$${}_{a}D_t^{r}f\left(t\right)=\underset{h\to 0}{lim}{h}^{-r}\sum _{j=0}^{⌊{\displaystyle \frac{t-a}{h}}⌋}{(-1)}^j\left({\displaystyle \genfrac{}{}{0pt}{}{r}{j}}\right)f(t-jh).$$

(9)

Podlubny [32] provides a detailed interpretation of the physical and geometric meaning behind fractional differentiation and integration. The RL and GL formulations are mathematically equivalent, and the GL form serves as the foundation for the discrete numerical implementation used in this study.

For numerical computation of the fractional-order derivative at the discrete time instant $t=ih$, we adopt the GL-based approximation

$$\left({\displaystyle \frac{i-L_m}{h}}\right)D_{ih}^{r}f\left(t\right)\approx h^{-r}\sum _{j=0}^i{(-1)}^j\left({\displaystyle \genfrac{}{}{0pt}{}{r}{j}}\right)f_{i-j},$$

(10)

where $L_m$ is the memory length, h the time step, and ${(-1)}^j\left({\displaystyle \genfrac{}{}{0pt}{}{r}{j}}\right)$ are the binomial coefficients $c_j^{\left(r\right)}$. These coefficients are recursively computed [33] using

$$\begin{array}{cc}\hfill c_0^{\left(r\right)}& =1,\hfill \\ \hfill c_j^{\left(r\right)}& =\left(1-{\displaystyle \frac{1+r}{j}}\right)c_{j-1}^{\left(r\right)},j\ge 1.\hfill \end{array}$$

(11)

Applying (11) to the fractional-order system (2) leads to a time-stepping update expressed in a finite-impulse-response (FIR) form of the GL method. Letting $N=\lfloor T_{\mathrm{sim}}/h\rfloor$, the discrete solution is obtained from

$$\begin{array}{cc}\hfill u_i& =w_{i-1}{h}^{q_1}-\sum _{j=\nu }^i{c}_j^{\left(q_1\right)}{u}_{i-j},\hfill \\ \hfill v_i& =w_{i-1}{h}^{q_2}-\sum _{j=\nu }^i{c}_j^{\left(q_2\right)}{v}_{i-j},\hfill \\ \hfill w_i& =\left(-a{u}_{i-1}-b{v}_{i-1}-c{w}_{i-1}+d{u}_{i-1}^3\right)h^{q_3}-\sum _{j=\nu }^i{c}_j^{\left(q_3\right)}{w}_{i-j},\hfill \end{array}$$

(12)

where $q_1,q_2,q_3$ denote the fractional derivative orders, $\overrightarrow{q}=(q_1,q_2,q_3)$ is the system order vector, and $c_j^{\left(q\right)}$ are the binomial weights obtained from (11). The lower summation index $\nu$ reflects the following memory truncation:

$$\nu =\left\{\begin{array}{cc}1,\hfill & i<L_m/h,\hfill \\ L_m/h,\hfill & i\ge L_m/h,\hfill \end{array}\right.$$

or simply $\nu =1$ for all i when the short-memory principle is not used. For numerical experiments, the simulation horizon is set to $T_{\mathrm{sim}}=1.5\mathrm{s}$ with a time increment $h=0.005$.

4. Numerical Solutions

The numerical solutions for system (2) given in Table 1, Table 2 and Table 3 represent the effect of fractional orders on the dynamics of the fractional-order Arneodo system. In the case of $(q_1,q_2,q_3)=(0.97,0.97,0.96)$ depicted in Table 1, states u, v, and w exhibit initial small oscillations and moderate growth. Divergence becomes distinctive only at later times due to the memory effect inherent in fractional dynamics. For $(q_1,q_2,q_3)=(0.96,0.96,0.96)$ as shown in Table 2, larger amplitude variations are accompanied by abrupt transitions in the system. This signals high sensitivity and chaotic behavior. In the mixed-order case $(q_1,q_2,q_3)=(0.97,0.96,0.95)$ shown in Table 3, solutions exhibit a mixture of behaviors from the previous cases: an initial moderate growth followed by a chaotic oscillation and high divergence in w; that means that non-uniform orders of fractions enhance the richness of dynamics. Hence, these results confirm that fractional orders have a significant influence on memory, sensitivity to initial conditions, and the onset of chaos in the system, whereas the numerical scheme used, namely of Grünwald-Letnikov scheme, is effective enough to catch such intricate dynamics.

Table 1. Solutions of system (2) for $(q_1,q_2,q_3)=(0.97,0.97,0.96)$.

t	u	v	w
1	0.084866402	−0.000359913	−0.352684968
2	0.029306692	−0.014764026	0.154806615
3	0.088279446	0.114983775	0.098081449
4	0.265233522	0.266903696	0.258663301
5	0.720892715	0.717896785	0.684585872
6	1.831494725	1.510460716	0.557768566
7	2.840953519	−0.320884293	−4.456545165
ABM	2.848573043	−0.320827460	−4.456422481

Table 2. Solutions of system (2) for $(q_1,q_2,q_3)=(0.96,0.96,0.96)$.

t	u	v	w
1	0.232508643	0.240651821	0.251331708
2	0.649028338	0.660051456	0.641785412
3	1.694547355	1.472048881	0.740915275
4	2.844600299	0.050174902	−4.218399192
5	1.168512325	−1.639973110	3.096412222
6	1.772563229	2.414867495	2.506844630
7	3.244323515	−2.007757272	−11.172282015
ABM	3.248662505	−2.011211727	−11.128636724

Table 3. Solutions of system (2) for $(q_1,q_2,q_3)=(0.97,0.96,0.95)$.

t	u	v	w
1	0.256492801	0.261113269	0.272858630
2	0.706399515	0.707266309	0.669360217
3	1.806973815	1.505196683	0.596901105
4	2.896784631	−0.276724010	−4.710927605
5	0.996149861	−1.780519168	3.702558690
6	1.466933645	2.340022923	2.410073621
7	3.438597118	−0.670632299	−10.351087789
ABM	3.438284188	−0.675353571	−10.310030545

We consider mixed fractional orders $(q_1,q_2,q_3)$ for the state variables to capture heterogeneous memory effects inherent in system components. Using different orders allows each variable to retain past information to a different degree, recognizing that some of the components may evolve on faster or slower time scales. This asymmetry makes more sense from both a modeling and physical perspective, as it offers greater freedom when modeling real-world systems where the model variables may exhibit different hereditary properties. It may also reveal more complex dynamics, including the emergence of hyperchaotic regimes not observable in the case of symmetric fractional orders. Mixed orders enhance the ability of the model to describe complex dynamics dependent on memory and provide deeper insight into the memory versus nonlinearity interplay. Table 1, Table 2 and Table 3 compare the numerical solutions of system (2) with the Adams–Bashforth–Moulton method for the respective fractional orders $q=0.97$, $q=0.96$, and $q=0.95$. In all these cases, it is seen that the proposed scheme is in excellent agreement with the ABM reference values, with minor deviations from the reference solution appearing only in the fourth or fifth decimal place. This demonstrates the accuracy and stability of the method at different orders of the fractional operator.

5. Dynamical Analysis

This section makes use of attractors and Lyapunov exponents in order to describe the sensitivity of the Lorenz system (2) quantitatively to initial conditions. The time-series plot shows the system’s chaotic behavior with no repeated patterns, while the bifurcation diagram summarizes how a small change in parameters can trigger large qualitative changes and marks the onset of chaos. The figures were drawn with the help of the package of MATLAB software package (R2024a).

5.1. Choas Behavior

The phase–space projections shown in Figure 2, Figure 3 and Figure 4 outline that changing the fractional orders q alters both the geometrical structure and the complexity of the system’s trajectories. For $q=[0.97,0.97,0.96]$, the attractor has well-defined lobes with smooth rotating motion and reflects strongly chaotic but organized geometry. When q is reduced to $q=[0.96,0.96,0.96]$, the trajectories of the system become a little more compressed and less symmetric, signaling that the intensity of chaos decreases because lower fractional orders have stronger memory effects. On the other hand, in the mixed order case $q=[0.97,0.96,0.95]$, one obtains an attractor that is distinctly more irregular, underlined by much longer loops and larger dispersion, once again pointing to the sensitive dependence of dynamics on the fractional orders. Finally, all these results confirm that small fluctuations in q substantially alter the attractor geometry and modify the degree of chaotic behavior, confirming that the fractional order is one of the most important determinants of the overall system dynamics.

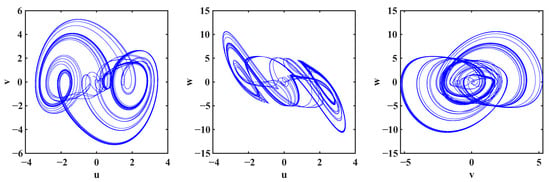
Figure 2. Projections of the system in phase space for $q=[0.97,0.97,0.96]$ with I.C. $(0.1,0.1,0.1)$.

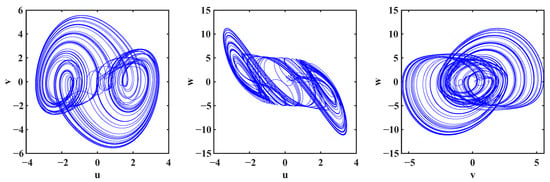
Figure 3. Phase–space projections for $q=[0.96,0.96,0.96]$ with I.C. $(0.1,0.1,0.1)$.

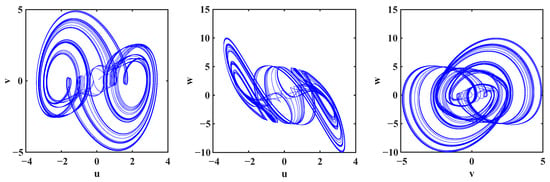
Figure 4. Phase–space trajectories for $q=[0.97,0.96,0.95]$ with I.C. $(0.1,0.1,0.1)$.

5.2. Time-Series Dynamics

The time-series evolution of the state variables $u\left(t\right)$, $v\left(t\right)$, and $w\left(t\right)$ with regard to different fractional orders, as depicted in Figure 5, Figure 6 and Figure 7, shows the dynamic behavior of the system. In particular, for the two parameter sets $q=[0.97,0.97,0.96]$ and $q=[0.97,0.96,0.95]$, the system shows dense, aperiodic oscillatory behavior that is typical of chaotic dynamics. Notice that the state trajectories do not converge to either a fixed equilibrium point or a simple limit cycle; instead, they fluctuate irregularly within a bounded range over the simulation interval $t\in [0,300]$. Such sensitivity to the fractional orders q indicates that even small variations in the derivative indices yield different trajectories that never repeat but retain the same nature in the chaotic attractor.

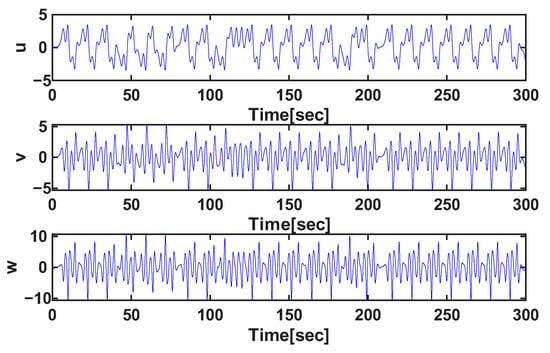
Figure 5. Projections of the phase space for $q=[0.97,0.97,0.96]$ starting I.C. $(0.1,0.1,0.1)$.

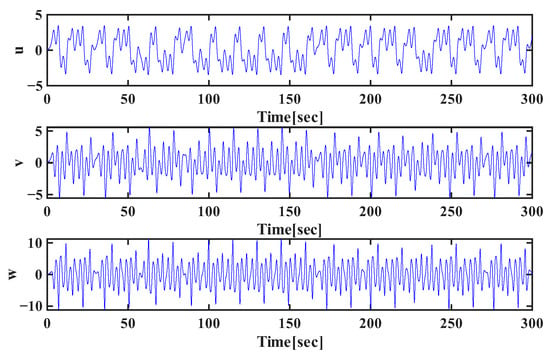
Figure 6. Phase–space projections for $q=[0.97,0.97,0.96]$ with I.C. $(0.1,0.1,0.1)$.

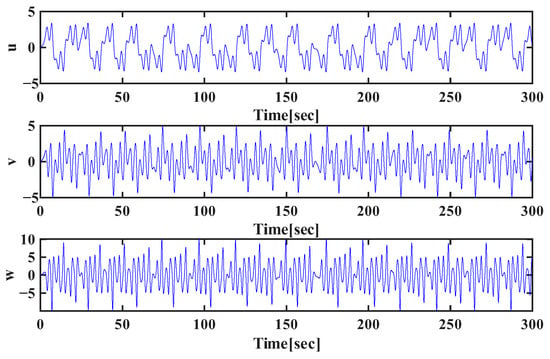
Figure 7. Phase–space trajectories corresponding to $q=[0.97,0.96,0.95]$ with I.C. $(0.1,0.1,0.1)$.

6. Lyapunov Exponent Analysis

In order to quantify the rich dynamics apparent in the phase portraits, the finite-time LEs were calculated, and the time evolution is shown in Figure 8. The plots indicate the convergence as the simulation time approaches $t=300$. In those cases for which chaos appears, the largest Lyapunov exponent ($L{E}_1$) converges to a value that is strictly positive, yielding the unquestionable signature of sensitivity to initial conditions and chaotic divergence. On the other hand, the sum of the LEs is negative ($\sum L{E}_i<0$), which confirms the dissipative nature of the system, with its trajectories flowing on a bounded strange attractor within the phase space.

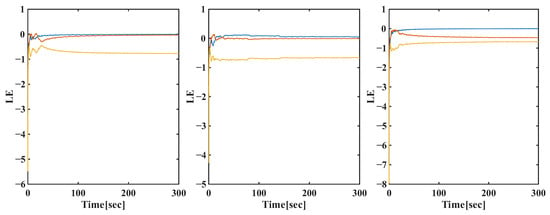
Figure 8. Lyapunov exponent dynamics for $q=0.95$, $0.96$, and $0.97$ (left to right).

7. Bifurcation Analysis

In this section, we investigate bifurcation analysis. Figure 9 shows the bifurcation diagram of the fractional-order Arneodo system versus the fractional order q, indicating a very complicated and, in fact, non-monotonic dependence on this control parameter. One can appreciate that the system goes through multiple transitions between stable periodic motion and robust chaos as the parameter q increases from $0.9$ to 1. For $q\ge 0.96$, one can observe a broad chaotic state as the scattering of the maximum and minimum values of u becomes dense. On the contrary, when q decreases, this system enters narrow stability windows, such as for $0.91<q<0.94$, where continuous and well-defined branches evolve through various bifurcations, corresponding to periodic orbits appearing after different bifurcations.

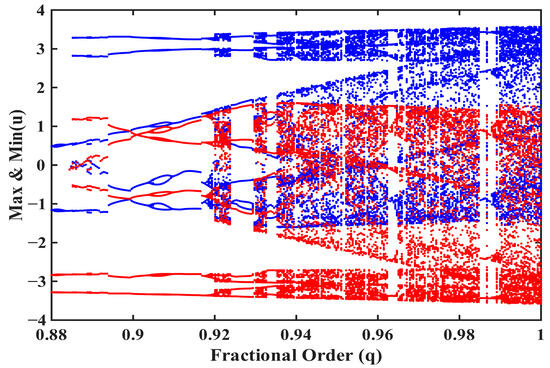
Figure 9. Bifurcation diagram of system (2) under fractional-order dynamics.

The periodic window for $q\in [0.882,0.886]$ is thus a real dynamical property of the system, confirmed by consistent time-series and phase–space trajectories. Tests with smaller step sizes and with different memory lengths demonstrated that its position is stable, and so it is not seriously affected by the Grünwald–Letnikov discretization. The window illustrates the sensitivity of fractional-order systems to small changes in their parameters. More detailed bifurcation analysis, including Floquet multipliers, is beyond the scope of the current paper.

8. Discussion

The results obtained in this paper provide a complete insight into the dynamics of the fractional-order Arneodo system under the Grünwald–Letnikov numerical discretization. The nature of fractional-order operators is intrinsically memory-dependent and hereditary, which significantly influences system evolution. It also allows modeling certain real-world dynamical phenomena more accurately than their classical integer-order counterparts. Stability analysis, based on the evaluation of Jacobian matrices for eigenvalues and the conditions of dissipativity, shows that fractional orders are critical in deciding the nature of the system equilibrium and that lower or non-uniform fractional orders may give rise to higher sensitivity and complex dynamics.

Numerical simulations show that these models represent a rich spectrum of behavior, ranging from regular oscillations to chaotic and hyperchaotic attractors. Table 1, Table 2 and Table 3 indicate the sensitivity of the response of the system to fractional orders. Small variations in their order produce very different trajectories with a greater divergence of the solutions and more irregular oscillations for larger time steps. Bifurcation diagrams underlie the complex behaviors developed as a function of fractional orders, confirming the conclusion that fractional dynamics offer more flexibility and finer control over the system’s behavior compared to integer-order models.

In such a context, the Grünwald–Letnikov scheme proves advantageous due to its simplicity, easy implementation, and stability for multi-dimensional fractional systems. In contrast to other methods, it performs discretization of the fractional derivative directly in the time domain and thus naturally preserves the memory effect. Hence, it can reproduce transient dynamics as well as long-term behavior quite accurately. This makes the method especially suitable for investigating sensitive nonlinear systems where the role of memory effects may be significant.

This paper thus confirms that fractional-order modeling, together with the GL numerical approach, enables (i) the accurate prediction of complex dynamics, (ii) the study of chaotic and hyperchaotic regimes, (iii) sensitivity analysis concerning fractional orders, and finally, a flexible framework that can be easily extended to variable-order derivatives, synchronization studies, control strategies, or hardware implementations. These advantages make the approach highly relevant for secure communications, random number generation, analysis of complex systems, and other areas that require the precise modeling of nonlinear dynamics.

It is evident from the above analysis that the fractional-order Arneodo system displays complex dynamics that are sensitive to the fractional orders being used. The GL discretization method successfully computes this phenomenon and provides a powerful, effective, and illustrative numerical approach toward the analysis of nonlinear fractional-order systems. Extensions of this setup can be made by considering variable-order systems, including other numerical approximation methods, or even carrying out experimental validations and practical implementations.

9. Conclusions

This article presents the fractional-order Arneodo system and investigates, using the Grünwald–Letnikov numerical method, the effects of memory on its nonlinear dynamics. The stability analysis, involving both eigenvalue evaluation and dissipativity criteria, confirmed that fractional order plays a crucial role in the determination of the behavior of this system. Various numerical simulations have shown a wide variety of phenomena, including the creation of new chaotic and hyperchaotic attractors, an increased sensitivity to initial conditions, and significant variations in complexity by changing the fractional order. Phase portraits, time series, Lyapunov exponents, and bifurcation diagrams all show that, contrary to its classical integer-order counterpart, the fractional framework provides a richer description and more flexibility. These results confirm that fractional calculus is an appropriate tool for describing complex dynamic phenomena in intricate real systems. The study of other numerical methods, variable-order generalization, and synchronization or control techniques is left for future work. Realistic parameter estimations and hardware implementations, including some engineering applications, could be carried out in the continuation of this work for its practical verification.