A Novel Sub-Abundance Map Regularized Sparse Unmixing Framework Based on Dynamic Abundance Subspace Awareness

Abstract

Sparse unmixing (SU) has become a research hotspot in hyperspectral image (HSI) analysis in recent years due to its interpretable physical mechanisms and engineering practicality. However, traditional SU methods are confronted with two core bottlenecks: Firstly, the high computational complexity of the abundance matrix inversion severely limits algorithmic efficiency. Secondly, the inherent challenges posed by large-scale highly coherent spectral libraries hinder improvement of unmixing accuracy. To overcome these limitations, this study proposes a novel sub-abundance map regularized sparse unmixing (SARSU) framework based on dynamic abundances subspace awareness. Specifically, first of all, we have developed an intelligent spectral atom selection strategy that employs a designed dynamic activity evaluation mechanism to quantify the participation contribution of spectral library atoms during the unmixing process in real time. This enables adaptive selection of critical subsets to construct active subspace abundance maps, effectively mitigating spectral redundancy interference. Secondly, we innovatively integrated weighted nuclear norm regularization based on sub-abundance maps into the model, deeply mining potential low-rank structures within spatial distribution patterns to significantly enhance the spatial fidelity of unmixing results. Additionally, a multi-directional neighborhood-aware dual total variation (DTV) regularizer was designed, which enforces spatial consistency constraints between adjacent pixels through a four directional (horizontal, vertical, diagonal, and back-diagonal) differential penalty mechanism, ensuring abundance distributions comply with physical diffusion laws of ground objects. Finally, to efficiently solve the proposed objective model, an optimization algorithm based on the Alternating Direction Method of Multipliers (ADMM) was developed. Comparative experiments conducted on two simulated datasets and four real hyperspectral benchmark datasets, alongside comparisons with state-of-the-art methods, validated the efficiency and superiority of the proposed approach.

1. Introduction

With the rapid development of hyperspectral imaging technology, hyperspectral remote sensing images have been widely applied in environmental monitoring [1], target detection [2], mineral exploration [3], and other fields. However, due to the insufficient spatial resolution and the spatial complexity of the distribution of materials, there are numerous mixed pixels in hyperspectral images (HSIs) [4]. The existence of mixed pixels hinders the refined application of HSIs [5]. To address the spectral mixing problem and effectively identify the spectral components and their proportions in each mixed pixel, hyperspectral unmixing (HU) technology has emerged and become an important step in the preprocessing of hyperspectral images. Its task is to estimate the spectral reflectance of pure materials (i.e., endmembers) and their proportion (i.e., fractional abundances) from the mixed pixels [6].

Up to now, based on different spectral mixing mechanisms, researchers have proposed the Linear Mixing Model (LMM) [7] and the Nonlinear Mixing Model (NLMM) [8]. The LMM assumes that the mixing of materials occurs at the macroscopic scale, and the incident solar photons interact with only one substance. Attributed to its computational efficiency, analytical tractability, and intuitive physical interpretability, the LMM has been extensively utilized in HU. Therefore, this paper carries out the unmixing research based on the LMM.

In the past few decades, researchers have proposed lots of unmixing methods based on the LMM, which can generally be classified into geometrical, statistical, sparse regression, and emerging methods (such as methods based on Non-negative Tensor Factorization (NTF) and methods based on Deep Learning (DL)). Specifically, geometrical methods are rooted in convex geometry principles and are bifurcated into two primary categories: pure pixel assumption frameworks and non-pure pixel assumption frameworks. Pure pixel methods demand the presence of at least one pure spectral pixel for each endmember within the HSI, where endmembers are identified as the vertices of the convex hull (simplex) in the HSI feature space. The representative algorithms include subspace projection [9] and maximum simplex volume maximization [10]. In contrast, non-pure pixel methods are anchored in the minimum simplex theory [11,12], where endmembers are theoretically estimated by solving for the optimal simplex vertices. This attribute enables the minimum simplex approach to effectively address scenarios with highly mixed spectral data, where conventional pure pixel methods often encounter limitations.

Statistical methods are based on probability and mathematical statistics theory and do not require the pure pixel assumption. The NMF method is the most representative method among them. NMF decomposes the non-negative hyperspectral data matrix into the product of a basis matrix and its coefficient matrix, corresponding to endmembers and abundances, respectively [13,14,15,16]. However, since the NMF model is based on mathematical statistics and optimization, it may obtain virtual endmembers without physical meaning. Moreover, due to the non-convexity of the NMF model, it cannot obtain the global optimal solution. The Non-negative Tensor Factorization (NTF) originates from the tensor decomposition theory and can be divided into four types according to different decomposition methods: Canonical Polyadic Decomposition (CPD) [17], Tucker Decomposition (TD) [18], Block Term Decomposition (BTD) [19,20,21], and Matrix–Vector NTF (MV-NTF). MV-NTF decomposes a tensor into the outer product form of a matrix and a vector [22]. Due to its clear physical meaning, it is widely used in unmixing. DL methods have strong nonlinear feature learning capabilities, can mine deep information in HSI, and can overcome the limitations of single-layer information [23,24]. However, DL methods require an amount of training and computational cost so there are shortcomings in timeliness.

In recent years, sparse unmixing (SU) has attracted widespread attention as a new semi-supervised method, which is mainly inspired by sparse representation theory. Iordache et al. [25] applied the sparse regression model to HSI unmixing and used $l_{1,1}$ regularization to enhance the sparsity of the representation coefficients (i.e., abundances), achieving effective abundance estimation (SUnSAL). Subsequently, the Total Variation (TV) regularizer was introduced into SU to improve the piecewise smoothness of the estimated abundance maps [26]. Inspired by this, many SU models using TV regularization have emerged [27,28,29]. Although TV-based methods can effectively enhance the piecewise smoothness of abundance maps, they increase computational costs. To address this issue, researchers proposed multi-scale methods to replace TV regularization. For example, Ricardo Augusto Borsoi et al. [30] proposed a new multi-scale spatial regularization SU method based on segmentation algorithms, decomposing the unmixing problem into two simple processes in the approximate image domain and the original image domain. Building on this, Taner Ince et al. combined the advantages of coupled spectral–spatial double-weighted SU [31] and designed the coarse abundances obtained from unmixing in the approximate image domain as a spatial–spectral weight matrix and used this weight matrix to design a new multi-scale regularization, achieving effective unmixing results with less time consumption [32]. However, multi-scale unmixing methods are prone to over-smoothing and local image blurring, and they are not as effective as TV regularization in preserving HSI detail features and edge information.

TV regularization excels in uncovering the spatial information within HSI and enhancing the piecewise smoothness of abundances by calculating differences along horizontal and vertical orientations. However, by analyzing the neighborhood structure of HSI, it can be seen that calculating differences only in the horizontal and vertical directions does not fully utilize the neighborhood information of pixels. For example, in addition to horizontal and vertical neighbors, the diagonal and back-diagonal directions are also important spatial structural information for a pixel. Traditional TV ignores this spatial structural prior, resulting in its inability to fully capture the local neighborhood structure of pixels. To address this deficiency, we propose a dual total variation (DTV) regularization method that incorporates differences in the horizontal, vertical, diagonal, and back-diagonal directions of pixels into the model to further encourage the piecewise smoothness of abundances. Similar ideas have also been studied and applied in LF image watermarking [33] and human parsing [34] to enhance structural preservation and spatial consistency.

In addition, methods based on graph Laplacian regularization [35] and joint sparse blocks and low-rank representations [36] have also shown excellent performance in preserving spatial correlations, resulting in highly effective unmixing outcomes. However, in the above methods, constraints are applied to the abundance matrix during SU. In fact, the structure of the abundance matrix is different from the original spatial structure of HSI, while all abundance maps (i.e., each row of the abundance matrix) are consistent with the spatial structure of HSI. Therefore, constraining each abundance map directly is more efficient than applying regularizations to the abundance matrix. However, the abundance matrix is overloaded with an excessive number of abundance maps, and the vast majority of these maps fail to make meaningful contributions to unmixing. In addition, the spectral library has a large scale and high coherence, which hinders the effective estimation of each abundance map. To address this issue, researchers have proposed some methods [37,38,39] to fine-tune the library atoms before unmixing to reduce the size of the spectral library. However, these methods all depend on the quality of the original hyperspectral data because they all learn active atoms from the given HSI. Therefore, these methods often fail to learn the correct active atoms when HSI is severely contaminated by noise. To solve this problem, Shen et al. proposed a layered sparse regression method [40] called LSU. This method decomposes SU into a multi-layer process in which each layer fine-tunes the library atoms. Although LSU can effectively overcome the noise influence of HSI, the design of multi-layer also brings considerable computational load to the model. In view of this, Qu et al. [41] proposed the NeSU-LP method, which divided the SU into two independent and continuous sub-processes, and completed the spectral library pruning at one time to obtain the ideal unmixing effect. However, this method cannot avoid the risk of incorrectly pruned active library atoms. Unlike LSU and NeSU-LP, the FaSUn method [42] considers a contribution matrix of the spectral library to adaptively update the activity of atoms in the library, rather than directly adjusting the spectral library. The combination of the spectral library and the contribution matrix is used to achieve semi-supervised unmixing. Although this approach avoids the noise influence of HSI and the cumbersome process of library atom adjustment, neither the contribution matrix nor its combination with the spectral library or abundance matrix has a clear physical meaning. Moreover, solving the contribution matrix and abundance matrix together brings a non-convex problem.

Different from the above methods, we propose a sub-abundance map regularization SU method that evaluates the activity of all abundance maps and constrains only the most active sub-abundance maps. This approach differs from other methods that directly apply regularization based on SUnSAL and also from semi-supervised methods with unclear physical meanings. Instead, it precisely imposes constraints on the active abundance maps and achieves precise regularization at the abundance map level while reducing the impact of the large scale and high coherence of the spectral library on SU and avoiding the potential risk of losing important library atoms due to spectral library pruning, thereby improving unmixing quality and efficiency. In the proposed model, we use a new singular value threshold-based discrimination method to determine the number of active sub-abundance maps in HSI. At the same time, we introduce weighted nuclear norm regularization and the designed DTV regularization to constrain the low rank and piecewise smoothness of the sub-abundance maps.

The main contributions of this paper are as follows:

• We propose a novel sub-abundance map regularized sparse unmixing (SARSU) framework based on dynamic abundance subspace awareness. This method introduces an intelligent spectral atom selection strategy that employs a dynamically designed activity evaluation mechanism to quantify the participation contribution of spectral library atoms during the unmixing process. By adaptively selecting key subsets, it constructs active subspace abundance maps to effectively mitigate spectral redundancy interference.
• A weighted nuclear norm regularization based on sub-abundance maps was developed to deeply mine potential low-rank structures within spatial distribution patterns, significantly improving the spatial accuracy of unmixing results. Furthermore, a multi-directional neighborhood-aware dual total variation (DTV) regularizer was introduced into the model. Through a four-directional (horizontal, vertical, diagonal, and back-diagonal) differential penalty mechanism, it ensures spatial consistency between adjacent pixels, enabling abundance distributions comply with the physical diffusion laws of ground objects.
• An efficient optimization algorithm based on the Alternating Direction Method of Multipliers (ADMM) was developed. Comprehensive experiments were conducted on two simulated datasets and four real hyperspectral benchmark datasets. The experimental results underwent rigorous analysis, and critical algorithm issues were thoroughly discussed. Through comparative performance analysis with state-of-the-art methods, the effectiveness and superiority of the proposed approach were validated.

The remainder of this paper is organized as follows. The proposed method is presented in Section 2. Section 3 describes our experimental results with simulated hyperspectral datasets. Section 4 describes our experiments with real hyperspectral datasets. Finally, some problem concerning our method is discussed in Section 5, and Section 6 provides some conclusions and some future research directions.

2. Proposed Model

2.1. Sparse Unmixing

Throughout this paper, all matrices appearing are denoted by uppercase letters, and vectors and scalars are denoted by lowercase letters.

The sparse unmixing assumes that an observed pixel spectrum in an HSI can be produced by a linear combination of endmember signatures and their corresponding abundances. Based on the sparse unmixing, the HSI dataset can be expressed as

$$X=AU+G,$$

(1)

where $X\in R_{+}^{l\times n}$ refers to the observation HSI matrix, with l bands and n pixels. Let $A\in R_{+}^{l\times d}$ be a large spectral library, where d is the number of spectral signatures in A, and $U\in R_{+}^{d\times n}$ denotes the abundance matrix corresponding to library A for the observed data X. $G\in R^{l\times n}$ is the error.

In general, two constraints—the abundance non-negative constraint (ANC) and the abundance sum-to-one constraint (ASC)— are added to restrict the SU model and can be formulated as

$$U\ge 0,1_d^{T}U=1_n^T,$$

(2)

where $1_d^T$ and $1_n^T$ represent all-one vectors with size d and size n, respectively.

It is worth mentioning that ASC is strongly criticized in the real scenario [25], so we only add ASC in the synthetic dataset experiments and do not use it in the real dataset experiments.

2.2. Sub-Abundance Map Regularization

In an HSI, the change between materials should be gradual, with only a minimal number of pixels at the edges exhibiting abrupt changes. Consequently, the entire HSI should exhibit piecewise smoothness, a characteristic that should consistently manifest in the abundance map. Furthermore, based on the material distribution patterns observed in real-world scenarios, the distribution of materials within an HSI tends to concentrate in specific areas. This implies that the abundance maps should possess the property of low rank. The piecewise smoothness and low rank of the abundance map offer valuable prior information for precise abundance estimation, ensuring the preservation of both the spatial characteristics of the image and its local similarity. To achieve this, it is both feasible and effective to incorporate a regularization term into the abundance map, thereby constraining its piecewise smoothness and low rank. By combining this with $l_{1,1}$ regularization, an SU problem can be formulated, incorporating both low-rank and piecewise smoothness constraints on the abundance maps, as follows:

$$\begin{array}{c}{\min }_U\frac{1}{2}\left|\right|Y-{AU\left|\right|}_F^2+{\alpha \left|\right|U\left|\right|}_{1,1}+\beta \phi \left(U\right)+\lambda \psi \left(U\right)\hfill \\ s.t.U\ge 0,\hfill \end{array}$$

(3)

where ${\parallel ·\parallel }_F$ is the Frobenius norm, ${\parallel U\parallel }_{1,1}={\sum }_{j=1}^n{\parallel u_j\parallel }_1$, $u_j$ denotes the column of the j-$th$ abundance matrix, and $\phi \left(U\right)$ and $\psi \left(U\right)$ represent low-rank and piecewise smoothness regularization, respectively. At this juncture, we neglect the ASC constraint. In model (3), the first term serves as the reconstruction term, and the second term introduces sparse regularization, while the third and fourth terms represent the low-rank regularization and the piecewise smooth regularization, respectively.

However, for SU, the large-scale spectral library leads to a large number of abundance maps in the abundance matrix, most of which are near-zero abundance maps that do not contribute to the unmixing. Constraining them one by one not only brings a lot of unnecessary computational overhead but also weakens the model’s attention to the abundance maps that contribute to the unmixing, thus limiting the unmixing efficiency. Therefore, we propose sub-abundance map regularization, which only imposes piecewise smooth and low-rank regularization constraints on the abundance maps of the ground objects in the scene (i.e., the contributing abundance maps) to reduce the computational overhead and improve the unmixing accuracy. Specifically, the SU model based on sub-abundance map regularization can be expressed as follows:

$$\begin{array}{c}{\min }_U\frac{1}{2}\left|\right|Y-{AU\left|\right|}_F^2+{\alpha \left|\right|U\left|\right|}_{1,1}+\beta {\displaystyle \sum _{i=1}^R}\phi \left({\widehat{U}}_i\right)+\lambda {\displaystyle \sum _{i=1}^R}\psi \left({\widehat{U}}_i\right)\hfill \\ s.t.U\ge 0.\hfill \end{array}$$

(4)

The first term of model (4) is the reconstruction term, and the second term is the sparsity regularization, both of which act on the abundance matrix. The third and fourth terms are the low-rank regularization term and the piecewise smooth regularization term acting on the sub-abundance map, respectively. ${\left\{{\widehat{U}}_i\right\}}_{i=1}^R$ is the set of matrices formed by expanding the R contributing sub-abundance maps separately along the spatial dimension. In order to determine the value of R and accurately identify the contributing abundance maps, we use the information of the clean HSI and the sparsity of each abundance map as prior knowledge for identification. Specifically, the value of R is determined by the following equation:

$$R=\sum _{i=1}^p({\sigma }_i>\epsilon ?1:0),$$

(5)

where ${\left\{{\sigma }_i\right\}}_{i=1}^p$ is an element in the singular-value matrix $\Sigma$, and p represents the number of non-zero-singular values in $\Sigma$. $\Sigma$ is obtained by the singular value decomposition of the denoised HSl, specifically

$$[UU,\Sigma ,VV]=SVD\left(estnoise\right(Y\left)\right).$$

(6)

where $\mathit{UU}$ and $\mathit{VV}$ represent the left singular matrix and the transpose of right singular matrix, respectively.

Since denoised HSI has a low-rank equivalent to the number of endmembers [43], it is theoretically feasible to take the number of large singular values of denoised HSI as the number of endmembers (that is, the number of contributing abundance maps) and then constrain the number of sub-abundance maps. It is worth mentioning that the value of $\epsilon$ determines the final number obtained in Equation (5) to a certain extent, so its value is very important. Since the large and small values in the singular value matrix have huge differences and there are jump changes, we choose $\epsilon$ = 1 × 10⁻⁴, which has been proved to achieve ideal results in the experiment, and we will prove it in Section 5.

In each iteration, the contribution of each abundance map is evaluated according to its sparsity, thus determining the sub-abundance maps that need to be constrained. Specifically, the selection of sub-abundance maps is determined by the following equation:

$${\left\{{\widehat{U}}_i\right\}}_{i=1}^R=\{Unfold(sort(\{\sum _{j=1}^{n}abs\left(U_{i,j}\right){\}}_{i=1}^d){)}_i{\}}_{i=1}^R.$$

(7)

where $abs(·)$ represents the absolute value of all elements of each abundance map, $sort(·)$ represents the order of the obtained sparse vector of the abundance maps from largest to smallest, the least sparse (that is, the largest contribution) R abundance maps are selected, and $Unfold(·)$ unfolds the abundance maps into a matrix according to spatial dimension.

By adopting the strategy of sub-abundance map regularization, it can not only save the computational cost but also avoid the error that may be caused by directly pruning the spectral library and has better fault tolerance. It can be observed that in model (4), the first two terms are a classical sparse regression problem, while the third and fourth terms are the regularization terms directly acting on the sub-abundance maps, and the two parts are relatively independent and unified with each other. This makes each iteration in the unmixing process actually focus on the optimization of the sub-abundance maps, which can effectively reduce the impact of the large-scale and high coherence of the spectral library on the unmixing. In addition, model (4) also has good generalization ability. In the extreme case, when $R=0$, model (4) degenerates to the original SU model, and when $R=d$, model (4) degenerates to the same SU model that regularizes all abundance maps as model (3).

2.3. Low-Rank Dual TV SU Model with Sub-Abundance Map Regularization

For model (4), we next specifically identify $\phi \left({\widehat{U}}_i\right)$ and $\psi \left({\widehat{U}}_i\right)$. Weighted kernel norm regularization has been proved to have good low-rank properties and can be used as an effective convex approximationof rank functions [44], so it has attracted extensive attention from researchers. Here, we use weighted kenel norm regularization to characterize the low-rank properties of sub-abundance maps. Specifically, $\phi \left({\widehat{U}}_i\right)$ is defined as follows:

$$\phi \left({\widehat{U}}_i\right)={||{\widehat{U}}_i||}_{W_i,\ast }=\sum _{j=1}^p{w}_{i,j}{\sigma }_j\left({\widehat{U}}_i\right),$$

(8)

where ${\sigma }_j\left({\widehat{U}}_i\right)$ represents the $\mathit{i}$ th nonzero singular value of ${\widehat{U}}_i$, where $W_i$ is the diagonal matrix of all $w_{i,j}$, and $w_{i,j}$ is the weight of the i-th nonzero singular value, which is defined as follows:

$$w_{i,j}={\displaystyle \frac{1}{(\sigma \left({\widehat{U}}_i\right)+1e-5)}}.$$

(9)

Next, we construct $\psi \left({\widehat{U}}_i\right)$. Recently, TV has been widely used in unmixing due to its excellent performance. By punishing the difference between adjacent pixels in the image, TV can promote the segmentation smooth of the image and retain the edge details well, which can effectively remove the influence of noise in the image. However, given a pixel $x(i,j)$, where $(i,j)$ is its coordinate in the spatial domain, the calculation of its prior to first-order difference design to four pixels is $x(i,j),x(i+1,j),x(i,j+1),x(i+1,j+1)$. When calculating the nearest neighbor gradient of a pixel, there are four gradients to choose from, namely, horizontal, vertical, diagonal, and back-diagonal. However, traditional TV only pays attention to the difference between horizontal and vertical directions but does not consider the intrinsic information between adjacent pixels in the diagonal and back-diagonal directions, which results in the spatial neighbor information of pixels not being fully explored and utilized. To solve this problem, we propose DTV regularization and design the difference of diagonal and back-diagonal directions as TV operator so as to make more use of spatial neighborhood information. The mathematical form of DTV is given below. Let X be a discrete image of $m\times n$. The Anisotropic DTV calculation based on $l_1$ norm is as follows:

$$\begin{array}{c}DTV\left(X\right)={\left|\right|X\left|\right|}_{TV}+\left|\right|X|{|}_{TVD}\hfill \\ =\{{\displaystyle \sum _{i=1}^{m-1}}{\displaystyle \sum _{j=1}^{n-1}}\left\{\right|x(i+1,j)-x(i,j)|+|x(i,j+1)-x(i,j)\left|\right\}\hfill \\ +\{{\displaystyle \sum _{i=1}^{m-1}}\left|x\right(i+1,n)-x(i,n\left)\right|+{\displaystyle \sum _{j=1}^{n-1}}\left|x\right(m,j+1)-x(m,j\left)\right|)\}\}\hfill \\ +{\displaystyle \sum _{i=1}^{m-1}}{\displaystyle \sum _{j=1}^{n-1}}\left\{\right|x(i+1,j+1)-x(i,j)|+|x(i+1,j)-x(i,j+1)|\}.\hfill \end{array}$$

(10)

For ease of presentation, we define $\nabla =\left[\begin{array}{c}{\nabla }_1\\ {\nabla }_2\end{array}\right]$, where ${\nabla }_1$ and ${\nabla }_2$ denote $\left|\right|.|{|}_{TV}$ and $\left|\right|.|{|}_{TVD}$, respectively. In order to distinguish the different importance of horizontal and vertical differences from diagonal and back-diagonal differences, we choose to bound them separately with different regularization parameters.

Finally, in view of the excellent performance of weighted $l_{1,1}$ regularization in promoting the row sparsity of the abundance matrix [45], we replace the $l_{1,1}$ regularization in model (4) with weighted $l_{1,1}$ regularization to enhance the utilization of spectral information in the unmixing process. Substituting Equations (8) and (10) together into model (4), the final model is obtained as follows:

$$\begin{array}{c}\underset{U}{\min }\frac{1}{2}\left|\right|Y-{AU\left|\right|}_F^2+\alpha \left|\right|W_s\otimes U{\left|\right|}_{1,1}+\beta \sum _{i=1}^R\left|\right|{\widehat{U}}_i|{|}_{W_i,\ast }+{\lambda }_1\sum _{i=1}^R\left|\right|{\widehat{U}}_i|{|}_{TV}+{\lambda }_2\sum _{i=1}^R\left|\right|{\widehat{U}}_i|{|}_{TVD}\hfill \\ s.t.U\ge 0.\hfill \end{array}$$

(11)

where ⊗ represents element-wise multiplication, $W_s={[w_{s,1},w_{s,2},\dots ,w_{s,d}]}^T\times ones\left(size\left(U\right)\right)$ is the weight matrix of the sparse regularization, the $ones(·)$ operator constructs matrix whose entries are all ones, and the $w_{s,i}$ is defined as

$$w_{s,i}={\displaystyle \frac{1}{{({\displaystyle \sum _{j=1}^n}{U_{i,j}}^2)}^{\frac{1}{2}}+1e-5}}.$$

(12)

Finally, for ASC, we take the approach in [16] and define the augmented matrix:

$$\overline{Y}=\left[\begin{array}{c}Y\\ \delta 1_n^T\end{array}\right],\overline{A}=\left[\begin{array}{c}A\\ \delta 1_d^T.\end{array}\right]$$

(13)

They are used in the unmixing process instead of the original HSI data matrix Y and spectral library A for iteration. It is worth mentioning that there are strong signature variability in real-world scenarios, which makes the use of ASC subject to strong criticisms [25]. Therefore, we only use ASC on synthetic datasets and do not enforce it in experiments on real datasets.

Obviously, model (11) is a constrained non-convex optimization problem, and its unconstrained equivalent form is as follows:

$$\begin{array}{c}\underset{U}{\min }\frac{1}{2}\left|\right|Y-{AU\left|\right|}_F^2+\alpha \left|\right|W_s\otimes U{\left|\right|}_{1,1}+\beta \sum _{i=1}^R\left|\right|{\widehat{U}}_i|{|}_{W_i,\ast }\hfill \\ +{\lambda }_1\sum _{i=1}^R\left|\right|{\widehat{U}}_i|{|}_{TV}+{\lambda }_2\sum _{i=1}^R\left|\right|{\widehat{U}}_i|{|}_{TVD}+l_{R^{+}}\left(U\right),\hfill \end{array}$$

(14)

where $l_{R^{+}}(·)$ is the indicative function defined as follows:

$$l_{R^{+}}\left(U\right)=\left\{\begin{array}{c}0,if(min\left(U_{i,j}\right)\ge 0,i=1,2,\dots ,n)\\ +\infty ,if(min\left(U_{i,j}\right)<0,i=1,2,\dots ,n).\end{array}\right.$$

(15)

In order to effectively solve Equation (14), we introduce auxiliary variables $V_1$, $V_2$, $V_3$, $V_4$, $V_5$, $V_6$, $V_7$ and convert them into the following equivalent form:

$$\begin{array}{c}{\min }_U\frac{1}{2}\left|\right|Y-V_1{\left|\right|}_F^2+\alpha \left|\right|W_s\otimes V_2|{|}_{1,1}+\beta {\displaystyle \sum _{i=1}^R}\left|\right|V_{3,i}|{|}_{W_i,\ast }+{\lambda }_1{\displaystyle \sum _{i=1}^R}\left|\right|V_{5,i}|{|}_1+{\lambda }_2{\displaystyle \sum _{i=1}^R}\left|\right|V_{7,i}|{|}_1+l_{R^{+}}\left(U\right)\hfill \\ s.t.V_1=AU,V_2=U,V_{3,i}={\widehat{U}}_i,V_{4,i}={\widehat{U}}_i,V_{5,i}={\nabla }_1{V}_{4,i},V_{6,i}={\widehat{U}}_i,V_{7,i}={\nabla }_2{V}_{6,i}.\hfill \end{array}$$

(16)

Further, the augmented Lagrange function of Equation (16) can be obtained as follows:

$$\begin{array}{c}{L}_{\mu }(U,V)={\displaystyle \frac{1}{2}}\left|\right|Y-V_1{\left|\right|}_F^2+\alpha \left|\right|W_s\otimes V_2|{|}_{1,1}\hfill \\ +\beta {\displaystyle \sum _{i=1}^R}\left|\right|V_{3,i}|{|}_{W_i,\ast }+{\lambda }_1{\displaystyle \sum _{i=1}^R}\left|\right|V_{5,i}|{|}_1+{\lambda }_2{\displaystyle \sum _{i=1}^R}\left|\right|V_{7,i}|{|}_1\hfill \\ +l_{R^{+}}\left(U\right)+\frac{\mu }{2}\left(\right||V_1-AU-D_1{\left|\right|}_F^2+\left|\right|V_2-U-D_2{\left|\right|}_F^2\hfill \\ +{\displaystyle \sum _{i=1}^R}\left|\right|V_{3,i}-{\widehat{U}}_i-D_{3,i}{\left|\right|}_F^2+{\displaystyle \sum _{i=1}^R}\left|\right|V_{4,i}-{\widehat{U}}_i-D_{4,i}{\left|\right|}_F^2\hfill \\ +{\displaystyle \sum _{i=1}^R}\left|\right|V_{5,i}-{\nabla }_1{V}_{4,i}-D_{5,i}{\left|\right|}_F^2+{\displaystyle \sum _{i=1}^R}\left|\right|V_{6,i}-{\widehat{U}}_i-D_{6,i}{\left|\right|}_F^2\hfill \\ +{\displaystyle \sum _{i=1}^R}\left|\right|V_{7,i}-{\nabla }_2{V}_{6,i}-D_{7,i}{\left|\right|}_F^2).\hfill \end{array}$$

(17)

where $\mu >0$ is the penalty parameter, and $D_1,D_2,D_3,D_4,D_5,D_6,D_7$ are the scaled Lagrange multipliers. Noting that Equation (17) is desepratable, and under the ADMM framework, it can be divided into various subproblems for solving, which are as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{V}_1:{\displaystyle \frac{1}{2}}\left|\right|Y-V_1{\left|\right|}_F^2+{\displaystyle \frac{\mu }{2}}\left|\right|V_1-AU-D_1{\left|\right|}_F^2\hfill \\ V_2:\alpha \left|\right|W_s\otimes V_2|{|}_{1,1}+{\displaystyle \frac{\mu }{2}}\left|\right|V_2-U-D_2{\left|\right|}_F^2\hfill \\ V_3:\beta \sum _{i=1}^R\left|\right|V_{3,i}|{|}_{W_i,\ast }+{\displaystyle \frac{\mu }{2}}\sum _{i=1}^R\left|\right|V_{3,i}-{\widehat{U}}_i-D_{3,i}{\left|\right|}_F^2\hfill \\ V_4:\sum _{i=1}^R(||V_{4,i}-{\widehat{U}}_i-D_{4,i}|{|}_F^2+\left|\right|V_{5,i}-{\nabla }_1{V}_{4,i}-D_{5,i}{\left|\right|}_F^2)\hfill \\ V_5:{\lambda }_1\sum _{i=1}^R\left|\right|V_{5,i}|{|}_1+{\displaystyle \frac{\mu }{2}}\sum _{i=1}^R\left|\right|V_{5,i}-{\nabla }_1{V}_{4,i}-D_{5,i}{\left|\right|}_F^2\hfill \\ V_6:\sum _{i=1}^R(||V_{6,i}-{\widehat{U}}_i-D_{6,i}|{|}_F^2+\left|\right|V_{7,i}-{\nabla }_2{V}_{6,i}-D_{7,i}{\left|\right|}_F^2)\hfill \\ V_7:{\lambda }_2\sum _{i=1}^R\left|\right|V_{7,i}|{|}_1+{\displaystyle \frac{\mu }{2}}\sum _{i=1}^R\left|\right|V_{7,i}-{\nabla }_2{V}_{6,i}-D_{7,i}{\left|\right|}_F^2\hfill \\ U:l_{R^{+}}\left(U\right)+{\displaystyle \frac{\mu }{2}}\left(\right||V_1-AU-D_1{\left|\right|}_F^2+\left|\right|V_2-U-D_2{\left|\right|}_F^2)\hfill \end{array}\right.\end{array}$$

2.4. Optimization Framework

The subproblems of $V_1$, $V_2$, and $V_6$ are differentiable and convex and can be solved by taking the derivative and setting it to 0. The updated formula is as follows:

$$V_1^{(k+1)}={(\mu I+I)}^{-1}(Y+\mu A{U}^{\left(k\right)}+\mu {D_1}^{\left(k\right)}),$$

(18)

$$\begin{array}{c}\hfill {V_{4,i}}^{(k+1)}\leftarrow {({{\nabla }_1}^T{\nabla }_1+I)}^{-1}[({{\widehat{U}}_i}^{\left(k\right)}+{D_{4,i}}^{\left(k\right)})+{{\nabla }_1}^T({V_{5,i}}^{\left(k\right)}-{D_{5,i}}^{\left(k\right)})],\end{array}$$

(19)

$$\begin{array}{c}\hfill {V_{6,i}}^{(k+1)}\leftarrow {({{\nabla }_2}^T{\nabla }_2+I)}^{-1}[({{\widehat{U}}_i}^{\left(k\right)}+{D_{6,i}}^{\left(k\right)})+{{\nabla }_2}^T({V_{7,i}}^{\left(k\right)}-{D_{7,i}}^{\left(k\right)})].\end{array}$$

(20)

where I is the identity matrix of size $n\times n$. Note that ${{\nabla }_1}^T{\nabla }_1$ and ${{\nabla }_2}^T{\nabla }_2$ only act on spatial domains and can be used band by band, and for each band, ${\nabla }_1$ and ${\nabla }_2$ are a convolution and can, therefore, be computed using the Fast Fourier transform diagonalization. In addition, for the subproblems of $V_3,V_4,V_5,V_6,V_7$, we take the method of updating the abundance maps one by one to solve and assign the values of all updated sub-abundance maps to the corresponding sub-abundance maps in the abundance matrix U after solving each subproblem.

The subproblems of $V_2,V_5,V_7$ can be solved using the well-known soft-thresholding method, which is defined as follows:

$$softTh(x,\alpha )=sign\left(x\right)max\{0,|x|-\alpha \},\alpha >0.$$

(21)

Therefore, the solution for $V_2,V_5,V_7$ can be expressed as

$${V_2}^{(k+1)}\leftarrow softTh(U^{\left(k\right)}+{D_2}^{\left(k\right)},{\displaystyle \frac{\alpha }{\mu }}{W}_s),$$

(22)

$${V_{5,i}}^{(k+1)}\leftarrow softTh({\nabla }_1{V_{4,i}}^{\left(k\right)}+{D_{5,i}}^{\left(k\right)},{\displaystyle \frac{{\lambda }_1}{\mu }}),$$

(23)

$${V_{7,i}}^{(k+1)}\leftarrow softTh({\nabla }_2{V_{6,i}}^{\left(k\right)}+{D_{7,i}}^{\left(k\right)},{\displaystyle \frac{{\lambda }_2}{\mu }}).$$

(24)

The subproblems of $V_3$ can be solved using the singular value soft threshold method. Assuming $X=UUdiag({\sigma }_1,\dots ,{\sigma }_p)VV$ is a singular value decomposition of X, the singular value soft threshold operator is defined as follows:

$$SV{T}_{w,\rho }\left(X\right)=UUdiag(({\sigma }_1-\rho w_1),\dots ,({\sigma }_p-\rho w_p))VV.$$

(25)

Obviously the closed solution of the $V_3$ subproblem can be expressed as

$${V_{3,i}}^{(k+1)}=SV{T}_{W_i,\frac{\beta }{\mu }}({{\widehat{U}}_i}^{\left(k\right)}+{D_{3,i}}^{\left(k\right)}).$$

(26)

The subproblems of U can be obtained by taking the derivative and setting the derivative to 0 and then projecting the solution into the non-negative quadrant, specifically

$$\begin{array}{c}\hfill U^{(k+1)}=max(0,{(A^{T}A+I)}^{-1}[A^T({V_1}^{\left(k\right)}-{D_1}^{\left(k\right)})+({V_2}^{\left(k\right)}-{D_2}^{\left(k\right)})]).\end{array}$$

(27)

Finally, update $D_1,D_2,D_3,D_4,D_5,D_6,D_7$ using the dual ascent method:

$${D_1}^{(k+1)}={D_1}^{\left(k\right)}-({V_1}^{\left(k\right)}-A{U}^{\left(k\right)}),$$

(28)

$${D_2}^{(k+1)}={D_2}^{\left(k\right)}-({V_2}^{\left(k\right)}-U^{\left(k\right)}),$$

(29)

$${D_{3,i}}^{(k+1)}={D_{3,i}}^{\left(k\right)}-({V_{3,i}}^{\left(k\right)}-{{\widehat{U}}_i}^{\left(k\right)}),$$

(30)

$${D_{4,i}}^{(k+1)}={D_{4,i}}^{\left(k\right)}-({V_{4,i}}^{\left(k\right)}-{{\widehat{U}}_i}^{\left(k\right)}),$$

(31)

$${D_{5,i}}^{(k+1)}={D_{5,i}}^{\left(k\right)}-({V_{5,i}}^{\left(k\right)}-{\nabla }_1{V_{4,i}}^{\left(k\right)}),$$

(32)

$${D_{6,i}}^{(k+1)}={D_{6,i}}^{\left(k\right)}-({V_{6,i}}^{\left(k\right)}-{{\widehat{U}}_i}^{\left(k\right)}),$$

(33)

$${D_{7,i}}^{(k+1)}={D_{7,i}}^{\left(k\right)}-({V_{7,i}}^{\left(k\right)}-{\nabla }_2{V_{6,i}}^{\left(k\right)}).$$

(34)

It should be noted that ${\left\{{\widehat{U}}_i\right\}}_{i=1}^R$ tends to be constant in the iteration, but when ${\left\{{\widehat{U}}_i\right\}}_{i=1}^R$ changes, $V_{3.i},V_{4.i},V_{5.i},V_{6.i},V_{7.i}$ should change uniformly, and Equation (30)–(34) should be replaced with the following updated formula:

$${D_{3,i}}^{(k+1)}=zeros(size({D_{3,i}}^{\left(k\right)})),$$

(35)

$${D_{4,i}}^{(k+1)}=zeros(size({D_{4,i}}^{\left(k\right)})),$$

(36)

$${D_{5,i}}^{(k+1)}=zeros(size({D_{5,i}}^{\left(k\right)})),$$

(37)

$${D_{6,i}}^{(k+1)}=zeros(size({D_{6,i}}^{\left(k\right)})),$$

(38)

$${D_{7,i}}^{(k+1)}=zeros(size({D_{7,i}}^{\left(k\right)})).$$

(39)

Next, we analyze the time complexity of the algorithm. The ADMM optimization framework including update $U,V_1,V_2,V_3,V_4,V_5,V_6,V_7,D_1,D_2,D_3,D_4,D_5,D_6,D_7$. The most expensive steps are U, whose computational complexity is $O\left(n{l}^2\right)$, and $V_4,V_6$, whose computational complexity is $O(nlogn)$, and the rest of the computational complexity is $O\left(n\right)$. Considering that there is usually $l^2>>logn$, the computational complexity of SARSU is $O\left(n{l}^2\right)$. Finally, the complete SARSU pseudocode is given in Algorithm 1.

Algorithm 1 Pseudocode of the SARSU algorithm

1:   Input: The observed data $\overline{Y}\in R^{l\times \mathrm{n}}$, the spectral library $\overline{A}\in R^{l\times d}$, the number of active abundance maps R, the weighted matrices $W_s$ and W, the parameters $\alpha$, $\beta$, ${\lambda }_1$, ${\lambda }_2$, $\mu$ and Maxiter. 2:   Output: abundance matrix $U\in R^{d\times n}$. 3:   Initialization: Set $\mathrm{k}=0$, $U^{\left(0\right)}\in R^{l\times d}$, ${\left\{{\widehat{U}}_i\right\}}_{i=1}^R\in R^{m1\times m2}$ and $V_1^{\left(0\right)},\dots ,V_7^{\left(0\right)}$, $D_1^{\left(0\right)},\dots ,D_7^{\left(0\right)}$. 4:   Repeat: 5:   Update $V_1$ by Equation (18). 6:   Update $V_2$ by Equation (22), update $w_s$ by Equation (12). 7:   Update $V_{3i}$ by Equation (26).   Update $V_{4i}$ by Equation (19).   Update $V_{5i}$ by Equation (23).   Update $V_{6i}$ by Equation (20).   Update $V_{7i}$ by Equation (24). 8:   Update U by Equation (27). 9:   Update Lagrange multipliers:   Update $D_1$ by Equation (28).   Update $D_2$ by Equation (29).   if ${\left\{{\widehat{U}}_i\right\}}_{i=1}^R$ has changed   Update $D_{3,i},D_{4,i},D_{5,i},D_{6,i},D_{7,i}$ by Equations (30)–(34).   else   Update $D_{3,i},D_{4,i},D_{5,i},D_{6,i},D_{7,i}$ by Equations (35)–(39). 10:  Update iteration: $\mathrm{k}\leftarrow \mathrm{k}+1$. 11:  Until Maxiter is reached.

3. Experiment on Synthetic Dataset

3.1. Experimental Settings

(1) Details of the experiment. Due to the global non-convexity of the proposed SARSU, some details such as initialization and parameter determination need to be specified in the method implementation. First, we have to determine the initialization of the abundance matrix U, and improper initialization may cause the algorithm to fall into a local minimum solution. Generally, there are two strategies for the initialization of abundance matrix U random initialization or pseudo-inverse initialization with spectral library. Random initialization is the random allocation of values between 0 and 1 as elements of the matrix U, while the latter is initialized using the initial decomposition $Y=AU$ of the image and the strategy of inverse solution U. In order to avoid the great uncontrollability of randomly initialized values, and the possibility of inappropriate initializations that cause the algorithm to fall into local minimum solutions, we choose pseudo-inverse initialization, that is, $U={\left(A^{T}A\right)}^{-1}{A}^{T}Y$. Secondly, the setting of augmented Lagrange penalty u directly affects the convergence speed of the algorithm. To this end, we adopt an adaptive update strategy by examining the ratio of the ADMM’s original and dual residuals in a given interval of iterations and update $\mu$ based on this. The reason for this is that both the original and dual residuals converge to 0, and we can make them converge uniformly by adjusting $\mu$. We use the following definitions of primal residual norm and dual residual norm as a measure of iteration completion:

$$\begin{array}{cc}\hfill r^{\left(k\right)}& =||[{V_1}^{\left(k\right)};{V_2}^{\left(k\right)};{V_3}^{\left(k\right)};{V_4}^{\left(k\right)};{V_5}^{\left(k\right)};{V_6}^{\left(k\right)};{V_7}^{\left(k\right)}]\hfill \\ & -[A{U}^{\left(k\right)};U^{\left(k\right)};{\widehat{U}}^{\left(k\right)};{\widehat{U}}^{\left(k\right)};{\nabla }_1{\widehat{U}}^{\left(k\right)};{\widehat{U}}^{\left(k\right)};{\nabla }_2{\widehat{U}}^{\left(k\right)}]{\left|\right|}_F^2,\hfill \end{array}$$

(40)

$$\begin{array}{c}\hfill d^{\left(k\right)}=\left|\right|[{V_1}^{\left(k\right)};\dots ;{V_7}^{\left(k\right)}]-[{V_1}^{(k-1)};\dots ;{V_7}^{(k-1)}]{\left|\right|}_F^2.\end{array}$$

(41)

In addition, we set a maximum number of iterations for the algorithm, such as 200. If either of the above two strategies is satisfied, the iteration ends. Empirically, we have found that a combination of these two strategies always produces satisfactory results.

(2) In this section, to prove the validity of our proposed SARSU, we select eight semi-supervised unmixing methods as comparison methods to evaluate the unmixing performance, namely, SUnSAL [25], SUnSAL_TV [26], JSpBLRU [36], MUA_SLIC [30], LSU [40], S2MSU [32], SUnCNN [23], and FaSUn [42]. As for the parameters of each method, we selected them according to the suggestions in the original paper and then carried out small tuning in the experiment. The parameter selection of all comparison methods and proposed methods is shown in

Table 1. Selection of parameters for each method.

Methods/Datasets	Synthetic Datasets	Real Datasets
SUnSAL [25]	$\lambda =0.5$	$\lambda =0.05$
SUnSAL_TV [26]	$\lambda =0.01,{\lambda }_{TV}=0.001,\mu =0.2$	$\lambda =0.01,{\lambda }_{TV}=0.0001,\mu =0.5$
JSpBLRU [36]	$d=7,\mu =0.01,\gamma =0.005,\tau =1$	$d=50,\mu =0.01,\gamma =0.0005,\tau =10$
MUA_SLIC [30]	${\lambda }_1=0.01,{\lambda }_2=0.1,\beta =0.01,slic\_size=6,slic\_reg=0.005$	${\lambda }_1=0.001,{\lambda }_2=0.01,\beta =10,slic\_size=200$, $slic\_reg=0.01$
LSU [40]	$\alpha =0.05,\beta =0.005,\mu =0.1$	$\alpha =0.05,\beta =5,\mu =0.1$
S2MSU [32]	$blocksize=5,stepsize=3,{\lambda }_{bar}=0.005,\lambda =0.05$	$blocksize=3,stepsize=2,{\lambda }_{bar}=0.005,\lambda =0.001$
SUnCNN [23]	$Iter$ = 12,000	$Iter=20,000$
FaSUn [42]	$T=10,000,T_A=T_B=5,{\mu }_1=50,{\mu }_2=2,{\mu }_3=1$	$T=10,000,T_A=T_B=5,{\mu }_1=400,{\mu }_2=20,{\mu }_3=1$

. All experiments were conducted in an environment with 12th Generation Intel Core i7-12700F and Windows 10.

(3) Synthetic datasets. This paper simulates two hyperspectral images, referred to as DC1 and DC2. Endmembers were randomly selected from the United States Geological Survey (USGS) spectral library, and corresponding abundance maps were generated to simulate possible spatial material distributions. The endmembers in the USGS library have 224 spectral bands, uniformly distributed in the range of 0.4–2.5 μm. We used a linear mixing model to generate the data, randomly selecting features from the USGS library as endmembers and applying the ASC to each simulated pixel, with an angle of at least 4.44° between any pair of spectral signatures. The images were contaminated by both white noise and spectrally correlated Gaussian noise generated by a low-pass filter. DC1 with $75\times 75$ pixels contains five endmembers, with each row being a mixture of different numbers of endmembers. Since it includes all possible mixing scenarios, it is often used in unmixing tasks to test algorithm performance. DC2 is composed of a linear mixture of nine endmembers and contains $100\times 100$ pixels. The abundance maps of DC2 were sampled from a Dirichlet distribution centered on a Gaussian random field, exhibiting piecewise smoothness and sharp edge transitions. The experiments were conducted on both DC1 and DC2 at signal-to-noise ratios (SNRs) of 20 dB, 30 dB, and 40 dB. Figure 1 shows the reflectance curves of each band of the endmembers selected by DC1 and DC2 and the synthetic images.

(4) Evaluation index. We use signal reconstruction error ($\mathit{SRE}$) as an evaluation index to evaluate the unmixing results, which is defined as follows:

$$SRE=20{log}_{10}{\displaystyle \frac{E\left(\right|\left|U\right|{|}_F^2)}{E(||U-\widehat{U}|{|}_F^2)}}.$$

(42)

where $E(·)$ represents the expectation operator, and the higher the $\mathit{SRE}$ value, the better the unmixing effect. We chose $\mathit{SRE}$ rather than root mean square error ($\mathit{RMSE}$) as an evaluation metric because $\mathit{SRE}$ is built on a logarithmic scale. When the reconstruction error is low, $\mathit{SRE}$ can better distinguish the unmixing performance of the model. This index is widely used in spectral-library-based unmixing methods.

In order to ensure the fair comparison of all methods, we use pseudo-inverse initialization to obtain the initial abundance of all methods. All the methods were tested ten times on the same image, and the optimal results of the ten times were selected for comparison. In order to restore the real unmixing scene as much as possible, we use the noisy image to initialize the abundance and unmixing.

3.2. Parameter Selection Experiment

In this experiment, we selected the four parameters $\alpha$, $\beta$, ${\lambda }_1$, and ${\lambda }_2$ in SARSU on DC1. With the image fixed and the SNR set to 30 dB, we first fixed the values of ${\lambda }_1$ and ${\lambda }_2$ and then optimized $\alpha$ and $\beta$. As shown in Figure 2a, when $\alpha =5\times {10}^{-3}$ and $\beta =1\times {10}^{-3}$, the $\mathit{SRE}$ value reaches the maximum, indicating the best unmixing results. Therefore, we selected $\alpha =5\times {10}^{-3}$ and $\beta =1\times {10}^{-3}$ and then optimized ${\lambda }_1$ and ${\lambda }_2$. As shown in Figure 2b, when $\alpha =5\times {10}^{-3}$ and $\beta =5\times {10}^{-4}$, the $\mathit{SRE}$ value reaches the maximum. Therefore, $\alpha =5\times {10}^{-3}$, $\beta =1\times {10}^{-3}$, ${\lambda }_1=5\times {10}^{-3}$, and ${\lambda }_2=5\times {10}^{-4}$ were selected in the subsequent experiments.

3.3. Noise Robustness Experiment

This experiment aims to evaluate the good performance and excellent robustness of the proposed SARSU method under different levels of Gaussian noise. The experiments are conducted on both DC1 and DC2, with noise levels selected as SNR = 20 dB, 30 dB, and 40 dB. To ensure the fairness of the experiment, all methods are compared under the same initialization conditions.

Figure 3 shows the $\mathit{SRE}$ results of each method under different SNR levels on DC1 and DC2. It can be clearly observed that as the SNR value increases, the $\mathit{SRE}$ values of all methods increase, indicating that the performance of all methods improves with the reduction in noise level. However, our method clearly achieves better results than other methods. Under all noise levels on both DC1 and DC2, the $\mathit{SRE}$ values obtained by our method are significantly superior to those of other methods, demonstrating better stability and noise robustness. This indicates that our sub-abundance map regularization strategy is successful. By directly integrating the low-rank and piecewise smoothness priors into the contributing abundance maps, it not only enhances their importance in unmixing but also effectively reduces the solution space, thereby further improving the algorithm’s performance. Figure 4 and Figure 5, respectively, display the estimated abundance maps of each method on DC1 and DC2 at 30 dB. It can be clearly seen that compared with other methods, our method achieves more desirable unmixing results and produces better abundance maps. At the 30 dB level, the abundance maps obtained by our method effectively eliminate the influence of noise, with smoother edges and better preservation of edge details, making them more consistent with the true abundance maps. Since the SNR of real images obtained by sensors is generally around this level, this indicates that our method is very promising for practical applications. This clearly confirms the effectiveness and advancement of SARSU in improving unmixing performance.

3.4. Convergence Analysis

The SARSU using the aforementioned stopping criterion is convergent. The convergence of the algorithm can be analyzed in a manner similar to that in [46,47]. We have demonstrated this in our experiments. As shown in Figure 6, the convergence curves of the objective function, primal residual, and dual residual in the DC1 experiment are presented. It can be seen from Figure 6a that the objective function value tends to flatten after 40 iterations and has essentially stabilized before 200 iterations. The primal and dual residual curves shown in Figure 6b also indicate that the primal and dual residuals oscillate and approach each other. As the number of iterations increases, the amplitude of oscillation gradually decreases until stabilization. By 200 iterations, the residuals have essentially completely converged to 0, which proves the convergence of SARSU.

3.5. Computational Cost Analysis

As is well known, the computational cost of the SU model is significantly influenced by the scale of the spectral library atoms. Particularly for algorithms with high time complexity, an increase in the number of spectral library atoms will lead to a substbackal rise in computational cost. We have previously analyzed the time complexity of SARSU. Now, we perform unmixing on each method using spectral libraries composed of different numbers of spectral library atoms. The number of atoms in the spectral library is set to 50, 100, 150, 240, 350, and 498, respectively, and the running time of each method is recorded. Figure 7 presents the running time curves of each method. It can be observed that our method, along with SUnSAL and MUA_SLIC, spends less time and has a relatively flat curve, indicating that the running time is not significantly affected by the number of spectral library atoms. Since SUnSAL does not include any additional regularization terms and MUA_SLIC employs a time-saving strategy based on multi-scale processing, they achieve fast running times. Our method, however, still maintains a rapid running time even after incorporating low-rank and piecewise smooth regularization terms for the abundance maps. This is attributed to our sub-abundance map regularization strategy, which balances unmixing performance and timeliness. Other methods exhibit a significant increase in running time with an increasing number of spectral library atoms. Notably, SUnCNN and LSU show the most pronounced increase. The former is limited by the time-consuming nature of deep learning, while the latter, due to its hierarchical characteristics, experiences an increase in the number of unmixing layers as the number of spectral library atoms increases, resulting in considerable time overhead. It is worth mentioning that JSpBLRU and SUnSAL_TV employ low-rank regularization and TV regularization on the abundance, respectively. However, their computational costs are much higher than that of the proposed method, which utilizes both types of regularization simultaneously.

Table 2. Running time (s) of each method on DC2, and the bold indicates the optimal value.

Datasets/Methods	SUnSAL	SUnSAL_TV	JSpBLRU	MUA_SLIC	LSU	S2MSU	SUnCNN	FaSUn	Proposed
DC2	6.75	87.53	37.58	15.94	116.24	22.51	173.27	91.60	20.82

presents the running time of each method on DC2. It can be seen from the table that the proposed method is only slower than SUnSAL and MUA_SLIC, and it has a significant advantage in running time compared with other methods, which once again confirms the superiority of the proposed method in terms of speed.

3.6. Ablation Experiment

To verify the effectiveness of the proposed method, we conducted ablation experiments on DC1. We designed six cases and performed experiments under SNR levels of 20, 30, and 40 dB. The six cases are as follows:

$$\begin{array}{c}{\min }_U\frac{1}{2}\left|\right|Y-{AU\left|\right|}_F^2+\alpha \left|\right|W_s\otimes U{\left|\right|}_{1,1}\hfill \\ s.t.U\ge 0,\hfill \end{array}$$

(43)

$$\begin{array}{c}{\min }_U\frac{1}{2}\left|\right|Y-{AU\left|\right|}_F^2+\alpha \left|\right|W_s\otimes U{\left|\right|}_{1,1}+\beta {\displaystyle \sum _{i=1}^R}\left|\right|{\widehat{U}}_i|{|}_{W_i,\ast }\hfill \\ s.t.U\ge 0,\hfill \end{array}$$

(44)

$$\begin{array}{c}{\min }_U\frac{1}{2}\left|\right|Y-{AU\left|\right|}_F^2+\alpha \left|\right|W_s\otimes U{\left|\right|}_{1,1}+\beta {\displaystyle \sum _{i=1}^R}\left|\right|{\widehat{U}}_i|{|}_{W_i,\ast }+{\lambda }_1{\displaystyle \sum _{i=1}^R}\left|\right|{\widehat{U}}_i|{|}_{TV}\hfill \\ s.t.U\ge 0,\hfill \end{array}$$

(45)

$$\begin{array}{c}{\min }_U\frac{1}{2}\left|\right|Y-{AU\left|\right|}_F^2+\alpha \left|\right|W_s\otimes U{\left|\right|}_{1,1}+\beta {\displaystyle \sum _{i=1}^R}\left|\right|{\widehat{U}}_i|{|}_{W_i,\ast }+{\lambda }_2{\displaystyle \sum _{i=1}^R}\left|\right|{\widehat{U}}_i|{|}_{TVD}\hfill \\ s.t.U\ge 0,\hfill \end{array}$$

(46)

$$\begin{array}{c}{\min }_U\frac{1}{2}\left|\right|Y-{AU\left|\right|}_F^2+\alpha \left|\right|W_s\otimes U{\left|\right|}_{1,1}+{\lambda }_1{\displaystyle \sum _{i=1}^R}\left|\right|{\widehat{U}}_i|{|}_{TV}+{\lambda }_2{\displaystyle \sum _{i=1}^R}\left|\right|{\widehat{U}}_i|{|}_{TVD}\hfill \\ s.t.U\ge 0,\hfill \end{array}$$

(47)

$$\begin{array}{c}{\min }_U\frac{1}{2}\left|\right|Y-{AU\left|\right|}_F^2+\alpha \left|\right|W_s\otimes U{\left|\right|}_{1,1}+\beta {\displaystyle \sum _{i=1}^R}\left|\right|{\widehat{U}}_i|{|}_{W_i,\ast }+{\lambda }_1{\displaystyle \sum _{i=1}^R}\left|\right|{\widehat{U}}_i|{|}_{TV}+{\lambda }_2{\displaystyle \sum _{i=1}^R}\left|\right|{\widehat{U}}_i|{|}_{TVD}\hfill \\ s.t.U\ge 0.\hfill \end{array}$$

(48)

Figure 8 presents the $\mathit{SRE}$ values of models (43)–(48) at SNR levels of 20 dB, 30 dB, and 40 dB. The figure clearly demonstrates the contributions of the low-rank regularization and the dual TV regularization to the models. It can be observed that the two TV regularizations have almost equal importance, especially at low SNR levels, where dual TV regularization can significantly improve the unmixing results. The difference between models (43) and (44) well illustrates the importance of the low-rank regularization, which can effectively promote the low-rank structure of the abundance maps and remove some outliers, thereby enhancing the unmixing results of the model. Model (48) is the complete model of the proposed method, and it achieves the best unmixing results by integrating both sub-abundance maps low-rank regularization and dual TV regularization.

4. Experiment on Real Dataset

4.1. Preparation Before the Experiment

In the experiments of this section, four real-world datasets were utilized: Samson, Urban, AVIRIS Cuprite, and Jasper Ridge. All competing methods were applied for unmixing and evaluation. These datasets are publicly available and widely adopted by researchers for unmixing tasks, providing effective validation of algorithm performance. Consistent with the synthetic dataset experiments, all methods employed pseudoinverse-based initialization. Due to the lack of ground-truth data for real-world validation, the RGB composite images of the four datasets are provided in Figure 9 for visual comparison.

Since real-world datasets lack ground-truth abundance maps, the unmixing performance cannot be directly evaluated using abundance-based metrics like the $\mathit{SRE}$, as done for synthetic datasets. To quantitatively assess the unmixing results, we adopt the image-level $\mathit{SRE}$ and $\mathit{RMSE}$, which are defined as follows:

$$SR{E}_{IM}=20{\log }_{10}{\displaystyle \frac{E\left(\right|\left|Y\right|{|}_F^2)}{E\left(\right||Y-AU|{|}_F^2)}},$$

(49)

$$RMSE=\sqrt{{\displaystyle \frac{\left|\right|Y-{AU\left|\right|}_F^2}{L\times N}}}.$$

(50)

where Y denotes the original HSI, A represents the spectral library, and U is the abundance matrix obtained after unmixing. The $SR{E}_{IM}$ can to some extent evaluate the quality of the unmixing results. The greater the value, the more effective the unmixing outcome will be.

4.2. Experiment Results

The Samson dataset was acquired using the Samson sensor and has $95\times 95$ pixels, 156 bands, and a spectral range of 0.041 to 0.889 μm. The scene is commonly assumed to include three endmembers: Soil, Tree, and Water. Figure 10 presents the abundance maps estimated by all methods on the Samson dataset. Notably, our method demonstrates desirable performance, particularly in estimating Water, where it achieves more precise spatial distribution and cleaner background separation compared to other approaches. The remaining methods also exhibit competent overall performance: SUnCNN and FaSUn yield satisfactory estimates for Soil, while SUnSAL_TV and MUA_SLIC effectively suppress noise but introduce varying degrees of oversmoothing.

The Jasper Ridge dataset was captured by the Airborne Visible Infrared Imaging Spectrometer (AVIRIS) sensor. It contains 224 bands with $100\times 100$ pixels and a spectral resolution of 9.46 nm. To mitigate atmospheric effects, several bands were removed, retaining 198 bands for unmixing. The scene is generally considered to include four endmembers: Tree, Water, Soil, and Road. Figure 11 presents the abundance maps estimated by different methods on the Jasper Ridge dataset. The results indicate that our method achieves overall satisfactory performance. Specifically, our method delivers superior estimates for Water, whereas SUnSAL, JSpBLRU, and S2MSU exhibit suboptimal performance in Water estimation. For Dirt and Road, all methods yield reasonable abundance estimates, with the exception of FaSUn, which underperforms in Road estimation. Overall, our method achieves robust abundance estimation accuracy.

The widely adopted AVIRIS Cuprite dataset was selected to evaluate the proposed method as it is a benchmark in hyperspectral unmixing. A sub-image from the sector ’f970619t01p02_r02_sc04.a.rfl’ (Available online at: https://avng.jpl.nasa.gov/pub/ABoselli/f970619t01p02_r02c/, accessed on 1 November 2025) with dimensions of $250\times 191$ pixels and 240 spectral bands was chosen for experimentation, where 188 bands were retained after removing noise-corrupted and water vapor absorption bands. Twelve minerals are hypothesized to be present in this dataset: Alunite GDS82 Na82, Andradite WS487, Buddingtonite GDS85D-206, Chalcedony CU91-6A, Dumortierite HS190.3B, Kaolin/Smect H89-FR-5 30K, Kaolin/Smect KLF508 85%K, Montmorillonite + Illi CM37, Muscovite GDS108, Nontronite NG-1.a, Pyrope WS474, and Sphene HS189.3B. Figure 12 displays the abundance maps estimated by different methods on the AVIRIS Cuprite dataset. Two key observations can be drawn: First, all algorithms achieve reasonable unmixing results. Second, our method accurately localizes regions with the highest mineral concentrations, which benefits from the sub-abundance map regularization effectively enforcing low-rank and piecewise smoothness properties of abundance maps, thereby preserving critical details while suppressing noise and outliers.

The Urban (available online at http://www.erdc.usace.army.mil/Media/Fact-Sheets/Fact-Sheet-Article-View/Article/610433/hypercube/#, accessed on 1 November 2025) dataset consists of $307\times 307$ pixels and contains 210 spectral bands. After removing noise-corrupted and water vapor absorption bands, 162 bands were retained for unmixing. As established in prior studies, the scene comprises six materials: Asphalt-road, Grass, Roof #1, Tree, Roof #2, and Concrete-road. Figure 13 presents the unmixing results of various algorithms on the Urban dataset. It is evident that our method achieves superior overall performance. Specifically, both our method and SUnCNN yield more complete and distinct abundance estimates for Grass, Roof #1, and Tree, while our method further produces smoother abundance maps with effective noise suppression. For Roof #2, our method, along with SUnSAL_TV, SUnSAL, and LSU, delivers satisfactory results, but our solution exhibits higher precision and cleaner background separation. All methods perform comparably well in estimating the Concrete-road abundance.

Table 3. $SR{E}_{IM}$ of all methods on real datasets, and the bolded parts indicate the optimal values.

Datasets/Methods	SUnSAL	SUnSAL_TV	JSpBLRU	MUA_SLIC	LSU	S2MSU	SUnCNN	FaSUn	Proposed
Samson	20.25	23.33	26.10	29.10	25.53	30.21	26.95	25.97	30.94
Jasper Ridge	18.82	27.36	22.47	21.10	27.11	26.81	26.04	28.52	31.85
AVIRIS Cuprite	23.12	30.66	26.35	23.08	33.13	35.42	32.72	29.33	36.17
Urban	19.96	28.36	26.39	27.79	28.62	28.05	27.16	24.39	28.87

and

Table 4. $\mathit{RMSE}$ of all methods on real datasets, and the bolded parts indicate the optimal values.

Datasets/Methods	SUnSAL	SUnSAL_TV	JSpBLRU	MUA_SLIC	LSU	S2MSU	SUnCNN	FaSUn	Proposed
Samson	0.024	0.017	0.011	0.009	0.013	0.012	0.017	0.015	$\mathbf{0}.\mathbf{006}$
Jasper Ridge	0.038	0.019	0.018	0.028	0.016	0.016	0.020	0.014	$\mathbf{0}.\mathbf{012}$
AVIRIS Cuprite	0.025	0.012	0.022	0.025	0.008	0.019	0.023	0.012	$\mathbf{0}.\mathbf{005}$
Urban	0.027	0.010	0.014	0.011	$\mathbf{0}.\mathbf{009}$	0.018	0.024	0.015	$\mathbf{0}.\mathbf{009}$

present the $\mathit{SRE}$ and $\mathit{RMSE}$ values obtained by all methods on four real-world datasets, respectively, with the highest values bolded and the second-highest values underlined. It is evident that our method achieves the best results across all real-world datasets, demonstrating the effectiveness of the proposed sub-abundance map regularization strategy in enhancing unmixing performance.

4.3. Running Time Analysis

The running times of all methods on four real-world datasets are summarized in

Table 5. Running time(s) of each method on real datasets, and the bolded parts indicate the optimal values.

Datasets/Methods	SUnSAL	SUnSAL_TV	JSpBLRU	MUA_SLIC	LSU	S2MSU	SUnCNN	FaSUn	Proposed
Samson	20.32	82.79	70.73	43.52	41.89	25.83	40.79	55.15	$\mathbf{18}.\mathbf{04}$
Jasper Ridge	39.68	117.25	85.45	57.34	131.56	58.51	127.21	104.07	$\mathbf{37}.\mathbf{54}$
AVIRIS Cuprite	$\mathbf{68}.\mathbf{27}$	245.83	233.62	88.05	432.76	152.96	765.53	155.28	109.05
Urban	$\mathbf{84}.\mathbf{08}$	591.19	464.83	139.90	837.30	354.23	1070.85	226.78	162.06

. It can be observed that our method maintains favorable time efficiency even under the complex scenarios of real datasets. Specifically, on the Samson and Jasper Ridge datasets, our method achieves the shortest runtime compared to SUnSAL. This is attributed to the fact that the complexity of real data requires SUnSAL to perform more iterations for convergence, while our method incorporates the low-rank and piecewise smoothness priors of abundance maps, which can speed up convergence. Additionally, the dual TV regularization employed in our framework captures twice the spatial information of conventional TV, thereby accelerating convergence. On the AVIRIS Cuprite and Urban datasets, our method also exhibits faster execution speeds compared to other methods that similarly adopt low-rank and TV regularization. These results collectively demonstrate the superiority of our approach in computational efficiency.

5. Discussion

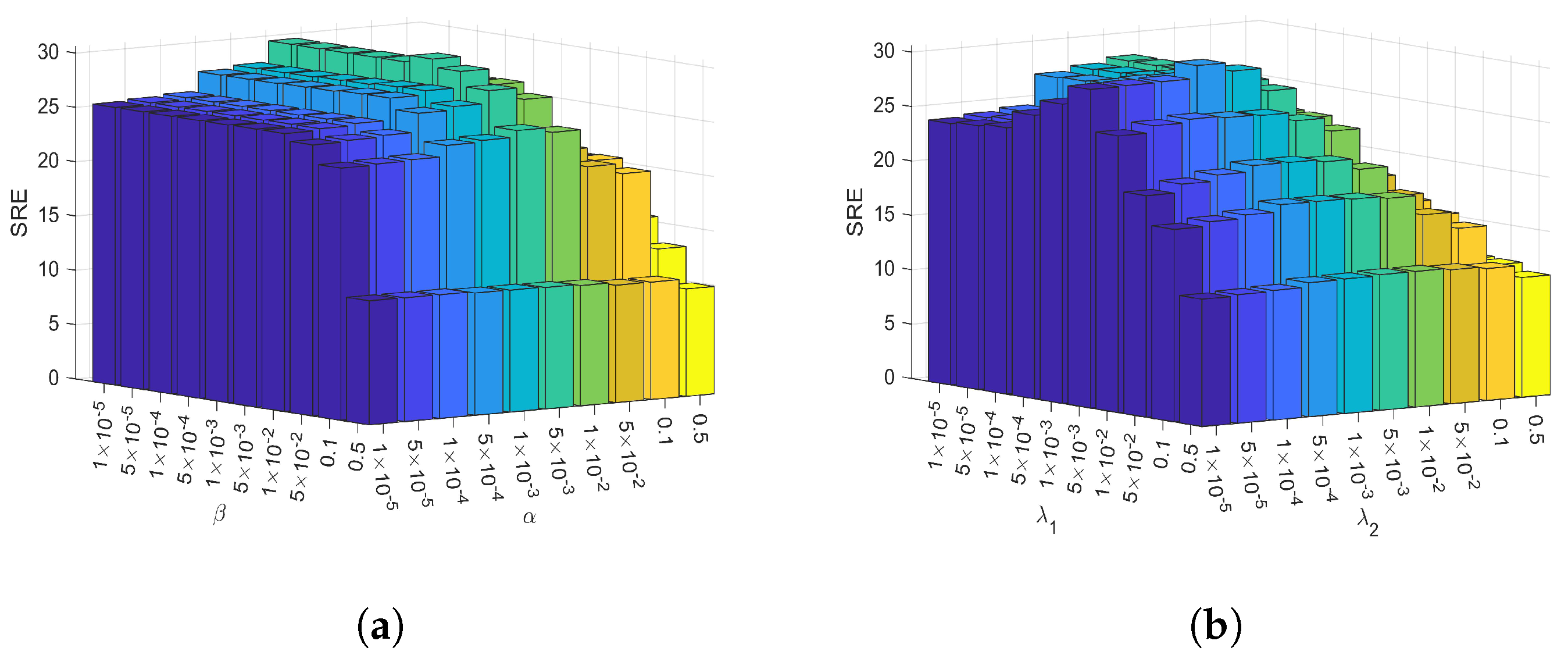
(1) The proposed active sub-abundance map number estimation strategy is based on the SVD of the denoised HSI. A clean HSI data matrix has a jump between large and small singular values (i.e., the large and small values in its singular value matrix are mutated). In order to prove the rationality of the threshold we selected, the two values of the singular value matrix of the denoised HSI data matrix of each dataset are statistically analyzed at the numerical jump.

Table 6. Two values of the singular value matrix of the denoised HSI data matrix at the numerical jump and number of active sub-abundance maps of each dataset.

Datasets	DC1	DC2	Samson	Jasper Ridge	AVIRIS Cuprite	Urban
Big singular value	1.90	4.36	0.10	4.73	0.69	1.81
Small singular value	$2.62\times {10}^{-12}$	$1.80\times {10}^{-13}$	$2.17\times {10}^{-14}$	$1.76\times {10}^{-10}$	$5.35\times {10}^{-13}$	$2.99\times {10}^{-13}$
Number of active sub-abundance maps	5	9	23	17	18	27
Number of endmember determined by VD	5	9	25	22	25	29
Number of endmember determined by Hysime	5	9	23	19	20	27
The true endmember number	5	9	Not available	Not available	Not available	Not available

presents two values of the singular value matrix of the denoised HSI data matrix at the numerical jump and number of active sub-abundance maps of each dataset. It can be seen that our selection of the threshold value of 1 $\times {10}^{-10}$ is reasonable and feasible and greatly reduces the number of sub-abundance maps that need to be regularized, saving computational overhead. To demonstrate the accuracy of this strategy, we included the results of the widely used VD [48] and Hysime [49] methods for determining the number of endmembers for comparison with our method. The experimental results proved the accuracy of this strategy.

(2) The sub-abundance map regularization strategy proposed in this paper can effectively reduce the regularization scale of the abundance matrix and save computational overhead. The inherent low-rank spatial prior of the abundance maps can be efficiently exploited by directly applying weighted nuclear norm regularization to the abundance maps. In addition, it can reduce the adverse effects of the large scale and high coherence of the spectral library on unmixing without pruning the spectral library, avoiding the risk of losing important library atoms in the pruning process. In SU, the proposed method can be applied in real scenarios as a practical fast method.

(3) Regarding the prediction of the number of active sub-abundance maps, besides the singular value thresholding method used in this paper, there are also many effective methods for estimating the number of endmembers that can be utilized. Firstly, the number of active sub-abundance maps is determined by estimating the number of endmembers, then they are specifically determined, and finally they are constrained. Such a series of operations can be used as a technical route of SU in future practice.

6. Conclusions

In this paper, we propose a novel sub-abundance map regularized sparse unmixing framework based on dynamic abundance subspace awareness, called SARSU. By constraining the contributing sub-abundance maps during the unmixing process, the method reduces the optimization complexity while mitigating the adverse effects of the large scale and high coherence of spectral libraries. For sub-abundance map regularization, a weighted nuclear norm regularization is employed to enforce the low-rank property of abundance maps, and a DTV regularization is designed to exploit additional spatial information and promote piecewise smoothness. The experimental results on both synthetic and real datasets demonstrate the effectiveness of the proposed method, achieving superior hyperspectral unmixing performance compared to other state-of-the-art sparse unmixing methods.

In future work, we will focus on addressing practical challenges and exploring solutions for sparse unmixing in real-world applications. Additionally, we will explore the method of combining semi-supervised models with deep priors in order to further develop a more ideal unmixing approach.