A Robust TEWMA–MA Control Chart Based on Sign Statistics for Effective Monitoring of Manufacturing Processes
Abstract
1. Introduction
2. The Conceptual Framework for the Control Chart
2.1. MA Control Chart
2.2. TEWMA Control Chart
2.3. Mixed MA–TEWMA Control Chart
2.4. Mixed TEWMA–MA Control Chart
2.5. Sign Statistics
2.6. Mixed MA–TEWMA Sign Control Chart
2.7. TEWMA–MA Sign Control Chart
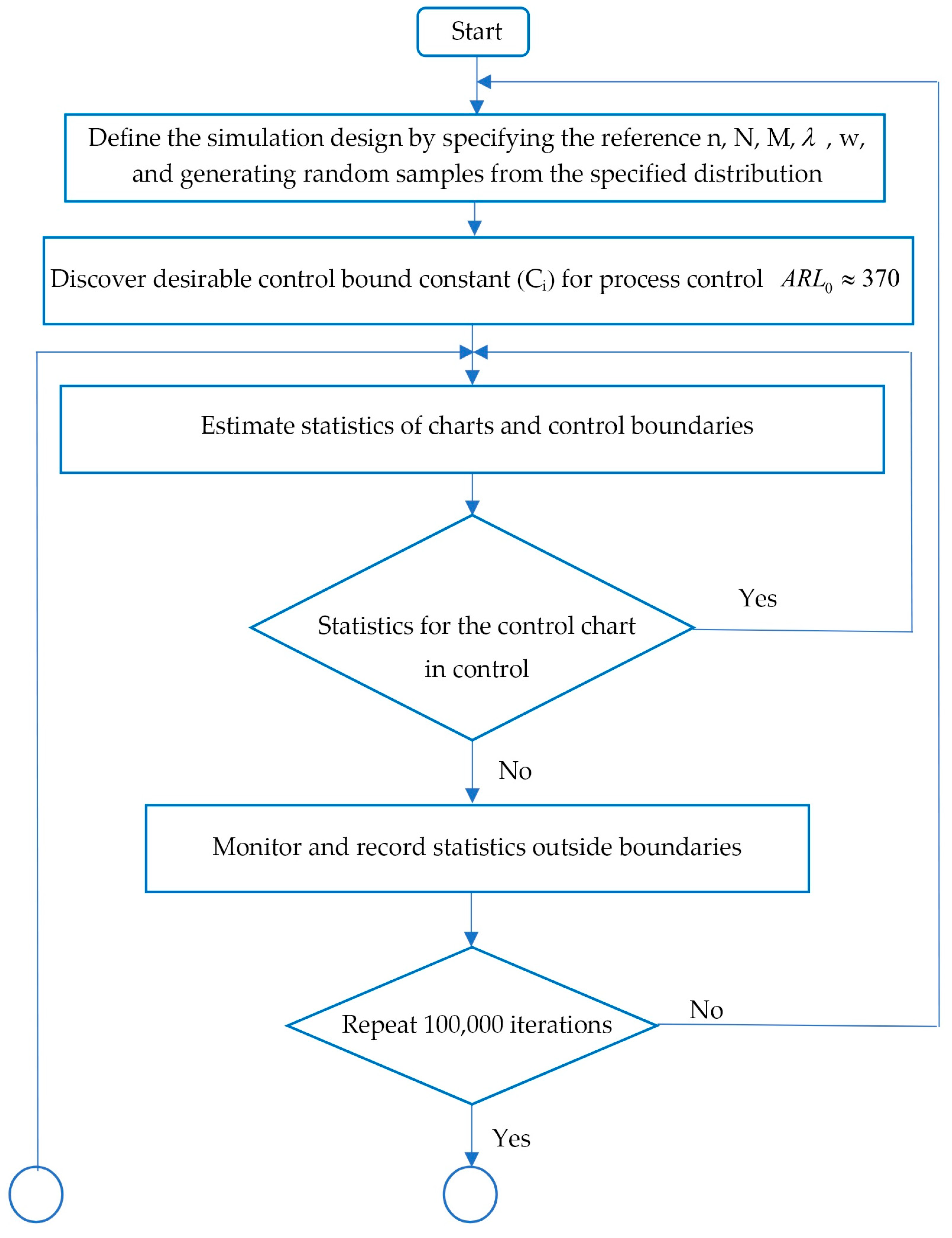
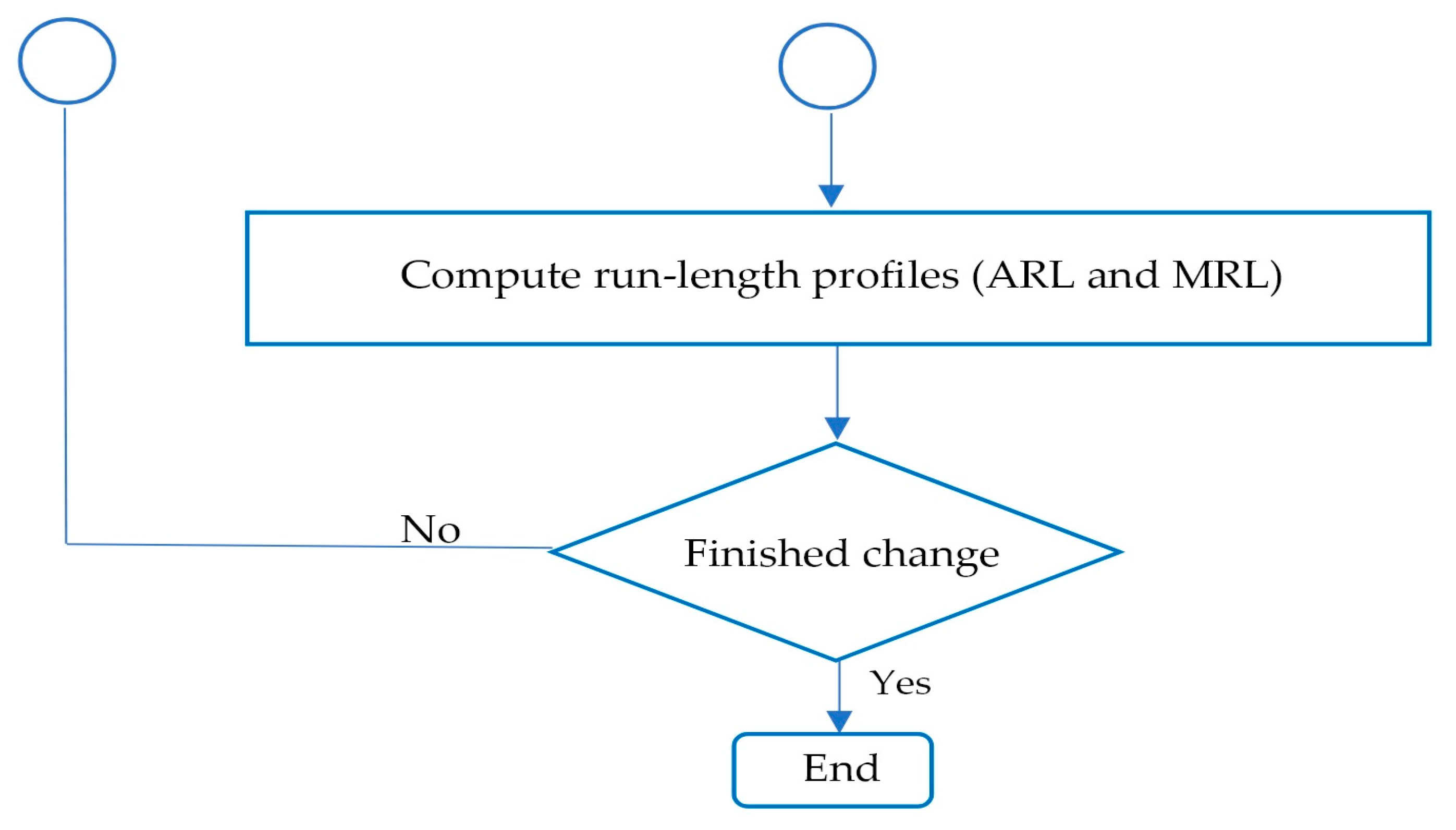
3. Methods for Evaluating Control Chart Performance
4. Simulation Results
4.1. Proposed TEWMA–MA Sign Control Chart
4.2. Performance Comparisons
4.3. Overall Performance Comparison
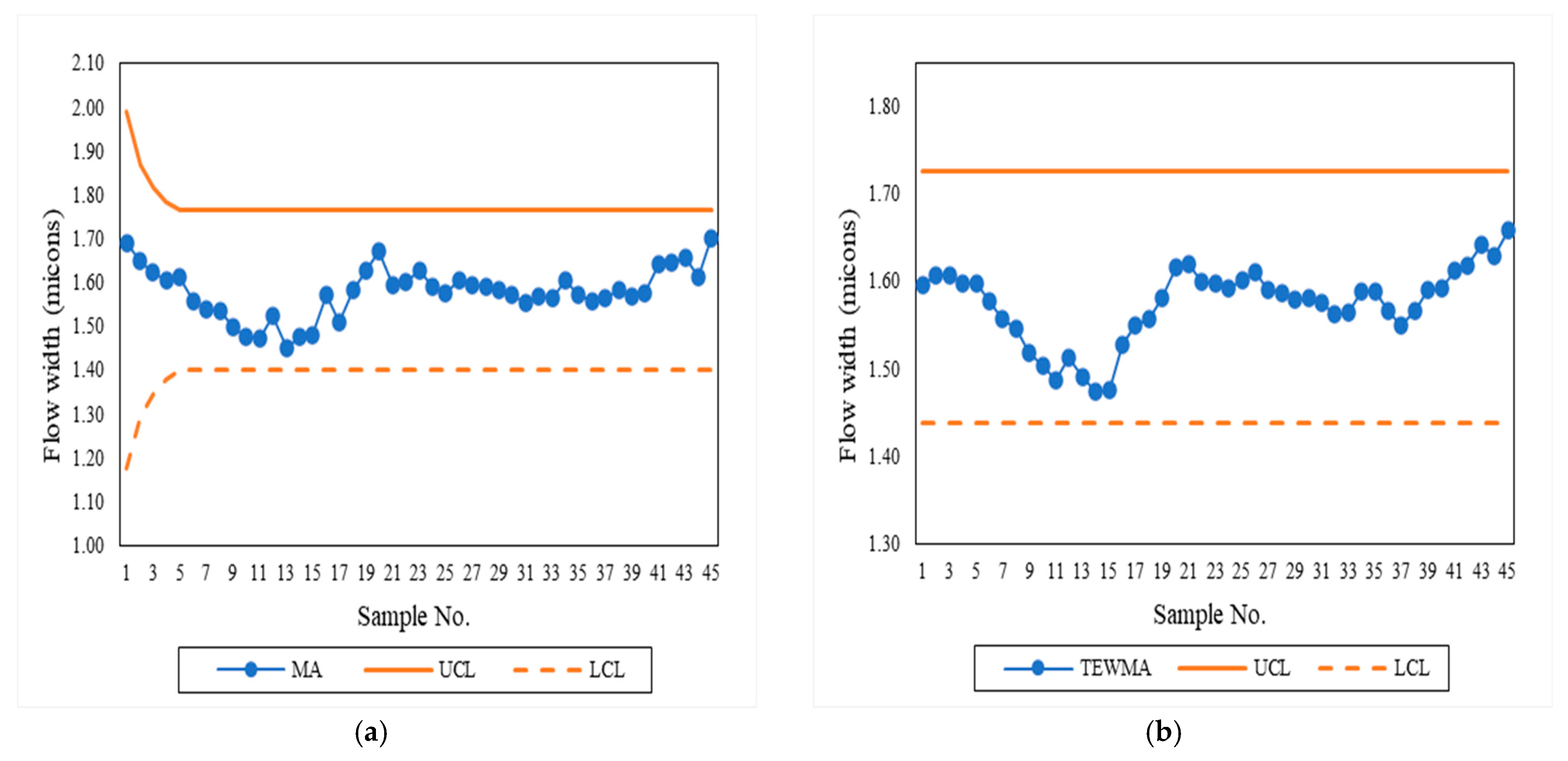
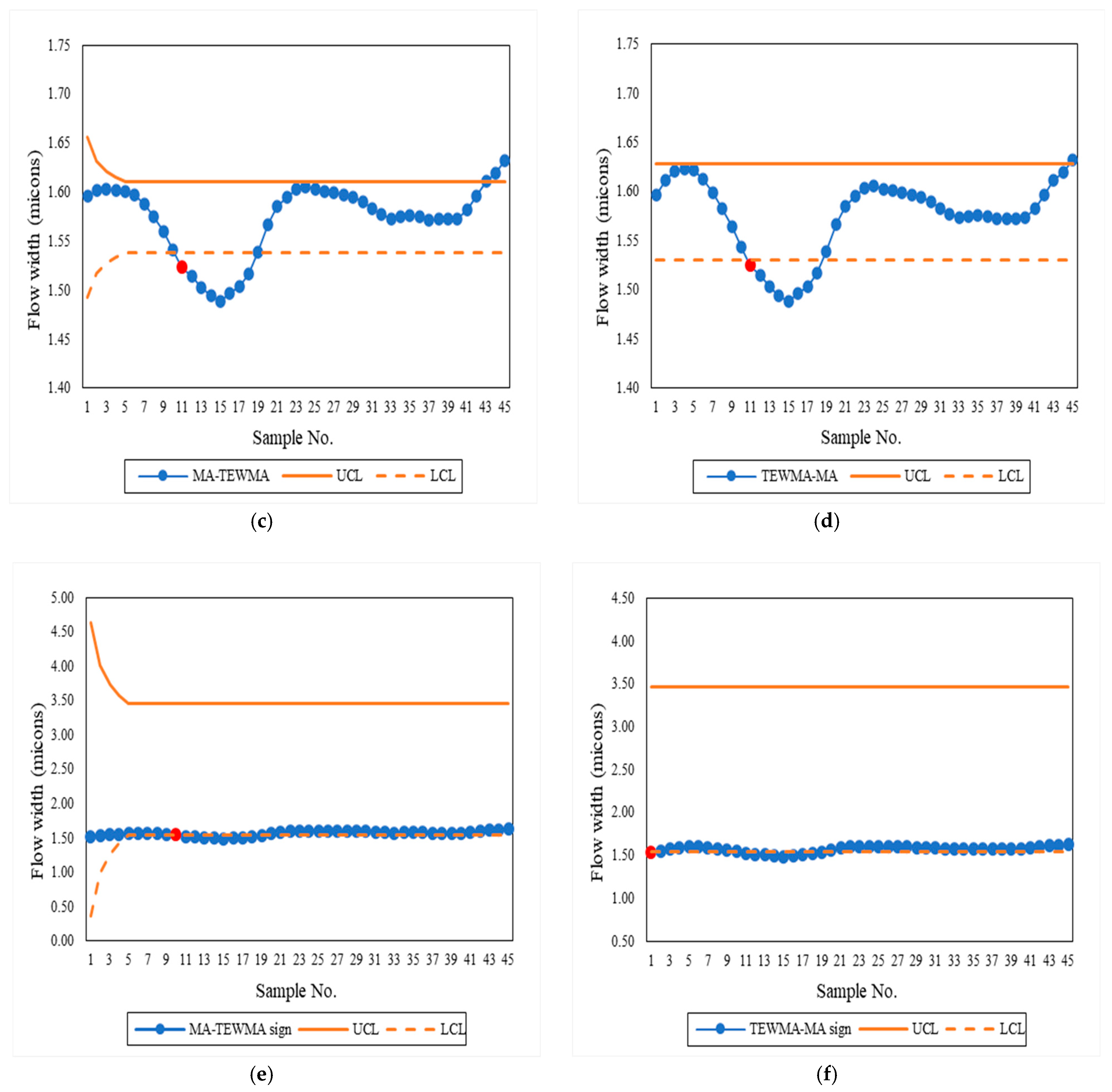
5. Empirical Application
6. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| EWMA | Exponentially weighted moving average |
| DEWMA | Double EWMA |
| TEWMA | Triple EWMA |
| MA | Moving average |
| DMA | Double MA |
| MEWMA | Modified EWMA |
| EEWMA | Extended EWMA |
| CUSUM | Cumulative sum |
| GWMA | Generally weighted moving average |
| HWMA | Homogeneously weighted moving average |
| DHWMA | Double HWMA |
| ARL | Average run length |
| SDRL | Standard deviation of run length |
| MRL | Median run length |
| PCI | Performance comparison index |
| AEQL | Average extra quadratic loss |
| RMI | Relative mean index |
| MC | Monte Carlo simulation |
Appendix A
Appendix B
References
- Shewhart, W.A. Economic Control of the Quality of the Manufactured Product; Macmillan and Company: London, UK, 1931. [Google Scholar]
- Page, E.S. Cumulative sum charts. Technometrics 1951, 3, 1–9. [Google Scholar] [CrossRef]
- Roberts, S.W. Control chart tests based on geometric moving average. Technometrics 1959, 42, 239–250. [Google Scholar] [CrossRef]
- Shamma, S.E.; Shamma, A.K. Development and evaluation of control charts using double exponentially weighted moving averages. J. Qual. Reliab. Manag. 1992, 9, 18–25. [Google Scholar] [CrossRef]
- Sheu, S.H.; Liu, T.C. The generally weighted moving average control chart for detecting small shifts in the process mean. Qual. Eng. 2003, 16, 203–231. [Google Scholar] [CrossRef]
- Khoo, M.B.C. A moving average control chart for monitoring the fraction non-conforming. Qual. Reliab. Eng. Int. 2004, 20, 617–635. [Google Scholar] [CrossRef]
- Khoo, M.B.C.; Wong, V.H. A double moving average control chart. Commun. Stat. Simul. Comput. 2008, 37, 1696–1708. [Google Scholar] [CrossRef]
- Khan, N.; Aslam, M.; Jun, C. Design of a control chart using a modified EWMA statistic. Qual. Reliab. Eng. Int. 2017, 41, 100–114. [Google Scholar] [CrossRef]
- Naveed, M.; Azam, M.; Khan, N.; Aslam, M. Design of a control chart using extended EWMA statistic. Technologies 2018, 6, 108–122. [Google Scholar]
- Alevizakos, V.; Chatterjee, K.; Koukouvinos, C. The triple exponentially weighted moving average control chart. Qual. Technol. Quant. Manag. 2021, 18, 326–354. [Google Scholar] [CrossRef]
- Graham, M.; Chakraborti, S.; Human, S. A nonparametric exponentially weighted moving average signed-rank chart for monitoring location. Comput. Stat. Data Anal. 2011, 55, 2490–2503. [Google Scholar] [CrossRef]
- Alevizakos, V.; Chatterjee, K.; Koukouvinos, C. A nonparametric triple exponentially weighted moving average sign control chart. Qual. Reliab. Eng. Int. 2021, 37, 1504–1523. [Google Scholar] [CrossRef]
- Taboran, R.; Sukparungsee, S.; Areepong, Y. Design of a new Tukey MA-DEWMA control chart to monitor process and its applications. IEEE Access 2021, 9, 102746–102757. [Google Scholar] [CrossRef]
- Taboran, R.; Sukparungsee, S. An Enhanced performance to monitor process mean with modified exponentially weighted moving average-sign control chart. Appl. Sci. Eng. Prog. 2022, 15, 5532. [Google Scholar] [CrossRef]
- Ali, S.; Abbas, Z.; Nazir, H.Z.; Riaz, M.; Zhang, X.; Li, Y. On developing sensitive nonparametric mixed control charts with application to manufacturing industry. Qual. Reliab. Eng. Int. 2021, 37, 2699–2723. [Google Scholar] [CrossRef]
- Mahmood, Y.; Khoo, M.B.C.; Teh, S.Y.; Saha, S. On designing TEWMA-Tukey control charts for normal and non-normal processes using single and repetitive sampling schemes. Comput. Ind. Eng. 2022, 170, 108343. [Google Scholar] [CrossRef]
- Abbas, Z.; Nazir, H.Z.; Akhtar, N.; Abid, M.; Riaz, M. Non-parametric progressive signed-rank control chart for monitoring the process location. J. Stat. Comput. Simul. 2022, 92, 2596–2622. [Google Scholar] [CrossRef]
- Talordphop, K.; Areepong, Y.; Sukparungsee, S. Design and analysis of extended exponentially weighted moving average signed-rank control charts for monitoring the process mean. Mathematics 2023, 11, 4482. [Google Scholar] [CrossRef]
- Raza, M.A.; Tariq, F.; Zaagan, A.A.; Engmann, E.M.; Mahnashi, A.M.; Meetei, M.Z. A nonparametric mixed exponentiallyweighted moving average-moving average control chart with an application to gas turbines. PLoS ONE 2024, 19, e0307559. [Google Scholar] [CrossRef]
- Raza, M.A.; Amin, A.; Aslam, M.; Nawaz, T.; Irfan, M.; Tariq, F. Nonparametric mixed exponentially weighted moving average-moving average control chart. Sci. Rep. 2024, 14, 6759. [Google Scholar] [CrossRef]
- Abid, M.; Sun, M.; Shabbir, A.; Bakr, M.E.; Abbas, T. An enhanced nonparametric quality control chart with application related to industrial process. Sci. Rep. 2024, 14, 13561. [Google Scholar] [CrossRef]
- Talordphop, K.; Areepong, Y.; Sukparungsee, S. Design of nonparametric extended exponentially weighted moving average-sign control chart. Appl. Sci. Eng. Prog. 2025, 18, 7272. [Google Scholar] [CrossRef]
- Montgomery, D.C. Introduction to Statistical Quality Control Case Study; John Wiley and Sons: New York, NY, USA, 2008. [Google Scholar]
| n | C | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.025 | 0.050 | 0.075 | 0.10 | 0.25 | 0.50 | 0.75 | |||
| 5 | 0.10 | 4.44 | 370.82 (261) | 321.80 (227) | 232.46 (166) | 160.18 (116) | 113.22 (83) | 32.74 (28) | 17.24 (16) | 13.39 (13) |
| 0.25 | 5.225 | 370.41 (257) | 339.69 (236) | 269.90 (188) | 201.16 (140) | 146.51 (102) | 32.51 (24) | 10.19 (9) | 6.48 (6) | |
| 0.50 | 5.193 | 370.34 (252) | 351.44 (239) | 301.85 (205) | 242.64 (165) | 188.49 (128) | 43.42 (29) | 8.85 (6) | 3.67 (3) | |
| 10 | 0.10 | 4.4375 | 370.86 (260) | 285.73 (202) | 170.43 (124) | 104.68 (78) | 70.29 (54) | 22.56 (21) | 13.53 (13) | 10.75 (11) |
| 0.25 | 5.23 | 370.75 (256) | 311.17 (215) | 211.02 (147) | 135.66 (95) | 89.15 (63) | 17.17 (14) | 6.65 (6) | 4.61 (4) | |
| 0.50 | 5.2185 | 370.72 (253) | 331.92 (226) | 250.22 (170) | 175.54 (120) | 121.10 (82) | 19.63 (13) | 3.92 (3) | 1.78 (1) | |
| n | C | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.025 | 0.050 | 0.075 | 0.10 | 0.25 | 0.50 | 0.75 | |||
| 5 | 0.10 | 12.7185 | 370.87 (269) | 241.68 (179) | 169.57 (129) | 127.00 (99) | 100.09 (80) | 45.26 (41) | 29.70 (29) | 25.04 (25) |
| 0.25 | 9.95 | 370.27 (260) | 257.78 (183) | 184.82 (132) | 137.64 (99) | 105.30 (76) | 34.98 (27) | 15.18 (13) | 10.84 (10) | |
| 0.50 | 7.927 | 370.68 (255) | 274.56 (191) | 207.44 (145) | 159.85 (111) | 125.31 (87) | 39.43 (28) | 12.22 (9) | 6.42 (5) | |
| 10 | 0.10 | 16.5975 | 370.78 (270) | 207.77 (157) | 134.37 (105) | 96.40 (78) | 75.00 (63) | 37.62 (36) | 27.06 (27) | 23.23 (2) |
| 0.25 | 12.32 | 370.59 (261) | 223.03 (158) | 143.68 (103) | 98.55 (72) | 71.31 (53) | 22.11 (18) | 11.31 (11) | 8.87 (9) | |
| 0.50 | 9.4675 | 370.88 (256) | 243.38 (168) | 166.07 (115) | 116.63 (81) | 84.42 (59) | 20.80 (15) | 6.33 (5) | 3.73 (3) | |
| Control Chart | Ci | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.025 | 0.050 | 0.075 | 0.10 | 0.25 | 0.50 | 0.75 | ||
| normal (0, 1) distribution | |||||||||
| MA | C1 = 2.885 | 370.87 (257) | 366.99 (254) | 354.01 (245) | 334.22 (232) | 310.96 (215) | 162.82 (113) | 51.28 (36) | 20.39 (14) |
| TEWMA | C2 = 2.44 | 370.86 (259) | 360.61 (251) | 333.63 (233) | 295.67 (208) | 255.25 (179) | 93.51 (67) | 28.43 (22) | 14.49 (12) |
| MA–TEWMA | C3 = 5.215 | 370.58 (259) | 359.73 (251) | 333.53 (234) | 294.75 (208) | 254.27 (179) | 93.43 (68) | 29.53 (23) | 15.98 (14) |
| TEWMA–MA | C4 = 5.24 | 370.65 (256) | 358.96 (248) | 332.33 (230) | 293.03 (203) | 252.17 (176) | 90.47 (64) | 26.83 (20) | 13.71 (12) |
| MA–TEWMA Sign | C5 = 5.1985 | 370.54 (260) | 340.14 (240) | 272.13 (193) | 204.41 (145) | 150.19 (107) | 36.28 (28) | 13.33 (12) | 9.45 (9) |
| TEWMA–MA Sign | C = 5.225 | 370.41 (257) | 339.69 (236) | 269.90 (188) | 201.16 (140) | 146.51 (102) | 32.51 (24) | 10.19 (9) | 6.48 (6) |
| Laplace (0, 1) distribution | |||||||||
| MA | C1 = 3.114 | 369.98 (257) | 369.45 (257) | 366.94 (255) | 360.60 (250) | 352.53 (245) | 278.06 (191) | 147.07 (102) | 74.07 (51) |
| TEWMA | C2 = 2.495 | 370.40 (261) | 366.21 (257) | 355.08 (249) | 337.02 (236) | 314.68 (220) | 168.26 (119) | 58.39 (43) | 27.25 (21) |
| MA–TEWMA | C3 = 5.3345 | 370.79 (261) | 366.71 (258) | 354.69 (249) | 335.50 (236) | 313.23 (220) | 166.47 (118) | 58.41 (43) | 28.30 (22) |
| TEWMA–MA | C4 = 5.3655 | 370.35 (256) | 366.53 (254) | 354.34 (245) | 334.97 (232) | 311.20 (215) | 163.49 (114) | 55.49 (40) | 25.80 (20) |
| MA–TEWMA Sign | C5 = 5.199 | 370.67 (259) | 326.22 (230) | 240.64 (171) | 168.72 (120) | 119.09 (86) | 29.91 (23) | 12.94 (12) | 9.72 (9) |
| TEWMA–MA Sign | C = 5.2253 | 370.26 (255) | 324.81 (225) | 237.66 (166) | 167.89 (115) | 115.18 (81) | 26.23 (20) | 9.81 (9) | 6.75 (6) |
| Control Chart | C | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.025 | 0.050 | 0.075 | 0.10 | 0.25 | 0.50 | 0.75 | ||
| exponential (1) distribution | |||||||||
| MA | C1 = 3.3435 | 370.52 (255) | 304.11 (209) | 253.37 (174) | 211.93 (146) | 179.71 (123) | 78.33 (54) | 30.77 (21) | 16.55 (12) |
| TEWMA | C2 = 2.4493 | 370.74 (258) | 294.94 (206) | 237.74 (166) | 193.94 (136) | 160.53 (113) | 65.25 (47) | 26.87 (20) | 16.25 (13) |
| MA–TEWMA | C3 = 5.23 | 370.51 (258) | 296.07 (207) | 239.49 (166) | 195.42 (137) | 162.12 (115) | 66.91 (48) | 28.52 (22) | 17.94 (14) |
| TEWMA–MA | C4 = 5.2625 | 370.35 (255) | 294.16 (203) | 236.44 (163) | 191.97 (133) | 158.38 (110) | 63.69 (45) | 26.07 (20) | 15.96 (13) |
| MA–TEWMA Sign | C5 = 9.9385 | 370.53 (262) | 259.32 (185) | 187.11 (135) | 140.42 (102) | 108.46 (80) | 38.37 (31) | 18.48 (17) | 14.00 (13) |
| TEWMA–MA Sign | C = 9.95 | 370.27 (260) | 257.78 (183) | 184.82 (132) | 137.64 (99) | 105.30 (76) | 34.98 (27) | 15.18 (13) | 10.84 (10) |
| gamma (4, 1) distribution | |||||||||
| MA | C1 = 3.022 | 370.92 (257) | 264.63 (183) | 192.79 (133) | 143.76 (99) | 109.43 (76) | 31.30 (22) | 9.09 (7) | 4.33 (3) |
| TEWMA | C2 = 2.436 | 370.49 (261) | 273.19 (191) | 190.63 (134) | 135.34 (96) | 98.41 (70) | 27.10 (21) | 10.70 (9) | 7.07 (6) |
| MA–TEWMA | C3 = 5.2075 | 370.43 (261) | 275.07 (194) | 192.12 (136) | 136.94 (97) | 99.73 (72) | 28.65 (22) | 12.39 (11) | 8.82 (8) |
| TEWMA–MA | C4 = 5.2328 | 370.26 (258) | 272.59 (189) | 188.65 (131) | 133.20 (93) | 96.03 (68) | 26.00 (20) | 10.48 (9) | 7.07 (6) |
| MA–TEWMA Sign | C5 = 7.29 | 370.99 (261) | 179.83 (129) | 100.58 (73) | 63.32 (47) | 43.73 (34) | 15.05 (14) | 9.90 (10) | 8.68 (9) |
| TEWMA–MA Sign | C = 7.305 | 370.61 (259) | 176.88 (125) | 97.05 (70) | 59.55 (44) | 40.02 (30) | 11.80 (10) | 6.86 (7) | 5.70 (5) |
| Control Chart | RMI | AEQL | PCI | Control Chart | RMI | AEQL | PCI |
|---|---|---|---|---|---|---|---|
| normal (0, 1) distribution | exponential (1) distribution | ||||||
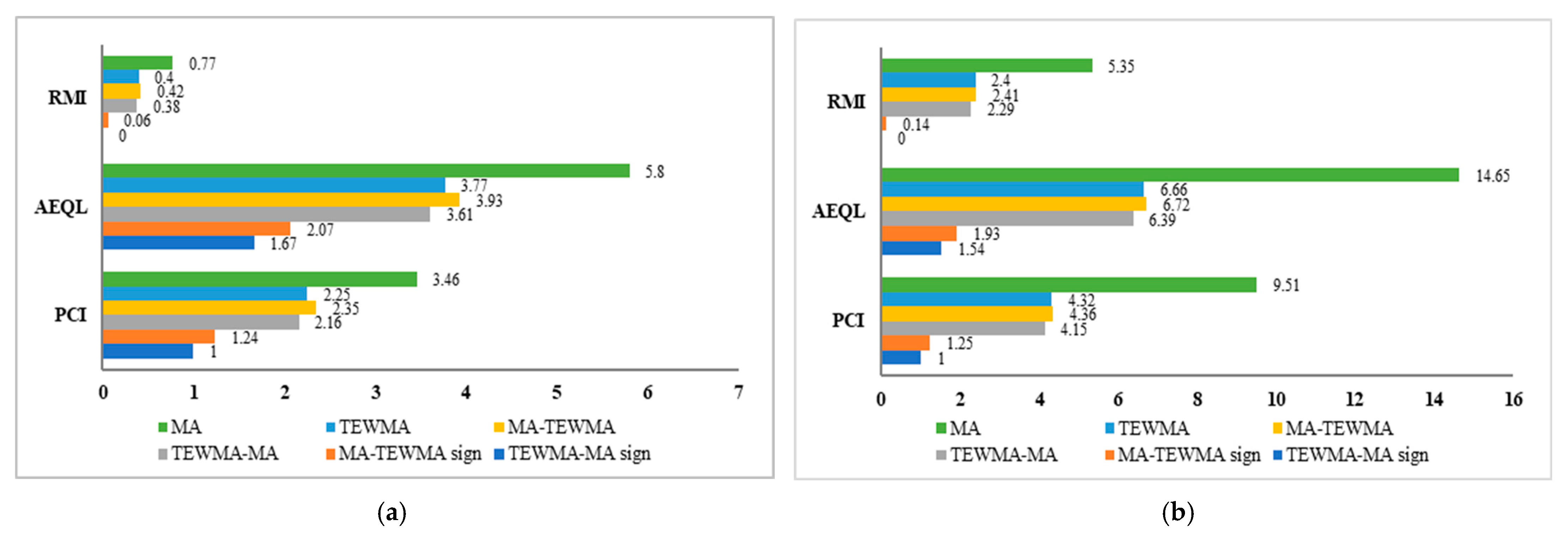
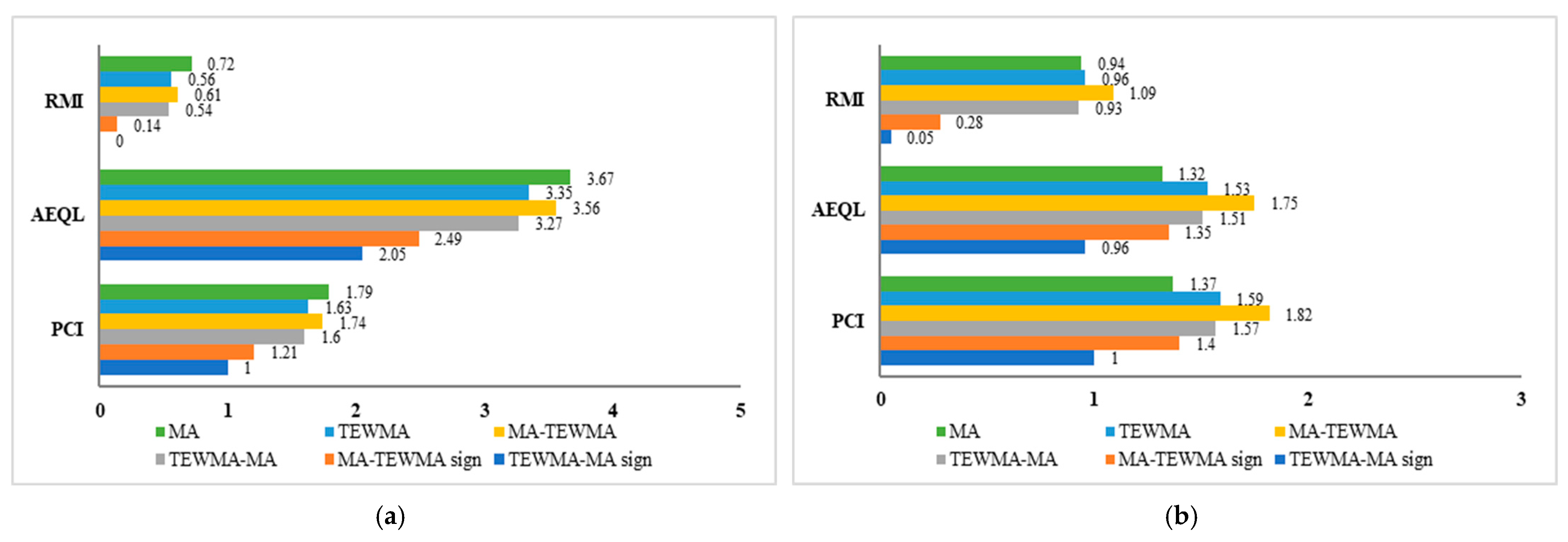
| MA | 0.77 | 5.80 | 3.46 | MA | 0.72 | 3.67 | 1.79 |
| TEWMA | 0.40 | 3.77 | 2.25 | TEWMA | 0.56 | 3.35 | 1.63 |
| MA–TEWMA | 0.42 | 3.93 | 2.35 | MA–TEWMA | 0.61 | 3.56 | 1.74 |
| TEWMA–MA | 0.38 | 3.61 | 2.16 | TEWMA–MA | 0.54 | 3.27 | 1.60 |
| MA–TEWMA Sign | 0.06 | 2.07 | 1.24 | MA–TEWMA Sign | 0.14 | 2.49 | 1.21 |
| TEWMA–MA Sign | 0 | 1.67 | 1.00 | TEWMA–MA Sign | 0 | 2.05 | 1.00 |
| Laplace (0, 1) distribution | gamma (4, 1) distribution | ||||||
| MA | 5.35 | 14.65 | 9.51 | MA | 0.94 | 1.32 | 1.37 |
| TEWMA | 2.40 | 6.66 | 4.32 | TEWMA | 0.96 | 1.53 | 1.59 |
| MA–TEWMA | 2.41 | 6.72 | 4.36 | MA–TEWMA | 1.09 | 1.75 | 1.82 |
| TEWMA–MA | 2.29 | 6.39 | 4.15 | TEWMA–MA | 0.93 | 1.51 | 1.57 |
| MA–TEWMA Sign | 0.14 | 1.93 | 1.25 | MA–TEWMA Sign | 0.28 | 1.35 | 1.40 |
| TEWMA–MA Sign | 0 | 1.54 | 1.00 | TEWMA–MA Sign | 0.05 | 0.96 | 1.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saesuntia, P.; Areepong, Y.; Sukparungsee, S. A Robust TEWMA–MA Control Chart Based on Sign Statistics for Effective Monitoring of Manufacturing Processes. Mathematics 2025, 13, 3789. https://doi.org/10.3390/math13233789
Saesuntia P, Areepong Y, Sukparungsee S. A Robust TEWMA–MA Control Chart Based on Sign Statistics for Effective Monitoring of Manufacturing Processes. Mathematics. 2025; 13(23):3789. https://doi.org/10.3390/math13233789
Chicago/Turabian StyleSaesuntia, Piyatida, Yupaporn Areepong, and Saowanit Sukparungsee. 2025. "A Robust TEWMA–MA Control Chart Based on Sign Statistics for Effective Monitoring of Manufacturing Processes" Mathematics 13, no. 23: 3789. https://doi.org/10.3390/math13233789
APA StyleSaesuntia, P., Areepong, Y., & Sukparungsee, S. (2025). A Robust TEWMA–MA Control Chart Based on Sign Statistics for Effective Monitoring of Manufacturing Processes. Mathematics, 13(23), 3789. https://doi.org/10.3390/math13233789







