Revisiting Wilf’s Question for Numerical Semigroups S₃ and Inequalities for Rescaled Genera

Abstract

We consider numerical semigroups $S_3=⟨d_1,d_2,d_3⟩$, which are minimally generated by three positive integers. We revisit the Wilf question for $S_3$ and, making use of identities for degrees of syzygies of such semigroups, we provide a short proof of existence of an affirmative answer. Finally, we find the upper and lower bounds for the rescaled genera of numerical semigroups $S_3$.

1. Introduction

Let a numerical semigroup $S_3$ be minimally generated by a set of natural numbers $\{d_1,d_2,d_3\}$, where

$$\begin{array}{c}\hfill gcd(d_1,d_2,d_3)=1,3\le d_1<d_2<d_3\le d_1{d}_2-d_1-d_2,\end{array}$$

(1)

and none of its generators is linearly representable by the rest of them. The generating function of $S_3$, denoted as $H\left(S_3;t\right)$, is defined as

$$\begin{array}{c}\hfill H\left(S_3;t\right)=\sum _{s\in S_3}{t}^s,t<1,0\in S_3.\end{array}$$

This function is referred to as the Hilbert series of $S_3$ and has a rational representation (Rep),

$$\begin{array}{c}\hfill H\left(S_3;t\right)={\displaystyle \frac{1-t^{x_1}-t^{x_2}-t^{x_3}+t^{y_1}+t^{y_2}}{\left(1-t^{d_1}\right)\left(1-t^{d_2}\right)\left(1-t^{d_3}\right)}},x_j,y_j\in {\mathbb{Z}}_{>},\end{array}$$

where $x_j$ and $y_j$ denote degrees of the syzygies. The Frobenius number, $F_3$, is the largest integer that cannot be represented as a linear combination of the elements in the triple $\{d_1,d_2,d_3\}$ with non-negative integer coefficients. When shifting by one unit to $c_3=F_3+1$, it is often used in commutative algebra and is referred to as the conductor of $S_3$. The largest degree, $g_3=max\left\{y_1,y_2\right\}$, is related to $F_3$ by the following equation:

$$\begin{array}{c}\hfill g_3=F_3+{\sigma }_1,{\sigma }_1=d_1+d_2+d_3.\end{array}$$

Here ${\mathsf{\Delta }}_3={\mathbb{Z}}_{>}\backslash S_3$ and $G_0=\#{\mathsf{\Delta }}_3$ stand for the set of non-representable integers (gaps) and the genus of the semigroup $S_3$, respectively.

The set ${\mathsf{\Delta }}_3$ comprises two sorts of gaps: (1) those $s\in {\mathsf{\Delta }}_3$ such that $F_3-s\notin {\mathsf{\Delta }}_3$ and (2) those $s\in {\mathsf{\Delta }}_3$ such that $F_3-s\in {\mathsf{\Delta }}_3$. Such a dichotomy in the set ${\mathsf{\Delta }}_3$ leads to a simple inequality:

$$\begin{array}{c}\hfill w_3\ge {\displaystyle \frac{1}{2}},w_3={\displaystyle \frac{G_0}{c_3}}.\end{array}$$

(2)

The equality $w_3=1/2$ is attained if and only if the semigroup is symmetric, in which case ${\mathsf{\Delta }}_3$ consists only of gaps of the first sort. In fact, (2) holds for semigroups $S_m$ of any m, i.e., $w_m=G_0/c_m\ge 1/2$, where $c_m$ denotes a conductor.

In 1978, Wilf [1] posed two questions, which are often referred to as Wilf’s questions (WQs). The first of them was the following: is it true that for a given $S_m$, the inequality

$$\begin{array}{c}\hfill w_m\le {\displaystyle \frac{m-1}{m}},\end{array}$$

(3)

holds, with equality only for the generators $m,m+1,\dots ,2m-1$? In a seminal paper [2], by means of an embedding procedure for a sequence of partial gapsets of semigroup $S_m$, it was shown that

$$\begin{array}{c}\hfill w_m\le {\displaystyle \frac{{\tau }_m}{{\tau }_m+1}},\end{array}$$

(4)

where ${\tau }_m$ denotes the type of $S_m$. Inequality (4) coincides with (3) if $m=2,3$, but it does not imply (3) for $m>3$. Over the last decade, a vast body of the literature [3,4,5,6,7] has been devoted to Wilf’s question. Despite the attention it has attracted in various special cases, it remains completely unsolved for the non-symmetric semigroups $S_m$, $m\ge 4$.

Based on the polynomial identities for the degrees of syzygies [8], the present paper suggests quite different approach to obtain an affirmative answer to WQ in semigroups $S_3$. Within this framework, we also derive the lower bound for $F_3$, as well as the lower and upper bounds for rescaled genera of $S_3$. From the perspective of WQ, the developed approach can be applied to semigroups $S_m$, $m\ge 4$. We discuss this broader perspective in the final section.

2. Syzygy Identities for Numerical Semigroups ${\mathit{S}}_{\mathbf{3}}$

Consider a numerical semigroup $S_3$ and write the polynomial identities (see [8], Theorem 1) for the degrees of syzygies $x_j$ and $y_j$. Denote by $X_r$ and $Y_r$ the following two power sums:

$$\begin{array}{c}\hfill \left(a\right)X_r=x_1^r+x_2^r+x_3^r,\left(b\right)Y_r=y^r+g_3^r,0\le x_j,y<g_3.\end{array}$$

(5)

Consider a set of polynomial equations for five real variables, $x_1$, $x_2$, $x_3$, y, and $g_3$:

$$\begin{array}{c}\left(a\right)Y_1-X_1=0,\hfill \\ \left(b\right)Y_2-X_2=2{\pi }_3,{\pi }_3=d_1{d}_2{d}_3,\hfill \\ \left(c\right)Y_{r+3}-X_{r+3}={\displaystyle \frac{(r+3)!}{r!}}{K}_r{\pi }_3,r\ge 0,K_r>0.\hfill \end{array}$$

(6)

The coefficients $K_r$ exhibit a linear combination of the higher genera $G_0,\dots ,G_r$ of the numerical semigroup $S_3$, i.e., $G_r={\sum }_{s\in {\mathsf{\Delta }}_3}{s}^r$ for $r\ge 0$ (see Formulas (22) and (23) in [9]).

E.g.,

$$\begin{array}{c}{K}_0=G_0+{\delta }_1,{\delta }_k={\displaystyle \frac{{\sigma }_k-1}{2^k}},\hfill \\ K_1=G_1+{\displaystyle \frac{{\sigma }_1}{2}}{G}_0+{\displaystyle \frac{3{\delta }_1^2+{\delta }_2}{6}},{\sigma }_k=d_1^k+d_2^k+d_3^k,\hfill \\ K_2=G_2+{\sigma }_1{G}_1+{\displaystyle \frac{3{\sigma }_1^2+{\sigma }_2}{12}}{G}_0+{\displaystyle \frac{{\delta }_1({\delta }_1^2+{\delta }_2)}{3}},\mathrm{etc}.\hfill \end{array}$$

(7)

Explicit expressions of $K_r$ are given in [9], in Formula (27).

2.1. Lower Bound of $g_3$

Utilizing Newton–Maclaurin inequalities (see [10], p. 52) for the power sums $X_j$ and $Y_j$,

$$\begin{array}{c}\hfill \left(a\right)3X_2>X_1^2,\left(b\right)2Y_2>Y_1^2,\end{array}$$

(8)

and substituting Equalities (6)a and (6)b into inequality (8)a, we get

$$\begin{array}{c}\hfill 3\left(Y_2-2{\pi }_3\right)>Y_1^2.\end{array}$$

(9)

By equality (5)b, we find a relationship between $Y_1$ and $Y_2$,

$$\begin{array}{c}\hfill Y_2=Y_1^2-2g_3{Y}_1+2g_3^2,\end{array}$$

(10)

and substitute it into (9). So, we find the following inequality:

$$\begin{array}{c}\hfill Y_1^2-3g_3{Y}_1+3g_3^2>3{\pi }_3,g_3<Y_1<2g_3.\end{array}$$

(11)

Denote u as the ratio $Y_1/g_3$ and rescale Inequality (11) by $g_3$, dividing by $g_3^2$, as follows:

$$\begin{array}{c}\hfill {\displaystyle \frac{g_3^2}{3{\pi }_3}}>P\left(u\right),P\left(u\right)={\displaystyle \frac{1}{u^2-3u+3}},u={\displaystyle \frac{Y_1}{g_3}},1<u<2.\end{array}$$

(12)

We find a range of $g_3$ where Inequality (12) is satisfied for any $u\in (1,2)$. Since a convex function $P\left(u\right)$ reaches its minimum $P\left(u\right)=1$ at $u=1,2$, we arrive at Davison’s lower bound [11] for $g_3$,

$$\begin{array}{c}\hfill g_3>\sqrt{3{\pi }_3}.\end{array}$$

(13)

In fact, more accurate reasoning [12], such as the constraint $Y_1\le 2g_3-1$, leads to a slightly stronger bound, $\sqrt{3}\sqrt{{\pi }_3+1}$.

2.2. Lower and Upper Bounds of $h_0=K_0/g_3$

We introduce elementary symmetric polynomials in three variables,

$$\begin{array}{c}\hfill {\mathcal{X}}_1=x_1+x_2+x_3,{\mathcal{X}}_2=x_1{x}_2+x_2{x}_3+x_3{x}_1,{\mathcal{X}}_3=x_1{x}_2{x}_3,\end{array}$$

which are related by Newton’s recursion identities to power sums $X_k$, defined in (5)a:

$$\begin{array}{c}\hfill {\mathcal{X}}_1=X_1,2{\mathcal{X}}_2=X_1^2-X_2,6{\mathcal{X}}_3=X_1^3-3X_1{X}_2+2X_3.\end{array}$$

(14)

Recall the Newton–Maclaurin inequalities (see [10], p. 52) for polynomials ${\mathcal{X}}_k(x_1,x_2,x_3)$:

$$\begin{array}{c}\hfill \left(a\right){\displaystyle \frac{{\mathcal{X}}_1}{3}}\ge {\left({\displaystyle \frac{{\mathcal{X}}_2}{3}}\right)}^{1/2}\ge {\mathcal{X}}_3^{1/3},\left(b\right){\left({\displaystyle \frac{{\mathcal{X}}_2}{3}}\right)}^2\ge {\displaystyle \frac{{\mathcal{X}}_1}{3}}{\mathcal{X}}_3.\end{array}$$

(15)

Consider the second inequality in (15)a, and substitute the identities from (14) into it:

$$\begin{array}{c}\hfill {(X_1^2-X_2)}^3\ge 6{(X_1^3-3X_1{X}_2+2X_3)}^2.\end{array}$$

Next, substitute the first three equalities (6)a,b,c into the last inequality:

$$\begin{array}{c}\hfill {(Y_1^2-Y_2+2{\pi }_3)}^3\ge 6{(Y_1^3-3Y_1{Y}_2+6Y_1{\pi }_3+2Y_3-12{\pi }_3{K}_0)}^2.\end{array}$$

(16)

Combining the identity for power sums, $2Y_3=3Y_1{Y}_2-Y_1^3$, and the relation in (10), we simplify (16) to obtain

$$\begin{array}{c}\hfill {(g_3{Y}_1-g_3^2+{\pi }_3)}^3\ge 27{\pi }_3^2{(Y_1-2K_0)}^2.\end{array}$$

(17)

We introduce two new variables, v and $h_0$:

$$\begin{array}{c}\hfill v={\displaystyle \frac{{\pi }_3}{g_3^2}},0<v<{\displaystyle \frac{1}{3}},h_0={\displaystyle \frac{K_0}{g_3}},{\displaystyle \frac{1}{2}}\le h_0\le w_3.\end{array}$$

(18)

Rescaling (17) by dividing both sides by $g_3^6$, we arrive at the following inequality:

$$\begin{array}{c}\hfill {(u-2h_0)}^2\le Q(u,v),Q(u,v)={\displaystyle \frac{{(u-1+v)}^3}{27v^2}}<Q(2,v).\end{array}$$

(19)

In (18), v is bounded from above due to the constraint in (13) and $h_0$ is bounded from below due to the constraint in (2).

Lemma 1.

$$\begin{array}{c}\hfill {\displaystyle \frac{1}{2}}\le h_0<{\displaystyle \frac{5}{9}}\simeq 0.5555.\end{array}$$

(20)

Proof. 

Determine the upper bound of $h_0$ and express Inequality (19) as

$$\begin{array}{c}\hfill u<2h_0+\sqrt{Q(2,v)}.\end{array}$$

On the other hand, the inequality $u<2$ always holds. To find the maximal value of $h_0$ while both inequalities are still satisfied, we must choose a value for v that provides the minimal value of $Q(2,v)$ within the interval $v\in (0,1/3)$. This occurs at at $v=1/3$.

Thus, we arrive at the equality

$$\begin{array}{c}\hfill 2h_0<2-\sqrt{Q(2,1/3)}={\displaystyle \frac{10}{9}},\end{array}$$

Combining the last inequality with (18), we finally obtain (20) and the Lemma is proven.  □

Figure 1 presents the plot of the function $\mathsf{\Phi }(u,v)={\displaystyle \frac{1}{2}}\left(u-\sqrt{Q(u,v)}\right)$ and the points $(u,v,h_0)$ for ten semigroups $S_3$.

2.3. Wilf’s Question for $S_3$

We prove that WQ has an affirmative answer for all non-symmetric semigroups $S_3$ and start with $\langle 3,d_2,d_3\rangle$. Using Lemma 6 in [13], which establishes inequalities for such semigroups, we get

$$\begin{array}{c}\hfill {\displaystyle \frac{3}{2}}{c}_3\le 3G_0<2c_3+1.\end{array}$$

(21)

By replacing the strict inequality on the r.h.s. of (21) with a non-strict one, $3G_0\le 2c_3$, we arrive at $w_3\le 2/3$.

Consider numerical semigroups $S_3$ with $d_1\ge 4$. Using the relation $g_3=c_3+2{\delta }_1$, the definition of $h_0$ (18), and the expression for $K_0$ (7), we can represent Inequality (20) in Lemma 1 for the upper bound as follows:

$$\begin{array}{c}\hfill w_3<{\displaystyle \frac{5}{9}}+{\displaystyle \frac{e_3}{9}},e_3={\displaystyle \frac{{\delta }_1}{c_3}}.\end{array}$$

(22)

A sufficient (not necessary) condition for an affirmative answer to WQ is the inequality $e_3\le 1$.

Theorem 1.

Let $S_3=\langle d_1,d_2,d_3\rangle$ be a non-symmetric numerical semigroup with $d_1\ge 4$. When its generators satisfy Condition (1), WQ is answered affirmatively for all semigroups $S_3$.

Proof. 

Instead of $e_3$, consider its inverse, $1/e_3$, and apply Inequality (13),

$$\begin{array}{c}\hfill {\displaystyle \frac{1}{e_3}}={\displaystyle \frac{g_3}{{\delta }_1}}-2>2\left({\displaystyle \frac{\sqrt{3{\pi }_3}}{{\sigma }_1-1}}-1\right)>2\left({\displaystyle \frac{\sqrt{3{\pi }_3}}{{\sigma }_1}}-1\right).\end{array}$$

(23)

According to Equation (23), a sufficient (but not necessary) condition to provide $e_3<1$ is the Diophantine inequality:

$$\begin{array}{c}\hfill {\rho }_3<{\displaystyle \frac{2}{\sqrt{3}}}\simeq 1.1547,d_1\ge 4,{\rho }_3={\displaystyle \frac{d_1+d_2+d_3}{\sqrt{d_1{d}_2{d}_3}}}.\end{array}$$

(24)

Analyze its solvability for different triples $\{d_1,d_2,d_3\}$. To perform this, represent (24) as follows:

$$\begin{array}{c}\hfill {(\sqrt{d_3}-\sqrt{d_2})}^2<2\left(\sqrt{{\displaystyle \frac{d_1}{3}}}-1\right)\sqrt{d_2{d}_3}-d_1,\end{array}$$

This necessarily yields a lower bound of the product $d_2{d}_3$:

$$\begin{array}{c}\hfill d_2{d}_3>C\left(d_1\right),C\left(d_1\right)={\displaystyle \frac{3}{4}}{\left({\displaystyle \frac{d_1}{\sqrt{d_1}-\sqrt{3}}}\right)}^2.\end{array}$$

(25)

Here, the concave function $C\left(d_1\right)$ reaches its minimum $C\left(12\right)=36$ (see Figure 2).

The criterion (25) must be supplemented by an additional restriction, $d_3>d_2>d_1$, or

$$\begin{array}{c}\hfill d_2{d}_3\ge (d_1+1)(d_1+2).\end{array}$$

The first values of the descendant sequence $C\left(d_1\right)$ are given below:

$$\begin{array}{c}\hfill C\left(4\right)=167.14,C\left(5\right)=73.81,C\left(6\right)=52.46,C\left(7\right)=44.02,\dots .\end{array}$$

The final criterion for generators $d_j$ to satisfy (25) reads

$$\begin{array}{c}\hfill \left(1\right)d_1=4,d_2{d}_3>167,\left(2\right)d_1=5,d_2{d}_3>73\left(3\right)d_1\ge 6.\end{array}$$

(26)

A brief analysis of (26) and the restriction $d_3<d_1{d}_2-d_1-d_2$ yields a short list of non-symmetric semigroups $S_3$ with $d_1=4,5$, where Inequality (24) might be broken. Below, we present

Table 1. Thirteen semigroups $S_3$, where ${\rho }_3>1.1547$.

${\mathit{S}}_3$	${\mathit{\rho }}_3$	${\mathit{e}}_3$	${\mathit{w}}_3$	${\mathit{h}}_0$
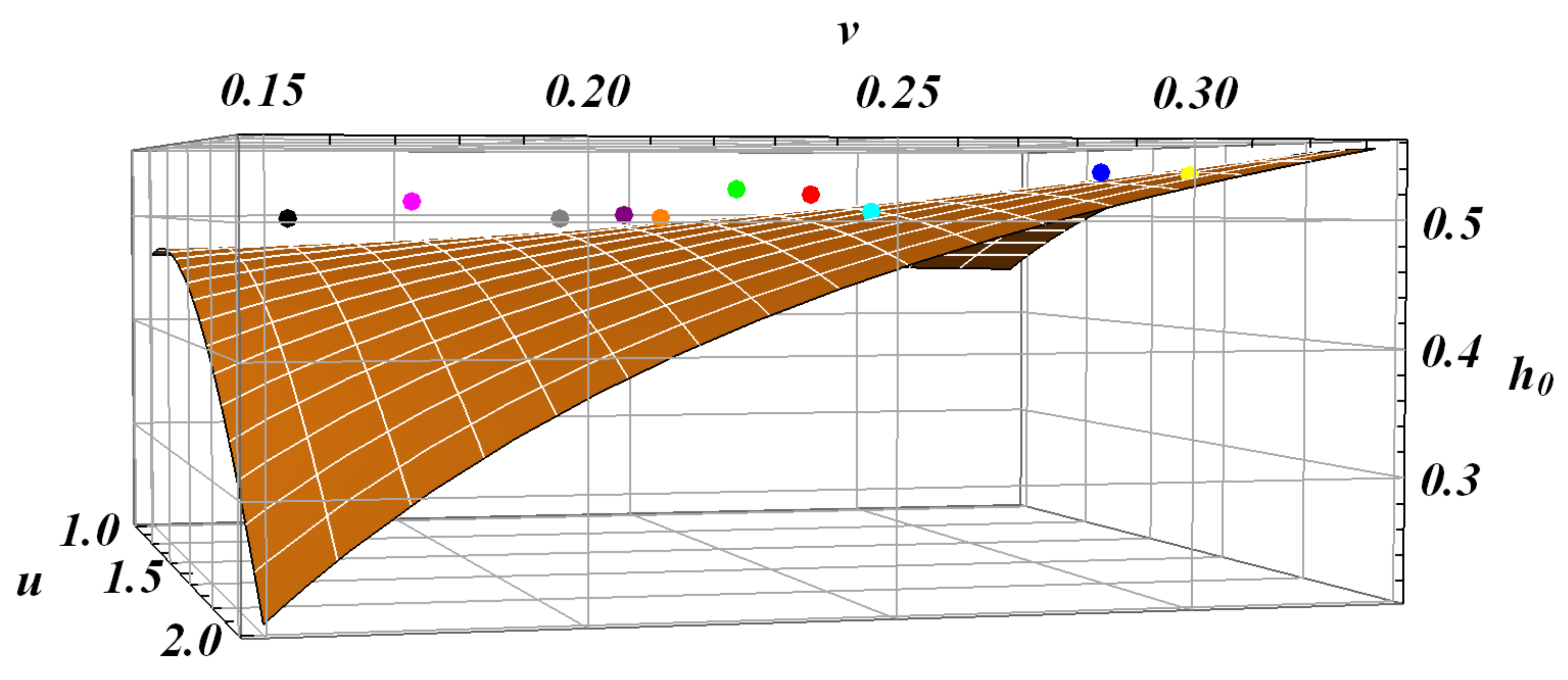
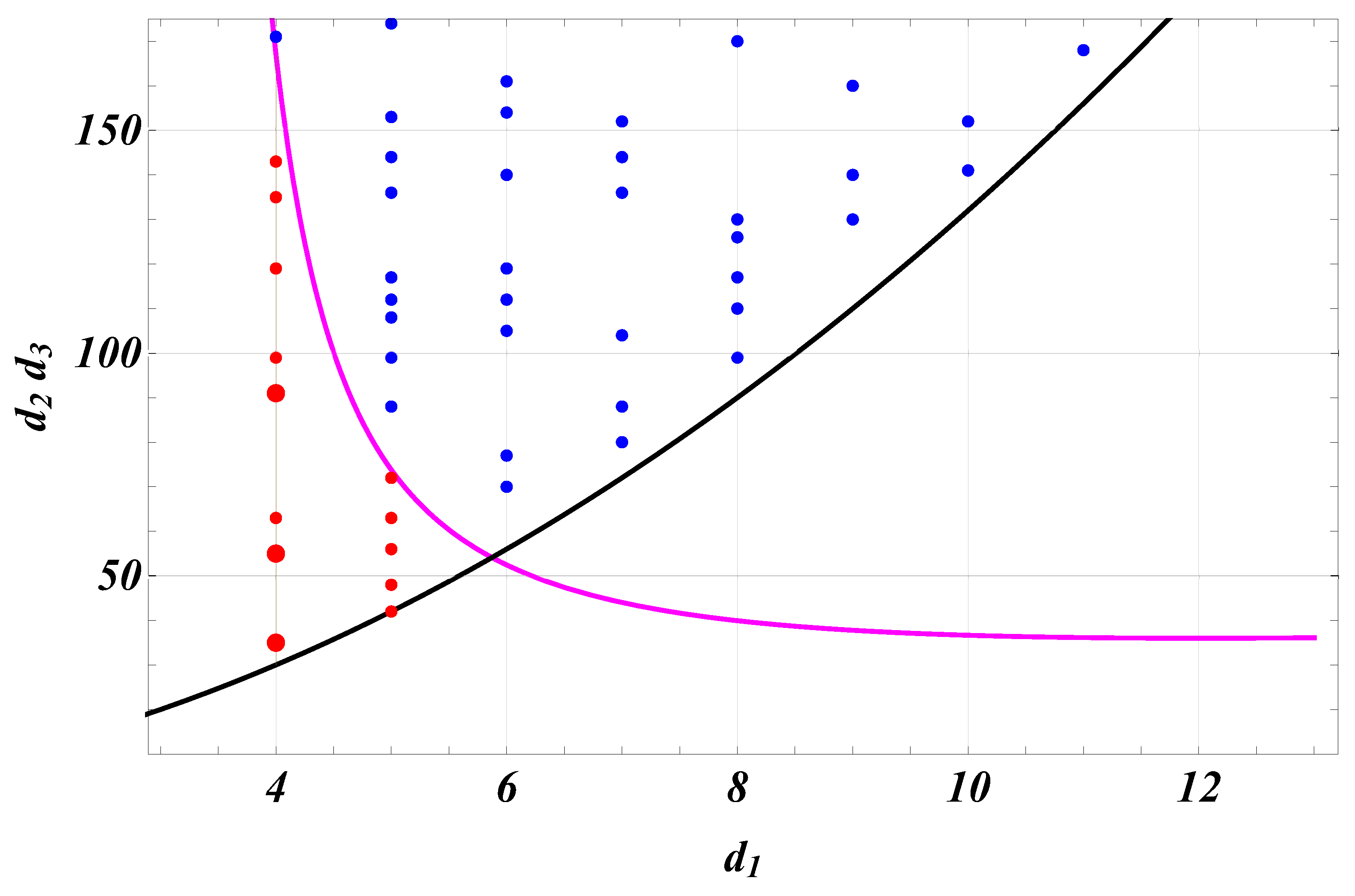
$\langle 4,5,7\rangle$	1.35225	1.07143	0.57143	0.52273
$\langle 4,7,9\rangle$	1.25988	0.86363	0.54545	0.51667
$\langle 4,5,11\rangle$	1.34840	1.18750	0.625	0.53704
$\langle 4,7,13\rangle$	1.25794	1.04545	0.63636	0.54412
$\langle 4,7,17\rangle$	1.28338	0.96428	0.57143	0.52439
$\langle 4,9,11\rangle$	1.20605	0.76667	0.53333	0.51316
$\langle 4,9,15\rangle$	1.20493	0.9	0.6	0.53571
$\langle 4,11,13\rangle$	1.17074	0.71053	0.52632	0.51087
$\langle 5,6,7\rangle$	1.24212	0.85	0.6	0.53704
$\langle 5,6,8\rangle$	1.22644	0.9	0.6	0.53571
$\langle 5,7,8\rangle$	1.19523	0.79167	0.58333	0.53226
$\langle 5,7,9\rangle$	1.18322	0.71429	0.57143	0.52941
$\langle 5,8,9\rangle$	1.15950	0.80769	0.61539	0.54412

, which lists the 13 semigroups $S_3$ for which ${\rho }_3>1.1547$.

The following 10 semigroups $S_3$ among the 13 listed in Table 1,

$$\langle 4,7,9\rangle ,\langle 4,7,17\rangle ,\langle 4,9,11\rangle ,\langle 4,9,15\rangle ,\langle 4,11,13\rangle ,\langle 5,6,7\rangle ,\langle 5,6,8\rangle ,\langle 5,7,8\rangle ,\langle 5,7,9\rangle ,\langle 5,8,9\rangle ,$$

have ${\rho }_3>1.1547$ and $e_3<1$, and, according to Inequality (22), provide $w_3<2/3$. The remaining three semigroups $S_3$,

$$\begin{array}{c}\hfill \langle 4,5,7\rangle ,\langle 4,5,11\rangle ,\langle 4,7,13\rangle ,\end{array}$$

(27)

have ${\rho }_3>1.1547$ and $e_3>1$. However, a direct calculation shows that

$$\begin{array}{c}\hfill w_3\left(\langle 4,5,7\rangle \right)=0.5714,w_3\left(\langle 4,5,11\rangle \right)=0.625,w_3\left(\langle 4,7,13\rangle \right)=0.6363.\end{array}$$

Thus, the theorem is proven.  □

2.4. Lower and Upper Bounds of Rescaled Genera $h_r=K_r/g_3^{r+1}$, $r\ge 1$

Having successfully calculated the bounds of the rescaled genus $h_0$ in Lemma 1, it makes sense to extend these calculations for the higher rescaled genera $h_r=K_r/g_3^{r+1}$ for numerical semigroups $S_3$, using the polynomial Equation (6) with $r\ge 1$. Utilizing the relationships among $h_r$ [9], we derive their expressions through the three independent parameters, u, v, and $h_0$. The calculation of the bounds for $h_r$ is noteworthy from several points of view, e.g., observing their change when passing from a non-symmetric semigroup $S_3$ to a symmetric one.

Consider the following four syzygy identities (6):

$$\begin{array}{c}\hfill Y_1-X_1=0,Y_2-X_2=2{\pi }_3,Y_3-X_3=6{\pi }_3{K}_0,Y_4-X_4=24{\pi }_3{K}_1.\end{array}$$

(28)

By substituting the polynomial relations $Y_4(Y_1,Y_2)$ and $X_4(X_1,X_2,X_3)$ into the fourth of these identities (see [9], Formula (37)),

$$\begin{array}{c}\hfill 2Y_4=Y_2^2+2Y_1^2{Y}_2-Y_1^4,6X_4=X_1^4-6X_1^2{X}_2+8X_1{X}_3+3X_2^2,\end{array}$$

we obtain

$$\begin{array}{c}\hfill 3(Y_2^2+2Y_1^2{Y}_2-Y_1^4)=X_1^4-6X_1^2{X}_2+8X_1{X}_3+3X_2^2+144{\pi }_3{K}_1.\end{array}$$

(29)

Continuing by substituting the first three identities from (28) and one more, $2Y_3=3Y_1{Y}_2-Y_1^3$, into (29), which yields

$$\begin{array}{c}\hfill Y_2=Y_1^2-4K_0{Y}_1+12K_1+{\pi }_3,\end{array}$$

and combining this result with Identity (10), we arrive at an equality in $h_1,h_0,u,$ and v:

$$\begin{array}{c}\hfill 12h_1=2u(2h_0-1)+2-v,h_1={\displaystyle \frac{K_1}{g_3^2}}.\end{array}$$

(30)

By utilizing the bounds (12), (17) and (20) for $u,v,$ and $h_0$, we derive both lower and upper bounds for $h_1$:

$$\begin{array}{c}\hfill 0.13889\simeq {\displaystyle \frac{5}{36}}<h_1<{\displaystyle \frac{11}{54}}\simeq 0.20370.\end{array}$$

(31)

Next, supplement identity (28) with another identity from (6):

$$\begin{array}{c}\hfill Y_5-X_5=60{\pi }_3{K}_2.\end{array}$$

(32)

Then, substitute the polynomial relations $Y_5(Y_1,Y_2)$ and $X_5(X_1,X_2,X_3)$ (see [9], Formula (37)), along with the other three first identities from (6) into (32). Skipping lengthy calculations, we present the final equality (see [9], Formula (39)),

$$\begin{array}{c}\hfill Y_1^3-2K_0{Y}_1^2+4{\pi }_3{K}_0+24K_2=Y_2(Y_1+2K_0),\end{array}$$

and combine it with identity (10). The result is presented in the rescaled variables $h_2,h_0,u,$ and v:

$$\begin{array}{c}\hfill 12h_2=(2h_0-1)u(u-1)+2h_0(1-v),h_2={\displaystyle \frac{K_2}{g_3^3}}.\end{array}$$

(33)

Making use of the bounds in (12), (17) and (20) for $u,v,$ and $h_0$, we arrive at lower and upper bounds for $h_2$:

$$\begin{array}{c}\hfill 0.05555\simeq {\displaystyle \frac{1}{18}}<h_2<{\displaystyle \frac{1}{9}}\simeq 0.11111.\end{array}$$

(34)

To study the bounds of the rescaled genera $h_r$, $r\ge 3$, we utilize Theorem 2 in [9], applying it to the semigroups $S_3$: there exists an algebraic equation, $R(h_0,h_1,h_2,h_r)=0$, where the polynomial $R(t_1,t_2,t_3,t_4)$ is irreducible over the ring $A[t_1,t_2,t_3,t_4]$. To avoid giving lengthy formulas for $R(h_0,h_1,h_2,h_r)$, which increase with r, we instead present the specific algebraic equation for $r=3$, making use of Formula (42) in [9]:

$$\begin{array}{c}\left(10h_3-18h_1^2+v{h}_0^2-{\displaystyle \frac{v^2}{24}}\right){\mathsf{\Delta }}_1={\mathsf{\Delta }}_2^2,\hfill \\ {\mathsf{\Delta }}_1=3h_1-2h_0^2+{\displaystyle \frac{v}{4}},{\mathsf{\Delta }}_2=6h_2-6h_0{h}_1+{\displaystyle \frac{v}{2}}{h}_0.\hfill \end{array}$$

(35)

Substituting Equalities (30) and (33) into Equality (35), we obtain

$$\begin{array}{c}\hfill {\mathsf{\Delta }}_1={\displaystyle \frac{1}{2}}(2h_0-1)(u-1-2h_0),{\mathsf{\Delta }}_2=u{\mathsf{\Delta }}_1,\end{array}$$

which substantially simplifies Equality (35):

$$\begin{array}{c}\hfill 10h_3=18h_1^2-v{h}_0^2+{\displaystyle \frac{v^2}{24}}+u^2{\mathsf{\Delta }}_1.\end{array}$$

Utilizing the bounds given in (12), (17), (20) and (31), we derive lower and upper bounds for $h_3$:

$$\begin{array}{c}\hfill 0.02443<h_3<0.07515.\end{array}$$

(36)

The following numerical calculations illustrate the upper and lower bounds in (20), (31), (34) and (36):

$$\begin{array}{c}\langle 3,4,5\rangle :h_0=0.535714,h_1=0.164116,h_2=0.072613,h_3=0.0381885,\hfill \\ \langle 4,7,13\rangle :h_0=0.544118,h_1=0.169406,h_2=0.0761945,h_3=0.0407323.\hfill \end{array}$$

2.5. Rescaled Genera $h_r$ in Symmetric Semigroups $S_3$

Every symmetric semigroup $S_3$ is a complete intersection [14]. Consequently, we can apply Formula (67) in [9] to calculate the first six rescaled genera $h_r$, $1\le r\le 6$, and determine their lower and upper bounds. Bearing in mind that

$$\begin{array}{c}\hfill h_0={\displaystyle \frac{1}{2}},u=1,0<v\le {\displaystyle \frac{1}{4}},\end{array}$$

we get

$$\begin{array}{c}{h}_1={\displaystyle \frac{1}{6}}\left(1-{\displaystyle \frac{1}{2}}v\right),0.14583\simeq {\displaystyle \frac{7}{48}}<h_1<{\displaystyle \frac{1}{6}}\simeq 0.16666,\hfill \\ h_2={\displaystyle \frac{1}{12}}(1-v),0.06250\simeq {\displaystyle \frac{1}{16}}<h_2<{\displaystyle \frac{1}{12}}\simeq 0.08333,\hfill \\ h_3={\displaystyle \frac{1}{20}}\left(1-{\displaystyle \frac{3}{2}}v+{\displaystyle \frac{1}{3}}{v}^2\right),0.03229\simeq {\displaystyle \frac{31}{960}}<h_3<{\displaystyle \frac{1}{20}}\simeq 0.05,\hfill \\ h_4={\displaystyle \frac{1}{30}}\left(1-2v+v^2\right),0.01875\simeq {\displaystyle \frac{3}{160}}<h_4<{\displaystyle \frac{1}{30}}\simeq 0.03333,\hfill \\ h_5={\displaystyle \frac{1}{42}}\left(1-{\displaystyle \frac{5}{2}}v+2v^2-{\displaystyle \frac{1}{4}}{v}^3\right),0.01181\simeq {\displaystyle \frac{127}{10752}}<h_5<{\displaystyle \frac{1}{42}}\simeq 0.02381,\hfill \\ h_6={\displaystyle \frac{1}{56}}\left(1-3v+{\displaystyle \frac{10}{3}}{v}^2-v^3\right),0.00791\simeq {\displaystyle \frac{85}{10752}}<h_6<{\displaystyle \frac{1}{56}}\simeq 0.01785.\hfill \end{array}$$

(37)

By utilizing (20) and comparing the upper and lower bounds in (31), (34) and (36) with those in (37), we conclude that the domain of variation for $h_r$, $0\le r\le 3$, in non-symmetric semigroups $S_3$ encompasses the corresponding upper and lower bounds in symmetric semigroups $S_3$:

$$\begin{array}{ccc}\hfill 0.5=0.5=& h_0& =0.5<0.55555,\hfill \\ \hfill 0.13889<0.14583<& h_1& <0.16666<0.20370,\hfill \\ \hfill 0.05555<0.06250<& h_2& <0.08333<0.11111,\hfill \\ \hfill 0.02443<0.03229<& h_3& <0.05000<0.07515.\hfill \end{array}$$

We leave open a question of whether such a property exists for the other rescaled genera $h_r$, with arbitrary $r\ge 4$, in numerical semigroups $S_3$.

3. Concluding Remarks

We have revisited the Wilf question for numerical semigroups $S_3$ and, making use of identities for the degrees of syzygies of such semigroups, suggested a quite different approach to the proof of existence of an affirmative answer.

The proof technique elaborated in Theorem 1 could be extended to numerical semigroups $S_m$ for higher values of $m\ge 4$. However, there are two difficulties that make such reasoning hard to implement:

• The number of degrees in all $m-1$ syzygies for arbitrary numerical semigroups $S_m$, $m\ge 4$, becomes unbounded (see [15] for $S_4$), while the number of polynomial equations, similarly to (6), up to degree m remains finite. This makes the algebraic estimation of $h_0$ extremely hard.
• The set of exceptional numerical semigroups $S_m$, similarly to (27), with ${\rho }_m$ and $e_m$ exceeding their critical values, must be finite; otherwise a direct verification becomes impossible.

We plan to address this question in a separate paper.