Kantorovich Extension of Parametric Generalized q-Schurer Operators and Their Approximation Properties

Abstract

This paper aims to extend, within the context of quantum calculus, the $\alpha$-Bernstein–Schurer operators ($\alpha \in [0,1]$) to Kantorovich form. Using the Ditzian–Totik modulus of continuity and the Lipschitz-kind maximal function for our recently extended operators, we first examine the Korovkin-type theorem before studying the global approximation and rate of convergence, respectively. Furthermore, Taylor’s formula is used to present Voronovskaja-type theorems. Lastly, the aforementioned operators are validated through the numerical results with graphical representation.

1. Introduction and Preliminaries

The Bernstein polynomial, a positive linear operator, was initially introduced by S. N. Bernstein in 1912 [1]. In his study, Bernstein showed that, under the assumption that $\psi \in C[0,1]$, the space of all continuous functions $\psi$ in $[0,1]$ is uniformly approximated by the Bernstein polynomial defined by [1]. The Weierstrass approximation theorem can be quickly shown using the Bernstein polynomial. Consequently, the well-known Bernstein operators $B_{\eta }$ for every $x\in [0,1]$ are as follows:

$$B_{\eta }(\psi ;x)=\sum _{\mu =0}^{\eta }\psi \left({\displaystyle \frac{\mu }{\eta }}\right)b_{\eta ,\mu }\left(x\right),$$

where $\eta \in \mathbb{N}$ (set of positive integers), and $b_{\eta ,\mu }\left(x\right)$ denotes the Bernstein polynomials of degree $\eta$ such that

$$b_{\eta ,\mu }\left(x\right)=\left({\displaystyle \genfrac{}{}{0pt}{}{\eta }{\mu }}\right)x^{\mu }{(1-x)}^{\eta -\mu }$$

where $\mu =0,1,\cdots ,$$\eta ;x\in \left[0,1\right]$, and

$$b_{\eta ,\mu }\left(x\right)=0(\mu <0or\mu >\eta ).$$

A notable application of these operators is their use in numerical differentiation and quadrature as discussed by Costabile et al. [2].

Recently, using the variant of the shape parameter $\alpha \in [-1,1]$, Chen et al. designed $\alpha$-Bernstein-type operators [3]. Furthermore, a number of researchers have studied operators of the $\alpha$-Bernstein type and computed convergence results. In this regard, a number of scholars have used many generalizations and modifications for these types of operators, and their approximation qualities have been investigated, as shown by, for example, the following: Ayman Mursaleen et al. defined Blending-type operators with shape parameter $\alpha$ [4] and also constructed wavelet-type Baskakov operators [5]; Aslan constructed bivariate GBS-associated $\lambda$-Bernstein–Kantorovich operators [6]; Cai constructed Bézier-type Kantorovich operators [7] while generalizing the Bernstein operators [8]; Kilicman et al. created Baskakov–Durrmeyer-type operators [9]; Mohiuddine and Özger created $\alpha$-type Bernstein–Kantorovich operators [10]; Mursaleen et al. presented q-Bernstein–Kantorovich-type operators [11,12]; Rao et al. obtained Szász–Kantorovich operators [13,14,15]; and Turhan et al. constructed Kantorovich-type Bernstein operators based on $(\alpha ,\lambda ,s)$ [16]. Moreover, Sehrawat et al. approximated Riemann–Liouville fractional Kantorovich-type operators [17], and S. Berwal et al. approximated Riemann–Liouville fractional-type operators based on parameter $\alpha$ [18]. They determined the convergence qualities and calculated the results of the Voronovskaja-type approximation.

Quantum calculus, often known as q-calculus, has various applications in the study of positive linear operators and approximation methods. The following are some essential components: Quantum calculus is used to define q-Bernstein operators, q-Bernstein–Kantorovich operators, and other operators, which provide better approximation results on certain classes of functions; define the shape-preserving properties of positive linear operators, such as monotonicity, convexity, and variation diminishing; study the approximation properties of positive linear operators, such as convergence, the rate of convergence, and asymptotic behavior; investigate the modulus of continuity, which is used to study the smoothness properties of functions; and so on. Moreover, positive linear operators and their approximation qualities can be studied effectively with quantum calculus, which has applications in approximation theory, numerical analysis, and computer-aided geometric design, among other areas. Finally, positive linear operators based on q-calculus have improved approximation and applications compared to classical positive linear operators; the q parameter allows for more flexibility in approximation, and it has many applications in computer-aided geometric design, numerical analysis, and other fields. Moreover, if we apply $q\to 1$, then q-Bernstein operators [19] are reduced to classical Bernstein operators [1], and q-Bernstein–Kantorovich operators [20] are reduced to Bernstein–Kantorovich operators [21]. So we can conclude that our constructed operators, the Kantorovich variation of $\alpha$-Bernstein–Schurer-type operators in q-calculus, are a type of mathematical operator that is used in quantum computing to approximate functions. These operators are a generalization of classical Bernstein–Kantorovich operators, $\alpha$-Bernstein–Kantorovich-type operators, Bernstein–Kantorovich–Schurer-type operators, and q-Bernstein–Kantorovich–Schurer-type operators.

The basic properties and attributes of q-integers are easily found (see [22,23,24]). For any $q\in (0,1)$ and $v\in \mathbb{N}$, the q-number is denoted by ${\left[v\right]}_q={\displaystyle \frac{1-q^v}{1-q}}$. Let $v=0$; then ${\left[v\right]}_q=0$, and for $v\in \mathbb{N}$, one can also write ${\left[v\right]}_q={\displaystyle \sum _{u=0}^{v-1}}{q}^u=1+q+q^2+\cdots +q^{v-1}$. The q-factorial is defined by ${\left[v\right]}_q!={\prod }_{j=1}^v{\left[j\right]}_q$. For $v=0$, we set ${\left[v\right]}_q!=1$.

Using the q-analog, Lupaş [25] introduced the first Bernstein polynomials, calculating various approximation properties and shape-preserving properties.

In 1962, Schurer [26] obtained a series of positive linear operators, denoted as $S_{\eta ,\mu }^P$, using a positive integer P for every $\eta \in \mathbb{N}$: defined for every $\psi \in C[0,P+1]$ and $S_{\eta ,\mu }^P:C\left[0,1+P\right]\to C[0,1]$ by

$$S_{\eta ,\mu }^P(\psi ;x)=\sum _{\mu =0}^{\eta +P}\psi \left({\displaystyle \frac{\mu }{\eta }}\right)s_{\eta ,P,\mu }\left(x\right)(x\in [0,1])$$

(1)

where the fundamental Bernstein–Schurer polynomials are $s_{\eta ,P,\mu }\left(x\right)$, such that

$$s_{\eta ,P,\mu }\left(x\right)=\left({\displaystyle \genfrac{}{}{0pt}{}{\eta +P}{\mu }}\right)x^{\mu }{(1-x)}^{\eta +P-\mu }(\mu =0,1,\cdots ,\eta +P).$$

(2)

Suppose that $\eta \in \mathbb{N},\psi \in C[0,P+1]$ in [27]; the q-analog of Bernstein–Schurer operators is constructed for any fixed positive integer P such as

$${\tilde{S}}_{\eta ,q,\mu }^P(\psi ;x)=\sum _{\mu =0}^{\eta +P}{\left[\begin{array}{c}\eta +P\\ \mu \end{array}\right]}_q{x}^{\mu }\prod _{r=0}^{\eta +P-\mu -1}(1-q^{r}x)\psi \left({\displaystyle \frac{{\left[\mu \right]}_q}{{\left[\eta \right]}_q}}\right),x\in [0,1].$$

(3)

The Bernstein operators $B_{\eta }(f;x)$ are obtained from the operators ${\tilde{S}}_{\eta ,q,\mu }^P(\psi ;x)$ in Equality (3) if $P=0$ and $q=1$. In this instance, the polynomials $s_{\eta ,P,\mu }$ yield the fundamental Bernstein polynomials $b_{\eta ,\mu }\left(x\right)$.

Most recently, the Bernstein-type operator by the use of shape parameter $\alpha$ was proposed by Özger et al. [28]. When P and $\eta \in \mathbb{N},\eta \ge 2$ are non-negative integers, the $\alpha$-Bernstein–Schurer-type operators ${\Phi }_{\eta ,\mu }^{\left(P,\alpha \right)}:C\left[0,1+P\right]\to C[0,1]$ are denoted by

$${\Phi }_{\eta ,\mu }^{\left(P,\alpha \right)}\left(\psi ;x\right)=\sum _{\mu =0}^{\eta +P}\psi \left({\displaystyle \frac{\mu }{\eta }}\right)Q_{\eta ,\mu }^{\left(P,\alpha \right)}\left(x\right),\left(x\in [0,1]\right),$$

(4)

where $\psi \in C\left[0,1+P\right]$, and $\alpha \in [0,1]$, and

$$\begin{array}{l}{Q}_{\eta ,\mu }^{\left(P,\alpha \right)}\left(x\right)=[\left(1-\alpha \right)x\left({\displaystyle \genfrac{}{}{0pt}{}{\eta +P-2}{\mu }}\right)+\left(1-\alpha \right)\left(1-x\right)\left({\displaystyle \genfrac{}{}{0pt}{}{\eta +P-2}{\mu -2}}\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +\alpha x\left(1-x\right)\left({\displaystyle \genfrac{}{}{0pt}{}{\eta +P}{\mu }}\right)]x^{\mu -1}{\left(1-x\right)}^{\eta +P-(\mu +1)}.\end{array}$$

(5)

The Kantorovich modification of the Bernstein operator was developed using the shape parameter $\alpha$ as described in [29].

$$M_{\eta ,i}^{\left(\alpha \right)}\left(f;x\right)=(\eta +1)\sum _{i=0}^{\eta }{P}_{\eta ,i}^{\left(\alpha \right)}\left(x\right){\mathit{\int }}_{{\displaystyle \frac{i}{\eta +1}}}^{{\displaystyle \frac{i+1}{\eta +1}}}f\left(\varphi \right)\mathrm{d}\varphi ,$$

(6)

where

$$\begin{array}{l}{P}_{\eta ,i}^{\left(\alpha \right)}\left(x\right)=[\left(1-\alpha \right)x\left({\displaystyle \genfrac{}{}{0pt}{}{\eta -2}{i}}\right)+\left(1-\alpha \right)\left(1-x\right)\left({\displaystyle \genfrac{}{}{0pt}{}{\eta -2}{i-2}}\right)\\ \hspace{1em}\hspace{1em}\hspace{1em} +\alpha x\left(1-x\right)\left({\displaystyle \genfrac{}{}{0pt}{}{\eta }{i}}\right)]x^{i-1}{\left(1-x\right)}^{\eta -(i+1)}.\end{array}$$

(7)

The Kantorovich modification of the $\alpha$-Bernstein–Schurer operator on the shape parameter $\alpha$ [30] is given by

$$K_{\eta ,P}^{\alpha }\left(\psi ;x\right)=(\eta +1)\sum _{\mu =0}^{\eta +P}{Q}_{\eta ,\mu }^{\left(P,\alpha \right)}\left(x\right){\int }_{{\displaystyle \frac{\mu }{\eta +1}}}^{{\displaystyle \frac{\mu +1}{\eta +1}}}\psi \left(\varphi \right)\mathrm{d}\varphi .$$

(8)

Most recently, by applying the shape parameter $\alpha$, another form of the q-analog of the Bernstein–Schurer type was presented by Nasiruzzaman and Aljohani [31], for all $\psi \in C\left[0,1+P\right]$ and $x\in [0,1]$, followed by

$${\Phi }_{\eta ,q}^{P,\alpha }\left(\psi ;x\right)=\sum _{\mu =0}^{\zeta }{p}_{\eta ,q,\mu }^{P,\alpha }\left(x\right)\psi \left({\displaystyle \frac{{\left[\mu \right]}_q}{{\left[\eta \right]}_q}}\right),$$

(9)

where we suppose that $\zeta =\eta +P$, and

$$\begin{array}{l}{p}_{\eta ,q,\mu }^{P,\alpha }\left(x\right)=[\left(1-\alpha \right)q^{\zeta -\mu -2}\left(1-q^{\zeta -(\mu +1)}x\right){\left[{\displaystyle \genfrac{}{}{0pt}{}{\zeta -2}{\mu -2}}\right]}_q\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\alpha x\left(1-q^{\zeta -\mu -1}x\right){\left[{\displaystyle \genfrac{}{}{0pt}{}{\zeta }{\mu }}\right]}_q+\left(1-\alpha \right)x{\left[{\displaystyle \genfrac{}{}{0pt}{}{\zeta -2}{\mu }}\right]}_q]x^{\mu -1}{\left(1-x\right)}_q^{\zeta -\mu -1}.\end{array}$$

(10)

Lemma 1

([31]). For the test function $\psi \left(\varphi \right)=1,\varphi ,$ the operators ${\Phi }_{\eta ,q}^{P,\alpha }$ defined in (9) have the following moments:

$$\begin{array}{l}{\Phi }_{\eta ,q}^{P,\alpha }\left(1;x\right)\hspace{1em}=1,\\ {\Phi }_{\eta ,q}^{P,\alpha }\left(\varphi ;x\right) ={\displaystyle \frac{{\left[\zeta \right]}_q}{{\left[\eta \right]}_q}}x.\end{array}$$

Lemma 2

([31]). Let $0\le \alpha \le 1$ and the test function $\psi \left(\varphi \right)={\varphi }^r,$ for $2\le r\le \zeta -1$; then operators ${\Phi }_{\eta ,q}^{P,\alpha }$ have the following equality:

$${\Phi }_{\eta ,q}^{P,\alpha }\left({\varphi }^r;x\right)=c_r{x}^r+c_{r-1}{x}^{r-1}+\cdots +c_{1}x+c_0,$$

where

$$c_r={\displaystyle \frac{q^{\frac{r(r-1)}{2}}{[\zeta -2]}_q!}{{[\zeta -r]}_q!{\left[\eta \right]}_q^r}}\{(1-\alpha ){[\zeta -r]}_q{[\zeta -1+r]}_q+\alpha {\left[\zeta \right]}_q{[\zeta -1]}_q\}.$$

Corollary 1

([31]). To obtain the moments of orders two, three, and four, suppose the test function $\psi \left(\varphi \right)={\varphi }^2,{\varphi }^3,{\varphi }^4$; then we have

$$\begin{array}{l}{\Phi }_{\eta ,q}^{P,\alpha }\left({\varphi }^2;x\right)=[{\displaystyle \frac{\left(1-\alpha \right)\left({[\zeta -1]}_q+q^{\zeta -1}\left(1+{\left[2\right]}_q\right)\right)}{{\left[\eta \right]}_q^2}}+{\displaystyle \frac{\alpha {\left[\zeta \right]}_q}{{\left[\eta \right]}_q^2}}]x\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +[{\displaystyle \frac{\left(1-\alpha \right){[\zeta -2]}_q\left(q{[\zeta -1]}_q+q^{\zeta }{\left[2\right]}_q\right)}{{\left[\eta \right]}_q^2}}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +{\displaystyle \frac{\alpha {[\zeta -1]}_q{\left[\zeta \right]}_q}{{\left[\eta \right]}_q^2}}]x^2\\ {\Phi }_{\eta ,q}^{P,\alpha }\left({\varphi }^3;x\right)=\left[{\displaystyle \frac{\left(1-\alpha \right)\left({[\zeta -1]}_q+q^{\zeta -1}\left(1+{\left[2\right]}_q\right)+\alpha {\left[\zeta \right]}_q\right)}{{\left[\eta \right]}_q^2}}\right]x\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +[{\displaystyle \frac{\left(1-\alpha \right)q{[\zeta -2]}_q\left({[\zeta -1]}_q+{\left[2\right]}_q{q}^{\zeta -1}\right)}{{\left[\eta \right]}_q^2}}\hspace{1em}\hspace{1em}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +{\displaystyle \frac{\alpha {\left[\zeta \right]}_q{[\zeta -1]}_q}{{\left[\eta \right]}_q^2}}]x^2\hspace{1em}\hspace{1em}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +[{\displaystyle \frac{\left(1-\alpha \right)q^3{[\zeta -2]}_q{[\zeta -3]}_q\left({[\zeta -1]}_q+q^{\zeta -1}{\left[3\right]}_q\right)}{{\left[\eta \right]}_q^3}}\hspace{1em}\hspace{1em}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +{\displaystyle \frac{\alpha q^3{[\zeta -1]}_q{\left[\zeta \right]}_q{[\zeta -2]}_q}{{\left[\eta \right]}_q^3}}]x^3\hspace{1em}\hspace{1em}\\ {\Phi }_{\eta ,q}^{P,\alpha }\left({\varphi }^4;x\right)=[{\displaystyle \frac{\left(1-\alpha \right)\left({[\zeta -1]}_q+q^{\zeta -1}\left(1+{\left[2\right]}_q\right)\right)}{{\left[\eta \right]}_q^2}}+{\displaystyle \frac{\alpha {\left[\zeta \right]}_q}{{\left[\eta \right]}_q^2}}]x\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +[{\displaystyle \frac{\left(1-\alpha \right){[\zeta -2]}_q\left(q{[\zeta -1]}_q+{\left[2\right]}_q{q}^{\zeta }\right)}{{\left[\eta \right]}_q^2}}\hspace{1em}\hspace{1em}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +{\displaystyle \frac{\alpha {\left[\zeta \right]}_q{[\zeta -1]}_q}{{\left[\eta \right]}_q^2}}]x^2\hspace{1em}\hspace{1em}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +[{\displaystyle \frac{\left(1-\alpha \right)q^3{[\zeta -2]}_q{[\zeta -3]}_q\left({[\zeta -1]}_q+q^{\zeta -1}{\left[3\right]}_q\right)}{{\left[\eta \right]}_q^3}}\hspace{1em}\hspace{1em}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +{\displaystyle \frac{\alpha q^3{\left[\zeta \right]}_q{[\zeta -1]}_q{[\zeta -2]}_q}{{\left[\eta \right]}_q^3}}]x^3\hspace{1em}\hspace{1em}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +[{\displaystyle \frac{\left(1-\alpha \right)q^6{[\zeta -2]}_q{[\zeta -3]}_q{[\zeta -4]}_q\left({[\zeta -1]}_q+q^{\zeta -1}{\left[4\right]}_q\right)}{{\left[\eta \right]}_q^4}}\hspace{1em}\hspace{1em}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +{\displaystyle \frac{\alpha q^6{\left[\zeta \right]}_q{[\zeta -1]}_q{[\zeta -2]}_q{[\zeta -3]}_q}{{\left[\eta \right]}_q^4}}]x^4.\end{array}$$

The structure of the current work is as follows. A novel family of the generalized Kantorovich variant of $\alpha$-Bernstein–Schurer-type operators via the q-analog is defined in the second section, along with a few basic features that are crucial to the theory of the uniform approximation of functions. The third section’s primary goal is to examine some significant findings regarding uniform convergence and estimates of the new linear positive operators, which are straightforward uses of the formulas and properties mentioned in the second section. In the fourth section, we quantitatively estimate the Voronovskaja-type theorem for the twice differentiable and bounded function. In the last section, we study some examples and conduct a graphical analysis. These findings not only enhance our understanding of the operators but also provide valuable insights into their practical applications in various mathematical fields. Ultimately, this research paves the way for the further exploration and refinement of approximation techniques.

2. Kantorovich-Type Operators and Moments

The main goal of this section is to obtain the approximation qualities and construct the Kantorovich variant of $\alpha$-Bernstein–Schurer-type operators via the q-analog. Functions of the Lebesgue integrable type can be approximated using Kantorovich generalizations to sequences of positive linear operators (PLOs). Kantorovich modifications entail substituting mean values in $\left[{\displaystyle \frac{\mu }{\eta +1}},{\displaystyle \frac{\mu +1}{\eta +1}}\right]$ for sample values $f\left({\displaystyle \frac{\mu }{\eta }}\right)$. We give the definition of a new family of Kantorovich variations of $\alpha$-Bernstein–Schurer-type operators via q-analogs in Equality (11). To acquire specific fundamental characteristics that are crucial to the notion of the uniform approximation of functions, we give Lemma (3), Corollary 2, and some theorems. In Lemma 3, we calculate moments by taking the test function $\psi \left(\varphi \right)={\varphi }^r$, and we find that the sequence of PLO ${\Psi }_{\eta ,q}^{P,\alpha }$ to the continuous function $\psi$ on the compact interval $[0,1]$ is the uniform convergence of the sequence ${\Phi }_{\eta ,q}^{P,\alpha }\left({\varphi }^r;x\right)\to {\varphi }^r$ for $r=0,1,2,3,4$. This result demonstrates the effectiveness of the PLO sequence in approximating continuous functions, highlighting its utility in various applications within functional analysis. Furthermore, it sets the foundation for exploring more complex scenarios and extending the results to higher-dimensional spaces. In Corollary 2, we calculate the moments, namely, ${\Psi }_{\eta ,q}^{P,\alpha }\left({(\varphi -x)}^r;x\right)$, for $r=1,2,4$, which play a crucial role in obtaining the convergence of operators (11) in spaces of a modulus of smoothness, Lipschitz maximal function, and Peetre’s K-functional.

We now define the Kantorovich extension of Bernstein–Schurer operators in the framework of q-calculus involving $\alpha$ (shape parameter) by taking into consideration positive integers P for any $\eta \in \mathbb{N}$, fixed $\alpha \in [0,1]$, and also assuming $1\le p<\infty$ and $\eta +P=\zeta$. We use ${\Psi }_{\eta ,q}^{P,\alpha }$ for operators acting on $L_p[0,1]\to L_p[0,1]$ and construct

$${\Psi }_{\eta ,q}^{P,\alpha }\left(\psi ;x\right)={[\eta +1]}_q\sum _{\mu =0}^{\zeta }{p}_{\eta ,q,\mu }^{P,\alpha }\left(x\right)q^{-\mu }{\int }_{{\displaystyle \frac{{\left[\mu \right]}_q}{{[\eta +1]}_q}}}^{{\displaystyle \frac{{[\mu +1]}_q}{{[\eta +1]}_q}}}\psi \left(\varphi \right){\mathrm{d}}_q\varphi ,$$

(11)

where $\psi \in L_p[0,1]$, $x\in [0,1]$, $(\eta \ge 2)$, and $p_{\eta ,q,\mu }^{P,\alpha }\left(x\right)$ defined by Equality (10).

Hereby, the symbol ${\left[m\right]}_q$, the q-integer, will be represented by $\left[m\right]$.

Instead of the operators based on Equality (9) in [31], the operators defined by Equality (11) are constructed over the broader class of functions such as $L_p,p\ge 1$.

To obtain the moments and central moments for operators ${\Psi }_{\eta ,q}^{P,\alpha }$ defined by (11), we use the equalities from Lemma 1 and Corollary 1.

Lemma 3.

Let the test function $\psi \left(\varphi \right)=1,\varphi ,{\varphi }^2,{\varphi }^3,{\varphi }^4$ be taken to operators ${\Psi }_{\eta ,q}^{P,\alpha }$ defined by (11); then we get the following identities:

$$\begin{array}{l}{\Psi }_{\eta ,q}^{P,\alpha }\left(1;x\right)\hspace{1em}\hspace{1em}=1;\\ {\Psi }_{\eta ,q}^{P,\alpha }\left(\varphi ;x\right)\hspace{1em}\hspace{1em}={\displaystyle \frac{\left[2\right]\left[\zeta \right]x+1}{\left[2\right][\eta +1]}};\\ {\Psi }_{\eta ,q}^{P,\alpha }\left({\varphi }^2;x\right)\hspace{1em} =\left[{\displaystyle \frac{\left(1-\alpha \right)\left([\zeta -1]+q^{\zeta -1}\left(1+\left[2\right]\right)+\alpha \left[\zeta \right]\right)}{{[\eta +1]}^2}}\right]x\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +[{\displaystyle \frac{\left(1-\alpha \right)q[\zeta -2]([\zeta -1]+\left[2\right]q^{\zeta -1})}{{[\eta +1]}^2}}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +{\displaystyle \frac{\alpha \left[\zeta \right][\zeta -1]}{{[\eta +1]}^2}}]x^2+{\displaystyle \frac{\left[\zeta \right]}{{[\eta +1]}^2}}{\displaystyle \frac{(2q+1)}{\left[3\right]}}x+{\displaystyle \frac{1}{\left[3\right]{[\eta +1]}^2}};\\ {\Psi }_{\eta ,q}^{P,\alpha }\left({\varphi }^3;x\right)\hspace{1em} ={\displaystyle \frac{\left[\eta \right]}{{[\eta +1]}^3}}[(1-\alpha )\left([\zeta -1]+q^{\zeta -1}(1+\left[2\right])\right)+\alpha \left[\zeta \right]]x\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +{\displaystyle \frac{\left[\eta \right]}{{[\eta +1]}^3}}[(1-\alpha )q[\zeta -1]([\zeta -2]\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +\left[2\right]q^{\zeta -1})+\alpha \left[\zeta \right][\zeta -1]]x^2\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +[{\displaystyle \frac{\left(1-\alpha \right)q^3[\zeta -2][\zeta -3]\left([\zeta -1]+q^{\zeta -1}\left[3\right]\right)}{{[\eta +1]}^3}}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +{\displaystyle \frac{\alpha q^3[\zeta -1]\left[\zeta \right][\zeta -2]}{{[\eta +1]}^3}}]x^3\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +{\displaystyle \frac{(1+2q+3q^2)}{\left[4\right]{[\eta +1]}^3}}[(1-\alpha )\left([\zeta -1]+q^{\zeta -1}(1+\left[2\right])\right)+\alpha \left[\zeta \right]]x\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +{\displaystyle \frac{(1+2q+3q^2)}{\left[4\right]{[\eta +1]}^3}}\left[(1-\alpha )q[\zeta -1]\right([\zeta -2]\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +\left[2\right]q^{\zeta -1})+\alpha \left[\zeta \right][\zeta -1]]x^2\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +{\displaystyle \frac{(1+3q)\left[\zeta \right]}{\left[4\right]{[\eta +1]}^3}}x+{\displaystyle \frac{1}{\left[4\right]{[\eta +1]}^3}};\end{array}$$

$$\begin{array}{l}{\Psi }_{\eta ,q}^{P,\alpha }\left({\varphi }^4;x\right)\hspace{1em} ={\displaystyle \frac{{\left[\eta \right]}^2}{{[\eta +1]}^4}}[(1-\alpha )\left([\zeta -1]+q^{\zeta -1}(1+\left[2\right])\right)+\alpha \left[\zeta \right]]x\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +[(1-\alpha )q[\zeta -2]([\zeta -1]+\left[2\right]q^{\zeta -1})\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +\alpha \left[\zeta \right][\zeta -1]]{\displaystyle \frac{{\left[\eta \right]}^2}{{[\eta +1]}^4}}{x}^2\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +{\displaystyle \frac{\left[\eta \right]}{{[\eta +1]}^4}}[(1-\alpha )q^3[\zeta -2][\zeta -3]\left([\zeta -1]+q^{\zeta -1}\left[3\right]\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +\alpha q^3[\zeta -1]\left[\zeta \right][\zeta -2]]x^3\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +[{\displaystyle \frac{\left(1-\alpha \right)q^6[\zeta -2][\zeta -3][\zeta -4]\left([\zeta -1]+q^{\zeta -1}\left[4\right]\right)}{{[\eta +1]}^4}}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +{\displaystyle \frac{\alpha q^6\left[\zeta \right][\zeta -1][\zeta -2][\zeta -3]}{{[\eta +1]}^4}}]x^4\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +{\displaystyle \frac{\left(1+2q+3q^2+4q^3\right)\left[\eta \right]}{{\left(\left[5\right][\eta +1]\right)}^4}}\left[(1-\alpha )\right([\zeta -1]\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +q^{\zeta -1}(1+\left[2\right]))+\alpha \left[\zeta \right]]x\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +{\displaystyle \frac{\left(1+2q+3q^2+4q^3\right)\left[\eta \right]}{\left[5\right]{[\eta +1]}^4}}[(1-\alpha )q[\zeta -1]([\zeta -2]+\left[2\right]q^{\zeta -1})\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +\alpha [\zeta -1]\left[\zeta \right]]x^2\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +{\displaystyle \frac{(1+2q+3q^2+4q^3)}{\left[5\right]{[\eta +1]}^4}}\left[(1-\alpha )q^3[\zeta -3][\zeta -2]\right([\zeta -1]\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +q^{\zeta -1}\left[3\right])+\alpha q^3[\zeta -1]\left[\zeta \right][\zeta -2]]x^3\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +{\displaystyle \frac{(1+3q+6q^2)}{\left[5\right]{[\eta +1]}^4}}[(1-\alpha )\left([\zeta -1]+q^{\zeta -1}(1+\left[2\right])\right)+\alpha \left[\zeta \right]]x\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +{\displaystyle \frac{(1+3q+6q^2)}{\left[5\right]{[\eta +1]}^4}}[(1-\alpha )q[\zeta -2]([\zeta -1]+\left[2\right]q^{\zeta -1})\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +\alpha \left[\zeta \right][\zeta -1]]x^2+{\displaystyle \frac{(1+4q)\left[\zeta \right]}{\left[5\right]{[\eta +1]}^4}}x+{\displaystyle \frac{1}{\left[5\right]{[\eta +1]}^4}}.\end{array}$$

Proof. 

To prove our equality, we take into account Lemma 1 and Corollary 1 and use the equality $[r+1]=q^r+\left[r\right]$ and $[r+1]=1+q\left[r\right]$. Thus, by applying the famous q-Jackson integral, we conclude that

$$\begin{array}{l}{\int }_J{\varphi }^r{\mathrm{d}}_q\varphi ={\int }_{J_1}{\varphi }^r{d}_{q}t-{\int }_{J_2}{\varphi }^r{d}_{q}t\\ \hspace{1em}\hspace{1em}\hspace{1em} ={\displaystyle \frac{1-q}{[\eta +1]}}\left\{[\mu +1]{\displaystyle \sum _{\eta =0}^{\infty }}\right({\displaystyle \frac{[\mu +1]}{[\eta +1]}}{q}^{\eta }{)}^r{q}^{\eta }\\ \hspace{1em}\hspace{1em}\hspace{1em} -\left[\mu \right]{\displaystyle \sum _{\eta =0}^{\infty }}\left({\displaystyle \frac{[\eta +1]}{\left[\mu \right]}}{)}^{-r}{q}^{\eta }\right\}\\ \hspace{1em}\hspace{1em}\hspace{1em} =(q-1)({\left(\left[\mu \right]\right)}^{r+1}-{\left([\mu +1]\right)}^{r+1}){\left([1+\eta ]\right)}^{-(r+1)}{\displaystyle \sum _{\eta =0}^{\infty }}{q}^{\eta (1+r)},\end{array}$$

where $J=\left[{\displaystyle \frac{\left[\mu \right]}{[\eta +1]}},{\displaystyle \frac{[\mu +1]}{[\eta +1]}}\right]$, $J_1=\left[0,{\displaystyle \frac{[\mu +1]}{[\eta +1]}}\right]$, and $J_2=\left[0,{\displaystyle \frac{\left[\mu \right]}{[\eta +1]}}\right]$. Therefore, it is easy to conclude that

$${\int }_J{\varphi }^r{\mathrm{d}}_q\varphi =\left\{\begin{array}{ll}{\displaystyle \frac{q^{\mu }}{[\eta +1]}}& \mathrm{for}r=0;\\ {\displaystyle \frac{q^{\mu }}{{\left([\eta +1]\right)}^2}}\left(\left[\mu \right]+{\displaystyle \frac{1}{\left[2\right]}}\right)& \mathrm{for}r=1;\\ {\displaystyle \frac{q^{\mu }}{{\left([\eta +1]\right)}^3}}({\left[\mu \right]}^2+{\displaystyle \frac{2q+1}{\left[3\right]}}\left[\mu \right]+{\displaystyle \frac{1}{\left[3\right]}})& \mathrm{for}r=2.\end{array}\right.$$

(12)

Thus, in the view of (12), the operators (11) give us

$$\begin{array}{l}{\Psi }_{\eta ,q}^{P,\alpha }\left(1;x\right)={\displaystyle \sum _{\mu =0}^{\zeta }}[1+\eta ]p_{\eta ,q,\mu }^{P,\alpha }\left(x\right)q^{-\mu }{\int }_J{\mathrm{d}}_q\varphi ,\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}={\displaystyle \sum _{\mu =0}^{\zeta }}[1+\eta ]p_{\eta ,q,\mu }^{P,\alpha }\left(x\right)q^{-\mu }{\displaystyle \frac{q^{\mu }}{[\eta +1]}}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}={\Phi }_{\eta ,q}^{P,\alpha }\left(1;x\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=1,\end{array}$$

$$\begin{array}{l}{\Psi }_{\eta ,q}^{P,\alpha }\left(\varphi ;x\right)={\displaystyle \sum _{\mu =0}^{\zeta }}[1+\eta ]p_{\eta ,q,\mu }^{P,\alpha }\left(x\right)q^{-\mu }{\int }_J\varphi {\mathrm{d}}_q\varphi ,\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}={\displaystyle \sum _{\mu =0}^{\zeta }}[1+\eta ]p_{\eta ,q,\mu }^{P,\alpha }\left(x\right)q^{-\mu }{\displaystyle \frac{q^{\mu }}{{\left([\eta +1]\right)}^2}}\left(\left[\mu \right]+{\displaystyle \frac{1}{\left[2\right]}}\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}={\displaystyle \frac{\left[\eta \right]}{\left(\right[\eta +1\left]\right)}}{\displaystyle \sum _{\mu =0}^{\zeta }}{p}_{\eta ,q,\mu }^{P,\alpha }\left(x\right)\left({\displaystyle \frac{\left[\mu \right]}{\left[\eta \right]}}\right)+{\displaystyle \frac{1}{\left[2\right]\left(\right[\eta +1\left]\right)}}{\displaystyle \sum _{\mu =0}^{\zeta }}{p}_{\eta ,q,\mu }^{P,\alpha }\left(x\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}={\displaystyle \frac{\left[\eta \right]}{\left(\right[\eta +1\left]\right)}}{\Phi }_{\eta ,q}^{P,\alpha }\left(\varphi ;x\right)+{\displaystyle \frac{1}{\left[2\right]\left(\right[\eta +1\left]\right)}}{\Psi }_{\eta ,q}^{P,\alpha }\left(1;x\right).\end{array}$$

For $\psi \left(\varphi \right)={\varphi }^2$,

$$\begin{array}{l}{\Psi }_{\eta ,q}^{P,\alpha }\left({\varphi }^2;x\right)={\displaystyle \sum _{\mu =0}^{\zeta }}[1+\eta ]p_{\eta ,q,\mu }^{P,\alpha }\left(x\right)q^{-\mu }{\int }_J{\varphi }^2{\mathrm{d}}_q\varphi ,\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} ={\displaystyle \sum _{\mu =0}^{\zeta }}[1+\eta ]p_{\eta ,q,\mu }^{P,\alpha }\left(x\right)q^{-\mu }{\displaystyle \frac{q^{\mu }}{{\left([\eta +1]\right)}^3}}({\left[\mu \right]}^2+{\displaystyle \frac{(2q+1)}{\left[3\right]}}\left[\mu \right]+{\displaystyle \frac{1}{\left[3\right]}})\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} ={\displaystyle \frac{{\left[\eta \right]}^2}{{[\eta +1]}^2}}{\displaystyle \sum _{\mu =0}^{\zeta }}{p}_{\eta ,q,\mu }^{P,\alpha }\left(x\right){\left({\displaystyle \frac{\left[\mu \right]}{\left[\eta \right]}}\right)}^2\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +{\displaystyle \frac{\left[\eta \right]}{{[\eta +1]}^2}}{\displaystyle \frac{(2q+1)}{\left[3\right]}}{\displaystyle \sum _{\mu =0}^{\zeta }}{p}_{\eta ,q,\mu }^{P,\alpha }\left(x\right)\left({\displaystyle \frac{\left[\mu \right]}{\left[\eta \right]}}\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +{\displaystyle \frac{1}{\left[3\right]{[\eta +1]}^2}}{\displaystyle \sum _{\mu =0}^{\zeta }}{p}_{\eta ,q,\mu }^{P,\alpha }\left(x\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} ={\displaystyle \frac{{\left[\eta \right]}^2}{{[\eta +1]}^2}}{\Phi }_{\eta ,q}^{P,\alpha }\left({\varphi }^2;x\right)+{\displaystyle \frac{\left[\eta \right]}{{\left([\eta +1]\right)}^2}}{\displaystyle \frac{(2q+1)}{\left[3\right]}}{\Phi }_{\eta ,q}^{P,\alpha }\left(\varphi ;x\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +{\displaystyle \frac{1}{\left[3\right]{[\eta +1]}^2}}{\Phi }_{\eta ,q}^{P,\alpha }\left(1;x\right).\end{array}$$

For $\psi \left(\varphi \right)={\varphi }^3$, if we use $[\mu +1]=q^{\mu }+\left[\mu \right]$ and $[\mu +1]=1+q\left[\mu \right]$, then from the above q-Jackson integral equality, it is easy to get

$$\begin{array}{l}{\int }_J{\varphi }^3{\mathrm{d}}_q\varphi ={\displaystyle \frac{q^{\mu }({[1+\mu ]}^3+{[1+\mu ]}^2\left[\mu \right]+{\left[\mu \right]}^2(1+q\left[\mu \right])+{\left[\mu \right]}^3)}{{[\eta +1]}^4(1+q+q^2+q^3)}}\\ \hspace{1em}\hspace{1em}\hspace{1em} ={\displaystyle \frac{q^{\mu }}{{[\eta +1]}^4\left[4\right]}}\{\left[4\right]{\left[\mu \right]}^3\\ \hspace{1em}\hspace{1em}\hspace{1em} +(1+2q+3q^2){\left[\mu \right]}^2+(1+3q)\left[\mu \right]+1\}\end{array}$$

$$\begin{array}{l}{\Psi }_{\eta ,q}^{P,\alpha }\left({\varphi }^3;x\right)={\displaystyle \sum _{\mu =0}^{\zeta }}[1+\eta ]p_{\eta ,q,\mu }^{P,\alpha }\left(x\right)q^{-\mu }{\int }_J{\varphi }^3{\mathrm{d}}_q\varphi ,\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} ={\displaystyle \frac{{\left[\eta \right]}^3}{{[\eta +1]}^3}}{\displaystyle \sum _{\mu =0}^{\zeta }}{p}_{\eta ,q,\mu }^{P,\alpha }\left(x\right){\left({\displaystyle \frac{\left[\mu \right]}{\left[\eta \right]}}\right)}^3\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +{\displaystyle \frac{\left(1+2q+3q^2\right){\left[\eta \right]}^2}{\left[4\right]{[\eta +1]}^3}}{\displaystyle \sum _{\mu =0}^{\zeta }}{p}_{\eta ,q,\mu }^{P,\alpha }\left(x\right){\left({\displaystyle \frac{\left[\mu \right]}{\left[\eta \right]}}\right)}^2\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +{\displaystyle \frac{(1+3q)\left[\eta \right]}{\left[4\right]{[\eta +1]}^3}}{\displaystyle \sum _{\mu =0}^{\zeta }}{p}_{\eta ,q,\mu }^{P,\alpha }\left(x\right)\left({\displaystyle \frac{\left[\mu \right]}{\left[\eta \right]}}\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +{\displaystyle \frac{1}{\left[4\right]{[\eta +1]}^3}}{\displaystyle \sum _{\mu =0}^{\zeta }}{p}_{\eta ,q,\mu }^{P,\alpha }\left(x\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} ={\displaystyle \frac{{\left[\eta \right]}^3}{{[\eta +1]}^3}}{\Phi }_{\eta ,q}^{P,\alpha }\left({\varphi }^3;x\right)+{\displaystyle \frac{(1+2q+3q^2){\left[\eta \right]}^2}{{\left(\left[4\right][\eta +1]\right)}^3}}{\Phi }_{\eta ,q}^{P,\alpha }\left({\varphi }^2;x\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +{\displaystyle \frac{(1+3q)\left[\eta \right]}{\left[4\right]{[\eta +1]}^3}}{\Phi }_{\eta ,q}^{P,\alpha }\left(\varphi ;x\right)+{\displaystyle \frac{1}{\left[4\right]{[\eta +1]}^3}}{\Phi }_{\eta ,q}^{P,\alpha }\left(1;x\right).\end{array}$$

In a similar way for $\psi \left(\varphi \right)={\varphi }^4$, we get

$$\begin{array}{l}{\int }_J{\varphi }^4{\mathrm{d}}_q\varphi ={\displaystyle \frac{q^{\mu }}{{[\eta +1]}^5\left[5\right]}}\{\left[5\right]{\left[\mu \right]}^4\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +(1+2q+3q^2+4q^3){\left[\mu \right]}^3+(1+3q+6q^2){\left[\mu \right]}^2+(1+4q)\left[\mu \right]+1\}\end{array}$$

$$\begin{array}{l}{\Psi }_{\eta ,q}^{P,\alpha }\left({\varphi }^4;x\right)={\displaystyle \sum _{\mu =0}^{\zeta }}[1+\eta ]p_{\eta ,q,\mu }^{P,\alpha }\left(x\right)q^{-\mu }{\int }_J{\varphi }^4{\mathrm{d}}_q\varphi ,\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} ={\displaystyle \frac{{\left[\eta \right]}^4}{{[\eta +1]}^4}}{\displaystyle \sum _{\mu =0}^{\zeta }}{p}_{\eta ,q,\mu }^{P,\alpha }\left(x\right){\left({\displaystyle \frac{\left[\mu \right]}{\left[\eta \right]}}\right)}^4\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +{\displaystyle \frac{\left(1+2q+3q^2+4q^3\right){\left[\eta \right]}^3}{\left[5\right]{[\eta +1]}^4}}{\displaystyle \sum _{\mu =0}^{\zeta }}{p}_{\eta ,q,\mu }^{P,\alpha }\left(x\right){\left({\displaystyle \frac{\left[\mu \right]}{\left[\eta \right]}}\right)}^3\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +{\displaystyle \frac{\left(1+3q+6q^2\right){\left[\eta \right]}^2}{\left[5\right]{[\eta +1]}^4}}{\displaystyle \sum _{\mu =0}^{\zeta }}{p}_{\eta ,q,\mu }^{P,\alpha }\left(x\right){\left({\displaystyle \frac{\left[\mu \right]}{\left[\eta \right]}}\right)}^2\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +{\displaystyle \frac{(1+4q)\left[\eta \right]}{\left[5\right]{[\eta +1]}^4}}{\displaystyle \sum _{\mu =0}^{\zeta }}{p}_{\eta ,q,\mu }^{P,\alpha }\left(x\right)\left({\displaystyle \frac{\left[\mu \right]}{\left[\eta \right]}}\right)+{\displaystyle \frac{1}{\left[5\right]{[\eta +1]}^4}}{\displaystyle \sum _{\mu =0}^{\zeta }}{p}_{\eta ,q,\mu }^{P,\alpha }\left(x\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} ={\displaystyle \frac{{\left[\eta \right]}^4}{{[\eta +1]}^4}}{\Phi }_{\eta ,q}^{P,\alpha }\left({\varphi }^4;x\right)+{\displaystyle \frac{\left(1+2q+3q^2+4q^3\right){\left[\eta \right]}^3}{\left[5\right]{[\eta +1]}^4}}{\Phi }_{\eta ,q}^{P,\alpha }\left({\varphi }^3;x\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +{\displaystyle \frac{\left(1+3q+6q^2\right){\left[\eta \right]}^2}{\left[5\right]{[\eta +1]}^4}}{\Phi }_{\eta ,q}^{P,\alpha }\left({\varphi }^2;x\right)+{\displaystyle \frac{(1+4q)\left[\eta \right]}{\left[5\right]{[\eta +1]}^4}}{\Phi }_{\eta ,q}^{P,\alpha }\left(\varphi ;x\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +{\displaystyle \frac{1}{\left[5\right]{[\eta +1]}^4}}{\Phi }_{\eta ,q}^{P,\alpha }\left(1;x\right).\end{array}$$

Thus finally, considering Lemma 1 and Corollary 1, we obtain the desired results. □

Corollary 2.

If the function $\phi \left(\varphi \right)=\varphi -x$ is taken to operators ${\Psi }_{\eta ,q}^{P,\alpha }$ defined by (11), then we get the following central moments of orders one, two, and four:

$$\begin{array}{l}{\Psi }_{\eta ,q}^{P,\alpha }\left(\phi \left(\varphi \right);x\right)\hspace{1em}\hspace{1em}={\Psi }_{\eta ,q}^{P,\alpha }\left(\varphi ;x\right)-x{\Psi }_{\eta ,q}^{P,\alpha }\left(1;x\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} =\left({\displaystyle \frac{\left[\zeta \right]}{[\eta +1]}}-1\right)x+{\displaystyle \frac{1}{\left[2\right][\eta +1]}};\\ {\Psi }_{\eta ,q}^{P,\alpha }\left({\left(\phi \left(\varphi \right)\right)}^2;x\right)\hspace{1em}={\Psi }_{\eta ,q}^{P,\alpha }\left({\varphi }^2;x\right)-2x{\Psi }_{\eta ,q}^{P,\alpha }\left(\varphi ;x\right)+x^2{\Psi }_{\eta ,q}^{P,\alpha }\left(1;x\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} =[{\displaystyle \frac{\left(1-\alpha \right)q[\zeta -2]([\zeta -1]+\left[2\right]q^{\zeta -1})}{{[\eta +1]}^2}}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +{\displaystyle \frac{\alpha [\zeta -1]\left[\zeta \right]}{{[\eta +1]}^2}}-2{\displaystyle \frac{\left[\zeta \right]}{[\eta +1]}}+1]x^2\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +[{\displaystyle \frac{\left(1-\alpha \right)\left([\zeta -1]+q^{\zeta -1}(1+\left[2\right])\right)}{{[\eta +1]}^2}}+{\displaystyle \frac{\alpha \left[\zeta \right]}{{[\eta +1]}^2}}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +{\displaystyle \frac{\left[\zeta \right]}{{[\eta +1]}^2}}{\displaystyle \frac{(2q+1)}{\left[3\right]}}-{\displaystyle \frac{2}{\left[2\right][\eta +1]}}]x+{\displaystyle \frac{1}{\left[3\right]{[\eta +1]}^2}};\\ {\Psi }_{\eta ,q}^{P,\alpha }\left({\left(\phi \left(\varphi \right)\right)}^4;x\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} ={\Psi }_{\eta ,q}^{P,\alpha }\left({\varphi }^4;x\right)-4x{\Psi }_{\eta ,q}^{P,\alpha }\left({\varphi }^3;x\right)+6x^2{\Psi }_{\eta ,q}^{P,\alpha }\left({\varphi }^2;x\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} -4x^3{\Psi }_{\eta ,q}^{P,\alpha }\left(\varphi ;x\right)+x^4{\Psi }_{\eta ,q}^{P,\alpha }\left(1;x\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} =\mathcal{O}\left({\displaystyle \frac{1}{{[\eta +1]}^4}}\right)(x^4+x^3+x^2+x+1).\end{array}$$

3. Convergence of Operators ${\Psi }_{\mathit{\eta },\mathit{q}}^{\mathit{P},\mathit{\alpha }}\left(\mathit{\psi };\mathit{x}\right)$

The approximation property of ${\Psi }_{\eta ,q}^{P,\alpha }$ represented by (11) is derived in this section. After obtaining the uniform convergence property for ${\Psi }_{\eta ,q}^{P,\alpha }\left(\psi ;x\right)$, we generate the local and global approximation using the Ditzian–Totik uniform modulus of smoothness. As a key finding in approximation theory, Theorem 2 yields the Bohman–Korovkin–Popoviciu-type theorem, which offers adequate circumstances for our sequence of PLO ${\Psi }_{\eta ,q}^{P,\alpha }$ to converge to an identical operator. A useful method for calculating the error of approximation of a function by a series of PLOs is the Ditzian–Totik modulus of smoothness. The relationship between the Ditzian–Totik modulus of smoothness of orders one and two is provided by Theorem 3. We can investigate the estimation of a function’s approximation error using a sequence of our PLO of order one thanks to Theorem 4. A class of function spaces known as Lipschitz function spaces is defined in terms of the Lipschitz continuity function. We estimate a direct-type approximation in the Lipschitz maximal function space in Theorem 5. This enables us to provide a thorough framework for examining the approximation’s behavior. We may further examine the efficacy and efficiency of the suggested approach in a variety of applications by utilizing these findings. Next, we use the Lipschitz-type maximum approximation and Peetre’s K-functional to deduce various theorems.

Theorem 1

([32,33]). Let ${\left\{L_{\eta }\right\}}_{\eta \ge 1}$ be a sequence of PLOs which acts on $C[a,b]$ to $C[a,b]$, and suppose that $L_{\eta }(1;x)\to 1,$$L_{\eta }(\varphi ;x)\to x,$ and $L_{\eta }({\varphi }^2;x)\to x^2,$ uniformly on $[a,b]$. Then, for any $f\in C[a,b]$, the operator $L_{\eta }\left(f\right)\to f$ is uniform on $[a,b]$.

Theorem 2.

Let $0<q<1$, $0\le \alpha \le 1$, $1\le p<\infty$, and the sequence of PLO ${\Psi }_{\eta ,q}^{P,\alpha }$ act on $L_p[0,1]\to L_p[0,1]$. Suppose that ${\Psi }_{\eta ,q}^{P,\alpha }({\varphi }^i;x)\to x^i$ is uniformly on $[0,1]$ for $i=0,1,2$. Then, for all classes of continuous function $\psi \in C[0,1+P]$, we get

$$\underset{\left[\eta \right]\to \infty }{\text{lim}}{\Psi }_{\eta ,q}^{P,\alpha }\left(\psi ;x\right)\to \psi \left(x\right)$$

which is uniformly convergent on $[0,1]$.

Proof. 

From Lemma 3, it is easy to get

$$\underset{\left[\eta \right]\to \infty }{\text{lim}}{\Psi }_{\eta ,q}^{P,\alpha }\left({\varphi }^i;x\right)=x^i(i=0,1,2).$$

Bohman–Korovkin–Popoviciu Theorem 1, which is uniformly convergent on $[0,1]$, makes it easy to obtain the sequence ${\Psi }_{\eta ,q}^{P,\alpha }\left(\psi ;x\right)\to \psi \left(x\right)$. This completes the proof. □

Next, we use the Ditzian–Totik smoothness properties for the maximum order of two to illustrate some global approximation results. We review the fundamental formulas for the uniform smoothness results of the maximum order of two in a manner that

$$\begin{array}{l}\omega (\psi ,\gamma ):=\underset{0<\left|\rho \right|\le \gamma }{\text{sup}}\underset{x,x+\rho \lambda \left(x\right)\in [0,1]}{\text{sup}}\left\{\right|\psi (x+\rho \lambda \left(x\right))-\psi \left(x\right)\left|\right\};\end{array}$$

$$\begin{array}{l}{\omega }_2^{\lambda }(\psi ,\gamma ):=\underset{0<\left|\rho \right|\le \gamma }{\text{sup}}\underset{x,x\pm \rho \lambda \left(x\right)\in [0,1]}{\text{sup}}\left\{\right|\psi (x+\rho \lambda \left(x\right))-2\psi \left(x\right)+\psi (x-\rho \lambda \left(x\right))\left|\right\}.\end{array}$$

Correspondingly, $\lambda \left(x\right)={\left[(x-a)(b-x)\right]}^{1/2}$ is the step-weight function. Suppose $\lambda$ is defined on $[a,b]$ (see [34]) if $x\in [a,b]$. Suppose $AC$ denotes a uniform continuous set. A mathematical idea utilized in approximation theory, specifically in the study of interpolation spaces and function approximation, is Peetre’s K-functional. Thus, Peetre’s K-functional on weight function $\lambda \left(x\right)$ is given by

$$\begin{array}{l}{K}_{2,\lambda \left(x\right)}(\psi ,\gamma )=\underset{h\in W^2\left(\lambda \right)}{\text{inf}}\left\{\left|\right|\psi -{h\left|\right|}_{C[0,1+\alpha ]}+\gamma \left|\right|{\lambda }^2{h}^{″}{\left|\right|}_{C[0,1+\alpha ]}:h\in C^2[0,1+\alpha ]\right\},\end{array}$$

and $\gamma >0$, $W^2\left(\lambda \right)=\{h\in C[0,1+\alpha ]:h^{\prime }\in AC[0,1+\alpha ],{\lambda }^2{h}^{″}\in C[0,1+\alpha ]\}$ and $C^2[0,1+\alpha ]=\{h\in C[0,1+\alpha ]:h^{\prime },h^{″}\in C[0,1+\alpha ]\}$.

Remark 1

([35]). There exists a absolute positive constant M such that

$$\begin{array}{l}{M}^{-1}{\omega }_2(\psi ,\sqrt{\gamma })\le K_{2,\lambda \left(x\right)}(\psi ,\gamma )\le M{\omega }_2(\psi ,\sqrt{\gamma }).\end{array}$$

(13)

The approximation properties of functions in different spaces are described by Peetre’s K-functional. In terms of the modulus of smoothness property, we obtain convergence by the use of weight functions $\lambda \left(x\right)$, which are as follows:

Theorem 3.

For any step-weight function $\lambda \left(x\right)$ such that ${\lambda }^2$ is concave and $(\lambda \ne 0)$ given, for all $\psi \in C[0,1+P]$, the operators ${\Psi }_{\eta ,q}^{P,\alpha }$ satisfy

$$\begin{array}{l}|{\Psi }_{\eta ,q}^{P,\alpha }\left(\psi ;x\right)-\psi \left(x\right)|\le M{\omega }_2\left(\psi ,{\displaystyle \frac{{[{\nu }_{\eta ,q}^{P,\alpha }\left(x\right)+{\theta }_{\eta ,q}^{P,\alpha }\left(x\right)]}^{1/2}}{2{\left[(x-a)(b-x)\right]}^{1/2}}}\right)+\omega \left(\psi ,{\displaystyle \frac{{\theta }_{\eta ,q}^{P,\alpha }\left(x\right)}{\lambda \left(x\right)}}\right),\end{array}$$

where $x\in [a,b]$, ${\theta }_{\eta ,q}^{P,\alpha }\left(x\right)={\Psi }_{\eta ,q}^{P,\alpha }(\phi \left(\varphi \right);x)$, and ${\nu }_{\eta ,q}^{P,\alpha }\left(x\right)={\Psi }_{\eta ,q}^{P,\alpha }({\left(\phi \left(\varphi \right)\right)}^2;x)$, and these are central moments defined by Corollary 2.

Proof. 

If we consider an auxiliary operator

$$\begin{array}{l}{\Omega }_{\eta ,q}^{P,\alpha }(\psi ;x)={\Psi }_{\eta ,q}^{P,\alpha }\left(\psi ;x\right)-\psi \left(x+{\theta }_{\eta ,q}^{P,\alpha }\left(x\right)\right)+\psi \left(x\right),\end{array}$$

(14)

where $\psi \in C[0,1+P]$, and $x\in [0,1]$, then from Lemma 3, it is easy to verify that

$${\Omega }_{\eta ,q}^{P,\alpha }(1;x)=1\mathrm{and}{\Omega }_{\eta ,q}^{P,\alpha }(\varphi ;x)=x,$$

${\Omega }_{\eta ,q}^{P,\alpha }(\phi \left(\varphi \right);x)=0$.

Take $y=(1-d)\varphi +dx$, for any $d\in [0,1]$. We suppose that ${\lambda }^2$ is a concave function defined on $[0,1]$; then consequently, we can derive ${\lambda }^2\left(y\right)\ge d{\lambda }^2\left(x\right)+(1-d){\lambda }^2\left(\varphi \right)$ and

$$\begin{array}{l}{\displaystyle \frac{|\varphi -y|}{{\lambda }^2\left(y\right)}}\le {\displaystyle \frac{d|x-\varphi |}{d{\lambda }^2\left(x\right)+(1-d){\lambda }^2\left(\varphi \right)}}\le {\displaystyle \frac{\left|\phi \right(\varphi \left)\right|}{{\lambda }^2\left(x\right)}}.\end{array}$$

(15)

We get the following identities:

$$\begin{array}{ll}|{\Omega }_{\eta ,q}^{P,\alpha }(\psi ;x)-\psi \left(x\right)|& \le |{\Omega }_{\eta ,q}^{P,\alpha }(\psi -h;x)|+|{\Omega }_{\eta ,q}^{P,\alpha }(h;x)-h\left(x\right)|+|\psi \left(x\right)-h\left(x\right)|\\ & \le {4\parallel \psi -h\parallel }_{C[0,1+\alpha ]}+|{\Omega }_{\eta ,q}^{P,\alpha }(h;x)-h\left(x\right)|.\end{array}$$

(16)

By Taylor’s series expansion, we can conclude that

$$\begin{array}{l}|{\Omega }_{\eta ,q}^{P,\alpha }(\psi ;x)-\psi \left(x\right)|\le {\Psi }_{\eta ,q}^{P,\alpha }\left(\right|{\int }_x^{\varphi }|\varphi -y||h^{″}\left(y\right)|{\mathrm{d}}_{q}y|;x)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +\left|{\int }_x^{{\displaystyle \frac{\left[\zeta \right]}{[\eta +1]}}x+{\displaystyle \frac{1}{\left[2\right][\eta +1]}}}|{\displaystyle \frac{\left[\zeta \right]}{[\eta +1]}}x+{\displaystyle \frac{1}{\left[2\right][\eta +1]}}-y|\left|h^{″}\left(y\right)\right|{\mathrm{d}}_{q}y\right|\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \le \parallel {\lambda }^2{h}^{″}{\parallel }_{C[0,1+\alpha ]}{\Psi }_{\eta ,q}^{P,\alpha }\left(\left|{\int }_x^{\varphi }{\displaystyle \frac{|\varphi -y|}{{\lambda }^2\left(y\right)}}{\mathrm{d}}_{q}y\right|;x\right)+{\parallel {\lambda }^2{h}^{″}\parallel }_{C[0,1+\alpha ]}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \times \left|{\int }_x^{{\displaystyle \frac{\left[\zeta \right]}{[\eta +1]}}x+{\displaystyle \frac{1}{\left[2\right][\eta +1]}}}\right|{\displaystyle \frac{\left[\zeta \right]}{[\eta +1]}}x+{\displaystyle \frac{1}{\left[2\right][\eta +1]}}-y\left|{\displaystyle \frac{{\mathrm{d}}_{q}y}{{\lambda }^2\left(y\right)}}\right|\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \le {\lambda }^{-2}\left(x\right){\parallel {\lambda }^2{h}^{″}\parallel }_{C[0,1+\alpha ]}{\Psi }_{\eta ,q}^{P,\alpha }({\left(\phi \left(\varphi \right)\right)}^2;x)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +{\lambda }^{-2}\left(x\right){\parallel {\lambda }^2{h}^{″}\parallel }_{C[0,1+\alpha ]}{\theta }_{\eta ,q}^{P,\alpha }\left(x\right).\end{array}$$

(17)

Peetre’s K-functional makes it simple to obtain derivations from Relations (13), (16), and (17)

$$\begin{array}{ll}|{\Omega }_{\eta ,q}^{P,\alpha }(\psi ;x)-\psi \left(x\right)|& \le {4\parallel \psi -h\parallel }_{C[0,1+\alpha ]}+{\lambda }^{-2}\left(x\right){\parallel {\lambda }^2{h}^{″}\parallel }_{C[0,1+\alpha ]}\left({\nu }_{\eta ,q}^{P,\alpha }\left(x\right)+{\theta }_{\eta ,q}^{P,\alpha }\left(x\right)\right)\\ & \le M{\omega }_2\left(\psi ,{\displaystyle \frac{1}{2}}\sqrt{{\displaystyle \frac{{\nu }_{\eta ,q}^{P,\alpha }\left(x\right)+{\theta }_{\eta ,q}^{P,\alpha }\left(x\right)}{\lambda \left(x\right)}}}\right).\end{array}$$

We now obtain the inequality due to the first order of the uniform modulus of smoothness.

$$\begin{array}{ll}|\psi \left({\displaystyle \frac{\left[\zeta \right]}{[\eta +1]}}x+{\displaystyle \frac{1}{\left[2\right][\eta +1]}}\right)-\psi \left(x\right)|& =|\psi \left(x+\lambda \left(x\right){\displaystyle \frac{{\theta }_{\eta ,q}^{P,\alpha }\left(x\right)}{\lambda \left(x\right)}}\right)-\psi \left(x\right)|\le \omega \left(\psi ,{\displaystyle \frac{{\theta }_{\eta ,q}^{P,\alpha }\left(x\right)}{\lambda \left(x\right)}}\right).\end{array}$$

Consequently, we ultimately obtain disparity:

$$\begin{array}{ll}|{\Psi }_{\eta ,q}^{P,\alpha }\left(\psi ;x\right)-\psi \left(x\right)|& \le |{\Omega }_{\eta ,q}^{P,\alpha }(\psi ;x)-\psi \left(x\right)|+|\psi \left({\displaystyle \frac{\left[\zeta \right]}{[\eta +1]}}x+{\displaystyle \frac{1}{\left[2\right][\eta +1]}}\right)-\psi \left(x\right)|\\ & \le M{\omega }_2\left(\psi ,{\displaystyle \frac{1}{2}}\sqrt{{\displaystyle \frac{{\nu }_{\eta ,q}^{P,\alpha }\left(x\right)+{\theta }_{\eta ,q}^{P,\alpha }\left(x\right)}{(x-a)(b-x)}}}\right)+\omega \left(\psi ,{\displaystyle \frac{{\theta }_{\eta ,q}^{P,\alpha }\left(x\right)}{\lambda \left(x\right)}}\right),\end{array}$$

which completes the desired proof. □

Below we obtain another approximation of properties for first-order continuously differentiable functions in Peetre’s K-functional by the use of Theorem 3. Thus we can state the theorem as follows:

Theorem 4.

Let $x\in [0,1]$ and $0<q<1$; then for all ${\psi }^{\prime }\in C[0,1+P]$, we get the following inequality:

$$\begin{array}{ll}|{\Psi }_{\eta ,q}^{P,\alpha }\left(\psi ;x\right)-\psi \left(x\right)|& \le {\nu }_{\eta ,q}^{P,\alpha }\left(x\right)\left|{\psi }^{\prime }\left(x\right)\right|+2\sqrt{{\nu }_{\eta ,q}^{P,\alpha }\left(x\right)}\omega \left({\psi }^{\prime },\sqrt{{\nu }_{\eta ,q}^{P,\alpha }(x)}\right),\end{array}$$

where ${\nu }_{\eta ,q}^{P,\alpha }\left(x\right)$ is defined in Theorem 3.

Proof. 

We know the relation

$$\begin{array}{l}\psi \left(\varphi \right)=\psi \left(x\right)+\left(\phi \left(\varphi \right)\right){\psi }^{\prime }\left(x\right)+{\int }_x^{\varphi }({\psi }^{\prime }\left(y\right)-{\psi }^{\prime }\left(x\right)){\mathrm{d}}_{q}y.\end{array}$$

(18)

For all $\varphi ,x\in [0,1]$, by applying the operators ${\Psi }_{\eta ,q}^{P,\alpha }$ to Equality (18), we obtain

$$\begin{array}{l}{\Psi }_{\eta ,q}^{P,\alpha }(\psi \left(\varphi \right)-\psi \left(x\right);x)={\psi }^{\prime }\left(x\right){\Psi }_{\eta ,P,\alpha }(\phi \left(\varphi \right);x)+{\Psi }_{\eta ,q}^{P,\alpha }\left({\int }_x^{\varphi }({\psi }^{\prime }\left(y\right)-{\psi }^{\prime }\left(x\right)){\mathrm{d}}_{q}y;x\right).\end{array}$$

For any $\gamma >0$, if $\psi \in C[0,1+P]$ and $x\in [0,1]$, then

$$|\psi \left(y\right)-\psi \left(x\right)|\le \omega (\psi ,\gamma )\left({\displaystyle \frac{|y-x|}{\gamma }}+1\right).$$

From the above explanations, we can deduce that

$$\left|{\int }_x^{\varphi }({\psi }^{\prime }\left(y\right)-{\psi }^{\prime }\left(x\right)){\mathrm{d}}_{q}v\right|\le \omega ({\psi }^{\prime },\gamma )\left({\displaystyle \frac{{\left(\phi \left(\varphi \right)\right)}^2}{\gamma }}+\left|\phi \left(\varphi \right)\right|\right).$$

Therefore, it is easy to find that

$$\begin{array}{ll}|{\Psi }_{\eta ,q}^{P,\alpha }\left(\psi ;x\right)-\psi \left(x\right)|& \le |{\psi }^{\prime }\left(x\right)\left|\right|{\Psi }_{\eta ,q}^{P,\alpha }(\phi \left(\varphi \right);x)|\\ & +\omega ({\psi }^{\prime },\gamma )\left\{{\displaystyle \frac{1}{\gamma }}{\Psi }_{\eta ,q}^{P,\alpha }({\left(\phi \right(\varphi \left)\right)}^2;x)+{\Psi }_{\eta ,q}^{P,\alpha }\left(\right|\phi \left(\varphi \right)|;x)\right\}.\end{array}$$

From the Cauchy–Schwarz inequality, we obtain

$${\Psi }_{\eta ,q}^{P,\alpha }\left(\right|\phi \left(\varphi \right)|;x)\le {\Psi }_{\eta ,q}^{P,\alpha }{(1;x)}^{{\displaystyle \frac{1}{2}}}{\Psi }_{\eta ,q}^{P,\alpha }{({\left(\phi \left(\varphi \right)\right)}^2;x)}^{{\displaystyle \frac{1}{2}}}={\Psi }_{\eta ,q}^{P,\alpha }{({\left(\phi \left(\varphi \right)\right)}^2;x)}^{{\displaystyle \frac{1}{2}}}.$$

Thus, we have

$$\begin{array}{ll}|{\Psi }_{\eta ,q}^{P,\alpha }\left(\psi ;x\right)-\psi \left(x\right)|& \le {\psi }^{\prime }\left(x\right){\Psi }_{\eta ,q}^{P,\alpha }({\left(\phi \right(\varphi \left)\right)}^2;x)\\ & +\omega ({\psi }^{\prime },\gamma )\left\{{\displaystyle \frac{1}{\gamma }}\sqrt{{\Psi }_{\eta ,q}^{P,\alpha }\left({\left(\phi \left(\varphi \right)\right)}^2;x\right)}+1\right\}{\Psi }_{\eta ,q}^{P,\alpha }{({\left(\phi \right(\varphi \left)\right)}^2;x)}^{{\displaystyle \frac{1}{2}}}.\end{array}$$

This completes the proof. □

The local direct approximation is now estimated using a Lipschitz function space, as we remember from [36] that the properties of such functions allow for better control over convergence rates. This approach not only enhances the accuracy of the estimates but also simplifies the computational processes involved.

$$\begin{array}{l}Li{p}_{\eta }\left(\theta \right):=\{\psi \in C[0,1]:|\psi \left(\varphi \right)-\psi \left(x\right)|\le M{\displaystyle \frac{{\left|\phi \right(\varphi \left)\right|}^{\theta }}{{({\beta }_1{x}^2+{\beta }_{2}x+\varphi )}^{\frac{\theta }{2}}}};x,\varphi \in [0,1]\},\end{array}$$

(19)

where $M>0$, ${\beta }_1,{\beta }_2\ge 0$, and $\theta \in \left(0.1\right]$.

The difference between the two functions at the values of two points are given by Inequality (19), and this provides a way to bound the error in approximating the Lipschitz function by a simpler function in terms of the Lipschitz constant M. Therefore, we derive Theorem 5 based on Inequality (19) to estimate the bound of error to approximate the Lipschitz function $\psi$.

Theorem 5.

Let $0<q<1$, and suppose that $Li{p}_{\eta }\left(\theta \right)$ is the Lipschitz inequality by (19); then for all $\psi \in Li{p}_{\eta }\left(\theta \right)$, there exists a positive M such that

$$\begin{array}{l}|{\Psi }_{\eta ,q}^{P,\alpha }\left(\psi ;x\right)-\psi \left(x\right)|\le M\sqrt{{\displaystyle \frac{{\left[{\nu }_{\eta ,q}^{P,\alpha }\left(x\right)\right]}^{\theta }}{{({\beta }_1{x}^2+{\beta }_{2}x)}^{\theta }}}},\end{array}$$

where $\theta \in (0,1]$.

Proof. 

Consider any $\psi \in Li{p}_{\eta }\left(\theta \right)$ and $\theta \in (0,1]$. First, we would like to show that our solution is valid for $\theta =1$. Because of this, we have

$$\begin{array}{ll}|{\Psi }_{\eta ,q}^{P,\alpha }\left(\psi ;x\right)-\psi \left(x\right)|& \le \psi \left(x\right)|{\Psi }_{\eta ,q}^{P,\alpha }(1;x)-1|+|{\Psi }_{\eta ,q}^{P,\alpha }\left(\right|\psi \left(\varphi \right)-\psi \left(x\right)|;x)|\\ & \le [\eta +1]{\displaystyle \sum _{\mu =0}^{\zeta }}{\int }_J|\psi \left(\varphi \right)-\psi \left(x\right)|{\mathrm{d}}_q\varphi q^{-\mu }{p}_{\eta ,q,\mu }^{P,\alpha }\left(x\right)\\ & \le M[\eta +1]{\displaystyle \sum _{\mu =0}^{\zeta }}{\displaystyle \frac{{\int }_J\left|\phi \right(\varphi \left)\right|{\mathrm{d}}_q\varphi }{{({\beta }_1{x}^2+{\beta }_{2}x+t)}^{\frac{1}{2}}}}{q}^{-\mu }{p}_{\eta ,q,\mu }^{P,\alpha }\left(x\right)\end{array}$$

for $\psi \in Li{p}_{\eta }\left(1\right)$; by using

$${({\beta }_1{x}^2+{\beta }_{2}x+\varphi )}^{-1/2}\le {({\beta }_1{x}^2+{\beta }_{2}x)}^{-1/2}({\beta }_1,{\beta }_2\ge 0,)$$

and applying the Cauchy–Schwarz inequality, one has

$$\begin{array}{ll}|{\Psi }_{\eta ,q}^{P,\alpha }\left(\psi ;x\right)-\psi \left(x\right)|& \le M{({\beta }_1{x}^2+{\beta }_{2}x)}^{-1/2}{\displaystyle \sum _{\mu =0}^{\zeta }}[\eta +1]{\int }_J|\phi \left(\varphi \right)|{\mathrm{d}}_{q}t{q}^{-\mu }{p}_{\eta ,q,\mu }^{P,\alpha }\left(x\right)\\ & =M{({\beta }_1{x}^2+{\beta }_{2}x)}^{-1/2}\left|{\Psi }_{\eta ,q}^{P,\alpha }(\phi \left(\varphi \right);x)\right|\\ & \le M|{\nu }_{\eta ,q}^{P,\alpha }{\left(x\right)|}^{1/2}{({\beta }_1{x}^2+{\beta }_{2}x)}^{-1/2}.\end{array}$$

Therefore, the statement is true if $\theta =1$. Furthermore, as per ${\Psi }_{\eta ,q}^{P,\alpha }\left(\psi ;x\right)$, the monotonicity property applying Holder’s inequality to $c=2/\theta$ and $d=2/(2-\theta )$ makes it evident that our statement is true for $\theta \in (0,1]$. This implies that

$$\begin{array}{l}\left|{\Psi }_{\eta ,q}^{P,\alpha }\left(\psi ;x\right)-\psi \left(x\right)\right|\hspace{1em}\le [\eta +1]{\displaystyle \sum _{\mu =0}^{\zeta }}{\int }_J|\psi \left(\varphi \right)-\psi \left(x\right)|{\mathrm{d}}_q\varphi q^{-\mu }{p}_{\eta ,q,\mu }^{P,\alpha }\left(x\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\le {\left({\displaystyle \sum _{\mu =0}^{\zeta }}[\eta +1]{\int }_J|\psi \left(\varphi \right)-\psi \left(x\right){|}^{{\displaystyle \frac{2}{\theta }}}{\mathrm{d}}_q\varphi q^{-\mu }{p}_{\eta ,q,\mu }^{P,\alpha }\left(x\right)\right)}^{{\displaystyle \frac{\theta }{2}}}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\times {\left({\displaystyle \sum _{\mu =0}^{\zeta }}{\Psi }_{\eta ,q}^{P,\alpha }\left(x\right)\right)}^{{\displaystyle \frac{2-\theta }{2}}}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\le M{\left({\displaystyle \sum _{\mu =0}^{\zeta }}{\displaystyle \frac{[\eta +1]{\int }_J{\left(\phi \left(\varphi \right)\right)}^2{\mathrm{d}}_q\varphi p_{\eta ,q,\mu }^{P,\alpha }\left(x\right)q^{-\mu }}{\varphi +{\beta }_1{x}^2+{\beta }_{2}x}}\right)}^{{\displaystyle \frac{\theta }{2}}}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\le M{\left\{{\displaystyle \sum _{\mu =0}^{\zeta }}[\eta +1]{\int }_J{\left(\phi \right(\varphi \left)\right)}^2{\mathrm{d}}_q\varphi q^{-\mu }{p}_{\eta ,q,\mu }^{P,\alpha }\left(x\right)\right\}}^{{\displaystyle \frac{\theta }{2}}}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\times {({\beta }_1{x}^2+{\beta }_{2}x)}^{-\theta /2}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\le M{({\beta }_1{x}^2+{\beta }_{2}x+\varphi )}^{-\theta /2}{\left[{\Psi }_{\eta ,q}^{P,\alpha }({\left(\phi \left(\varphi \right)\right)}^2;x)\right]}^{{\displaystyle \frac{\theta }{2}}}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=M\sqrt{{\displaystyle \frac{{\left[{\nu }_{\eta ,q}^{P,\alpha }\left(x\right)\right]}^{\theta }}{{({\beta }_1{x}^2+{\beta }_{2}x)}^{\theta }}}}.\end{array}$$

These explanations complete the proof of the desired Theorem 5. □

4. Voronovskaja-Type Approximation

An approximation theory conclusion that characterizes the asymptotic behavior of a series of linear operators is called the Voronovskaja-type approximation. In approximation theory, the Voronovskaja-type approximation has numerous uses, such as calculating the error of a function’s approximation by a series of linear operators, examining the convergence of linear operator sequences, and creating novel approaches to function approximation. Theorem 6 is a generalization of the classical Voronovskaja theorem, which is defined for the twice differentiable function. Several PLO sequences have been subjected to the Voronovskaja-type theorem for bounded functions. Compared to the standard Voronovskaja theorem, the Voronovskaja-type theorem for limited functions is a broader finding that may be extended to a larger class of functions. Thus, we present Theorem 7 for any limited functions $\psi \in C_B[0,1+P]$. The approximation theory of the quantitative Voronovskaja type for ${\Psi }_{\eta ,q}^{P,\alpha }$ is mainly inspired by [28,37]. We employ the concept of the modulus of smoothness, which is described as follows, for this:

$$\begin{array}{l}{\omega }_u(\mu ,\gamma ):=\underset{0<\left|\rho \right|\le \gamma }{\text{sup}}\left\{|\mu \left(x+{\displaystyle \frac{\rho u\left(x\right)}{2}}\right)-\mu \left(x-{\displaystyle \frac{\rho u\left(x\right)}{2}}\right)|\right\},\end{array}$$

where $0\le x\pm {\displaystyle \frac{\rho u\left(x\right)}{2}}\le 1$. In this case, $\mu \left(x\right)\in C[0,1+P]$ together with $u\left(x\right)={(x-x^2)}^{1/2}$, and the associated Peetre’s K-functional is defined by

$$\begin{array}{l}{K}_u(\mu ,\gamma )=\in {\mu }_{v\in {\omega }_u[0,1+P]}\left\{\left|\right|\mu -v\left|\right|+\gamma \left|\right|u{v}^{\prime }\left|\right|:v^{\prime }\in C[0,1+P],\gamma >0\right\},\end{array}$$

where ${\omega }_u[0,1+P]=\{v:v\in AC[0,1+\alpha ],\parallel u{v}^{\prime }\parallel <\infty \}$, and $AC[0,1+P]$ is denoted for the set of functions on interval $[z_1,z_1]\subset [0,1+P]$ that are completely absolutely continuous. A constant $M>0$ exists such that

$$\begin{array}{l}{K}_u(\mu ,\gamma )\le M{\omega }_u(\mu ,\gamma ).\end{array}$$

Theorem 6.

Let $0<q<1$, and suppose that the sequence of positive linear operators acts on ${\Psi }_{\eta ,q}^{P,\alpha }:C[0,1]\to C[0,1]$; then for all $\mu ,{\mu }^{\prime },{\mu }^{″}\in C[0,1+P]$, we get

$$\begin{array}{l}|{\Psi }_{\eta ,q}^{P,\alpha }\left(\mu ;x\right)-\mu \left(x\right)-{\nu }_{\eta ,q}^{P,\alpha }\left(x\right){\mu }^{\prime }\left(x\right)-{\displaystyle \frac{{\theta }_{\eta ,q}^{P,\alpha }\left(x\right)+1}{2}}{\mu }^{″}\left(x\right)+1|\\ \le {\displaystyle \frac{\Omega }{[\eta +1]}}{u}^2\left(x\right){\omega }_u\left({\mu }^{″},{\displaystyle \frac{1}{\sqrt{[\eta +1]}}}\right),\end{array}$$

where $x\in [0,1]$, $\Omega >0$ is a constant, and ${\theta }_{\eta ,q}^{P,\alpha }\left(x\right)$ and ${\nu }_{\eta ,q}^{P,\alpha }\left(x\right)$ are defined by Theorem 3.

Proof. 

Consider $\mu \in C[0,1+P]$; then

$$\mu \left(\varphi \right)-\mu \left(x\right)-\left(\phi \left(\varphi \right)\right){\mu }^{\prime }\left(x\right)={\int }_x^{\varphi }(\varphi -y){\mu }^{″}\left(y\right){\mathrm{d}}_{q}y,$$

which leads to

$$\begin{array}{l}\mu \left(\varphi \right)-\mu \left(x\right)-\left(\phi \left(\varphi \right)\right){\mu }^{\prime }\left(x\right)-{\displaystyle \frac{{\mu }^{″}\left(x\right)}{2}}\left({\left(\phi \right(\varphi \left)\right)}^2+1\right)\le {\int }_x^{\varphi }(\varphi -y)[{\mu }^{″}\left(y\right)-{\mu }^{″}\left(x\right)]{\mathrm{d}}_{q}y.\end{array}$$

(20)

Applying ${\Psi }_{\eta ,q}^{P,\alpha }\left(\mu ;x\right)$ to (20),

$$\begin{array}{l}|{\Psi }_{\eta ,q}^{P,\alpha }\left(\mu ;x\right)-\mu \left(x\right)-{\Psi }_{\eta ,q}^{P,\alpha }(\phi \left(\varphi \right);x){\mu }^{\prime }\left(x\right)-{\displaystyle \frac{{\mu }^{″}\left(x\right)}{2}}\left({\Psi }_{\eta ,q}^{P,\alpha }({\left(\phi \left(\varphi \right)\right)}^2;x)+{\Psi }_{\eta ,q}^{P,\alpha }(1;x)\right)|\\ \le {\Psi }_{\eta ,q}^{P,\alpha }\left(|{\int }_x^{\varphi }|\varphi -y||{\mu }^{″}\left(y\right)-{\mu }^{″}\left(x\right)|{\mathrm{d}}_{q}y|;x\right).\end{array}$$

(21)

Based on the equality of the right side of (21), we can estimate the following:

$$\begin{array}{l}|{\int }_x^{\varphi }|\varphi -y||{\mu }^{″}\left(y\right)-{\mu }^{″}\left(x\right)|{\mathrm{d}}_{q}y|\le 2\parallel {\mu }^{″}{-g\parallel \left(\phi \right(\varphi \left)\right)}^2+2\parallel u{g}^{\prime }\parallel u^{-1}\left(x\right){\left|\phi \left(\varphi \right)\right|}^3,\end{array}$$

(22)

where $\mu \in {\omega }_u[0,1+\alpha ]$. Suppose there exists $\Omega >0$ and

$$\begin{array}{l}{\Psi }_{\eta ,q}^{P,\alpha }({\left(\phi \right(\varphi \left)\right)}^2;x)\le {\displaystyle \frac{2^{-1}\Omega }{[\eta +1]}}{u}^2\left(x\right)\mathrm{and}{\Psi }_{\eta ,q}^{P,\alpha }({\left(\phi \right(\varphi \left)\right)}^4;x)\le {\displaystyle \frac{2^{-1}\Omega }{{[\eta +1]}^2}}\left(u^4\left(x\right)\right).\end{array}$$

(23)

Based on the Cauchy–Schwarz inequality, we can write that

$$\begin{array}{ll}& |{\Psi }_{\eta ,q}^{P,\alpha }\left(\mu ;x\right)-\mu \left(x\right)-{\Psi }_{\eta ,q}^{P,\alpha }(\phi \left(\varphi \right);x){\mu }^{\prime }\left(x\right)-{\displaystyle \frac{{\mu }^{″}\left(x\right)}{2}}\left({\Psi }_{\eta ,q}^{P,\alpha }({\left(\phi \right(\varphi \left)\right)}^2;x)+{\Psi }_{\eta ,q}^{P,\alpha }(1;x)\right)|\\ & \le 2\parallel {\mu }^{″}-v\parallel {\Psi }_{\eta ,q}^{P,\alpha }({\left(\phi \right(\varphi \left)\right)}^2;x)+2\parallel u{v}^{\prime }\parallel u^{-1}\left(x\right){\Psi }_{\eta ,q}^{P,\alpha }{\left(\right|\phi \left(\varphi \right)|}^3;x)\\ & \le {\displaystyle \frac{\Omega }{{[\eta +1]}^4}}(x^2+x)\parallel {\mu }^{″}-v\parallel +2\parallel u{v}^{\prime }\parallel u^{-1}\left(x\right){\left\{{\Psi }_{\eta ,q}^{P,\alpha }({\left(\phi \left(\varphi \right)\right)}^2;x)\right\}}^{1/2}{\left\{{\Psi }_{\eta ,q}^{P,\alpha }({\left(\phi \left(\varphi \right)\right)}^4;x)\right\}}^{1/2}\\ & \le {\displaystyle \frac{\Omega }{{[\eta +1]}^2}}{u}^2\left(x\right)\left\{\parallel {\mu }^{″}{-v\parallel +[\eta +1]}^{-1/2}\parallel u{v}^{\prime }\parallel \right\}.\end{array}$$

By calculating the infimum over all $v\in {\omega }_u[0,\alpha +1]$, we discover that

$$\begin{array}{ll}& |{\Psi }_{\eta ,q}^{P,\alpha }\left(\mu ;x\right)-\mu \left(x\right)-{\mu }^{\prime }\left(x\right){\nu }_{\eta ,q}^{P,\alpha }\left(x\right)-{\mu }^{″}\left(x\right){\displaystyle \frac{1+{\theta }_{\eta ,q}^{P,\alpha }\left(x\right)}{2}}+1|\\ & \le {\displaystyle \frac{\Omega }{[\eta +1]}}{u}^2\left(x\right){\omega }_u\left({\mu }^{″},{\displaystyle \frac{1}{\sqrt{[\eta +1]}}}\right),\end{array}$$

which completes our results. □

Theorem 7.

Let $0<q<1$ and operators ${\Psi }_{\eta ,q}^{P,\alpha }$ be defined from $C[0,1]$ to $C[0,1]$; then for all $\mu \in C_B[0,1+P]$, we deduce

$$\begin{array}{l}\underset{\left[\eta \right]\to \infty }{\text{lim}}[\eta +1]\left[{\Psi }_{\eta ,q}^{P,\alpha }\left(\mu ;x\right)-\mu \left(x\right)-{\nu }_{\eta ,q}^{P,\alpha }\left(x\right){\mu }^{\prime }\left(x\right)-{\displaystyle \frac{{\theta }_{\eta ,q}^{P,\alpha }\left(x\right)+1}{2}}{\mu }^{″}\left(x\right)\right]=0,\end{array}$$

where the collection of all bounded and continuous functions on $[0,1+P]$ is represented by the notation $C_B[0,1+P]$.

Proof. 

Assuming $\mu \in C_B[0,1+P]$, we may apply Taylor’s series formula to determine

$$\begin{array}{l}\mu \left(\varphi \right)-\mu \left(x\right)=\left(\phi \left(\varphi \right)\right){\mu }^{\prime }\left(x\right)+{\displaystyle \frac{1}{2}}{\left(\phi \left(\varphi \right)\right)}^2{\mu }^{″}\left(x\right)+R_x\left(\varphi \right){\left(\phi \left(\varphi \right)\right)}^2.\end{array}$$

(24)

For $R_x\left(\varphi \right)\to 0$, the Peano form of the remainder is defined as $\varphi \to x$, where $R_x\left(\varphi \right)\in C[0,1]$. When we apply the operators ${\Psi }_{\eta ,q}^{P,\alpha }(·;x)$ to the equality (24), we obtain

$${\Psi }_{\eta ,q}^{P,\alpha }\left(\mu ;x\right)-\mu \left(x\right)={\mu }^{\prime }\left(x\right){\Psi }_{\eta ,q}^{P,\alpha }(\phi \left(\varphi \right);x)+{\displaystyle \frac{{\mu }^{″}\left(x\right)}{2}}{\Psi }_{\eta ,q}^{P,\alpha }({\left(\phi \left(\varphi \right)\right)}^2;x)+{\Psi }_{\eta ,q}^{P,\alpha }({\left(\phi \left(\varphi \right)\right)}^2{R}_x\left(\varphi \right);x).$$

From the Cauchy–Schwarz property, we get

$$\begin{array}{l}{\Psi }_{\eta ,q}^{P,\alpha }({\left(\phi \right(\varphi \left)\right)}^2{R}_x\left(\varphi \right);x)\le \sqrt{{\Psi }_{\eta ,q}^{P,\alpha }\left(R_x^2\right(\varphi );x)}\sqrt{{\Psi }_{\eta ,q}^{P,\alpha }({\left(\phi \left(\varphi \right)\right)}^4;x)}.\end{array}$$

(25)

We clearly observe here that ${\text{lim}}_{\left[\eta \right]\to \infty }{\Psi }_{\eta ,q}^{P,\alpha }(R_x^2\left(\varphi \right);x)=0$, and therefore

$$\underset{\left[\eta \right]\to \infty }{\text{lim}}[\eta +1]\left\{{\Psi }_{\eta ,q}^{P,\alpha }({\left(\phi \left(\varphi \right)\right)}^2{R}_x\left(\varphi \right);x)\right\}=0.$$

(26)

Thus, we have

$$\begin{array}{l}\underset{\left[\eta \right]\to \infty }{\text{lim}}[\eta +1]\{{\Psi }_{\eta ,q}^{P,\alpha }\left(\mu ;x\right)-\mu \left(x\right)\}=\underset{\left[\eta \right]\to \infty }{\text{lim}}[\eta +1]\{{\Psi }_{\eta ,q}^{P,\alpha }(\phi \left(\varphi \right);x){\mu }^{\prime }\left(x\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+{\displaystyle \frac{{\mu }^{″}\left(x\right)}{2}}{\Psi }_{\eta ,q}^{P,\alpha }({\left(\phi \right(\varphi \left)\right)}^2;x)+{\Psi }_{\eta ,q}^{P,\alpha }({\left(\phi \right(\varphi \left)\right)}^2{R}_x\left(\varphi \right);x)\}.\end{array}$$

Thus, in the view of Equality (26), we have our proof of Theorem 7. □

5. Numerical and Graphical Results

To illustrate the approximation behavior of the proposed modified Kantorovich-type q-Bernstein–Schurer operators ${\Psi }_{\eta ,q}^{P,\alpha }$, we consider the test function

$$\psi \left(x\right)=sin{x}^{15},x\in [0,1].$$

The computations are carried out for the parameters $q=0.9$, $p=2$, and $\alpha =0.3$. The operator values are evaluated for different values of the shape parameter $\eta =10,20,30$. The Jackson-type q-integral is employed in the definition of the Kantorovich modification to ensure improved smoothness and approximation accuracy.

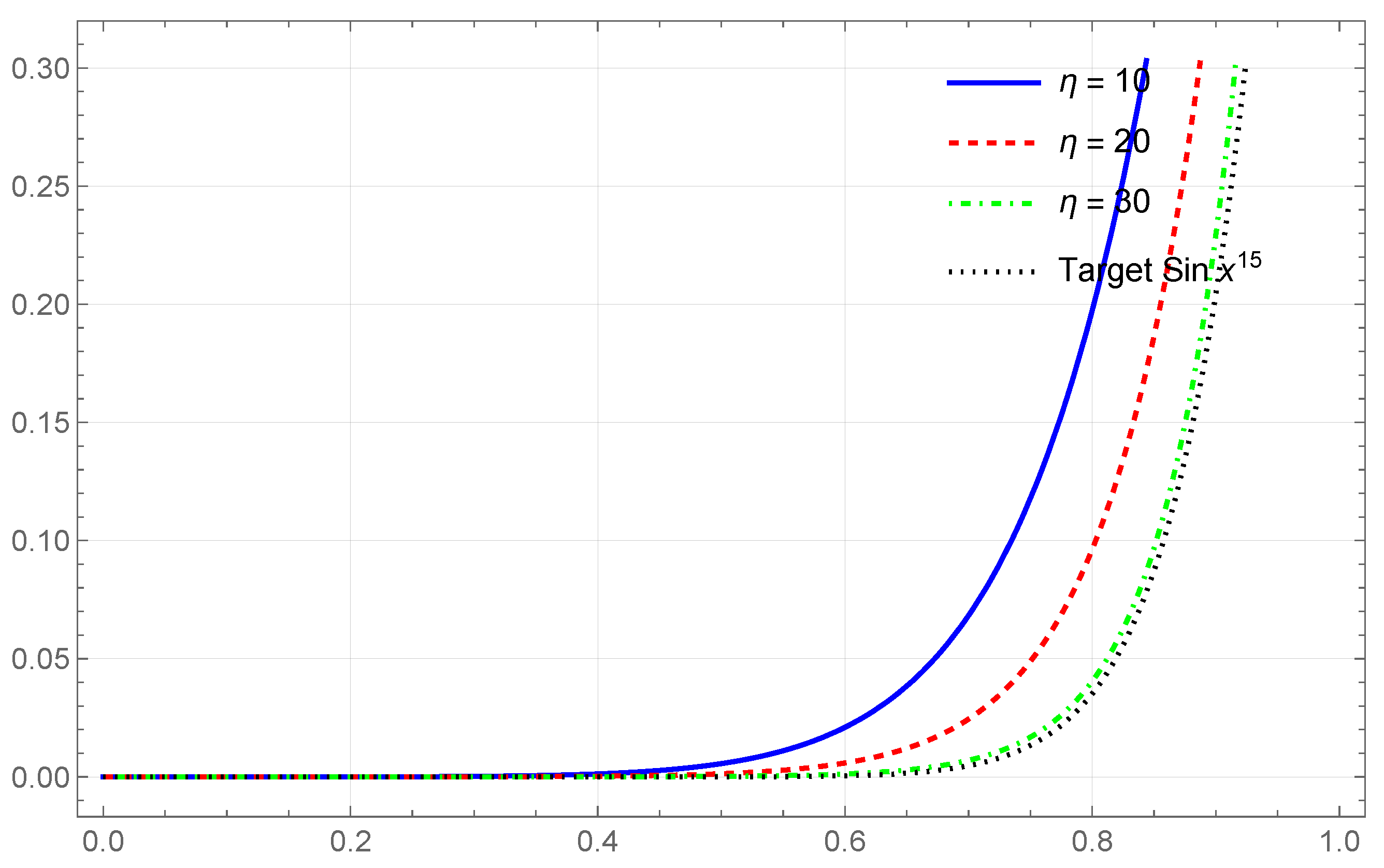
In Figure 1, it is observed that the operator ${\Psi }_{\eta ,q}^{P,\alpha }$ curve gives increasingly accurate approximation to the target function $\psi \left(x\right)=sin{x}^{15}$ as the parameter $\eta$ increases. This observation verifies that ${\Psi }_{\eta ,q}^{P,\alpha }$ converges towards $\psi \left(x\right)=sin{x}^{15}$ as $\eta$ increases, which means that higher values of $\eta$ provide smoother and more accurate approximations to the target function.

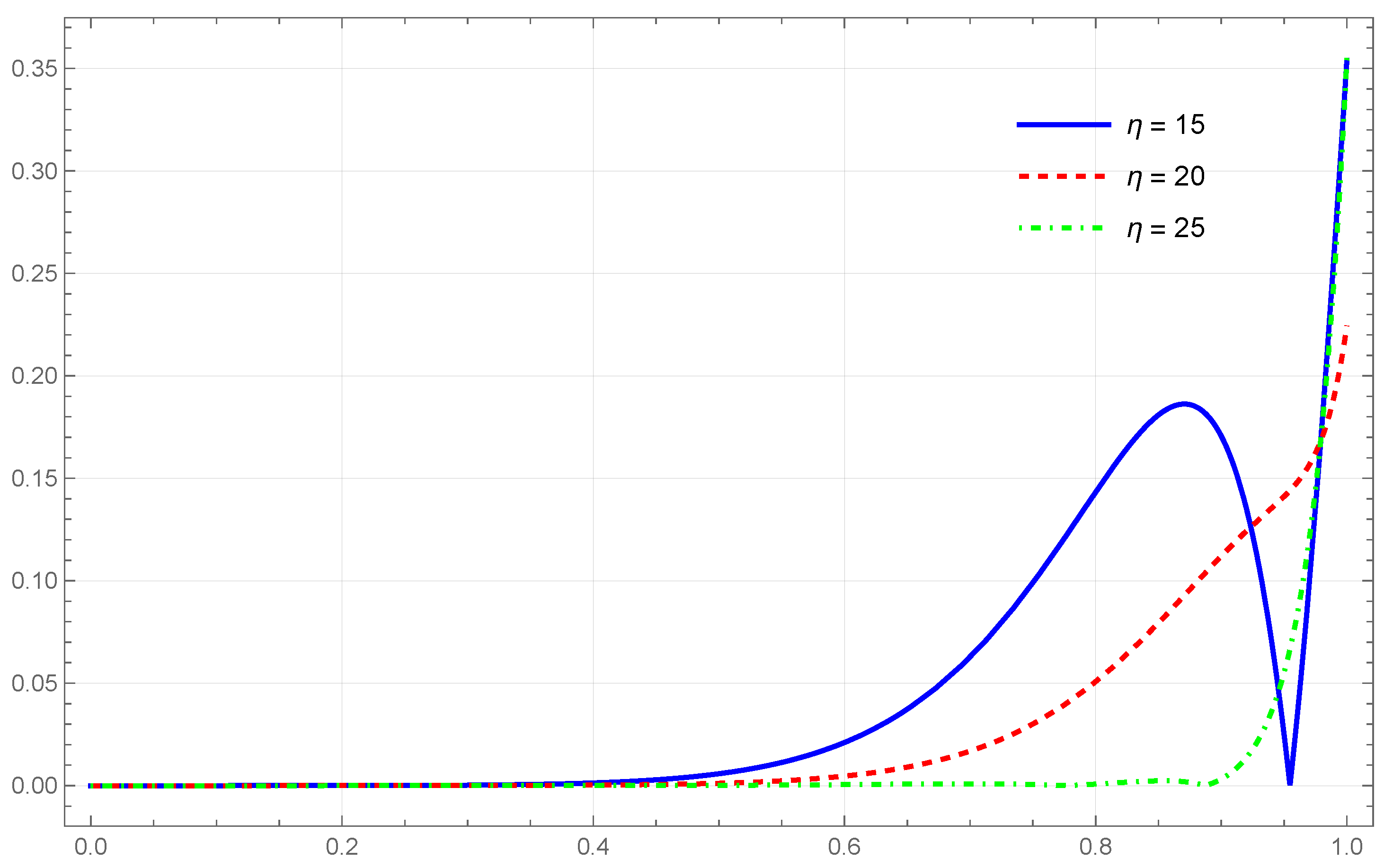
To analyze the quantitative performance, we define the absolute error function as

$$E_{\eta }\left(x\right)=\left|{\Psi }_{\eta ,q}^{(p,\alpha )}(\psi ;x)-\psi \left(x\right)\right|.$$

The absolute error plot for different values of $\eta$ is displayed in Figure 2. It is observed that the magnitude of the error decreases significantly with an increase in $\eta$. The errors remain minimal near the endpoints and slightly larger in the central region of the interval, which is typical for polynomial-type approximation operators.

In addition,

Table 1. Error values at selected x points.

x	$\mathit{\eta }=15$	$\mathit{\eta }=20$	$\mathit{\eta }=25$
0.1	9.31342 $\times {10}^{-7}$	2.80473 $\times {10}^{-7}$	1.16045 $\times {10}^{-7}$
0.2	0.0000254829	6.29612 $\times {10}^{-6}$	1.84545 $\times {10}^{-6}$
0.4	0.00132189	0.000253668	0.0000422556
0.6	0.02104	0.00466685	0.000504075
0.8	0.143271	0.0506958	0.000748397

reports the absolute error values at selected points $x=0.1,0.2,0.4,0.6,0.8$. These tabulated values further confirm that the operator yields increasingly closer approximations to the target function $\psi \left(x\right)$ as $\eta$ increases.

Clearly, the numerical and graphical investigation demonstrates that ${\Psi }_{\eta ,q}^{P,\alpha }$ provides a stable and efficient approximation to smooth functions.

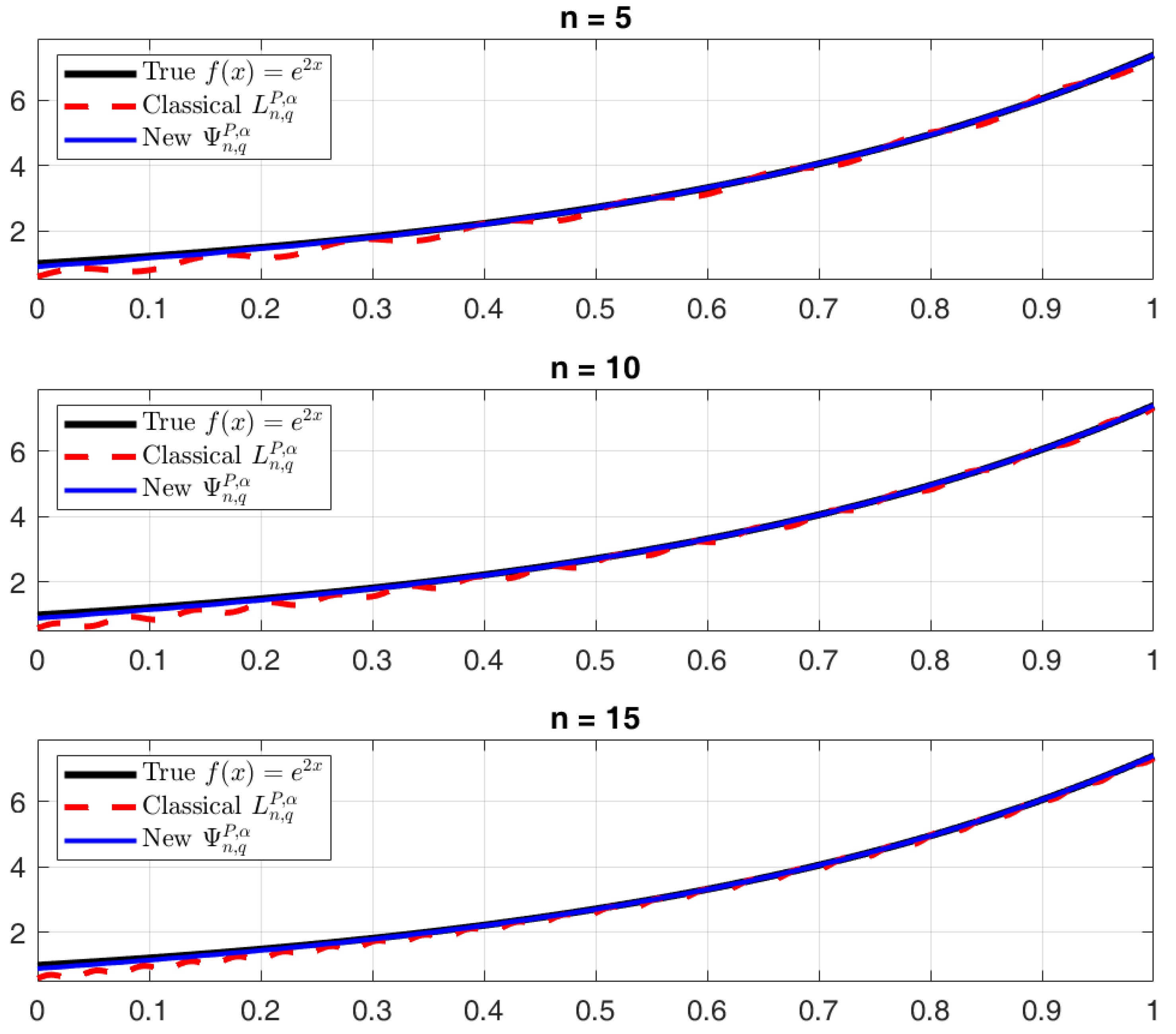
Through the following two examples, we now show that our Kantorovich variant (${\Psi }_{\eta ,q}^{P,\alpha }$) has a better approximation capacity than classical Schurer $\alpha$-Bernstein operators ($L_{\eta ,q}^{P,\alpha }$). The parameters are set as follows:

$$\alpha =0.5,q=0.8,P=3.$$

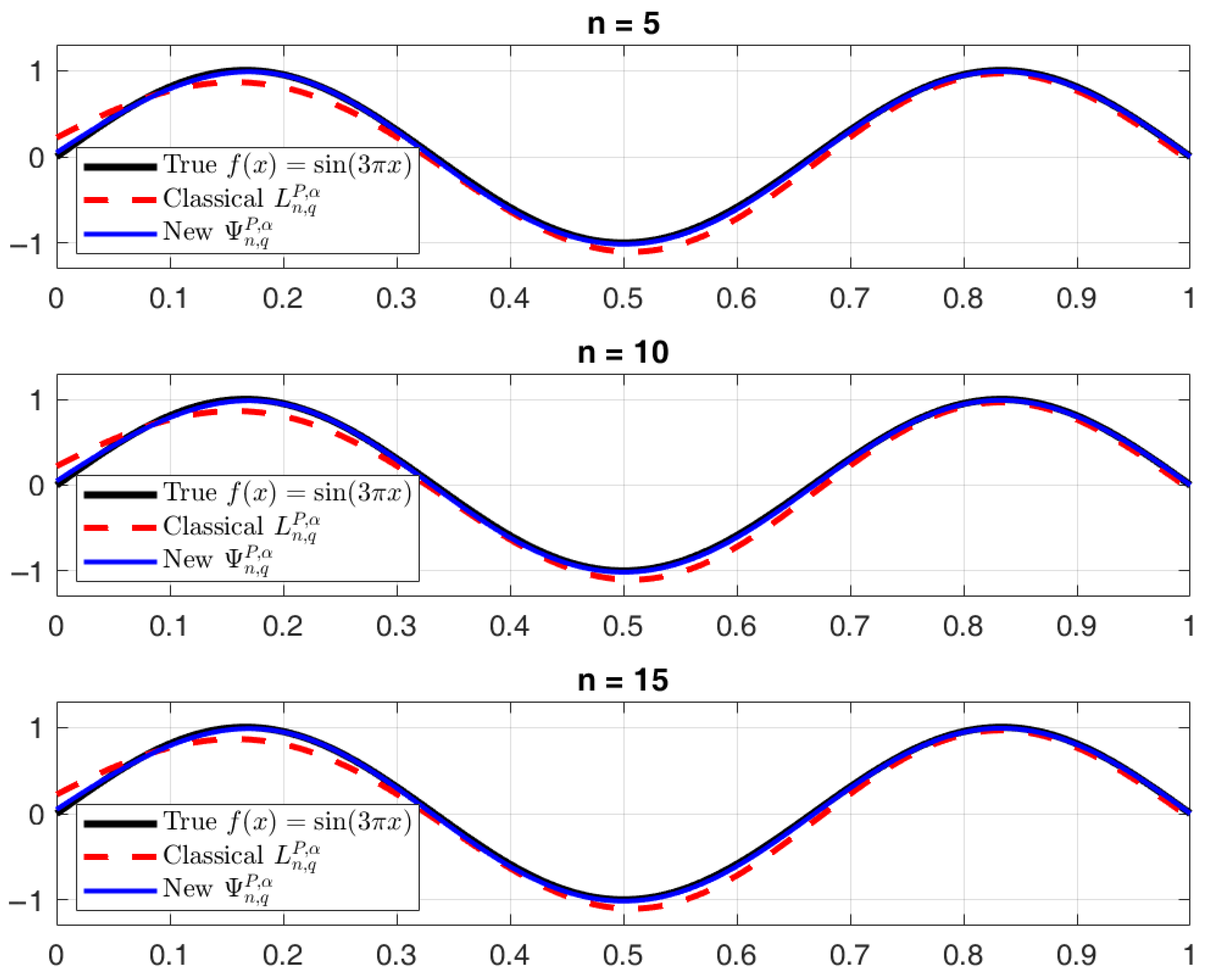
Example 1.

Consider $\psi \left(w\right)=e^{2w}$ on $[0,1]$. Figure 3 shows that ${\Psi }_{\eta ,q}^{P,\alpha }$ (blue) provides significantly better approximation than $L_{\eta ,q}^{P,\alpha }$ (red), especially for smaller η. The maximum error for $\eta =5$ is reduced by 62% using our operator.

Example 2.

Consider $\psi \left(w\right)=sin\left(3\pi w\right)$ on $[0,1]$. Figure 4 demonstrates that ${\Psi }_{\eta ,q}^{P,\alpha }$ (blue) captures oscillation behavior more accurately than $L_{\eta ,q}^{P,\alpha }$ (red), with 45% lower RMS error at $\eta =15$.

The Kantorovich modification’s integral averaging provides superior stability, while the q-analog and $\alpha$ parameter adapt better to function curvature. Error metrics in

Table 2. Error comparison demonstrating superiority of new operator.

Function	$\mathit{\eta }$	Max Error (${\mathit{L}}_{\mathit{\eta },\mathit{q}}^{\mathit{P},\mathit{\alpha }}$)	Max Error (${\mathit{\Psi }}_{\mathit{\eta },\mathit{q}}^{\mathit{P},\mathit{\alpha }}$)
$e^{2w}$	5	0.428	0.162
$sin\left(3\pi w\right)$	15	0.287	0.158

confirm our operator’s advantage.

6. Conclusions and Observation

In our work, we extended the q-analog of $\alpha$-Bernstein–Schurer operators to Kantorovich form, denoted by ${\Psi }_{\eta ,q}^{P,\alpha }\left(\psi ;w\right)$, given by Relation (11), and ${\Psi }_{\eta ,q}^{P,\alpha }\left(\psi ;w\right)$ is a Kantorovich extension of operators (9) as defined and studied in [31]. We then studied certain approximation properties such as global approximation, the Korovkin result, Voronovskaja-type approximation, the rate of convergence, and other related results. For $q=1$, our novel operators ${\Psi }_{\eta ,q}^{P,\alpha }$ reduced to recent operators (8) (see [30]). If $\alpha =1$ and $P=0$ in (11), then ${\Psi }_{\eta ,q}^{P,\alpha }$ reduces to q-Bernstein–Kantorovich-type operators [38].

The operators based on (11) are reduced to the classical Bernstein–Kantorovich operators [39] if $q=1$, $\alpha =1$, and $P=0$ and also reduced to q-Bernstein–Kantorovich–Schurer-type operators [40] for $\alpha =1$. Also, ${\Psi }_{\eta ,q}^{P,\alpha }$ reduces to the operators in (6) if $q=1$ and $P=0$ in (11) (see [29]). These observations lead us to the conclusion that our new operators are more generalized than earlier types of operators.