Let’s Make a Deal: Sleeping Beauty and Monty Hall Are the Same “Paradox”

Abstract

The Monty Hall problem and the Sleeping Beauty paradox are two of the best-known problems in probability theory and information theory. The essence of both is asking what credence a player should give to one of two options, when the options presented have been informed by a decision made by another intelligent agent, based on information unavailable to the player. The solution to the Monty Hall problem is largely well established, but there is no such consensus for Sleeping Beauty. While most commenters advocate for the so-called thirder solution, there remains a robust defence of the dissenting halfer viewpoint. Here, we demonstrate that these two famous problems can be simulated from the same simple experiment and thus are, in fact, entirely equivalent. As such, we also advocate for the thirder solution to Sleeping Beauty, in line with the equivalent result for Monty Hall. Despite this defence of the thirder position, we argue that many of the published statements made in favour of this conclusion are either misleading or incorrect, owing to ambiguous notation regarding frames of reference and knowledge. Similar issues have led to flawed attempts at resolving other paradoxes, including the Two Envelope paradox and the Absent-Minded Driver paradox.

1. Introduction

In probability theory and information theory, few problems are as famous and widely known outside of academic circles as the Monty Hall Problem [1]. Nowadays, its solution is largely uncontroversial. The roots of the question are in the gameshow Let’s Make a Deal and named after the show’s host, Monty Hall. In the mathematical literature, the problem dates to a letter published in the American Statistician by Steve Selvin [2]. In essence, the problem is described below.

A gameshow host has three doors and places a sportscar behind one of these and a goat behind each of the other two. The host continues to remember which door the car is behind. A contestant (with no information about the prizes’ locations) selects a door but does not open it. The host then opens one of the two doors not selected by the contestant, chosen such that one of the goats is revealed. The contestant is then offered the opportunity to open the door initially selected or to switch to the one remaining unopened door and claim the prize behind whichever door is finally selected. Assuming the contestant would prefer to win the sportscar than a goat, what should the contestant do?

The solution to this problem is accepted to be that the contestant should switch at the second stage. A number of arguments have been advanced to explain this conclusion but the simplest is perhaps that switching is the correct choice if the contestant’s initial choice was a door with a goat (2 in 3 chance) and sticking with the original choice is correct only if the initial choice was the sportscar (1 in 3 chance). This is equivalent to the statement that, after the host has opened one door, the contestant should have only 1/3 credence that the initially selected door contains the sportscar. This result is consistent with what is seen through repeated simulations and backed up by the Weak Law of Large Numbers [3].

An equally well-known, but far more controversial problem in the field, is the Sleeping Beauty paradox [4,5,6]. In this problem, a fair coin is flipped on Sunday and Sleeping Beauty is put to sleep. She knows that if the coin lands Heads, she will be awakened once, on Monday only. If the coin lands Tails, she will be awakened twice, once on Monday and once on Tuesday. Additionally, she knows that after each awakening, she will have her memory of this awakening wiped, so she will have no information as to whether any awakening is her first or her second time. Upon each awakening, she will be asked “What is your credence that the coin landed Heads?”, before being put back to sleep.

Solutions to this problem tend to fall into one of two main categories. The so-called halfer position [7,8,9] maintains that she obtains no new information each time she is awakened (since she knows she will be awakened), so her credence should not shift from that which she had on Sunday before the process began. As the coin is fair, her credence that the coin landed Heads was and should remain 1/2.

The other common answer is the thirder position. This argument is supported by the Weak Law of Large Numbers, essentially that if the experiment were repeated indefinitely, then on 1/3 of the occasions Sleeping Beauty was awakened, the coin would have landed Heads since Heads results in just one awakening and Tails results in two [10,11]. This places her rational credence that the coin landed Heads as 1/3.

2. Materials and Methods

2.1. Monty Hall Simulation

Here, I will argue that these two problems are, in fact, entirely equivalent. To do so, let us first consider an alternative equivalent description of the Monty Hall problem. A fair six-sided die will be rolled. Depending on the outcome of this roll, the three prizes will be assembled as described in

Table 1. The six possible orderings of prizes, allocated by the outcome of a single roll of a fair six-sided die.

	1 on Die	2 on Die	3 on Die	4 on Die	5 On Die	6 On Die
Door A	Sportscar	Sportscar	Monday Goat	Tuesday Goat	Monday Goat	Tuesday Goat
Door B	Monday Goat	Tuesday Goat	Sportscar	Sportscar	Tuesday Goat	Monday Goat
Door C	Tuesday Goat	Monday Goat	Tuesday Goat	Monday Goat	Sportscar	Sportscar

, where the two goats are now called Monday Goat and Tuesday Goat.

If the contestant initially selects a door with a goat behind it, then the host must open the one remaining door with a goat. If the contestant selects a door with the sportscar, then the host opens the door revealing Monday Goat. This is equivalent to the classic Monty Hall formulation, but with the host making the decision in advance as to which door will be opened in the event of having two goats to select from. It is assumed that the contestant cannot distinguish Monday Goat from Tuesday Goat, but the host can.

Before selecting a door, the contestant is asked “What is your credence that the die roll showed an even number?” and “What is your credence that the die roll showed an odd number?”. The unconditional answer to both questions should be 1/2, since by the problem definition, the six-sided die is fair. The contestant then selects a door, and the host opens a different door and asks either the contestant’s credence about the die roll showing an odd number or showing an even number, depending on the initial choice.

For example, if the contestant selects Door A and Door B is then opened, this eliminates any possibility of the die roll showing 3 or 4 (since the contestant can now see a goat and not the sportscar) and also eliminates the possibility of the die showing a 2 (since, if the contestant’s initial choice had been the sportscar, then Monday Goat would have been revealed, not Tuesday Goat). The second question would therefore be “What is your credence that the die roll showed an even number?”. For the same reason, if the contestant selects Door A and Door C is then opened, then the possibilities of the die showing 1, 5 or 6 would be eliminated, hence the question would be “What is your credence that the die roll showed an odd number?”. In all cases, the answer to this second question should be 1/3.

In this case, even though the initial questions (“What is your credence that the die roll showed an even number?” and “What is your credence that the die roll showed an odd number?”) should both have the answer 1/2, the imposition of the game’s rules and hence the contestant’s frame of reference introduces a latent factor associated with the question “What is your credence that your initial door choice concealed the sportscar?”. The solution to this is 1/3. Crucially, however, when the second question about the die’s result is asked, the contestant’s credence should be dependent upon the credence given to the “What is your credence that your initial door choice concealed the sportscar?” question. If the contestant has selected the sportscar, then the answer to the die roll question is 0. If the contestant has not selected the sportscar, the answer to the die roll question is 1/2. The contestant, however, has no way of knowing which of these realities the game is in. With 1/3 credence of being in the 0 credence reality (i.e., having selected the sportscar) and 2/3 credence of being in the 1/2 credence reality (i.e., not having selected the sportscar), the contestant’s overall credence is therefore (1/3)(0) + (2/3)(1/2) = 1/3. This is the widely accepted solution.

2.2. Sleeping Beauty Simulation

Returning now to the Sleeping Beauty paradox, this can similarly be framed in terms of the die roll. Specifically, there are three days immediately after the experiment begins:

• Sunday. She knows she will not be awoken again, analogous to knowing the sportscar will not be revealed by the host;
• Monday. She has 50% credence both of the die landing on an odd number and of the die landing on an even number if it is Monday (although she cannot ever be sure that it is Monday);
• Tuesday. She has 0% credence in the statement implied by the second question (although, again, she cannot ever be sure that it is Tuesday).

Consider now the Monty Hall problem, with the word “Sunday” written on the sportscar and the word “Monday” written on one goat and “Tuesday” written on the other such that these words are all unseen by the contestant. The allocation of these can again be set with a single roll of a fair six-side die, as illustrated in

Table 2. The six possible orderings of the three words corresponding to days of the week, allocated by the outcome of a single roll of a fair six-sided die.

	1 on Die	2 on Die	3 On Die	4 On Die	5 on Die	6 on Die
Door A	Sunday	Sunday	Monday	Tuesday	Monday	Tuesday
Door B	Monday	Tuesday	Sunday	Sunday	Tuesday	Monday
Door C	Tuesday	Monday	Tuesday	Monday	Sunday	Sunday

.

3. Results

As long as Sleeping Beauty is provided with the same information as a contestant on Monty Hall’s show, and someone (herself, or an outside agent, it does not matter) selects a door to trigger the reveal of a goat, the logic remains consistent. She knows that, unconditionally, her credence of the fair die showing an odd number is 1/2 and that her credence of an even number is 1/2. The critical point is, knowing the rules of this setup and the initially chosen door, her credence at the second stage should be either 0 or 1/2, with the latter twice as probable as the former. As with the Monty Hall contestant, Sleeping Beauty’s overall credence should then be (1/3)(0) + (2/3)(1/2) = 1/3.

Take the same scenario as illustrated above. When she awakes, she chooses Door A and is asked “What is your credence that the die roll showed an even number?”. According to the rules of the game, Door B is then opened, revealing a goat. She, crucially, does not know which goat this is. If she knew she was looking at Tuesday Goat, then her credence of the die roll showing an even number would be 0, since she would know it landed showing 5. If she knew she was looking at Monday Goat, then her credence of an odd number would be 1/2 since either a 1 or a 6 on the die roll would be equally probable. Congruent with the previous simulation, she has no way to distinguish between the two goats, so she is left to conclude that she is in one of three equally probable scenarios, that the die landed 1, landed 5 or landed 6. This leads her to have credence 1/3 that the die landed on an odd number.

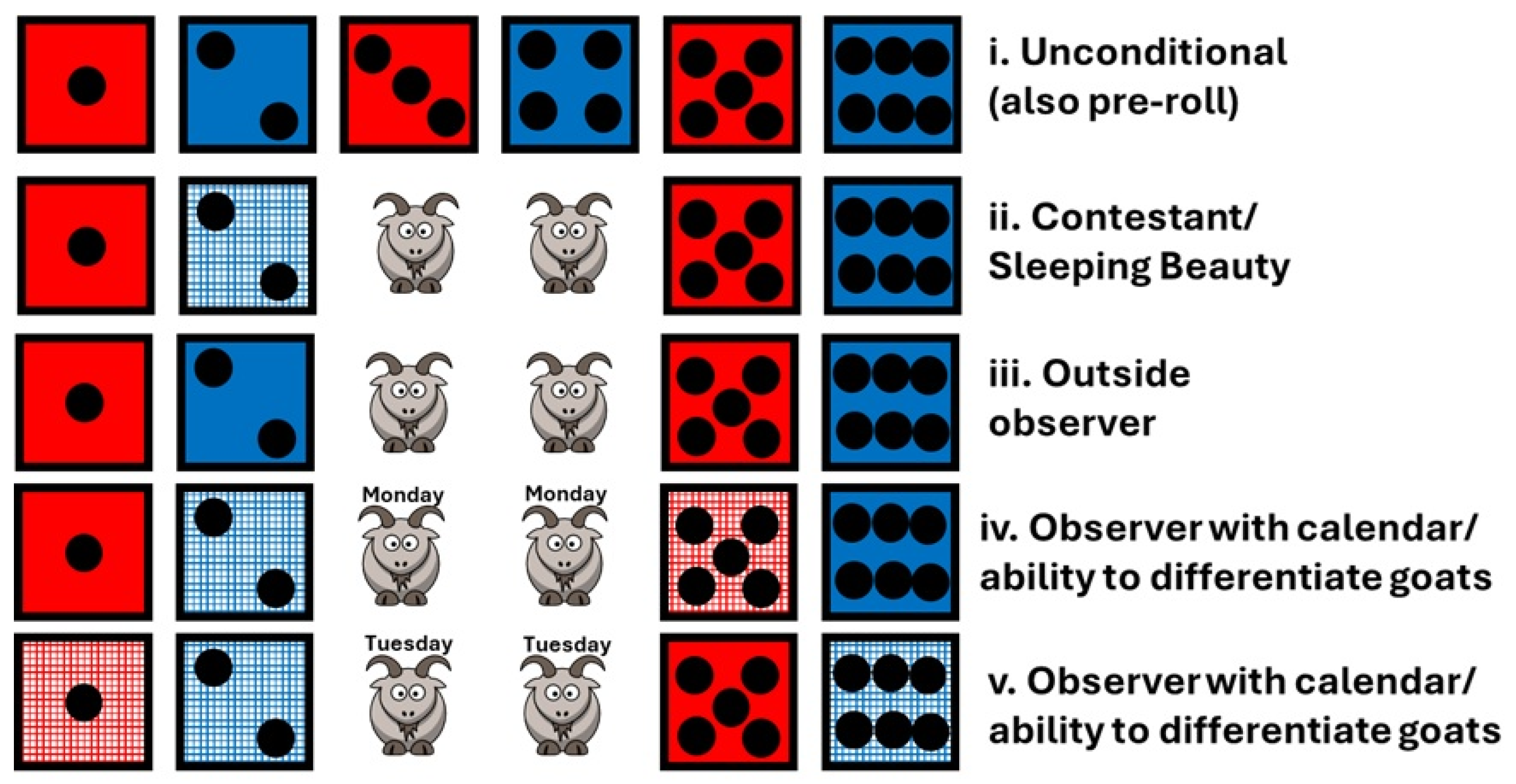
Figure 1 illustrates this equivalence. The roll of a fair six-sided die, then the unconditional credence given of an even number should be, by definition, 1/2, since 2, 4 and 6 are three of the six equally probable outcomes. This corresponds to sample space (i). below. Below this is the reference of either Monty Hall’s contestant or Sleeping Beauty (ii). With knowledge only of the game’s rules and which option was originally selected, the die result of a 2 is also eliminated as a possibility. With 1, 5 and 6 as the equally probable options remaining, the credence given to the die having landed on an even number is therefore 1/3. Also illustrated are the sample spaces by an observer who either does not know the rules of the game or does not know the initial choice (iii). This observer would simply eliminate 3 and 4 as options and hence conclude that the die was equally likely to have shown an odd or an even number. The last two scenarios (iv and v) are the ones which arise from ambiguous conditional probability/credence not applicable to either problem. They suppose that an observer or player could, in fact, condition on either the day of the week on which goat was revealed. In these scenarios, credence associated with the die showing an even number is either 1/2 (if Monday or Monday Goat is known) or 0 (if Tuesday or Tuesday Goat is known.).

In both problems, there is a latent factor which cannot be known by the contestant. For Monty Hall, if the contestant could know that the initial selection was correct, then it would be certain that the revealed goat would be Monday Goat and hence that the resulting credence for the question should be 0. If the contestant could know that the initial selection was incorrect, then it would be equally probable whether the goat was Monday Goat or Tuesday Goat and hence equally probable that the die result was odd or even.

4. Discussion

Given that the same underlying experiment can be used to simulate both famous problems, why is there consensus for Monty Hall but not Sleeping Beauty? The most prominent reason is perhaps that, even amongst proponents of the thirder position, many ambiguous or even misleading statements have been made. The published literature includes many arguments [11] which rest on Sleeping Beauty making assessments of her belief regarding statements such as P(Heads|Monday). This, however, is not information which she ever has or to which she could even assign belief. She can never know it is Monday without being awake and it is illogical to suppose that she should marginalise out knowledge of her wakefulness while assuming or knowing it is Monday. In fact, despite staunchly advocating for the thirder position, we argue that the correct credence for P(Heads|Monday) is 1/2. This, however, is irrelevant to Sleeping Beauty, as this is not the same as P(Heads|Awake) and she should certainly not have credence that P(Monday|Awake) = 1 since she knows that she may be awoken on either Monday or Tuesday. A similar distinction has previously been drawn by Joseph Halpern [12] differentiating between the event “it is Monday” and “Sleeping Beauty is awake and perceives it to be Monday”. The former event could be held by anyone, with or without knowledge of this game and its rules, whereas the latter could not.

This is not simply inexactness in notation, but rather a problem which leads to misinterpretation of the initial problem. An example of this is the modification of the original problem whereby the coin is not flipped until Monday night. This argument (correctly) states that when awoken on Monday, Sleeping Beauty’s credence that the coin landed (or, more precisely, will land) Heads should obviously be 1/2 [8]. In this sense, we are advocating for the so-called double halfer position that P(Heads) = P(Heads|Monday) = 1/2. This, however, is the correct answer to a completely different problem. In the original problem, there is no possibility of her ever knowing that it is Monday, only that she is awake. Correctly applied, the conditional event Heads|Monday describes the belief of someone who has no knowledge of Sleeping Beauty’s status (awake or asleep) and only has knowledge (or belief) that today is Monday. Given that a fair coin flip’s outcome is independent of the day of the week, this credence should be 1/2. Statements regarding what Sleeping Beauty should believe have to consider her frame of reference, i.e., that she is awake.

Extending the Logical Framework

To extend the analogy with the Monty Hall problem, there is a difference between the belief which someone who observes only that one door has been opened compared with the contestant, who knows which door was initially chosen and how the rules of the game have been applied. The non-contestant observer would see a door open and hence know that two of the six die outcomes had been eliminated. The contestant would know, with knowledge of which door had been initially chosen, that three of the die roll outcomes had been eliminated.

This attempt to evaluate self-locating probabilities (e.g., conditioning on Sleeping Beauty knowing the day of the week or on Monty Hall’s contestant knowing if the initial selection is the sportscar) has plagued numerous attempts to resolve similar problems. Probably the most notable of these is the Two Envelope paradox [13] whereby a contestant selects one of two envelopes, where is it known that one envelope contains twice as much money as the other. Upon opening the chosen envelope, the contestant can see how much money is in the selected envelope and then switch to the other envelope or keep the initial amount. Say, for example, that the contestant’s chosen envelope contains $20. The contestant then argues that it is equally probable that the other envelope contains $10 or $40 and so the expected value of the other envelope must be $25. In reality, of course, the value in the first envelope provides no information as to whether it is the larger or smaller value. If the values before observation are, say, X and 2X, the flawed argument above effectively assumes that X is known to be $20 and that the other envelope is an unknown 1/2X or 2X and compares these two statements. Similarly, the Absent-Minded paradox [14] cannot be resolved by conditioning on which junction the driver is at, when all that driver can ever know is that he/she is at a junction and not which junction that is.

One possible criticism of the proposed equivalence is that time is explicitly present in the original formulation (i.e., Tuesday unambiguously follows Monday) and that in the duration of the problem, Sleeping Beauty will be questioned on her credence either twice or three times. These features are not present in the proposed die-based formulation. This, however, does not invalidate the equivalence since Sleeping Beauty has no conception of time or the ordering of awakenings in any case. Just as Rachel Briggs, William Talbot [15] and others have argued [16], attempts to apply general concepts in a memory-loss scenario are often problematic.

5. Conclusions

There have been attempts to reconcile the thirder and halfer positions, often suggesting that the original problem formulation is ambiguous, as is the case with similarly famous problems such as the Boy or Girl paradox [17] whereby the mechanism by which the information “at least one son” is obtained is unclear. No such ambiguity inherently exists for the Sleeping Beauty problem. The statements of when and under which conditions she is awoken are clear and unambiguous. Confusion, however, does arise when conditional notation becomes poorly defined and attempts are made to condition on information which is never in the original problem, such as knowledge of the day of the week without knowledge of her waking status. While the double halfer argument is correct for an outside observer, it is not a frame of reference which Sleeping Beauty herself could ever hold, thus it is not the solution to the original problem.

The work here is, in essence, a discussion paper presenting a simple experiment which can simulate both the Monty Hall problem and the Sleeping Beauty paradox. As such, we argue that this demonstrates that these should not be regarded as two different problems, rather two different wordings of the same problem. In doing so, we advocate for the established thirder position in the Monty Hall problem as the unambiguous solution for Monty Hall as well.