Application of Markov Models to Cost-Effectiveness Analysis in the Selection of Patients for Liver Transplantation
Abstract
1. Introduction
2. Methodology
2.1. Clinical and Probabilistic Assumptions
- (i)
- Adult patients (≥18 years old);
- (ii)
- Patients with early to intermediate HCC;
- (iii)
- Patients without regional nodal or distant metastases;
- (iv)
- Patients without comorbidities that could affect quality of life or life expectancy;
- (v)
- Molecular analyses performed on explant specimens (diseased liver removed from transplanted patients) were equivalent to molecular analyses performed on a biopsy sample (pre-transplant);
- (vi)
- The probability of mortality for relapsed patients who received different treatments (such as resection, ablation, or systemic therapy) was equal to that of patients who only received systemic therapy;
- (vii)
- The probability of mortality for patients without recurrence was assumed to be equal to the all-cause mortality of HCC patients who underwent transplantation in the U.S. during 2017;
- (viii)
- The probability of transplant-related mortality was not applied to patients who relapsed within the first three months;
- (ix)
- Costs did not include all expenses related to hospital infrastructure, such as laboratories;
- (x)
- In any given month, the probability of a patient being in a specific health state depends solely on the patient’s health state in the preceding month (Markov property).
2.2. Health Economic Model: Markov Model
2.2.1. Formulation of the Markov Model
2.2.2. Costs and Health Economic Measures
- : Cost of the HP kit plus the labour required to perform it.
- : Cost of the ultrasound-guided liver biopsy.
- : Minimum cost needed before transplantation.
- : Cost related to liver transplant.
- : Costs of hospitalisation and nursing care immediately after the transplant.
- : Monthly cost of patient follow-up.
- : Monthly cost of systemic therapy.
- : Cost incurred by the hospital when a patient dies.
- : Cost of the first month related to extra post-operative care.
- : Costs of the second and third months related to extra post-operative care.
- : Monthly QALY in the first three months post-transplant.
- : Monthly QALY of a cancer-free patient after transplantation.
- : Monthly QALY for a patient experiencing recurrence after transplantation.
- : represents the monthly discount rate for QALYs (annual rate of 3%).
- -
- , : total months of RFS for all patients who did not experience recurrence, within and outside criterion c, respectively;
- -
- , : total months of RFS for all patients who experienced recurrence, within and outside criterion c, respectively;
- -
- , : total months lost due to recurrence, for all patients who experienced recurrence, within and outside criterion c, respectively.
- -
- : Estimated recurrence-free survival at time t, i.e., , where T is a randomvariable that describes the time until recurrence;
- -
- : Number of observed recurrences at ;
- -
- : Number of patients at risk just before .
2.3. Parameters of the Markov Model
- Post-transplant mortality [28]: Derived from a study that specifically analysed HCC patients who underwent liver transplantation, ensuring clinical comparability.
- Mortality unrelated to recurrence [39]: Obtained from an annual nationwide U.S. registry reporting outcomes of liver transplant recipients, ensuring representativeness for post-transplant survival.
- Mortality following recurrence [40,41]: This parameter was among the most challenging to estimate due to the heterogeneity of treatment and the limited sample sizes reported across available studies. Two studies were selected—one conducted in Latin America and another in the U.S.—that provided survival curves for patients with recurrent HCC treated with any available therapy. These studies were considered appropriate because they included sufficiently medium sample sizes and represented populations with a high incidence of HCC and predominantly Caucasian or Hispanic, supporting partial comparability with the U.S. context, particularly for the Latin American study [40].
2.4. Description of the Deterministic Sensitivity Analysis
3. Results
3.1. Characterisation of the Cohort
3.2. Base-Case Scenario
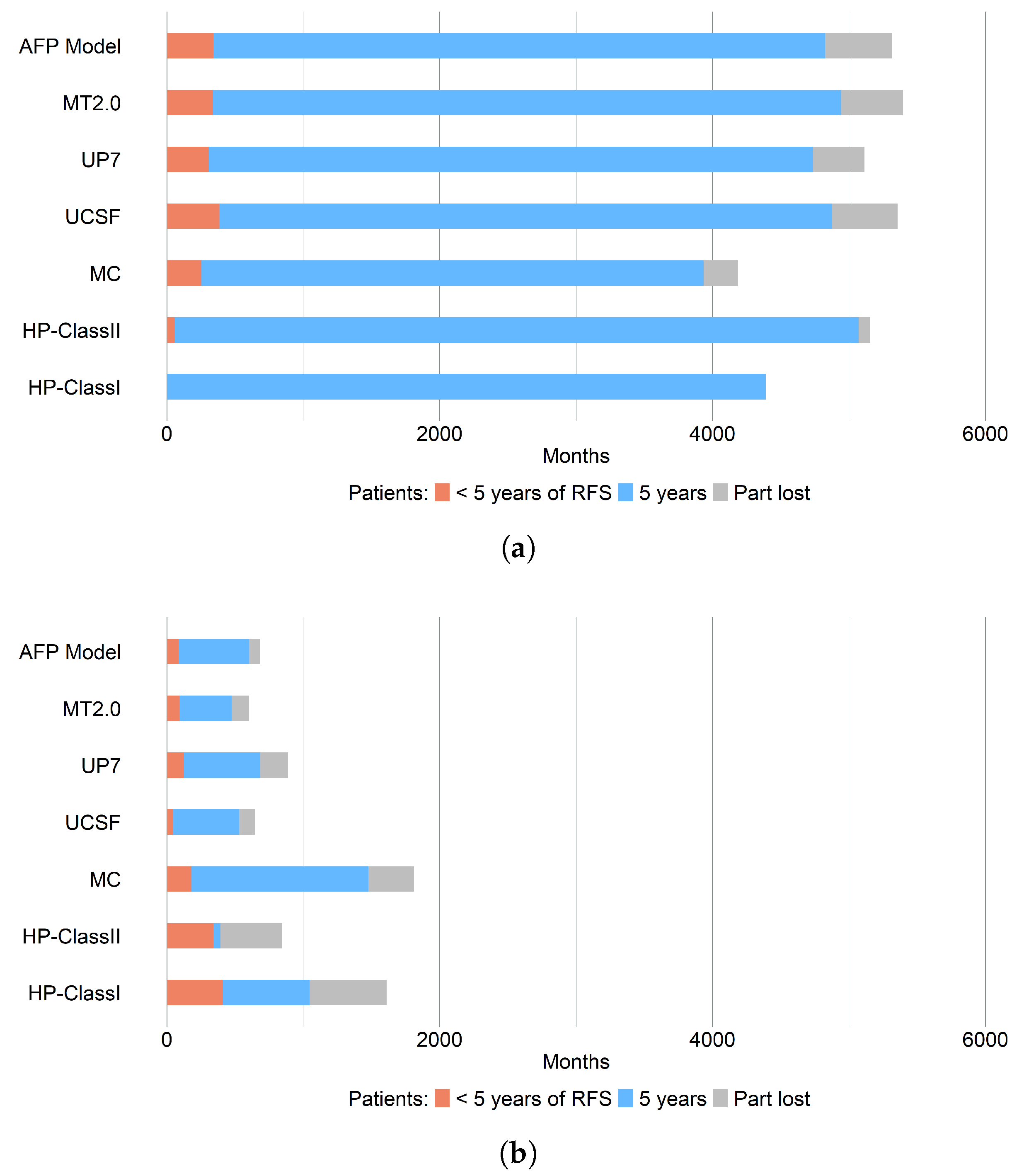
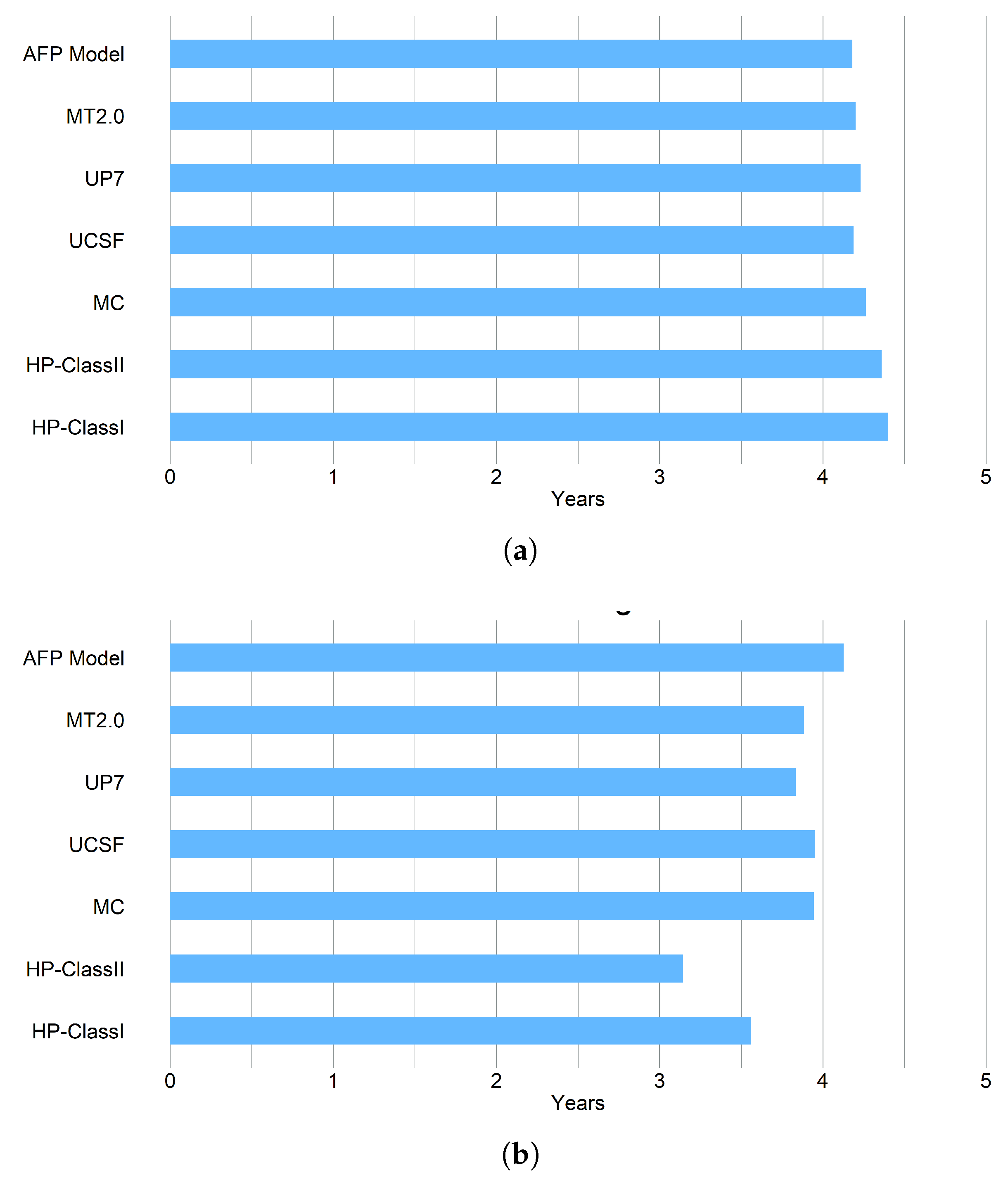
3.2.1. Recurrence-Free Survival, RFS
3.2.2. Life Years Gained, LYG
3.2.3. QALYs
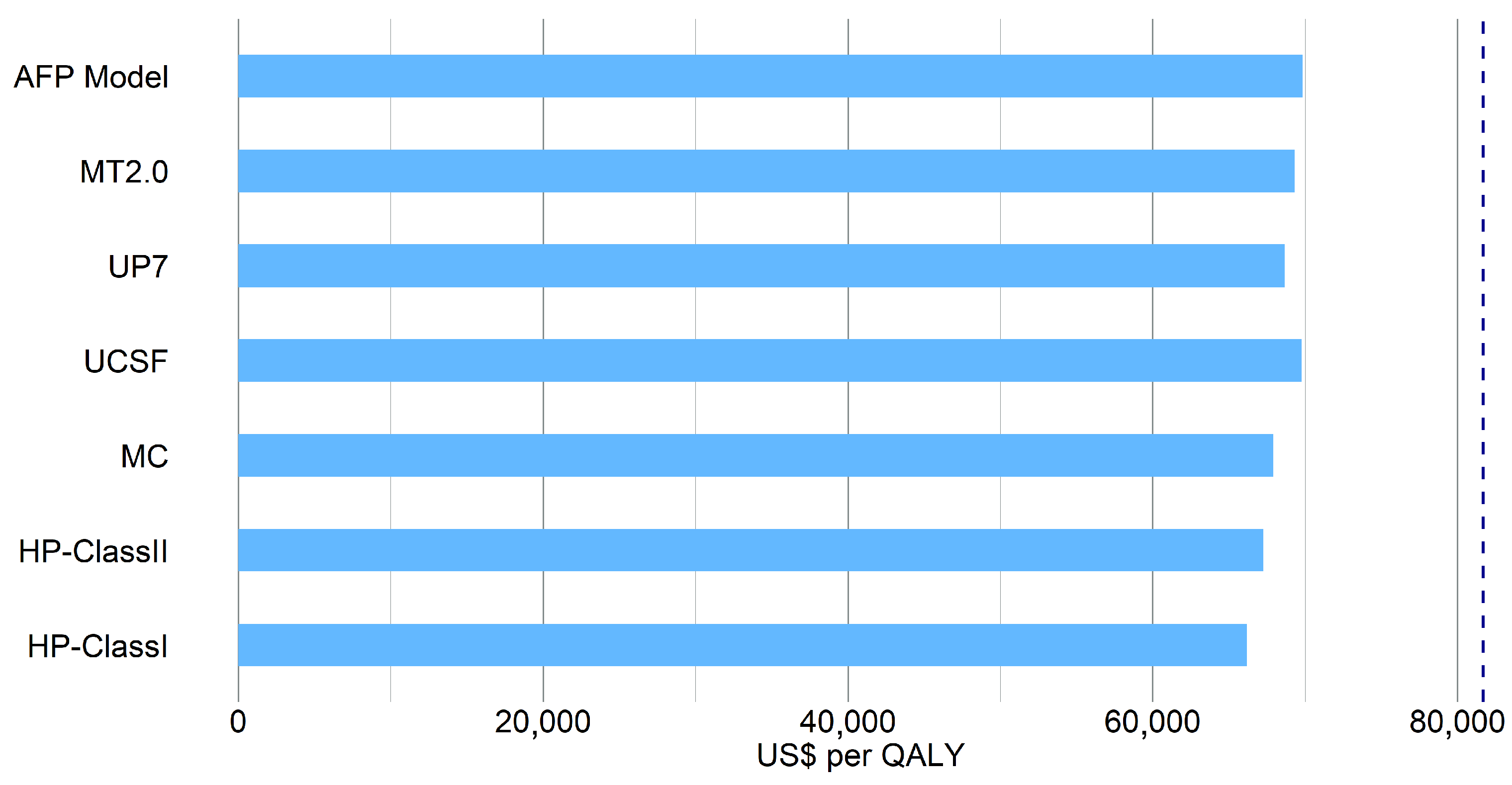
3.2.4. Costs
3.2.5. Cost-Effectiveness Analysis
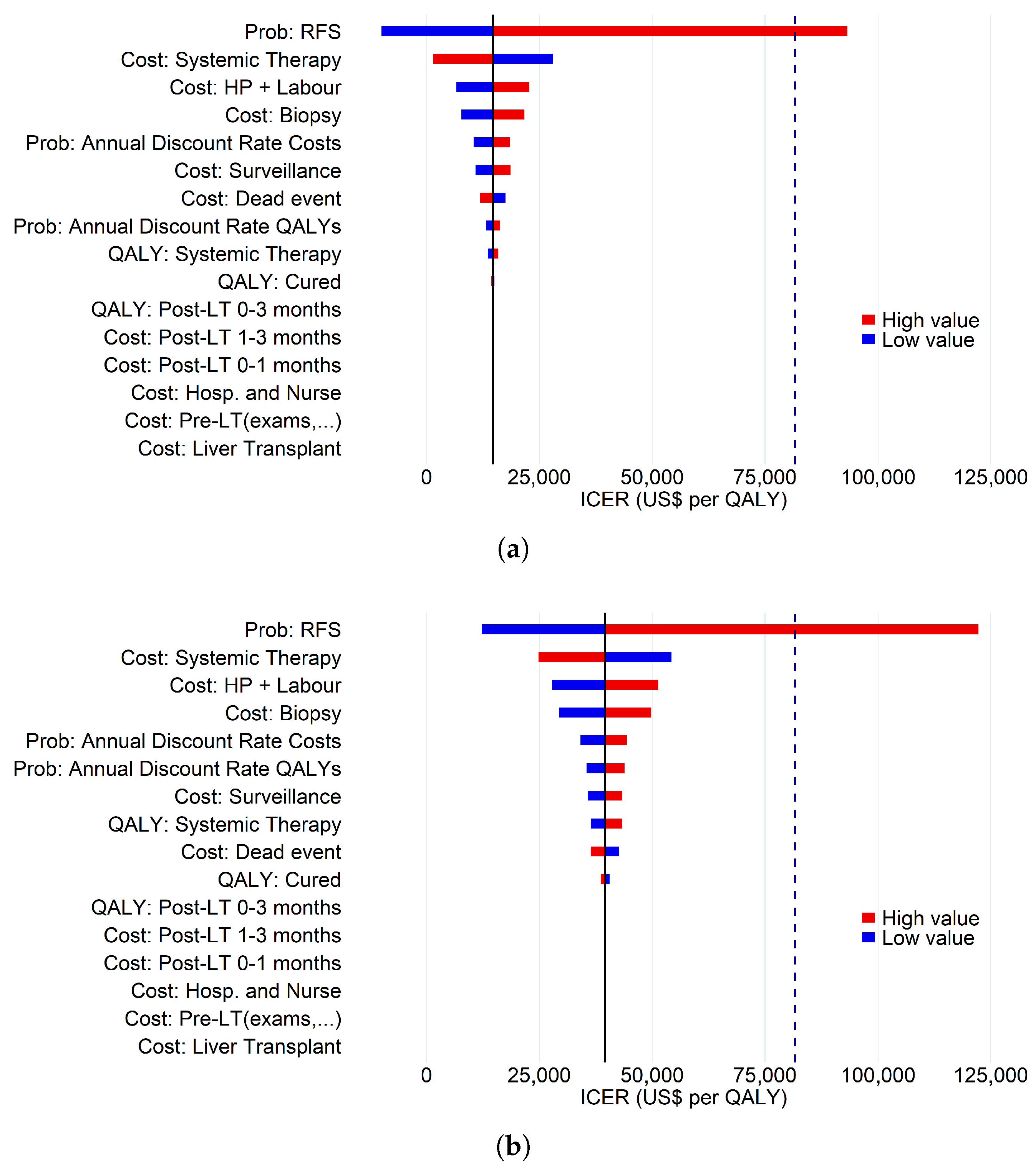
3.3. Deterministic Sensitivity Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ferlay, J.; Ervik, M.; Lam, F.; Laversanne, M.; Colombet, M.; Mery, L.; Piñeros, M.; Znaor, A.; Soerjomataram, I.; Bray, F. Global Cancer Observatory: Cancer Today (Version 1.1); International Agency for Research on Cancer: Lyon, France, 2024; Available online: https://gco.iarc.who.int/today (accessed on 15 June 2024).
- Rumgay, H.; Ferlay, J.; de Martel, C.; Georges, D.; Ibrahim, A.S.; Zheng, R.; Wei, W.; Lemmens, V.E.; Soerjomataram, I. Global, regional and national burden of primary liver cancer by subtype. Eur. J. Cancer 2022, 161, 108–118. [Google Scholar] [CrossRef]
- Galle, P.R.; Forner, A.; Llovet, J.M.; Mazzaferro, V.; Piscaglia, F.; Raoul, J.L.; Schirmacher, P.; Vilgrain, V. EASL clinical practice guidelines: Management of hepatocellular carcinoma. J. Hepatol. 2018, 69, 182–236. [Google Scholar] [CrossRef]
- Rich, N.E.; Yopp, A.C.; Singal, A.G.; Murphy, C.C. Hepatocellular carcinoma incidence is decreasing among younger adults in the United States. Clin. Gastroenterol. Hepatol. 2020, 18, 242–248. [Google Scholar] [CrossRef]
- Rich, N.E.; Hester, C.; Odewole, M.; Murphy, C.C.; Parikh, N.D.; Marrero, J.A.; Yopp, A.C.; Singal, A.G. Racial and ethnic differences in presentation and outcomes of hepatocellular carcinoma. Clin. Gastroenterol. Hepatol. 2019, 17, 551–559. [Google Scholar] [CrossRef]
- World Health Organization. International Agency for Research on Cancer Cancer Today; World Health Organization: Geneva, Switzerland, 2016. [Google Scholar]
- Tsilimigras, D.I.; Aziz, H.; Pawlik, T.M. Critical analysis of the updated Barcelona clinic liver cancer (BCLC) group guidelines. Ann. Surg. Oncol. 2022, 29, 7231–7234. [Google Scholar] [CrossRef]
- Aksoy, S.O.; Unek, T.; Sevinc, A.I.; Arslan, B.; Sirin, H.; Derici, Z.S.; Ellidokuz, H.; Sagol, O.; Agalar, C.; Astarcioglu, I. Comparison of resection and liver transplant in treatment of hepatocellular carcinoma. Exp. Clin. Transpl. 2020, 18, 712–718. [Google Scholar] [CrossRef]
- Golabi, P.; Fazel, S.; Otgonsuren, M.; Sayiner, M.; Locklear, C.T.; Younossi, Z.M. Mortality assessment of patients with hepatocellular carcinoma according to underlying disease and treatment modalities. Medicine 2017, 96, e5904. [Google Scholar] [CrossRef]
- Llovet, J.; Kelley, R.; Villanueva, A.; Singal, A.; Pikarsky, E.; Roayaie, S.; Lencioni, R.; Koike, K.; Zucman-Rossi, J.; Finn, R. Hepatocellular Carcinoma Nat Rev Dis Primers. 7: 6. Article10 2021, 1038, 1038. [Google Scholar]
- Line, P.D. Selection criteria in liver transplantation for hepatocellular carcinoma: An ongoing evolution. BJS Open 2022, 6, zrac024. [Google Scholar] [CrossRef]
- Pinto-Marques, H.; Cardoso, J.; Silva, S.; Neto, J.L.; Goncalves-Reis, M.; Proenca, D.; Mesquita, M.; Manso, A.; Carapeta, S.; Sobral, M.; et al. A gene expression signature to select hepatocellular carcinoma patients for liver transplantation. Ann. Surg. 2022, 276, 868–874. [Google Scholar] [CrossRef]
- Llovet, J.M.; Pena, C.E.; Lathia, C.D.; Shan, M.; Meinhardt, G.; Bruix, J. Plasma biomarkers as predictors of outcome in patients with advanced hepatocellular carcinoma. Clin. Cancer Res. 2012, 18, 2290–2300. [Google Scholar] [CrossRef]
- Duvoux, C.; Roudot-Thoraval, F.; Decaens, T.; Pessione, F.; Badran, H.; Piardi, T.; Francoz, C.; Compagnon, P.; Vanlemmens, C.; Dumortier, J.; et al. Liver transplantation for hepatocellular carcinoma: A model including α-fetoprotein improves the performance of Milan criteria. Gastroenterology 2012, 143, 986–994. [Google Scholar] [CrossRef]
- Mazzaferro, V.; Regalia, E.; Doci, R.; Andreola, S.; Pulvirenti, A.; Bozzetti, F.; Montalto, F.; Ammatuna, M.; Morabito, A.; Gennari, L. Liver transplantation for the treatment of small hepatocellular carcinomas in patients with cirrhosis. New Engl. J. Med. 1996, 334, 693–700. [Google Scholar] [CrossRef]
- Yao, F.Y.; Ferrell, L.; Bass, N.M.; Watson, J.J.; Bacchetti, P.; Venook, A.; Ascher, N.L.; Roberts, J.P. Liver transplantation for hepatocellular carcinoma: Expansion of the tumor size limits does not adversely impact survival. Hepatology 2001, 33, 1394–1403. [Google Scholar] [CrossRef]
- Mazzaferro, V.; Llovet, J.M.; Miceli, R.; Bhoori, S.; Schiavo, M.; Mariani, L.; Camerini, T.; Roayaie, S.; Schwartz, M.E.; Grazi, G.L.; et al. Predicting survival after liver transplantation in patients with hepatocellular carcinoma beyond the Milan criteria: A retrospective, exploratory analysis. Lancet Oncol. 2009, 10, 35–43. [Google Scholar] [CrossRef]
- Mazzaferro, V.; Sposito, C.; Zhou, J.; Pinna, A.D.; De Carlis, L.; Fan, J.; Cescon, M.; Di Sandro, S.; Yi-Feng, H.; Lauterio, A.; et al. Metroticket 2.0 model for analysis of competing risks of death after liver transplantation for hepatocellular carcinoma. Gastroenterology 2018, 154, 128–139. [Google Scholar] [CrossRef]
- Ophiomics—Precision Medicine. Available online: https://www.ophiomics.com/ (accessed on 12 April 2025).
- Barton, P.; Bryan, S.; Robinson, S. Modelling in the economic evaluation of health care: Selecting the appropriate approach. J. Health Serv. Res. Policy 2004, 9, 110–118. [Google Scholar] [CrossRef] [PubMed]
- Sánchez-Périz, I.; Barrachina-Martínez, I.; Díaz-Carnicero, J.; Climent, A.M.; Vivas-Consuelo, D. Cost-Effectiveness Mathematical Model to Evaluate the Impact of Improved Cardiac Ablation Strategies for Atrial Fibrillation Treatment. Mathematics 2023, 11, 915. [Google Scholar] [CrossRef]
- Henderson, R.H.; Sampson, C.; Pouwels, X.G.; Harvard, S.; Handels, R.; Feenstra, T.; Bhandari, R.; Sepassi, A.; Arnold, R. Mapping the Landscape of Open Source Health Economic Models: A Systematic Database Review and Analysis: An ISPOR Special Interest Group Report. Value Health 2025, 28, 813–820. [Google Scholar] [CrossRef]
- Ross, A.; Kim, J.; McKay, M.; Pappas, E.; Hardaker, N.; Whalan, M.; Peek, K. The economics of a national anterior cruciate ligament injury prevention program for amateur football players: A Markov model analysis. Med. J. Aust. 2024, 221, 149–155. [Google Scholar] [CrossRef]
- Wu, W.; Tang, F.; Wang, Y.; Yang, W.; Zhao, Z.; Gao, Y.; Dong, H. Cost-effectiveness analysis of combination therapies involving novel agents for first/second-relapse patients with multiple myeloma: A Markov model approach with calibration techniques. Health Econ. Rev. 2025, 15, 21. [Google Scholar] [CrossRef]
- Wen, C.; Wang, X.; Shu, J.; Ruan, Y.; Xie, J.; Cheng, X.; Qi, B.; En, H.; Qin, G.; Huang, L.; et al. Estimated cost-effectiveness of early screening strategies for newborn hearing impairment using a Markov model. Front. Public Health 2025, 13, 1498860. [Google Scholar] [CrossRef]
- Worthington, J.; He, E.; Caruana, M.; Wade, S.; de Graaff, B.; Nguyen, A.L.T.; George, J.; Canfell, K.; Feletto, E. A Health Economic Evaluation of Routine Hepatocellular Carcinoma Surveillance for People with Compensated Cirrhosis to Support Australian Clinical Guidelines. MDM Policy Pract. 2025, 10, 23814683251344962. [Google Scholar] [CrossRef]
- Younossi, Z.M.; Paik, J.M.; Henry, L.; Pollock, R.F.; Stepanova, M.; Nader, F. Economic evaluation of non-invasive test pathways for high-risk metabolic dysfunction-associated steatotic liver disease (MASLD) in the United Kingdom (UK). Ann. Hepatol. 2025, 30, 101789. [Google Scholar] [CrossRef]
- Patel, M.V.; Davies, H.; Williams, A.O.; Bromilow, T.; Baker, H.; Mealing, S.; Holmes, H.; Anderson, N.; Ahmed, O. Transarterial therapies in patients with hepatocellular carcinoma eligible for transarterial embolization: A US cost-effectiveness analysis. J. Med. Econ. 2023, 26, 1061–1071. [Google Scholar] [CrossRef]
- Wu, X.; Kwong, A.; Heller, M.; Lokken, R.P.; Fidelman, N.; Mehta, N. Cost-effectiveness analysis of interventional liver-directed therapies for downstaging of HCC before liver transplant. Liver Transplant. 2024, 30, 151–159. [Google Scholar] [CrossRef] [PubMed]
- Rognoni, C.; Ciani, O.; Sommariva, S.; Bargellini, I.; Bhoori, S.; Cioni, R.; Facciorusso, A.; Golfieri, R.; Gramenzi, A.; Mazzaferro, V.; et al. Trans-arterial radioembolization for intermediate-advanced hepatocellular carcinoma: A budget impact analysis. BMC Cancer 2018, 18, 715. [Google Scholar] [CrossRef] [PubMed]
- Perelman, J.; Soares, M.; Mateus, C.; Duarte, A.; Faria, R.; Ferreira, L.; Saramago, P.; Veiga, P.; Furtado, C.; Caldeira, S.; et al. Methodological Guidelines for Economic Evaluation Studies of Health Technologies; INFARMED—National Authority of Medicines and Health Products, IP: Lisbon, Portugal, 2019. [Google Scholar]
- Qu, Z.; Krauth, C.; Amelung, V.E.; Kaltenborn, A.; Gwiasda, J.; Harries, L.; Beneke, J.; Schrem, H.; Liersch, S. Decision modelling for economic evaluation of liver transplantation. World J. Hepatol. 2018, 10, 837. [Google Scholar] [CrossRef] [PubMed]
- Sanders, G.D.; Neumann, P.J.; Basu, A.; Brock, D.W.; Feeny, D.; Krahn, M.; Kuntz, K.M.; Meltzer, D.O.; Owens, D.K.; Lisa, A. Prosser, L.A.; et al. Recommendations for Conduct, Methodological Practices, and Reporting of Cost-Effectiveness Analyses: Second Panel on Cost-Effectiveness in Health and Medicine. J. Am. Med. Assoc. 2016, 316, 1093–1103. [Google Scholar] [CrossRef]
- Chong, C.A.; Gulamhussein, A.; Heathcote, E.; Lilly, L.; Sherman, M.; Naglie, G.; Krahn, M. Health-state utilities and quality of life in hepatitis C patients. Am. J. Gastroenterol. 2003, 98, 630–638. [Google Scholar] [CrossRef]
- Bertram, M.Y.; Lauer, J.A.; De Joncheere, K.; Edejer, T.; Hutubessy, R.; Kieny, M.P.; Hill, S.R. Cost–effectiveness thresholds: Pros and cons. Bull. World Health Organ. 2016, 94, 925. [Google Scholar] [CrossRef] [PubMed]
- Rand, L.Z.; Melendez-Torres, G.J. Alternatives to the quality-adjusted life year: How well do they address common criticisms? Health Serv. Res. 2023, 58, 433–444. [Google Scholar] [CrossRef]
- Anchisi, M. Métodos Não Paramétricos Para Análise de Dados de Sobrevivência. Master’s Thesis, Faculdade de Ciências, Universidade de Lisboa, Lisboa, Portugal, 2011. [Google Scholar]
- Rocha, C.; Papoila, A.L. Análise de Sobrevivência; Sociedade Portuguesa de Estatística, SPE: Lisboa, Portugal, 2009; ISBN 978-972-8890-22-3. [Google Scholar]
- Kwong, A.J.; Kim, W.R.; Lake, J.R.; Schladt, D.P.; Schnellinger, E.M.; Gauntt, K.; McDermott, M.; Weiss, S.; Handarova, D.K.; Snyder, J.J.; et al. OPTN/SRTR 2022 annual data report: Liver. Am. J. Transplant. 2024, 24, S176–S265. [Google Scholar] [CrossRef]
- Maccali, C.; Chagas, A.L.; Boin, I.; Quiñonez, E.; Marciano, S.; Vilatobá, M.; Varón, A.; Anders, M.; Duque, S.H.; Lima, A.S.; et al. Recurrence of hepatocellular carcinoma after liver transplantation: Prognostic and predictive factors of survival in a Latin American cohort. Liver Int. 2021, 41, 851–862. [Google Scholar] [CrossRef]
- Roayaie, S.; Schwartz, J.D.; Sung, M.W.; Emre, S.H.; Miller, C.M.; Gondolesi, G.E.; Krieger, N.R.; Schwartz, M.E. Recurrence of hepatocellular carcinoma after liver transplant: Patterns and prognosis. Liver Transplant. 2004, 10, 534–540. [Google Scholar] [CrossRef]
- Pereira, H. Cost-Effectiveness Analysis of Selection Criteria for Liver Transplantation in Patients with Hepatocellular Carcinoma. Master’s Thesis, Faculdade de Ciências, Universidade de Lisboa, Lisboa, Portugal, 2025. [Google Scholar]
- U.S. Bureau of Labor Statistics. CPI Inflation Calculator. Available online: https://www.bls.gov/data/inflation_calculator.htm (accessed on 18 July 2024).
- Younossi, Z.M.; Teran, J.C.; Ganiats, T.G.; Carey, W.D. Ultrasound-Guided Liver Biopsy for Parenchymal Liver Disease (An Economic Analysis). Dig. Dis. Sci. 1998, 43, 46–50. [Google Scholar] [CrossRef]
- Cadier, B.; Bulsei, J.; Nahon, P.; Seror, O.; Laurent, A.; Rosa, I.; Layese, R.; Costentin, C.; Cagnot, C.; Durand-Zaleski, I.; et al. Early detection and curative treatment of hepatocellular carcinoma: A cost-effectiveness analysis in France and in the United States. Hepatology 2017, 65, 1237–1248. [Google Scholar] [CrossRef] [PubMed]
- Andrade, R.; Perez-Rojas, J.; da Silva, S.G.; Miskinyte, M.; Quaresma, M.C.; Frazão, L.P.; Peixoto, C.; Cubells, A.; Montalvá, E.M.; Figueiredo, A.; et al. HepatoPredict Accurately Selects Hepatocellular Carcinoma Patients for Liver Transplantation Regardless of Tumor Heterogeneity. Cancers 2025, 17, 500. [Google Scholar] [CrossRef] [PubMed]
- O’Neill, A. Gross Domestic Product (GDP) per Capita in the United States in Current Prices from 1987 to 2029. Available online: https://www.statista.com/statistics/263601/gross-domestic-product-gdp-per-capita-in-the-united-states/ (accessed on 18 July 2024).
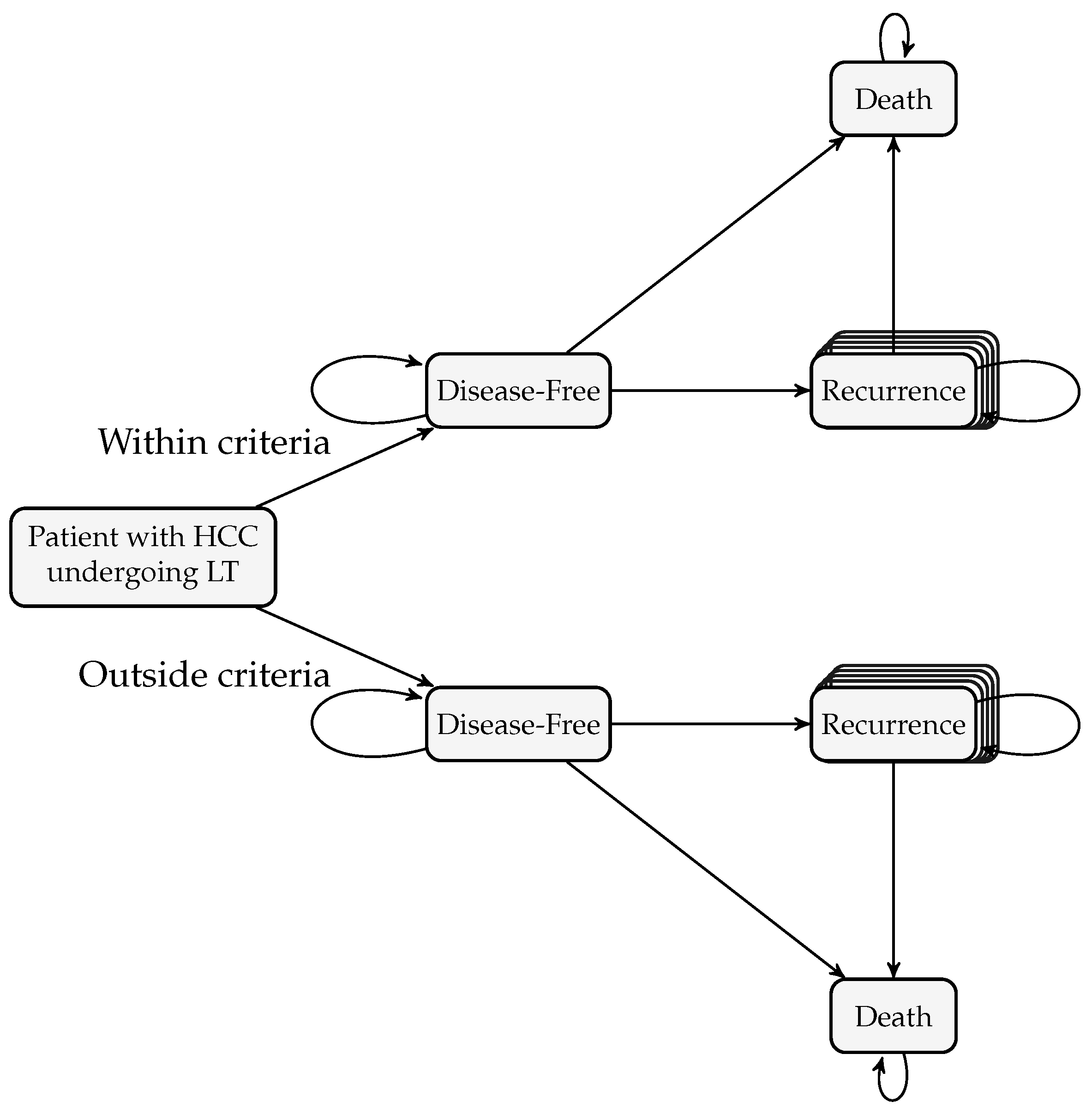
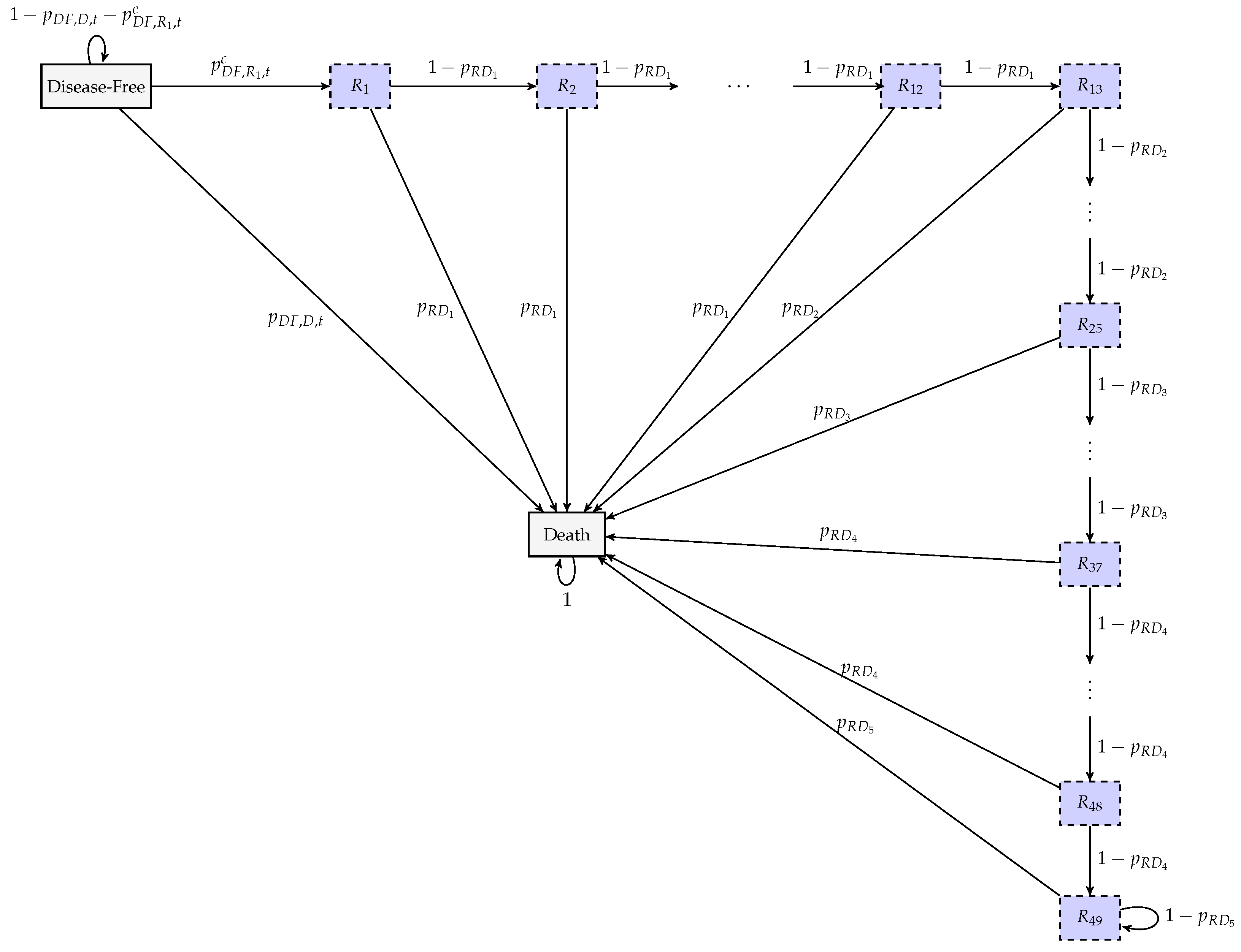

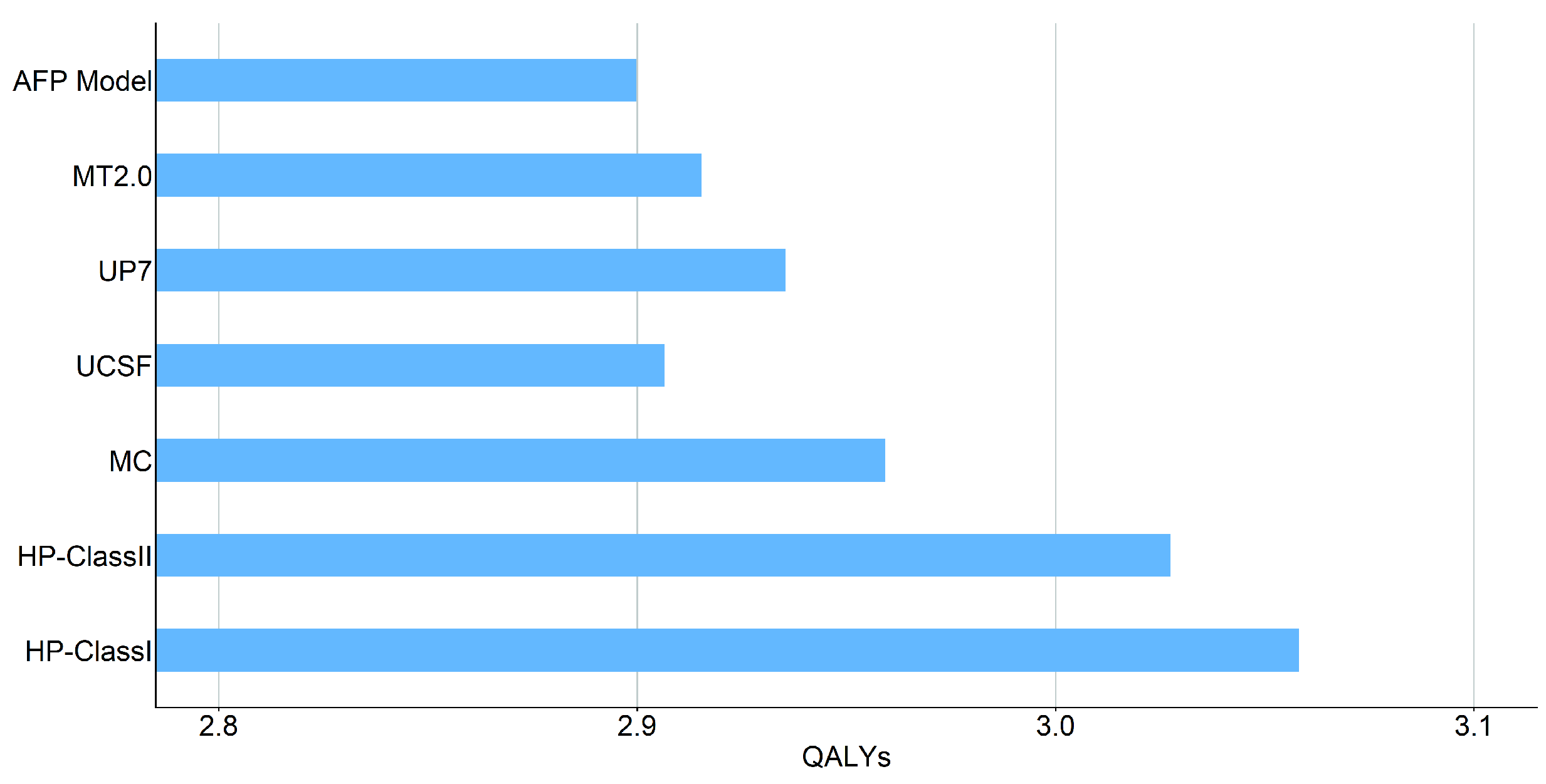
| Criterion | Inclusion Rules |
|---|---|
| MC * [15] | Single tumour ≤ 5 cm OR |
| Number of tumours ≤ 3 AND all tumour size ≤ 3 cm | |
| UCSF [16] | Single tumour ≤ 9 cm OR |
| Number of tumours ≤ 3 AND largest tumour size ≤ 4.5 cm AND total tumour diameter cm | |
| UCSF [16] | Single tumour ≤ 9 cm OR |
| Number of tumours ≤ 3 AND largest tumour size ≤ 4.5 cm AND total tumour diameter cm | |
| UP7 ** [17] | Number of tumours + largest tumour size ≤ 7 cm |
| AFP Model [14] | Tumour size: ≤3 cm, 0 points; 3–6 cm, 1 point; >6 cm, 4 points. Number of tumours: 1–3, 0 points; ≥4, 2 points. AFP level: ≤100 ng/mL, 0 points; 100–1000 ng/mL, 2 points; >1000 ng/mL, 3 points. Sum of points ≤ 2 points |
| MT2.0 [18] | Number of tumours + largest tumour size (cm) < 7 AND AFP level < 200 ng/mL OR |
| Number of tumours + largest tumour size (cm) < 5 AND AFP level < 400 ng/mL OR | |
| Number of tumours + largest tumour size (cm) < 4 AND AFP level < 1000 ng/mL |
| Parameter | Designation | Monthly Probability (%) |
|---|---|---|
| Post-transplant mortality (first 3 months) | 1.39% | |
| Mortality without recurrence in 4–12 months | 0.42% | |
| Mortality without recurrence in the 2nd year | 0.25% | |
| Mortality without recurrence in the 3rd year | 0.25% | |
| Mortality without recurrence in the 4th year | 0.33% | |
| Mortality without recurrence in the 5th year | 0.33% | |
| Mortality with recurrence in the 1st year | 6.26% | |
| Mortality with recurrence in the 2nd year | 3.65% | |
| Mortality with recurrence in the 3rd year | 3.35% | |
| Mortality with recurrence in the 4th year | 4.08% | |
| Mortality with recurrence in the 5th year | 2.91% |
| Parameter | Cost Designation | Reference | Cost (U.S. $) |
|---|---|---|---|
| Health State One-Off Costs | |||
| Biopsy | [44] | 3467.05 | |
| Hospitalisation and nurse appointments | [28] | 687.64 | |
| HP kit + Labour | − | 4000.00 | |
| Liver Transplant | [28] | 119,616.88 | |
| Pre-Liver Transplant | [28] | 1055.12 | |
| End of life cost | [28] | 23,091.60 | |
| Health State Cycle Costs | |||
| Post-transplant 0–1 months | [28] | 3338.09 | |
| Post-transplant 1–2 and 2–3 months | [28] | 1595.33 | |
| Surveillance | [28] | 1278.47 | |
| Systemic Therapy | [28] | 23,496.49 | |
| Parameter | QALYs Designation | Monthly QALYs (SE) | Annual QALYs (SE) |
|---|---|---|---|
| QALYPost.LT | Patients without recurrence in the first three months | 0.0575 (0.0058) | 0.69 (0.07) |
| QALYDF | Patients without recurrence after the 3rd month | 0.0625 (0.0008) | 0.75 (0.01) |
| QALYR | Patients with recurrence | 0.0583 (0.0042) | 0.70 (0.05) |
| Parameter | Median (, ) |
|---|---|
| Tumour number | 1 (1, 2) |
| Largest tumour size | 3 (2.1, 3.9) |
| Total tumour volume | 14.1 (5.8, 33.5) |
| Total tumour diameter | 3.4 (2.5, 5.3) |
| Levels of alpha-fetoprotein (AFP) | 9.7 (4.3, 38) |
| Criterion | N.º Patients Within Criteria (%) |
|---|---|
| HP-ClassI * | 109 (73.15%) |
| HP-ClassII * | 128 (85.91%) |
| UP7 | 127 (85.23%) |
| MC | 104 (69.80%) |
| UCSF | 133 (89.26%) |
| AFP Model | 132 (88.59%) |
| MT2.0 | 134 (89.93%) |
| RFS 5-year (CI) | Within Criteria | Outside Criteria |
|---|---|---|
| HP-Class I *,† | 100% | 39.35% |
| — | (23.56%, 54.80%) | |
| HP-Class II * | 97.23% | 6.35% |
| (91.63%, 99.10%) | (00.48%, 24.15%) | |
| UP7 | 86.54% | 63.16% |
| (78.64%, 91.67%) | (37.20%, 80.77%) | |
| MC | 88.04% | 71.61% |
| (79.41%, 93.20) | (54.43%, 83.24%) | |
| UCSF | 84.02% | 75.00% |
| (76.06%, 89.52%) | (40.84%, 91.17%) | |
| AFP Model | 84.28% | 75.49% |
| (76.17%, 89.81%) | (46.91%, 90.08%) | |
| MT2.0 | 85.49% | 63.49% |
| (77.66%, 90.74) | (33.12%, 82.97%) |
| Criterion | Year | Total | |||||
|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | (5 Years) | |
| HP-ClassI * | 128,826.69 | 22,407.16 | 13,920.03 | 13,110.28 | 12,454.89 | 11,617.85 | 202,336.90 |
| HP-ClassII * | 128,826.69 | 23,539.06 | 13,941.42 | 13,003.63 | 12,314.77 | 11,954.31 | 203,579.88 |
| UP7 | 121,359.64 | 24,652.01 | 15,200.91 | 14,463.07 | 13,905.15 | 11,923.46 | 201,504.24 |
| MC | 121,359.64 | 24,450.14 | 14,124.37 | 14,224.09 | 14,369.60 | 12,295.66 | 200,823.50 |
| UCSF | 121,359.64 | 25,055.66 | 15,764.60 | 14,644.83 | 13,654.56 | 12,177.06 | 202,656.35 |
| AFP Model | 121,359.64 | 25,721.53 | 15,294.15 | 14,678.85 | 13,717.67 | 11,728.74 | 202,500.58 |
| MT2.0 | 121,359.64 | 25,090.01 | 15,273.56 | 14,692.59 | 13,748.93 | 11,801.30 | 201,966.03 |
| Criterion | Costs (US $) | QALYs | ICER |
|---|---|---|---|
| MC | 200,883.76 | 2.96 | − |
| HP-ClassI * | 202,336.90 | 3.06 | 14,689.58 |
| HP-ClassII * | 203,579.32 | 3.03 | 39,542.98 |
| UP7 | 201,407.00 | 2.94 | |
| UCSF | 202,738.45 | 2.91 | |
| AFP Model | 202,461.82 | 2.90 | |
| MT2.0 | 202,062.32 | 2.92 |
| Criterion | Costs (US $) | QALYs | ICER |
|---|---|---|---|
| Lower Bound for RFS | |||
| MC | 204,646.32 | 2.83 | − |
| HP-ClassI * | 202,336.90 | 3.06 | |
| HP-ClassII * | 205,994.44 | 2.94 | 12,152.11 |
| UP7 | 205,009.55 | 2.81 | |
| UCSF | 206,201.50 | 2.79 | |
| AFP Model | 206,095.59 | 2.77 | |
| MT2.0 | 205,453.50 | 2.80 | |
| Upper Bound for RFS | |||
| MC | 198,336.24 | 3.01 | − |
| HP-ClassI * | 202,336.90 | 3.06 | 92,462.87 |
| HP-ClassII * | 202,747.23 | 3.05 | 123,291.52 |
| UP7 | 199,064.99 | 2.99 | |
| UCSF | 200,074.83 | 2.97 | |
| AFP Model | 199,919.30 | 2.97 | |
| MT2.0 | 199,495.13 | 2.98 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pereira, H.; Fonseca, R.J.; Mouriño, H. Application of Markov Models to Cost-Effectiveness Analysis in the Selection of Patients for Liver Transplantation. Mathematics 2025, 13, 3683. https://doi.org/10.3390/math13223683
Pereira H, Fonseca RJ, Mouriño H. Application of Markov Models to Cost-Effectiveness Analysis in the Selection of Patients for Liver Transplantation. Mathematics. 2025; 13(22):3683. https://doi.org/10.3390/math13223683
Chicago/Turabian StylePereira, Hugo, Raquel J. Fonseca, and Helena Mouriño. 2025. "Application of Markov Models to Cost-Effectiveness Analysis in the Selection of Patients for Liver Transplantation" Mathematics 13, no. 22: 3683. https://doi.org/10.3390/math13223683
APA StylePereira, H., Fonseca, R. J., & Mouriño, H. (2025). Application of Markov Models to Cost-Effectiveness Analysis in the Selection of Patients for Liver Transplantation. Mathematics, 13(22), 3683. https://doi.org/10.3390/math13223683






