Abstract
Model Predictive Control (MPC) predicts the vehicle’s motion within a fixed time window, known as the prediction horizon, and calculates potential collision risks with obstacles in advance. It then determines the optimal steering input to guide the vehicle safely around obstacles. For example, when a sudden obstacle appears, sensors detect it, and MPC uses the vehicle’s current speed, position, and heading to predict its driving trajectory over the next few hundred milliseconds to several seconds. If a collision is predicted, MPC computes the optimal steering path among possible avoidance trajectories that are feasible within the vehicle’s dynamics. The vehicle then follows this input to steer away from the obstacle. In the proposed method, MPC is combined with Adaptive Artificial Potential Field (APF). The APF dynamically adjusts the repulsive force based on the distance and relative speed to the obstacle. MPC predicts the optimal driving path and generates control inputs, while the avoidance vector from APF is integrated into MPC’s constraints or cost function. Simulation results demonstrate that the proposed method significantly improves obstacle avoidance response, steering smoothness, and path stability compared to the baseline MPC approach.
Keywords:
Adaptive Artificial Potential Field (APF); obstacle avoidance; trajectory planning; exponential repulsive force; path smoothness; reactive navigation; local planner; sensitivity tuning; autonomous systems; motion stability; parameter adaptation; real-time control MSC:
37M10
1. Introduction
Systems such as mobile robots, UAVs, and self-driving cars must operate in environments where static and dynamic obstacles are present. Ensuring safe, efficient, and real-time obstacle avoidance in these dynamic scenarios is a central challenge in modern robotics. To address this, a wide range of motion-planning strategies have been proposed, including optimization-based approaches, reactive methods, and learning-based techniques.
Model Predictive Control (MPC) has become a popular approach due to its ability to anticipate future states over a prediction horizon and incorporate system constraints directly into the control formulation. For example, Dynamic Control Barrier Functions (DCBFs) integrated with MPC enable real-time avoidance of dynamic obstacles based on LiDAR-based prediction and clustering [1].
However, MPC is not the only solution. Gradient-based trajectory optimization using B-splines has also proven to be effective for real-time dynamic obstacle avoidance in cluttered environments, utilizing signed distance fields and receding-horizon re-planning [2]. Metaheuristic approaches, such as Modified Bat Swarm Optimization (MFBA), introduce adaptive search mechanisms and obstacle-aware replanning to generate smooth, collision-free paths [3].
In robotic manipulation scenarios, reactive methods in real time, such as the Intelligent Circular Field (ICF) planner, can generate dynamically feasible avoidance behaviors in the presence of moving obstacles, without relying on pre-computed maps [4]. Similarly, global–local hybrid planners use occupancy grid maps and trajectory evaluation via cost functions that consider dynamic obstacle proximity, static map data, and goal alignment [5].
Traditional reactive algorithms, such as the dynamic window approach (DWA) and the vector field histogram (VFH), remain widely used due to their low computational cost and the ability to handle real-time sensor data [6,7]. Furthermore, fuzzy logic controllers enable context-sensitive behavior, adjusting robot movement based on the type and distance of surrounding obstacles—especially useful in human–robot interaction environments [8].
Learning-based methods, including Reinforcement Learning (RL) and behavior prediction models, show strong generalization to highly dynamic settings. Algorithms such as the Learning-based Motion Behavior Rule-Based Controller (LMBRC) and Nonparametric Velocity Obstacles (NPVOs) outperform traditional planners in high-speed or highly uncertain environments [9]. Finally, trajectory smoothing through Quadratic Programming (QP) has been explored to refine discrete paths while preserving safety and dynamic feasibility [10].
Collision avoidance is one of the core functionalities necessary for safe and reliable operation of autonomous vehicles. Among various control strategies, Model Predictive Control (MPC) has gained significant attention due to its ability to explicitly handle system dynamics and constraints within an optimization framework. However, for real-time obstacle avoidance, MPC alone may not respond fast enough to dynamic environments. To complement this, Artificial Potential Fields (APFs) are often integrated into MPC frameworks due to their simplicity and efficiency in modeling repulsive and attractive forces within the vehicle’s local environment.
Despite its advantages, traditional APF-based approaches often struggle in complex, dynamic environments, such as high-speed traffic or multi-obstacle scenarios. A key limitation is the fixed nature of APF parameters, which may not properly reflect the urgency of threats from fast-moving or suddenly appearing obstacles. Recent research has attempted to overcome this by introducing adaptive components into the APF-MPC structure.
For instance, in [11], an improved APF was proposed where a risk-level factor and velocity-sensitive coefficient are introduced into the repulsive potential function. This enables dynamic adjustment of the repulsion strength and range based on the obstacle’s motion, thereby enhancing early collision prediction and avoidance. Similarly, ref. [12] incorporates an adjustment factor into both the attractive and repulsive potentials to improve the adaptability of path planning near road boundaries and moving obstacles. These modifications allow for the APF to respond more realistically to real-world dynamics.
In addition, the study in [13] employs adaptive MPC, where the prediction horizon is modified in real time based on vehicle speed and surrounding conditions. By combining this with a safety–distance model, improved tracking accuracy and responsiveness to environmental changes are achieved.
While these contributions mark significant progress, most of the existing approaches lack an explicit modeling of how sensitive the system should be to rapid or high-risk obstacle behavior. In dynamic driving scenarios—such as lane changes, merging, or emergency braking—a controller must not only detect obstacles but also evaluate how urgently to respond. This motivates the introduction of a sensitivity coefficient, a new parameter that quantifies the responsiveness of the repulsive field to variations in obstacle threat level.
Therefore, in this work, we propose a novel collision avoidance strategy for autonomous vehicles that integrates MPC with an adaptive APF enhanced by a sensitivity coefficient. The sensitivity coefficient dynamically scales the repulsive potential based on real-time relative velocity, distance, and acceleration. This allows the controller to
Increase repulsion early when a fast-approaching object is detected;
Reduce unnecessary evasive action when obstacles pose minimal threat;
Ensure smoother and more stable trajectories in cluttered environments.
By integrating this sensitivity-aware potential field into the MPC framework, the proposed method balances safety, reactiveness, and trajectory smoothness, contributing to more robust autonomous navigation in uncertain and dynamic environments.
Autonomous vehicles require robust collision-avoidance mechanisms to navigate dynamic environments safely. Among various strategies, Model Predictive Control (MPC) stands out for its ability to handle multi-objective optimization under constraints, while Artificial Potential Field (APF) methods are valued for their intuitive repulsive/attractive-force-based path shaping. Prior work by Song et al. (2021) implemented an improved APF integrated with safety–distance modeling and MPC for generating safe, reactive trajectories in dynamic scenarios [14]. Similarly, Ref. [15] proposed a hierarchical two-level MPC framework, using potential field methods to assess collision risk and generate cost functions for path planning, with a lower-level MPC handling trajectory tracking. In the present study, we extend these foundational concepts by developing a real-time MPC strategy augmented with an adaptive APF, which dynamically adjusts repulsive forces based on obstacle behavior and road context. Ref. [11] proposes a method that combines Event-triggered Model Predictive Control (EMPC) with an Adaptive Artificial Potential Field (APF) to achieve stable obstacle avoidance and trajectory tracking. In particular, the APF-based cost function is integrated directly into the objective function of the MPC framework, ensuring both the stability and feasibility of the control strategy. Ref. [16] enhances the classical APF by introducing safety–distance constraints and velocity-dependent repulsion forces, which are then integrated into an MPC framework for lateral control and a Fuzzy-PID controller for longitudinal control. The approach achieves smooth lane changes while maintaining dynamic obstacle avoidance and velocity tracking in real-time environments. Ref. [17] offers a comparative analysis between Artificial Potential Fields (APFs) and Control Barrier Functions (CBFs). It demonstrates that traditional APF methods can be interpreted as a specific case of CBFs under certain assumptions. The paper further evaluates the advantages and limitations of each method in terms of safety guarantees and real-time applicability in autonomous navigation systems. Ref. [18], inspired by electrostatic line charges, introduces a novel APF formulation for integration into MPC. The approach allows for adaptive shaping of repulsive fields according to road geometry and obstacle type. Simulation results show significant improvements in success rates and collision avoidance compared to conventional APF-MPC systems, especially in emergency scenarios. This approach ensures both smooth trajectory planning and adherence to safety constraints (e.g., road width and vehicle geometry) while maintaining recursive feasibility and practical stability, as demonstrated through experimental validation. Our contributions build upon earlier strategies by introducing adaptivity into the APF to better predict and smoothly avoid dynamic obstacles using MPC.
In this work, we build upon these foundations and explore a predictive-control-based framework for dynamic obstacle avoidance, evaluating its performance relative to these alternative strategies.
2. Materials and Methods
The state space model for kinematic model is given as
where the state, control, and disturbance inputs are defined as follows:
and the system matrices are the following:
where
- : Predicted state vector at time step k;
- : Reference state vector at time step k;
- : Control input at time step k;
- Q: State weighting matrix ();
- R: Input weighting matrix ();
- N: Prediction horizon;
- : Longitudinal velocity of the vehicle [m/s];
- y: Lateral displacement of the vehicle [m];
- : Lateral velocity of the vehicle [m/s];
- : Yaw angle of the vehicle [rad];
- : Desired yaw angle [rad];
- r: Yaw rate (angular velocity) of the vehicle [rad/s];
- : Steering angle [rad];
- : Steering rate (control input) [rad/s];
- : Desired yaw rate (external disturbance);
- a: Distance from the vehicle’s center of gravity (CG) to the front axle [m];
- b: Distance from CG to the rear axle [m];
- m: Mass of the vehicle [kg];
- : Yaw moment of inertia of the vehicle [kg·m2];
- : Cornering stiffness of the front tires [N/rad];
- : Cornering stiffness of the rear tires [N/rad].
The Model Predictive Control (MPC) for the steering system can be formulated as follows:
The original method given in [18] is described as follows: The current position is shown as
The target position is described as
The position at the t-th prediction step is given as
The attractive and repulsive forces are given as
and
The total force is given as
The time step is given as
The list of obstacles is given as
The adaptive repulsive coefficient is given as
- : mobile platform’s longitudinal position;
- : i-th obstacle’s longitudinal position;
- : The distance between mobile platform and obstacle;
- : repulsive distance threshold;
- .
For each i-th obstacle, the repulsive force is calculated from
For all prediction steps , compute and construct the reference trajectory as follows:
The total artificial potential force is given as
Using the step size , compute the next position as follows:
The algorithm iteratively updates and moves along the horizon over steps, predicting the next position at each step by considering the attractive force toward the goal and the adaptive repulsive forces from obstacles.
The following revisement is illustrated in the experiment to improve the previous theory introduced in [18]:
- Maintain the actual magnitude of without normalization.→ This preserves movement while promoting obstacle avoidance.
- Increase the movement coefficient ().→ For example, or higher. (The value of controls the sensitivity of the repulsive force in the APF method. Choosing too low a value, such as = 0.01, may result in a very weak repulsive force that does not sufficiently push the vehicle away from obstacles in a timely manner, increasing the risk of collision).
- Modify the design of for a more sensitive response.→ Use instead of to adjust sensitivity.
- Introduce a minimum movement threshold.→ If is too small, the system may be forced to push.
The kinematic system model is given as
where
- : Position;
- : Yaw angle (heading direction);
- : Velocity;
- : Acceleration control input;
- : Steering angle.
2.1. Optimization Problem Formulation
The Model Predictive Control problem is formulated to minimize the tracking error and control effort over a prediction horizon N, subject to vehicle dynamics and constraints. The optimization problem is as follows:
where
- : state vector at time k;
- : control input (acceleration and steering angle);
- : reference state at step k, generated by the adaptive APF;
- : state-tracking weight matrix;
- : control effort weight matrix;
- : vehicle kinematic update function as defined in Equation (21).
The short-term reference trajectory generated by the Adaptive Artificial Potential Field (APF) is defined as follows:
Each position is updated according to the following equation:
where
- ;
- .
The above equation increases gradually as the distance d decreases, following a linearly decaying polynomial form. This results in a relatively smooth and moderate repulsive behavior.
In contrast, the following equation exhibits an exponential-like growth as , leading to a much more sensitive response when the system approaches an obstacle. As the system approaches an obstacle, increasing the value of ∂ results in a more sensitive response.
There is a reason why we revise the equation from polynomial decay to exponential decay.
2.2. Polynomial Decay Method
- Formula:
- Characteristics:
- –
- As the distance decreases, the force increases gradually.
- –
- When far from obstacles, the effect is almost negligible. Even when approaching, the increase is smooth rather than abrupt.
- –
- Therefore, the behavior is smooth but may lead to a delayed response in actual collision risk situations, resulting in a “lack of safety” issue.
2.3. Exponential Method
- Formula:
- Characteristics:
- –
- As (i.e., when approaching an obstacle), the force grows explosively.
- –
- Even small changes in distance trigger a very sensitive response.
- –
- Thus, in real robotic systems, when approaching obstacles, the robot reacts much faster with evasive maneuvers.
2.4. Why Was It Changed? (Reasoning)
- Ensuring SafetyThe polynomial model does not generate a large force until the robot gets very close to the obstacle. Therefore, a fast-moving robot may fail to respond sufficiently before collision. In contrast, the exponential model produces a rapidly increasing force as it approaches the obstacle, enabling safer avoidance.
- Sensitivity AdjustmentBy tuning the parameter , the sensitivity can be easily adjusted. This allows fine-tuning according to the environment or specific robot characteristics.
- Adaptability to Real EnvironmentsIn industrial sites or complex environments, a strong avoidance response near obstacles is essential. Hence, the exponential model is considered more practical for real-world applications.
The parameter serves as a switch that adjusts the slope (rate of increase) of the exponential function.
- If is large even small changes in distance cause the repulsive force to grow explosively (very sensitive).
- If is small the exponential growth becomes more gradual, and the obstacle response is less sensitive.
Thus, is a tuning parameter that controls sensitivity and the safety margin. In real robotic environments, setting too high may result in unnecessarily aggressive evasive maneuvers (oscillations), while setting it too low may cause delayed reactions, increasing the risk of collision.
Sensitivity Control: As the robot approaches an obstacle, we want the evasive response to increase sharply. Linear or quadratic functions cannot generate the desired “explosive” reaction right before collision. In contrast, the exponential function increases output exponentially even for small changes in input, allowing the robot to respond very sensitively near obstacles.
Safety Assurance: In real robotic systems, inertia poses a risk of collision if the robot reacts too late when close to an obstacle. Therefore, once the distance falls below a certain threshold, a sharply increasing repulsive force is applied to trigger rapid evasive maneuvers.
3. Results
When a sudden obstacle appears, visualized as a red object in the simulator, the Adaptive Artificial Potential Field (APF) method generates a virtual target point by combining a repulsive force directed away from the obstacle with an attractive force toward the original goal. This virtual target guides the MPC to perform a smooth and safe avoidance maneuver. The experiment was implemented based on code given in Appendix A. The scenario is described in Figure 1.
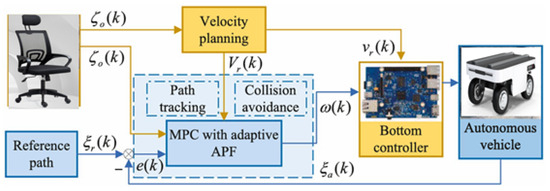
Figure 1.
Scenario: The dynamical obstacle (chair) was interrupted after the mobile platform moved in three seconds. The Model Predictive Control avoids dynamical obstacles (the chair in our case).
3.1. APF-to-MPC Command Mapping
The APF does not directly output a torque; instead, it defines a desired heading from the net artificial force:
A yaw-rate (angular-velocity) reference is then obtained as a finite-difference target:
- 1.
- Velocity-Planning Model
The Velocity-Planning block in Figure 1 is responsible for generating a safe and feasible reference velocity, denoted as , based on the dynamic environment, particularly moving or static obstacles represented by . This module considers the relative position and motion of obstacles and utilizes this information to compute a safe velocity trajectory for the autonomous vehicle.
Mathematically, this can be expressed as follows:
where is a function or algorithm that maps obstacle information to a velocity reference. This function may involve the following:
- Safety constraints (e.g., minimum stopping distance);
- Kinematic or dynamic limits of the vehicle;
- Heuristics or optimization techniques for dynamic obstacle avoidance.
- 2.
- Integration with Model Predictive Control (MPC)
The Model Predictive Control (MPC) with adaptive Artificial Potential Field (APF) uses the reference velocity , along with the reference path , actual vehicle state , and obstacle information , to compute the optimal control inputs for the vehicle.
The MPC solves an optimization problem over a prediction horizon N as follows:
where
- : Reference state;
- : Actual state of the vehicle;
- : Angular velocity control input;
- : Weighting matrices for tracking error and control effort;
- : Vehicle motion model including the influence of .
3.2. Adaptive Artificial Potential Field (APF)
The APF enhances collision avoidance by dynamically adjusting the repulsive potential based on real-time obstacle data. The repulsive potential and resulting force are adjusted adaptively to reflect the velocity and proximity of obstacles.
- 3.
- System Workflow
The overall control loop proceeds as follows:
- Obstacle state is detected.
- Velocity-Planning block computes a safe velocity .
- MPC uses , path-tracking objectives, and APF constraints to compute optimal control .
- Bottom controller sends and to the autonomous vehicle.
- The vehicle updates its state , which is fed back to the MPC.
The control performance is evaluated qualitatively and comparatively by analyzing the behavior of the autonomous vehicle in response to a dynamic obstacle, across both the existing (original) and improved MPC with adaptive APF models.
- The key criteria used to evaluate and compare performance include the following:
Using the existing design method introduced in [18], the result is given in Figure 2.
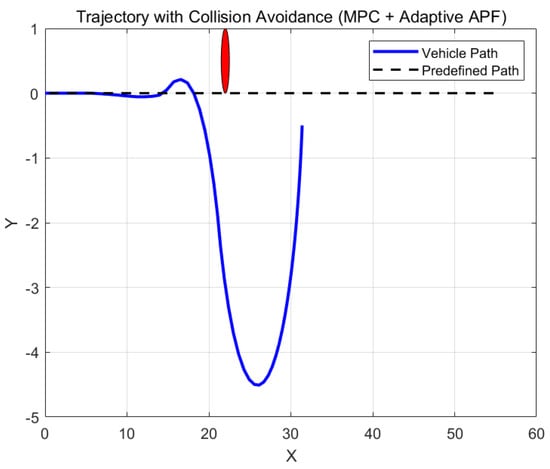
Figure 2.
The dynamical obstacle avoidance using existing Model Predictive Control.
When applying the improved model predictive control method, the result is given in Figure 3.
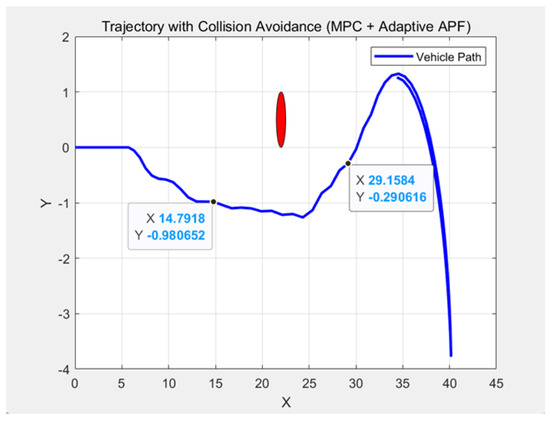
Figure 3.
The dynamical obstacle avoidance using improved Model Predictive Control. (x and y are in meters).
The “uncontrolled response” after obstacle avoidance that you observed—especially in the original MPC model (e.g., Figure 2 or the second graph)—typically happens due to limitations in trajectory recovery and inadequate repulsive force management after avoidance.
The comparison between the existing design algorithm and our improved MPC (Model Predictive Control) is given in Table 1 and Table 2. The second graph shows a better performance.

Table 1.
Key criteria for evaluating and comparing control performance.

Table 2.
Comparison of performance between the improved and original methods.
4. Discussion
The comparative results highlight the effectiveness of the proposed improvements in adaptive artificial potential field (APF)-based trajectory planning. One of the most notable advantages is the enhanced responsiveness to obstacles. By avoiding normalization of the total force vector and introducing an exponential repulsive force formulation, the system becomes significantly more sensitive as it approaches nearby obstacles. This allows for earlier and smoother avoidance maneuvers, which are critical in real-time navigation scenarios. The smoothness of the post-avoidance path is also greatly improved. Unlike the original method, which often results in sharp and unnatural curves due to sudden changes in the repulsive force, our approach maintains continuity and stability in the generated trajectory. This is particularly beneficial for applications, such as autonomous driving or mobile robotics, where abrupt changes can compromise safety or passenger comfort. Moreover, the modified repulsive force equation—by incorporating a tunable exponential sensitivity—allows for finer control over how aggressively the system responds to obstacles. This flexibility enables adaptation to different environments or task-specific requirements, offering a more generalizable solution. However, the increased sensitivity may also lead to overly cautious behavior in densely cluttered environments, where the system could react too strongly to minor obstacles. This could potentially lead to inefficient detours or oscillatory behavior if not properly tuned. Additionally, the performance heavily depends on careful parameter selection (e.g., , , ), which may require environment-specific tuning or learning-based adaptation mechanisms. Future work may explore integrating learning-based strategies to automatically adapt APF parameters in dynamic environments, or combining the approach with global path-planning methods to ensure both local reactivity and global optimality.
5. Conclusions
In this study, we presented an improved obstacle avoidance method based on Adaptive Artificial Potential Field (APF) principles. Comparative analysis between the proposed approach and the original method demonstrates significant improvements in multiple aspects of trajectory planning and control. The proposed method exhibits faster and smoother responses to obstacles, enabling more natural and stable steering behavior. Unlike the original approach, which often results in sharp and aggressive turns, our method ensures a gradual and continuous trajectory even in the presence of nearby obstacles. This is achieved by adaptively tuning the repulsive force using a distance-sensitive exponential formulation, which allows for more responsive behavior as the system approaches obstacles. Furthermore, the improved design enhances goal recovery performance, allowing the system to efficiently re-align with the intended direction after avoidance maneuvers. Overall path stability is also improved, showing minimal oscillations and avoiding sudden, unstable reactions observed in the original approach. These enhancements contribute to a safer and more reliable navigation framework, particularly in dynamic or cluttered environments, and demonstrate the effectiveness of our approach in real-time trajectory generation for autonomous systems.
Author Contributions
Writing—original draft, H.Y.; Visualization, H.Y.; Validation, S.C.; Supervision, S.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (No. RS-2020-NR049604, 100%).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| APF | Adaptive Potential Field |
| MPC | Model Predictive Control |
| DWA | Dynamic Window Approach |
Appendix A
| Nx = 4; Ny = 2; Nu = 2; |
| Np = 10; Nc = 3; Ts = 0.1; Nsteps = 100; |
| L = 2.5; |
| f = @(x, u)[ |
| x(4)*cos(x(3)); |
| x(4)*sin(x(3)); |
| x(4)/L * tan(u(2)); |
| u(1) |
| ]; |
| h = @(x, u)[x(1); x(2)]; |
| mpcobj = nlmpc(Nx, Ny, Nu); |
| mpcobj.Ts = Ts; |
| mpcobj.PredictionHorizon = Np; |
| mpcobj.ControlHorizon = Nc; |
| mpcobj.Model.StateFcn = f; |
| mpcobj.Model.OutputFcn = h; |
| mpcobj.MV(1).Min = -3; mpcobj.MV(1).Max = 3; |
| mpcobj.MV(2).Min = -0.4; |
| mpcobj.MV(2).Max = 0.4; |
| mpcobj.Weights.OutputVariables = [1 1]; |
| mpcobj.Weights.ManipulatedVariables = [0.1 0.1]; |
| mpcobj.Weights.ManipulatedVariablesRate = [0.01 0.01]; |
| x = zeros(Nx, Nsteps+1); |
| x(:,1) = [0; 0; 0; 0]; |
| = [0; 0]; |
| ob = cell(1, Nsteps); |
| for k = 1:Nsteps |
| xk = x(:,k); |
| obs = getObstacles(k); |
| obk = obs; |
| = computeAdaptiveAPF4(xk, obs, Np); |
| updateMPCConstraints(mpcobj, xk, obs); |
| [uk, ] = nlmpcmove(mpcobj, xk, , ); |
| x(:,k+1) = xk + f(xk, uk) * Ts; |
| = uk; |
| end |
| figure; |
| plot(x(1,:), x(2,:), ‘b’, ‘LineWidth’, 2); |
| hold on; |
| plotObstacles(obend); |
| xlabel(‘X [m]’); ylabel(‘Y [m]’); |
| title(‘Trajectory with Collision Avoidance (MPC + Adaptive APF)’); |
| legend(‘Vehicle Path’, ‘Obstacles’); |
| grid on; |
References
- Zeng, W.; Tomizuka, M. Real-Time Obstacle Avoidance for a Mobile Robot Using CNN-Based Sensor Fusion. arXiv 2025, arXiv:2509.08095. [Google Scholar]
- Jongseo, C.; Hyuntai, C.; Hyunwoo, P.; Daehyeok, K.; Doosan, B.; Sang-Hyun, L. Safe and Efficient Trajectory Optimization for Autonomous Vehicles using B-spline with Incremental Path Flattening. arXiv 2022, arXiv:2311.02957. [Google Scholar]
- Ismail, F.B.; Zain, A.M. Path Planning of an Autonomous Mobile Robot in a Dynamic Environment using Modified Bat Swarm Optimization. arXiv 2019, arXiv:1807.05352. [Google Scholar] [CrossRef]
- Hou, Y.; Meike, T.; Zhang, J.; Knoll, A. Informed Circular Fields for Global Reactive Obstacle Avoidance of Robotic Manipulators. arXiv 2022, arXiv:2212.05815. [Google Scholar]
- Zhong, J.; Zhang, M.; Chen, Z.; Wang, J. Dynamic Obstacle Avoidance for Mobile Robots Based on 2D Differential Euclidean Signed Distance Field Maps in Park Environment. World Electr. Veh. J. 2024, 15, 320. [Google Scholar] [CrossRef]
- Fox, D.; Burgard, W.; Thrun, S. The Dynamic Window Approach to Collision Avoidance. IEEE Robot. Autom. 1997, 4, 23–33. [Google Scholar] [CrossRef]
- Borenstein, J.; Koren, Y. The Vector Field Histogram—Fast Obstacle Avoidance for Mobile Robots. IEEE Trans. Robot. Autom. 1991, 7, 278–288. [Google Scholar] [CrossRef]
- Sousa, L.C.; Silva, Y.M.; Schettino, V.B.; Santos, T.M.; Zachi, A.R.; Gouvêa, J.A.; Pinto, M.F. Obstacle Avoidance Technique for Mobile Robots at Autonomous Human-Robot Collaborative Warehouse Environments. Sensors 2025, 25, 2387. [Google Scholar] [CrossRef] [PubMed]
- Guan, L.; Lu, Y.; He, Z.; Chen, X. Intelligent Obstacle Avoidance Algorithm for Mobile Robots in Uncertain Environment. J. Robot. 2022, 2022, 8954060. [Google Scholar] [CrossRef]
- Kenneth, R.S.; Naoki, U.; Shigenori, S. Real-time smooth trajectory generation for nonholonomic mobile robots using Bezier curves. Robot. Comput.-Integr. Manuf. 2016, 41, 31–42. [Google Scholar]
- Zhao, L.; Liu, H.; Niu, W. Collision Avoidance of Driving Robotic Vehicles Based on Model Predictive Control with Improved APF. Machines 2025, 13, 696. [Google Scholar] [CrossRef]
- Wang, S.; Lin, F.; Wang, T.; Zhao, Y.; Zang, L.; Deng, Y. Autonomous Vehicle Path Planning Based on Driver Characteristics Identification and Improved Artificial Potential Field. Actuators 2022, 11, 52. [Google Scholar] [CrossRef]
- Miao, B.; Han, C. Intelligent vehicle obstacle avoidance path-tracking control based on adaptive model predictive control. Mech. Sci. 2023, 14, 247–258. [Google Scholar] [CrossRef]
- Feng, S.; Qian, Y.; Wang, Y. Collision avoidance method of autonomous vehicle based on improved artificial potential field algorithm. Sage J. 2021, 14, 3416–3430. [Google Scholar] [CrossRef]
- Yang, H.; Wang, Z.; Xia, Y.; Zuo, Z. EMPC with Adaptive APF for Obstacle Avoidance and Trajectory Tracking. ISA Trans. 2023, 135, 438–448. [Google Scholar] [CrossRef] [PubMed]
- Singletary, A.; Klingebiel, K.; Bourne, J.; Browning, A.; Tokumaru, P.; Ames, A.D. Comparative Analysis: Control Barrier Functions and Artificial Potential Fields for Obstacle Avoidance. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021; pp. 8129–8136. Available online: https://ieeexplore.ieee.org/document/9636670 (accessed on 16 December 2021).
- Shang, X.; Eskandarian, A. Emergency Collision Avoidance Using MPC and Line-Charge-Inspired APF. arXiv 2023, arXiv:2211.06574v3. [Google Scholar]
- Yang, H.; He, Y.; Xu, Y.; Zhao, H. Collision avoidance for autonomous vehicles based on MPC with adaptive APF. IEEE Trans. Intell. Veh. 2024, 9, 1559–1570. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).