A Methodological Framework for Analyzing and Differentiating Daily Physical Activity Across Groups Using Digital Biomarkers from the Frequency Domain
Abstract
1. Introduction
1.1. PA Variables in the Time Domain
1.2. PA Variables in Frequency Domain
2. Materials and Methods
2.1. Motivating Studies and Physical Activity Observations
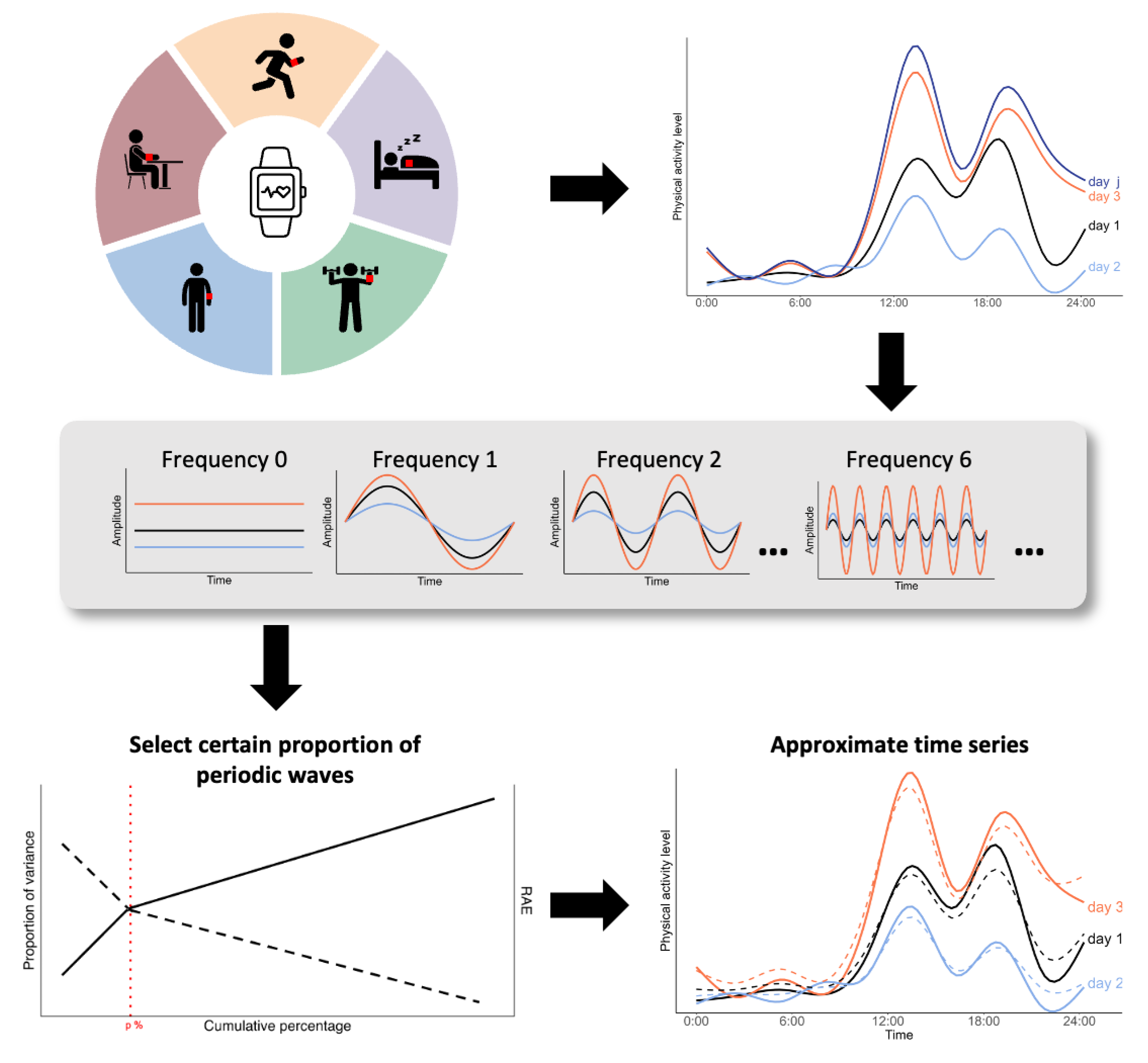
2.2. Properties of Frequency Domain Variables
2.3. Approximate Activity Curve and Dimension Reduction
3. Results
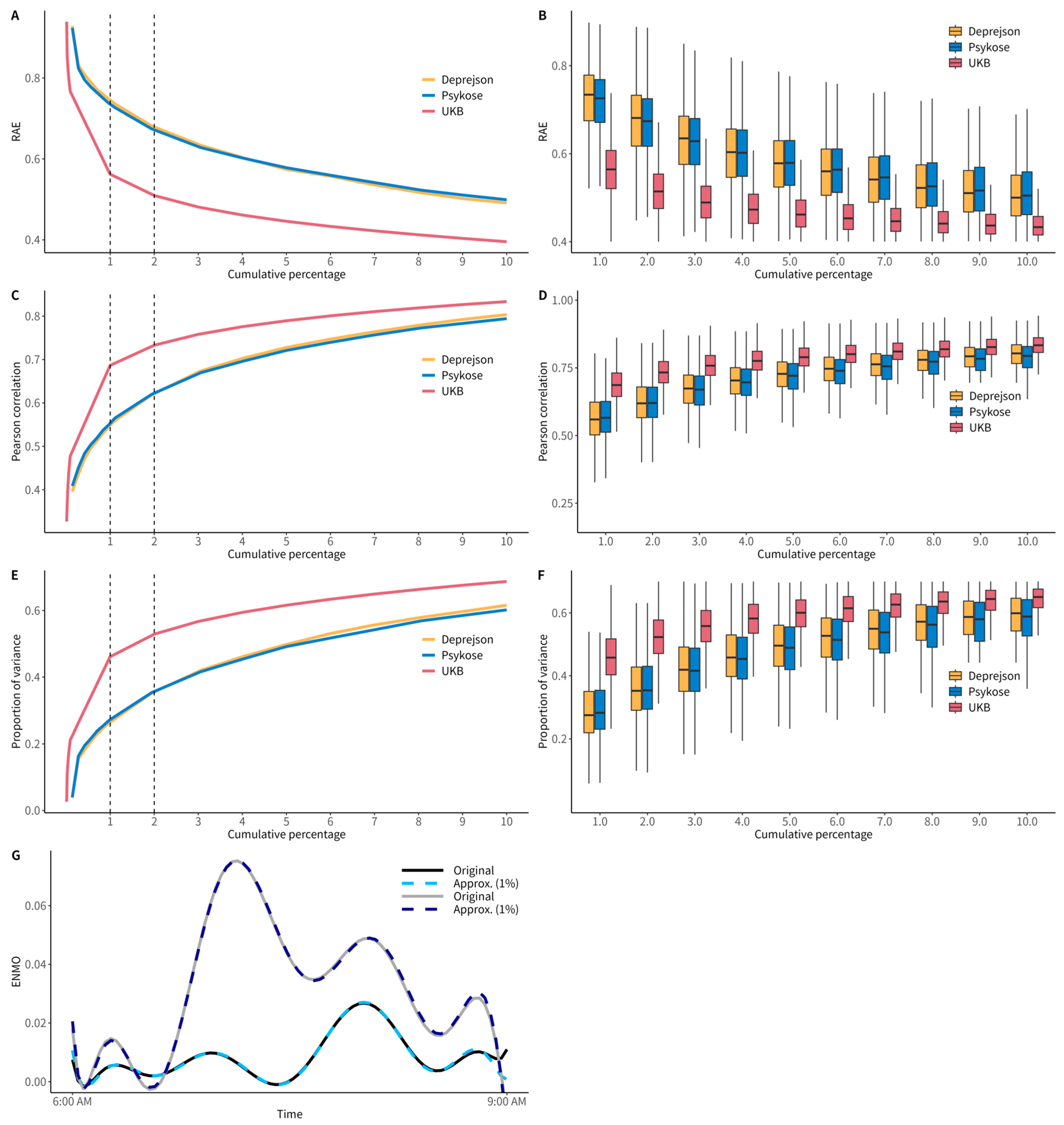
3.1. DFT Variables Approximate PA Well
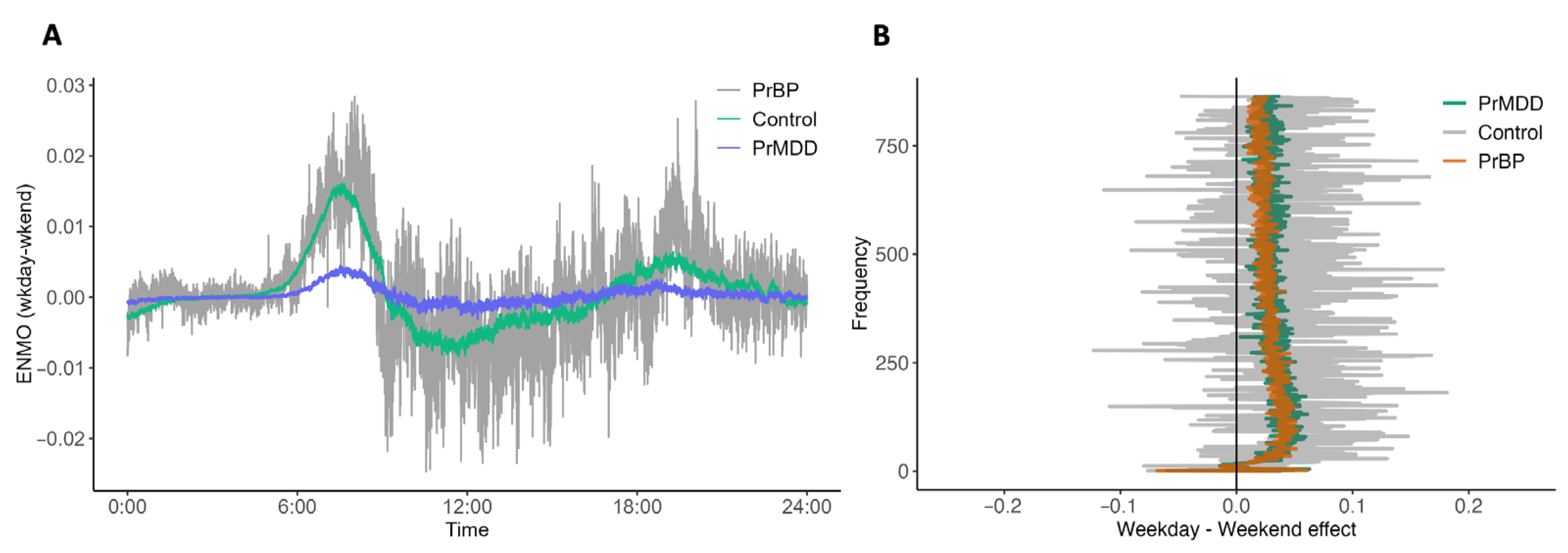
3.2. DFT-Based Variables Are Associated with Group Status and Weekend/Weekday Effects
3.3. Evaluating DFT-Based Variables: Impact on Classification Performance and Variable Influence in Association Studies
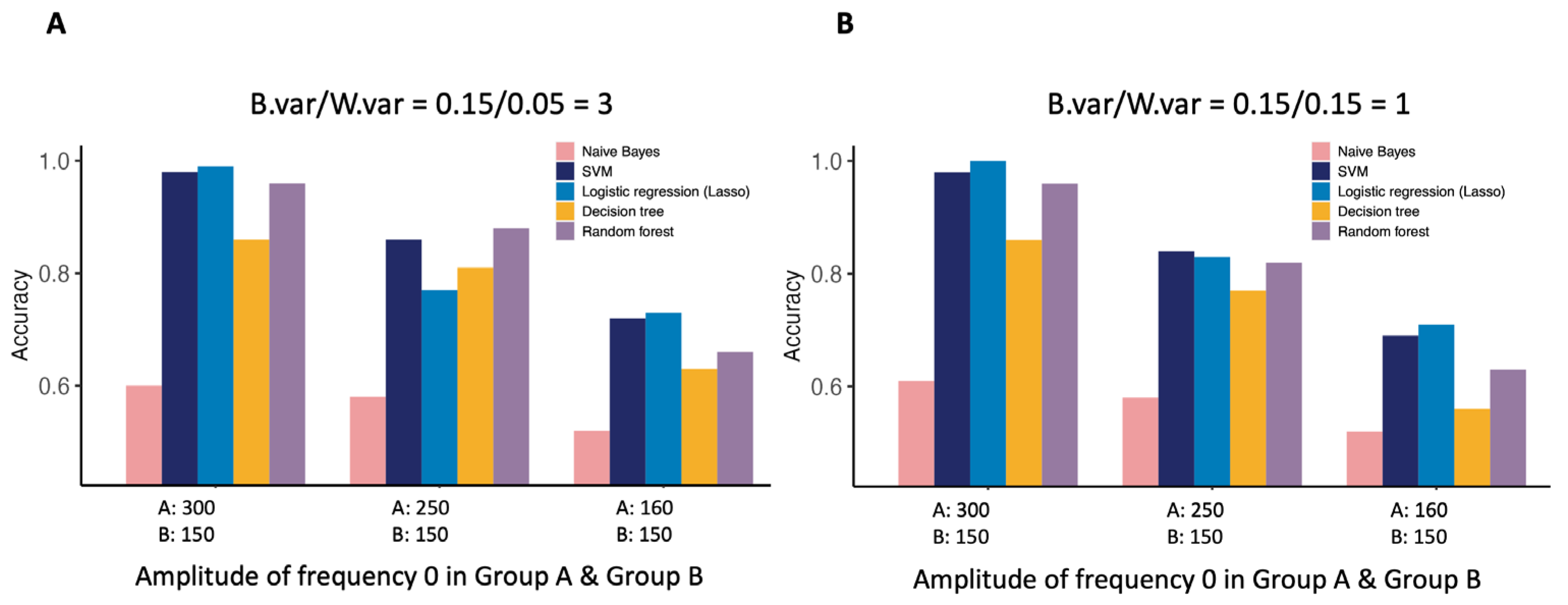
3.4. DFT Variables in Simulation Studies for Classification
4. Discussion
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AC | Activity count |
| AI | Activity index |
| BMI | Body Mass Index |
| ENMO | Euclidean Norm Minus One |
| FFT | Fast Fourier transform |
| FPC | Functional Principal Component |
| FPCA | Functional Principal Component Analysis |
| GLMM | Generalized linear mixed-effect model |
| IFFT | Inverse fast Fourier transform |
| IS | Inter-day stability |
| IV | Intra-day variability |
| L5 | The least active 5 h |
| M10 | The most active 10 h |
| PA | Physical activity |
| PrBP | Probable bipolar |
| PrMDD | Probable major depression |
| RA | Relative amplitude |
| RAE | Relative absolute error |
| RAR | Rest-activity rhythm |
| SMOTE | Synthesized minority oversampling technique |
| SPT | The sleep period time |
| SVM | Support vector machine |
| UKB | UK Biobank |
Appendix A
Appendix A.1. Three Motivating Studies
Appendix A.2. Definition of RAE and Expl.var
Appendix A.3. Simulation Settings
Appendix B. Mathematical Framework: Sparse Fourier Approximation Proof
Appendix B.1. Preliminaries
- Fourier Basis Theorem: the set forms an orthogonal basis for Then, any admits the expansionwhere , ,
- Parseval’s Identitywhich states that the total time-domain energy equals the sum of squared Fourier coefficients.
Appendix B.2. Coefficient Decay for Smooth Signals
- Lemma (Coefficient Bound).
- If , then ,
- Main Theorem.
- Let and be the total number of FFT modes. Let be the proportion of the selected FFT modes and . Define the truncated sum keeping only modes from both ends:Then, .
- (1)
- Parseval’s Identity:
- (2)
- Apply coefficient bound:
- (3)
- Estimate Tail Sum:
- (4)
- Square Root:
- Remark
References
- Straczkiewicz, M.; James, P.; Onnela, J.P. A systematic review of smartphone-based human activity recognition methods for health research. npj Digit. Med. 2021, 4, 148. [Google Scholar] [CrossRef] [PubMed]
- Babu, M.; Lautman, Z.; Lin, X.; Sobota, M.; Snyder, M. Wearable devices: Implications for precision medicine and the future of health care. Annu. Rev. Med. 2024, 75, 401–415. [Google Scholar] [CrossRef]
- Lee, T.; Chen, C.; Chen, I.; Chen, H.; Liu, C.; Wu, S.; Hsiao, C.K.; Kuo, P.-H. Dynamic bidirectional associations between global positioning system mobility and ecological momentary assessment of mood symptoms in mood disorders: Prospective cohort study. J. Med. Internet Res. 2024, 26, e55635. [Google Scholar] [CrossRef]
- Opoku Asare, K.; Terhorst, Y.; Vega, J.; Peltonen, E.; Lagerspetz, E.; Ferreira, D. Predicting depression from smartphone behavioral markers using machine learning methods, hyperparameter optimization, and feature importance analysis: Exploratory study. JMIR Mhealth Uhealth 2021, 9, e26540. [Google Scholar] [CrossRef]
- Jeganathan, V.S.; Golbus, J.R.; Gupta, K.; Luff, E.; Dempsey, W.; Boyden, T.; Rubenfire, M.; Mukherjee, B.; Klasnja, P.; Kheterpal, S.; et al. Virtual AppLication-supported Environment To INcrease Exercise (VALENTINE) during cardiac rehabilitation study: Rationale and design. Am. Heart J. 2022, 248, 53–62. [Google Scholar] [CrossRef]
- Leroux, A.; Xu, S.; Kundu, P.; Muschelli, J.; Smirnova, E.; Chatterjee, N.; Crainiceanu, C. Quantifying the predictive performance of objectively measured physical activity on mortality in the UK Biobank. J. Gerontol. A Biol. Sci. Med. Sci. 2021, 76, 1486–1494. [Google Scholar] [CrossRef]
- Graham, B.; Farrell, M. Mortality prediction using data from wearable activity trackers and individual characteristics: An explainable artificial intelligence approach. Expert. Syst. Appl. 2025, 267, 126195. [Google Scholar] [CrossRef]
- Boruvka, A.; Almirall, D.; Witkiewitz, K.; Murphy, S.K. Assessing time-varying causal effect moderation in mobile health. J. Am. Stat. Assoc. 2018, 113, 1112–1121. [Google Scholar] [CrossRef] [PubMed]
- NeCamp, T.; Sen, S.; Frank, E.; Walton, M.A.; Ionides, E.L.; Fang, Y.; Tewari, A.; Wu, Z. Assessing real-time moderation for developing adaptive mobile health interventions for medical interns: Micro-randomized trial. J. Med. Internet Res. 2020, 22, e15033. [Google Scholar] [CrossRef]
- Golbus, J.R.; Dempsey, W.; Jackson, E.A.; Nallamothu, B.K.; Klasnja, P. Microrandomized trial design for evaluating just-in-time adaptive interventions through mobile health technologies for cardiovascular disease. Circ. Cardiovasc. Qual. Outcomes 2021, 14, e006760. [Google Scholar] [CrossRef] [PubMed]
- Doherty, A.; Jackson, D.; Hammerla, N.; Plötz, T.; Olivier, P.; Granat, M.H.; White, T.; van Hees, V.T.; Trenell, M.I.; Owen, C.G.; et al. Large scale population assessment of physical activity using wrist worn accelerometers: The UK biobank study. PLoS ONE 2017, 12, e0169649. [Google Scholar] [CrossRef]
- Bai, J.; Di, C.; Xiao, L.; Evenson, K.R.; LaCroix, A.Z.; Crainiceanu, C.M.; Buchner, D.M. An activity index for raw accelerometry data and its comparison with other activity metrics. PLoS ONE 2016, 11, e0160644. [Google Scholar] [CrossRef]
- van Hees, V.T.; Gorzelniak, L.; Dean León, E.C.; Eder, M.; Pias, M.; Taherian, S.; Ekelund, U.; Renström, F.; Franks, P.W.; Horsch, A.; et al. Separating movement and gravity components in an acceleration signal and implications for the assessment of human daily physical activity. PLoS ONE 2013, 8, e61691. [Google Scholar] [CrossRef]
- van Hees, V.T.; Sabia, S.; Jones, S.E.; Wood, A.R.; Anderson, K.N.; Kivimäki, M.; Frayling, T.M.; Pack, A.I.; Bucan, M.; Trenell, M.I.; et al. Estimating sleep parameters using an accelerometer without sleep diary. Sci. Rep. 2018, 8, 12975. [Google Scholar] [CrossRef] [PubMed]
- van Hees, V.T.; Migueles, J.; Fang, Z.; Zhao, J.; Heywood, J.; Mirkes, E.; Sabia, S.; Patterson, M.R.; Pujol, J.C.; Kushleyeva, L.; et al. R Package GGIR: Raw Accelerometer Data Analysis. Version 2.3.0. Available online: https://CRAN.R-project.org/package=GGIR (accessed on 7 June 2023).
- Bai, J.; Goldsmith, J.; Caffo, B.; Glass, T.A.; Crainiceanu, C.M. Movelets: A dictionary of movement. Electron. J. Stat. 2012, 6, 559–578. [Google Scholar] [CrossRef] [PubMed]
- Xue, X.N.; Qi, Q.; Sotres-Alvarez, D.; Roesch, S.C.; Llabre, M.M.; Bainter, S.A.; Mossavar-Rahmani, Y.; Kaplan, R.; Wang, T. Modeling daily and weekly moderate and vigorous physical activity using zero-inflated mixture Poisson distribution. Stat. Med. 2020, 39, 4687–4703. [Google Scholar] [CrossRef]
- Van Someren, E.J.; Swaab, D.F.; Colenda, C.C.; Cohen, W.; McCall, W.V.; Rosenquist, P.B. Bright light therapy: Improved sensitivity to its effects on rest-activity rhythms in Alzheimer patients by application of nonparametric methods. Chronobiol. Int. 1999, 16, 505–518. [Google Scholar] [CrossRef]
- Feng, H.; Yang, L.; Ai, S.; Liu, Y.; Zhang, W.; Lei, B.; Chen, J.; Liu, Y.; Chan, J.W.Y.; Chan, N.Y.; et al. Association between accelerometer-measured amplitude of rest-activity rhythm and future health risk: A prospective cohort study of the UK Biobank. Lancet Healthy Longev. 2023, 4, e200–e210. [Google Scholar] [CrossRef]
- Rykov, Y.; Thach, T.Q.; Bojic, I.; Christopoulos, G.; Car, J. Digital biomarkers for depression screening with wearable devices: Cross-sectional study with machine learning modeling. JMIR Mhealth Uhealth 2021, 9, e24872. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Li, H.; Keadle, S.K.; Matthews, C.E.; Carroll, R.J. A review of statistical analyses on physical activity data collected from accelerometers. Stat. Biosci. 2019, 11, 465–476. [Google Scholar] [CrossRef]
- Ashraf, M.; Anowar, F.; Setu, J.H.; Chowdhury, A.I.; Ahmed, E.; Islam, A.; Al-Mamun, A. A survey on dimensionality reduction techniques for time-series data. IEEE Access 2023, 11, 42909–42923. [Google Scholar] [CrossRef]
- Sharma, A.; Purwar, A.; Lee, Y.D.; Lee, Y.S.; Chung, W.Y. Frequency based classification of activities using accelerometer data. In Proceedings of the 2008 IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems, Seoul, Republic of Korea, 20–22 August 2008; IEEE: New York, NY, USA, 2008. [Google Scholar]
- Cochran, W.T.; Cooley, J.W.; Favin, D.L.; Helms, H.D.; Kaenel, R.A.; Lang, W.W.; Maling, G.C.; Nelson, D.E.; Rader, C.M.; Welch, P.D. What is the fast Fourier transform? Proc. IEEE 1967, 55, 1664–1674. [Google Scholar] [CrossRef]
- Vähä-Ypyä, H.; Vasankari, T.; Husu, P.; Suni, J.; Sievänen, H. A universal, accurate intensity-based classification of different physical activities using raw data of accelerometer. Clin. Physiol. Funct. Imaging 2015, 35, 64–70. [Google Scholar] [CrossRef] [PubMed]
- Belcher, B.R.; Berrigan, D.; Dodd, K.W.; Emken, B.A.; Chou, C.P.; Spruijt-Metz, D. Physical activity in US youth: Impact of race/ethnicity, age, gender, & weight status. Med. Sci. Sports Exerc. 2010, 42, 2211–2221. [Google Scholar] [CrossRef]
- Garcia-Ceja, E.; Riegler, M.; Jakobsen, P.; Tørresen, J.; Nordgreen, T.; Oedegaard, K.J.; Fasmer, O.B. Depresjon: A motor activity database of depression episodes in unipolar and bipolar patients. In Proceedings of the 9th ACM Multimedia Systems Conference, Amsterdam, The Netherlands, 12–15 June 2018. [Google Scholar]
- Jakobsen, P.; Garcia-Ceja, E.; Stabell, L.A.; Oedegaard, K.J.; Berle, J.O.; Thambawita, V.; Hicks, S.A.; Halvorsen, P.; Fasmer, O.B.; Riegler, M.A. Psykose: A motor activity database of patients with schizophrenia. In Proceedings of the 2020 IEEE 33rd International Symposium on Computer-Based Medical Systems, Rochester, MN, USA, 28–30 July 2020. [Google Scholar]
- Bhatia, R. Convergence in L2 and L1. In Fourier Series; American Mathematical Society/MAA Press: Washington, DC, USA, 2005; Chapter 4. [Google Scholar] [CrossRef]
- Ramsay, J.O.; Silverman, B.W. Functional Data Analysis; Springer: New York, NY, USA, 2005. [Google Scholar]
- Black, M.; Brunet, J. Exploring the effect of an eHealth intervention on women’s physical activity: Design and rationale for a randomized controlled trial. Digit. Health 2022, 8, 20552076221093134. [Google Scholar] [CrossRef]
- Ramirez, V.; Shokri-Kojori, E.; Cabrera, E.A.; Wiers, C.E.; Merikangas, K.; Tomasi, D.; Wang, G.-J.; Volkow, N.D. Physical activity measured with wrist and ankle accelerometers: Age, gender, and BMI effects. PLoS ONE 2018, 13, e0195996. [Google Scholar] [CrossRef]
- Li, X.; Zhang, Y.; Jiang, F.; Zhao, H. A novel machine learning unsupervised algorithm for sleep/wake identification using actigraphy. Chronobiol. Int. 2020, 37, 1002–1015. [Google Scholar] [CrossRef] [PubMed]
- Ogbagaber, S.B.; Cui, Y.; Li, K.; Iannotti, R.J.; Albert, P.S. A hidden Markov modeling approach combining objective measure of activity and subjective measure of self-reported sleep to estimate the sleep-wake cycle. J. Appl. Stat. 2022, 51, 370–387. [Google Scholar] [CrossRef]
- Migueles, J.H.; Rowlands, A.V.; Huber, F.; Sabia, S.; van Hees, V.T. GGIR: A research community–driven open source R package for generating physical activity and sleep outcomes from multi-day raw accelerometer data. J. Meas. Phys. Behav. 2019, 2, 188–196. [Google Scholar] [CrossRef]
- Su, C.H. An Exploratory Analysis of Sleep and Activity Variables from Wearable Device in UK Biobank Study. Master’s thesis, National Taiwan University, Taipei, Taiwan, 2022.
- Smith, D.J.; Nicholl, B.I.; Cullen, B.; Martin, D.; Ul-Haq, Z.; Evans, J.; Gill, J.M.R.; Roberts, B.; Gallacher, J.; Mackay, D.; et al. Prevalence and characteristics of probable major depression and bipolar disorder within UK biobank: Cross-sectional study of 172,751 participants. PLoS ONE 2013, 8, e75362. [Google Scholar] [CrossRef] [PubMed]
- Berle, J.O.; Hauge, E.R.; Oedegaard, K.J.; Holsten, F.; Fasmer, O.B. Actigraphic registration of motor activity reveals a more structured behavioural pattern in schizophrenia than in major depression. BMC Res. Notes 2010, 3, 149. [Google Scholar] [CrossRef] [PubMed]
- Jakobsen, P.; Garcia-Ceja, E.; Riegler, M.; Stabell, L.A.; Nordgreen, T.; Torresen, J.; Fasmer, O.B.; Oedegaard, K.J. Applying machine learning in motor activity time series of depressed bipolar and unipolar patients compared to healthy controls. PLoS ONE 2020, 15, e0231995. [Google Scholar] [CrossRef] [PubMed]
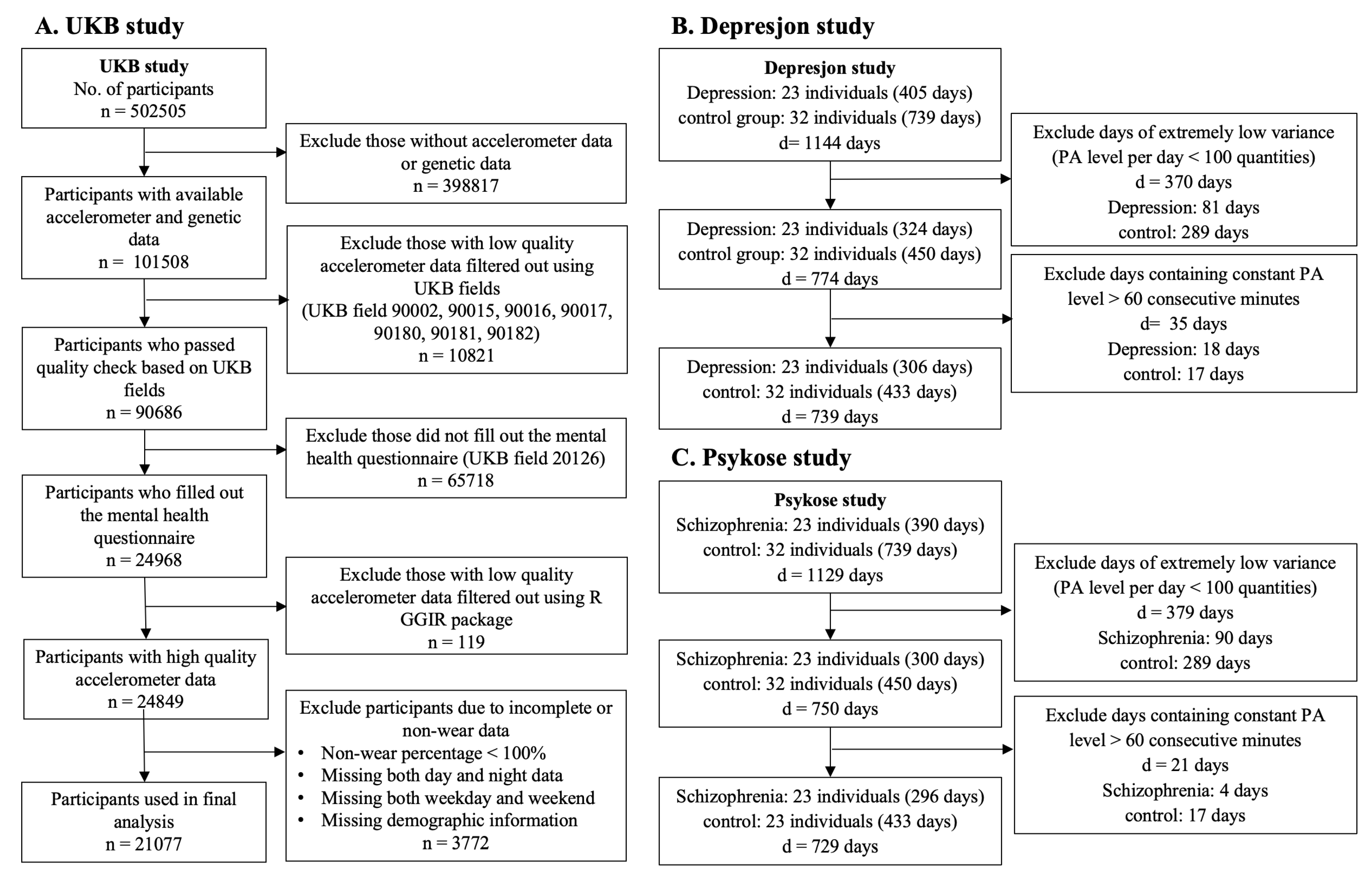



| UK Biobank | Psykose | Depresjon | |
|---|---|---|---|
| Sample size | 21,077 | 54 | 55 |
| Age range | 40~70 | 21~69 | 21~69 |
| Sex F:M | 11,500:9577 | 23:31 | 30:25 |
| Wearable device | Axivity Ax3 | Actiwatch AW4 | Actiwatch AW4 |
| Sampling frequency | 100 Hz | 32 Hz | 32 Hz |
| Metric of PA level | ENMO | Activity count | Activity count |
| Range of PA level | 0~8 g | 0~8 | 0~8 |
| No. of observations per day for analysis | 17,280 | 1440 | 1440 |
| No. of available days per individual | 2~6 | 6~21 | 9~21 |
| Accuracy | Sensitivity | Specificity | F1 Score | |
|---|---|---|---|---|
| Baseline model (demographic information) | ||||
| Naive Bayes | 0.72 (0.013) | 0.61 (0.035) | 0.80 (0.035) | 0.64 (0.016) |
| SVM | 0.72 (0.013) | 0.61 (0.035) | 0.80 (0.035) | 0.64 (0.016) |
| Logistic regression (Lasso) | 0.72 (0.013) | 0.61 (0.035) | 0.80 (0.035) | 0.64 (0.016) |
| Decision tree (C5.0) | 0.72 (0.013) | 0.64 (0.047) | 0.78 (0.041) | 0.64 (0.016) |
| Random forest | 0.72 (0.013) | 0.61 (0.035) | 0.80 (0.035) | 0.64 (0.016) |
| Baseline model + RAR Variables (L5, M10, RA, IV) | ||||
| Naive Bayes | 0.81 (0.006) | 0.71 (0.013) | 0.88 (0.006) | 0.75 (0.009) |
| SVM | 0.84 (0.006) | 0.74 (0.013) | 0.91 (0.009) | 0.79 (0.006) |
| Logistic regression (Lasso) | 0.81 (0.006) | 0.77 (0.013) | 0.84 (0.013) | 0.77 (0.006) |
| Decision tree (C5.0) | 0.82 (0.006) | 0.75 (0.019) | 0.87 (0.009) | 0.77 (0.013) |
| Random forest | 0.85 (0.006) | 0.80 (0.009) | 0.88 (0.013) | 0.82 (0.009) |
| Baseline model + FPCA Variables (FPC1–11 score) | ||||
| Naive Bayes | 0.80 (0.012) | 0.85 (0.011) | 0.77 (0.015) | 0.78 (0.016) |
| SVM | 0.91 (0.006) | 0.91 (0.011) | 0.91 (0.006) | 0.89 (0.008) |
| Logistic regression (Lasso) | 0.87 (0.005) | 0.86 (0.012) | 0.88 (0.007) | 0.85 (0.007) |
| Decision tree (C5.0) | 0.83 (0.006) | 0.81 (0.015) | 0.86 (0.014) | 0.80 (0.007) |
| Random forest | 0.87 (0.008) | 0.87 (0.014) | 0.89 (0.009) | 0.85 (0.008) |
| Baseline model + DFT variables (amplitudes of frequency 0–14) | ||||
| Naive Bayes | 0.81 (0.006) | 0.79 (0.013) | 0.82 (0.009) | 0.77 (0.013) |
| SVM | 0.85 (0.006) | 0.81 (0.009) | 0.87 (0.006) | 0.81 (0.009) |
| Logistic regression (Lasso) | 0.85 (0.003) | 0.81 (0.006) | 0.88 (0.006) | 0.82 (0.006) |
| Decision tree (C5.0) | 0.82 (0.006) | 0.74 (0.013) | 0.87 (0.013) | 0.77 (0.013) |
| Random forest | 0.87 (0.009) | 0.80 (0.016) | 0.92 (0.009) | 0.84 (0.016) |
| Baseline model + RAR Variables (L5, M10, RA, IV) + DFT variables (amplitudes of frequency 0–14) | ||||
| Naive Bayes | 0.81 (0.009) | 0.79 (0.016) | 0.82 (0.009) | 0.78 (0.013) |
| SVM | 0.84 (0.006) | 0.79 (0.013) | 0.88 (0.006) | 0.80 (0.009) |
| Logistic regression (Lasso) | 0.85 (0.006) | 0.81 (0.013) | 0.88 (0.006) | 0.82 (0.009) |
| Decision tree (C5.0) | 0.81 (0.006) | 0.74 (0.013) | 0.87 (0.013) | 0.76 (0.009) |
| Random forest | 0.87 (0.009) | 0.80 (0.016) | 0.92 (0.009) | 0.84 (0.013) |
| Baseline model + FPCA Variables (FPC1–11 score) + DFT variables (amplitudes of frequency 0–14) | ||||
| Naive Bayes | 0.81 (0.009) | 0.82 (0.014) | 0.81 (0.010) | 0.78 (0.013) |
| SVM | 0.91 (0.006) | 0.90 (0.009) | 0.92 (0.006) | 0.89 (0.008) |
| Logistic regression (Lasso) | 0.89 (0.007) | 0.88 (0.014) | 0.90 (0.007) | 0.87 (0.009) |
| Decision tree (C5.0) | 0.85 (0.009) | 0.82 (0.013) | 0.88 (0.014) | 0.82 (0.011) |
| Random forest | 0.89 (0.011) | 0.84 (0.022) | 0.92 (0.009) | 0.86 (0.017) |
| Accuracy | Sensitivity | Specificity | F1 Score | |
|---|---|---|---|---|
| Baseline model (demographic information) | ||||
| Naive Bayes | 0.52 (0.001) | 0.54 (0.003) | 0.50 (0.003) | 0.53 (0.001) |
| SVM | 0.52 (0.001) | 0.63 (0.001) | 0.41 (0.001) | 0.57 (0.001) |
| Logistic regression (Lasso) | 0.52 (0.001) | 0.52 (0.032) | 0.52 (0.031) | 0.51 (0.022) |
| Decision tree | 0.52 (0.001) | 0.63 (0.001) | 0.41 (0.001) | 0.57 (0.001) |
| Random forest | 0.52 (0.001) | 0.59 (0.027) | 0.45 (0.026) | 0.55 (0.014) |
| Baseline model + RAR Variables (L5, M10, RA, IV) | ||||
| Naive Bayes | 0.53 (0.001) | 0.77 (0.002) | 0.29 (0.003) | 0.62 (0.001) |
| SVM | 0.56 (0.001) | 0.58 (0.005) | 0.53 (0.003) | 0.57 (0.002) |
| Logistic regression (Lasso) | 0.53 (0.001) | 0.52 (0.019) | 0.54 (0.018) | 0.52 (0.010) |
| Decision tree (C5.0) | 0.55 (0.001) | 0.58 (0.014) | 0.52 (0.001) | 0.57 (0.007) |
| Random forest | 0.56 (0.001) | 0.63 (0.006) | 0.50 (0.008) | 0.59 (0.002) |
| Baseline model + FPCA Variables (FPC1–11 score) | ||||
| Naive Bayes | 0.53 (0.001) | 0.84 (0.001) | 0.22 (0.001) | 0.64 (0.001) |
| SVM | 0.58 (0.001) | 0.66 (0.003) | 0.50 (0.003) | 0.61 (0.001) |
| Logistic regression (Lasso) | 0.54 (0.001) | 0.56 (0.009) | 0.52 (0.008) | 0.55 (0.004) |
| Decision tree (C5.0) | 0.58 (0.002) | 0.70 (0.026) | 0.46 (0.031) | 0.62 (0.008) |
| Random forest | 0.78 (0.001) | 0.78 (0.001) | 0.78 (0.001) | 0.78 (0.001) |
| Baseline model + DFT variables (amplitudes of frequency 0–172) | ||||
| Naive Bayes | 0.54 (0.011) | 0.83 (0.001) | 0.26 (0.001) | 0.65 (0.001) |
| SVM | 0.75 (0.001) | 0.68 (0.001) | 0.82 (0.001) | 0.73 (0.001) |
| Logistic regression (Lasso) | 0.55 (0.001) | 0.58 (0.013) | 0.53 (0.014) | 0.56 (0.005) |
| Decision tree (C5.0) | 0.81 (0.001) | 0.74 (0.001) | 0.88 (0.001) | 0.79 (0.001) |
| Random forest | 0.84 (0.001) | 0.76 (0.001) | 0.93 (0.001) | 0.83 (0.001) |
| Baseline model + RAR Variables (L5, M10, RA, IV) + DFT variables (amplitudes of frequency 0–172) | ||||
| Naive Bayes | 0.55 (0.001) | 0.83 (0.001) | 0.26 (0.001) | 0.65 (0.001) |
| Logistic regression (Lasso) | 0.55 (0.001) | 0.59 (0.013) | 0.52 (0.013) | 0.57 (0.006) |
| SVM | 0.75 (0.001) | 0.68 (0.001) | 0.82 (0.001) | 0.73 (0.001) |
| Decision tree (C5.0) | 0.81 (0.001) | 0.74 (0.001) | 0.88 (0.001) | 0.79 (0.001) |
| Random forest | 0.85 (0.002) | 0.76 (0.001) | 0.94 (0.003) | 0.83 (0.001) |
| Baseline model + FPCA Variables (FPC1–11 score) + DFT variables (amplitudes of frequency 0–172) | ||||
| Naive Bayes | 0.55 (0.001) | 0.83 (0.001) | 0.26 (0.001) | 0.65 (0.001) |
| SVM | 0.75 (0.001) | 0.68 (0.001) | 0.82 (0.001) | 0.73 (0.001) |
| Logistic regression (Lasso) | 0.55 (0.001) | 0.53 (0.018) | 0.58 (0.018) | 0.54 (0.009) |
| Decision tree (C5.0) | 0.76 (0.001) | 0.74 (0.002) | 0.78 (0.001) | 0.75 (0.001) |
| Random forest | 0.84 (0.001) | 0.76 (0.002) | 0.93 (0.001) | 0.83 (0.001) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, Y.-T.; Hsiao, C.K.; Chattopadhyay, A.; Lu, T.-P.; Kuo, P.-H.; Wang, C. A Methodological Framework for Analyzing and Differentiating Daily Physical Activity Across Groups Using Digital Biomarkers from the Frequency Domain. Mathematics 2025, 13, 3616. https://doi.org/10.3390/math13223616
Liang Y-T, Hsiao CK, Chattopadhyay A, Lu T-P, Kuo P-H, Wang C. A Methodological Framework for Analyzing and Differentiating Daily Physical Activity Across Groups Using Digital Biomarkers from the Frequency Domain. Mathematics. 2025; 13(22):3616. https://doi.org/10.3390/math13223616
Chicago/Turabian StyleLiang, Ya-Ting, Chuhsing Kate Hsiao, Amrita Chattopadhyay, Tzu-Pin Lu, Po-Hsiu Kuo, and Charlotte Wang. 2025. "A Methodological Framework for Analyzing and Differentiating Daily Physical Activity Across Groups Using Digital Biomarkers from the Frequency Domain" Mathematics 13, no. 22: 3616. https://doi.org/10.3390/math13223616
APA StyleLiang, Y.-T., Hsiao, C. K., Chattopadhyay, A., Lu, T.-P., Kuo, P.-H., & Wang, C. (2025). A Methodological Framework for Analyzing and Differentiating Daily Physical Activity Across Groups Using Digital Biomarkers from the Frequency Domain. Mathematics, 13(22), 3616. https://doi.org/10.3390/math13223616







