Can the Collateral Value of a Data Asset Be Increased by Insurance?

Abstract

As an emerging production factor, data assets are gaining strategic prominence, yet their application in collateralized financing faces persistent challenges, including illiquidity and risk evaluation complexities. This study introduces an innovative $P_{max}$ model to enhance the Collateral Value of data assets through insurance mechanisms, systematically demonstrating the feasibility conditions under which risk transfer optimizes asset valuation and delineating implementation pathways to integrate data insurance with asset-backed financing. Building on the theoretical framework of Value-at-Risk (VaR), this study develops a dynamic valuation model to assess the value of the collateral before and after insurance. Our analysis shows that insurance coverage for potential losses significantly enhances financing viability when premiums satisfy $P_{max}$. Empirical analysis employing Monte Carlo simulations reveals a nonlinear positive correlation between pledgees’ risk tolerance thresholds and the maximum acceptable premium $P_{max}$. This study bridges theoretical gaps in understanding insurance-value relationships for data assets while providing conceptual foundations and operational blueprints to standardize data markets and foster financial innovation.

1. Background and Problem

As a crucial strategic resource in the digital economy era, the potential in value of data is being unleashed in the process of iterative technological upgrades. Through its profound permeation in circulation and transaction ecosystems, data have transcended the value boundaries of traditional production factors. Its value configuration is undergoing a paradigmatic transition from fundamental resource to strategic assets with transformative significance, progressively evolving into the central dynamic driving systemic reconstruction of social production.

In the digital economy era, data have been strategically positioned as a “new factor of production” and have emerged as a core driver of economic development. Its recognition as a distinct asset class has gained substantial traction within both academic and industrial domains. The 2023 White Paper on Data Asset Management Practice (Version 6.0), published by the China Academy of Information and Communications Technology (CAICT), has formally operationalized technical criteria for data asset management. This authoritative framework underscores that data assets must exhibit defining attributes, including electronic traceability, transactional measurability, capacity to generate socioeconomic value, and unambiguous ownership. Concurrently, the 2023 Guidelines for Data Asset Valuation issued by the China Appraisal Society (CAS) codify data assets as legally owned or controlled data resources that are monetarily quantifiable and capable of delivering direct or indirect economic benefits to identifiable entities.

Tracing the academic lineage, Ref. [1] was the first to systematically propose the concept of “data assets” in academia, defining them as “various types of digital media with usage rights and encoded in binary form.” This definition broke through the functional boundaries of traditional information carriers, elevating data from a technical resource to an asset category for the first time. It emphasized the core features of usage rights and digital encoding, thereby laying the foundation for subsequent theoretical research and industrial practice in data assets. From an information management perspective, Ref. [2] constructed a demand-oriented dynamic assetization model, emphasizing that only data units meeting specific needs can be transformed into assets and that the scale of assets exhibits elasticity with demand fluctuations. The report of [3] demonstrates the productive asset attributes of data from a macroeconomic perspective and proposes pathways for data capitalization. These theoretical developments indicate that data assets not only carry information value, but are also deeply embedded in the social production system in the form of resources and factors of production, demonstrating unique strategic value.

In the academic exploration of data asset valuation methodologies, scholars have developed diverse systematic approaches to assess economic worth. The income approach estimates the present value of future earnings generated by data assets using a reasonable discount rate. The cost approach accounts for process-related expenses, including data collation and maintenance costs. The market approach bases the discounted value on premiums paid by specific business partners. Notably, many studies measure the value of data assets from the perspective of value loss. Ref. [4] discussed the protection of data assets in the context of the digital economy, emphasizing the maximum potential loss of assets within a specific time frame. Ref. [5] discussed how the rise of the data economy is changing the nature of income sources and risks, analyzing how to measure data as an intangible asset from the perspectives of value and risk.

It is worth noting that risk factors constitute a critical dimension that cannot be overlooked in the valuation of data assets. Based on the theory of intangible assets, Ref. [6] explored the valuation and pricing of data assets for internet platform enterprises, with particular emphasis on the impact of risk and uncertainty on data value. Ref. [7] constructed a three-dimensional value valuation model of “development–application–risk” for enterprise data assets based on the concept of data potential and the entire data life cycle, enabling a more comprehensive value assessment. This shows that considering the risks of data assets can significantly improve the accuracy and comprehensiveness of data asset value assessment.

Accurately identifying and scientifically classifying the risks of data assets are crucial prerequisites for building effective risk management mechanisms and achieving reasonable pricing of data assets. By systematically clarifying the sources of risk and their impact mechanisms, it is possible not only to optimize resource allocation efficiency and enhance the utilization and market competitiveness of data assets, but also to comprehensively safeguard and enhance the intrinsic value of data assets. Existing literature on data asset risk mainly focuses on dimensions such as data security risk and liability risk.

In terms of data security risks, Ref. [8] pointed out that data security issues mainly stem from external attacks and internal threats, permeating every stage of data collection, storage, and processing. Ref. [9] proposed that enterprise IT data security mainly faces four core risks: data security, privacy protection, system reliability, and storage security. Ref. [10] analyzed the impact of data breaches on corporate value, revealing that secondary breaches cause greater harm, financial information leaks are the most severe, and replacing the CEO after the first violation can prevent future losses.

At the level of liability risk, Ref. [11] pointed out that while anonymization techniques (such as k-anonymity) are widely used for privacy protection in medical big data, their potential re-identification risks (e.g., through linkage attacks using external data) may lead to sensitive information disclosure, thereby resulting in legal compliance responsibilities and ethical risks. Ref. [12] discussed big technology and data privacy. Ref. [13] highlighted that predictive analytics using big data and AI, which infer sensitive attributes (e.g., health, ethnicity, income) by linking individual behavioral data to anonymized datasets, creates liability risks if such predictions result in privacy breaches or unauthorized disclosures about third parties.

As the market value of data assets as a new production factor becomes increasingly prominent, managing related risks has become a focus of industry attention. Drawing on mature models such as cyber insurance [14,15,16], intellectual property insurance [17,18] and technology transformation insurance, data asset insurance has entered the stage of practical exploration as an innovative risk management tool. This trend not only reflects the recognition of data assets as insurable objects but also highlights the real market demand for risk hedging mechanisms for data elements.

On the other hand, the financial attributes of data assets mean they can be used as collateral to help enterprises obtain funding. Ref. [19] proposed a data valuation model to enable companies to use data assets as collateral for loans in financial transactions. Ref. [20] reported focuses on the mechanisms through which digital assets (such as tokenized bonds, securities, and funds) optimize financing processes and enhance credit trust via Distributed Ledger Technology (DLT).

It is generally believed that by introducing data asset insurance, enterprises can demonstrate to financial institutions that their data assets are effectively protected, thereby reducing the risk assessment of pledge financing. Data asset insurance can not only enhance the market recognition of data assets as collateral, but also, through risk transfer and guarantee mechanisms, significantly improve the operability and security of data asset pledge financing. This provides strong support for activating enterprise data assets and broadening financing channels, while also promoting the healthy development of the data element market.

In financial market risk research, the VaR (Value at Risk) model is widely used to assess and quantify market risk.VaR emerged from the need for a single, comprehensible metric to capture market risk, famously endorsed by J.P. Morgan’s RiskMetrics system [21]. Mathematically, for a random loss variable L and a confidence level $\alpha$, ${\mathrm{VaR}}_{\alpha }\left(L\right)$ is the $\alpha$-quantile of the loss distribution. The link to insurance was established formally in the economic decision-theoretic literature. In the seminal work on premium principles, Ref. [22] laid the groundwork for considering upper-tail risks. This was later advanced by [23], who explicitly defined a mean-shortfall criterion. From this perspective, a risk measure focusing on a quantile naturally leads to an insurance contract with a deductible at that quantile. An insurance policy that indemnifies the loss ${(L-{\mathrm{VaR}}_{\alpha }\left(L\right))}_{+}$ is a quantile insurance contract. The insured retains all losses below the $\alpha$-quantile while transferring the tail risk to the insurer. Therefore, VaR is not merely a risk measure; it also serves as the contractual trigger point for a class of optimal insurance contracts. Given the beneficial role of VaR theory in risk management, it has also been widely applied in various specific fields. In the field of railway hazardous materials transportation, Ref. [24] proposed a method based on the VaR model, aiming to minimize the risks of railway hazardous materials transportation by optimizing train configurations. Ref. [25] incorporated weather factors into the VaR model in their research, validating it through historical data and the bootstrap method, thereby offering a new perspective for derivative valuation. The integration of the VaR model with other methods has demonstrated significant advantages in financial market risk management. It not only enhances the precision and flexibility of risk management but also provides robust support for enterprises in navigating complex market environments.

Based on this, our study innovatively evaluates data assets from a risk measurement perspective. We classify data asset risks into three stages: holding, operation, and value-added. Furthermore, we propose a $P_{max}$ model for enhancing the pledged value of data assets through insurance. By introducing the VaR method, this study systematically examines the changes in the pledged value of data assets before and after insurance, clarifying the specific pathways and conditions under which insurance can enhance the market value of data assets by reducing risk and strengthening financing capability. This opens up new ideas for data asset appreciation and market application. The research in this paper not only fills the gap in existing studies on the relationship between data asset insurance and value but also provides theoretical support and practical guidance for data asset pledge financing, promoting the healthy development of the data element market.

The remainder of this paper is organized as follows. Section 2 develops a risk-based valuation framework for data assets, in which risks are classified according to the stages of holding, operation, and value addition. Section 3 presents the theoretical $P_{max}$ model, establishing the feasibility conditions under which insurance arrangements can raise collateral value. This section also examines the standard deviation premium principle within the same framework. Section 4 offers a numerical illustration based on Monte Carlo simulation, which verifies the $P_{max}$ model and explores how risk tolerance influences both the maximum acceptable premium and the corresponding increase in collateral value. The paper concludes with Section 5, which summarizes key findings and discusses their broader implications.

2. Risk-Based Valuation of Data Assets

2.1. Data Assets and Risks

From a mathematical perspective, data assets can be conceptually identified as the totality of their future returns and losses (assuming discounting where appropriate), so that a data asset can be typically represented by $X=U-L$, where $U\ge 0$ is the totality of its returns and $L\ge 0$ the totality of its losses. Since these returns and losses are subject to stochastic and uncertain factors—such as market conditions and technological failures—the values of data assets are treated as random variables. We would like to note that, clearly, U and L can be and are not necessarily the positive part $X_{+}=max\{X,0\}$ and negative part $X_{-}=-min\{X,0\}$ of X extensively referred to in mathematics. For example, if U and L are supposed statistically independent and following exponential distributions $\mathrm{Exp}\left({\lambda }_U\right)$ with density ${\lambda }_U{e}^{-{\lambda }_{U}x}(x>0)$ and $\mathrm{Exp}\left({\lambda }_L\right)$ with density ${\lambda }_L{e}^{-{\lambda }_{L}x}(x>0)$, then X follows an asymmetric Laplace distribution with density ${\displaystyle \frac{{\lambda }_U{\lambda }_L}{{\lambda }_U+{\lambda }_L}}\left\{\begin{array}{cc}{e}^{-{\lambda }_{U}x},\hfill & x\ge 0\hfill \\ e^{-{\lambda }_{L}x},\hfill & x<0\hfill \end{array}\right.$. Thus $X_{+}$ is distributed as: $Pr(X_{+}=0)={\displaystyle \frac{{\lambda }_U}{{\lambda }_U+{\lambda }_L}}$ and $X_{+}$ has density ${\displaystyle \frac{{\lambda }_U{\lambda }_L}{{\lambda }_U+{\lambda }_L}}{e}^{-{\lambda }_{U}x}$ when $x>0$, so that U is absolutely different from $X_{+}$ in distribution.

The sources of risk-related losses are diverse. Specifically, these losses can be categorized diversely in different stages within the data asset lifecycle: holding, operation, and value-addition. This classification not only enables more precise identification and management of stage-specific risks, but also provides a solid theoretical basis for risk quantification and value assessment.

During the holding stage, risks primarily take the form of data leakage or damage. Although data assets at this stage have not yet entered active use or transaction, and thus exert only a minor direct impact on value realization, such losses are typically permanent, jeopardizing the integrity and availability of the data.

The operational stage is characterized by potential risks arising from the circulation and use of data assets, such as data breaches, legal compliance issues, or credit risks. In this stage, as data assets are leveraged to deliver products or services, their economic value and operational effectiveness become directly apparent. The risks encountered here tend to correlate strongly with asset value, and the resulting losses are often considered general losses within the insurance industry.

Risks encountered during the value-addition stage often stem from issues like legal liabilities emerging in the course of data product development. This stage is pivotal for generating further economic value through the development and utilization of data assets. Risks at this stage are most closely correlated with asset value and can substantially constrain value creation, frequently resulting in significant potential losses.

For an illustrative breakdown, see

Table 1. Categories of Data Asset Risks.

	Holding Data Assets	Operating Data Assets	Value-Addition of Data Assets
Type of Risk	Fundamental Risk	Operational Risk	Incremental Risk
Correlation with Asset Value	Low Relatively	High	High
Form of Loss	Permanent Loss	General Loss	Potential Loss

below:

2.2. Risk-Based Valuation of Data Assets

From an operational perspective, data asset valuation has typically employed market-based model, economic models and dimensional models [26]. However, from a theoretical standpoint, data asset valuation fundamentally represents a risk measurement exercise because, as established earlier, a data asset can be conceptualized as a random variable encompassing the totality of its future returns and losses. Consequently, as a standard practice in risk management, the determined value depends not only on the distribution of these returns and losses (appropriately discounted), but also critically on the valuator’s specific purposes. This implies that the same data asset may yield different valuations based on the assessment purpose.

When considering the perspective of a pledgee (such as a financial institution), the primary purpose of valuation is to establish appropriate credit limits for the asset holder. For the pledgee, this valuation can be formalized as: determining the maximum of the deterministic quantities $v\ge 0$ such that $Pr(X\le v)\le \alpha$, i.e.,

$$V=max\{v\ge 0:Pr(X\le v)\le \alpha \}=F_X^{-1}\left(\alpha \right),$$

(1)

where in (1), $\alpha$ represents a small predetermined risk threshold of the pledgee, typically 5% or 1%, and $F_X$ is the distribution function of random variable X. The value V (referred to as collateral value) ensures that the probability of the data asset X falling below V does not exceed $\alpha$. Expressed differently, if a bank extends credit V against the data asset, the probability of the asset’s return dropping below this credit amount (potentially triggering insolvency) remains bounded by the predefined risk level $\alpha$. Clearly, if $Pr(X\le 0)>\alpha$, then the data asset X is not valuable at the risk level $\alpha$ in the pledgee’s perspective. Different risk thresholds typically lead to different values of a same data asset.

From an insurer’s perspective, the analytical focus shifts to potential losses. As aforementioned, an asset is represented as $X=U-L$, where $U\ge 0$ and $L\ge 0$ represent respectively the future random return and random loss of asset X and an insurer is not concerned with the whole data asset X itself but possibly a part $L_I$ of the loss L such that $L_I\le L$. $L_I$ will be referred to as insured loss. The insurer valuates the data asset’s risk profile L (if $Pr(L=0)<1$) to determine an appropriate underwriting premium. The objective becomes: for a given risk threshold $\beta$, identify the minimum of the numbers $v\ge 0$ such that $Pr(L\le v)\ge 1-\beta$, i.e.,

$$p=min\{v\ge 0:Pr(L\le v)\ge 1-\beta \}.$$

(2)

In words, the insurer seeks to ensure that the probability of losses not exceeding p is at least $1-\beta$. The value p can be understood as the value of the data asset X in the insurer’s perspective.

The valuation methodology above corresponds to the VaR approach widely employed in risk management. As demonstrated, banks and insurers arrive at distinct valuation assessments (V and p respectively) for the same data asset due to their fundamentally different purposes. This valuation differential creates the economic basis for insurance instruments to enhance the collateral value of data assets in secured financing arrangements.

3. Increasing Collateral Value of Data Assets Through Insurance

Let X denote a data asset (discounted if necessary), where X is a real-valued random variable and can take either positive or negative values (a profit is positive, a loss is negative). Obviously, a data asset that takes positive values with probability 1 does not require insurance, and a random variable that takes negative values with probability 1 has no collateral value. Therefore, this study only focuses on data assets where the probabilities of taking positive and negative values are both nonzero.

As discussed in Section 2, the data assets are valuated within the VaR risk measurement framework. VaR is based on the definition of loss. The VaR at a threshold $\alpha \in (0,1)$ is the minimal number y such that the probability of the loss $Y:=-X$ not exceeding y is at least $(1-\alpha )$. Mathematically, ${\mathrm{VaR}}_{\alpha }\left(X\right)$ is the $(1-\alpha )$ quantile of Y, that is,

$${\mathrm{VaR}}_{\alpha }\left(X\right)=F_Y^{-1}(1-\alpha )=-sup\{x\in \mathcal{R}:F_X\left(x\right)\le \alpha \},$$

(3)

where $F_X\left(x\right)=Pr(X\le x)$ is the probability distribution function of X. This is the general definition of VaR, and these two expressions are equivalent.

From the insurer’s perspective, using VaR to assess the value of a data asset is equivalent to the quantile premium principle. That is, for a given confidence level $\alpha$, the premium p for a risk or loss L is set as the minimal y such that the probability of L exceeding y does not exceed $\alpha$. This means that an insurer, according to their risk tolerance (indicated by $\alpha$), determines a premium level that covers loss in most cases (with probability $1-\alpha$). Mathematically, for $0<\alpha <1$, p is the solution to $F_L\left(p\right)=1-\alpha$ or $Pr\{L>p\}=\alpha$, and can be denoted as $p=F_L^{-1}(1-\alpha )$.

3.1. Insurance and Collateral Value Based on VaR Measurement

As mentioned above, from the perspective of the insurer, according to the premium pricing principle based on VaR,

$$p=F_L^{-1}(1-\alpha )\mathrm{or}Pr(L>p)=\alpha ,$$

(4)

where p is the premium determined by the insurer based on the risk volatility of data assets, and $\alpha$ is the insurer’s risk tolerance. The above formula indicates that the probability of the insured risk loss exceeding the premium equals $\alpha$.

From the perspective of the pledgee, under the VaR principle, the financing collateral value of the data asset X, denoted $V\left(X\right)$, is

$$Pr\left(X\le V\left(X\right)\right)=\beta \mathrm{or}V\left(X\right)=F_X^{-1}\left(\beta \right),$$

(5)

where $\beta$ is the pledgee’s risk tolerance. The formula shows that the probability of the pledgee suffering a loss because the value of the pledged asset X is less than the estimated asset value $V\left(X\right)$ equals $\beta$.

3.2. Changes in Insurance Coverage and the Collateral Value of Data Assets

Assume that X consists of U and the risk loss L, i.e., before insurance, the value of the data asset is

$$X=U-L,$$

(6)

where L is the loss portion of the data asset that is covered by insurance (other uncovered parts are included in U). Before insurance, from the perspective of the pledgee, the financing pledge value of the data asset is

$$V_{\beta }\left(X\right)=F_X^{-1}\left(\beta \right)=F_{U-L}^{-1}\left(\beta \right).$$

(7)

If the risk loss L of the data asset is insured, with a premium of p, the post-insurance data asset becomes $\tilde{X}$, where the pre-insurance asset U is reduced by the premium expenditure p, and the original loss L changes to $L-f\left(L\right)$ due to the insurance compensation function (8),

$$\tilde{X}=U-p-L+f\left(L\right).$$

(8)

Here, U represents the (discounted) future return of the data asset,$p$ is the premium paid at the time of insurance, L represents the inherent loss of the data asset caused by risk events, and $f\left(L\right)$ represents the compensation function provided by the insurer after loss occurs.

Suppose the insurance provides full compensation, i.e., $f\left(L\right)=L$, then $\tilde{X}=U-p.$ Therefore, after insurance, from the pledgee’s perspective, the financing collateral value of the data asset becomes

$$V_{\beta }\left(\tilde{X}\right)=F_{\tilde{X}}^{-1}\left(\beta \right)=F_{U-p}^{-1}\left(\beta \right).$$

(9)

Obviously, when $V_{\beta }\left(\tilde{X}\right)>V_{\beta }\left(X\right)$, utilizing insurance rights can increase the financing collateral value of the data asset.

Next, we demonstrate the conditions under which $V_{\beta }\left(\tilde{X}\right)>V_{\beta }\left(X\right)$. For any y, define

$$g(p,y)=Pr(U-L\ge y)-Pr(U-p\ge y)=\int {[\overline{F}}_{U|L}(x+y)-{\overline{F}}_{U|L}(p+y)]d{F}_L\left(x\right).$$

Note that $g(p,y)$ satisfies: if L is “non-degenerate”, then $g(p,y)$ is non-decreasing with respect to p; $g\left(L_{min}\right)<0$ and $g\left(L_{max}\right)>0$. Define

$$P_{max}\left(y\right)=max\left\{p:g\left(p\right)<0\right\}\in \left(L_{min},L_{max}\right),$$

(10)

then ${p\le P}_{max}\left(y\right)$ implies $Pr(U-L\ge y)\le Pr(U-p\ge y)$. In other words, if y is the pre-insurance collateral value of the data asset $U-L$ (i.e., $Pr(U-L\ge y)=1-\beta$), then it must be that $Pr(U-p\ge y)\ge 1-\beta$; therefore, the post-insurance collateral value from the perspective of the pledgee (i.e., $U-p$) will certainly exceed y.

Let $y_{\beta }$ be the value of y that satisfies $Pr(U-L\ge y)=1-\beta$, and let $P_{max}(\beta )=P_{max}(y_{\beta })$. Then $P_{max}(\beta )$ (abbreviated as $P_{max}$) is the maximum premium for which the collateral value of the data asset can be increased. The pledgee’s risk tolerance $\beta$ varies, and the corresponding $P_{max}$ is also different. In addition, $P_{max}$ is related to the joint distribution of $(U,L)$. As long as the insurance premium $p\le P_{max}$, the post-insurance collateral value will exceed the pre-insurance value.

The above principle of enhancement can also be further described from the perspective of the insurer. Let ${\alpha }_{min}(\beta )=Pr({L\ge P}_{max})$, then $p\le P_{max}(\beta )$ is equivalent to $\alpha \ge {\alpha }_{min}(\beta )$ (abbreviated as ${\alpha }_{min}$ below); that is, if the insurer’s risk tolerance is greater than or equal to ${\alpha }_{min}$, the financing collateral value of the data asset can be enhanced via insurance rights.

When $p\le P_{max}$ as stated above, the financing collateral value of the data asset can be increased by the rights of insurance. At this time, the net financing enhancement for the data asset holder (pledge value increase minus premium expenditure) is denoted as follows:

$$U(\alpha ,\beta )=V_{\beta }\left(\tilde{X}\right)-V_{\beta }\left(X\right)={F_{U-p}^{-1}\left(\beta \right)-F_{U-L}^{-1}\left(\beta \right)=F}_U^{-1}\left(\beta \right)-F_L^{-1}(1-\alpha )-F_{U-L}^{-1}\left(\beta \right).$$

(11)

The net financing enhancement depends on $U,L$, and $\alpha ,\beta$.

Figure 1 illustrates the value composition of data assets and their relationships with insurance and pledge financing. The data asset holder defines the asset value as future returns minus losses (i.e., X = $U-L$). At this point, the data asset holder assesses the asset for financing, while the pledgee, based on their risk tolerance, expresses the value as $V_{\beta }\left(X\right)=F_X^{-1}\left(\beta \right)=F_{U-L}^{-1}\left(\beta \right)$, where $\beta$ represents the pledgee’s risk tolerance.

Under the condition that $p<P_{max}$, the holder pays an insurance premium p, calculated as $p=F_L^{-1}(1-\alpha )$, where $\alpha$ denotes the insurer’s risk tolerance. After insurance is procured, the collateral value of the data asset becomes $\tilde{X}=U-p$. At this point, when seeking financing from a pledgee with the same risk tolerance, the value is expressed as $V_{\beta }\left(\tilde{X}\right)=F_{\tilde{X}}^{-1}\left(\beta \right)=F_{U-p}^{-1}\left(\beta \right)=F_U^{-1}\left(\beta \right)-p$.

Moreover, Figure 1 demonstrates that, under the protection of the insurance mechanism, the potential loss borne by the data asset holder is reduced, thereby enhancing the value of the pledge financing to a certain extent. The specific increase can be defined as $U(\alpha ,\beta )=V_{\beta }\left(\tilde{X}\right)-V_{\beta }\left(X\right)={F_{U-p}^{-1}\left(\beta \right)-F_{U-L}^{-1}\left(\beta \right)=F}_U^{-1}\left(\beta \right)-F_L^{-1}(1-\alpha )-F_{U-L}^{-1}\left(\beta \right)$. We name this model the $P_{max}$ model, as it provides an intuitive and integrated framework for understanding insurance, financing, and risk management of data assets.

3.3. Innovative Analysis of the Standard Deviation Premium Principle Under the ${\mathit{P}}_{max}$ Model Framework

When U and L follow normal distributions, the VaR criterion can be simplified to the standard deviation principle. According to the standard deviation premium principle, the corresponding insurance premium is

$$p=E\left(L\right)+\eta {\sigma }_L,$$

where $\eta$ represents the insurer’s risk safety loading coefficient. A larger $\eta$ indicates lower risk tolerance $\alpha$ for the insurer. Here, ${\sigma }_L$ is the standard deviation of the risk loss and $E\left(L\right)$ is the expected value of the risk loss of the digital asset.

The valuation of data assets can be considered as the expected value of the data asset X = U–L, see Equation (6). Due to the existence of digital asset risk, its valuation is less than the mathematical expectation. We can also use the standard deviation principle to view the valuation of data assets. Thus, before insurance, the asset valuation is

$$V_{\beta }\left(X\right)=E\left(U\right)-E\left(L\right)-k{\sigma }_{U-L}.$$

(12)

Here, $E\left(U\right)$ and $E\left(L\right)$ denote the expected values, ${\sigma }_{U-L}$ is the standard deviation of U–L, and k is a function of $\beta$ representing the pledgee’s risk safety loading coefficient. A larger k means lower risk tolerance $\beta$ for the pledgee, making their valuation of data assets more conservative. The standard deviation principle ranks among the most frequently applied and easily interpretable premium principles in insurance practice. Its primary advantage stems from a transparent structure: the premium consists of the expected loss, covering the average claim, augmented by a risk load that scales with the statistical volatility of the loss. This offers a clear mechanism for insurers to price uncertainty. The link to the VaR framework is particularly clear under the normality assumption, where the VaR itself becomes a linear function of the standard deviation. Consequently, in such a context, the standard deviation principle serves as a practical approximation to a VaR-based premium, combining computational simplicity with sound theoretical grounding.

From the same perspective, Equation (8), after insurance, the insured data asset $\tilde{X}$ is

$$\tilde{X}=U-p=U-E\left(L\right)-\eta {\sigma }_L.$$

(13)

Here, it is also assumed that the insurance provides full risk compensation. After insurance, the pledged financing value of the asset as follows:

$$V_{\beta }\left(\tilde{X}\right)=E\left[U-E\left(L\right)-\eta {\sigma }_L\right]-k{\sigma }_{U-E\left(L\right)-\eta ·{\sigma }_L}=E\left(U\right)-E\left(L\right)-\eta {\sigma }_L-k{\sigma }_U.$$

(14)

Therefore, $V_{\beta }\left(\tilde{X}\right)\ge V_{\beta }\left(X\right)$ is equivalent to $k{\sigma }_{U-L}\ge \eta {\sigma }_L+k{\sigma }_U$, which is also equivalent to

$${\displaystyle \frac{k}{\eta }}\ge {\displaystyle \frac{{\sigma }_L}{{\sigma }_{U-L}-{\sigma }_U}}.$$

If U and L are independent, then $k/\eta \ge 1$, which means the pledgee’s safety loading coefficient is greater than that of the insurer. As the risk manager, the insurer generally has a higher risk tolerance. Therefore, $k/\eta \ge 1$ can generally be satisfied.

Assuming the risk tolerance $\beta$ of the pledgee is determined in the process of data asset pledge financing, then $k$ is also determined. At this point, $k/\eta \ge 1$ is equivalent to ${\eta \le \eta }_{max}\left(\beta \right)$. Accordingly, the insurer’s risk tolerance ${\alpha \ge \alpha }_{min}$, and the premium $p\le P_{max}$. That is, when these conditions are met, the use of insurance rights can enhance the value of data assets. This conclusion is consistent with that under the VaR risk measurement approach.

3.4. ${\mathit{P}}_{max}$ Model Contributions and Comparison

The $P_{max}$ model is the first to formally integrate insurance pricing (from the insurer’s perspective) with collateral valuation (from the pledgee’s perspective) within a unified VaR framework for data assets. It quantitatively establishes the maximum acceptable premium $P_{max}$ as a critical threshold for value enhancement, presents a novel contribution by being the first to formally integrate insurance pricing, from the insurer’s perspective, with collateral valuation, from the pledgee’s perspective, within a unified VaR framework tailored for data assets. This integration quantitatively establishes the maximum acceptable premium $P_{max}$ as a critical threshold for enhancing collateral value, thereby providing a clear criterion for evaluating the financial viability of insuring data assets.

Compared to existing models, prevailing data asset valuation methods primarily focus on the intrinsic value of the data asset itself, only qualitatively considering risks as an adjunct to the core valuation approach. Furthermore, the Value-at-Risk model itself has not yet been systematically applied to the valuation or value measurement of data assets. Therefore, our model innovatively adapts the VaR framework to establish a theoretical foundation for data asset pledging. Crucially, $P_{max}$ model serves as a practical decision-making tool by explicitly answering the critical question: “Under what premium conditions does insuring a data asset become financially viable for increasing its collateral value?” This dynamic integration of risk transfer (insurance) with asset financing represents a key advancement.

4. Numerical Example Verification of the ${\mathit{P}}_{max}$ Model

This section aims to verify the theoretical feasibility of the $P_{max}$ model through a concrete numerical example and to visually demonstrate the quantitative relationships among key variables, such as the risk tolerance of the pledgee $\beta$, the maximum acceptable premium $P_{max}$ and the enhancement of the net value $U(\alpha ,\beta )$, thus making the theoretical framework more tangible. To achieve this, we first need to specify the distributional assumptions for the core variables $(U,L)$.

We assume $U\sim N(1000,{200}^2)$, where the mean $\mu =1000$ and the variance ${\sigma }^2={200}^2$. The mean parameter for this assumption is primarily informed by the concept of industry benchmark financial impact from the IBM “Cost of a Data Breach Report 2024”, mapped to the expected value of the data asset’s potential return. The variance parameter captures the volatility in value realization. This setting provides a representative theoretical scenario. It is assumed that there is no loss in $80\%$ of cases, while in $20\%$ of cases, a risk loss occurs and the amount of loss typically exhibits heavy-tailed characteristics, which we assume follows a log-normal distribution. Therefore, we can assume that the risk loss L of the data asset follows a mixed distribution:$80\%\ast 0+20\%\ast logN(e^4,1)$.

In this section, we abbreviate $V_{\beta }\left(X\right)$ as $V\left(X\right)$. To calculate $P_{max}$. Based on the above distributions of $(U,L)$, we use Monte Carlo simulation to generate a dataset comprising 100,000 pairs of $(U,L)$, then calculate $P_{max}$ for different values of $\beta$, and plot a comparison chart of the pledged value of data assets before and after insurance.

Table 2. ${\alpha }_{min}$ and $P_{max}$ under different $\beta$.

$\mathit{\beta }$	${\mathit{P}}_{max}$	${\mathit{\alpha }}_{min}$
0.20	51.5630	0.1712
0.15	60.3923	0.1634
0.10	76.6382	0.1492
0.05	116.8998	0.1189
0.01	176.2326	0.0865

shows that, under a fixed $\alpha$, for different values of $\beta$, both $P_{max}$ and ${\alpha }_{min}$ can be calculated. According to the data in the table, as the value of $\beta$ decreases, $P_{max}$ increases nonlinearly, while ${\alpha }_{min}$ shows a decreasing trend. This means that as the pledgee’s risk tolerance increases (i.e., $\beta$ decreases), the critical value of the maximum premium that allows insurance rights to enhance the collateral value becomes higher, implying that the actual required premium also increases.

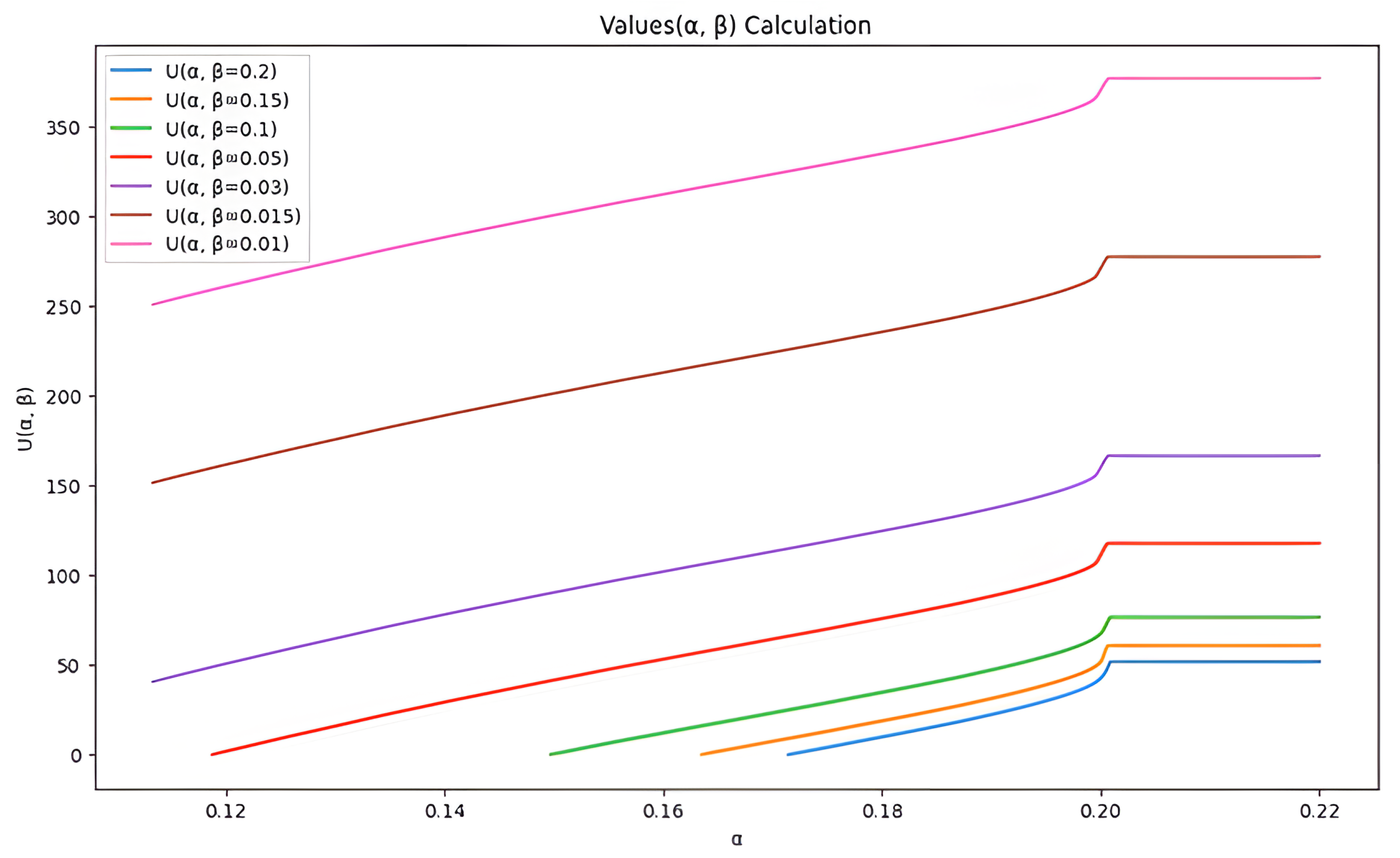
Further calculations reveal how $U(\alpha ,\beta )$ varies with $\alpha$ for different $\beta$, as shown in Figure 2 below. The following conclusions can be observed:

(1)

As $\alpha$ increases, the value of $U(\alpha ,\beta )$ for all curves exhibits an upward trend; that is, as the insurer’s risk tolerance decreases, the amount by which the financing value increases will also rise.

(2)

The degree to which different $\beta$ values affect the increase in financing value varies. A larger $\beta$ (e.g., 0.2) corresponds to the smallest $U(\alpha ,\beta )$ at the same $\alpha$ value, while a smaller $\beta$ (e.g., 0.01) shows a relatively higher value. This indicates that in the data asset value model, the value of $\beta$ has a significant effect on the amount by which the financing value increases, and this effect is independent of $\alpha$. This provides important guidance for subsequent risk management and decision-making.

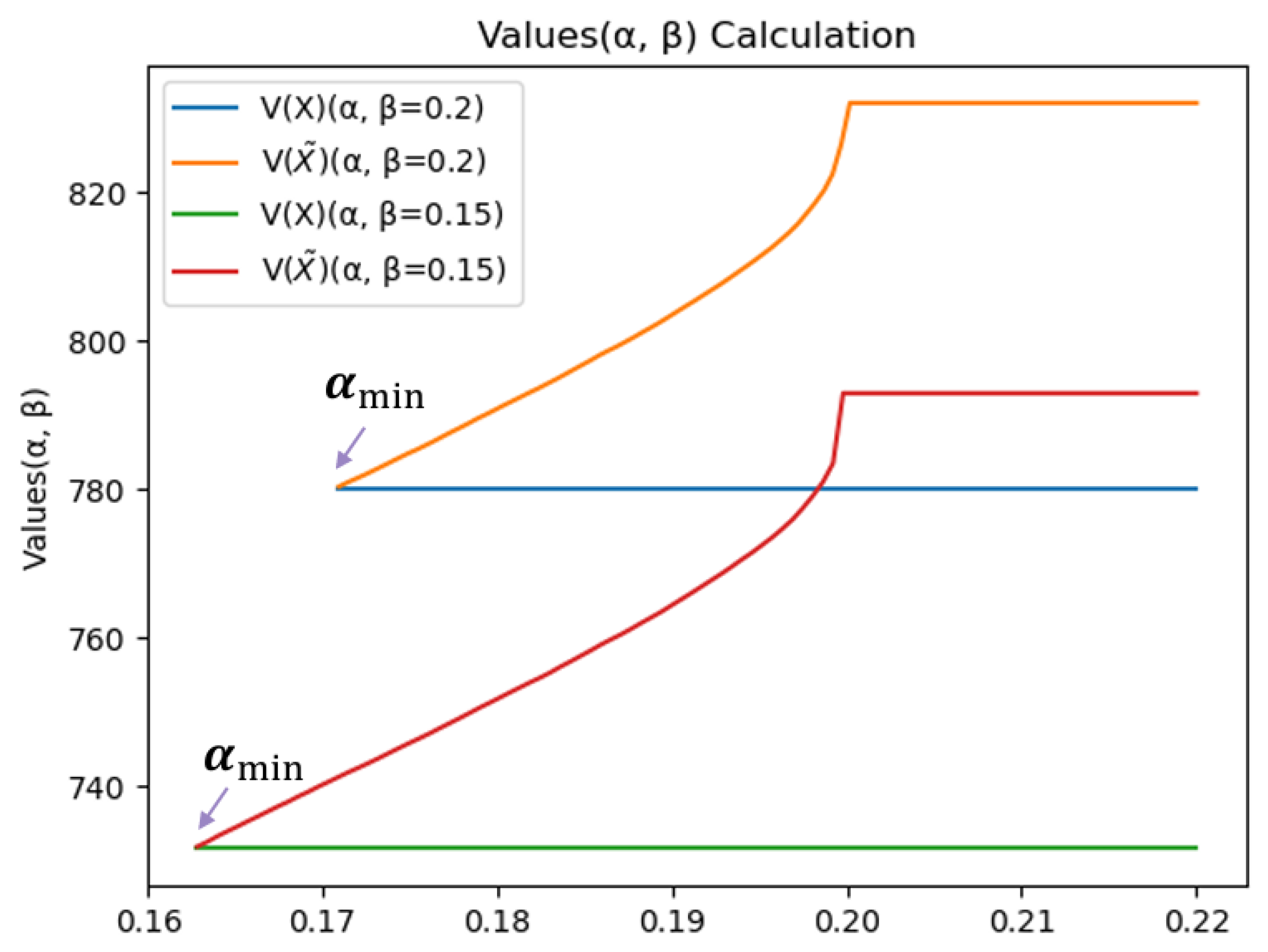
Further analysis, as shown in Figure 3 below, reveals that given a fixed $\beta$, the value of $V\left(X\right)$ for uninsured data assets remains constant. For insured data assets, when assessing the collateral value, the value of $V\left(\tilde{X}\right)$ depends on the insurer’s risk tolerance $\alpha$ for a given $\beta$. For the insurer, the greater the value of $\alpha$, the higher the insurer’s risk tolerance, and the greater the collateral value value $V\left(\tilde{X}\right)$ of the insured data asset. Therefore, as $\alpha$ increases, the corresponding increase in the collateral value after insurance, $U(\alpha ,\beta )$, also becomes larger. The corresponding values ${\alpha }_{min}$ and $P_{max}$ can thus be obtained: only when the insurer’s tolerance $\alpha$ is greater than ${\alpha }_{min}$ is it possible to enhance the collateral value of the data asset through insurance. When $\alpha$ exceeds the probability of loss occurrence, $V\left(\tilde{X}\right)$ reaches its maximum, and the increase in the collateral value $U(\alpha ,\beta )$ also reaches its maximum.

The parameters and distributions specified for U and L in this example are chosen to clearly demonstrate the model’s mechanics. The core conclusion of the model—the existence of a critical premium $P_{max}$ that enables insurance to enhance collateral value—is robust to the specific parameter choices, as it is rooted in the risk quantification logic of VaR and the risk transfer function of insurance. Naturally, if the distribution or parameters of U were changed (e.g., increased variance indicating higher risk), the specific numerical values in Table 2 and Figure 2 and Figure 3 would change accordingly (e.g., the base collateral value $V\left(X\right)$ might decrease). However, the qualitative trends, such as the negative correlation between $P_{max}$ and $\beta$ and the positive correlation between $U(\alpha ,\beta )$ and $\alpha$, are expected to hold. Future research will utilize real-world data to calibrate the distributions and parameters for more thorough robustness checks.

5. Concluding Remarks and Practical Application

This study introduces the $P_{max}$ model, a novel framework that quantifiably integrates insurance mechanisms into the valuation and financing of data assets. Our analysis, grounded in the VaR framework and supported by numerical simulations, yields the following principal findings:

First, by categorizing data asset risks across the holding, operational, and value-addition stages, we establish that the correlation between risk and asset value increases progressively. The insurance mechanism, by transferring these quantified risks, directly targets and mitigates the tail risks that most concern pledgees. Our Monte Carlo simulations (Section 4) visually demonstrate that this risk transfer is the foundational mechanism enabling the enhancement of collateral value.

Second, and most critically, the $P_{max}$ model provides a precise decision-making tool, which represents a key advancement over traditional valuation methods. It moves beyond qualitative risk consideration by explicitly answering the pivotal question: “Under what premium conditions does insurance become financially viable?” Our analytical and numerical results (e.g., Table 2 and Figure 2) confirm that when the premium $p\le P_{max}$, which is nonlinearly influenced by the pledgee’s risk tolerance $\beta$, the post-insurance collateral value $V\left(\tilde{X}\right)$ unequivocally exceeds its pre-insurance counterpart $V\left(X\right)$. This dynamic integration of risk transfer with asset financing is a core contribution of our study.

Furthermore, the “market mechanism + insurance” dual credit enhancement model proposed is not merely conceptual. The model’s structure implies that standardized platforms reduce valuation uncertainty (a component of U-L, thereby raising the base value $V\left(X\right)$ upon which the insurance mechanism then superposes a further layer of protection and value enhancement via the $P_{max}$ condition. This synergy offers a clear pathway to reduce credit risk premiums for financial institutions.

This study is motivated by the core dilemma faced by data assets in collateralized financing: on one hand, data as a new factor of production carries significant strategic value; on the other hand, its characteristics—difficult-to-quantify risks and insufficient liquidity—severely constrain its financialization. The $P_{max}$ model proposed in this paper is designed to systematically address this dilemma, providing an operational pathway of “risk quantification–insurance enhancement–value uplift” for realizing the value of data assets.

It is acknowledged that, from a theoretical perspective, the $P_{max}$ model requires further refinement. For instance, future work could incorporate more realistic insurance contract terms, such as deductibles and coinsurance provisions. Additionally, it is crucial to investigate whether consistent conclusions can be derived under alternative premium principles, particularly when accounting for the heavy-tailed characteristics of data asset losses.

In practice, the model can be implemented through the following steps: First, based on the full lifecycle risk categorization of data assets (holding, operational, value-addition), use the VaR framework to quantify their risk exposure and base collateral value $V\left(X\right)$. Second, determine a reasonable premium p according to the insurer’s risk tolerance $\alpha$, and use the $P_{max}$ model to assess whether purchasing insurance is economically viable. Finally, when $p\le P_{max}$, the data asset holder can transform the asset into a more recognized form of collateral $\tilde{X}$ through insurance, thereby securing a higher financing amount $V\left(\tilde{X}\right)$ from financial institutions.

Looking ahead, with the maturation of data asset registration, valuation, and trading systems, as well as the enrichment of data insurance products, the $P_{max}$ model can be further embedded into on-market transactions and securitization processes, forming a closed-loop ecosystem of “market valuation + insurance enhancement + collateralized financing.” This will not only activate the financing function of corporate data assets but also promote the standardization and financial innovation of the data element market, ultimately contributing to the high-quality development of the digital economy.