Abstract
Social media platforms produce extensive user–item interaction data that demand advanced analytical models for effective personalization. This study investigates the link prediction task within social recommendation systems using Graph Neural Networks (GNNs). A hybrid framework is proposed that integrates Graph Convolutional Networks (GCNs) with dual similarity metrics combining cosine and dot product measures to enhance link prediction accuracy. Experiments conducted on the Ciao and Epinions datasets using the Graph Convolutional Network (GCN) demonstrate superior performance compared with baseline models such as GraphRec and GraphSAGE. The proposed approach effectively captures latent interaction patterns, providing a robust foundation for more accurate and personalized recommendation systems on social media platforms.
MSC:
68T07; 68R10; 68T05
1. Introduction
Social media serves as a powerful communication tool, allowing users to instantly exchange ideas, information, and updates. Whether for staying connected with friends and family, discovering news, pursuing hobbies or networking professionally, social media has become an essential part of everyday life for millions of people, shaping the way we interact and engage with the digital world.
Recommendation tools have been introduced to enhance the functionality of social media platforms [1,2,3,4,5,6,7]. These services are used to help personalize users’ experiences by suggesting relevant content, friends, or groups based on a user’s interests and activity patterns. By analyzing data such as user preferences, past interactions, and trending topics, recommendation algorithms deliver tailored content that is more likely to engage each individual. This helps users discover relevant posts, news, and accounts they might not have found otherwise, creating a more engaging and efficient browsing experience. The ultimate goal of these recommendation tools is to keep users more connected to the content they care about and encourage interactions that align with their interests.
In this system type, data are represented as a graph, with nodes symbolizing entities, such as users in a social network, and edges representing the associations or connections between these entities [1,2,3,8]. These systems rely on predicting possible links between nodes by computing similarity scores, which are measures of how closely two nodes are related based on various factors such as similar interests, common connections, or other relationship patterns.
These systems rely on predicting possible links between nodes by computing similarity scores, which quantify how closely two nodes are related based on factors such as shared interests, common connections, or other relational patterns. To improve the accuracy of such predictions, we utilized the Deep Graph Library (DGL) [9,10], which provides efficient tools for building graph neural networks while leveraging existing deep learning frameworks. Within this framework, various models can be employed to learn node representations; in particular, Graph Convolutional Networks (GCNs), GraphSAGE, and GraphR are widely used techniques for learning node representations in graph-structured data, yet they differ in their mechanisms for aggregating neighborhood information. GCNs compute node embeddings by aggregating features from all neighboring nodes through a weighted, normalized sum, providing a global view of the local graph structure. GraphSAGE extends this idea by introducing flexible sampling of neighbors and allowing different aggregation functions, which enhances scalability and adapts to large and dynamic graphs. GraphR, on the other hand, emphasizes capturing the types of relationships in relational graphs, enabling the model to encode edge heterogeneity explicitly. Together, these methods illustrate the spectrum of strategies for graph representation learning, ranging from uniform neighbor aggregation to sampling-based and relation-aware techniques, providing context for the design choices in our proposed model.
In this work, we propose a link prediction framework based on Graph Neural Networks (GNNs) to model complex and dynamic interactions in social networks. We utilize the Ciao and Epinions datasets [11], representing user trust relationships, and represent user–product interactions as graphs. Each node is characterized by a feature vector combining normalized degree, cosine similarity, and dot product similarity to capture local structural patterns [12,13,14,15]. By integrating dual similarity measures, the framework effectively predicts user–item links, enhances personalization, and improves recommendation accuracy compared to baseline methods [16,17,18,19,20,21,22].
We summarize the main contributions of this paper as follows:
- Novel Link Prediction Framework: We propose a new method for enhancing link prediction in social networks using Graph Neural Networks (GNNs), specifically addressing complex and dynamic interactions between nodes.
- Graph Representation with GCN: We leverage the Graph Convolutional Network (GCN) model to capture structural and relational information effectively, enabling better node embeddings for link prediction.
- Dual Similarity Measures for Feature Enhancement: We integrate both dot product and cosine similarity to capture complementary relational cues between nodes, improving prediction accuracy.
- Empirical Validation: The proposed approach is extensively evaluated on the Ciao and Epinions datasets, demonstrating superior performance compared to conventional methods, thus confirming its effectiveness.
The remainder of the article is structured as follows: We present a concise overview of related work commonly discussed in Section 2. In Section 3, we delve into a comprehensive explanation of our approach to social recommendation based on graph neural networks (GNNs). Finally, we will wrap up with the experimental results and our concluding remarks.
2. Related Works
The use of Graph Neural Networks (GNNs) in the social recommendation context is explored in [1,4,23,24]. Its primary focus is to improve the accuracy of recommendation systems by taking advantage of the social relationships between users [5,25,26]. To accomplish the study, the researchers used various datasets, including Yelp, Epinions, Ciao, and Douban, which provide data on reviews and social interactions. A GNN model was developed based on this data to predict the relationship between a user and a recommended item (such as a product or service).
This work focuses on such techniques as graph neural networks, neighborhood aggregation, embedding, and stochastic gradient descent. By taking into account past interactions and social network structure, these techniques allow models to capture the complex relationships between users and recommended items. By taking into account past interactions and social network structure, these techniques enable GNN models to capture the complex relationships between users and recommended items. Special emphasis is placed on the similarity between users and recommended items, which is evaluated using metrics such as shared neighbors, content, interactions, and user information. These metrics are integrated into the GNN model to improve the relevance of recommendations. In summary, the paper “Graph Neural Network for Social Recommendations” presents an innovative approach to combine a graph neural network with social data to improve the quality of recommendation systems. This research opens a new perspective on social recommendation by effectively utilizing the large amount of data available in social networks.
In [27], an innovative approach to inductive learning in large-scale graph representations is discussed. The goal of this method is to induce both structural features and node properties in the graph, enabling efficient generalization to new nodes and graphs. GraphSAGE uses a neural network architecture to collect local information from the neighbors of a given node, allowing for the production of vector representations (embeddings) for each node while preserving its local context. Its inductive approach, which allows it to generate representations for nodes not present during training, is a key aspect of GraphSAGE. This makes it possible for the model to effectively generalize to invisible nodes and graphs even without the need for retraining. The article discusses various information aggregation strategies, including mean aggregation, max pooling, and LSTM-based aggregation, which allow the model to take advantage of different structural aspects of the graph. These temporal aggregation techniques allow GraphSAGE to learn rich and informative node descriptions, which can be applied to diverse topics such as node classification, link prediction, and recommendation.
In continuation with the related studies, a previous study [28] investigates state-of-the-art techniques in graph neural networks (GNNs), which integrate external knowledge into the learning process. The authors point out that conventional GNNs have difficulties in exploiting external information, such as knowledge bases and ontologies. To address this issue, they developed a framework that allows GNNs to incorporate this knowledge to improve graph representation and predictive capabilities. The mechanism of attention used in this model helps to evaluate the relevance of external knowledge when propagating the network information. By incorporating this kind of knowledge, models can more accurately capture complex relationships between entities in the graph, thus improving the accuracy of tasks such as classification and link prediction.
While earlier works have focused on conventional approaches, a recent article [29] explores a new way to study social recommendation using channel-based graph neural networks (GNN). The authors emphasize the significance of social interactions in recommendation systems, and they present a model that can effectively incorporate this information. The study model uses several channels to capture different types of social interactions, including friendship and online communication. Using GNN, the model produces a hidden representation for each channel, allowing it to understand the nuances of social relationships within the network. By linking these representations, the model provides more concise and personalized recommendations that take into account all aspects of social interaction.
In line with the ongoing discussion, the authors of [30] highlight the role of users’ social data in improving recommendation systems. The authors use the social interactions between users to propose a model called Social Attention Memory Network (SAMN), which provides more suitable recommendations. They used a dataset from WeChat Moments which contains information on user interactions such as sharing, commenting, and posting. The SAMN model employs several basic techniques, including graph neural networks, attention-based memory, and stochastic gradient descent. These techniques allow the model to capture the complexity of social network structures and identify key connections between users. A key feature of SAMN is its attention-based memory, which allows the model to prioritize the most relevant social interactions when making recommendations. This approach emphasizes the importance of social ties in the recommendation process.
In the same direction, another study [31] proposes a new similarity measure based on user preference models, specifically tailored for collaborative filtering. Two distinct user preference models are introduced: the first captures the proportion of movie genres a user has watched, and the second focuses on the average ratings given to different genres. From these models, two new similarity measures are developed.
Evaluations conducted using the MovieLens dataset show promising results. The similarity measure based on genre-watching ratios consistently outperforms traditional methods across all metrics. Meanwhile, the measure based on average genre ratings achieves comparable accuracy to Pearson correlation, but with significantly lower computational complexity, as it does not require identifying correlated items.
This approach demonstrates how incorporating user preference models can enhance the performance and efficiency of collaborative filtering systems.
In addressing similar challenges, in [24], the authors present a novel Graph Neural Network (GNN) architecture for efficient and accurate link prediction, addressing the limitations of existing node-wise and edge-wise methods. Node-wise approaches are fast at inference but struggle to distinguish structurally similar (isomorphic) nodes due to limited representational power. In contrast, edge-wise methods offer higher accuracy by generating edge-specific subgraph embeddings, but at the cost of increased computational complexity.
To overcome this trade-off, the proposed architecture introduces a unique use of negative sampling during the forward pass—a key innovation. Unlike traditional models that consider contrastive (positive vs. negative) pairs only during training (i.e., in the backward pass), this method incorporates both positive and negative edges directly into the forward pass. Node embeddings are framed as solutions to an energy minimization problem that encourages clear separation between positive and negative samples.
This design maintains the efficiency of node-wise models while improving accuracy to be competitive with edge-wise approaches. Extensive experiments validate the effectiveness of the proposed method across various benchmarks.
Despite the potential of social information to enhance recommendations, existing approaches often struggle with redundant data and fail to account for the differing influence of users and their social connections. To address this, authors in [4] propose USLGCN (User Preference and Social Relationship-aware Light Graph Convolutional Networks), a framework that leverages both user interactions and social relationships to improve recommendation performance. The model employs a subgraph classification strategy to partition the user–item interaction and social graphs into distinct subgraphs, capturing user-specific influences while reducing redundant or negative information. A graph fusion module then integrates information across subgraphs to further enhance robustness.
Building on the need to model diverse user interactions more effectively, the novel social recommendation disentangled learning framework (LDGSR) proposed in [32] addresses the limitations of existing recommender systems, which often struggle to capture diverse user behaviors across domains and fail to accurately represent user preferences.
With a similar focus, the study in [7] proposes a data-driven methodology that combines advanced preprocessing, feature selection, and model training to analyze gender-based behavioral patterns. The preprocessing steps included min–max normalization and the conversion of numerical variables into categorical formats. To capture complex behavioral relationships, a Degree-free Graph Neural Network (GNN) was employed.
To further capture complex relationships beyond pairwise connections, researchers have turned to hypergraph-based approaches that generalize traditional graph neural networks (GNNs) [10,33,34,35]. Building on GNNs, hypergraph neural networks (HGNNs) extend their capabilities to model higher-order interactions.
In parallel with these advances, link prediction has been extensively studied in the context of social networks, recommendation systems, and graph-based modeling. Beyond these traditional areas, recent studies have highlighted its usefulness in other domains. For instance, in drug–drug interaction (DDI) prediction, drugs are represented as nodes and known interactions as edges within a graph. Predicting potential interactions can help identify side effects, optimize drug combinations, and explore opportunities for drug repurposing [32].
Building upon these applications, recent developments in graph neural networks have greatly advanced link prediction and recommendation tasks in complex social and knowledge networks. The Synergetic Fusion-based Graph Convolutional Network (SFGCN) introduced a unified fusion mechanism that integrates both structural and attribute-based information to produce richer node and edge embeddings, leading to more accurate predictions across several benchmark datasets [36]. Subsequently, the Light Graph Convolutional Network with Knowledge-Aware Attention (LGKAT) improved recommendation accuracy by jointly exploiting user–item graphs and knowledge graphs, where a lightweight GCN architecture and personalized attention mechanism effectively captured subtle semantic relationships [37]. In parallel, the Granular Concept-Enhanced Relational Graph Convolutional Network (GCR-GCN) addressed the limited relational scope of standard R-GCN models by incorporating Formal Concept Analysis, thereby enhancing interpretability and relational reasoning beyond immediate node neighborhoods [38,39]. Altogether, these studies illustrate an ongoing shift toward hybrid graph learning models that merge structural, semantic, and conceptual information. Despite these advances, further research is needed to achieve an optimal trade-off between model expressiveness, interpretability, and computational efficiency.
These examples illustrate the versatility of link prediction approaches for uncovering hidden relationships in complex networks, improving recommendation quality, and supporting decision-making across different fields. Motivated by these applications, our proposed NALP framework leverages node features, graph structure, and similarity measures to enhance link prediction accuracy in user–product recommendation scenarios, demonstrating its adaptability to various networked domains.
3. Methodology
This section presents the New Approach for Link Prediction (NALP), a hybrid graph neural network framework developed to enhance prediction accuracy and robustness. The methodology is structured around four key components: graph construction using GNN model, feature extraction and link prediction via similarity calculation.
The New Approach For Link Prediction (NALP) revolves around the development of a system capable of predicting relationships between users and product categories. The primary goal of this approach is to analyze interactions that often form a complex web of relationships that are not immediately visible. To address these challenges, the research focuses on representing the user–product interaction data as a graph structure, and the link prediction problem forms the core of this study. By predicting the likelihood of a link between users and product categories, the system can suggest relevant product categories to users, thereby enhancing their browsing experience and improving the efficiency of recommendation systems by narrowing down potential options.
The developed system is based on three steps, as shown in Figure 1. The first step involves feature extraction using embedding vectors. The second phase uses the extracted features to generate graphs based on edges and nodes. In our approach, nodes represent either users or categories, while edges represent the interactions between a user and a category. After feature extraction and GNN construction, we move to the third phase of our approach, which focuses on link prediction and similarity calculation. The GNN is used again to perform classification on edges and nodes.
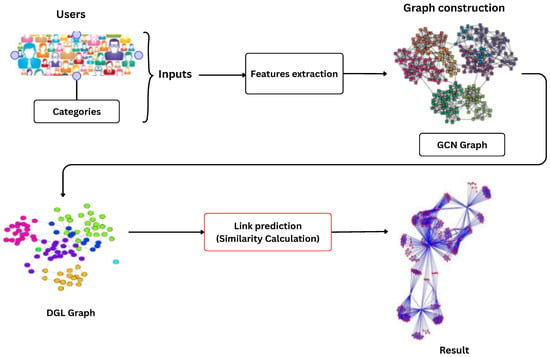
Figure 1.
Overall architecture of the proposed approach with four components: feature extraction, graph construction, link prediction and similarity calculation.
Algorithm 1 provides a detailed description of the training and evaluation pipeline used for link prediction.
| Algorithm 1: Graph Neural Network Training on Ciao and Epinions Subgraph |
 |
3.1. Feature Extraction
We used embedding vectors to extract features. These vectors transform source nodes and destination nodes into matrices of values that learn to represent users and categories. These matrices are iteratively updated by propagating information along the edges of the graph.
Using embeddings in this context offers several benefits, including the ability to capture complex, nonlinear relationships between users and categories, as well as improved algorithm performance in terms of accuracy and convergence speed. These features enable the creation of more robust and adaptive recommendation models that can dynamically adjust to new information and changes in user behavior.
3.2. Graph Neural Network (GNN)
3.2.1. Graph Convolutional Network (GCN)
In this step, we used a Graph Neural Network (GNN) to build the graph, utilizing the Graph Convolutional Network (GCN) model, a neural network architecture designed for graph-structured data [1,6,25,26,40]. In the context of product evaluation, the GCN is applied to predict links between users and product categories within a graph dataset. To achieve this, the GCN uses the features of graph nodes (representing users and categories) to learn the relationships and patterns that exist among them.
GCN’s use convolution layers to manipulate information from each node by summarizing the features of its neighboring nodes and edges, thus creating a new representation that both captures the local structure and the interconnections in the graph. This allows GCNs to efficiently learn the representations for each node by sensing the patterns in its local neighborhood, which is particularly useful for tasks such as node classification, link prediction, and graph classification.
The convolution operation in GCNs typically involves the transformation of the features of each node, their combination with the features of its neighbors, and the passing of the aggregated information through a nonlinear activation function. By overlapping multiple convolutional layers, the network can learn more and more complex and abstract representations, as well as capture information from more distant nodes in the graph. This allows GCNs to exploit the unique structure of graph data to make accurate and significant predictions, building hierarchical representations of nodes and edges.
The architecture of a GCN, as illustrated in Figure 2, is used to process graph-structured data by means of convolutional layers, which operate on nodes and their links. In GCNNs, each layer actually updates the representation of a node by combining features from its neighboring nodes and edges, allowing the network to capture local structure and relationships in the graph. The process typically begins by assigning initial features to each node. Then, as information passes through each convolutional layer, nodes iteratively integrate features from their neighbors, helping to learn both direct and indirect relationships. Nonlinear activation functions are applied after each layer to enhance feature learning, and stacking multiple convolutional layers allows the network to capture patterns across different levels of the graph. Finally, GCNNs can use pooling or readout functions to create an overall representation of the graph.
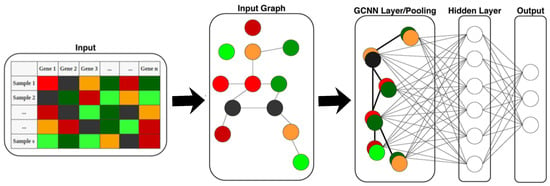
Figure 2.
The GCN architecture [41].
3.2.2. GraphSAGE (Graph Sample and Aggregate)
GraphSAGE is a scalable and inductive framework for learning node embeddings in graph-structured data [26,42,43,44,45]. Unlike traditional methods that process the entire graph, GraphSAGE samples a fixed number of neighbors for each node and aggregates their features using functions like mean, pooling, or LSTM-based operations. This iterative process allows nodes to incorporate information from their local neighborhood while maintaining scalability, even for large or dense graphs. A key advantage of GraphSAGE is its inductive capability, meaning it can generate embeddings for previously unseen nodes without retraining, making it suitable for dynamic graphs. In link prediction tasks, GraphSAGE computes embeddings for nodes, which are then combined or scored to estimate the likelihood of a connection, offering an efficient solution for evolving networks and large-scale applications [26,42,43,44].
3.2.3. GraphRec (Graph-Based Recommendation)
GraphRec is a recommendation system framework that utilizes graph structures to model relationships between users and items [46,47,48,49].
By representing users, items, and their interactions as a graph, GraphRec leverages graph neural networks (GNNs) to learn embeddings for each node, capturing both direct and indirect connections within the graph. These embeddings help in predicting user preferences and generating personalized recommendations. The model considers not only user–item interactions but also the relationships between users and items, allowing it to uncover latent patterns and improve recommendation accuracy [46,47,48,49].
3.3. Link Prediction via Node Similarity
In this phase, we perform link prediction to estimate the likelihood of connections between nodes in the graph. To improve the performance, we utilized the Deep Graph Library (DGL) [9,10], which provides efficient tools for building graph neural networks while leveraging existing deep learning frameworks, as illustrated in Figure 3. Node attributes are used to train the model, enabling it to predict whether a connection exists between two nodes—for example, whether a user will interact with a specific product category based on prior interactions.

Figure 3.
Example of relations between Users and Rated Product Categories on the Ciao dataset.
Once the embeddings are learned, we compute the similarity between nodes, framing similarity estimation as the link prediction task. High similarity scores indicate a strong potential connection, while low scores suggest weak or absent links. By integrating node features, graph structure, and similarity measures, this unified framework enhances the accuracy and interpretability of predicted links.
3.3.1. Cosine Similarity
Cosine similarity is widely used in link prediction tasks to evaluate how closely the embeddings of two nodes in a graph are aligned, irrespective of their scale or magnitude [32,40]. This makes it especially useful for assessing the similarity of relationships in high-dimensional spaces.
The goal is to measure the similarity between two vectors by calculating the cosine of the angle between them. It provides a normalized measure of similarity, focusing on the direction of the vectors rather than their magnitude.
The formula for cosine similarity between two vectors u and v is as follows: Cosine similarity:
3.3.2. The Dot Product
The dot product serves as a similarity measure, estimating the likelihood of a connection between the two nodes. It is often used as an input feature in link prediction models or directly as a scoring mechanism to rank potential links [50,51].
The dot product measure is used to quantify the similarity between the embeddings of two nodes in a graph. These embeddings represent the nodes in a vector space, capturing their structural and relational features.
For two nodes u and v represented by their embeddings u and v, where is the angle between the vectors u and v, the scalar product is calculated as: Dot product:
3.3.3. Jaccard Similarity
Jaccard similarity is a metric used to measure the similarity between two nodes based on the overlap of their neighborhoods in a graph. It evaluates the likelihood of a link between two nodes by quantifying the proportion of their shared neighbors relative to their combined neighbors [23,44].
For two nodes u and v in a graph, let A and B denote the sets of neighbors of u and v, respectively. The Jaccard similarity is defined as follows:
Jaccard similarity:
4. Experiments
The programming and experiments were conducted using Google Colaboratory (Google LLC, Mountain View, CA, USA) in conjunction with a local machine equipped with an Intel(R) Core(TM) i7-7500U CPU @ 2.70 GHz (up to 2.90 GHz), 8 GB RAM (7.88 GB usable), and a 224 GB SSD (PNY CS900 240GB, PNY Technologies Inc., Parsippany, NJ, USA). The system operated on a 64-bit Microsoft Windows 10 (Microsoft Corporation, Redmond, WA, USA) environment running on an x64-based processor.
4.1. Used Dataset
We used two real-world datasets, Ciao [11] and Epinions [16], to evaluate our proposed approach. A summary of the Ciao and Epinions dataset characteristics is provided in Table 1. Ciao is a benchmark dataset for graph-based and socially-aware recommendation systems. It contains 7375 users, 105,114 items, and 284,086 explicit user–item ratings, with a sparsity of 0.04%. Additionally, it includes 111,781 directed trust relationships among users. This combination of sparse interaction data and social trust information makes it suitable for evaluating models that consider both collaborative filtering and social influence, such as GraphRec and GCN-based approaches. The dataset was divided into training (55%), validation (40%), and test (5%) subsets using the train_test_split_edges utility from PyTorch Geometric (PyG) 2.7.0. Ratings are provided in a matrix file with columns representing user ID, product ID, category ID, rating, and usefulness.

Table 1.
Summary of Ciao and Epinions Dataset Characteristics.
Epinions is an online review platform that captures both user–item interactions and explicit trust relationships. The dataset contains 75,879 users and 508,837 social links, along with ratings, reviews, and comments. Its dual nature allows testing of trust-aware recommendation methods and social network analysis techniques.
For model training, we used a subgraph of 3000 nodes, trained for 30 epochs with a hidden dimension of 64. These settings preserve the structural patterns of the original graphs while maintaining computational efficiency. Further tuning can be applied to improve performance.
4.2. Experiments Details
In this section, we will present the experiments achieved and discuss the obtained results.
Link Prediction
Graph Visualization is an optional graph-based visualization, designed to illustrate the relationships between users and the product categories they have rated.
Figure 3 presents a graph-based visualization that illustrates the relationships between users and rated product categories on the Ciao dataset. In this graph, each node represents either a user or a product category, while each edge signifies a rating interaction between them. The use of node colors, assigned by category, enhances visual clarity and helps distinguish between different product types. As presented in Figure 4, this visualization is particularly valuable for understanding the structure and distribution of user preferences. It allows for the identification of popular categories, highly active users, and potential clusters of users who share similar interests. Such patterns are crucial for developing and interpreting graph-based models, such as Graph Convolutional Networks (GCNs), which rely on both node attributes and edge connectivity to learn effective representations.

Figure 4.
Example of Link prediction between Users and Product Categories on the Ciao dataset.
For link prediction, numerous experiments have been conducted on the Ciao and Epinions datasets. Our study evaluated the performance of different recommendation algorithms, focusing on GraphSAGE, GraphRec, and GCN. To improve node feature representation, we experimented with various similarity-based enhancements, including combinations of Jaccard similarity and Cosine similarity with node degree, Jaccard and Cosine with dot product similarity, Jaccard and Cosine similarity alone, and Cosine similarity combined with dot product similarity. These configurations allowed us to assess how different feature representations impact the effectiveness of link prediction on both datasets.
All experiments were conducted under a consistent training setup: the number of nodes (NUM_NODES = 3000) and training epochs (EPOCHS = 30) were fixed, with regularization parameters held constant (dropout = 0.1, weight_decay = 1 × 10−5). Prior to drafting the manuscript, exploratory trials were conducted to assess the impact of key parameters, including the number of nodes, hidden dimension (HIDDEN), number of epochs, and learning rate (LR). Although detailed results from these preliminary tests were not retained, they guided the selection of hyperparameters that consistently yielded stable and reliable performance. Across reasonable ranges (NUM_NODES: 1000–5000; HIDDEN: 32–128; EPOCHS: 20–100; LR: 0.001–0.01), performance remained nearly stable, with variations typically within ±1–2%. These observations indicate that the improvements reported are primarily due to the proposed similarity combination mechanism rather than specific hyperparameter settings.
We conducted link prediction experiments on two publicly available social trust datasets obtained from the Stanford Network Analysis Project (SNAP) repository: Epinions (soc-Epinions1.txt.gz) and Ciao (soc-Slashdot0902.txt.gz or ciao.txt.gz). In both datasets, nodes represent users and edges denote trust relationships. The original directed graphs were converted to an undirected form, and self-loops were removed prior to processing. For computational efficiency, 3000 nodes were extracted using NetworkX, and node indices were relabeled sequentially. Each node was represented by a feature vector composed of its normalized degree and a metric similarity with neighbors, forming a feature matrix. The dataset was divided into training (55%), validation (40%), and test (5%) subsets using the train_test_split_edges utility from PyTorch Geometric. Negative samples were generated uniformly at random in equal numbers to the positive edges in each split. The proposed link prediction model employed a six-layer Graph Convolutional Network (GCN) with 64 hidden units per layer, ReLU activation, a dropout rate of 0.1, and a final embedding dimension of 64. This configuration enables the model to capture multi-level structural dependencies while ensuring effective regularization and robust learning across datasets.
4.3. Results and Discussion
Three algorithms, GraphSAGE, GraphRec, and GCN, were utilized for comparison, as shown in Table 2, each with distinct approaches and performance levels. GraphSAGE, GraphRec, and GCN are three prominent graph-based algorithms used in learning node representations for tasks such as recommendation and link prediction. GCN (Graph Convolutional Network) is a foundational model that performs message passing by aggregating features from neighboring nodes in a fixed way, assuming the entire graph is available during training. It works well in semi-supervised settings but is less scalable to large graphs due to its reliance on full neighborhood aggregation. GraphSAGE improves scalability by sampling a fixed-size set of neighbors for each node, enabling inductive learning and better generalization to unseen nodes. It supports various aggregation functions such as mean, LSTM, and pooling, offering flexibility. GraphRec is specifically tailored for recommender systems and integrates both user–item interaction graphs and behavioral signals to capture richer user preferences. While GraphRec and GraphSAGE offer specialized advantages, GCN outperformed both models in the Ciao dataset significantly in our experiments, achieving an accuracy of 87.6%. This result demonstrates the strong representational power of GCN when applied in a well-connected, dense graph setting, despite its transductive limitations.

Table 2.
Comparative Analysis of Graph Neural Network Approaches: GCN, GraphSAGE, and GraphRec.
GraphSAGE achieved an accuracy of 74.2%, making it the least accurate of the three. GraphSAGE operates through an inductive framework, enabling it to learn node representations by sampling and aggregating features from a node’s neighbors. Despite its ability to generalize to unseen nodes, its relatively lower accuracy indicates limitations in fully capturing complex relationships in this dataset. GraphRec demonstrated a marked improvement over GraphSAGE, with an accuracy of 76.5%. This algorithm specifically leverages social data by combining graph neural networks with social interaction information, enhancing the recommendation system’s ability to provide more relevant suggestions based on user interactions. Its higher accuracy showcases the advantage of incorporating social context, making it well-suited for recommendation tasks in social networks.
GCN outperformed the other two algorithms significantly, achieving an accuracy of 87.6%. GCN’s architecture allows it to learn representations by applying convolutional operations on graph data, capturing local and global structures within the graph. This strong performance highlights GCN’s capability to detect intricate patterns and connections between nodes, making it highly effective for tasks requiring a precise understanding of graph structures.
On the Epinions dataset, the accuracy of GCN and GraphRec models reached 67.31%, significantly higher than GraphSAGE at 53.85%. This indicates that GCN and GraphRec better capture structural dependencies and trust relationships in the network, whereas GraphSAGE’s neighborhood sampling may lose important information in sparse trust graphs. Overall, these results suggest that GCN’s architecture, which leverages convolution on graph-structured data, provides superior predictive accuracy, particularly in applications involving complex user–item relationships.
We tried to enhance the node feature representation by combining Jaccard similarity and Cosine similarity with the basic node degree. First, for each node, we calculated the Jaccard similarity with its neighbors: for a given node, we measured the overlap between its neighbors and the neighbors of each of its adjacent nodes, summing these values to produce a single score per node. This captures local structural similarity in the graph. Next, we computed the cosine similarity between the degree vectors of all nodes, producing a similarity matrix that reflects the similarity of nodes’ connectivity patterns. For each node, we summed the cosine similarities with its neighbors to obtain a second feature. Finally, we combined the normalized node degree, the Jaccard similarity score, and the cosine similarity sum into a single feature vector for each node.
Jaccard and Cosine dot similarity combination
The node features are enriched by combining four complementary similarity measures to capture both local and global structural information. First, each node’s degree is normalized to represent its basic connectivity. Then, Jaccard similarity is computed as the sum of overlap ratios between the node’s neighbors and the neighbors of each neighbor, capturing local neighborhood similarity. Next, cosine similarity is calculated between the degree vectors of nodes, and the sum of cosine similarities with a node’s neighbors is used as an additional feature, representing a more global structural similarity. Finally, dot product similarity is computed between the degree vectors and summed over neighbors, providing another perspective on connectivity strength. These four features—degree, Jaccard, cosine-sum, and dot-sum—are concatenated into a single feature vector for each node, which is then used as input to graph neural network models.
Jaccard and dot product similarity
Jaccard and Cosine similarity combination
In this approach, each node in the graph is represented by a feature vector that captures both structural similarity and connection strength. First, for each node, the Jaccard similarity is computed by summing the pairwise Jaccard indices between the node and each of its neighbors, which reflects how similar their neighborhoods are. Second, the dot product similarity is calculated by taking the dot product of the node’s degree with the degrees of its neighbors, providing a measure of connectivity magnitude between nodes. These two similarity measures are then concatenated into a single feature vector per node, forming a combined representation that encodes both local neighborhood overlap (Jaccard) and relative node importance (dot product).
Cosine and dot product similarity combination
In this approach, we enhance node features for link prediction by combining cosine similarity and dot product similarity. Cosine similarity measures the directional similarity between nodes’ feature vectors, capturing how similar their connectivity patterns are regardless of magnitude. Dot product similarity, on the other hand, measures the magnitude-aligned similarity, emphasizing nodes with both high and aligned degrees. By combining these two measures, we generate a richer feature representation that captures both the relative orientation and the magnitude of nodes’ connectivity patterns. These combined features are then used as input to the GCN, providing more informative embeddings that improve the model’s ability to predict links accurately.
Our study highlighted the effectiveness of different recommendation algorithms when applied to the Ciao and Epinions datasets. The performance of certain algorithms, like GCN, was particularly impressive, reaching 90.15% accuracy for the Ciao dataset. Additionally, analyzing various combinations of similarity calculation techniques paired with GCN revealed interesting trends, showing how these methods impact the accuracy of link predictions.
These results emphasize the importance of carefully selecting the algorithm and methods best suited to the dataset’s specific characteristics and the recommendation objectives. Ultimately, our study provides a strong foundation for future research aimed at enhancing social network-based recommendation systems.
The results presented in Table 3 clearly show the impact of different similarity techniques on GCN performance for link prediction on the Ciao and Epinions datasets. Using Jaccard similarity alone yields the lowest accuracy (45.33% on Ciao), reflecting its limitation in capturing only the local neighborhood overlap. Combining Jaccard with Cosine similarity improves performance slightly (53.36% on Ciao), indicating that incorporating vector orientation information helps, but is still insufficient. Adding dot product similarity to Jaccard and Cosine features marginally increases accuracy (55.37% on Ciao), as the dot product captures magnitude-based similarity which complements the previous measures. Dot similarity alone performs better than Jaccard-based combinations (55.42% on Ciao), highlighting the effectiveness of magnitude-aligned information in link prediction. The combination of Jaccard and dot similarity shows an interesting improvement (61.9% on Ciao), but its performance on Epinions drops, suggesting dataset- specific interactions.

Table 3.
Comparison of Similarity Techniques Performances using GCN.
The most significant improvement is observed with the Cosine similarity + dot similarity combination (90.15% on the Ciao dataset). This combination is effective because Cosine similarity captures the relative orientation of node feature vectors, emphasizing structural patterns, while dot similarity incorporates magnitude information, highlighting highly connected or influential nodes. Together, they provide a more comprehensive representation of node relationships, allowing the GCN to generate embeddings that are both directionally and numerically informative, which directly translates to higher link prediction accuracy. This demonstrates that combining complementary similarity measures can significantly enhance model performance compared to using any single measure or partially combined features. On the Epinions dataset, the results indicate that combining cosine similarity with dot similarity yields the best performance, reaching 73.33%, which significantly outperforms all other techniques. Using dot similarity alone also provides relatively strong results (57.59%), while the combination of cosine, Jaccard, and dot similarity achieves 55.21%. In contrast, techniques relying solely on Jaccard similarity or its combinations perform poorly, with accuracies around 45–50%, highlighting their limited ability to capture meaningful relationships in this dataset. Interestingly, while cosine similarity alone achieves a high accuracy on the Ciao dataset, its performance drops considerably on Epinions (52.63%), suggesting that interaction patterns in Epinions are better captured when cosine similarity is reinforced with dot similarity. Overall, the highest score of 73.33% can be considered acceptable and remains comparable to the performance reported by several state-of-the-art methods, emphasizing the effectiveness of combining cosine and dot similarity for trust-aware recommendation on the Epinions dataset.
To gain a deeper understanding of this improvement, we analyzed the learned embeddings and observed distinct structural patterns depending on the similarity measure applied.
When using cosine similarity alone, node embeddings are projected onto a hypersphere, leading to well-aligned directions but limited sensitivity to the magnitude of relationships. This normalization effect emphasizes angular proximity but tends to compress the inter-cluster distances, which may obscure subtle relationship strengths.
Conversely, dot product similarity captures magnitude variations effectively, amplifying the influence of highly connected nodes, but sometimes at the cost of losing fine-grained angular distinctions between less prominent nodes.
The proposed Cosine + Dot Product hybrid approach overcomes these limitations by simultaneously considering both direction and magnitude. This fusion produces embeddings that form more cohesive and semantically meaningful clusters, where nodes belonging to the same community or user category are not only directionally aligned but also appropriately scaled according to their interaction intensity.
Such a balance between angular uniformity and magnitude discrimination leads to a better preservation of relational structure in the embedding space, explaining the observed improvements in link prediction accuracy and stability across datasets.
In essence, this hybrid measure allows the GNN to learn embeddings that are both compact and discriminative, enhancing its generalization ability over single-similarity methods. The results show that the accuracy obtained on the Epinions dataset is lower than on Ciao, which can be explained by structural and distributional differences between the two networks. The Ciao dataset tends to have denser connections and more clustered communities, making similarity measures such as Cosine and Dot more informative and reliable in capturing user relationships. In contrast, Epinions is often sparser, with more heterogeneous and noisy connections, which reduces the ability of local similarity features to reflect meaningful structural patterns. Furthermore, the degree distribution in Epinions is more irregular, leading to less stable feature combinations when using Cosine and Dot similarity. As a result, while the same similarity-based techniques achieve high accuracy on Ciao, their effectiveness is diminished on Epinions due to its more complex and less predictable topology.
Furthermore, we compare in Table 4 our proposed method NALP against six state-of-the-art approaches published in [16]. These baselines can be grouped into two categories:

Table 4.
Comparison of Similarity Techniques performances employing GCN.
- -
- Network embedding methods: GAT [17], SGC [18], STNE [19], and SNEA [20].
- -
- Trust evaluation methods: DeepTrust [13] and AtNE-Trust [15].
GAT [17]: An attention-based graph neural network that assigns different weights to neighbors, thereby enhancing the aggregation process.
SGC [18]: A simplified graph convolutional model that reduces complexity by removing nonlinearities and collapsing weight matrices between layers.
STNE [19]: A social trust network embedding method designed to preserve both node–latent factor relations and trust transfer patterns for trust prediction.
SNEA [20]: A signed network embedding approach that incorporates a masked self-attention mechanism to compute neighbor importance coefficients.
DeepTrust [21]: A trust evaluation model grounded in homophily theory, which integrates user commenting behaviors and object-related features to assess trustworthiness.
AtNE-Trust [22]: A deep trust prediction framework that learns user embeddings by considering both their dual roles (trustor and trustee) and their connectivity properties.
On the Epinions dataset, although some approaches, such as STNE (79.51%) and SGC (78.62%), achieve slightly higher performances, our method, NALP, remains competitive with an accuracy of 73.33%, placing it within the same range as other state-of-the-art methods like SNEA (74.63%) and AtNE-Trust (74.35%). Moreover, compared to models such as DeepTrust, which only reaches 58.38%, our approach demonstrates a clear superiority and confirms its robustness. These results highlight that, even if NALP is not the top performer on Epinions, it still provides an effective and comparable solution to advanced existing methods, while achieving remarkable performance on the Ciao dataset (90.15%), which underscores its adaptability and overall competitiveness.
5. Conclusions
In this paper, we present an innovative approach to advance link prediction in social media networks by harnessing the power of graph neural networks (GNNs). Our approach is centered on the implementation of the Graph Convolutional Network (GCN) model, a neural network architecture that excels at handling graph-structured data, making it well-suited for complex social networks. By leveraging the Deep Graph Library (DGL), we were able to streamline and improve the computational efficiency of our model, enabling scalable and faster graph processing.
To refine the prediction accuracy further, we combined the scalar product and cosine similarity methods. The scalar product approach measures the degree of alignment between vector representations of nodes, while cosine similarity evaluates the angle between node vectors, providing complementary perspectives on potential connections within the graph. This dual-method approach exploits the strengths of both techniques and enhances the model’s sensitivity to subtle relational cues.
The results show that our approach provides a significant improvement in accuracy, outperforming conventional techniques by effectively identifying and predicting links within the social network. This advance demonstrates the potential of combining GCN, DGL, and dual similarity measures to optimize link prediction, providing a robust solution for more personalized and responsive recommendation systems on social media platforms.
Applying the model to domains beyond social networks offers an exciting opportunity to explore its versatility and effectiveness in various networked environments. In academic research, for instance, citation networks rely on link prediction to identify meaningful connections between papers, aiding in discovering related work and fostering collaboration. In bioinformatics, predicting protein–protein interactions or gene–disease associations can significantly advance scientific research, as accurate link predictions can accelerate the identification of functional relationships in biological networks. Testing the model in these domains not only helps validate its generalizability but also uncovers any specific modifications required to handle unique data structures, interaction types, or domain-specific challenges.
Author Contributions
All authors contributed significantly to the development of this work. S.G. carried out the implementation of the proposed models, conducted experiments, and performed data analysis. S.Y. contributed to the comparative study, validation, and interpretation of the results. W.B. and T.B. conceptualized the study and designed the methodology. S.Y., W.B. and T.B. supervised the overall research process, assisted with the literature review, and reviewed and approved the final version of the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported and funded by the Deanship of Scientific Research at Imam Mohammad Ibn Saud Islamic University (IMSIU) (grant number IMSIU-DDRSP2501).
Data Availability Statement
We used the Ciao dataset available online at: https://www.kaggle.com/datasets/aravindaraman/ciao-data (accessed on 22 July 2025) and the Epinions dataset available online at: https://snap.stanford.edu/data/soc-Epinions1.html (accessed on 8 August 2025).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ma, G.; Ahmed, N.K.; Willke, T.L.; Yu, P.S. Deep graph similarity learning: A survey. Data Min. Knowl. Discov. 2021, 35, 688–725. [Google Scholar] [CrossRef]
- Li, Y.; Zhong, N.; Taniar, D.; Zhang, H. MCGNet+: An improved motor imagery classification based on cosine similarity. Brain Inform. 2022, 9, 3. [Google Scholar] [CrossRef]
- Romanova, A. GNN graph classification method to discover climate change pat-ternsy. In Proceedings of the International Conference on Artificial Neural Networks, Proceedings of the 32nd International Conference on Artificial Neural Networks, Heraklion, Greece, 26–29 September 2023; Springer: Cham, Switzerland, 2023; pp. 388–397. [Google Scholar]
- Zhang, H.; Li, H.; Li, Z.; Chen, P. User preference and social relationship-aware recommendations base on a novel light graph convolutional network. J. Supercomput. 2025, 81, 27. [Google Scholar] [CrossRef]
- Akkaya, B. Current Trends in Recommender Systems: A Survey of Approaches and Future Directions. Comput. Sci. 2025, 10, 53–91. [Google Scholar]
- Li, Y.; Feng, H.; Zeng, Y.; Zhao, X.; Chai, J.; Fu, S.; Ye, C.; Zhang, S. Light disentangled graph learning for social recommendation. World Wide Web 2025, 28, 29. [Google Scholar] [CrossRef]
- Chattopadhyay, S.; Kumar, S.; Kumar, M.S.; Balasubramanian, K.; Pujar, R.P. Novel Method for Predicting Consumer Purchase Behaviour on E-Commerce Platforms through Graph Neural Network Model. In Proceedings of the International Conference on Intelligent Computing and Knowledge Extraction (ICICKE), Bengaluru, India, 6–7 June 2025; pp. 1–6. [Google Scholar]
- Wang, X.; Zhang, H.; Liu, Y.; Zhang, J. Graph neural networks for social recommendation. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 Januray–1 February 2019; Volume 33, pp. 4602–4609. [Google Scholar]
- Dalvi, A.; Honavar, V. Hyperdimensional representation learning for node classification and link prediction. In Proceedings of the Eighteenth ACM International Conference on Web Search and Data Mining, Hannover, Germany, 10–14 March 2025; pp. 88–97. [Google Scholar]
- Wang, L.; Han, M. High-order Graph Neural Networks with Common Neighbor Awareness for Link Prediction. In Proceedings of the 2025 Joint International Conference on Automation-Intelligence-Safety (ICAIS) & International Symposium on Autonomous Systems (ISAS), Xi’an, China, 23–25 May 2025; pp. 1–5. [Google Scholar]
- Ciao. Available online: https://www.ciao.co.uk (accessed on 22 July 2025).
- Levy, A.; Shalom, B.R.; Chalamish, M. A guide to similarity measures and their data science applications. J. Big Data 2025, 12, 188. [Google Scholar] [CrossRef]
- Firuzbakht, S.; Khansari, M. TwitterTagNet: An extensive graph dataset for node classification in co-occurring hashtag networks. Soc. Netw. Anal. Min. 2025, 15, 17. [Google Scholar] [CrossRef]
- Mishra, A. Graph-Based Methods for e-Commerce Data Science Applications. Ph.D. Thesis, The Pennsylvania State University, University Park, PA, USA, 2025. [Google Scholar]
- Contreras-Velasco, O.; Jones, N.P.; Argomedo, D.W.; Sullivan, J.P.; Callaghan, C. Uncovering hidden alliances in organized crime networks with machine learning: From node similarity to graph neural networks. J. Comput. Soc. Sci. 2025, 8, 101. [Google Scholar] [CrossRef]
- Yu, Z.; Jin, D.; Huo, C.; Wang, Z.; Liu, X.; Qi, H.; Wu, J.; Wu, L. Kgtrust: Evaluating trustworthiness of siot via knowledge enhanced graph neural networks. In Proceedings of the ACM Web Conference 2023, Austin, TX, USA, 30 April–4 May 2023; pp. 727–736. [Google Scholar]
- Velickovic, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph Attention Networks. arXiv 2018, arXiv:1710.10903. [Google Scholar]
- Wu, F.; Souza, A., Jr.; Zhang, T.; Fifty, C.; Yu, T.; Weinberger, K. Weinberger Simplifying Graph Convolutional Networks. In Proceedings of the 36th International Conference on Machine Learning, ICML, Long Beach, CA, USA, 2–15 June 2019; pp. 6861–6871. [Google Scholar]
- Xu, P.; Hu, W.; Wu, J.; Liu, W.; Du, B.; Yang, J. Social Trust Network Embedding. In Proceedings of the 2019 IEEE International Conference on Data Mining (ICDM), Beijing, China, 8–11 November 2019; pp. 678–687. [Google Scholar]
- Li, Y.; Tian, Y.; Zhang, J.; Chang, Y. Learning Signed Network Embedding via Graph Attention. Proc. AAAI Conf. Artif. Intell. 2020, 34, 4772–4779. [Google Scholar] [CrossRef]
- Wang, Q.; Zhao, W.; Yang, J.; Wu, J.; Hu, W.; Xing, Q. DeepTrust: A Deep User Model of Homophily Effect for Trust Prediction. In Proceedings of the 2019 IEEE International Conference on Data Mining (ICDM), Beijing, China, 8–11 November 2019; pp. 618–627. [Google Scholar]
- Wang, Q.; Zhao, W.; Yang, J.; Wu, J.; Zhou, C.; Xing, Q. DeepTrust: AtNE-Trust: Attributed Trust Network Embedding for Trust Prediction in Online Social Networks. In Proceedings of the 2020 IEEE International Conference on Data Mining (ICDM), Sorrento, Italy, 17–20 November 2020; pp. 601–610. [Google Scholar]
- Han, X.; Xie, X.; Zhao, R.; Li, Y.; Ma, P.; Li, H.; Chen, F.; Zhao, Y.; Tang, Z. Calculating the similarity between prescriptions to find their new indications based on graph neural network. Chin. Med. 2023, 19, 124. [Google Scholar] [CrossRef]
- Wang, Y.; Hu, X.; Gan, Q.; Huang, X.; Qiu, X.; Wipf, D. Efficient link prediction via gnn layers induced by negative sampling. IEEE Trans. Knowl. Data Eng. 2025, 37, 253–264. [Google Scholar] [CrossRef]
- Choudhary, S.; Kumar, G. Enhancing link prediction in dynamic social networks through hybrid GCN-LSTM models. Knowl. Inf. Syst. 2025, 67, 6717–6751. [Google Scholar] [CrossRef]
- Ga, S.; Cho, P.H.; Moon, G.E.; Jung, S. Efficient GNN-based social recommender systems through social graph refinement. J. Supercomput. 2025, 81, 215. [Google Scholar] [CrossRef]
- Hamilton, W.; Ying, R.; Leskovec, J. Inductive representation learning on large graphs. arXiv 2017, arXiv:1706.02216. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, F.; Zhang, M.; Leskovec, J.; Zhao, M.; Li, W.; Wang, Z. Knowledge-aware graph neural networks with label smoothness regularization for recommender systems. In Proceedings of the 25th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 968–977. [Google Scholar]
- Wang, Y.; Sun, M.; Zhu, X.; Zhang, C. Multi-channel graph neural networks for social recommendation. In Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval, Virtual, 25–30 June 2020; pp. 135–144. [Google Scholar]
- Zheng, Y.; Zhang, H.; Ma, Y.; Chen, E. Joint deep modeling of users and items using reviews for recommendation. In Proceedings of the Tenth ACM International Conference on Web Search and Data Mining, Cambridge, UK, 6–10 February 2017; Volume 35, pp. 425–434. [Google Scholar]
- Cheng, Q.; Wang, X.; Yin, D.; Niu, Y.; Xiang, X.; Yang, J.; Shen, L. The new similarity measure based on user preference models for collaborative filtering. In Proceedings of the 2015 IEEE International Conference on Information and Automation, Lijiang, China, 8–10 August 2015; pp. 577–582. [Google Scholar]
- Li, D.; Yang, Y.; Cui, Z.; Yin, H.; Hu, P.; Hu, L. LLM-DDI: Leveraging Large Language Models for Drug-Drug Interaction Prediction on Biomedical Knowledge Graph. IEEE J. Biomed. Health Inform. 2025, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Yang, M.-R.; Xu, X.-J. Recent Advances in Hypergraph Neural Networks. J. Oper. Res. Soc. China 2025. [Google Scholar] [CrossRef]
- Tan, G. NAH-GNN: A graph-based framework for multi-behavior and high-hop interaction recommendation. PloS ONE 2025, 20, e0321419. [Google Scholar] [CrossRef] [PubMed]
- Xu, R.; Liu, G.; Wang, Y.; Zhang, X.; Zheng, K.; Zhou, X. Adaptive hypergraph network for trust prediction. In Proceedings of the 2024 IEEE 40th International Conference on Data Engineering (ICDE), Utrecht, The Netherlands, 13–16 May 2024; pp. 2986–2999. [Google Scholar]
- Lee, S.-W.; Tanveer, J.; Rahmani, A.M.; Alinejad-Rokny, H.; Khoshvaght, P.; Zare, G.; Alamdari, P.M.; Hosseinzadeh, M. SFGCN: Synergetic Fusion-based Graph Convolutional Networks Approach for link prediction in social networks. Inf. Fusion 2025, 114, 102684. [Google Scholar] [CrossRef]
- Hassanzadeh, R.; Majidnezhad, V.; Arasteh, B. A novel recommender system using light graph convolutional network and personalized knowledge-aware attention sub-network. Sci. Rep. 2025, 15, 15693. [Google Scholar] [CrossRef]
- Dai, Y.; Yan, M.; Li, J. Granular concept-enhanced relational graph convolution networks for link prediction in knowledge graph. Inf. Sci. 2025, 694, 121698. [Google Scholar] [CrossRef]
- Bansal, S.; Gowda, K.; Kumar, N. Multilingual personalized hashtag recommendation for low-resource Indic languages using graph-based deep neural network. EXpert Syst. Appl. 2024, 236, 121188. [Google Scholar] [CrossRef]
- Leskovec, J. Graphsage: Inductive representation learning on large graphs. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Ramirez, R.; Chiu, Y.C.; Hererra, A.; Mostavi, M.; Ramirez, J.; Chen, Y.; Jin, Y.F. Classification of cancer types using graph convolutional neural networks. Front. Phys. 2020, 8, 203. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Ong, G.P.; Chen, X. GraphSAGE-based traffic speed forecasting for segment network with sparse data. IEEE Trans. Intell. Transp. Syst. 2020, 23, 1755–1766. [Google Scholar] [CrossRef]
- Zhang, T.; Shan, H.-R.; Little, M.A. Causal GraphSAGE: A robust graph method for classification based on causal sampling. Pattern Recognit. 2022, 128, 108696. [Google Scholar] [CrossRef]
- Sun, Q.; Wei, X.; Yang, X. GraphSAGE with deep reinforcement learning for financial portfolio optimization. Expert Syst. Appl. 2022, 238, 122027. [Google Scholar] [CrossRef]
- Pompeu, M.L.F.; Holanda Filho, R. Identification Based on GraphSAGE Algorithm. In Proceedings of the Complex Networks & Their Applications XIII, Proceedings of the Thirteenth International Conference on Complex Networks and Their Applications: COMPLEX NETWORKS, Istanbul, Turkey, 10–12 December 2024; Springer Nature: Cham, Switzerland, 2025; Volume 1187, pp. 28–36. [Google Scholar]
- Lee, J.-W.; Kim, J.-H. GraphRec-based Korean expert recommendation using author contribution index and the paper abstracts in marine. Eng. Appl. Artif. Intell. 2024, 133, 108219. [Google Scholar] [CrossRef]
- Liao, D.; Yu, H. PEVGraphRec: A PEV method-based graph neural networks for social recommendations. In Proceedings of the International Conference on Statistics, Data Science, and Computational Intelligence, Qingdao, China, 19–21 August 2022; Volume 12510, pp. 414–420. [Google Scholar]
- Si, G.; Xu, S.; Li, Z.; Zhang, J. Rec-GNN: Research on social recommendation based on graph neural networks. In Proceedings of the 2022 International Conference on Computer Science, Information Engineering and Digital Economy, Guangzhou, China, 28–30 October 2022; pp. 478–485. [Google Scholar]
- Gao, J.; Zhang, Y.; Zhang, Y. Graph Diffusion Social Recommendation. IEEE Trans. Consum. Electron. 2025. [Google Scholar] [CrossRef]
- Zhang, M.; Wu, S.; Gao, M.; Jiang, X.; Xu, K.; Wang, L. Personalized graph neural networks with attention mechanism for session-aware recommendation. IEEE Trans. Knowl. Data Eng. 2023, 34, 3946–3957. [Google Scholar] [CrossRef]
- Lavryk, Y.; Kryvenchuk, Y. Product Recom-mendation System Using Graph Neural Network. In MoMLeT + DS 2023, Proceedings of the 5th International Workshop on Modern Machine Learning Technologies and Data Science, Lviv, Ukraine, 3 June 2023; CEUR: Kyiv, Ukraine, 2023; pp. 182–192. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).