Convergence by Class of Kantorovich-Type q-Szász Operators and Comprehensive Results

Abstract

In this paper, we primarily use Stancu variants of Kantorovich-type operators to investigate the convergence and other associated properties of new Szász–Mirakjan operators. We compute the moments and central moments of the new Szász–Mirakjan operators by q-integers and propose their modified Kantorovich form. More specifically, we examine the convergence characteristics in the space of continuous functions. With the use of the modulus of continuity and the integral modulus of continuity, we determine the degree of convergence. Additionally, we obtain the Voronovskaja type theorems. To validate convergence, we conclude with a numerical example and graphical illustration of the operator sequences.

1. Introduction and Basic Definitions

By presenting the Bernstein polynomials in 1912, S. N. Bernstein provided a brief and straightforward demonstration of the Weierstrass approximation theorem [1]. These operators can only be applied to bounded intervals on $[0,1]$. In 1950, Szász introduced another form of positive linear operators to approximate a class of functions over the unbounded interval $[0,\infty )$, known as the Szász–Mirakjan operators. Lupaş [2] and Phillips [3] introduced the q-analogue of Bernstein polynomials independently. Since then, the q-calculus has been used to study and generalize a number of polynomials. Thus, for all $x\in [0,1]$ and $\psi \in C[0,1]$, the famous Bernstein operators are given by

$$B_{\eta }(\psi ;x)=\sum _{\mu =0}^{\eta }\psi \left({\displaystyle \frac{\mu }{\eta }}\right)b_{\eta ,\mu }\left(x\right),$$

where $\eta \in \mathbb{N}$ (set of natural numbers) and $b_{\eta ,\mu }\left(x\right)$ are the Bernstein polynomials of degree at most $\eta$ defined by

$$b_{\eta ,\mu }\left(x\right)=\left({\displaystyle \genfrac{}{}{0pt}{}{\eta }{\mu }}\right)x^{\mu }{(1-x)}^{\eta -\mu }\left(\mu =0,1,\cdots ,\eta ;x\in \left[0,1\right]\right)$$

and

$$b_{\eta ,\mu }\left(x\right)=0(\mu <0or\mu >\eta ).$$

It is very easy to verify the recursive relation for the Bernstein basis function $b_{\eta ,\mu }\left(x\right)$ given by

$$b_{\eta ,\mu }\left(x\right)=(1-x)b_{\eta -1,\mu }\left(x\right)+x{b}_{\eta -1,\mu -1}\left(x\right).$$

The q-calculus proved to be a highly useful tool and a useful bridge between mathematics and physics. Here, we go over a few key words and symbols associated with the q-calculus. It is easy to find the fundamental characteristics and qualities of q-integers (see [4,5]). The q-integers for any $\gamma \in \mathbb{N}$, ${\left[\gamma \right]}_q={\displaystyle \frac{1-q^{\gamma }}{1-q}}=\left[\gamma \right]$ (we denote over the article). The binomial coefficient for q-integers is given by for each $q\in (0,1)$ and $0\le {\ell }_2\le {\ell }_1$, $\left[\begin{array}{c}{\ell }_1\\ {\ell }_2\end{array}\right]={\displaystyle \frac{\left[{\ell }_1\right]!}{[{\ell }_1-{\ell }_2]!\left[{\ell }_2\right]!}}$. The q-exponential function $e_q\left(x\right)={\displaystyle \sum _{k=0}^{\infty }}{\displaystyle \frac{x^k}{\left[k\right]!}}$ and $E_q\left(x\right)={\displaystyle \sum _{k=0}^{\infty }}{q}^{{\displaystyle \frac{k(k-1)}{2}}}{\displaystyle \frac{x^k}{\left[k\right]!}}$. For any $\ell \in \mathbb{N}$, the q-binomial polynomial is given by ${(1+\gamma )}_q^{\ell }=(1+\gamma )(1+q\gamma )\cdots (1+q^{\ell -1}\gamma )$, and if $\ell =0$, then ${(1+\gamma )}_q^{\ell }=1$.

Following the Bernstein analysis, the Bernstein operators rapidly extended and have subsequently undergone further expansions aimed at approximating functions. The Szász–Mirakjan operators were given the following new generalized Kantorovich variation for any $0<q<1$ and f be continuous in $[0,\infty )\to \mathbb{R}$ by [6]:

$${\mathcal{K}}_{r,q}(f;x)=\sum _{k=0}^{\infty }{q}^{{\displaystyle \frac{k(k-1)}{2}}}{\displaystyle \frac{{\left[r\right]}^k{x}^k}{\left[k\right]!}}{\displaystyle \frac{1}{E_q\left(\left[r\right]x\right)}}{\int }_0^1\cdots {\int }_0^{1}f\left({\displaystyle \frac{\left[k\right]q^{1-k}+u_1+\cdots +u_n}{\left[r\right]}}\right)\mathrm{d}{u}_1\cdots \mathrm{d}{u}_n.$$

(1)

Definition 1

([4,5]). The definition of the q-Jackson integral from 0 to $\mathcal{A}\in \mathbb{R}$ is

$${\int }_0^{\mathcal{A}}f\left(x\right){\mathrm{d}}_{q}x=\mathcal{A}(1-q)\sum _{s=0}^{\infty }f\left(\mathcal{A}{q}^s\right)q^s.$$

(2)

The more generic q-Jackson integral on interval $[A,B]$, however, is provided by

$${\int }_A^{B}f\left(x\right){\mathrm{d}}_{q}x={\int }_0^{B}f\left(x\right){\mathrm{d}}_{q}x-{\int }_0^{A}f\left(x\right){\mathrm{d}}_{q}x.$$

(3)

From Lemma 2.1, [7], for any $r\in \mathbb{N}$ and $0<q<1$, we have the new form of Szász operators denoted as ${\mathcal{S}}_{r,q}(f;x)$ such that

$${\mathcal{S}}_{r,q}(f;x)=\sum _{k=0}^{\infty }{q}^{{\displaystyle \frac{k(k-1)}{2}}}{\displaystyle \frac{{\left[r\right]}^k{x}^k}{\left[k\right]!}}{\displaystyle \frac{1}{E_q\left(\left[r\right]x\right)}}f\left({\displaystyle \frac{\left[k\right]}{q^{k-2}\left[r\right]}}\right),$$

(4)

and for the test function $f(ı)=1,ı,{ı}^2,{ı}^3,{ı}^4$, operators ${\mathcal{S}}_{r,q}$ have the following properties:

$$\begin{array}{ccc}\hfill {\mathcal{S}}_{r,q}(1;x)& & =1;\hfill \\ \hfill {\mathcal{S}}_{r,q}(ı;x)& & =qx;\hfill \\ \hfill {\mathcal{S}}_{r,q}({ı}^2;x)& & =q{x}^2+{\displaystyle \frac{q^2}{\left[r\right]}}x;\hfill \\ \hfill {\mathcal{S}}_{r,q}({ı}^3;x)& & =x^3+{\displaystyle \frac{q(1+2q)}{\left[r\right]}}{x}^2+{\displaystyle \frac{q^3}{{\left[r\right]}^2}}x;\hfill \\ \hfill {\mathcal{S}}_{r,q}({ı}^4;x)& & ={\displaystyle \frac{1}{q^2}}{x}^4+{\displaystyle \frac{3q^2+2q+1}{q\left[r\right]}}{x}^3+{\displaystyle \frac{q(1+3q+3q^2)}{{\left[r\right]}^2}}{x}^2+{\displaystyle \frac{q^4}{{\left[r\right]}^3}}x.\hfill \end{array}$$

2. New Operators and Basic Moments

In this section, we give an extension of the operators [7] using the Stancu-type form of Kantorovich operators. These extensions allow for a broader application of the operators in various mathematical contexts, enhancing their utility in approximation theory. By exploring the properties of these Stancu-type modifications, we can gain deeper insights into their convergence behavior and efficiency. We generalize the operators (4) in the Kantorovich meaning of the Stancu form in the q-integral Jackson formula. In the interval $\left[{\displaystyle \frac{k}{r+1}},{\displaystyle \frac{k+1}{r+1}}\right]$, the mean values of f are substituted by use the sample values are $f\left({\displaystyle \frac{k}{r}}\right)$. We refer to [8,9,10,11,12,13,14,15,16,17,18,19] for Kantorovich type operators. We establish a new Szász–Kantorovich in a generalized form of the Stancu type, based on the basic definitions of q-integers $0<q<1$. Furthermore, we explore various convergence results and provide examples that lead to flexibility in approximation theory. Let we denote here, $[0,\infty )$ by ${\mathcal{R}}^{+}$. Thus, we take $0\le {\displaystyle \frac{l_1}{[r+1]+d_1}}\le {\displaystyle \frac{[k+1]+l_1}{[r+1]+d_1}}$ for $r\in \mathbb{N}$ and $l_1,d_1$ with $0\le l_1\le d_1$. For all $f\in C{\mathcal{R}}^{+}$ and $x\in {\mathcal{R}}^{+}$ we define the operators ${\mathcal{N}}_{r,k,q}^{l_1,d_1}:C[0,\infty )\to \mathbb{R}$ as follows:

$${\mathcal{N}}_{r,k,q}^{l_1,d_1}(f;x)=([r+1]+d_1)\sum _{k=0}^{\infty }{q}^{{\displaystyle \frac{k(k-1)}{2}}}{\displaystyle \frac{{\left[r\right]}^k{x}^k}{\left[k\right]!}}{\displaystyle \frac{1}{E_q\left(\left[r\right]x\right)}}{\int }_{{\displaystyle \frac{q\left[k\right]+l_1}{[r+1]+d_1}}}^{{\displaystyle \frac{[k+1]+l_1}{[r+1]+d_1}}}f\left(ı\right){\mathrm{d}}_q(ı),$$

(5)

where $\mathbb{N}$ is the set of positive numbers, $\mathbb{R}$ is the set of real numbers and $C{\mathcal{R}}^{+}$ set of all continuous function defined on ${\mathcal{R}}^{+}$. While the new variant of classical new Szász–Kantorovich-type operator of order one based on q-integers can be represented as:

$${\mathcal{M}}_{r,k,q}^{l_1,d_1}(f;x)=\left([r+1]\right)\sum _{k=0}^{\infty }{q}^{{\displaystyle \frac{k(k-1)}{2}}}{\displaystyle \frac{{\left[r\right]}^k{x}^k}{\left[k\right]!}}{\displaystyle \frac{1}{E_q\left(\left[r\right]x\right)}}{\int }_{{\displaystyle \frac{q\left[k\right]}{[r+1]}}}^{{\displaystyle \frac{[k+1]}{[r+1]}}}f\left(ı\right){\mathrm{d}}_q(ı).$$

(6)

Lemma 1.

Let the test function $f(ı)=1,ı,{ı}^2,{ı}^3,{ı}^4$. For $0<q<1$ operators ${\mathcal{N}}_{r,k,q}^{l_1,d_1}$ defined by (5) satisfy:

$$\begin{array}{ccc}\hfill \left(1\right){\mathcal{N}}_{r,k,q}^{l_1,d_1}(1;x)& & =1;\hfill \\ \hfill \left(2\right){\mathcal{N}}_{r,k,q}^{l_1,d_1}(ı;x)& & ={\displaystyle \frac{2q^2\left[r\right]}{\left[2\right]([r+1]+d_1)}}x+{\displaystyle \frac{1+2l_1}{\left[2\right]([r+1]+d_1)}};\hfill \\ \hfill \left(3\right){\mathcal{N}}_{r,k,q}^{l_1,d_1}({ı}^2;x)& & ={\displaystyle \frac{3q^3{\left[r\right]}^2}{\left[3\right]{([r+1]+d_1)}^2}}{x}^2+{\displaystyle \frac{3q^2(q^2+1+2l_1)\left[r\right]}{\left[3\right]{([r+1]+d_1)}^2}}x\hfill \\ & & +{\displaystyle \frac{1+3l_1+3l_1^2}{\left[3\right]{([r+1]+d_1)}^2}};\hfill \\ \hfill \left(4\right){\mathcal{N}}_{r,k,q}^{l_1,d_1}({ı}^3;x)& & ={\displaystyle \frac{4q^3{\left[r\right]}^3}{\left[4\right]{([r+1]+d_1)}^3}}{x}^3+{\displaystyle \frac{2q^3(2q+4q^2+3+6l_1){\left[r\right]}^2}{\left[4\right]{([r+1]+d_1)}^3}}{x}^2\hfill \\ & & +{\displaystyle \frac{q^2\left(4q^4+6q^2(3+2l_1)+12l_1(1+l_1)\right)\left[r\right]}{\left[4\right]{([r+1]+d_1)}^3}}x\hfill \\ & & +{\displaystyle \frac{{(1+l_1)}^4-l_1^4}{\left[4\right]{([r+1]+d_1)}^3}};\hfill \\ \hfill \left(5\right){\mathcal{N}}_{r,k,q}^{l_1,d_1}({ı}^4;x)& & ={\displaystyle \frac{5q^2{\left[r\right]}^4}{\left[5\right]{([r+1]+d_1)}^4}}{x}^4+{\displaystyle \frac{5q^3\left(1+2q+3q^2+2(1+l_1)\right){\left[r\right]}^3}{\left[5\right]{([r+1]+d_1)}^4}}{x}^3\hfill \\ & & +{\displaystyle \frac{5q^3\left(q^2+3q^3+3q^4+2q^2(1+2q)(1+2l_1)+6(1+l_1)\right){\left[r\right]}^2}{\left[5\right]{([r+1]+d_1)}^4}}{x}^2\hfill \end{array}$$

$$\begin{array}{ccc}& & +{\displaystyle \frac{5q^2\left(q^6+2q^4(1+2l_1)+6q^2(1+l_1)+5{(1+l_1)}^4-5l_1^4\right)\left[r\right]}{\left[5\right]{([r+1]+d_1)}^4}}x\hfill \\ & & +{\displaystyle \frac{{(1+l_1)}^5-l_1^5}{\left[5\right]{([r+1]+d_1)}^4}}.\hfill \end{array}$$

Proof. 

It is evident from the q-Jackson integral that we have

$$\begin{array}{ccc}\hfill {\int }_{\mathcal{I}}{ı}^{\beta }{\mathrm{d}}_q(ı)& & ={\int }_{{\mathcal{I}}_1}{ı}^{\beta }{\mathrm{d}}_q(ı)-{\int }_{{\mathcal{I}}_2}{ı}^{\beta }{\mathrm{d}}_q(ı)\hfill \\ & & =(1-q){\displaystyle \frac{[k+1]+l_1}{[r+1]+d_1}}\sum _{m=0}^{\infty }({\displaystyle \frac{[k+1]+l_1}{[r+1]+d_1}}{q}^m{)}^{\beta }{q}^m\hfill \\ & & -(1-q){\displaystyle \frac{q\left[k\right]+l_1}{[r+1]+d_1}}\sum _{m=0}^{\infty }({\displaystyle \frac{q\left[k\right]+l_1}{[r+1]+d_1}}{q}^m{)}^{\beta }{q}^m\hfill \\ & & ={\displaystyle \frac{(1-q)}{{([r+1]+d_1)}^{\beta +1}}}({([k+1]+l_1)}^{\beta +1}-{(q\left[k\right]+l_1)}^{\beta +1})\sum _{m=0}^{\infty }{q}^{m(1+\beta )},\hfill \end{array}$$

where $\mathcal{I}=\left[{\displaystyle \frac{q\left[k\right]+l_1}{[r+1]+d_1}},{\displaystyle \frac{[k+1]+l_1}{[r+1]+d_1}}\right]$, ${\mathcal{I}}_1=\left[0,{\displaystyle \frac{[k+1]+l_1}{[r+1]+d_1}}\right]$ and ${\mathcal{I}}_2=\left[0,{\displaystyle \frac{q\left[k\right]+l_1}{[r+1]+d_1}}\right]$. Thus, we take into account the $[k+1]=1+q\left[k\right]$ and get

$${\int }_{\mathcal{I}}{ı}^{\beta }{\mathrm{d}}_q(ı)=\left\{\begin{array}{cc}{\displaystyle \frac{1}{[r+1]+d_1}}\hfill & \mathrm{for}\beta =0;\hfill \\ {\displaystyle \frac{1}{\left[2\right]{\left([r+1]+d_1\right)}^2}}\left(1+2l_1+2q\left[k\right]\right)\hfill & \mathrm{for}\beta =1;\hfill \\ {\displaystyle \frac{1}{\left[3\right]{\left([r+1]+d_1\right)}^3}}(3q^2{\left[s\right]}^2+3q(1+2l_1)\left[k\right]\hfill \\ +1+3l_1+3l_1^2)\hfill & \mathrm{for}\beta =2\hfill \end{array}\right.$$

(7)

and

$${\int }_{\mathcal{I}}{ı}^{\beta }{\mathrm{d}}_q(ı)=\left\{\begin{array}{c}{\displaystyle \frac{1}{\left[4\right]{\left([r+1]+d_1\right)}^4}}(4q^3{\left[k\right]}^3+6(1+2l_1)q^2{\left[k\right]}^2\hfill \\ +12l_1(1+l_1)q\left[k\right]+{(1+l_1)}^4-l_1^4)\hfill & \mathrm{for}\beta =3;\hfill \\ {\displaystyle \frac{1}{\left[5\right]{\left([r+1]+d_1\right)}^5}}(5q^4{\left[k\right]}^4+10(1+2l_1)q^3{\left[k\right]}^3\hfill \\ +30(1+l_1)q^2{\left[k\right]}^2\hfill \\ +5q\left[k\right]\left({(1+l_1)}^4-l_1^4\right)+{(1+l_1)}^5-l_1^5)\hfill & \mathrm{for}\beta =4.\hfill \end{array}\right.$$

(8)

Thus in the view of (7) for $\beta =0,1,2,$ we get

$$\begin{array}{ccc}\hfill {\mathcal{N}}_{r,k,q}^{l_1,d_1}(1;x)& & =([r+1]+d_1)\sum _{k=0}^{\infty }{q}^{{\displaystyle \frac{k(k-1)}{2}}}{\displaystyle \frac{{\left[r\right]}^k{x}^k}{\left[k\right]!}}{\displaystyle \frac{1}{E_q\left(\left[r\right]x\right)}}{\int }_{\mathcal{I}}{\mathrm{d}}_q(ı)\hfill \\ & & =([r+1]+d_1)\sum _{k=0}^{\infty }{q}^{{\displaystyle \frac{k(k-1)}{2}}}{\displaystyle \frac{{\left[r\right]}^k{x}^k}{\left[k\right]!}}{\displaystyle \frac{1}{E_q\left(\left[r\right]x\right)}}{\displaystyle \frac{1}{([r+1]+d_1)}}\hfill \\ & & ={\mathcal{S}}_{r,q}(1;x)\hfill \\ & & =1;\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {\mathcal{N}}_{r,k,q}^{l_1,d_1}(ı;x)& & =([r+1]+d_1)\sum _{k=0}^{\infty }{q}^{{\displaystyle \frac{k(k-1)}{2}}}{\displaystyle \frac{{\left[r\right]}^k{x}^k}{\left[k\right]!}}{\displaystyle \frac{1}{E_q\left(\left[r\right]x\right)}}{\int }_{\mathcal{I}}ı{\mathrm{d}}_q(ı)\hfill \\ & & ={\displaystyle \frac{2q\left[r\right]}{\left[2\right]([r+1]+d_1)}}\sum _{k=0}^{\infty }{q}^{{\displaystyle \frac{k(k-1)}{2}}}{\displaystyle \frac{{\left[r\right]}^k{x}^k}{\left[k\right]!}}{\displaystyle \frac{1}{E_q\left(\left[r\right]x\right)}}{\displaystyle \frac{\left[k\right]}{\left[r\right]}}\hfill \\ & & +{\displaystyle \frac{1+2l_1}{\left[2\right]([r+1]+d_1)}}\sum _{k=0}^{\infty }{q}^{{\displaystyle \frac{k(k-1)}{2}}}{\displaystyle \frac{{\left[r\right]}^k{x}^k}{\left[k\right]!}}{\displaystyle \frac{1}{E_q\left(\left[r\right]x\right)}}\hfill \\ & & ={\displaystyle \frac{2q\left[r\right]}{\left[2\right]([r+1]+d_1)}}{\mathcal{S}}_{r,q}(ı;x)+{\displaystyle \frac{1+2l_1}{\left[2\right]([r+1]+d_1)}}{\mathcal{S}}_{r,q}(1;x)\hfill \\ & & ={\displaystyle \frac{2q^2\left[r\right]}{\left[2\right]([r+1]+d_1)}}x+{\displaystyle \frac{1+2l_1}{\left[2\right]([r+1]+d_1)}};\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {\mathcal{N}}_{r,k,q}^{l_1,d_1}({ı}^2;x)& & =([r+1]+d_1)\sum _{k=0}^{\infty }{q}^{{\displaystyle \frac{k(k-1)}{2}}}{\displaystyle \frac{{\left[r\right]}^k{x}^k}{\left[k\right]!}}{\displaystyle \frac{1}{E_q\left(\left[r\right]x\right)}}{\int }_{\mathcal{I}}{ı}^2{\mathrm{d}}_q(ı)\hfill \\ & & ={\displaystyle \frac{3q^2{\left[r\right]}^2}{\left[3\right]{([r+1]+d_1)}^2}}\sum _{k=0}^{\infty }{q}^{{\displaystyle \frac{k(k-1)}{2}}}{\displaystyle \frac{{\left[r\right]}^k{x}^k}{\left[k\right]!}}{\displaystyle \frac{1}{E_q\left(\left[r\right]x\right)}}{\displaystyle \frac{{\left[k\right]}^2}{{\left[r\right]}^2}}\hfill \\ & & +{\displaystyle \frac{3q(1+2l_1)\left[r\right]}{\left[3\right]{([r+1]+d_1)}^2}}\sum _{k=0}^{\infty }{q}^{{\displaystyle \frac{k(k-1)}{2}}}{\displaystyle \frac{{\left[r\right]}^k{x}^k}{\left[k\right]!}}{\displaystyle \frac{1}{E_q\left(\left[r\right]x\right)}}{\displaystyle \frac{\left[k\right]}{\left[r\right]}}\hfill \\ & & +{\displaystyle \frac{1+3l_1+3l_1^2}{\left[3\right]{([r+1]+d_1)}^2}}\sum _{k=0}^{\infty }{q}^{{\displaystyle \frac{k(k-1)}{2}}}{\displaystyle \frac{{\left[r\right]}^k{x}^k}{\left[k\right]!}}{\displaystyle \frac{1}{E_q\left(\left[r\right]x\right)}}\hfill \\ & & ={\displaystyle \frac{3q^2{\left[r\right]}^2}{\left[3\right]{([r+1]+d_1)}^2}}{\mathcal{S}}_{r,q}({ı}^2;x)+{\displaystyle \frac{3q(1+2l_1)\left[r\right]}{\left[3\right]{([r+1]+d_1)}^2}}{\mathcal{S}}_{r,q}(t;x)\hfill \\ & & +{\displaystyle \frac{1+3l_1+3l_1^2}{\left[3\right]{([r+1]+d_1)}^2}}{\mathcal{S}}_{r,q}(1;x)\hfill \\ & & ={\displaystyle \frac{3q^2{\left[r\right]}^2}{\left[3\right]{([r+1]+d_1)}^2}}\left(q{x}^2+{\displaystyle \frac{q^2}{\left[r\right]}}x\right)+{\displaystyle \frac{3q^2(1+2l_1)\left[r\right]}{\left[3\right]{([r+1]+d_1)}^2}}x\hfill \\ & & +{\displaystyle \frac{1+3l_1+3l_1^2}{\left[3\right]{([r+1]+d_1)}^2}}.\hfill \end{array}$$

We take in account (8) $f(ı)={ı}^3,{ı}^4$, thus we get

$$\begin{array}{ccc}\hfill {\mathcal{N}}_{r,k,q}^{l_1,d_1}({ı}^3;x)& & =([r+1]+d_1)\sum _{k=0}^{\infty }{q}^{{\displaystyle \frac{k(k-1)}{2}}}{\displaystyle \frac{{\left[r\right]}^k{x}^k}{\left[k\right]!}}{\displaystyle \frac{1}{E_q\left(\left[r\right]x\right)}}{\int }_{\mathcal{I}}{ı}^3{\mathrm{d}}_q(ı)\hfill \\ & & ={\displaystyle \frac{4q^3{\left[r\right]}^3}{\left[4\right]{([r+1]+d_1)}^3}}\sum _{k=0}^{\infty }{q}^{{\displaystyle \frac{k(k-1)}{2}}}{\displaystyle \frac{{\left[r\right]}^k{x}^k}{\left[k\right]!}}{\displaystyle \frac{1}{E_q\left(\left[r\right]x\right)}}{\displaystyle \frac{{\left[k\right]}^3}{{\left[r\right]}^3}}\hfill \\ & & +{\displaystyle \frac{6q^2(1+2l_1){\left[r\right]}^2}{\left[4\right]{([r+1]+d_1)}^3}}\sum _{k=0}^{\infty }{q}^{{\displaystyle \frac{k(k-1)}{2}}}{\displaystyle \frac{{\left[r\right]}^k{x}^k}{\left[k\right]!}}{\displaystyle \frac{1}{E_q\left(\left[r\right]x\right)}}{\displaystyle \frac{{\left[k\right]}^2}{{\left[r\right]}^2}}\hfill \\ & & +{\displaystyle \frac{12q{l}_1(1+l_1)\left[r\right]}{\left[4\right]{([r+1]+d_1)}^3}}\sum _{k=0}^{\infty }{q}^{{\displaystyle \frac{k(k-1)}{2}}}{\displaystyle \frac{{\left[r\right]}^k{x}^k}{\left[k\right]!}}{\displaystyle \frac{1}{E_q\left(\left[r\right]x\right)}}{\displaystyle \frac{\left[k\right]}{\left[r\right]}}\hfill \\ & & +{\displaystyle \frac{{(1+l_1)}^4-l_1^4}{\left[4\right]{([r+1]+d_1)}^3}}\sum _{k=0}^{\infty }{q}^{{\displaystyle \frac{k(k-1)}{2}}}{\displaystyle \frac{{\left[r\right]}^k{x}^k}{\left[k\right]!}}{\displaystyle \frac{1}{E_q\left(\left[r\right]x\right)}}\hfill \\ & & ={\displaystyle \frac{4q^3{\left[r\right]}^3}{\left[4\right]{([r+1]+d_1)}^3}}{\mathcal{S}}_{r,q}({ı}^3;x)+{\displaystyle \frac{6q^2(1+2l_1){\left[r\right]}^2}{\left[4\right]{([r+1]+d_1)}^3}}{\mathcal{S}}_{r,q}({ı}^2;x)\hfill \\ & & +{\displaystyle \frac{12q{l}_1(1+l_1)\left[r\right]}{\left[4\right]{([r+1]+d_1)}^3}}{\mathcal{S}}_{r,q}(ı;x)+{\displaystyle \frac{{(1+l_1)}^4-l_1^4}{\left[4\right]{([r+1]+d_1)}^3}}{\mathcal{S}}_{r,q}(1;x)\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {\mathcal{N}}_{r,k,q}^{l_1,d_1}({ı}^4;x)& & =([r+1]+d_1)\sum _{k=0}^{\infty }{q}^{{\displaystyle \frac{k(k-1)}{2}}}{\displaystyle \frac{{\left[r\right]}^k{x}^k}{\left[k\right]!}}{\displaystyle \frac{1}{E_q\left(\left[r\right]x\right)}}{\int }_{\mathcal{I}}{ı}^4{\mathrm{d}}_q(ı)\hfill \\ & & ={\displaystyle \frac{5q^4{\left[r\right]}^4}{\left[5\right]{([r+1]+d_1)}^4}}\sum _{k=0}^{\infty }{q}^{{\displaystyle \frac{k(k-1)}{2}}}{\displaystyle \frac{{\left[r\right]}^k{x}^k}{\left[k\right]!}}{\displaystyle \frac{1}{E_q\left(\left[r\right]x\right)}}{\displaystyle \frac{{\left[k\right]}^4}{{\left[r\right]}^4}}\hfill \\ & & +{\displaystyle \frac{10q^3(1+2l_1){\left[r\right]}^3}{\left[5\right]{([r+1]+d_1)}^4}}\sum _{k=0}^{\infty }{q}^{{\displaystyle \frac{k(k-1)}{2}}}{\displaystyle \frac{{\left[r\right]}^k{x}^k}{\left[k\right]!}}{\displaystyle \frac{1}{E_q\left(\left[r\right]x\right)}}{\displaystyle \frac{{\left[k\right]}^3}{{\left[r\right]}^3}}\hfill \\ & & +{\displaystyle \frac{30q^2(1+l_1){\left[r\right]}^2}{\left[5\right]{([r+1]+d_1)}^4}}\sum _{k=0}^{\infty }{q}^{{\displaystyle \frac{k(k-1)}{2}}}{\displaystyle \frac{{\left[r\right]}^k{x}^k}{\left[k\right]!}}{\displaystyle \frac{1}{E_q\left(\left[r\right]x\right)}}{\displaystyle \frac{{\left[k\right]}^2}{{\left[r\right]}^2}}\hfill \\ & & +{\displaystyle \frac{5q\left({(1+l_1)}^4-l_1^4\right)\left[r\right]}{\left[5\right]{([r+1]+d_1)}^4}}\sum _{k=0}^{\infty }{q}^{{\displaystyle \frac{k(k-1)}{2}}}{\displaystyle \frac{{\left[r\right]}^k{x}^k}{\left[k\right]!}}{\displaystyle \frac{1}{E_q\left(\left[r\right]x\right)}}{\displaystyle \frac{\left[k\right]}{\left[r\right]}}\hfill \\ & & +{\displaystyle \frac{{(1+l_1)}^5-l_1^5}{\left[5\right]{([r+1]+d_1)}^4}}\sum _{k=0}^{\infty }{q}^{{\displaystyle \frac{k(k-1)}{2}}}{\displaystyle \frac{{\left[r\right]}^k{x}^k}{\left[k\right]!}}{\displaystyle \frac{1}{E_q\left(\left[r\right]x\right)}}\hfill \\ & & ={\displaystyle \frac{5q^4{\left[r\right]}^4}{\left[5\right]{([r+1]+d_1)}^4}}{\mathcal{S}}_{r,q}({ı}^4;x)+{\displaystyle \frac{10q^3(1+2l_1){\left[r\right]}^3}{\left[5\right]{([r+1]+d_1)}^4}}{\mathcal{S}}_{r,q}({ı}^3;x)\hfill \\ & & +{\displaystyle \frac{30q^2(1+l_1){\left[r\right]}^2}{\left[5\right]{([r+1]+d_1)}^4}}{\mathcal{S}}_{r,q}({ı}^2;x)+{\displaystyle \frac{5q\left({(1+l_1)}^4-l_1^4\right)\left[r\right]}{\left[5\right]{([r+1]+d_1)}^4}}{\mathcal{S}}_{r,q}(ı;x)\hfill \\ & & +{\displaystyle \frac{{(1+l_1)}^5-l_1^5}{\left[5\right]{([r+1]+d_1)}^4}}{\mathcal{S}}_{r,q}(1;x).\hfill \end{array}$$

Thus we complete the required results of Lemma 1. □

Corollary 1.

Let us denote the function ${(ı-x)}^j$ by ${\theta }_j$ for any $j=1,2,3,4$, then the central moments of order one and two for the operators ${\mathcal{N}}_{r,k,q}^{l_1,d_1}$ can be represented by:

$$\begin{array}{ccc}\hfill {\mathcal{N}}_{r,k,q}^{l_1,d_1}\left({\theta }_1;x\right)& & =({\displaystyle \frac{2q^2\left[r\right]}{\left[2\right]([r+1]+d_1)}}-1)x+{\displaystyle \frac{1+2l_1}{\left[2\right]([r+1]+d_1)}};\hfill \\ \hfill {\mathcal{N}}_{r,k,q}^{l_1,d_1}\left({\theta }_2;x\right)& & =({\displaystyle \frac{3q^3{\left[r\right]}^2}{\left[3\right]{([r+1]+d_1)}^2}}+1-{\displaystyle \frac{4q^2\left[r\right]}{\left[2\right]([r+1]+d_1)}})x^2\hfill \\ & & +({\displaystyle \frac{3q^2(q^2+1+2l_1)\left[r\right]}{\left[3\right]{([r+1]+d_1)}^2}}-{\displaystyle \frac{2(1+2l_1)}{\left[2\right]([r+1]+d_1)}})x\hfill \\ & & +{\displaystyle \frac{1+3l_1+3l_1^2}{\left[3\right]{([r+1]+d_1)}^2}};\hfill \end{array}$$

Corollary 2.

The central moments of order four for the operators ${\mathcal{N}}_{r,k,q}^{l_1,d_1}$ are written as follows:

$$\begin{array}{ccc}\hfill {\mathcal{N}}_{r,k,q}^{l_1,d_1}\left({\theta }_4;x\right)& & =\{{\displaystyle \frac{5q^2{\left[r\right]}^4}{\left[5\right]{([r+1]+d_1)}^4}}-{\displaystyle \frac{16q^3{\left[r\right]}^3}{\left[4\right]{([r+1]+d_1)}^3}}\hfill \\ & & +{\displaystyle \frac{18q^3{\left[r\right]}^2}{\left[3\right]{([r+1]+d_1)}^2}}-{\displaystyle \frac{8q^2\left[r\right]}{\left[2\right]([r+1]+d_1)}}+1\}{x}^4\hfill \\ & & +\{{\displaystyle \frac{5q^3\left(1+2q+3q^2+2(1+l_1)\right){\left[r\right]}^3}{\left[5\right]{([r+1]+d_1)}^4}}\hfill \\ & & -{\displaystyle \frac{8q^3(2q+4q^2+3+6l_1){\left[r\right]}^2}{\left[4\right]{([r+1]+d_1)}^3}}\hfill \end{array}$$

$$\begin{array}{ccc}& & +{\displaystyle \frac{3q^2(q^2+1+2l_1)\left[r\right]}{\left[3\right]{([r+1]+d_1)}^2}}-{\displaystyle \frac{4(1+2l_1)}{\left[2\right]([r+1]+d_1)}}\}{x}^3\hfill \\ & & +\{{\displaystyle \frac{5q^3\left(q^2+3q^3+3q^4+2q^2(1+2q)(1+2l_1)+6(1+l_1)\right){\left[r\right]}^2}{\left[5\right]{([r+1]+d_1)}^4}}\hfill \\ & & -{\displaystyle \frac{4q^2\left(4q^4+6q^2(3+2l_1)+12l_1(1+l_1)\right)\left[r\right]}{\left[4\right]{([r+1]+d_1)}^3}}\hfill \\ & & +{\displaystyle \frac{6(1+3l_1+3l_1^2)}{\left[3\right]{([r+1]+d_1)}^2}}\}{x}^2\hfill \\ & & +\{{\displaystyle \frac{5q^2\left(q^6+2q^4(1+2l_1)+6q^2(1+l_1)+5{(1+l_1)}^4-5l_1^4\right)\left[r\right]}{\left[5\right]{([r+1]+d_1)}^4}}\hfill \\ & & -{\displaystyle \frac{4{(1+l_1)}^4-4l_1^4}{\left[4\right]{([r+1]+d_1)}^3}}\}x+{\displaystyle \frac{{(1+l_1)}^5-l_1^5}{\left[5\right]{([r+1]+d_1)}^4}}.\hfill \end{array}$$

3. Convergence in Weighted Space

We recall the weighted spaces of the functions on ${\mathcal{R}}^{+}$, in accordance with Gadžiev’s [20], and further circumstances under which the corresponding theorem of P. P. Korovkin applies for such a kind of functions. Let $x\to \xi \left(x\right)$ be a continuous and strictly increasing function and $\nabla \left(x\right)=1+{\xi }^2\left(x\right)$, ${lim}_{x\to \infty }\nabla \left(x\right)=\infty$. Let $B_{\nabla }{\mathcal{R}}^{+}$ be a set of functions defined on ${\mathcal{R}}^{+}$ and satisfying

$$\left|f\left(x\right)\right|\le C_f\nabla \left(x\right)\},$$

(9)

where $C_f$ is a constant depending only on f. Its subset of continuous functions will be denoted by $C_{\nabla }{\mathcal{R}}^{+}$, i.e., $C_{\nabla }{\mathcal{R}}^{+}=B_{\nabla }{\mathcal{R}}^{+}\cap C{\mathcal{R}}^{+}$. It is well known (see [20]) that a sequence of linear positive operators ${\left\{K_m\right\}}_{m\ge 1}$ maps $C_{\nabla }{\mathcal{R}}^{+}$ into $B_{\nabla }{\mathcal{R}}^{+}$ if and only if

$$|K_m(\nabla ;x)|\le C\nabla \left(x\right)\},$$

(10)

where $\nabla \left(x\right)=1+{\xi }^2\left(x\right)$, $x\in {\mathcal{R}}^{+}$, C is a positive constant. We note that $B_{\nabla }{\mathcal{R}}^{+}$ is a normed space with the norm

$${\parallel f\parallel }_{\nabla }=\underset{x\in {\mathcal{R}}^{+}}{sup}{\displaystyle \frac{\left|f\right(x\left)\right|}{\nabla \left(x\right)}}.$$

Finally, let $C_{\nabla }^0{\mathcal{R}}^{+}$ is a subset of $C_{\nabla }{\mathcal{R}}^{+}$, such that the limit

$$\underset{m\to \infty }{lim}={\displaystyle \frac{f\left(x\right)}{\nabla \left(x\right)}}=C_f$$

exists and is finite. Moreover, Let $B[0,1]$ be the space of all bounded functions on $[0,1]$ and $C[0,1]$ be the space of all continuous functions f on $[0,1]$ equipped with norm

$${\parallel f\parallel }_{\infty }=\underset{x\in [0,1]}{sup}\left|f\left(x\right)\right|,$$

where $f\in C[0,1]$, then the famous Korovkin Theorem [21] give us:

Theorem 1

([21]). For the sequences of any positive linear operators ${\left\{K_m\right\}}_{m\ge 1}$ acting from $C[0,1]$ into $B[0,1]$, we have

$$\underset{m\to \infty }{lim}{\parallel K_m({ı}^j;x)-x^j\parallel }_{\infty }=0,j=0,1,2,$$

if and only if, for all $f\in C[0,1]$,

$$\underset{m\to \infty }{lim}{\parallel K_m(f(ı);x)-f\left(x\right)\parallel }_{\infty }=0.$$

Theorem 2

([20,22]). For the sequences of any positive linear operators ${\left\{K_m\right\}}_{m\ge 1}$ acting from $C_{\nabla }{\mathcal{R}}^{+}$ into $B_{\nabla }{\mathcal{R}}^{+}$, if we have

$$\underset{m\to \infty }{lim}{\parallel K_m({ı}^j;x)-x^j\parallel }_{\nabla }=0,j=0,1,2,$$

then for any $f\in C_{\nabla }^0{\mathcal{R}}^{+}$,

$$\underset{m\to \infty }{lim}{\parallel K_m(f(ı);x)-f\left(x\right)\parallel }_{\nabla }=0.$$

Theorem 3.

Let ${\mathcal{N}}_{r,k,q}^{l_1,d_1}$ be the operators defined by (5) and $\nabla \left(x\right)=1+x^2$. Then for every $\phi \in C_{\nabla }^0{\mathcal{R}}^{+}$ and $0<q<1$ we get

$$\begin{array}{c}\hfill \underset{\left[r\right]\to \infty }{lim}\Vert {\mathcal{N}}_{r,k,q}^{l_1,d_1}\left(\phi \right)-\phi {\left|\right|}_{\nabla }=0.\end{array}$$

Proof. 

Using the Korovkin’s theorem analogues, we obtain the results of Theorem 3 and note that

$$\begin{array}{c}\hfill \underset{\left[r\right]\to \infty }{lim}{\parallel {\mathcal{N}}_{r,k,q}^{l_1,d_1}\left({ı}^j\right)-x^j\parallel }_{\nabla }=0,forj=0,1,2.\end{array}$$

Easily obtainable from the Lemma 1

$$\parallel {\mathcal{N}}_{r,k,q}^{l_1,d_1}{\left(1\right)-1\parallel }_{\nabla }=\underset{x\in {\mathcal{R}}^{+}}{sup}{\displaystyle \frac{|{\mathcal{N}}_{r,k,q}^{l_1,d_1}(1;x)-1|}{\nabla \left(x\right)}}=0.$$

For $j=1$, we have

$$\begin{array}{ccc}\hfill \parallel {\mathcal{N}}_{r,k,q}^{l_1,d_1}{(ı;x)-x\parallel }_{\nabla }& & =\underset{x\in {\mathcal{R}}^{+}}{sup}{\displaystyle \frac{\left|{\mathcal{N}}_{r,k,q}^{l_1,d_1}(ı;x)-x\right|}{\nabla \left(x\right)}}\hfill \\ & & =\underset{x\in {\mathcal{R}}^{+}}{sup}{\displaystyle \frac{x}{\nabla \left(x\right)}}|{\displaystyle \frac{2q^2\left[r\right]}{\left[2\right]([r+1]+d_1)}}-1|\hfill \\ & & +\underset{x\in {\mathcal{R}}^{+}}{sup}{\displaystyle \frac{1}{\nabla \left(x\right)}}\left|{\displaystyle \frac{1+2l_1}{\left[2\right]([r+1]+d_1)}}\right|.\hfill \end{array}$$

It is simple to get $\parallel {\mathcal{N}}_{r,k,q}^{l_1,d_1}{(ı;x)-x\parallel }_{\nabla }\to 0$, if $\left[r\right]\to \infty ,$ since we have ${\displaystyle \frac{2q^2\left[r\right]}{\left[2\right]\left(\right[r+1]+d1)}}\to 1$ and ${\displaystyle \frac{1}{(q\left[r\right]+1+d_1)}}\to 0$. Similarly, for $j=2$, we get that

$$\begin{array}{ccc}\hfill \parallel {\mathcal{N}}_{r,k,q}^{l_1,d_1}({ı}^2;x)-x^2{\parallel }_{\nabla }& & =\underset{x\in {\mathcal{R}}^{+}}{sup}{\displaystyle \frac{\left|{\mathcal{N}}_{r,k,q}^{l_1,d_1}({ı}^2;x)-x^2\right|}{\nabla \left(x\right)}}\hfill \\ & & =\underset{x\in {\mathcal{R}}^{+}}{sup}{\displaystyle \frac{x^2}{\nabla \left(x\right)}}|{\displaystyle \frac{3q^3{\left[r\right]}^2}{\left[3\right]{([r+1]+d_1)}^2}}-1|\hfill \\ & & +\underset{x\in {\mathcal{R}}^{+}}{sup}{\displaystyle \frac{x}{\nabla \left(x\right)}}\left|{\displaystyle \frac{3q^2(q^2+1+2l_1)\left[r\right]}{\left[3\right]{([r+1]+d_1)}^2}}\right|\hfill \\ & & +\underset{x\in {\mathcal{R}}^{+}}{sup}{\displaystyle \frac{1}{\nabla \left(x\right)}}\left|{\displaystyle \frac{1+3l_1+3l_1^2}{\left[3\right]{([r+1]+d_1)}^2}}\right|\hfill \\ & & \le \underset{x\in {\mathcal{R}}^{+}}{max}{\displaystyle \frac{x^2}{\nabla \left(x\right)}}|{\displaystyle \frac{3q^3{\left[r\right]}^2}{\left[3\right]{([r+1]+d_1)}^2}}-1|\hfill \end{array}$$

$$\begin{array}{ccc}& & +\underset{x\in {\mathcal{R}}^{+}}{max}{\displaystyle \frac{x}{\nabla \left(x\right)}}\left|{\displaystyle \frac{3q^2(q^2+1+2l_1)\left[r\right]}{\left[3\right]{([r+1]+d_1)}^2}}\right|\hfill \\ & & +\underset{x\in {\mathcal{R}}^{+}}{max}{\displaystyle \frac{1}{\nabla \left(x\right)}}\left|{\displaystyle \frac{1+3l_1+3l_1^2}{\left[3\right]{([r+1]+d_1)}^2}}\right|\hfill \\ & & \le \underset{\left[r\right]\to \infty }{lim}\underset{q\to 1}{lim}max|{\displaystyle \frac{3q^3{\left[r\right]}^2}{\left[3\right]{([r+1]+d_1)}^2}}-1,\hfill \\ & & {\displaystyle \frac{3q^2(q^2+1+2l_1)\left[r\right]}{\left[3\right]{([r+1]+d_1)}^2}},{\displaystyle \frac{1+3l_1+3l_1^2}{\left[3\right]{([r+1]+d_1)}^2}}|.\hfill \end{array}$$

This makes it easy to get that $\parallel {\mathcal{N}}_{r,k,q}^{l_1,d_1}\left({ı}^2\right)-x^2{\parallel }_{\nabla }\to 0.$ □

Theorem 4.

For all $\phi \in C_{\nabla }^0{\mathcal{R}}^{+}$ and $0<q<1$, the operators ${\mathcal{N}}_{r,k,q}^{l1,d1}$ satisfying

$$\begin{array}{c}\hfill \underset{\left[r\right]\to \infty }{lim}\underset{x\in {\mathcal{R}}^{+}}{sup}{\displaystyle \frac{|{\mathcal{N}}_{r,k,q}^{l_1,d_1}(\phi ;x)-\phi \left(x\right)|}{{(\nabla \left(x\right))}^{1+p}}}=0,\end{array}$$

where the number p is a fixed positive number.

Proof. 

By taking into consideration the inequality $|\phi \left(x\right)|\le {\left|\right|\phi \left|\right|}_{\xi }(1+x^2)$, we can obtain equality for any real $x_0>0$.

$$\begin{array}{ccc}\hfill & & \underset{\left[r\right]\to \infty }{lim}\underset{x\in {\mathcal{R}}^{+}}{sup}{\displaystyle \frac{|{\mathcal{N}}_{r,k,q}^{l_1,d_1}(\phi ;x)-\phi \left(x\right)|}{{(\nabla \left(x\right))}^{1+p}}}\hfill \\ & & \le \underset{x\le x_0}{sup}{\displaystyle \frac{|{\mathcal{N}}_{r,k,q}^{l_1,d_1}(\phi ;x)-\phi \left(x\right)|}{{(\nabla \left(x\right))}^{1+p}}}+\underset{x\ge x_0}{sup}{\displaystyle \frac{|{\mathcal{N}}_{r,k,q}^{l_1,d_1}(\phi ;x)-\phi \left(x\right)|}{{(\nabla \left(x\right))}^{1+p}}}\hfill \\ & & \le \Vert {\mathcal{N}}_{r,k,q}^{l_1,d_1}(\phi ;x)-\phi \left(x\right){\Vert }_{C[0,x_0]}\hfill \\ & & +{\Vert \phi \Vert }_{\nabla }\underset{x\ge x_0}{sup}{\displaystyle \frac{|{\mathcal{N}}_{r,k,q}^{l_1,d_1}(1+{ı}^2;x)-\phi \left(x\right)|}{{(\nabla \left(x\right))}^{1+p}}}+\underset{x\ge x_0}{sup}{\displaystyle \frac{\left|\phi \right(x\left)\right|}{{(\nabla \left(x\right))}^{1+p}}}\hfill \\ & & ={\mathcal{Q}}_1+{\mathcal{Q}}_2+{\mathcal{Q}}_3,\left(wesuppose\right).\hfill \end{array}$$

Therefore, we get that

$${\mathcal{Q}}_3=\underset{x\ge x_0}{sup}{\displaystyle \frac{\left|\phi \right(x\left)\right|}{{(\nabla \left(x\right))}^{1+p}}}\le \underset{x\ge x_0}{sup}{\displaystyle \frac{{\Vert \phi \Vert }_{\nabla }(1+x^2)}{{(\nabla \left(x\right))}^{1+p}}}\le {\displaystyle \frac{{\Vert \phi \Vert }_{\nabla }}{{(1+x_0^2)}^p}}.$$

(11)

According to this, Lemma 1

$$\begin{array}{c}\hfill \underset{\left[r\right]\to \infty }{lim}\underset{x\ge x_0}{sup}{\displaystyle \frac{{\mathcal{N}}_{r,k,q}^{l_1,d_1}(1+{ı}^2;x)}{\nabla \left(x\right)}}=1.\end{array}$$

Now, for each and every Since there are some positive integers $r_1$ for ${ϵ}^{*}>0,$ we have equality for all $r\ge r_1$.

$$\begin{array}{c}\hfill \underset{x\ge x_0}{sup}{\displaystyle \frac{{\mathcal{N}}_{r,k,q}^{l_1,d_1}(1+{ı}^2;x)}{\nabla \left(x\right)}}\le {\displaystyle \frac{{(1+x_0^2)}^p}{{\left|\right|\phi \left|\right|}_{\nabla }}}{\displaystyle \frac{{ϵ}^{*}}{3}}+1.\end{array}$$

For all $r\ge r_1$

$${\mathcal{Q}}_2={\left|\right|\phi \left|\right|}_{\nabla }\underset{x\ge x_0}{sup}{\displaystyle \frac{{\mathcal{N}}_{r,k,q}^{l_1,d_1}(1+{ı}^2;x)}{{(\nabla \left(x\right))}^{1+p}}}\le {\displaystyle \frac{{\Vert \phi \Vert }_{\nabla }}{{(1+x_0^2)}^p}}+{\displaystyle \frac{{ϵ}^{*}}{3}}.$$

(12)

The equality light (11) and (12) make it clear that

$$\begin{array}{c}\hfill {\mathcal{Q}}_2+{\mathcal{Q}}_3\le 2{\displaystyle \frac{{\left|\right|\phi \left|\right|}_{\nabla }}{{(1+x_0^2)}^p}}+{\displaystyle \frac{{ϵ}^{*}}{3}}.\end{array}$$

For every $r\ge r_1$, we obtain ${\displaystyle \frac{{\Vert \phi \Vert }_{\nabla }}{{(1+x_0^2)}^p}}\le {\displaystyle \frac{{ϵ}^{*}}{6}}$ by selecting any real $x_0$, if so large.

$${\mathcal{Q}}_2+{\mathcal{Q}}_3\le {\displaystyle \frac{2{ϵ}^{*}}{3}}.$$

(13)

Conversely, if we take $r_2\ge r$, then it is clear that

$${\mathcal{Q}}_1=\left|\right|{\mathcal{N}}_{r,k,q}^{l_1,d_1}(\phi ;x)-\phi \left(x\right){\left|\right|}_{C[0,x_0]}\le {\displaystyle \frac{{ϵ}^{*}}{3}}.$$

(14)

Lastly, in the final section, we take $r_3=max(r_1,r_2)$. This allows us to easily obtain our results of Theorem 4 by combining the equality (13) and (14).

$$\begin{array}{c}\hfill \underset{x\in {\mathcal{R}}^{+}}{sup}{\displaystyle \frac{|{\mathcal{N}}_{r,k,q}^{l_1,d_1}(\phi ;x)-\phi \left(x\right)|}{{(\nabla \left(x\right))}^{1+p}}}<{ϵ}^{*}.\end{array}$$

□

4. Order of Convergence ${\mathcal{N}}_{\mathbf{r},\mathbf{k},\mathbf{q}}^{{\mathbf{l}}_{\mathbf{1}},{\mathbf{d}}_{\mathbf{1}}}$

In operator theory, the rate at which a sequence of operators approaches a limit or an objective is known as the rate of convergence. Let $f\in C\mathcal{R}\cup \left\{0\right\}$ be the set of all functions on $\mathcal{R}\cup \left\{0\right\}$ that are uniformly continuous. The modulus of continuation of f for order one is then provided by: for all $\tilde{\delta }>0$:

$$\begin{array}{c}\hfill \tilde{\omega }(f;\tilde{\delta })=\underset{|{ı}_1-{ı}_2|\le \tilde{\delta }}{sup}|f\left({ı}_1\right)-f\left({ı}_2\right)|,{ı}_1,{ı}_2\in \mathcal{R}\cup \left\{0\right\},\end{array}$$

$$\begin{array}{c}\hfill |f\left({ı}_1\right)-f\left({ı}_2\right)|\le \left(1+{\displaystyle \frac{|{ı}_1-{ı}_2|}{{\tilde{\delta }}^2}}\right)\tilde{\omega }(f;\tilde{\delta }).\end{array}$$

(15)

Additionally, the modulus of continuity for the function f defined on the closed interval $[0,\lambda ]$ is as follows for each positive real $\lambda$:

$$\begin{array}{c}\hfill {\tilde{\omega }}_{\lambda }(f;\tilde{\delta })=\underset{|{\Omega }_r\left(x\right)|\le \tilde{\delta }}{sup}\underset{x,ı\in [0,\lambda ]}{sup}|f(ı)-f\left(x\right)|.\end{array}$$

(16)

Theorem 5

([23]). Let $[u_1,v_1]\subseteq [u_2,v_2]$ and consider the sequence of positive and linear operators ${\left\{K_m\right\}}_{m\ge 1}$ acting from $C[u_1,v_1]$ into $C[u_2,v_2]$, then

1. 

for every $f\in C[u_1,v_1]$ and all $x\in [u_2,v_2]$ operators $K_m$ satisfying:

$$\begin{array}{ccc}\hfill |K_m(f;x)-f\left(x\right)|& \le & \left|f\left(x\right)\right||K_m(1;x)-1|\hfill \\ & & +\{K_m(1;x)+{\displaystyle \frac{1}{\tilde{\delta }}}\sqrt{K_m({\theta }_2;x)}\sqrt{K_m(1;x)}\}\tilde{\omega }(f;\tilde{\delta }),\hfill \end{array}$$

2. 

for every $g^{\prime }\in C[u_1,v_1]$ and $x\in [u_2,v_2],$ operators $K_m$ satisfying:

$$\begin{array}{ccc}\hfill |K_m(g;x)-g\left(x\right)|& \le & \left|g\left(x\right)\right||K_m(1;x)-1|+|g^{\prime }\left(x\right)\left|\right|K_m({\theta }_1;x)|\hfill \\ & & +K_m({\theta }_2;x)\{\sqrt{K_m(1;x)}+{\displaystyle \frac{1}{\tilde{\delta }}}\sqrt{K_m({\theta }_2;x)}\}\tilde{\omega }(g^{\prime };\tilde{\delta }).\hfill \end{array}$$

Theorem 6.

Let $0<q<1$ and $x\in \mathcal{R}\cup \left\{0\right\}$, then for every $f\in C\mathcal{R}\cup \left\{0\right\}$ operators ${\mathcal{N}}_{r,k,q}^{l_1,d_1}$ satisfying:

$$\begin{array}{ccc}\hfill |{\mathcal{N}}_{r,k,q}^{l_1,d_1}(f;x)-f\left(x\right)|& \le & 2\tilde{\omega }\left(f;\sqrt{{\tilde{\delta }}_{r,q}\left(x\right)}\right),\hfill \end{array}$$

where $\tilde{\delta }=\sqrt{{\mathcal{N}}_{r,k,q}^{l_1,d_1}({\theta }_2;x))}=\sqrt{{\delta }_{r,k,q}^{l_1,d_1}\left(x\right)}$.

Proof. 

Given the findings of Corollary 1 and Theorem 5, it is evident that

$$\begin{array}{ccc}\hfill |{\mathcal{N}}_{r,k,q}^{l_1,d_1}(f;x)-f\left(x\right)|& \le & |f\left(x\right)\Vert {\mathcal{N}}_{r,k,q}^{l_1,d_1}(1;x)-1|+\{{\mathcal{N}}_{r,k,q}^{l_1,d_1}(1;x)\hfill \\ & & +{\displaystyle \frac{1}{\tilde{\delta }}}\sqrt{{\mathcal{N}}_{r,k,q}^{l_1,d_1}({\theta }_2;x)}\sqrt{{\mathcal{N}}_{r,k,q}^{l_1,d_1}(1;x)}\}\tilde{\omega }(f;\tilde{\delta }),\hfill \end{array}$$

where if we take $\tilde{\delta }=\sqrt{{\delta }_{r,k,q}^{l_1,d_1}\left(x\right)}=\sqrt{{\mathcal{N}}_{r,k,q}^{l1,d1}({\theta }_2;x)}$ then easy to get results. □

Theorem 7.

Consider $0<q<1$, $x\in \mathcal{R}\cup \left\{0\right\}$ and $g^{\prime }\in C\mathcal{R}\cup \left\{0\right\}$. Then, operators ${\mathcal{N}}_{r,k,q}^{l_1,d_1}$ satisfying:

$$\begin{array}{ccc}\hfill |{\mathcal{N}}_{r,k,q}^{l_1,d_1}(g;x)-g\left(x\right)|& & \le \left|\right({\displaystyle \frac{2q^2\left[r\right]}{\left[2\right]([r+1]+d_1)}}-1)x+{\displaystyle \frac{1+2l_1}{\left[2\right]([r+1]+d_1)}}|\left|{\xi }^{\prime }\left(x\right)\right|\hfill \\ & & +2{\delta }_{r,k,q}^{l_1,d_1}\left(x\right)\tilde{\omega }\left(g^{\prime };\sqrt{{\delta }_{r,k,q}^{l_1,d_1}\left(x\right)}\right),\hfill \end{array}$$

where $\tilde{\delta }=\sqrt{{\delta }_{r,k,q}^{l_1,d_1}\left(x\right)}=\sqrt{{\mathcal{N}}_{r,k,q}^{l_1,d_1}({\theta }_2;x)}$.

Proof. 

Taking into account the findings of Theorem 5 and Corollary 1, it is clear that

$$\begin{array}{ccc}\hfill |{\mathcal{N}}_{r,k,q}^{l_1,d_1}(g;x)-g\left(x\right)|& & \le |{\mathcal{N}}_{r,k,q}^{l_1,d_1}(1;x)-1\Vert g\left(x\right)|+|g^{\prime }\left(x\right)\Vert {\mathcal{N}}_{r,k,q}^{l_1,d_1}({\theta }_1;x)|\hfill \\ & & +{\mathcal{N}}_{r,k,q}^{l_1,d_1}({\theta }_2;x)\{\sqrt{{\mathcal{N}}_{r,k,q}^{l_1,d_1}(1;x)}+{\displaystyle \frac{1}{\tilde{\delta }}}\sqrt{{\mathcal{N}}_{r,k,q}^{l_1,d_1}({\theta }_2;x)}\}\tilde{\omega }\left(g^{\prime };\tilde{\delta }\right)\hfill \\ & & \le |{\displaystyle \frac{2q^2\left[r\right]}{\left[2\right]([r+1]+d_1)}}x+{\displaystyle \frac{1+2l_1}{\left[2\right]([r+1]+d_1)}}-x|\left|g^{\prime }\left(x\right)\right|\hfill \\ & & +{\mathcal{N}}_{r,k,q}^{l_1,d_1}({\theta }_2;x)\{\sqrt{{\mathcal{N}}_{r,k,q}^{l_1,d_1}(1;x)}+{\displaystyle \frac{1}{\tilde{\delta }}}\sqrt{{\mathcal{N}}_{r,k,q}^{l_1,d_1}({\theta }_2;x)}\}\tilde{\omega }\left(g^{\prime };\tilde{\delta }\right)\hfill \\ & & \le \left|\right({\displaystyle \frac{2q^2\left[r\right]}{\left[2\right]([r+1]+d_1)}}-1)x+{\displaystyle \frac{1+2l_1}{\left[2\right]([r+1]+d_1)}}|\left|g^{\prime }\left(x\right)\right|\hfill \\ & & +2{\delta }_{r,k,q}^{l_1,d_1}\left(x\right)\tilde{\omega }\left(g^{\prime };\sqrt{{\delta }_{r,k,q}^{l_1,d_1}\left(x\right)}\right),\hfill \end{array}$$

where, $\tilde{\delta }=\sqrt{{\delta }_{r,k,q}^{l_1,d_1}\left(x\right)}=\sqrt{{\mathcal{N}}_{r,k,q}^{l_1,d_1}({\theta }_2;x)}$, then it is easy to get our desired results. □

Theorem 8.

Suppose that $0<q<1$ and $x\in [0,\Lambda ]$ with $\Lambda >0$. Then, for all $f\in C\mathcal{R}\cup \left\{0\right\}$ we get the inequality:

$$\begin{array}{c}\hfill \parallel {\mathcal{N}}_{r,k,q}^{l_1,d_1}{(f;x)-f\left(x\right)\parallel }_{C[0,\Lambda ]}\le 4C_f(1+{\Lambda }^2){\tilde{\delta }}_{r,q}(\Lambda )+2{\tilde{\omega }}_{\Lambda +1}(f;\sqrt{{\tilde{\delta }}_{r,q}(\Lambda )}),\end{array}$$

where ${\displaystyle {\tilde{\delta }}_{r,q}(\Lambda )=\underset{x\in [0,\Lambda ]}{max}{\mathcal{N}}_{r,k,q}^{l_1,d_1}({\theta }_2;x)}$ and ${\tilde{\omega }}_{\Lambda +1}(f;\tilde{\delta })$ obtained on $[0,\Lambda +1]\subset \mathcal{R}\cup \left\{0\right\}$, and $C_f$ is constant and depends on f.

Proof. 

Consider the inequality for any $x\in [0,\Lambda ]$, $ı\in \mathcal{R}\cup \left\{0\right\}$, and $\Delta >0$.

$$\begin{array}{c}\hfill |f(ı)-f\left(x\right)|\le 4C_f(1+{\Lambda }^2)({\theta }_2+\left({\displaystyle \frac{|{\theta }_1|}{\Delta }}+1\right){\tilde{\omega }}_{\Lambda +1}(f;\Delta ).\end{array}$$

Apply ${\mathcal{N}}_{r,k,q}^{l_1,d_1}$ to get

$$\begin{array}{ccc}\hfill |{\mathcal{N}}_{r,k,q}^{l_1,d_1}(f;x)-f\left(x\right)|& \le & 4M_f(1+{\Lambda }^2){\mathcal{N}}_{r,k,q}^{l_1,d_1}({\theta }_2;x)\hfill \\ & & +\left(1+{\displaystyle \frac{{\mathcal{N}}_{r,k,q}^{l_1,d_1}\left(\right|{\theta }_1|;x)}{\Delta }}\right){\tilde{\omega }}_{\Lambda +1}(f;\Delta )\hfill \\ & \le & 4M_f(1+{\Lambda }^2)\Delta +\left(1+{\displaystyle \frac{\sqrt{{\mathcal{N}}_{r,k,q}^{l_1,d_1}({\theta }_2;x)}}{\Delta }}\right){\tilde{\omega }}_{\Lambda +1}(f;\Delta ),\hfill \end{array}$$

where suppose ${\displaystyle \Delta =\sqrt{{\Delta }_{r,k,q}^{l_1,d_1}\left(\lambda \right)}=\underset{x\in [0,\Lambda ]}{max}\sqrt{{\mathcal{N}}_{r,k,q}^{l_1,d_1}({\theta }_2;x)}}$. □

5. Approximation in Lipschitz Class

In this section, the rate of convergence in terms of the Lipschitz maximum function is determined for the operators ${\mathcal{N}}_{r,k,q}^{l_1,d_1}$. The Lipschitz space that we use, [24], contains the following relations:

$$\begin{array}{c}\hfill Li{p}_{\mathcal{P}}^{{\gamma }_1,{\gamma }_2}\left(\alpha \right):=\left\{\chi \in C_B\mathcal{R}\cup \left\{0\right\}:|\chi (ı)-\chi \left(x\right)|\le M{\displaystyle \frac{{|ı-x|}^{\alpha }}{{(ı+{\gamma }_{1}x+{\gamma }_2{x}^2)}^{\frac{\alpha }{2}}}}:x,ı\in \mathcal{R}\cup \left\{0\right\}\right\},\end{array}$$

where the set of all continuously bounded functions on $\mathcal{R}\cup \left\{0\right\}$ be $C_B\mathcal{R}\cup \left\{0\right\}$ and has explicit properties for $M>0$, $0<\alpha \le 1$, ${\gamma }_1,{\gamma }_2>0$.

Theorem 9.

Take $x\in \mathcal{R}\cup \left\{0\right\}$, $0<q<1$ and $\chi \in Li{p}_{\mathcal{P}}^{{\gamma }_1,{\gamma }_2}\left(\alpha \right)$. Then, for $0<\alpha \le 1$, the operators ${\mathcal{N}}_{r,k,q}^{l_1,d_1}$ satisfy:

$$\begin{array}{c}\hfill |{\mathcal{N}}_{r,k,q}^{l_1,d_1}(\chi ;x)-\chi \left(x\right)|\le M{\left({\displaystyle \frac{{\delta }_{r,k,q}^{l_1,d_1}\left(x\right)}{{\gamma }_{1}x+{\gamma }_2{x}^2}}\right)}^{{\displaystyle \frac{\alpha }{2}}},\end{array}$$

(17)

where ${\gamma }_1,{\gamma }_2\in (0,\infty )$ and ${\delta }_{r,k,q}^{l_1,d_1}\left(x\right)={\mathcal{N}}_{r,k,q}^{l_1,d_1}({\theta }_2;x)$ given by Theorem 7.

Proof. 

Take $\alpha =1$ and $x\in \mathcal{R}\cup \left\{0\right\}$, then

$$\begin{array}{ccc}\hfill |{\mathcal{N}}_{r,k,q}^{l_1,d_1}(\chi ;x)-\chi \left(x\right)|& & \le {\mathcal{N}}_{r,k,q}^{l_1,d_1}\left(\right|\chi (ı)-\chi \left(x\right)|;x)\hfill \\ & & \le M{\mathcal{N}}_{r,k,q}^{l_1,d_1}\left({\displaystyle \frac{|{\theta }_1|}{{(ı+{\gamma }_{1}x+{\gamma }_2{x}^2)}^{\frac{1}{2}}}};x\right).\hfill \end{array}$$

From hypothesis for all $x\in \mathcal{R}$, we know ${\displaystyle \frac{1}{ı+{\gamma }_{1}x+{\gamma }_2{x}^2}<\frac{1}{{\gamma }_{1}x+{\gamma }_2{x}^2}}$, therefore,

$$\begin{array}{ccc}\hfill |{\mathcal{N}}_{r,k,q}^{l_1,d_1}(\chi ;x)-\chi \left(x\right)|& & \le {\displaystyle \frac{M}{{({\gamma }_{1}x+{\gamma }_2{x}^2)}^{\frac{1}{2}}}}{\left({\mathcal{N}}_{r,k,q}^{l_1,d_1}({\theta }_2;x)\right)}^{{\displaystyle \frac{1}{2}}}\hfill \\ & & \le M{\left({\displaystyle \frac{{\delta }_{r,k,q}^{l_1,d_1}}{{\gamma }_{1}x+{\gamma }_2{x}^2}}\right)}^{{\displaystyle \frac{1}{2}}}.\hfill \end{array}$$

Therefore, for $\alpha =1$, the Theorem 9 holds true. Now, if we enter the well-known Hölder’s inequality if $\alpha \in (0,1)$, we get

$$\begin{array}{ccc}\hfill |{\mathcal{N}}_{r,k,q}^{l_1,d_1}(\chi ;x)-\chi \left(x\right)|& & \le {\left({\mathcal{N}}_{r,k,q}^{l_1,d_1}{\left(\right|\chi (ı)-\chi \left(x\right)|}^{{\displaystyle \frac{2}{\alpha }}};x)\right)}^{{\displaystyle \frac{\alpha }{2}}}\hfill \\ & & \le M{\left({\mathcal{N}}_{r,k,q}^{l_1,d_1}\left({\displaystyle \frac{|{\theta }_1{|}^2}{(ı+{\gamma }_{1}x+{\gamma }_2{x}^2)}};x\right)\right)}^{{\displaystyle \frac{\alpha }{2}}}\hfill \\ & & \le M{\left({\displaystyle \frac{{\mathcal{N}}_{r,k,q}^{l_1,d_1}\left(\right|{\theta }_1{|}^2;x)}{{\gamma }_{1}x+{\gamma }_2{x}^2}}\right)}^{{\displaystyle \frac{\alpha }{2}}}\hfill \\ & & \le M{\left({\displaystyle \frac{{\delta }_{r,k,q}^{l_1,d_1}\left(x\right)}{{\gamma }_{1}x+{\gamma }_2{x}^2}}\right)}^{{\displaystyle \frac{\alpha }{2}}}.\hfill \end{array}$$

Hence, we get the proof. □

In order to find the operators ${\mathcal{N}}_{r,k,q}^{l_1,d_1}$ local approximation in Lipschitz space, we use the function results from [25], which are as follows:

$$\begin{array}{c}\hfill {\tilde{\omega }}_{\alpha }(\chi ;x)=\underset{ı\ne x,ı\in (0,\infty )}{sup}{\displaystyle \frac{\left|\chi \right(ı)-\chi (x\left)\right|}{|{\theta }_1{|}^{\alpha }}},\alpha \in (0,1]\mathrm{and}x\in \mathcal{R}\cup \left\{0\right\}.\end{array}$$

(18)

Theorem 10.

Take $0<q<1$ and $\chi \in C_B\mathcal{R}\cup \left\{0\right\}$, then for any $\alpha \in (0,1]$ operators ${\mathcal{N}}_{r,k,q}^{l_1,d_1}$ provide the inequality:

$$\begin{array}{c}\hfill |{\mathcal{N}}_{r,k,q}^{l_1,d_1}(\chi ;x)-\chi \left(x\right)|\le {\left({\delta }_{r,k,q}^{l_1,d_1}\left(x\right)\right)}^{{\displaystyle \frac{\alpha }{2}}}{\tilde{\omega }}_{\alpha }(\chi ;x).\end{array}$$

Proof. 

Easily we see that

$$\begin{array}{c}\hfill |{\mathcal{N}}_{r,k,q}^{l_1,d_1}(\chi ;x)-\chi \left(x\right)|\le {\mathcal{N}}_{r,k,q}^{l_1,d_1}\left(\right|\chi (ı)-\chi \left(x\right)|;x).\end{array}$$

Apply equality (18), and it is clear to obtain from Ḧolder’s inequality

$$\begin{array}{ccc}\hfill |{\mathcal{N}}_{r,k,q}^{l_1,d_1}(\chi ;x)-\chi \left(x\right)|& \le & {\tilde{\omega }}_{\alpha }(\chi ;x){\mathcal{N}}_{r,k,q}^{l_1,d_1}\left(\right|{\theta }_1{|}^{\alpha };x)\le {\tilde{\omega }}_{\alpha }(\chi ;x){\left({\mathcal{N}}_{r,k,q}^{l_1,d_1}\left(\right|{\theta }_1{|}^2;x)\right)}^{{\displaystyle \frac{\alpha }{2}}},\hfill \end{array}$$

which completes the result. □

6. Direct Approximation

Some direct approximation results based on the prominent K-functional characteristic are presented in this section. A straightforward estimate Theorems in mathematical analysis show how a function’s smoothness affects how well simpler functions, such as polynomials, can approximate it. Recall the many K-functional characteristics from [26], such as the following: We assume that $C_B\mathcal{R}\cup \left\{0\right\}$ is a class of all continuous and bounded functions constructed for the interval $\mathcal{R}\cup \left\{0\right\}$. For any $\tilde{\Delta }>0$ property of the K-functional for any $\chi \in C\mathcal{R}\cup \left\{0\right\}$ is provided by:

$${\mathcal{K}}_{\rho }(\chi ;\tilde{\Delta })=inf\left\{\left(\left|\right|\chi -{\rho \left|\right|}_{C_B\mathcal{R}\cup \left\{0\right\}}+\tilde{\Delta }{\left|\left|{\rho }^{″}\right|\right|}_{C_B\mathcal{R}\cup \left\{0\right\}}\right):\rho ,{\rho }^{\prime }\in C_B^2\mathcal{R}\cup \left\{0\right\}\right\},$$

(19)

$$C_B^r\mathcal{R}\cup \left\{0\right\}=\left\{\chi :\chi \in C_B\mathcal{R}\cup \left\{0\right\},r\in N;suchthat\underset{x\to \infty }{lim}{\displaystyle \frac{f\left(x\right)}{1+x^2}}=k_{\chi }<\infty \right\}.$$

(20)

For a real number M that is absolutely positive, one has

$$\begin{array}{c}\hfill {\mathcal{K}}_{\rho }(\chi ;\tilde{\Delta })\le M\left\{min(1,\tilde{\Delta })+{\overline{\omega }}_2(\chi ;\sqrt{\tilde{\Delta }}){\Vert \chi \Vert }_{C_B\mathcal{R}\cup \left\{0\right\}}\right\},\end{array}$$

${\overline{\omega }}_2(\chi ;\tilde{\Delta })$ is the modulus of continuity maximum order two, such that

$${\tilde{\omega }}_2(\chi ;\tilde{\Delta })=\underset{0<\vartheta <\tilde{\Delta }}{sup}\underset{x\in \mathcal{R}\cup \left\{0\right\}}{sup}|\chi (x+2\vartheta )-2\chi (x+\vartheta )+\chi \left(x\right)|.$$

(21)

On the other hand, the usual modulus of continuity is provided by

$$\tilde{\omega }(\chi ;\tilde{\Delta })=\underset{0<\vartheta <\tilde{\Delta }}{sup}\underset{x\in [0,\infty )}{sup}|\chi (x+\vartheta )-\chi \left(x\right)|.$$

(22)

Theorem 11.

Suppose $C_B^2\mathcal{R}\cup \left\{0\right\}$ denotes the second order continuously bounded function on $\mathcal{R}\cup \left\{0\right\}$. For an arbitrary $\phi \in C_B^2\mathcal{R}\cup \left\{0\right\}$, let we define the auxiliary operators ${\mathcal{O}}_{r,k,q}^{l_1,d_1}$ such that:

$${\mathcal{O}}_{r,k,q}^{l_1,d_1}(\phi ;x)={\mathcal{N}}_{r,k,q}^{l_1,d_1}(\phi ;x)+\phi \left(x\right)-\phi \left\{\right({\displaystyle \frac{2q^2\left[r\right]}{\left[2\right]([r+1]+d_1)}})x+{\displaystyle \frac{1+2l_1}{\left[2\right]([r+1]+d_1)}}\}.$$

(23)

Then, for any $\chi \in C_B^2\mathcal{R}\cup \left\{0\right\}$ we get the following inequality:

$$\begin{array}{c}\hfill \left|{\mathcal{O}}_{r,k,q}^{l_1,d_1}(\chi ;x)-\chi \left(x\right)\right|\le \left\{{\delta }_{r,k,q}^{l_1,d_1}\left(x\right)+\left[\right({\displaystyle \frac{2q^2\left[r\right]}{\left[2\right]([r+1]+d_1)}}-1)x+{\displaystyle \frac{1+2l_1}{\left[2\right]([r+1]+d_1)}}{]}^2\right\}\Vert {\chi }^{″}\Vert \end{array}$$

where Theorem 7 defines ${\delta }_{r,k,q}^{l_1,d_1}\left(x\right)$.

Proof. 

If $\chi (ı)=1$ and any $\chi \in C_B^2\mathcal{R}\cup \left\{0\right\}$, then it is clear that ${\mathcal{O}}_{r,k,q}^{l_1,d_1}(1;x)=1$ and for $\chi (ı)=ı$

$$\begin{array}{c}\hfill {\mathcal{O}}_{r,k,q}^{l_1,d_1}(t;x)={\mathcal{N}}_{r,k,q}^{l_1,d_1}(ı;x)+x-\left\{\right({\displaystyle \frac{2q^2\left[r\right]}{\left[2\right]([r+1]+d_1)}})x+{\displaystyle \frac{1+2l_1}{\left[2\right]([r+1]+d_1)}}\}=x.\end{array}$$

We have

$$\begin{array}{c}\hfill \Vert {\mathcal{N}}_{r,k,q}^{l_1,d_1}(\phi ;x)\Vert \le \Vert \phi \Vert ,\end{array}$$

and

$$\begin{array}{c}\hfill \mid {\mathcal{O}}_{r,k,q}^{l_1,d_1}(\phi ;x)\mid \le \mid {\mathcal{N}}_{r,k,q}^{l_1,d_1}(\phi ;x)\mid +\mid \phi \left(x\right)\mid +\left|\phi \right({\mathcal{N}}_{r,k,q}^{l_1,d_1}(ı;x)\left)\right|\le 3\Vert \phi \Vert .\end{array}$$

(24)

The Taylor series expression for any $\chi \in C_B^2\mathcal{R}\cup \left\{0\right\}$ gives us

$$\begin{array}{c}\hfill \chi (ı)=\chi \left(x\right)+\left({\theta }_1\right){\chi }^{\prime }\left(x\right)+{\int }_x^t(ı-\vartheta ){\chi }^{″}\left(\vartheta \right)\mathrm{d}\vartheta .\end{array}$$

Operating ${\mathcal{O}}_{r,k,q}^{l_1,d_1},$ it is simple to get

$$\begin{array}{ccc}& & {\mathcal{O}}_{r,k,q}^{l_1,d_1}(\chi ;x)-\chi \left(x\right)\hfill \\ & & ={\xi }^{\prime }\left(x\right){\mathcal{O}}_{r,k,q}^{l_1,d_1}({\Omega }_r\left(x\right);x)+{\mathcal{O}}_{r,k,q}^{l_1,d_1}\left({\int }_x^{ı}(ı-\vartheta ){\chi }^{″}\left(\vartheta \right){\mathrm{d}}_q\vartheta ;x\right)\hfill \\ & & ={\mathcal{O}}_{r,k,q}^{l_1,d_1}\left({\int }_x^{ı}(ı-\vartheta ){\chi }^{″}\left(\vartheta \right){\mathrm{d}}_q\vartheta ;x\right)\hfill \\ & & ={\mathcal{N}}_{r,k,q}^{l_1,d_1}\left({\int }_x^{ı}(ı-\vartheta ){\chi }^{″}\left(\vartheta \right){\mathrm{d}}_q\vartheta ;x\right)+{\int }_x^x(x-\vartheta ){\chi }^{″}\left(\vartheta \right){\mathrm{d}}_q\vartheta ;x\hfill \\ & & -{\int }_x^{{\mathcal{N}}_{r,k,q}^{l_1,d_1}(ı;x)}\left({\mathcal{N}}_{r,k,q}^{l_1,d_1}(ı;x)\right)-\vartheta ){\xi }^{″}\left(\vartheta \right){\mathrm{d}}_q\vartheta ;\hfill \end{array}$$

$$\begin{array}{ccc}& & \mid {\mathcal{O}}_{r,k,q}^{l_1,d_1}(\chi ;x)-\chi \left(x\right)\mid \hfill \\ & & \le \left|{\mathcal{N}}_{r,k,q}^{l_1,d_1}\left({\int }_x^{ı}(ı-\vartheta ){\chi }^{″}\left(\vartheta \right){\mathrm{d}}_q\vartheta ;x\right)\right|\hfill \\ & & +\left|{\int }_x^{{\mathcal{N}}_{r,k,q}^{l_1,d_1}(ı;x)}\right({\mathcal{N}}_{r,k,q}^{l_1,d_1}(ı;x))-\vartheta ){\chi }^{″}\left(\vartheta \right){\mathrm{d}}_q\vartheta |.\hfill \end{array}$$

We know the inequality

$$\begin{array}{c}\hfill \left|{\int }_x^{ı}(ı-\vartheta ){\chi }^{″}\left(\vartheta \right){\mathrm{d}}_q\vartheta \right|\le {\left({\Omega }_r\left(x\right)\right)}^2\Vert {\chi }^{″}\Vert \end{array}$$

and

$$\begin{array}{ccc}& & \left|{\int }_x^{{\mathcal{N}}_{r,k,q}^{l_1,d_1}(ı;x)}\right({\mathcal{N}}_{r,k,q}^{l_1,d_1}(ı;x))-\vartheta ){\chi }^{″}\left(\vartheta \right){\mathrm{d}}_q\vartheta |\hfill \\ & & \le \left\{\right({\displaystyle \frac{2q^2\left[r\right]}{\left[2\right]([r+1]+d_1)}}-1)x+{\displaystyle \frac{1+2l_1}{\left[2\right]([r+1]+d_1)}}{\}}^2\Vert {\chi }^{″}\Vert .\hfill \end{array}$$

Thus we get

$$\begin{array}{ccc}\hfill \mid {\mathcal{O}}_{r,k,q}^{l_1,d_1}(\chi ;x)-\chi \left(x\right)\mid & & \le \{{\mathcal{N}}_{r,k,q}^{l_1,d_1}\left({\theta }_2;x\right)\hfill \\ & & +\left(\right({\displaystyle \frac{2q^2\left[r\right]}{\left[2\right]([r+1]+d_1)}}-1)x+{\displaystyle \frac{1+2l_1}{\left[2\right]([r+1]+d_1)}}{)}^2\}\Vert {\chi }^{″}\Vert .\hfill \end{array}$$

This completes our result. □

Next, we use the Ditzian–Totik uniform modulus of smoothness for the maximal second order to provide some global approximation results. We review the standard basic formulas for the first- and second-order uniform modulus of smoothness in a way that

$$\begin{array}{c}\hfill \omega (f,\Delta ):=\underset{0<\left|\rho \right|\le \Delta }{sup}\underset{x,x+\rho \Lambda \left(x\right)\in \mathcal{R}\cup \left\{0\right\}}{sup}\left\{\right|\chi (x+\rho \Lambda \left(x\right))-\chi \left(x\right)\left|\right\};\end{array}$$

$$\begin{array}{c}\hfill {\omega }_2^{\Lambda }(\chi ,\Delta ):=\underset{0<\left|\rho \right|\le \Delta }{sup}\underset{x,x\pm \rho \Lambda \left(x\right)\in \mathcal{R}\cup \left\{0\right\}}{sup}\left\{\right|\chi (x+\rho \Lambda \left(x\right))-2\chi \left(x\right)+\chi (x-\rho \Lambda \left(x\right))\left|\right\},\end{array}$$

Given that the admissible step-weight function $\Lambda$ is specified on $[{\sigma }_1,{\sigma }_2]$, $\Lambda \left(x\right)={\left[(x-{\sigma }_1)({\sigma }_2-x)\right]}^{1/2}$ is entered if $x\in [{\sigma }_1,{\sigma }_2]$ (see [27]). The Peetre’s K-functional is provided by, and $AC$ stands for the set of all absolutely continuous functions.

$$\begin{array}{c}\hfill K_{2,\Lambda \left(x\right)}(\chi ,\Delta )=\underset{\phi \in W^2(\Lambda )}{inf}\left\{\Vert \chi -{\phi \Vert }_{C\mathcal{R}\cup \left\{0\right\}}+\Delta \Vert {\Lambda }^2{\phi }^{″}{\Vert }_{C\mathcal{R}\cup \left\{0\right\}}:\phi \in C^2\mathcal{R}\cup \left\{0\right\}\right\},\end{array}$$

where we have $\Delta >0$, $W^2(\Lambda )=\{\phi \in C\mathcal{R}\cup \left\{0\right\}:{\phi }^{\prime }\in AC\mathcal{R}\cup \left\{0\right\},{\Lambda }^2{\phi }^{″}\in C\mathcal{R}\cup \left\{0\right\}\}$ and $C^2\mathcal{R}\cup \left\{0\right\}=\{\phi \in C\mathcal{R}\cup \left\{0\right\}:{\phi }^{\prime },{\phi }^{″}\in C\mathcal{R}\cup \left\{0\right\}\}$.

Remark 1

([28]). One has for every absolute positive constant M

$$\begin{array}{c}\hfill M^{-1}{\omega }_2(\chi ,\sqrt{\Delta })\le K_{2,\Lambda \left(x\right)}(\chi ,\Delta )\le M{\omega }_2(\chi ,\sqrt{\Delta }).\end{array}$$

(25)

Theorem 12.

Let $0<q<1$ and $x\in \mathcal{R}\cup \left\{0\right\}$. In addition, we suppose Λ be the step-weight function with $(\Lambda \ne 0)$ from the modulus of smoothness such that ${\Lambda }^2$ is concave. Then, for all $\chi \in AC\mathcal{R}\cup \left\{0\right\}$ the operators ${\mathcal{O}}_{r,k,q}^{l_1,d_1}$ give the following identity:

$$\begin{array}{c}\hfill |{\mathcal{O}}_{r,k,q}^{l_1,d_1}\left(\chi ;x\right)-\chi \left(x\right)|\le M{\omega }_2\left(\chi ,{\displaystyle \frac{{[d_{r,k,q}^{l_1,d_1}\left(x\right)+l_{r,k,q}^{l_1,d_1}\left(x\right)]}^{1/2}}{2{\left[(x-{\sigma }_1)({\sigma }_2-x)\right]}^{1/2}}}\right)+\omega \left(\chi ,{\displaystyle \frac{l_{r,k,q}^{l_1,d_1}\left(x\right)}{\Lambda \left(x\right)}}\right),\end{array}$$

where $l_{r,k,q}^{l_1,d_1}\left(x\right)={\mathcal{N}}_{r,k,q}^{l_1,d_1}({\theta }_1;x)$ and $d_{r,k,q}^{l_1,d_1}\left(x\right)={\mathcal{N}}_{r,k,q}^{l_1,d_1}({\theta }_2;x).$

Proof. 

We can write the auxiliary operators:

$$\begin{array}{c}\hfill {\mathcal{O}}_{r,k,q}^{l_1,d_1}(\chi ;x)={\mathcal{N}}_{r,k,q}^{l_1,d_1}\left(\chi ;x\right)+\chi \left(x\right)-\chi \left(l_{r,k,q}^{l_1,d_1}\left(x\right)+x\right),\end{array}$$

(26)

where $\chi \in C\mathcal{R}\cup \left\{0\right\}$ and $x\in \mathcal{R}\cup \left\{0\right\}$, it is simple to obtain the following relations using by Lemma 1. ${\mathcal{O}}_{r,k,q}^{l_1,d_1}(1;x)=1\mathrm{and}{\mathcal{O}}_{r,k,q}^{l_1,d_1}(ı;x)=x,$${\mathcal{O}}_{r,k,q}^{l_1,d_1}({\theta }_1;x)=0$.

Assume that $x=\rho x+(1-\rho )ı$, $\rho \in [0,1]$. The concavity of ${\Lambda }^2$ on $[0,1]$ implies that ${\Lambda }^2\left(x\right)\ge l{\Lambda }^2\left(x\right)+(1-l){\Lambda }^2(ı)$ and

$$\begin{array}{c}\hfill {\displaystyle \frac{|ı-x|}{{\Lambda }^2\left(x\right)}}\le {\displaystyle \frac{\rho |x-ı|}{\rho {\Lambda }^2\left(x\right)+(1-\rho ){\Lambda }^2(ı)}}\le {\displaystyle \frac{|{\Omega }_r\left(x\right)|}{{\Lambda }^2\left(x\right)}}.\end{array}$$

(27)

The identities we acquire are as follows:

$$\begin{array}{cc}\hfill |{\mathcal{O}}_{r,k,q}^{l_1,d_1}(\chi ;x)-\chi \left(x\right)|& \le |{\mathcal{O}}_{r,k,q}^{l_1,d_1}(\chi -\phi ;x)|+|{\mathcal{O}}_{r,k,q}^{l_1,d_1}(\phi ;x)-\phi \left(x\right)|+|\chi \left(x\right)-\phi \left(x\right)|\hfill \\ \hfill & \le {4\parallel \chi -\phi \parallel }_{C[0,\infty )}+|{\mathcal{O}}_{r,q}^{\zeta ,\alpha }(\phi ;x)-\phi \left(x\right)|.\hfill \end{array}$$

(28)

We can reproduce from the Taylor’s series that

$$\begin{array}{ccc}\hfill |{\mathcal{O}}_{r,k,q}^{l_1,d_1}(\phi ;x)-\phi \left(x\right)|& \le & {\mathcal{N}}_{r,k,q}^{l_1,d_1}\left(\left|{\int }_x^{ı}|ı-x||{\phi }^{″}\left(x\right)|{\mathrm{d}}_{q}x\right|;x\right)\hfill \\ \hfill & & +\left|{\int }_x^{{\mathcal{O}}_{r,k,q}^{l_1,d_1}(ı;x)}\right|{\mathcal{O}}_{r,k,q}^{l_1,d_1}(ı;x)-x\left|\left|{\phi }^{″}\left(x\right)\right|{\mathrm{d}}_{q}x\right|\hfill \\ \hfill & \le & \parallel {\Lambda }^2{\phi }^{″}{\parallel }_{C\mathcal{R}\cup \left\{0\right\}}{\mathcal{O}}_{r,k,q}^{l_1,d_1}\left(\left|{\int }_x^{ı}{\displaystyle \frac{|ı-\Im |}{{\Lambda }^2\left(x\right)}}{\mathrm{d}}_{q}x\right|;x\right)+{\parallel {\Lambda }^2{\phi }^{″}\parallel }_{C\mathcal{R}\cup \left\{0\right\}}\hfill \\ \hfill & & \times \left|{\int }_x^{{\mathcal{O}}_{r,k,q}^{l_1,d_1}(ı;x)}\right|{\mathcal{O}}_{r,k,q}^{l_1,d_1}(ı;x)-x\left|{\displaystyle \frac{{\mathrm{d}}_{q}x}{{\Lambda }^2\left(x\right)}}\right|\hfill \\ \hfill & \le & {\Lambda }^{-2}\left(x\right){\parallel {\Lambda }^2{\phi }^{″}\parallel }_{C\mathcal{R}\cup \left\{0\right\}}{\mathcal{N}}_{r,k,q}^{l_1,d_1}({\left({\Omega }_r\left(x\right)\right)}^2;x)\hfill \\ \hfill & & +{\Lambda }^{-2}\left(x\right){\parallel {\Lambda }^2{\phi }^{″}\parallel }_{C\mathcal{R}\cup \left\{0\right\}}{l}_{r,k,q}^{l_1,d_1}\left(x\right).\hfill \end{array}$$

(29)

Using Peetre’s K-functional, it is simple to obtain from the relation (25), (28) and (29).

$$\begin{array}{cc}\hfill |{\mathcal{O}}_{r,k,q}^{l_1,d_1}(\chi ;x)-\chi \left(x\right)|& \le {4\parallel \chi -\phi \parallel }_{C\mathcal{R}\cup \left\{0\right\}}+{\Lambda }^{-2}\left(x\right){\parallel {\Lambda }^2{\phi }^{″}\parallel }_{C\mathcal{R}\cup \left\{0\right\}}\left(d_{r,k,q}^{l_1,d_1}\left(x\right)+l_{r,k,q}^{l_1,d_1}\left(x\right)\right)\hfill \\ \hfill & \le M{\omega }_2\left(\chi ,{\displaystyle \frac{1}{2}}\sqrt{{\displaystyle \frac{d_{r,k,q}^{l_1,d_1}\left(x\right)+l_{r,k,q}^{l_1,d_1}\left(x\right)}{\Lambda \left(x\right)}}}\right).\hfill \end{array}$$

We have the inequality by follow the uniform modulus of smoothness’s first order.

$$\begin{array}{cc}\hfill |\chi \left({\mathcal{N}}_{r,k,q}^{l_1,d_1}(ı;x)\right)-\chi \left(x\right)|& =|\chi \left(x+\Lambda \left(x\right){\displaystyle \frac{l_{r,k,q}^{l_1,d_1}\left(x\right)}{\Lambda \left(x\right)}}\right)-\chi \left(x\right)|\le \omega \left(\chi ,{\displaystyle \frac{l_{r,k,q}^{l_1,d_1}\left(x\right)}{\Lambda \left(x\right)}}\right).\hfill \end{array}$$

Consequently, we ultimately obtain the disparity.

$$\begin{array}{cc}\hfill |{\mathcal{N}}_{r,k,q}^{l_1,d_1}\left(\chi ;x\right)-\chi \left(x\right)|& \le |{\mathcal{O}}_{r,k,q}^{l_1,d_1}(\chi ;x)-\chi \left(x\right)|+|\chi \left({\mathcal{N}}_{r,k,q}^{l_1,d_1}(ı;x)\right)-\chi \left(x\right)|\hfill \\ \hfill & \le M{\omega }_2\left(\chi ,{\displaystyle \frac{1}{2}}\sqrt{{\displaystyle \frac{d_{r,k,q}^{l_1,d_1}\left(x\right)+l_{r,k,q}^{l_1,d_1}\left(x\right)}{(x-{\sigma }_1)({\sigma }_2-x)}}}\right)+\omega \left(\chi ,{\displaystyle \frac{l_{r,k,q}^{l_1,d_1}\left(x\right)}{\Lambda \left(x\right)}}\right).\hfill \end{array}$$

It completes Theorem 12’s desired proof. □

7. Voronovskaja-Type Approximation Theorems

This section was mostly inspired by the paper [29,30,31] to compute the quantitative Voronovskaja-type approximations. We utilize the modulus of smoothness findings discussed in the previous section. The definition of this modulus of smoothness is as follows:

$$\begin{array}{c}\hfill {\omega }_{\chi }(f,\Delta ):=\underset{0<\left|\rho \right|\le \Delta }{sup}\left\{|f\left(x+{\displaystyle \frac{\rho \chi \left(x\right)}{2}}\right)-f\left(x-{\displaystyle \frac{\rho \chi \left(x\right)}{2}}\right)|,x\pm {\displaystyle \frac{\rho \chi \left(x\right)}{2}}\in \mathcal{R}\cup \left\{0\right\}\right\}.\end{array}$$

In this case, $f\in C\mathcal{R}\cup \left\{0\right\}$ and $\chi \left(x\right)={(x+x^2)}^{1/2}$, along with the associated Peetre’s K-functional, are called

$$\begin{array}{c}\hfill K_{\chi }(f,\Delta )=\underset{g\in {\omega }_{\chi }\mathcal{R}\cup \left\{0\right\}}{inf}\left\{\Vert f-g\Vert +\Delta \Vert \chi g^{\prime }\Vert :g^{\prime }\in C\mathcal{R}\cup \left\{0\right\},\Delta >0\right\},\end{array}$$

$AC\mathcal{R}\cup \left\{0\right\}$ refers to the set of absolutely continuous functions on an interval. $[a,b]\subset \mathcal{R}\cup \left\{0\right\}$ and ${\omega }_{\chi }\mathcal{R}\cup \left\{0\right\}=\{g:g\in AC\mathcal{R}\cup \left\{0\right\},\parallel \chi g^{\prime }\parallel <\infty \}$. A constant $M>0$ exists in such a way

$$\begin{array}{c}\hfill K_{\chi }(f,\Delta )\le M{\omega }_{\chi }(f,\Delta ).\end{array}$$

Theorem 13.

Late $0<q<1$ and $x\in C\mathcal{R}\cup \left\{0\right\}$. Then, for every $f,f^{\prime },f^{″}\in C\mathcal{R}\cup \left\{0\right\}$, the operators ${\mathcal{N}}_{r,k,q}^{l_1,d_1}$ defined by (5) satisfy:

$$\begin{array}{c}\hfill |{\mathcal{N}}_{r,k,q}^{l_1,d_1}\left(f;x\right)-f\left(x\right)-d_{r,k,q}^{l_1,d_1}\left(x\right)f^{\prime }\left(x\right)-{\displaystyle \frac{l_{r,k,q}^{l_1,d_1}\left(x\right)+1}{2}}{f}^{″}\left(x\right)+1|\le {\displaystyle \frac{M}{{\left([r+1]\right)}^2}}{\chi }^2\left(x\right){\omega }_{\chi }\left(f^{″},{\displaystyle \frac{1}{[r+1]}}\right),\end{array}$$

where $M>0$ be any constant and $l_{r,k,q}^{l_1,d_1}\left(x\right)$, $d_{r,k,q}^{l_1,d_1}\left(x\right)$ are given according to Theorem 12.

Proof. 

If we take into consideration al $f\in C\mathcal{R}\cup \left\{0\right\}$

$$f(ı)-f\left(x\right)=\left({\theta }_1\right)f^{\prime }\left(x\right)+{\int }_x^{ı}(ı-x)f^{″}\left(x\right){\mathrm{d}}_{q}x,$$

then easy to get

$$\begin{array}{c}\hfill f(ı)-f\left(x\right)\le \left({\theta }_1\right)f^{\prime }\left(x\right)+{\displaystyle \frac{f^{″}\left(x\right)}{2}}\left({\theta }_2+1\right)+{\int }_x^{ı}(ı-x)[f^{″}\left(x\right)-f^{″}\left(x\right)]{\mathrm{d}}_{q}x.\end{array}$$

(30)

Applying ${\mathcal{N}}_{r,k,q}^{l_1,d_1}$ to (30),

$$\begin{array}{cc}\hfill & |{\mathcal{N}}_{r,k,q}^{l_1,d_1}\left(f;x\right)-f\left(x\right)-{\mathcal{N}}_{r,k,q}^{l_1,d_1}({\theta }_1;x)f^{\prime }\left(x\right)-{\displaystyle \frac{f^{″}\left(x\right)}{2}}\left({\mathcal{N}}_{r,k,q}^{l_1,d_1}({\theta }_2;x)+{\mathcal{N}}_{r,k,q}^{l_1,d_1}(1;x)\right)|\hfill \\ \hfill & \le {\mathcal{N}}_{r,k,q}^{l_1,d_1}\left(|{\int }_x^{ı}|ı-x||f^{″}\left(x\right)-f^{″}\left(x\right)|{\mathrm{d}}_{q}x|;x\right).\hfill \end{array}$$

(31)

We can estimate from the right side equality (31):

$$\begin{array}{c}\hfill |{\int }_x^{ı}|ı-x||f^{″}\left(x\right)-f^{″}\left(x\right)|{\mathrm{d}}_{q}x|\le 2\parallel f^{″}-g\parallel ({\theta }_2+2\parallel \chi g^{\prime }\parallel {\chi }^{-1}\left(x\right){\left|{\Omega }_r\left(x\right)\right|}^3,\end{array}$$

(32)

where $f\in {\omega }_{\chi }\mathcal{R}\cup \left\{0\right\}$. A constant $M>0$ is exists and satisfying:

$$\begin{array}{c}\hfill {\mathcal{N}}_{r,k,q}^{l_1,d_1}({\theta }_2;x)\le {\displaystyle \frac{M}{2{\left([r+1]\right)}^2}}{\chi }^2\left(x\right)\mathrm{and}{\mathcal{N}}_{r,k,q}^{l_1,d_1}(({\theta }_4;x)\le {\displaystyle \frac{M}{2{[r+1]}^4}}{\chi }^4\left(x\right).\end{array}$$

(33)

The Cauchy–Schwarz properties can be used to determine that

$$\begin{array}{cc}\hfill & |{\mathcal{N}}_{r,k,q}^{l_1,d_1}\left(f;x\right)-f\left(x\right)-{\mathcal{N}}_{r,k,q}^{l_1,d_1}({\theta }_1;x)f^{\prime }\left(x\right)-{\displaystyle \frac{f^{″}\left(x\right)}{2}}\left({\mathcal{N}}_{r,k,q}^{l_1,d_1}({\theta }_2;x)+{\mathcal{N}}_{r,k,q}^{l_1,d_1}(1;x)\right)|\hfill \\ \hfill & \le 2\parallel f^{″}-g\parallel {\mathcal{N}}_{r,k,q}^{l_1,d_1}({\theta }_2;x)+2\parallel \chi g^{\prime }\parallel {\chi }^{-1}\left(x\right){\mathcal{N}}_{r,k,q}^{l_1,d_1}\left(\right|{\theta }_1{|}^3;x)\hfill \\ \hfill & \le {\displaystyle \frac{M}{{\left([r+1]\right)}^2}}(x^2+x)\parallel f^{″}-g\parallel +2\parallel \chi g^{\prime }\parallel {\chi }^{-1}\left(x\right){\left\{{\mathcal{N}}_{r,k,q}^{l_1,d_1}({\theta }_2;x)\right\}}^{1/2}\{{\mathcal{N}}_{r,k,q}^{l_1,d_1}{\left(({\theta }_4;x)\right\}}^{1/2}\hfill \\ \hfill & \le {\displaystyle \frac{M}{{\left([r+1]\right)}^2}}{\chi }^2\left(x\right)\left\{\parallel f^{″}-g\parallel +{\displaystyle \frac{1}{[r+1]}}\parallel \chi g^{\prime }\parallel \right\}.\hfill \end{array}$$

We determine that by calculating the infimum over all $g\in {\omega }_{\chi }\mathcal{R}\cup \left\{0\right\}$,

$$\begin{array}{c}\hfill |{\mathcal{N}}_{r,k,q}^{l_1,d_1}\left(f;x\right)-f\left(x\right)-d_{r,k,q}^{l_1,d_1}\left(x\right)f^{\prime }\left(x\right)-{\displaystyle \frac{l_{r,k,q}^{l_1,d_1}\left(x\right)+1}{2}}{f}^{″}\left(x\right)+1|\le {\displaystyle \frac{M}{{\left([r+1]\right)}^2}}{\chi }^2\left(x\right){\omega }_{\chi }\left(f^{″},{\displaystyle \frac{1}{[r+1]}}\right).\end{array}$$

This concludes the proof. □

Theorem 14.

For any $f\in C_B\mathcal{R}\cup \left\{0\right\}$ and $x\in \mathcal{R}\cup \left\{0\right\}$ we can write:

$$\begin{array}{c}\hfill \underset{\left[r\right]\to \infty }{lim}{\left([r+1]\right)}^2\left[{\mathcal{N}}_{r,k,q}^{l_1,d_1}\left(f;x\right)-f\left(x\right)-d_{r,k,q}^{l_1,d_1}\left(x\right)f^{\prime }\left(x\right)-{\displaystyle \frac{l_{r,k,q}^{l_1,d_1}\left(x\right)+1}{2}}{f}^{″}\left(x\right)\right]=0,\end{array}$$

where $0<q<1$ and the collection of all bounded and continuous function on $\mathcal{R}\cup \left\{0\right\}$ is denoted by $C_B\mathcal{R}\cup \left\{0\right\}$.

Proof. 

If $f\in C_B\mathcal{R}\cup \left\{0\right\}$, then Taylor’s series expansion leads to the conclusion that

$$\begin{array}{c}\hfill f(ı)=f\left(x\right)+\left({\theta }_1\right)f^{\prime }\left(x\right)+{\displaystyle \frac{1}{2}}{\left({\theta }_1\right)}^2{f}^{″}\left(x\right)+{\left({\theta }_1\right)}^2{R}_x(ı),\end{array}$$

(34)

The Peano form of remainder is defined as $R_x(ı)\to 0$ as $ı\to x$, where $R_x(ı)\in C\mathcal{R}\cup \left\{0\right\}$. By using the operators ${\mathcal{N}}_{r,k,q}^{l_1,d_1}(·;x)$ on the equality (34), we may obtain

$${\mathcal{N}}_{r,k,q}^{l_1,d_1}\left(f;x\right)-f\left(x\right)=f^{\prime }\left(x\right){\mathcal{N}}_{r,k,q}^{l_1,d_1}({\theta }_1;x)+{\displaystyle \frac{f^{″}\left(x\right)}{2}}{\mathcal{N}}_{r,k,q}^{l_1,d_1}({\theta }_2;x)+{\mathcal{N}}_{r,k,q}^{l_1,d_1}({\left({\theta }_1\right)}^2{R}_x(ı);x).$$

Cauchy–Schwarz inequality gives us

$$\begin{array}{c}\hfill {\mathcal{N}}_{r,k,q}^{l_1,d_1}({\left({\theta }_1\right)}^2{R}_x(ı);x)\le \sqrt{{\mathcal{N}}_{r,k,q}^{l_1,d_1}(R_x^2(ı);x)}\sqrt{{\mathcal{N}}_{r,k,q}^{l_1,d_1}({\theta }_4;x)}.\end{array}$$

(35)

Here, we can plainly see ${lim}_{\left[r\right]\to \infty }{\mathcal{N}}_{r,k,q}^{l_1,d_1}(R_x^2(ı);x)=0$ and therefore

$$\underset{\left[r\right]\to \infty }{lim}{\left([r+1]\right)}^2\left\{{\mathcal{N}}_{r,k,q}^{l_1,d_1}({\theta }_2{R}_x(ı);x)\right\}=0.$$

Thus, we have

$$\begin{array}{ccc}\hfill \underset{\left[r\right]\to \infty }{lim}{\left([r+1]\right)}^2\{{\mathcal{N}}_{r,k,q}^{l_1,d_1}\left(f;x\right)-f\left(x\right)\}& & =\underset{\left[r\right]\to \infty }{lim}{\left([r+1]\right)}^2\{{\mathcal{N}}_{r,k,q}^{l_1,d_1}({\theta }_1;x)f^{\prime }\left(x\right)\hfill \\ & & +{\displaystyle \frac{f^{″}\left(x\right)}{2}}{\mathcal{N}}_{r,k,q}^{l_1,d_1}({\theta }_2;x)+{\mathcal{N}}_{r,k,q}^{l_1,d_1}({\theta }_2{R}_x(ı);x)\}.\hfill \end{array}$$

□

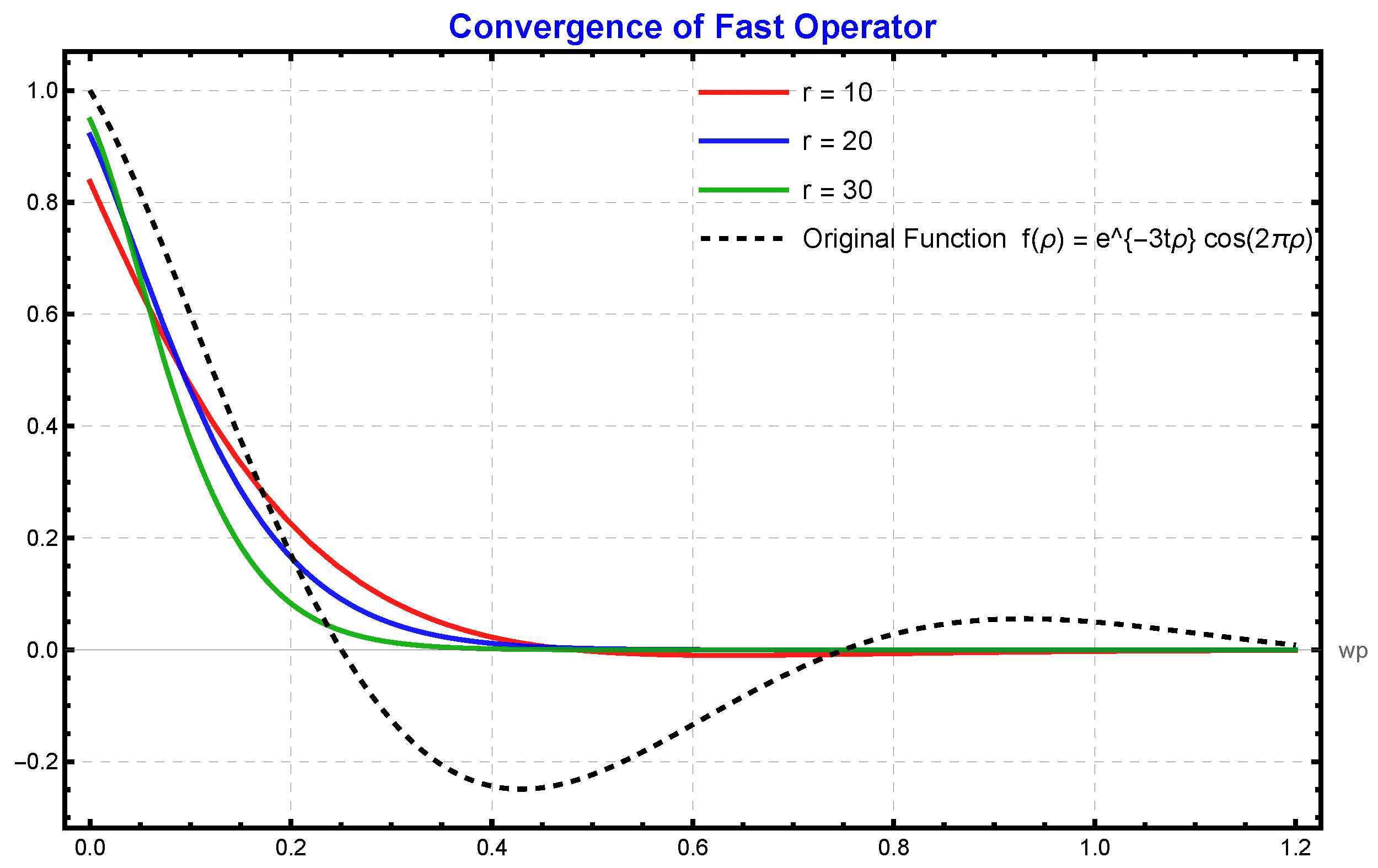
8. Numerical Illustration and Convergence Behavior

To illustrate the approximation behavior of the proposed operator, we consider the test function

$$f(\wp )=e^{-3\wp }cos(2\pi \wp ),\wp \in [0,1.2].$$

The operator under consideration is defined as

$${\mathcal{N}}_{r,k,q}^{t_1,{\mathfrak{d}}_1}(f;\wp )=(r+1)\sum _{k=0}^{\infty }{\displaystyle \frac{q^{k(k-1)/2}{r}^k{\wp }^k}{\Gamma (k+1)}}{e}^{-r\wp }{\int }_{k/(r+1)}^{(k+1)/(r+1)}f\left(t\right)dt,$$

where the integral is evaluated numerically using the midpoint rule. The parameter r denotes the order of the operator, and $q=0.8$ is chosen for illustration.

8.1. Graphical Analysis

Figure 1 shows the convergence of the operator ${\mathcal{N}}_{r,k,q}^{t_1,{\mathfrak{d}}_1}(.;.)$ towards the original function $f(\wp )$ for $r=10,20,$ and 30. The black dashed line represents the exact function, while the colored lines represent the operator approximations. It is evident that as r increases, the curves corresponding to ${\mathcal{N}}_{r,k,q}^{t_1,{\mathfrak{d}}_1}(.;.)$ approach $f(\wp )$ uniformly.

Figure 1. Convergence of the Fast Operator ${\mathcal{N}}_{r,k,q}^{t_1,{\mathfrak{d}}_1}(.;.)$ to $f(\wp )=e^{-3\wp }cos(2\pi \wp )$ for $r=10,20,30$.

8.2. Numerical Results

The computed numerical values of the operator for various r and selected points of ℘ are reported in Table 1. The results clearly show that the operator values converge to the true function as r increases.

Table 1. Numerical values of ${\mathcal{N}}_{r,k,q}^{t_1,{\mathfrak{d}}_1}(.;.)$ for $r=10,20,30$.

℘	$\mathit{f}\left(\mathit{\wp }\right)$	${\mathcal{N}}_{10,\mathit{k},\mathit{q}}^{{\mathit{t}}_1,{\mathfrak{d}}_1}$	${\mathcal{N}}_{20,\mathit{k},\mathit{q}}^{{\mathit{t}}_1,{\mathfrak{d}}_1}$	${\mathcal{N}}_{30,\mathit{k},\mathit{q}}^{{\mathit{t}}_1,{\mathfrak{d}}_1}$
0.0	1.0000	0.9846	0.9925	0.9961
0.2	0.0685	0.0738	0.0704	0.0691
0.4	$-0.1353$	$-0.1246$	$-0.1305$	$-0.1332$
0.6	$-0.1111$	$-0.1002$	$-0.1068$	$-0.1095$
0.8	0.0593	0.0627	0.0608	0.0599
1.0	0.1481	0.1529	0.1500	0.1490
1.2	0.0189	0.0217	0.0201	0.0193

9. Numerical Example and Error Analysis

In this section, we study the convergence behavior of the proposed operator, denoted by ${\mathcal{N}}_r(f;\rho )$, towards the target function

$$f\left(\rho \right)=e^{-3\rho }cos\left(2\pi \rho \right),$$

for various values of the parameter r. The operator has been implemented numerically for $q=0.8$, and the absolute error

$$E_r\left(\rho \right)=\left|{\mathcal{N}}_r(f;\rho )-f\left(\rho \right)\right|$$

has been evaluated over the interval $\rho \in [0,1.2]$.

Figure 2 illustrates the pointwise behavior of the absolute error for different values of r. It is observed that the error curves flatten and approach zero as r increases, indicating faster convergence. Additionally, the logarithmic plot provides a clearer visualization of the rate of error decay, especially for smaller error magnitudes. These results demonstrate that the proposed operator exhibits good approximation characteristics and converges rapidly to the target function for moderately large values of r.

Figure 2. Pointwise absolute error curves for $r=10,20,30$.

The overall numerical evidence supports the theoretical findings and confirms that the operator ${\mathcal{N}}_r(f;\rho )$ provides an effective and stable approximation for smooth functions such as the chosen test function $f\left(t\right)=e^{-3t}cos\left(2\pi t\right)$.

Discussion

The above results confirm that the proposed operator ${\mathcal{N}}_{r,k,q}^{t_1,{\mathfrak{d}}_1}(.;.)$ approximates the target function efficiently as r increases. The numerical and graphical evidence demonstrates the uniform convergence and supports the theoretical findings derived from the Korovkin-type approximation theorem.

10. Conclusions & Observation

Our new operators (5) are plainly the modified Kantorovich variation of operators [7]. For taking $l_1=d_1=0$ in equality (5) then reduced to equality of the new Szász–Mirakjan Kantorovich operators obtained by (6). Therefore, we can say that our new operators (5) are an extension of the classic Szász–Mirakjan Kantorovich operators, q-Szász–Mirakjan Kantorovich operators, and earlier versions of Szász–Mirakjan Kantorovich-type operators [7]. Consequently, we conclude that our new operators are stronger than the ones that were previously studied.