Approximation Properties of a Fractional Integral-Type Szász–Kantorovich–Stancu–Schurer Operator via Charlier Polynomials
Abstract
1. Introduction
- For , and , this operator reduces to the operator defined in [33].
- For , the operator is generalized to the operator defined in [30].
2. Main Results
3. Convergence Analysis of
4. Voronovskaya- and Grüss–Vororonovskaya-Type Estimates
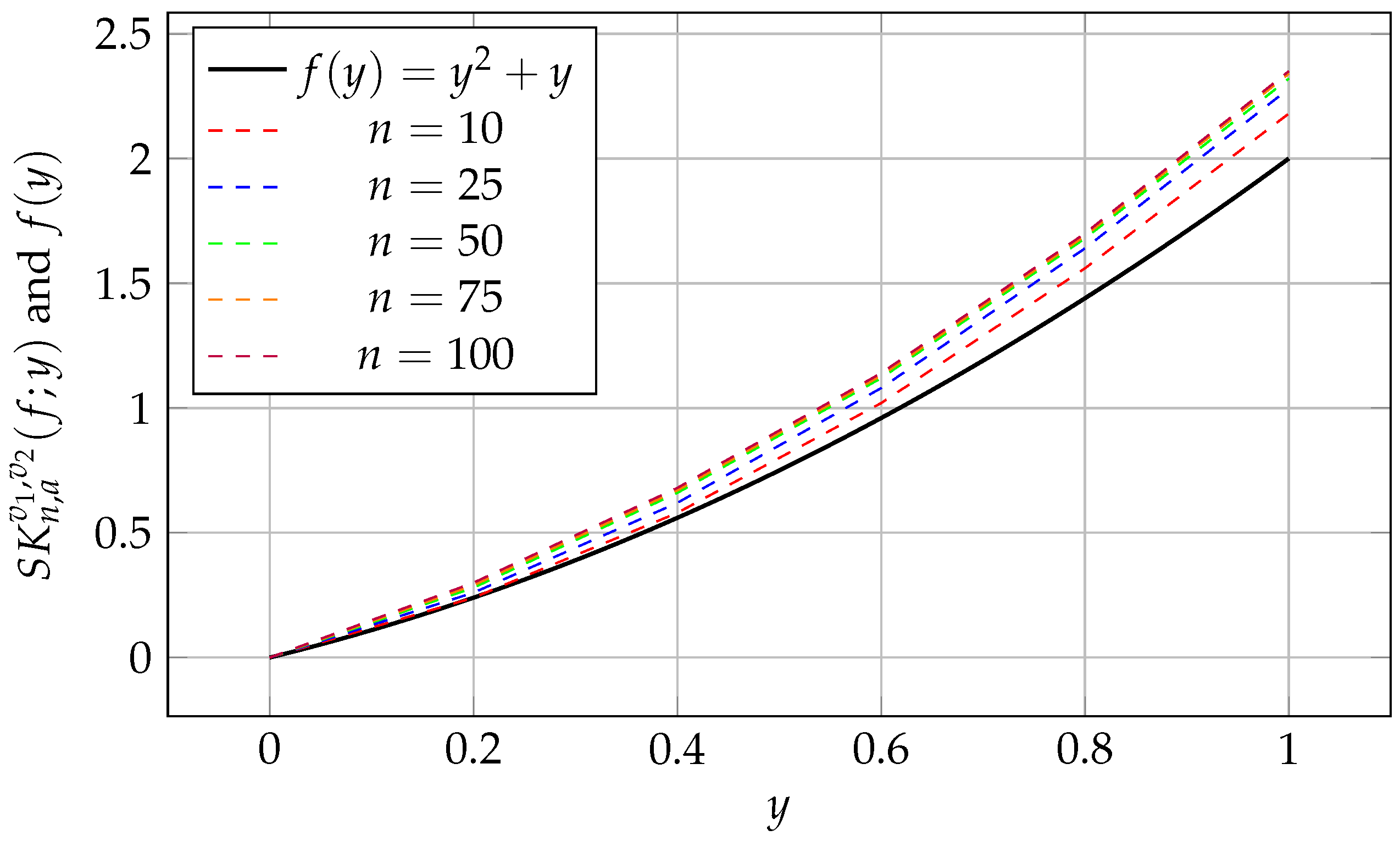
5. Numerical Validation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Correction Statement
References
- Bernstein, S.N. Démonstration du théoréme de Weierstrass fondée sur le calcul des probabilités. Commun. Kharkov Math. Soc. 1912, 13, 1–2. [Google Scholar]
- Szász, O. Generalization of Bernstein’s polynomials to the infinite interval. J. Res. Nat. Bur. Stds. 1950, 45, 239–245. [Google Scholar] [CrossRef]
- Özger, F.; Ersoy, M.T.; Özger, O.Z. Existence of solutions: Investigating Fredholm integral equations via a fixed-point theorem. Axioms 2024, 13, 261. [Google Scholar]
- Özger, F.; Aslan, R.; Ersoy, M. Some Approximation Results on a Class of Szász-Mirakjan-Kantorovich Operators Including Non-negative parameter α. Numer. Funct. Anal. Optim. 2025, 46, 461–484. [Google Scholar]
- Ayman-Mursaleen, M.; Nasiruzzaman, M.; Rao, N.; Dilshad, M.; Nisar, K.S. Approximation by the modified λ-Bernstein-polynomial in terms of basis function. AIMS Math. 2024, 9, 4409–4426. [Google Scholar] [CrossRef]
- Ayman-Mursaleen, M. Quadratic function preserving wavelet type Baskakov operators for enhanced function approximation. Comput. Appl. Math. 2025, 44, 395. [Google Scholar] [CrossRef]
- Braha, N.L.; Loku, V.; Mansour, T.; Mursaleen, M. A new weighted statistical convergence and some associated approximation theorems. Math. Meth. Appl. Sci. 2022, 45, 5682–5698. [Google Scholar] [CrossRef]
- Ansari, K.J.; Mursaleen, M.; Al-Abeid, A.H. Approximation by Chlodowsky variant of Szász operators involving Sheffer polynomials. Adv. Oper. Theory 2019, 4, 321–341. [Google Scholar] [CrossRef]
- Ansari, K.J.; Usta, F. On a modified Bernstein operators approximation method for computational solution of Volterra integral equation. J. Inequalities Appl. 2025, 2025, 8. [Google Scholar] [CrossRef]
- Khan, A.; Mansoori, M.; Khan, K.; Mursaleen, M. Phillips-type q-Bernstein operators on triangles. J. Funct. Spaces 2021, 2021, 6637893. [Google Scholar] [CrossRef]
- Acar, T.; Acu, A.M.; Manav, N. Approximation of functions by genuine Bernstein-Durrmeyer type operators. J. Math. Inequalities 2018, 12, 975–987. [Google Scholar] [CrossRef]
- Acar, T.; Acu, A.M.; Muraru, C.V.; Radu, V.A. Some approximation properties by a class of bivariate operators. Math. Methods Appl. Sci. 2019, 42, 5551–5565. [Google Scholar] [CrossRef]
- Aslan, R. Rate of approximation of blending type modified univariate and bivariate λ-Schurer-Kantorovich operators. Kuwait J. Sci. 2024, 51, 100168. [Google Scholar] [CrossRef]
- Mohiuddine, S.A.; Singh, K.K.; Alotaibi, A. On the order of approximation by modified summation-integral-type operators based on two parameters. Demo. Math. 2023, 56, 20220182. [Google Scholar] [CrossRef]
- Mohiuddine, S.A.; Özger, Z.O.; Özger, F.; Alotaibi, A. Construction of a new family of modified Bernstein-Schurer operators of different order for better approximation. J. Nonlinear Convex Anal. 2024, 25, 2059–2082. [Google Scholar]
- Mursaleen, M.; Ansari, K.J.; Khan, A. Approximation properties and error estimation of q-Bernstein shifted operators. Numer. Algorithms 2020, 84, 207–227. [Google Scholar] [CrossRef]
- Mursaleen, M.; Tabassum, S.; Fatma, R. On q-statistical summability method and its properties. Iran. J. Sci. Technol. Trans. 2022, 46, 455–460. [Google Scholar] [CrossRef]
- Malik, G.; Khan, T.; Mursaleen, M. Approximation properties and q-statistical convergence of Kantorovich variant of Stancu type Lupaş operators. Filomat 2023, 37, 10107–10124. [Google Scholar] [CrossRef]
- Nasiruzzaman, M.; Srivastava, H.M.; Mohiuddine, S.A. Approximation process based on parametric generalization of Schurer–Kantorovich operators and their bivariate form. Proc. Nat. Acad. Sci. India Sect. 2023, 93, 31–41. [Google Scholar] [CrossRef]
- Nasiruzzaman, M.; Mohammed, A.O.; Serra-Capizzano, T.S.; Rao, N.; Mursaleen, M.A. Approximation results for Beta Jakimovski-Leviatan type operators via q-analogue. Filomat 2023, 37, 8389–8404. [Google Scholar] [CrossRef]
- Rao, N.; Farid, M.; Ali, R. A Study of Szász–Durremeyer-Type Operators Involving Adjoint Bernoulli Polynomials. Mathematics 2024, 12, 3645. [Google Scholar] [CrossRef]
- Rao, N.; Farid, M.; Jha, N.K. Szász-integral operators linking general-Appell polynomials and approximation. AIMS Math. 2025, 10, 13836–13854. [Google Scholar] [CrossRef]
- Alamer, A.; Nasiruzzaman, M. Approximation by Stancu variant of λ-Bernstein shifted knots operators associated by bézier basis function. J. King Saud Univ. Comput. Inf. Sci. 2024, 36, 103333. [Google Scholar] [CrossRef]
- Cai, Q.B.; Khan, A.; Mansoori, M.S.; Iliyas, M.; Khan, K. Approximation by λ-Bernstein type operators on triangular domain. Filomat 2023, 37, 1941–1958. [Google Scholar] [CrossRef]
- Cai, Q.B.; Aslan, R.; Özger, F.; Srivastava, H.M. Approximation by a new Stancu variant of generalized (λ, μ)-Bernstein operators. Alex. Eng. J. 2024, 107, 205–214. [Google Scholar] [CrossRef]
- Aslan, R. Some approximation properties of Riemann-Liouville type fractional Bernstein-Stancu-Kantorovich operators with order of α. Iran. J. Sci. 2025, 49, 481–494. [Google Scholar] [CrossRef]
- Braha, N.L.; Mansour, T.; Mursaleen, M.; Acar, T. Convergence of-Bernstein operators via power series summability method. J. Appl. Math. Comput. 2021, 65, 125–146. [Google Scholar] [CrossRef]
- Berwal, S.; Mohiuddine, S.A.; Kajla, A.; Alotaibi, A. Approximation by Riemann–Liouville type fractional α-Bernstein–Kantorovich operators. Math. Methods Appl. Sci. 2024, 47, 8275–8288. [Google Scholar] [CrossRef]
- Baxhaku, B.; Agrawal, P.N.; Bajpeyi, S. Riemann–Liouville Fractional Integral Type Deep Neural Network Kantorovich Operators. Iran. J. Sci. 2024, 49, 711–724. [Google Scholar] [CrossRef]
- Kajla, A.; Agrawal, P.N. Szász-Kantorovich type operators based on Charlier polynomials. Kyungpook Math. J. 2016, 56, 877–897. [Google Scholar] [CrossRef]
- Ansari, K.J.; Sharma, V.; Samei, M.E. Charlier polynomial-based modified Kantorovich-Szász type operators and related approximation outcomes. J. Anal. 2024, 32, 3315–3333. [Google Scholar] [CrossRef]
- Varma, S.; Taşdelen, F. Szász type operators involving Charlier polynomials. Math. Comput. Model. 2012, 56, 118–122. [Google Scholar] [CrossRef]
- Ansari, K.J.; Mursaleen, M.; Shareef, K.M.; Ghouse, M. Approximation by modified Kantorovich–Szász type operators involving Charlier polynomials. Adv. Differ. Equ. 2020, 2020, 192. [Google Scholar] [CrossRef]
- Korovkin, P. On convergence of linear positive operators in the space of continuous functions (russian). Dokl. Akad. Nauk. SSSR (NS) 1953, 90, 961. [Google Scholar]
- Ditzian, Z.; Totik, V. K-functional and weighted moduli of smoothness. J. Approx. Theory 1990, 63, 3–29. [Google Scholar] [CrossRef][Green Version]
- Ditzian, Z.; Totik, V. Moduli of Smoothness; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 9. [Google Scholar]
- Özarslan, M.A.; Aktuğlu, H. Local approximation for certain King type operators. Filomat 2013, 27, 173–181. [Google Scholar] [CrossRef]
- Gonska, H.; Rasa, I. A Voronovskaya estimate with second order modulus of smoothness. Proc. Math. Inequal. 2008.
- Gonska, H.H. Degree of approximation by Lacunary interpolators:(0,⋯,r−2,r) interpolation. Rocky Mt. J. Math. 1989, 19, 157–171. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rao, N.; Farid, M.; Jha, N.K. Approximation Properties of a Fractional Integral-Type Szász–Kantorovich–Stancu–Schurer Operator via Charlier Polynomials. Mathematics 2025, 13, 3039. https://doi.org/10.3390/math13183039
Rao N, Farid M, Jha NK. Approximation Properties of a Fractional Integral-Type Szász–Kantorovich–Stancu–Schurer Operator via Charlier Polynomials. Mathematics. 2025; 13(18):3039. https://doi.org/10.3390/math13183039
Chicago/Turabian StyleRao, Nadeem, Mohammad Farid, and Nand Kishor Jha. 2025. "Approximation Properties of a Fractional Integral-Type Szász–Kantorovich–Stancu–Schurer Operator via Charlier Polynomials" Mathematics 13, no. 18: 3039. https://doi.org/10.3390/math13183039
APA StyleRao, N., Farid, M., & Jha, N. K. (2025). Approximation Properties of a Fractional Integral-Type Szász–Kantorovich–Stancu–Schurer Operator via Charlier Polynomials. Mathematics, 13(18), 3039. https://doi.org/10.3390/math13183039






