Abstract
To analyze unbalanced electrical systems, the mathematical technique “symmetrical components method” developed by Charles LeGeyt Fortescue in the early 20th century has been very successful in this field. By decomposing three-phase systems into three symmetrical components: positive sequence, negative sequence, and zero sequence, the Fortescue theory provides an important analyzing method. It allows for the calculation of these symmetrical components, which helps in understanding and addressing issues related to unbalance in amplitude within electrical systems. This theory deals only with amplitude unbalances in electrical systems to analyze and solve those problems. Since this technique is limited only to amplitude unbalance, our objective is to propose a modified Fortescue theory, which will resolve frequency unbalance problems in electrical systems. The new balanced components, at the conclusion of this new theory, will be used as references to be assigned in the adopted control strategies in a subsequent research paper.
Keywords:
frequency unbalance; amplitude unbalance; Fortescue theory; symmetrical components; electrical systems MSC:
93-10; 37C20; 90C31; 65L07
1. Introduction and Literature Review
The global energy landscape is undergoing a profound transformation, driven by the dual imperatives of climate change mitigation and energy security. The depletion of conventional oil reserves and the carbon-intensive nature of fossil fuels have significantly disrupted the global carbon cycle, leading to an accelerated accumulation of greenhouse gases and alarming climate change [1]. This reality, compounded by a growing imbalance between energy production and consumption, has galvanized the international research community to rapidly integrate renewable energy sources (RES) primarily solar photovoltaic (PV) and wind power into electrical grids [2,3].
However, the stochastic and intermittent nature of these resources poses major challenges to the stability, power quality, and reliability of modern power systems. Ensuring the balance of future energy systems will require advanced strategies for seamless integration and continuous service, even under dynamic and unbalanced operating conditions [4,5]. A critical aspect of this challenge is managing electrical power quality, particularly when RES are connected to the grid under non-ideal conditions. These conditions often manifest as imbalances in voltage and current amplitude and frequency, which can cause equipment malfunction, reduced efficiency, and voltage flicker [6].
The foundational framework for analyzing unbalanced three-phase systems was established by Charles LeGeyt Fortescue in 1918 with his introduction of the Symmetrical Components Method (SCM) [7]. This seminal technique decomposes an unbalanced three-phase system into three sets of balanced sequences: the positive sequence (representing normal balanced operation), the negative sequence (representing phase imbalance), and the zero sequence (representing ground or neutral currents). For nearly a century, Fortescue’s theory has been the cornerstone of power system analysis, fault detection, and protection design, proving highly effective for handling imbalances in voltage or current amplitude under a constant grid frequency [8,9].
However, the effectiveness of SCM is intrinsically tied to the assumption of a single, stable system frequency. As established in fundamental textbooks and reaffirmed in contemporary reviews like [10], the classical transformation matrices are valid only when the phase angles evolve at a synchronous speed, .
The large-scale integration of RES, which are interfaced through power electronic converters, has fundamentally altered power system dynamics. Unlike synchronous generators with significant rotational inertia that stabilize grid frequency, converter-based resources can exhibit rapid frequency variations due to several factors:
- ✓
- Intermittency of RES: Sudden variations in solar irradiance or wind speed cause immediate fluctuations in the power output frequency [11].
- ✓
- Low Grid Inertia: In weak grids or microgrids, low inertia makes the system frequency highly susceptible to fluctuations from load changes and generation imbalances [12,13].
- ✓
- Inverter Control Dynamics: Complex control loops in grid-following and grid-forming inverters can introduce frequency oscillations, particularly during unbalanced grid conditions [14,15].
When a PV generator operates at a frequency that deviates from the grid’s, a fundamental synchronization problem arises at the Point of Common Coupling (PCC). This frequency mismatch means the inverter’s output is no longer synchronized with the grid voltage, directly manifesting as voltage flicker and power oscillations at the beat frequency. These effects severely degrade power quality for other local loads.
This situation is critically exacerbated by the behavior of grid-following inverters, which rely on Phase-Locked Loops (PLLs) for synchronization. A fluctuating PV frequency can cause PLL instability, leading to control failures and potentially triggering protective shutdowns. Such a trip not only results in a loss of generation but also injects further instability into the grid by suddenly removing active power. Consequently, rather than acting as a stable power source, a PV system with frequency fluctuations becomes a source of disturbance, undermining local power quality and threatening the stability of the microgrid or weak grid to which it is connected.
The principal advantage of Fortescue’s method over direct analytical techniques for resolving asymmetrical faults lies in its powerful decomposition of a complex, unbalanced system into decoupled positive, negative, and zero-sequence networks. This transformation simplifies calculation by reducing the problem to the analysis of simpler, single-phase equivalent circuits. Furthermore, it provides unparalleled physical insight by directly quantifying imbalance through the negative-sequence component. This capability not only enables root-cause analysis and accurate assessment of harmful effects like machine heating but also forms the critical foundation for designing sensitive and selective protective relaying systems. As such, Fortescue’s method offers a standardized and comprehensive framework that direct techniques lack.
These frequency deviations create a scenario where the fundamental assumption of the classical Fortescue theory is violated. When , the traditional sequence components, as calculated by the fixed Fortescue operator , are no longer constant in a rotating reference frame but become oscillatory, leading to inaccurate analysis and ineffective control [16]. Recognizing the limitations of classical methods, researchers have developed advanced techniques to handle unbalanced conditions, primarily focusing on amplitude unbalance but laying the groundwork for frequency-variation analysis. Dual/Second-Order Generalized Integrator (DSOGI) and Dual Synchronous Reference Frame (DSRF) PLL: These techniques are highly effective for decomposing sequences under amplitude unbalance. The DSRF-PLL, for instance, uses two rotating frames (positive and negative) to extract DC components from each sequence [17,18]. However, their performance degrades under frequency variations, as the filters and controllers are tuned for a nominal frequency [19].
Advanced Phase-Locked Loops (PLLs): Numerous enhanced PLL structures, such as the Decoupled Double Synchronous Reference Frame (DDSRF) PLL [20] and adaptive PLLs [21], have been proposed to improve synchronization under unbalanced and distorted grids. While robust to amplitude imbalances, their response to rapid frequency changes can be slow or oscillatory, and they do not provide a generalized theoretical framework for sequence decomposition under frequency unbalance.
Signal Processing Approaches: Methods based on the Kalman Filter [22], the Teager Energy Operator [23], and mathematical morphology [24] have been applied for frequency estimation and flicker detection. These are excellent for measurement but are not inherently designed to reconstruct balanced sequence components for control purposes under combined amplitude and frequency imbalance [25]. A critical gap identified in the literature is the absence of a unified theoretical extension of Fortescue’s method that explicitly accounts for frequency unbalance. Existing solutions are often control-centric or signal-processing-based, addressing the symptom rather than redefining the underlying analytical model [26]. As demonstrated, the classical Fortescue theory is inadequate for systems experiencing frequency deviations, a common occurrence in RES-dominated grids. While modern control techniques offer practical workarounds, they lack the foundational analytical elegance and generality of Fortescue’s approach [27].
This paper links this gap by proposing a Modified Fortescue Theory. The core contribution is the introduction of a new transformation operator, , which incorporates the frequency deviation term . This modification allows for the decomposition of a three-phase system with simultaneous amplitude and frequency unbalance [28] into three distinct, balanced sequences. The resulting components are constant in their respective reference frames, providing ideal references for control systems. This theoretical advancement is not merely an academic exercise; it is a necessary step towards developing more robust and intelligent control strategies for future power systems [29]. By providing a mathematically sound basis for analyzing frequency unbalance, this work paves the way for enhanced stability, power quality, and reliability in the era of renewable energy. The final objective of this work is to study the behavior of currents and voltages when a renewable energy source is connected to a three-phase electrical grid under conditions of both amplitude and frequency unbalance [30]. The classical analytical tools, while powerful, are insufficient to fully address the complexities introduced by frequency deviations. This paper, therefore, introduces a Modified Fortescue Theory to resolve frequency unbalance problems, providing new balanced components that will serve as references for advanced control strategies in subsequent research.
Our paper is structured to systematically develop and validate the proposed Modified Fortescue Theory. It begins with a system description and mathematical presentation, establishing the foundational models and highlighting the limitations of the classical theory under frequency unbalance. The subsequent section analyzes the influence of the PV generator frequency variation on system performance, demonstrating the resulting oscillations and flicker phenomena. Following this, a load voltage calculation method is detailed to model the system’s behavior under these unbalanced conditions. The core of our contribution is then presented in the strategy for evaluating the load voltage sequences, which introduces the new transformation operator and derives the balanced sequence components. The validity and effectiveness of the proposed theory are subsequently demonstrated through Section 6. Finally, the paper concludes by summarizing the key findings, emphasizing the significance of the work, and outlining potential future research directions.
2. System Description and Mathematical Presentation
The benchmark system, shown in Figure 1, models a three-phase PV generator connected to the main grid. The PV source is interfaced at the Point of Common Coupling (PCC), which also supplies a local three-phase load. This topology is ideal for analyzing key power quality issues. Specifically, we investigate the system’s response to a frequency deviation between the PV generator and the grid (), as well as to voltage amplitude sags [31], thereby simulating realistic grid fault conditions.
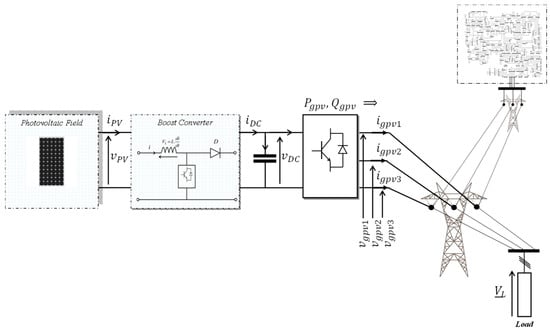
Figure 1.
Photovoltaic generator connected to grid.
This paper establishes the theoretical foundation for advanced control strategies to enable the robust integration of renewable energy sources—such as photovoltaic, wind, and hybrid systems—into modern power grids. The work is motivated by a critical limitation of the classical Fortescue theory: its restriction to amplitude unbalance and its inability to handle the frequency unbalance inherent to inverter-based resources. To address this gap, we introduce a novel theoretical identification method that precisely traces the origin of fluctuations in a three-phase system [32] under simultaneous amplitude and frequency deviations. The system is modeled using complex phasors, as defined in Equation (1), where the quantities and are complex numbers of the form .
The angular position is defined by the relation , where represents the grid’s fundamental angular velocity. When the three-phase system is unbalanced in amplitude , its behavior can be decomposed into symmetrical components. The positive, negative, and zero sequences, which characterize different aspects of the system’s response, are calculated using the standard Fortescue transformations given in Equations (2)–(4) [33,34]:
The decomposition yields three sets of symmetrical components: the positive-sequence , the negative-sequence , and the zero-sequence , derived from the unbalanced system using the Fortescue operator . The characteristic spatial orientation of each sequence, which provides a clear means of differentiation, is depicted in Figure 2 [35].
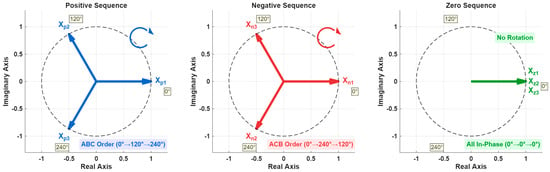
Figure 2.
Spatial distribution of different sequences.
The system under study, illustrated in Figure 1, comprises a photovoltaic (PV) generator defined by its three-phase voltages ( and currents ( interfaced with a three-phase electrical grid, supplying a three-phase load . Under ideal synchronous conditions, the PV generator frequency matches the grid frequency . However, in practice, the intermittent nature of solar generation inevitably introduces a frequency deviation . To analyze this effect, a deviation of is considered.
Similarly, while the objective is to maintain balanced voltage amplitudes at the load, real-world grid conditions often lead to imbalances. To simulate this, a 10% voltage drop in phase 1 is applied at t = 0.5 s. The frequency deviation between the PV generator and the grid is quantified by Equation (5):
The frequency variation directly impacts the mathematical description of the three-phase system established in Equation (1). To account for this deviation, the system’s representation is modified by introducing the angular displacement , leading to the revised expressions given in Equation (6):
The system in Figure 1 was simulated in MATLAB/Simulink R2025a under conditions of simultaneous frequency and amplitude unbalance. Figure 3 shows the resulting load voltage over time, illustrating the resulting flicker phenomenon [36]. The electrical parameters and simulation settings used for this study are detailed in Table 1.
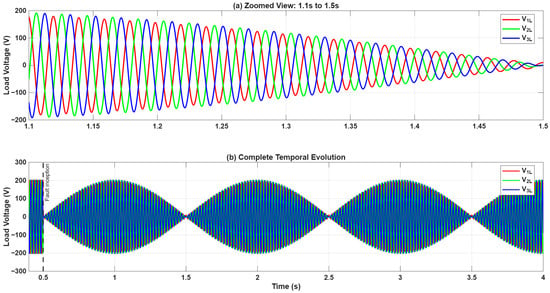
Figure 3.
Temporal evolution of load voltage.

Table 1.
Electrical system and simulation parameters.
To obtain the simulation results shown in Figure 3, fundamental circuit laws were applied to the electrical system comprising the photovoltaic generator, the load, and the electrical grid. The voltage across a single phase of the load is given by the following expression: where and represent the resistance and inductance of the single-phase load, respectively, and is the current through it. The current in the single-phase load is defined as: where and are the currents in the first phase of the photovoltaic generator and the electrical grid, respectively. Applying Kirchhoff’s voltage law to the PV generator-load loop yields: where is the first-phase voltage of the photovoltaic generator, is its current, and are the resistance and inductance of its first phase, respectively. Similarly, applying Kirchhoff’s voltage law to the electrical grid-load loop gives: where is the first-phase voltage of the electrical grid, is its current, and are the resistance and inductance of the grid’s first phase.
Figure 3 demonstrates the onset of pronounced load voltage fluctuations; a phenomenon known as voltage flicker; immediately after the fault occurrence at t = 0.5 s. Considering a three-phase system with amplitude unbalance and a modified pulsation (), its direct and quadrature axis components are given by Equation (7):
In summary, the integration of renewable energy poses significant challenges to grid stability, particularly through power quality issues arising from operational imbalances. Although classical Fortescue theory offers a foundational framework for analyzing amplitude unbalance, its limitations are critically exposed under the dynamic conditions of modern power systems, where frequency deviations are increasingly prevalent. This gap necessitates an expanded analytical approach to accurately characterize system behavior during loss of synchronization.
The following section addresses this exact scenario by analyzing the direct impact of PV generator frequency variations on system performance. The results demonstrate that even a minimal deviation—as small as 1 Hz—between the generator frequency () and the grid frequency () propagates through the system, causing measurable oscillations in key operational parameters. This empirical evidence underscores the critical need for the modified theoretical framework introduced in this work.
3. PV Generator Frequency Variation Influence
To quantitatively assess the impact of frequency unbalance on system stability, a case study was conducted on the power system illustrated in Figure 1. A random fault scenario was simulated, inducing a frequency deviation in the photovoltaic (PV) generator such that its operating frequency diverges from the grid frequency by . This perturbation creates an asynchronous operating condition between the generator and the grid. Under these circumstances, the direct and quadrature axis components of the load voltage, [37], which are typically constant in a perfectly synchronized steady state, exhibit significant oscillatory behavior. The resulting temporal evolution, depicted in Figure 4, clearly demonstrates the destabilizing effect of frequency unbalance, manifesting as sustained oscillations that compromise power quality and highlight the insufficiency of conventional control strategies based solely on the classical Fortescue decomposition.
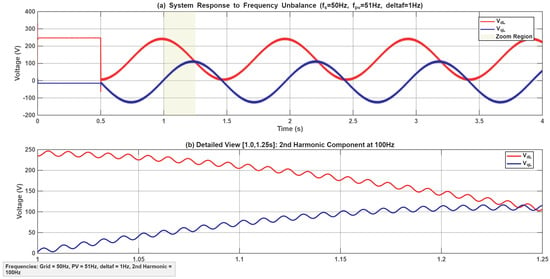
Figure 4.
Temporal evolution of components.
The positive-sequence components of the load voltage system , expressed in the reference frame, exhibit oscillations at the perturbation frequency of .
Furthermore, these signals are characterized by a secondary frequency component at 100 Hz, which corresponds to twice the grid frequency (2 × 50 Hz). It is important to note that this 100 Hz component is distinct from the classical “dual frequency” phenomenon [38], as it is not a harmonic of the 1 Hz fundamental perturbation. Consequently, the temporal evolution of both the positive-sequence components and the negative-sequence components , referenced to the positive and negative synchronous reference frames (PSF and NSF), respectively [39], are presented in Figure 5 and Figure 6.
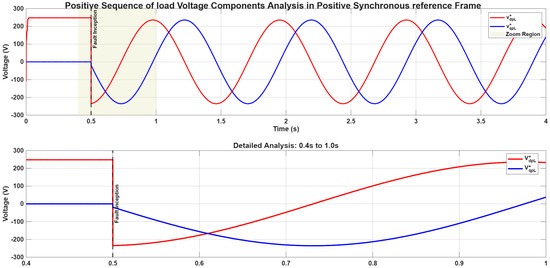
Figure 5.
Temporal evolutions of the positive sequence components of the load voltages system relative to the positive synchronous reference frame (PSF).
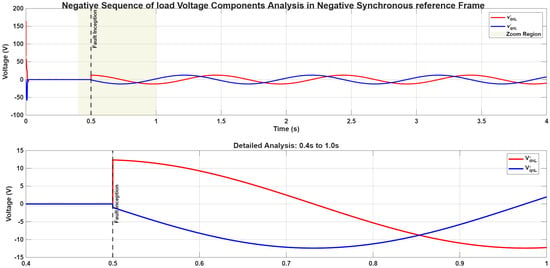
Figure 6.
Temporal evolutions of the negative sequence components of the load voltages system relative to the negative synchronous reference frame (NSF).
To investigate the origins of the fluctuations observed in the positive sequence and negative sequence components, the mathematical expressions for the positive , negative , and zero sequence components are derived with respect to the positive and negative synchronous reference frames (PSF, NSF). These formulations are presented in Equation 8 [40].
Consequently, the axis components for these sequences are formulated as shown in Equations (9) and (10).
The classical Fortescue theory is inadequate for identifying the origin of fluctuations in sequence components caused by PV generator frequency variations or grid faults. Under these dynamic conditions, the standard Fortescue operator fails to provide an accurate sequence decomposition, as it is strictly limited to systems with amplitude perturbations. To overcome this limitation, we are introducing a new transformation operator, denoted as . Developed from the principles in [41], this modified operator is specifically designed to handle the challenges of variable-frequency environments.
In the system of Equations (11), the angular displacement is defined as . Utilizing this new operator, the system of Equations (6) can be reformulated as follows:
To compensate for frequency variation, we introduce a phase correction factor, . This leads to a new transformation matrix that replaces the one used in classical Fortescue theory. The modified matrix decomposes the system into three balanced subsystems: direct (positive-sequence), inverse (negative-sequence), and homopolar (zero-sequence). The new positive-sequence components are thus defined as follows:
Thus, expanding Equation (13) yields the following expressions for the new positive-sequence components:
Following an analogous procedure to that applied for the positive sequence, the negative-sequence components are derived as follows:
Thus, expanding Equation (15) yields the following expressions for the new negative-sequence components:
The zero-sequence components are similarly derived using the following matrix relationship:
After expansion, the new zero-sequence components are given by the system of Equation (18).
This section has established the core theoretical framework for handling frequency unbalance through the novel transformation operator and its corresponding matrix. This development enables the decomposition of an unbalanced system into balanced positive-, negative-, and zero-sequence subsystems, specifically for scenarios involving frequency deviations from PV generator integration. With this analytical foundation in place, the subsequent Section 4 will detail the computational model for determining the load voltage under these unbalanced conditions. This application will quantify the concrete impact of combined PV generator frequency and amplitude variations on electrical load operation.
4. Load Voltage Computing Method
To apply the modified Fortescue theory in practice, a precise method for calculating load voltage under imbalance conditions is required. This section presents a computational model for determining load voltage dynamics during simultaneous PV-grid frequency and amplitude variations.
The system topology is shown in Figure 7, a detailed single-line diagram of the grid-connected PV system. The model comprises three primary components:
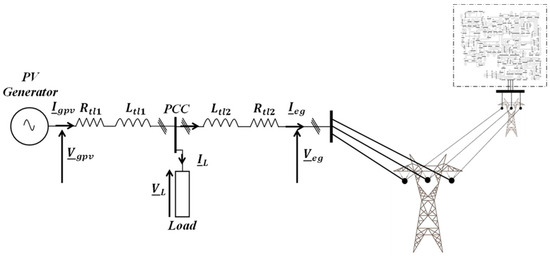
Figure 7.
Scheme model topology.
- ✓
- The Photovoltaic (PV) Generator: Represented as an ideal three-phase voltage source, it is characterized by its generated currents and voltages . Its interface with the grid includes a line impedance [42], modeled by a resistance and an inductance .
- ✓
- The Electrical Load: A local three-phase load is connected at the Point of Common Coupling (PCC), drawing a current at a voltage . The load itself is modeled with its own impedance [43].
- ✓
- The Electrical Grid: Modeled as a second ideal three-phase voltage source with currents and voltages , representing the main grid. Its connection to the PCC also includes a line impedance [42].
This configuration creates two primary current paths: one from the PV generator to the load, and another from the main grid to the load. The load voltage is the critical variable at the PCC [44], determined by the interaction of these two sources and the load impedance. The objective of the calculating method is to derive considering the potential frequency deviation of the PV generator and possible voltage amplitude sags [45].
The calculation begins by defining the balanced three-phase voltage systems for both the PV generator and the electrical grid, as shown in Equations (19) and (20). To analyze these quantities in a rotating reference frame [46] that simplifies the control and analysis, Park’s transformation [47] is applied. The PV generator voltages are transformed using the Park matrix referenced to the PV generator’s angle as per Equation (21). Similarly, the grid voltages are transformed using , referenced to the grid angle , as per Equation (22). By applying Kirchhoff’s voltage laws to the loops formed between the PV generator, the grid, and the load, the dynamic equations for the system in the reference frame are established. These equations, presented in Equations (24)–(26), form a complete set of differential equations that describe the system’s electrical dynamics. Solving this system of equations allows for the precise computation of the load voltage components and under the defined unbalanced operating conditions, thereby providing a direct link between the theoretical sequences derived in the previous section and their practical manifestation in the system’s voltages.
As shown in Figure 7, the balanced voltages for the PV generator system are given by the following equations:
Similarly, the balanced voltages for the electrical grid are given by the system of Equation (20).
The PV generator voltages are transformed into the Park reference frame using the Park matrix , as defined in Equation (21). Similarly, the three-phase grid voltages are transformed using the Park matrix , given by Equation (22).
The Park matrix , which is used in both Equations (21) and (22), is defined in Equation (23).
In the preceding equations, the angles are defined as and . Based on the interaction between the PV generator and the electrical load, the system dynamics are described by equation set (24).
Similarly, for the loop comprising the grid and the load, the -axis components of the grid voltage and the load voltage are given by Equations (25) and (26), respectively.
Under normal operating conditions, in the absence of disturbances and with the PV generator connected to the grid supplying the load, the grid and the PV generator share the same frequency, as stated in Equation (27).
When a fault occurs, causing a frequency deviation in the PV generator relative to the grid, Equation (27) is no longer valid and is replaced by Equation (28).
The system was simulated in MATLAB/Simulink with a PV generator frequency variation as defined by Equation (28). The results, shown in Figure 8, demonstrate the emergence of a voltage flicker phenomenon in the load voltage, consistent with prior research [48,49,50]. This flicker not only disrupts industrial equipment but also has documented adverse physiological effects on humans. Its severity is rigorously quantified according to standard EN 61000-4-15 [51], which defines the methodologies for flicker measurement and assessment [52].
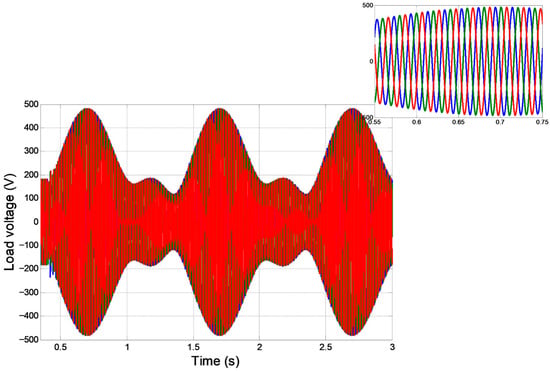
Figure 8.
Temporal evolution of the load voltages.
Following the frequency deviation , the -axis components of the load voltages exhibit sustained oscillations. As illustrated in Figure 9, these oscillations occur precisely at the deviation frequency , demonstrating a direct propagation of the disturbance from the PV generator through the system to the load bus.
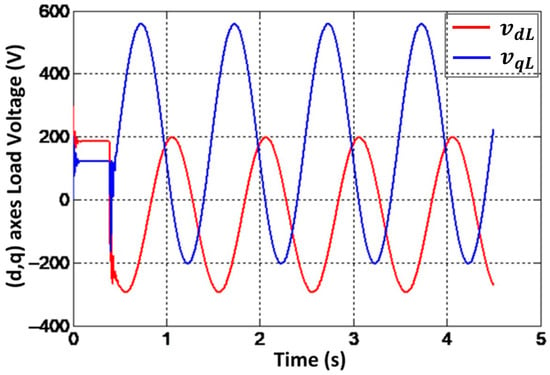
Figure 9.
Temporal evolution of components: case of frequency variation.
The second case study examines an amplitude imbalance, simulated by applying a 10% voltage drop to the first phase of the photovoltaic generator. This single-phase fault induces significant oscillations in the load voltage’s direct and quadrature components (). As Figure 10 shows, these oscillations occur at twice the grid frequency (), a characteristic signature of unbalanced conditions in three-phase systems [53]. This result demonstrates how a localized amplitude disturbance propagates through the system, manifesting as a second-harmonic oscillation in the synchronous reference frame [54].
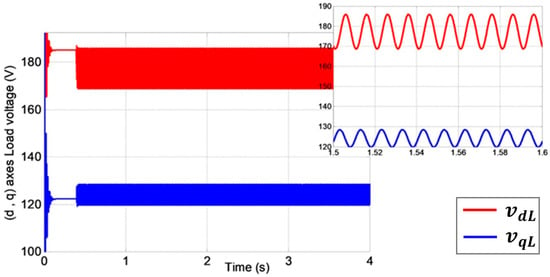
Figure 10.
Temporal evolution of components: case of voltage drops.
5. Strategy for Evaluating the Sequences of Load Voltage
Building upon the previous section’s method for calculating load voltage, this section provides a critical analysis of its sequence components. While the conventional Fortescue decomposition is effective for amplitude unbalance, it fails under frequency deviations. To address this, we develop a comprehensive strategy for evaluating load voltage sequences using the novel transformation operator and the modified symmetrical components theory. Our objective is to deconstruct the fluctuating load voltage into its positive, negative, and zero sequences under frequency unbalance. This decomposition precisely identifies the origins of the observed oscillations, thereby establishing a foundation for their effective mitigation through advanced control strategies.
Due to random disturbances, the frequency of the electrical quantities exchanged between the PV generator and the load deviates from the grid frequency by a value of , as defined by the following relationship:
Under these conditions of frequency unbalance, the standard Fortescue theory is invalidated, as the amplitudes of the symmetrical sequences become oscillatory. To demonstrate this limitation, the positive sequence components of the load voltage are evaluated using the conventional theory as follows [55]:
Expanding Equation (30) yields the temporal expressions for the positive sequence components , as given in Equation (31).
To address the limitations of the conventional Fortescue theory under frequency unbalance, the new transformation operator is applied. This operator compensates for the frequency deviation, enabling a correct evaluation of the positive sequence components of the load voltage system. The calculation, based on this modified approach, is defined by Equation (32).
Developing the expression in Equation (32) leads to a new temporal form for the positive sequence components , which is fundamentally different from the result obtained using the standard Fortescue theory in Equation (31). Crucially, the frequency deviation term cancels out in the derivation, resulting in the simplified and balanced expressions given in Equation (33). This elimination demonstrates the new operator’s ability to compensate for the frequency unbalance, producing a steady-state sequence.
The expressions for the positive sequence components derived in Equation (33) can be succinctly generalized into a single, condensed mathematical form presented in Equation (34). This formulation provides a unified representation for the three phases , significantly streamlining subsequent analysis and implementation in control algorithms.
Applying the same methodological framework established for the positive sequence, the negative sequence components of the load voltage system are now derived. This involves utilizing the new transformation operator within a dedicated transformation matrix for the negative sequence, as defined in Equation (35).
The expansion of the transformation in Equation (35) yields the explicit time-domain expressions for the negative sequence load voltage components . These temporal expressions, detailed in Equation (36), reveal the specific oscillatory behavior of the negative sequence under the influence of the frequency unbalance, completing the symmetrical component analysis initiated for the positive sequence.
For mathematical consistency and compactness, the negative-sequence components are also expressed in a generalized form. Analogous to the positive-sequence formulation, this provides a unified expression for the three phases:
Completing the symmetrical component analysis, the zero sequence components of the load voltage system are derived. This is achieved by applying the transformation defined in Equation (38), which utilizes the new operator to extract the zero sequence under frequency unbalance conditions.
The zero-sequence component can be consolidated into the compact form of Equation (39). This generalized representation simplifies the expression considerably, yielding a concise and versatile formula suitable for computational analysis and control system design.
Having independently derived the positive , negative , and zero sequence components using the modified theory, the final step is to reconstruct the original load voltage vector . This reconstruction is performed by summing the respective sequences according to the fundamental principle expressed in Equation (40), thereby verifying the consistency and completeness of the decomposition process.
The final load voltage vector is synthesized from its individual sequence components using Equation (40). By substituting the compact forms of the positive-, negative-, and zero-sequence components (Equations (34), (37), and (39)) into this superposition, we arrive at the comprehensive result in Equations (41) and (42). This derivation culminates in a simplified expression that accurately represents the original unbalanced system.
To analyze the dynamic behavior of each symmetrical component, the load voltage sequences are transformed into their respective Park components within the Positive (PSF) and Negative (NSF) Synchronous Reference Frames. Figure 11 illustrates this essential relationship, which forms the basis for the subsequent control strategy.
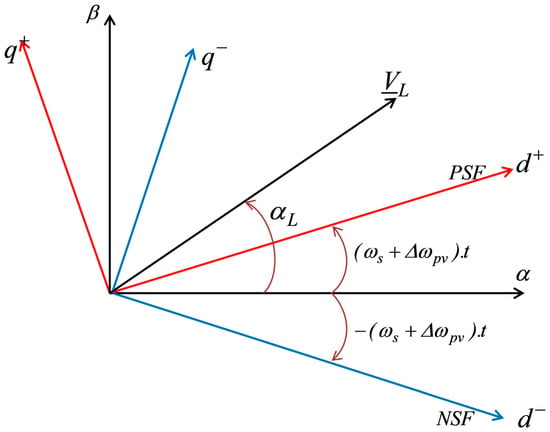
Figure 11.
Reference frame study.
The positive sequence components of the load voltage are transformed into the synchronous positive reference frame (PSF) using the Park transformation matrix defined in Equation (43). This operation projects the balanced positive sequence onto a rotating reference frame aligned with the grid voltage vector, converting the three-phase quantities into DC components under ideal balanced conditions.
Substituting the explicit form of the Park transformation matrix into Equation (43) yields the expanded expression given in Equation (44). This step provides the complete mathematical operation for converting the positive sequence voltages into their direct and quadrature-axis components within the positive synchronous reference frame.
Substituting the time-domain expressions for the positive sequence voltages into the transformation of Equation (44) allows for the analytical derivation of the dq-axis components . The resulting expressions, given in Equation (45), reveal that under the defined conditions, the quadrature and zero-sequence components become zero, while the direct-axis component reflects the average amplitude of the three phases. This result confirms the effective transformation of the balanced positive sequence into a pure DC quantity in the synchronous frame.
The negative sequence voltage components are transformed into the Negative Synchronous Reference Frame (NSF) using the Park transformation matrix defined in Equation (46). This specific transformation, denoted as , is designed to effectively isolate and analyze the negative sequence by rotating in the direction opposite to the positive sequence, converting its oscillatory nature into simplified components.
Substituting the explicit form of the Negative Synchronous Reference Frame (NSF) Park transformation matrix into the general framework of Equation (46) yields the expanded matrix Equation (47). This step provides the complete computational formulation required to project the negative sequence voltages onto the dq-axes of the NSF, explicitly defining the trigonometric operations for this specific transformation.
Substituting the analytical expressions for the negative sequence voltages into the transformation matrix of Equation (47) allows for the derivation of the corresponding dq-axis components in the NSF. The resulting expressions, given in Equation (48), demonstrate a key characteristic: the quadrature and zero-sequence components resolve to zero, while the direct-axis component is a function of the voltage amplitudes. This confirms the successful isolation of the negative sequence into a simplified, non-oscillatory form within its dedicated reference frame.
The balanced dq-axis components, essential for robust control, are synthesized by subtracting the negative-sequence components in the NSF (Equation (48)) from the positive-sequence components in the PSF (Equation (45)). As defined in Equation (49), this operation yields balanced references (). Crucially, this subtraction cancels the oscillatory terms caused by system unbalance, resulting in steady-state DC quantities that are immune to imbalances.
This analytical development successfully reconstructs perfectly balanced direct and quadrature-axis components for the voltage and current systems by strategically combining the positive and negative sequences within their respective synchronous reference frames (PSF and NSF). The specific balanced components, defined as and , constitute the principal result of this methodology. These components are impervious to the oscillations caused by system unbalance and will serve as the critical reference signals to be assigned within the advanced control strategies developed in a subsequent publication.
The core objective of this theoretical framework is to precisely identify the origin of fluctuations during unbalanced conditions. To achieve this, the analysis within the Positive and Negative Synchronous Frames (PSF and NSF) must account for the interaction between sequence components. This analysis is based on the following fundamental relationships:
The transformation of sequence components between the Positive and Negative Synchronous Reference Frames (PSF and NSF) is governed by a fundamental kinematic relationship. A component in one frame is converted to the other by accounting for the relative angular displacement of , as defined by the following equations:
Therefore, by strategically combining sequence components from the PSF and NSF, we reconstruct a set of perfectly balanced voltage components. These synthesized components, defined in Equation (52), provide the essential balanced references () for the load voltage. As they are impervious to the imbalances studied here, they form the direct foundation for the control strategies developed in subsequent research.
The subscript denotes “balanced,” indicating components synthesized to be free from oscillatory effects caused by system unbalance. The resulting signals, and , are thus designated as critical reference signals. These references will be fed to the controller of the grid-interfacing PV inverter to ensure stable, high-quality power injection, even in the presence of upstream imbalances.
The Modified Fortescue Theory developed in this work provides the foundation for an advanced, robust control system for grid-connected PV inverters. The transition from theory to practice involves a structured implementation strategy where these balanced components serve as the critical input to an intelligent controller. The proposed implementation is architected as follows:
- ✓
- Real-Time Signal Conditioning Block: A dedicated processing unit must be implemented in the inverter’s digital signal processor (DSP) to execute the modified symmetrical components transformation in real-time. This block will continuously sample the three-phase voltages at the Point of Common Coupling (PCC), compute the frequency deviation , and apply the new transformation operator to generate the perfectly balanced reference signals and , as defined by Equation (52). These signals, being constant in the synchronous reference frame even under grid imbalance, form the ideal setpoints for the control system.
- ✓
- Controller Core: The balanced references and are fed into a Controller as the target setpoints. The controller is designed to regulate the inverter’s output currents by processing the error and its derivative between these balanced references and the measured inverter currents in the frame. The key advantage here is that the controller’s decision-making is based on clean, non-oscillatory error signals, allowing its rule base to operate effectively without being misled by the oscillatory components traditionally induced by grid imbalances.
- ✓
- Actuation and Modulation Stage: The output of the controller (the commanded inverter voltage in the frame) is transformed back to the three-phase stationary frame using an inverse Park transformation. These voltage commands are then synthesized by the inverter’s power switches using a Space Vector Pulse Width Modulation (SVPWM) technique, renowned for its high DC-link utilization and low harmonic distortion.
In conclusion, this implementation strategy directly leverages the core contribution of this paper: the generation of imbalance-immune reference signals. By integrating these signals into a controller, the inverter is endowed with the capability to maintain stable, high-quality power injections and provide effective grid support, even in the presence of severe amplitude and frequency unbalances. This paves the way for the development of a new generation of highly resilient and intelligent grid-connected renewable energy systems.
6. Results and Discussion
This section presents the simulation results and a detailed discussion that validates the limitations of the classical Fortescue theory under frequency unbalance and demonstrates the efficacy of the proposed Modified Fortescue Theory.
6.1. Limitations of Classical Theory in Describing Frequency Unbalance Phenomena
The initial simulation of the system depicted in Figure 1, under a frequency deviation of between the PV generator and the grid, clearly illustrates the problem. As shown in Figure 3, the load voltage exhibits significant fluctuations, a phenomenon known as voltage flicker, immediately after the fault inception at t = 0.5 s. This flicker is a direct consequence of the frequency unbalance, which the classical grid control systems, based on a single-frequency assumption, cannot compensate for.
Further analysis in the synchronous reference frame provides deeper insight. The axis components of the load voltage , presented in Figure 4, are not constant as they would be in a perfectly balanced and synchronous system. Instead, they exhibit persistent oscillations at the frequency of the deviation, . This oscillation confirms that the standard Park transformation, which locks onto the grid frequency , is unable to decouple the variables when the source (PV generator) operates at a different frequency.
Most critically, the application of the classical Fortescue transformation to this scenario leads to erroneous results. When the positive and negative sequence components of the load voltage are extracted using the standard operator and observed in their respective Positive and Negative Synchronous Frames (PSF, NSF), they are not constant. As evidenced in Figure 5 and Figure 6, both sequences and contain oscillatory components. Specifically, these signals oscillate at two distinct frequencies: the primary oscillation at and a secondary component at 100 Hz (twice the grid frequency). This outcome is pivotal: it demonstrates that under frequency unbalance, the classical Fortescue theory fails to produce its fundamental output constant, balanced sequence components. The sequences themselves become unbalanced and time-varying, rendering them useless as stable references for high-performance control systems.
6.2. Development and Validation of the Modified Fortescue Theory
The limitation of the classical approach requires a fundamental revision of the transformation principle. The core of our solution is the introduction of a new transformation operator, , defined in Equation (11). This operator is modified to explicitly account for the phase drift caused by the frequency difference: . The factor acts as a frequency compensation term, effectively aligning the reference frame with the average or intended system dynamics despite the presence of .
The derivation of the new sequence components using the modified transformation matrix (Equations (13), (15) and (17)) yields a critical result. After mathematical development, the expressions for the new positive sequence components (Equation 14) simplify to a form where the disturbance term is eliminated:
The same applies to the negative and zero sequences (Equations (16) and (18)). This is the principal theoretical result: the proposed modification successfully decouples the frequency unbalance, yielding sequence components that are functions only of the fundamental grid frequency and the amplitudes . Consequently, these new sequences are perfectly balanced and constant, fulfilling the original purpose of symmetrical component analysis even in the presence of a frequency deviation.
6.3. Reconstruction of Balanced References for Control Applications
The practical value of this theoretical development is demonstrated through the reconstruction of balanced axis components for control purposes. By processing the load voltages with the modified theory, we obtain the new positive and negative sequences. Their representation in the PSFs and NSFs, as detailed in Equations (43)–(48), results in constant values for the direct and quadrature components .
The key innovation for control strategy is introduced in Equation (52): the construction of a balanced reference signal by subtracting the negative-sequence component in the NSF from the positive-sequence component in the PSF.
This operation, , yields a constant value proportional to the sum of the voltage amplitudes of the two unaffected phases, as shown in Equation (49). This balanced component is completely devoid of the oscillations caused by the frequency unbalance. It represents a “clean” reference signal that accurately reflects the state of the system after rejecting the imbalance disturbance.
The ability to generate such balanced references is a breakthrough for controlling power converters under non-ideal conditions. In a standard controller, the oscillations in the components (Figure 9) would propagate through the control loops, causing oscillatory current injections, power pulsations, and potential instability. By using the proposed and as references, a controller can be designed to drive the system towards a truly balanced operating point, effectively mitigating the flicker and ensuring stable power injection even during frequency transients. This provides a mathematically rigorous foundation for the next generation of “grid-supporting” and “grid-forming” inverters that must remain stable in the increasingly complex and variable-frequency environment of modern power grids.
6.4. Comparative Analysis: Amplitude vs. Frequency Unbalance
The paper further contrasts the effects of frequency unbalance with the well-understood case of amplitude unbalance. When a 10% voltage drop in one phase is simulated (amplitude unbalance), the resulting oscillations in the components, shown in Figure 10, occur at twice the grid frequency (100 Hz). This 100 Hz ripple is a known phenomenon, addressed by techniques like the DDSRF-PLL [56]. However, the oscillation at 1 Hz due to frequency unbalance is a fundamentally different and more challenging problem, as it is not a harmonic but a sub-synchronous modulation of the fundamental component, which cannot be filtered out by conventional means without affecting the controller’s dynamic response. This comparison underscores the necessity of the proposed theory, as it addresses a distinct class of power quality issues that existing methods are not designed to handle.
6.5. Limitations of the Proposed Method
This study’s methodology is developed under the defined condition of symmetrical frequency fluctuation across the three phases of the PV generator. While this work focuses on this specific case, the derived framework establishes a foundation for future adaptation to address scenarios involving asymmetrical (phase-dependent) frequency fluctuations.
7. Conclusions
This paper has established a novel theoretical framework by extending the classical Fortescue symmetrical components theory to address the critical challenge of frequency unbalance in modern electrical systems, a phenomenon increasingly prevalent with the high penetration of renewable energy sources like photovoltaics. The conventional Fortescue decomposition, while robust for amplitude unbalances, proves inadequate under frequency deviations, leading to oscillatory sequence components and compromised power quality, as demonstrated by the flicker phenomenon observed in our simulations.
The core contribution of this work is the introduction of a modified transformation theory, centered on the new operator , which successfully compensates for frequency variations. This modification allows for the derivation of balanced positive, negative, and zero sequence components even when the PV generator frequency deviates from the grid frequency . The culmination of this analytical effort is the synthesis of perfectly balanced direct and quadrature-axis voltage components, and , which are impervious to both amplitude and frequency imbalances. These components are not merely a theoretical result; they are specifically engineered to serve as the foundational reference signals for advanced control systems.
The immediate and practical application of this methodology lies in the control of the three-phase voltage source converter (VSC) that interfaces the PV generator with the power grid. The balanced references and can be directly integrated into a high-performance control loop. Specifically, these DC-like reference signals will be used as the setpoints for the inner current controllers in the synchronous reference frame. The output of these controllers, the required converter voltage vectors, will then be synthesized using the Space Vector Pulse Width Modulation (SVPWM) technique [57].
The application of SVPWM is particularly suitable for this context due to its inherent advantages: it provides superior DC-link voltage utilization, generates lower total harmonic distortion (THD) compared to conventional sinusoidal PWM, and offers a digital implementation that is ideal for modern microprocessor-based controllers. By feeding the SVPWM algorithm with the voltage commands derived from the balanced references and , the inverter will generate switching signals that produce a three-phase voltage waveform which counteracts the effects of the source imbalance. This ensures that the power injected into the grid remains stable and of high quality, even during disturbances, thereby mitigating flicker and protecting sensitive equipment.
In conclusion, this paper provides the essential theoretical groundwork for a new generation of robust control strategies. The proposed modified Fortescue theory delivers the precise reference quantities needed to effectively decouple the converter operation from system imbalances. The subsequent research will detail the implementation of an intelligent control scheme, leveraging these balanced references within a fuzzy logic-based controller to dictate the SVPWM-driven inverter, ultimately assigning remarkable fault-tolerant capabilities to grid-connected PV systems and enhancing the stability and reliability of future power networks.
Author Contributions
Conceptualization, B.M. and C.N.; Methodology, K.M.; Software, K.M.; Validation, K.M. and C.N.; Formal analysis, B.M., A.Y. and E.T.; Investigation, B.M. and A.Y.; Resources, K.M.; Data curation, A.Y.; Writing—original draft, K.M. and B.M.; Writing—review and editing, K.M.; Visualization, E.T.; Supervision, C.N. and E.T.; Project administration, A.Y. and E.T.; Funding acquisition, A.Y. and E.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by [Northern Border University, Saudi Arabia] grant number [NBU-CRP-2025-2448] And the APC was funded by [NBU-CRP-2025-2448].
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
The authors extend their appreciation to the Northern Border University, Saudi Arabia, for supporting this work through project number “NBU-CRP-2025-2448”.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Calvin, K.; Dasgupta, D.; Krinner, G.; Mukherji, A.; Thorne, P.W.; Trisos, C.; Romero, J.; Aldunce, P.; Barrett, K.; Blanco, G.; et al. Climate Change 2023: Synthesis Report; Lee, H., Romero, J., Eds.; Contribution of Working Groups I, II and III to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2023. [Google Scholar] [CrossRef]
- Tang, Z.; Yang, Y.; Blaabjerg, F. Power electronics: The enabling technology for renewable energy integration. CSEE J. Power Energy Syst. 2021, 8, 39–52. [Google Scholar] [CrossRef]
- Papon, P.; AIE (Agence Internationale de L’énergie). World Energy Outlook; AIE: Paris, France, 2024; 398p, Available online: https://iea.blob.core.windows.net/assets/6a25abba-1973-4580-b6e3-ba014a81b458/WorldEnergyOutlook2024.pdf (accessed on 1 September 2025).
- Cavus, M. Advancing Power Systems with Renewable Energy and Intelligent Technologies: A Comprehensive Review on Grid Transformation and Integration. Electronics 2025, 14, 1159. [Google Scholar] [CrossRef]
- Ahmad, G.; Hassan, A.; Islam, A.; Shafiullah, M.; Abido, M.A.; Al-Dhaifallah, M. Distributed Control Strategies for Microgrids: A Critical Review of Technologies and Challenges. IEEE Access 2025, 13, 60702–60719. [Google Scholar] [CrossRef]
- Razmi, D.; Lu, T.; Papari, B.; Akbari, E.; Fathi, G.; Ghadamyari, M. An overview on power quality issues and control strategies for distribution networks with the presence of distributed generation resources. IEEE Access 2023, 11, 10308–10325. [Google Scholar] [CrossRef]
- Fortescue, C.L. Method of symmetrical co-ordinates applied to the solution of polyphase networks. Trans. Am. Inst. Electr. Eng. 2009, 37, 1027–1140. [Google Scholar] [CrossRef]
- Grainger, J.J.; Stevenson, W.D. Power System Analysis; McGraw-Hill: Columbus, OH, USA, 1994; Available online: http://thuvienso.bvu.edu.vn/handle/TVDHBRVT/14336 (accessed on 1 September 2025).
- Mikulović, J.; Šekara, T.; Forcan, M. Power definitions for three-phase systems in terms of instantaneous symmetrical components. Int. J. Electr. Power Energy Syst. 2023, 147, 108808. [Google Scholar] [CrossRef]
- Bialobrzheskyi, O.V.; Rod’KIn, D. A positive, negative and zero sequences electric power, to improve upon the standard IEEE 1459–2010. COMPEL-Int. J. Comput. Math. Electr. Electron. Eng. 2023, 42, 402–424. [Google Scholar] [CrossRef]
- Latoufis, K.C.; Vassilakis, A.I.; Grapsas, I.K.K.; Hatziargyriou, N.D. Design Optimization and Performance Evaluation of Passive Filters for Acoustic Noise Mitigation in Locally Manufactured Small Wind Turbines. IEEE Trans. Ind. Appl. 2024, 60, 4350–4365. [Google Scholar] [CrossRef]
- Njoka, G.M.; Mogaka, L.; Wangai, A. Impact of variable renewable energy sources on the power system frequency stability and system inertia. Energy Rep. 2024, 12, 4983–4997. [Google Scholar] [CrossRef]
- Islam, K.; Kim, D.; Abu-Siada, A. A review on adaptive power system protection schemes for future smart and micro grids, challenges and opportunities. Electr. Power Syst. Res. 2024, 230, 110241. [Google Scholar] [CrossRef]
- Ma, Z.; Wang, Z.; Cheng, R. Analytical large-signal modeling of inverter-based microgrids with koopman operator theory for autonomous control. IEEE Trans. Smart Grid 2023, 15, 1376–1387. [Google Scholar] [CrossRef]
- Issa, W.; Sharkh, S.; Abusara, M. A review of recent control techniques of drooped inverter-based AC microgrids. Energy Sci. Eng. 2024, 12, 1792–1814. [Google Scholar] [CrossRef]
- Subedi, S.; Gui, Y.; Xue, Y. Applications of data-driven dynamic modeling of power converters in power systems: An overview. IEEE Trans. Ind. Appl. 2025, 61, 2434–2456. [Google Scholar] [CrossRef]
- Mousavi, M.H.; Ahmadi, M.; Moradi, H. Decoupled Double Synchronous Reference Frame Sequence Extraction Technique: A Compact Review on Applications in Microgrids. In Proceedings of the 2024 9th International Conference on Technology and Energy Management (ICTEM), Mazandaran, Iran, 14–15 February 2024; IEEE: New York, NY, USA, 2024; pp. 1–7. [Google Scholar] [CrossRef]
- Dai, Z.; Li, G.; Yang, Y.; Wang, G.; Li, B.; Wang, Y. A Complex-Type Voltage Normalization Method for Three-Phase Synchronous Reference Frame Phase-Locked Loop. IEEE Trans. Power Electron. 2024, 39, 5873–5882. [Google Scholar] [CrossRef]
- Peng, Q.; Yang, J.; Guenter, S.; Buticchi, G.; Tan, N.M.L.; Wheeler, P. On the synchronous reference frame impedance and stability characteristics of more electric aircraft electrical power distribution systems. IEEE Trans. Transp. Electrif. 2024, 11, 3037–3049. [Google Scholar] [CrossRef]
- Hussein, A.A.; Ahmed, A.H.; Mohammed, N.M. An enhanced implementation of SRF and DDSRF-PLL for three-phase converters in weak grid. Int. J. Emerg. Electr. Power Syst. 2023, 24, 273–286. [Google Scholar] [CrossRef]
- Wang, R.; Xie, F.; Zhang, B.; Qiu, D.; Xiao, W. Modeling and Stability Analysis of Two-stage Photovoltaic Grid-connected System Based on Phase-by-phase Angle Analysis. IEEE J. Emerg. Sel. Top. Power Electron. 2025. [Google Scholar] [CrossRef]
- Dedović, M.M.; Avdaković, S.; Musić, M.; Kuzle, I. Enhancing power system stability with adaptive under frequency load shedding using synchrophasor measurements and empirical mode decomposition. Int. J. Electr. Power Energy Syst. 2024, 160, 110133. [Google Scholar] [CrossRef]
- Reza, S.; Hossain, M.; Hellany, A. Teager Energy Operator-Based Single-Phase Grid Synchronization Method. In Proceedings of the IECON 2024-50th Annual Conference of the IEEE Industrial Electronics Society, Chicago, IL, USA, 3–6 November 2024; IEEE: New York, NY, USA, 2024; pp. 1–7. [Google Scholar] [CrossRef]
- Guo, Z. Three-phase unbalanced voltage sag detection method based on morphological filtering. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2022; p. 012035. [Google Scholar] [CrossRef]
- Cvetanovic, R.; Janda, Z. A fast finite sample count symmetric component extraction method for use in grid side converters. Int. J. Electr. Power Energy Syst. 2022, 137, 107857. [Google Scholar] [CrossRef]
- Sun, W.; Lin, X.; Huang, L.; Mu, D.; Zhang, H. Distributed sliding mode control for reactive power sharing in an islanded microgrid. Electr. Power Syst. Res. 2024, 231, 110342. [Google Scholar] [CrossRef]
- Mirza, S.; Hussain, A. New approaches in finite control set model predictive control for grid-connected photovoltaic inverters: State of the art. Solar 2024, 4, 491–508. [Google Scholar] [CrossRef]
- Lacerda, V.A.; Araujo, E.P.; Cheah-Mañe, M.; Gomis-Bellmunt, O. Phasor modeling approaches and simulation guidelines of voltage-source converters in grid-integration studies. IEEE Access 2022, 10, 51826–51838. [Google Scholar] [CrossRef]
- Jigyasu, D.; Kumar, S.; Vats, S. Introduction to artificial intelligence-empowered electric vehicles in smart grids. In Artificial Intelligence-Empowered Modern Electric Vehicles in Smart Grid Systems; Elsevier: Amsterdam, The Netherlands, 2024; pp. 3–31. [Google Scholar] [CrossRef]
- Yagüe, Y.; Sauro, J. Stability Analysis of Unbalanced Microgrids with Grid-Forming and Grid-Following Electronic Power Converters. Available online: http://hdl.handle.net/10803/690653 (accessed on 1 September 2025).
- Lv, S.; Zheng, C.; Jiang, J.; Deng, J. Fault Ride-Through Strategy for Grid-Forming Photovoltaic Systems under Unbalanced Voltage. In Proceedings of the 2025 2nd International Conference on Smart Grid and Artificial Intelligence (SGAI), Changsha, China, 21–23 March 2025; IEEE: New York, NY, USA, 2025; pp. 406–410. [Google Scholar] [CrossRef]
- Shahin, M.; Topriska, E.; Gormley, M.; Nour, M. Design and field implementation of smart grid-integrated control of PV inverters for autonomous voltage regulation and VAR ancillary services. Electr. Power Syst. Res. 2022, 208, 107862. [Google Scholar] [CrossRef]
- Gebru, F.M.; Salau, A.O.; Mohammed, S.H.; Goyal, S.B. Analysis of 3-phase symmetrical and unsymmetrical fault on transmission line using Fortescue Theorem. WSEAS Trans. Power Syst. 2022, 17, 316–323. [Google Scholar] [CrossRef]
- Abasi, M. Accurate Fault Location Algorithm for Untransposed Transmission Lines Based on Network Phasor Equations in Positive-, Negative-, and Zero-Sequences Domain During Fault. IEEE Access 2024, 12, 104742–104754. [Google Scholar] [CrossRef]
- Pietrzak, P.; Wolkiewicz, M. On-line detection and classification of PMSM stator winding faults based on stator current symmetrical components analysis and the KNN algorithm. Electronics 2021, 10, 1786. [Google Scholar] [CrossRef]
- Łowczowski, K.; Nadolny, Z. Voltage Fluctuations and Flicker in Prosumer PV Installation. Energies 2022, 15, 2075. [Google Scholar] [CrossRef]
- Roos, M.; Nguyen, P.; Morren, J.; Slootweg, J.G. Direct-quadrature sequence models for energy-function based transient stability analysis of unbalanced inverter-based microgrids. IEEE Trans. Smart Grid 2021, 12, 3692–3704. [Google Scholar] [CrossRef]
- Wang, J.; Ma, K.; Tang, W.; Cai, X.; Zheng, L.; Li, X.; Wang, A. Dual-frequency bands grid impedance emulator for stability test of grid-connected converters. IEEE Trans. Power Electron. 2022, 37, 13070–13080. [Google Scholar] [CrossRef]
- Zou, Z.; Liu, X.; Chen, W.; Buticchi, G.; Wang, X.; Liserre, M. Design of filter-based stabilizing control for PLL-synchronized converters. IEEE Trans. Ind. Electron. 2024, 71, 14208–14219. [Google Scholar] [CrossRef]
- Du, W.; Nguyen, Q.H.; Wang, S.; Kim, J.; Liu, Y.; Zhu, S.; Tuffner, F.K.; Huang, Z. Positive-sequence modeling of droop-controlled grid-forming inverters for transient stability simulation of transmission systems. IEEE Trans. Power Deliv. 2024, 39, 1736–1748. [Google Scholar] [CrossRef]
- Waseem, F.; Khan, U.A. A Seamless Synchronization of the Synchronverter with an Unbalanced Grid. SSRN 2025. [Google Scholar] [CrossRef]
- Zhang, M.; Mu, L.; Chen, G.; Fang, C. A circulating current suppression strategy of VSG based on adaptive virtual complex impedance. Electr. Power Syst. Res. 2024, 228, 110065. [Google Scholar] [CrossRef]
- Osorio-Vásquez, D.; García-Ceballos, C.; Mora-Flórez, J. Enhanced distance-based protection for high impedance faults considering dynamic load modelling. Results Eng. 2024, 22, 102278. [Google Scholar] [CrossRef]
- Alturki, Y.A.; Alhussainy, A.A.; Alghamdi, S.M.; Rawa, M. A Novel Point of Common Coupling Direct Power Control Method for Grid Integration of Renewable Energy Sources: Performance Evaluation among Power Quality Phenomena. Energies 2024, 17, 5111. [Google Scholar] [CrossRef]
- Guan, X.; Liu, W.; Zhang, X.; Ruan, P.; Zhang, R.; Yi, H. Asymmetric Voltage Sag Detection Method Based on Delay Small Angle Method and Moving Average Filter. In Proceedings of the 2024 IEEE 4th New Energy and Energy Storage System Control Summit Forum (NEESSC), Hohhot, China, 29–31 August 2024; IEEE: New York, NY, USA, 2024; pp. 34–41. [Google Scholar] [CrossRef]
- Lunt, P.; Hill, P.; Reiter, J.; Preiss, P.M.; Gałka, M.; Jochim, S. Realization of a Laughlin state of two rapidly rotating fermions. Phys. Rev. Lett. 2024, 133, 253401. [Google Scholar] [CrossRef]
- Wang, R.; Gu, Q.; Lu, S.; Tian, J.; Yin, Z.; Yin, L.; Zheng, W. FI-NPI: Exploring optimal control in parallel platform systems. Electronics 2024, 13, 1168. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, P.; Ji, H.; Zhao, J.; Xi, W.; Wu, J.; Wang, C. Combined central-local voltage control of inverter-based DG in active distribution networks. Appl. Energy 2024, 372, 123813. [Google Scholar] [CrossRef]
- Hossain, R.; Gautam, M.; Olowolaju, J.; Livani, H.; Benidris, M. Multi-agent voltage control in distribution systems using GAN-DRL-based approach. Electr. Power Syst. Res. 2024, 234, 110528. [Google Scholar] [CrossRef]
- Zeng, Q.; Yang, X.; Bu, E.; Liu, Z.; Ji, F.; Yuan, F.; Jin, Y.; Gao, X.; Li, C. Comprehensive experimental investigation of dynamic response to fluctuating load of proton exchange membrane water electrolyzer. Int. J. Hydrog. Energy 2025, 103, 310–326. [Google Scholar] [CrossRef]
- Silsüpür, M.; Türkay, B.E. Flicker source detection methods based on IEC 61000-4-15 and signal processing techniques—A review. Balk. J. Electr. Comput. Eng. 2015, 3. [Google Scholar] [CrossRef]
- Enayati, J.; Asef, P.; Benoit, A. A Hybrid Artificial Intelligence Method for Estimating Flicker in Power Systems. arXiv 2015, arXiv:2506.13611. [Google Scholar] [CrossRef]
- Abdo, A.; Siam, J.; Abdou, A. Fault Detection and Fault Tolerant Control of Single Phasing on Three-Phase System. IEEE Trans. Instrum. Meas. 2025, 74, 1–11. [Google Scholar] [CrossRef]
- Gao, J.; Zou, C. Inter-turn short circuit fault diagnosis methods for eVTOL propulsion motor based on back EMF harmonic analysis. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2025; p. 012055. [Google Scholar] [CrossRef]
- Pavankumar, Y.; Debnath, S.; Paul, S. An optimization based resilient control strategy for voltage unbalance compensation in grid connected microgrid system. Electr. Eng. 2025, 107, 205–222. [Google Scholar] [CrossRef]
- Rajak, M.K.; Pudur, R. Mathematical modelling and dynamic optimization of phase-locked loop systems using hybrid PSO-gradient descent approach. Syst. Sci. Control Eng. 2025, 13, 2448636. [Google Scholar] [CrossRef]
- Satpathy, S.; Das, P.P.; Bhattacharya, S. A Digital Three Level Space Vector Modulator for High Frequency Vector Sequence Generation. IEEE J. Emerg. Sel. Top. Ind. Electron. 2025, 6, 1879–1885. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).