Abstract
While recent advances have successfully integrated neural networks with physical models to derive numerical solutions, there remains a compelling need to obtain exact analytical solutions. The ability to extract closed-form expressions from these models would provide deeper theoretical insights and enhanced predictive capabilities, complementing existing computational techniques. In this paper, we study the nonlinear Gardner equation and the (2+1)-dimensional Zabolotskaya–Khokhlov model, both of which are fundamental nonlinear wave equations with broad applications in various physical contexts. The proposed models have applications in fluid dynamics, describing shallow water waves, internal waves in stratified fluids, and the propagation of nonlinear acoustic beams. This study integrates a modified generalized Riccati equation mapping approach and a novel generalized -expansion method with neural networks for obtaining exact solutions for the suggested nonlinear models. Researchers are currently investigating potential applications of these neural networks to enhance our understanding of complex physical processes and to develop new analytical techniques. The proposed strategies incorporate the solutions of the Riccati problem into neural networks. Neural networks are multi-layer computing approaches including activation and weight functions among neurons in input, hidden, and output layers. Here, the solutions of the Riccati equation are allocated to each neuron in the first hidden layer; thus, new trial functions are established. We evaluate the suggested models, which lead to the construction of exact solutions in different forms, such as kink, dark, bright, singular, and combined solitons, as well as hyperbolic and periodic solutions, in order to verify the mathematical framework of the applied methods. The dynamic properties of certain wave-related solutions have been shown using various three-dimensional, two-dimensional, and contour visualizations. This paper introduces a novel framework for addressing nonlinear partial differential equations, with significant potential applications in various scientific and engineering domains.
Keywords:
neural networks methods; Gardner’s equation; analytical solutions; (2+1)-dimensional Zabolotskaya–Khokhlov model MSC:
35C08; 35A20; 35B10; 35L05
1. Introduction
Nonlinear evolution equations (NLEEs) are very important since they are used in many different fields of research and industry [1]. Researchers have been very interested in nonlinear wave structures in the last several decades since they have different features that may be seen in many areas of modern science [2]. Due to the inadequacy of linear models in accurately depicting complex nonlinear systems, investigations into real-world systems have progressively focused on nonlinear science. In order to accurately characterize these systems, it is now necessary to incorporate new techniques that address the increasing complexity [3,4]. In many scientific fields, nonlinear partial differential equations (NLPDEs) are fundamental for understanding nonlinear wave phenomena in many physical and industrial systems [5,6,7]. NLPDEs have garnered a lot of interest in the nonlinear sciences due to their many applications. Considering the practical importance of NLPDEs, many researchers are trying to find new and accurate ways to solve them. Consequently, NLPDE research has become quite popular recently. To learn about the features of the nonlinear model, analytical and exact solutions are required. In order to guarantee the accuracy of soliton solutions to NLPDEs using symbolic computations, researchers have devised a wide range of effective approaches [8].
In recent years, with the rise of artificial intelligence, many scientific and technological fields have utilized deep learning [9,10]. Using neural networks to solve differential and integral equations has become an active and essential research topic [11] due to its great expressibility in function approximation [12]. Significant attention has been generated by the use of physics-informed neural networks [13] to solve PDEs. In addressing NLPDEs, data-driven and computational neural networks are mainly replacing conventional numerical and analytical methods. Neural networks are able to handle complex, high-dimensional problems of various types by solving them using physical principles or data, bypassing the necessity for discretization or solvability restrictions. Without making any assumptions, they may use universal approximation to express complicated nonlinear relationships. Due to the limitations of PDEs, sparse or noisy input solutions are produced when physics-informed neural networks are developed. Similarly, NLPDEs may be solved and the inverse case with unknown parameters can be determined using neural networks. Despite stability and generalization problems, they are a powerful and versatile approach to scientific machine learning because of their ability to handle irregular domains, provide adaptive refinement, and conduct parallel computation. The integration of computational mathematics and engineering with previously established analytical methods has facilitated the advancement of these fields.
The nonlinear phenomena of many important structures may be more clearly defined with the help of solitons, particularly due to the recent advances in a number of modern analytical approaches. Solitons are characterized by their remarkably uniform shapes and speeds after collision; solitons are produced in relation to optical frequency [14,15]. In addition to approaching a constant at infinity, kink solutions are asymptotic waves that rise or fall from one asymptotic state to another. While the geometry of kink solutions remains constant, the widths may fluctuate, much like those of classical particles. In the normal dispersion domain, solitons are communicated as dark ones, while in the anomalous dispersion domain, they are transmitted as bright ones. Understanding the dynamics of nonlinear wave propagation via different types of wave-guides is crucial given today’s rapid advancement of information technology and telecom technology, and optical solitons play a key role in this. Research on NLPDEs is crucial for many nonlinear processes in order to further soliton theory and its applications in related domains.
The formation of exact solutions of different physical processes improves the comprehension of physical phenomena. They serve as the foundation for further study. The interactions of the physical system may be independently described as either an ODE or a PDE to obtain exact results. PDEs are the only method for quantitatively modeling complex natural and industrial systems. Numerous scholars have devised other techniques to address these challenges. A wide range of approaches have been successfully employed during recent years: the new Jacobi elliptic function expansion method [16] is employed to investigate various soliton solutions of the NLPDE describing nonlinear low-pass electrical lines. The enhanced generalized exponential rational function approach [17] is used to examine interaction phenomena and solitary wave dynamics of the ultrasonic model, the auxiliary equation method [18] is employed to study the Nizhnik–Novikov–Vesselov equations, and chaotic and sensitivity analyses, as well as the solitary wave solutions of the truncated fractional telegraph equation, are examined in [19]. In similar way, the Riccati equation mapping method is applied to study Brownian motion in the stochastic Schrödinger wave equation [20], the optical solitons of cubic–quartic NLSEs are investigated using the Bernoulli -expansion method [21], the modified Sardar sub-equation method is employed to investigate the extended NLSE and the impact of the third-order dispersion parameter in the proposed model [22], and the neural network method is applied for the exact solutions of NLPDEs [23], etc.
This study presents a novel integration of modified generalized Riccati equation mapping neural networks (MGREMMNNs) with a generalized -expansion neural network technique to investigate analytical solutions of Gardner’s equation and the (2+1)-dimensional Zabolotskaya–Khokhlov (ZK) model. By combining symbolic analytical methods with machine learning architectures, the proposed approach overcomes the limitations of traditional analytical techniques. In this framework, the solutions of Riccati and -type equations are embedded as activation functions in the neural network, while the network output, computed via feedforward processing, serves as a trial function for solving the nonlinear partial differential equation. The novelty of this approach lies in its systematic and physically meaningful construction of trial functions using neural networks, which ensures high accuracy and eliminates computational errors. The methodology not only reproduces known solutions from the existing literature but also facilitates the generation of entirely new analytical solutions. Furthermore, the neural network architecture offers flexibility and adaptability, allowing the number of layers, neurons, and activation functions to be adjusted to suit a wide range of nonlinear systems. The scientific and technological significance of this hybrid approach is substantial. By capturing the complex interactions between nonlinearity and other factors, it provides a powerful and versatile tool for solving nonlinear problems across multiple disciplines. Overall, the proposed methods offer both theoretical insights and practical alternatives, with important implications for the advancement of nonlinear dynamics and applied mathematical research.
The remaining content of this article is structured as follows: Section 2 delineates the MGREMM and the novel generalized -expansion approach, the neural networks model, the used neural networks methods, and their graphical representations. Section 3 and Section 4 delineate the use of the presented methodologies for computing the required soliton solutions of the prescribed NLPDE. Section 5 provides a comprehensive elucidation of the visual depiction of the solutions. Section 6 contains the concluding remarks.
2. Description of the Applied Techniques
2.1. The Modified Generalized Riccati Equation Mapping Method
This subsection summarizes the key points discussed in the MGREMM [24] with regard to dealing with NLPDEs. For any specified PDE including the variables x and t
where represent their respective partial derivatives of U. The MGREMM can be used to solve the ODE with Solutions are presented as follows.
- Case-I: When , , and , then
- Case-II: When , , and , thenwhere denote real numbers, with .
- Case-III: When , then
- Case-IV: When , thenwhere is a constant.
2.2. New Generalized -Expansion Method
In this subsection, we outline the main steps of the new generalized -expansion method [25] for solving the PDE presented in Equation (1). In the proposed method, the solutions are obtained by assuming that , with satisfying the condition
where are constants. Furthermore, the solutions are presented as follows.
- Family-I: When then
- Family-II: When then
- Family-III: When then
- Family-IV: When then
- Family-V: When thenwhere are constants.
2.3. Neural Network Model
In order to obtain exact solutions to Equation (1), we employ the trial function with the neural network (NN) model. As the trial function, we use the NNs’ output. Subsequently, we characterize the trial function for the recommended technique by means of the following:
stands for the weight’s coefficient to provide the output layer U’s last hidden layer . F is the activation function that may be used, and . Parameters known as weights and the bias terms from the -th neuron of the layer preceding it are included in the proposed neural network model. These parameters are also included in the output of the output layer. The mathematical illustration of the in the layer is as follows:
with
Forward propagation is the mechanism by which the model of the neural network receives information obtained from the input layer and passes it on to the output layer, where it is processed by the activation function and weighted sum of neurons to produce the final output.
Figure 1 properly depicts the suggested neural network approach.
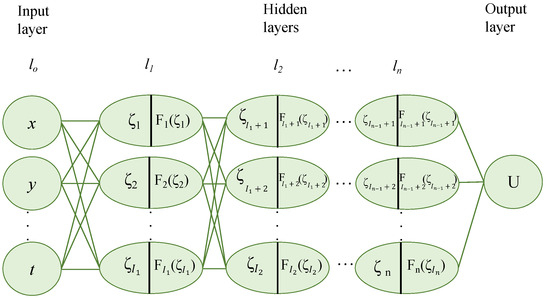
Figure 1.
NN model.
2.4. MGREMM Neural Networks
The MGREMM neural networks (MGREMMNNs) are a novel technique that integrates the NN model with the MGREMM. The key concept behind MGREMMNNs is the notion that the activation functions for the first hidden layer can be used for the solutions to the analytical method known as the MGREMM. Assuming the trial functions work as expected, the PDE will be transformed into algebraic equations. The first hidden layer’s activation functions in the NN model will be chosen as the solutions of the MGREMM by connecting NNs with the MGREMM. More exact solutions to PDEs may be found in this way. The suggested procedure consists of the following major steps:
- Step-1: We can determine the Riccati equation as the required equation by applying the MGREMM and the first hidden layer of activation functions for the NN model.
- Step-2: Making use of the activation function regarding the hidden layer as chosen in step 1, the MGREMMNN model will be constructed. With as input variables, with this approach, one may choose a subsequent hidden layer according to the particular requirements. Then, using the feedforward technique, you may obtain the output. The NN model is shown in Figure 2.
- Step-3: A forward-propagation MGREMMNN model may be used to derive the trial functions of PDE solutions.
- Step-4: By plugging the MGREMMNN trial functions into the appropriate PDEs, a system of algebraic equations is obtained.
- Step-5: Various potential solutions are investigated by algebraic equations involving and the function ; by setting the coefficients of every single term to zero for the equations generated in step-4, a set of algebraic equations may be produced.
- Step-6: A thorough examination of such algebraic equations must precede the selection of the best possible coefficient solutions from among all those that fulfill the criteria. These numbers are put back into the trial function to obtain the first U solutions that are explicit. Equations (2)–(4) may be used to provide an exact solution to Equation (1).
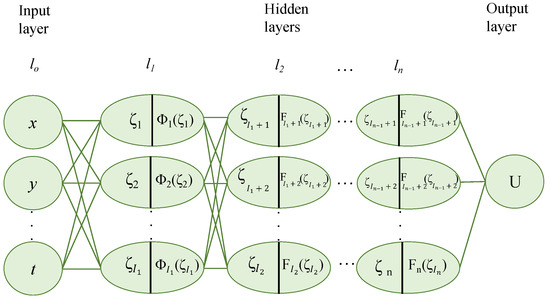
Figure 2.
NN model for MGREMM neural networks.
This approach accomplishes its objective of identifying more exact solutions by designating an appropriate number of neurons (MGREMM solutions) in the first hidden layer for the NN approach, which is an evident advantage.
2.5. Generalized -Expansion Neural Network Technique
This approach [26] facilitates the discovery of analytical solutions to NLPDEs by parameterizing a trial function using a neural network. The application of this function converts the governing PDE into a system of nonlinear algebraic equations. The parameters of the network (i.e., its weights and biases) are subsequently computed as the solution to this system. For discussing the solutions of the nonlinear system, we utilize a specified explicit model within the feedforward computation of the NNs, as shown in Figure 3.
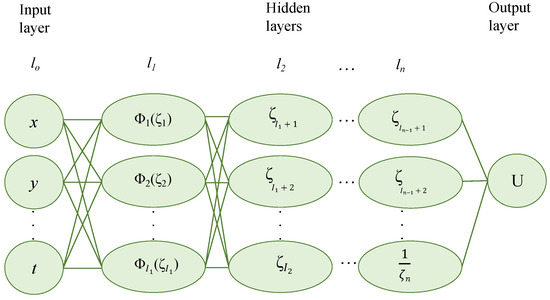
Figure 3.
NN model for generalized -expansion neural network technique.
In the proposed method, the activation function is used, which was defined in Section 2.2. Moreover, by using steps-4, -5, and -6 from Section 2.4, we obtain the desired results.
3. Applications of the Proposed Techniques for Gardner’s Equation
This section aims to investigate the nonlinear PDE known as Gardner’s equation. We apply the 2-2-2-1 MGREMMNN model and novel generalized -expansion neural network technique, which employs U, named as the trial function, to identify solutions to Gardner’s equation.
The MGREMMNN model uses two neurons for both the input and hidden layers and uses the trial function for PDE solutions as its output equation U as follows:
where
whereas , indicates the activation function corresponding to where are the real parameters to be identified subsequently.
To make the calculation simple, we employ the 2-2-2-1 MGREMMNN technique. In other words, x and t serve as inputs, and the activation functions for the first hidden layer are the Riccati equation solutions, denoted as . In contrast, the activation functions for the second layer are the identity function and the square function . This NN output is the trial function of PDEs, and the result represents the following:
where
A straightforward explanation of the 2-2-2-1 MGREMMNN model is provided in Figure 4. In order to simplify the calculation, set and in the actual computation. Thus, the formula for the 2-2-2-1 MGREMMNN model is as follows:
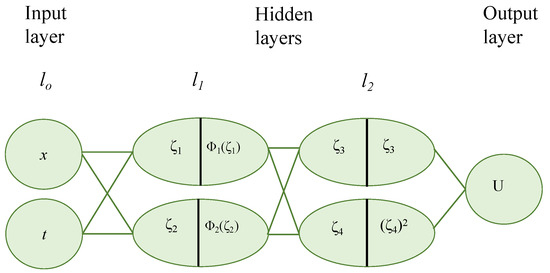
Figure 4.
The 2-2-2-1 NN model of Equation (17).
Moreover, the analytical solutions of Gardner’s equation are also discussed by applying the generalized extended neural network method, which comprises two hidden layers, each of which contains two neurons, as illustrated in Figure 5. The first hidden layer neurons’ activation functions are all ; however the second hidden layer’s third and fourth neurons’ activation functions are the identity mappings and , accordingly. As a result, we have the trial function as follows:
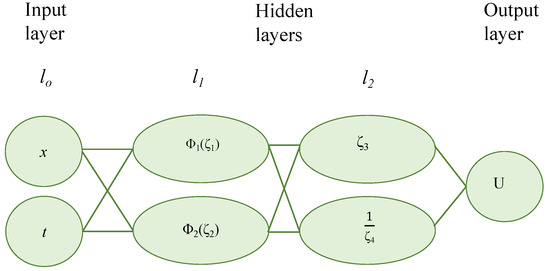
Figure 5.
The 2-2-2-1 NN model of Equation (18).
3.1. Gardner’s Equation
This subsection aims to study the soliton solutions of the nonlinear Gardner equation introduced in 1967 [27]. It developed as part of the Miura transformation, which connects solutions to the KdV and mKdV equations. The Gardner equation is an interpolating equation that links the solution spaces of KdV and mKdV. In this work, we study Gardner’s equation [28,29,30], read as
where is wave amplitude and are constants determining nonlinearity and dispersion. In addition, for ℏ Equation (19) transforms to the mKdV equation, while for ℵ it transforms to the classical KdV equation, where and are quadratic and cubic nonlinearities, respectively. Equation (19) models nonlinear waves in fluid dynamics, plasma physics, optics, and Bose–Einstein condensates. Furthermore, the proposed model has been studied from different perspectives in the literature. In [28] the -expansion method and the generalized projective Ricatti method are applied to investigate the soliton solutions of the proposed model, while in [29] the improved -expansion and wave Ansatz methods are applied for investigating Equation (19). Similarly, in [30] the exp-function method is applied to study various soliton solutions of the suggested model. In this work, we study the soliton solutions of Equation (19), applying the newly integrated neural network method.
3.2. Modified Generalized Riccati Equation Mapping Neural Network Method
In this subsection, we calculate the soliton solution of Gardner’s equation by applying the suggested technique; by manipulating Equations (17) and (19) and solving the system of algebraic equations, we have the following solutions.
- (I) When , , , and , , , and , the following solutions are provided.The kink-type soliton solution:The singular soliton solution:The bright–dark soliton solution:The singular soliton solution:When , we obtain the singular solitons as follows:When , , we have the following singular soliton solutions:
- (II) When , , , and , , , we have the following periodic solutions:When , the following solutions can be acquired:When , we obtain the periodic solutions as follows:
- (III) When , the soliton solutions are as follows:
- (IV) When , , we havewhere denote the real numbers such that .
3.3. New Generalized -Expansion Neural Network Method
The solutions of the proposed method can be written as follows by tackling Equations (18) and (19) and solving the system of algebraic equations.
- Family-I: When and , , we obtain the singular solution
- Family-II: When and , , we have the periodic solution
- Family-III: When and, we obtain the singular soliton
- Family-IV: When and, we have the periodic solution
4. Applications of the Proposed Techniques for the (2+1)-Dimensional Zabolotskaya–Khokhlov Model
This section aims to briefly describe how the proposed methods can be applied to the nonlinear PDE known as the ZK model, where its other details are already described in Section 2. We apply the 3-2-2-1 MGREMMNN model and novel generalized -expansion neural network technique, which employs U, named as the trial function, to identify solutions to the ZK model.
The MGREMMNN model has three neurons for input as well as two neurons for each hidden layer and uses the trial function for PDE solutions as its output equation U as follows:
where
whereas , indicates the activation function corresponding to where are the real parameters to be identified subsequently.
To make the calculation simple, we employ the 3-2-2-1 MGREMMNN technique. In other words, x, y, and t serve as inputs, and the activation functions for the first hidden layer are the Riccati equation solutions, denoted as . In contrast, the activation functions for the second layer are the identity function and the square function . This NN output is the trial function of PDEs, and the result represents the following:
where
In order to simplify the calculation, set and in the actual computation. Thus, the formula for the 3-2-2-1 MGREMMNN model is as follows:
A straightforward explanation of the 3-2-2-1 MGREMMNN model is provided in Figure 6.
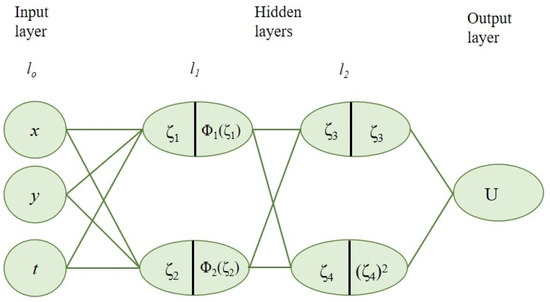
Figure 6.
The 3-2-2-1 NN model of Equation (53).
Moreover, the analytical solutions of the ZK model are also discussed by applying the generalized extended neural network method, which comprises two hidden layers, each of which contains two neurons, as illustrated in Figure 7. The first hidden layer neurons’ activation functions are all ; however the second hidden layer’s third and fourth neurons’ activation functions are the identity mappings and , accordingly. As a result, we have the trial function as follows:
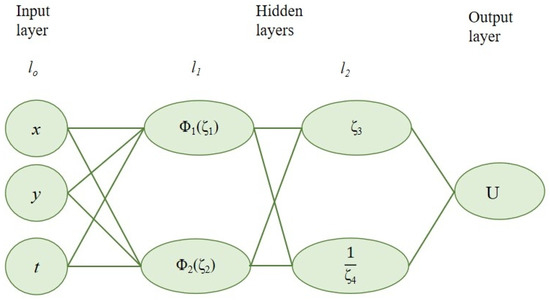
Figure 7.
The 3-2-2-1 NN model of Equation (54).
4.1. The (2+1)-Dimensional Zabolotskaya–Khokhlov Model
In this subsection, we calculate the soliton solutions of the (2+1)-dimensional ZK model [31,32,33], read as
where is the wave field describing how the nonlinear acoustic disturbance evolves in space and time. In addition, the (2 + 1)-dimensional ZK equation models the propagation of weakly nonlinear and weakly diffracting sound beams in fluids and gases. It describes the balance between nonlinearity, dispersion, and diffraction in nonlinear acoustic waves. This model has important applications in nonlinear acoustics, plasma physics, and fluid dynamics, particularly for studying finite-amplitude sound beams and nonlinear wave interactions.
4.2. Modified Generalized Riccati Equation Mapping Neural Network Method
In this subsection, we calculate the soliton solution of the ZK equation by applying the suggested technique; by manipulating Equations (53) and (55) and solving the system of algebraic equations, we have the following solutions.
- (I) When , , , and , , the following solutions are provided. Please check that the intended meaning has been retained. The kink-type soliton solution:The soliton solution:The bright–dark soliton solution:The combined soliton solution:When we obtain the soliton solutions as follows:
- (II) When , , and , we have the following periodic solutions:When , and the following solutions can be acquired:
- (III) When , the soliton solutions are as follows:
- (IV) When , and we havewhere denote the real numbers such that .
4.3. New Generalized -Expansion Neural Network Method
The solutions of the proposed method can be written as follows by tackling Equations (54) and (55) and solving the system of algebraic equations.
- Family-I: When and , we get the solution
- Family-II: When and , we have the periodic solution
- Family-III: When and , we obtain
- Family-IV: When and , we have the periodic solution
5. Discussion and Graphical Illustrations of Some Selected Derived Solutions
In this paper, we have examined a variety of the solutions like kink, dark, bright–dark, dark–singular, combined singular, and other types of solutions with the assistance of the application of neural network methods. The dynamics of some of the derived solutions are graphically illustrated in Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16 and Figure 17 with 2-dimensional, 3-dimensional, and contour plots based on the suitable selection of the parameters. The kink-type soliton in Equation (20) is visualized by 2-dimensional, 3-dimensional, and contour plots in Figure 8 with the parametric values , . Kink-type solitons model nonlinear waves in shallow water and stratified fluids, crucial for tsunamis and internal waves. Three-dimensional graphs visualize wave evolution, 2D plots track soliton profiles, and contour maps show energy distribution. Applications include ocean engineering, climate modeling, and tsunami prediction. These graphs enhance understanding of soliton dynamics in geophysical and fluid systems. The bright–dark soliton in Equation (22) is depicted by 2-dimensional, 3-dimensional, and density plots in Figure 9 for the parameters Combined bright–dark solitons in fluids model nonlinear wave interactions, enhancing understanding of energy localization and wave stability. They describe coupled phenomena in stratified oceans and atmospheric waves, improving rogue wave prediction. Their dual nature aids in optical–fluid analogies, bridging studies in nonlinear optics and hydrodynamics. These solitons optimize wave energy transport in geophysical and engineering applications. Moreover, the imaginary behavior of the solution in Equation (29) is plotted in three-dimensional, two-dimensional, and contour graphs in Figure 10 for the parameters . This shows the dynamics of the dark soliton. Dark solitons in optical systems enable stable signal transmission in fibers and all-optical switching due to their robustness against perturbations. In fluids, they model density dips in Bose–Einstein condensates and oceanic internal waves, aiding nonlinear wave studies. Their phase-jump property is key for vortex dynamics and turbulence analysis. Applications span telecommunications, quantum fluids, and geophysical fluid diagnostics. Figure 11 is sketched for for the parameters . Furthermore, the dynamics of the solution in Equation (30) is depicted in Figure 12 for the parameters , . This figure shows that the soliton maintains its overall shape and amplitude, demonstrating the hallmark features of soliton dynamics, namely stability and shape preservation due to a balance between nonlinearity and dispersion. The slight broadening over time suggests minimal dispersive effects, but no significant deformation or radiation is observed. This behavior confirms the solitary wave nature of the solution, propagating without losing its identity. The periodic wave solution in Equation (33) is plotted in Figure 13 for the values , . Moreover, the in Equation (35) is sketched for the values , in Figure 14. The periodic type dynamics for the solution in Equation (40) is plotted in Figure 15 with the parametric values . Many usages of periodic solutions can be found in advanced signal processing techniques. The oscillatory nature of such solutions is used for wavelength conversion and other signal processing applications in optical communication systems. Furthermore, dynamics of the solution are shown in Figure 16 for the parametric values . Such types of solution visualizations are crucial for analyzing nonlinear wave stability in fluids/optics and optimizing soliton-based signal transmission in fibers or oceanic waves. Applications include modeling internal waves in stratified fluids and designing robust optical communication systems. The parameters , are used for the physical behavior of the solution in Figure 17. Moreover, the dynamical behavior of the solution is plotted in Figure 18 for the values , . Figure 19 depicts the dynamics of the Re for the values , . By examining the solution profile plots for various parameter combinations, the visual representation exposes insight into the behavior and relationships of the soliton solutions. By simulating various soliton solutions in different forms, the 3D plots shed light on the spatial and temporal development of solitons. Solitons’ stability, oscillation, and propagation may be better understood with the help of these visuals. Contrarily, two-dimensional graphs highlight the exact spatial organization of solitons, allowing us to study the distribution of amplitudes, peak intensities, and localization degrees of solitons in the system. Contour profiles provide a compact, two-dimensional representation of wave behavior, capturing amplitude, phase, and energy distribution across a system. They are indispensable for visualizing nonlinear dynamics, soliton interactions, and wavefront evolution in diverse media like fluids, plasmas, and optical fields. By revealing gradients, critical points, and stability thresholds, they enable precise analysis in ocean engineering, fiber optics, and quantum systems. Their universal applicability makes them a cornerstone in theoretical research, experimental validation, and industrial problem-solving for wave-dominated phenomena. These simulations are useful for studying soliton interaction because they provide high- and low-density regions, which provide information on soliton merging, energy exchange, modulation, and soliton interaction.
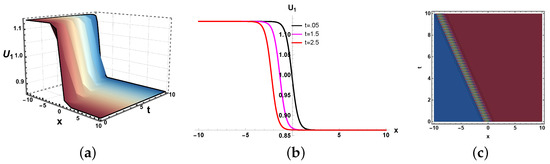
Figure 8.
(a) Three dimensional, (b) two dimensional and (c) contour plots of solution (20).
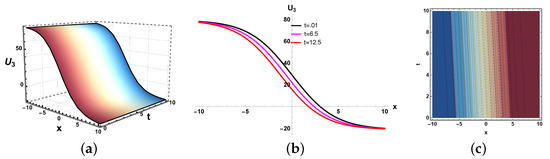
Figure 9.
(a) Three dimensional, (b) two dimensional and (c) contour plots of real behavior of solution (22).
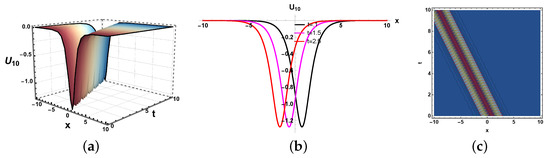
Figure 10.
(a) Three dimensional, (b) two dimensional and (c) contour plots of imaginary behavior of solution (29).
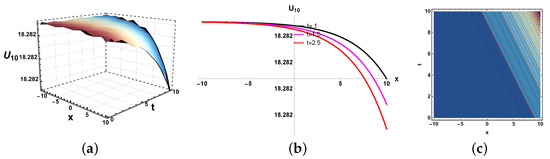
Figure 11.
(a) Three dimensional, (b) two dimensional and (c) contour plots of real behavior of solution (29).
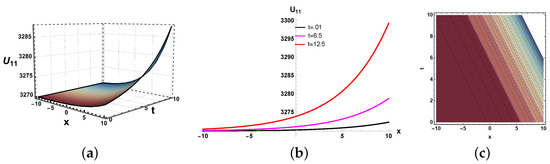
Figure 12.
(a) Three dimensional, (b) two dimensional and (c) contour plots of solution (30).
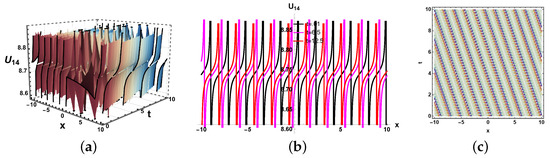
Figure 13.
(a) Three dimensional, (b) two dimensional and (c) contour plots of solution (33).
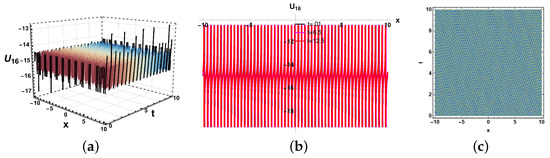
Figure 14.
(a) Three dimensional, (b) two dimensional and (c) contour plots of solution (35).
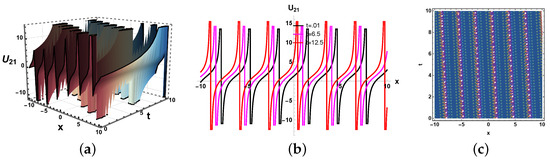
Figure 15.
(a) Three dimensional, (b) two dimensional and (c) contour plots of solution (40).
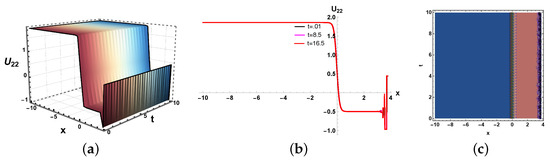
Figure 16.
(a) Three dimensional, (b) two dimensional and (c) contour plots of solution (41).
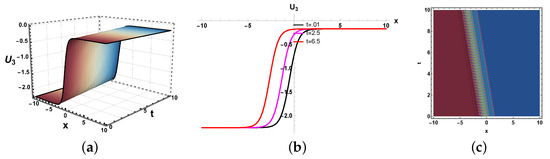
Figure 17.
(a) Three dimensional, (b) two dimensional and (c) contour plots of solution (47).
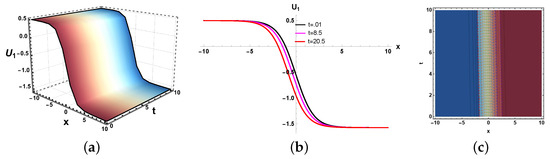
Figure 18.
(a) Three dimensional, (b) two dimensional and (c) contour plots of solution (56).
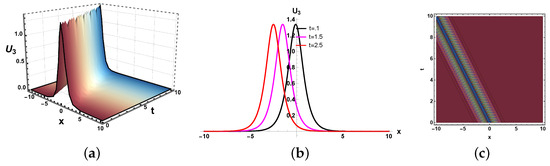
Figure 19.
(a) Three dimensional, (b) two dimensional and (c) contour plots of solution (58).
6. Conclusions
Recent advances in computational mathematics have introduced neural network-based frameworks as transformative tools for solving PDEs. While physics-informed neural networks and Deep Neural Networks have gained traction, their reliance on numerical approximations often overlooks the intrinsic mathematical elegance of PDEs. A groundbreaking shift is underway: hybrid methodologies now merge neural networks with symbolic computation, transcending mere curve-fitting to achieve exact analytical solutions. This fusion of data-driven learning and rigorous mathematical derivation unlocks unprecedented precision, bridging the gap between numerical pragmatism and theoretical exactness—ushering in a new era of equation-solving sophistication. In this work, a novel approach known as MGREMMNNs and a new generalized -expansion neural network method are introduced. This approach is a combination of analytical methods and neural networks that is used to compute analytical solutions of the nonlinear Gardner equation and ZK model. The proposed method has the capacity to overcome the limitations of traditional analytical methods. For analytical methods, the NLPDE is firstly transformed into a nonlinear ODE by employing suitable transformations. The preferred analytical approach is thereafter used in accordance with the balancing principle. Nonetheless, this sometimes does not provide integers essential for the application of the analytical technique, while in this approach, the solutions are derived directly from the PDE via the use of the suggested method. The neural network model’s forward propagation is used to build the trial functions by adding the findings of the proposed methods to the model’s first hidden layer. Setting the coefficients of each term equal to zero is achieved by the application of trial functions. These algebraic equations may be solved to obtain these coefficients. They can be further applied to obtain the solution of the model in the proposed techniques. These methodologies possess the capacity to provide novel insights and comprehension of various NLPDEs, potentially facilitating future progress in multiple scientific domains. By using these tools, researchers may enhance their understanding of the behavior of nonlinear systems and events.
Author Contributions
Conceptualization, J.M.; methodology, F.Y.; software, J.M.; validation, A.R.A.; formal analysis, J.M. and A.R.A.; investigation, F.Y. and U.Y.; resources, U.Y.; qriting—original draft, J.M. and A.R.A.; writing—review and editing, U.Y.; visualization, F.Y.; supervision, F.Y.; project administration, U.Y.; funding acquisition, A.R.A. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported and funded by the Deanship of Scientific Research at Imam Mohammad Ibn Saud Islamic University (IMSIU) (grant number IMSIU-DDRSP2502).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Gepreel, K.A. Analytical methods for nonlinear evolution equations in mathematical physics. Mathematics 2020, 8, 2211. [Google Scholar] [CrossRef]
- Yang, J. Nonlinear Waves in Integrable and Nonintegrable Systems; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2010. [Google Scholar]
- Baber, M.Z.; Shahzad, T.; Mohammed, W.W.; Ahmed, N.; Ceesay, B.; Yasin, M.W. Impact of Brownian motion on the optical soliton solutions for the three component nonlinear Schrödinger equation. Sci. Rep. 2025, 15, 25860. [Google Scholar] [CrossRef]
- Demirbilek, U. Analytical study on the generalized q-deformed Sinh–Gordon (Eleuch) equation. Comput. Math. Math. Phys. 2025, 65, 825–839. [Google Scholar] [CrossRef]
- Baber, M.Z.; Yasin, M.W.; Ahmed, N.; Ali, S.M.; Ali, M. Dynamical analysis and optical soliton wave profiles to GRIN multimode optical fiber under the effect of noise. Nonlinear Dyn. 2024, 112, 20183–20198. [Google Scholar] [CrossRef]
- Muhammad, J.; Bilal, M.; Rehman, S.U.; Nasreen, N.; Younas, U. Analyzing the decoupled nonlinear Schrödinger equation: Fractional optical wave patterns in the dual-core fibers. J. Opt. 2024, 1–12. [Google Scholar] [CrossRef]
- Bulut, H.; Demirbilek, U.; Çelik, E. Dynamical Soliton Solutions of (2+1)-Dimensional Paraxial Wave and (4+1)-Dimensional Fokas Wave Equations with Truncated M-Fractional Derivative Using an Efficient Technique. J. Math. 2025, 2025, 6659392. [Google Scholar] [CrossRef]
- Mehdi, K.B.; Mousa, A.A.A.; Baloch, S.A.; Demirbilek, U.; Ghallab, A.; Siddique, I.; Zulqarnain, R.M. Exploration of Soliton Dynamics and Chaos in the Landau-Ginzburg-Higgs Equation Through Extended Analytical Approaches. J. Nonlinear Math. Phys. 2025, 32, 22. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, Z.; Lei, Z.; Omura, M.; Wang, R.L.; Gao, S. Dendritic deep learning for medical segmentation. IEEE/CAA J. Autom. Sin. 2024, 11, 803–805. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, H.; Jiang, X. Physics-informed neural network algorithm for solving forward and inverse problems of variable-order space-fractional advection–diffusion equations. Neurocomputing 2023, 535, 64–82. [Google Scholar] [CrossRef]
- Zhang, Z.; Bao, F.; Ju, L.; Zhang, G. Transferable neural networks for partial differential equations. J. Sci. Comput. 2024, 99, 2. [Google Scholar] [CrossRef]
- Liu, Y.; Mao, T.; Zhou, D.X. Approximation of functions from Korobov spaces by shallow neural networks. Inf. Sci. 2024, 670, 120573. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Chen, X.; Yan, X.; Zhang, X.; Wang, F.; Suzuki, T.; Ohishi, Y.; Cheng, T. Highly sensitive nonlinear temperature sensor based on soliton self-frequency shift technique in a microstructured optical fiber. Sens. Actuators A Phys. 2022, 334, 113333. [Google Scholar] [CrossRef]
- Zayed, E.M.; Alngar, M.E.; Shohib, R.; Biswas, A.; Yildirim, Y.; Moraru, L.; Georgescu, P.; Iticescu, C.; Asiri, A. Highly Dispersive Solitons in Optical Couplers with Metamaterials Having Kerr Law of Nonlinear Refractive Index. Ukr. J. Phys. Opt. 2024, 25, 01001–01019. [Google Scholar] [CrossRef]
- Zayed, E.M.; Alurrfi, K.A. A new Jacobi elliptic function expansion method for solving a nonlinear PDE describing the nonlinear low-pass electrical lines. Chaos Solitons Fractals 2015, 78, 148–155. [Google Scholar] [CrossRef]
- Younas, U.; Muhammad, J.; Ali, Q.; Sediqmal, M.; Kedzia, K.; Jan, A.Z. On the study of solitary wave dynamics and interaction phenomena in the ultrasound imaging modelled by the fractional nonlinear system. Sci. Rep. 2024, 14, 26080. [Google Scholar] [CrossRef]
- Zhang, S.; Xia, T. A generalized new auxiliary equation method and its applications to nonlinear partial differential equations. Phys. Lett. A 2007, 363, 356–360. [Google Scholar] [CrossRef]
- Younas, U.; Muhammad, J.; Murad, M.A.; Almutairi, D.K.; Khan, A.; Abdeljawad, T. Investigating the truncated fractional telegraph equation in engineering: Solitary wave solutions, chaotic and sensitivity analysis. Results Eng. 2025, 25, 104489. [Google Scholar] [CrossRef]
- Hamad, I.S.; Ali, K.K. Investigation of Brownian motion in stochastic Schrödinger wave equation using the modified generalized Riccati equation mapping method. Opt. Quantum Electron. 2024, 56, 996. [Google Scholar] [CrossRef]
- Hosseini, K.; Samadani, F.; Kumar, D.; Faridi, M. New optical solitons of cubic-quartic nonlinear Schrödinger equation. Optik 2018, 157, 1101–1105. [Google Scholar] [CrossRef]
- Muhammad, J.; Ali, Q.; Younas, U. On the analysis of optical pulses to the fractional extended nonlinear system with mechanism of third-order dispersion arising in fiber optics. Opt. Quantum Electron. 2024, 56, 1168. [Google Scholar] [CrossRef]
- Wang, J.; Liu, Y.; Yan, L.; Han, K.; Feng, L.; Zhang, R. Fractional sub-equation neural networks (fSENNs) method for exact solutions of space–time fractional partial differential equations. Chaos Interdiscip. J. Nonlinear Sci. 2025, 35, 043110. [Google Scholar] [CrossRef]
- Kumar, S.; Hamid, I.; Abdou, M.A. Dynamic frameworks of optical soliton solutions and soliton-like formations to Schrödinger–Hirota equation with parabolic law non-linearity using a highly efficient approach. Opt. Quantum Electron. 2023, 55, 1261. [Google Scholar] [CrossRef]
- Naher, H.; Abdullah, F.A. New approach of (G′/G)-expansion method and new approach of generalized (G′/G)-expansion method for nonlinear evolution equation. AIP Adv. 2013, 3, 032116. [Google Scholar] [CrossRef]
- Liu, Y.; Yuan, S.; Zhang, R.; Yan, L.; Dong, H.; Feng, L. A novel G′G-expansion neural networks method for exactly explicit solutions of nonlinear partial differential equations. Nonlinear Dyn. 2025, 113, 26603–26630. [Google Scholar] [CrossRef]
- Gardner, C.S.; Greene, J.M.; Kruskal, M.D.; Miura, R.M. Method for solving the Korteweg-deVries equation. Phys. Rev. Lett. 1967, 19, 1095. [Google Scholar] [CrossRef]
- Akram, G.; Arshed, S.; Sadaf, M.; Mariyam, H.; Aslam, M.N.; Ahmad, R.; Khan, I.; Alzahrani, J. Abundant solitary wave solutions of Gardner’s equation using three effective integration techniques. Results Phys. 2023, 44, 106187. [Google Scholar] [CrossRef]
- Gunerhan, H. Exact traveling wave solutions of the Gardner’s equation by the improved expansion method and the wave ansatz method. Math. Probl. Eng. 2020, 2020, 5926836. [Google Scholar] [CrossRef]
- Wang, K.J. Traveling wave solutions of the Gardner equation in dusty plasmas. Results Phys. 2023, 44, 106187. [Google Scholar] [CrossRef]
- Li, B.Q.; Wang, C. N-soliton solutions for (2+1)-dimensional nonlinear dissipative Zabolotskaya-Khokhlov system. Adv. Mater. Res. 2012, 424, 564–567. [Google Scholar] [CrossRef]
- Kumar, M.; Kumar, R.; Kumar, A. On similarity solutions of Zabolotskaya–Khokhlov equation. Comput. Math. Appl. 2014, 68, 454–463. [Google Scholar] [CrossRef]
- Han, T.; Rezazadeh, H.; Rahman, M.U. High-order solitary waves, fission, hybrid waves and interaction solutions in the nonlinear dissipative (2+1)-dimensional Zabolotskaya-Khokhlov model. Phys. Scr. 2024, 99. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).