Pull-Based Output Rate Control of a Flexible Job Shop in a Multi-Shop Production Chain

Abstract

This paper addresses the problem where optimizing a single production shop within a production chain may not improve the overall performance of the entire chain. To overcome this and synchronize the efficiency of each shop, methods are proposed to align the output rate of an upstream shop with the limited intake rate of its downstream shop. In the proposed methods, the output rate of the upstream shop is used to guide job scheduling, processing, and resource allocation in the shop. Simulation results from a real-world case study demonstrate that implementing this pull-based system reduces job earliness and tardiness by over 90% in the tested factory, where the upstream shop is a flexible job shop, leading to lower inventory costs, idling costs, and labor costs.

1. Introduction

The concept of pull production was introduced long ago, and numerous related studies have been conducted since then. However, most existing approaches assume either a linear production line or a single-shop environment where all jobs follow identical routing sequences [1,2,3,4]. Their methods focus on coordinating production between consecutive stages. For example, the market demand triggers the release of jobs from the final operation, which in turn pulls jobs from its immediate predecessor. This pull process continues upstream until the first operation draws in the raw materials.

In real-world production environments, multiple production shops (or independent production stages) are often connected in series [5]. Based on our investigation of many manufacturing factories in Taiwan and Japan, a common issue exists: even when a production shop is optimized for a specific objective, this optimization does not necessarily contribute to improving the performance of the entire production chain. For example, minimizing the total completion time of all jobs (i.e., makespan) in one shop may result in the problem of being unable to transfer those jobs to the downstream shop, because the downstream shop might still be busy and unable to accept additional jobs due to limited capacity. This mismatch can lead to an accumulation of completed jobs between shops, increasing inventory levels and costs for storage and management. Previous research findings also suggested that there is a clear tradeoff between minimizing the makespan and just-in-time (JIT) production [6]. Conversely, when the pull concept is applied to optimize the whole production chain, it becomes challenging to control the production speed of each individual shop so that it aligns with the intake rate of the next shop in the sequence.

This study addresses this gap by proposing a new pull-based control framework specifically designed for a flexible job shop (FJS) constrained by a downstream shop with limited intake capacity. Unlike prior pull and hybrid systems, the proposed approach integrates detailed job scheduling within the FJS with due-date assignment mechanisms that synchronize its output pace to the downstream shop’s intake rate. Through this integration, our method not only optimizes the internal efficiency of the FJS but also ensures smooth and capacity-aligned flow across production shops.

The proposed approach is based on a real factory case in Japan, where one of the production shops operates in an FJS environment. In such a complex production environment, jobs follow diverse processing routes and revisit certain machines, making traditional pull control between individual machines infeasible. Moreover, the shop faces the problem of unsmooth job flows to the downstream shop, where some operations are strictly limited in speed and capacity. Though the case might be specific, the underlying structure of the problem—an FJS upstream constrained by limited intake capacity of a downstream shop—is not rare in various industries. Examples may include food processing, pharmaceuticals, and semiconductor manufacturing [7,8,9,10], where upstream production must be tightly coordinated with bottleneck operations or limited-capacity finishing stages.

Existing studies on FJS problems focus on one single shop and mostly aim at objectives such as minimizing the makespan, flow time, tardiness [11,12], processing costs [13], and machine idle time [14]. They assign due dates by using benchmark or shop floor data. Some studies propose combinations of dispatching rules [11,12] and optimization algorithms such as Artificial Bee Colony [13] and deep Q network [14] to cope with dynamics including new job arrivals and machine failures, but none of them take into consideration the needs or limitations of a downstream shop. To make up this void and help a real factory we visited improve production performance, this study proposes a solution aiming at controlling an FJS’s production speed to align with the limited intake rate of its downstream production shop.

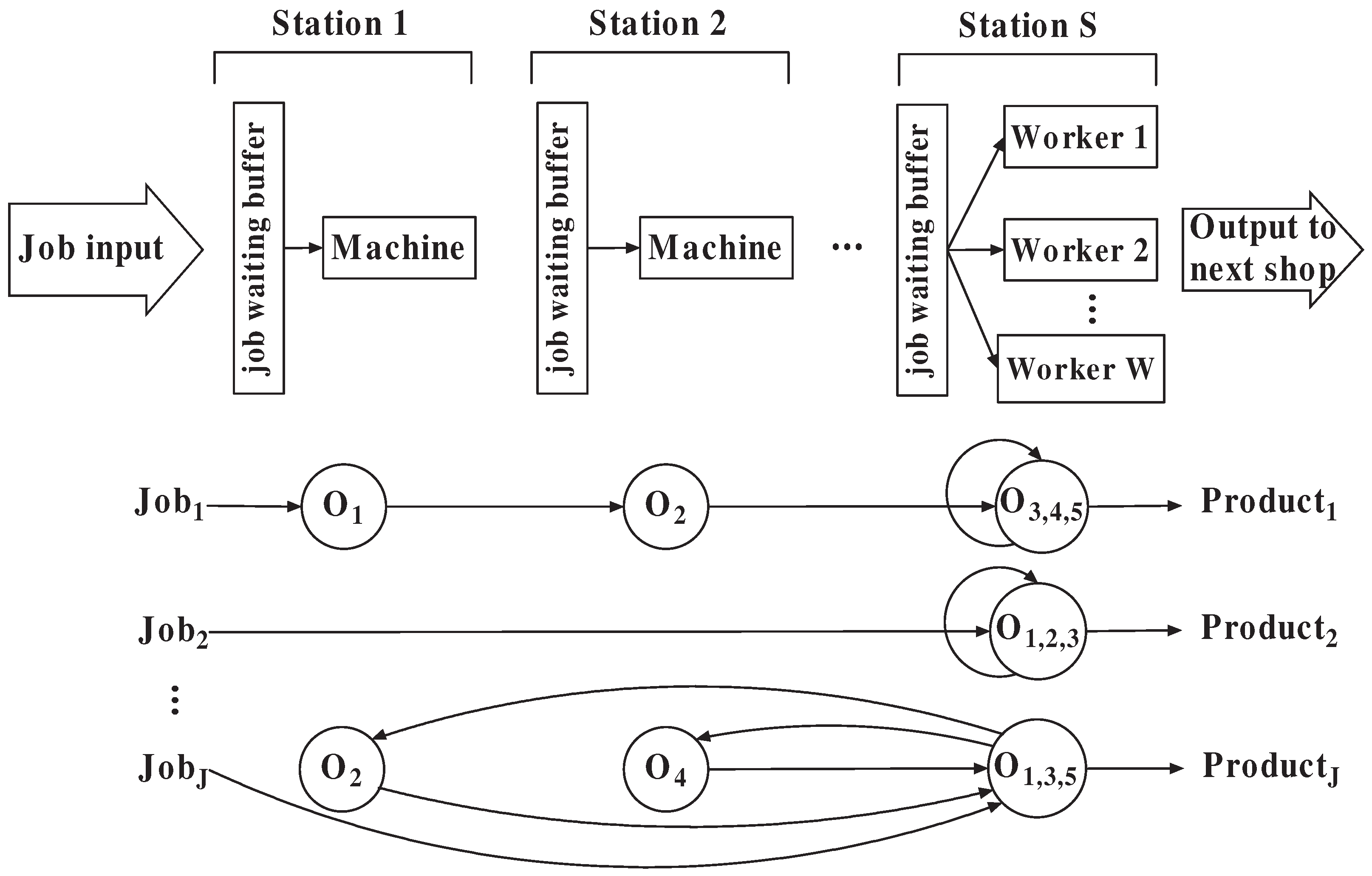
The FJS in the factory consists of multiple stations through which jobs go in predefined sequences. One of the stations has multiple workers performing the same work independently, while each of the other stations contains one machine. The worker station is frequently revisited by jobs, whereas the machine stations are accessed less often. However, many worker operations take only one-tenth as much time as a machine operation. Jobs arrive at the shop once per day in a batch. Transportation time between stations is considered negligible.

Figure 1 illustrates the FJS environment and provides an example of predefined job routings. In the figure, the number beside the letter “O” on each job’s routing indicates the job’s ith operation. For example, job 1’s first operation is performed in station 1, second operation is performed in station 2, and third, fourth, and fifth operations are performed in station S.

To ensure a smooth job flow between this production shop and the subsequent one, this study proposes controlling the completion times of jobs based on the intake rate of the successor shop. Each job is assigned a due date $D_j$, which is determined based on the successor shop’s intake rate. Let $C_j$ denote job j’s completion time, then if a job is completed earlier than $D_j$, its earliness is defined as $E_j=D_j-C_j$; if it is completed later, its tardiness is defined as $T_j=C_j-D_j$. The objective is to minimize the total earliness and tardiness of all jobs. For evaluation, the average earliness and tardiness of all jobs are used:

$$Minimize\sum _{j=1}^{J}max(E_j,T_j)/J.$$

(1)

In Equation (1), J represents the number of jobs received in one day. While the objective function allows a job to be completed after its due date $D_j$, the factory prefers that all jobs be completed on or before their due dates. Therefore, the proposed job scheduling method prioritizes completing jobs early rather than late. The following assumptions are made in this study:

• Assumptions

(1)

The processing of a job is non-preemptive.

(2)

Machines do not fail.

(3)

The job waiting buffer at each station is unlimited.

The main contributions of this study include modeling a real-world FJS where both machines and workers are required to perform operations, and proposing methods for achieving JIT production in the modeled shop. The methods extend the pull-based production concept to the complex FJS-downstream settings by developing algorithms that (1) assign job due dates based on scheduling and downstream constraints, (2) control the production pace of the FJS to match the downstream intake rate, and (3) maintain internal efficiency within the FJS while ensuring synchronized flow across shops.

The remainder of this paper is organized as follows: the proposed model and methods are detailed in Section 2, they are evaluated through computer simulations and analysis in Section 3, and the findings are summarized and directions for future research are discussed in Section 4.

2. Methodology

Notation
m	index of machine
M	number of machine stations
$RSJ$	jobs that go through the machine requiring rescheduling
$J\left(m\right)$	jobs going through machine m
$bT(m,j)$	processing time of job j before it arrives at machine m
$cT(m,j)$	completion time of job j on machine m
j	index of job
$T(m,j)$	processing time of job j on machine m
$RSM$	machines requiring rescheduling
$E{T}_j$	earliest completion time of job j
$ddI$	interval between two consecutive due dates
H	hours for which the schedule is made
w	number of workers at the worker station
$W{P}_j$	total processing time of job j at the worker station
$w\left[i\right]$	the ith worker
b	total idle time of workers before $D_j$
$a_{w\left[i\right]}$	idle time of the ith worker after the due date of his previously assigned job

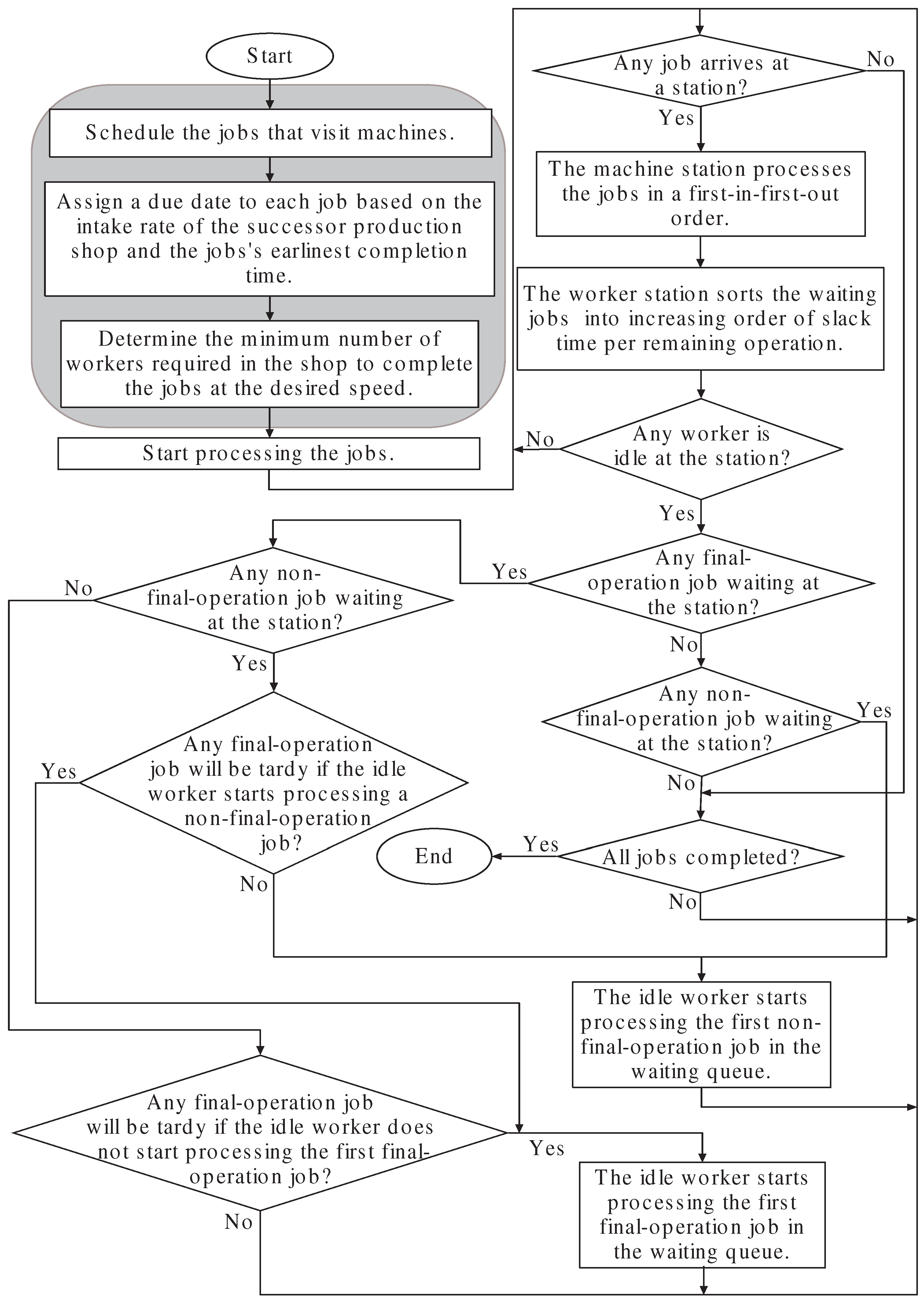
This study proposes a scheduling and production control method for the FJS production shop described. The method includes two stages: an offline scheduling stage and an online processing control stage. The offline stage schedules jobs that go through the machine stations, assigns a due date to each job based on the intake rate of the downstream production shop, and determines the minimum number of workers required to complete all the jobs by their respective due dates. The online stage determines the processing sequence of the waiting jobs at the worker station and controls the start time of processing the jobs at their final operations.

The advantage of this semi-offline, semi-online approach, compared to methods that rely entirely on offline solutions, is its low computational cost, which enables faster calculation speed and makes it suitable for solving large-scale problems. All the algorithms presented are original heuristics, rather than adaptations of existing methods.

The first step of the offline scheduling stage is to schedule the jobs that go through the machine stations. This process is illustrated in the pseudocode Algorithm 1. The goal is to ensure that jobs going through the same machine arrive one after another in a sequence so that no job has to wait long for the machine. This effectively eliminates the possibility of long waiting times at any machine station, because a machine operation takes much longer time than a worker operation.

In Algorithm 1, line 6 gets the jobs that need to go through a machine. This step ensures that only the machine (bottleneck) operations are included in the scheduling. Line 8 sorts the jobs in increasing order of their processing times before they arrive at the machine. This step provides a possible arrival sequence of the jobs at the machine. Lines 14–20 compute for each of these jobs its expected completion time by the machine if the machine processes the jobs in the order obtained in line 8. When a job assigned to the current machine also has operations on another machine that has already been scheduled, conflicts may arise if the new completion time violates the precedence of that downstream machine. In such a case, the affected jobs are rescheduled to ensure feasibility and preserve the processing order across machines. This feedback step is described by lines 2–4, 10–13 and 21–28. It enables adjustment of the schedule whenever the sequencing on one machine impacts previously scheduled machines.

Algorithm 1: Schedule the jobs that go through machines

After the schedule is created, the due date of each job is assigned based on its completion time on the final machine it goes through as well as the intake rate of the subsequent production shop. This process is described in the pseudocode Algorithm 2, which first calculates the earliest completion time for each job (lines 1–3) and then sets the job’s due date according to the intake rate of the next production shop (lines 4–12). The intake rate represents how frequently the subsequent production system can accept new jobs and is expressed as a time interval between consecutive intakes. This procedure effectively spaces the job due dates in a way that matches the flow capacity of the next shop. If the upstream schedule produces jobs faster than the downstream intake allows, the due dates will automatically be extended to maintain synchronization.

The purpose of this algorithm is to ensure smooth job flow between multiple shops and to prevent overloading or idling in the downstream shop. By integrating scheduling information from Algorithm 1 with the downstream intake constraint, it minimizes waiting times and ensures a balanced and continuous flow throughout the multi-shop production system.

Algorithm 2: Due date setting

Finally, Algorithm 3 is proposed to determine the minimum number of workers required to execute the production schedule generated by Algorithm 1, thereby establishing a link between job scheduling and workforce planning. While Algorithms 1 and 2 focus on aligning production pace and due dates with downstream capacity, Algorithm 3 quantifies the human resource requirement necessary to implement that schedule at the lowest possible labor cost.

Algorithm 3: Determine number of workers

Algorithm 3 starts by reading the detailed job due dates obtained from Algorithm 2. Based on this information, it computes the number of workers by checking if their total working time would be longer than the total processing time of worker operations. The algorithm assumes that if a worker finishes a job early, any remaining idle time before the job’s due date can be used to process other operations, provided sufficient time is available to complete them. This represents an idealized utilization scenario, which may not be perfectly achievable in practice due to the non-preemptive nature of operations. Therefore, the worker count derived from this algorithm should be interpreted as the minimum feasible number rather than an exact operational requirement.

The three algorithms described above constitute the offline scheduling stage. After being combined with the online processing control stage, they form the complete workflow of the proposed method, as illustrated in Figure 2.

In Figure 2, the offline scheduling stage is shown with a grey background, whereas the online processing control stage appears on a white background. During the online stage, machines process jobs in their order of arrival. Workers process jobs in the sequence of slack time per remaining operation, with priority given to jobs at their final operations. If a final-operation job would be tardy, a worker will process it first. This ensures that final-operation jobs wait only when there is sufficient time before their due dates. By allowing waiting, earliness is reduced, and as the due date approaches, the worker processes the job immediately, minimizing tardiness.

3. Simulation and Analysis

The proposed method is simulated using the real factory data. The FJS environment consists of 21 stations, including 1 worker station and 20 machine stations. There are 6 workers in the worker station. Jobs arrive once per day and must be completed within 16 h. All completed jobs are delivered to a downstream production shop, which has a maximum intake rate of one job per 20 min.

Currently, jobs in the production shop are processed based on empirical rules. Although it is possible to complete all the jobs within the required 16-h timeframe, many of the jobs end up as intermediate inventory because they are completed much earlier and need to wait through many intervals before entering the downstream shop. However, the last few jobs are often completed just near the end of the 16-h timeframe.

The routing and processing time for each job are presented in

Table 1. Routing and processing time of each job.

$\mathit{j}\setminus$op	1	2	3	4	5	6	7	8	9	10
1	1/10	2/240	1/10	1/60	1/170	1/20
2	1/50	1/10	3/180	1/10	1/60	1/20
3	1/10	1/10	3/180	1/10	1/60	1/10
4	1/2	3/240	1/10	1/20
5	1/45	1/5	4/420	1/15
6	1/35	1/5	5/180	1/90	1/20
7	1/35	1/10	5/180	1/45	1/7
8	1/25	1/5	5/120	1/120	1/35	1/15
9	1/20	1/35	1/10	1/20
10	1/20	1/5	5/120	1/15	1/70	1/35	1/10
11	1/5	6/60	1/20	1/5	7/120	1/15	8/360	1/15	1/10
12	1/5	8/30	1/10	1/5	9/60	1/40	1/15
13	1/10	10/60	1/10	1/160
14	1/10	11/60	1/20	1/160
15	1/25	1/10	10/60	1/20	1/160
16	1/40	1/10	10/60	1/20	1/20	1/60
17	1/10	1/10	11/240	1/30	1/80
18	1/10	12/180	1/20	1/45
19	1/10	12/180	1/20	1/75
20	1/5	13/90	1/14	1/1	14/15	1/2	1/1	15/5	1/30	1/7
21	1/25	1/10	16/60	1/2	1/35	1/11
22	1/6	1/5	17/10	1/9	1/25
23	1/5	17/120	1/15
24	1/5	18/60	1/10	19/30	1/15	1/10
25	1/2	20/180	1/2	1/2	15/10	1/2	1/25	1/7
26	1/10	1/5	18/60	1/5	1/10	15/30	1/15	1/10
27	1/5	1/2	20/180	1/2	15/10	1/2	1/15	1/10
28	1/30	1/10	19/120	1/20	1/20
29	1/5	20/120	1/5	1/5	21/300	1/15
30	1/10	16/60	1/10	1/45	1/50
31	1/10	16/60	1/10	1/45	1/45

, where jobs are listed vertically and their operations horizontally. Each cell shows the station index and the corresponding processing time for an operation. Station 1 represents the worker station, while the remaining stations are machine stations.

According to the shop floor information described above, the parameters in the proposed method are set as follows: $M=20$, $H=16\times 60$, and $ddI=20$. Using the proposed Algorithm 3, the minimum number of workers required for the provided data is determined to be $w=4$.

The evaluation is made based on the following performance measures, with several due date-related dispatching rules—EDD (earliest due date), MDD (modified due date), and MST (minimum slack time)—selected for comparison. These rules are found to be among the most effective for completing jobs while minimizing either tardiness alone [15,16,17] or the total of earliness and tardiness [18,19]. They are widely employed for performance comparison in studies on dynamic FJS problems [14,17,20,21].

Table 2. Performance comparison between existing scheduling rules and the proposed method.

	${\mathit{D}}_{\mathit{J}}$	${\mathit{C}}_{\mathit{J}}$	$\overline{\mathit{ET}}$	$\mathit{\sigma }\left(\mathit{ET}\right)$	${\mathit{J}}_{\mathit{t}}$	${\overline{\mathit{E}}}_{\mathit{e}}$	$\mathit{\sigma }\left(\mathit{E}\right)$	${\overline{\mathit{T}}}_{\mathit{t}}$	$\mathit{\sigma }\left(\mathit{T}\right)$
EDD	820	1316	149.0	108.11	10	120.2	57.68	209.5	159.91
	840	1316	156.1	102.16	10	140.2	57.68	189.5	159.91
	860	1316	163.7	98.77	9	153.3	65.09	189.1	156.33
	880	1316	172.1	97.28	8	165.8	73.04	190.4	152.58
	900	1316	181.8	96.91	8	185.8	73.04	170.4	152.58
MDD	820	1271	152.0	106.93	10	122.4	53.90	214.3	159.05
	840	1276	160.3	100.56	9	136.3	59.57	219.0	152.13
	860	1271	168.0	94.31	8	149.7	66.64	220.6	141.03
	880	1286	177.0	92.83	8	168.7	67.89	200.9	146.87
	900	1291	186.4	92.56	7	180.5	76.95	206.4	139.75
MST	820	1031	128.2	50.94	12	124.5	45.50	134.2	54.60
	840	1031	132.7	52.77	12	144.5	45.50	114.2	54.60
	860	1031	137.3	63.37	11	156.3	45.50	102.8	54.60
	880	1031	143.5	63.37	10	168.2	45.50	91.7	54.60
	900	1031	151.6	74.49	9	180.4	72.00	81.4	34.07
PSM	820	916	28.8	32.46	15	11.1	6.37	49.1	33.79
	840	840	20.8	16.86	15	11.4	6.57	32.3	15.53
	860	860	11.4	11.49	11	12.8	6.86	14.7	16.03
	880	880	7.3	7.57	2	10.2	7.45	11.0	6.24
	900	900	7.6	9.66	0	10.3	9.92	0.0	-

presents the simulation results, where PSM denotes the proposed scheduling method. $D_J$ starts from 820 because it is the earliest possible completion time of the last job according to the results obtained by Algorithm 2. As shown in the table, $C_J$ changes in line with $D_J$ under PSM, indicating the effectiveness of the proposed online processing control stage, where jobs are ordered depending on both due dates and slack time per remaining operation.

It is observed that when the due date parameter $D_J$ = 900 (equivalent to 15 h), the proposed scheduling method successfully completes all jobs without any instances of tardiness. Furthermore, the average earliness in job completion times from their respective due dates is limited to just 7.6 min, indicating a high level of scheduling precision. From the perspective of JIT production, where minimizing both early and tardy job completions is critical, this outcome is notably effective. In comparison to alternative scheduling rules, the proposed method demonstrates clear superiority across multiple performance indicators, including the average earliness and tardiness ($\overline{ET}$), the number of tardy jobs ($J_t$), and the corresponding standard deviations. These improvements suggest that the proposed method not only ensures timeliness, reducing inventory space and management, but also provides higher efficiency and less labor costs.

Figure 3 illustrates the performance differences between the methods based on the measures $\overline{ET}$, ${\overline{E}}_e$, and ${\overline{T}}_t$. The proposed method achieves an $\overline{ET}$ that is approximately one-fifth or less compared to the other methods, an ${\overline{E}}_e$ that is around one-tenth or lower, and a ${\overline{T}}_t$ that is even reduced to zero when all the jobs are completed within 15 h.

Table 3. Result of one-way ANOVA test.

		Sum of Squares	Degrees of Freedom	Mean Square	F-Value	p-Value
$\overline{ET}$	Between groups	78,410.768	3	26,136.922	200.169	0.0000 ∗
	Within groups	2089.184	16	130.574
${\overline{E}}_e$	Between groups	75,599.002	3	25,199.667	61.433	0.0000 ∗
	Within groups	6563.120	16	410.195
${\overline{T}}_t$	Between groups	113,707.398	3	37,902.466	143.675	0.0000 ∗
	Within groups	4220.900	16	263.806

Note: ^∗ marks statistical significance at the 0.05 level.

shows the result of an analysis of variance (ANOVA) test. ANOVA is widely used to check if a method has a significant impact on a performance measure. The closer to 0 the p-value is, the larger the significance is; and the closer to 1, the less the significance is. Usually, if the p-value is less than 0.05, it is believed that the corresponding method has a significant impact on the performance measure. Since the results in Table 3 all have a p-value of 0.0000, they represent a significant improvement under the three performance measures by using the proposed method.

4. Conclusions

This study applies the pull production concept to a production chain consisting of several sequentially connected production shops. In this framework, the production speed of each individual shop is not set independently but is instead governed by the demand rate of the subsequent downstream shop. This demand-driven approach ensures that each shop aligns its output pace with the needs (required input pace) of the next, thereby promoting synchronization across the entire production chain. The determined production speeds are then used as key parameters in guiding both job scheduling and processing decisions within a shop.

The research focuses on a real-world FJS environment as a case study. For this setting, a comprehensive control method for scheduling and job processing is developed. The proposed method is divided into two stages: an offline stage and an online stage. The offline stage is responsible for determining the appropriate due dates for each job and calculating the minimum number of workers required in the shop. These outputs contribute to a smoother job flow between adjacent shops and facilitate the elimination of surplus labor resources, enhancing overall efficiency. Meanwhile, the online stage dynamically manages the execution phase of production. It determines the optimal job processing sequence in real time and decides the precise start times for processing jobs at their final operations. This ensures responsiveness to current shop-floor conditions such as delay in worker operations and helps maintain alignment with the upstream-downstream synchronization goals.

The proposed method might be integrated into Manufacturing Execution Systems (MESs) as a plug-in or decision-support module that receives live job status data. It can provide dynamic scheduling recommendations or real-time control feedback. It may also help update job processing schedules in ERP systems.

Although the method is specifically developed for FJS environments, several key principles embedded in the method such as prioritizing scheduling bottleneck stations, synchronizing production rates between adjacent shops, eliminating redundant workers, sequencing jobs in a rational and efficient order, and actively managing the completion timing of jobs nearing their final operations offer valuable insights for addressing a broader range of general scheduling and production control problems.

Future work would focus on generalizing the method to other contexts including multi-factory environments where similar production constraints exist, or further considering machine failures, to validate the method’s applicability.