Abstract
Fast-growing technology and the development of IT services give the idea of founding a new application of stochastic processes and their properties. We give a new connection between electronic process management and a stochastic process named the bivariate Pólya–Aeppli counting process. This process is applied as a counting process in the mathematical construction of the given model and it has been introduced as a counting process in electronic process management. In our current study, we assume a company that has two locations in two countries—Bulgaria and Romania. For seamless communication and data sharing, the integrated factories leverage the System Applications and Products in Data Processing (SAP) system. By combining these functions into one structure, we optimize coordination, streamline operations, and improve the company’s productivity and profitability. The automated tools within the system facilitate uninterrupted production and secure supply chains and thus the decision making is improved. A key benefit of these tools is to boost production and procurement activities for success in today’s competitive market which results in cost savings, will increase visibility, and also will improve rapid decision making.
Keywords:
stochastic processes; electronic process management; enterprise resource planning; SAP system; cloud computing; industrial systems MSC:
60G07; 90B06; 91B32
1. Introduction
The development of modern business is closely related to the technological development of the world. Enterprise resource planning (ERP) software provides a centralized database from various company departments for the small, medium, and large enterprises on the market [1,2,3]. Shehab et al. [1] present an integrative review of ERP systems covering their architecture and implementation phases, demonstrating how these systems unify data across business functions. O’Connor and Dodd [2] discuss achieving enterprise-wide integration with ERP in capital projects, highlighting the benefits of centralizing departmental data on a single platform. O’Leary [3] offers a comprehensive overview of ERP systems—encompassing their life cycle, electronic commerce integration, and risk considerations—underlining the value of consolidating diverse processes into one system.
However, implementing a full ERP suite is not always a justified investment for small companies, since they usually work with a smaller volume of data. It may be more practical for a small enterprise to purchase only the ERP module that covers its current needs and plan for possible module upgrades as the business grows [4,5]. Jawad and Balázs [4] conduct a review of modern ERP optimization techniques (including the use of machine learning), implying that adopting ERP in a modular, needs-driven fashion can yield efficiency gains without excessive upfront costs. Katuu [5] traces the evolution of ERP systems and notes that recent innovations (like cloud computing) enable flexible, modular ERP solutions—allowing smaller firms to start with basic functionality and expand their systems over time as requirements increase.
Modern ERP solutions offer increased productivity and efficiency, especially with the advent of cloud-based architectures. This shift is of great importance for the resources, budget, and infrastructure traditionally required for ERP implementation, and many of these costs are becoming a thing of the past. Parr and Shanks [6] propose a structured model for ERP project implementation that improves process efficiency and helps maximize productivity gains from ERP. Dumitriu and Popescu [7] emphasize that adopting a cloud-based enterprise architecture can significantly reduce on-premises infrastructure needs and associated costs for ERP systems. Similarly, Biagi and Russo [8] demonstrate that aligning ERP data models with IT governance can streamline operations and eliminate redundant resource usage, further reducing overhead.
ERP software is designed to store large amounts of data about business operations, and these systems are typically flexible—allowing the software to scale and adapt in tandem with business growth [9,10,11]. Rao [9] notes that ERP capabilities can be aligned with evolving business needs so that, as an organization expands, the system can scale to accommodate new processes. Gaol et al. [10] report that, in the automotive industry, ERP implementation yielded improved process efficiency and was able to support a broader scope of operations as the company grew. Stergiou and Psannis [11] explore the integration of digital twin and IoT technologies in cloud environments, highlighting the need for ERP architectures that are flexible and scalable enough to incorporate such emerging technologies as business demands evolve.
One of the main benefits of an ERP system is that it integrates data from different operations into a centralized workspace which is fully traceable, minimizing the possibility of errors in process execution. Another benefit is that the system maintains a history of all operations, making data verification a quick and easy process. Thus, at any moment in the company’s processes, one can identify the person responsible for performing a given operation [12,13]. Chehri et al. [12] illustrate that implementing an enterprise IoT strategy in conjunction with ERP provides real-time visibility of operations, allowing every action to be traced to the individual responsible. Likewise, Chen et al. [13] show how an ERP-based inventory management system logs maintenance and operational activities in detail, enabling immediate accountability for each task.
1.1. ERP Software Can Be Used to Optimize the Production Process in the Following Ways
- Data from accounting, customer relationship management (CRM), order management, and the supply chain, among other departments, are collected by the ERP system [14,15];
- The ERP system consolidates the data into a single dashboard which is easy to navigate. It provides greater efficiency, accuracy, and a good insight into the internal processes;
- ERP efficiency is essential and it ensures that the customers remain satisfied and loyal users to the business itself.
When a company is seeking a suitable solution which would help it to integrate into the market, the ERP system’s functionality is important for its integration and development. This is the extent to which the system covers the information needs of the enterprise.
1.2. Main Processes
The main processes that a system should use include:
- the commercial process—from meetings and contacts through to the conclusion of deals, monitoring the development of relationships;
- the processes of acquiring—the necessary technical means and materials;
- the planning of the necessary resources—human and material resources, time, correct implementation of the commitments that is undertaken;
- the cash flows—monitoring, authorization, planning, reporting;
- condition of the material base;
- accounting reporting—other supporting activities—less important, but the possibilities for implementing a single system should be assessed.
Important features of a robust ERP system include using a single integrated database (enabling multi-company work in one data repository), the ability to consolidate information from all companies, and the ability to connect to accompanying systems such as web portals or other software used by different partners [16,17,18,19]. Chatterjee et al. [16] underscore that a unified data repository, combined with integrated CRM tools, is crucial for successful digital transformation, reflecting the need for a single source of truth in enterprise systems. El Hail and El Koraichi [17] demonstrate that linking an ERP with web-based CRM and e-business platforms can enhance supply chain performance, highlighting the importance of connectivity to external systems. Sologia et al. [18] evaluate ERP implementations and conclude that cross-departmental information consolidation is a key factor in their success. Additionally, Antwi and Avickson [19] show how integrating an SAP ERP with AI and data analytics platforms extends its functionality and exemplifies the system’s capacity to incorporate diverse external services.
The reliability of an ERP system depends not only on the level of integration but also on proper implementation and maintenance, as well as an architecture designed to handle the expected load [20,21,22]. Al-Banna et al. [20] examine the integration of ERP with Industry 4.0 technologies, finding that well-integrated systems lead to more resilient and reliable operations. Tarigan et al. [21] report that firms achieve better performance when their ERP is implemented with careful attention to integration and upkeep, indicating greater reliability in day-to-day operations. Furthermore, SAP technical documentation [22] notes that modern in-memory ERP architectures (like SAP S/4HANA) are engineered to support high transaction volumes and complex analytics, ensuring the system remains stable and efficient under heavy usage demands.
The main goal of ERP systems is to fully serve the needs of the corporate organization. In this study, we use the SAP ERP system. Cloud ERP systems increase the business efficiency of the enterprise, automate processes, and improve productivity through AI assistants.
The current study presents specific use cases of ERP systems and cloud computing technologies in industrial systems:
- Optimization of production: ERP systems share data from different departments such as CRM, supply chain, and accounting, providing a dashboard that increases production efficiency and minimizes errors.
- Corporate integration: A company with branches in different countries such as Bulgaria, Greece, and Romania can use cloud ERP systems to centralize and share data and improve coordination between them.
- Business process automation (BPA)/BA: SAP S/4HANA presents modules for finance, supply chain, sales, manufacturing and human resources, IoT, AI, and machine learning to automate operations.
- Accessibility: SAP Fiori presents access to ERP systems on web and mobile platforms, increasing accessibility and improving user experience in industrial applications.
- Real-time analytics and cybersecurity: Cloud ERP presents business continuity through real-time data analytics and cybersecurity.
The use of ERP highlights how these systems not only optimize business operations but also enable cross-border collaboration and data-driven decision making across industries.
ERP [14] is a multi-functional business management information system with integrated software modules that support the core business processes of a company. ERP systems optimize and automate processes, allowing companies to track key business processes such as production, delivery, and inventory management in real time. They can monitor operational resources, the fulfillment of company obligations, facilitate information flow between different functions in enterprises, and provide full visibility of the company’s core business processes.
For our study, we utilize the SAP S/4HANA ERP system, which introduces significant improvements over earlier SAP ERP solutions [23]. Cloud ERP platforms like S/4HANA increase enterprise efficiency by automating processes and even providing AI-driven assistance in operations. Notably, SAP S/4HANA employs a three-layer architecture (presentation, application, and database) and runs on an in-memory database for high-speed processing, while using SAP Fiori as a modern, user-friendly interface [24]. Built on the SAP NetWeaver Application Server, S/4HANA supports application development in ABAP and Java, and it integrates with the SAP Business Technology Platform (BTP) for extended cloud and analytics capabilities [25,26,27]. Bögelsack et al. [25] describe the deployment of S/4HANA in hyperscaler cloud environments, highlighting how its NetWeaver-based design facilitates integration with cloud services. Bagga [26] details SAP’s Integration Suite (a component of BTP), demonstrating how S/4HANA connects to external applications and services through standardized APIs. Brinkkemper [27] discusses principles of continuous enterprise system innovation, principles that are reflected in S/4HANA’s adaptable architecture and its support for ongoing improvement.
Innovations such as artificial intelligence (AI), machine learning, and the Internet of Things (IoT) can be seamlessly incorporated into this modern ERP environment [26]. Bagga [26] illustrates that SAP S/4HANA’s cloud integration framework enables these advanced technologies to plug into ERP workflows without disrupting core operations. A functional ERP architecture is illustrated in Figure 1 for reference, and further details on typical ERP architectures are available in the literature [28,29,30,31]. Wang [28] provides an educational perspective by integrating SAP into an information systems curriculum, which sheds light on SAP ERP’s modular architecture and how its components are taught. Brinkkemper and Pachidi [29] propose a method for modeling the functional architecture of enterprise software, delineating how different ERP modules interact within a system. Plattner and Leukert [30] discuss the in-memory SAP HANA technology underpinning S/4HANA, explaining how this design yields real-time data processing and analytics in modern ERPs. Singh [31] outlines the SAP Activate implementation methodology for S/4HANA, offering practical insight into deploying an ERP system in phased stages that align with its architectural layers.
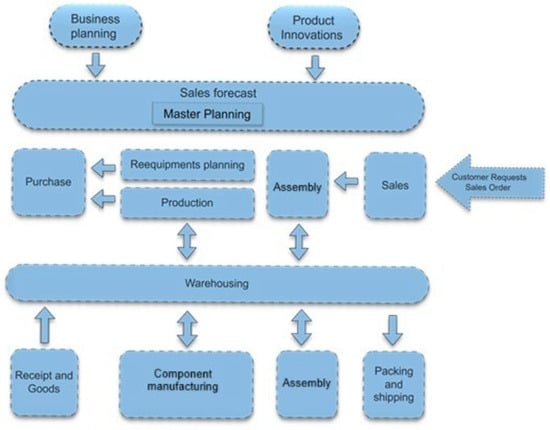
Figure 1.
An example of functional architecture of ERP.
1.3. Main Functionalities in SAP S/4HANA
The main functionalities that are present in SAP S/4HANA are:
- Finance Accounting (FI)—automation of financial operations and real-time reporting;
- Supply Chain Management (SCM)—inventory optimization and IoT integration;
- Sales and Distribution (SD)—streamlined order management and sales analytics;
- Production Planning (PP)—IoT-driven production tracking and efficiency gains;
- Human Capital Management (HCM)—automation of HR tasks and workforce planning;
- Analytics and Reporting—advanced data visualization via SAP Analytics Cloud.
SAP ERP systems also integrate with other commonly used modules such as CRM, SRM, and PLM to support all core business functions [32,33,34,35]. Keijzer [32] highlights that SAP S/4HANA’s embedded analytics module is tightly integrated into the system, providing real-time insights within the ERP environment. Sharma [33] provides a quantitative study on SAP S/4HANA in the retail sector, demonstrating significant financial benefits that result from integrating various functional modules (e.g., linking sales, inventory, and finance data for better decision making). An industry source [34] enumerates the standard modules of SAP S/4HANA (including CRM, SRM, and PLM) and describes how they interoperate as a unified suite to cover end-to-end business processes. Furthermore, Lazarova and Sapundzhi [35] explore a stochastic modeling approach using ERP data from supply chain management, illustrating how information from different ERP modules can feed into advanced analytics and improve decision-making processes.
1.4. Stochastic Modeling in ERP Systems
Another interesting scientific aspect of this paper is introduced in [36]. An interesting investigation on this topic is the bivariate Pólya–Aeppli stochastic process introduced in [37]. The Pólya–Aeppli process is a compound Poisson process with geometric compounding distribution and it is introduced in [38] and characterized in [39]. The simplicity of the Pólya–Aeppli process motivates the construction of the bivariate Pólya–Aeppli process. It is applied in a bivariate risk model with the bivariate Pólya–Aeppli counting process. By applying the Pólya–Aeppli process in the digital world and in the further development of the ERP systems, business processes are further developed, efficiency in CRM, production and financial processes is improved, and potential risks are predicted.
The main focus of this work is the application of this stochastic process which is also a birth process in the electronic industry. There are several approaches to extending the univariate distribution to a bivariate form in the literature. One approach is to obtain the bivariate Poisson distribution by using the trivariate reduction method and after that compounding this bivariate Poisson distribution with the geometric distribution, see [40].
Stochastic processes could be modeled to manage cloud databases by incorporating the inherent randomness and variability of workloads and resource demands, enabling more efficient resource allocation, performance optimization, and cost reduction. They involve and use techniques like predictive analysis, automated resource allocation, and real-time monitoring to optimize performance and resource utilization, ensuring high availability and efficient data management [41].
The current study has a significant role because we give the idea of using some stochastic elements of a constructed bivariate process and its nice properties that can be applied in business management [42,43].
The use of stochastic processes in cloud ERP is scientifically applicable due to their ability to model uncertainty, variability, and time-dependent event patterns. The two-dimensional Pólya–Aeppli process is well suited to finding discrete events that are clustered and dependent—a common feature in ERP data, such as transaction records, updates, and user interactions.
Unlike simpler counting models, this process allows for better correlation between correlated streams of events, such as those occurring across different company sites. Using such stochastic simulations to model ERP data streams, we gain a deeper understanding of system behavior and an analytical tool to optimize data-driven industrial decision making.
Stochastic models could improve demand forecasting by incorporating historical data and statistical methods to predict future demand with a range of possibilities, rather than a single point forecast.
By considering the probability of different demand scenarios, stochastic models optimize the inventory levels, minimizing the risk of stockouts or overstocking. This supports the determination of the optimal production schedule, considering the potential for disruptions in supply or demand and allowing for flexibility in production capacity. With the correct definition of the corresponding safety, the optimal level of minimum or maximum stock needed is determined to buffer against uncertainty in demand or supply.
The cloud ERP systems are established as a standard system on the Bulgarian market. We consider one mother company located in Greece and two location business centers in Bulgaria and Romania. The cloud database information events of the Bulgarian company are counted by a process which is a sum of two Pólya–Aeppli processes with different parameters. The cloud database information events of the Romanian company are counted by another stochastic process which is again a sum of two Pólya–Aeppli processes but its parameters are quite different from the parameters given for the Bulgarian company. As the bivariate process is a birth process [37] then any additional data can be easily counted by it. The next section gives an overview of this approach.
1.5. Objective, Relevance, and Novelty of the Study
The main objective of this study is to introduce a novel approach for modeling cloud-based enterprise resource planning (ERP) data flows in industrial systems using a stochastic framework based on the bivariate Pólya–Aeppli counting process. Although ERP systems are widely adopted for managing business operations, the underlying data patterns—especially those related to real-time, distributed production environments—are often complex, bursty, and interdependent. Traditional Poisson-based models fall short in capturing this behavior due to their equidispersion property and lack of correlation structure. Existing research primarily focuses on deterministic optimization or high-level system design, with limited attention to the probabilistic modeling of ERP-generated event data in cloud-based and multi-site settings. This study bridges that gap by proposing a mathematically rigorous, yet practically applicable model that captures the stochastic dynamics of real-time ERP data flows across interconnected production sites. The proposed bivariate Pólya–Aeppli process enables the quantification of dependent data events, offering a foundation for future performance evaluation and predictive control in cloud-integrated industrial systems.
The relevance of this study lies in its timely response to the increasing complexity of data-driven operations in global manufacturing and logistics. As enterprises adopt intelligent cloud ERP platforms like SAP S/4HANA, there is a pressing need for advanced mathematical tools that can both model and optimize the flow of digital information across distributed systems. According to recent market analyses, over 90% of large-scale enterprises have implemented ERP systems, with cloud-based ERP adoption projected to reach USD 100 billion by 2026. Yet, the statistical modeling of ERP-generated event data remains largely unexplored in the literature. By integrating a theoretically grounded stochastic model with a real-world ERP architecture, this study offers a dual contribution: it provides a rigorous mathematical framework for analyzing cloud-based data processes, and it proposes an application pathway that enhances process visibility, automation, and decision making in industrial settings. The model is especially suited for systems where transaction logs, updates, and production events exhibit overdispersion and intersite dependencies, thereby offering a new lens through which ERP system performance can be evaluated and improved.
To highlight the contribution of the study, Table 1 provides a comparative review of key related works and demonstrates the unique positioning of our methodology.

Table 1.
Comparative literature review.
Evident from Table 1, prior works have either focused on qualitative insights [5], architecture overviews [1], or applied machine learning techniques without explicit modeling of ERP event distributions [4]. While the bivariate Pólya–Aeppli process has been explored in risk modeling [37], its application to ERP systems is unstudied so far.
The innovation in this study is based on the integration of ERP systems, such as SAP S/4HANA, with stochastic modeling using the bivariate Pólya–Aeppli process. The use of this model is popular in risk and statistical analyses, but in this paper, we aim to apply the model innovatively in the field of cloud ERP systems and business process management in the electronics industry. This study bridges these gaps by introducing a stochastic framework that is both mathematically rigorous and practically aligned with real ERP architectures such as SAP S/4HANA. In it, we propose a new approach to quantifying and managing business events in distributed systems (e.g., Bulgarian and Romanian cloud data centers) using real-time analytics, IoT, AI, and machine learning capabilities coupled with stochastic modeling, offering a powerful tool for performance forecasting, real-time analytics, and data-driven optimization in distributed cloud environments. In addition to improving data analysis efficiency and accuracy, this research will improve business continuity through real-time decision making and provide a new theoretical framework for analyzing ERP data streams using combined distribution processes.
The rest of the paper is structured as follows: Section 2 presents the theoretical foundation of the bivariate Pólya–Aeppli process and its application in modeling cloud-based ERP data events and further shows the methodology of the study in a great detail. Section 3 discusses the results concerning the integration of this stochastic framework within a real-world SAP S/4HANA architecture, including organizational configuration and production planning across distributed manufacturing sites. Section 4 provides a discussion of the study’s contributions, significance, and comparison with existing literature. Finally, Section 5 concludes the paper with a summary of findings, future research directions, and the potential impact of the proposed methodology on industrial process optimization and decision making.
2. Materials and Methods
2.1. The Bivariate Pólya–Aeppli Process and Its Application to Cloud Database Information Events
The widely used model for count data is the Poisson process with intensity and probability mass function (PMF) given by:
One of the good properties of the Poisson process is that this process has the equidispersion property which means that its variance and mean are equal. In many practical applications the equidispersion property cannot be used, especially if there are count data. This fact motivates many authors to search for more flexible models in time for such data. The most popular and useful generalization of the Poisson process is the compound Poisson process which is suitable for cluster data. In [38], a compound Poisson process with geometric counting distribution is defined and called the Pólya–Aeppli process with parameters and The notation of the Pólya–Aeppli process is given by A counting process [38] is said to be a Pólya–Aeppli process if it starts at zero, i.e., , it has independent, stationary increments, and for each , is Pólya–Aeppli distributed. The Pólya–Aeppli process is a time-homogeneous process which for the parameter value becomes a homogeneous Poisson process. So, we have a homogeneous process with an additional parameter. The additional parameter has an interpretation as a correlation coefficient, see [44]. In the present paper we are interested in four independent Pólya–Aeppli processes denoted by , i.e.,
In [37], the following construction of two Pólya–Aeppli stochastic processes and with different parameters is used:
The compounding distribution of the stochastic processes and , as they are Pólya–Aeppli processes, is a geometric distribution with success probability The compounding distribution of the stochastic processes and is again the geometric distribution but with success probability
The joint probability generating function of the obtained bivariate Pólya–Aeppli process has the following form [37]:
where is the probability generating function (PGF) of the geometric distribution given by:
Definition (see [37]): A stochastic process with corresponding bivariate probability distribution of (), corresponding to (4) and (5), is referred to as a bivariate Pólya–Aeppli process BivPAP(), with parameters , and
In order to apply the Pólya–Aeppli process to model ERP data events, it is essential to estimate the arrival rate parameter , which represents the mean number of event clusters (or bursts) occurring per unit time. Given a time series of event data—such as database update timestamps, production log entries, or transaction records—the estimation of can be performed using the method of moments or maximum likelihood estimation (MLE). A common approach involves dividing the observed number of event clusters over a fixed time interval , denoted by , and computing the estimator . To distinguish clusters from individual events within a cluster, a threshold interarrival time can be defined based on empirical observations or domain knowledge, allowing the grouping of closely spaced events into single bursts. When full timestamps are available, this preprocessing enables reliable estimation of both and the compounding parameter from the data. In cloud ERP systems, where event logs are typically timestamped and stored in real time, this estimation can be automated, enabling adaptive tuning of the model to reflect current system dynamics.
Based on the construction and the properties of the bivariate Pólya–Aeppli process we give an application of this process in production management. The main production of the company is wireless access points—routers. The cloud database information events of the Romanian location center are counted by the process and cloud database information events of the Bulgarian location center are counted by the process Both companies function in SAP as one company code but each location has a separate plant in the organizational structure.
The purpose of this study is to implement an ERP system for the mother company with two business locations. It will help explain the processes of the company’s conception, planning, development, testing, and implementation of some specific SAP solutions and individual modules for the specified business departments.
We give attention to the SAP system which is mostly used for seamless communication and data sharing among the mother business company and the other two centers.
2.2. Detailed Methodology
The methodology proposed in this study integrates advanced stochastic process theory with cloud-based ERP system modeling to address the complexities of real-time information flows in industrial settings. The core of the methodology lies in constructing a bivariate Pólya–Aeppli (BivPAP) counting process as a mathematical tool for capturing the clustered and interdependent nature of ERP data events—such as database transactions, production log updates, or inventory changes—across two geographically distributed production sites.
The initial step involves the definition of four independent univariate Pólya–Aeppli processes each representing a stream of discrete events within the system. These are then combined to form two aggregate processes: and , which model the ERP data flow in Romania and Bulgaria, respectively. The resulting bivariate process captures the bursty and correlated behavior of digital records in distributed production environments. To account for clustering and overdispersion, the processes use geometric compounding distributions with different parameters for each location, reflecting localized event dynamics.
In contrast to traditional ERP data models—which often rely on deterministic flows or simple Poisson processes assuming independence and uniform arrival rates—our methodology provides a more nuanced, probabilistically sound model that incorporates intersite correlation, time dependency, and data clustering. This offers an analytical foundation for real-time monitoring, demand forecasting, and performance evaluation.
A key innovation of the proposed methodology is its applicability to cloud-integrated ERP systems, such as SAP S/4HANA, where transactional data from multiple locations are processed and stored centrally. By aligning the stochastic process structure with the organizational structure of ERP modules (e.g., separate plants, unified company code), the model allows for real-time data quantification and simulation. This also enables the future implementation of adaptive ERP analytics that respond dynamically to the statistical properties of business events.
We outline below the sequential steps of the methodology in detail:
- System Definition and ERP Structure MappingDefine the ERP system structure in terms of business logic, company code, production plants, and transactional modules. In our case study, two plants (Bulgaria and Romania) are modeled under a unified SAP company code using SAP S/4HANA Cloud.
- ERP Data IdentificationIdentify the discrete event streams to be modeled (e.g., database transactions, inventory updates, production log entries). These are timestamped events representing ERP data flows.
- Selection of Modeling FrameworkChoose the bivariate Pólya–Aeppli (BivPAP) process as the modeling tool due to its ability to capture overdispersion and interdependence between event streams.
- Construction of the Stochastic ModelConstruct four independent Pólya–Aeppli processes (two per location) and aggregate them to form two compound processes:
- : ERP events in the Romanian plant;
- : ERP events in the Bulgarian plant.
These are then jointly modeled as a bivariate Pólya–Aeppli process . - Parameter ConfigurationAssign process parameters reflecting real-world ERP data characteristics for each location. Parameters differ across plants to capture local variability and dependencies.
- Simulation and AnalysisSimulate ERP data streams based on the BivPAP model to analyze burst behavior, correlations, and ERP system load over time.
- Validation and Future IntegrationPlan empirical validation using real ERP logs to estimate model parameters via maximum likelihood or moment-based estimation. Integrate the model into predictive analytics tools for process monitoring and optimization.
The methodology is illustrated via a flowchart, see Figure 2. The methodology is novel in its application of a two-dimensional stochastic birth process to industrial ERP systems. While most prior works focus on optimization heuristics, AI, or high-level architecture, we propose a mathematically grounded framework that captures both time-dependent dynamics and site-specific interactions in cloud ERP environments.
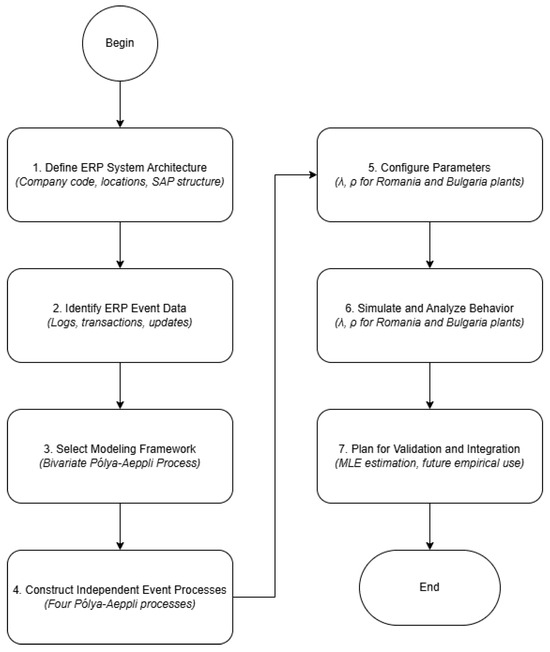
Figure 2.
Flowchart of the methodology.
In future work, this methodology can be extended through empirical validation using timestamped ERP logs. Parameters such as the arrival rate and compounding parameter will be estimated from real data using statistical methods (e.g., maximum likelihood estimation and cluster analysis), making the approach not only theoretically robust but also practically implementable in smart industrial environments.
3. Results
The integration of cloud computing platforms with ERP systems presents new challenges and opportunities for modeling distributed industrial data flows. This section explores how the architecture and configuration of SAP S/4HANA Cloud [45,46] enable the practical deployment of the stochastic methodology proposed in this paper.
We consider a case study of an industrial enterprise with a central office in Bulgaria and a subsidiary plant in Romania. These facilities share a unified SAP company code but operate as distinct production plants in the ERP hierarchy. Such a configuration presents complex intersite event dynamics that justify the use of a two-dimensional stochastic framework.
3.1. Organizational Modeling in SAP S/4HANA
The company is structured using standard SAP organizational elements, including:
- A single company code controlling financial processes (Figure 3);
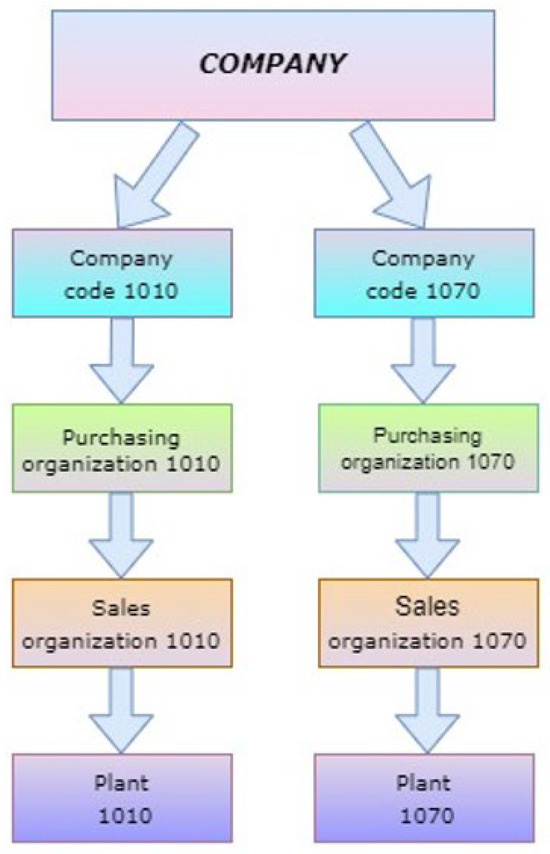 Figure 3. Company’s organization structure.
Figure 3. Company’s organization structure. - Two plants (Bulgaria and Romania), each with its own production and material planning units;
- Centralized procurement and logistics operations housed in the head office.
From a mathematical modeling perspective, this organizational configuration defines the support structure for two correlated data streams: ERP events generated at the Bulgarian and Romanian plants. These streams correspond to production records, inventory transactions, and real-time database updates—precisely the types of discrete, timestamped events modeled by the bivariate Pólya–Aeppli process.
3.2. SAP Module Interaction and Data Generation
SAP modules such as Materials Management (MM), Production Planning (PP), and Financial Accounting (FI) generate timestamped event data (Figure 4). These include:
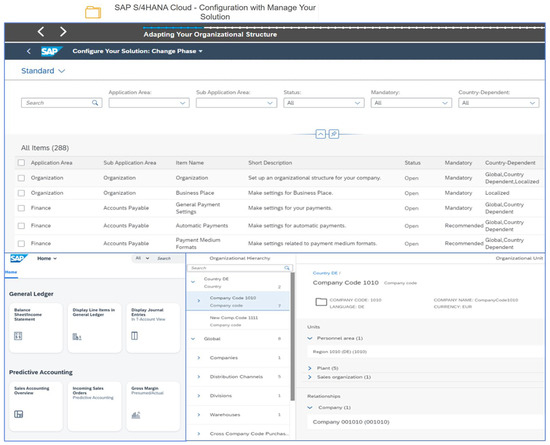
Figure 4.
Configuration of company’s solution.
- Creation and execution of production orders;
- Updates to stock levels and inventory transactions;
- Logging of goods receipts and invoice verifications.
Each of these operations contributes to a cumulative ERP event stream for each location. The heterogeneity and asynchronous nature of these processes produce bursty and interdependent event patterns—characteristics that deviate from the assumptions of traditional Poisson models and are better captured by our stochastic approach.
3.3. ERP-Driven Motivation for Stochastic Modeling
SAP S/4HANA provides cloud-native support for distributed plants under one company code. However, synchronization delays, processing overlaps, and variability in production load introduce nontrivial statistical behavior in the event logs. For example (Figure 5):
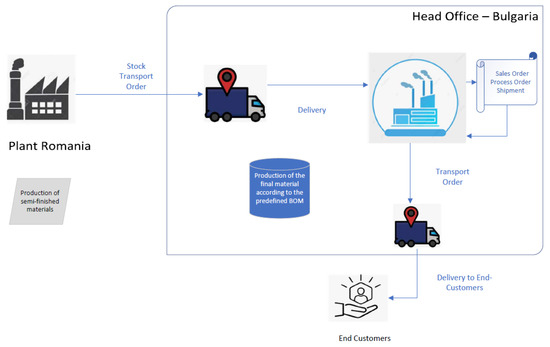
Figure 5.
Bulgarian Head Office.
- Romanian subcomponents are shipped to Bulgaria, introducing temporal dependencies between production events across sites.
- Material Requirements Planning (MRP) and safety stock definitions introduce bounded stochasticity in inventory triggers.
- Real-time analytics modules record correlated bursts of ERP activity during production surges.
These factors provide empirical justification for modeling ERP event processes as interdependent, overdispersed point processes. The bivariate Pólya–Aeppli model offers both a theoretical and computational advantage in this context by capturing:
- Event clustering via geometric compounding;
- Intersite correlation through joint distributions;
- Flexibility in parameterization to reflect local dynamics.
3.4. Conceptual Architecture for Model Implementation
Figure 6 presents a high-level schematic of how the bivariate Pólya–Aeppli model integrates with the SAP S/4HANA Cloud configuration. Each plant generates a stream of ERP events, modeled by a univariate Pólya–Aeppli process. These are jointly captured by the bivariate model, enabling both monitoring and predictive analytics across the enterprise. Event streams from distributed plants are modeled by the bivariate Pólya–Aeppli process to capture burstiness, overdispersion, and correlation.
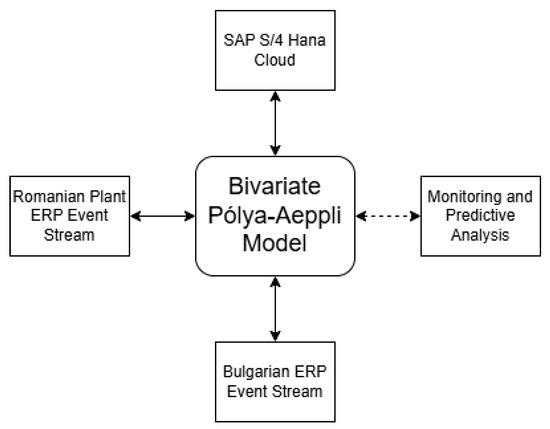
Figure 6.
Conceptual integration of stochastic ERP event modeling within the SAP S/4HANA Cloud architecture.
3.5. Simulation of Production Process—Case Study
In our case study, the main product is manufactured in Bulgaria, but some of the parts are produced in Romania. Figure 7 provides an example for the production of one final good through the bill of material (BOM) from different materials with different MRP structures. The BOM is a formally structured list of the components that make up a product. The list contains the object number of each component as well as the quantity and the unit of measurement.
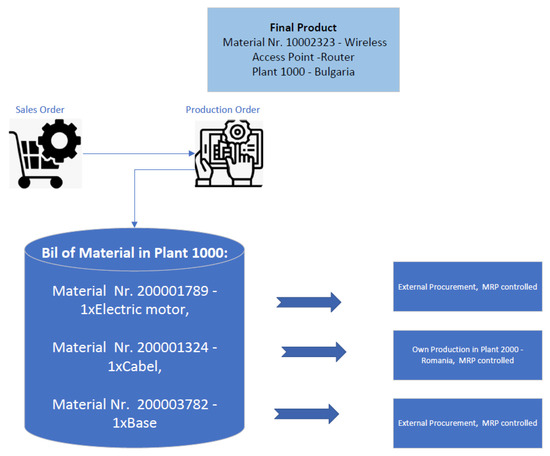
Figure 7.
Production of one final good.
As discussed earlier, in our case study the final product is produced in Bulgaria, but one of the components is a product originating from the plant in Romania. All the configurations for the material planning are performed from the Consumption-Based Planning menu, as the system could automatically generate purchase and production orders, preventing interruptions in production and creating a secure supply chain (Figure 8).

Figure 8.
BOM configuration in SAP.
The modern development of digital technologies has turned ERP systems into a very important tool for increasing the efficiency, automation, and integration of business processes in enterprises. Modern business management platforms such as SAP S/4HANA provide many opportunities for increasing the productivity of companies through real-time data analysis, use of cloud technologies, and automation of business processes. Cloud technologies associated with ERP systems integrate important business functionalities such as supply chains, sales, manufacturing, management, and many others and ensure a seamless flow of data. ERP platforms are becoming increasingly flexible and allow users to adapt to the changing business environment. With these systems, users have access to a lot of information in real time, which allows them to make informed decisions very quickly.
In the presented study, we consider a two-dimensional stochastic Pólya–Aeppli process that tracks events in a cloud environment, demonstrating how ERP systems can optimize production management through appropriate data modeling. A case study from a Greek company with Bulgarian and Romanian subsidiaries illustrates the role of SAP in unifying business operations while enabling local management. Businesses must invest in ERP systems to remain competitive in the digital economy. By leveraging cloud infrastructure, intelligent automation, and real-time data analytics, companies can streamline their business processes, improve decision making, and drive sustainable growth in their businesses.
4. Discussion
This study introduced a novel methodological framework that applies the bivariate Pólya–Aeppli (BivPAP) stochastic process to model cloud ERP data flows in distributed industrial environments. The main objective—to develop a mathematical model capable of capturing the time-dependent, correlated, and clustered behavior of ERP event data—was achieved by constructing two aggregate Pólya–Aeppli processes corresponding to different factory locations and combining them into a bivariate structure. Through this model, we demonstrated how complex production data, such as real-time cloud database updates, can be represented and analyzed in a mathematically rigorous way.
The significance of these results lies in the integration of advanced stochastic modeling into cloud ERP systems, a direction that has been largely underexplored in existing literature. While many previous studies focus on deterministic optimization approaches, rule-based automation, or high-level software architecture [1,2,3,36], they often lack formal mathematical tools to address the inherent randomness and correlation of ERP-generated data. In contrast, the proposed BivPAP-based approach provides a quantitative and probabilistic structure that captures both the frequency and dependence of events occurring in distributed locations. This is particularly relevant for multi-plant ERP systems like SAP S/4HANA, where synchronized operations depend heavily on the timing and reliability of data events across different units.
By demonstrating how ERP event streams—such as transaction logs, inventory movements, and production logs—can be modeled as birth processes with geometric clustering, we provide a theoretical tool that lays the groundwork for predictive analytics, system diagnostics, and real-time optimization. The proposed framework also opens new possibilities for coupling stochastic models with machine learning, IoT sensor data, and adaptive supply chain optimization, further enhancing its relevance in the context of Industry 4.0.
Although the present paper is largely conceptual and theoretical, it sets the stage for a future case-study-based validation, where model parameters such as the arrival rate and compounding parameter will be estimated from real ERP data. This will allow for empirical performance analysis and direct comparisons with traditional Poisson-based or rule-driven models used in current ERP decision-support systems.
The results obtained in this paper align with the study’s objective by delivering a new mathematical modeling framework for cloud ERP systems. The contribution is twofold: first, it introduces the BivPAP process into a new application domain—enterprise systems modeling—and second, it highlights its theoretical and practical advantages over existing models, particularly in terms of flexibility, accuracy, and the ability to model complex interdependent event streams.
5. Conclusions
The present paper gives an interesting approach of using some stochastic elements of the bivariate Pólya–Aeppli counting process and its nice properties that can be applied in production management with some data sources. The stochastic process is a bivariate birth process and this property can be used for data that can increase in time. We also introduce the cloud ERP system which is in fact established as a standard system on the Bulgarian market. The main production of the company that we are interested in is concerned with wireless access points—routers. The business model that we are interested in is a mother company located in Greece with two business centers in two countries—Bulgaria and in Romania. The cloud database information events for the routers’ production of the Romanian company are counted by a stochastic process which is a sum of two Pólya–Aeppli processes with different parameters. The parameters of the second stochastic process that counts the routers’ production cloud database information events (record, log entry, update) of the Bulgarian company are quite different from the parameters of the process determined to count the cloud database information events of the Romanian company, but they correlate. Both the companies function in SAP as one company code while each location has a separate plant in the organizational structure. The purpose of this study is to implement the ERP system between the mother company and the two business locations. The most important thing for each business location is the definition and planning of their own organizational structure which can be performed through the implementation of SAP S/4HANA Cloud configuration. The company’s model is developed and configured in SAP S/4HANA Cloud, public edition, and supports scalability and traceability in real time according to the dynamic global production and logistics.
To demonstrate the improvements in system productivity and efficiency, it is advisable to use real data or practical case studies. Specifically, a comparative analysis will be conducted between a traditional ERP architecture and the implemented SAP-S/4HANA-Cloud-based solution. This analysis will measure key performance indicators such as order processing time, inventory accuracy, production automation levels, report generation speed, and reductions in IT infrastructure costs. For instance, monitoring the production of wireless routers at the Bulgarian and Romanian locations will enable the assessment of how the ERP system enhances logistics coordination and resource planning in real time—minimizing delays and improving the traceability of production stages.
Integrated AI technology, predictive analytics, and blockchain technologies can also significantly enhance ERP systems through safe, transparent, and secure transactions. IoT’s increasing role will provide expanded data for stochastic modeling, improving forecasting and resource planning.
The current study leaves open the question of further research into hybrid models that combine stochastic processes and AI. They are expected to improve business process automation, forecasting, and supply chain management.
Cloud ERP systems continue to evolve, and their integration with new mathematical tools will be important for the development of the next generation of intelligent industrial systems.
Author Contributions
Conceptualization, F.S. and M.L.; methodology, F.S. and V.D.; software, S.G. and V.T.; validation, F.S., V.D. and M.L.; formal analysis, F.S., M.L. and M.T.; investigation, F.S. and M.L.; resources, V.D. and S.G.; data curation, V.D.; writing—original draft preparation, F.S. and M.L.; writing—review and editing, F.S., V.D., M.L., S.G., M.T. and V.T.; visualization, M.L. and V.T.; supervision, F.S. and M.L.; project administration, S.G. and V.T.; funding acquisition, M.L and S.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Bulgarian National Science Fund under Project KP-06-M 62/1 “Numerical deterministic, stochastic, machine and deep learning methods with applications in computational, quantitative, algorithmic finance, biomathematics, ecology and algebra” from 2022 and by the Scientific Research fund of Ruse University under Project No. FNSE-02.
Data Availability Statement
The data that support the funding of this study are available within the article.
Acknowledgments
The authors would like to thank the anonymous reviewers, whose valuable comments helped to improve the quality of the paper.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Shehab, E.M.; Sharp, M.W.; Supramaniam, L.; Spedding, T.A. Enterprise resource planning: An integrative review. Bus. Process Manag. J. 2004, 10, 359–386. [Google Scholar] [CrossRef]
- O’Connor, J.T.; Dodd, S.C. Achieving integration on capital with enterpriseresource-planning systems. Autom. Constr. 2000, 9, 515–524. [Google Scholar] [CrossRef]
- O’Leary, D.E. Enterprise Resource-Planning Systems: Systems, Life Cycle, Electronic Commerce, and Risk; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar] [CrossRef]
- Jawad, Z.N.; Villányi, B. Designing Predictive Analytics Frameworks for Supply Chain Quality Management: A Machine Learning Approach to Defect Rate Optimization. Platforms 2025, 3, 6. [Google Scholar] [CrossRef]
- Katuu, S. Enterprise Resource Planning: Past, Present, and Future. New Rev. Inf. Netw. 2020, 25, 37–46. [Google Scholar] [CrossRef]
- Parr, A.; Shanks, G. A model of ERP project implementation. J. Inf. Technol. 2000, 15, 289–303. [Google Scholar] [CrossRef]
- Dumitriu, D.; Popescu, M.A. Enterprise architecture framework design in IT management. Procedia Manuf. 2020, 46, 932–940. [Google Scholar] [CrossRef]
- Biagi, V.; Russo, A. Data Model Design to Support Data-Driven IT Governance Implementation. Technologies 2022, 10, 106. [Google Scholar] [CrossRef]
- Rao, S.S. Enterprise resource planning: Business needs and technologies. Ind. Manag. Data Syst. 2000, 100, 81–88. [Google Scholar] [CrossRef]
- Gaol, F.L.; Deniansyah, M.F.; Matsuo, T. The measurement impact of ERP system implementation on the automotive industry business process efficiency. Int. J. Bus. Inf. Syst. 2023, 43, 429–442. [Google Scholar] [CrossRef]
- Stergiou, C.L.; Psannis, K.E. Digital twin intelligent system for industrial internet of things-based big data management and analysis in cloud environments. Virtual Real. Intell. Hardw. 2022, 4, 279–291. [Google Scholar] [CrossRef]
- Chehri, A.; Zimmermann, A.; Schmidt, R.; Masuda, Y. Theory and Practice of Implementing a Successful Enterprise IoT Strategy in the Industry 4.0 Era. Procedia Comput. Sci. 2021, 192, 4609–4618. [Google Scholar] [CrossRef]
- Chen, J.; Gusikhin, O.; Finkenstaedt, W.; Liu, Y.N. Maintenance, Repair, and Operations Parts Inventory Management in the Era of Industry 4.0. IFAC-PapersOnLine 2019, 52, 171–176. [Google Scholar] [CrossRef]
- Jawad, Z.N.; Balázs, V. Machine learning-driven optimization of enterprise resource planning (ERP) systems: A comprehensive review. Beni-Suef Univ. J. Basic Appl. Sci. 2024, 13, 4. [Google Scholar] [CrossRef]
- Tortorella, G.; Fogliatto, F.S.; Gao, S.; Chan, T.K. Food supply chain resilience through digital transformation: A mixed-method approach. Int. J. Logist. Manag. 2021, 33, 547–556. [Google Scholar] [CrossRef]
- Perez-Vega, R.; Hopkinson, P.; Singhal, A.; Mariani, M.M. From CRM to social CRM: A bibliometric review and research agenda for consumer research. J. Bus. Res. 2022, 151, 1–16. [Google Scholar] [CrossRef]
- Chatterjee, S.; Chaudhuri, R.; Vrontis, D.; Jabeen, F. Digital transformation of organization using AI-CRM: From microfoundational perspective with leadership support. J. Bus. Res. 2022, 153, 46–58. [Google Scholar] [CrossRef]
- El Hail, C.; El Koraichi, M. Enhancing Supply Chain Management PerformanceThrough E-CRM Implementation. Int. J. Supply Chain Manag. 2024, 12, 56–64. [Google Scholar] [CrossRef]
- Sologia, F.E.; Witjaksono, R.W.; Ramadani, L. Evaluation of the Successful Implementation of EnterpriseResource Planning Based on SAP Using the DeLone & McLeanModel. Int. J. Community Serv. Learn. 2024, 8, 29–40. [Google Scholar] [CrossRef]
- Antwi, B.O.; Avickson, E.K. Integrating SAP, AI, And Data Analytics for Advanced Enterprise Management. Int. J. Res. Publ. Rev. 2024, 5, 621–636. [Google Scholar] [CrossRef]
- Al-Banna, A.; Rana, Z.A.; Yaqot, M.; Menezes, B. Interconnectedness between Supply Chain Resilience, Industry 4.0, and Investment. Logistics 2023, 7, 50. [Google Scholar] [CrossRef]
- Tarigan, Z.J.H.; Siagian, H.; Jie, F. Impact of Enhanced Enterprise Resource Planning (ERP) on Firm Performance through Green Supply Chain Management. Sustainability 2021, 13, 4358. [Google Scholar] [CrossRef]
- SAP S/4HANA. Available online: https://www.leanix.net/en/wiki/tech-transformation/sap-ecc-vs-hana-vs-r3-vs-s4hana (accessed on 6 March 2025).
- Bavaraju, A. SAP Fiori Implementation and Development; SAP Press: Walldorf, Germany, 2016. [Google Scholar]
- Steckenborn, T. Schnelleinstieg SAP Business Technology Platform (BTP)–Services und Integration; Espresso Tutorials GmbH: Gleichen, Germany, 2022. [Google Scholar]
- Bögelsack, A.; Bögelsack, A.; Chakraborty, U.; Kumar, D. SAP S/4HANA Systems in Hyperscaler Clouds. Deploying SAP S/4HANA in AWS, Google Cloud, and Azure; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Bagga, J. A Practical Guide to SAP Integration Suite; Springer Books: Berlin/Heidelberg, Germany, 2023. [Google Scholar]
- Brinkkemper, S. Dynamic Enterprise Innovation: Establishing Continuous Improvement in Business; van Es, R., Ed.; Baan Business Innovation: Barneveld, The Netherlands, 1998. [Google Scholar]
- Wang, M. Integrating SAP to Information Systems Curriculum: Design and Delivery. Inf. Syst. Educ. J. 2011, 9, 97–104. [Google Scholar]
- Brinkkemper, S.; Pachidi, S. Functional architecture modeling for the software product industry. In European Conference on Software Architecture; Springer: Berlin/Heidelberg, Germany, 2010; pp. 198–213. [Google Scholar]
- Plattner, H.; Leukert, B. The In-Memory Revolution: How SAP HANA Enables Business of the Future; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Singh, V. Manage Your SAP Projects with SAP Activate: Implementing SAP S/4HANA; Packt Publishing Ltd.: Birmingham, UK, 2017. [Google Scholar]
- Keijzer, F. SAP S/4HANA Embedded Analytics; Apress: New York, NY, USA, 2021. [Google Scholar] [CrossRef]
- Sharma, C. Financial advantages of leveraging SAP S/4HANA integration in retail: A quantitative study. World J. Adv. Eng. Technol. Sci. 2021, 1, 98–113. [Google Scholar] [CrossRef]
- SAP S/4 HANA Modules. Available online: https://www.erpresearch.com/en-us/sap-s/4-hana-modules (accessed on 6 March 2025).
- Lazarova, M.; Sapundzhi, F. Stochastic Modeling with Applications in Supply Chain Management and ICT Systems. Computation 2023, 11, 21. [Google Scholar] [CrossRef]
- Lazarova, M.; Minkova, L. A risk model with a bivariate Polya-Aeppli counting process. AIP Conf. Proceeding 2022, 2505, 100003. [Google Scholar] [CrossRef]
- Minkova, L.D. The Polya-Aeppli process and ruin problems. J. Appl. Math. Stoch. Anal. 2004, 3, 221–234. [Google Scholar] [CrossRef]
- Chukova, S.; Minkova, L.D. Characterization of the Polya-Aeppli process. Stoch. Anal. Appl. 2013, 31, 590–599. [Google Scholar] [CrossRef]
- Minkova, L.D.; Balakrishnan, N. On a bivariate Pólya-Aeppli distribution. Commun. Stat.-Theory Methods 2014, 43, 5026–5038. [Google Scholar] [CrossRef]
- T-distributed Stochastic Neighbour Embedding. Available online: https://help.sap.com/docs/SAP_HANA_PLATFORM/319d36de4fd64ac3afbf91b1fb3ce8de/t-distributed-stochastic-neighbour-embedding-3de9095.html (accessed on 6 March 2025).
- Lazarova, M.D.; Sapundzhi, F.I. Stochastic processes with applications in supply chain management of electronic industry. In Proceedings of the International Conference on Statistics and Machine Learning in Electronics, Sofia, Bulgaria, 12–13 May 2022. Complex Control. Syst. 2022, 4, 41–45. Available online: http://ir.bas.bg/ccs/2022/9_lazarova.pdf (accessed on 6 March 2025).
- Lazarova, M.D.; Minkova, L.D. Non-central Polya-Aeppli process and ruin probability. Ann. Acad. Rom. Sci. Ser. Math. Appl. 2019, 11, 312–321. [Google Scholar]
- Minkova, L.D. A Generalization of the Classical Discrete Distributions. Commun. Statist. Theory Methods 2002, 31, 871–888.1. [Google Scholar] [CrossRef]
- SAP S/4HANA Cloud. Available online: https://www.sap.com/products/erp.html (accessed on 6 March 2025).
- SAP Business Configuration. Available online: https://help.sap.com/docs/btp/sap-business-technology-platform/fiori-apps-business-configuration (accessed on 6 March 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).